Mechanistic Basis for the Binding of RGD- and AGDV-Peptides to the Platelet Integrin αIIbβ3

Abstract

Binding of soluble fibrinogen to the activated conformation of the integrin αIIbβ3 is required for platelet aggregation and is mediated exclusively by the C-terminal AGDV-containing dodecapeptide (γC-12) sequence of the fibrinogen γ chain. However, peptides containing the Arg-Gly-Asp (RGD) sequences located in two places in the fibrinogen Aα chain inhibit soluble fibrinogen binding to αIIbβ3 and make substantial contributions to αIIbβ3 binding when fibrinogen is immobilized and when it is converted to fibrin. Here, we employed optical trap-based nanomechanical measurements and computational molecular modeling to determine the kinetics, energetics, and structural details of cyclic RGDFK (cRGDFK) and γC-12 binding to αIIbβ3. Docking analysis revealed that NMR-determined solution structures of cRGDFK and γC-12 bind to both the open and closed αIIbβ3 conformers at the interface between the αIIb β-propeller domain and the β3 βI domain. The nanomechanical measurements revealed that cRGDFK binds to αIIbβ3 at least as tightly as γC-12. A subsequent analysis of molecular force profiles and the number of peptide-αIIbβ3 binding contacts revealed that both peptides form stable bimolecular complexes with αIIbβ3 that dissociate in the 60–120 pN range. The Gibbs free energy profiles of the αIIbβ3–peptide complexes revealed that the overall stability of the αIIbβ3-cRGDFK complex was comparable with that of the αIIbβ3–γC-12 complex. Thus, these results provide a mechanistic explanation for previous observations that RGD- and AGDV-containing peptides are both potent inhibitors of the αIIbβ3–fibrinogen interactions and are consistent with the observation that RGD-motifs, in addition to AGDV, support interaction of αIIbβ3 with immobilized fibrinogen and fibrin.

Graphical abstract

Integrins are ubiquitous α/β transmembrane heterodimers that mediate essential cell–matrix and cell–cell adhesion interactions by binding to specific macromolecular protein ligands. Each integrin subunit consists of a large extracellular headpiece, a transmembrane helix, and a short cytoplasmic tail^1–3 and complementary subunits interacting via a large interface between the α subunit β propeller domain and the β subunit βI domain to form a ligand-binding headpiece (Figure 1). Nonactivated low affinity integrins appear to have a bent configuration with a “closed” headpiece, whereas activated high affinity integrins are extended molecules with an “open” headpiece that enables high affinity ligand binding.⁴

Figure 1.

Schematic representation of the αIIbβ3 ectodomain in its closed conformation (State 1, panel a), several intermediate conformations (States 2–7; panel b), and its open conformation (State 8; panel c). The closed State 1 and open State 8 were reconstructed using crystal structures from the PDB: 3FCS⁶⁰ and 2VDO,⁹ respectively. Shown in different colors are the subdomains of αIIb and β3 ectodomain. Panel b illustrates intermediate structural changes that occur in the αIIb β-propeller domain and the β3 βI domain (crystal structures from PDB: entries 3ZDY and 3ZE0) during αIIbβ3 activation. As an example, panel b also depicts structural alterations highlighted in red color that accompany the transition from State 2 to State 7.⁷ Headpiece conformations corresponding to States 3–6 are very similar to the conformations associated with States 2 and 7 and are not presented.

The major platelet integrin αIIbβ3 mediates primary hemostasis by enabling the formation of occlusive platelet aggregates at sites of vascular injury. Platelet aggregation occurs when soluble fibrinogen binds to the open conformation of the αIIbβ3 headpiece. Because the equilibrium dissociation constant (K_d) for fibrinogen binding to active αIIbβ3 of ~100 nM is 100-fold lower than the concentration of fibrinogen in plasma,⁵ the αIIbβ3 headpiece is immediately occupied by fibrinogen when platelets are activated in a plasma environment. Accordingly, αIIbβ3 activation is tightly regulated to prevent the spontaneous formation of intravascular platelet aggregates.⁶ In this context, it is important to note that the transition of αIIbβ3 from its bent inactive to its fully extended active conformation occurs in a stepwise fashion through a number of discernible intermediate conformational states (Figure 1).^6,7

Soluble fibrinogen binding to the open αIIbβ3 headpiece is mediated exclusively by the AGDV-containing sequence located at the C-terminus of the fibrinogen γ chain.⁸ However, the binding site for peptides corresponding to the Arg-Gly-Asp (RGD) sequences located in two places in the fibrinogen Aα chain overlaps with the binding site for the γ chain sequence,⁹ and RGD-containing peptides are potent inhibitors of soluble fibrinogen binding to αIIbβ3.¹⁰ The interaction of αIIbβ3 with peptides containing the γ chain and RGD sequences has been extensively studied. NMR studies and constrained molecular dynamics (MD) simulations of RGD peptide binding to αIIbβ3 have revealed the importance of the conformation of the RGD backbone, the spatial orientation of the charged Arg and Asp side chains, and the role of the hydrophobic moiety flanking the Asp residue in their interaction with αIIbβ3.^11–14 However, these studies have not provided a mechanistic basis for the interaction of RGD sequences with αIIbβ3.

Previously, we observed that either of the two Aα chain RGD motifs and the γ chain C-terminus make substantial contributions to αIIbβ3 headpiece binding when fibrinogen is immobilized rather than soluble and when fibrinogen is converted to fibrin by thrombin.¹⁵ Here, we used optical trap-based single-molecule force spectroscopy to measure the nanomechanical strength of complexes between αIIbβ3 and γC-12, a dodecapeptide corresponding to C-terminus of the fibrin(ogen) γ chain, and cRGDFK, a cyclic RGD-peptide, and found that the resistance of the bimolecular complexes between αIIbβ3 and cRGDFK and αIIbβ3 and γC-12 to forced dissociation was comparable, although there was a small, but consistent, increase in the stability of the αIIbβ3–cRGDFK complexes. Then, using docking analysis and molecular dynamics (MD)-based molecular modeling, we found that the αIIbβ3–cRGDFK complex was slightly more stable than the αIIbβ3–γC-12, although the difference was again relatively small. Thus, these observations indicate there is little, if any, difference in the ability of αIIbβ3 to interact with the γ-chain sequence and the RGD motifs in immobilized fibrinogen and fibrin. Nonetheless, because there are twice as many RGD motifs than AGDV sequences, it is likely that RGD assumes an enhanced physiologic importance when platelets interact with immobilized fibrinogen or polymerized fibrin.

MATERIALS AND METHODS

Proteins and Peptides

The peptide cyclo[Arg-Gly-Asp-D-Phe-Lys(Cys)] (cRGDFK) was purchased from Peptides International, Louisville, Kentucky; the fibrinogen γC-dodeca-peptide (His-His-Leu-Gly-Gly-Ala-Lys-Gln-Ala-Gly-Asp-Val, γC-12) was obtained from Bachem Americas, Torrance, California. Dextran from Leuconostoc spp. (M_W = 110 000) was supplied by Fluka Chemie AG (Switzerland). Sodium periodate (NaIO₄), sodium borohydride (NaBH₄), ethanolamine, and n-octyl-β-D-glucosidewere purchased from Sigma-Aldrich Co. (St. Louis, MO). NH₂-functionalized latex beads were purchased from Bangs Laboratories, Inc. (Fisher, IL). Human αIIbβ3 was purified as described.¹⁶

Optical Trap-Based Force Spectroscopy

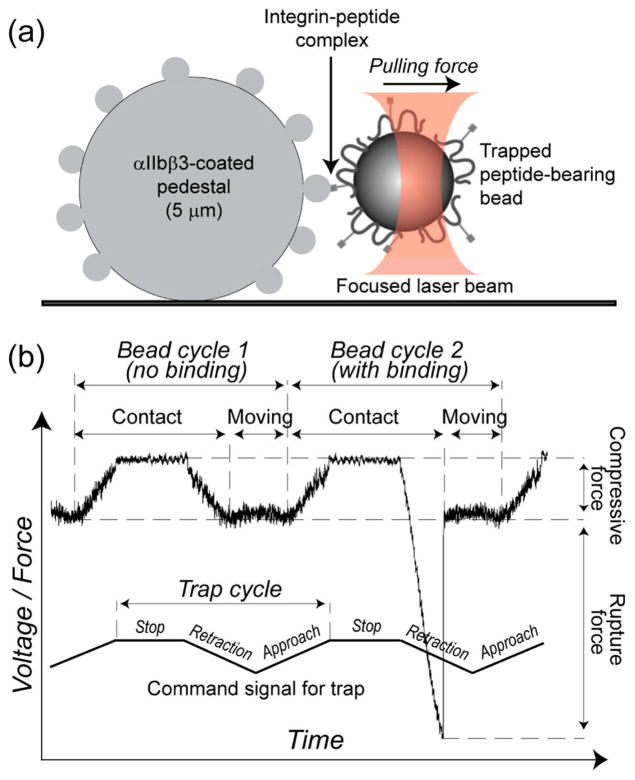
To quantify peptide binding to αIIbβ3, we used optical trap-based force spectroscopy, a method to measure single-molecule nanomechanics that we applied previously to study various receptor–ligand interactions, including αIIbβ3-fibrinogen and αIIbβ3-fibrin^15,17–19 as well as αIIbβ3-peptide¹⁶ and other receptor–ligand^20–22 complexes. In this method, each of two contacting surfaces is coated with one type of interacting molecule. Here, purified human αIIbβ3 was immobilized on micron-size stationary silica beads, whereas peptides were bound covalently to freely moving latex beads. Under visual microscopic control and at room temperature, a bead coated with either cRGDFK or γC-12 was trapped in a fluid chamber by a focused laser beam and moved in an oscillatory fashion so that it tapped a stationary αIIbβ3-coated pedestal anchored to the bottom surface of the flow chamber. When the immobilized peptide on the bead interacted with αIIbβ3 on the pedestal, tension was produced when the bead was displaced from the laser focus until the αIIbβ3–peptide bond ruptured. The applied force was recorded and displayed as a signal proportional to the strength of receptor–ligand binding (Figure 2). These rupture force signals were on the order of pico-Newtons, and they quantitatively characterized the bimolecular interactions of αIIbβ3 with the ligand peptides.

Figure 2.

Panel a: Schematic representation of the experimental system used to study bimolecular αIIbβ3–peptide interactions. A peptide-functionalized dextran-coated latex bead is trapped by a focused laser beam and oscillated toward or away from a silica pedestal coated with αIIbβ3, touching it repeatedly. If the surface-bound peptide and αIIbβ3 interact, a tensile (rupture) force is generated when the bead is moved away from the pedestal. Panel b: A typical force trace from single-molecule measurements of αIIbβ3–peptide interactions. The command signal of the optical trap (lower broken line) oscillates the peptide-coated latex bead with a truncated triangular waveform. This brings peptide on the bead and αIIbβ3 on the pedestal into proximity and stops the bead in an extreme position, keeping the peptide and αIIbβ3 in contact for a designated time. When there is no αIIbβ3–peptide contact, there is no rupture force signal (cycle 1). When αIIbβ3 and peptide interact, a rupture force that separates the bead and the pedestal is generated (cycle 2, negative rupture force signal). The approach-retraction cycle can be applied repeatedly, enabling the calculation of a binding probability P_b(T) as a function of contact time T (eq 1, Materials and Methods).

To synthesize peptide-coated latex beads, we utilized a double oxidation procedure to couple biologically active peptides to latex beads that is based on the ability of oxidized 110-kDa-dextran to form a Schiff base with primary amines.¹⁶ First, dextran was covalently bound to the latex beads, thereby providing a relatively inert surface with a low nonspecific background when the beads interacted with αIIbβ3-coated pedestals. The beads were then modified to bind the bioactive peptides cRGDFK and γC-12 as previously described.¹⁶ Purified human αIIbβ3 was bound covalently to 5-μm spherical silica pedestals anchored to the bottom of a flow chamber as previously described.¹¹ Briefly, pedestals coated with a thin layer of polyacrylamide were activated with glutaraldehyde, after which Mn²⁺-activated αIIbβ3 was immobilized for 2 h at 4 °C. αIIbβ3 was activated using 1 mM Mn²⁺ because we previously found that Mn²⁺ treatment increases the probability of specific αIIbβ3–ligand interactions.^17,23 The chamber was then washed to remove noncovalently adsorbed protein, blocked with bovine serum albumin (BSA), and equilibrated with 0.1 M HEPES buffer, pH 7.4, containing 150 mM NaCl, 3 mM CaCl₂, 1 mM MnCl₂, 2 mg/mL BSA, and 0.1% (v/v) Triton X-100 before rupture force measurements were performed. The αIIbβ3 coating concentration at which the cumulative probability of fibrinogen binding reached saturation was determined experimentally.¹⁵

The experimental protocol we used to measure αIIbβ3–peptide interactions was similar to the one we previously used to study the strength of αIIbβ3–peptide bonds,¹⁶ but with an important modification of the trapped bead motion protocol (Figure 2). Briefly, a latex bead coupled to a peptide was trapped by laser light and brought to a distance of 2–3 μm from an αIIbβ3-coupled pedestal. After the bead was oscillated at 10 Hz with a 0.8 μm peak-to-peak amplitude (2000 pN/s loading rate), the bead was brought into intermittent contact with the pedestal by micromanipulation using a keyboardcontrolled piezoelectric stage. The duration of contact between the interacting surfaces or the stopping time was precisely controlled and arbitrarily varied between 0.01 and 2 s, so that the oscillation frequency changed accordingly but without variations in the pulling or loading rate. Data acquisition was initiated at the first contact between the bead and the pedestal. Rupture force signals following repeated contacts between the pedestal and the bead were collected for periods of about 1 min. Each signal was counted as a discrete binding event provided that the rupture force was >10 pN because optical artifacts observed with or without trapped latex beads produced signals that appeared as forces below 10 pN. Because signals between 10 pN and 20 pN were found to be nonspecific,¹⁶ they were also excluded from subsequent analysis. Only a small percentage of contact/detachment cycles resulted in effective receptor–ligand binding/unbinding events, so that data from 10 experiments representing 10³ to 10⁴ individual measurements were combined. The percentages of binding/unbinding events at a contact duration time T enabled us to plot and analyze the force-free binding probability as a function of T as described below.

Kinetic Analysis of αIIbβ3–Peptide Interactions

In the binding phase of a measurement, where there is only one receptor–ligand bound state (LR), reversible association–dissociation kinetics is governed by the on-rate k_on and the off-rate k_off. Further, the binding probability P_b(T) describes the likelihood of observing these transitions during contact duration time T. It can be demonstrated that for single-step kinetics, P_b(T) is given by eq 1:¹⁷

$$P_{\mathrm{b}}(T)=\frac{k_{\text{on}}{d}_{max}}{k_{\text{on}}{d}_{max}+k_{\text{off}}}(1-exp[-(k_{\text{on}}{d}_{max}+k_{\text{off}})T])$$ (1)

where d_max = max{d_L,d_R} is the surface density of the species (L for peptide and R for αIIbβ3) present in excess and k_on and k_off are the force-free on- and off-rates, respectively. In these experiments, αIIbβ3 is present in excess over γC-12 and cRGDFK. Hence, d_max ≈ d_R and the kinetic rate constants (k_on, k_off), the equilibrium dissociation constant (K_d = k_off/k_on), and the binding probability P_b for the ligand-bound form of αIIbβ3 are obtained by numerically fitting the average experimental kinetic curves to eq 1. Here, d_R, obtained using radioactively labeled proteins, equaled about 3000 molecules/(μm²)¹⁷ and was used to convert the apparent on-rate k_ond_R into the true kinetic on-rate k_on. Using the on- and off-rates, we obtained the equilibrium dissociation constant K_d = k_off/k_on or the binding affinity constant K_b = 1/K_d.

¹H NMR Spectroscopy

To resolve the three-dimensional (3D) structure of γC-12 and cRGDFK in solution, we used high-resolution ¹H NMR spectroscopy. 1D ¹H and 2D ¹H–¹H NMR spectra of cRGDFK in PBS buffer (pH 7.4) containing 50 mM sodium dodecyl sulfate (SDS) were recorded in a 500 MHz NMR spectrometer (Bruker, AVANCE II-500). The 1D ¹H and 2D ¹H–¹H NMR spectra of γC-12 in PBS were obtained using a 700 MHz NMR spectrometer (Bruker, AVANCE III-700) equipped with a quadruple resonance (¹H, ¹³C, ¹⁵N, and ³¹P) CryoProbe. For all NMR measurements, the temperature was set to 298 K. The spectrometers operated in the internal stabilization mode for the resonance line ²H. The ¹H NMR spectra were recorded using 90° pulses, a relaxation delay of 2 s, and a spectral width of 12.00 ppm (Figures S1 and S2). For the assignment of signals in the ¹H NMR spectra, we used 2D TOtal Correlation SpectroscopY (TOCSY).²⁴ Chemical shifts were measured relative to 4,4-dimethyl-4-silapentan-1-sulfonic acid (DSS). Peptides were dissolved in buffer containing a mixture of H₂O and D₂O immediately before the measurements were performed. The 2D ¹H–¹H NOESY NMR spectra²⁵ were recorded in a phase-sensitive mode with 1024 points in the F2-dimension and 256 points in the F1-dimension with exponential filtration. Mixing times were set to τ_m = 0.10, 0.15, 0.20, 0.25, 0.35, 0.40, 0.45, and 0.50 s (Tables S1 and S2).

For structure determination, NMR-based 3D peptide conformations were subjected to restrained MD simulations with the XPLOR-NIH package.²⁶ Structures were energy-minimized, heated to 1000 K in 6000 steps, and then cooled to 50 K with 100 K increments in 3000 steps. The obtained structures were energy-minimized again over 1000 steps using the steepest descent algorithm, which was followed by 1000 steps of the conjugate gradient minimization. Using the initial set of 200 structures, 20 structures were selected for subsequent MD simulations. Finally, 10 structures with the lowest energy were collected. The program MolProbity^27,28 was used to assess the overall quality of the structures.

Molecular Modeling of αIIbβ3–Peptide Interactions

Crystal structures of the open and closed conformations of the αIIbβ3 headpiece were obtained from the Protein Data Bank (PDB). The PDB entry codes are 3ZDX for the closed conformation and 3ZE2 for the open conformation of αIIbβ3.⁷ The structures were energy-minimized and equilibrated for 10 ns using the AMBER force-field.²⁹ All-atom MD simulations were carried out using the Generalized Born implicit solvent model implemented in the AMBER package accelerated on Graphic Processing Units (GPUs).^29,30 Equilibrium MD simulations were performed at a constant temperature of 300 K with the integration time step of 2 fs. The final structures of the αIIbβ3 headpiece from the MD equilibrium simulation runs were utilized in subsequent molecular modeling.

To generate structures for cRGDFK and γC-12 bound to the αIIbβ3 headpiece and to compare their corresponding association energies, we used a docking protocol implemented in AutoDock Vina software.³¹ In the docking analysis, the αIIbβ3 headpiece structures were constrained, whereas the peptides were treated as flexible. To generate the input files, we used the AutoDockTools option in the MGLTools package.³² In “blind docking”, we set a grid size of 15 nm in the x-, y-, and z- directions; the center of the cell was the center of mass of the αIIbβ3 headpiece. For each peptide and αIIbβ3 headpiece conformer pair, we performed four separate docking runs using different random seeds. In each run, we selected a number of peptide conformations (up to nine) with minimum docking energy. The conformations were further analyzed using lab-written scripts. The end-to-end distances were calculated for the C_α-atoms of His1 and Val12 of γC-12 and for the C_ζ-atom of Arg1 and C_γ-atom of Asp3 of cRGDFK.

Energy of αIIbβ3 Headpiece–Peptide Interactions

To determine the binding energy of the interaction of the αIIbβ3 headpiece with cRGDFK and γC-12, we performed all-atom MD simulations of the energy-minimized bimolecular complexes obtained from peptide docking to the two αIIbβ3 conformers. We employed the Solvent Accessible Surface Area (SASA) model of implicit solvation³³ implemented in our in-house software package.³⁴

Force-ramp peptide unbinding simulations which mimic dynamic force spectroscopic measurements¹⁶ in vitro were carried out using the time-dependent force protocol f(t) = κ(ν_ft − Δx), where ν_f is the pulling speed, κ is the cantilever spring constant, and Δx is the displacement of a tagged residue from its initial position. In the simulations, we constrained the C_α-atoms of Leu1 and Pro452 in αIIb and the C_α-atoms of Glu108 and Arg352 in β3. The pulling force was applied to the C_α-atoms of His1 or Val12 in γC-12 and Lys5 in cRGDFK in a direction perpendicular to the peptide–αIIbβ3 binding interface. The output from the simulations for each complex, carried out with ν_f = 2 × 10⁴ μm/s and κ = 100 pN/nm, was used to profile the force for αIIbβ3–peptide noncovalent bond rupture (F) as a function of bond extension (Δx).

Umbrella Sampling simulations were performed to resolve the free energy landscape (ΔG) for the bimolecular interactions of cRGDFK and γC-12 with αIIbβ3 as a function of Δx.^35,36 This approach has been used previously to access the thermodynamics of protein–ligand interactions in bimolecular complexes.^37–39 Using this technique requires generation of initial conformations (windows), which span the entire range of reaction coordinates for unbinding, Δx. Each conformation is subjected to long equilibration simulations. The mean force potential is constructed using the weighted histogram analysis method (WHAM).^40,41 To obtain a set of initial structures for cRGDFK and γC-12 bound to each αIIbβ3 headpiece conformation, we ran 10 ns equilibration simulations for each bimolecular complex. To generate a set of structures for an entire range of Δx, we carried out force-ramp simulations in which we constrained the center of mass of each subunit of the αIIbβ3 headpiece and the C_α-atoms of the N- and C-terminal residues. In these dynamic force measurements in silico, the pulling force was applied to the C_α-atoms of His1 in the γC-12 and Lys5 in cRGDFK through a virtual cantilever (κ = 100 pN/nm and ν_f = 2× 10⁴ μm/s). To eliminate the contribution to ΔG from the γC-12 conformational fluctuations, we constrained the C_α-atoms of the peptide relative to each other using the harmonic potential with ~1 kcal/mol stiffness. The force was applied to the center of mass of the constrained γC-12. We generated a total of 240 sampling conformations for γC-12 (with the width w = 0.2 Å) and 90 conformations for cRGDFK (with w = 0.3 Å). These constructs were then used in subsequent 50 ns equilibration runs with constrained the displacement of the peptide center of mass.

RESULTS

Two-Dimensional Kinetics of αIIbβ3 Binding to cRGDFK and γC-12

To compare the time-dependence of γC-12 and cRGDFK binding and unbinding to αIIbβ3, the probability of forming αIIbβ3-peptide complexes P_b(T) was studied as a function of the precisely controlled duration of contact T between interacting surfaces coated with αIIbβ3 and peptide. This experimental method is a part of a more general binding–unbinding correlation spectroscopy method (BUCS)¹⁷ that can be used to explore the kinetics of formation and dissociation of bimolecular complexes.^42,43 In the experimental setup, a command signal from an optical trap oscillates a peptide-coated bead between two fixed positions with a truncated triangular waveform, thereby keeping it in contact with an αIIbβ3-coated pedestal for a prescribed contact time T (Figure 2). This is followed by bead retraction, which in the case of successful noncovalent bond formation results in the linear generation of tensile force until a bond rupture occurs. To exclude nonspecific interactions, only bond rupture forces >20 pN were considered to represent valid αIIbβ3–peptide interactions, based on control experiments indicating that force signals <20 pN mainly represent nonspecific background.¹⁶

Measurements of binding probability P_b(T) as a function of contact duration T generated characteristic curves for γC-12 and cRGDFK with an exponentially increasing likelihood for αIIbβ3–peptide binding that reached a plateau when the contact time approached T ≈ 1 s (Figure 3a), the time required to fully populate the stable high-affinity headpiece conformation (Figure 3b). Nonetheless, while the curves for γC-12 and cRGDFK were similar, they had different slopes and plateau levels reflecting somewhat different kinetics of αIIbβ3 binding. This enabled us to directly estimate model-free two-dimensional kinetic parameters for each peptide using eq 1 and a surface density of reactive αIIbβ3 molecules (d_R) of ~3000 molecules/μm² or 0.5 × 10⁻¹² mol/cm². The average true first-order binding rate constants (k_on) were (2.5 ± 0.9) × 1012 cm²/(mol·s) for γC-12 and (3.0 ± 0.8) × 10¹² cm²/(mol·s) for cRGDFK, with a difference close to but not reaching the level of statistical significance (p = 0.063, a Mann–Whitney test). The average unbinding rate constants k_off were 2.05 ± 0.59 s⁻¹ for γC-12 and 1.53 ± 0.57 s⁻¹ for cRGDFK and were significantly different (p = 0.012). The corresponding average binding affinity constants (K_b), calculated as K_b = k_on/k_off, were (1.22 ± 0.61) × 10¹² cm²/mol and (1.96 ± 0.65) × 10¹² cm²/mol for γC-12 and cRGDFK, respectively. Although the binding affinity constant for cRGDFK was greater than the binding affinity constant for γC-12, the difference is close to but does not reach the level of statistical significance (p = 0.059). This indicates that cRGDFK binding to αIIbβ3 is somewhat stronger, or at least is not weaker, than γC-12 binding to αIIbβ3.

Figure 3.

Panel a: Averaged kinetic curves showing the binding probability P_b(T) as a function of contact duration T for γC-12 and cRGDFK binding to αIIbβ3. The experimental data (blue circles and red squares) were fitted with an exponential probability function (eq1 in Materials and Methods). Panel b: Profiles of average rupture force F (n = 10)as a function of contact duration T for the γC-12 (blue circles) and cRGDFK (red squares). The data shown are a mean and standard deviation from at least 10 experiments.

In Silico Analysis of the Strength of αIIbβ3–Peptide Binding

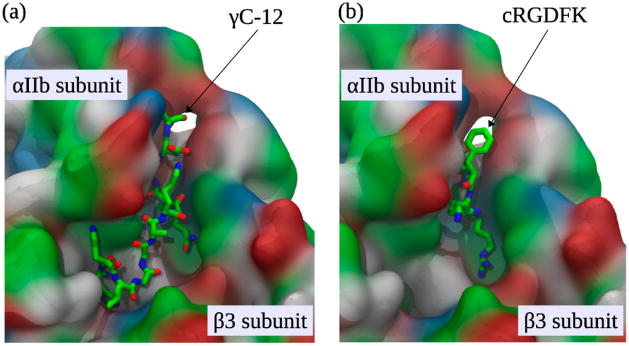
For a more comprehensive analysis of the strength of αIIbβ3 binding to cRGDFK and γC-12, we performed dynamic force-ramp measurements in silico, employing the all-atom MD simulations in implicit water and using a time-dependent pulling force to dissociate the αIIbβ3–peptide complexes. To enable these studies, we used NMR to obtain three-dimensional (3D) structures for cRGDFK and γC-12. Ensembles of these structures are shown in Figure 4, and a detailed discussion of the structures is provided in the Supporting Information. To begin the MD studies, we equilibrated the αIIbβ3 headpiece in its open and closed conformational states (Figure 1) by performing several 10 ns long equilibrium MD simulations. The equilibrium conformations were then used in conjunction with structure-based molecular docking to explore the association of γC-12 and cRGDFK with both αIIbβ3 conformational states. As expected, we found that both γC-12 and cRGDFK interacted with αIIbβ3 via the previously described RGD-binding site located in the interface between the αIIb β-propeller and the β3 βI domain (Figure 5).⁹

Figure 4.

¹H NMR-based solution structures of the αIIbβ3–binding peptides cRGDFK and γC-12. Panel a: cRGDFK, an overlay of 10 structures with a minimum energy. Panel b: γC-12, an overlay of 10 structures with a minimum energy. Calculations were made in X-PLOR-NIH.²⁶ The structures were visualized with VMD.⁶¹

Figure 5.

Representative conformations of γC-12 (Panel a) and cRGDFK (Panel b) bound to the αIIbβ3 headpiece (shown in licorice representation). The αIIbβ3 headpiece is displayed in the open conformation using solvent accessible surface area representation colorized according to the type of amino acid residue: red, acidic amino acids; blue, basic amino acids; green and white, polar and nonpolar (hydrophobic) residues, respectively.

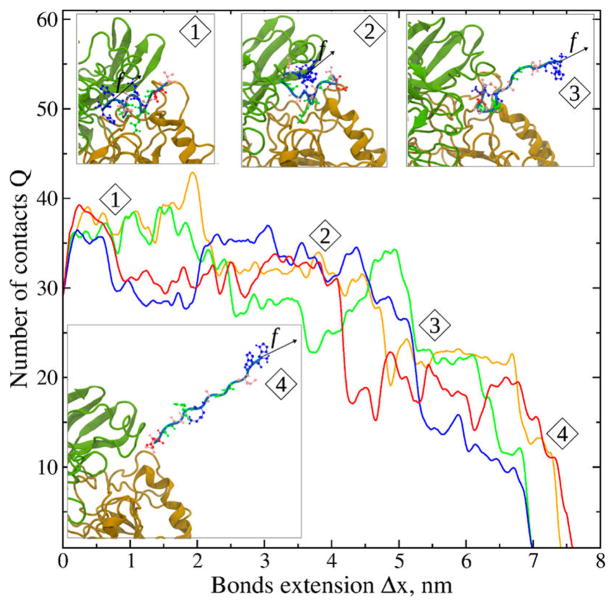
Next, we selected an αIIbβ3–peptide complex structure with the largest docking energy and pro3led the complex molecular response to an applied pulling force as a function of noncovalent bond extension, a measure of the strength of bimolecular interactions (Figure S3). We also analyzed the dependence of noncovalent bond extension on the number of contacts between residues of the peptide and the αIIbβ3 headpiece. A pair of amino acids in the αIIbβ3 headpiece and in the peptide was considered to form a strong binding contact if the distance between the centers-of-mass of their side chains was persistently shorter than a commonly accepted 6 Å cutoff for at least 50% of the simulation time.^37,44

The profiles of force–bond extension curves (Figure S3) exhibit multiple sharp negative peaks, i.e., distinct force drops, which occur due to partial rupture of binding contacts. They reflect force-induced structural transitions (F^tr) that occur prior to complete dissociation of the complex. The last peak, which is accompanied by a force drop to zero, corresponds to complete complex dissociation. For this reason, we call this the dissociation (or rupture) force (F^diss). We found that the dissociation of αIIbβ3 headpiece–peptide complexes occurred via multistep transitions with the αIIbβ3–γC-12 complex dissociating in three steps when the headpiece was open and in two steps when it was closed (Figure S3a–d). By contrast, αIIbβ3–cRGDFK complexes dissociated via two distinct pathways regardless of the αIIbβ3 headpiece conformation (Figure S3e,f).

When γC-12 was bound to the open αIIbβ3 headpiece and His1 of γC-12 was the tagged residue (i.e., the residue to which the force was applied at the C_α-atom), a first structural transition occurred at a tension of F^tr ≈ 69 pN due to γC-12 unraveling (snapshot 1 in Figure 6), and a second transition at F^tr ≈ 93 pN corresponded to γC-12 unfolding and the rupture of 17 contacts with the αIIbβ3 headpiece (Table S3; Figure 6, snapshot 2). The complex dissociated at F^diss ≈112 pN when persistent contacts between the AGD-motif of γC-12 and β3 ruptured. This pattern of dissociation was unchanged when Val12 was the tagged residue instead of His1 (Table S3).

Figure 6.

Dynamics of the force-induced dissociation of the complex between γC-12 and the αIIbβ3 headpiece in its open conformation. Shown are four representative profiles of the total number of residue–residue contacts stabilizing the bound state (Q) as a function of extension of αIIbβ3–γC-12 noncovalent bonds (Δx) from the force-ramp simulations (pulling speed v_f = 2 × 10⁴ μm/s and cantilever spring constant κ = 100 pN/nm). The tagged residue in γC-12 is His1. The structural snapshots numbered 1–4 correspond to the similarly numbered regions in the red curve of Q vs Δx and display the progress of forced dissociation from the initial bound state (structure 1), to the partially stretched state (structure 2), and to the partially and fully dissociated states (structures 3 and 4, respectively). The αIIb β-propeller and the β3 βI domain are colored in green and orange, respectively; γC-12 is shown in gray with its residues in ball-and-stick representation colorized according to the residue type: red for acidic amino acids, blue for basic amino acids, green and pink for hydrophobic polar and nonpolar residues, respectively.

By contrast, when γC-12 was bound to the closed αIIbβ3 headpiece, structural transitions occurred in two, rather than three, steps. The first structural transition occurred at F^tr ≈ 102 pN and F^tr ≈ 75 pN when His1 and Val12 were the tagged residues, respectively (Table S3; Figure S3c,d). Further, when His1 was tagged, the complex dissociated at F^diss ≈ 125 pN, but when force was applied to Val12, 50% of the time the complex dissociated at F^diss ≈ 82 pN, while in the other trajectories, it dissociated at F^diss ≈ 149 pN due to the formation of strong interactions between residues His1, His2, Leu3 of γC-12 and Tyr160 and Tyr190 of αIIb.

Regardless of the conformation of the αIIbβ3 headpiece, αIIbβ3–cRGDFK complexes dissociated via two distinct pathways (Figure S3e,f). Pathway 1, observed 66% of the time, was characterized by high bond rupture forces of F^diss ≈ 159 pN, a large number of binding contacts (~20) and a relatively long bond lifetime of ~0.24 μs. Pathway 2, observed 34% of the time, was characterized by a smaller rupture force of F^diss ≈ 112 pN, a smaller number of contacts (~10) and a short bond lifetime of ~0.17 μs. (Table S3; Figures S3e and S4). Structure analysis revealed that αIIbβ–cRGDFK interactions in Pathway 1 were mediated by strong contacts between Arg1 and Lys5 in cRGDFK and residues in the αThr150–αArg165 loop in αIIbβ3, whereas cRGDFK in Pathway 2 formed stable contacts with the αThr150–αArg165 loop, but only through Arg1 (snapshot 2b in Figure S4). Structure analysis and profiles for the closed αIIbβ3–cRGDFK complex were similar, although rupture forces were slightly lower: F^diss ≈ 105 pN for Pathway 1 and F^diss ≈ 79 pN for Pathway 2 (Table S3; Figure S3f). Subsequent analysis of the dynamics of stable contacts revealed that cRGDFK formed similar stable binding contacts with αIIbβ3 headpiece as γC-12 (Figures S5 and S6), but the cRGDFK–αIIbβ3 contacts persisted while the pulling force was ramped up and disrupted simultaneously just before complete ligand dissociation occurred (Figure S6; Supporting Information Movie S2). During dissociation of γC-12, unlike cRGDFK, the duration of each stable contact was shorter: they dissociated and reformed upon peptide unfolding (Figure S5; Supporting Movie S1). Still, the overall total number of stable binding contacts for γC-12 was higher than for cRGDFK. This explains the similar dissociation forces but shorter bond lifetimes and lack of intermediate transition states for αIIbβ3–cRGDFK compared to αIIbβ3–γC-12.

Stability of αIIbβ3 Headpiece Binding to cRDGFK and γC-12

The stability of bimolecular complexes like those of γC-12 and cRGDFK with αIIbβ3 can be defined by their docking energies. The docking energies for cRGDFK binding to the closed and open αIIbβ3 headpiece were 6.8 ± 0.4 and 7.0 ± 0.3 kcal/mol, with maximum energies of 7.7 and 7.5 kcal/mol, respectively, whereas the docking energies for γC-12 binding to closed and open αIIbβ3 were 6.5 ± 0.4 and 6.4 ± 0.5 kcal/mol, respectively, with maximum docking energies of 7.1 kcal/mol for both conformational states (Table 1). The differences in the docking energies of cRGDFK and γC-12 were moderate but statistically significant (p < 0.05, a Mann–Whitney test). Thus, the data indicate that RGDFK and γC-12 interact well with both closed and open αIIbβ3, although the bimolecular complexes formed by cRGDFK and αIIbβ3 are somewhat more stable.

Table 1.

Parameters for γC-12 and cRGDFK Binding to the Closed and Open Conformations of the αIIbβ3 Headpiece^a

αIIbβ3 headpiece	γC-12			cRGDFK
	Eav, kcal/mol (n)	Emax, kcal/mol	X, Å	Eav, kcal/mol (n)	Emax, kcal/mol	X, Å
Closed state (3ZDX: molecule 1)	6.5 ± 0.4 (8)	7.1	14.2 ± 4.3	6.8 ± 0.4 (27)	7.7	11.7 ± 1.4
open state (3ZE2: molecule 2)	6.4 ± 0.5 (16)	7.1	14.5 ± 5.1	7.0 ± 0.3 (6)	7.5	12.4 ± 1.5

^aShown are the docking energy (E_av) averaged over the number of peptide conformations shown in parentheses (n), the maximum docking energy (E_max) across the available peptide conformations, and the peptide end-to-end distances (X). The absolute values of E_av and E_max correspond to peptides bound to the canonical RGD-binding sites in the αIIbβ3 headpiece. Note: the difference between the energy parameters for γC-12 and cRGDFK was significant at p < 0.05.

The Gibbs free energy of dissociation of the αIIbβ3–peptide complexes (ΔG) was profiled as a function of noncovalent bond extension using Umbrella Sampling simulations, a technique widely used to access the free-energy landscapes of proteins and protein–protein complexes.³⁷ The results of these calculations, shown in Figure 7, enabled us to extract the following quantitative measures of αIIbβ3–peptide interactions: the average free energy for binding (ΔG_b); the width of the bound state energy well (Δx_b), which characterizes the flexibility of the protein–peptide complex at equilibrium; and the transition state distance at which the complex dissociates (Δx^‡), which quantifies the conformational tolerance for noncovalent bond dissociation.

Figure 7.

Plots of the Gibbs free energy landscape for unbinding ΔG vs noncovalent bond extension Δx for complexes between the αIIbβ3 headpiece and γC-12 (panel a) and cRGDFK (panel b). ΔG profiles were generated using the Umbrella Sampling simulation technique for the open conformation (blue curve) and closed conformation (red curve) of the αIIbβ3 headpiece. Inset: ΔG profiles for the αIIbβ3–γC-12 complex with unsuppressed peptide unraveling.

The values of ΔG_b, Δx_b, and Δx^‡ for the complexes of the αIIbβ3 headpiece with γC-12 and cRGDFK are shown in Table 2. For γC-12 and the open αIIbβ3 headpiece, ΔG_b = 29.2 kcal/mol, Δx_b = 0.81 nm and Δx^‡ = 5.1 nm and ΔG_b was 37.5 kcal/mol, Δx_b = 0.76 nm, and Δx^‡ = 4.6 nm for γC-12 with the closed αIIbβ3 headpiece (inset in Figure 7a). These values contain significant entropic contributions due to the extended structure of γC-12, allowing it to unravel and reduce/adopt tension, thereby prolonging lifetime of the integrin-peptide complex (Figures S3a and S3b). To suppress the entropic contribution of γC-12 to the binding energy, we carried out Umbrella Sampling simulations with the C_α-atoms of γC-12 constrained relative to each other, thereby making the peptide rigid and preventing it from force-induced elongation and unraveling during dissociation. As a result of these constraints, the Gibbs free energy and the transition distance decreased from ΔG_b = 29.2 kcal/mol to ΔG_b = 13.5 kcal/mol, implying that the folded conformation of γC-12 increases the mechanical stability of the γC-12–αIIbβ3 complex (Figure 7a). These constraints made cRGDFK and γC-12 equally inflexible. For cRGDFK, ΔG_b was 16.1 kcal/mol for open αIIbβ3 and 15.6 kcal/mol for closed αIIbβ3, which are slightly greater than for the constrained γC-12 peptide. The bonds in the cRGDFK–αIIbβ3 complex were also more extensible compared to the constrained γC-12–αIIbβ3 complex with Δx^‡ = 2.6 nm and Δx_b = 0.79 nm for open αIIbβ3 and Δx^‡ = 2.0 nm and Δx_b = 0.70 nm for the closed αIIbβ3 headpiece (Figure 7; Table 2).

Table 2.

Parameters for αIIbβ3–Peptide Complexes Obtained Using the Umbrella Sampling Simulations: ΔG_b, Binding Energy; Δx_b, Width of the Bound State Basin; Δx^‡, Transition State Distance^a

peptide	ΔGb, kcal/mol	Δx‡, nm	Δxb, nm
γC-12 and open αIIbβ3	13.5 (29.2)	1.9 (5.1)	0.75 (0.81)
γC-12 and closed αIIbβ3	13.9 (37.5)	2.2 (4.6)	0.71 (0.76)
cyclic RGDFK and open αIIbβ3	16.1	2.6	0.79
cyclic RGDFK and closed αIIbβ3	15.6	2.0	0.70

^aValues obtained without suppression of γC-12 forced unraveling are given in parentheses.

To probe the structural bases for the observed differences in thermodynamic stability, we analyzed binding contacts between residues in αIIbβ3 and γC-12 and residues in αIIbβ3 and cRGDFK using the output from the Umbrella Sampling simulations. We identified two types of contacts between residues Arg1, Asp3, and Lys5 of cRGDFK and the αIIbβ3 headpiece residues: electrostatic bonds involving Asp159 in αIIb and residues Glu220, Asp251, Arg214 in β3, and polar interactions involving β3 residues Ser121, Tyr122, Ser123, and Asn215. Three types of contacts were identified between γC-12 and the αIIbβ3 headpiece residues: electrostatic bonds between αIIb residue Asp159 and γC-12 residues His1 and His2; hydrophobic interactions involving αIIb residue Val156, β3 residue Ala218 and γC-12 residues Gly4, Ala9, Gly10; and polar interactions of β3 residues Ser121, Ser123, and Asn215 with γC-12 residue Gln8. Stronger electrostatic interactions dominated the cRGDFK-αIIbβ3 complex, making it slightly more stable than the γC-12-αIIbβ3 complex in which weaker hydrophobic and polar interactions were predominant. However, the overall number and the nature of the binding contacts in these complexes, namely, fewer strong bonds in cRGDFK- αIIbβ3 and more weak bonds in γC-12-αIIbβ3 make the difference in overall binding energies insignificant.

It is noteworthy that for cRGDFK bound to open αIIbβ3, the profile ΔG vs Δx plateaued at 1 nm bond extension, corresponding to ~5 kcal/mol due to bond tension (Figure 7b). Thus, there is a lower-affinity bound state for cRGDFK that is captured in the Umbrella Sampling simulations that was undetected in the docking analysis. This explains the emergence of Pathway 1 and Pathway 2 in the unbinding scenarios observed in the force-ramp simulations. Taken together, these results indicate that the strength of the cRGDFK–αIIbβ3 and γC-12–αIIbβ3 complexes is similar. Further, they show that the conformational flexibility of γC-12 and the related entropy penalty reduce the strength and thermodynamic stability of its complex with αIIbβ3.

DISCUSSION

The impetus for the studies reported here was our previous observation that whereas platelet aggregation via fibrinogen is exclusively mediated by binding of the γ chain C-terminal dodecapeptide to the αIIbβ3 headpiece, αIIbβ3 appears to interact with both the dodecapeptide and either of the fibrinogen Aα chain RGD motifs when fibrinogen is immobilized or converted to fibrin.¹⁵ Thus, to understand the physical bases underlying these observations, we have employed state-of-the-art single-molecule experimental and computational techniques to explore the kinetics and energy of the interactions of a cyclic RGD peptide, cRGDFK, and a peptide corresponding to the C-terminal 12 residues of the fibrinogen γ chain, γC-12, with the closed and open conformations of the αIIbβ3 headpiece.⁷

First, we measured the kinetics and strength of cRGDFK and γC-12 binding to immobilized αIIbβ3 using optical trap-based force spectroscopy.^{17–20,23,37,45–47} We found the rupture force values for the complex of αIIbβ3 with cRGDFK were comparable to those we observed for the αIIbβ3–γC-12 complex, indicating that the strength of the complexes is comparable. Further, the on-rate and off-rate of cRGDFK binding were slightly greater and smaller, respectively, than the corresponding parameters for γC-12, resulting in a slightly greater affinity constant, although this difference did not reach statistical significance. Thus, these results indicate there is little, if any, difference in the ability of αIIbβ3 to interact with the γ-chain sequence and the α chain RGD motifs when fibrinogen is immobilized fibrinogen or is converted to fibrin.

Previous rupture force measurements of peptides bound to the αIIbβ3 headpiece generally agree with these conclusions, although reported values are slightly less than the ones we determined here, perhaps due to the higher force-loading rate used in our experiments.^16,48,49 Moreover, the calculated values of the rupture forces reported here are also qualitatively consistent with our previous studies in which we found that cRGD- αIIbβ3 interactions had a greater binding strength than that of αIIbβ3 with γC-12.¹⁶ Further, the two-pathway unbinding of cRGDFK in the MD simulations agrees with a bimodal distribution of rupture forces observed experimentally.¹⁶ Similar to our results, Lee and Marchant, using atomic force microscopy and live platelets, found that the kinetic off-rate (k_off) was significantly greater for γC-12 than for RGD-containing peptides, indicating that the γC-12–αIIbβ3 complex dissociates faster under tension than does the cRGDFK-αIIbβ3 complex.⁴⁸ Lastly, based on a theoretical model, Dutta et al.⁴⁹ found that the dissociation energy of a cyclic RGD peptide cHarGD [cyclo (S,S)-L-lysyl-L-tyrosyl-glycyl-L-cystinyl-L-homoarginyl-glycyl-L-aspartyl-L-trytopanyl-L-prolyl-L-cystine] was ~7–9 kcal/mol, less than the value we obtained for cRGDFK (~16 kcal/mol), but within the same order of magnitude.

To decipher the mechanisms underlying the experimental differences we observed using optical force spectroscopy, we turned to computational modeling using the reported crystal structures of the open and closed αIIbβ3 headpiece⁷ and NMR structures for cRGDFK and γC-12 that we determined experimentally. It is important to note that the structures we found for cRGDFK and γC-12 peptides were consistent with previously reported NMR and crystallographic structures for cyclic RGD peptides and for γC-12.^13,50–55

Mimicking atomic force microscopy and optical trap-based force spectroscopy experiments,^56–58 we performed in silico dynamic force-ramp measurements to provide information about the kinetics and pathways of dissociation of αIIbβ3–peptide complexes. Profiles of rupture force versus noncovalent bond extension confirmed that cRGDFK and γC-12 form stable bimolecular complexes with rupture forces in the 60–120 pN range. Further, application of pulling force was accompanied by substantial 2–6 nm bond extensions, indicating that the peptide molecules and their binding interfaces with αIIbβ3 are flexible.

The forced dissociation simulations were complemented by mapping the free energy landscapes for peptide binding and unbinding using the Umbrella Sampling technique. Umbrella Sampling is an advanced computational tool^37–39 which can be utilized to quantitatively describe the thermodynamics of the noncovalent interactions. While molecular docking provides fast preliminary screening of energy-minimized stable conformations, Umbrella Sampling is a numerically accurate but more computationally demanding method for the estimation of the Gibbs free energy changes which accompany bimolecular interactions (ΔG_b). In our studies, ΔG_b corresponds to the total equilibrium work required to dissociate the noncovalent bond stabilizing a αIIbβ3–peptide complex. The higher values of ΔG_b are indicative of stronger coupling, and they correspond to higher binding affinity. We found that the binding energy for the open αIIbβ3 headpiece was insignificantly higher for cRGDFK (ΔG_b = 16.1 kcal/mol) than for γC-12 (ΔG_b = 13.5 kcal/mol). This correlates with a difference in the critical bond extension before breakage, Δx^‡ = 2.6 nm for cRGDFK and 1.9 nm for the γC-12. These results agree with the kinetic parameters obtained from the force spectroscopy experiments, indicating that the affinity of the αIIbβ3 headpiece for cRGDFK is slightly greater than its affinity for γC-12, but this difference does not reach statistical significances.

Our contact analysis is consistent with X-ray data,^7,9 indicating the importance of αIIb residue Asp159 and β3 residues Ser121, Tyr122, Ser123, Arg214, Asn215, and Ala218 for binding of γC-12 and RGD-containing peptides. However, the dynamics displayed in our simulations reveals additional transient contacts not observed in the static X-ray structure (Figures S5 and S6). Analysis of binding contacts showed that the longer γC-12 molecule formed more contacts with αIIbβ3 compared to the shorter cRGDFK peptide (Figures 5 and S4). However, whereas the cRGDFK–αIIbβ3 complex was stabilized by strong electrostatic interactions, the γC-12–αIIbβ3 complex was formed from weaker hydrophobic contacts. Moreover, conformational flexibility of the γC-12 peptide significantly contributed to the thermodynamic stability of the αIIbβ3 headpiece-γC-12 complex. In particular, stretching γC-12 by ~3.0 nm required a ΔG_b of ~16 kcal/mol, suggesting that γC-12 binding to αIIbβ3 requires that the peptide adopt an energetically costly folded conformation. In other words, the Gibbs free energy for cRGDFK binding to αIIbβ3 headpiece is predominantly enthalpic due to strong electrostatic interactions, whereas the extended structure and unfolding of γC-12 introduced a significant entropic contribution into the values of ΔG_b we have obtained for γC-12 binding to αIIbβ3 headpiece (Table 2). Thus, overall, cRGDFK is a little “better αIIbβ3 binder” and, hence, a stronger competitive inhibitor, compared to free γC-12. Nonetheless, intact ligands such as soluble fibrinogen do not bind to αIIbβ3 on resting platelets,⁵ indicating that the ability of small peptide ligands such as cRGDFK and γC-12 to bind to αIIbβ3 cannot fully account for the ability of αIIbβ3 to bind large intact macromolecular ligands.⁵⁹

In summary, we have measured the kinetics and have probed the strength of γC-12 and cRGDFK peptide binding and unbinding to αIIbβ3 using optical trap-based single-molecule force spectroscopy, and we have quantified the energy of these interactions with the crystallographically resolved open and closed conformations of the αIIbβ3 headpiece using advanced molecular modeling techniques. This has enabled us to determine the stability of the αIIbβ3–peptide complexes and the dynamics of interatomic contacts, suggesting that both the RGD and AGDV motifs in immobilized fibrinogen and fibrin are almost equally important for the interaction of these molecules with platelets. Although the differences we detected between αIIbβ3 binding to single cRGDFK and γC-12 molecules were small, their cumulative effect is likely to be biologically significant when αIIbβ3 on platelets interacts with multiple immobilized fibrinogen molecules and with polymerized fibrin. On the other hand, the relative contribution of RGD motifs to the αIIbβ3-mediated adhesion of platelets to immobilized fibrinogen and fibrin is likely enhanced because there are twice as many RGD sites as there are AGDV sites in these molecules.