Abstract
The wrist is essential for hand function. Yet, due to the complexity of the wrist and hand, studies often examine their biomechanical features in isolation. This approach is insufficient for understanding links between orthopaedic surgery at the wrist and concomitant functional impairments at the hand. We hypothesize that clinical reports of reduced force production by the hand following wrist surgeries can be explained by the surgically-induced, biomechanical changes to the system, even when those changes are isolated to the wrist. This study develops dynamic simulations of lateral pinch force following two common surgeries for wrist osteoarthritis: scaphoid-excision four-corner fusion (SE4CF) and proximal row carpectomy (PRC). Simulations of lateral pinch force production in the nonimpaired, SE4CF, and PRC conditions were developed by adapting published models of the nonimpaired wrist and thumb. Our simulations and biomechanical analyses demonstrate how the increased torque-generating requirements at the wrist imposed by the orthopaedic surgeries influence force production to such an extent that changes in motor control strategy are required to generate well-directed thumb-tip end-point forces. The novel implications of our work include identifying the need for surgeries that optimize the configuration of wrist axes of rotation, rehabilitation strategies that improve post-operative wrist strength, and scientific evaluation of motor control strategies following surgery. Our simulations of SE4CF and PRC replicate surgically-imposed decreases in pinch strength, and also identify the wrist's torque-generating capacity and the adaptability of muscle coordination patterns as key research areas to improve post-operative hand function.
Keywords: wrist, thumb, computer simulation, proximal row carpectomy, scaphoid-excision four-corner fusion
Introduction
A healthy wrist is essential for hand function. Every day we produce forces with our hands in order to grasp objects, push buttons, or feel surfaces. Producing these forces requires the coordinated action of over three dozen muscles and muscle compartments, many of which originate in the forearm, cross the wrist, and insert into the hand. This anatomical design means that muscle activity (Johnston et al. 2010) and maximal grip force (O'Driscoll et al. 1992; Ambike et al. 2013) vary with wrist posture.
As multi-body, multi-joint systems, the distinct complexities of the wrist and hand often necessitate isolated study. Experimental studies, for example, have separately examined kinematics of the carpal (e.g., Ruby et al. 1988; Neu et al. 2001; Crisco et al. 2005; Eschweiler et al. 2016; Eschweiler et al. 2016), carpometacarpal (e.g., Buffi et al. 2013), and phalangeal (e.g., Hollister et al. 1992; Hess et al. 2013) joints. Even simulation studies rarely integrate the wrist and hand because the computational challenges associated with building robust musculoskeletal models of these intricate, low mass, low inertia systems are substantial. For example, many of the most detailed simulation studies analyzing force production by the hand exclude the wrist. Instead, these studies have elucidated the biomechanics of force production at the index finger (Valero-Cuevas et al. 1998; Wu et al. 2008; Lee and Kamper 2009), the thumb (Valero-Cuevas et al. 2003; Goehler and Murray 2010; Wohlman and Murray 2013), and the end-points of multiple digits to produce coordinated grip forces (Esteki and Mansour 1997; Sancho-Bru et al. 2003) in isolation from the proximal upper limb.
Studying the wrist and hand in isolation precludes understanding the ubiquitous links between loss of function at the wrist and concomitant functional impairments in the hand. Such understanding is critical for designing effective clinical interventions. For example, Adamczykand Crago (2000) utilized biomechanical simulation of the wrist, index finger, and thumb to demonstrate that, following C5/C6 tetraplegia, functional electrical stimulation (FES) can best modulate prehensile grasp forces if the controller accounts for the mechanical couplings between the wrist and hand in such a way that control of wrist posture becomes independent from control of grasp force. Importantly, Adamczyk and Crago (2000) designed an FES controller to restore wrist and hand function in individuals whose primary injury involves a severely damaged nervous system. Substantial impairment also occurs when the disease state and clinical intervention primarily affect the musculoskeletal system. For example, the two most common orthopaedic surgeries used to treat wrist osteoarthritis, scaphoid-excision four-corner fusion (SE4CF) and proximal row carpectomy (PRC), alter the geometry of the wrist extensively (Fig. 1, inset). While effective at reducing pain, these surgeries degrade kinematic motion at the wrist and also impair functional performance at the hand (Wolff et al. 2015). Loss of grip and pinch strength, in particular, are widely reported as debilitating functional impairments (Nagelvoort et al. 2002; Bain and Watts 2010; Richou et al. 2010). Yet, the biomechanical mechanisms by which isolated wrist surgery alters force production at the hand remain largely unknown.
Figure 1.

Simulation framework implemented for the (A) simulations of joint torque, (B) simulations of muscle control strategy, and (C) the simulations of muscle for transmission. The nonimpaired, SE4CF, and PRC models as well as the lateral pinch tasks are shown in the insert. For the SE4CF model, the scaphoid was removed and the remaining carpal bones were fused using a weld joint. For the PRC model, the lunate, scaphoid, and triquetrum were removed and the remaining carpal bones were translated proximally to establish an interface between the radius and capitate. Unless otherwise noted, simulations were performed for all three models for seven lateral pinch tasks (target thumb-tip endpoint force from 0 to 60N in increments of 10N).
In this study, we evaluate how altering the wrist through orthopaedic surgery influences hand function, in the context of SE4CF and PRC. We hypothesize that reduced force production by the hand can be explained by the surgically-induced, biomechanical changes to the system, even when those changes are isolated to the wrist. To test this hypothesis, we leverage available biomechanical data characterizing the wrist surgeries (Blankenhorn et al. 2007; Nichols et al. 2015; Nichols et al. 2016; Nichols et al. 2017) and computational advances in biomechanical simulation of force development at the thumb (Valero-Cuevas et al. 2003; Goehler and Murray 2010; Wohlman and Murray 2013) to develop dynamic musculoskeletal simulations of lateral pinch force that integrate the wrist and thumb. We then utilize these simulations to specifically examine how having a nonimpaired versus a surgically-altered wrist influences joint torques, muscle force transmission, and muscle control strategies during lateral pinch.
Methods
Dynamic musculoskeletal models of the nonimpaired, SE4CF, and PRC conditions were developed to examine how surgically altering the wrist affects lateral pinch force production. The models were developed in SIMM (v. 6.2.1, Musculo graphics Inc.; Delp and Loan 1995), and then imported into OpenSim (v. 3.3; Delp et al. 2007) to perform all simulations. Simulations of a lateral pinch task separately examined how the nonimpaired, SE4CF, and PRC wrists influence (i) the joint torques necessary to produce thumb-tip endpoint forces, (ii) the transformation of muscle forces into a thumb-tip endpoint force, and (iii) the muscle control strategies required for thumb-tip endpoint force production.
Musculoskeletal Models
The dynamic musculoskeletal models of the nonimpaired, SE4CF, and PRC conditions were developed by adapting previously published models of the nonimpaired wrist (Saul et al. 2015) and thumb (Wohlman and Murray 2013). Condition-specific bone geometry, joint kinematics, and muscle moment arms at the wrist for each model were based on experimental data, as described below.
The nonimpaired model included bone geometry, masses, and inertial parameters for the humerus, ulna, radius, and proximal carpal bones as described by Saul et al. (2015). The hand from Saul et al. (2015) was divided into multiple segments to enable modeling the thumb as separate segments for the first metacarpal, proximal phalanx, and distal phalanx (Table 1). Joint kinematics and muscle-tendon actuators were included for only the wrist and thumb. Wrist kinematics (Saul et al. 2015) defined two degrees-of-freedom (flexion-extension and radial-ulnar deviation), based on experimentally measured joint axes of rotation (Ruby et al. 1988). Thumb kinematics (Holzbaur et al. 2005) defined four degrees-of-freedom (carpometacarpal flexion-extension, carpometacarpal abduction-adduction, metacarpophalangeal flexion-extension, and interphalangeal flexion-extension), based on experimental measurements (Hollister et al. 1992; Hollister et al. 1995). Fourteen muscle-tendon actuators were modeled using the dynamic Hill-type model described by Millard et al. (2013). These actuators included the five primary wrist muscles, four extrinsic thumb muscles, and five intrinsic thumb muscles (see Table 2 for muscle names and abbreviations). The nonimpaired muscle lines of action and muscle force-generating parameters have been previously described (Wohlman and Murray 2013; Saul et al. 2015).
Table 1. Inertial parameters for palm and thumba.
| Segment | Mass (kg) | Center of Mass (m) | Inertia (kg m2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rx | Ry | Rz | Ixx | Ixy | Ixz | Iyy | Iyz | Izz | ||
| Palm | 0.4648 | −0.0067 | −0.0389 | 0.0038 | −1.1E-04 | −9.0E-07 | −2.0E-07 | −6.0E-05 | −1.2E-05 | −1.5E-04 |
| First Metacarpal | 0.0160 | 0.0078 | −0.0147 | −0.0060 | 1.2E-06 | 4.7E-07 | 2.5E-07 | 7.1E-07 | −4.1E-07 | 1.3E-06 |
| Proximal Phalanx | 0.0079 | 0.0096 | −0.0163 | −0.0063 | 2.6E-07 | 9.5E-08 | 3.8E-08 | 1.6E-07 | −6.3E-08 | 2.9E-07 |
| Distal Phalanx | 0.0031 | 0.0056 | −0.0104 | −0.0044 | 4.6E-08 | 1.4E-08 | 7.0E-09 | 3.2E-08 | −1.0E-08 | 5.0E-08 |
The origin of the palm segment is in the center of the capitate. All other segment origins are consistent with those defined in Holzbaur et al. (2005). The xyz convention for all segments in the neutral position of the right arm is defined such that anterior, superior, and lateral are respectively aligned with the positive direction of the x, y, and z axes.
Table 2. List of Modeled Wrist and Thumb Muscles.
| Group | Abbreviation | Muscle Name |
|---|---|---|
| Primary Wrist Muscles | ECRB | extensor carpi radialis brevis |
| ECRL | extensor carpi radialis longus | |
| ECU | extensor carpi ulnaris | |
| FCR | flexor carpi radialis | |
| FCU | flexor carpi ulnaris | |
| Extrinsic Thumb | APL | abductor pollicis longus |
| EPB | extensor pollicis brevis | |
| Muscles | EPL | extensor pollicis longus |
| FPL | flexor pollicis longus | |
| Intrinsic Thumb Muscles | ADPo | adductor pollicis oblique head |
| ADPt | adductor pollicis transverse head | |
| APB | abductor pollicis brevis | |
| FPB | flexor pollicis brevis | |
| OPP | Opponenes pollicis |
To develop models of SE4CF and PRC, we altered the nonimpaired model to reflect the bone geometry, joint axes of rotation, and muscle lines of action following these surgeries. Bone geometry was modeled as previously described (Nichols et al. 2013). Implemented axes of rotation were based on cadaveric experiments that measured wrist kinematics following SE4CF (Nichols et al. 2017) and PRC (Blankenhorn et al. 2007). Additionally, in both models, the muscle lines of action of the primary wrist and extrinsic thumb muscles were adjusted to replicate experimentally measured wrist flexion-extension and radial-ulnar deviation moment arms following SE4CF and PRC (Nichols et al. 2015; Nichols et al. 2016). Muscle force-generating parameters associated with the Hill-type model were equivalent across the nonimpaired, SE4CF, and PRC models.
Simulations of Joint Torques
To compare the joint torques necessary to produce a given level of lateral pinch force across wrist conditions, we implemented a computed torque control algorithm (Fig. 1A) (Delp et al. 2007). Each simulation required maintaining a target posture while producing a target thumb-tip endpoint force. These simulations did not include muscle-tendon units. Thus, differences in the resulting torques isolate the effects of wrist kinematics on the transformation from joint torque to thumb-tip endpoint force.
For each model, seven simulations of lateral pinch were performed. The outputs of each simulation were joint torques at the wrist, carpometacarpal, metacarpophalangeal, and interphalangeal joints. The inputs were the target joint posture and endpoint force (direction and magnitude) defining the simulated lateral pinch task (Fig. 1, inset). In all simulations, the target joint posture defined a neutral wrist position (0° flexion-extension and 0° radialulnar deviation) and a thumb positioned in a lateral pinch posture (15° carpometacarpal extension, 20° carpometacarpal adduction, 20° metacarpophalangeal flexion, and 40° interphalangeal flexion). The target thumb-tip endpoint force varied in magnitude (0 to 60N in increments of 10N), but was always directed in a pure palmar direction. The range of endpoint forces was chosen to include the average maximum lateral pinch force (51.9N) reported in a human subjects study (Valero-Cuevas et al. 2003). In all simulations, the target thumb-tip endpoint force was maintained for at least 0.5 seconds, which was enough simulation time to ensure an equilibrium posture was reached. Here, an equilibrium posture is the joint posture that can be statically maintained while producing the target endpoint force; importantly, given the dynamic nature of the simulations, the equilibrium posture is not necessarily equivalent to the target posture. For simulations with a target thumb-tip endpoint force above 10N, a linear increase from 10N to the target thumb-tip endpoint force was required for the computed torque control optimization algorithm to find an appropriate solution space (Fig. 1, inset). Thus, to accommodate this linear increase, total simulation time varied between 1 and 3 seconds based on thumb-tip endpoint force magnitude.
The calculated torques were decomposed into standard anatomical reference frames to allow direct comparison across the nonimpaired, SE4CF, and PRC models. This was necessary because computed torque control calculates the torques about the joint axes of rotation, which were defined differently for the wrist in each model. Thus, for each simulation, the torques about the flexion-extension and radialulnar deviation axes of rotation were decomposed to define a total wrist torque. Similarly, the torques about the carpometacarpal flexion-extension and carpometacarpal abduction-adduction axes of rotation were decomposed to define a total carpometacarpal joint torque. Flexion, ulnar deviation, and abduction torques were defined as positive.
Simulations of Muscle Control Strategy
To compare the muscle control strategies necessary to produce lateral pinch forces in the nonimpaired, SE4CF, and PRC models, computed muscle control simulations (Thelen and Anderson 2006) were performed (Fig. 1B). Similar to the simulations of joint torque, each simulation involved producing a well-directed thumb-tip endpoint force while maintaining a prescribed, static posture. However, these simulations included muscle-tendon units. Thus, differences in the calculated muscle control strategy (i.e., muscle activations) provide insights into whether or not the simulated muscle-tendon units have the ability to compensate for surgical changes to wrist joint kinematics and musculoskeletal geometry.
In each computed muscle control simulation, the inputs were identical to those in the simulations of joint torque and defined the target joint posture and endpoint force (direction and magnitude) of the seven lateral pinch tasks described in the previous section. The outputs were a set of controls describing the muscle activations and joint torques necessary to produce the target lateral pinch force. Muscle activations were defined on a scale from 0 to 1, thereby representing levels of activation ranging from a muscle that is not active (activation=0) to one that is maximally activated (activation=1). We defined the simulations such that muscle activations would be calculated for each of the fourteen muscles included in the models, and additional joint torques (i.e., reserve torques) would be calculated at the wrist. This means that the thumb joint torques were fully described by modeled muscle actions, while wrist joint torques were described by modeled muscle actions and additional torque generators. The additional torque generators represent the wrist joint torque generated by the extrinsic finger muscles, which were not included in the models but are known to contribute to wrist torque (Brand and Hollister 1999). The muscle activations and reserve torques at the wrist were compared across the nonimpaired, SE4CF, and PRC models.
Simulations of Muscle Force Transmission
To compare how effectively muscle force is transformed into lateral pinch force across wrist conditions, forward dynamic simulations were performed (Fig. 1C). Each simulation involved utilizing a given set of muscle activations to produce a lateral pinch force. Because muscle activations were held constant across wrist models, any differences in the simulated pinch force vectors arise from changes to wrist joint kinematics and musculoskeletal geometry imposed by the surgeries.
In each forward dynamic simulation, the inputs were the muscle activations required to reproduce lateral pinch tasks in the nonimpaired model, calculated using computed muscle control. Similar to the simulations of muscle control strategy, computed muscle control simulations were performed to determine the muscle activations for the seven previously described lateral pinch tasks. These simulations were defined such that the outputs were the muscle activations corresponding to the fourteen muscles included in the model. Unlike the simulations of muscle control strategy, no additional torques (i.e., reserve torques) were simulated, meaning that the required joint torques were fully produced by the modeled muscles.
To ensure that the calculated muscle activations produced the desired lateral pinch tasks, the muscle activations were first used as inputs to forward dynamic simulations using the nonimpaired model. After verifying correct thumb-tip endpoint force production, the same muscle activations were input into forward dynamic simulations using the SE4CF and PRC models. The output of these simulations, which defined the thumb-tip endpoint force (magnitude and direction) as well as joint posture (wrist and thumb) were compared across the nonimpaired, SE4CF, and PRC models. Flexion, ulnar deviation, and abduction were defined as positive joint angles.
Results
All simulations, except two, ran to completion without error. The computed muscle control simulation to produce 60N endpoint force without reserve torques using the nonimpaired model failed, indicating that additional joint torques, such as those produced by the extrinsic finger muscles, are necessary to reach the 60N force magnitude. Given that the muscle activations from this simulation were required inputs for the forward simulation, forward simulations were not completed for a target endpoint force of 60N. Additionally, the computed muscle control simulation to produce 60N of endpoint force with reserve torques using the PRC model failed; full activation of the primary thumb flexor (FPL) was insufficient to produce this magnitude of force in this condition.
Altering only the wrist axes of rotation changes the joint torques required to produce endpoint forces at the thumb-tip. Regardless of the magnitude of endpoint force simulated, the wrist joint torque required to produce well-directed thumb-tip endpoint forces were larger in the SE4CF and PRC models than those required in the nonimpaired model (Fig. 2). The PRC model required the largest wrist joint torque, which was more than 3.6 times larger than that required in the nonimpaired model (cf., Fig. 2A, red line compared to black line for thumb-tip endpoint forces greater than or equal to 10N). The joint torques required at the carpometacarpal, metacarpophalangeal, and interphalangeal joints were similar across all models (Fig. 2B-D).
Figure 2.
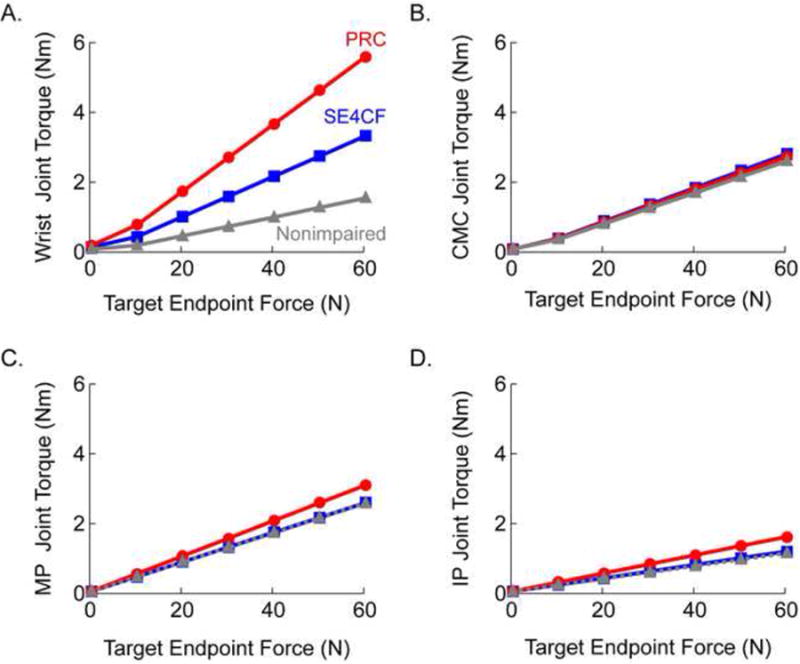
Magnitude of joint torque required to produce a range of endpoint forces at the thumb-tip in the nonimpaired (grey), SE4CF (blue), and PRC (red) models. Joint torque versus target endpoint force are reported at the (A) wrist, (B) carpometacarpal joint, (C) metacarpophalangeal joint, and (D) interphalangeal joint.
Producing equivalent, well-directed thumb-tip endpoint forces while maintaining a given posture requires different control strategies in the nonimpaired, SE4CF, and PRC models. For example, muscle activations for the majority of simulated muscles changed substantially across simulations using the nonimpaired, SE4CF, and PRC models (cf. Fig. 3, muscle activations changed by greater than 10 percent following at least one surgery for 8 of the 14 muscles). The changes in muscle activation included primary wrist muscles, extrinsic thumb muscles, and intrinsic thumb muscles (Fig. 3). The additional torque generators, which represent the joint torque that the extrinsic finger muscles would be required to produce, further suggest that different control strategies must be implemented following wrist surgery (Fig. 4). Notably, to produce a 20N lateral pinch force, the PRC model requires an ulnar extension torque that is greater than that generated by a fully activated ECU, the only primary wrist muscle to act as both an ulnar deviator and wrist extensor (cf., Fig. 4B, positive torque about radial-ulnar axis represents wrist extension, and Fig. 4D, positive torque about palmar-dorsal axis represents ulnar deviation).
Figure 3.
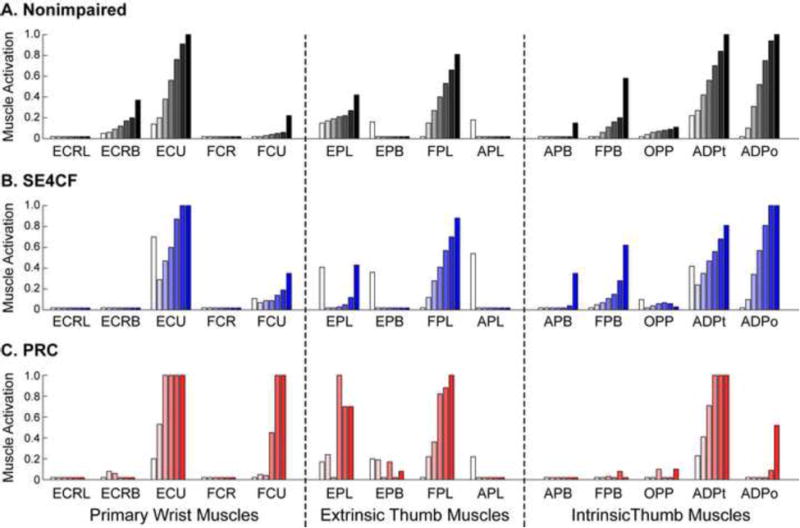
Muscle activations for the (A) nonimpaired, (B) SE4CF, and (C) PRC models. For each muscle, activation levels are displayed for increasing levels of target force (i.e., white bar represents 0N target force, each progressively darker bar represents a 10N increase in target force). Note, the target force of 60N is not displayed for the PRC models, as this simulation failed to run to completion.
Figure 4.

(A) Magnitude of additional torque required at the wrist during the computed muscle control simulations using the nonimpaired (gray), SE4CF (blue), and PRC (red) models. (B-D) The reserve torque decomposed into (B) radial-ulnar, (C) proximal-distal, and (D) palmar-dorsal components. The example shown is for simulations to produce at 20N thumb-tip endpoint force, the force necessary for most activities of daily living (Smaby et al. 2004). This example is representative of the differences in torque seen across models for all force magnitudes. Note, magnitudes for all results in Fig 4B arose from only wrist extension torques; magnitudes in Fig. 4D resulted from only ulnar deviation torques.
Given the same muscle activations, the SE4CF and PRC models produce thumb-tip endpoint forces that are smaller in magnitude (Table 3) and misdirected (Fig. 5) compared to those produced by the nonimpaired model. The misdirection of the force depended on the surgery; SE4CF produced force in palmar and medial directions, PRC produced force in palmar and proximal directions (Fig. 5). The posture at equilibrium was also different across the three models. In addition to changes in thumb joint posture (Fig. 5), the wrist moved by nearly 10° in both surgical models (Table 4). The equilibrium wrist posture was neutral for the nonimpaired model, combined radial-extension for SE4CF, and radial deviation for PRC (Fig. 5).
Table 3. Endpoint Force Produced at Thumb-tip (Output from Forward Dynamics).
| Target Force Magnitude (N) | Endpoint Force Magnitude (N) | ||
|---|---|---|---|
| Nonimpaired | SE4CF | PRC | |
| 0 | 0.8 | 1.1 | 0.7 |
| 10 | 10.0 | 9.2 | 8.7 |
| 20 | 20.1 | 18.2 | 17.9 |
| 30 | 30.1 | 27.6 | 27.0 |
| 40 | 39.9 | 37.1 | 36.2 |
| 50 | 50.2 | 47.1 | 46.2 |
| 60 | Simulation Not Performed# | ||
| Average*(% of nonimpaired) | 100% | 92.1 ± 1.3% | 89.8 ± 1.8 % |
Activations from the computed muscle control simulation to produce 60N endpoint force without reserve torques are a necessary input for this simulation. These input values were not available because this simulation failed to run to completion without error.
Average (± standard deviation) excludes target force magnitude of zero.
Figure 5.
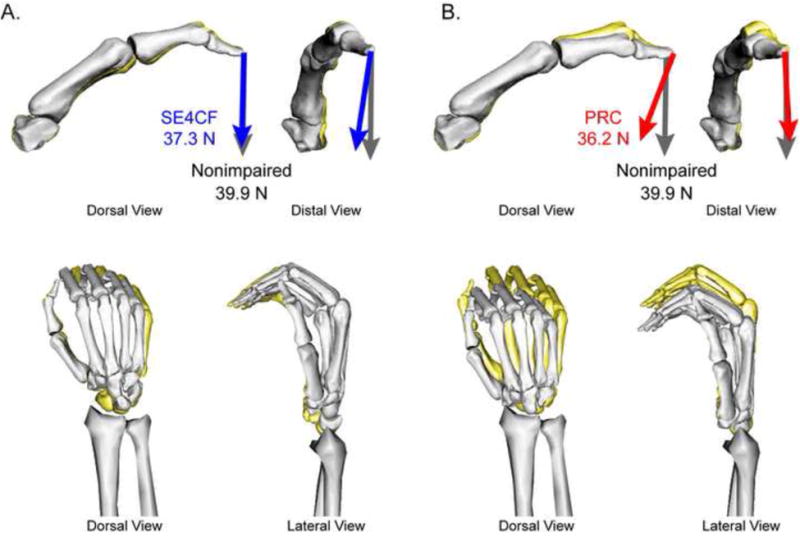
Final equilibrium joint posture and thumb-tip endpoint force produced during the forward simulations. For comparison, results from the (A) SE4CF (gray bones and blue arrows) and (B) PRC models (gray bones and red arrows) are superimposed on those of the nonimpaired model (yellow bones and gray arrows). For each model, the arrow represents the thumb-tip endpoint force (direction and magnitude) and the bone geometry illustrates the thumb (top) and wrist (bottom) posture during force production. The example shown is for forward simulations using the nonimpaired muscle activations corresponding to a 40N thumb-tip endpoint force; this example is representative of the direction in thumb-tip endpoint forces for all targeted force magnitudes.
Table 4. Average Joint Posture During Force Production (Output from Forward Dynamics)*.
| Model | Ulnar Deviation | Wrist Flexion | CMC Flexion | CMC Abduction | MP Flexion | IP Flexion |
|---|---|---|---|---|---|---|
| Target Posture | 0 | 0 | -15 | -20 | 20 | 40 |
| Nonimpaired | 0.0 ± 0.5 | -0.7 ± 1.2 | -13.8 ± 0.7 | -18.3 ± 2.9 | 17.6 ± 1. 6 | 43.1 ± 3.0 |
| SE4CF | -7.8 ± 0.5 | 1.5 ± 0.2 | -9.8 ± 0.4 | -18.3 ± 1.4 | 23.7 ± 0.4 | 36.3 ± 0.3 |
| PRC | -6.7 ± 1.6 | 0.0 ± 1.3 | -8.4 ± 1.8 | -24.0 ± 2.7 | 26.1 ± 0.5 | 24.6 ± 3.6 |
All values reported in degrees; standard deviations represent variation across simulations of different force magnitude. Ulnar deviation, flexion, and abduction are defined as positive.
Discussion
In this study, we examined how drastic surgical changes to the musculoskeletal design of the wrist influence hand function. We specifically studied SE4CF and PRC, two wrist surgeries that unintentionally result in long-term impairments in hand function (Bain and Watts 2010; Richou et al. 2010). Through simulations, we demonstrate that surgically altering wrist kinematics and muscle moment arms substantially influences the joint torques, muscle force transmission, and muscle control strategies associated with the production of lateral pinch force. Notably, our simulations demonstrate that following wrist surgery increased torque-generating requirements at the wrist (Fig. 2) influence force production to such an extent that changes in muscle control strategy are required to generate well-directed thumb-tip end-point forces (Fig. 3).
Overall, our simulations identify novel directions for future research to improve clinical outcomes following S4CF and PRC. For example, from the simulations of joint torque, we conclude that surgically altering wrist kinematics limits the capacity to produce lateral pinch force. This is highlighted by the fact that the nearly orthogonal axes of rotation imposed by PRC result in an almost fourfold increase in the torque-generating requirements to produce thumb-tip endpoint force (Fig. 2). Clinically, this result implies the need for surgeries that optimize the configuration of wrist axes of rotation, rehabilitation strategies that improve post-operative wrist strength, or a combination of these approaches. Based on our results, we now hypothesize that increasing torque-generating capacity following surgery could allow individuals to stabilize the wrist and generate desired forces at the hand. Notably, wrist torque is not routinely measured following surgery. In fact, to our knowledge, there are no research studies that quantify wrist strength following either SE4CF or PRC. Thus, the ability to coordinate wrist torque and hand force, and the extent to which clinical interventions that improve wrist strength also improve hand strength is an open area for investigation.
Similarly, the simulations of muscle force transmission and muscle control highlight the need to further examine motor learning following SE4CF and PRC, as post-operative hand function could potentially be improved by learning new muscle coordination patterns. For example, the muscle force transmission simulations demonstrate that a nonimpaired control strategy results in a 10 percent decrease in thumb-tip forces following surgery (Table 3). Thus, immediately following surgery, before individuals have had time to learn and adopt a new muscle control strategy, ineffective control likely contributes to post-operative impairments in hand function. The extent to which individuals can learn a new muscle control strategy is unknown; however, the ability of such motor learning to improve function is supported by the simulations to examine muscle control. These simulations indicate that control strategies exist that allow production of the same magnitude of well-directed force following SE4CF (up to the 60N evaluated here), and PRC (up to 50N) (Fig. 3), and therefore could potentially be learned. Given that post-operative impairments in hand strength are reported following SE4CF and PRC (Bain and Watts 2010; Richou et al. 2010), further study is necessary to test the extent individuals alter their motor control strategies following surgery as well as to what extent rehabilitation could lead to optimized control strategies that improve lateral pinch strength.
All of the results presented in this study rely upon musculoskeletal simulations. These simulations provided an idealized environment to study the biomechanically complex process of force production by the hand following SE4CF and PRC. However, the results from our “simulation-only” study remain theoretical. Despite this limitation, our results are important because they identify novel, biomechanically-driven hypotheses to be experimentally tested. We have previously demonstrated that hypotheses derived from theoretical simulations and limited quantitative data improved the design and analysis of biomechanical experiments (Nichols et al. 2016). Such experiments can also simultaneously address issues associated with external validation of our models. For example, the nonimpaired thumb model (excluding the wrist) was validated by replicating cadaveric and in vivo data (see Wohlman and Murray 2013). The endpoint forces simulated with the SE4CF and PRC models have not been evaluated against similar data, despite being based on experimental data (Blankenhorn et al. 2007; Nichols et al. 2015; Nichols et al. 2016; Nichols et al. 2017). While many studies summarize clinical outcomes of these surgeries, studies that provide the scope and quantitative detail needed to validate our biomechanicalsimulationsdonotexist.Experimentalvalidationisalsoneededtoinformexpansion of the models to include finger kinematics, which were excluded from this study, as well as extrinsic finger muscles, which we represented as reserve torques.
In this study, we advance the work of Adamczyk and Crago (2000) by evaluating decreases in external pinch force production due to an impaired musculoskeletal system instead of an injured nervous system. Our simulations of SE4CF and PRC replicate surgically-imposed decreases in pinch strength, and also identify the wrist's torque-generating capacity and muscle coordination patterns as key research areas to improve post-operative hand function.
Acknowledgments
This work was funded by the National Institutes of Health (NIH F31 AG041627 and NIH R01 EB011615).
Footnotes
Conflict of Interest Statement: The authors have no conflicts of interest to disclose.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adamczyk MM, Crago PE. Simulated feed forward neural network coordination of hand grasp and wrist angle in a neuroprosthesis. IEEE Trans Rehabil Eng. 2000;8(3):297–304. doi: 10.1109/86.867871. [DOI] [PubMed] [Google Scholar]
- Ambike SS, Paclet F, Latash ML, Zatsiorsky VM. Grip-force modulation in multi-finger prehension during wrist flexion and extension. Exp Brain Res. 2013;227(4):509–22. doi: 10.1007/s00221-013-3527-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bain GI, Watts AC. The outcome of scaphoid excision and four-corner arthrodesis for advanced carpal collapse at a minimum of ten years. J Hand Surg Am. 2010;35(5):719–25. doi: 10.1016/j.jhsa.2010.01.025. [DOI] [PubMed] [Google Scholar]
- Blankenhorn BD, Pfaeffle HJ, Tang P, Robertson D, Imbriglia J, Goitz RJ. Carpal kinematics after proximal row carpectomy. J Hand Surg Am. 2007;32(1):37–46. doi: 10.1016/j.jhsa.2006.10.014. [DOI] [PubMed] [Google Scholar]
- Brand PW, Hollister AM. Clinical mechanics of the hand. St. Louis, MO: Mosby, Inc; 1999. [Google Scholar]
- Buffi JH, Crisco JJ, Murray WM. A method for defining carpometacarpal joint kinematics from three-dimensional rotations of the metacarpal bones captured in vivo using computed tomography. J Biomech. 2013;46(12):2104–8. doi: 10.1016/j.jbiomech.2013.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crisco JJ, Coburn JC, Moore DC, Akelman E, Weiss AP, Wolfe SW. In vivo radiocarpal kinematics and the dart thrower's motion. J Bone Joint Surg Am. 2005;87(12):2729–40. doi: 10.2106/JBJS.D.03058. [DOI] [PubMed] [Google Scholar]
- Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. Opensim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007;54(11):1940–50. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- Delp SL, Loan JP. A graphics-based software system to develop and analyze models of musculoskeletal structures. Comput Biol Med. 1995;25(1):21–34. doi: 10.1016/0010-4825(95)98882-e. [DOI] [PubMed] [Google Scholar]
- Eschweiler J, Stromps JP, Fischer M, Schick F, Rath B, Pallua N, Radermacher K. A biomechanical model of the wrist joint for patient-specific model guided surgical therapy: Part 2. Proc Inst Mech Eng H. 2016;230(4):326–34. doi: 10.1177/0954411916635443. [DOI] [PubMed] [Google Scholar]
- Eschweiler J, Stromps JP, Fischer M, Schick F, Rath B, Pallua N, Radermacher K. Development of a biomechanical model of the wrist joint for patient-specific model guided surgical therapy planning: Part 1. Proc Inst Mech Eng H. 2016;230(4):310–25. doi: 10.1177/0954411916632791. [DOI] [PubMed] [Google Scholar]
- Esteki A, Mansour JM. A dynamic model of the hand with application in functional neuromuscular stimulation. Ann Biomed Eng. 1997;25(3):440–51. doi: 10.1007/BF02684185. [DOI] [PubMed] [Google Scholar]
- Goehler CM, Murray WM. The sensitivity of endpoint forces produced by the extrinsic muscles of the thumb to posture. J Biomech. 2010;43(8):1553–9. doi: 10.1016/j.jbiomech.2010.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hess F, Furnstahl P, Gallo LM, Schweizer A. 3d analysis of the proximal interphalangeal joint kinematics during flexion. Comput Math Methods Med. 2013;2013:138063. doi: 10.1155/2013/138063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollister A, Buford WL, Myers LM, Giurintano DJ, Novick A. The axes of rotation of the thumb carpometacarpal joint. J Orthop Res. 1992;10(3):454–60. doi: 10.1002/jor.1100100319. [DOI] [PubMed] [Google Scholar]
- Hollister A, Giurintano DJ, Buford WL, Myers LM, Novick A. The axes of rotation of the thumb interphalangeal and metacarpophalangeal joints. Clin Orthop Relat Res. 1995;320:188–93. [PubMed] [Google Scholar]
- Holzbaur KR, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Ann Biomed Eng. 2005;33(6):829–40. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
- Johnston JA, Bobich LR, Santello M. Coordination of intrinsic and extrinsic hand muscle activity as a function of wrist joint angle during two-digit grasping. Neurosci Lett. 2010;474(2):104–8. doi: 10.1016/j.neulet.2010.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SW, Kamper DG. Modeling of multiarticular muscles: Importance of inclusion of tendon-pulley interactions in the finger. IEEE Trans Biomed Eng. 2009;56(9):2253–62. doi: 10.1109/TBME.2009.2019119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millard M, Uchida T, Seth A, Delp SL. Flexing computational muscle: Modeling and simulation of musculotendon dynamics. J Biomech Eng. 2013;135(2):021005. doi: 10.1115/1.4023390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagelvoort RW, Kon M, Schuurman AH. Proximal row carpectomy: A worthwhile salvage procedure. Scand J Plast Reconstr Surg Hand Surg. 2002;36(5):289–99. doi: 10.1080/028443102320791842. [DOI] [PubMed] [Google Scholar]
- Neu CP, Crisco JJ, Wolfe SW. In vivo kinematic behavior of the radio-capitate joint during wrist flexion-extension and radio-ulnar deviation. J Biomech. 2001;34(11):1429–38. doi: 10.1016/s0021-9290(01)00117-8. [DOI] [PubMed] [Google Scholar]
- Nichols JA, Bednar MS, Havey RM, Murray WM. Wrist salvage procedures alter moment arms of the primary wrist muscles. Clin Biomech. 2015;30(5):424–430. doi: 10.1016/j.clinbiomech.2015.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols JA, Bednar MS, Murray WM. Orientations of wrist axes of rotation influence torque required to hold the hand against gravity: A simulation study of the nonimpaired and surgically salvaged wrist. J Biomech. 2013;46(1):192–196. doi: 10.1016/j.jbiomech.2012.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols JA, Bednar MS, Murray WM. Surgical simulations based on limited quantitative data: Understanding how musculoskeletal models can be used to predict moment arms and guide experimental design. PLOS One. 2016;11(6):e0157346. doi: 10.1371/journal.pone.0157346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols JA, Havey RM, Bednar MS, Murray WM. Decoupling the wrist: A cadaveric experiment examining wrist kinematics following midcarpal fusion and scaphoid excision J ApplBiomech. 2017;33(1):12–23. doi: 10.1123/jab.2015-0324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Driscoll SW, Horii E, Ness R, Cahalan TD, Richards RR, An KN. The relationship between wrist position, grasp size, and grip strength. J Hand Surg Am. 1992;17(1):169–77. doi: 10.1016/0363-5023(92)90136-d. [DOI] [PubMed] [Google Scholar]
- Richou J, Chuinard C, Moineau G, Hanouz N, Hu W, Le Nen D. Proximal row carpectomy: Long-term results. Chir Main. 2010;29(1):10–5. doi: 10.1016/j.main.2009.10.003. [DOI] [PubMed] [Google Scholar]
- Ruby LK, Cooney WP, 3rd, An KN, Linscheid RL, Chao EY. Relative motion of selected carpal bones: A kinematic analysis of the normal wrist. J Hand Surg Am. 1988;13(1):1–10. doi: 10.1016/0363-5023(88)90189-x. [DOI] [PubMed] [Google Scholar]
- Sancho-Bru JL, Perez-Gonzalez A, Vergara M, Giurintano DJ. A 3d biomechanical model of the hand for power grip. J BiomechEng. 2003;125(1):78–83. doi: 10.1115/1.1532791. [DOI] [PubMed] [Google Scholar]
- Saul KR, Hu X, Goehler CM, Vidt ME, Daly M, Velisar A, Murray WM. Benchmarking of dynamic simulation predictions in two software platforms using an upper limb musculoskeletal model. Comput Methods Biomech Biomed Engin. 2015;18(13):1445–58. doi: 10.1080/10255842.2014.916698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smaby N, Johanson ME, Baker B, Kenney DE, Murray WM, Hentz VR. Identification of key pinch forces required to complete functional tasks. J Rehabil Res Dev. 2004;41(2):215–24. doi: 10.1682/jrrd.2004.02.0215. [DOI] [PubMed] [Google Scholar]
- Thelen DG, Anderson FC. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. J Biomech. 2006;39(6):1107–15. doi: 10.1016/j.jbiomech.2005.02.010. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Johanson ME, Towles JD. Towards a realistic biomechanical model of the thumb: The choice of kinematic description may be more critical than the solution method or the variability/uncertainty of musculoskeletal parameters. J Biomech. 2003;36(7):1019–30. doi: 10.1016/s0021-9290(03)00061-7. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Zajac FE, Burgar CG. Large index-fingertip forces are produced by subject-independent patterns of muscle excitation. J Biomech. 1998;31(8):693–703. doi: 10.1016/s0021-9290(98)00082-7. [DOI] [PubMed] [Google Scholar]
- Wohlman SJ, Murray WM. Bridging the gap between cadaveric and in vivo experiments: A biomechanical model evaluating thumb-tip endpoint forces. J Biomech. 2013;46(5):1014–20. doi: 10.1016/j.jbiomech.2012.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolff AL, Garg R, Kraszewski AP, Hillstrom HJ, Hafer JF, Backus SI, Lenhoff ML, Wolfe SW. Surgical treatments for scapholunate advanced collapse wrist: Kinematics and functional performance. J Hand Surg Am. 2015 doi: 10.1016/j.jhsa.2015.04.035. [DOI] [PubMed] [Google Scholar]
- Wu JZ, An KN, Cutlip RG, Krajnak K, Welcome D, Dong RG. Analysis of musculoskeletal loading in an index finger during tapping. J Biomech. 2008;41(3):668–76. doi: 10.1016/j.jbiomech.2007.09.025. [DOI] [PubMed] [Google Scholar]


