Abstract
Brain Computer Interfaces (BCI) seek to infer some task symbol, a task relevant instruction, from brain symbols, classifiable physiological states. For example, in a motor imagery robot control task a user would indicate their choice from a dictionary of task symbols (rotate arm left, grasp, etc.) by selecting from a smaller dictionary of brain symbols (imagined left or right hand movements). We examine how a BCI infers a task symbol using selections of brain symbols. We offer a recursive Bayesian decision framework which incorporates context prior distributions (e.g. language model priors in spelling applications), accounts for varying brain symbol accuracy and is robust to single brain symbol query errors. This framework is paired with Maximum Mutual Information (MMI) coding which maximizes a generalization of ITR. Both are applicable to any discrete task and brain phenomena (e.g. P300, SSVEP, MI). To demonstrate the efficacy of our approach we perform SSVEP “Shuffle” Speller experiments and compare our recursive coding scheme with traditional decision tree methods including Huffman coding. MMI coding leverages the asymmetry of the classifier’s mistakes across a particular user’s SSVEP responses; in doing so it offers a 33% increase in letter accuracy though it is 13% slower in our experiment.
Index Terms: BCI, SSVEP Shuffle Speller, Decision Tree, Huffman Coding, Mutual Information, Discrete Memoryless Channel
I. Introduction
We suggest that there is much to be gained by considering a BCI in two distinct parts. In one, a BCI must correctly classify a brain symbol1. In another, a BCI must map an estimated brain symbol(s) to some task symbol (move wheelchair forward, type “A”, rotate robot arm clockwise, etc). In this work, we focus exclusively on the latter, the scheme which maps a sequence of brain symbols to a task symbol. We refer to this second function as the “coding scheme” of a BCI and begin with a brief review of existing solutions.
A. SSVEP
SSVEP, with its large dictionary of brain symbols, is well suited for a simple “one-to-one” coding scheme which assigns each task symbol its own unique brain symbol. For instance, QWERTY-style BCI keyboards exist where each character is assigned a unique SSVEP frequency [1]. Other keyboards vary the stimulation elements by using mixed frequency and phase flashing [2], arbitrary binary patterns [3], or quantized sinusoids [4]. Cao et al. offer a variation on the theme, a system which reserves two brain symbols to flip forward and backward through different one-to-one task symbol menus [5]. Many of these one-to-one systems show impressive performance by leveraging the large number of SSVEP brain symbols available. However, there is no guarantee that such a large quantity of brain symbols are available in all locked-in users and increasing the number of brain symbols may come with a penalty in classification accuracy [6].
Cursor control is an alternative coding scheme which assigns brain symbols to cursor directions [7], [8], [9]. In such a system, the user directs a cursor over a large, arbitrary menu of task symbols. Cursor systems often require fewer brain symbols than one-to-one coding schemes.
Decision trees, as exemplified in [10] or [11], also offer the ability to choose among a large dictionary of task symbols with few brain symbols. In this coding scheme, task symbols are partitioned among the brain symbols. With each round, the task symbols associated with the estimated brain symbol are re-partitioned while others are discarded. The process continues until a unique task symbol remains. Note that absent any backspace capability, any single brain symbol query error yields a task symbol decision error.
B. Motor Imagery
Hex-o-spell and its variants can be considered a combination cursor/decision tree coding scheme [12], [13]. Task symbols are visually partitioned into the six slices of a hexagon. The system then queries the user as to whether his or her selection is in the currently highlighted slice. The user responds using two state motor imagery and the process continues as a decision tree by zooming in on slices the user selects until a unique task symbol remains.
C. P300
P300 coding schemes, because of the necessarily temporal nature of P300 stimuli, must be more creative. Rapid serial visual presentation (RSVP) spellers show sequences of single task symbols and ask the user to generate the P300 signal when their target task symbol is present [14], [15]. Alternatively, P300 matrix spellers flash sets of characters and infer the user’s target character by identifying the intersection of all sets where the P300 is present [16]. Waal et al. apply this paradigm to tactile BCIs by mapping task symbol sets to fingers via tactile stimulators [17]. Carefully choosing the sets of flashing characters reduces the number of queries per decision [18]. Zhou et al. search for the optimal flashing pattern by maximizing an estimation of the system’s practical ITR [19]. Matrix spellers show promise when combined with generative brain symbol models, as in [20], which could potentially be used to construct coding schemes which optimize system performance according to a given criterion.
D. Combined Brain Symbols
Combining BCI modalities opens up new coding opportunities. Xu et al. develop a matrix speller that uses both P300 and SSVEP to find the intended character; brain symbols alternate between flickering and timed events in order to leverage both phenomena [21], [22]. Similarly, Yin et al. offer task symbol arrangements which leverage both P300 and SSVEP stimulation to uniquely identify the target task symbol [23], [24]. Li et al. combine modalities to add an idle state to a wheelchair control BCI [25].
E. Task Symbol Context
Task symbol context prior distributions can limit the load placed on user querying via BCI, as language models do for spelling applications [26]. Disregarding context can dramatically reduce efficiency. The speller design shown in Fig. 4 of [10] assigns about 70% of the task symbol probability to a single brain symbol by assigning the “first” few task symbols to a the first brain symbol. Such an initial query, on average, offers relatively weak evidence in making inferences about the target task symbols (see Sec IV-C for discussion). On the other hand, Volosyak et al use context to great effect in reorganizing the layout of characters in a cursor-based SSVEP speller BCI [27]. Hohne et al introduce a T9 predictive text system to an auditory BCI speller [28]. Word prediction is found to reduce the estimated typing time by half in a motor imagery speller [29]. Word level inference via graphical models is used to increases communication rates in [30]. Perhaps most famously, Wills and MacKay build Dasher [31], a two brain symbol speller in the spirit of Shayevitz’s Posterior Matching paradigm [32]. Dasher selections are made by moving a cursor up or down across a line whose length is divided according to the probability of the task symbol. There are many systems which use Huffman coding, which offers the fewest queries, on average, to uniquely resolve a task symbol [33], [34].
Fig. 4.
Sequential coding of a hypothetical motor imagery wheelchair BCI example. Each decision requires two queries.
F. BCI Channel Modelling
With a channel model a BCI designer can explicitly optimize characteristics of interest. Omar et al apply a binary symmetric model with noiseless feedback to a two-state motor imagery BCI [35]. By doing so they import well known feedback coding schemes and all the rigor and optimal performance which comes with them [32]. The binary symmetric channel is a step in the right direction for motor imagery though it leaves much to be desired in the context of P300 or SSVEP as there are no garauntees that brain symbols are confused symmetrically2.
G. Our Contribution
In this work, we build a decision framework that takes both task symbol context and the varying accuracy of inferring a user’s brain symbols into account. Given discrete task symbols, we model the BCI as a memoryless channel. By memoryless we mean that the previous query’s brain symbol inference has no impact on the current query’s brain symbol inference. (See Appendix A for how P300 can be considered memoryless). With this assumption, we offer a Bayesian update rule that integrates query evidence into a task decision framework (Sec III). We examine various coding schemes on the framework, including decision trees and Huffman codes similar to those described above, as well as our own recursive codes (Sec IV) that are robust to single query errors. Finally, in Sec VI, we present results from 10 users who used each coding scheme in an SSVEP speller paradigm (see Fig. 1 for overview).
Fig. 1.

The SSVEP Shuffle Speller associates a letter (task symbol) with a particular SSVEP response (brain symbol) by placing it near the LED array which stimulates that response. The square and less-than characters represent space and backspace respectively. See Section VI-A or https://www.youtube.com/watch?v=JNFYSeIIOrw for further detail.
II. Terminology and Notation
We use the term brain symbol to refer to a classifiable physiological state. For example, right hand imagined movement, P300 present, or the response to a flickering 10Hz LED are brain symbols of motor imagery, P300, and SSVEP respectively. We denote the brain symbol as random variable X which takes a value . A task symbol is an application specific decision. For example, a letter is a spelling task symbol while “drive left” is a wheelchair control task symbol. We denote the task symbol as random variable M which takes a value with known context prior PM(m).
We reserve the term query to refer to a classification on X, the set of brain symbols. We reserve the term decision to refer to a classification on M, the set of task symbols. Finally, we use the term sequence to refer to the set of queries required to make a single decision.
BCI channel has a slightly unconventional meaning here, referring to a mapping from ground truth brain symbols to their estimates. A BCI channel can be considered to be the concatenation of a user’s physiological response function with a classifier and all of its parameters. By fixing a particular user-classifier pair, we can quantify the BCI channel’s performance as the distribution . Intuitively, this distribution describes how often the classifier confuses one brain signal with another. This conditional distribution is referred to as the confusion matrix.
III. Decision Framework
We seek a decision framework that:
Performs inference over a task symbol set which is much larger than the brain symbol set (NM > NX)
Leverages context prior distributions over a task symbol set (PM)
Leverages the varying accuracy of brain symbols (i.e. the confusion matrix ) for inference on task symbols
Offers a principled mechanism to decide on a task symbol which is robust to single classification errors
We propose the framework depicted in Fig. 2. It assumes knowledge of the confusion matrix, which can be estimated by normalizing a count of how often brain symbols are confused for one another in a given training set.
Fig. 2.
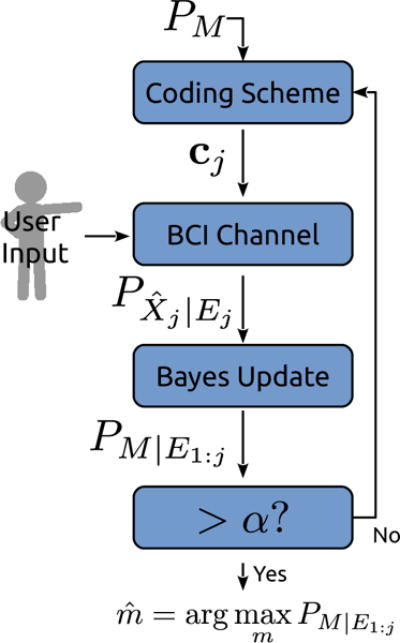
BCI Decision Framework.
In usage, an encoding vector cj assigns each task symbol a brain symbol:
| (1) |
where j is the query index and each is the brain symbol associated with task mi during query j. Note that cj will often map multiple task symbols to a single brain symbol. The user attempts to produce the brain symbol associated with their target task symbol. Evidence, ej, is collected and classified by the BCI to produce , a distribution3 over the estimated brain symbol. A Bayesian update which incorporates this latest query evidence yields If confidence threshold α is exceeded a decision is made, otherwise another query is performed by incrementing j. Evidence is aggregated such that each query’s posterior is the next query’s prior. The recursive Bayesian update is given as:
| (2) |
where E1:j−1 is all previous evidence, is the classifier’s estimate of the intended brain symbol in the most recent query and
| (3) |
which expresses the system’s belief in each task symbol before the current query’s evidence is incorporated. A derivation is given in Appendix B.
While this framework meets all four requirements listed above, its speed and accuracy are highly dependent on the particular coding scheme used to generate c from the latest distribution over M. We describe different coding schemes in the following section.
IV. Coding Methods
The first two coding schemes, Sequential and Huffman, are decision tree style methods which successively “zoom-in” on a particular task symbol after many queries. Decision tree methods do not use the recursive nature of the decision framework given in Fig. 2 and are included for comparison. Instead, they make a decision when only one viable task symbol remains. Later on, we propose Uniform or Maximum Mutual Info (MMI) coding, which query until a sufficiently high confidence is reached.
A. Sequential Coding
Sequential codes perform as many queries as would be needed to uniquely resolve all task symbols in an error free BCI system. Task symbols are assigned to codewords (sequences of brain symbols) arbitrarily, often associating the task symbols to codewords by their index. Specifically, a sequential codebook is built by counting in base NX, the most significant digit of each number is used for the first query (see Fig. 3).
Fig. 3.
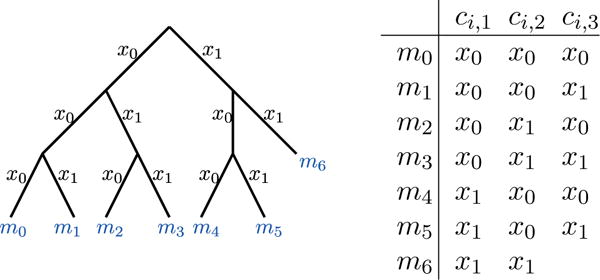
Sequential coding tree (NX = 2,NM = 7) and corresponding codebook. ci,j denotes the brain symbols assigned to task symbol mi in query j of a decision sequence.
There is much room for improvement from sequential decision trees. Notice that in the example of Fig. 3 m6 requires only two queries to make a decision while the rest require three. To capitalize on this benefit, we should re-index task symbols to ensure that m6 is the most probable based on contextual information. Sequential coding offers no guarantee that we are assigning faster codewords, those which require fewer quieries, to more frequent task symbols.
B. Huffman Coding
Huffman codes minimize how many queries it takes, on average, to resolve a particular task symbol:
| (4) |
where we use L(m) to denote the number of queries it takes to resolve a particular task message (“L” for codeword length). For example, in Fig. 3 L(m1) = 3 while L(m6) = 2. We demonstrate Huffman coding by way of example, for a rigorous treatment see [37].
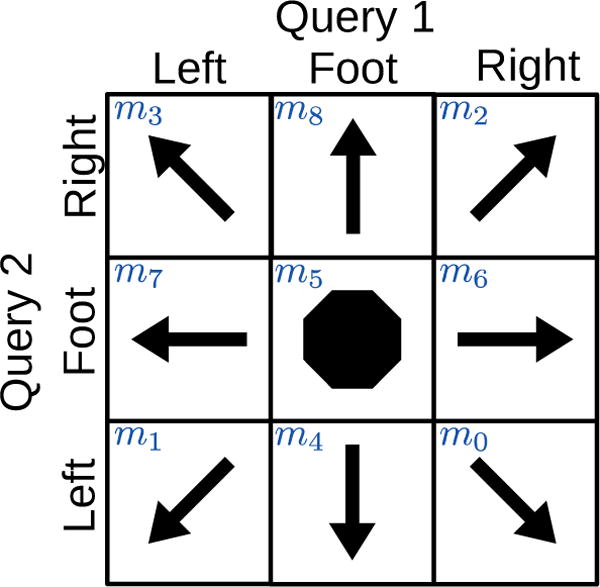
Let us examine the task of driving a wheelchair with NM = 9 different task symbols using NX = 3 brain symbols (motor imagery left, right, and foot). Fig. 4 shows a (re-indexed) sequential code for this task. We might expect the user to drive forward (m8) more often than reverse-right (m0). Huffman codes leverage such context prior information to minimize the average number of queries per decision. In this toy example the Huffman code given by Fig. 5 minimizes the expected number of queries per decision to 1.53, a significant speedup from the 2 given by sequential coding.
Fig. 5.
Huffman coding tree (NX = 3, NM = 9) and corresponding codebook for the example of Fig. 4. This code offers an average of 1.53 queries per decision.
Any decision tree method, including both Sequential and Huffman coding, suffer from the fact that an error in a single query forces a wrong decision and removes the user’s target task symbol for the remainder of the sequence. For example, in the code given by Fig. 5, if the target task symbol is m7 but the user incorrectly chooses x0 in the first query there is no way to “go back up” the tree; they must continue to traverse downwards towards a set of non-target task symbols. We call these queries where the target is not present “impossible’.
C. Uniform Coding
We remind the reader that the following two proposed coding schemes are recurisve in that they perform queries until a sufficiently high confidence is reached to make a decision. Because of this there are no “impossible” queries as no task symbol is ever precluded until a decision is made. Additionally, “codewords” of recursive methods are all one brain symbol long and need not be unique.
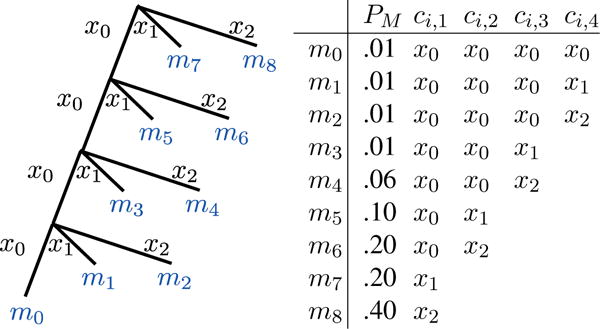
To motivate Uniform Coding, let us first imagine designing the worst possible code, assigning all task symbols to a single brain symbol. Under any classification evidence supplied, the Bayesian update, (2) and (3), will not shift the posterior away from the prior distribution. Fortunately, the opposite of this worst-case scenario code offers strong performance. Uniform coding seeks to spread task symbols among brain symbols such that the brain symbol probability distribution is as uniform as possible.
Extending the motor imagery wheelchair example used in Sec IV-B to Uniform Codes yields Fig. 6. Note that m8 is so privileged by its probability mass that it earns its own unique brain symbol. on the other hand, m0,…,m5 are so rare that Uniform Coding is willing to accept that if the set is selected, , we still cannot distinguish from among them.
Fig. 6.
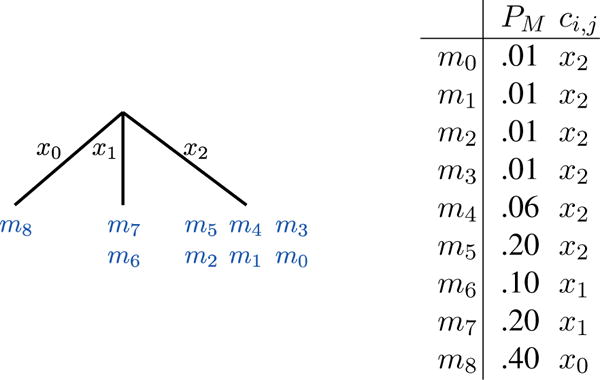
Uniform Coding “tree” (NX = 3, NM = 9). Both MMI and Uniform Coding build a “tree” before each query according to the latest .
More formally, we choose cuni as
| (5) |
where
| (6) |
On first sight, one might suspect that uniform codes struggle to decide in favor of uncommon task symbols. However, as a sequence progresses a target task symbol increases its probability through query evidence updating, eventually earning its own unique brain symbol. Further, because every task symbol is shown in every query, Uniform codes, like MMI codes below, never frustrate the user with “impossible” queries. Despite these advantages, Uniform codes still leave room for improvement.
Consider the confusion matrix for a hypothetical motor imagery BCI in Table I. Uniform codes entrust each brain symbol with as equal probability mass as possible even though a “foot” classification is weaker evidence. In line with this example, real user-classifier pairs offer no guarantee of identical accuracies and uniform errors across brain symbols. The final coding scheme, MMI, explicitly leverages the relative accuracies of brain symbols in encoding task symbols.
TABLE I.
An example confusion matrix which contains accurate (Left and Right) and inaccurate (Foot) brain symbols. The classifier is often inaccurate when the user is trying to generate the Foot response. Uniform codes do not leverage the relative accuracy of inferring brain symbols while MMI Codes do.
| Target X | |||||
|---|---|---|---|---|---|
|
|
Left | Right | Foot | ||
| Estimat | Left | .95 | .025 | .33 | |
| Right | .025 | .95 | .33 | ||
| Foot | .025 | .025 | .33 | ||
D. Maximum Mutual Information (MMI) Coding
The ideal query would shift our current knowledge of the task symbol, , from its previous form as much as possible. In this sense, the ideal query ought to maximize our expectation of this shift, as quantified by the Kullback Leibler divergance. Again, to simplify notation, we drop the query indexing variable j:
| (7) |
where I is the mutual information function, H is the entropy function and the last equality comes from the fact that H(M) does not depend on c. From the final equality we see our objective has another intuitive motivation; MMI codes minimize the uncertainty in task symbol M after being given brain symbol estimate . Further:
| (8) |
where we have applied (3) in the last equality.
Alternatively, this objective can be motivated as a particular extension of the Information Transfer Rate (ITR). ITR measures the rate of information common to both the target brain symbol X and estimated brain symbol (see Sec V). This common information represents how confidently the BCI estimates the user’s target brain symbol X. Of course, in and of itself, determining a user’s intended brain symbol is only of academic interest; we ultimately seek to determine which task symbol M the user wishes to select. With this in mind, it is natural to think that the mutual information between task symbol M and estimated brain symbol is a closely related objective.
Using the most accurate brain symbols offers strong evidence in making a task symbol decision. Of course, it is not wise to assign all task symbols to the most accurate brain symbol; a system would struggle to distinguish among task symbols. MMI codes balance these effects. Empirically, we observe that the final query of most MMI sequences uniquely assigns the most probable task symbol with the strongest brain symbol; such a configuration offers the strongest evidence for (or against) the selection of this task symbol.
If a particular confusion matrix is symmetric, it can be seen (See Theorem 7.2.1 [37]) that the distribution PX which maximizes the mutual information is uniform. In particular, symmetric confusion matrices imply equivalence between Uniform and MMI codes. As we will see in Sec VI, MMI codes gain a performance advantage over Uniform codes only for confusion matrices which are far from symmetric.
V. Performance Metrics
We evaluate the performance of our classifiers using ITR:
| (9) |
where is the mutual information between the target and estimate of the brain symbol and T is the stimulation time. This version of ITR is consistent with the common definition:
| (10) |
where p is the accuracy of all brain symbols though it doesn’t assume that all brain symbols are equally accurate or that PX is uniform. Throughout this work we use “ITR” and “ITR* ” to mean the quantities given by (9) and (10) respectively.
The difference can be significant, as it is in Table III. ITR* is often lower than ITR because mistakes under a symmetric channel are uniformly distributed among all brain symbols, offering the weakest evidence (see noisy typewriter example in [37]). For further details on both definitions of ITR see [38], [39], [40], [41], [42].
TABLE III.
Performance of SSVEP classifier per user coding scheme pair. Acci denotes the accuracy of the ith brain symbol, . All ITRs reported in bits/min, see Sec V for ITR detail. AccM denotes the average letter decision accuracy across all copy phrase tasks of a particular user and coding scheme. The ‘Sim’ row is not counted in the ‘Mean’ row, see Sec VI-C for detail.
| User | E[AccX ] | ITR | ITR* | Acc1 | Acc2 | Acc3 | Acc4 | Acc5 | Acc6 | Sequential Code | Huffman Code | Uniform Code | Max M-Info Code | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AccM |
|
AccM |
|
AccM |
|
AccM |
|
||||||||||
| 1 | 0.88 | 25 | 16 | 0.85 | 1.00 | 0.75 | 0.90 | 0.95 | 0.80 | 0.49 | 2.0 | 0.57 | 2.1 | 1.00 | 1.8 | 1.00 | 1.5 |
| 2 | 0.82 | 22 | 14 | 0.95 | 0.85 | 0.60 | 0.70 | 0.85 | 0.95 | 0.82 | 2.0 | 0.76 | 1.7 | 1.00 | 1.8 | 1.00 | 1.9 |
| 3 | 0.94 | 30 | 20 | 0.90 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.62 | 2.0 | 0.73 | 1.7 | 1.00 | 1.7 | 0.83 | 1.9 |
| 4 | 0.91 | 26 | 18 | 0.85 | 0.95 | 0.80 | 0.90 | 0.95 | 1.00 | 0.90 | 2.0 | 0.83 | 1.5 | 0.95 | 1.6 | 0.90 | 1.5 |
| 5 | 0.75 | 17 | 11 | 0.80 | 0.65 | 0.75 | 0.65 | 0.85 | 0.80 | 0.46 | 2.0 | 0.57 | 1.8 | 1.00 | 2.3 | 1.00 | 3.2 |
| 6 | 0.66 | 18 | 8 | 0.95 | 0.90 | 0.60 | 0.55 | 0.65 | 0.30 | 0.30 | 2.0 | 0.16 | 1.8 | 1.00 | 4.2 | 1.00 | 3.2 |
| 7 | 0.88 | 24 | 16 | 0.90 | 1.00 | 0.80 | 0.85 | 0.85 | 0.85 | 0.58 | 2.0 | 0.72 | 1.9 | 0.89 | 1.9 | 1.00 | 1.6 |
| 8 | 0.90 | 25 | 17 | 0.95 | 0.95 | 0.90 | 0.90 | 0.95 | 0.75 | 0.51 | 2.0 | 0.60 | 1.8 | 1.00 | 2.8 | 0.95 | 1.9 |
| 9 | 0.89 | 25 | 17 | 0.85 | 0.85 | 0.85 | 0.90 | 0.95 | 0.95 | 0.25 | 2.0 | 0.24 | 1.7 | 0.95 | 4.3 | 0.79 | 1.8 |
| 10 | 0.91 | 27 | 18 | 1.00 | 1.00 | 1.00 | 0.85 | 0.85 | 0.75 | 0.74 | 2.0 | 0.91 | 1.7 | 1.00 | 1.6 | 0.96 | 1.5 |
| Mean | 0.85 | 23.8 | 15.5 | 0.90 | 0.91 | 0.80 | 0.82 | 0.88 | 0.81 | 0.57 | 2.0 | 0.61 | 1.77 | 0.98 | 2.4 | 0.94 | 2.0 |
| Sim | 0.65 | 12.6 | 10.9 | 0.90 | 0.80 | 0.70 | 0.60 | 0.50 | 0.40 | 0.783 | 2.00 | 0.684 | 1.845 | 0.984 | 4.66 | 0.991 | 3.59 |
VI. Experiment
We aim to validate the efficacy of our recursive Bayesian decision framework (Fig. 2) using MMI coding against other methods. To do so, we perform online experiments using different coding schemes in an SSVEP speller paradigm.
A. SSVEP Shuffle Speller
SSVEP Shuffle Speller associates task and brain symbols by placing them near each other (see Fig. 1). Users are instructed to gaze at the LED nearest their target letter. We have named it the “Shuffle” speller because after each query the letters are shuffled around the monitor, moving to the box associated with their next brain symbol4. This animation was created in an attempt to make it as easy as possible for a user to track their letter. We are wary of the potential difficulties the shuffling may have in locked in users. As a preliminary exploration, users were given a user experience survey (Appendix ??) upon completion of the experiment. Despite these positive results, we still have many reservations about the eye gaze requirements of the shuffle speller. We use it here only as a test bed for our different coding schemes.
We have chosen SSVEP as it offers a large dictionary of classifiable brain symbols to demonstrate coding schemes, but we remind the reader that the particular choice of BCI modality (SSVEP, MI, or P300), classifier, and even user performance are encapsulated in the confusion matrix . One could imagine building a Motor Imagery “Shuffle” Speller that associates each set of characters in Fig. 1 with an imagined body movement. See Appendix A for a P300 example.
B. Setup
Ten neurotypical people volunteered for experiments. The volunteers included 6 men and 4 women ages 24–34, all with normal or corrected to normal vision. Each user gave written informed consent according to Northeastern’s IRB protocol and was paid for their participation.
LEDs stimulated at 6 equally spaced frequencies in the alpha range:
| (11) |
and were classified using the CCA-KDE method described in Appendix C. All queries were 5 seconds long and the training session consisted of 20 ground truth queries for each target frequency in (11).
We compute the Uniform code by noting that its objective is identical to the “Partition Problem”, whose solution we approximate using a well known greedy algorithm [43]. Specifically, we assign the task symbols in order of decreasing probability, mapping each to the brain symbol which currently has the lowest probability (6).
As we do not have a closed form solution of (7) for MMI codes, computation was done via a gradient ascent hill climbing algorithm (see [44]). In particular, we start with a random c and iterate over the task symbols. For each m, we choose for it the brain symbol x which optimizes (7) and stop our iteration when a local maximum is reached. We do this for 20 random c initializations and choose the maximum of these local optima as our MMI code approximation.
The experiment consists of 5 copy phrase tasks. In each task, the user was asked to spell a sequence of characters from a particular word. The copy phrase tasks were selected for a varying range of difficulty (see Table II). Character probabilities were determined using an n-gram language model trained on a one million sentence New York Times corpus (see [45] Section 3 for full details). Character probabilities were computed under the assumption that all previously typed characters were correct, and were normalized to allow for a backspace probability fixed at 5%.
TABLE II.
Copy Phrase Tasks. denotes the context prior given for the ith target character under the assumption that all previous characters were selected correctly with certainty.
| Idx | Context | Target |
|
|
|
|
|
|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | <none> | SPEAR | 0.07 | 0.03 | 0.28 | 0.32 | 0.04 | |||||
| 2 | He could not stand | THE | 0.67 | 0.73 | 0.69 | |||||||
| 3 | It went a | MILE | 0.07 | 0.18 | 0.20 | 0.30 | ||||||
| 4 | Tropical | HUTS | 0.01 | 0.06 | 0.02 | 0.01 | ||||||
| 5 | Go to college | FOR | 0.51 | 0.91 | 0.89 |
A probability threshold of α = .85 was used to make decisions in the recursive codes; no threshold was used in decision tree codes. Decision tree codes made decisions at the end of each tree branch as the maximum a posteriori task symbol.
C. Simulation
Remember that MMI coding is only advantageous over Uniform when the confusion matrix is far from symmetric (see last paragraph of Sec IV-D). To explicitly examine this case we define confusion matrix:
| (12) |
Which is equivalent to a user who has an accuracy of {.9, .8, .7, .6, .5, .4} across different stimuli (11); mistakes are uniformly distributed among remaining stimuli. Note that no real SSVEP data was used in this simulation. Instead, we generate a Monte Carlo “SSVEP classification” by assigning a 90% belief to X = xi where xi is drawn according to and xj is fixed by a particular code vector (1). Remaining probability mass is distributed uniformly in We perform 100 Monte Carlo decision sequences for each coding scheme and target character pair where target character prior probabilities are given in Table II. Results are shown in the last row of Table III.
VII. Results
As can be seen in Fig. 7, decision tree style codes (Sequential and Huffman) were much less accurate and slightly faster than recursive codes (Uniform and MMI). This makes intuitive sense as no threshold need be met in a decision tree style decision. As expected, Huffman codes were slightly faster than sequential codes (see Sec IV-B) as they leveraged the context prior to minimize the number of queries per decision. Remember that we call a query “impossible” if the user’s target character is not present for selection. Across all users, 14% of Sequential Code queries were impossible while only 4% of Huffman queries were impossible. Uniform and MMI coding do not produce impossible queries.
Fig. 7.
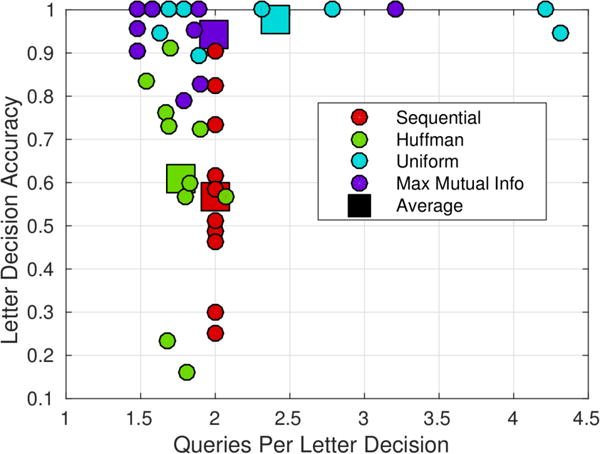
Letter decision accuracy and speed (queries per letter decision). Each circle is a user-coding scheme pair averaged across all queries of all decisions of all copy phrase tasks.
Among the recursive codes, MMI codes offer an increase in speed at a small cost in accuracy over Uniform codes. Remember that MMI codes consider the accuracy of brain symbol classication in assigning task symbols to brain symbols. The difference between these codes is slight due to the fact that the confusion matrices of many users were close to symmetric (see Table III for accuracies of each brain symbol). Remember that for symmetric confusion matrices a uniform distribution over PX, (6), optimizes both the Uniform and MMI objectives. This explanation is further supported by the fact that the simulation (See Sec VI-C), built to have a non symmetric confusion matrix, had a significant boost in speed using MMI codes against Uniform codes (see Table III). Because MMI coding avoids less accurate brain symbols, it earns more confident classifier outputs (Fig. 8). Because MMI coding is a generalization of Uniform coding, we suggest using MMI coding and tuning the decision threshold α to achieve a given accuracy.
Fig. 8.
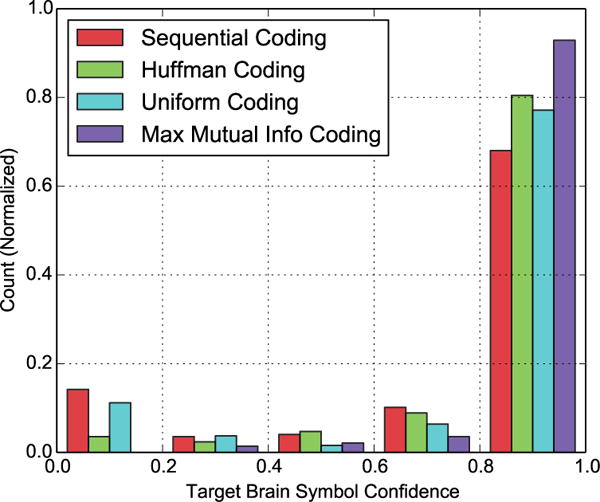
A histogram of Target Brain Symbol Confidence (i.e. classifier output) across coding schemes. Max Mutual Info coding keeps the user-classifier pair in its comfort zone by avoiding less accurate brain symbols. As a result, it produces more confident brain symbol classifications.
Empirically, recursive codes spent fewer queries on decisions which initially had a higher probability from the language model (see Fig. 9). Intuitively, characters which had a higher initial probability required fewer queries to raise their probability beyond the threshold.
Fig. 9.
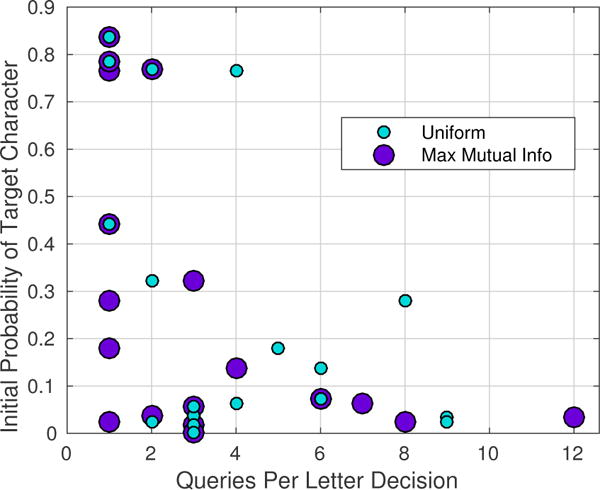
Speed (queries per letter decision) vs initial probability of target character. Each circle represents a decision sequence of User 6. Note that recursive codes efficiently spend more queries on more challenging target characters (those with lower probability).
In summary, decision tree methods were quick but relatively inaccurate. Both uniform and MMI codes have high accuracy as they perform queries until a sufficiently high confidence is reached; though MMI also leverages the varying accuracy of the different brain symbols to decide more quickly. This is most notable in the case of the simulated user whose accuracy was constructed to vary the most across brain symbols.
VIII. Conclusion
We have presented a Bayesian decision framework which:
Performs inference over a task symbol set which is much larger than the brain symbol set (NM > NX)
Leverages a context prior distribution over a task symbol set (PM)
Leverages the varying accuracy of brain symbols (i.e. the confusion matrix ) for inference on task symbols
Offers a principled mechanism to decide on a task symbol which is robust to single query errors
This framework employs a coding scheme which maps task symbols to brain symbols by leveraging the latest distribution over task symbols. We offer recursive codes which perform queries until a decision confidence is reached; this property makes them robust to single query error. MMI codes, in particular, offer a strong trade-off point between decision accuracy and queries per decision (Fig. 7). MMI codes achieve their competitive advantage by leveraging both the context prior of task symbols as well as the confusion between brain symbols inherent to a particular user-classifier pair.
We would like to highlight that (2) and (3) are applicable to all circumstances which have some training set for a user-classifier pair. Incorporating these Bayesian updates will appropriately consider brain symbol confusion in the user or classifier. This can offer some measure confidence in decisions even if the classifier itself offers only point estimates.
Acknowledgments
We would like to thank Umut Orhan of Honeywell whose insights and criticisms were extremely formative in converging on the final MMI coding scheme. Additionally, thanks to Betts Peters of Oregon Health and Science University for her thorough revisions.
This work was supported by NSF (CNS-1136027, IIS-1149570), NIH (R01DC009834), NIDRR (H133E140026).
Biographies

Matt Higger will receive a PhD in Electrical and Computer Engineering from Northeastern University in 2016. His research interests include information theory, signal processing and machine learning. Like many BCI researchers, he hopes his work has a positive impact on people.

Fernando Quivira received the BS degree in Electrical and Computer Engineering from Northeastern University. Since then, he has been with the Cognitive Systems Laboratory (CSL) at Northeastern University where he is currently a PhD candidate. His main areas of research interest are statistical signal processing and machine learning.

Murat Akcakaya received Ph.D. in Electrical Engineering from Washington University in St. Louis, MO, in December 2010. He is an Assistant Professor in the Electrical and Computer Engineering Department of the University of Pittsburgh. His research interests are in the areas of statistical signal processing and machine learning.

Mohammad Moghadamfalahi (S’14) received the B.Sc. degree in electrical engineering from Amirkabir University, Tehran, Iran, 2008. Since 2012, he has been working as a Ph.D. student in Cognitive System Laboratory (CSL), at ECE Department of Northeastern University, Boston, MA, USA, on BCIs, machine learning, and statistical signal processing.

Hooman Nezamfar has a B.S. degree in electrical engineering, and an M.S. degree in communication systems. He is currently a Ph.D. candidate and a member of Cognitive Systems Laboratory (CSL) at Northeastern University. His research includes BCIs, probabilistic modelling, and embedded systems.

Mujdat Cetin received the Ph.D. degree from Boston University, worked at MIT, and is now a faculty member at Sabanci University. Dr. Cetins research interests lie within the field of statistical signal processing, and include computational imaging, sparse signal and image representation, brain-computer interfaces, biomedical image analysis, and image segmentation.

Deniz Erdogmus received BS in EE and Mathematics (1997), and MS in EE (1999) from the Middle East Technical University, PhD in ECE (2002) from the University of Florida, where he was a postdoc until 2004. He is currently a research professor at Northeastern University ECE. His research focuses on statistical signal processing and machine learning with applications to biomedical signal/image processing and cyberhuman systems.
APPENDIX A Appendix: P300 as a Memoryless Channel
Readers who are familiar with the P300 ought to object strongly to modeling P300 generation as a memoryless channel; by its very nature the P300 is dependent on the task symbols shown beforehand! We suggest a slight abstraction to remedy this. Let us redefine a P300 query as the selection of one time bin from a set of time bins where a user may have generated a unique P300 signal. In this sense, our redefined “brain symbol” corresponds to the time bin where the P300 is present. In this way, the confusion matrix expresses confusion of P300 targets in time. In particular, it may be the case that errors are more prevalent in time bins immediately before or after the target time bin. Additionally, it may also be the case that the P300 is easier or more difficult at the start or end of a query. MMI codes would explicitly mitigate these effects.
Appendix B Appendix: recursive Bayesian Update
We remind the reader that we use PM to express the naive prior distribution over task symbols (ie language model). The remaining expressions in this section are valid when conditioned on E1:j−1 though we drop this conditioning to simplify notation. Dropping the conditioning in this manner is equivalent to computing before the evidence of the first query has been received.
| (13) |
where the second equality comes from the fact that given X, is independent of M and the third equality uses a Kronecker delta to express the fact that PX|M(x|m) = 1 if cm = x and is 0 otherwise. Further, we compute:
| (14) |
where the last equality is a result of (13). Finally:
| (15) |
which applies Bayes rule in the first equality and (13) and (14) in the second.
Appendix C Appendix: SSVEP Classifier (CCA-KDE)
We use CCA-KDE ([41]) because it produces a principled estimate of the posterior distribution of our target brain symbol which is helpful, though not necessary, in the framework of Fig. 2.
A. Canonical Correlation Analysis (CCA)
Lin et al. [46] introduce CCA, a dimensionality reduction method which captures the correlation between multiple electrodes of EEG signal and multiple harmonics of each target frequency. In particular, for each fi ∈ F a template is built:
| (16) |
for t = where H is the number of harmonics considered, fs is the sampling frequency and T is the query length in seconds. CCA maximizes Pearson’s correlation coefficient between a linear combination of electrodes of EEG data as well as an additional linear combination over the template signals in Yi (see [47]).
We collect a feature vector of maximal Pearson’s coefficients to each template as:
| (17) |
where ρi is the maximum correlation coefficient to the ith template. In most CCA methods, the estimate is chosen as the maximal correlation coefficient. CCA is still an exciting and active area of development within the BCI community [48], [49], [50], [51], [52].
B. Kernel Density Estimation (KDE)
CCA-KDE explicitly estimates the distribution of the CCA coefficients eCCA on its true stimulation frequency x. In particular, it uses training data of N stimulation queries and approximates Pe|X as a mixture:
| (18) |
where Nj is the number of samples from class x and K(·|,Σ) is a Gaussian kernel. The covariance matrix is chosen according to Silverman’s rule [53]. Please see [54] for a thorough treatment of KDE.
Footnotes
A complete package containing code and data for this paper is available at: https://repository.library.northeastern.edu/collections/neu:rx9149848
We use the term brain symbol to refer to a classifiable physiological state. For example, right hand imagined movement, P300 present, or the response to a flickering 10Hz LED are brain symbols of motor imagery, P300, and SSVEP respectively.
Since our paper was submitted for review, similar to our approach, another paper which describes an adaptive query strategy for a discrete memoryless channel has been published [36]. However, there is an important fundamental difference between the approaches of these two papers: unlike the above mentioned published work, our optimization searches over all possible code vectors (1) without requiring our task or brain symbols to be in any particular order. Furthermore, this work compares multiple different encodings of task symbols as brain symbols.
We assume that the classification scheme outputs a distribution , rather than a point estimate . In the event that the classifier only provides a point estimate, it can be assumed that the decision is made with certainty. The Bayesian update (2), by itself, appropriately introduces uncertainty into the decision.
An altenative to animated shuffling could be to assign color codes to brain symbols and in a static matrix of letters, change the coloring of letters without moving them. The tuning of visual aspects to suit human factors is outside the scope of this work
References
- 1.Hwang H-j, Lim J-h, Jung Y-j, Choi H, Woo S, Im C-h. Development of an SSVEP-based BCI spelling system adopting a QWERTY-style LED keyboard. Journal of Neuroscience Methods. 2012;208(1):59–65. doi: 10.1016/j.jneumeth.2012.04.011. [DOI] [PubMed] [Google Scholar]
- 2.Nakanishi M, Wang Y, Wang Y-T, Mitsurkura Y, Jung T-P. A high speed brain speller using steady state visual evoked potentials. Int J Neur Syst. 2014 Sep;24(06):1450019. doi: 10.1142/S0129065714500191. [DOI] [PubMed] [Google Scholar]
- 3.Rosenstiel W, Bogdan M, Spu M. Online Adaptation of a c-VEP Brain-Computer Interface (BCI) Based on Error-Related Potentials and Unsupervised Learning. PloS one. 2012;7(12) doi: 10.1371/journal.pone.0051077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chen X, Chen Z, Gao S, Gao X. A high-ITR SSVEP-based BCI speller. Brain-Computer Interfaces. 2014 Sep;Sep;:1–11. [Google Scholar]
- 5.Cao T, Wang X, Wang B, Wong CM, Wan F, Mak PU, Mak P-i, Vai MI. A High Rate Online SSVEP Based Brain-Computer Interface Speller. IEEE EMBS Conference on Neural Engineering. 2011:465–468. [Google Scholar]
- 6.Nicolas-Alonso LF, Gomez-Gil J. Brain computer interfaces, a review. Sensors. 2012;12(2):1211–1279. doi: 10.3390/s120201211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Allison BZ, Brunner C, Altstatter C, Wagner IC, Grissmann S, Neuper C. A hybrid ERD/SSVEP BCI for continuous simultaneous two dimensional cursor control. Journal of Neuroscience Methods. 2012 Aug;209(2):299–307. doi: 10.1016/j.jneumeth.2012.06.022. [DOI] [PubMed] [Google Scholar]
- 8.Volosyak I. SSVEP-based Bremen-BCI interface-boosting information transfer rates. Journal of Neural Engineering. 2011 Jun;8(3):036020. doi: 10.1088/1741-2560/8/3/036020. [DOI] [PubMed] [Google Scholar]
- 9.Bacher D, Jarosiewicz B, Masse NY, Stavisky SD, Simeral JD, Newell K, Oakley EM, Cash SS, Friehs G, Hochberg LR. Neural point-and-click communication by a person with incomplete locked-in syndrome. Neurorehabilitation and Neural Repair. 2014 Nov;29(5):462–471. doi: 10.1177/1545968314554624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Combaz A, Chatelle C, Robben A, Vanhoof G, Goeleven A, Thijs V, Van Hulle MM, Laureys S. A comparison of two spelling Brain-Computer Interfaces based on visual P3 and SSVEP in Locked-In Syndrome. PloS one. 2013 Jan;8(9):e73691. doi: 10.1371/journal.pone.0073691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cecotti H. A Self-Paced and Calibration-Less SSVEP-Based Brain Computer Interface Speller. IEEE transactions on neural systems and rehabilitation engineering. 2010;18(2):127–133. doi: 10.1109/TNSRE.2009.2039594. [DOI] [PubMed] [Google Scholar]
- 12.Blankertz B, Dornhege G, Krauledat M, Schroeder M, Williamson J, Murray-Smith R, Muller K-R. The Berlin Brain-Computer Interface presents the novel mental typewriter Hex-o-Spell. 3rd International BrainComputer Interface Workshop and Training Course. 2006:2–3. [Google Scholar]
- 13.Treder M, Schmidt N, Blankertz B. Gaze-independent braincomputer interfaces based on covert attention and feature attention. Journal of neural engineering. 2011 Dec;8(6) doi: 10.1088/1741-2560/8/6/066003. [DOI] [PubMed] [Google Scholar]
- 14.Acqualagna L, Blankertz B. Gaze-independent BCI-spelling using rapid serial visual presentation (RSVP) Clinical Neurophysiology. 2013 May;124(5):901–8. doi: 10.1016/j.clinph.2012.12.050. [DOI] [PubMed] [Google Scholar]
- 15.Orhan U. RSVP keyboard: an EEG based BCI typing system with context information fusion. Electrical Engineering Dissertations. 2014;85 [Google Scholar]
- 16.Farwell La, Donchin E. Talking off the top of your head: toward a mental prosthesis utilizing event-related brain potentials. Electroencephalography and clinical neurophysiology. 1988;70:510–523. doi: 10.1016/0013-4694(88)90149-6. [DOI] [PubMed] [Google Scholar]
- 17.Waal MVD, Severens M, Geuze J. Introducing the tactile speller : an ERP-based brain computer interface for communication. Journal of Neural Engineering. 2012;045002 doi: 10.1088/1741-2560/9/4/045002. [DOI] [PubMed] [Google Scholar]
- 18.Polprasert C, Kukieattikool P, Demeechai T, Ritcey Ja, Siwamogsatham S. New stimulation pattern design to improve P300-based matrix speller performance at high flash rate. Journal of Neural Engineering. 2013 Jun;10(3):036012. doi: 10.1088/1741-2560/10/3/036012. [DOI] [PubMed] [Google Scholar]
- 19.Zhou Z, Yin E, Liu Y, Jiang J, Hu D. A novel task-oriented optimal design for P300-based brain-computer interfaces. Journal of Neural Engineering. 2014;056003 doi: 10.1088/1741-2560/11/5/056003. [DOI] [PubMed] [Google Scholar]
- 20.Martens SMM, Leiva JM. A generative model approach for decoding in the visual event-related potential-based brain-computer interface speller. Journal of Neural Engineering. 2010 Apr;7(2) doi: 10.1088/1741-2560/7/2/026003. [DOI] [PubMed] [Google Scholar]
- 21.Xu M, Qi H, Wan B, Yin T, Liu Z. A hybrid BCI speller paradigm combining P300 potential and the SSVEP. Journal of Neural Engineering. 2013;026001 doi: 10.1088/1741-2560/10/2/026001. [DOI] [PubMed] [Google Scholar]
- 22.Xu M, Chen L, Zhang L, Qi H, Ma L, Tang J, Wan B, Ming D. A visual parallel-BCI speller based on the timefrequency coding strategy. Journal of Neural Engineering. 2014 Apr;11(2):026014. doi: 10.1088/1741-2560/11/2/026014. [DOI] [PubMed] [Google Scholar]
- 23.Yin E, Zhou Z, Jiang J, Chen F, Liu Y, Hu D. A novel hybrid BCI speller based on the incorporation of SSVEP into the P300 paradigm. Journal of Neural Engineering. 2013;026012 doi: 10.1088/1741-2560/10/2/026012. [DOI] [PubMed] [Google Scholar]
- 24.Yin E, Zhou Z, Jiang J, Chen F, Liu Y, Hu D. A speedy hybrid BCI spelling approach combining P300 and SSVEP. IEEE Transactions on Biomedical Engineering. 2014 Feb;61(2):473–83. doi: 10.1109/TBME.2013.2281976. [DOI] [PubMed] [Google Scholar]
- 25.Li Y, Pan J, Wang F, Yu Z. A Hybrid BCI System Combining P300 and SSVEP and Its Application to Wheelchair Control. IEEE Transactions on Biomedical Engineering. 2013 Nov;60(11):3156–66. doi: 10.1109/TBME.2013.2270283. [DOI] [PubMed] [Google Scholar]
- 26.Mora-Cortes A, Manyakov N, Chumerin N, Van Hulle M. Language Model Applications to Spelling with Brain-Computer Interfaces. Sensors. 2014;14:5967–5993. doi: 10.3390/s140405967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Volosyak I, Moor A, Grser A. A dictionary-driven ssvep speller with a modified graphical user interface. In: Cabestany J, Rojas I, Joya G, editors. Advances in Computational Intelligence. Vol. 6691. Springer Berlin Heidelberg; 2011. pp. 353–361. (ser Lecture Notes in Computer Science). [Google Scholar]
- 28.Höhne J, Schreuder M, Blankertz B, Tangermann M. A novel 9-class auditory ERP paradigm driving a predictive text entry system. Frontiers in neuroscience. 2011 Jan;5(August):99. doi: 10.3389/fnins.2011.00099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tiziano DAlbis. PhD dissertation. Politecnico di Milano; 2008. A Predictive Speller for a Brain-Computer Interface Based on Motor Imagery. [Google Scholar]
- 30.Saa JFD, de Pesters A, Mc Farland D, Cetin M. Word-level language modeling for p300 sellers based on discriminative graphical models. Journal of Neural Engineering. 2015;12(2):026007. doi: 10.1088/1741-2560/12/2/026007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wills Sa, MacKay DJC. DASHER - An efficient writing system for brain-computer interfaces? IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2006;14(2):244–246. doi: 10.1109/TNSRE.2006.875573. [DOI] [PubMed] [Google Scholar]
- 32.Shayevitz O, Feder M. Optimal feedback communication via posterior matching. Information Theory, IEEE Transactions …. 2011;57(3):1186–1222. [Google Scholar]
- 33.Perdikis S, Leeb R, Williamson J, Ramsay A, Tavella M, Desideri L, Hoogerwerf E-J, Al-Khodairy A, Murray-Smith R, Millan JDR. Clinical evaluation of BrainTree, a motor imagery hybrid BCI speller. Journal of Neural Engineering. 2014 Jun;11(3):036003. doi: 10.1088/1741-2560/11/3/036003. [DOI] [PubMed] [Google Scholar]
- 34.Roark B, Gibbons C, Fried-Oken M. Binary coding with language models for eeg-based access methods. International Society for Augmentative and Alternative Communication Biennial Conference. 2010 [Google Scholar]
- 35.Omar C, Akce A, Johnson M, Bretl T, Ma R, Maclin E, Mccormick M, Coleman TP. A Feedback Information-Theoretic Approach to the Design of BrainComputer Interfaces. International journal of human-computer interaction. 2011;27(1):5–23. [Google Scholar]
- 36.Akce A, Norton J, Bretl T. An ssvep-based brain computer interface for text spelling with adaptive queries that maximize information gain rates. Neural Systems and Rehabilitation Engineering, IEEE Transactions on. 2015 Sep;23(5):857–866. doi: 10.1109/TNSRE.2014.2373338. [DOI] [PubMed] [Google Scholar]
- 37.Cover TM, Thomas JA. Elements of Information Theory Wiley-Interscience. 2012 [Google Scholar]
- 38.Fatourechi M, Mason S, Birch G, Ward R. Is Information Transfer Rate a Suitable Performance Measure for Self-paced Brain Interface Systems? 2006 IEEE International Symposium on Signal Processing and Information Technology. 2006 Aug;:212–216. [Google Scholar]
- 39.Billinger M, Daly I, Kaiser V, Jin J, Allison B, Mller-Putz G, Brunner C. Is it significant? guidelines for reporting bci performance. In: Allison BZ, Dunne S, Leeb R, Milln J Del R, Nijholt A, editors. Towards Practical Brain-Computer Interfaces. Springer Berlin Heidelberg; 2013. pp. 333–354. (ser Biological and Medical Physics, Biomedical Engineering). [Google Scholar]
- 40.Nykopp T. Statistical Modelling Issues for the Adaptive Brain Interface. University of Helsinki. 2001 [Google Scholar]
- 41.Higger M, Akcakaya M, Nezamfar H, LaMountain G, Orhan U, Erdogmus D. A bayesian framework for intent detection and stimulation selection in ssvep bcis. Signal Processing Letters, IEEE. 2015 Jun;22(6):743–747. [Google Scholar]
- 42.Speier W, Arnold C, Pouratian N. Evaluatin true bci communication rate through mutual information and language models. PLOS ONE. 2013;8(10):e78432, 10. doi: 10.1371/journal.pone.0078432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Graham RL. Bounds on multiprocessing timing anomalies. SIAM Journal on Applied Mathematics. 1969;17(2):416–429. [Google Scholar]
- 44.Nocedal J, Wright S. Numerical Optimization (Springer Series in Operations Research and Financial Engineering) Springer; 2006. [Google Scholar]
- 45.Orhan U, Erdogmus D, Roark B, Oken B, Fried-Oken M. Offline analysis of context contribution to ERP-based typing BCI performance. Journal of neural engineering. 2013 Dec;10(6):066003. doi: 10.1088/1741-2560/10/6/066003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lin Z, Zhang C, Wu W, Gao X. Frequency recognition based on canonical correlation analysis for SSVEP-based BCIs. Biomedical Engineering, IEEE …. 2006:1–13. doi: 10.1109/tbme.2006.886577. [DOI] [PubMed] [Google Scholar]
- 47.Bin G, Lin Z, Gao X, Hong B, Gao S. The SSVEP topographic scalp maps by canonical correlation analysis. Annual International Conference of the IEEE Engineering in Medicine and Biology Society. 2008 Jan;2008:3759–62. doi: 10.1109/IEMBS.2008.4650026. [DOI] [PubMed] [Google Scholar]
- 48.Pan J, Gao X, Duan F, Yan Z, Gao S. Enhancing the classification accuracy of steady-state visual evoked potential-based brain-computer interfaces using phase constrained canonical correlation analysis. Journal of neural engineering. 2011 Jun;8(3):036027. doi: 10.1088/1741-2560/8/3/036027. [DOI] [PubMed] [Google Scholar]
- 49.Zhang Y, Zhou G, Jin J, Wang X, Cichocki A. Frequency Recognition in SSVEP-based BCI using Multiset Canonical Correlation Analysis. International Journal of Neural Systems. 2013:1–7. doi: 10.1142/S0129065714500130. [DOI] [PubMed] [Google Scholar]
- 50.Zhang Y, Zhou G, Jin J, Wang M, Wang X, Cichocki A. L1-regularized Multiway canonical correlation analysis for SSVEP-based BCI. IEEE transactions on neural systems and rehabilitation engineering. 2013 Nov;21(6):887–96. doi: 10.1109/TNSRE.2013.2279680. [DOI] [PubMed] [Google Scholar]
- 51.Akcakaya M, Peters B, Moghadamfalahi M, Mooney AR, Orhan U, Oken B, Erdogmus D, Fried-Oken M. Noninvasive brain-computer interfaces for augmentative and alternative communication. IEEE reviews in biomedical engineering. 2014 Jan;7:31–49. doi: 10.1109/RBME.2013.2295097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhu D, Bieger J, Garcia Molina G, Aarts RM. A survey of stimulation methods used in SSVEP-based BCIs. Computational intelligence and neuroscience. 2010 Jan;2010:702357. doi: 10.1155/2010/702357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Silverman BW. Density Estimation for Statistics and Data Analysis (Chapman & Hall/CRC Monographs on Statistics & Applied Probability) Chapman and Hall/CRC; 1986. [Google Scholar]
- 54.Bishop CM. Pattern Recognition and Machine Learning (Information Science and Statistics) Springer; 2007. [Google Scholar]


