Bayesian Switching Factor Analysis for Estimating Time-varying Functional Connectivity in fMRI

Abstract

There is growing interest in understanding the dynamical properties of functional interactions between distributed brain regions. However, robust estimation of temporal dynamics from functional magnetic resonance imaging (fMRI) data remains challenging due to limitations in extant multivariate methods for modeling time-varying functional interactions between multiple brain areas. Here, we develop a Bayesian generative model for fMRI time-series within the framework of hidden Markov models (HMMs). The model is a dynamic variant of the static factor analysis model (Ghahramani and Beal, 2000). We refer to this model as Bayesian switching factor analysis (BSFA) as it integrates factor analysis into a generative HMM in a unified Bayesian framework. In BSFA, brain dynamic functional networks are represented by latent states which are learnt from the data. Crucially, BSFA is a generative model which estimates the temporal evolution of brain states and transition probabilities between states as a function of time. An attractive feature of BSFA is the automatic determination of the number of latent states via Bayesian model selection arising from penalization of excessively complex models. Key features of BSFA are validated using extensive simulations on carefully designed synthetic data. We further validate BSFA using fingerprint analysis of multisession resting-state fMRI data from the Human Connectome Project (HCP). Our results show that modeling temporal dependencies in the generative model of BSFA results in improved fingerprinting of individual participants. Finally, we apply BSFA to elucidate the dynamic functional organization of the salience, central-executive, and default mode networks—three core neurocognitive systems with central role in cognitive and affective information processing (Menon, 2011). Across two HCP sessions, we demonstrate a high level of dynamic interactions between these networks and determine that the salience network has the highest temporal flexibility among the three networks. Our proposed methods provide a novel and powerful generative model for investigating dynamic brain connectivity.

1. Introduction

Precise characterization of dynamic connectivity is critical for understanding the intrinsic functional organization of the human brain (Biswal et al., 1995; Buckner et al., 2013; Menon, 2015a; Power et al., 2013; Cole et al., 2014; Rosenberg et al., 2016; Greicius et al., 2003; Zalesky et al., 2014). Recent studies suggest that intrinsic functional connectivity is non-stationary (Allen et al., 2014; Chang and Glover, 2010; Deco et al., 2008; Rabinovich et al., 2012; Breakspear, 2004). However, most studies characterizing time-varying intrinsic functional connectivity still rely primarily on a sliding window approach (Allen et al., 2014), in which a fixed length window is advanced across time providing a measure of temporal change in covariance between brain regions computed within each sliding window. The resulting matrices across time are then clustered together to infer the underlying brain states. However, a limitation of this approach is that the size of the sliding window and the number of clusters, which greatly influence the estimation of underlying dynamic brain networks (Leonardi and Van De Ville, 2015; Lindquist et al., 2014), are often set arbitrarily. It is now increasingly clear that new computational techniques are needed to overcome limitations of extant methods for quantifying time-varying changes in connectivity (Baker et al., 2014; Calhoun et al., 2014; Karahanoǧlu and Van De Ville, 2015; Menon, 2015a; Vidaurre et al., 2016).

Recent attempts at addressing limitations of the sliding-window based approaches include temporal independent component analysis (Smith et al., 2012) and graph theory based methods including dynamic condition correlation (Lindquist et al., 2014), and dynamic connectivity regression (Cribben et al., 2012). Evolutionary models are another family of techniques for modeling time-series in which observed data at a given time depend on the previous data via a linear or nonlinear transformation function, (Harrison et al., 2003; Rogers et al., 2010; Smith et al., 2010; Samdin et al., 2016; Fiecas and Ombao, 2016; Ting et al., 2015).

An alternate approach we develop here is based on the general framework of probabilistic generative models which are appealing as they can provide a more mechanistic understanding of the latent processes that generate observed brain dynamics. Crucially, probabilistic generative models provide more precise quantitative information about key properties of dynamic functional brain organization, including temporal evolution of brain states, occupancy rate and lifetime of individual states, and transition probabilities between states.

Most generative models for assessing dynamic brain connectivity are based on hidden Markov models (HMMs). HMMs are statistical Morkov models which have been extensively used in various applications for modeling time-series (Rabiner, 1989; Murphy, 2012; Bishop, 2006). HMMs have been previously largely applied to EEG and MEG data, e.g., (Baker et al., 2014). However, their applications to dynamic functional connectivity analysis of the fMRI data have been relatively limited (Højen-Sørensen and Hansen, 2000; Eavani et al., 2013; Suk et al., 2015; Robinson et al., 2015) given their potentials. Crucially, HMMs assume that observations are coupled through a set of temporally-dependent latent-state (hidden-state) variables, where the dependence is expressed as a first-order Markov chain. Hence, unlike the sliding window approach which requires explicit specification of the window length, they provide a systematic and principled way of capturing long-term correlations using Markovian assumptions (Bishop, 2006; Murphy, 2012).

Here we develop a novel generative model for characterizing time-varying functional connectivity between distributed brain regions, using a Bayesian switching factor analysis (BSFA) framework that combines hidden Markov models (HMM) (Mackay, 1997) with static factor analysis (Ghahramani and Beal, 2000) in a unified Bayesian framework. BSFA belongs to the class of matrix factorization models. More specifically, as discussed by Singh and Gordon (2008), if we assume no constraints on the factors, matrix factorization can be seen as factor analysis where an increase in the influence of one latent variable (factor) does not require a decrease in the influence of other latent variables. In BSFA, each instance of the regional time-series is generated from latent states that are linked through a first-order Markov chain. The number of latent states is learnt from the data using Bayesian model selection which automatically penalizes excessively complex models (Mackay, 1997). Crucially, observations in each state are generated from a linear mapping of sources in a latent subspace which may have significantly lower dimensionality than the observed data. The dimensionality of the latent subspace is allowed to vary across states and its optimal value is determined within the Bayesian framework using automatic relevance determination (Neal, 1996; MacKay, 1996). Furthermore, the noise variance is allowed to vary across states and brain regions which, in principle, shall give the model potential to control for measurement noise. On synthetic data, we demonstrate that this feature of the model is useful for reducing the effect of additive noise on dynamic brain connectivity.

Another important feature of our BSFA is that it is formulated in a fully Bayesian framework. This approach overcomes limitations of extant HMM methods that are based on a maximum likelihood (ML) estimation. Specifically, ML-based HMM methods require a priori specification of the number of hidden states, which are not known a priori in fMRI data. Furthermore, specifying a larger or smaller number of states may overfit or underfit the data respectively. In contrast to the commonly used ML-based approaches for inferring model parameters, we use a variational Bayes inference framework (Jordan et al., 1999; Jaakkola, 2000) which provides several advantages, including (1) a regularization framework that reduces overfitting by penalizing complex models; (2) an explicit way of computing a predictive likelihood which can be used in prediction analysis, e.g., fingerprint and signature identifications, (Finn et al., 2015); (3) a theoretical framework for incorporating prior beliefs in the learning through assignment of prior distributions over model parameters, if such prior information is available; (4) a lower bound on the marginal-likelihood that can be used as model evidence. We show that our BSFA accurately estimates the key parameters of time-varying functional connectivity—the number of states, covariance associated with each state, occurrence and lifetime of individual states, and transition probability between states.

In the following, we first describe our BSFA and discuss a variational approach for estimating time-varying functional connectivity in resting-state fMRI (rs-fMRI) data. We then evaluate the performance of BSFA using synthetic data by varying model complexity (number of latent states), data dimensionality (number of brain regions) and measurement noise. We further evaluate BSFA using real rs-fMRI data by performing a predictive “fingerprint” analysis using multisession rs-fMRI data from individual participants. The fingerprint analysis examines whether the latent dynamics uncovered by BSFA is “informative” such that dynamics learnt in one session can uniquely predict data in the other session from the same subject.

Finally, we apply our framework to uncover intrinsic dynamic functional interactions within a triple-network model encompassing the salience network (SN), the central-executive network (CEN), and the default mode network (DMN)—three core neurocognitive systems that play a central role in cognitive and affective information processing (Menon, 2011). We used two independent cohorts of HCP data because our goal was to demonstrate the robustness and replicability of our key neuroscientific findings across the cohorts. Specifically, using two independent cohorts of HCP data, we showed that the salience network has the highest level of temporal flexibility among the three.

2. Methods

2.1. Bayesian switching factor analysis

2.1.1. Generative model

Let ${\mathit{y}}_t^s$ denote a D-dimensional vector of voxel time-series measured from subject s at time t, that is ${\mathit{y}}_t^s={(y_{t1}^s,\dots ,y_{\mathit{\text{tD}}}^s)}^{\top }$, where D is the number of ROIs, and ⊤ denotes the transpose operator. We collect a sequence of T measurements of ${\mathit{y}}_t^s$ for S subjects in Y̲ = {Y^s | s = 1, …, S}, where ${\mathit{Y}}^s=({\mathit{y}}_1^s,\dots ,{\mathit{y}}_T^s)$. We then assume each observation, ${\mathit{y}}_t^s$ is generated from a linear transformation of a number of latent source factors, ${\mathit{x}}_t^s={(x_{1t}^s,\dots ,x_{\mathit{\text{Pt}}}^s)}^{\top }$, of lower dimensionality in a latent subspace followed by noise in the measurement, e_t, and decoded by a fixed amount of bias in the data space, μ, (Bishop, 2006, Chapter 12) (Everitt, 1984; Ghahramani and Hinton, 1997) as:

$${\mathit{y}}_t^s=\mathit{U}{\mathit{x}}_t^s+\mathit{\mu }+{\mathit{e}}_t=\left(\sum _{p=1}^P{\mathit{u}}_p{x}_{\mathit{\text{pt}}}^s\right)+\mathit{\mu }+{\mathit{e}}_t,\forall t=1,\dots ,T$$ (1)

where U is the linear transformation matrix known as the factor loading matrix, and P is the dimensionality of the latent space where in general P < D. With the normality assumption, it is assumed that the latent source factors follow independent zero-mean unit-variance Gaussian distributions, and that the noise has a zero-mean Gaussian distribution with diagonal covariance matrix, i.e., e_t ~ 𝒩 (0, Ψ). Thus the marginal distribution of ${\mathit{y}}_t^s$ follows a Gaussian distribution as: $p({\mathit{y}}_t^s|\mathit{\mu },\mathit{U},\mathbf{\Psi })=𝒩(\mathit{\mu },\mathit{U}{\mathit{U}}^{\top }+\mathbf{\Psi })$, (Ghahramani and Hinton, 1997). Generally the underlying distribution of the voxel time-series measurements is multi-modal as observations are lied on a globally non-linear manifold. However, a single factor analyzer is a linear model which can only model a portion of this nonlinear manifold where it is locally linear. One simple solution to tackle nonlinearity is to use a parametric mixture model of factor analyzers which models the data point ${\mathit{y}}_t^s$ as a weighted average of factor analyzer densities, (Ghahramani and Hinton, 1997; Ghahramani and Beal, 2000). However, mixture models come with a strong assumption on the observed data that measurements are independent and identically distributed (i.i.d.), (Bishop, 2006, Chapter 9). Recent findings however suggest that the brain networks are not static and functional interactions between distributed brain regions are temporally dependent (Allen et al., 2014; Chang and Glover, 2010). Thus the i.i.d. assumption may not hold in practice.

In the following, we derive a dynamic variant of the static factor analysis model (Ghahramani and Beal, 2000) suitable for dynamic functional connectivity analysis of fMRI time-series. To weaken the i.i.d. assumption and allow a mechanism for capturing time-dependent functional-connectivity variations in fMRI data, we assume that observations are independent but they are generated from a set of latent state variables (commonly known as hidden state variables) which are connected to each other through a first-order Markov chain, as shown in Figure 1. This family of models is known as the hidden Markov models (HMM). The latent state variable at time t is shown by ${\mathit{z}}_t^s$ which is a 1-of-K discrete vector with elements of $z_{\mathit{\text{kt}}}^s$, i.e., ${\mathit{z}}_t^s={(z_{1t}^s,\dots ,z_{\mathit{\text{Kt}}}^s)}^{\top }$. Given the latent state variables ${\mathit{z}}_t^s$, the marginal density of ${\mathit{y}}_t^s$ is expressed as:

$$p({\mathit{y}}_t^s|{\mathit{z}}_t^s,\mathit{\mu },\mathit{U},\mathbf{\Psi })=\prod _{k=1}^K\int p({\mathit{y}}_t^s|{\mathit{x}}_{\mathit{\text{kt}}}^s,z_{\mathit{\text{kt}}}^s,{\mathit{\mu }}_k,{\mathit{U}}_k,{\mathbf{\Psi }}_k)p({\mathit{x}}_{\mathit{\text{kt}}}^s)d{\mathit{x}}_{\mathit{\text{kt}}}^s=\prod _{k=1}^K{\left[𝒩\right({\mathit{\mu }}_k,{\mathit{U}}_k{\mathit{U}}_k^{\top }+{\mathbf{\Psi }}_k\left)\right]}^{z_{\mathit{\text{kt}}}^s}.$$ (2)

For all 1 ≤ i, j ≤ K, the elements of an HMM can be formally defined as:

• initial state probability distribution $\mathit{\pi }=\{{\pi }_k|{\sum }_{k=1}^K{\pi }_k=1,\forall k=1,\dots ,K\}$

• state transition probability distribution $\mathit{A}=\{[a_{\mathit{\text{ij}}}]|{\sum }_{j=1}^K{a}_{\mathit{\text{ij}}}=1,\forall i,j=1,\dots ,K\}$

• emission probability distribution ${\mathit{O}}_t^s=\{{𝒪}_{\mathit{\text{kt}}}^s|\forall k=1,\dots ,K\}$, where ${𝒪}_{\mathit{\text{kt}}}^s$ is an important quantity for which we shall derive an explicit expression given by Equation (11).

Let $\underset{¯}{\mathit{Z}}=\{{\mathit{Z}}^s=({\mathit{z}}_1^s,\dots ,{\mathit{z}}_T^s)|\forall s=1,\dots ,S\}$ denote a set of latent states for all subjects. Given A and π, the probability mass for the state variables can be expressed as

$$p(\underset{¯}{\mathit{Z}}|\mathit{\pi },\mathit{A})=\prod _{s=1}^{S}p({\mathit{z}}_1^s|\mathit{\pi })\prod _{t=2}^{T}p({\mathit{z}}_t^s|{\mathit{z}}_{t-1}^s,\mathit{A}),$$ (3)

from which the joint distribution over observations and latent state variables is given by

$$p(\underset{¯}{\mathit{Y}},\underset{¯}{\mathit{Z}}|\underset{¯}{\mathit{X}},\mathit{\theta },\mathit{\varphi })=\prod _{s=1}^{S}p({\mathit{z}}_1^s|\mathit{\pi })[\prod _{t=2}^{T}p({\mathit{z}}_t^s|{\mathit{z}}_{t-1}^s,\mathit{A})\left]\right[\prod _{t=1}^T\prod _{k=1}^{K}p({\mathit{y}}_t^s|z_{\mathit{\text{kt}}}^s,{\mathit{x}}_{\mathit{\text{kt}}}^s,{\mathit{\varphi }}_k)].$$ (4)

where $\underset{¯}{\mathit{X}}=\{{\mathit{X}}_k^s=({\mathit{x}}_{k1}^s,\dots ,{\mathit{x}}_{k,T}^s)|\forall s,k\}$, θ = {π, A} and ϕ = {μ, U, Ψ} to keep the notation uncluttered. Note that θ and ϕ are learnt in a group level using sufficient statistics accumulated from all subjects. Latent state variables ${\mathit{z}}_t^s$ and latent source factors are inferred for each subject using group-learnt model parameters θ and ϕ. We refer to the model in Equation (4) as the switching factor analysis.

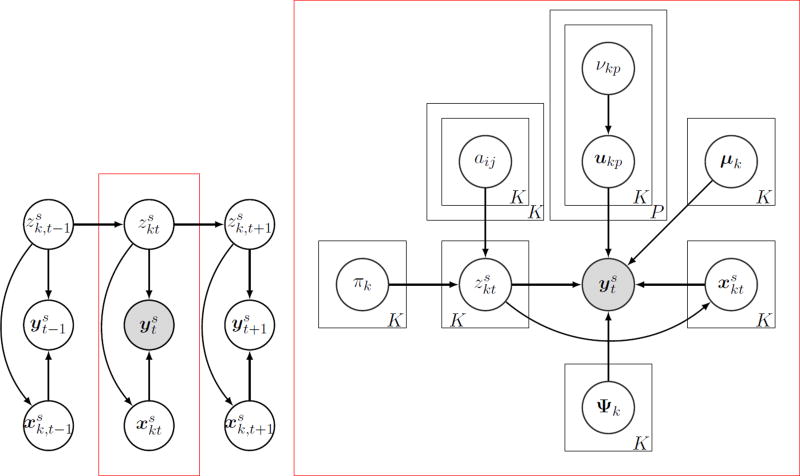
Figure 1.

Directed acyclic graph representing the Bayesian switching factor analysis (BSFA) model. ${\mathit{y}}_t^s$ is the observed variable, $z_{\mathit{\text{kt}}}^s$ is the k-th latent state variable, and ${\mathit{x}}_{\mathit{\text{kt}}}^s$ is the latent source factor (latent subspace variable) associated with the k-th latent state variable at time t for a given subject s. (left) Allowed dependencies among observations, latent state variables and latent subspace variables. Given the latent states, observations and latent subspace variables are conditionally independent. However, latent states are connected to each other using a first-order Markov chain. (right) Generative model at a given time t (indicated with a red box). π_k and a_ij, ∀_{i, j} ∈ K, are HMM parameters indicating the initial state probability distribution and the state transition probability distribution. μ_k is the fixed bias in the data, Ψ_k is the noise covariance matrix at state k, u_kp is the p-th column of the factor loading matrix and at the k-th state, and ν_kp is the prior on the variance of the u_kp, known as ARD prior which controls the dimensionality of the latent subspace. Black boxes indicate replications over latent variables and model parameters.

2.1.2. Bayesian inference

In a fully Bayesian view to uncertainty, all uncertain quantities are treated as random variables. The Bayesian framework allows to incorporate prior knowledge in a coherent way, and provides a principled basis to determine the model complexity—the number of states, K, and the dimensionality of the latent space, P. Contrary to the maximum likelihood approach, a Bayesian approach attempts to integrate over possible settings of all random variables rather than optimizing them. The resulting quantity is known as the marginal likelihood. The marginal likelihood for the BSFA is given by

$$p(\underset{¯}{\mathit{Y}})=\prod _{s=1}^S\prod _{t=1}^T\prod _{k=1}^K\iiint p({\mathit{y}}_t^s,z_{\mathit{\text{kt}}}^s,{\mathit{x}}_{\mathit{\text{kt}}}^s,{\mathit{\varphi }}_k,{\mathit{\theta }}_k)d{\mathit{x}}_{\mathit{\text{kt}}}^{s}d{\mathit{\varphi }}_{k}d{\mathit{\theta }}_k,$$ (5)

where $p({\mathit{y}}_t^s,z_{\mathit{\text{kt}}}^s,{\mathit{x}}_{\mathit{\text{kt}}}^s,{\varphi }_k,{\mathit{\theta }}_k)$ is the joint probability distribution over all variables given by

$$p({\mathit{y}}_t^s,z_{\mathit{\text{kt}}}^s,{\mathit{x}}_{\mathit{\text{kt}}}^s,{\mathit{\varphi }}_k,{\mathit{\theta }}_k)=p({\mathit{y}}_t^s|z_{\mathit{\text{kt}}}^s,{\mathit{x}}_{\mathit{\text{kt}}}^s,{\mathit{\varphi }}_k)p({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)p(z_{\mathit{\text{kt}}}^s|{\mathit{\theta }}_k)p({\mathit{\theta }}_k)p({\mathit{\varphi }}_k),$$ (6)

where p(θ_k) and p(ϕ_k) are the prior distributions. The choice of prior distributions are discussed in Appendix A. A graphical representation of the BSFA is shown in Figure 1. This illustrative graph shows allowed dependencies across various variables in the model. Given the observed data and the assigned priors over all variables, the posterior distribution may be inferred using Bayes’s rule as $p(\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\varphi ,\mathit{\theta }|\underset{¯}{\mathit{Y}})=\frac{p(\underset{¯}{\mathit{Y}},\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\varphi ,\mathit{\theta })}{p(\underset{¯}{\mathit{Y}})}$, where p(Y̲) is the marginal likelihood given by Equation (5) and p(Y̲, Ẕ, X̲, ϕ, θ) is the joint distribution given by Equation (6). Working directly with the posterior distribution is precluded by the the need to compute the marginal likelihood of the observations. Thus, directly computing the posterior may not be analytically possible. In the following, we approximate the posterior using a family of optimization methods known as variational inference (Jordan et al., 1999; Wainwright and Jordan, 2007). Variational inference is based on reformulating the problem of computing the posterior distribution as an optimization problem. In this paper, we work with a particular class of variational methods known as mean-field methods, which are based on optimizing Kullback-Leibler divergence (Jordan et al., 1999). We aim to minimize the Kullback-Leibler divergence between the variational posterior distribution, shown as q(Ẕ, X̲, ϕ, θ), and the true posterior distribution, p(Ẕ, X̲, ϕ, θ|Y̲), which can be expressed as:

$$𝒟[q(\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })\Vert p(\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta }|\underset{¯}{\mathit{Y}})]=-{\langle \text{log}\frac{p(\underset{¯}{\mathit{Y}},\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })}{q(\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })}\rangle }_{q(\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })}+\text{log}p(\underset{¯}{\mathit{Y}}),$$ (7)

where the operator 〈·〉 takes the expectation of variables in its argument with respect to the variational distribution q(·), e.g., 〈f (x)〉_g(x) = ∫ f (x)g(x)dx. The minimization of Equation (7) is equivalent to the maximization of a lower bound, ℒ, on the log marginal likelihood defined as:

$$ℒ={\langle \text{log}\frac{p(\underset{¯}{\mathit{Y}},\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })}{q(\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })}\rangle }_{q(\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })}.$$ (8)

For the mean-field framework to yield a computationally efficient inference method, it is necessary to choose a family of distributions q(Ẕ, X̲, ϕ, θ) such that we can tractably optimize the lower bound. We now approximate the true posterior distribution using a partly factorized approximation in the form of

$$p(\underset{¯}{\mathit{Y}},\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })\simeq q(\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })=q(\mathit{\varphi })q(\underset{¯}{\mathit{X}}|\underset{¯}{\mathit{Z}})q(\underset{¯}{\mathit{Z}})q(\mathit{\theta }).$$ (9)

Given our choice of factorization in Equation (9), we can express the lower bound, Equation (8), explicitly as

$$ℒ=\underset{ℒ(\underset{¯}{\mathit{Y}}|\underset{¯}{\mathit{Z}})}{\underbrace{{\langle {\langle \text{log}\frac{p(\underset{¯}{\mathit{Y}},\underset{¯}{\mathit{X}},\mathit{\varphi }|\underset{¯}{\mathit{Z}},\mathit{\theta })}{q(\underset{¯}{\mathit{X}},\mathit{\varphi }|\underset{¯}{\mathit{Z}})}\rangle }_{q(\underset{¯}{\mathit{X}},\mathit{\varphi }|\underset{¯}{\mathit{Z}})}\rangle }_{q(\underset{¯}{\mathit{Z}})}}}+{\langle {\langle \text{log}\frac{p(\underset{¯}{\mathit{Z}},\mathit{\theta })}{q(\underset{¯}{\mathit{Z}})q(\mathit{\theta })}\rangle }_{q(\mathit{\theta })}\rangle }_{q(\underset{¯}{\mathit{Z}})}.$$ (10)

Note that in Equation (10) the lower bound has been separated into two parts. The first part, ℒ(Y̲ | Ẕ), is the Ẕ-conditional expected value calculated using q(X̲, ϕ|Ẕ) across X̲ and ϕ related only to the generation of Y̲. This part is calculated as a function of any given Ẕ. The second term depends only on the Markov-chain model for the latent variables Ẕ. Thus, the total lower bound can be maximized by alternating optimization of each of these two parts, while the other part of the model is kept unaltered.

2.1.3. Posterior distribution of the model parameters

q(X̲, ϕ|Ẕ) and q(θ) are obtained by maximizing ℒ(Y̲ |Ẕ). As the result of working with the conjugate priors, the resulting posteriors will follow the same functional forms as their priors. Explicit expressions for computing q(X̲, ϕ|Ẕ) and q(θ) are summarized in Appendix B.

2.1.4. Posterior distribution of the latent state variables

q(Ẕ) is obtained by maximizing the second term in the lower bound expression by Equation (10), and using the Markov properties for Ẕ. In practice, a variant of the forward algorithm and backward algorithm can be used to efficiently compute the necessary marginal probabilities, namely, ${\langle {\mathit{z}}_t^s\rangle }_{q({\mathit{z}}_t^s)}$ and ${\langle {\mathit{z}}_t^s{\mathit{z}}_{t-1}^s\rangle }_{q({\mathit{z}}_t^s)}$ (Appendix D). Computation of these statistics using the forward and backward algorithms requires the emission probability distribution, ${\mathit{O}}_t^s=\{{𝒪}_{\mathit{\text{kt}}}^s|\forall k\}$, which is given by:

$${𝒪}_{\mathit{\text{kt}}}^s=\text{exp}(ℒ({\mathit{y}}_t^s|z_{\mathit{\text{kt}}}^s=1)),\forall k=1,\dots ,K$$ (11)

where

$$ℒ({\mathit{y}}_t^s|z_{\mathit{\text{kt}}}^s=1)={\langle \text{log}p({\mathit{y}}_t^s|z_{\mathit{\text{kt}}}^s,{\mathit{x}}_{\mathit{\text{kt}}}^s,{\mathit{\varphi }}_k)\rangle }_{q({\mathit{x}}_{\mathit{\text{kt}}}^s,{\mathit{\varphi }}_k|z_{\mathit{\text{kt}}}^s)}-{\langle \text{log}q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)\rangle }_{q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)}.$$ (12)

Details of the forward-backward computations are discussed in Appendix D and an explicit expression for computation of Equation (12) is given by Equation (D.2).

2.1.5. Algorithm

The algorithm starts with initialization of the variational parameters. The optimization of the variational posterior distribution q(Ẕ, X̲, ϕ, θ) involves cycling between optimization of q(Ẕ), q(X, ϕ, θ). First, we use the current distributions over the model parameters to evaluate ${\langle z_{\mathit{\text{kt}}}^s\rangle }_{q(z_{\mathit{\text{kt}}}^s)}$ and ${\langle z_{\mathit{\text{it}}}^s{z}_{j,t-1}^s\rangle }_{q({\mathit{z}}_t^s)}$. Next, these quantities are used to re-estimate the variational distribution over the parameters, q(ϕ_k, θ_k), from which $q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)$ is updated for all k = 1, …, K. These steps are repeated until convergence is achieved, that is when ℒ^iter − ℒ^iter−1 < thr, where ℒ is the model evidence (lower bound) given by Equation (10) and thr is a small value. In our simulations, the threshold was set to 10⁻³. In general, less than 200 iterations are often enough to achieve convergence. The variational procedure is guaranteed to converge (Bishop, 2006, Chapter 10) as the lower bound is convex in each of the factors in Equation (9). A summary of the algorithm is presented in Algorithm 1. An implementation of BSFA in Matlab is available upon request.

2.2. Functional MRI data

2.2.1. HCP Dataset

Two sessions (hereafter Sessions 1 and 2) of minimally processed rs-fMRI data were obtained from the Human Connectome Project (HCP¹). Seventy-four subjects (age: 22–35 years old, 28 males) were selected from 500 subjects based on the following criteria: (1) individuals were unrelated; (2) range of head motion in any translational direction was less than 1 mm; (3) average scan-to-scan head motion was less than 0.2 mm and (4) maximum scan-to-scan head motion was less than 1 mm.

2.2.2. Resting-state fMRI acquisition

For each subject, 1200 volumes were acquired using multi-band, gradient-echo planar imaging with the following parameters: TR, 720 ms; TE, 33.1 ms; flip angle, 52°; field of view, 280 × 180 mm; and matrix, 140 × 90. During scanning, each subject has eyes open with relaxed fixation on a projected bright crosshair on a dark black screen.

2.2.3. Preprocessing

The same processing steps were applied to volumetric data from each session. Spatial smoothing with a Gaussian kernel of 6 mm FWHM was first applied to the minimally pre-processed data to

Algorithm 1.

Bayesian Switching Factor Analysis

step 1: initialization

• set the number of states, K (the initial value of K is usually set to a large value, and during learning those states with small contributions will get weights close to zero);

• set the intrinsic dimensionality of the latent subspace, P, (in general P is set to be smaller than data dimension, P < D, however, in a fully noninformative initialization, one can simply set P = D − 1);,

• set the prior distribution parameters (Appendix A);

• initialize ${\langle {\mathit{z}}_t^s\rangle }_{q({\mathit{z}}_t^s)}$ (e.g., using K-means algorithm, with Euclidean distance as the similarity measure);

repeat

step 2: optimization of the model parameters (variational-maximization step)

• update q(ϕ) and $q({\mathit{x}}_{\mathit{\text{kt}}}^s)$ using update Equations (B.4), (B.5) and (B.11);

• update q(θ) using update Equations (B.2), (B.3);

step 3: optimization of the latent state variables (variational-expectation step)

• update ${\langle {\mathit{z}}_t^s\rangle }_{q({\mathit{z}}_t^s)}$ using update Equation (D.7);

• update ${\langle {\mathit{z}}_t^s{\mathit{z}}_{t-1}^s\rangle }_{q({\mathit{z}}_t^s)}$ using update Equation (D.8);

step 4: optimization of the posterior hyperparameters

• update posterior hyperparameters using Equations (E.2)–(E.6);

step 5: check for convergence

• evaluate lower bound, ℒ, from Equation (10) using Equation (F.1).

until convergence (ℒiter − ℒiter − 1 < thr)

improve signal-to-noise ratio as well as anatomy correspondence between individuals. A multiple linear regression approach with 12 realignment parameters (three translations, three rotations and their first temporal derivatives) was applied to the smoothed data to reduce head-motion-related artifacts. To further remove physiological noise, independent component analysis (ICA) was applied to the preprocessed data using Melodic ICA version 3.14 (Multivariate Exploratory Linear Optimized Decomposition into Independent Components²). ICA components for white matter and cerebrospinal fluid were first identified and their corresponding ICA time-series were then extracted and regressed out of the preprocessed data.

2.2.4. Regions of interest

ROIs were independently defined using 20 clusters from the SN, CEN and DMN based on a previously published study (Shirer et al., 2012) as shown in Figure 3A and Table G.2. The first eigenvalue time-series from each ROI was extracted from each subject. The first eight volumes were discarded to minimize non-equilibrium effects in fMRI signals. High-pass filtering (f > 0.008 Hz) was applied on ROI time-series to remove low frequency signals related to drift. The resulting time-series were linearly detrended and normalized.

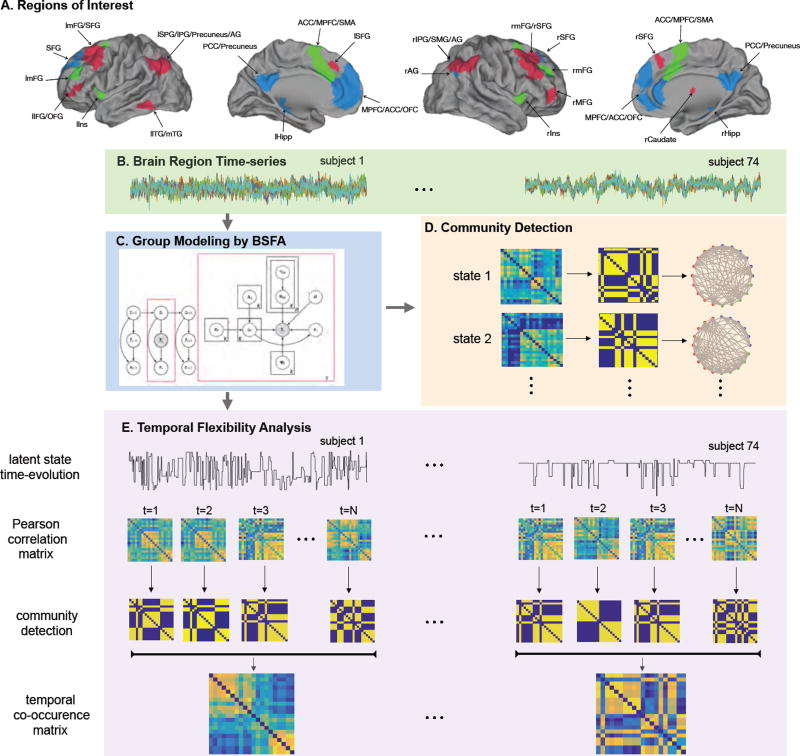
Figure 3.

Schematic illustration of the functional connectivity analysis. (A) Regions of interest (ROIs) defined using 20 clusters from the SN, CEN and DMN based on Shirer et al. (2012) study. List of ROIs and their abbreviations are given in Table G.2. (B) Brain ROI time-series of the HCP rs-fMRI data. (C) Group modeling of the ROI time-series using BSFA. (D) Steps involved in computing the community structure of the latent states after modeling. (E) Steps involved in temporal flexibility analysis.

2.3. Predictive fingerprint analysis of HCP multiple-session rs-fMRI data

Unlike the simulation analysis, since the real underlying dynamics in the real rs-fMRI data are unknown, it is impossible to directly evaluate BSFA based on the key metrics of temporal dynamics of brain states. Hence, a predictive fingerprint analysis is used to assess the validity of the underlying dynamics uncovered using BSFA. The underlying hypothesis is that if BSFA is able to uncover the underlying brain dynamics, the model learnt from Session 1 (training session) is able to best predict data of Session 2 (test session) from the same participant, compared to its prediction on data from other participants. To further demonstrate that BSFA is able to capture informative temporal structures across time-series in rs-fMRI data, we compare BSFA with the static mixture model of factor analyzers (MFA), (Ghahramani and Beal, 2000), which discards the temporal dependencies by imposing the i.i.d. assumptions on the data observations. In the following, we first derive the predictive likelihood and then use it to conduct fingerprint analysis.

2.3.1. Predictive likelihood for the BSFA

Let y′ denote a data sample from the test set for a given subject. Associated with this observation, there is a corresponding latent state variable z′ and a representation of y′ on the latent subspace x′, for which the predictive density is then given by

$$p(\mathit{y}\prime |\underset{¯}{\mathit{Y}})=\sum _{z\prime }\iint p(\mathit{y}\prime |\mathit{z}\prime ,\mathit{x}\prime ,\mathit{\varphi },\mathit{\theta }|\underset{¯}{\mathit{Y}})p(\mathit{x}\prime ,\mathit{\varphi },\mathit{\theta }|\underset{¯}{\mathit{Y}})d\mathit{x}\prime d\mathit{\varphi }d\mathit{\theta },$$ (13)

Algorithm 2.

Predictive likelihood for the BSFA

step 1: Compute $q({\mathit{x}}_{\mathit{\text{kt}}}^{\prime })$ for the new data vector ${\mathit{y}}_t^{\prime }$ using Equation (B.11). Note that only $q({\mathit{x}}_{\mathit{\text{kt}}}^{\prime })$ requires to be updated and posterior distribution of all other model parameters remain unaltered.

step 2: Compute the emission probability distribution, Equation (11), for the new data, ${\mathit{y}}_t^{\prime }$, using updated $q({\mathit{x}}_{\mathit{\text{kt}}}^{\prime })$ and the posterior distribution of the other model parameters, q(Ψ), q(U).

step 3: Compute sufficient statistics of the latent state variables, ${\langle {\mathit{z}}_t^s\rangle }_{q({\mathit{z}}_t^s)}$ and ${\langle {\mathit{z}}_t^s{\mathit{z}}_{t-1}^s\rangle }_{q({\mathit{z}}_t^s)}$, using Equations (D.7) and (D.8).

step 4: Compute the lower bound on the logarithm of the predictive density by computing Equation (10).

where p(y′ |z′,x′, ϕ, θ) is the true posterior distribution. Directly computing p(y′ |Y̲) is not possible as the true posterior is not available in closed form. It is possible, to obtain an approximate to the predictive density by replacing the true posterior distribution with its variational approximation,

$$p(\mathit{y}\prime |\underset{¯}{\mathit{Y}})\approx \sum _{\mathit{z}\prime }\iint p(\mathit{y}\prime |\mathit{z}\prime ,\mathit{\varphi },\mathit{\theta })q(\mathit{\varphi })q(\mathit{\theta })d\mathit{\varphi }d\mathit{\theta }.$$ (14)

This approach has been previously studied by Beal (2003). The approximate solution by Equation (14) is still intractable. However, it is now possible to compute a lower bound on the logarithm of the approximate predictive density. The resulting quantity is called log-predictive likelihood. A summary of the approach is given in Algorithm 2. Note that log-predictive likelihood is a marginalized quantity meaning that uncertainty in the estimation of the model parameters has been integrated out. Marginalization is the key in making the Bayesian predictive density robust to the overfitting.

2.3.2. Predictive likelihood using static model (MFA)

To show the effect of capturing temporal dependencies in better modeling of fMRI time-series, we compare our BSFA with static variant of this model, MFA. Note that MFA is a special case of BSFA that assumes all observations are strictly independent and identically distributed. In other words, MFA assumes that there are no temporal dependencies in the rs-fMRI time-series.

2.3.3. Fingerprint analysis

Fingerprint analysis was carried out through a training phase and a test phase. Data from one scan session are treated as the training set and data from the other session are treated as test set. At the training phase, the underlying generative model for each subject is learnt using BSFA model (Algorithm 1). The model for the i-th subject in the training set is shown as $M_{\text{train}}^{\{i\}}$ which is computed for all subjects separately, i = 1, …, 74. At the test phase, data from the test set are compared against trained models. To test whether the generative model built using training data for a given subject would predict brain region time-series of the same subject in the test set, we computed the predictive likelihood of test data from Equation (14) and using Algorithm 2. Let $p(y_{\text{test}}^{\{i\}}|M_{\text{train}}^{\{j\}})$ denote the predictive likelihood for the i-th subject from the test set using the j-th model from the train set. We then computed $p(y_{\text{test}}^{\{i\}}|M_{\text{train}}^{\{j\}})$ for a given subject i of the test set and for all models j = 1, …, 74 from the train set. The predicted identity is the one with the highest predictive likelihood. Formally it can be expressed as:

$$i^{\ast }={\text{argmax}}_{j}p(y_{\text{test}}^{\{i\}}|M_{\text{train}}^{\{j\}}),\forall j=1,\dots ,74.$$ (15)

The hypothesis is that the predictive likelihood is maximized when i* = i = j. Schematic illustration of the fingerprint analysis using BSFA is shown in Figure 2.

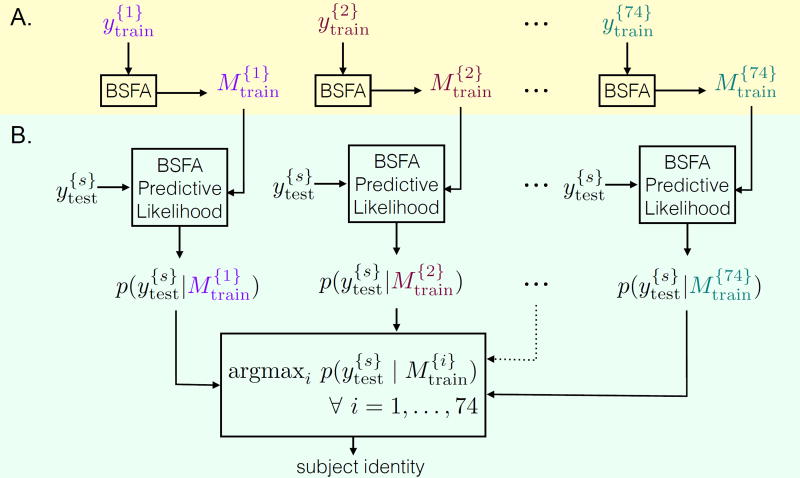
Figure 2.

Schematic illustration of fingerprint analysis using BSFA. (A) Training phase: data from each subject in the train set is modeled using BSFA (Algorithm 1). $y_{\text{train}}^{\{i\}}$ shows data from the i-th subject in the train set and $M_{\text{train}}^{\{i\}}$ shows the corresponding model. (B) Test phase: data from a given subject s from the test set, $y_{\text{test}}^{\{s\}}$, are compared against all the trained models (Algorithm 2). The predicted identity is the one with the highest predictive likelihood.

We tested identification rate across all subjects i = 1, …, 74. The success rate was measured as the percentage of subjects whose identities were correctly predicted out of the total number of subjects (the chance probability is $\frac{1}{74}$). We repeated the same analysis using Session 2 as the train set and Session 1 as the test set.

2.4. Dynamic functional connectivity analysis of HCP rs-fMRI data

2.4.1. Modeling

Resting-state fMRI data from Session 1 and 2 were separately modeled using BSFA (Algorithm 1). BSFA was initialized in a noninformative fashion (Appendix A). The model used no prior information about the optimal number of states and the optimal dimensionality of the latent subspace in each state. The model was initialized with 30 states. Note that the initially assigned model complexity is not critical since during optimization those states with little role in explaining data are automatically pruned out from the model based on the Bayesian model selection. The intrinsic dimensionality of the latent subspace at each state was set to one less than the number of ROIs. However, the optimal dimensionality of the latent subspace is automatically determined from the data and can vary across subjects and states. The estimated generative model consists of posterior distributions of all model parameters and latent state variables.

2.4.2. Transition probability between states

Transition probabilities between latent states are given by:

$$\hat{\mathit{A}}=[{\hat{a}}_{\mathit{\text{ij}}}]\text{ where }{\hat{a}}_{\mathit{\text{ij}}}=\text{exp }\left({\langle \text{log}{a}_{\mathit{\text{ij}}}\rangle }_{q(\mathit{A})}\right),\forall i,j=1,\dots ,K$$ (16)

where 〈log a_ij〉_q(A) is given by Equation (C.1). Diagonal values on  give the self-transition probabilities and off-diagonal values give the cross-transition probabilities.

2.4.3. Temporal evolution of states

Temporal evolution of the latent states indicates the latent state to which a given time point belongs and it is given by the Viterbi path which is defined as the most likely sequence of latent states in the sequence of observed data and is computed using Viterbi algorithm (Bishop, 2006, Chapter 12). Explicitly, the temporal evolution of states for a given subject s is expressed by the Viterbi path and is computed using estimated output probability distribution ${𝒪}_{\mathit{\text{kt}}}^s$, given by Equation (11), and the estimated transition probabilities given by Equation (16). Note that, as the model parameters (HMM model parameters θ = {π, A}, and factor analysis model parameters, ϕ = {μ, U, Ψ}) are learnt in a group-level fashion using sufficient statistics from all subjects (Appendix B), there is a one-to-one matching between states across subjects such that a given state i would correspond to the same state for all subjects, s = 1, …, S. Thus, we can compute variations in estimated number of states across subjects using temporal evolution of states.

2.4.4. Occupancy rate and mean life

The occupancy rate for state i and subject s is computed as:

$$\text{Occupancy Rate}(i,s)=\frac{{\sum }_{t=1}^T\delta (z_{\mathit{\text{it}}}^s=1)}{T}\times 100,$$ (17)

where $\delta (z_{\mathit{\text{it}}}^s=1)$ is the Dirac delta function which is one if the current state at time t is the i-th state. To know at which state we are at a given time, we will use the temporal evolution of states. Occupancy rate is computed for all states and across all subjects. The mean life time of a state is the average time that a given state i continuously persists before switching to another state (Ryali et al., 2016). This quantity can be simply computed from the temporal evolution of states. As there is a one-to-one matching between states across subjects, we can compute how occupancy rate and mean life vary across subjects.

2.4.5. Mean and covariance

Using estimated posterior distribution of the model parameters, estimated group-level mean and covariance for each state are given by:

$${\text{mean}}_k={\overline{\mathit{\mu }}}_k,{\overline{\mathit{\mu }}}_k=[{\overline{\mu }}_{\mathit{\text{kd}}},\forall d=1,\dots ,D],,\forall k=1,\dots ,K$$ (18)

$${\text{cov}}_k=\left({\overline{\dot{\mathit{u}}}}_k{\overline{\dot{\mathit{u}}}}_k^{\top }\right)+{\mathbf{\Psi }}^{-1},{\overline{\dot{\mathit{u}}}}_k=[{\overline{\dot{\mathit{u}}}}_{\mathit{\text{kd}}},\forall d=1,\dots ,D],\forall k=1,\dots ,K$$ (19)

where μ̄_kd, ${\overline{\dot{\mathit{u}}}}_{\mathit{\text{kd}}}$ and Ψ⁻¹ are given by Equations (B.10), (B.9), and (E.1), respectively. Note that, using temporal evolution of states and estimated covariance of states, we can now compute changes in covariance over time.

2.4.6. Community detection

We first computed the Pearson correlation matrices from the estimated covariance matrices for each state using Equation (19), and then determined the dynamic functional community structure under each state by applying the Louvain community detection algorithm (Blondel et al., 2008) on the estimated correlation matrices. The resolution parameter of the modularity maximization of the quality function in Louvain algorithm was set to 1 (default value). Community detection analysis is illustrated in Figure 3D.

2.4.7. Temporal flexibility

To investigate dynamic interactions between brain nodes, we first computed the temporal co-occurrence matrix. The following steps are performed for a given subject as shown in Figure 3C:

• step 1: group level modeling of the brain regions time-series using BSFA;

• step 2: computing the temporal evolution of brain states from the trained model;

• step 3: computing the Pearson correlation matrix from the estimated covariance matrices;

• step 4: extracting the community structure computed using the Louvain community detection algorithm from the Pearson correlation matrices for each detected brain state at each time point given by the temporal evolution of states;

• step 5: constructing an adjacency matrix W_ijts for each subject using the extracted community structure matrix such that W_ijts = 1 if node i and node j are in the same community at time point t for individual s, otherwise W_ijts = 0;

• step 6: computing the temporal co-occurrence matrix as the temporal mean of the adjacency matrix: $C_{\mathit{\text{ijs}}}=\frac{{\sum }_{t=1}^T{W}_{\mathit{\text{ijts}}}}{T}$

Each element of the temporal co-occurrence matrix measures the proportion of times that two brain regions are part of the same community. A high value indicates that the two corresponding brain regions co-participate in the same community more frequently. Based on the temporal co-occurrence matrix C_ijs and the static modular organization of nodes, we characterized the dynamic property of each node using temporal flexibility. Specifically, the temporal flexibility of node i and participant s was computed as:

$$f_{\mathit{\text{is}}}=\frac{{\sum }_{j\notin u_i}{C}_{\mathit{\text{ijs}}}}{{\sum }_{j\ne i}{C}_{\mathit{\text{ijs}}}}$$ (20)

where C_ijs is the temporal co-occurrence matrix for individual s and u_i is the community to which node i belongs. Σ_j∉ui C_ijs measures the frequency with which node i engages in interactions with nodes outside its native community. Σ_j≠i C_ijs measures the total interactions with all nodes. Therefore, temporal flexibility captures the tendency of each node to deviate from its own native static community and interact with outside nodes (Chen et al., 2016).

3. Results and Discussion

3.1. Performance of BSFA on synthetic data

3.1.1. Experiment I: Applying BSFA—an example

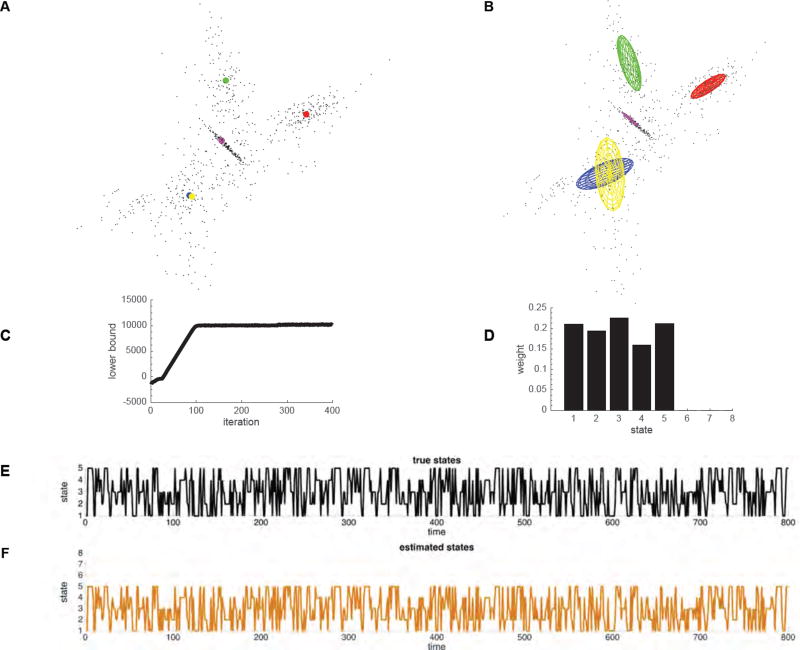
We first illustrate key features of BSFA by estimating the number of latent states and the temporal evolution of the identified states in synthetic data. Specifically, synthetic data were generated using the generative model in Equations (1) and (4) with the following parameters: 800 data samples drawn from each of 5 Gaussian clusters (latent states) with intrinsic dimensionality of 2 embedded at random orientations in a 3-dimensional space. The Gaussian clusters were randomly generated (ellipsoids in Figure 4A), and we used a random temporal evolution of states in data generation (Figure 4E). We added a zero-mean Gaussian distribution with variance of 0.01 across all dimensions as sensor noise (Table 1–I).

Figure 4.

Visualization of BSFA performance on toy data described in § 3.1.1. (A) Data samples and 5 Gaussian cluster centers. Each Gaussian cluster (latent state) is shown in a unique color. (B) Gaussian ellipses after learning given by the mean and covariance computed from the model. (C) The lower bound values (model evidence) during learning at each iteration. (D) The occupancy rate of each state. (E) True temporal evolution of states in data generation. (F) Estimated temporal evolution of the latent states computed using the Viterbi algorithm.

Table 1.

Parameters used in data generation of experiments I–IV.

Experiment	no. samples	no. of states	no. of ROIs	latent space dim.	noise variance
I	800	5	3	2	0.01
II	1200	10	20	10	0.01
III	400	4	14:2:60	7:1:30	0.01
IV	1200	5	20	10	0.01–1000

BSFA was initialized in a noninformative fashion (Appendix A). The initial number of states was set to 8. The intrinsic dimensionality within each state was set to 2 (one less than the actual data dimension).

As shown in Figure 4B,C, BSFA converged to the correct solution of 5 latent states, each with its unique mean and covariance (ellipsoids in Figure 4B). Figure 4D shows the occupancy rate of each state. As shown in this figure, from initially assigned 8 states, BSFA correctly determined that only 5 states have significant contributions in explaining data. Figure 4C shows the estimated model evidence computed using equation (10) at each iteration of the optimization process; the model evidence serves as a measure of convergence. Figure 4F shows the recovered temporal evolution of states estimated using the Viterbi Algorithm. This example demonstrates that BSFA could recover latent states and state dynamics.

3.1.2. Experiment II: Model selection—robust estimation of the number of latent states with respect to the initially assigned model complexity

We next demonstrate robust estimation of the number of latent states, which is particularly important in the context of unsupervised learning of structure in fMRI data. In this experiment, we show that BSFA can reliably estimate the latent states regardless of the initially assigned model complexity. For this purpose, synthetic data were generated using the generative model in Equations (1), (4) with the following parameters: 1200 data samples drawn from each of 10 latent states (Gaussian clusters) with intrinsic dimensionality of 10 embedded at random orientations in a 20-dimensional space and a random temporal evolution of states. We added a zero-mean Gaussian distribution with variance of 0.01 across all dimensions as sensor noise (Table 1–II).

We then trained models using various initial model complexities. The initial model complexity was varied through varying the number of states from 6 to 20 with a step size of 2. The intrinsic dimensionality within each state was set to one less than the actual data dimension. The experiment was repeated for 10 runs with random initializations of BSFA at each run (Appendix A).

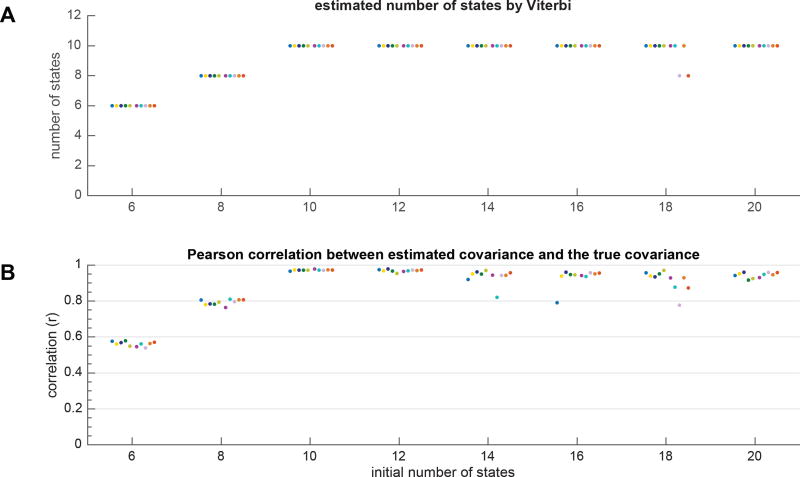
Figure 5A shows the estimated number of states at each experimental condition by Viterbi algorithm, and Figure 5B shows the Pearson correlation between the estimated covariance and true covariance matrices averaged across all states at each run. Ideally, when the estimated covariance from the model is identical to the true covariance, the correlation becomes 1. Each experimental condition is shown with a unique color. The results can be summarized as follows: (a) when the initial model complexity is not sufficient, the model uses all available model complexity and none of the states are pruned out from the model, implying that one would need to increase the initial model complexity by assigning larger number of states; (b) when the initial model complexity is sufficient, that is when the initial number of states is equal or greater than the true number of states, in most cases BSFA could reliably estimate the true number of states as well as the true covariance estimated with each state by pruning out those states which had close to zero contribution in explaining the data generation. The results here show that the Bayesian model selection in BSFA works as expected, that is arbitrarily increasing model complexity has little effect on the overall performance so that BSFA can successfully regulate its complexity and reduce overfitting.

Figure 5.

Evaluation of BSFA performance with respect to model complexity. Model complexity was varied by changing the initial number of states. Data were generated as detailed in § 3.1.2. Experiment was repeated for 10 runs and at each run, the trained models were initialized randomly. Each run is shown in a unique color. (A) The estimated number of states in each run and for each condition. The results are plotted as “·” symbols with small horizontal perturbations for better visualization. Note that some solutions found suboptimal local maxima, but this happened very infrequently. (B) Pearson correlation between true covariance matrix used in the data generation and the estimated covariance matrix computed from the model averaged across all states. If the true and estimated covariance matrices are identical, the Pearson correlation becomes one.

3.1.3. Experiment III: Scalability with dimensionality—performance of BSFA as a function of data dimension (number of ROIs)

Next we evaluated model performance in handling relatively large number of ROIs in relation to more limited number of data samples. In this experiment, we varied the dimensionality of data while keeping the number of data samples fixed. For this purpose, the synthetic data were generated using the generative model in Equations (1), (4). We generated 400 data samples drawn from 4 latent states (Gaussian clusters with random mean vectors and covariance matrices) and using random temporal evolution of states. The data dimensionality was varied from 14 to 60 (with a step size of 2) and the intrinsic dimensionality in the data generation within each state was set to the half of the data dimensionality. We added a zero-mean Gaussian distribution with variance of 0.01 across all dimensions as sensor noise (Table 1–III).

BSFA was initialized in a noninformative fashion (Appendix A). The initial number of states was set to 10. The intrinsic dimensionality within each state was set to one less than the actual data dimension. The experiment was repeated for 10 runs.

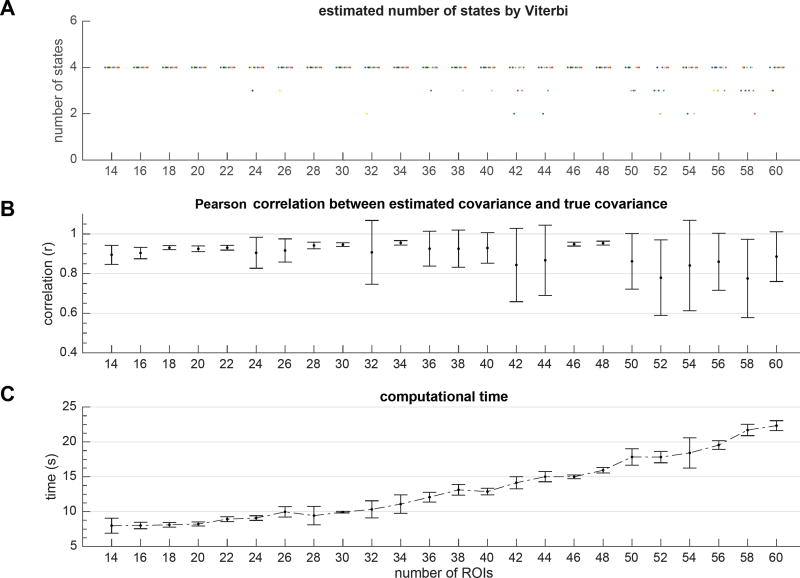
Figure 6A illustrates the remaining (estimated) number of states after convergence at each condition shown with a unique color and, Figure 6B shows the Pearson correlation between the estimated covariance and true covariance matrices averaged across all states and all runs. Figure 6C shows the average amount of computational time averaged across all runs. The following observations are notable: a) BSFA scales well with the data dimensionality, and with increasing data dimensions, the computational complexity increases approximately linearly; b) with increasing data dimension, the chance of falling into local optima increases. This is expected because limited data samples cannot provide statistically sufficient evidence for as many states and intrinsic dimensions. As a result, with various random initializations, it is more likely BSFA falls into bad local optima and hence unable to uncover true underlying number of states. In such cases naturally the error in estimation of covariance is larger. In our experiments, an approximate 10:1 ratio of number of samples to number of ROIs was generally sufficient for robust estimation of the number of latent states.

Figure 6.

Evaluation of BSFA performance with respect to number of ROIs. Data were generated as described in § 3.1.3. Experiment repeated for 10 runs and for each run, trained models were initialized randomly. (A) The estimated number of states in each run and for each condition is given by Viterbi algorithm. The results are plotted as “·” symbols with small horizontal perturbations for better visualization. Each run is shown in a unique color. Note that some solutions found suboptimal local maxima, but this happened very infrequently. However, with increase in the number of ROIs for a fixed amount of data, chance of falling into bad optimal solutions increases. (B) The Pearson correlation between true covariance and estimated covariance matrices averaged across states and runs. (C) Computational time averaged across runs.

3.1.4. Experiment IV: Robustness to noise—effect of measurement noise on the performance of BSFA

Finally, we examined the effect of noise on the performance of BSFA in handling model complexity and estimation of covariance. For this purpose, synthetic data were generated using the generative model in Equations (1), (4) with the following parameters: 1200 data samples with data dimensionality of 20, five latent states embedded in an intrinsic 10-dimensional space, each latent state associated with a unique mean and covariance specified by a Gaussian distribution, and a random temporal evolution of states. The noise variance in the data generation was varied from 0.01 to 1000 (Table 1–IV).

BSFA was initialized in a noninformative fashion (Appendix A). The initial number of states was set to 10. The intrinsic dimensionality within each state was set to one less than the actual data dimension. To smooth out the effect of random initialization, the experiment was repeated for 10 runs.

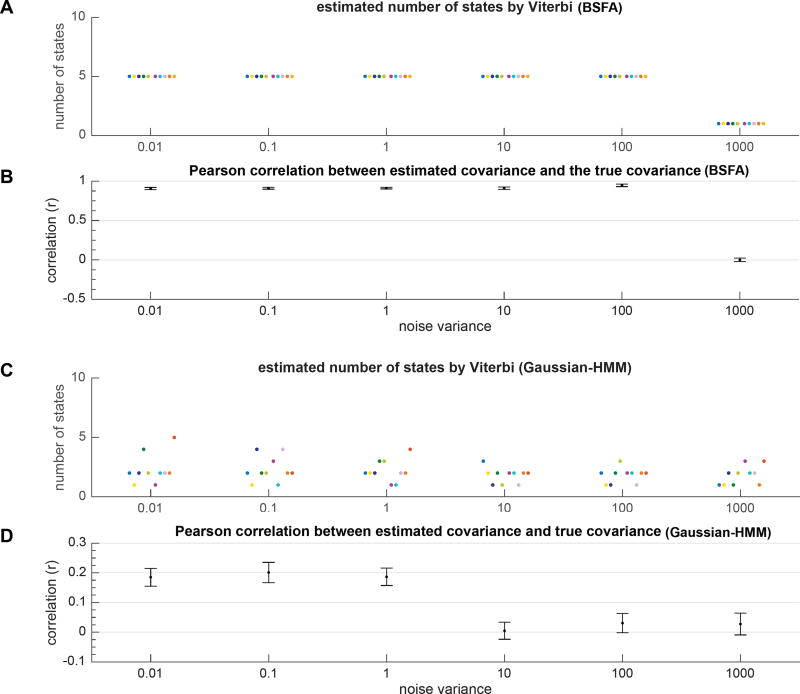
Figure 7A,B shows the estimated number of states by Viterbi and error in estimation of the covariance matrix averaged across all runs. Each run is shown by a unique color. We also compared the performance of BSFA with a model variant that does not incorporate noise in the model in order to demonstrate the advantages of our BSFA in handing noise. For comparison, we used the Bayesian Gaussian hidden Markov model (Ryali et al., 2016) as a closely related model to BSFA which assumes that data samples at each latent state are generated from a Gaussian distribution (we refer to this model as Gaussian-HMM). In contrast to BSFA, the generative model in Gaussian-HMM does not account for noise in the data. As the result, as shown in Figure 7C,D, the model fails to uncover the true number of latent states used in data generation and thus performs poorly in estimation of the covariance matrices.

Figure 7.

Performance of BSFA versus Gaussian-HMM models with respect to observation noise. Data were generated as described in § 3.1.4. The noise variance in data generation was varied from 0.01 to 1000. Experiment was repeated for 10 runs with random initializations. Each run is shown in a unique color. The results are plotted as “·” symbols with small horizontal perturbations for better visualization. (A) Estimated number of states in each run and for each condition given by Viterbi algorithm and computed using BSFA. (B) Pearson correlation between true covariance and estimated covariance matrices averaged across all states and all runs computed from BSFA. (C) Estimated number of states in each run and for each condition given by Viterbi algorithm and computed using Gaussian-HMM model. (D) Pearson correlation between true and estimated covariance matrices computed from Gaussian-HMM model.

3.2. Performance of BSFA on experimental data—fingerprint analysis on HCP rs-fMRI datasets

3.2.1. Regulating model complexity

As noted above, BSFA can effectively determine model complexity on simulation data. The goal here is to further validate this feature of the method using the fingerprint identification analysis on actual fMRI data. For this purpose, we applied BSFA to HCP rs-fMRI data and computed the identification success rate averaged across all runs and across two scan sessions. BSFA was initialized in a noninformative fashion (Appendix A). The initial number of latent states was varied from 4 to 10. The intrinsic dimensionality of the latent space during experiments was set to account for 70% of variation in data. The optimal values for the number of latent states and the intrinsic dimensionality of each state are subject specific and are learnt automatically from the data.

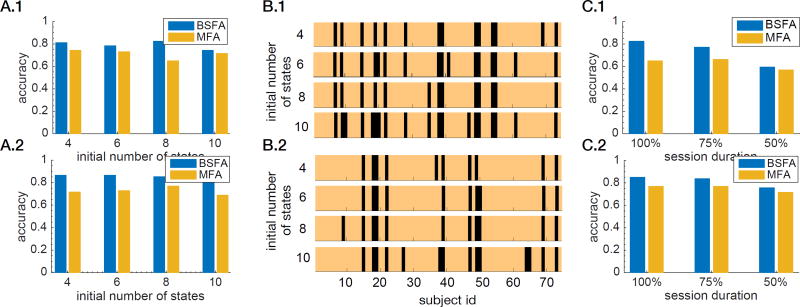
Figure 8A shows the identification success rate with respect to the initially assigned number of states. The results show that identification rate only slightly varies with respect to the number of states. Figure 8B shows the identified subject ids with respect to the number of states. The copper colors indicate the correctly identified participants and black colors indicate the misidentified participants. It is notable that, regardless of the initial model complexity, similar participants were successfully identified. This consistency in identification of the subjects’ IDs further illustrates BSFA’s strength in handling its model complexity.

Figure 8.

Fingerprint identification of HCP rs-fMRI datasets. (A) Identification success rate for various initially assigned model complexities on (A.1) Session 1 as training session and Session 2 as test session, and (A.2) Session 2 as training session and Session 1 as test session. The model complexity was varied through varying the initial number of states. (B) Identified subject ids with respect to various model complexities for the BSFA model. The copper colors indicate the correctly Identified subjects and black colors indicate the misIdentified subjects on (B.1) Session 1 as training session and Session 2 as test session, and (B.2) Session 2 as training session and Session 1 as test session. (C) Comparison between BSFA and MFA with respect to various scan durations of the test session for (C.1) Session 1 as training session and Session 2 as test session, and (C.2) Session 2 as training session and Session 1 as test session.

3.2.2. Effect of including temporal dependence on modeling of HCP rs-fMRI data

Our aim here is to use fingerprint analysis to validate the hypothesis that there are informative temporal dependencies across time points in the rs-fMRI data and including those temporal structures in modeling of data from a given session may contribute to better prediction on data from the other session. For this purpose, we compared the performance of BSFA with MFA. As discussed above, MFA is a special case of BSFA that assumes all observations are independent, and that there are no temporal dependencies in the rs-fMRI time-series. We used exactly the same initializations for both methods. Figure 8A shows the identification success rate with respect to the initially assigned model complexity (number of components). Similar to BSFA, MFA can effectively regulate the model complexity. Next, we compared performance of BSFA and MFA for various durations of scan session in the test phase. In this experiment, the initial number of states for both models (BSFA and MFA) is set to 8, as we have previously shown in Figures 8A that both models can handle the assigned model complexity and avoid overfitting. Figure 8C shows the result of this comparison. We note that BSFA consistently has a higher accuracy compared to MFA. The results suggest that BSFA is able to capture additional informative participant-specific temporal dynamics in the rs-fMRI data, compared to the static model which ignores the richness of the underlying temporal dynamics.

3.3. Performance of BSFA on experimental data—dynamic functional organization of the salience network, default mode network, and central-executive network examined using BSFA

The salience network (SN), the central-executive network (CEN) and the default mode network (DMN) are three core neurocognitive systems that play a central role in cognitive and affective information processing (Menon, 2011, 2015b; Menon and Uddin, 2010; Cai et al., 2015). Crucially, brain regions encompassing these networks are commonly involved in a wide range of cognitive tasks (Dosenbach et al., 2008; Seeley et al., 2007). These networks have previously been investigated using static connectivity measures (Shirer et al., 2012), as a result their dynamic temporal interaction is not known. In a recent study we showed that the SN demonstrated the highest levels of flexibility in time-varying connectivity with other brain networks, including the fronto-parietal network, the cingulate-opercular network and the ventral and dorsal attention networks (Chen et al., 2016). However, that study used a sliding temporal window of 30 seconds duration, leaving unclear the generality of our findings. Here we take advantage of BSFA latent dynamics model, with no assumptions of window length or number of underlying states, to investigate dynamic interactions between the three networks and, crucially, to determine whether SN nodes have higher temporal flexibility than those of the DMN and CEN. Accordingly, we applied BSFA to rs-fMRI data from the HCP to uncover dynamic functional interactions between SN, CEN and DMN. The nodes of the three networks were identified as described in Section 2.2.4. We performed separate analyses on two HCP datasets from Sessions 1 and 2, importantly, to demonstrate the test-retest reliability and robustness of all our findings across two Sessions.

3.3.1. Identification of dynamic brain states

HCP Session 1

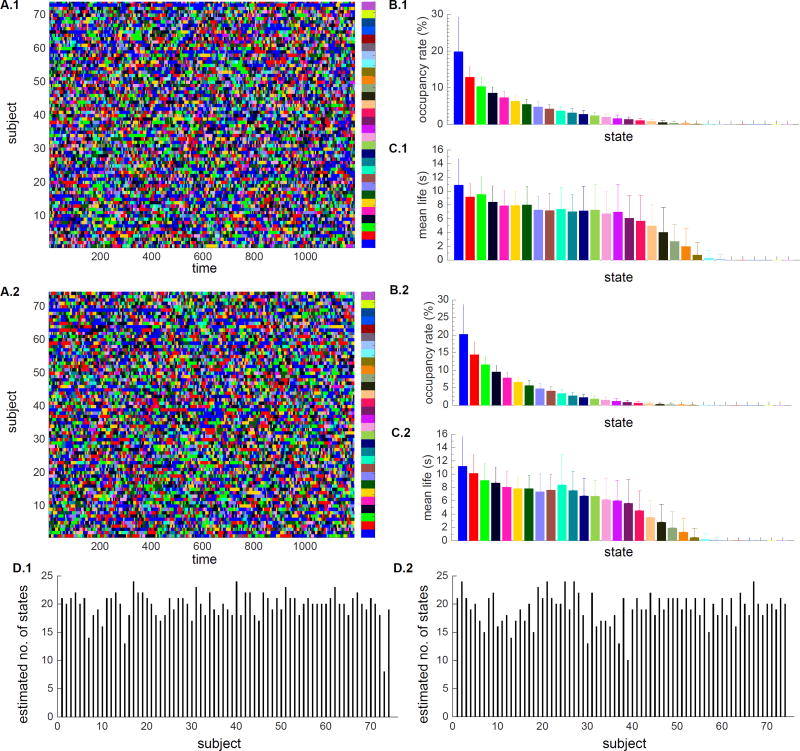
We used BSFA to uncover the temporal evolution of latent states in each participant (Figure 9A.1), the occupancy rate of each state averaged across all subjects (Figure 9B.1), the mean life of each state averaged across all subjects (Figure 9C.1), and estimated number of states for each subject (Figure 9D.1). As discussed earlier in Section 2.4.3, there is only a one-to-one matching between states across subjects of a given session, however, across sessions, states are not matched. As a convention, states are ranked and color-coded based on their occupancy rate such that the first state has the highest occupancy rate. Nonetheless, the same color-code across two sessions does not necessarily correspond to the same state. Out of initially assigned 30 states, there are 24 states with occupancy greater than about zero. On average, subjects have 19.75 states (with standard deviation of 2.4, Figure 9D.1). The first 6 states have occupancy greater than 6% and together they account for approximately 61% of the total occupancy. Among the remaining 24 states, 19 states have mean life greater than 3 seconds. The first 6 states have mean life of about 8 seconds indicating temporal persistence over durations much shorter than the length of the scan (864 seconds).

Figure 9.

Occupancy rate and mean life in rs-fMRI data from Sessions 1 and 2. States are sorted and color-coded based on their occupancy rate such that state 1 has the highest occupancy rate. Each state is shown in a unique color. Within each session, there is a one-to-one matching between states across subjects. However, two states with the same color-code across two sessions, do not necessarily point to the same state. The choice of color is primarily based on the state occupancy rates in each session. (A) Temporal evolution of latent states for each subject in (A.1) Session 1 and (A.2) Session 2 (B) Mean and standard deviation of the occupancy rate of each state averaged across subjects for (B.1) Session 1 and (B.2) Session 2. (C) Mean and standard deviation of the mean life of each state averaged across subjects for (C.1) Session 1 and (C.2) Session 2. (D) Estimated number of states for each subject for (D.1) Session 1 and (D.2) Session 2.

HCP Session 2

A similar analysis was conducted on Session 2 data. BSFA uncovered the temporal evolution of latent states in each participant, the occupancy rate of each state averaged across all subjects, the mean life of each state averaged across all subjects, and estimated number of states for each subject (Figure 9A.2, B2, C2, D.2). States are ranked and color-coded based on their occupancy rate. Two states with the same color-code across two sessions do not necessarily correspond to the same state. Out of initially assigned 30 states, 24 states have occupancy greater than about zero. On average, subjects have 19.2 states (with standard deviation of 2.7, Figure 9D.2). The first 6 states, similar to Session 1, have occupancy greater than 6% and together they account for 66% of the total occupancy. Among the remaining 24 states, 18 states have mean life greater than 3 seconds. The first 6 states have mean life of about 8 seconds. Thus, the overall pattern of latent states, occupancy rates and mean life of states is consistent across two sessions.

3.4. Transition between dynamic functional states

HCP Session 1

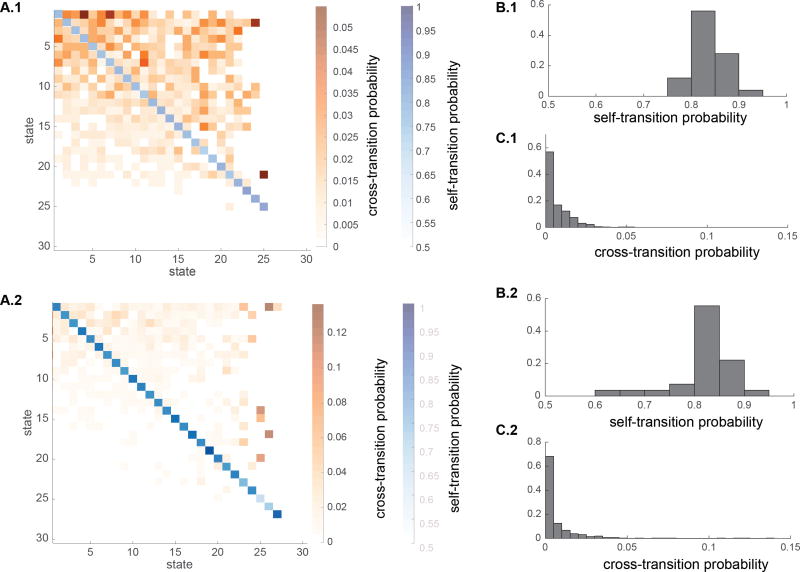
Next we assessed transition probabilities between states (Figure 10A.1). Self-transition probabilities are shown with continuous blue colors and cross transition probabilities are shown with continuous orange colors. As before, states are sorted based on their occupancy rate with the first state having the highest occupancy. Figure 10B.1 shows the histogram of self-transition probabilities. Self-transition probabilities vary between range of 0.76 and 0.94 with average of 0.83. Figure 10C.1 shows histogram of the cross-transition probabilities. Cross-transition probabilities vary between about 0 and 0.055 with average of 0.0097.

Figure 10.

Transition probabilities between dynamic states in HCP rs-fMRI data. Because states are not matched across sessions, for the purpose of visualization, states are ranked based on their occupancy rate such that the first state has the highest occupancy rate. (A) Self-transition and cross-transition probabilities in (A.1) Session 1 and (A.2) Session 2. Self-transition probabilities are shown with continuous blue colors and cross transition probabilities are shown with continuous orange colors. States are sorted based on their occupancy rate with the first state having the highest occupancy. (B) Histogram of self-transition probabilities in (B.1) Session 1 and (B.2) Session 2. (C) Histogram of the cross-transition probabilities in (C.1) Session 1 and (C.2) Session 2.

HCP Session 2

Figure 10A.2 shows transition probabilities between states. Figure 10B.2 shows the histogram of self-transition probabilities. Self-transition probabilities vary between 0.62 and 0.96 with average of 0.82, suggesting stability of individual states when they occur. Figure 10C.2 shows histogram of the cross-transition probabilities. Cross-transition probabilities vary between 0 and 0.136 with average of 0.010. Thus, the pattern of transition probabilities is consistent across sessions.

3.5. Dynamic functional networks

To characterize connectivity patterns associated with each brain state, we used a community detection algorithm on the estimated Pearson correlations in each state and examined functional connectivity between ROIs. The salient features of the dynamic functional network structure in each HCP session are described below.

HCP Session 1

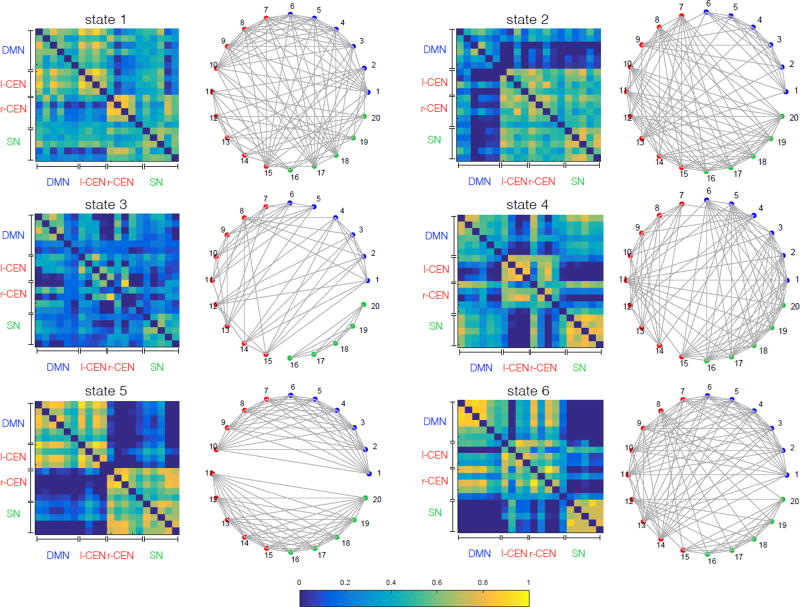
Pearson correlation matrices of the first 6 states which have percent occupancy greater than 6% each and their corresponding community structure are shown in Figure 11, with each ROI depicted in a unique color corresponding to the static network it belongs to. Blue color shows 6 nodes corresponding to DMN, green color shows 5 nodes corresponding to SN, and red color shows 9 nodes corresponding to left and right CEN (Table G.2).

Figure 11.

Pearson correlation matrices of the first 6 states with occupancy rate greater than 6% (left) and their corresponding community structures (right) on rs-fMRI from Session 1. Community structures are computed using modularity maximization approach (§ 2.4.6). Results show a high level of dynamic functional interactions between nodes of the salience, default mode and central-executive networks.

HCP Session 2

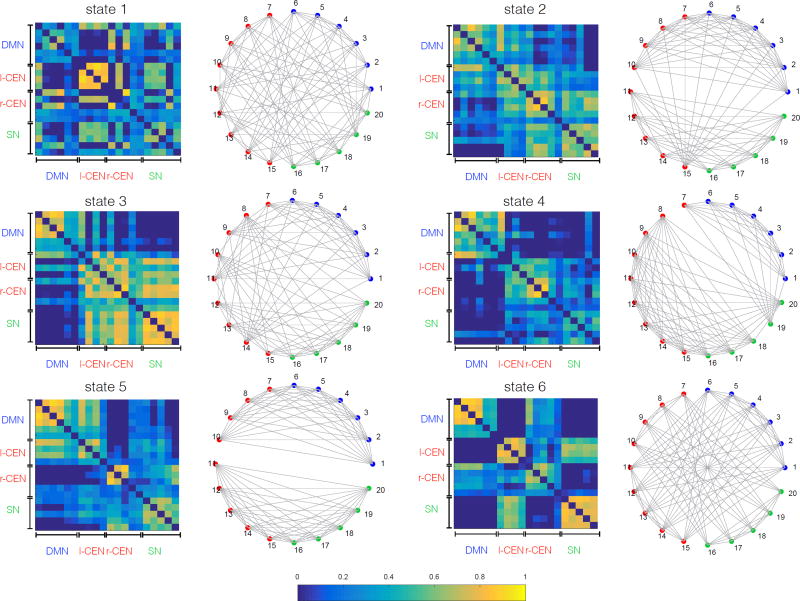
Pearson covariance matrices of the first 6 states which have occupancy greater than 6% and their corresponding community structure are shown in Figure 12.

Figure 12.

Pearson correlation matrices of the first 6 states with occupancy rate greater than 6% (left) and their corresponding community structures (right) on rs-fMRI from Session 2. Community structures are computed using modularity maximization approach (§ 2.4.6). Similar to Session 1 (Figure 11), results reveal a high level of dynamic functional interactions between nodes of the salience, default mode and central-executive networks. Note that there is no one-to-one correspondence between state covariance matrices shown in this figure and the ones shown in Figure 11. States are sorted based on their occupancy rate.

Note that states in Figure 11 and Figure 12 are sorted based on their occupancy rate. However, we emphasize that sorting based on the fractional occupancy does not guarantee a one-to-one correspondence between states across the two sessions, and it reflects a general difficulty in matching states without imposing a common model. For direct comparison, one would need to match states ad-hoc for example based on their covariance structure but this can be non-trivial in practice. A more appropriate way would be to combine data from both sessions within a common BSFA model. However, our choice of performing separate analyses on data from the two sessions was based on our goal of demonstrating the robustness of our key neuroscientific findings across sessions, as described in the next section. Note that our subsequent analysis in § 3.6 does not require explicit matching of the states between sessions. Results in Figure 11 and Figure 12 may be seen as intermediate steps toward our higher-level temporal flexibility analysis.

Taken together, these results demonstrate that although the DMN, SN, CEN have separately previously been identified using static network analysis, BSFA demonstrates frequent and dynamically changing cross-network interactions.

3.6. Temporal flexibility of individual brain regions

In addition to characterization of brain states and the associated dynamics as described above, BSFA provides a quantitative framework to examine graph-theoretic properties that capture and measure topological structure of a brain region or network of interest. To demonstrate this, we computed temporal flexibility of the 20 ROIs. Temporal flexibility is a measure of how frequently a brain region interacts with regions belonging to other dynamic functional networks across time (Chen et al., 2016).

HCP Session 1

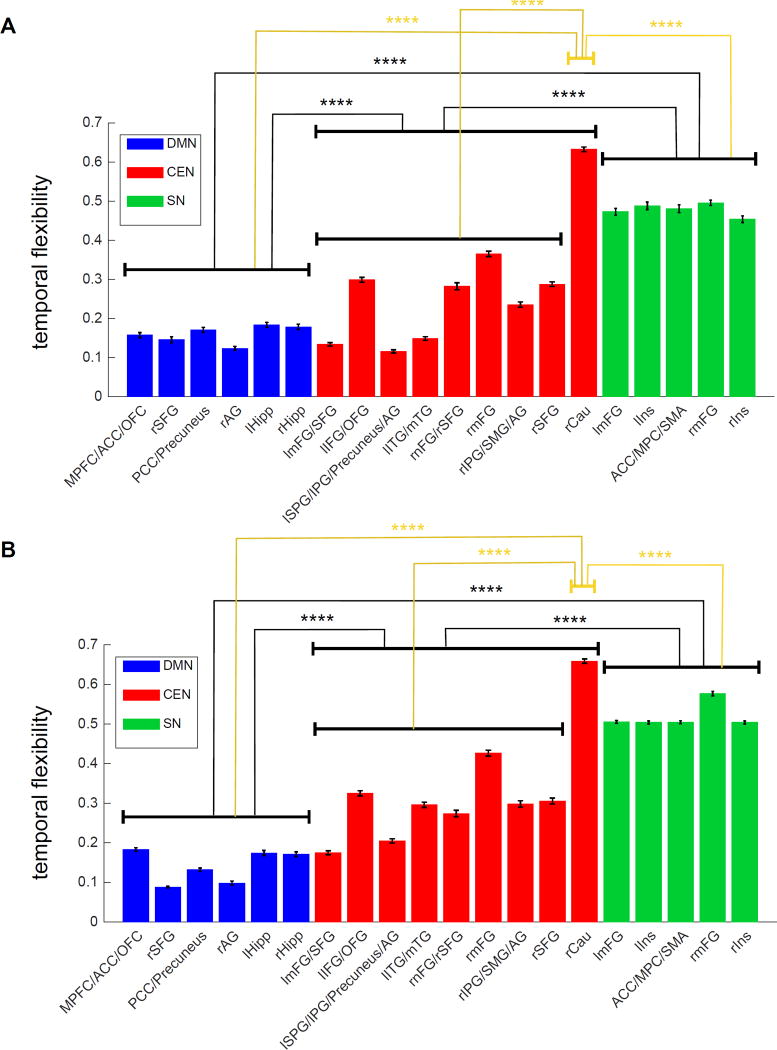
The temporal flexibility of each ROI is shown in Figure 13A. Brain regions in the SN showed the highest temporal flexibility.

Figure 13.

Average and standard deviation of the temporal flexibility across all subjects on HCP rs-fMRI data with 20 ROIs from (A) Session 1 and (B) Session 2 (****: p<10⁻⁴).

HCP Session 2

As in HCP Session 1, SN showed the highest temporal flexibility (Figure 13B).

Thus, BSFA consistently identifies SN nodes as having a significantly higher temporal flexibility, compared to nodes of the CEN and DMN (p<10⁻⁴). These results converge on recent findings using a brain wide analysis using 264 nodes spanning multiple brain systems which found SN nodes had the highest level of temporal flexibility (Chen et al., 2016). The present results obtained using a generative model with no assumptions of window length further bolster the previous findings.

It is notable that the right Caudate showed the highest level of temporal flexibility among all brain regions examined here, including SN, in both Session 1 and 2 (p<10⁻⁴). The high level of temporal flexibility of the right Caudate suggests that, despite being identified as part of the same network by static connectivity analysis, this region has a highly differentiated network dynamics distinct from other prefrontal, parietal and temporal nodes of the CEN. Our findings point to a unique temporal property of the Caudate and other subcortical nodes consistent with results from a prior study (Chen et al., 2016). Further research is required to investigate the behavioral significance and dynamic functional role of our novel findings.

These findings are important because they further demonstrate that BSFA can identify key features of brain dynamics in a robust and consistent manner with minimal assumptions. In this context, an important challenge for future work is extending BSFA to the whole brain, a key limitation here is the approximate 10:1 ratio of time points to number of ROIs required to to obtain reliable estimates of latent states in HMM models, as demonstrated in our simulations above (see Appendix H for practical considerations in analysis of large number of ROIs). Nevertheless, it is highly encouraging that despite the complexity of human brain dynamics, our findings provide convergent evidence for distinct dynamic functional features associated with the SN and further demonstrate the usefulness of BSFA models.

4. Conclusion

We developed a novel generative method for modeling time-varying functional connectivity in fMRI data: Bayesian switching factor analysis (BSFA). Key strengths of BSFA include: (1) a generative model which provides useful information about underlying structure of the brain dynamic functional networks including: time evolution of brain states and transition probabilities between states as a function of time; (2) regulating the model complexity by automatic determination of the number of latent states (brain states) via Bayesian model selection and the automatic determination of intrinsic dimensionality of the latent subspace at each latent state via Bayesian automatic relevance determination.

Key features of the method were validated using extensive simulations. We then applied BSFA to model dynamic temporal structures in fMRI data. Fingerprint analysis of multisession resting-state fMRI data from the Human Connectome Project (HCP) demonstrated that BSFA is able to successfully capture the subject-specific temporal dynamics. We further demonstrated that modeling temporal dependencies in the BSFA generative model results in improved fingerprinting of individual participants. BSFA models revealed a high level of dynamic temporal interactions between brain networks previously identified as being temporally segregated and independent. Crucially, BSFA revealed a high level of dynamic functional interactions between nodes of the salience, default mode and central-executive networks, and furthermore, identified salience network nodes as having higher temporal flexibility than nodes of the other two networks. Finally, BSFA findings demonstrated strong test-retest reliability.

Overcoming the curse of dimensionality when the number of brain regions is large (~200) remains an important challenge for future work on HMM-based generative models of experimental fMRI data. Finally, it is important to note that although in this study experiments were carried out on resting-state fMRI data, BSFA can be used for dynamic brain connectivity analysis of task-based fMRI time-series. Future studies will examine this further.

Appendix A

Parameter priors for BSFA

Following Bayesian HMM by Mackay (1997), the prior distributions on the HMM model parameters are chosen as follows:

$$p(\mathit{\pi })=\text{Dir}({\alpha }_{\mathit{\pi }}^{\ast }{\mathit{m}}^{\ast }),\text{ such that }{\mathit{m}}^{\ast }={[\frac{1}{K},\dots ,\frac{1}{K}]}^{\top },$$ (A.1)

$$p(\mathit{A})=\prod _{i=1}^{K}p({\mathit{a}}_i)=\prod _{i=1}^K\text{Dir}({\alpha }_{{\mathit{a}}_i}^{\ast }{\mathit{m}}^{\ast }),\text{ such that }{\mathit{m}}^{\ast }={[\frac{1}{K},\dots ,\frac{1}{K}]}^{\top },$$ (A.2)

where, for instance, $\text{Dir}({\alpha }_{\mathit{\pi }}^{\ast }{m}^{\ast })$ is a symmetric Dirichlet distribution with strength ${\alpha }_{\mathit{\pi }}^{\ast }$. a_i indicates the i-th row of the transition matrix A. For a noninformative initialization, we set ${\alpha }_{\mathit{\pi }}^{\ast }={\alpha }_{{\mathit{a}}_i}^{\ast }=1$, ∀i = 1,…, K.

For the other model parameters, we use the same choice of priors as proposed by Ghahramani and Beal (2000) for the static factor analysis model. The priors are chosen to be conjugate to the likelihood terms.

$$p(\mathit{U}|\mathit{\nu })\mathit{=}\prod _{k=1}^K\prod _{d=1}^{D}p({\dot{\mathit{u}}}_{\mathit{\text{kd}}}|{\mathit{\nu }}_k)=\prod _{k=1}^K\prod _{d=1}^D𝒩(\mathbf{0},\text{diag}{({\mathit{\nu }}_k)}^{-1}),$$ (A.3)

where u̇_kd shows the d-th row of the factor loading matrix U at the k-th state and 0 is a P-dimensional vector of zero values.

$$p(\mathit{\nu })=\prod _{k=1}^K\prod _{p=1}^{P}p({\nu }_{\mathit{\text{kp}}})=\prod _{k=1}^K\prod _{p=1}^P𝒢(a^{\ast },b^{\ast }),$$ (A.4)

where a* and b* are shape and inverse-scale hyperparameters for a Gamma distribution. For a noninformative initialization we set these parameters as: a* = b* = 1. The same prior values can be used for all k, p.

$$p(\mathit{\mu })=\prod _{k=1}^{K}p({\mathit{\mu }}_k)=\prod _{k=1}^K𝒩({\mathit{\mu }}^{\ast },\text{diag}{({\mathit{\nu }}^{\ast })}^{-1}).$$ (A.5)

For a noninformative initialization we set μ* = 0_D, ∀ k = 1,…, K, where 0_D is a D-dimensional zero vector and ν* = 10⁻³ × 1_D, where 1_D is a D-dimensional vector of unit values.

Appendix B

Posterior distribution of the model parameters

Let us start with rewriting the posterior distribution of the model parameters, q(Ẕ, X̱, ϕ, θ), given by equation (9):

$$q(\underset{¯}{\mathit{Z}},\underset{¯}{\mathit{X}},\mathit{\varphi },\mathit{\theta })=q(\underset{¯}{\mathit{X}},\mathit{\varphi }|\underset{¯}{\mathit{Z}})q(\underset{¯}{\mathit{Z}})q(\mathit{\theta })=q(\underset{¯}{\mathit{X}}|\underset{¯}{\mathit{Z}})q(\underset{¯}{\mathit{Z}})q(\mathit{U}|\mathit{\nu })q(\mathit{\nu })q(\mathit{\mu })q(\mathit{A})q(\mathit{\pi }),$$ (B.1)

where we have used θ = {π, A}, and ϕ = {μ, U, Ψ}. In this section, we summarize the exact form of these distributions and the necessary summary of statistics.

$$q(\mathit{\pi })=\text{Dir}({\mathit{\alpha }}_{\mathit{\pi }}),\text{ where }{\mathit{\alpha }}_{\mathit{\pi }}=\sum _{s=1}^S({\alpha }_{\mathit{\pi }}^{\ast }{\mathit{m}}^{\ast })+{\langle {\mathit{z}}_1^s\rangle }_{q({\mathit{z}}_1^s)}$$ (B.2)

$$q(\mathit{A})=\prod _{i=1}^{K}q({\mathit{a}}_i)=\prod _{i=1}^K\text{Dir}({\mathit{\alpha }}_{{\mathit{a}}_i}),\text{ where }{\mathit{\alpha }}_{\mathit{A}}=\left[\begin{array}{c}\hfill {\mathit{\alpha }}_{{\mathit{a}}_1}\hfill \\ \hfill {\mathit{\alpha }}_{{\mathit{a}}_K}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\alpha }_{{\mathit{a}}_1}^{\ast }{\mathit{m}}^{\ast \top }\hfill \\ \hfill {\alpha }_{{\mathit{a}}_K}^{\ast }{\mathit{m}}^{\ast \top }\hfill \end{array}\right]+\sum _{s=1}^s\sum _{t=2}^T{\langle {\mathit{z}}_{t-1}^s{\mathit{z}}_t^s\rangle }_{q({\mathit{z}}_t^s)}$$ (B.3)

$$q(\mathit{\nu })=\prod _{k=1}^K\prod _{d=1}^{D}q({\nu }_{\mathit{\text{kd}}})=\prod _{k=1}^K\prod _{d=1}^D𝒢(a_k,b_k),\text{ where }{a}_k=a^{\ast }+\frac{D}{2},b_k=b^{\ast }+\frac{1}{2}\sum _{d=1}^D{\langle {\mathit{u}}_{\mathit{\text{kd}}}^{\top }{\mathit{u}}_{\mathit{\text{kd}}}\rangle }_{q(\mathit{U})}$$ (B.4)

$$q\left(\right[\begin{array}{c}\hfill \mathit{U}\hfill \\ \hfill \mathit{\mu }\hfill \end{array}\left]\right)=\prod _{k=1}^K\prod _{d=1}^{D}q\left(\right[\begin{array}{c}\hfill {\dot{\mathit{u}}}_{\mathit{\text{kd}}}\hfill \\ \hfill {\mu }_{\mathit{\text{kd}}}\hfill \end{array}\left]\right)=\prod _{k=1}^K\prod _{d=1}^D𝒩\left(\right[\begin{array}{c}\hfill {\overline{\dot{\mathit{u}}}}_{\mathit{\text{kd}}}\hfill \\ \hfill {\overline{\mu }}_{\mathit{\text{kd}}}\hfill \end{array}],{\mathrm{\Gamma }}_{\mathit{\text{kd}}}),\text{where }{\mathrm{\Gamma }}_{\mathit{\text{kd}}}=\left[\begin{array}{cc}\hfill {({\sum }_{\mathit{\text{kd}}}^{\mathit{\text{UU}}})}^{-1}\hfill & \hfill {\left({\sum }_{\mathit{\text{kd}}}^{\mathit{U}\mathit{\mu }}\right)}^{-1}\hfill \\ \hfill {\left({\sum }_{\mathit{\text{kd}}}^{\mathit{\mu }\mathit{U}}\right)}^{-1}\hfill & \hfill {({\sum }_{\mathit{\text{kd}}}^{\mathit{\mu }\mathit{\mu }})}^{-1}\hfill \end{array}\right],$$ (B.5)

and

$${({\sum }_{\mathit{\text{kd}}}^{\mathit{\text{UU}}})}^{-1}=\text{diag }\left({\langle {\mathit{\nu }}_k\rangle }_{q({\mathit{\nu }}_k)}\right)+{\mathrm{\Psi }}_{\mathit{\text{dd}}}^{-1}\sum _{s=1}^S\sum _{t=1}^T{\langle z_{\mathit{\text{kt}}}^s\rangle }_{q(z_{\mathit{\text{kt}}}^s)}{\langle {\mathit{x}}_{\mathit{\text{kt}}}^s{{\mathit{x}}_{\mathit{\text{kt}}}^s}^{\top }\rangle }_{q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)}$$ (B.6)

$${\left({\sum }_{\mathit{\text{kd}}}^{\mathit{U}\mathit{\mu }}\right)}^{-1}={\left({\sum }_{\mathit{\text{kd}}}^{\mathit{\mu }\mathit{U}}\right)}^{-1}={\mathrm{\Psi }}_{\mathit{\text{dd}}}^{-1}\sum _{s=1}^S\sum _{t=1}^T{\langle z_{\mathit{\text{kt}}}^s\rangle }_{q(z_{\mathit{\text{kt}}}^s)}{\langle {\mathit{x}}_{\mathit{\text{kt}}}^s\rangle }_{q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)}$$ (B.7)

$${({\sum }_{\mathit{\text{kd}}}^{\mathit{\mu }\mathit{\mu }})}^{-1}={\nu }_d^{\ast }+{\mathrm{\Psi }}_{\mathit{\text{dd}}}^{-1}\sum _{s=1}^S\sum _{t=1}^T{\langle z_{\mathit{\text{kt}}}^s\rangle }_{q(z_{\mathit{\text{kt}}}^s)}$$ (B.8)

$${\overline{\dot{\mathit{u}}}}_{\mathit{\text{kd}}}={[{\mathrm{\Gamma }}_{\mathit{\text{kd}}}]}_{\mathit{\text{UU}}}\left({\mathrm{\Psi }}_{\mathit{\text{dd}}}^{-1}\sum _{s=1}^S\sum _{t=1}^T{\langle z_{\mathit{\text{kt}}}^s\rangle }_{q(z_{\mathit{\text{kt}}}^s)}{𝒴}_{\mathit{\text{dt}}}^s{\langle {\mathit{x}}_{\mathit{\text{kt}}}^s\rangle }_{q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)}\right),$$ (B.9)

$${\overline{\mu }}_{\mathit{\text{kd}}}={[{\mathrm{\Gamma }}_{\mathit{\text{kd}}}]}_{\mathit{\mu }\mathit{\mu }}({\mathrm{\Psi }}_{\mathit{\text{dd}}}^{-1}\sum _{s=1}^S\sum _{t=1}^T{\langle z_{\mathit{\text{kt}}}^s\rangle }_{q(z_{\mathit{\text{kt}}}^s)}{𝒴}_{\mathit{\text{dt}}}^s+{\nu }_d^{\ast }{\mu }_d^{\ast }).$$ (B.10)

$$q({\mathit{x}}_t^s|{\mathit{z}}_t^s)=\prod _{k=1}^{K}q({\mathit{x}}_{\mathit{\text{kt}}}^s)=\prod _{k=1}^K𝒩({\overline{\mathit{x}}}_{\mathit{\text{kt}}}^s,{\mathbf{\sum }}_k),$$ (B.11)

where

$${\mathbf{\sum }}_k^{-1}=\mathit{I}+{\langle {\mathit{U}}_k^{\top }{\mathbf{\Psi }}^{-1}{\mathit{U}}_k\rangle }_{\left[\begin{array}{c}\hfill q({\mathit{U}}_k)\hfill \\ \hfill q({\mathit{\mu }}_k)\hfill \end{array}\right]}$$ (B.12)

$${\overline{\mathit{x}}}_{\mathit{\text{kt}}}^s={\mathbf{\sum }}_k{\langle {\mathit{U}}_k^{\top }{\mathbf{\Psi }}^{-1}({\mathit{y}}_t^s-{\mathit{\mu }}_k)\rangle }_{\left[\begin{array}{c}\hfill q({\mathit{U}}_k)\hfill \\ \hfill q({\mathit{\mu }}_k)\hfill \end{array}\right]}$$ (B.13)

Note that (µ_k)_q(µk), 〈ν_kp〉_q(νkp), ${\langle {\mathit{u}}_{\mathit{\text{kp}}}^{\top }{\mathit{u}}_{\mathit{\text{kp}}}\rangle }_{q(\mathit{U})},{\langle {\mathit{x}}_{\mathit{\text{kt}}}^s{{\mathit{x}}_{\mathit{\text{kt}}}^s}^{\top }\rangle }_{q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)}$, and ${\langle {\mathit{x}}_{\mathit{\text{kt}}}^s\rangle }_{q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)}$ are given by the known statistics of their associated distributions. For example, 〈ν_kp〉_q(νkp) is given by the mean value of the Gamma distribution expressed by Equation (B.4) which will be updated at each iteration of the optimization.

Appendix C

Updating HMM model parameters

$${\langle \text{log }{a}_{\mathit{\text{ij}}}\rangle }_{q(\mathit{A})}=\psi ({\alpha }_{a_{\mathit{\text{ij}}}})-\psi \left(\sum _{l=1}^K{\alpha }_{a_{i,l}}\right),\forall i,j=1,\dots ,K$$ (C.1)

$${\langle \text{log }{\pi }_k\rangle }_{q({\pi }_k)}=\psi ({\alpha }_{{\pi }_k})-\psi \left(\sum _{j=1}^K{\alpha }_{{\pi }_j}\right),\forall k=1,\dots ,K$$ (C.2)

where ψ(·) indicates the mathematical digamma function, α_aij is the j-th element of α_ai given by Equation (B.3), and similarly, α_πk is the k-th element of α_π given by Equation (B.2).

Appendix D

Posterior distribution of the latent state variables

We compute the sufficient statistics for the posterior distribution of the latent state variables, ${\langle {\mathit{z}}_t^s\rangle }_{q({\mathit{z}}_t^s)}$ and ${\langle {\mathit{z}}_t^s{\mathit{z}}_{t-1}^s\rangle }_{q({\mathit{z}}_t^s)}$, using a variant of forward and backward algorithm. For this purpose, we start with computation of the emission probability distribution given by Equations (11). Using the results in Appendix B, we obtain an explicit expression for the computation of the emission probability distribution as

$${𝒪}_{\mathit{\text{kt}}}^s=\text{exp}(ℒ({\mathit{y}}_t^s|z_{\mathit{\text{kt}}}^s=1)),$$ (D.1)

where

$$ℒ({\mathit{y}}_t^s|z_{\mathit{\text{kt}}}^s=1)={\langle \text{log }p({\mathit{y}}_t^s|z_{\mathit{\text{kt}}}^s,{\mathit{x}}_{\mathit{\text{kt}}}^s,{\mathit{U}}_k,{\mathbf{\Psi }}_k,)\rangle }_{q({\mathit{U}}_k)q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)}-{\langle \text{log }q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s\rangle }_{q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)}=\frac{1}{2}\text{log}|{\mathbf{\sum }}_k|-\frac{1}{2}\text{trace }({\mathrm{\Psi }}^{-1}{\langle ({\mathit{y}}_t^s-[\begin{array}{c}\hfill {\mathit{U}}_k\hfill \\ \hfill {\mathit{\mu }}_k\hfill \end{array}\left]\right[\begin{array}{c}\hfill {\mathit{x}}_{\mathit{\text{kt}}}^s\hfill \\ \hfill 1\hfill \end{array}\left]\right){({\mathit{y}}_t^s-[\begin{array}{c}\hfill {\mathit{U}}_k\hfill \\ \hfill {\mathit{\mu }}_k\hfill \end{array}\left]\right[\begin{array}{c}\hfill {\mathit{x}}_{\mathit{\text{kt}}}^s\hfill \\ \hfill 1\hfill \end{array}\left]\right)}^{\top }\rangle }_{\left[\begin{array}{c}\hfill q({\mathit{U}}_k)\hfill \\ \hfill q({\mathit{\mu }}_k)\hfill \end{array}\right]q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)})$$ (D.2)

Forward Algorithm

The forward procedure is initialized for t = 1 as

$${\alpha }_{i1}^s={\stackrel{\sim }{a}}_{\mathit{\text{Ki}}}{𝒪}_{\mathit{\text{it}}}^s,\text{ where }{\stackrel{\sim }{a}}_{\mathit{\text{ij}}}=\text{exp }\left({\langle \text{log}{a}_{\mathit{\text{ij}}}\rangle }_{q(\mathit{A})}\right),\forall 1\le i\le K.$$ (D.3)

Then, the forward iteration can formally run for t = 2,…, T as

$${\alpha }_{\mathit{\text{jt}}}^s=\sum _{i=1}^K{\alpha }_{t-1,i}^s{\stackrel{\sim }{a}}_{\mathit{\text{ij}}}{𝒪}_{\mathit{\text{jt}}}^s,\forall 1\le j\le K.$$ (D.4)

For later use in the computation of the lower bound, we compute the the normalization constant C as

$$C=\sum _{s=1}^S\sum _{k=1}^K{\alpha }_{\mathit{\text{kT}}}^s.$$ (D.5)

Backward Algorithm

To supplement the forward calculation, we need a backward variable to represent the observed conditions after time t. The backward variable is initialized as ${\beta }_{\mathit{\text{jT}}}^s=1$ for all j = 1,…, K. The backward variable is recursively defined for t = T − 1,…, 1 as

$${\beta }_{\mathit{\text{it}}}^s=\sum _{j=1}^K{\stackrel{\sim }{a}}_{\mathit{\text{ij}}}{𝒪}_{j,t+1}^s{\beta }_{j,t+1}^s,\forall 1\le i\le K.$$ (D.6)

Finally, ${\langle z_{\mathit{\text{kt}}}^s\rangle }_{q(z_{\mathit{\text{kt}}}^s)}$ and ${\langle z_{\mathit{\text{it}}}^s{z}_{j,t-1}^s\rangle }_{q({\mathit{z}}_t^s)}$ are given by:

$${\langle z_{\mathit{\text{it}}}^s\rangle }_{q(z_{\mathit{\text{it}}}^s)}=\frac{{\alpha }_{\mathit{\text{it}}}^s{\beta }_{\mathit{\text{it}}}^s}{{\sum }_{k=1}^K{\alpha }_{\mathit{\text{kt}}}^s{\beta }_{\mathit{\text{kt}}}^s},$$ (D.7)

$${\langle z_{\mathit{\text{it}}}^s{z}_{j,t-1}^s\rangle }_{q(z_t^s)}=\frac{{\alpha }_{j,t-1}^s{\stackrel{\sim }{a}}_{\mathit{\text{ij}}}{𝒪}_{\mathit{\text{it}}}^s{\beta }_{\mathit{\text{it}}}^s}{{\sum }_{k=1}^K{\sum }_{l=1}^K{\alpha }_{l,t-1}^s{\stackrel{\sim }{a}}_{\mathit{\text{kl}}}{𝒪}_{\mathit{\text{kt}}}^s{\beta }_{\mathit{\text{kt}}}^s},\forall 1\le i,j\le K.$$ (D.8)

Appendix E

Optimization of the posterior hyperparameters

We take a similar approach as in the static variant of the factor analysis (Ghahramani and Beal, 2000; Beal, 2003) for the optimization of the hyperparameters α*m*, a*, b*, μ*, ν*, Ψ (Ghahramani and Beal, 2000).

$${\mathbf{\Psi }}^{-1}=\text{diag }\left(\frac{1}{\mathit{\text{TS}}}\sum _{s=1}^S\sum _{t=1}^T\sum _{k=1}^K{\langle ({\mathit{y}}_t^s-[\begin{array}{c}\hfill {\mathit{U}}_k\hfill \\ \hfill {\mathit{\mu }}_k\hfill \end{array}\left]\right[\begin{array}{c}\hfill {\mathit{x}}_{\mathit{\text{kt}}}^s\hfill \\ \hfill 1\hfill \end{array}\left]\right){({\mathit{y}}_t^s-[\begin{array}{c}\hfill {\mathit{U}}_k\hfill \\ \hfill {\mathit{\mu }}_k\hfill \end{array}\left]\right[\begin{array}{c}\hfill {\mathit{x}}_{\mathit{\text{kt}}}^s\hfill \\ \hfill 1\hfill \end{array}\left]\right)}^{\top }\rangle }_{\left[\begin{array}{c}\hfill q({\mathit{U}}_k)\hfill \\ \hfill q({\mathit{\mu }}_k)\hfill \end{array}\right]q({\mathit{x}}_{\mathit{\text{kt}}}^s|z_{\mathit{\text{kt}}}^s)q(z_{\mathit{\text{kt}}}^s)}\right)$$ (E.1)

Hyperparameters a*, b* are computed from the following fixed-point Equations

$$\psi ({\alpha }^{\ast })=\text{log}(b^{\ast })+\frac{1}{\mathit{\text{KP}}}\sum _{k=1}^K\sum _{p=1}^P{\langle \text{log}{\nu }_{\mathit{\text{kp}}}\rangle }_{q({\nu }_{\mathit{\text{kp}}})},$$ (E.2)

$$b^{\ast -1}=\frac{1}{a^{\ast }\mathit{\text{KP}}}\sum _{k=1}^K\sum _{p=1}^P{\langle {\nu }_{\mathit{\text{kp}}}\rangle }_{q({\nu }_{\mathit{\text{kp}}})}$$ (E.3)

The scale prior $m_k^{\ast }=\frac{1}{K}$ is fixed and ${\alpha }_{\mathit{\pi }}^{\ast }={\alpha }_{{\mathit{a}}_i}^{\ast }={\alpha }^{\ast }$ are given for all i = 1,…, K as:

$$\psi ({\alpha }^{\ast })-\psi (\frac{{\alpha }^{\ast }}{K})=\frac{1}{K}\sum _{k=1}^K\psi (\alpha )-\psi (\alpha m_k).$$ (E.4)

$${\mathit{\mu }}^{\ast }=\frac{1}{K}\sum _{k=1}^K{\langle {\mathit{\mu }}_k\rangle }_{q({\mathit{\mu }}_k)},$$ (E.5)

$${\mathit{\nu }}^{\ast }=[{\nu }_1^{\ast },\dots ,{\nu }_D^{\ast }],\text{ with }{\nu }_d^{\ast }=\frac{1}{K}\sum _{k=1}^K\langle ({\mu }_{\mathit{\text{kd}}}-{\mu }_d^{\ast })({\mu }_{\mathit{\text{kd}}}-{\mu }_d^{\ast })\rangle q({\mathit{\mu }}_k),$$ (E.6)

where the update for ν* uses the already updated μ*, and 〈logν_kp〉_q(νkp) is given by the known sufficient statistics of its distribution, Equation (B.4).

Appendix F

Lower bound evaluation

The lower bound is computed from Equation (10) and it is explicitly expressed as:

$$ℒ=\text{log}C+{\langle \text{log}\frac{p(\mathit{A})}{q(\mathit{A})}\rangle }_{q(\mathit{A})}+{\langle \text{log}\frac{p(\mathit{\pi })}{q(\mathit{\pi })}\rangle }_{q(\mathit{\pi })},$$ (F.1)

where C is given by Equation (D.5), and other terms can be easily computed from the functional forms of the priors and posterior parameters computed in the previous sections.

Appendix G

List of regions of interest

Table G.2.

List of regions of interest (ROIs) and their abbreviations defined using 20 clusters from the SN, CEN and DMN. ROIs are defined according to Supplementary Table S1 from (Shirer et al., 2012).

List of 20 ROIs
DMN	1 MPFC/ACC/OFC	Medial Prefrontal Cortex/Anterior Cingulate Cortex/Orbitofrontal Cortex
	2 rSFG	Right Superior Frontal Gyrus
	3 PCC/Precuneus	Posterior Cingulate Cortex/Precuneus
	4 rAG	Right Angular Gyrus
	5 lHipp	Left Hippocampus
	6 rHipp	Right Hippocampus
CEN	7 lmFG/SFG	Left Middle Frontal Gyrus/Superior Frontal Gyrus
	8 lIFG/OFG	Left Inferior Frontal Gyrus/Orbitofrontal Gyrus
	9 lSPG/IPG/Precuneus/AG	Left Superior Partial Gyrus/Inferior Parietal Gyrus/Precuneus/Angular Gyrus
	10 lITG/mTG	Left Inferior Temporal Gyrus/Middle Temporal Gyrus
	11 rmFG/rSFG	Right Middle Frontal Gyrus/Right Superior Frontal Gyrus
	12 rmFG	Right Middle Frontal Gyrus
	13 rIPG/SMG/AG	Right Inferior Parietal Gyrus/Supramarginal Gyrus, Angular Gyrus
	14 rSFG	Right Superior Frontal Gyrus
	15 rCau	Right Caudate
SN	16 lmFG	Left Middle Frontal Gyrus
	17 lIns	Left Insula
	18 ACC/MPC/SMA	Anterior Cingulate Cortex/Medial Prefrontal Cortex/Supplementary Motor Area
	19 rmFG	Right Middle Frontal Gyrus
	20 rIns	Right Insula

Appendix H

Scalability: practical considerations

As in principal component analysis (PCA), in practice, BSFA model requires P ≪ D in Equation (1), i.e., the number of latent source factors (equivalent of principal components in PCA) needs to be less than the size of the observed data (here number of ROIs). In the simulations, we initialized BSFA fully non-informatively by setting the dimensionality of the latent source factors to one less than data dimension (using P = D − 1). The optimal number of latent source factors for each state was then determined within the Bayesian framework. However, in analysis of large number of ROIs, e.g., whole brain analysis, a fully noninformative initialization, P = D − 1, could be problematic: firstly due to the computational complexity and secondly due to limited amount of data, automatic model selection in BSFA may fail to discard all the excess variations in data which may result in underfitting. In such cases, one would need to initialize BSFA semi-informative by bounding the dimensionality of the latent source factors to use a certain percentile of variations in the observations, for example, 90% of variations in data. In this way, optimal number of latent source factors for each latent state can still be determined automatically from data but they are now bounded.