Actin cortex architecture regulates cell surface tension

Abstract

Animal cell shape is largely determined by the cortex, a thin actin network underlying the plasma membrane in which myosin-driven stresses generate contractile tension. Tension gradients result in local contractions and drive cell deformations. Previous cortical tension regulation studies have focused on myosin motors. Here, we show that cortical actin network architecture is equally important. First, we observe that actin cortex thickness and tension are inversely correlated during cell cycle progression. We then show that the actin filament length regulators CFL1, CAPZB, DIAPH1 regulate mitotic cortex thickness and find that both increasing and decreasing thickness decreases tension in mitosis. This suggests that the mitotic cortex is poised close to a tension maximum. Finally, using a computational model, we identify a physical mechanism by which maximum tension is achieved at intermediate actin filament lengths. Our results indicate that actin network architecture, alongside myosin activity, is key to cell surface tension regulation.

Introduction

Animal cell shape is controlled primarily by the cell cortex, a thin network of actin filaments, myosin motors and actin-binding proteins that lies directly beneath the plasma membrane¹. Local changes in cortex mechanical properties, particularly in cortical tension, drive cellular deformations, such as those occurring during mitotic cell rounding, cytokinesis, migration, and tissue morphogenesis^2–10. Thus, understanding cortical tension regulation is essential for understanding how cells change shape^1–3.

Cortical tension is primarily generated by myosin-II motors, which create contractile stresses by pulling actin filaments with respect to one another^11,12. As such, myosin-II function in cortical tension regulation has been studied extensively^1,9,13,14. In contrast, little is known about the role of actin filament properties and organization. Models of tension generation commonly assume that actin acts as a mere scaffold, and tension is determined by myosin amounts and activity^13,15–17. A recent experimental study reports that cortical actin thickness decreases as tension increases from prometaphase to metaphase and concludes that modulating myosin recruitment, rather than actin, controls cortical tension¹⁴. In contrast, recent in vitro studies of actomyosin networks have demonstrated that modulating actin architecture without changing myosin concentration or activity can considerably affect tension^18–21. Given that actin filaments provide the substrate for myosin motors, the spatial organization of actin likely influences tension in the cortex as well. Yet, the contribution of actin network properties to cellular tension regulation remains an open question.

One major challenge to investigating the link between cortical organization and tension is that cortex thickness is below the resolution of diffraction-limited light microscopy^22,23. To address this challenge, we recently developed a sub-resolution image analysis method to quantify cortex thickness and density in live cells²⁴. Here, we use this method to investigate whether cortex thickness contributes to cortical tension regulation.

We first compared interphase and mitotic cells, as cortical tension is known to be higher in mitosis^{6,7,9,25–27}. We found that mitotic cells have higher tension but a thinner cortex compared to interphase cells. Using targeted genetic perturbations, we identified proteins controlling actin filament length as the main regulators of mitotic cortex thickness. Strikingly, both increasing and decreasing thickness resulted in a strong decrease in mitotic cortical tension. Finally, using a computational model, we identified a physical mechanism suggesting that in the mitotic cortex, filament length is optimised for maximum tension generation. Together, our experiments and model show that in addition to myosin activity, actin filament network architecture is a key regulator of contractile tension in the cell cortex.

Results

The mitotic cortex is thinner and has higher tension than the interphase cortex

We investigated changes in actin network architecture between interphase and mitosis, as cortical tension is known to be higher in mitosis^6,9,25. We first verified the tension difference using atomic force microscopy in adherent HeLa cells synchronized in interphase and prometaphase (Fig. 1a-c, Supplementary Fig. 1). Interphase cells were detached such that they acquired a spherical morphology, comparable to mitotic cells (Fig. 1a,b). To rule out potential effects of cell detachment, we repeated the measurements in suspension (S)-HeLa cells, a sub-line derived from adherent HeLa cells, which display a rounded morphology throughout the cell cycle. We observed an increase in cortex tension from interphase to mitosis in both HeLa and S-HeLa cells (Fig. 1c,d).

Figure 1. The mitotic cortex is thinner and has higher tension than the interphase cortex.

(a) Schematic representation of cortex thickness and tension measurements in adherent HeLa cells in interphase (trypsinized) and mitosis. (b) Adherent HeLa (HeLa) and suspension HeLa (S-HeLa) cells synchronized in interphase (G1/S) and mitosis (prometaphase) expressing GFP-Actin and mCherry-CAAX. Images are representative of 3, 13, 6, 5 independent experiments and 41, 100, 47, 27 cells). Scale bars = 10 μm. (c, d) Boxplots comparing cortex tension and cortex thickness, h, between interphase (blue) and mitotic (red) HeLa (c) and S-HeLa cells (d). Points represent individual measurements (n=12, 13, 41, 100 cells pooled across at least 3 independent experiments; p=0.0009, 1.4x10^-15 for adherent HeLa cells and n=40, 42, 47, 27 cells (outliers included) pooled across 5-6 independent experiments; p=7.9x10^-5, 2.4x10^-8 for S-HeLa cells). The points plotted with 'X' were determined to be outliers (see Methods for details) and were not considered for statistical analysis. (e) Representative images of interphase and mitotic Normal Rat Kidney (NRK) cells (trypsinized) expressing GFP-Actin and mCherry-CAAX and mouse embryonic stem cells (Mouse ESC) expressing LifeAct-GFP and labelled with plasma membrane binding dye Cell Mask Orange™ (CMO). Mouse ESCs were cultured in 2i/LIF medium, where they display a rounded morphology throughout the cell cycle. Images are representative of 2-3 independent experiments (11, 13, 22, 13 cells). Scale bars = 10 μm. (f) Boxplot comparing cortex thickness between interphase and mitotic NRK and mouse ESCs. Points represent individual measurements (n=11, 13, 22, 13 cells pooled across 2-3 independent experiments; p=0.0016, 2.6x10^-5). (g) Scanning electron micrographs of membrane extracted cortices of adherent HeLa (left) and S-HeLa (right) cells blocked in interphase and mitosis (representative of 11-18 cells from 1 to 2 independent experiments). Scale bars = 100 nm. Insets: lower magnification images of whole cells; boxed areas indicate the high magnification regions; scale bars = 10 μm. See Supplementary Fig. 2h-j for quantifications. Welch's t-test p-values: **p<0.01; ***p<0.001. For all boxplots in this figure and all subsequent figures, the box extends from the lower to upper quartile of the data, and the line denotes the median. Whiskers extend to include the most extreme values within 1.5 times the interquartile range below and above the lower and upper quartiles, respectively.

We then asked if the cortex tension increase correlated with changes in cortex architecture. As a basic readout, we measured cortical thickness using the sub-resolution localisation method we recently developed²⁴ (Fig. 1a,b). Interestingly, we found that thickness was lower in mitosis compared to interphase in both adherent HeLa and S-HeLa cells, indicating an inverse correlation between cortex thickness and tension during the cell cycle (Fig. 1c,d). To exclude the influence of potential changes in effective membrane width on thickness measurements (Fig. 1a), we checked that the width of the plasma membrane linescan did not considerably change between interphase and mitosis (Supplementary Fig. 2a). Moreover, the reduced cortex thickness in mitosis could not be attributed simply to a redistribution of cortical material due to cell volume increase between interphase and mitosis²⁸ (Supplementary Fig. S2b and Supplementary Table 1). We verified that neither trypsinisation, nor the method used to immobilise interphase cells, nor the treatment used for synchronisation affected cortex thickness measurements (Supplementary Fig. 2c,d). Finally, we compared cortex thickness in mitosis and interphase in detached normal rat kidney (NRK) cells, which are adherent throughout the cell cycle, and naïve mouse embryonic stem cells (mESCs), which are non-transformed and have a round morphology throughout the cell cycle (Fig. 1e). We observed a decrease in cortex thickness between interphase and mitosis in both cell lines (Fig. 1f), suggesting that mitotic cortex thinning is a widespread feature among different cell types.

We further probed cortex architecture by investigating cortex density and ultrastructure. We first quantified cortical actin density, which is an output of our thickness extraction method²⁴, and total amounts of cortical actin (Supplementary Fig. 2e). We observed a modest, but significant increase in cortex density, but not change in cortical actin amounts, from interphase to mitosis (Supplementary Fig. 2f,g). We then visualized the outer surface of the cortex in interphase and mitotic HeLa and S-HeLa cells using scanning electron microscopy (Fig. 1g). The cortical network appeared slightly less homogenous in interphase, with a higher incidence of larger gaps; away from these gaps, network mesh size and organization in interphase and mitosis were largely comparable (Fig. 1g and Supplementary Fig. 2h-j). Based on these data, we concluded that changes in actin density and surface organization between interphase and mitosis were less prominent than the observed changes in cortex thickness. We thus focused on cortex thickness as a first-order readout of cortical nanoscale architecture for the remainder of the study.

Proteins controlling actin filament length regulate cortex thickness

To investigate if changes in cortex thickness could affect cortical tension directly, we searched for thickness regulators by performing a targeted siRNA screen of key actin-binding proteins (ABPs). We explored four categories of ABPs: contractility-related proteins, cortex-membrane linkers, actin crosslinkers and actin filament length regulators. Each ABP was depleted using siRNA previously shown to reduce expression, or siRNA pools (Supplementary Table 2). The three members of the ezrin, radixin and moesin (ERM) family of actin-membrane linkers were depleted together to avoid compensation effects; we also included the kinase SLK in our targeted screen, which regulates ERM activity in mitosis^29,30. To rule out compensation between the two heavy chains of myosin-II, MYH9 and MYH10, we also tested the effect of the myosin inhibitor blebbistatin (Supplementary Fig. 3a). We confirmed the reduction in mRNA levels by qPCR (Supplementary Fig. 4, Supplementary Table 3). We then blocked treated cells in mitosis and measured cortex thickness (Fig. 2).

Figure 2. Actin filament length-regulating proteins control cortex thickness in mitosis.

Box plots comparing relative cortex thickness in mitotic HeLa cells depleted for contractility-related ABPs (a), cortex-membrane linkers (b), crosslinkers (c) and actin filament length regulators (d). Relative cortex thickness values were obtained by dividing cortex thickness in siRNA-depleted cells (Target) by the median of the corresponding scrambled control (Scr.). Points represent individual measurements (n=14, 26, 18, 23, 10, 25, 21, 17; 14, 24, 20, 17, 40, 33, 13, 9, 13, 12, 17, 17, 26, 17, 21, 7; 38, 18, 38, 16, 38, 16, 27, 16; 21, 18, 8, 12, 38, 17, 40, 44, 21, 16, 20, 20, 21, 25, 40, 23, 8, 13, 13, 16 cells pooled across 2-3 independent experiments; p=0.61, 0.86, 0.15, 0.57; 0.99, 0.47, 0.36, 0.45, 0.82, 0.35, 0.06, 0.36; 0.84, 0.48, 0.80, 0.20; 0.91, 0.0028, 0.0004, 0.034, 0.65, 3.6x10^-6, 0.57, 0.64, 0.47, 0.37). Details on the siRNA treatments are given in Supplementary Table 2; depletion levels were checked by qPCR (Supplementary Fig. 4). Welch's t-test p-values: *p<0.05, **p<0.01 and ***p<0.001.

Surprisingly, we found no significant effect on cortex thickness following depletion of ABPs involved in contractility generation, membrane-to-cortex attachment, or actin crosslinking (Fig. 2a-c). In contrast, we found that several ABPs regulating actin assembly and disassembly, and thus actin filament length significantly affected cortex thickness (Fig. 2d). Specifically, we found that depletion of the barbed end-capping protein CAPZB³¹ and the actin-severing protein CFL1^32,33 led to an increase in mitotic cortex thickness, whereas depletion of the actin-nucleating and elongating formin DIAPH1^34–36 led to a thickness decrease. CFL1 knockdown and treatment with the actin filament stabilising drug Jasplakinolide were previously found to increase cortex thickness²⁴, supporting these findings. Depletion of the ARPC2 subunit of the Arp2/3 complex also led to a decrease in cortex thickness. However, we did not observe any change in thickness upon depletion of ARPC1B, another Arp2/3 subunit, or following treatment with the Arp2/3 inhibitor CK-666 (Supplementary Fig. 3a). Therefore, we focused on CAPZB, CFL1, and DIAPH1 for the rest of the study. Together, our candidate knockdown approach revealed that proteins regulating actin filament length are the primary regulators of thickness of the mitotic cortex.

Perturbation of actin filament length-regulating proteins causes a decrease in tension

We next asked whether perturbation of the three thickness regulating proteins identified in our screen also affected tension. Although knockdown of CAPZB or CFL1 caused an increase in cortex thickness and DIAPH1 knockdown caused a decrease in thickness (Fig. 3a-c), cortical tension decreased in all three conditions (Fig. 3d). We also observed a decrease in average cortical stress, extracted from thickness and tension, in all three knockdown conditions (Supplementary Table 4). Furthermore, stabilisation of actin filaments with Jasplakinolide, which increases cortical thickness²⁴, also led to a tension decrease in mitotic cells (Supplementary Fig. 3b). Together, these data indicate that the relationship between tension and thickness during mitosis is non-monotonic, and treatments leading to either an increase or decrease in cortex thickness result in lower tension.

Figure 3. Perturbation of actin filament length-regulating proteins causes a decrease in cortex tension.

(a) Representative images of mitotic HeLa cells expressing GFP-Actin and mCherry-CAAX treated with siRNA against capping protein subunit beta (CAPZB), cofilin1 (CFL1) and diaphanous1 (DIAPH1). Images are representative of 3-4 independent experiments (17, 44 and 20 cells). Scale bar = 10 μm. (b) Western blots of CAPZB, CFL1 and DIAPH1 levels after siRNA depletion compared to corresponding scrambled controls (Scr.). Representative blots from 3 independent experiments for CAPZB and DIAPH1 and 1 experiment for CFL1, confirming results from Clark et al.²⁴. GAPDH was used as the loading control. See Supplementary Fig. 7 for uncropped western blots. (c, d) Boxplots comparing cortex thickness (c, the same data are presented, normalized, in Fig. 2) and cortex tension (d) between cells treated with scrambled (Scr., black) siRNA or siRNA targeted against CAPZB, CFL1 or DIAPH1 (Target, red). Points represent individual measurements (n=38, 17, 40, 44, 20, 20 cells pooled across 3-4 independent experiments, p=0.0004, 0.034, 3.6x10^-6 for thickness measurements; n=7, 14, 17, 24, 14, 20 cells pooled across 2-5 independent experiments, p=0.0046, 0.0315, 0.0006 for tension measurements). (e) Representative images of mitotic HeLa cells expressing myosin-IIA heavy chain MYH9-GFP, treated with siRNA against CAPZB, CFL1, DIAPH1 and corresponding scrambled controls (Scr.). Images are representative of 1-3 independent experiments (28, 35, 22, 28, 23, 38 cells). Scale bars = 10 μm. (f) Boxplots comparing the cortex-to-cytoplasm intensity ratio of MYH9-GFP for all conditions in (e) (n=28, 35, 22, 28, 23, 38 cells pooled across 1-3 independent experiments; p=0.96, 0.0055, 0.088). Welch's t-test p-values: ^nsp>0.05, *p<0.05, **p<0.01 and ***p<0.001.

We verified that thickness changes following knockdown of CAPZB, CFL1 or DIAPH1 were not due to changes in effective plasma membrane width or cell size (Supplementary Fig. 3c-e). We then checked for possible changes in cortex density and amounts. We found that cortex density was unchanged in CAPZB and CFL1 knockdown cells but slightly increased upon CFL1 depletion (Supplementary Fig. 3f), while total cortical actin amounts followed the same pattern as cortex thickness (Supplementary Fig. 3g).

Previous studies have focused on myosin activity as the primary determinant of cortical tension. We thus investigated levels of total and phosphorylated myosin in the different conditions. We observed a slight increase in myosin regulatory light chain (MRLC) expression following CAPZB and DIAPH1 knockdown, but no substantial change in phosphorylated MRLC levels following any of the knockdowns (Supplementary Fig. 3h,i). We then investigated myosin localization using HeLa cells expressing myosin-IIA heavy chain (MYH9) fused to GFP. The cortex-to-cytoplasm ratio of MYH9-GFP intensity was unchanged following CAPZB and DIAPH1 depletion, and even slightly higher following CFL1 knockdown (Fig. 3e,f). Together, our results suggest that modulating cortex thickness by actin filament length regulators decreases mitotic cortex tension, and that this tension change does not result from a decrease in myosin-II levels or localization at the cortex.

A computational model predicts maximum cortex tension at intermediate actin filament lengths

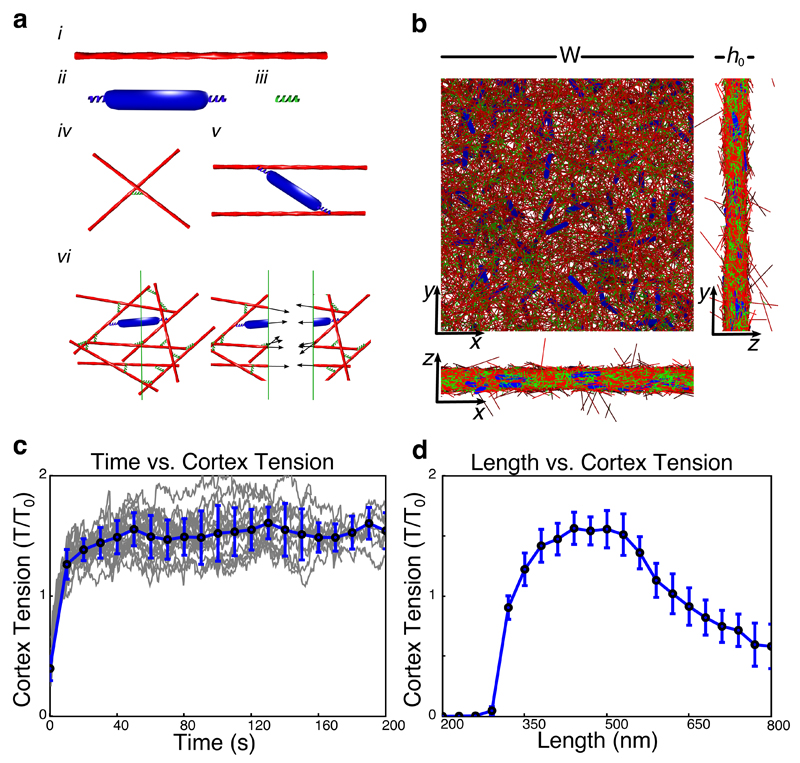
To investigate how changes in actin filament length could affect cortex tension, we developed a computational model of the actin cortex. The components of the model are actin filaments, myosin minifilaments and crosslinkers (Fig. 4ai-iii, Supplementary Fig. 5a, Supplementary Table 5). For simplicity, actin filaments are described as rigid rods (see Supplementary Note for details). Filaments are bound to each other by passive crosslinkers with finite length that behave as linear springs (Fig. 4aiv). Myosin minifilaments are represented as rigid rods that can bind to actin filaments and walk towards their plus ends (Fig. 4av). Resistance to motor walking is described by an effective friction (Supplementary Table 5). Filament centre-of-mass positions are chosen randomly within a box of equal length and width W and initial seeding thickness h₀ (Fig. 4b, Supplementary Fig. 5b, see Supplementary Note for details).

Figure 4. A computational model of cortex tension generation predicts maximal tension at intermediate actin filament length.

(a) Components of the simulation: i. actin filament, ii. myosin minifilament, iii. crosslinker, iv. example of crosslinked actin filaments, v. example of a myosin motor binding two actin filaments, vi. tension measurement by slicing the network, arrows represent forces within the network components. (b) Projections of an initialized simulation from the top (xy) and the sides (xz, yz). W: width of simulation box, h₀: seeding thickness. (c) Plot of tension (T/T₀) as a function of time for an ensemble of simulations with filament length of 500 nm (see Supplementary Table 5 for the other parameters). Gray lines represent measurements for a single plane in a simulation; blue circles are mean values (±SD) for each time point, n=9 simulations. The magnitude at which tension saturates in the simulations is comparable to experimental tension values with our choice of myosin stall force (see Discussion of Model Assumptions in the Supplementary Note). (d) Plot of cortex tension as a function of actin filament length. Blue dots represent mean tension values after 25 s (±SD) calculated from 9 simulations. In c and d, tension is normalized to T₀ = 230 pN/μm (see Supplementary Note for details).

To investigate cortical tension generation, we simulated networks of filaments in three dimensions with periodic boundary conditions along the x and y dimensions and free boundary conditions along the z direction (Fig. 4b, Supplementary Fig. 5b). We then measured the tension exerted in the network in transversal cross-sections over time (Fig. 4avi,c, Supplementary Fig. 5c,d). We found that after transient network reorganization (~20 s), tension appeared to fluctuate around a steady-state value (Fig. 4c).

We then tested how cortical tension varies with actin filament length (Supplementary Movies 1–3). The seeding thickness, h₀, was taken proportional to filament length, while the actin density and number of myosin motors in the cortex were kept constant, as suggested by our experiments (Supplementary Fig. 3f,h,i, Fig. 3e,f). We found that tension strongly varied with filament length, with a tension maximum at intermediate lengths (Fig. 4d).

We tested the robustness of our results to variability in filament length, and found that various Gaussian distributions in length did not affect our conclusions (Supplementary Fig. 5e). To test whether changing thickness could affect cortex tension independently of filament length, we performed simulations with varying seeding thickness but fixed cortex density, filament length and number of motors. We found that while thin networks (<200 nm) produced slightly lower tension, for thicker networks, tension changed very little with seeding thickness, and no maximum was observed (Supplementary Fig. 5f). This suggests that filament length, and not simply seeding thickness, influences tension in our simulations. Finally, we performed simulations with varying filament length, but fixed seeding thickness, actin density, and thus total cortical actin amount. We found that maximal tension was obtained for intermediate filament length (Supplementary Fig. 5g). Together, these results indicate that changing actin filament length can modulate cortical tension and that the non-monotonic tension-filament length relationship is not dependent on changes in the total amount of cortical material.

We next investigated the physical mechanism underlying the tension maximum at intermediate filament lengths. To this aim, we examined tension acting within myosin motors, and tension acting within the actin and crosslinker network (Fig. 5a). We observed that while tension within myosins increases with actin filament length and eventually saturates, tension in the actin network exhibits a maximum as a function of filament length. This indicates that the non-monotonic tension-filament length relationship arises from the response of the actin network to myosin-induced stresses. We thus analysed the behaviour of the actin network in our simulations. We calculated local isotropic strain and two-dimensional (2D) network stress for short (200 nm), intermediate (500 nm) and long (740 nm) actin filaments (Fig. 5b,c, Supplementary Movies 1–3). We found that strain distributions have as many stretched as compressed regions, as expected in a non-deformable simulation box (Fig. 5d). The network displays higher strain for shorter filaments, indicating that short filament networks are more compliant (Fig. 5d). In contrast, stress distributions are asymmetric, with more regions under positive (tensile) stress than negative (compressive) stress, resulting in networks under overall contractile tension (Fig. 5e). This 2D stress asymmetry is higher for shorter filaments, suggesting that larger local network deformation promotes stress asymmetry (Fig. 5e).

Figure 5. Local network behaviour in response to myosin-induced stresses.

(a) Plot of cortex tension as a function of actin filament length separating the total tension (blue) into the tension exerted within myosin motors (green) and the network tension exerted within actin filaments and crosslinkers (red). (b) Example of triangulation used for measuring strain in the network. The black lines are triangles before network deformation, white lines are triangles after deformation, red arrows are the displacement field. Green box marks the zoomed inset (right). (c) Projections of simulated cortical networks with different actin filament lengths (l_a). xy (top) and xz (bottom) projections were generated after 100 s of simulation runs. The whitened section of the network in the xz view is not shown in the xy view. (d,e) Local strain (d) and local 2D network stress (e) distributions in the deformed networks for filament lengths of 200 nm (left), 500nm (middle) and 740 nm (right) (see Supplementary Note for a description of strain calculation). (d) Positive strain corresponds to stretched regions, negative strain to compressed regions. The strain distributions are largely symmetric, and shorter filament networks exhibit higher strain than networks with longer filaments. (e) Network stress distributions are asymmetric, with larger positive stresses. Stress asymmetry is more pronounced for shorter filament networks. Distribution asymmetry is quantified with the parameter a= (T₊ − T₋)/(T₊ + T₋), with T₊ and T₋ the sum of positive and negative local stresses, and normalized to T₀ = 230 pN/μm.

In order to generate high tension, actin networks must (1) be dense and connected enough and (2) display an asymmetry in stress favouring positive stress build-up. In the short filament case, the network has high stress asymmetry, but appears not connected enough for stress generation at the network level. In the long filament case, myosins generate high tension, but stress asymmetry is low, presumably because of high network rigidity, resulting in low overall tension. At intermediate filament length, myosins generate sufficient tension, and stress asymmetry is high, resulting in contractile tension build up. Together, this results in maximum tension at intermediate filament length.

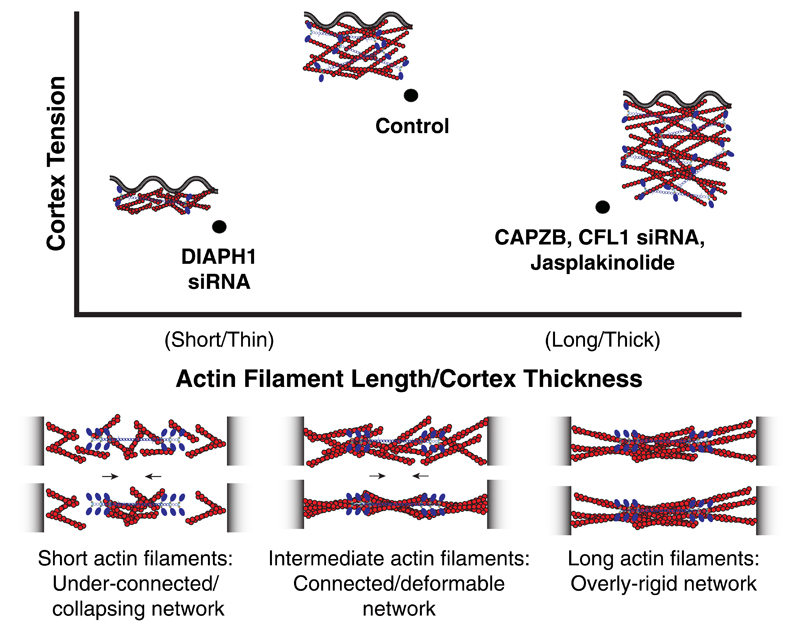
Our simulations provide a physical mechanism that could account for our experimental observations (Fig. 3), and suggest that cortical actin filaments in mitosis are close to an optimal, intermediate filament length for maximal tension generation (Fig. 6). More generally, our model identifies a mechanism by which cortical tension can be modulated independently of changes in myosin motor density and activity, by fine-tuning actin filament structural properties.

Figure 6. Actin cortex architecture regulates cortical tension.

Our experimental measurements and simulations indicate that cortical tension is maximum at intermediate actin filament length and intermediate cortex thickness (top panel). Conditions that either increase or decrease cortex thickness/actin filament length result in lower tension in mitotic cells. Our simulations suggest a physical mechanism for this non-monotonic relationship (bottom panel). While networks of short filaments are too poorly connected to allow for build up of myosin-induced stresses, networks of long filaments are too rigid to allow for sufficiently asymmetric stress generation. At intermediate filament lengths, networks are sufficiently connected for tension generation, and sufficiently compliant to promote stress asymmetry and the build up of positive tensile stresses, leading to an overall high contractile tension.

Discussion

In this study, we asked whether changing the nanoscale architecture of the cortical actin network could modulate cell surface tension independently of myosin activity. To investigate the effect of cortex thickness, a first-level readout of cortex architecture, on cortical tension, we used a targeted RNAi screen to find thickness regulators. Interestingly, only a few of the proteins tested strongly affected cortical thickness. Functional redundancy may have masked the effects of some of the proteins tested. Nonetheless, neither depletion of myosin-II heavy chains (MYH9 and MYH10), nor inhibition of myosin-II activity with blebbistatin, significantly affected cortex thickness (Fig. 2a and Supplementary Fig. 3a). This suggests that myosin-II, a likely candidate for thickness regulation, as contractility could lead to cortex compaction by aligning actin filaments, has no effect on cortical thickness. Furthermore, neither depletion of the three ERM family proteins together nor depletion of their mitotic regulator SLK had any significant effect on thickness (Fig. 2b). This suggests that membrane-to-cortex attachment, which is strongly modulated by ERM proteins^37,38, is not a regulator of cortical thickness.

All of the hits identified in our targeted screen are actin filament length regulators. No method is currently available to directly measure filament length in the cellular cortex. However, both cofilin and capping protein reduce filament length in vitro^39,40 and DIAPH1 not only nucleates but also elongates actin filaments⁴¹. Recent work indicates that capping protein and formins can even form a complex at filament ends to precisely regulate filament length⁴⁰. These studies suggest that these proteins should affect cortical actin filament length in the same way.

Both increasing and decreasing cortex thickness led to a strong tension decrease in mitotic cells. To explore physical mechanisms that could account for these observations, we developed a computational model of the contractile cortex. The model builds on previous work on tension generation in 2D networks^42,43 and expands them to investigate the influence of actin organization in 3D. For simplicity, we did not incorporate steric interactions, explicit diffusion, filament bending or turnover (Supplementary Note). Our simplified model nonetheless indicates that at fixed myosin levels, maximum tension is generated for intermediate actin filament lengths under a large range of conditions (Supplementary Fig. 5e-g). The non-monotonic tension-filament length relationship appears to arise from an asymmetry in actin network response to myosin forces, which generate more tensile (positive) than compressive (negative) stresses (Figs. 5,6). This effect is maximal at intermediate filament lengths, where the network is both sufficiently connected, which is required for stress generation by myosins, and sufficiently compliant, which promotes stress asymmetry. A similar behaviour at the level of individual filaments, which can buckle under compression, thus relaxing negative stresses while accumulating positive stresses, has been proposed previously to account for positive tension build-up in isotropic networks^19,44,45. Interestingly, in our simulations asymmetric stress generation is achieved without introducing filament bending. It will be interesting to investigate the combined effect of filament bending and the asymmetric network response displayed by our simulations.

Tension regulation by fine-tuning filament length could provide a flexible way to modulate tension, as it can be achieved rapidly and by a multitude of different mechanisms. The cortex thinning between interphase and mitosis (Fig. 1) could result from filament shortening. However, the three hits identified in our mitotic thickness screen do not appear to directly control this cortex thinning (Supplementary Fig. 6). Given the complexity of the cellular changes at mitosis entry, many players likely act in a coordinated manner to effect the concomitant actin architecture remodelling. Surprisingly, Ect2, a key cortex regulator at the interphase-mitosis transition²⁷, does not appear to regulate cortex thickness (Fig. 2a). It is possible that Ect2 mainly modulates myosin activity, while other proteins affect actin organization. Elucidating how exactly cortex architecture is controlled during this transition will be an important question for future studies.

Myosins have been commonly assumed to be the primary regulators of cortical tension^13–15. Our study identifies actin filament length as an additional key regulator. Importantly, the tension decrease upon depletion of filament length regulators is comparable to the tension decrease upon myosin-II inhibition (Fig. 3d and Supplementary Fig. 3b). Thus, modulating actin filaments and myosin activity could play equally important roles in tension regulation. A recent in vitro study shows that the degree of network connectivity modulates actomyosin contractility¹⁸. This is consistent with our model, as increasing filament length effectively increases the crosslinking level, and thus network connectivity. However, redundancy between the multiple cortical crosslinkers⁴⁶ and the fact that myosin itself acts as a crosslinker⁴⁷ make the direct study of crosslinkers influence on tension more difficult in cells than in vitro. Nonetheless, crosslinking could provide yet another level of tension regulation.

Together, our study highlights that cortical tension, and the resulting cellular surface tension, are not controlled by myosin-II activity alone and can be regulated at multiple levels. Future studies will be required to dissect the relative contributions of different mechanisms of tension regulation during specific tension-driven cellular shape changes.

Methods

Cell culture, plasmids and experimental treatments

Wild type HeLa cells were a gift from the MPI-CBG Technology development studio (TDS, Dresden, Germany). Suspension HeLa line (S-HeLa) was derived from HeLa TDS by constant culturing on low-adherent flasks (Cat no. 3815, Corning). Normal Rat Kidney (NRK) cells were a gift from the lab of Mark Marsh (MRC-LMCB, University College London). Adherent HeLa, S-HeLa, and NRK cells were cultured in DMEM (Gibco, Invitrogen/Life Technologies) supplemented with 10% heat-inactivated foetal bovine serum (FBS; Gibco), 100 U/ml Penicillin, 100 μg/ml Streptomycin and 2 mM L-Glutamine at 37°C with 5% CO₂. The Lifeact mES cells were provided by the lab of Kevin Chalut (Wellcome Trust/Medical Research Council Cambridge Stem Cell Institute). mESCs were cultured on 0.1% gelatin at all times in 2i-LIF medium, as described in Pagliara et al.⁴⁸, which is N2B27 medium (Invitrogen) supplemented with MEK inhibitor (1 μM PD0325901), GSK3 inhibitor (3 μM CHIR99021) and Leukemia inhibitory factor (LIF). None of the cell lines used in this study were found in the database of commonly misidentified cell lines maintained by ICLAC and NCBI Biosample. The cell lines used in this study were not authenticated and were not tested for mycoplasma contamination.

EGFP-CAAX was a gift from John Carroll (Monash University, Australia). EGFP was replaced with mCherry by restriction digest by M. Bergert to create the mCherry-CAAX fusion. The GFP-actin construct was obtained by cloning human beta-actin into pEGFP-C2 (Clontech, Takara Bio Europe). Jasplakinolide (Invitrogen/Life Technologies, Darmstadt, Germany) was added to final concentrations of 20 nM. Blebbistatin (+/-) (Tocris Biosystems) and CK-666 (Merck Millipore) were both used at a final concentration of 100μM. All drug treatments were performed for ~20 min to ~1 h before imaging and equivalent volume of DMSO was used as a control.

Cell cycle synchronization and preparation for microscopy

Cells were synchronized in interphase (G1/S-phase) by single thymidine block. The block was performed by incubating cells overnight (~16-24 hours) in 2 mM thymidine²⁴. For measurements in adherent cells, cells were detached from the dish using Trypsin-EDTA (Cat no. 25300-054, Life Technologies) and immobilized for imaging by either confining the cells in 25 μm wide PDMS channels (prepared as described in Bergert et al.¹⁰) or by brief centrifugation on poly-L-lysine (PLL) coated 35 mm glass bottom dishes. For enzyme-free detachment of interphase cells, “Cell Dissociation Buffer, enzyme-free” (Cat no. 13151014, Thermo Fisher Scientific) was used. To enrich cells in mitosis (prometaphase), the cells were treated with 2 μM S-Trityl-L-Cysteine (STLC)⁴⁹ for a 5-7 hours before imaging. For electron microscopy and tension measurement experiments, the STLC treatments were performed overnight.

Transfection

Cells were plated on 35 mm glass-bottom imaging dishes (Willco wells HBST-3522) at least 16 hours prior to transfection. For plasmids, 0.3-0.5 μg DNA was transfected by lipofection (Lipofectamine 2000, Cat no. 11668-027, Life Technologies) according to manufacturer’s instructions. siRNAs were transfected using Lipofectamine RNAiMax (Invitrogen, Life Technologies) for specified treatment times (Supplementary Table 2). Detailed information about siRNA treatments is given in Supplementary Table 2.

Confocal imaging and cortex thickness measurements

For all live cortex thickness measurements, two-colour image stacks (30-70 z-slices, 100 nm intervals) were acquired around the equatorial plane of rounded cells using a 60X colour-corrected objective (1.40 NA OSC2 PlanApoN) mounted on an Olympus FV1200 microscope. For chromatic correction 200 nm diameter multicolour tetraspeck beads (Invitrogen) were imaged using the same settings as used for the cells and chromatic shift was calculated as described previously²⁴. After correcting for the chromatic shift in x, y, z, and magnification using custom software written in MATLAB, a single equatorial plane was selected for each image using Fiji image analysis software⁵⁰. Cortex thickness and density were then extracted using the protocol detailed in Clark et al.²⁴, the custom software for image analysis and linescan extraction is available publicly (details in Code availability section below). For membrane width measurements, we measured the full width at the half-maximum (FWHM) of the plasma membrane intensity peak by interpolating the x-position on the linescan on either side of the peak by linear interpolation of the two closest points. The half-maximum was defined as half of the difference between peak intensity and intracellular background. Cell radius measurements were performed by fitting the cell segmentation used for thickness analysis to a circle.

Western blotting

For western blotting, cells transiently transfected with siRNA and synchronized in specific cell cycle stages were centrifuged at 1000g for 3 min. The pellet was washed with PBS and then lysed using RIPA lysis buffer (Santa Cruz Biotechnology, Santa Cruz, CA, USA). The lysates were clarified by centrifugation at 8000g for 4 min at 4°C, diluted 1:1 with 2x Laemmli buffer (Sigma-Aldrich), incubated for 5 min at 95°C and loaded onto NuPage 4-12% Bis-Tris gradient gels (Invitrogen/Life Technologies). Primary antibodies used were 1:500 Anti-mDia1 (Cat. No. 96784 Abcam), 1:1000 Anti-CAPZB (AB6017 Millipore), 1:1000 Anti-CFL1 (3318s Cell signaling), 1:100,000 Anti-GAPDH (1D4, NB300-221 Novus Biologicals). Myosin amount and activity were assessed by running whole cell lysates on NuPage 14% Tris-Glycine gels (Invitrogen/Life Technologies). Primary antibodies used were 1:1000 pMLC-2 (Ser19) (3671S Cell Signaling), 1:2000 MLC-2 (M4401 Sigma-Aldrich), 1:2,000 Anti-GAPDH (1D4, NB300-221 Novus Biologicals), 1:2000 Anti-β-Actin (C4, sc-47778 Santa Cruz), and 1:2,000 anti-α-Tubulin (T5168 Sigma Aldrich). All secondary antibodies (Anti-rabbit IgG: NA934V; Anti-mouse IgG: NXA931 from GE Healthcare) were used at 1:5,000 for 1 hour at RT.

Quantification of Western blots

Protein levels relative to their corresponding loading control (glyceraldehyde 3-phosphate dehydrogenase, GAPDH) were quantified using Fiji. A rectangular region of interest was drawn around the protein band, and intensity in the box was measured using the Integrated density (IntDen) function in Fiji. A second region of interest of the same dimensions was then used to measure the background intensity in a region of the blot image in an area devoid of any bands. The background intensity was subtracted from the protein intensity. This procedure was performed for all the proteins of interest and normalized to the background-subtracted intensity of the corresponding GAPDH bands.

Quantification of cortical MYH9-GFP intensity

To determine the cortex-to-cytoplasm ratio for MYH9, images of cells expressing MYH9-GFP were segmented based on the MYH9 signal, and an average linescan of 100 pixels (with the peak of the cortical signal in the middle) was extracted, as for cortex thickness measurements. The cytoplasmic background intensity was defined as the mean intensity of the first 20 pixels of the linescan (i.e. in a ~1.4 μm region, ~5.5 μm away from the peak cortical signal), and the cortex intensity was defined as the mean intensity of the 13 pixels surrounding the peak of the cortical signal (i.e. within a ~900 nm region around the peak). These ranges were optimized based on visual inspection of the linescans.

RNA extraction and Quantitative Real-Time PCR (qPCR)

Total RNA from HeLa cells was extracted using the RNeasy Mini Kit (Qiagen, Hilden, Germany). Total RNA was reverse-transcribed using the cDNA Reverse Transcription Kit (Applied Biosystems, Carlsbad, CA, USA) following the manufacturer's instructions. Gene expression levels of endogenous controls GAPDH and beta-actin (ACTB) were determined using pre-validated TaqMan Gene Expression Assays (Applied Biosystems). Expression levels of queried and control genes were determined using assays designed with the Universal Probe Library from Roche. The PCR reactions were performed on an ABI Real Time 7900HT cycler and analyzed with SDS 2.2 software. qPCR was performed with TaqMan Gene Expression Master Mix (Applied Biosystems), and all samples were tested in duplicate. mRNA levels of queried genes were normalized to the averaged levels of GAPDH and ACTB, and relative abundance was calculated by normalizing values from cells treated with control and targeted siRNA pools by dividing by the control value. The genes tested and corresponding forward and reverse primers are listed in Supplementary Table 3.

Scanning electron microscopy

Sample preparation for scanning electron microscopy was performed using a protocol detailed in Bovellan et al.³⁴ with minor modifications. Briefly, cell cycle synchronized cells (in interphase or mitosis) were plated onto 12 mm etched grid coverslips (Cat no. 1943-10012A, SciQuip Ltd). Immediately prior to fixation, the cells were washed with PBS before being transferred to cytoskeleton buffer (50mM Imidazole, 50mM KCl, 0.5mM MgCl₂, 0.1mM EDTA, 1mM EGTA, pH 6.8) containing 0.5% Triton-X and 0.25% glutaraldehyde for 5 min. This first fixation/extraction was followed by a second extraction using 2% Triton-X and 1% CHAPS in cytoskeleton buffer for 5 min before washing the coverslips thrice with cytoskeleton buffer. The rest of the protocol was identical to the protocol described in Bovellan et al.³⁴. The cells were DAPI stained (1:1000) and imaged for identification of coordinates of interphase and mitotic cells on grid coverslips. The cells were then dehydrated with serial ethanol dilutions, dried in a critical point dryer, coated with 5-6nm platinum-palladium and imaged using the inlens detector of a JEOL7401 Field Emission Scanning Electron Microscope (JEOL, Tokyo, Japan).

Quantification of holes in SEM images

400 pixels x 400 pixels (532 μm x 532 μm) sections were cropped from SEM images for HeLa and S-HeLa focusing on regions devoid of microvilli. Using a custom plugin developed in Fiji, pores were segmented in a semi-automated manner through intensity thresholding and size exclusion. Pore contours were then corrected manually as necessary. From the final segmentation mask, areas of holes were calculated and used to quantify the distribution of pore sizes and the percentage of area covered by pores.

Cortex tension measurements

For tension measurements, cells were resuspended in 10% FBS Leibovitz’s L-15 media (Gibco, Life Technologies) before each experiment and plated on glass bottom dishes (HBSt-3522, WillCo dish). In order to visualize the cell periphery, CellMask Deep Red plasma membrane stain (Life Technologies) was added to a final concentration of 0.5 μg/ml. To verify the cell cycle stage, DNA was labelled with Hoechst 33342 (Life Technologies) at a final concentration of 10 μg/ml.

Tension measurements were performed using a Nanowizard1 Atomic Force Microscope (JPK Instruments) mounted on an IX81 inverted confocal microscope (Olympus). Tipless silicon nitride cantilevers (HQ:CSC38/tipless/NoAl, Mikromasch) were chosen with a nominal spring constant of 0.03-0.09 N/m. Sensitivity was calibrated by acquiring a force curve on a glass coverslip and spring constant was calibrated by the thermal noise fluctuation method. The spring constant estimated for each experiment ranged between 0.07 and 0.12 N/m. The calibrated cantilever was positioned within 15 μm above the selected cell and lowered at a speed of 0.5 μm/s. We chose a set-point force of 10 nN, which produced an average cell compression of 1-4 μm. During the constant height compression (for 300 s), the force acting on the cantilever was recorded. After initial force relaxation, the force value was measured (red arrow, Supplementary Fig. 1c) and a confocal stack of the cell for cell height measurement was acquired using a 60X / 1.35 NA UPlanSAPO oil immersion objective (Olympus) (Supplementary Fig. 1a).

The calculation of cortex tension is based on Fischer-Friedrich et al.²⁵. Briefly, assuming negligible adhesion between the cell and the dish and cantilever, the force balance at the contact point reads:

$$T=\frac{F\left(\frac{r_{mid}^2}{r_c^2}-1\right)}{2\pi r_{mid}}$$ (1)

where r_mid is the radius of the maximum cross sectional area of the selected cell (orange line in Supplementary Fig. 1b), r_c is the radius of the contact area of the cell with the cantilever (blue line in Supplementary Fig. 1b), and F is the force exerted by the cell on the cantilever (Supplementary Fig. 1c). In order to avoid errors due to direct measurement of r_c, the contact radius was calculated using the following formula⁵¹

$$A_c=A_{mid}-\left(\frac{\pi }{4}\right)h_{cell}^2$$ (2)

where A_c is the contact area between the cell and the cantilever, A_mid is the cell maximum cross sectional area, and h_cell is the cell height (green line, Supplementary Fig. 1b). h_cell was extracted from the reconstructed confocal stack of the plasma membrane. To account for optical aberrations in cell height measurements due to mismatch in refractive index between the objective immersion medium, glass, cell cytoplasm, and culture medium⁵², we applied a correction factor estimated following the method similar to that described in Diaspro et al.⁵³. In brief, we used mES cells, which are small enough for their size to be directly measured using the AFM piezo motor (limited to a range of 15 μm), and compared cell heights obtained from confocal stacks to heights from direct AFM measurements. Linear fitting was then used to compute the correction factor relating the apparent cell height from confocal stacks to the AFM-measured height (Supplementary Fig. 1d). This correction factor was then applied to calculate h_cell for larger cells for which only confocal measurements could be used. Cortical tension was then calculated using Eq. 1.

3D Simulations of tension generation in the cortex

We generated 3D simulations of a cortical network with three components: actin filaments, myosin minifilaments, and crosslinkers (Fig. 4a, Supplementary Fig. 5a). Actin filaments and myosin minifilaments are modelled as rigid rods with finite lengths l_a and l_m, respectively. Myosin minifilament heads interact with actin filaments through a spring-like interaction. Similarly, crosslinkers that attach two actin filaments are treated as short springs.

The simulation is initialized as N_f actin filaments are placed within a box of square surface (side width W) and seeding thickness h₀ (Fig. 4b, Supplementary Fig. 5b). Crosslinkers are introduced in the system with an actin binding probability p_x. Finally, myosin minifilaments initially bind to actin filaments in a straight, unstretched configuration.

After initialization, the simulation is updated in two stages at every step of iteration. In the first stage, myosin minifilaments bind, unbind, and bound minifilaments walk towards plus ends of actin filaments. In the second stage, the network configuration is mechanically relaxed.

The simulation is run for 200s and updated every 10^-3 s. Network surface tension is measured by slicing the network with a plane and calculating the total force F acting in the direction normal to that plane (Fig. 4avi). Tension is then calculated by dividing F by the width of the simulation box W. To obtain average steady-state tensions plotted in Figs. 4d and 5a, tension values are averaged between t₀= 25 s and the total simulation time = 200 s.

To explore the relationship between actin filament length and tension in the network, varying actin filament lengths were used as input while keeping the mean actin density constant in the network, in accordance with experimental observations. A more complete description can be found in the Supplementary Note.

Statistics and Reproducibility

Boxes in all boxplots extend from the 25th to 75th percentiles, with a line at the median. Whiskers extend to x1.5 the interquartile range (IQR) or the max/min data points if they fall within x1.5 IQR. Each dot on the boxplots represents a measurement from a single cell. For comparisons of means between categories, Welch's t-test (2-tailed, no assumption of variance) was performed, and p-values were obtained from a t-value lookup table. Welch's t-test p-values: *p<0.05, **p<0.01, and ***p<0.001. For the cortex tension data in Fig. 1d (left), outliers were determined based on the following criteria: (1) deviation from the majority of the data based on visual inspection of the normal probability plot, (2) values greater than 1.5x the interquartile range beyond the third quartile⁵⁴, (3) the modified Z-score was greater than 3.5 (see Ref55), (4) the Grubbs' test statistic was greater than the critical value (at p<0.05)⁵⁶. For the Grubbs' test, tests for each outlier were performed sequentially, removing outliers individually. All statistical analyses and plotting were performed using Python (www.python.org), using the Numeric Python (NumPy), Scientific Python (SciPy), and Matplotlib packages.