Abstract
Arsenic is a toxic and carcinogenic contaminant of potential concern. Ettringite [Ca6Al2(SO4)3(OH)12·26H2O] has the ability to incorporate oxyanions as a solid solution with SO42−, which could lower the soluble oxyanion concentrations. Therefore, ettringite containing SO42− and AsO43− has been synthesized. Results indicated that AsO43− could substitute for SO42− inside the channels of ettringite in the form of HAsO42−, and a linear correlation existed between Xinitial solution and Xsolid. The thermodynamic characterization of the solid samples was investigated by means of Visual MINTEQ, a freeware chemical equilibrium model, and the solubility product logK of -48.4 ± 0.4 was calculated for HAsO4–ettringite at 25°C. The Lippmann phase diagram and XHAsO4–XHAsO4,aq plot showed that the solid solution series containing arsenate has HAsO4-poor aqueous solutions in equilibrium. These findings can be helpful to arsenate solidification and arsenate leaching modeling projects.
Introduction
Arsenic (As) is known to be toxic, carcinogenic, and possibly teratogenic to humans [1–3]. In nature, As is released to the environment through volcanism and weathering. As is also produced by anthropogenic activities, such as mineral processing and melting, coal combustion, and extensive use of As-containing compounds, such as wood preservatives, desiccants, and herbicides, resulting in high concentrations of As in water and soil [4].
Ettringite, a hydrous calcium aluminum sulfate mineral with the formula Ca6(Al(OH)6)2(SO4)3·26H2O, is an important hydration product of cement and alkaline wastes [5, 6]. Ettringite forms a hexagonal prismatic crystal, which is constructed of the columns of composition {Ca6[Al(OH)6]2·24H2O}6+ through electrostatic interactions with {(SO4)3·2H2O}6− in the channels between the columns [7]. The full or partial SO42− ions in the channels can be replaced by some oxyanions (i.e., CrO42−, SeO42−, SeO32−, MoO42−, and VO43−) to form a solid solution [8–13]. Ettringite and its solid solution have low solubility. Robert reported on SO4–ettringite and CrO4–ettringite with the pKsp of -44.8 [14]and -41.4 [5], respectively. Therefore, ettringite and ettringite analogs are important potential candidates for the immobilization of contaminant ions.
Indeed, AsO43− substitution for SO42− in ettringite has been previously observed [15, 16]. However, to date there are no investigations focusing on the solid composition analysis and thermodynamic data of AsO4/SO4–ettringite solid solutions. The purpose of the present study is to investigate the changes in solid-phase characteristics, solid composition, and solubility resulting from AsO43− substitutions in the ettringite structure. The results of this investigation will be helpful in modeling the potential for ettringite to control AsO42− concentrations.
Experimental materials and methods
Materials
All chemicals used in this study were at least of pro-analytical grade. The following substances were used: CaCO3 powder, NaAlO2 powder, Na2SO4, Na3AsO4·12H2O, sucrose, and HNO3. Deionized water used in this study was boiled, followed by cooling under soda lime in a N2 (g)-filled glove box to eliminate CO2 (aq).
All polyethylene bottles, tubes, and glassware were soaked in acid solution (5% HNO3) for at least 24 h and rinsed using ultrapure water three times prior to each experiment. All handling of materials, the solid solution synthesis, the sample filtration, the sample drying, and the pH measurements were conducted in a glovebox filled with N2 to prevent possible CO2 contamination.
Solid solution synthesis and experiments
The solid solution was synthetized on the basis of Hassett and McCarthy’s “modified saccharate method” [17]. Initially, a solution containing a mixture of NaAlO2, Na2SO4, and Na3AsO4·12H2O was prepared with a range of arsenate/sulfate ratios (the total number of moles of SO4 and AsO4 was constant). A soluble calcium complex prepared by dissolving CaO in a 10% sucrose solution was added slowly (4 mL/min to 7 mL/min) to the mixed solution while stirring. A twofold excess of NaAlO2 was used to prevent the precipitation of calcium arsenate or sulfate, which would be difficult to separate from the ettringite solid solution. The liquid-to-solid ratio was 20 mL/g. The sample was stirred for 12 h and equilibrated in a thermostatic oscillator for 48 h at a constant temperature of 25°C. Afterward, the sample was centrifuged for 15 min at 4,500 rpm. The supernatant was filtered using 0.45 μm nylon membrane filters following pH measurement. The solution was stored at 4°C for analyzing for elemental composition after being acidified with concentrated HNO3. The solid phase was washed with acetone after being filtered, and was dried in a desiccator.
Characterization of the solid phase
After drying, part of the solid phase was ground with an agate mortar to <60 μm for analysis by X-ray diffraction (XRD), infrared (IR) analysis, and chemical analysis. XRD analysis was used to determine the purity and crystallinity of the phases, and data were collected on an X’Pert PRO Polycrystalline X-ray Diffractometer from PANalytical Company using Cu Ka radiation. The diffraction scans ranged from 5° to 60° 2θ with a step interval of 0.0263° 2θ and a counting time of 4 s/step. The IR spectra were recorded on a Thermo Nicolet Nexus Series using potassium bromide pellets in the range of 4,000 cm−1 to 400 cm−1 with a resolution of 2 cm−1 to confirm arsenate in the samples. The morphology of the samples was determined by scanning electron microscopy (SEM) using a ZEISS SIGMA 500 equipped with a Bruker Quantax EDS detector, which can also provide the information on the surface composition.
Chemical analysis
Part of powder sample was dissolved in a 1% solution of HNO3. Then, solid stoichiometry was determined using ICP-OES for calcium, sodium, aluminum, and arsenic and using ion chromatography for sulfur.
Solubility study and geochemical model
Finely ground synthetic solid samples were mixed with distilled deionized water (1:10 (w/v)) and equilibrated in a shaker bath for 100 days at 25 ± 1°C. The supernatant was isolated by centrifugation and passage through a 0.45 μm nylon membrane filter, and the concentrations of calcium, sodium, aluminum, arsenic, and sulfur in the filtrate were determined. Ionic species and their activities were calculated from the experimental values of ionic concentrations and pH values using Visual MINTEQ (Version 3.1).
Visual MINTEQ is a freeware chemical equilibrium model, which was developed from the DOS program MINTEQA2 and originally coded by the US EPA. Visual MINTEQ can calculate the speciation of inorganic ions and complexes in water [18]. And the databases used by Visual MINTEQ (Version 3.1) included pertinent and updated thermodynamic data from available literature (Table 1).
Table 1. Thermodynamic data supplemented to the Visual MINTEQ (Version 3.1) database.
| Reaction | logKsp | Source |
|---|---|---|
| H2O-H+ = OH- | -13.99 | [19] |
| Aqueous species | ||
| Ca2++AsO43− = CaAsO4− | 4.36 | [20] |
| Ca2++H++AsO43− = CaHAsO40 | 14.31 | [20] |
| Ca2++2H++AsO43− = CaH2AsO4+ | 19.66 | [20] |
| Ca2++H2O-H+ = CaOH+ | -12.83 | [19] |
| Al3++H2O = AlOH2++H+ | -4.97 | [21] |
| Al3++2H2O = Al(OH)2++2H+ | -10.11 | [21] |
| Al3++3H2O = Al(OH)30+3H+ | -16.67 | [21] |
| Al3+-4H2O = Al(OH)4-+4H+ | -23 | [21] |
| AsO43-+H+ = HAsO42- | 11.8 | [22] |
| AsO43-+2H+ = H2AsO4- | 18.79 | [22] |
| AsO43-+3H+ = H3AsO40 | 21.09 | [22] |
| Al3++2SO42- = Al(SO4)2- | 5.58 | [23] |
| Al3++SO42- = AlSO4+ | 3.84 | [23] |
| SO42-+H+ = HSO4- | 1.99 | [23] |
| Ca2++SO42- = CaSO40 | 2.36 | [23] |
| Solid phases | ||
| Ca5(AsO4)3OH = 5Ca2++3AsO43−+H2O−H+ | −26.12 | [20] |
| Ca3(AsO4)2·xH2O = 3Ca2++2AsO43−+xH2O | −21.25 | [20] |
| Ca4(OH)2(AsO4)24H2O = 4Ca2++2AsO43−+6H2O–2H+ | −1.20 | [20] |
| Ca(H2AsO4)2 = Ca2++2H++2AsO43− | −35.62 | [20] |
| CaHAsO4 = Ca2++H++AsO43− | -10.55 | [20] |
| Ca(OH)2 = Ca2++2H2O-2H+ | 22.7 | [19] |
| Al2O3,corundum = 2Al3++3H2O-6H+ | 16.93 | [21] |
| Al2O3,g-alumina = 2Al3++3H2O-6H+ | -18.33 | [21] |
| Al(OH)3,amph = Al3++3H2O-3H+ | 10.8 | [24] |
| AlOOHboehmite = Al3++2H2O-3H+ | 7.64 | [19] |
| AlOOHdisapore = Al3++2H2O-3H+ | 7.01 | [19] |
| Al(OH)3,gibbsite = Al3++3H2O-3H+ | 7.75 | [19] |
| CaSO4·2H2O = Ca2++SO42-+2H2O | -4.61 | [23] |
| CaSO4·2H2O = Ca2++SO42- | -4.36 | [23] |
| AlOHSO4 = Al3++SO42-+H2O-H+ | -3.23 | [23] |
| Al4(OH)10SO4 = 4Al3++SO42-+10H2O-10H+ | 22.7 | [23] |
| Ca6[Al(OH)6]2(SO4)3·26H2O = 6Ca2++2Al(OH)4-+SO42-+4OH-+26H2O | 44.8 | [14] |
Results and discussion
Solid phases of the solid solution series
Table 2 lists the chemical composition of the solid solution series, which shows that the solids had relatively constant Ca and Al ratios at variable SO4:AsO4 ratios in the initial solution. The ideal stoichiometry of ettringite is 6Ca:2Al:3SO4. However, small deviations from the ideal stoichiometry were observed, which might have resulted from the synthesis method and the amount of water present [25]. Nevertheless, the Ca/Al ratio in the solid with no sulfur was 4.7, and far greater than the ideal value 3, which occurred in despite of the two-fold excess of soluble Al in the synthesis solution. This could be the result of the production of Ca phases (such as portlandite, calcite or calcium-arsenic compound). Furthermore, the molar ratio of AsO4 to (AsO4 + SO4) in the initial solution (which is represented by Xinitial solution) was not obtained in the solid. At low molar ratio (Xinitial solution < 0.3), the solids were more enriched in AsO4 than the original solution, whereas the solids had more SO4 at high molar ratio (Xinitial solution > 0.3). Linear regression analysis of the data of the molar ratio of AsO4 to (AsO4 + SO4) in solids (which is represented by Xsolid) and the initial solution led to the following equation: Xsolid = 0.7858Xinitial solution + 0.0409 with a coefficient of correlation of 0.994. This equation can be used to approximately estimate the solution mix ratio of SO4 to AsO4 required to prepare a particular solid solution composition.
Table 2. Chemical composition of solid digest analyses of synthesized solid solution series.
| Initial solution (AsO4)/(SO4+AsO4) | Measured solid digest concentrations in mol/L | Molar ratios Ca:Al:(SO4+AsO4) normalized to 6Ca | Solid product (AsO4)/(SO4+AsO4) | Final solutions in precipitation experiments | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Xinitial solution | Ca | Al | SO4 | AsO4 | Ca | Al | SO4 | AsO4 | SO4+AsO4 | Xsolid | pH | log{HAsO4} | XHAsO4, aq |
| 0.00 | 2.35 | 0.75 | 1.14 | 0.00 | 6.0 | 1.9 | 2.9 | 0.0 | 2.9 | 0 | 11.53 | 0 | 0 |
| 0.03 | 2.35 | 0.74 | 1.09 | 0.05 | 6.0 | 1.9 | 2.8 | 0.1 | 2.9 | 0.04 | 11.53 | -5.17 | 0.0018 |
| 0.07 | 2.31 | 0.71 | 1.03 | 0.11 | 6.0 | 1.8 | 2.7 | 0.3 | 2.9 | 0.09 | 11.52 | -5.12 | 0.0051 |
| 0.10 | 2.31 | 0.71 | 0.99 | 0.14 | 6.0 | 1.8 | 2.6 | 0.4 | 2.9 | 0.12 | 11.51 | -4.76 | 0.0053 |
| 0.30 | 2.33 | 0.65 | 0.79 | 0.34 | 6.0 | 1.7 | 2.0 | 0.9 | 2.9 | 0.3 | 11.43 | -4.82 | 0.0051 |
| 0.60 | 2.08 | 0.63 | 0.49 | 0.55 | 6.0 | 1.8 | 1.4 | 1.6 | 3.0 | 0.53 | 11.48 | -4.76 | 0.0078 |
| 0.80 | 2.30 | 0.66 | 0.43 | 0.80 | 6.0 | 1.7 | 1.1 | 2.1 | 3.2 | 0.65 | 11.52 | 5.2 | 0.0203 |
| 1.00 | 2.11 | 0.45 | 0.00 | 1.12 | 6.0 | 1.3 | 0.0 | 3.2 | 3.2 | 1 | 11.54 | -4.85 | 1 |
Sharp peaks in the X-ray diffractograms (Fig 1) of the synthesis products indicated good crystallinity, and ettringite was the only stable crystalline phase except the sample h. Although the low intensities of the diffraction peaks are obtained in the pure As-sample (Fig 1h), the ettringite phase clearly can be recognized. The peaks showed slight shifts to higher angles (smaller d-spacing) with substitution of AsO4 for SO4 (including the sample h). This decrease in basal spacing implied that the interchannel for sulfate and water molecules was compressed after AsO4 uptake, which can be attributed to the intercalation of an arsenate anion in exchange for sulfate and the displacement of the ordered water molecules [26, 27]. The solids with high arsenic content (Xsolid > 0.5) evidently had lower intensities of the diffraction peaks, which indicated lower crystallinity of samples. The peak intensity (around 9.9°) decreased with increasing As content in the solid solution series, and disappear when there was no sulfur. That was due to the elevated electron density in the structure, which resulted from the substitution of SO4 by AsO4. A new peak (around 12.6°) appeared when As contents in the samples were higher than 0.65. This could be attributed to CaAl2O4·10H2O. And there was another new peak at 30.4° in sample h, which was due to Ca3(AsO4)2·10H2O. The peak intensity around 37.3°rapidly decreased with As increasing in solid samples, which may be attributed to As substitute for partial H2O in the channel of ettringite. And the rapid decrease of the peak (37.3°) caused a false appearance of peak split in f, g and h.
Fig 1. X-ray diffractograms of the solid solution series of AsO4–ettringite and SO4–ettringite.
a, b, c, d, e, f, g, and h correspond to the samples with Xsolid of 0, 0.04, 0.09, 0.12, 0.30, 0.53, 0.65, and 1.00, respectively.
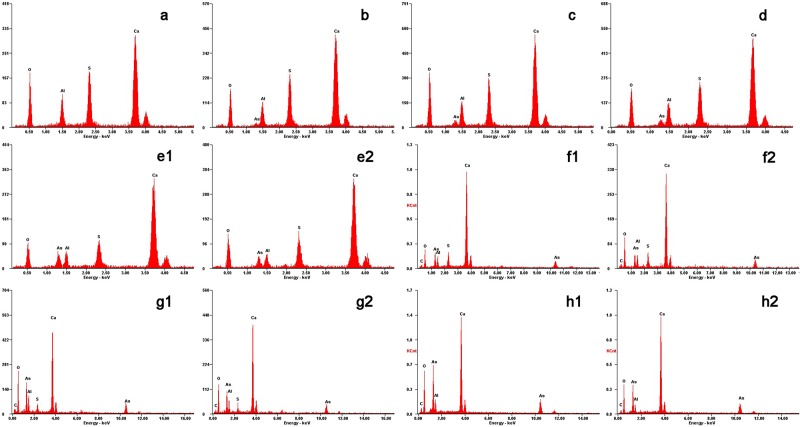
The poorer crystalline solid with increasing As content in the samples could also be observed through the SEM micrographs of the samples (Fig 2). The club-shaped ettringite particles were approximately 5 μm to 12 μm in length when arsenic was absent. However, the grain length of ettringite decreased to <1 μm with increases in solid-phase arsenic concentration, and the length-to-diameter ratio was lower. Typical ettringite rods dominated when As contents in samples were lown(<0.3), while some irregular particles attached to the rods with short length at higher As content. The irregular particles also contained the same elements with the prisms, which were showed from EDS mapping (Fig 3).
Fig 2. SEM micrographs of the solid solution series of AsO4–ettringite and SO4–ettringite.
a, b, c, d, e, f, g, and h correspond to the samples with Xsolid of 0, 0.04, 0.09, 0.12, 0.30, 0.53, 0.65, and 1.00, respectively.
Fig 3. EDS mapping of the solid solution series of AsO4–ettringite and SO4–ettringite.
The selected points for EDS were the square boxes in Fig 2.
Oxyanion speciation could be confirmed by Fourier transform infrared (FTIR) spectroscopy. Fig 4 shows the spectra of the solid solution series of AsO4-SO4-ettringite. The assignments of vibration are shown in Table 3. As indicated by the peak intensities, the SO4 concentration in the solid solutions decreased with the increase in the solid phase AsO4 concentration. The FTIR spectra of solid solutions exhibited an As–O stretching peak at 855 cm−1, which was higher than 810 cm−1 reported by Siebert H. [28]. AsO43- was protonated to form HAsO42−, which caused the As–OH symmetric stretch to shift to higher wavenumbers [29]. Thus, AsO43− substituted SO42− inside the channels in the form of HAsO42−, which was also demonstrated in dissolution experiments because HAsO42− was the dominant form of arsenic in the equilibrated solutions. Strong and broad OH bands around 3432 cm-1 and 2950 cm-1 developed with increases in solid phase AsO4 concentration, and the new band (around 2950 cm-1) may have been due to the formation of H-bonds between AsO4 and structural OH or H2O. Possible weak carbonate bands at 1421 cm−1 existed in the spectra [30, 31], which could indicate carbonate contamination, but in less than 5%, because no compound containing carbonate was observed from the X-ray diffractograms.
Fig 4. FTIR spectra of the solid solution series of AsO4–ettringite and SO4–ettringite.
a, b, c, d, e, f, g, and h correspond to the samples with Xsolid of 0, 0.04, 0.09, 0.12, 0.30, 0.53, 0.65, and 1.00, respectively.
Table 3. IR spectra of the solid solution series of AsO4–ettringite and SO4–ettringite and band assignments.
| Frequency (cm−1) | Vibrations |
|---|---|
| 553 | Al(OH)6 |
| 619 | SO4 |
| 855 | HAsO4 |
| 1112 | SO4 |
| 1421 | Possible CO3 |
| 1668 | H2O |
| 3432 | H-boned OH |
| 3635 | Non-H-boned OH |
Solid solution solubility products
The ion concentrations in solution of the dissolution experiments were shown in Table 4. And the Ca:Al:SO4:AsO4 ratios in solution were different from those of the solid, suggesting non-stoichiometric dissolution. This was expected, since the presence of secondary phases (Ca-As compound, gypsum and Al-hydroxide) leaded to reduction of dissolved Ca, Al, SO4 and AsO4 concentrations in solution.
Table 4. Ion concentrations in solution in the dissolution experiments (mmol/L).
| Sample(Xsolid) | Ca | Al | SO4 | AsO4 | pH | log{HAsO4} | XHAsO4,aq |
|---|---|---|---|---|---|---|---|
| 0.00 | 2.984 | 1.032 | 5.261 | 0.000 | 10.85 | 0 | 0 |
| 0.04 | 3.004 | 1.010 | 5.105 | 0.020 | 10.80 | -5.3 | 0.0019 |
| 0.09 | 2.692 | 0.857 | 4.452 | 0.081 | 10.90 | -4.89 | 0.0053 |
| 0.12 | 2.677 | 0.811 | 4.067 | 0.088 | 10.97 | -4.91 | 0.0056 |
| 0.30 | 2.530 | 0.842 | 4.315 | 0.094 | 11.09 | -4.94 | 0.0049 |
| 0.53 | 1.745 | 1.912 | 2.902 | 0.131 | 11.32 | -4.87 | 0.0082 |
| 0.65 | 1.836 | 2.206 | 1.268 | 0.160 | 11.34 | -4.86 | 0.0186 |
| 1.00 | 1.751 | 1.579 | 0.000 | 0.174 | 11.41 | -5.06 | 1 |
The chemical speciation of the ions and saturation index (SI) calculations were performed using the geochemical speciation model Visual MINTEQ 3.1. Activity coefficients of aqueous species were calculated with the geochemical speciation model Visual MINTEQ 3.1 using the Davies equation:
| (1) |
In the precipitation experiments, the results showed the saturation index (SI) of ettringite, Ca4(OH)2(AsO4)2·4H2O, Ca3(AsO4)2·xH2O at low molar ratio (X initial solution, <0.3), and ettringite, Al(OH)3, boehimte, Ca5(AsO4)3OH, Ca3(AsO4)2·xH2O, biaspore, gibbsite at higher molar ratio, and Al(OH)3, boehimte, Ca5(AsO4)3OH, Ca3(AsO4)2·xH2O, diaspore, gibbsite, without sulfate were above 0. However, ettringite was the only the stable phase except the sample without sulfate. This indicated the content of the other phases was below XRD detection limit even though these phases were present. However, both the XRD result of the sample without sulfate and the saturation index (SI) indicated Ca3(AsO4)2·10H2O was present. In the dissolution experiments, the saturation index (SI) of Al(OH)3, boehimte, Ca5(AsO4)3OH, diaspore, ettringite, gibbsite at X solid <0.3, and Al(OH)3, Boehimte, Ca5(AsO4)OH, diaspore, ettringite, gibbsite, Ca4(OH)2(AsO4)2·4H2O at higher X solid were above 0.
FTIR spectroscopy analysis of the solid samples and chemical analysis of the liquid phase revealed that AsO43− substituted for SO42− inside the channels in the form of HAsO42−. Thus, HAsO42− will be used for the thermodynamic study of the solid solution series.
The solubility products of the solid solution series was calculated according to the following reaction:
| (2) |
The curly brackets {} denote aqueous activities. The Ksp calculated are shown in Fig 5. The calculated AsO4–ettringite and SO4–ettringite solubility products change as a function of XHAsO4 for mixed phases, with a linear correlation between logKsp and XHAsO4. This finding indicates that solid solutions exist. Solubility calculations of all precipitation and dissolution experiments resulted in a mean logKAs-ettringite = -48.4 ± 0.4 and KSO4–ettringite = -43.9 ± 0.6. The solubility of SO4–ettringite in the current study was higher than that determined by Barbara and Thomas (-44.9) [14, 32], which could be due to a small CO2 amount in the system that lowers the pH. Certainly other factors, such as the choice of the activity coefficient model, analytical errors, and the presence of other complexes not included in the activity calculations, may affect estimates based on minimizing the variance in Ksp.
Fig 5. Solid mole fraction/solubility products plot for the system HAsO4–ettringite and SO4–ettringite solid solution at 25°C.
The calculated Ksp of the solid solutions fits best to the nonideal model.
The aqueous solubility of the binary solid solution system HAsO4–ettringite and SO4–ettringite could be predicted by plotting the Lippmann’s solidus and solutus relationships on the ordinate against two superimposed scales, i.e., XHAsO4 and XHAsO4,aq, on the abscissa, which could provide the solid-phase and aqueous-phase compositions for a series of possible thermodynamic equilibrium states [33–35]. In this case, the solidus and solutus equations can be expressed as follows:
| (3) |
and
| (4) |
where the curly brackets {} denote aqueous activities; XHAsO4 and XSO4 are the mole fractions of HAsO4 and SO4 (XSO4 + XHAsO4 = 1) in the solid, respectively; XHAsO4,aq and XSO4,aq are the activity fractions of HAsO42− and SO42− ions in the aqueous solution, respectively; KHAsO4 and KSO4 are the solubility products of pure HAsO4–ettringite and SO4–ettringite, respectively; and γHAsO4 and γSO4 are solid activity coefficients.
The solid-phase activity coefficients determined from the modified Guggenheim regular excess free energy model [36]can be expressed as follows:
| (5) |
| (6) |
Regular nonideal solid solutions only need one Guggenheim fitting parameter (a0), which was determined by the MBSSAS code [33, 37]. A value of a0 = 1.69 was obtained. Thus, Eqs 5 and 6 can be simplified as follows:
| (7) |
| (8) |
The Lippmann diagram for this system at 25°C is shown in Fig 6. The calculated ΣΠ of the solid solution series fits best to the nonideal model.
Fig 6. Lippmann diagram for the system HAsO4/SO4–ettringite solid solution series at 25°C.
The pure HAsO4–ettringite and SO4–ettringite endmember solubility products in this system differ by four orders of magnitude. As a result, a strong preferential distribution of the less soluble endmember toward the solid phase was observed. This expression (Eq 9) can be used to construct a XHAsO4–XHAsO4,aq plot (Fig 7), which describes the coexisting compositions of solid and aqueous solutions under equilibrium conditions.
Fig 7. Solid mole fraction/aqueous activity fraction plot for the system HAsO4/SO4 –ettringite solid solutions at 25°C.
| (9) |
Fig 7 shows that the XHAsO4–XHAsO4,aq curve approximates to two straight lines forming a right angle, which implies that HAsO4-poor aqueous solutions are in equilibrium with HAsO4-rich solid phases in a wide XHAsO4 range.
In summary, ettringite containing SO42− or HAsO42− has been synthesized, and its thermodynamic data were first published. The results revealed that HAsO4–ettringite and SO4–ettringite solid solutions exist and that this solid solution had HAsO4-poor aqueous solutions in equilibrium. This finding implies that ettringite (AFt-phase) may play an important role in AsO43− solidifying mechanisms in the cement matrix and should be considered in AsO43− leaching modeling projects.
Supporting information
a, b, c, d, e, f, g, and h correspond to the samples with Xsolid of 0, 0.04, 0.09, 0.12, 0.30, 0.53, 0.65, and 1.00, respectively.
(ZIP)
a, b, c, d, e, f, g, and h correspond to the samples with Xsolid of 0, 0.04, 0.09, 0.12, 0.30, 0.53, 0.65, and 1.00, respectively.
(ZIP)
Acknowledgments
We thank the research group of solid waste treatment and disposal of Wuhan University for their comments on an earlier draft of this manuscript.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This work was funded by Science and Technology Department of Hubei Province (URL: http://www.hbstd.gov.cn/), grant number: 2016ACA162. Two authors, MZ and HH, received the funding. The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Mollah MYA, Lu F, Cocke DL. An X-ray diffraction (xrd) and fourier transform infrared spectroscopic (FT-IR) characterization of the speciation of arsenic (v) in portland cement type-V. Science of the Total Environment, 1998; 224: 57–68. [DOI] [PubMed] [Google Scholar]
- 2.Garry MR, Santamaria AB, Williams AL, Desesso JM. In utero arsenic exposure in mice and early life susceptibility to cancer. Regulatory Toxicology and Pharmacology. 2015; 73: 378–390. doi: 10.1016/j.yrtph.2015.07.023 [DOI] [PubMed] [Google Scholar]
- 3.Rudnai T, Sándor J, Kádár M, Borsányi M, Béres J, Métneki J, et al. Arsenic in drinking water and congenital heart anomalies in Hungary. International Journal of Hygiene & Environmental Health, 2014; 217(8):813. [DOI] [PubMed] [Google Scholar]
- 4.Moon DH, Dermatas D, Menounou N. Arsenic immobilization by calcium–arsenic precipitates in lime treated soils. Science of the Total Environment. 2004; 330: 171–185. doi: 10.1016/j.scitotenv.2004.03.016 [DOI] [PubMed] [Google Scholar]
- 5.Perkins RB, Palmer CD. Solubility of Ca6[Al(OH)6]2(CrO4)3∙26H2O, the chromate analog of ettringite:5±75°C. Applied Geochemistry. 2000; 15: 1203–1218. [Google Scholar]
- 6.Scholtzová E, Kucková L, Kožíšek J, Tunega D. Structural and spectroscopic characterization of ettringite mineral–combined DFT and experimental study. Journal of Molecular Structure, 2015; 1100: 215–224. [Google Scholar]
- 7.Iwaida T, Yano K, Tanaka S, Nagasaki S. Synthesis and characterization of sulfate-iodate ettringite; and their potential role in immobilization of 129I. Journal of Nuclear Fuel Cycle & Environment. 2001; 7: 57–63. [Google Scholar]
- 8.Poellmann H, Kuzel HJ, Wenda R. Solid solution of ettringites: Part II Incorporation of B(OH)4 and CrO42- in 3CaO∙Al2O3∙3CaSO4∙32H2O. Cement and Concrete Research. 199; 23: 422–430. [Google Scholar]
- 9.Moon DH, Grubb DG, Reilly TL. Stabilization/solidification of selenium-impacted soils using Portland cement and cement kiln dust. Journal of Hazardous Materials, 2009; 168(2–3):944–951. doi: 10.1016/j.jhazmat.2009.02.125 [DOI] [PubMed] [Google Scholar]
- 10.Ochs M, Lothenbach B, Giffaut E. Uptake of oxo-anions by cements through solid-solution formation: Experimental evidence and modelling. Radiochimica Acta. 2002; 90: 639–646. [Google Scholar]
- 11.Zhang M, Reardon EJ. Removal of B, Cr, Mo, and Se from wastewater by incorporation into hydrocalumite and ettringite. Environmental Science & Technology. 2003; 37: 2947–2952. [DOI] [PubMed] [Google Scholar]
- 12.Cornelis G, Saikia N, Van Gerven T, Vandecasteele, C. Leaching of antimony and molybdenum from municipal solid waste incinerator residues. WASCON2006, Science and engineering of recycling for environmental protection location. 2006.
- 13.Frost RL, López A, Xi YF, Scholz R, Costa GM, Lima RMF, et al. The spectroscopic characterization of the sulphate mineral ettringite from Kuruman manganese deposits, South Africa. Vibrational Spectroscopy, 2013; 68(35): 266–271. [Google Scholar]
- 14.Perkins RB, Palmer CD. Solubility of ettringite (Ca6[Al(OH)6]2(SO4)3∙26H2O) at 5–75°C. Geochimica et Cosmochimica Acta. 1999; 63: 1969–1980. [Google Scholar]
- 15.Kumarathasan P, McCarthy GJ, Hasset DJ, Pflughoeft-Hassett DF. Oxyanion substituted ettringites: synthesis and characterization, and their potential role in immobilization of As, B, Cr, Se, and V. Mat. MRS Online Proceeding Library. 1990; 178: 83–104. [Google Scholar]
- 16.Myneni SCB, Traina SJ, Logan TJ, Waychunas GA. Oxyanion behavior in alkaline environments: sorption and desorption of arsenate in ettringite. Environmental Science & Technology. 1997; 31: 1761–1768. [Google Scholar]
- 17.Hassett DJ, McCarthy GJ, Kumarathasan P, Pflughoeft-Hassett DF. Synthesis and characterization of selenate and sulfate-selenate ettringite strcuture phases. Materials Research Bulletin, 1990; 25: 1347–1354. [Google Scholar]
- 18.KTH, Department of Sustainable Development, Environmental Science and Engine. Visual MINTEQ ver. 3.0/3.1, 2010; http://hem.bredband.net/b108693/index.html.
- 19.Shock EL, Sassani DC, Willis M, Sverjensky DA. Inorganic species in geologic fluids: correlations among standard molal thermodynamic properties of aqueous ions and hydroxide complexes. Geochimica et Cosmochimica Acta, 1997, 61(5): 907–950. [DOI] [PubMed] [Google Scholar]
- 20.Bothe JV, Brown PW. The stabilities of calcium arsenates at 23±18°C. Journal of Hazardous Materials. 1999; B69: 197–207. [DOI] [PubMed] [Google Scholar]
- 21.Nordstrom DK, May HM. Aqueous equilibrium data for mononuclear aluminum species. The environmental chemistry of aluminum, 1996, 2: 39–80. [Google Scholar]
- 22.Henke K. Arsenic: Environmental Chemistry, Health Threats and Waste Treatment. 2009.
- 23.KTH, Department of Sustainable Development, Environmental Science and Engine. MINTEQA2_Database (Aqueous species database and Solid phase database); https://vminteq.lwr.kth.se/download/.
- 24.Nordstrom DK, Plummer LN, Langmuir D, Busenberg E, May HM, Jones BF, et al. Revised chemical equilibrium data for major water–mineral reactions and their limitations In: Melchior D.C., Bassett R.L. (Eds.), Chemical Modeling of Aqueous Systems II: ACS Symposium Series. American Chemical Society, Washington DC, 1990, pp. 398–413. [Google Scholar]
- 25.Leisinger SM, Lothenbach B, Saout GL, Kägi R, Wehrli B, Johnson CA. Solid solutions between CrO4- and SO4-ettringite Ca6(Al(OH)6)2[(CrO4)x(SO4)1-x]3∙26H2O. Environmental Science & Technology. 2010; 44: 8983–8988. [DOI] [PubMed] [Google Scholar]
- 26.Choi WH, Ghorpade PA, Kim KB, Shin JW, Park JY. Properties of synthetic monosulfate as a novel material for arsenic removal. Journal of Hazardous Materials. 2012; 227:402–409. doi: 10.1016/j.jhazmat.2012.05.082 [DOI] [PubMed] [Google Scholar]
- 27.Prasanna SV, Kamath PV. Synthesis and characterization of arsenate-intercalated layered double hydroxides (LDHs): Prospects for arsenic mineralization. Journal of Colloid and Interface Science. 2009; 331: 439–445. doi: 10.1016/j.jcis.2008.11.054 [DOI] [PubMed] [Google Scholar]
- 28.Siebert H. Anwendungen der schwingungsspektroskopie in deranorganischen chemie. Springer-Verlag; 1966. [Google Scholar]
- 29.Myneni SCB, Traina SJ, Waychunas GA, Logan TJ. Experimental and theoretical vibrational spectroscopic evaluation of arsenate coordination in aqueous solutions, solids, and at mineral-water interfaces. Geochimica et Cosmochimica Acta. 1998; 62: 3285–3300. [Google Scholar]
- 30.Reig FB, Adelantado JVG, Moreno MCMM. FTIR quantitative analysis of calcium carbonate (calcite) and silica (quartz) mixtures using the constant ratio method. Application to geological samples. Talanta. 2002; 58: 811–821. [DOI] [PubMed] [Google Scholar]
- 31.Suksomrana W, Molloy R. Hydroxyapatite prepared by co-precipitation with calcium carbonate:effects of digested calcium carbonate and phosphate sources. Naresuan University Journal: Science and Technology. 2017; 25(1):57–66. [Google Scholar]
- 32.Lothenbach B, Matschei T, Möschner G, Glasser FP. Thermodynamic modelling of the effect of temperature on the hydration and porosity of Portland cement. Cement and Concrete Research. 2008; 38:1–18. [Google Scholar]
- 33.Glynn PD, Reardon EJ. Solid-solution aqueous-solution equilibria thermodynamic theory and representation. American Journal of Science. 1990; 290:164–201. [Google Scholar]
- 34.Prieto M, Fernández-González A, Becker U, Putnis A. Computing Lippmann Diagrams from direct calculation of mixing properties of solid solutions: application to the barite-celestite system. Aquatic Geochemistry. 2000; 6:133–146. [Google Scholar]
- 35.OECD Nuclear Energy Agency. Chemical Thermodynamics Chemical Thermodynamics of Solid Solutions of Interest in Radioactive Waste Management. SourceOECD Nuclear Energy, 2007; i-289(289). [Google Scholar]
- 36.Redlich O, Kister AT. Algebraic representation of the thermodynamic properties and the classification of solutions. Industrial and Engineering Chemistry. 1948; 40, 345–348. [Google Scholar]
- 37.Glynn PD. MBSSAS: A code for the computation of Margules parameters and equilibrium relations in binary solid-solution aqueous-solution systems. Computers and Geoscience. 1991; 17: 907–966. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
a, b, c, d, e, f, g, and h correspond to the samples with Xsolid of 0, 0.04, 0.09, 0.12, 0.30, 0.53, 0.65, and 1.00, respectively.
(ZIP)
a, b, c, d, e, f, g, and h correspond to the samples with Xsolid of 0, 0.04, 0.09, 0.12, 0.30, 0.53, 0.65, and 1.00, respectively.
(ZIP)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.