Abstract
Cerebral microdialysis is widely used in neurocritical care units. The goal of this study was to establish the reference interval for the interstitial fluid concentrations of energy metabolites and glycerol by using the extrapolation to zero-flow methodology in anesthetized patients and by constant perfusion at 0.3 µL/min in awake patients. A CMA-71 probe was implanted during surgery in normal white matter of patients with posterior fossa or supratentorial lesions, and the perfusion flow rate was randomized to 0.1, 0.3, 0.6, 1.2, and 2.4 µL/min. Within 24 h of surgery, perfusion was restarted at a constant 0.3 µL/min in fully awake patients. The actual interstitial fluid metabolite concentrations were calculated using the zero-flow methodology. In vitro experiments were also conducted to evaluate the reproducibility of the in vivo methodology. Nineteen patients (seven males) with a median age of 44 years (range: 21–69) were included in the in vivo study. The median (lower–upper) reference interval values were 1.57 (1.15–4.13 mmol/L) for glucose, 2.01 (1.30–5.31 mmol/L) for lactate, 80.0 (54.4–197.0 µmol/L) for pyruvate, and 49.9 (23.6–227.3 µmol/L) for glycerol. The reference intervals reported raises the need to reconsider traditional definitions of brain metabolic disturbances and emphasize the importance of using different thresholds for awake patients and patients under anesthesia.
Keywords: Brain metabolism, cerebral microdialysis, lactate, reference intervals, traumatic brain injury
Introduction
Cerebral microdialysis (MD) was introduced by Bito et al.1 for in vivo dialysis of the canine brain and is now used for an extensive array of applications that explore the regional chemistry of the human brain. The first known application of cerebral MD in humans was reported by Meyerson et al.,2 who implanted microdialysis probes during thalamotomy procedures in patients with Parkinson’s disease. Since that time, cerebral MD has been increasingly used as a neuromonitoring technique in neurocritical patients with traumatic brain injury (TBI), middle cerebral artery infarction, and spontaneous subarachnoid hemorrhage (SAH) to monitor cerebral energy metabolism during the acute phase after injury or stroke.3
One problem inherent to microdialysis is the fact that the dialysate concentration of any substance is never a perfect mirror of the interstitial levels but instead represents a variable fraction of the actual values.3–6 Since its introduction, a recurrent problem with cerebral MD has been the lack of a reliable in vivo calibration method, which prevents accurate in vivo concentrations from being established.7 The approach most frequently used to evaluate MD efficiency for any substance is to use the in vitro relative recovery (RR), which is defined as the ratio of the concentration in the dialysate to the true in vitro concentration of a given substance.8 In clinical practice, the true substance concentration in the interstitial fluid (ISF) is calculated by measuring the concentration in the dialysate and dividing that concentration by the in vitro RR expressed as a fraction of 1.5 The validity of this approach rests on the principle that the in vitro and in vivo conditions are similar; however, this assumption is far from true.5 The RR in vitro depends primarily on the physical properties of the membrane, the temperature of the medium, the perfusion flow rate, the characteristics of the sample matrix, and the diffusion coefficient of the substance of interest.3–5,8 However, these results are difficult to extrapolate to the brain, due to the effect of the tissue properties on the diffusion of analytes. The ISF space in any organ is an inhomogeneous and tortuous medium; therefore, the in vitro RR can only provide a rough estimate of the efficiency of MD probes in vivo.5,9
The main study reporting the reference intervals (RIs) for analytes involved in monitoring brain energy metabolism in neurocritical patients was conducted by Reinstrup et al.10 in patients who underwent neurosurgical procedures under general anesthesia. Other authors have reported brain metabolite levels in the normal brains of patients with central nervous system tumors,11 in awake epileptic patients,12,13 and in patients with spontaneous SAH.14 However, in most of these studies, the true ISF concentrations were unknown, and the reference limits were estimated from the concentrations in the dialysate and from the in vitro RR for the specific metabolite. Consequently, the normal ranges for brain lactate, the lactate-to-pyruvate (LP) ratio, and what has been considered the “anaerobic threshold,” are still quite arbitrary. In human studies, the upper reference limit for lactate in normal brain tissue is unexpectedly variable and ranges from 1.50 to 5.1 mmol/L.11,13,15–17 This variability remains an important obstacle for adequately evaluating metabolic findings in neurocritical patients, as well as for making physiopathological interpretations and assessing clinical relevance.
To overcome the limitations of in vitro studies, three different methods have been proposed to estimate the true ISF concentration of any analyte of interest. These methods are (1) the extrapolation to zero-flow rate method (ZFM),18 (2) the no-net flux method, and (3) the slow perfusion rate.7,19 All three methods are considered reliable and yield similar results, as shown in the experimental studies conducted by Menacherry et al.7 Here, we present the results of a human study in which the reference limits for analytes involved in energy metabolism (i.e., glucose, lactate, and pyruvate) and for glycerol (a biomarker of cell damage) were determined in a cohort of patients who were observed twice: while anesthetized and while fully awake.
In anesthetized patients, we used the extrapolation to ZFM, and in awake patients we employed perfusion at a constant infusion speed of 0.3 µL/min, the infusion rate recommended by a recent consensus conference on neuromonitoring.20 The RIs reported here provide additional support for the thresholds suggested by the most recent consensus conference on microdialysis neuromonitoring,20 highlighting the importance of lactate in brain energetics and raising the need to reconsider traditional definitions of metabolic disturbances observed in neurocritical patients. Our study emphasizes the importance of using different thresholds for awake patients and patients under anesthesia or deep sedation.
Materials and methods
The present study was divided into three separate sections: (1) preliminary in vitro experiments to confirm the RR of the CMA-71 probes (M Dialysis AB, Stockholm, Sweden) for the analytes of interest, (2) an in vitro evaluation of the reproducibility of the “ZFM” used in the in vivo setting to calculate the brain tissue concentrations of the metabolites, and (3) a study of the brain ISF concentrations of glucose, lactate, pyruvate, and glycerol—and their reference limits—in patients who underwent neurosurgical procedures both under general anesthesia and while fully awake after surgery.
In vitro RR experiments
In vitro RR experiments were conducted to confirm the efficient recovery of CMA-71 probes that have been previously described by others.9,21 The experiments were conducted using an in vitro setup that was described by our group elsewhere.22 In brief, the experiments involved placing each CMA-71 catheter into two different matrix solutions (MA-1 and MA-2), which had different concentrations of glucose, lactate, pyruvate, and glycerol (Sigma-Aldrich, St Louis, MO, USA). The study matrices composition is described in Table S1 in Supplementary information. A total volume of 2.5 mL of the matrix solution was placed in a 5-mL glass tube (BD Vacutainer®) in a dry bath (Labnet International, Edison, NJ, USA) set at a temperature of 37℃.
The tips of the CMA-71 probes were placed in the matrix, and the microdialysis (MD) catheters were connected to a CMA-402 pump (M Dialysis AB) and perfused at 0.3 µL/min (18 µL/h) with an isotonic solution that had the same ionic composition as the matrix but contained an additional 3% albumin. Our in vitro experiments were conducted without stirring. The main reason to avoid stirring was that it produced significant variability in the volume recovered in the microvial (see Supplementary information).
When steady-state conditions were achieved, the experiments were initiated by perfusing the in vitro probes at a constant flow rate of 0.3 µL/min and collecting one microvial per hour for six consecutive hours; six microvials were obtained for each matrix in each catheter. The matrix solution was analyzed before and resampled after each microvial collection to control for all of the variables that can modify the initial analyte concentration in the medium, such as evaporation, solute depletion by the dialysis procedure, etc. A total volume of 140 µL was removed from the matrix at the end of the 6-h experiment. Both dialysate and matrix samples were analyzed in the ISCUSflex analyzer (M Dialysis AB). The RR was calculated using the following equation:
| (1) |
where Cmd and Cmatrix are the analyte concentrations in the microdialysate and in the matrix, respectively.
In vitro extrapolation to zero-flow rate
To test in vitro the extrapolation to ZFM that was used during surgery in the included patients, a second experiment was conducted in which CMA-71 probes pertaining to two different lots (M Dialysis AB, lots #T23301 and #T24612) were placed in a matrix with the same solute concentrations described for MA-2 in the previous section. The catheter was connected to a 1-mL disposable syringe (Luer-Lok™, New Jersey, USA) placed in a microinfusion pump (CMA-402, M Dialysis AB). The CMA-402 is a variable flow rate pump that enables the adjustment of the infusion rate between 0.1 and 20 µL/min. For these experiments, the same isotonic solution used in the in vitro RR experiments was infused. For each catheter, the flow rate was changed randomly to the following rates: 0.1, 0.3, 0.6, 1.2, and 2.4 µL/min. Each flow rate was maintained for 1 h, except for the 0.1 µL/min flow rate, which was maintained for 2 h to compensate for the low recovery volume. Microvials were collected every 30 min for the 2.4–0.3 µL/min infusion rates and hourly for the 0.1 µL/min flow rate. Each catheter experiment yielded a total of 10 determinations (two for each infusion rate). The metabolite concentrations in the matrix were analyzed at the beginning and at the end of each experiment. All analyses were conducted in the ISCUSflex analyzer.
The actual concentrations of matrix metabolites were estimated using the ZFM described by Jacobson et al.18 This method determines the analyte concentration through the determination of the relation between the perfusion flow rate (F), the probe’s membrane area, and the transference coefficient. This relation is defined by the following equation:
| (2) |
where Cdial is the analyte concentration in the dialysate, C0 the matrix concentration of the analyte of interest, r the average mass transfer coefficient, A the surface of the microdialysis membrane, and F the infusion flow rate. The external concentration (C0) can be estimated by fitting a nonlinear regression model to the dialysate concentrations obtained at different perfusion rates.7,18 According to this method, at a theoretical flow rate of 0 µL/min, the metabolite concentration of the dialysate is considered to be equal to the true concentration in the matrix.18,23 Because the first dialysate sample at each flow rate is heavily influenced by the previous flow rate (due to the dead liquid volume of the outlet tube [∼5.1 µL]), the first sample was always discarded and was not included in the calculations; therefore, at any flow rate, only the second determination was used to fit the curve. The catheters used in these experiments were never infused for more than 96 h.
Determination of the brain tissue metabolites concentrations
Patient selection and study design
A prospective study was conducted in patients aged above 18 years who underwent surgical treatment under standard general anesthesia to treat posterior fossa and supratentorial lesions at Vall d’Hebron University Hospital (VHUH), between November 2012 and January 2016. To enroll patients in the study, the inclusion criteria were: (1) posterior fossa or supratentorial lesions requiring the implantation of an external ventricular catheter for the drainage of cerebrospinal fluid (CSF); (2) no neuroradiological abnormalities in the white/gray matter in the supratentorial compartment where the MD probe will be implanted in magnetic resonance imaging (MRI) sequences evaluated in the following MRI sequences: T1W, T2W, and FLAIR; (3) a normal ventricular size defined as an Evan Index below or equal to 0.30 or moderate ventricular enlargement without clinical symptoms of intracranial hypertension;24 and (4) written informed consent signed by the patient or the next-of-kin. The study was approved by the Institutional Ethics Committee of the VHUH (protocol number approval PR/AG-140-2011). All provisions of the Declaration of Helsinki were followed.
Surgical procedure
According to the manufacturer’s specifications, the CMA-71 probe has a nominal cut-off of “around 100 kDa”.25 CMA-71 probes were placed with the patient under general anesthesia at the same time the external ventricular drainage was placed, through a small hole in the duramater at ∼3 mm from the ventriculostomy entry. The position of the probe in the normal white matter was confirmed by a control computed tomography (CT) scan conducted within the first 24 h after probe implantation (Figure S1 in the Supplement). Patients with any hemorrhagic or hypodense lesion around the probe detected in the control CT were excluded from analysis. The MD probe was connected through a 150-cm length extension line, with 1.58 mL residual volume (Prolonsend® PA-150, Sendal, Cáceres, Spain) primed with CNS perfusion fluid (M Dialysis AB), to a 1-mL disposable syringe (Luer-Lok™) placed in the microinfusion pump CMA-402 and perfused at 0.3 µL/min during 1 h with CNS perfusion fluid (M Dialysis AB). The first sample from the first hour was always discarded to allow stabilization of the system. Then, for each patient, the perfusion flow rate was varied randomly, and the same methodology described in the in vitro section was applied except in the first four patients, where microvials were collected hourly for all infusion rates and just one microvial was collected for each infusion rate. Once all the experiment was completed, and if the duration of the surgery allowed it, the perfusion rate was changed to 0.3 µL/min rate, and microvials were collected each hour until the surgery was completed. At the end of the surgical procedure, the perfusion of the cerebral catheter was interrupted until the patient was fully awake in the reanimation unit.
During the surgical procedure, blood and CSF samples were also collected periodically. Blood gas analysis was performed in a Co-oximeter (1200 RAPIDLab Systems, Siemens, Munich, Germany). The CSF samples were centrifuged at 4000 rpm during 10 min, and the supernatant was analyzed in the ISCUSflex analyzer.
Microdialysis in the awake patient
Within 24 h after surgery and when the patient was extubated and fully conscious, the MD probe was reconnected to a CMA-106 microinfusion pump (M Dialysis AB), and the perfusion was restarted. In this second part of the study, the flow rate was maintained at a constant rate of 0.3 µL/min, and the samples were collected hourly. Blood and CSF samples were also collected and processed using the same methodology previously described. All monitoring data obtained during the study were collected in a Microsoft Excel spread sheet (Microsoft, Redmond, Washington, USA).
Statistical analysis
Statistical analyses were performed with R software v3.2.2 (R Foundation for Statistical Computing, Vienna, Austria; http://www.R-project.org) and the integrated development environment R Studio v0.99.491 (RStudio, Inc., Boston, MA, USA; http://www.rstudio.com). Unless otherwise specified, differences were considered statistically significant for p ≤ 0.05.
For estimating the true concentrations in the matrices (in vitro experiments) and in the brain ISF (in vivo experiments) with the ZFM, all the flow rate-concentration pairs were plotted in a scatter plot and analyzed by using the function and the R packages “nlstools” and “minpack.lm.”26,27 The R code (available on request) used the original equation described by Jacobson et al.18 The goodness of fit for the exponential model with the total data was evaluated based on visual inspection of the residuals calculated from the fit and testing the normality of the residuals with the Shapiro–Wilk test and the randomness of residuals with the runs test.
RI calculation. The Horn’s algorithm28 implemented in the package “referenceIntervals” was applied to detect outliers. Each detected outlier was reviewed, and if the patient or the data were considered doubtful, the case was eliminated of the RIs calculation. To calculate the brain upper and lower RI limits for each analyte, we used the distribution-free nonparametric method described in the NCCLS and Clinical and Laboratory Standards Institute (CLSI) guidelines C28-A3 for estimating percentiles intervals29,30 by using the package “referenceIntervals” for R.31
Results
In vitro RR of metabolites
Four catheters were used in these experiments. We observed minimal differences between the initial and the final concentrations of the matrix metabolites, with a mean reduction of approximately 5.5%. Although these differences were statistically significant, we considered them methodologically irrelevant. The denominator used for the RR calculation (equation (1)) was always the mean concentration of the matrix sampled before and after each microvial change. The four catheters included in the analysis yielded a total of 48 samples. The RR for each metabolite is summarized in Table 1. The mean RR for all metabolites was approximately 95%, similar to the findings published by others who used the CMA-71 probe.32 We did not find any significant difference between the two matrices studied (see Table 1); furthermore, the RR inter-catheter agreement was excellent, with differences always below 5%.
Table 1.
In vitro relative recoveries.
| Metabolite | Mean ± SD | Median (min–max) | p value |
|---|---|---|---|
| Glucose (mmol/L) | 91 ± 5 | 91 (80–103) | |
| MA-1 | 92 ± 4 | 91 (85–101) | 0.39 |
| MA-2 | 91 ± 5 | 92 (80–103) | |
| Lactate (mmol/L) | 95 ± 6 | 95 (83–109) | |
| MA-1 | 95 ± 5 | 95 (85–109) | 0.92 |
| MA-2 | 94 ± 6 | 96 (83–107) | |
| Pyruvate (µmol/L) | 104 ± 17 | 100 (83–150) | |
| MA-1 | 109 ± 20 | 97 (89–150) | 0.13 |
| MA-2 | 100 ± 13 | 101 (83–128) | |
| Glycerol (µmol/L) | 90 ± 6 | 91 (73–105) | |
| MA-1 | 92 ± 4 | 93 (82–99) | 0.09 |
| MA-2 | 89 ± 7 | 90 (73–105) |
Means and medians are expressed as percent recovery, as explained in the text (equation (1)). Comparisons between matrices were made using the Kruskal–Wallis test; no statistically significant differences were observed.
In vitro extrapolation to zero-flow
Seven catheters were included in this experiment. For each catheter, the metabolite concentrations at a theoretical flow rate of 0 µL/min were calculated using a nonlinear regression model. The matrix concentration (C0 in equation (2)) was calculated as the y-intercept, as described. A k value (where k = rA in equation (2)) was also determined for each metabolite. Figure 118 shows examples of the ZFM applied both in vitro and in vivo. The goodness of fit for the exponential model in vitro was excellent for all metabolites. The concentrations estimated at 0 µL/min with the nonlinear regression model were compared with the measured concentrations in the matrices (Table 2). To minimize errors, the matrix concentration used in the analysis was the mean concentration for each metabolite at the start and the end of the experiment. In all metabolites and for all catheters, we found a high agreement between the estimated concentrations and the true concentrations in the medium. The differences between both concentrations were not statistically significant (see Table 2) (Wilcoxon test for paired samples).
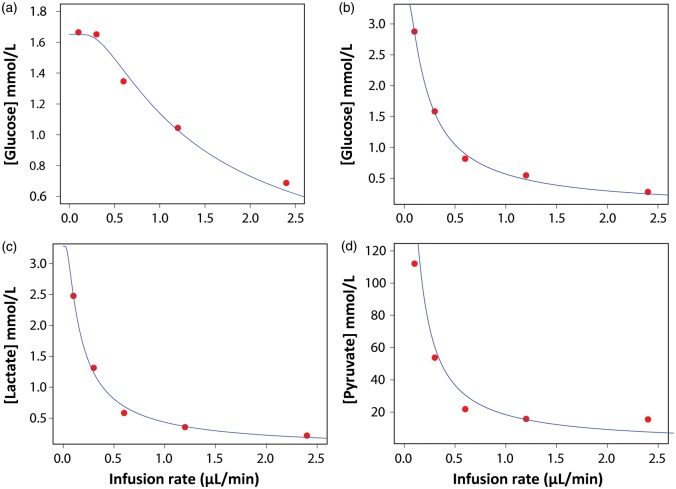
Figure 1.
Example of the graphical representation of the extrapolation to zero-flow method. Using non-linear curve fitting to the equation described by Jacobson et al.18 (see equation (2) in the manuscript), the concentration in the matrix and in the extracellular fluid (C0 in equation (2)) corresponds to the y-intercept. (a) In vitro extrapolation of the glucose data for catheter # 5. The estimated C0 was 1.65 mmol/L, the value of k (where k = rA in equation (2)) was 1.17 mm/min, and the measured C0 for glucose was 2.06 mmol/L. (b) In vivo extrapolation of the glucose data for patient # 12 (C0 = 3.43 mmol/L, k = 0.18 mm/min). (c) In vivo extrapolation of the lactate data for patient # 12 (C0 = 3.28 mmol/L, k = 0.14 mm/min). (d) In vivo extrapolation of the pyruvate data for patient #12 (C0 = 169 mmol/L, k = 0.11 mm/min).
Table 2.
In vitro estimated concentrations using the extrapolation to zero-flow methodology against true concentrations.
| Estimated concentration | Measured concentration | p value | |
|---|---|---|---|
| Glucose (mmol/L) | 1.97 (1.59–2.19) | 2.06 (1.93–2.25) | 0.16 |
| Lactate (mmol/L) | 2.01 (1.71–2.44) | 2.15 (2.05–2.37) | 0.09 |
| Pyruvate (µmol/L) | 106.7 (87.3–143.9) | 119.5 (108.5–127.5) | 0.38 |
| Glycerol (µmol/L) | 242.1 (160.6–284.5) | 231.6 (200.1–295.0) | 0.11 |
In these experiments, seven catheters were used. Data summarized correspond to the data for each metabolite in all experiments. Data are expressed as median (min–max). Comparisons between estimated and measured concentrations were made using the Wilcoxon test for paired samples; no statistically significant differences were observed.
Descriptive data of included patients
A total of 19 patients were included, 16 with a posterior fossa lesion and 3 with a supratentorial lesion. All presented normal-appearing gray and white matter in the MRI. The 19-patient cohort included 7 males and 12 females with a median age of 44 (range: 21–69 years) and a median Evans index of 0.28 (min: 0.20, max: 0.33). Table 3 shows a summary of the clinical data.
Table 3.
Demographic and clinical characteristics of the patients included in the study.
| Case No. | Age (years)/sex | Diagnosis of pathology | Evans index | Duration of microdialysis on surgery (h) | Duration of microdialysis on awakeness (h) | Anesthesia |
|---|---|---|---|---|---|---|
| 1 | 38/F | Cerebellar tonsil lesión | 0.28 | 4.67 | 7.42 | Inhalation |
| 2 | 32/F | Ependymoma | 0.28 | 8.00 | 11.90 | TIVA |
| 3 | 61/F | Atypical fibrous meningioma | 0.33 | 6.83 | NA | Inhalation |
| 4 | 21/F | Hemangioblastoma | 0.29 | 3.30 | 5.17 | Inhalation |
| 5 | 43/F | Chiari malformation | 0.27 | 4.93 | 13.17 | Inhalation |
| 6 | 22/M | Classic medulloblastoma | 0.27 | 7.72 | 7.42 | Inhalation |
| 7 | 34/F | Cerebellar metastasis | 0.24 | 10.83 | 5.08 | Inhalation |
| 8 | 60/F | Vestibular Schwannoma | 0.30 | 6.53 | 15.83 | Inhalation |
| 9 | 65/M | Cerebellar metastasis | 0.31 | 5.00 | 5.33 | Inhalation |
| 10 | 65/F | Hemangioblastoma | 0.28 | 5.00 | 9.33 | Inhalation |
| 11 | 66/M | Cerebellar metastasis | 0.28 | 8.00 | NA | Inhalation |
| 12 | 55/F | Anaplasic glioma | 0.30 | 5.83 | 7.67 | Inhalation |
| 13 | 42/M | Transitional meningioma | 0.24 | 6.83 | 39.00 | Inhalation |
| 14 | 31/M | Vestibular schwannoma | 0.21 | 6.50 | 14.00 | Inhalation |
| 15 | 69/F | Mixed meningioma | 0.27 | 6.25 | 10.00 | TIVA |
| 16 | 32/F | Central neurocytoma | 0.30 | 5.08 | 13.42 | TIVA |
| 17 | 65/F | Low grade glioma | 0.20 | 7.10 | 14.00 | TIVA |
| 18 | 66/M | Cerebellar metastasis | 0.29 | 7.17 | 13.17 | TIVA |
| 19 |
44/M |
Epidermoid cyst |
0.30 |
7.17 |
12.67 |
TIVA |
| Median | 44/M | 0.28 | 6.53 | 11.90 |
M: male; F: female; TIVA: total intravenous anesthesia; NA: not applicable.
Brain tissue concentrations in anesthetized patients
In 3 of the 19 patients, the intraoperative data were discarded; for one, the surgery was too short to obtain data for all the perfusion flow rates, and for the other two patients, the volume recovered was not correct. The remaining 16 patients had valid intraoperative data, which were included in the analysis. For each patient, the extracellular fluid concentration was determined with the ZFM, as already described. In some patients, the non-linear curve fitting to the equation did not result in a correct estimated C0 value because the iterative procedure of the “nls” function did not successfully converge to a certain value. This unsuccessful convergence was because the equation is too complex for the amount of data we had. In order to simplify the equation, we obtained a fixed k value for each metabolite by merging the data for all patients. We used the obtained k to estimate the C0 by non-linear curve fitting for each individual patient.
Of these 16 patients, the data from the first three patients were excluded from the RIs calculation at 0.3 µL/min because the microdialysis sampling methodology used during surgery was modified after the fourth patient, so as to avoid generating inaccurate values from the dead volume inside the outlet tube (∼5.1 µL). The data for the analyzed metabolites calculated by the ZFM and those measured at a flow rate of 0.3 µL/min in anesthetized patients are summarized in Table 4 and Figures 2 and 3. Median plasma levels for glucose and lactate were 7.13 (min, max: 4.99–9.88 mmol/L) and 2.03 (min, max: 1.24–5.04 mmol/L), respectively.
Table 4.
Brain tissue concentrations of metabolites.
| Condition | Glucose (mmol/L) |
Lactate (mmol/L) |
Pyruvate (µmol/L) |
Glycerol (µmol/L) |
LP ratio |
LG ratio |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Median (min–max) | RIa | Median (min–max) | RIa | Median (min–max) | RIa | Median (min–max) | RIa | Median (min–max) | RIa | Median (min–max) | RIa | |
| ZFM (n = 16) | 1.57 (1.12–4.70) | 1.15–4.13 | 2.01 (1.37–5.44) | 1.3–5.31 | 80.0 (53.9–223.3) | 54.4–197.0 | 49.9 (21.7–228.7) | 23.6–227.3 | 27.5 (14.9–39.5) | 15.6–39.2 | 1.33 (0.46–3.64) | 0.49–3.47 |
| Anesthetized (0.3 µL/min) (n = 15) | 1.25 (0.64–3.53) | 0.68–3.11 | 1.40 (1.10–3.84) | 1.11–3.63 | 73.8 (36.6–149.7) | 39.0–137.1 | 53.8 (24.4–205.1) | 25.3–202.9 | 23.3 (12.8–34.5) | 13.1–34.3 | 1.42 (0.50–2.78) | 0.52–2.57 |
| Awake (0.3 µL/min) (n = 17) | 1.55 (0.29–3.01) | 0.43–2.94 | 3.41 (1.56–5.62) | 1.64–5.50 | 137.1 (85.0–192.0) | 86.1–188.7 | 79.8 (29.3–346.4) | 31.7–338.7 | 24.9 (16.9–35.1) | 18.3–33.5 | 2.32 (0.62–15.0) | 0.65–11.3 |
ZFM: zero-flow method; RI: reference interval; LP: lactate-to-pyruvate ratio; LG: lactate-to-glucose ratio.
2.5% and 97.5% percentile values, as lower and upper reference interval limits, respectively. All data were recorded from white matter.
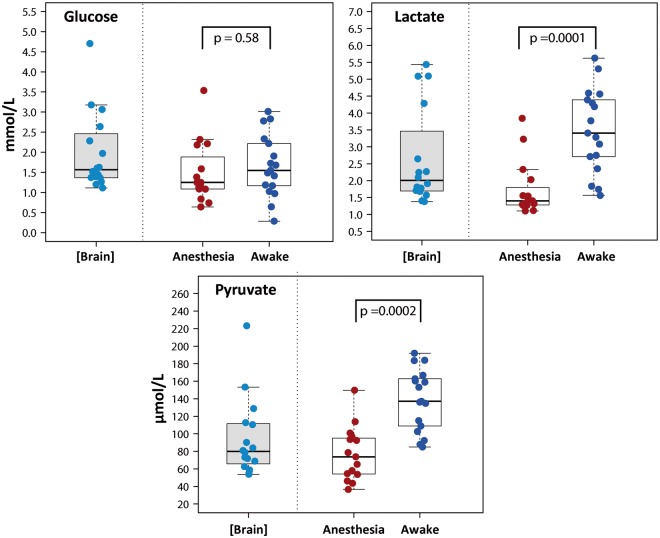
Figure 2.
Box plots showing the concentrations of glucose, lactate, and pyruvate obtained with the extrapolation to zero-flow method [Brain] and at a perfusion flow of 0.3 µL/min under different conditions: anesthesia and awake. A summary of the data is shown in Table 4. All data were recorded from white matter. Anesthetized values were compared with awake values by the Wilcoxon signed-rank test. Lactate and pyruvate concentrations were significantly higher when the patients were awake. No significant differences were observed in glucose concentration. NS: statistically non-significant.
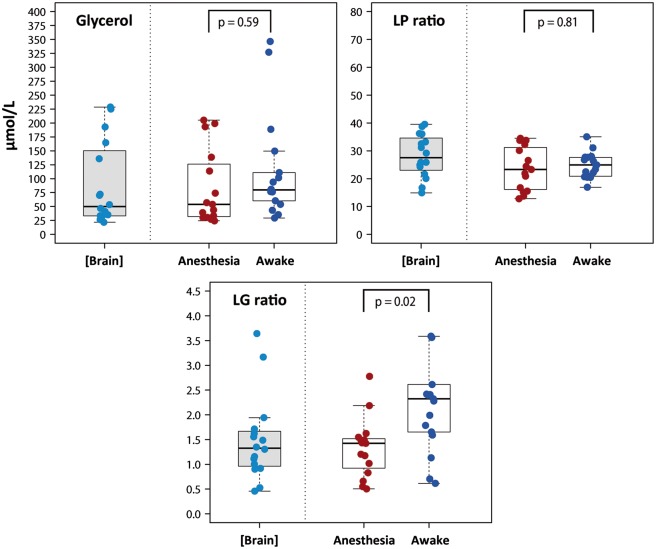
Figure 3.
Box plots showing the concentrations of glycerol, LP ratios, and LG ratios, all of which were obtained with the extrapolation to zero-flow method [Brain] and at a perfusion flow of 0.3 µL/min under different conditions: anesthesia and awake. All data were recorded from white matter. A summary of the data is shown in Table 4. Anesthetized values were compared with awake values by the Wilcoxon signed-rank test. No significant differences were observed in glycerol concentration and in the LP ratio. The LG ratio was significantly higher in patients who were awake compared with patients under anesthesia. NS: statistically non-significant; LP: lactate-to-pyruvate; LG: lactate-to-glucose.
The in vivo RR at a perfusion flow rate of 0.3 µL/min was calculated by taking into account the estimated tissue concentration for each analyte obtained with the ZFM. The in vivo median RR values were 80% for glucose (min: 56, max: 96), 75% for lactate (min: 59, max: 92), 83% for pyruvate (min: 66, max: 100), and 89% for glycerol (min: 69, max: 103).
Brain tissue concentrations in awake patients
In 2 of the 19 patients, data could not be obtained due to a malfunction in the microdialysis probe. The median values for the 17 remaining patients at a fixed perfusion flow of 0.3 µL/min are summarized in Table 4 and are also shown in the box plots presented in Figures 2 and 3. Table 4 shows the upper and lower reference limits found by the nonparametric method. Levels at a perfusion flow rate of 0.3 µL/min were significantly higher for lactate, pyruvate, and lactate-to-glucose (LG) ratio levels when the patient was fully awake, as compared to the values obtained when the patient was under anesthesia. However, we did not find statistically significant differences between the glucose, glycerol, and LP ratio levels of awake versus anesthetized patients (Figures 2 and 3). Median plasma levels for glucose and lactate were 7.72 (min, max: 5.11–8.22 mmol/L) and 1.40 (min, max: 0.55–3.80 mmol/L), respectively.
Discussion
Cerebral MD is not yet used as a routine neuromonitoring tool, but it is a mature powerful research tool that is widely used in many neurocritical care units worldwide. However, unless probes are calibrated in vivo, the microdialysate does not give the absolute brain concentration of the analytes of interest, but only provides an estimate.3 In vivo calibration methods are time-consuming, cannot be routinely conducted at the bedside and present ethical constraints. Therefore, in clinical practice, the true concentrations are estimated from the absolute values given by the analyzer and the known in vitro RR for the analyte of interest, although in vitro conditions are rarely reproduced in vivo. In clinical practice, thresholds that were determined for a fixed flow perfusion rate of 0.3 µL/min are typically used because this is the flow rate recommended by the 2014 consensus statement and is the most commonly used rate in the cerebral MD literature.20 A direct consequence of these variable approaches is that researchers have used different cut-off levels for the RIs of energy metabolites, introducing significant variability and biases when explaining cerebral MD data and interpreting findings observed in neurocritical patients. These implications are especially relevant for the definition of brain hypoxia/ischemia and hyperglycolysis. In addition, ambiguous RIs in any neuromonitoring tool create significant uncertainty among clinicians about correct patient management. In our study, we enrolled a cohort of homogeneous patients who were studied twice: once while under general anesthesia and once when they were fully awake. In this cohort, we determined the actual brain concentrations for each analyte by using the Jacobson et al.18 methodology. In addition, we followed the statistical methods recommended by the latest version of the CLSI to identify outliers and to perform the calculations necessary to set valid biological RIs.33
Brain glucose thresholds
Reinstrup et al.10 established the traditional clinical upper threshold for MD brain glucose at 3.5 mmol/L. This upper limit was similar to the values found in our awake and anesthetized patients at the same perfusion rate. This threshold corresponds to a true ISF glucose of ∼4 mmol/L, similar to the upper reference limit calculated for [Glu]brain in our anesthetized patients (Table 4). This cut-off agrees with the upper limit determined in awake epileptic patients (3.1 mmol/L),12,13 and to the upper threshold in the CSF determined for adults.34 Therefore, taking together all these studies, it can be safely assumed that in patients under general anesthesia or heavy sedation, an upper limit of 3.5 mmol/L is appropriate when using the standard flow rate of 0.3 µL/min. Our lower [Glu]brain was 0.43 mmol/L in the absence of hypoglycemia and with normal or moderately increased glucose plasma levels, a threshold significantly lower than the lower limit reported for the CSF (2.8 mmol/L).34 Based on our data, [Glu]brain < 0.43 mmol/L should be indicative of substrate limitation or ischemia, which reinforces the reference limits recommended by the 2014 cerebral microdialysis consensus statement.20 Our data also support the findings of Abi-Saab et al.13, who showed that [Glu]brain levels are substantially lower than [Glu]plasma.
All metabolites in our study presented wide reference ranges, which demonstrate the variability in metabolite levels between different subjects and under different conditions (under general anesthesia or awake). Our data highlight that no single metabolic value can be interpreted outside the context of the patient. The importance of monitoring systemic parameters in parallel to brain MD must be emphasized. In patients with SAH, Schlenk et al.35 showed that hyperglycemic episodes were not reflected in the levels of [Glu]brain but episodes of [Glu]brain < 0.6 mmol/L induced metabolic derangements in the brain and a significant increase in [Gly]brain and in the LPR. In the case of lactate, we reported previously on the misleading interpretation of an isolated increase in [Lac]brain and the low level of agreement between [Lac]brain and the LPR in indicating brain metabolic dysfunction.36 In monitoring brain metabolism, integrating all data is essential and, in the case of ischemia, the use of multiparametric monitoring may help in interpreting them. The use of a regional method for monitoring rCBF or PtiO2 close to the MD probe may aid interpretation of the absolute and/or the observed values. This is crucial for attributing any metabolic abnormality to either ischemic or non-ischemic episodes by considering both the PtiO2 values and brain glucose levels. A reduced PtiO2 and/or reduced [Glu]brain, the latter in the absence of hypoglycemia, is a clear indication of ischemia.
The anaerobic threshold revisited
As we discussed in a previous paper, the best available estimate for upper brain lactate levels derives from studies of CSF and from a few studies of patients operated on in neurosurgical procedures in whom brain MD were monitored under general anesthesia and using different anesthetic management techniques.36 These studies and others—conducted in severe TBI and patients with SAH—found that certain lactate thresholds were related to poor clinical outcomes, and the upper limit for brain lactate most widely used in neurocritical patients is extremely variable (range: 1.50 to 5.10).11,13,16,17,37 The 2014 cerebral microdialysis consensus statement recommended 4 mmol/L as the upper reference limit.20 Reinstrup et al. found a mean lactate of 1.2 ± 0.6 mmol/L (in anesthetized patients and at a perfusion rate of 1 µL/min), which translates to 2.82 mmol/L at 0.3 µL/min assuming the in vivo RR of 32% observed in our study at such perfusion rate. The recommended 4 mmol/L upper reference limit is based on the Reinstrup et al. study, and three additional studies conducted in patients with spontaneous SAH (i.e., comatose or requiring external ventricular drainage) or severe TBI.16,37 Indeed, Oddo et al. used a threshold of 4 mmol/L, based on findings in patients with severe TBI and a poor outcome.16
Our data suggest that the upper lactate reference limit in anesthetized patients, when used independently of the LP ratio, should be reduced to ∼3.5 mmol/L when using a fixed perfusion rate of 0.3 µL/min. This corresponds to a true ISF lactate of ∼5 mmol/L, as shown in our cohort by using the ZFM. However, values above 3.0 mmol/L were unusual (13%), and most patients had an ISF lactate ≤ 3 mmol/L (Figure 2). Differences in the depth of anesthesia or anesthetic agents used might account for these differences. In awake patients, the upper lactate level should be raised significantly such that an upper level of 5.5 mmol/L falls within the normal range.
This recommendation is consistent with prior findings where a true ISF upper lactate limit of 5.7 mmol/L was observed in the non-epileptic cortex and hippocampus of 38 awake epileptic patients during the interictal period.12 Also, other studies suggest that lactate increases in the brain during physiological stimulation, due to a transient boost of glycolysis that occurs as a normal response to physiologic stimulation.38 A second relevant finding in our study was that the [Lac]brain is usually higher than expected in both the awake and anesthetized patient. Our findings support the 1994 astrocyte-neuron lactate model suggested by Pellegrin and Magistretti, which suggests that lactate is an effective fuel for the brain.39 Therefore, lactate formed within the brain parenchyma from glycolysis in astrocytes may be used by activated neurons that take lactate from the ISF by MCT-2.39 Our data support the notion that an increase in lactate by itself does not indicate ischemia if the LP ratio is below 35 and may only indicate active aerobic metabolism with increased glycolysis.
Thresholds for pyruvate and the lactate–pyruvate ratio
Increases in lactate can be indicative of either hyperglycolysis or hypoxia/ischemia. In patients with spontaneous SAH, Oddo et al.37 found that brain lactate elevations (>4 mmol/L) were more often caused by cerebral hyperglycolysis than by brain hypoxia and that hypoxic lactate was associated with increased mortality whereas hyperglycolysis was a predictor of good outcomes.37 LP ratio is generally thought to be a more reliable indicator of anaerobic metabolism than lactate alone and furthermore is unaffected by changes in the probes’ recovery. When oxygen is present, pyruvate is converted into acetyl-CoA in order to enter the citric acid cycle. At 0.3 µL/min, we found a lower pyruvate limit of 39 µmol/L in anesthetized patients, corresponding to a true [Pyr]brain of ∼55 µmol/L. This value was similar to the lower limit obtained by Reinstrup et al.10
Our upper limit for the LP ratio was 34.2 at a perfusion rate of 0.3 µL/min, and it was 39.2 when using the ZFM data (Table 4); this corresponds to a LP ratio that is above 35–40, as suggested by the 2014 microdialysis consensus conference.20 Therefore, the limit of 25 we suggested in a previous paper is likely too low to indicate ischemic or non-ischemic brain hypoxia or mitochondrial dysfunction.36 As additional data are not available, a pragmatic upper limit for the LP ratio in both awake and anesthetized patients appears to be 35, and this threshold should be used in future classifications of the metabolic disturbances in neurocritical patients.
Glycerol
Glycerol (Gly) is an end product of phospholipid degradation. Some studies have used it as a biomarker for cell membrane deterioration (and therefore cell destruction) in TBI injury and other acute brain injuries.40,41 In a small cohort of TBI patients, Peerdeman et al.40 found that values of [Gly]brain > 150 µmol/L in the normal-appearing regions of the brain had a positive predictive value of 100% for an unfavorable outcome. In a previous paper, where we studied the ionic profile of normal and injured brains, we found a significant increase in [Gly]brain in both the ischemic and traumatic core,42 but the [Gly]brain levels were always below the upper reference threshold in both the normal-appearing brain and the traumatic penumbra. Our findings indicate that a [Gly]brain < 209 µmol/L is a good predictor for tissue viability, with high sensitivity (99.4%) but modest specificity (52.0%). In our study, the upper reference limit for [Gly]brain at a perfusion rate of 0.3 µL/min was 203 µmol/L, corresponding to a [Gly]brain of 227 µmol/L. In awake patients, two cases had [Gly]brain above 300 µmol/L without any abnormalities in the control CT scan around the tip of the MD probe.
The effects of anesthesia on brain metabolism
We obtained energy metabolites values in the same patients under two conditions: while anesthetized and while fully awake. We consistently found that upper reference limits were significantly higher in awake patients for pyruvate, lactate, and the LG ratio (Figures 2 and 3), but remained unchanged for glucose, the LP ratio, and glycerol. Although our data need further verification in larger cohorts, they suggest that anesthesia depresses the glycolytic pathway and that brain lactate levels increase when the patient is awake. However, increased lactate was never accompanied by an increase in the LPR, indicating a normal redox status. In humans, positron emission tomography studies have shown that both isoflurane and propofol may reduce whole brain glucose metabolism by ∼50%.43–45 Volatile anesthetics also reduce CMR and energy consumption, as well as protect the brain against short-term ischemia. Similar neuroprotective effects have been shown for isoflurane, sevoflurane, or desflurane.46 Similar to propofol, volatile anesthetics induce a strong concentration-dependent suppression of electroencephalographic (EEG) activity and therefore of the brain’s functional metabolism.
Following the lactate-shuttle hypothesis,39 a drug-induced reduction in synaptic activity during anesthesia may cause a reduction in aerobic glycolysis and therefore in [Lac]brain. Our data suggest that reference limits for neurocritical patients—in whom both propofol and midazolam are widely used—should be identical to those obtained in patients under general anesthesia.
Recent experimental models in rats showed that brain lactate was fivefold higher for isoflurane compared with propofol anesthesia and that this increase was independent of blood lactate levels.47,48 Horn and Klein48 concluded that volatile anesthetics like isoflurane, halothane, and sevoflurane, but not intravenous anesthetics, caused a specific, dose-dependent rise in extracellular lactate and pyruvate levels in mice brains. We obtained data during anesthesia in 14 patients (nine anesthetized with desflurane and five with continuous infusion of propofol); no statistically significant difference in lactate or ISF glucose levels between both groups was observed (data not shown). Our data suggest that the changes in the metabolomic profile shown with volatile anesthetics can be species-specific and must be verified in the human brain before any conclusion can be reached.
Study limitations and future directions
RI estimation methodology has significantly evolved over the past few decades. Once RIs are established, the immediate clinical consequence is that any value outside this range is flagged.30 Although our cohort was accurately selected, our samples were not representative of healthy individuals, which limits the generalizability of our findings. In addition, NCCLS guidelines recommend the use of nonparametric RIs and that sample sizes consist of at least 120 values.30 For obvious reasons, to include 120 patients in a single-center study is difficult, and therefore, a multicenter study is needed. The ZFM described by Jacobson in 1985 relies on the fact that the brain concentration stays constant during the study.6 This assumption could be challenged in our study, as the median experiment time in our cohort was 6.5 h. However, we believe that, under general anesthesia and when surgery was uneventful and with no intraoperative adverse events, the margin of error introduced by the length of the experiment is acceptable and that the randomization of the perfusion rates that we performed reduced the risk of bias. The differences in the depth of anesthesia or the different anesthetic agents used might account for some of the differences among studies. The reliability of future studies could be significantly improved if a measure of brain activity suppression (EEG or bispectral index) was included in routine monitoring.
In our in vitro experiments, we did not use stirring because it produced significant and unpredictable changes in volume recovery, as explained in the in vitro experiments section. However, in non-agitated solutions, changes in solute concentration can occur at the surface of any porous semipermeable membrane, as long as the membrane shows different permeability for the various components of the solution. This phenomenon is known as polarization by concentration, and its immediate consequence is that concentrations at the membrane surface are not the same as in the bulk fluid (matrix) and can produce overestimates or underestimates of the true concentration (see Supplementary information).49,50 In our in vitro experiments, we cannot disregard the possibility that this phenomenon was the cause of underestimating the true concentrations in the matrices. Therefore, we believe this may affect all concentrations and the true in vitro concentrations calculated by the ZFM. However, the main goal of these experiments was to replicate Jacobson’s finding and to show that this method can be applied in vivo. This phenomenon could also justify the approximately 5% difference in RR found for all metabolites in our in vitro studies and the statistically non-significant underestimation shown in Table 2 between the estimated in vitro concentrations and the real concentrations in the matrices (except for glycerol).
An additional limitation of the Jacobson method, when used in vivo, is that it inherently assumes that the unperturbed tissue next to the probe is representative of tissue far from the probe. However, it has been shown that the physical insertion of any probe into the brain causes a local injury that initiates a progressive inflammatory tissue response that alters the microenvironment and the function of the tissue from which metabolites are sampled (see Supplementary information).51 In addition, our studies were limited in time and therefore only the more acute changes induced by inserting a probe need to be taken into consideration. We excluded all patients with any CT scan abnormality after insertion, and therefore, we minimized the odds of obvious bleeding or edema around the probe.
MD has—with its present methodology—some intrinsic and unavoidable limitations. Probably the most important one is that it only provides an estimate of the time-averaged metabolic profile of the time—30–60 min—before the microvials are collected. Therefore, MD is quite insensitive to rapid changes in metabolite levels. However, trends are still very useful as a method for identifying brain tissue at risk for patients in neurocritical care, detecting changes in metabolic profiles, and detecting ischemia. The future of the technique is real-time online techniques already introduced into clinical research. Rogers et al.52 reported on the use of continuous online MD by using microfluidic sensors to study glucose, lactate, and potassium in cortical spreading depolarization.53 Ideally, when commercially available and approved for human use, continuous MD might improve its temporal resolution and therefore will be able to detect metabolic changes that are short in duration and thus missed with conventional MD.
We believe one of the next steps in neurocritical care is to establish a clear classification of the metabolic disturbances found in patients who suffer acute brain damage and to clarify its pathophysiology. Ideally, both cerebral MD and PtiO2 monitoring should be conducted in order to define hypoxic-induced metabolic crisis from aerobic hyperglycolysis or mitochondrial dysfunction, in which oxygen limitation is not the cause. A better characterization of the metabolic response of the brain to injury and its pathophysiology is an essential step for implementing better and more targeted therapeutic strategies for managing patients with acute brain damage.
Supplementary Material
Acknowledgements
The authors thank all subjects for their participation in this study. They would like to thank DG Rossiter, Adjunct Associate Professor in the Section of Soil & Crop Sciences, Cornell University, USA for his help in the use of the nls function and the “nlstools” package.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The Neurotraumatology and Neurosurgery Research Unit is supported by a Grant from the Department d’Universitats, Recerca i Societat de la Informació de la Generalitat de Catalunya (SGR 2014-844). This work has been supported in part by the Fondo de Investigación Sanitaria (Instituto de Salud Carlos III) with grant FIS PI11/00700, which was co-financed by the European Regional Development Fund (ERDF) and awarded to Dr J. Sahuquillo. A. Sánchez-Guerrero is the recipient of personal pre-doctoral grant from the Instituto de Salud Carlos III (grant number FI12/00074).
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Authors’ contributions
Authors’ contributions to the study and manuscript preparation include the following: Conception and design: JS and ASG. Acquisition of data: IC, EC, GMB, MAP, ASG, MVJ, and DGS. Analysis and interpretation of data: JS, MAP, and ASG. Statistical analysis: JS, KM, and ASG. Drafting the article: JS and ASG. Critically revising the article: all authors. Reviewed submitted version of manuscript: all authors. Approved the final version of the manuscript on behalf of all authors: JS. Study supervision: JS.
Supplementary material
Supplementary material for this paper can be found at http://jcbfm.sagepub.com/content/by/supplemental-data
References
- 1.Bito L, Davson H, Levin E, et al. The concentrations of free amino acids and other electrolytes in cerebrospinal fluid, in vivo dialysate of brain, and blood plasma of the dog. J Neurochem 1966; 13: 1057–1067. [DOI] [PubMed] [Google Scholar]
- 2.Meyerson BA, Linderoth B, Karlsson H, et al. Microdialysis in the human brain: extracellular measurements in the thalamus of parkinsonian patients. Life Sci 1990; 46: 301–308. [DOI] [PubMed] [Google Scholar]
- 3.Nordstrom CH. Cerebral energy metabolism and microdialysis in neurocritical care. Childs Nerv Syst 2010; 26: 465–472. [DOI] [PubMed] [Google Scholar]
- 4.Benveniste H, Huttemeier PC. Microdialysis: theory and application. Prog Neurobiol 1990; 35: 195–215. [DOI] [PubMed] [Google Scholar]
- 5.Benveniste H. Brain microdialysis. J Neurochem 1989; 52: 1667–1679. [DOI] [PubMed] [Google Scholar]
- 6.Hutchinson PJ, O’Connell MT, Al-Rawi PG, et al. Clinical cerebral microdialysis–determining the true extracellular concentration. Acta Neurochir Suppl 2002; 81: 359–362. [DOI] [PubMed] [Google Scholar]
- 7.Menacherry S, Hubert W, Justice JB., Jr In vivo calibration of microdialysis probes for exogenous compounds. Anal Chem 1992; 64: 577–583. [DOI] [PubMed] [Google Scholar]
- 8.Ungerstedt U, Rostami E. Microdialysis in the human brain: clinical applications. In: Westerink BHC, Cremers TIFH. (eds). Handbook of microdialysis: methods, applications and perspectives, 1st edn Amsterdam: Elsevier Academic Press, 2007, pp. 697. [Google Scholar]
- 9.Janle EM, Cregor M. Ultrafiltrate and microdialysis DL probe in vitro recoveries: electrolytes and metabolites. Curr Sep 1996; 15: 31–34. [PubMed] [Google Scholar]
- 10.Reinstrup P, Ståhl N, Mellergård P, et al. Intracerebral microdialysis in clinical practice: baseline values for chemical markers during wakefulness, anesthesia, and neurosurgery. Neurosurgery 2000; 47: 701–709. [DOI] [PubMed] [Google Scholar]
- 11.Langemann H, Alessandri B, Mendelowitsch A, et al. Extracellular levels of glucose and lactate measured by quantitative microdialysis in the human brain. Neurol Res 2001; 23: 531–536. [DOI] [PubMed] [Google Scholar]
- 12.Cavus I, Kasoff WS, Cassaday MP, et al. Extracellular metabolites in the cortex and hippocampus of epileptic patients. Ann Neurol 2005; 57: 226–235. [DOI] [PubMed] [Google Scholar]
- 13.Abi-Saab WM, Maggs DG, Jones T, et al. Striking differences in glucose and lactate levels between brain extracellular fluid and plasma in conscious human subjects: effects of hyperglycemia and hypoglycemia. J Cereb Blood Flow Metab 2002; 22: 271–279. [DOI] [PubMed] [Google Scholar]
- 14.Schulz MK, Wang LP, Tange M, et al. Cerebral microdialysis monitoring: determination of normal and ischemic cerebral metabolisms in patients with aneurysmal subarachnoid hemorrhage. J Neurosurg 2000; 93: 808–814. [DOI] [PubMed] [Google Scholar]
- 15.Sanchez JJ, Bidot CJ, O’Phelan K, et al. Neuromonitoring with microdialysis in severe traumatic brain injury patients. Acta Neurochir Suppl 2013; 118: 223–227. [DOI] [PubMed] [Google Scholar]
- 16.Timofeev I, Carpenter KL, Nortje J, et al. Cerebral extracellular chemistry and outcome following traumatic brain injury: a microdialysis study of 223 patients. Brain 2011; 134: 484–494. [DOI] [PubMed] [Google Scholar]
- 17.Vilalta A, Sahuquillo J, Merino MA, et al. Normobaric hyperoxia in traumatic brain injury. Does brain metabolic state influence the response to hyperoxic challenge? J Neurotrauma 2011; 28: 1139–1148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jacobson I, Sandberg M, Hamberger A. Mass transfer in brain dialysis devices: a new method for the estimation of extracellular amino acids concentration. J Neurosci Meth 1985; 15: 263–268. [DOI] [PubMed] [Google Scholar]
- 19.Lönnroth P, Jansson PA, Smith U. A microdialysis method allowing characterization of intercellular water space in humans. Am J Physiol 1987; 253: E228–E231. [DOI] [PubMed] [Google Scholar]
- 20.Hutchinson PJ, Jalloh I, Helmy A, et al. Consensus statement from the 2014 International Microdialysis Forum. Intensive Care Med 2015; 41: 1517–1528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hutchinson PJ, Oconnell MT, AlRawi PG, et al. Clinical cerebral microdialysis: a methodological study. J Neurosurg 2000; 93: 37–43. [DOI] [PubMed] [Google Scholar]
- 22.Martínez-Valverde T, Vidal-Jorge M, Montoya N, et al. Brain microdialysis as a tool to explore the ionic profile of the brain extracellular space in neurocritical patients: a methodological approach and feasibility study. J Neurotrauma 2015; 32: 7–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chefer VI, Thompson AC, Zapata A, et al. Overview of Brain Microdialysis. Curr Protoc Neurosci 2009; CHAPTER 7: Unit7.1. [DOI] [PMC free article] [PubMed]
- 24.Evans JWA. An encephalographic ratio for estimating ventricular enlargement and cerebral atrophy. Arch Neurol Psychiatr 1942; 47: 931–937. [Google Scholar]
- 25.CMA 71 High Cut-Off Brain Microdialysis Catheter. http://www.dipylonmedical.com/basic-research/microdialysis-catheters/cma-71 (accessed 28 September 2016).
- 26.Baty F, Ritz C, Charles S, et al. A toolbox for nonlinear regression in R: the package nlstools. J Stat Software 2015; 66: 21. [Google Scholar]
- 27.minpack.lm: R Interface to the Levenberg-Marquardt nonlinear least-squares algorithm found in MINPACK, plus support for bounds, https://CRAN.R-project.org/package=minpack.lm (accessed 28 September 2016).
- 28.Horn PS, Feng L, Li Y, et al. Effect of outliers and nonhealthy individuals on reference interval estimation. Clin Chem 2001; 47: 2137–2145. [PubMed] [Google Scholar]
- 29.Horn PS, Pesce AJ, Copeland BE. A robust approach to reference interval estimation and evaluation. Clin Chem 1998; 44: 622–631. [PubMed] [Google Scholar]
- 30.Horn PS, Pesce AJ. Reference intervals: an update. Clin Chim Acta 2003; 334: 5–23. [DOI] [PubMed] [Google Scholar]
- 31.referenceIntervals: Reference Intervals. R package version 1.1.1, http://CRAN.R-project.org/package=referenceIntervals (accessed 28 September 2016).
- 32.Hutchinson PJ, O’Connell MT, Nortje J, et al. Cerebral microdialysis methodology-evaluation of 20 kDa and 100 kDa catheters. Physiol Meas 2005; 26: 423–428. [DOI] [PubMed] [Google Scholar]
- 33.CLSI. EP28-A3C. Defining, establishing, and verifying reference intervals in the clinical laboratory; approved guideline, 3 rd edn Wayne: Clinical and Laboratory Standards Institute, 2008. [Google Scholar]
- 34.Leen WG, Willemsen MA, Wevers RA, et al. Cerebrospinal fluid glucose and lactate: age-specific reference values and implications for clinical practice. PLoS One 2012; 7: e42745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schlenk F, Nagel A, Graetz D, et al. Hyperglycemia and cerebral glucose in aneurysmal subarachnoid hemorrhage. Intensive Care Med 2008; 34: 1200–1207. [DOI] [PubMed] [Google Scholar]
- 36.Sahuquillo J, Merino MA, Sánchez-Guerrero A, et al. Lactate and the lactate-to-pyruvate molar ratio cannot be used as independent biomarkers for monitoring brain energetic metabolism: a microdialysis study in patients with traumatic brain injuries. PLoS One 2014; 9: e102540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Oddo M, Levine JM, Frangos S, et al. Brain lactate metabolism in humans with subarachnoid hemorrhage. Stroke 2012; 43: 1418–1421. [DOI] [PubMed] [Google Scholar]
- 38.Prichard J, Rothman D, Novotny E, et al. Lactate rise detected by 1 H NMR in human visual cortex during physiologic stimulation. Proc Natl Acad Sci U S A 1991; 88: 5829–5831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pellerin L, Magistretti PJ. Glutamate uptake into astrocytes stimulates aerobic glycolysis: a mechanism coupling neuronal activity to glucose utilization. Proc Natl Acad Sci USA 1994; 91: 10625–10629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Peerdeman SM, Girbes AR, Polderman KH, et al. Changes in cerebral interstitial glycerol concentration in head-injured patients; correlation with secondary events. Intensive Care Med 2003; 29: 1825–1828. [DOI] [PubMed] [Google Scholar]
- 41.Merenda A, Gugliotta M, Holloway R, et al. Validation of brain extracellular glycerol as an indicator of cellular membrane damage due to free radical activity after traumatic brain injury. J Neurotrauma 2008; 25: 527–537. [DOI] [PubMed] [Google Scholar]
- 42.Martinez-Valverde T, Sanchez-Guerrero A, Vidal-Jorge M, et al. Characterization of the ionic profile of the extracellular space of the injured and ischemic brain: a microdialysis study. J Neurotrauma Epub ahead of print 27 June 2016. DOI: 10.1089/neu.2015.4334. [DOI] [PubMed] [Google Scholar]
- 43.Alkire MT, Haier RJ, Shah NK, et al. Positron emission tomography study of regional cerebral metabolism in humans during isoflurane anesthesia. Anesthesiology 1997; 86: 549–557. [DOI] [PubMed] [Google Scholar]
- 44.Sun X, Zhang H, Gao C, et al. Imaging the effects of propofol on human cerebral glucose metabolism using positron emission tomography. J Int Med Res 2008; 36: 1305–1310. [DOI] [PubMed] [Google Scholar]
- 45.Inoue S, Kawaguchi M. Intravenous anesthetics and neuroprotection. In: Uchino H, Ushijima K, Ikeda Y. (eds). Neuroanesthesia and cerebrospinal protection, Tokyo: Springer, 2015, pp. 93–102. [Google Scholar]
- 46.Mishima Y, Ushijima K. Volatile anesthetics and neuroprotection. In: Uchino H, Ushijima K, Ikeda Y. (eds). Neuroanesthesia and cerebrospinal protection, Tokyo: Springer, 2015, pp. 83–92. [Google Scholar]
- 47.Makaryus R, Lee H, Yu M, et al. The metabolomic profile during isoflurane anesthesia differs from propofol anesthesia in the live rodent brain. J Cereb Blood Flow Metab 2011; 31: 1432–1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Horn T, Klein J. Lactate levels in the brain are elevated upon exposure to volatile 1anesthetics: a microdialysis study. Neurochem Int 2010; 57: 940–947. [DOI] [PubMed] [Google Scholar]
- 49.Song L, Elimelech M. Theory of concentration polarization in crossflow filtration. J Chem Soc Faraday Trans 1995; 91: 3389–3398. [Google Scholar]
- 50.Ibarz A, Barbosa-Cánovas GV. Separation processes by membranes. Unit operations in food engineering, Boca Raton: CRC Press, 2003, pp. 265–308. [Google Scholar]
- 51.Kozai TD, Jaquins-Gerstl AS, Vazquez AL, et al. Brain tissue responses to neural implants impact signal sensitivity and intervention strategies. ACS Chem Neurosci 2015; 6: 48–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Rogers ML, Feuerstein D, Leong CL, et al. Continuous online microdialysis using microfluidic sensors: dynamic neurometabolic changes during spreading depolarization. ACS Chem Neurosci 2013; 4: 799–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hamaoui K, Gowers S, Damji S, et al. Rapid sampling microdialysis as a novel tool for parenchyma assessment during static cold storage and hypothermic machine perfusion in a translational ex vivo porcine kidney model. J Surg Res 2016; 200: 332–345. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.