Abstract
IntraVoxel Incoherent Motion (IVIM) is a magnetic resonance imaging (MRI) technique capable of measuring perfusion-related parameters. In this manuscript, we show that the mono-exponential model commonly used to process IVIM data might be challenged, especially at short diffusion times. Eleven rat datasets were acquired at 7T using a diffusion-weighted pulsed gradient spin echo sequence with b-values ranging from 7 to 2500 s/mm2 at three diffusion times. The IVIM signals, obtained by removing the diffusion component from the raw MR signal, were fitted to the standard mono-exponential model, a bi-exponential model and the Kennan model. The Akaike information criterion used to find the best model to fit the data demonstrates that, at short diffusion times, the bi-exponential IVIM model is most appropriate. The results obtained by comparing the experimental data to a dictionary of numerical simulations of the IVIM signal in microvascular networks support the hypothesis that such a bi-exponential behavior can be explained by considering the contribution of two vascular pools: capillaries and somewhat larger vessels.
Keywords: Cerebral blood flow, intravoxel incoherent motion, magnetic resonance imaging, microcirculation, perfusion
Introduction
Perfusion imaging has been shown useful in a wide variety of clinical applications, including the classification of tumors,1 the identification of stroke regions2 and the characterization of numerous other diseases.3,4 MRI provides access to perfusion related parameters, either using external tracers (contrast agents) or completely noninvasively. Contrast agents are contraindicated in patients at risk for nephrogenic systemic fibrosis, and gadolinium deposits have been detected in the brain of patients who underwent multiple contrast-enhanced MRI scans.5,6 The Arterial Spin Labeling (ASL) technique, which uses blood as an endogenous tracer, has been used as an alternative, noninvasive approach for measuring cerebral perfusion in clinical settings.7 However, ASL suffers from low signal-to-noise ratio and a dependence on transit time presenting limitations in slow flow conditions, such as stroke. Besides, ASL leads to high specific absorption rates (SAR) restricting its repeated use for fragile subjects (children). Another noninvasive approach which is becoming popular in research and clinical applications is IntraVoxel Incoherent Motion (IVIM) imaging.8,9 IVIM imaging is a variant of diffusion MRI relying on the assumption that flow of blood within capillary networks can be considered as a pseudo diffusion process characterized by a pseudo diffusion coefficient D*.10 Besides D*, IVIM imaging also provides estimates of the flowing blood volume fraction, fIVIM. Relationships linking the IVIM outputs to classical perfusion parameters have been proposed.11
The original IVIM model10 describes the signal attenuation with the diffusion weighting as a mono-exponential decay, assuming blood changes flowing direction several times during the measurement (“diffusion”) time. At very short diffusion times, when blood remains in a single straight but randomly oriented capillary segment, the signal attenuation becomes a sinc function.9,10 Kennan et al.12 have proposed a model based on velocity autocorrelation functions to cover intermediate situations between the two extreme regimes, mono-exponential and sinc. Arguing that the Gaussian phase approximation assumed by Kennan et al. is invalid in some cases, Wetscherek et al.13 introduced a model based on normalized phase distributions. These two models assume that only flow in capillaries contributes to the IVIM signal. Noticing some disagreement between experimental data and the standard mono-exponential model, other authors have suggested models which take into account not only capillaries but all types of vessels.14,15
Overall, there is a general consensus that the current mono-exponential IVIM model is appropriate to fit experimental data at long diffusion times, but might not be accurate at small time scales. Here, we introduce a bi-exponential IVIM model (not to be confounded with the bi-exponential model used to separate diffusion and IVIM effects16), accounting for two different vascular pools, as an alternative to the mono-exponential model. We demonstrate that this bi-exponential model fits the experimental data better than the standard mono-exponential model, especially at short diffusion times. By comparing the experimental data to numerical simulations of the flow within a microvascular network, we show that the IVIM signal can be indeed related to two distinct pools of vessels.
Materials and methods
Theory
Extraction of the IVIM component from the raw MR signal
Using a pulsed gradient MRI sequence, the attenuation of the MRI signal due to diffusion and IVIM effects10,17 can be expressed as
| (1) |
with where . and are the fractions of diffusion and IVIM components, respectively, with and , where is the blood volume fraction and S0 is the overall signal when b = 0 (it should be noted that tissue and blood contribute to S0 with different T2 and T1-weightings). Fdiff(b) and FIVIM(b) are, respectively, the diffusion and IVIM signals as a function of diffusion weighting.
Given that the pseudo diffusion coefficient associated with the IVIM effect, D*, is much higher than the water molecular diffusion in tissues, at high b-values, the MR signal originates solely from water molecules diffusing in the extravascular compartment (pure diffusion effect). At small b-values, both diffusion17 and flowing blood effects (IVIM effect) are present and one has to remove the tissue diffusion component to isolate the blood compartment. To increase robustness (as there are fewer parameters to estimate for each step), this is typically done using a two-step process,18,19 first removing the extravascular component found by fitting the experimental data for high b-values (above 400–600 s/mm2) with a diffusion model and then fitting the residual signal at low b values.16 In this work, we used the Kurtosis20,21 model (equation (2)) to fit the diffusion component:
| (2) |
where is the apparent diffusion coefficient obtained when b approaches 0, and K is the Kurtosis parameter which characterizes the deviation from the exponential decay.
Different IVIM models
Making the hypothesis that the microvascular network can be modeled by a series of straight tubes randomly oriented in space and distributed over 4π, the expression for depends on the mean vessel length, L, the mean blood flow velocity, v, and the diffusion encoding time defined as Δ + δ.22 Several models have been proposed to describe this dependency.
Mono-exponential IVIM model
When blood spins change vessels many times during the diffusion encoding time, their movements can be modeled by a random walk. The expression for is thus exponential
| (3) |
where Db is the diffusion coefficient of water in blood and , so-called the “pseudo-diffusion coefficient”, can be approximated by (Le Bihan et al.10), L and v being the mean vessel length and mean blood flow velocity, respectively.
Sinc IVIM model 10
When blood spins stay in the same vessel during the diffusion encoding time, i.e. they do not change direction and the blood flow velocity is assumed to be constant, the expression for becomes
| (4) |
with . A can also be defined in this regime by calculating the Taylor expansion limited to the first orders of . obtained in this case is (Le Bihan23), where has units of time ( for a PGSE sequence with ). It can be seen that is independent of L, as spins never get to probe the entire segment.
Intermediate regime (Kennan model 12 )
The Kennan model uses a velocity autocorrelation function to describe the spins’ dynamics. This function can be applied to a capillary network with a distribution of segments of different lengths. After integrating the expression of the signal attenuation, taking into consideration the strength of the applied diffusion encoding gradients, the sequence timing parameters and the assumed velocity autocorrelation function for capillary blood, the model equation12 becomes
| (5) |
The two parameters extracted from this model are the mean squared blood flow velocity and T0, the correlation time which corresponds to the average time the spins stay in a given segment. This model converges toward the mono-exponential and the sinc regimes at long and short diffusion times, respectively, and it is expected to also cover intermediate regimes.
Bi-exponential IVIM model
As we will present later, in some cases, the mono-exponential model is not sufficient to describe the IVIM signal. Here we introduce a bi-exponential IVIM model to better describe the IVIM signal decay
| (6) |
The physical interpretation behind this model is that, instead of reflecting only one vascular pool, i.e. the capillaries, the IVIM signal incorporates contributions coming from two different vascular components: a slow component, characterized by and , and a faster component, characterized by and with . Depending on the experimental parameters and the vascular properties, one can also consider models consisting of a combination of two sinc functions or one exponential and one sinc function. However, as indicated in previous literature reports,13,24 when considering a Gaussian distribution of blood flow velocities, the IVIM signal plotted against b-value decays smoothly even when spins do not change direction multiple times (closer to the sinc regime), suggesting that fitting with a decaying exponential is a reasonable choice.
As mentioned earlier, other models considering more than one vascular pool were previously suggested. Henkelman et al. proposed a model which involves two pools associated with the arterial and venous trees.14 Our model also assumes two vascular pools but, unlike Henkelman’s, these pools are not of arterial and venous origins, and they are separated based on their respective blood velocities and geometries.
Animal procedures
Dark Agouti male rats (NR = 11, 240–360 g, 3–21 months, Janvier, Saint Isle, France) were used in this study. The animals were housed two per cage and they had ad libitum access to food and water. All animal experiments were conducted according to recommendations of the EU Directive 2010/63/EU for care and use of laboratory animals. The protocol was approved by the Comité d'EThique en Expérimentation Animale Commissariat à l'Energie Atomique et aux énergies alternatives Direction des Sciences du Vivant Ile de France (CETEA CEA DSV IdF) under protocol ID 10_032. This manuscript is in compliance with the ARRIVE guidelines (Animal Research: Reporting in Vivo Experiments).
Throughout the experiments, the animals, anesthetized with 1.5–2% isoflurane in a 1:2 O2:air mixture, were monitored for respiration rate (30–50 breath per min) and temperature, maintained at a constant 36.5 ± 0.5℃ with a heated air circuit device (SA Instruments, Inc, USA). To avoid motion-related artifacts, the head was immobilized using a bite bar and ear pins connected to the nose cone.
MRI acquisitions
Data were collected using a horizontally oriented 7T small animal MRI scanner (Biospec, Bruker BioSpin, Etlingen, Germany) equipped with a 740 mT/m gradient coil system. A 3 × 3 cm2 four-element phased-array receiver coil and a 7.2 cm (inside diameter) volume transmit coil (Bruker BioSpin, Etlingen, Germany) were used. After scout scans, the magnetic field homogeneity was ensured through the FASTMAP method (Paravision 5.1) followed by the MAPSHIM method to shim specifically in the region of interest.
Coronal DW-MRI images were acquired using a standard pulsed-gradient spin-echo EPI sequence with a GRAPPA reconstruction (acceleration factor 2) and 30 b-values (20 b-values ranging from 7 to 500 s/mm2 and 10 b-values ranging from 500 to 2500 s/mm2). The acquisition parameters were set as follows: gradient directions [X = 1, Y = 1, Z = 1], [X = 0, Y = 1, Z = 0] and [X = 0, Y = 0, Z = 1], diffusion gradient duration time δ = 3 ms, diffusion gradient separation times Δ = 14, 24 and 34 ms, in-plane resolution 250 × 250 µm2, matrix size 80 × 80, field of view 20 × 20 mm2, slice thickness 1.5 mm, 1 segment, echo time TE = 45 ms, repetition time TR = 1 000 ms, six averages, six repetitions, two slices. Data with strong motion artifacts were discarded and the acquisition repeated. For one rat, only five repetitions could be included.
Because our model includes a somewhat fast flow component, we checked for possible inflow effects by using two different TRs, 1000 and 3000 ms (gradient direction [X = 0, Y = 1, Z = 0], Δ = 14 ms) on four animals. When the TR is short compared to the T1 relaxation time, the longitudinal magnetization of tissue spins does not fully recover from the slice radiofrequency excitation between two repetitions, while fresh flowing spins entering the voxel are fully magnetized, which slightly enhances their relative contribution to the signal. This “inflow” effect depends on the fraction of fresh spins entering the slice, hence the dependence on blood velocity, and will lead to an overestimation of ffast. By increasing the repetition time, tissue spins recover their magnetization and the apparent increase in the signal due to flowing spins vanishes, restoring the correct value for ffast.
Data analysis
IVIM/diffusion MRI images were processed using in-house software written in MATLAB (MathWorks, Massachusetts, USA). First, assuming isotropic IVIM and diffusion effects in the regions of interest (ROIs) at the acquired resolution, the signals from the different gradient diffusion directions were averaged. Afterwards, ROIs were drawn manually on the cortical gray matter and on the thalamus of the left hemisphere and averaged over the two acquired slices. The ROIs consisted of approximately 132 ± 37 and 125 ± 33 pixels for each slice for the left cortex (LC), and 90 ± 18 and 88 ± 15 pixels for each slice for the left thalamus (LT), respectively. IVIM parameters were obtained from the signal attenuation, , in two steps. First, we estimated the diffusion component, , for b >500 s/mm2 using the diffusion Kurtosis model. The maximum b-value used for this fit, 2500 s/mm2, is smaller than the limiting value of blim = 3000 s/mm2 for which the Kurtosis model was reported to be adequate. The blim value was calculated using blim < 3/(ADC0* K) and considering typical brain values for ADC0 and K of roughly 1 µm2/ms and 1, respectively.20 Second, we fitted the IVIM component, , obtained from the residual signal, after the diffusion component has been removed for data corresponding to b < 500 s/mm2 (equation (2)), with three different models, mono-exponential, Kennan, and bi-exponential according to equations (3), (5), and (6), respectively. The adequacy of the chosen b threshold value was confirmed after examination of many cases, as the residual signal taken after removing diffusion effects was found not to differ significantly from noise for b-values above 500 s/mm2.
Numerical simulations of the IVIM signal in microvascular networks
IVIM MRI signals coming from microvascular networks were numerically simulated using MATLAB. Considering an isochromat characterized by the position vector in the vascular compartment and solving the Bloch equations25 while neglecting relaxation effects and water diffusion in blood, the expression of the complex transverse magnetization associated to this isochromat at t = TE can be written as
| (7) |
where i is the imaginary unit, the phase shift accumulated by the isochromat at t = TE, γ the gyromagnetic ratio of protons and the gradient encoding vector. We specify that , with G the gradient amplitude and the gradient direction. For a PGSE sequence, is expressed as:
where t1 and t2 correspond to the beginning of the first and second gradient pulses, respectively and .
Considering one isochromat trajectory that includes N segments, with lengths Lk, orientations , , and constant flow velocity v, we define , the time to traverse the segment k, such that is the cumulative time to get to the end of segment k. The accumulated phase becomes
| (8) |
Here, we suppose that , and .
We modeled the blood flow in the microvascular network as a pseudo-random walk along straight line segments with the segment orientations following a uniform distribution in the unit sphere in 3D. This choice allowed us to perform an analytical integration on the unit sphere and removed the need to sample the segment orientations in the numerical simulations. In essence, we integrated (where is given in equation (8)) analytically over all possible orientations for each segment k, assuming that is uniformly distributed in the unit sphere. The end result is that the MRI signal associated to all the isochromats that see N segments of lengths Lk, , during TE under the uniform orientation distribution assumption is (see online supplementary Appendix 1 for details)
| (9) |
It can be demonstrated (see online supplementary Appendix 2) that equation (9) is valid in both the exponential and the sinc regimes.
In the numerical simulations, we allowed the segment lengths and the blood velocities of the isochromat trajectories to follow Gaussian distributions. We varied the choice of the mean value and the standard deviation of the Gaussian distributions for both velocities and segment lengths. For a given Gaussian distribution of lengths, with the mean value and the standard deviation , and a given Gaussian distribution of velocities, with the mean value and the standard deviation , we took 1000 different trajectories. One velocity v was associated with each trajectory which consisted of N segments with lengths . The number of segments, N, was defined as the smallest value for which , with Nmax = 50. All trajectories resulting in more than 50 segments were not taken into account. To compute for this sample, we plugged and v into equation (9). The averaged over the 1000 samples was defined as the simulated signal for the distribution choice .
We computed for 72 values of , spanning the interval 8–150 µm, with a 2 µm step, and 100 values of , spanning the interval 0.1–10 mm/s, with a 0.1 mm/s step. To reduce the complexity of the problem of fitting experimental data to simulations, we used only one value for the relative standard deviation, namely 50%. In other words, the standard deviation was fixed at for each choice of and fixed at for each value of . The simulated for each combination of and was assembled to build a dictionary of simulated signals.
We note here two particular choices made for our numerical simulations: (1) the length distributions were truncated at 5 µm, meaning that if a sampled length was smaller than 5 µm, it was removed from the sample; (2) the velocity distributions were truncated to stay in the range of 0.01–20 mm/s. The choice of this range was motivated to include not only capillaries but also larger vessels, the upper limit representing the blood flow velocity in pial arterioles.26
In a further step, drawing an analogy with the bi-exponential model, two simulated signals representing two pools, one for a slow pool, (mean values ), and another one for a fast pool, (mean values ), were combined and compared to the experimental signals. This comparison aimed to identify the mean values (lengths and velocities) best matching the experimental signals for the two pools in equation (6), where for and , we used the values found experimentally
| (10) |
As the self-diffusion of water molecules in the intravascular compartment was not taken into account in the simulations whereas it was included in the IVIM model, the simulated signals were not compared directly to the experimental signals but to where Db is the blood diffusion coefficient, set to mm2/s (Li et al.27).
Statistical analysis
The statistical analysis for the comparison between the three models was performed using the corrected Akaike information criterion (AICc) for a small number of samples28 (NS < 30)
with Nb the number of b-values used to fit the signals, MSE the mean squared error and k the number of parameters in the model, taking into account that the Gaussian noise hypothesis for the signal residuals counts as 1 additional parameter according to the AIC theory. Hence, k = 3, 4, and 5 for the mono-exponential, Kennan and bi-exponential models, respectively.
The reported AICc values have been calculated using only experimental and fitted signals corresponding to b-values < 500 s/mm2 (residual IVIM component of the signal) (hence Nb = 20). The Akaike weight,29 , was then calculated as the probability that model i is the best model given the data and the set of candidate models30
where K is the number of compared models (here K = 3). A weight > 0.90 indicates that robust inferences can be made using the associated model.
The AICc calculations were done using MATLAB while the other statistical analyses were conducted using the R software.31 First, the statistical significance of the difference between the AICc of the bi- and mono-exponential models was assessed using a Wilcoxon signed rank test. Then, to assess the existence of a dependence of the diffusion and bi-exponential models parameters on the diffusion time and/or ROI, we used the two-way ANOVA test. If the two-way ANOVA was statistically significant with regards to Δ, the Tukey’s Honest Significant Difference (HSD) test was used, allowing the identification of the diffusion times for which the parameter means were significantly different. When one or both assumptions of the two-way ANOVA were not met, we used a non-parametric version of the two-way ANOVA, the Scheirer–Ray–Hare test. If the p-value of the Scheirer–Ray–Hare test was statistically significant with regards to Δ, the Games–Howell post hoc test was used, allowing the identification of the diffusion times for which the parameter means were significantly different.
To evaluate the goodness of fit of the experimental data compared to the dictionary of simulated signals, the error ɛ between them was calculated using the normalized l2-norm formula
where and represent the simulated signals from the dictionary and the experimental signal, respectively. An ɛ less than 10% was considered an acceptable match between the experimental data and a particular combination of simulated signals.
Results
Model comparison
For one diffusion time (Δ = 24 ms), examples of the IVIM signal versus the b-value along fitted signals for the bi-, mono-exponential and Kennan models for the two ROIs are given in Figure 1. The error bars come from averaging over the directions, repetitions and slices. In the upper right corners, the ROI masks have been drawn on the DW images (in white).
Figure 1.
Examples of IVIM data fitted with the bi-, mono-exponential and Kennan models. Typical IVIM signal, for one animal, resulting from the subtraction of the diffusion component from the total MRI signal versus b-value for Δ = 24 ms. The black circles represent the experimental data. The black, blue, and red lines correspond to the three fitting models, the bi-, mono-exponential and Kennan models, respectively. The ROI masks are given in the upper right corners: (a, b) LC, (c, d) LT. The curves were fit to the data with b-values ranging from 0 to 500 s/mm2. Error bars represent SD. Scale bar: 5 mm.
The Akaike weights for the mono-exponential (AWM), Kennan (AWK) and bi-exponential (AWB) models for the two ROIs have been calculated and are shown in Figure 2. Although no statistical difference was found (p > 0.05), we observe AWK < AWM for all ROIs and diffusion times. Given this, for the rest of the analysis, we only compared the bi- and mono-exponential models. For 61 out of 66 data points, AWB > AWM. A Wilcoxon signed rank test gives a p < 0.0001 when comparing the AICc values, showing a significant difference between the AICc of the two models. The black circles draw attention to the datasets for which AWB is smaller than AWM. One can notice that they are all observed for Δ = 34 ms, suggesting that the bi-exponential model is a better model to describe the IVIM signal than the standard mono-exponential model at short diffusion times, but that the two models converge at longer diffusion times.
Figure 2.
Akaike weights for the three fitting models and diffusion times. Akaike weights for each model and ROI for 11 datasets: (a) LC, (b) LT. The black dotted lines separate the data between the diffusion times. The black circles highlight the cases for which AWB < AWM.
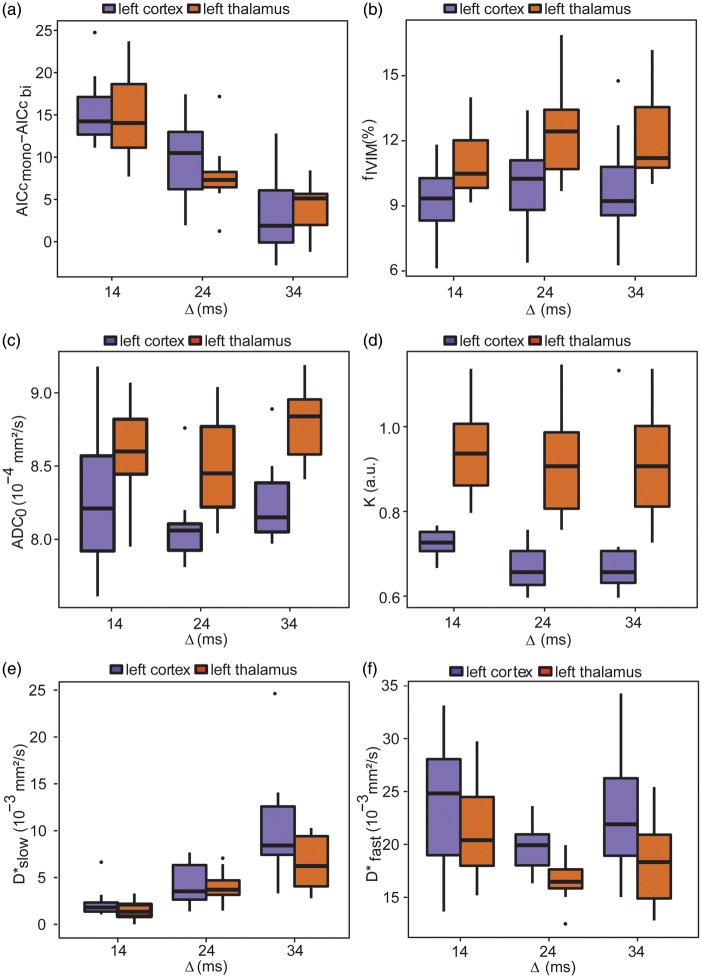
Figure 3(a) displays the box-and-whisker plot for the difference in AICc between the mono- and bi-exponential models against the diffusion time for the two ROIs. As shown in Table 1, the two-way ANOVA test shows that the AICc is not different according to the ROI location, but is significantly different between diffusion times (p < 0.0001). The Tukey’s HSD test indicates that the differences in AICc are significantly different between all diffusion times. Specifically, we see a decrease in the difference in AICc between the two models when the diffusion time increases.
Figure 3.
Box-and-whisker plots of the model parameters against the diffusion time and ROI. Box-and-whisker plots of the difference in AICc of the mono- and bi-exponential models and the parameters of the Kurtosis and bi-exponential models against the diffusion time for the two ROIs: (a) AICcmono–AICcbi, (b) fIVIM,(c) ADC0, (d) K, (e) D*slow, and (f) D*fast. Error bars represent SD (NR = 11).
Table 1.
Changes in the difference in AICc and the IVIM parameters with the different diffusion times and ROIs.
| Parameter | Δ = 14 ms (1) (mean ± SD) |
Δ = 24 ms (2) (mean ± SD) |
Δ = 34 ms (3) (mean ± SD) |
Two-way ANOVA or Scheirer–Ray–Hare test p-value |
Comparison Group | Tukey’s HSD or Games–Howell post hoc test p-value | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| LC | LT | LC | LT | LC | LT | ROI | Δ | Δ | ||
| AICcmono–AICcbi | 15.00 ± 4.63 | 15.09 ± 4.74 | 9.45 ± 4.34 | 7.55 ± 3.75 | 3.18 ± 4.64 | 3.64 ± 3.20 | 0.58 | 1.11 × 10−11 | 1 vs. 2 | 2.89 × 10−5 |
| 1 vs. 3 | <1 × 10−7 | |||||||||
| 2 vs. 3 | 4.30 × 10−4 | |||||||||
| ADC0 (10−4 mm2/s) | 8.29 ± 0.43 | 8.57 ± 0.36 | 8.10 ± 0.24 | 8.47 ± 0.34 | 8.33 ± 0.48 | 8.77 ± 0.27 | 1.30 × 10 − 6 | 0.044 | 1 vs. 2 | 0.27 |
| 1 vs. 3 | 0.60 | |||||||||
| 2 vs. 3 | 0.036 | |||||||||
| K | 0.74 ± 0.02 | 0.94 ± 0.11 | 0.68 ± 0.05 | 0.92 ± 0.12 | 0.67 ± 0.05 | 0.91 ± 0.13 | 4.08 × 10 − 9 | 0.62 | – | – |
| fIVIM (%) | 9.37 ± 1.84 | 11.08 ± 1.61 | 10.02 ± 2.05 | 12.44 ± 2.44 | 9.53 ± 1.85 | 12.08 ± 2.21 | 5.74 × 10 − 5 | 0.17 | – | – |
| ffast (%) | 77.35 ± 11.54 | 78.16 ± 9.48 | 81.86 ± 6.32 | 70.12 ± 11.75 | 55.36 ± 26.79 | 48.52 ± 23.65 | 0.24 | 1.61 × 10 − 5 | 1 vs. 2 | 0.85 |
| 1 vs. 3 | 3.2 × 10 − 4 | |||||||||
| 2 vs. 3 | 7.7 × 10 − 4 | |||||||||
| D*slow (10−3 mm2/s) | 2.25 ± 1.58 | 1.53 ± 1.03 | 4.28 ± 2.25 | 4.10 ± 1.62 | 10.44 ± 5.91 | 6.48 ± 2.83 | 0.11 | 6.83 × 10 − 7 | 1 vs. 2 | 1.4 × 10 − 4 |
| 1 vs. 3 | 9.7 × 10 − 6 | |||||||||
| 2 vs. 3 | 2.2 × 10 − 3 | |||||||||
| D*fast (10−3 mm2/s) | 23.92 ± 6.09 | 21.32 ± 4.68 | 19.92 ± 2.30 | 16.52 ± 1.90 | 23.16 ± 6.45 | 18.23 ± 4.02 | 0.0039 | 0.017 | 1 vs. 2 | 0.0054 |
| 1 vs. 3 | 0.50 | |||||||||
| 2 vs. 3 | 0.18 | |||||||||
Note: IVIM parameters for the three diffusion times and two ROIs (NR = 11) and results of the statistical tests on the dependence of the parameters against Δ and the ROIs. The values reported here for D*slow and D*fast are obtained by removing the contribution due to water diffusion in blood from the values obtained by fitting the experimental data. The two-way ANOVA was used as initial statistical test. When the assumptions of the two-way ANOVA were not met, i.e. for all parameters except the difference in AICc, ADC0 and fIVIM, the Scheirer–Ray–Hare test was used. The Tukey’s HSD and Games–Howell post hoc test were used when a significant difference was found for Δ with the two-way ANOVA or Scheirer–Ray–Hare test, respectively; Groups 1, 2, and 3 correspond to Δ = 14 ms, 24 ms and 34 ms, respectively. p < 0.05, highlighted in bold, are considered statistically significant.
Dependence of the model parameters on the diffusion time
Table 1 gathers the means ± SD and the results of the statistical tests for all parameters of the Kurtosis model, for diffusion, and of the bi-exponential model, for IVIM. Figure 3(b) to (f) shows the box-and-whisker plots for fIVIM, ADC0, K, D*slow, and D*fast against the diffusion time for the two ROIs.
ADC0 was found significantly different between Δ = 24 and 34 ms. K and fIVIM were not significantly influenced by the diffusion time in the range used in this study. We found, however, a significant difference for these parameters and ADC0 between the two ROIs. IVIM parameters, ffast and D*slow, were not significantly different between the two ROIs while D*fast was found lower in the thalamus. D*slow significantly increased with the diffusion time. D*fast was higher for Δ = 34 than for Δ = 24 ms, although not statistically significant. However, there was a significant decrease in D*fast between Δ = 14 and Δ = 24 ms and fslow was found higher for Δ = 34 ms compared to Δ = 24 ms.
The cortical capillary blood volume fraction was calculated as fIVIM,corr*fslow, where fIVIM,corr is the estimated blood volume fraction corrected for T2 differences between tissue and blood. Taking T2 of the blood 34.4 ms (30% arterial blood with T2 = 68 ms and 70% venous blood with T2 = 20 ms15,32) and T2 of the cortex 56.5 ms,33 we obtain the corrected fIVIM,corr values of 15.6%, 16.7%, and 15.9% for Δ = 14, 24, and 34 ms, respectively. For Δ = 14 and 24 ms, we obtain fIVIM,corr*fslow = 3.5 and 3%, respectively. We note that these values are in agreement with the cortical capillary blood volume fraction of 3.1% found in rats previously.34 For Δ = 34 ms, this value was, however, found to be higher (7.1%).
To study the signal evolution of the two pools separately, we simulated the IVIM signal for five diffusion times, Δ = 3, 14, 24, 34, and 60 ms for typical values of the lengths and blood flow velocities for the two pools considering that they represent capillaries and medium-size arterioles: vslow = 1 mm/s,35 Lslow = 40 µm, vfast = 5 mm/s,26 and Lfast = 150 µm. In Figure 4, we show the simulated signals for the two components at b = 50 s/mm2 weighted by the blood volume fractions fslow = 23 % and ffast = 77% against the diffusion time. ffast*FSim/fast is nine times smaller for Δ = 60 ms compared to Δ = 3 ms whereas fslow*FSim/slow barely changes.
Figure 4.
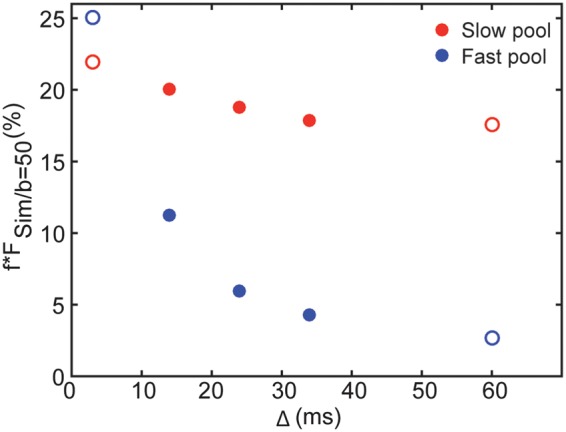
Simulated IVIM signals at b = 50 s/mm2 against the diffusion time for the slow and fast pools. Simulated IVIM signals for the slow and fast pools at b = 50 s/mm2 weighted by the blood volume fractions fslow = 23% and ffast = 77% against the diffusion time for vslow = 1 mm/s, Lslow = 40 µm, vfast = 5 mm/s and Lfast = 150 µm. The red and blue circles represent the slow and fast pools, respectively. The filled circles correspond to the diffusion times acquired in this study, for Δ = 14, 24 and 34 ms, and the empty circles to two extreme diffusion times, for Δ = 3 and 60 ms.
Dependence of the model parameters on the repetition time
As our bi-exponential model includes a fast flow component, we checked for inflow effects. Indeed, with increasing TR, we observed a major decrease in fIVIM and an increase in fslow while D*slow and D*fast stay constant (Table 2). As a result, even though the bi-exponential behavior was present for both repetition times, the quality of the fits was significantly better for TR = 1000 ms. Interestingly, the product fIVIM * fslow was similar at both TRs (3.3% at TR = 1000 ms and 3.7% at TR = 3000 ms) suggesting that the slow flow component does not present inflow effects, while the contribution of the fast flow component to the overall IVIM effects increases when TR gets shorter.
Table 2.
Changes in the IVIM parameters with TR.
| TR (ms) | fIVIM (%) | fslow (%) | D*slow (10−3 mm2/s) | D*fast (10−3 mm2/s) |
|---|---|---|---|---|
| 1000 | 13.41 ± 0.55 | 24.39 ± 10.84 | 2.01 ± 0.33 | 27.28 ± 1.97 |
| 3000 | 6.36 ± 1.06 | 57.94 ± 10.36 | 1.96 ± 0.70 | 25.76 ± 3.21 |
Note: IVIM parameters for two different repetition times on an ROI on the LC and one slice (NR = 4).
Comparison of the data with numerical simulations
The comparison with numerical simulations was performed for Δ = 24 ms. Four parameters were allowed to change in the dictionary of simulated signals: Lslow, vslow, Lfast and vfast (mean values). To assess goodness of fit, ɛ was calculated between simulated and experimental signals.
In Figure 5(a), in red, we show the 10% ɛ isolines for the slow pool obtained by fixing Lfast and vfast to 50 µm and 4 mm/s, respectively. The area between two isolines encompasses all acceptable combinations of Lslow and vslow that match the experimental data for this particular set of Lfast and vfast. Similarly, we obtain the 10% ɛ isolines for the fast pool (in blue) by fixing Lslow and vslow (Lslow = 40 µm, vslow = 1 mm/s). The isolines’ shapes are similar for both pools, with the slow pool thinner and shifted to the left compared to the fast pool, clearly demonstrating that the two pools are well separated with the slow pool associated with a smaller blood flow velocity than the fast pool. The vessel length is difficult to determine and Figure 5(a) shows that nearly all probed vessel lengths can yield an acceptable match with the data. To better illustrate this, in Figure 5(b) and (c), we plot the experimental signal along with simulated signals with the same blood flow velocity, vfast = 3 mm/s, but with two different vessel lengths for the fast pool, Lfast = 70 and 150 µm, and with the same vslow = 1 mm/s and Lslow = 40 µm for the slow pool. The two different lengths give a match with a similar quality confirming that the vessel length cannot be determined in this comparison (ɛ = 6.50% and 6.38%, respectively). A similar example can be given for two different vessel lengths associated with the slow pool. This incapability to determine the vessel lengths suggests that the two pools are closer to the sinc regime than to the exponential regime.
Figure 5.

Contour plots of the 10% errors isolines for different vessel lengths and blood flow velocities and examples of IVIM signals superimposed with simulated signals. (a) 10% isolines for different combinations of vessel lengths and blood flow velocities. The red curves correspond to the slow pool for vfast = 4 mm/s, Lfast = 50 µm and the blue curves to the fast pool for vslow = 1 mm/s, Lslow = 40 µm. (b, c) Examples of IVIM signal superimposed with simulated signals versus b-value for Δ = 24 ms in the LC. The black circles stand for the experimental data and the blue solid lines for the simulated signals with the same vslow = 1 mm/s and Lslow = 40 µm but with two different combinations of vfast and Lfast, vfast = 3 mm/s, Lfast = 70 µm, ɛ = 6.50% and vfast = 3 mm/s, Lfast = 150 µm, ɛ = 6.38%, respectively. Error bars represent SD from the averaging step.
Discussion
In this manuscript, we propose a bi-exponential model to fit the IVIM data at short diffusion times. We show that, for the datasets in this work, this model performs better than both the mono-exponential and the Kennan models proposed previously.
We hypothesize that the bi-exponential behavior seen in the IVIM data reflects the contribution of flow in two distinct vascular pools: a slow and a fast flowing pool corresponding to capillaries and medium-sized vessels, respectively. This hypothesis is supported by several observed relationships between the model parameters when varying experimental parameters. The presence of more than two vascular pools was also considered. However, a tri-exponential IVIM model did not fit the current data better than the bi-exponential model presented here. Therefore, while the presence of three or more pools is possible, such additional pools would present very low volume fractions.
We varied TR to examine the inflow effect, which should impact fast flowing blood. We showed that inflow effects had a negligible impact on the estimated volume fraction of the slow pool but significantly impacted the volume fraction of the fast pool. This is consistent with the fast pool signal coming from faster moving blood than for the slow pool. As a result, the global fIVIM fraction (or the fIVIM value of the IVIM mono-exponential model) could be overestimated when inflow effects are present (small number of slices, short TR).
We found a ffast-value that is smaller at the longest diffusion time for Δ = 34 ms compared to Δ = 24 ms, in agreement with a transition to a mono-exponential behavior at longer diffusion times as indicated by the AICc analysis. Combined with the fact that fIVIM is independent of the diffusion time, this observation also implies that while both pools, slow and fast, are initially present at b = 0 s/mm2, the decay of the IVIM signal corresponding to the fast pool is much faster as the diffusion time increases, eventually becoming difficult or even impossible to estimate. In addition, this could explain why the slow pool volume fraction we found in the cortical ROI was higher for the longest Δ (34 ms) while in agreement with other literature reports for Δ = 14 and 24 ms.34 Indeed, by simulating the two components of the IVIM signal separately for five diffusion times, we show in Figure 4 that FSim/fast decreases more than nine times going from Δ = 3 ms to Δ = 60 ms while FSim/slow practically does not change.
D*slow significantly increased with the diffusion time, suggesting a sinc (equation (3)) or intermediate regime for the slow pool. Also in agreement with a sinc regime, D*fast was higher for Δ = 34 ms than for Δ = 24 ms, although not statistically significant. Going from Δ = 14 to Δ = 24 ms, we see, however, a significant decrease in D*fast. This decrease could result from an additional dephasing effect present only at very short diffusion times. It is reasonable to consider that flow in the slow pool has a plug flow profile. However, if the fast pool corresponds to medium-sized vessels in between capillaries and pial arterioles (diameters ranging between 10 (Stefanovic et al.36) and 50 µm (Ma et al.26) and blood flow velocities ranging between 2 (Unekawa et al.35) and 20 mm/s (Jensenet al.37)), blood flow is expected to be laminar. In this case, an additional phase dispersion,38 , should be considered to the overall IVIM signal decay of the fast flow component
with , where is the variance in the laminar flow velocity field. This contribution is significant only for observation times on the order of the fluid element correlation time, defined as
where d is the blood vessel diameter. A simple estimation, assuming d = 40 µm and a mean blood flow velocity v = 5 mm/s, leads to ms, implying that cannot be neglected when Δ = 14 ms. At Δ = 24 ms, on the other hand, is negligible and, as a result, we witness a decrease in the measured .
By matching the experimental data with numerically simulated signals, we noticed that the vessel length could not be estimated accurately. Indeed, determining the vessel length is an ill-posed problem if we consider that, on average, spins do not get to probe the entire vessel segment during the diffusion encoding time. This observation supports our experimental results suggesting that the two pools are in a sinc or intermediate regime for the diffusion times used in this study, in agreement with recent findings showing that the pseudo-diffusion (exponential) IVIM regime is not always valid in the brain.39
ADC0 was found to be significantly influenced by the diffusion time between Δ = 24 and 34 ms. This trend is coherent with previous results from Pyatigorskaya et al.,40 although no significant difference was found between all diffusion times.
We report a significant difference in ADC0, K and fIVIM with the two ROIs studied, justified by the different composition and organization of the two structures. No significant difference was found for ffast and D*slow for the two ROIs, probably due to vascular similarities between the two regions.
The cut-off b-value to separate between diffusion and IVIM components used in this study, b = 500 s/mm2, is higher than the one usually applied for the rat brain, 300–400 s/mm2 (Iima et al.41). Due to the high SNR (≅ 44 at b = 500 s/mm2) made possible by the high field used and the many averages employed, we noticed that the IVIM signal was still present at b = 400 s/mm2 and therefore increased the cut-off value.
It is worth noting that formerly Neil et al. reported that the IVIM signal obtained by using a modified DW sequence in which the tissue component was directly suppressed can be better fit to a bi-exponential than a mono-exponential function.42 The authors attributed this bi-exponential behavior to an incomplete saturation of the extravascular spins. In the analysis we performed, extra care was taken to ensure that the tissue diffusion component has been completely removed, leaving the vascular component as the only possible contributor to the observed bi-exponential IVIM signal.
In this study, given the relatively coarse spatial resolution and the large size of the ROIs considered, we assumed diffusion and perfusion isotropy. We acquired and averaged data along three different diffusion encoding directions in order to eliminate possible gradient hardware differences and to increase the SNR. However, an investigation of IVIM anisotropy would be interesting and could provide key insights into the local geometry of the vasculature.
Our simulations could be improved in several ways. First, the vessel diameter could be added as a structural parameter of the network, allowing the definition of a vessel velocity profile. Second, the Gaussian distribution for the blood flow velocity could be replaced by a more accurate representation of the blood flow velocity in the vascular network, which could be different for the two pools. Finally, with the hypothesis that both pools are close to the sinc regime (few number of direction changes during the measured diffusion time, hence long segments), the assumption of a uniform distribution for the vessel orientations in the voxel (with a fixed vascular volume fraction) may not be valid for all combinations of vessel lengths and blood flow velocities. More complex simulations could lead to a more accurate prediction of the IVIM signal over a large range of diffusion times.
Conclusion
This study demonstrates that a bi-exponential IVIM model describes the IVIM MRI signal at short diffusion times better than the standard mono-exponential IVIM model. As validated by numerical simulations, this bi-exponential behavior reflects the presence of two separate vascular pools, corresponding to two different flow regimes. While at long diffusion times the faster pool is difficult to detect, and the bi- and mono-exponential models converge, employing IVIM at short diffusion times can provide valuable information not only regarding the capillary network but also larger vessels. There are clinical implications to this finding, as lesions or response to therapy might potentially be characterized by a differential balance between the fast and slow vascular pools.
Supplementary Material
Acknowledgment
The authors wish to thank Boucif Djemai and Erwan Selingue for their excellent technical assistance.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The research was supported by the ANR Grant ANR-13-NEUC-0002-01 and the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under Award Number R01EB018107. The content is solely the responsibility of the authors and does not necessarily represent the official views of the ANR or NIH.
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Authors’ contributions
LC and DLB designed and supervised the research. GF and LC performed all in-vivo experiments. GF, AC, JRL, and DLB designed the numerical simulations. GF, DLB, LC, and JRL analyzed the data. GF, DLB, LC, JRL, AC, and BS interpreted the data. GF, LC, JRL, and DLB wrote the manuscript.
Supplementary material
Supplementary material for this paper can be found at http://jcbfm.sagepub.com/content/by/supplemental-data
References
- 1.Iima M, Yano K, Kataoka M, et al. Quantitative non-Gaussian diffusion and intravoxel incoherent motion magnetic resonance imaging: differentiation of malignant and benign breast lesions. Invest Radiol 2015; 50: 205–211. [DOI] [PubMed] [Google Scholar]
- 2.Hu L, Hong N, Zhu W. Quantitative measurement of cerebral perfusion with intravoxel incoherent motion in acute ischemia stroke: initial clinical experience. Chin Med J 2015; 128: 2565–2569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ebrahimi B, Rihal N, Woollard JR, et al. Assessment of renal artery stenosis using intravoxel incoherent motion diffusion-weighted magnetic resonance imaging analysis. Invest Radiol 2014; 49: 640–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chung SR, Lee SS, Kim N, et al. Intravoxel incoherent motion MRI for liver fibrosis assessment: a pilot study. Acta Radiol 2014; 56: 1428–1436. [DOI] [PubMed] [Google Scholar]
- 5.Kanda T, Ishii K, Kawaguchi H, et al. High signal intensity in the dentate nucleus and globus pallidus on unenhanced T1-weighted MR images: relationship with increasing cumulative dose of a gadolinium-based contrast material. Radiology 2014; 270: 834–841. [DOI] [PubMed] [Google Scholar]
- 6.Kanda T, Osawa M, Oba H, et al. High signal intensity in dentate nucleus on unenhanced T1-weighted mr images: association with linear versus macrocyclic gadolinium chelate administration. Radiology 2015; 275: 803–809. [DOI] [PubMed] [Google Scholar]
- 7.Alsop DC, Detre JA, Golay X, et al. Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: a consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magn Reson Med 2014; 73: 102–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yao Y, Zhang S, Tang X, et al. Intravoxel incoherent motion diffusion-weighted imaging in stroke patients: initial clinical experience. Clin Radiol 2016; 71(9): 938. e11–16. [DOI] [PubMed] [Google Scholar]
- 9.Federau C, O'Brien K, Meuli R, et al. Measuring brain perfusion with intravoxel incoherent motion (IVIM): initial clinical experience. J Magn Reson Imag 2014; 39: 624–632. [DOI] [PubMed] [Google Scholar]
- 10.Le Bihan D, Breton E, Lallemand D, et al. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 1988; 168: 497–505. [DOI] [PubMed] [Google Scholar]
- 11.Le Bihan D, Turner R. The capillary network: a link between IVIM and classical perfusion. Magn Reson Med 1992; 27: 171–178. [DOI] [PubMed] [Google Scholar]
- 12.Kennan RP, Gao JH, Zhong J, et al. A general model of microcirculatory blood flow effects in gradient sensitized MRI. Med Phys 1994; 21: 539–545. [DOI] [PubMed] [Google Scholar]
- 13.Wetscherek A, Stieltjes B, Laun FB. Flow-compensated intravoxel incoherent motion diffusion imaging. Magn Reson Med 2015; 74: 410–419. [DOI] [PubMed] [Google Scholar]
- 14.Henkelman RM, Neil JJ, Xiang QS. A quantitative interpretation of IVIM measurements of vascular perfusion in the rat brain. Magn Reson Med 1994; 32: 464–469. [DOI] [PubMed] [Google Scholar]
- 15.Duong TQ, Kim SG. In vivo MR measurements of regional arterial and venous blood volume fractions in intact rat brain. Magn Reson Med 2000; 43: 393–402. [DOI] [PubMed] [Google Scholar]
- 16.Iima M, Le Bihan D. Clinical intravoxel incoherent motion and diffusion MR imaging: past, present, and future. Radiology 2016; 278: 13–32. [DOI] [PubMed] [Google Scholar]
- 17.Le Bihan D, Turner R. Intravoxel incoherent motion imaging using spin echoes. Magn Reson Med 1991; 19: 221–227. [DOI] [PubMed] [Google Scholar]
- 18.Fujima N, Yoshida D, Sakashita T, et al. Intravoxel incoherent motion diffusion-weighted imaging in head and neck squamous cell carcinoma: assessment of perfusion-related parameters compared to dynamic contrast-enhanced MRI. Magn Reson Imag 2014; 32: 1206–1213. [DOI] [PubMed] [Google Scholar]
- 19.Su S, Catherall M, Payne S. The influence of network structure on the transport of blood in the human cerebral microvasculature. Microcirculation 2012; 19: 175–187. [DOI] [PubMed] [Google Scholar]
- 20.Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed 2010; 23: 698–710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chabert S, Meca C, Le Bihan D. Relevance of the information about the diffusion distribution in vivo given by kurtosis in q-space imaging. Proc Intl Soc Mag Reson Med 2004; 11: 1238. [Google Scholar]
- 22.Lori NF, Conturo TE, Le Bihan D. Definition of displacement probability and diffusion time in q-space magnetic resonance measurements that use finite-duration diffusion-encoding gradients. J Magn Reson 2003; 165: 185–195. [DOI] [PubMed] [Google Scholar]
- 23.Le Bihan D. Magnetic resonance imaging of perfusion. Magn Reson Med 1990; 14: 283–292. [DOI] [PubMed] [Google Scholar]
- 24.Nevo U, Ozarslan E, Komlosh ME, et al. A system and mathematical framework to model shear flow effects in biomedical DW-imaging and spectroscopy. NMR Biomed 2010; 23: 734–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Torrey H. Bloch equations with diffusion terms. Phys Rev 1956; 104: 563–565. [Google Scholar]
- 26.Ma YP, Koo A, Kwan HC, et al. On-line measurement of the dynamic velocity of erythrocytes in the cerebral microvessels in the rat. Microvasc Res 1974; 8: 1–13. [DOI] [PubMed] [Google Scholar]
- 27.Li JG, Stanisz GJ, Henkelman RM. Integrated analysis of diffusion and relaxation of water in blood. Magn Reson Med 1998; 40: 79–88. [DOI] [PubMed] [Google Scholar]
- 28.Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control 1974; 19(6): 716–723.
- 29.Wagenmakers E, Farrell S. AIC model selection using Akaike weights. Psychon Bull Rev 2004; 11: 192–196. [DOI] [PubMed] [Google Scholar]
- 30.Burnham KP, Anderson DR. Kullback-Lebibler information as a basis for strong inference in ecological studies. Wildlife Res 2001; 28: 111–119. [Google Scholar]
- 31.https://www.R-project.org/ (accessed 30 September 2015).
- 32.Krishnamurthy LC, Liu P, Xu F, et al. Dependence of blood T(2) on oxygenation at 7 T: in vitro calibration and in vivo application. Magn Reson Med 2014; 71: 2035–2042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Liachenko S, Ramu J. Quantification and reproducibility assessment of the regional brain T2 relaxation in naïve rats at 7T. J Magn Reson Imag Epub ahead of print 7 July 2016. DOI: 10.1002/jmri.25378. [DOI] [PubMed] [Google Scholar]
- 34.Dunn JF, Roche MA, Springett R, et al. Monitoring angiogenesis in brain using steady-state quantification of DeltaR2 with MION infusion. Magn Reson Med 2004; 51: 55–61. [DOI] [PubMed] [Google Scholar]
- 35.Unekawa M, Tomita M, Takashi O, et al. Frequency distribution function of red blood cell velocities in single capillaries of the rat cerebral cortex using intravital laser-scanning confocal microscopy with highspeed camera. Asian Biomed 2008; 2: 203–218. [Google Scholar]
- 36.Stefanovic B, Hutchinson E, Yakovleva V, et al. Functional reactivity of cerebral capillaries. J Cereb Blood Flow Metab 2008; 28: 961–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jensen LJ, Holstein-Rathlou N. The vascular conducted response in cerebral blood flow regulation. J Cereb Blood Flow Metab 2013; 33: 649–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Callaghan P. Principles of nuclear magnetic resonance microscopy, Corby: Oxford Science Publications (Ed.), 1991. [Google Scholar]
- 39.Ahlgren A, Knutsson L, Wirestam R, et al. Quantification of microcirculatory parameters by joint analysis of flow-compensated and non-flow-compensated intravoxel incoherent motion (IVIM) data. NMR Biomed 2016; 29: 640–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pyatigorskaya N, Le Bihan D, Reynaud O, et al. Relationship between the diffusion time and the diffusion MRI signal observed at 17.2 Tesla in the healthy rat brain cortex. Magn Reson Med 2014; 72: 492–500. [DOI] [PubMed] [Google Scholar]
- 41.Iima M, Reynaud O, Tsurugizawa T, et al. Characterization of glioma microcirculation and tissue features using intravoxel incoherent motion magnetic resonance imaging in a rat brain model. Invest Radiol 2014; 49: 485–490. [DOI] [PubMed] [Google Scholar]
- 42.Neil JJ, Bosch CS, Ackerman JJ. An evaluation of the sensitivity of the intravoxel incoherent motion (IVIM) method of blood flow measurement to changes in cerebral blood flow. Magn Reson Med 1994; 32: 60–65. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.