Reliability of infarct volumetry: Its relevance and the improvement by a software-assisted approach

Abstract

Despite the efficacy of neuroprotective approaches in animal models of stroke, their translation has so far failed from bench to bedside. One reason is presumed to be a low quality of preclinical study design, leading to bias and a low a priori power. In this study, we propose that the key read-out of experimental stroke studies, the volume of the ischemic damage as commonly measured by free-handed planimetry of TTC-stained brain sections, is subject to an unrecognized low inter-rater and test-retest reliability with strong implications for statistical power and bias. As an alternative approach, we suggest a simple, open-source, software-assisted method, taking advantage of automatic-thresholding techniques. The validity and the improvement of reliability by an automated method to tMCAO infarct volumetry are demonstrated. In addition, we show the probable consequences of increased reliability for precision, p-values, effect inflation, and power calculation, exemplified by a systematic analysis of experimental stroke studies published in the year 2015. Our study reveals an underappreciated quality problem in translational stroke research and suggests that software-assisted infarct volumetry might help to improve reproducibility and therefore the robustness of bench to bedside translation.

Introduction

Although decades of translational research revealed several promising drug candidates, the reperfusion of the occluded brain vessels remains the only specific treatment option for ischemic stroke so far. Regardless of recanalization and reperfusion, several potential neuroprotective drugs have been shown to have a positive effect on infarct size in experimental stroke models. However, none of these substances could prove its efficacy in clinical trials.^1,2

In general, an alarming problem in experimental research is that reproduction of published results fails in 75–80% of cases.³ Researchers may overestimate the effect of their interventions because they are susceptible to different types of bias. Once the interventions are subjected to rigorous prospective evaluation and reporting as is the standard for randomized controlled trials (RCTs) with patients, interventions that were successful in experimental studies often cannot meet their proposed expectations.⁴

On the preclinical side, this “translational roadblock” is in parts a result of methodological and statistical flaws, which have been shown to be frequent among experimental stroke studies.^5,6 Although the stroke therapy academic industry roundtable (STAIR) preclinical recommendations emphasized as early as 1999 the importance of methodological criteria like a priori sample size calculation, proper blinding, and randomization, studies still suffer from these methodological quality issues.^7,8 The latest update of the STAIR criteria therefore recommends the replication of experiments in an independent laboratory to improve the reproducibility of positive results, comparable to multi-center, RCTs in clinical research.^9,10

Infarct volume is the central outcome parameter in evaluating the potency of neuroprotective drugs. In order to identify and quantify the ischemic damage, the agent 2,3,5-Triphenyltetrazolium hydrochloride (TTC) is frequently used in brain slices. TTC is reduced by enzymes of vital mitochondria and converted into its insoluble form of formazan, staining healthy tissue in a deep red color, whereas tissue damaged by ischemia remains unstained.¹¹ Notably, most investigators still rely on a manual measurement by delineating the unstained border in scanned brain slices to determine infarct sizes.¹² We hypothesize, that being largely dependent on subjective judgment, especially at areas of low contrast, this method is highly susceptible to produce biased especially in the case of a poor study design, such as insufficient blinding.^13,14 Furthermore, we believe that this subjective bias reduces the reproducibility of infarct volumetry among different raters as well as the same rater in a test-retest situation. The resulting imprecision might hamper the usability of this method in multi-center studies. A first analysis of inter-rater reliability in manual infarct volumetry has been shown in a recently published preclinical RCT.¹⁵ However, to our knowledge, no systematic analysis of inter-rater and test-retest analysis of infarct volumetry has been performed so far.

In this paper, we demonstrate the impact of low reliability of manual infarct volumetry in TTC-stained mouse brain slices on statistical power, the precision of the observed effect and hence the reproducibility of obtained results. In addition, we conducted a systematic literature analysis of experimental stroke studies published in 2015, allowing the investigation of the effects of reliability with realistic statistical data. We furthermore show how an increase in reliability by a newly developed, user friendly ImageJ macro improves the strength of infarct size determination.

Materials and methods

Experimental model of middle cerebral artery occlusion and staining

A total of 15 male C57Bl/6 mice (Charles River Laboratories, Sulzfeld, Germany), housed under standard conditions with 12 hours of light/dark cycle and free access to food and water, were used at 10–12 weeks of age. All experiments were approved by the local governmental authorities (Regierungspräsidium Darmstadt, Germany) and conducted in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and the current Animal Research: Reporting of In Vivo Experiments guidelines (http://www.nc3rs.org/ARRIVE). Sample size of animals with MCAO was chosen a priori according to achieve a power of >0.8 at an ICC difference of at least 0.05.

Focal cerebral ischemia was induced by transient middle cerebral artery occlusion (tMCAO) as described previously.¹⁶ Briefly, mice were anesthetized with 1.5–2.5% isoflurane (Forene®; Abbott, Wiesbaden, Germany) and 0.1 mg/kg buprenorphine (Temgesic®; Essex Pharma, Munich, Germany) under spontaneous respiration. The right carotid bifurcation was exposed through a midline cervical incision and a custom made filament (tip diameter 0.23 +|− 0.02 mm, coating length 9–10 mm, Doccol, Sharon, USA) was advanced into the internal carotid artery to occlude the middle cerebral artery. After an occlusion time of 1 h (n = 7) or 3 h (n = 8), the filament was withdrawn to initiate reperfusion. After 6–8 h, an additional dose of 0.1 mg/kg buprenorphine was applied; 24 h after reperfusion, mice were lethally anaesthetized and perfused transcardially with saline solution. One mouse died before reaching the end-point and was not used for analysis. Despite being sufficient for the hypothesis tested here, we do not recommend usage of occlusion times of 3 h or more in neuroprotective studies due to high morbidity and mortality of animals. Besides, a 24-h end-point is by some authors considered to be a too narrow time frame, as the ischemic lesion might be growing afterwards and behavioral data are hampered by the influence of anesthesia and surgery. Brains were removed and cut into 2 mm thick coronal slices using a mouse brain matrix (ASI Instruments, Warren, USA). The slices were stained with a 2% solution of 2,3,5-triphenyltetrazoliumchloride (TTC) in phosphate-buffered saline (pH 7.4) for 15 min at 37℃. Subsequently, slices were arranged between transparent foils and front, and back surfaces of the slices were scanned with a flatbed color scanner (CanoScan LiDE 100; Canon, Tokyo, Japan; settings: 600dpi, full colors) against a black background. The resulting images were saved in tagged image file format (TIFF).

Design

Eleven raters (MD and PhD students) working in neuro-vascular laboratories at three German university hospitals (Frankfurt, München and Würzburg) and frequently employing TTC staining were asked to manually measure cerebral infarct volumes of 15 mice as described below. Measurements were repeated four months later applying our newly designed ImageJ macro. Infarct sizes of five mice were measured again four weeks after the respective first measurement with raters being blinded to this repetition to assess test-retest reliability. None of the raters was involved in conducting or evaluating this study. Reporting was conducted according to GRRAS guidelines.¹⁷

Manual measurement of infarct volumes

Raters were provided with front and back surface scans of the first three rostral slices of each mouse brain as well as detailed instructions in order to minimize bias due to different tracing principles (supplemental method 5). Briefly, areas of infarct and ipsi- and contralesional hemispheres were quantified by planimetry after region borders were manually delineated (ImageJ software; National Institute of Health, Bethesda, USA).¹⁸ Area dimensions were obtained from slices of both front and back surfaces and imported into a predefined Excel template. The infarct and hemispherical areas of each side were multiplied by half of each slice’s thickness (1 mm) and the following equation was applied to calculate edema-corrected infarct volumes.^19,20 Infarct sizes were given as percentage of the contralateral hemisphere.

We also asked the raters to state the time they needed from starting the measurements until entering the results in the provided excel templates (in total 20 measurements of 15 infarcts, of which 5 were measured twice).

Automated infarct volumetry by an ImageJ macro

For the measurement of infarct size by the macro, the same images used for manual measurement were taken without further processing or editing.

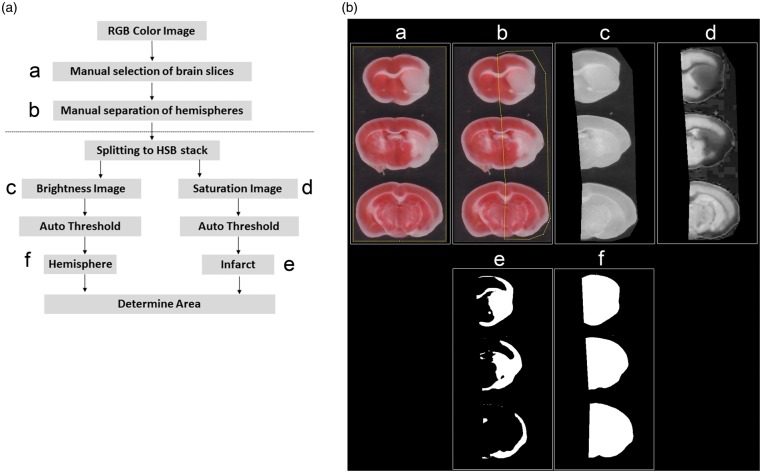
The ImageJ macro follows the following principles (Figure 1(a); for the full macro code see supplemental method 1): The user is asked to choose an image and a working directory and to select the brain slices subjected to measurement. Subsequently, the hemispheres are separated along the midline by overlaying a polygon on the ipsilesional hemisphere. After splitting in the components hue, saturation and brightness, image segmentation is performed by applying the “Default AutoThreshold” algorithm provided with ImageJ.²¹ The resulting segmented images represent either the infarcted or viable tissue, depending on whether bright or saturated images were thresholded (Figure 1(a) and (b)). By executing this algorithm for both hemispheres independently, areas of ischemic damage and of ipsi- and contralesional hemispheres were determined. Resulting segmented pictures and result charts were saved automatically allowing visual confirmation. Resulting values were imported into a predefined Excel template and edema corrected infarct volumes were calculated by the above given equation.

Figure 1.

Implementation of an ImageJ macro using automated thresholding (a) Overview of the algorithm, the letters a–f indicate the different steps of the macro, corresponding images are shown in (b) and the corresponding macro code is shown in supplemental methods 1. (b) Example of the image processing by the macro.

Optionally, the macro is able to measure the unstained area of the contralateral hemisphere as well. The resulting values were not used in our calculation but may be of interest as quality standard or in future applications.

Systematic analysis of the literature

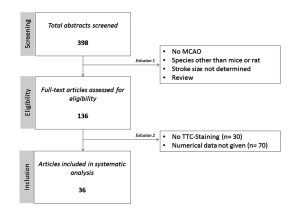
The systematic analysis followed a predefined protocol and was based on the results of experimental stroke studies on neuroprotective strategies published in 2015. Within PubMed, we searched for original papers by MeSH terms involving three search components: “mice” or “rats,” “ischemic stroke,” and “(neuroprotective) treatment” (for the complete search term see supplemental method 2). Results were restricted to studies published in English. Studies were included if they (1) were performed in mice or rats in vivo; (2) applied MCA occlusion; (3) assessed the effect of a treatment on infarct size; (4) used TTC-stained brain slices for infarct volumetry; and (5) reported numerical values for mean infarct sizes, either standard deviation (SD) or standard error of the mean (SEM) and sample size (for flow-diagram of inclusion process see supplemental method 2).

From the 36 included studies, bibliographic data and study characteristics were registered (for details see supplemental method 2). We extracted data for mean infarct sizes, sample size, SD or SEM in the treatment as well as the control group. For studies with multiple treatments and dosing, the data of the first significant results shown with the lowest dose administered were extracted. In cases of sample sizes reported as a range, the lowest number was considered. SEMs were converted to SD by the formula: $\mathrm{SD}=\mathrm{SEM}\times \sqrt{n}$. Because in small studies the observed variance is not a precise estimate of the true variance, we computed pooled coefficients of variation $(\mathrm{CV}=\frac{\mathrm{SD}}{\mathrm{mean}})$. To calculate the ${\mathrm{CV}}_{\mathrm{pooled}}$, we obtained the CV and the sample size for both control and treatment group from each individual study. Taking into account all these values, the ${\mathrm{CV}}_{\mathrm{pooled}}$ for each group was calculated according to the formula reported in Kleikers et al.²²

$${\mathrm{CV}}_{\mathrm{pooled}}=\sqrt{\frac{\sum {\mathrm{CV}}^2\times (n-1)}{\sum (n-1)}}$$

Statistical analysis

Inter-rater and test-retest reliability were calculated using the packages “irr” (Version 0.84) and “agRee” (Version 0.4-0) for the open-source software “R” (Version 3.2.2).^23–25 For the intraclass coefficient (ICC) of inter-rater and test-retest reliability, a two-way model was chosen, using single values.²⁶ Given the exploratory nature of our study, power of the ICC comparison was analyzed post hoc according to Zou²⁷ and Rathbone et al.²⁸ using the R-package “ICC.sample.size” (Version 1.0). The point estimate of the within-subject coefficient of variation (WSCV) was calculated using the package “agRee”.²⁹

Correlation and agreement of measurements between manual and automated method were analyzed by Pearson correlation and Bland–Altman blot.³⁰ Agreement between repeated measurements for the test-retest situation was also analyzed by Bland–Altman Blots. The (dis-)advantages of the different reliability parameters are discussed in the supplemental methods section of this paper (supplemental method 4).

For post hoc power analysis of the systematic analysis of the literature, we calculated standardized effect sizes according to the method of ‘Cohen’s d’:

$\mathrm{Cohen}\text{'}sd\text{'}=\frac{\mathrm{absolute}\mathrm{effect}\mathrm{size}(\%\mathrm{of}\mathrm{control})}{\mathrm{pooled}\mathrm{CV}(\%\mathrm{of}\mathrm{control})}$.³¹ Post hoc power analysis was performed with the R-package “pwr” (Version 1.2-0).³²

Power estimation of bootstrapped samples was also performed with the R-package “pwr,” using resampling with estimated true SDs, as well as pooled n and effect size derived from the systematic analysis. The true SD was estimated with the ICC for test-retest reliability (see below) using the formula

$$\mathrm{True}\mathrm{SD}=\sqrt{\mathrm{reliability}\times \mathrm{pooled}\mathrm{observed}{\mathrm{SD}}^2}$$

(for the full R code see supplemental method 3).

In order to analyze the effect of reliability on the precision of the observed effect, we took advantage of the assumptions that a. the t-test can be seen as a linear model $(\mathrm{stroke}\mathrm{size}=\beta *\mathrm{treatment}\mathrm{group})$ and b. measurement error can be added as a random error term $(\mathrm{stroke}\mathrm{size}=\beta *\mathrm{treatment}\mathrm{group}+\mathrm{measurement}\mathrm{error})$. The measurement error term consists of a normal distribution around 0 with the SDs of the measurement error alone. The resulting β-coefficients of this model reflect the observed effect, or the difference between the means of both groups. This linear model was repeated 9999 times with bootstrapping samples from the two normal distributions (treatment vs. control). The sample size used here was again the mean number of animals for each group used in previous studies as revealed in our systematic analysis of the literature (for the full R code see supplemental method 3).

Results

Establishment and validation of the ImageJ macro

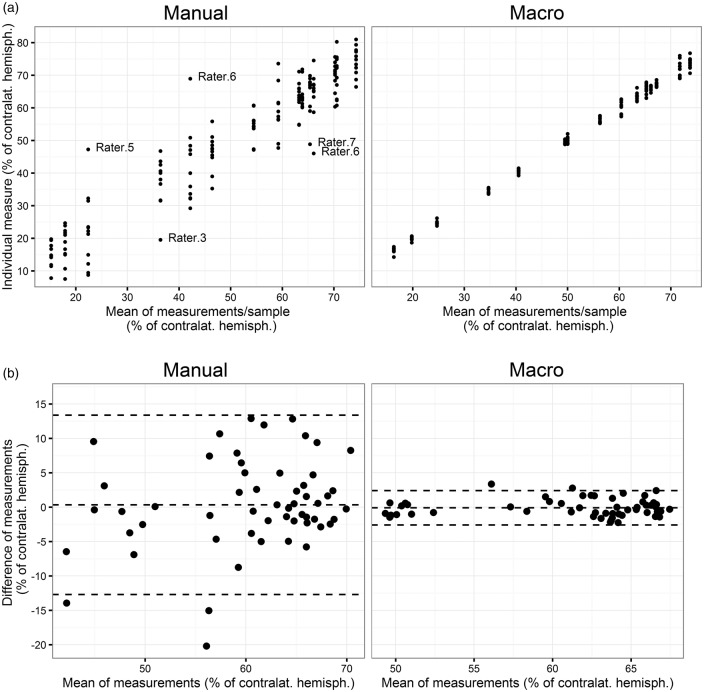
The ImageJ macro written for this project allowed 78.5% time saving (32 ± 11 min vs. 233 ± 53 min for 20 infarcts, according to the raters’ statements). All users were able to apply the macro after a short introduction. Experience level or research center had no influence on the usability of the macro. The macro recognized infarcts in all samples in a comprehensive way, as shown by examples in Figure 1. The mean measurements of all 15 infarcts by 11 raters using the macro correlated well with the values of the mean of 15 measurements with the actual standard, the delineation of the infarct by hand (see Figure 2(a), R²: 0.965, p < 0.001). The Bland–Altman analysis (Figure 2(b), mean difference: 0.371, lower limit: −6.980, upper limit: 7.722; all values as infarct size as % of contralateral hemisphere) showed no relevant systematic bias and confirmed the validity of the macro. As shown in Figure 1(b), the macro also recognizes to some extent white matter in the ipsilateral hemisphere as infarct; however, this has little relevance for the validity of our macro (Figure 2(b)).

Figure 2.

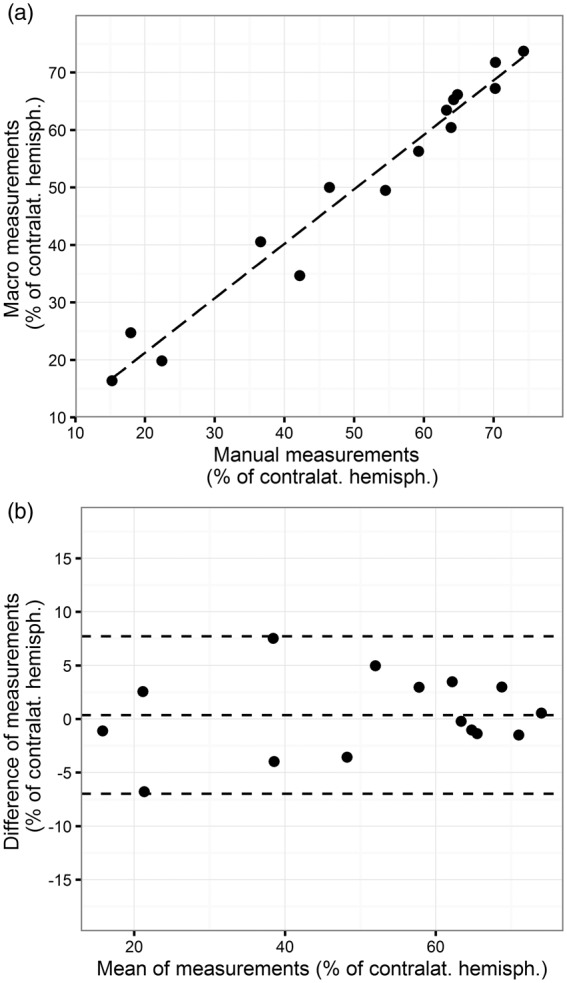
Validity of infarct volumetry with an ImageJ macro. (a) Correlation of manual infarct volumetry with automated infarct volumetry. To reduce the effects of reliability, means of measurements by 11 raters were correlated. (b) The Bland–Altman plot shows the average of the differences between the measurements with both methods. The central dashed line near zero indicates the lack of systematic bias, the upper and the lower line indicate the limits of agreement. The difference between the measurements of both methods does not differ between small values or large values, indicating high consistency among different infarct sizes.

Reliability of manual versus automated infarct volumetry

Three different approaches to investigate inter-rater reliability were applied: The ICC was used to analyze consistency and agreement between different raters (n = 15). We determined lower ICC values for consistency as well as agreement for the manual infarct volumetry compared to the measurement by the ImageJ macro (see values and confidence intervals in Table 1). As a second index of reliability, we calculated the WSCV, which is independent of the study population. Again the macro showed a much smaller WSCV confirming the presence of a difference between the reliability of the manual approach and the automated analysis (see Table 1 for values and confidence intervals). To illustrate the difference of inter-rater reliability, all single measurements were plotted against the mean of each sample for both the manual method as well as the macro (Figure 3(a)).

Table 1.

Inter-rater agreement of manual vs. auto.

	ICC(2,1) consistency	95% conf. interval	ICC(2,1) agreement	95% conf. interval	WSCV	95% conf. interval
Manual	0.908	0.832 to 0.962	0.895	0.811 to 0.956	0.133	0.103 to 0.162
Macro	0.996	0.993 to 0.999	0.996	0.991 to 0.998	0.024	0.019 to 0.030

ICC: intraclass correlation coefficient; WSCV: within-subject coefficient of variation.

Figure 3.

Inter-rater and test-retest reliability of manual infarct volumetry versus measurement with a macro. (a) Infarct volumetry by the conventional manual method (left) and with an ImageJ macro (right) plotted for each sample. The plot shows the disagreement between raters, which is similar across different infarct sizes. Outliers are identified by local-weighted regression (>2× the standard residual) in order to analyze the influence of single raters. (b) Test-retest reliability of the two different methods for infarct volumetry, analyzed with the Bland–Altman plot.

The comparison of test-retest or intra-rater reliability revealed a substantial difference between both methods. Corresponding to the inter-rater reliability, test-retest ICC values were considerably lower for the manual measurement compared to the automated analysis (Table 2). This improvement in reliability by the automated infarct volumetry was again recapitulated by the WSCV (Table 2) and Bland–Altman plots (Figure 3(b)). The manual method showed a mean difference between measurements of +0.346 (all values in % of contralateral hemisphere) with an upper limit of +13.381 % and a lower limit of −12.688 %; the values for the macro method were: mean difference: −0.081%, lower limit: −2.581 % and upper limit: +2.420 %.

Table 2.

Test-retest reliability.

	ICC(2,1) agreement	95% conf. interval	WSCV	95% conf. interval
Manual	0.681	0.508 to 0.801	0.077	0.062 to 0.092
Macro	0.978	0.962 to 0.987	0.014	0.012 to 0.017

ICC: intraclass correlation coefficient; WSCV: within-subject coefficient of variation.

Analysis of infarct volumetry in the literature

The search identified 398 studies in total, of which 136 articles were selected for full text screening. TTC staining was the most frequently applied method for infarct volume assessment (106 out of 136 studies). Notably, only 36 out of 106 studies reported all data by numerical means and therefore were eligible for systematic analysis (for flow-diagram of inclusion process and study characteristics see supplemental method 2).

Sample sizes ranged from 4 to 14 animals per group, mean sample size for control was 7.69 ± 2.22 animals per group and 7.53 ± 2.14 animals per group for treatment. In total 548 mice were included in our systematic analysis. Only 3 out of 36 studies (8.33%) reported to have carried out an a priori sample size calculation. The remaining 33 studies did not reveal how sample size was determined. Absolute effect sizes varied between 15.4% and 79.19% of the respective mean of the control group with an average effect size of 40.99 % ± 14.94 for all included studies; 10 out of 36 studies (27.78%) reported blinding for infarct volumetry. Remarkably only one of the studies reported a non-significant change in infarct volume. Due to the fact that within small studies, the observed variance is not a precise estimate of the true variance, we computed pooled coefficients of variation (CV of 0.3 for the control group and 0.5 for the treatment group). This in turn resulted in the same SD in absolute numbers. ImageJ was the most frequently applied software for infarct measurement. Interestingly, none of the studies reported to have used an automated method of infarct volumetry.

Next, we performed a post hoc power analysis on all included studies and assessed their power to detect a standardized effect size (or Cohen’s d) of 1.37 (resulting from an absolute effect size of 41% and a SD of 30% of control infarct volume) with a significance level α ≤ 0.05. Average statistical power of the studies included was 64.83 ± 13.54% and only 8 out of 36 studies (22.22%) achieved a sufficient level of power (1−β ≥ 0.8).

Effects of reliability on power and precision of effect estimation

In line with the t-test assumptions, i.e. that the variables follow a normal distribution, we resampled from the distributions based on the pooled effect (Mean: 0.6 vs. 1.0); CVs (0.5 vs. 0.3) and sample size (n = 8) of the systematic analysis. The repeated resampling, also known as bootstrapping, and testing from these distributions allows an accurate analysis of the true relationship between treatment and control population.

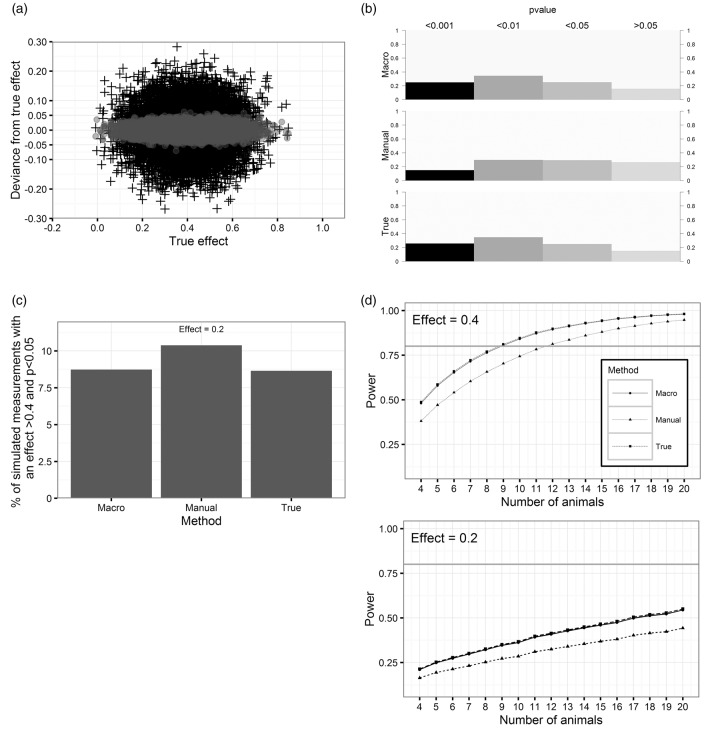
Figure 4(a) and (b) shows the resulting imprecision of the observed effects after resampling from the distributions of treatment group and control group with the three (none, manual measurement and macro) measurement errors, respectively. As expected, infarct volumetry with the macro results in a very low imprecision due to the small measurement error.

Figure 4.

Simulated effects of the reliabilities on the precision of the observed effect, p-values, effect inflation and power. (a) Effect of reliability on the precision of the estimate. The crosses show the difference of the observed effect with manual measurement error to the effect without measurement error (mean = 0.4). Gray dots indicate the imprecision using the macro. (b) Distribution of observed p-values of simulated measurements by the different methods (mean effect = 0.4). (c) Percentage of observed effects >0.4 and p < 0.05 if true mean effect is 0.2. (d) Estimation of power/sample sizes for different reliabilities and effects of 0.4 and 0.2.

The repeated t-tests of the bootstrapped samples from both groups result in different levels of significance (Figure 4(b)). P-values of the measurement with the macro have the same distribution as the measurement without error. However, using the manual method, the distribution of p-values is shifted towards p > 0.05.

To address the question to which degree measurement error affects the chance to observe an effect of >0.4 at the significance level of p < 0.05 although the true mean difference of the populations is actually lower, a problem also known as effect inflation, we simulated the distributions for a mean effect of 0.2 with the different measurement errors. As illustrated in Figure 4(c), 10.4% of the observations with the manual method actually indicate a difference of >0.4 at p < 0.05. For the macro as well as comparisons without measurement error, this chance is slightly smaller (8.7%).

Kanyongo et al.³³ showed the appliance of simulations to correct the power calculations of the t-test for reliability. By following their procedure (Figure 4(d)), we demonstrate that the increase of reliability from 0.681 (manual measurement) to 0.978 (macro) leads to an increase of power and reduces the number of animals required to reach the adequate statistical power (1−β ≥ 0.8). With a hypothetical effect of 0.2, which is not unlikely to be the true effect due to effect inflation as shown above, even a sample size of 20 would not reach adequate power (for a given effect size = 0.2, the animal number needed to reach a power of 0.8 would be n = 60, 45, 44 for manual, macro and true error, respectively).

Discussion

In this paper, we demonstrate the impact of low reliability of infarct volumetry, one of the most frequently used outcome parameters in preclinical stroke research, on precision of the observed effect and its implications for power calculations. We furthermore show how a simple increase in reliability may aid to improve this particular read-out.

The common way of measuring infarct volume by delineating the unstained area of TTC stainings is not only a time consuming process. The investigator’s decision of where to draw the border between stained and unstained tissue inherent in this method is prone for bias and inconsistency. The goal of this report was therefore to establish and validate an automated image analysis method for quantification of infarct volumes based on TTC-stained brain sections.

A first description of an automated procedure to determine infarct sizes from TTC-stained rat brain slices by spectral analysis was published by Goldlust et al.³⁴ A second algorithm with improved applicability was provided by Schneider et al.¹⁸ and Regan et al.³⁵ in form of an ImageJ macro. Lately, Lee et al.³⁶ developed a program called “InfarctSizer” which computes the infarct volume proportional to the pixel intensity. There are several reasons why their methodology has not become the standard of infarct size assessment. First of all, parameters of the algorithm (e.g. the applied threshold to separate infarcted and healthy tissue) had to be defined by the user in preceding experiments. This results again in a factor prone to subjective bias, as well as additional work and time. The macro shown here overcomes this issue by using an automatic, unbiased thresholding technique. In support of these arguments, we show the superiority of our macro compared to two other software-assisted approaches including “InfarctSizer” (see supplemental method 6). Additionally, images had to fit specific requirements (as the exact positioning of the slices) and preprocessing was required before analysis was carried out. As shown above, the macro established by us, circumvents this problem by allowing preprocessing within the software. Finally, until today it could not be shown that besides a doubtless time saving effect, automated assessment of infarct sizes is indeed superior to a manual measurement with regard to reliability.

First of all, we provide evidence for the validity of the infarct volumetry with the macro by comparing the results of this method in the hands of 11 new users of the macro to the results of manual infarct volumetry of the same individuals who were all familiar with TTC staining and Image J-based free-hand planimetry. Taking advantage of a regression to the mean, a comparison of measurements with the macro by 11 raters with the mean of each 15 manual measurements is a good indicator for validity. Importantly, we did not observe any systematic bias for certain infarct sizes as shown by the mean difference in the Bland–Altmann plot. A drawback of the assessment of validity in this case is the inevitable fact, that we cannot compare our results with the true infarct size, as we believe that there is no method available allowing a nearly perfect accuracy of measurement. Additionally, the limitations of the TTC staining itself are beyond the topic of this paper. A frequent concern of auto-thresholding is its non-adjustability in cases of poorly stained specimens. However, we want to point out that careful handling of the sections and appliance of a strict staining protocol avoids this problem. Furthermore, we recommend the analysis of the measured non-stained area in the contralateral hemisphere, which should be below 17% of the hemisphere. With slight modifications, the macro is also applicable for other staining protocols, other species or histological methods such as Nissl-staining of viable neuronal tissue (supplemental Figures 2.5 and supplemental method 7).

In the following reliability analysis (Tables 1 and 2 and Figure 3), we investigated inter-rater reliability as well as test-retest reliability, and show the increase of reliability using a macro instead of infarct volumetry by hand. Our findings are in line with a previous analysis of inter-rater reliability by Llovera et al.¹⁵ in manual infarct volumetry, which showed acceptable ICC values in a heterogeneous infarct population and particular wide limits of agreement in the Bland–Altman plot. Importantly, all reliability estimates used here indicate a higher reliability of infarct volumetry with a software-assisted approach. The meaning, advantages, and disadvantages of reliability estimates are described elsewhere.³⁷ In summary, as Rankin and Stokes³⁸ pointed out, there is no reliability estimate which can be applied universally. Thus, we decided to show three different parameters of reliability, the intraclass-coefficient (ICC), the WSCV as well as visual inspection of Bland–Altman plots (the latter only for test-retest reliability). The confidence intervals of all parameters analyzed indicate a strong increase of reliability by using a macro. Test-retest reliability reflects the consistency of results and therefore validity of any experiment. In addition to test-retest reliability, inter-rater reliability gains of importance if studies are supposed to be reproduced by other research groups or in the case of translational multi-center studies.

To demonstrate the impact of test-retest reliability, we evaluated the infarct volumetry in studies published in 2015 (Table 3, for details see supplemental method 2). As our data indicates, statistical power has improved in our selection of studies as compared to former analyses of post hoc power in experimental stroke research.⁵ However, only a minority of the analyzed studies conducted an a priori sample size calculation. This is in line with a recent comparative analysis of in vivo research showing that the prevalence of sample size calculation has been extraordinary low with 0.7% and was not associated with the impact factor.¹⁴ We did not investigate publication bias or the likelihood of excess significance. Nonetheless, the remarkably large effect sizes and the fact, that only one of the studies published a non-significant result, suggest a high risk for such biases and therefore inflated effect sizes.^39,40

Table 3.

Pooled parameters derived from results from published studies in 2015, used for systematic analysis.

	Number of animals	Infarct size (relative to control)	CV	Effect	Cohens’ d	Post hoc power
Control	8	1	0.3	0.4	1.33	0.65
Treatment	8	0.60	0.5

An obvious consequence of low reliability is its effect on the precision of the observed effect. Figure 4(a) shows the extent to which the reliability of the manual measurement affects the deviance of observed effects from the true distribution of an effect of 0.4 due to measurement error.

Furthermore, we analyzed the p-values of the simulated tests, as it is common practice to interpret the “level of significance” as a “weight of evidence,” a problem which is controversially discussed in science.⁴¹ Supporting this controversy, our simulation shows that the distribution of the simulated tests’ p-values is spread among all different levels of significance although the effect is large (0.4). The main reason for the inaccuracy of a single p-value is again the sample size; however, as Figure 4(b) shows, a decrease of measurement error decreases the likelihood of receiving a non-significant p-value by 50%.

In reality, investigators do not know the true distribution of their values we predefined here by using pooled parameters from literature. Only the results of one single experiment with two different experimental groups are available for analysis under the assumption that they represent a random sample of a larger population. The imprecision of a method increases the likelihood of false-positive large effects, e.g. to detect an effect of 0.4 although it is actually 0.2 (Figure 4(c)), a problem which is not considered in the usual power calculation. The true, but smaller effect could not only be discussed as clinically non-relevant (as a benchmark: clinical trials on mechanical revascularization in stroke have shown a reduction in infarct volume of 58%) but again has the consequence that the power calculation is too optimistic (Figure 4(d)) and hence reproducibility is very difficult, an effect described as “the winner’s curse.”^42,43 Importantly, the studies in our systematic analysis were severely underpowered to detect such small effects at the significance level of α ≤ 0.05 (Figure 4(d)). On the other hand, a true effect of 0.4 might be lost in noise by measurement error, if the result only depends on one experiment in which the comparison of means indicates an effect of less than 40%.⁴⁴

In order to improve statistical power, one has to decide either to compensate low reliability by an increase of sample size (with the required sample size following the relationship n’ = n/reliability) or to improve the reliability of the test.^45,46 As the error of the method of volumetry can be seen as additive random error which increases the SD, the higher SD obtained with manual measurements results in a lower power. The correction of the SD for this measurement error (reliability = 1.0) leaves the true sample SD. A measurement method with perfect reliability would result in a decrease of the required sample size to achieve a power of 80% or a higher power for a given sample size. Interestingly, even with perfect reliability (r = 1.0), the number of animals per group to detect an effect of 40% would have been n = 9 instead of average n = 7.6 obtained in our literature analysis. Moreover, with the manual measurement, a power of 80% would have been achieved with as much as 12 animals per group (Figure 4(d)).

Although we did not investigate a relationship between experience of the rater and reliability, for a single center study, the hypothetical alternative to the analysis with a software-assisted approach of infarct volumetry would be a single highly trained rater who repeatedly measures the same infarcts. However, the very time consuming training of a rater would have to be comprehensible and replicable for the scientific community and it is unclear whether such a training effect would be stable over time. Even with replicates it is impossible to detect and control for all cognitive biases which arise by the human decision making process of defining the ischemic area in each single measurement.

This study was not designed to investigate the effect a software-assisted approach of infarct volumetry has on systematic, confirmatory bias. Confirmatory bias can both increase the reported effect as well as decreasing it (reverse bias). The relevance of this bias increases with decreasing measurement error. In translational stroke research, systematic factors like the lack of reporting of the drop-out of dead animals⁴⁷ and insufficient blinding might be of importance. Importantly, the advantages of an automatic infarct volumetry we show here are independent of a lack of factors like insufficient blinding. In order to reduce the likelihood of some aspects of confirmatory bias, we recommend journals favor the publication of the raw data as it was done in a recently published preclinical RCT,¹⁵ allowing the research community to quickly reanalyze the data, easily done by using the macro published here.

In summary, our data clearly demonstrate that low reliability of infarct volumetry directly effects the observed variance by increasing measurement error. The increased variance in turn decreases power and precision. Therefore, improvement of reliability of infarct volumetry reduces required sample sizes substantially, enabling satisfying statistical power with realistic sample sizes and therefore may contribute to an important reduction in study cost and time, as well as the reproducibility of promising experimental stroke studies. Additionally, a reduction of sample sizes by such a simple improvement of reliability avoids unnecessary suffering of animals from these very large infarcts.⁴⁸

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: We acknowledge the support of the German Research Foundation (SFB 1039), the Leducq Foundation (Sphingonet, to W. Pfeilschifter) and the Else Kröner Fresenius-Stiftung (Translational Research Innovation Pharma graduate school, Dr. Hans Kröner Graduiertenkolleg).

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Authors’ contributions

FF, RB, KD, and WP designed the experiments, FF and RB performed the analysis and FF, RB, WP, PK, and ArL wrote the manuscript. AlL and RV performed MCAOs. FB, MB, JC, YK, HK, SL, RS, KS, and LS performed measurements of infarct sizes.

Supplementary material

Supplementary material for this paper can be found at http://jcbfm.sagepub.com/content/by/supplemental-data