An Interoperable Similarity-based Cohort Identification Method Using the OMOP Common Data Model Version 5.0

Abstract

Cohort identification for clinical studies tends to be laborious, time-consuming, and expensive. Developing automated or semi-automated methods for cohort identification is one of the “holy grails” in the field of biomedical informatics. We propose a high-throughput similarity-based cohort identification algorithm by applying numerical abstractions on electronic health records (EHR) data. We implement this algorithm using the Observational Medical Outcomes Partnership (OMOP) Common Data Model (CDM), which enables sites using this standardized EHR data representation to avail this algorithm with minimum effort for local implementation. We validate its performance for a retrospective cohort identification task on six clinical trials conducted at the Columbia University Medical Center. Our algorithm achieves an average area under the curve (AUC) of 0.966 and an average Precision at 5 of 0.983. This interoperable method promises to achieve efficient cohort identification in EHR databases. We discuss suitable applications of our method and its limitations and propose warranted future work.

Introduction

Computational reuse of electronic health records (EHR) promises to accelerate biomedical discoveries [1, 2]. Identification of patients with certain phenotypes or meeting a set of eligibility criteria using the EHR supports numerous applications, including study recruitment, phenotype modeling, comparative effectiveness research, and so on. Many methods have been developed for EHR-based cohort identification [3]. Clinically supervised rule-based algorithms have been used for cohort identification. However, this school of methods is laborious and lack scalability [4], and hence often fails to facilitate efficient study recruitment, especially for multi-site studies [5]. There is a need for unsupervised and data-driven approaches to improve the efficiency and cost-effectiveness of cohort identification for clinical studies [6]. Machine learning methods for cohort identification have been developed, including discriminative techniques, [7] such as support vector machines (SVM) [8] and Random Forests [9]. Their major limitation is their requirement of using controls in addition to cases for algorithm training, because getting a reliable set of controls to train a cohort identification algorithm is equally tedious and challenging as is defining cases.

The use of case-based reasoning or similarity-based approaches [10, 11], which starts with only a handful of cases to identify other similar cases, is a promising alternative. Case-based reasoning (CBR) has previously shown success in identifying cohorts for clinical trials [12], in identifying treatments for patients of Alzheimer’s Disease [13], in healthcare planning [14], health event predictions [15], and pharmacovigilance [16]. Learning from past patients that are similar to a patient of interest has also been identified as a tool to guide clinical care at the point of care [17]. A related study identified similarities between patient treatment event series to perform patient trace identification and anomaly detection [18]. The method is primarily promising for identifying patient cohorts that have similar health event series over a large time period. Cohort identification for clinical studies, however, requires the identification of patients who are similar to each other at a certain point in time, in particular, the time of recruitment for clinical studies. This article focuses on building a time-specific CBR-based cohort identification algorithm. CBR approaches bypass the difficulty in transforming eligibility criteria to EHR-compatible rules and are immune from EHR database terminology heterogeneity and data quality imperfections, which often impede other cohort recruitment methods [19]. Prior studies using CBR for cohort identification have largely ignored the numerical details present in different data types in the EHR to build relatively simple CBR models. For example, Kopcke et al. used only diagnosis and procedure codes for cohort identification while ignoring clinical laboratory variables [9]. Miotto et al. used simplified abstractions of all data types (i.e., either presence or absence or averages) as predictors of potential cases [12].

To address the limitations in these methods, this study aims to support similarity-based cohort identification by using numerical abstractions of all major structured data in the EHR, i.e., patient demographics, diagnoses, medications, laboratory results, and procedures. EHR data is highly time-dependent and often consists of a large amount of complex longitudinal data [20]. EHR data also suffer from biases, incompleteness, and representational heterogeneities across institutions [6, 21]. Hence, appropriate preprocessing, abstraction, and summarization of EHR data [22, 23] are indispensable prior to the application of cohort identification algorithms. Methods for data abstractions have been used to build similarity-based personalized patient prediction models [24, 25]. However, prior similarity-based personalized prediction and cohort identification systems were not based on a widely adopted common data standard and hence have limited interoperability with heterogeneous clinical databases [3]. If a cohort identification algorithm developed at one institution needs to be reused at another institution, data extraction and transformation need to be redeveloped anew. This process is costly and can introduce interpretation variations.

To further enhance CBR-based recruitment methods, this study contributes a CBR-based approach that does not define rules for patient search but uses a set of seed cases to automatically train a similarity-based patient matching algorithm. This study makes three major contributions. First, this method uses numerical abstractions of EHR data in order to achieve more precise cohort identification than an earlier method [12]. Second, this method uses a scalable approach for data preprocessing and abstraction, which is independent of the heterogeneities, discrepancies, and incompleteness of EHR data. Third, our method employs the Observational Medical Outcomes Partnership (OMOP) Common Data Model (CDM) [26] standard, which is widely adopted by the Observational Health Data Sciences and Informatics (OHDSI) [27] community, to represent EHR data in this shared information model and to enable the interoperability between this cohort identification method and heterogeneous EHR databases.

Material and methods

Dataset

We assess the use of our algorithm in a recruitment task for six clinical trials in conjunction with Columbia University Medical Center’s Clinical Data Warehouse (CDW). Trials are chosen on the basis of their sample sizes. Specifically, trials that have at least 100 enrolled participants, or cases, in the EHR, are selected for this study. The trials used, their trial identification numbers, start and end dates, and the number of previously identified cases with EHR data are shown in Table 1.

Table 1.

Clinical trial identification numbers, trial conditions, start and end dates, and the number of previously identified cases (or trial participants) in the EHR, for the six clinical trials used in this study

Trial NCT ID	Condition	Start Date	End Date	No. of available cases in the CDW
T1: NCT00995150	Contraception	November 2009	December 2021	139
T2: NCT00831116	Myocardial Infarction, Angina, Coronary Artery Disease, Myocardial Ischemia	February 2009	November 2016	463
T3: NCT01019369	Contraception	March 2010	November 2012	133
T4: NCT02033694	Coronary Artery Disease,Atherosclerosis	January 2014	March 2018	148
T5: NCT00530894	Critical Aortic Stenosis	April 2007	March 2017	294
T6: NCT01314313	Symptomatic Severe Aortic Stenosis	March 2011	September 2020	562

The gold standards for training and validating our algorithm are the set of enrolled participants for these six trials (shown in the last column of Table 1), who have all been manually confirmed by clinical research coordinators. We also use a random sample of 30,000 unknown patients in the EHR, who were not enrolled in any of these six trials, in the evaluation of our method.

Data collection and processing

We use patient demographics, laboratory results, conditions, medications, and procedures as features for our cohort identification algorithm. Age, gender, laboratory results, conditions, medications, and procedures were extracted using the OMOP CDM version 5 data standard. The OMOP CDM [28] is a relational data model, centered at the patient, which contains demographics, clinical observations, observation periods, drug exposure, condition occurrences, procedures, and visits mapped to a standard vocabulary from a host of disparate source vocabularies. The source vocabularies range from Health Level 7 (HL7) [29], Office of Management and Budget (OMB) codes [30], and Center for Disease Control and Prevention (CDC) [31] codes for demographics, International Classification of Diseases (ICD) 9, ICD 10 [32], and Systematic Nomenclature of Medicine-Clinical Terms (SNOMED-CT) [33] for conditions and procedures, Logical Observation Identifiers Names and Codes (LOINC) [34], United Codes for Units of Measure (UCUM) [35] codes, and SNOMED-CT codes [33] for observations, and the Cerner Multum Lexicon Drug Database [36], and National Drug Codes (NDC) [37] for drugs. In addition to these codes, institution specific source vocabularies (e.g., Medical Entities Dictionary (MED) [38] which is a repository of concepts used at the New York Presbyterian Hospital including the Unified Medical Language System (UMLS) [39], ICD 9 Clinical Modification (ICD-9-CM) [32], and LOINC [34]) also map to the standard OMOP vocabulary at the institution level. For our study, age (at the start of the trial) and patient gender (male or female) constitute patient demographics. Distinct laboratory tests are identified by the source MED [38] code, and medical conditions are defined by the source ICD 9 codes [32] assigned to the patients in the enrollment window of each trial. Patient medications are defined by either the MED [38] or the NDC [37] codes assigned to the patient during the enrollment window of the trial. Patient procedures are defined by the ICD 9 [32] and Current Procedural Terminology (CPT) codes [40] assigned to the patient during the enrollment window of the trial. We use the source vocabularies at our site to identify EHR data types due to incompleteness in the source vocabulary to OMOP vocabulary mapping at our site. However, we develop queries that are generalizable to the complete mapped OMOP vocabulary at any OMOP CDM v5 database. We make the associated source and OMOP concept-based queries available as an R package in the following Github repository:

https://github.com/scdbmi/StudyProtocolSandbox/tree/master/phenotypeDataExtraction

The conceptual framework for similarity-based cohort identification

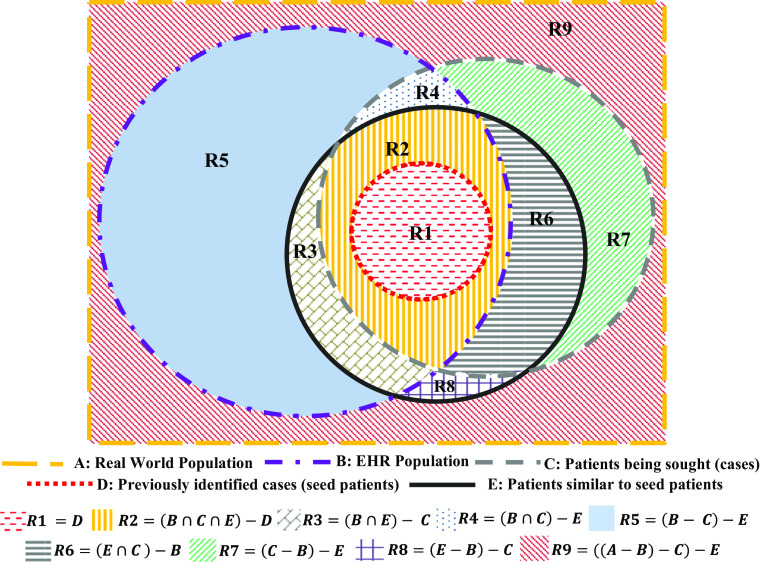
The populations that are typically associated with a clinical cohort identification task are illustrated by the Venn diagram in Fig. 1. The boundaries of the various shapes in Fig. 1 denote particular populations and are labeled by bold capital alphabets shown in the legend. Population A represents the universe of all patients. Population B represents patients that are recorded in the EHR of a particular institution. Population C consists of patients being sought (cases). Population D represents patients who have previously been identified as cases and are also present in the EHR. This population represents seed patients for the cohort identification task. In reality, population C is often not well defined due to the ambiguity and complexity of EHR-based phenotyping algorithms [4] and clinical study eligibility criteria [19]. Identification of population C requires a lot of manual effort in transforming these poorly defined eligibility criteria to EHR-compatible phenotyping rules. Similarity-based cohort identification methods aim to bypass this problem by identifying a population E to represent patients who are similar to the seed patient population D. This population E then represents potential cases for the cohort identification task at hand. It should be noted here that similarity between two populations is defined later in this article in terms of the cosine distance between feature representations of the respective populations (Eq. (2)).

Fig. 1.

Populations and sub-populations associated with a cohort identification task: a similarity-based cohort identification algorithm uses the seed patient population D to identify new cases in sub-populations R2 and R3

These populations partition A into various sub-populations shown with different colored patterns in Fig. 1. Next, we describe the characteristics of each of these sub-populations denoted by R1, R2,…, R9. The operator “−” here denotes the set difference operator. Thus, for any two populations Y and Z, Y − Z represents all members of Y that are not members of Z.

R1 = D represents patients who are known to be cases and have EHR data. These patients are the seed patients to be used for similarity-based identification of more potential cases.

R2 = (B ∩ C ∩ E)  − D represents patients in the EHR who are similar to previously identified cases and are also actual cases that have not yet been identified (so that they do not yet belong to R1). This is the sub-population that our algorithm will help identify. Thus, R2 represents the true positives of our algorithm.

R3 = (B ∩ E) − C represents patients who are similar to previously identified cases but are not cases. This represents the false positives of our algorithm.

R4 = (B ∩ C) − E represents patients in the EHR who are not similar to previously identified cases but who are actually cases. This represents the false negatives of our algorithm.

R5 = (B −  C) − E represents patients in the EHR who are not similar to previously identified cases and are not cases. This represents the true negatives of our algorithm.

R6 = (E ∩ C ) − B represents patients who would be similar to previously identified cases (if their records were available) and who are cases but who do not have data in the EHR.

R7 = (C −  B) − E represents patients who are cases but are not in the EHR and would not be similar to previously identified cases (if their records were available).

R8 = (E − B) − C represents patients who would be similar to previously identified cases (if their records were available) but would not be cases and are not in the EHR.

R9 = ((A − B) − C) − E represents patients who would not be similar to identified cases (if records of their phenotypic traits were available), would not be cases, and are not in the EHR.

EHR-based cohort identification algorithms disregard R6, R7, R8, and R9, as these patient sub-populations do not have EHR data. However, these sub-populations are defined here for the completeness of the Venn Diagram shown in Fig. 1. A similarity-based cohort identification algorithm uses the seed sub-population of patients, R1, to identify new patients falling into regions R2 and R3. A manual review by clinicians will then follow to screen patients in R2 and R3 and verify how many of these patients are true cases, i.e., R2. All the patients classified into R4 are true controls if the algorithm has 100% negative predictive value. Therefore, an ideal similarity-based cohort identification algorithm should maximize the sensitivity and specificity until the recruitment target for the cohort identification task is reached [41]. The errors associated with a similarity-based cohort identification algorithm can be defined as follows:

• Type I error: members in R3 who are falsely identified as cases (false positives)

• Type II error: members in R4 who are not identified as cases (false negatives)

The evaluation metrics for a similarity-based cohort identification algorithm are defined below.

Precision = R2/(R2 + R3), which measures the fraction of patients identified by the cohort identification algorithm that are true cases.

Sensitivity = R2/(R2 + R4), which measures the ability of the similarity-based algorithm to identify true cases.

Specificity = R5/(R3 + R5), which measures the ability of the similarity-based algorithm to identify true controls.

Accuracy = (R2 + R5)/(R2 + R3 + R4 + R5), which measures the ability of the similarity-based algorithm to recognize cases and controls.

It should be noted that this similarity-based cohort identification algorithm is not exhaustive in its recommendation of all possible cases but only suggests a list of patients who are similar to known cases. The patients recommended by the algorithm are “potentially eligible” [41] for the cohort identification task at hand and need to then be reviewed by a clinical researcher in order to find true cases among them. This approach is designed to recommend “worthy review” candidates to clinical researchers. Without the use of our method, clinical researchers would have to perform chart reviews for patients in R2, R3, R4, and R5 to find potential cases. In contrast, our algorithm enables researchers to focus on patients that are in sub-populations R2 and R3, which significantly reduces the manual burden and expedites the cohort identification task.

Algorithm design

We train our algorithm using half of the cases for each trial and test it using the other half of the cases and the 30,000 randomly selected patients. These form the training and test sets, respectively.

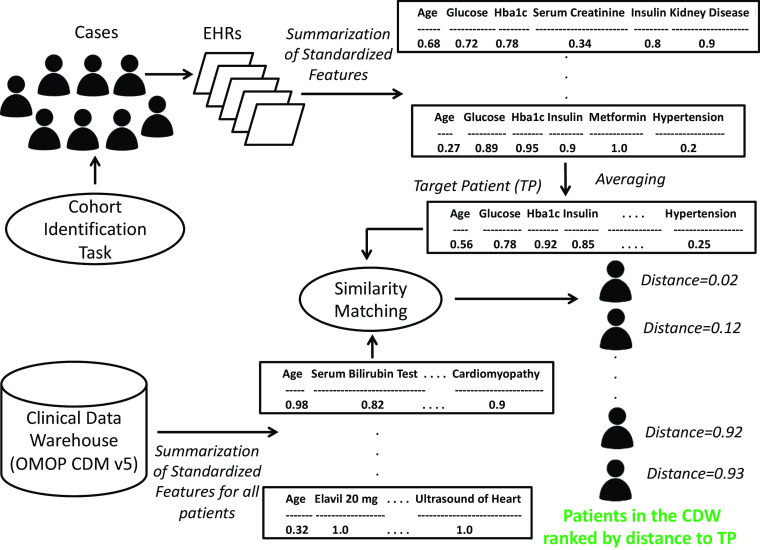
The similarity-based cohort identification algorithm is demonstrated in Fig. 2. We formally define our similarity-based cohort identification algorithm as follows:

1. Extract records of demographics, laboratory results, conditions, medications, and procedures for all training and testing patients from the CDW, using the standardized OMOP CDM v5 data standard.

2. For each patient, we create a patient feature vector (Fig. 2), which contains a scaled summary of each demographic, laboratory result, condition, medication, and procedure that the patient has. To address data incompleteness and different numbers and scales of readings present for each patient, we summarize and normalize all data types for each patient as follows.

   • (2.1)
     First, we summarize all data types for each patient using the following metrics:

     1. Each laboratory test for a patient may contain one to multiple readings within the enrollment window of a trial, and various approaches exist for summarizing laboratory measurements independent of time [42]. Median has been shown to be one of the more robust and stable estimates of central tendency, as compared to other measures such as the mean [43, 44]. Hence, we use the median of the laboratory results instead of other non-robust statistics such as the mean, most recent measurement, all of which are highly susceptive to noise and statistical outliers [44]. Laboratory results are also sparsely represented in the EHR; just the presence or absence of a lab test is often an important indicator for a patient’s condition and is used in addition to its median (if present).
     2. Each medical condition is summarized by the number of times a patient has a certain diagnosis code prior to the enrollment end date of the trial.
     3. Each medication is summarized by the number of times a patient is exposed to a particular medication within the enrollment window of the trial.
     4. Each procedure is summarized by the number of times a patient underwent a certain procedure during the enrollment window of the trial.
   • (2.2)
     Secondly, we normalize all summarized features to a unit scale between 0 and 1. This is done to ensure that all features are on the same arithmetic scale prior to additional computation and similarity-based comparison.

Fig. 2.

Method for building the target patient for a cohort identification task using the summarized EHR traits for n previously identified cases and using it to rank patients in the CDW based on similarity to the target patient; this figure shows the summarized and normalized feature vectors for different patients as well as for the target patient

Following steps (2.1) and (2.2), we obtain a normalized and summarized patient feature vector for each patient, which is shown in Fig. 2.

• (3)Perform feature selection. Features which are present for at least 50% of training patients are selected to be included in the target patient representation derived in the next step, such that number of features does not fall below a value of ε. ε was empirically found to be 30 for our experiments. If this feature selection step causes the number of features to fall below ε, then only features that are present for a non-trivial number of training patients are selected to be included in the target patient. We perform feature selection, because the number of features that are present across all training patients is very large, and including all of them in our classification and ranking methods would cause overfitting due to the curse of dimensionality problem that affects high-dimensional statistical models [45].
• (4)Find the mean of the normalized feature vectors, aggregated by feature, over all training cases. When computing the mean across all training cases, if a feature is not present for a particular case, then it is assigned a value of 0 for that case, prior to computing the mean of that feature across all cases. The Target patient, TP, is defined as follows:

$$\mathit{TP}=\left[\frac{1}{n}\sum _{m=1}^n{T}_{m1}\frac{1}{n}\sum _{m=1}^n{T}_{m2}\dots \frac{1}{n}\sum _{m=1}^n{T}_{\mathit{ml}}\right]$$ 1

where T _m1 , T _m2 ,  … T _ml, are the normalized l features for the m ^th training case. Each of the l features is averaged across the n training cases to obtain the target patient.

• (5)For each patient in the test set of a trial, find the cosine distance of its normalized feature vector to the target patient’s feature vector, obtained in step 4 [46], i.e., find |T _i − TP|, where T _i ,  i = 1 , 2 , 3 … s are the normalized feature vectors for the s testing patients and TP is the target patient’s feature vector. If a feature is not present for a particular test patient but exists in the target patient’s feature vector, then that particular feature is assigned a value of 0 in the test patient’s feature vector, prior to computing the cosine distance. Since the target patient represents the gold standard for a particular cohort identification task, if a feature is not present in the target patient’s feature vector but is present in a test patient’s feature vector, then that feature is removed from the test patient’s feature vector prior to computing the test patient’s cosine distance to the target patient.
• (6)
  Classification:

  • (6.1) Classify a patient as eligible if his or her cosine distance to the target patient of the trial is less than a certain threshold, i.e.,

$$\left|T_i-\mathit{TP}\right|<P_t\left(\left|T_{\forall i}-\mathit{TP}\right|\right)\mathrm{for}i=1,2,3\dots s,$$ 2

where P _t(|T _∀i − TP|) is the t ^th percentile of cosine distances of all testing patient vectors to the target patient vector TP. The symbol ∀i represents “for all i”.

• (6.2) Vary t in Eq. (2) over different values from 0 to 100, in steps of 1, to plot the Receiver Operating Characteristic (ROC) curve. The optimal value of t is obtained from this ROC curve, and the area under the curve (AUC) is the AUC computed for this optimal value t. P _t(|T _∀i − TP|) for the optimal value of t then represents the optimal cosine distance to the target patient.

• (7)
  Ranking:

  • (7.1) Rank the s patients in the test set in ascending order of cosine distances computed in step (5). The higher up a patient is in this list, the more similar the patient is to TP and the more likely the patient is to be a case for the trial.
  • (7.2) Evaluate this ranked list of patients using evaluation measures discussed in Section 3.4 (2).

We make all our MATLAB software developed for this algorithm available at the following github repository:

https://github.com/scdbmi/Similarity-based-Cohort-Identification

Algorithm evaluation

The evaluation of our method is done using the testing set for each trial, and the results reported in Section 3, Table 2, Table 3, and Fig. 2 are obtained using only this testing set for each trial, consisting of 30,000 randomly selected EHR patients and half of the cases for each trial. The eligibility statuses of these 30,000 randomly selected EHR patients are unknown, but we make the assumption of ineligibility for these patients and use them to compute the ROC curves and the AUC. Our assumption is based on the fact that these patients were not selected by clinical research coordinators for recruitment after their manual search for eligible patients in the database. The precision metrics computed for our method (described in (2) below), however, do not make any assumptions for these 30,000 patients and are thus, more accurate measures of evaluation for our algorithm. We evaluate the performance of our cohort identification algorithm using the following metrics.

1. Classification performance metrics

Table 2.

Trial wise and average classification results: AUC scores and corresponding optimal threshold on the cosine distance to TP for the classifier

Trial	Optimal AUC	Optimal threshold on the Cosine Distance to TP
T1	0.999	0.993
T2	0.999	0.937
T3	0.795	0.949
T4	0.999	0.944
T5	0.999	0.978
T6	0.999	0.946
Average	0.966	0.958

Table 3.

Trial wise and average ranking results: precision at k (k=5, 10, 20, 30), MAP, and MRR scores

Trial	P5	P10	P20	P30	MAP	MRR
T1	1.000	1.000	1.000	0.830	0.526	1.000
T2	0.900	0.950	0.800	0.717	0.304	1.000
T3	1.000	1.000	0.950	0.870	0.526	1.000
T4	1.000	0.900	0.800	0.683	0.555	1.000
T5	1.000	1.000	1.000	1.000	0.631	1.000
T6	1.000	1.000	1.000	0.983	0.856	1.000
Average	0.983	0.975	0.925	0.847	0.566	1.000

The ROC curve is used to determine the optimum value of t in Eq. (2) for each cohort identification task. The AUC for this optimal cosine distance represents the AUC for each trial.

• (2)Information retrieval performance metrics

Precision at k, which represents the fraction of true positives in the top-k of the ranked list of test patients, is used to evaluate the ranking performance of our algorithm. We use four values of k, namely, k = 5, k = 10, k = 20, and k = 30. The second metric of evaluation we use is the mean average precision (MAP) which is the average of the precision evaluated at each index of the ranked list where a patient is correctly identified [12]. Finally, the mean reciprocal rate (MRR) represents the inverse of the rank of the first correctly identified patient [12].

• (3)Robustness metric

We conduct one-way analyses of variance (ANOVAs) [47] to evaluate the robustness of our cohort identification algorithm to changes in (1) the condition that is being studied by the cohort identification task and (2) the number of cases used to train the algorithm. For these comparisons, the significance level α is selected to be 0.05.

Results

The performance of our algorithm for each of the six cohort identification tasks, i.e., the six clinical trials listed in Table 1 is reported in this section.

1. Classification performance measure:

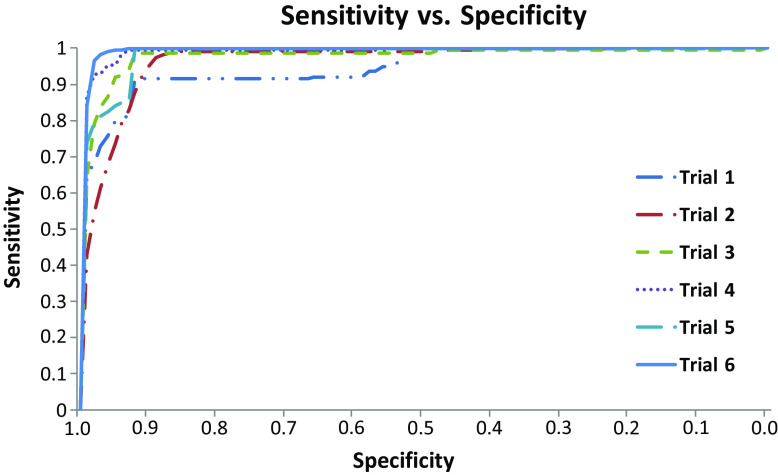
Table 2 shows the optimal AUC and the optimal cosine distance that it corresponds to, for each of the six clinical trials evaluated in this study. It can be seen that with the exception of T3, an optimal AUC of almost 1 is achieved for all the trials. The sensitivity versus specificity curves, obtained by varying the threshold t (in Eq. 2) from 0 to 100 in steps of 1, for the six trials are shown in Fig. 3.

• (2)Information Retrieval Performance Measures:

Fig. 3.

Sensitivity versus specificity plots for the six trials, plotted for various thresholds on the cosine distance from the target patient TP (t in Equation (2) varied from 0 to 100, in steps of 1)

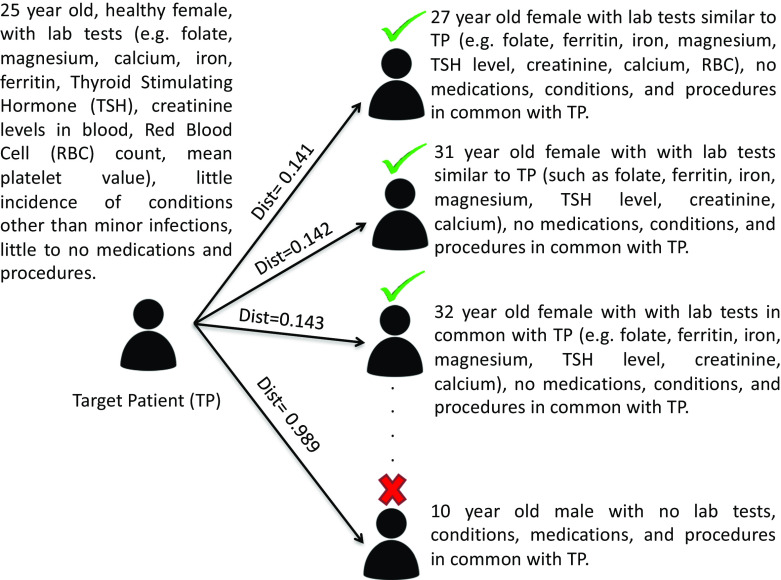
Table 3 shows the information retrieval performance metrics for each of the six testing trials. The average Precision at 5 (P5), Precision at 10 (P10), Precision at 20 (P20), Precision at 30 (P30), MAP, and MRR across the six trials are 0.983, 0.975, 0.925, 0.847, 0.566, and 1.000, respectively. Figure 4 shows an example of how the similarity matching algorithm ranks patients based on the target patient for Trial T1, which is an intrauterine contraception trial accepting healthy women of ages 16–45 years at enrollment [48]. The higher up a patient is in the ranked list and the lower its distance from the target patient, the more phenotypically similar the patient is to the target patient.

• (3)Robustness:

Fig. 4.

An example of the similarity based ranked list of test patients obtained using the target patient representation derived for Trial 1; the term 'dist' here refers to the cosine distance. The patients marked with a green tick and a red cross would be deemed similar and dissimilar to the target patient respectively

Both the factors, namely the trial condition and the number of cases used to train the cohort identification algorithm, demonstrated non-significant influences on each of the performance metrics, i.e., AUC, P5, P10, P20, P30, MAP, and MRR. In other words, a one-way ANOVA resulted in a p value > 0.05 for each influence-metric pair.

Discussion

Applications and merits of our method

The cohort identification framework proposed here helps identify patients being sought by performing a similarity-based matching to previously identified cases. We demonstrate the usefulness of our method for a specific application of cohort identification, namely, clinical trial recruitment. In comparison to a previous study on similarity-based clinical trial eligibility screening that does not use numeric summaries of the EHR data types [12], our method enables an improvement in performance of 136.87 and 200.93% for the precision at k (k = 5, k = 10) metrics, and of 39.47% for the MRR metric.

A practical application of this algorithm in a cohort identification setting would be to use the set of cases as and when they become available to train our cohort identification algorithm. An alert system can then be implemented in the EHR so that whenever our method identifies a potential case, a clinical researcher is alerted to perform a review of the recommended patient. In a real-time cohort identification setting, the threshold parameter (t in Eq. (2)) in our patient identification algorithm can also be tuned to meet the recruitment needs. This threshold can be increased if a large number of patients have to be recruited and decreased otherwise.

The target patient representation that we use can be trained on as few as one identified case. Despite this important advantage of using the target patient representation, it should be noted that using only a small number of training cases is likely to lead to poor performance in cohort identification. The larger the number of cases, the better would be the performance of this method. However, practical recruitment constraints may often limit the number of cases available for training. In such a situation, the advantage of our method over other standard machine learning approaches becomes salient. As described in Miotto et al. 2015, it is worth noting that in comparison to other classifiers, our method is the most cost-effective as it relies on the storage and use of only a target patient summary representation for each cohort identification task based on formerly identified cases [12].

One advantage of this algorithm is that it is implemented using the OMOP CDM v5 [26], which makes it interoperable with other CDM-compliant databases developed by the OHDSI consortium [27]. This can save researchers the tedious effort of transforming site-specific cohort identification algorithms to the data terminologies being used at the researcher’s site. This will also help validate our proposed cohort identification algorithm at other sites that are part of the collaborative OHDSI network. We make all the software developed for data extraction and algorithm implementation available to researchers, who can apply our algorithm to cohort identification tasks at their site.

Caution in the appropriate use of our method

The representativeness of the cases used to train our cohort identification algorithm heavily biases the selection of new potential cases for the task. For example, if the training cases are all female, then all recommended potential cases will also be only female and may not be representative of the target population. In other words, if the identified cases are already biased towards certain population subgroups, our methods will only amplify this bias. Thus, the choice of a representative and unbiased set of cases to train our cohort identification model is vital to using patient similarity for selecting new potential cases that are well representative of the target population for the cohort identification task. The number of previously identified cases whose data is used to train our cohort identification model also affects the goodness of our model. The larger the number of previously identified cases used to train our model, the better our model will perform in the cohort identification task.

On the other hand, a largely heterogeneous population of cases can also compromise the usefulness of similarity-based cohort identification methods. It remains unknown if identified cases for a cohort identification task will be homogeneous enough for modeling a target patient and for finding potential cases. This is particularly problematic for clinical study recruitment tasks, as clinical trial participants have been shown to often be heterogeneous [49]. Therefore, similarity-based methods for clinical trial recruitment may have unaccounted sources of variance due their implicit assumption of homogeneity. In such a situation, a heterogeneity or subgroup analysis would need to be performed in order to reveal how many participant subgroups exist in the previously identified cases, or the seed patients. Such an analysis can then inform the design of more sophisticated similarity matching techniques that would take these subgroups into account, instead of assuming a homogeneous set of previously identified cases.

Finally, the similarity-based cohort identification method proposed here aims to maximize the recall of the cohort identification task, without much regard for precision. Thus, the aim of a similarity-based cohort identification task is to maximize the number of cases being recommended by the algorithm, so that these cases can then be reviewed by clinical researchers and the recruitment targets for a cohort identification task be reached on time. However, there may also be a number of false positives among the recommended cases. Thus, any clinical researcher who wishes to use our method for precise cohort identification should ensure that a manual review follows the use of our algorithm in order to find the true positives among all the cases being recommended by our method and use only the true positives for the clinical research that the cohort identification task is designed for. Moreover, this similarity-based algorithm performs better with the inclusion of continuous data types (e.g., laboratory results), and clinical researchers using this algorithm are recommended to include these numerically rich data types for more precise cohort identification (whenever available).

Limitations and future work

This study has multiple limitations. The first limitation is the relatively small number of cases used in the training and evaluation of this method. The seed patients had to be confirmed by clinical trial coordinators for the selected studies so that our study was constrained by their availability. The set of cases (Population D in Fig. 1 ) may also have been biased towards population sub-types due to unknown recruitment constraints. The small number of cases not only limited and potentially biased our training data set but also limited the sophistication of the target patient representation to a simple mean of all training patients. A larger number of cases would enable us to use more sophisticated distribution fitting approaches [50]. In the future, we would like to use a larger and more representative sample to serve as the gold standard (true cases). For this, we need to measure the representativeness of populations enrolled in clinical studies. This will be an extension of our work on quantifying clinical study eligibility-based representativeness [51].

Moreover, we used a randomly selected unknown EHR patient sample to evaluate our algorithm, because we did not have access to true controls. Some of these randomly selected unknown EHR patients may be eligible cases for the cohort identification task, and this will create a bias in the evaluation strategy used here. One way to address this in the future would be to perform a manually review to derive controls. Use of true controls will help us evaluate our algorithm using measures such as recall, specificity, and accuracy, in addition to the measures of precision used here.

Since our method currently uses only structured phenotypic traits, our method might not help clinical studies that rely heavily on clinical features available in free-text clinical notes, such as the “ability to run 5 miles on the treadmill” or “family history of breast cancer”. In the future, we would like to extend our similarity-based cohort identification algorithm to include unstructured free-text clinical notes to address this limitation.

In our experiments reported here, we use only the Columbia University Medical Center’s CDW as our EHR source. Routine clinical data, such as those recorded in EHRs are collected primarily for clinical and billing purposes, and reuse of this type of data for research should always be treated with caution, and our data set is no exception. There are often severely limiting data quality issues with the EHR, such as missing values, sampling biases, and incorrectness [52, 53], and this invariably implies that a certain margin of error exists in research using EHRs. In the future, we plan to validate our algorithm using EHRs at other sites that are part of the collaborative OHDSI framework [27]. We also plan to conduct a comprehensive evaluation of the effect of EHR data quality on cohort identification algorithms.

Conclusions

This article proposes a portable high-throughput similarity-based cohort identification algorithm using the OMOP CDM v5 framework. Its performance is promising in selected clinical trials. Validation of our algorithm at other OHDSI sites and a practical evaluation of our method in a real-time cohort identification setting are immediate next steps for this research.

Authors’ contributions

Chunhua Weng designed and supervised the research and edited the manuscript substantially. Shreya Chakrabarti performed data extraction, data analysis, writing, and MATLAB software development for the algorithm. Vojtech Huser developed R software for the OMOP CDM-based data extraction. Anando Sen and David J. Albers contributed to the methods and the manuscript editing. Gregory W. Hruby and Alexander Rusanov contributed to the development of the conceptual framework of this research.

Compliance with ethical standards

Conflict of interest

None.