Conditional Analysis of Multiple Quantitative Traits Based on Marginal GWAS Summary Statistics

Abstract

There has been an increasing interest in joint association testing of multiple traits for possible pleiotropic effects. However, even in the presence of pleiotropy, most of the existing methods cannot distinguish direct and indirect effects of a genetic variant, say SNP, on multiple traits, and a conditional analysis of a trait adjusting for other traits is perhaps the simplest and most common approach to addressing this question. However, without individual-level genotypic and phenotypic data but with only GWAS summary statistics, as typical with most large-scale GWAS consortium studies, we are not aware of any existing method for such a conditional analysis. We propose such a conditional analysis, offering formulas of necessary calculations to fit a joint linear regression model for multiple quantitative traits. Furthermore, our method can also accommodate conditional analysis on multiple SNPs in addition to on multiple quantitative traits, which is expected to be useful for fine mapping. We provide numerical examples based on both simulated and real GWAS data to demonstrate the effectiveness of our proposed approach, and illustrate possible usefulness of conditional analysis by contrasting its result differences from those of standard marginal analyses.

1 Introduction

There is an increasing interest in association analysis of multiple traits with many new tests being recently proposed; see, e.g. He et al. (2013), Jiang et al. (2014), Zhang et al. (2014), Wang et al. (2016), Kim et al. (2016) and Schaid et al. (2016) and references therein. There are two main reasons: one is to increase statistical power and the other is to detect pleotropic effects, which may shed light on underlying biology and for possible repurposing the use of existing drugs. However, as pointed out by Schaid et al. (2016), almost all existing methods test with a null hypothesis of no associated trait, which may be rejected even in the absence of pleiotropy if only one of the multiple traits is indeed associated; they cannot tell whether there is indeed pleiotropy. Accordingly, several methods have appeared to explore which of the multiple traits are indeed associated (Stephens, 2013; Majumdar et al., 2016). In particular, Schaid et al. (2016) proposed a formal testing framework to sequentially test for the number of associated traits. However, even in the presence of multiple associated traits, these approaches cannot distinguish direct and indirect associations. For example, if it is known two traits are associated with one SNP, it is unknown whether one of the traits is a mediator between the SNP and the other trait, the answer to which would be of interest. For this purpose, a conditional analysis would be useful: we can test for possible association between a trait and an SNP by conditioning on all other traits; if the effect of the trait being tested is indirect and solely through some other trait as a mediator, it will not be significantly associated with the SNP in the conditional analysis, though it may be marginally associated with the SNP (without adjusting for other traits) in a standard GWAS analysis. With the availability of individual-level genotypic and phenotypic data, such a conditional analysis is straightforward. However, due to confidentiality concerns or logistic reasons, often we only have summary statistics available from a GWAS or a meta-analysis of multiple GWAS. Most existing association testing methods for multiple traits are applicable only to individual-level data, though a few exceptions exist for marginal analyses (Zhu et al., 2015; Kim et al., 2015; Cichonska et al., 2016; Kwak, & Pan, 2016, 2017). A major contribution here is to extend a conditional analysis of multiple quantitative traits to GWAS summary statistics without individual-level data. Our idea is similar to conditional analysis of a single quantitative trait on multiple SNPs with only GWAS summary statistics (Yang et al., 2012). The difference is that, in our approach we use the GWAS summary statistics to estimate the correlations among the multiple quantitative traits, while in the latter a reference panel of individual-level genotypic data is used to estimate the correlations (LD) among the SNPs. We will also combine the two approaches for a joint conditional analysis of multiple traits and multiple SNPs. The proposed approach will be useful to sort out specific effects of the SNPs in a locus associated with one or more traits, e.g. in fine mapping. It can be also used to infer the causal relationships among multiple quantitative traits as in structural equation modeling (Li et al., 2006).

A caveat of our approach is that we implicitly assume that a set of multiple traits is collected on each subject, as in usual multivariate analyses. However, for GWAS summary statistics, this assumption may not exactly hold due to missing values of one or more traits on some subjects. This can be easily seen from unequal numbers of subjects across the multiple traits for the same SNP in a typical dataset of GWAS summary statistics. The consequence is biased parameter estimation with the bias increasing with the proportion of non-overlapping subjects across the traits. In the extreme case that no more than one trait is collected from any subject, then the multiple traits will be estimated as uncorrelated, implying that a conditional analysis of multiple traits will be equal to marginal analyses on each trait separately. We will use simulations to demonstrate this phenomenon. Finally, we will apply our proposed method to two large GWAS datasets, confirming differences between usual marginal analyses and a conditional analysis.

2 Methods

2.1 Adjusting for One Phenotype

We first consider the simplest case with two traits and a single SNP. Denote the two traits as Y₁ = (y_i1)_n×1 and Y₂ = (y_i2)_n×1, and the additive coding of the SNP as X₁ = (x_i1)_n×1, where n is the number of subjects. We assume that both the two traits and the SNP have been centered so that an intercept is not needed in a regression analysis. Given a dataset of GWAS summary statistics, we have the estimates $\widehat{{\beta }_1},\widehat{{\beta }_2}$ and $\widehat{\text{var}}(\widehat{{\beta }_1}),\widehat{\text{var}}(\widehat{{\beta }_2})$ from a marginal analysis with marginal linear models

$${\mathbf{Y}}_1={\mathbf{X}}_1{\beta }_1+{\mathbf{e}}_1$$

$${\mathbf{Y}}_2={\mathbf{X}}_1{\beta }_2+{\mathbf{e}}_2$$

$${\mathbf{e}}_i~\mathrm{N}(\mathbf{0},{{\sigma }_i}^2{\mathbf{I}}_n)i=1,2$$

Now our goal is to obtain parameter estimates from a conditional analysis with a joint linear regression model

$${\mathbf{Y}}_1=({\mathbf{X}}_1{\mathbf{Y}}_2)\left(\begin{array}{c}\hfill b_1\hfill \\ \hfill b_2\hfill \end{array}\right)+\mathbf{e}$$

where b₁, b₂ are the joint effects, and e~N(0, σ_J²I_n). In particular, b₁ is the parameter of interest, giving conditional association of the SNP with trait 1 after adjusting for trait 2. Based on the ordinary least squares estimator, we have

$$\left(\begin{array}{c}\hfill \widehat{b_1}\hfill \\ \hfill \widehat{b_2}\hfill \end{array}\right)={\left(\begin{array}{cc}\hfill {\mathbf{X}}_1\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{Y}}_2\prime {\mathbf{X}}_1\hfill \\ \hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_2\hfill & \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_2\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_1\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_1\hfill \end{array}\right)$$

$$\widehat{\text{var}}\left(\begin{array}{c}\hfill \widehat{b_1}\hfill \\ \hfill \widehat{b_2}\hfill \end{array}\right)={\left(\begin{array}{cc}\hfill {\mathbf{X}}_1\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{Y}}_2\prime {\mathbf{X}}_1\hfill \\ \hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_2\hfill & \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_2\hfill \end{array}\right)}^{-1}{{\hat{\sigma }}_J}^2$$

where σ̂_J² is the estimated residual variance for the joint model.

σ̂_J² can be calculated as

$${{\hat{\sigma }}_J}^2=\frac{{\mathbf{Y}}_1\prime {\mathbf{Y}}_1-\left(\begin{array}{c}\hfill \widehat{b_1}\hfill \\ \hfill \widehat{b_2}\hfill \end{array}\right)\prime \left(\begin{array}{c}\hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_1\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_1\hfill \end{array}\right)}{n-2}$$

Hence, we only need X₁′X₁, X₁′Y₁, X₁′Y₂, Y₁′Y₁, Y₂′Y₂ and Y₁′Y₂ to estimate the coefficients and their covariance matrix.

We can obtain X₁′Y₁, X₁′Y₂, Y₁′Y₁ and Y₂′Y₂ using the following equations

$$\widehat{{\beta }_1}=\frac{{\mathbf{X}}_1\prime {\mathbf{Y}}_1}{{\mathbf{X}}_1\text{'}{\mathbf{X}}_1}$$

$$\widehat{{\beta }_2}=\frac{{\mathbf{X}}_1\prime {\mathbf{Y}}_2}{{\mathbf{X}}_1\text{'}{\mathbf{X}}_1}$$

$${\widehat{{\sigma }_1}}^2=\frac{{\mathbf{Y}}_1\prime {\mathbf{Y}}_1-{\mathbf{X}}_1\prime {\mathbf{X}}_1{\widehat{{\beta }_1}}^2}{n-1}={\mathbf{X}}_1\prime {\mathbf{X}}_1\widehat{\text{var}}(\widehat{{\beta }_1})$$

$${\widehat{{\sigma }_2}}^2=\frac{{\mathbf{Y}}_2\prime {\mathbf{Y}}_2-{\mathbf{X}}_1\prime {\mathbf{X}}_1{\widehat{{\beta }_2}}^2}{n-1}={\mathbf{X}}_1\prime {\mathbf{X}}_1\widehat{\text{var}}(\widehat{{\beta }_2})$$

where $\widehat{{\sigma }_1}$ and $\widehat{{\sigma }_2}$ are the estimated residual variances for the two marginal models.

Suppose X₂, X₃, … X_m+1 are some other SNPs that do not have marginal associations with both Y₁ and Y₂. Following Kim et al. (2015), if we have the Z-scores Z₁ = (Z_i1)_m×1 for β₁ in the marginal models Y₁ = X_i+1β₁ + e₁, and Z₂ = (Z_i2)_m×1 for Y₂ = X_i+1β₂ + e₂, and if the sample size is large (as usual in GWAS), we can estimate Y₁′Y₂ as $\sqrt{{\mathbf{Y}}_1\prime {\mathbf{Y}}_1{\mathbf{Y}}_2\prime {\mathbf{Y}}_2}\text{cor}({\mathbf{Z}}_1,{\mathbf{Z}}_2)$, since we have

$$\frac{{\mathbf{Y}}_1\prime {\mathbf{Y}}_2}{\sqrt{{\mathbf{Y}}_1\prime {\mathbf{Y}}_1{\mathbf{Y}}_2\prime {\mathbf{Y}}_2}}\approx \text{cor}({\mathbf{Y}}_1,{\mathbf{Y}}_2)\approx \text{cor}({\mathbf{Z}}_1,{\mathbf{Z}}_2)$$

where cor(Z₁, Z₂) is the sample Pearson correlation between the two sets of the Z-statistics Z₁ and Z₂.

When the summary statistics are fixed, the calculated X₁′Y₁, X₁′Y₂, Y₁′Y₁ and Y₂′Y₂ are proportional to X₁′X₁. As a result, Y₁′Y₂ is also proportional to X₁′X₁, and the calculated coefficients and covariance do not depend on the value of X₁′X₁ we specify. Hence, we can simply set X₁′X₁ to 1.

As a result, we have

$$\left(\begin{array}{c}\hfill \widehat{b_1}\hfill \\ \hfill \widehat{b_2}\hfill \end{array}\right)={\left(\begin{array}{cc}\hfill 1\hfill & \hfill \widehat{{\beta }_2}\hfill \\ \hfill \widehat{{\beta }_2}\hfill & \hfill S_2\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill \widehat{{\beta }_1}\hfill \\ \hfill \text{cor}({\mathbf{Z}}_1,{\mathbf{Z}}_2)\sqrt{S_1{S}_2}\hfill \end{array}\right)$$

$${{\hat{\sigma }}_J}^2=\frac{S_1-\left(\begin{array}{c}\hfill \widehat{b_1}\hfill \\ \hfill \widehat{b_2}\hfill \end{array}\right)\prime \left(\begin{array}{c}\hfill S_1\hfill \\ \hfill \text{cor}({\mathbf{Z}}_1,{\mathbf{Z}}_2)\sqrt{S_1{S}_2}\hfill \end{array}\right)}{n-2}$$

$$\widehat{\text{var}}\left(\begin{array}{c}\hfill \widehat{b_1}\hfill \\ \hfill \widehat{b_2}\hfill \end{array}\right)={\left(\begin{array}{cc}\hfill 1\hfill & \hfill \widehat{{\beta }_2}\hfill \\ \hfill \widehat{{\beta }_2}\hfill & \hfill S_2\hfill \end{array}\right)}^{-1}{{\hat{\sigma }}_J}^2$$

where $S_1=(\mathrm{n}-1)\widehat{\text{var}}(\widehat{{\beta }_1})+{\widehat{{\beta }_1}}^2,S_2=(\mathrm{n}-1)\widehat{\text{var}}(\widehat{{\beta }_2})+{\widehat{{\beta }_2}}^2$. Again Z₁, Z₂ are the Z-scores for a large number, say a few hundreds of thousands, of some null SNPs’ for Y₁, Y₂ respectively, drawn from the given GWAS summary statistics.

We note that in practice, the subjects used to generate summary statistics for Y₁ and Y₂ may not be exactly the same, which may lead to biased estimates; the degree of the bias increases with the proportion of the subjects who did not have all the measurements for all the traits. For operational purpose, we can set n as the number of all subjects and carry on the above process.

2.2 Adjusting for Multiple Phenotypes and Multiple SNPs

We extend our method to the general situation where Y₂ includes more than one phenotype, and X₁ includes more than one SNP. Suppose Y₂ = (y_ik)_n×(K−1), k = 2, … K, where (K − 1) is the number of phenotypes we want to adjust for in the joint model; X₁ = (x_il)_n×L, where L is the number of SNPs. Based on the given GWAS data, we have the summary statistics $\hat{{\beta }_{\mathit{\text{kl}}}}$ and $\widehat{\text{var}}(\hat{{\beta }_{\mathit{\text{kl}}}})$ in marginal analyses with marginal linear models

$${\mathbf{Y}}_{(k)}={\mathbf{X}}_{1l}{\beta }_{\mathit{\text{kl}}}+{\mathbf{e}}_{\mathit{\text{kl}}},$$

where Y_(k) is the kth column of (Y₁ Y₂), k = 1, … K, X_1l = (x_il)_n×1, and e_kl~N(0, σ_kl²I_n). Now we are interested in inference for conditional analysis with a joint (full) linear regression model

$${\mathbf{Y}}_1=({\mathbf{X}}_1{\mathbf{Y}}_2)\left(\begin{array}{c}\hfill {\mathbf{b}}_1\hfill \\ \hfill {\mathbf{b}}_2\hfill \end{array}\right)+\mathbf{e}$$

where b₁, b₂ are the joint effects, and e~N(0, σ_J²I_n).

In practice, due to missing values, different summary statistics often came from different numbers of individuals. Suppose n_kl is the sample size used to calculate $\hat{{\beta }_{\mathit{\text{kl}}}}$ and $\widehat{\text{var}}(\hat{{\beta }_{\mathit{\text{kl}}}})$, and n is the number of all subjects; we assume $n=\underset{kl}{\text{max}}{n}_{\mathit{\text{kl}}}$. Each sample of n_kl < n individuals is regarded as a random sample from the n subjects.

Similar to what we did before, we have

$$\left(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array}\right)={\left(\begin{array}{cc}\hfill {\mathbf{X}}_1\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_2\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_2\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_1\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_1\hfill \end{array}\right)$$

$$\widehat{\text{var}}\left(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array}\right)={\left(\begin{array}{cc}\hfill {\mathbf{X}}_1\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_2\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_2\hfill \end{array}\right)}^{-1}{{\hat{\sigma }}_J}^2$$

The residual variance σ̂_J² can be estimated as

$${{\hat{\sigma }}_J}^2=\frac{{\mathbf{Y}}_1\prime {\mathbf{Y}}_1-\left(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array}\right)\prime \left(\begin{array}{c}\hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_1\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_1\hfill \end{array}\right)}{n-(K+L-1)}$$

Denote the (k − 1)th column of Y₂ by Y_(k) and Y₁ by Y₍₁₎. We have

$${\mathbf{Y}}_2=({\mathbf{Y}}_{(2)}\dots {\mathbf{Y}}_{(K)})$$

$${\mathbf{Y}}_2\prime {\mathbf{Y}}_2={({\mathbf{Y}}_{(k)}\prime {\mathbf{Y}}_{(q)})}_{k=2,\dots ,K;q=2,\dots ,K}$$

$${\mathbf{X}}_1\prime {\mathbf{X}}_1={({\mathbf{X}}_{1i}\prime {\mathbf{X}}_{1j})}_{L\times L}$$

$${\mathbf{X}}_1\prime {\mathbf{Y}}_2={({\mathbf{X}}_{1i}\prime {\mathbf{Y}}_{(k)})}_{i=1,\dots ,L;k=2,\dots ,K}$$

$${\mathbf{Y}}_1\prime {\mathbf{Y}}_2={({\mathbf{Y}}_1\prime {\mathbf{Y}}_{(k)})}_{k=2,\dots ,K}$$

We can obtain X_1l′Y_(k), Y_(k)′Y_(k) using

$$\hat{{\beta }_{\mathit{\text{kl}}}}\prime =\frac{{\mathbf{X}}_{1l}\prime {\mathbf{Y}}_{(k)}}{{\mathbf{X}}_{1l}\prime {\mathbf{X}}_{1l}}$$

$$\frac{{\mathbf{Y}}_{(k)}\prime {\mathbf{Y}}_{(k)}-{\mathbf{X}}_{11}\prime {\mathbf{X}}_{11}{\widehat{{\beta }_{k1}}}^{\prime 2}}{n-1}={\mathbf{X}}_{11}\prime {\mathbf{X}}_{11}\widehat{\text{var}}(\widehat{{\beta }_{k1}}\prime )$$

Note that $\hat{{\beta }_{\mathit{\text{kl}}}}\prime$ is the estimated coefficient using all n subjects. It is different from the $\hat{{\beta }_{\mathit{\text{kl}}}}$ we have, which only used n_kl subjects. We can replace the unknown $\hat{{\beta }_{\mathit{\text{kl}}}}\prime$ by $\hat{{\beta }_{\mathit{\text{kl}}}}$, assuming the sample size is large enough (which is the case in GWAS). As for $\widehat{\text{var}}(\widehat{{\beta }_{k1}}\prime )$, we should replace it by $n_{k1}\widehat{\text{var}}(\widehat{{\beta }_{k1}})/n$ because the sample size does influence the variance of the estimator. Then we have

$$\hat{{\beta }_{\mathit{\text{kl}}}}=\frac{{\mathbf{X}}_{1l}\prime {\mathbf{Y}}_{(k)}}{{\mathbf{X}}_{1l}\prime {\mathbf{X}}_{1l}}$$

$$\frac{{\mathbf{Y}}_{(k)}\prime {\mathbf{Y}}_{(k)}-{\mathbf{X}}_{11}\prime {\mathbf{X}}_{11}{\widehat{{\beta }_{k1}}}^2}{n-1}=\frac{n_{k1}}{n}{\mathbf{X}}_{11}\prime {\mathbf{X}}_{11}\widehat{\text{var}}(\widehat{{\beta }_{k1}})$$

When n is large, we can also use

$${\mathbf{Y}}_{(k)}\prime {\mathbf{Y}}_{(k)}-{\mathbf{X}}_{11}\prime {\mathbf{X}}_{11}{\widehat{{\beta }_{k1}}}^2\approx n_{k1}{\mathbf{X}}_{11}\prime {\mathbf{X}}_{11}\widehat{\text{var}}(\widehat{{\beta }_{k1}})$$

As before, given the GWAS data of summary statistics, we have Z-statistics Z_k for Y_(k) versus SNPs that are not significant for all phenotypes, which are used to estimate Y_(k)′Y_(q) as $\sqrt{{\mathbf{Y}}_{(k)}\prime {\mathbf{Y}}_{(k)}{\mathbf{Y}}_{(q)}\prime {\mathbf{Y}}_{(q)}}\text{cor}({\mathbf{Z}}_k,{\mathbf{Z}}_q)$ when k ≠ q.

If we can get individual level data $\stackrel{\sim }{{\mathbf{X}}_1}$ from some reference panel for the L SNPs of interest, we can estimate X₁′X₁ as Σ, where Σ is the sample variance-covariance matrix obtained from $\stackrel{\sim }{{\mathbf{X}}_1}$.

To summarize, if we have $\hat{{\beta }_{\mathit{\text{kl}}}}$ and $\widehat{\text{var}}(\hat{{\beta }_{\mathit{\text{kl}}}})$ for Y_(k)~X_1l (k = 1 … K, l = 1 … L) and n_kl, the sample size to get the summary statistics, as well as Σ, an estimate of the variance-covariance matrix of the SNPs, and Z_k, Z-scores for Y_(k) versus null SNPs, we can use the following procedure to get the coefficients and the variance estimates:

$${\mathbf{X}}_1\prime {\mathbf{X}}_1=\sum ={({\mathrm{s}}_{\mathit{\text{ij}}})}_{L\times L}$$

$${\mathbf{X}}_1\prime {\mathbf{Y}}_1=\left(\begin{array}{cccc}\hfill s_{11}& 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0& s_{22}\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮& ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0& 0\hfill & \hfill \cdots \hfill & \hfill s_{\mathit{\text{LL}}}\hfill \end{array}\right)(\widehat{{\beta }_{11}}\widehat{{\beta }_{12}}\dots \widehat{{\beta }_{1L}})\prime$$

$${\mathbf{X}}_1\prime {\mathbf{Y}}_2=\left(\begin{array}{cccc}\hfill s_{11}& 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0& s_{22}\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮& ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0& 0\hfill & \hfill \cdots \hfill & \hfill s_{\mathit{\text{LL}}}\hfill \end{array}\right)\left(\begin{array}{cccc}\hfill \widehat{{\beta }_{21}}& \widehat{{\beta }_{31}}\hfill & \hfill \cdots \hfill & \hfill \widehat{{\beta }_{K1}}\hfill \\ \hfill \widehat{{\beta }_{22}}& \widehat{{\beta }_{32}}\hfill & \hfill \cdots \hfill & \hfill \widehat{{\beta }_{K2}}\hfill \\ \hfill ⋮& ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \widehat{{\beta }_{2L}}& \widehat{{\beta }_{3L}}\hfill & \hfill \cdots \hfill & \hfill \hat{{\beta }_{\mathit{\text{KL}}}}\hfill \end{array}\right)$$

$${\mathbf{Y}}_{(k)}\prime {\mathbf{Y}}_{(k)}=n_{k1}{s}_{11}\widehat{\text{var}}(\widehat{{\beta }_{k1}})+s_{11}{\widehat{{\beta }_{k1}}}^2$$

$${\mathbf{Y}}_{(k)}\prime {\mathbf{Y}}_{(q)}=\sqrt{{\mathbf{Y}}_{(k)}\prime {\mathbf{Y}}_{(k)}{\mathbf{Y}}_{(q)}\prime {\mathbf{Y}}_{(q)}}\text{cor}({\mathbf{Z}}_k,{\mathbf{Z}}_q),k\ne q$$

$${\mathbf{Y}}_1\prime {\mathbf{Y}}_1={\mathbf{Y}}_{(1)}\prime {\mathbf{Y}}_{(1)}$$

$${\mathbf{Y}}_2\prime {\mathbf{Y}}_2={({\mathbf{Y}}_{(i)}\prime {\mathbf{Y}}_{(j)})}_{i=2\dots K;j=2\dots K}$$

$${\mathbf{Y}}_1\prime {\mathbf{Y}}_2=={({\mathbf{Y}}_{(1)}\prime {\mathbf{Y}}_{(j)})}_{j=2\dots K}$$

$$\left(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array}\right)={\left(\begin{array}{cc}\hfill {\mathbf{X}}_1\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_2\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_2\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_1\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_1\hfill \end{array}\right)$$

$${{\hat{\sigma }}_J}^2=\frac{{\mathbf{Y}}_1\prime {\mathbf{Y}}_1-\left(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array}\right)\prime \left(\begin{array}{c}\hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_1\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_1\hfill \end{array}\right)}{n-(K+L-1)}(n=\text{max}(n_{\mathit{\text{kl}}}))$$

$$\widehat{\text{var}}\left(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array}\right)={\left(\begin{array}{cc}\hfill {\mathbf{X}}_1\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_2\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_2\hfill \end{array}\right)}^{-1}{{\hat{\sigma }}_J}^2$$

Note that the calculated $(\widehat{{\mathbf{b}}_{\mathbf{1}}},\widehat{{\mathbf{b}}_{\mathbf{2}}})\prime$ does not depend on the choice of n, but σ̂_J² does. When there are many non-overlapping subjects, e.g. if $\underset{k,l}{\text{min}}(n_{\mathit{\text{kl}}})/\underset{k,l}{\text{max}}(n_{\mathit{\text{kl}}})$ is small, we shall obtain biased estimates of σ̂_J² and other parameters.

From our experience, the estimate of X₁′X₁ tends to affect the result. In some cases, it may even make some diagonal elements of $\widehat{\text{var}}\left(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array}\right)$ negative. To fix this problem, we may use a modified version of $\mathbf{A}=\left(\begin{array}{cc}\hfill {\mathbf{X}}_1\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{X}}_1\prime {\mathbf{Y}}_2\hfill \\ \hfill {\mathbf{Y}}_2\prime {\mathbf{X}}_1\hfill & \hfill {\mathbf{Y}}_2\prime {\mathbf{Y}}_2\hfill \end{array}\right)$ when calculating $\left(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array}\right)$ and $\widehat{\text{var}}\left(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array}\right)$. Inspired by Cichonska et al. (2016), we can use (A + λI)/(λ + 1), where I is an identity matrix and λ > 0 is a small positive number to be manually selected. In the data analysis part, we still used the default λ = 0 unless specified otherwise.

2.3 Hypothesis Testing

Denote (b₁, b₂)′ and $(\widehat{{\mathbf{b}}_{\mathbf{1}}},\widehat{{\mathbf{b}}_{\mathbf{2}}})\prime$ by b and b̂. Since we are able to obtain b̂ and $\widehat{\text{var}}(\hat{\mathbf{b}})$, we can test any null hypothesis in the form of Cb = l by the Wald test, where C is a rank Q matrix with (K + L) columns and Q rows, l is a Q dimensional vector. If Q is greater than 1, the test is testing multiple hypothesis, otherwise a single hypothesis. The test statistic is

$$T=\left[\mathbf{C}\right(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array})-\mathbf{l}]\prime {\left[\mathbf{C}\widehat{\text{var}}\right(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array})\mathbf{C}\prime ]}^{-1}\left[\mathbf{C}\right(\begin{array}{c}\hfill \widehat{{\mathbf{b}}_{\mathbf{1}}}\hfill \\ \hfill \widehat{{\mathbf{b}}_{\mathbf{2}}}\hfill \end{array})-\mathbf{l}]$$

Under the null hypothesis, T approximately follows a chi-squared distribution with Q degrees of freedom.

3 Results

3.1 Simulations

To evaluate the effectiveness of our proposed approach, we first compared the performance of using summary statistics only with that of using individual-level data in a simulation study with one SNP and two traits. We generated the genotypes of a single SNP from a binomial distribution with frequency f₀. Then we generated Y₂ using the model Y₂ = X₁β₂ + e₁, and Y₁ using the model ${\mathbf{Y}}_1=({\mathbf{X}}_1{\mathbf{Y}}_2)\left(\begin{array}{c}\hfill b_1\hfill \\ \hfill b_2\hfill \end{array}\right)+{\mathbf{e}}_2$, where e_i follows a standard normal distribution. To obtain the Z-scores, we generated 500 independent null SNPS with varying allele frequencies f~U [0.08,0.2] and then estimated their marginal effect sizes and variances. The sample size was set to n. We compared our approach using only summary statistics with the golden standard approach of using individual-level data.

Next, we did simulations to assess the influence of non-overlapping subjects. After generating the data for n subjects, we only used the first n₁ subjects to obtain summary statistics for Y₁, and the last n₂ subjects for Y₂. When building the model based on individual data, we only used the overlapping subjects. We obtained the means and the standard deviations using 100 iterations. We also compared the results with marginal estimates.

In addition, we looked at the performance of the new method for adjusting for multiple traits and multiple SNPs. A new simulation was conducted based on a dataset from the Genetic Investigation of Anthropometric Traits (GIANT) consortium (Randall et al., 2013). The dataset contains summary statistics for the marginal effects of each single SNPs on each of the anthropometric traits like body mass index (BMI), hip circumference (HIP), waist circumference (WC) and weight, etc., stratified by sex.

For this simulation, we only simulated data for males. We chose 8 SNPs that are marginally significant for the four traits (p-value < 5e-8) but not highly correlated. We generated the genotypes from a multivariate binomial distribution based on the 8 SNPs’ minor allele frequencies and their correlations estimated from the reference panel. In this step, we multiplied the correlation between each pair of SNPs by 0.8 to avoid numerical problems. We also standardized the genotypes. Then we simulated HIP and WC using the estimated models for HIP~SNP₁ + SNP₂ + SNP₃ + SNP₄, WC~SNP₅ + SNP₆ + SNP₇ + SNP₈. Next, we generated BMI using the estimated model for BMI~HIP + WC + SNP₁ + SNP₂ + ⋯ + SNP₈. The sample size was set to 2000. After that, we conducted the marginal analysis. Then we did the conditional analysis using the obtained summary statistics.

The results shown in Table 4 indicate that the regression coefficient estimates from the conditional model tended to be more accurate than those from the marginal models, and that they had smaller standard errors, suggesting possible power gains from conditional analyses.

Table 4.

Estimated coefficients, standard errors and p-values

SNP	marginal	s.e.	conditional	s.e.	“true”
rs10852521	−0.027	0.0055	−0.171	0.0047	−0.168
rs11075985	0.093	0.0051	0.134	0.0040	0.118
rs11075987	−0.019	0.0055	−0.163	0.0031	−0.192
rs11075989	0.057	0.0054	−0.043	0.0035	−0.050
rs11642841	0.070	0.0053	0.026	0.0029	0.006
rs12149832	0.084	0.0052	0.085	0.0032	0.068
rs8057044	0.106	0.0050	0.278	0.0031	0.304
rs9922619	0.042	0.0055	−0.092	0.0033	−0.076

The marginal models are BMI~SNP_i. The conditional model is BMI~HIP + WC + SNP₁ + SNP₂ + ⋯ + SNP₈. The true model was generated using the original GWAS data. The covariance for SNPs was estimated from the 381 European subjects from the 1000 Genomes Project data (The 1000 Genomes Project Consortium 2015). When building the conditional model for simulated data, we multiplied non-diagonal elements of the variance-covariance matrix by 0.8, since the same adjustment was made to generate these data. 2000 independent null SNPs with MAF f~U [0.1, 0.5] were simulated to estimate the correlation between traits. λ = 0.01.

3.2 BCX Data

The Blood Cell Consortium (BCX) data (Chami et al., 2016) contains summary statistics for single SNP effects on red blood cell traits. We applied the method to traits red blood cell count (RBC) and hematocrit (HCT) for European subjects, denoted by Y₁ and Y₂. We examined each SNP that has both significant marginal effects on BCX and HCT. The number of such SNPs is 25. We used the Z-scores for those 206751 SNPs in the same chromosome that were not marginally associated with either trait.

Y₂ in every case turned out to be highly significant, while only 15 SNPs (e.g. rs218237, rs172629) remained significant (p-value < 5e-8) after adjusting for Y₂ in conditional analyses. This might suggest that the other SNPs (e.g. rs11611647, rs837763) influence RBC through HCT. Table 4 shows some examples.

3.3 GIANT Data

We applied the methods to the GIANT data. Before conducting the analysis, for each sex, we estimated the correlations among the traits using 2723514 SNPs that were not marginally significant for BMI, HIP, WC and weight (i.e. p-value > 5e-8) for men and 2723477 SNPs for women. The number of subjects used to obtain the summary statistics varies a lot, depending on SNPs, traits and genders, as shown in Table 5.

Table 5.

Marginal and conditional effect on RBC

SNP	Chr	gene	MAF	Marginal			Conditional (on HCT)
				$\widehat{{\beta }_1}$	s.e.	P	$\widehat{b_1}$	s.e.	P
rs218237	4		0.1143	−0.106	0.009	9e-33*	−0.075	0.008	1e-21*
rs2293767	7	ZAN	0.3012	0.066	0.007	6e-22*	0.044	0.006	3e-13*
rs10247980	7	ZAN	0.33	0.063	0.007	1e-20*	0.042	0.006	2e-12*
rs11611647	12		0.2227	−0.049	0.007	1e-11*	−0.030	0.006	2.0e-6
rs837763	16		0.5676	−0.035	0.006	3e-8*	−0.015	0.006	0.006
rs10495928	2	PRKCE	0.3171	−0.057	0.006	2e-19*	−0.017	0.006	0.003

First, we looked at the data for males. We considered those SNPs that were marginally significant for BMI, HIP, WC and weight (p-value < 5e-8). Only 44 SNPs satisfied this condition, and they were all mapped to gene FTO on chromosome 16. Since these SNPs were highly correlated, we chose 8 of them so that the correlation matrix estimated from the reference panel was not nearly singular. The panel we used was the 381 European subjects from the 1000 Genomes Project data (The 1000 Genomes Project Consortium, 2015). If the absolute value of the correlation between two SNPs was greater than 0.98, we excluded the second one. We list the effective sample sizes in Table 6. Note that, due to the inclusion of some family-based studies in the meta-analysis, the effective sample sizes may not be integers.

Table 6.

Estimated correlation between traits using Z_k’s and the range of sample size for each trait (Upper: Men; Lower: Women)

Correlation	BMI (221, 58665)	HIP (118, 32851)	WC (118, 38313)	Weight (113, 58351)
BMI (124, 67959)	1	0.54	0.70	0.84
HIP (120, 40358)	0.63	1	0.68	0.61
WC (120, 47322)	0.72	0.70	1	0.70
Weight (125, 67594)	0.89	0.66	0.72	1

We conducted a conditional analysis with a joint (full) model for BMI vs. the other traits plus the 8 SNPs. We also considered models adjusting for traits only or for SNPs only. The four types of models can be viewed as BMI~SNP_i (marginal), BMI~SNP_i + HIP + WC + Weight (adjusted for only the traits), BMI~SNP₁ + SNP₂ + ⋯ + SNP₈ (adjusted for only the SNPs) and BMI~HIP + WC + Weight + SNP₁ + SNP₂ + ⋯ + SNP₈ (adjusted for both the traits and SNPs).

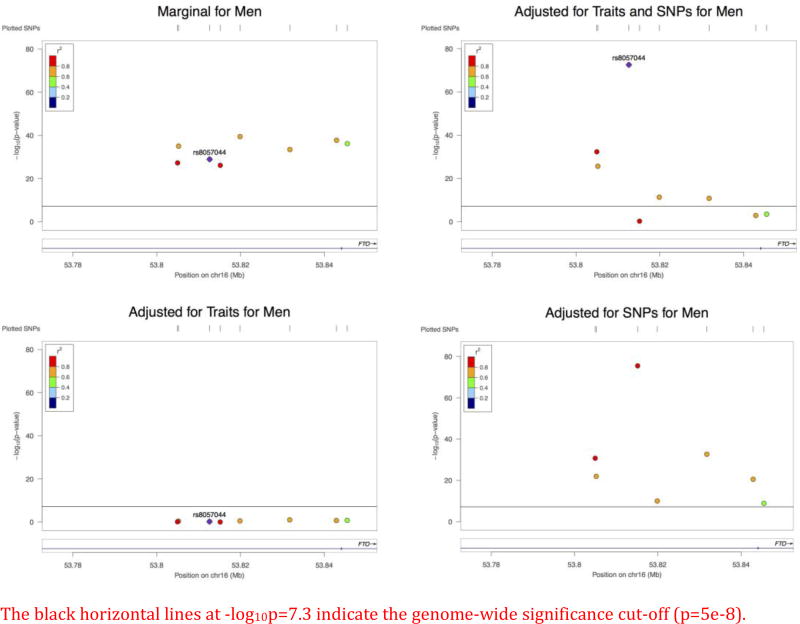
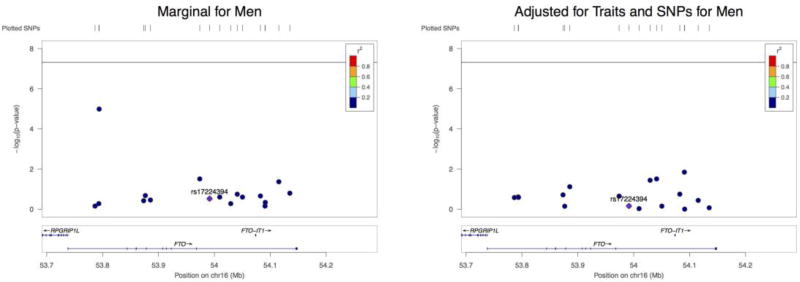
As shown in Figure 1, after adjusting for both SNPs and traits, three marginally significant SNPs became insignificant, while one became more significant (rs8057044). If we only adjusted for traits, all 8 SNPs became insignificant. The estimated effects were all very small. If we only adjusted for SNPs, a few SNPs retained much larger effect sizes. The effect size of rs8057044 was much larger than those of the other SNPs, yielding p-value 0. Note that SNP rs11075987 was insignificant in the full model, but highly significant in the partial model only adjusting for SNPs, which demonstrates the effects of conditional analysis.

Figure 1.

The effect of each SNP on BMI in different models (Men)

The black horizontal lines at −log₁₀p=7.3 indicate the genome-wide significance cut-off (p=5e-8).

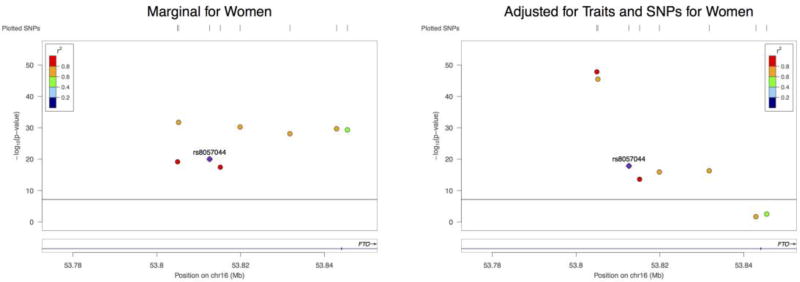
Next, we built the joint model with the same SNPs for females. The results are shown in Figure 2. After adjusting for SNPs and traits, 2 SNPs became insignificant. The most significant SNP in our analysis for males, rs8057044, was much less significant for females: the estimated effect sizes were 0.239 and 0.095, with the standard errors 0.013 and 0.011, respectively. In contrast, in the marginal models, the corresponding effect sizes were 0.072 and 0.058 respectively. The joint analysis seems able to better capture the sex difference for this SNP.

Figure 2.

The effect of each SNP on BMI in different models (Women)

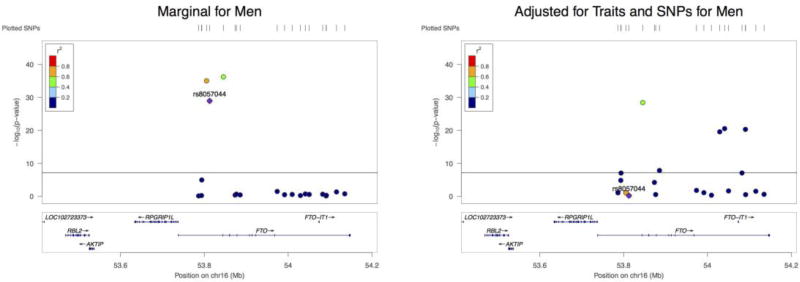
Furthermore, we considered both marginally significant and insignificant SNPs mapped to gene FTO. We looked at the 8 significant SNPs from above plus 20 SNPs that are not marginally significant for BMI in the male data. Again we selected 20 SNPs so that none of the pairwise correlation was greater than 0.9, while intentionally reserving rs8057044. Then we built the joint models for men and women respectively.

As shown in Figure 3, some SNPs (e.g. rs9922370, rs12447427, rs12596862) that were not marginally significant for association with BMI became highly significant in the joint model for men. However, their estimated effect sizes were not as large in the joint model for women. Note that the reference panel we used was not stratified by sex.

Figure 3.

The effect of each SNP on BMI in different models

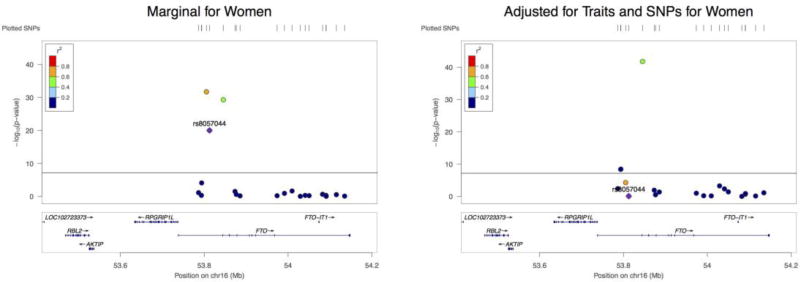
We also only looked at the 17 marginally insignificant SNPs among the selected SNPs. As shown in Figure 4, none of them became significant in the joint model, suggesting that their significant results obtained earlier were due to their correlations with other marginally significant SNPs.

Figure 4.

The effect of each SNP on BMI in different models (Men)

4 Discussion

We have presented the conditional analysis adjusting for one or more traits and possibly for one or more SNPs using only GWAS summary statistics. Our simulation study confirmed that when an SNP influences one trait through another trait, the conditional analysis is more reliable than the marginal analysis to detect the mediating effects, thus distinguishing direct and indirect effects.

We applied our analysis to the BCX data for the subjects of European ancestry. Among the 25 SNPs that were both marginally significant for RBC and HCT, 10 of them became insignificant for RBC after adjusting for HCT. This may suggest these SNPs affect RBC through HCT, though it may be also due to reduced power in conditional analysis. We also applied our analysis to the GIANT data. We found that the joint models could reduce the number of significant SNPs, and more importantly, possibly better distinguish sex-specific associations.

We assume that all the traits were collected from the same set of subjects, which may not hold in practice due to missing values, as often shown in varying samples sizes for trait-specific summary statistics in GWAS data. If this assumption is violated, we may obtain estimates with bias, whose degree depends on the proportion of non-overlapping subjects. In the worst case of no-overlapping subjects among the multiple traits, a conditional analysis reduces to marginal analysis (because the traits would be estimated to be uncorrelated to each other).

In addition to conditional analysis of multiple traits to unravel specific pleiotropic effects, our proposed method can also be applied to conditional analysis of both multiple traits and multiple SNPs. We expect that our proposed method will be useful in future fine mapping studies.

The proposed method is implemented as an R function available at https://github.com/yangq001/conditional.

Table 1.

Estimated coefficients, standard errors and p-values when all subjects are overlapped

f0 = 0.1, (β2, b1, b2) = (1, 0.8, 1.2), n = 500
	$\widehat{b_1}$	s.e.	P	$\widehat{b_2}$	s.e.	P
summary	0.89	0.155	8e-9	1.20	0.044	2e-167
individual	0.90	0.157	2e-8	1.19	0.044	2e-98
f0 = 0.1, (β2, b1, b2) = (1, 0.8, 1.2), n = 2000
	$\widehat{b_1}$	s.e.	P	$\widehat{b_2}$	s.e.	P
summary	0.78	0.078	2e-23	1.16	0.022	0
individual	0.76	0.077	9e-23	1.17	0.022	0
f0 = 0.1, (β2, b1, b2) = (0.5, 0, 0.5), n = 2000
	$\widehat{b_1}$	s.e.	P	$\widehat{b_2}$	s.e.	P
summary	−0.06	0.074	0.45	0.49	0.022	3e-110
individual	−0.05	0.074	0.51	0.50	0.022	<2e-16

As shown in Table 1, the results of the two approaches were quite close, confirming the effectiveness of our proposed method.

Table 2.

Estimated coefficients, standard errors and p-values when non-overlapping subjects exist for the two traits

f0 = 0.1, (β2, b1, b2) = (1, 0.8, 1.2), n = 500, n1 = 400, n2 = 500
	Mean( $\widehat{b_1}$)	SD	Mean( $\widehat{b_2}$)	SD
summary	0.82	0.22	1.18	0.09
individual	0.79	0.18	1.21	0.05
marginal	2.07	0.25	2.03	0.23
f0 = 0.1, (β2, b1, b2) = (1, 0.8, 1.2), n = 500, n1 = 500, n2 = 400
	Mean( $\widehat{b_1}$)	SD	Mean( $\widehat{b_2}$)	SD
summary	1.07	0.20	0.94	0.07
individual	0.80	0.18	1.21	0.05
marginal	2.03	0.23	2.01	0.25
f0 = 0.1, (β2, b1, b2) = (1, 0.8, 1.2), n = 500, n1 = 400, n2 = 400
	Mean( $\widehat{b_1}$)	SD	Mean( $\widehat{b_2}$)	SD
summary	1.16	0.26	0.84	0.10
individual	0.79	0.21	1.21	0.06
marginal	2.07	0.25	2.01	0.25

As shown in Table 2, the presence of non-overlapping subjects did affect the results of our method. The main reason is due to the poor approximation cor(Y₁, Y₂) ≈ cor(Z₁, Z₂) in this case. Table 3 shows the averages of the estimated correlations based on 20 samples for varying degrees of overlapping subjects. We generated one set of (Y₁, Y₂), and then simulated (Z₁, Z₂) 20 times for each set-up. It is clear that as the proportion of the non-overlapping subjects increased, the bias of the correlation estimates also increased.

Table 3.

The correlation between Y₁, Y₂ and Z₁, Z₂ under each setting

n = 500	n1 = 500, n2 = 500	n1 = 400, n2 = 500	n1 = 500, n2 = 400	n1 = 400, n2 = 400
cor(Y1, Y2)	0.77
cor(Z1, Z2)	0.77	0.71	0.69	0.59

Since the estimated correlation between Y₁ and Y₂ was under-biased, $\widehat{b_2}$ became underestimated. Meanwhile, $\widehat{b_1}$ was inflated. Nevertheless, the estimates from our conditional analysis were still better than those from marginal analysis (i.e. closer to the true parameters in the conditional model).

Table 7.

Effective sample size for each trait-SNP pair (men)

SNP	BMI	HIP	WC	Weight
rs10852521	58612.9	32844.1	38299.9	58317.5
rs11075985	58612.1	32843.3	38299.4	58316.7
rs11075987	58615.9	32846.5	38302.5	58320.5
rs11075989	58618.1	32848.3	38304.2	58322.7
rs11642841	58604.5	32841.8	38297.5	58309.1
rs12149832	58597.6	32838.7	38294.8	58302.2
rs8057044	58556.0	32791.5	38247.5	58260.7
rs9922619	58615.8	32846.2	38302.3	58320.4

The (effective) sample size did not vary much among these SNPs for a given trait, but it did vary across the traits, suggesting at least about 1/4 of the subjects were not overlapped, thus cautions are needed with regard to possible biases of the parameter estimates.