Biomechanical Behavior of Bioprosthetic Heart Valve Heterograft Tissues: Characterization, Simulation, and Performance

Abstract

The use of replacement heart valves continues to grow due to the increased prevalence of valvular heart disease resulting from an ageing population. Since bioprosthetic heart valves (BHVs) continue to be the preferred replacement valve, there continues to be a strong need to develop better and more reliable BHVs through and improved the general understanding of BHV failure mechanisms. The major technological hurdle for the lifespan of the BHV implant continues to be the durability of the constituent leaflet biomaterials, which if improved can lead to substantial clinical impact. In order to develop improved solutions for BHV biomaterials, it is critical to have a better understanding of the inherent biomechanical behaviors of the leaflet biomaterials, including chemical treatment technologies, the impact of repetitive mechanical loading, and the inherent failure modes. This review seeks to provide a comprehensive overview of these issues, with a focus on developing insight on the mechanisms of BHV function and failure. Additionally, this review provides a detailed summary of the computational biomechanical simulations that have been used to inform and develop a higher level of understanding of BHV tissues and their failure modes. Collectively, this information should serve as a tool not only to infer reliable and dependable prosthesis function, but also to instigate and facilitate the design of future bioprosthetic valves and clinically impact cardiology.

INTRODUCTION

The valves of the heart are responsible for controlling the unidirectional flow of blood through the body. Annually each valve opens and close 30–40 million times, for a total of ~3 billion cycles in a lifetime.²¹⁰ Valvular heart disease is clinically typified by gradual narrowing of the valve due to calcification of the leaflets or regurgitation through the valve due to insufficient valve closure in one of four heart valves. Stenotic (too narrow and hardened to fully open) or incompetent (unable to close completely) valves cause blood flow in between the several heart chambers to become pathological, imposing an increased mechanical load on the ventricle and leading to ventricular chamber enlargement, thickening, and progressive contractile failure. Valve repair or replacement are two available therapies to correct diseased valves, preserve cardiac function, and ultimately necessary to prevent congestive heart failure and death. According to the American Heart Association (AHA), the overall prevalence of any heart valve disease is 2.5%, and clinically diagnosed (moderate or greater) prevalence of 1.8% with an annual mortality of over 22,000.^{63,64,146,158} Valve replacement surgery, first performed in 1960, has significantly reduced the mortality rate of patients with valvular heart disease.^14,154,159 As reported by The Society of Thoracic Surgeons 59,555 Americans underwent valve replacement surgery in 2014 (48,060 AV replacement, 9595 MV replacement, 1900 both AV and MV replacement). Of the various types of heart valves, the aortic valve (AV) has been studied most, followed next by the mitral valve (MV), whereas fewer studies have been performed on the valves of the pulmonary circulation, the pulmonary valve (PV) and the tricuspid valve. This is primarily due to the fact that the AV and MV are more commonly diseased than the PV, as indicated by AHA statistics, and more frequently warrant replacement surgery. While important differences exist in valve geometries and function, the mechanics of the AV are primarily used as a baseline for the development of models of heart valve function. Valve repair is a feasible alternative for valve replacement and is an attractive approach in the treatment of severe mitral valve regurgitation. Ring annuloplasty allows robust and predictable mitral valve reconstructions and surgical corrections to restore leaflet mobility, enlarge coaptation surface, and promote favorable remodeling of the annulus to offer optimal and stable orifice area.¹⁰⁶ However, meta-analyses indicate that mitral valve repair or mitral valve replacement are indeed head-to-head in comparison: replacement was associated with a higher 30-day mortality (as the procedure is much more drastic and entails higher inherent risks), whereas repair is associated with higher rates of mitral regurgitation occurrence and the need for reoperation.¹⁷²

Current clinical implants used for surgical valve replacement utilize either mechanical valves (usually made of pyrolytic carbon or titanium) or valves constructed from biologically-derived soft tissues. Although mechanical prosthetic valves are very durable, they introduce a large degree of pathologic blood flow patterns, elicit a substantial thrombogenic response, and require lifelong post-operative anticoagulation therapy with its inherent risks.¹⁵⁴ Bioprosthetic heart valves (BHVs), on the other hand, are comprised of decellularized bovine or porcine tissues (prosthesis constructed with either the native valve leaflets per se, or with connective tissues, most commonly the pericardium) and offer a higher degree of functionality including improved hemodynamics and a higher resistance to thrombosis. Although they are chemically fixed, these tissues are still prone to valve calcification, structural deterioration, and eventual failure.^166,226 Durability is the major limitation of current BHV technology—the 15-year durability of heterograft BHVs in the aortic position is less than 50% for middle-aged patients and slightly better for older patients, however BHVs continue to be the preferred replacement valve.¹⁷⁹ Regardless of its shortcomings, heart valve replacement has had a substantial impact on cardiac surgery with a consistently increasing number of surgeries per year (Fig. 1), and more recently on interventional cardiology with catheter based techniques. This may have saved the lives of millions of patients with valvular diseases, who before the advent of replacement therapies were faced with very limited clinical options and death by congestive heart failure as the likely result. The very first successful heart valve surgery was mitral commissurotomy performed in 1923 by Elliott Cutler.³¹ The introduction of the heart–lung bypass machine in the 1950s allowed for entire valve replacement surgeries. In 1960, pioneer surgeons Nina S. Braunwald and Dwight E. Harken implanted the first artificial mitral and aortic valves respectively.^14,82 BHVs have been a popular choice among surgeons since they were made commercially available in the 1960s (Fig. 1). The Hancock porcine BHV, first implanted in 1970 and starting clinical trials in 1972, was the first glutaraldehyde-fixed BHV commercially available for widespread use in humans in mid-to-late 1970s.³² Over the years, heart valve technology has improved slowly and steadily, providing significant increases in durability for both mechanical and bioprosthetic valves. However, the gold standard of current valve replacement technology utilizes essentially the same principles and concepts of the past. Progress within the field and development of novel technology has been limited by apprehension created by a few notable setbacks. While most mechanical valves tend to be very durable, the Bjork-Shiley mechanical prosthetic valve had a critical design flaw that caused the valve to fail in vivo, leading to numerous deaths¹⁰ (and may explain the drop in mechanical valve surgeries in 1977, Fig. 1). Setbacks have been observed in BHVs, usually as a result of attempts to increase the durability of BHVs through various fixation chemistries. A notable case is the Oxford Photofix stentless valve, a xenograft valve fixed with a dye-mediated photoxidiation process that failed numerous times in clinical studies due to cusp abrasion and perforation.¹⁷⁷ Regardless and despite of the many setbacks, significant developments have improved valve technology progressively over the years—examples of such are anti-calcification treatments such as α-amino oleic acid, Polysorbate 80, and ethanol pretreatment, some of which have now been implemented in current technology present in commercial valves.^60,105

FIGURE 1.

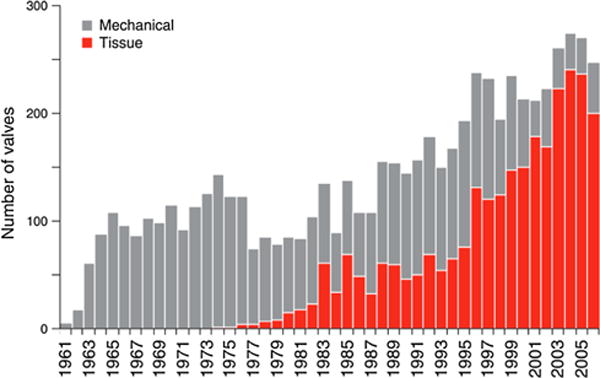
Increase in use of tissue valves for aortic valve replacement, reaching ~80% in recent years. Data from a total of 6648 patients treated at the Providence St. Vincent Hospital, Portland, Oregon, USA. Adapted with permission from Starr.¹⁸⁷

The development of stentless valves provided an alternative delivery method for BHVs, however these did not really offer a superior alternative to stented valves as both have excellent clinical outcomes at short- and mid-term.^3,46 However, stentless valves offer significant hemodynamic advantages, e.g., larger effective orifice area, better coronary flow, and lower trans-aortic pressure difference.^150,152 Stentless valves also offer superior biomechanical properties by preserving increased distensability and lowering leaflet stress in comparison to stented valves, and may be advantageous in specific surgical cases such as AV endocarditis, aortic root pathologies, and may improve post-operative function in impaired ventricles.⁵¹ The most recent development in BHV technology is the percutaneous (or transcatheter) valve replacement, which involves replacement of the aortic valve in a minimally invasive procedure with catheterization from a large blood vessel, most commonly the femoral artery. This procedure makes replacing failed BHVs less invasive and less risky (as several classes of patients may not be suited for open heart surgery), and initially posed substantial technological challenges on prosthesis design and required substantial refinement of the delivery technique. Currently, large randomized trials among high- and intermediate-risk patients with aortic stenosis have shown similar survival rates of transcatheter aortic valve replacement and surgical aortic valve replacement.¹²⁵ Currently, bovine pericardium (BP) and porcine AV tissues are still the only clinically approved xenograft biomaterial for BHVs and as such are the most frequently studied and employed sources of tissue (Fig. 2). Other tissue sources have been pursued, but none has reached clinical widespread application.

FIGURE 2.

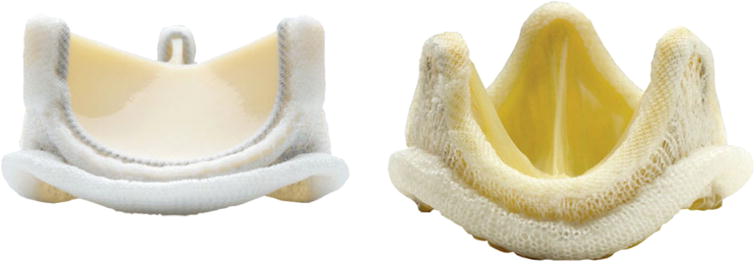
Carpentier-Edwards (a) BP and (b) PAV bioprostheses. With permission from http://www.edwards.com/.

BHVs have become the preferred replacement valve. The sustained growth of AV and MV replacement surgeries, the lack of substantial technological breakthroughs in the field over the last decades (Fig. 3), and the continuous need to improve BHV durability, promote a strong necessity to develop a higher understanding of the mechanisms involved in BHV function and failure. Critical BHV engineering aims to ensure valve functionality for its clinical performance with a combination of hemodynamic, biomechanical and biological aspects, e.g., sufficient effective orifice area, transvalvular pressure gradient, good leaflet coaptation without regurgitation, among others, and to predict and extend as much as possible valve durability. The major hurdle on the technology is simply the lifespan of the BHV implant, and substantial clinical impact can be achieved with its improvement, even if only slightly (e.g., increases of 3–5 years).¹⁰⁰

FIGURE 3.

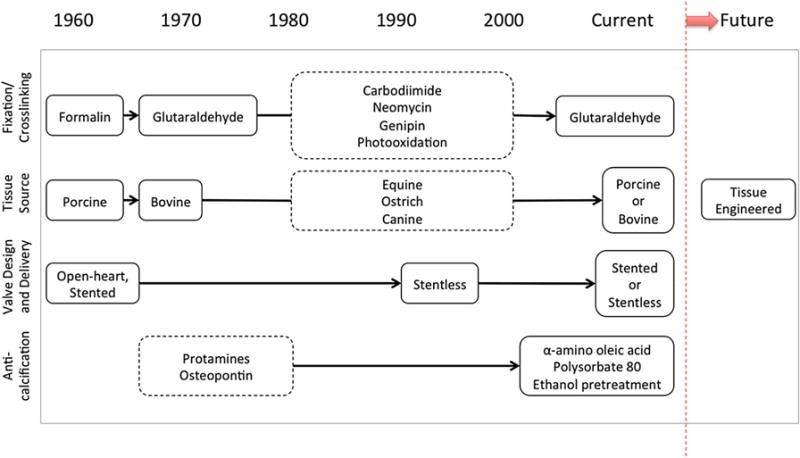
History of technological developments in the processing of BHVs: note that current standards are relatively unchanged from the advent of commercial BHVs and that the future prospects point to tissue engineered heart valves.

This review seeks to establish the need for rational methodologies and quantitative approaches to optimize BHV design by providing a comprehensive overview of the different types of BHVs, chemical fixation treatments, the mechanical properties of various tissues used for BHVs, methods to characterize them, and experimental results that provide insight on the mechanisms of BHV in vivo function and failure (Fig. 4). Additionally, this review provides a detailed summary of the computational biomechanical simulations that have been used to aid in better understanding these tissues and their failure modes. The inclusion of high fidelity anatomical descriptions and better microstructural and macrostructural models of BHV material response into in silico environments for organ-level simulations under physiological and pathological conditions will certainly be of great importance towards the improvement of BHV technology in the future. The integration of modeling and simulation into technology development will not only guide and inform subsequent R&D steps with critical quantitative data and rational methods (instead of solely relying on trial-and-error), but also will allow different insights into the problems and better analysis and interpretation of empirical data.

FIGURE 4.

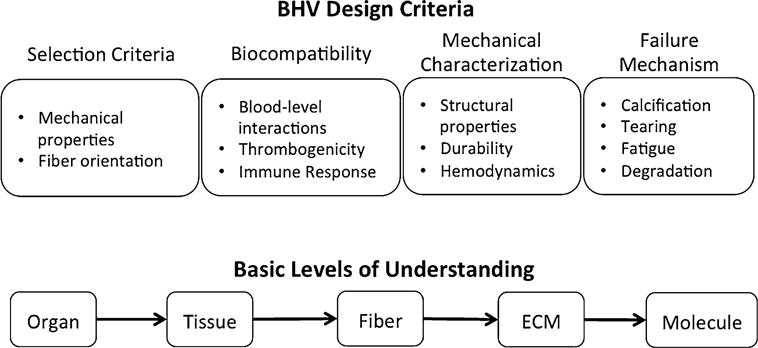
Important considerations in BHV processing including design criteria and basic levels of tissue understanding.

PRIMARY TISSUE SOURCES

Bovine Pericardium

The pericardial sac is a multi-layered connective tissue that surrounds and protects the heart: the visceral layer (also known as the epicardium) lies next to the cardiac muscle and is separated from the parietal layer by the pericardial cavity. Pericardium is primarily composed of collagen but also contains glycoproteins, glycosaminoglycans (GAGs) and cells. The collagen fiber distribution in pericardium is generally anisotropic and the overall collagen orientation and organization varies regionally. Structural variability and fiber alignment is high in pericardial tissue, which was characterized using small angle light scattering (SALS)^83,84 (Fig. 5). In SALS, laser light is passed through a tissue and the scattered light is quantified to determine the spatial distribution of structural orientation, i.e., identifying preferred-fiber direction (PD) and cross-preferred fiber direction (XD) and their degree of orientation, and thus allowing for the selection of structurally uniform specimens. Specimens pre-sorted by SALS were evaluated for biaxial mechanical properties and resulted in a much higher degree of uniformity and more consistent biomechanical data than results from previously reported non-sorted tissue tests.¹⁶³ In general, there are significant intra- and inter-sac variations in fibrous structure, which emphasizes the need for the careful selection of tissue for BHVs to achieve the highest degree of uniformity in the fiber orientation, uniform tissue thickness, and most importantly, reliable process reproducibility. Upon tissue selection aided by SALS, bovine pericardium (BP) can be chemically fixed, cut to size in the shape of a leaflet, and then affixed to a mechanical support to be sutured into the aortic wall (Fig. 2a).

FIGURE 5.

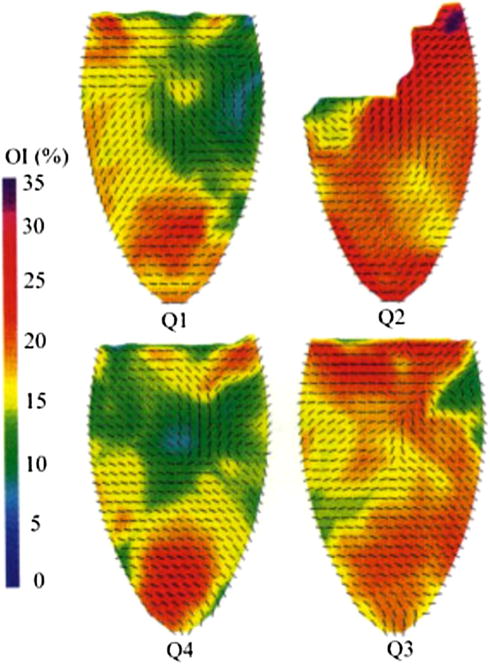
Preferred fiber direction of the BP sac displayed as vectors superposed onto color representation orientation index. Adapted with permission from Hiester and Sacks.⁸⁴

Porcine Aortic Valve Leaflet

The aortic valve (AV) has three leaflets, also known as cusps, which enable unidirectional flow from the left ventricle to the aorta and are comprised of three distinct layers: the fibrosa, spongiosa, and ventricularis.^176,210 The fibrosa faces the aorta and is composed primarily of Type I collagen fibers, highly aligned in the circumferential direction (Fig. 6). The ventricularis faces the left ventricle and is composed of a mix of elastin and collagen. Valve leaflets contain a relatively low elastin content when compared with collagen (13 to 50% dry weight). During diastolic loading there is considerable realignment of collagen fibers extending passively as the cusps undergo beyond 50% strain. The elastin in the ventricularis exerts compressible forces to keep the fibrosa in its undulated confirmation in unloaded leaflets, and is responsible for ensuring the elastic recovery mechanisms.²²² The spongiosa is the middle layer between the fibrosa and the ventricularis and contains mostly water and glycosaminoglycans (GAGs), which have been shown to have no significant effects on static mechanical properties of biological tissues.¹¹³ In addition to the valvular extracellular matrix (ECM) components, the aortic valve is also rich in valvular interstitial cells (VICs) distributed throughout the valve, as well as valvular endothelial cells (VECs) at the bloodcontacting surfaces. These cells help contribute to the maintenance of the valvular ECM and are linked with structural growth, remodeling, and repair. To prepare porcine AVs (PAVs) as BHVs, they must first be explanted, decellularized, and chemically fixed before being affixed to a mechanical support for implantation (Fig. 2b). While the decellularization process is necessary to remove viable porcine cells and to decrease the risk of an immune response, it hampers other key features of heart valve function, in particular the biochemical processes occurring within the native valves. Liao et al.¹²⁸ showed that decellularization causes a substantial loss in valve stiffness, but also significant microscopic ECM disruption. The purpose of these cells, although much remains unknown, is to maintain the structure and to respond to environmental changes; if no longer present, the valve may indeed be more prone to failure and the natural mechanisms of ECM remodeling and repair are not present.

FIGURE 6.

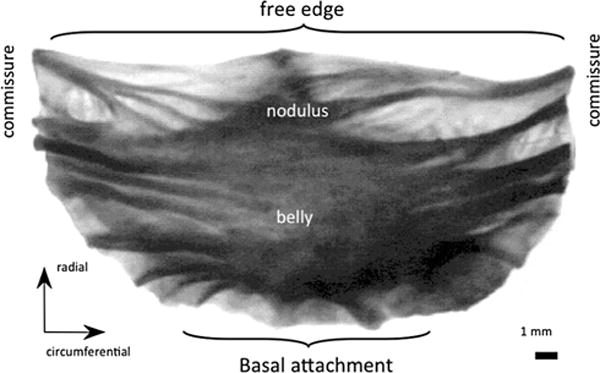
Notable regions and orientation for the aortic valve.⁹¹

Other Tissue Sources

Although bovine pericardium and porcine aortic tissues are the current standard materials for BHV construction, allograft and homograft biomaterials have also been used. Various other tissue sources have been evaluated as potential candidates for BHVs, including porcine pericardium, jugular vein valve,¹⁵⁶ pulmonary valve, and intestinal mucosal membrane; however, these are less common alternatives, and additionally, the performance of the porcine pulmonary valve was shown to be far inferior to the porcine aortic BHV.¹⁰¹ More exotic tissue sources including equine,⁸¹ canine,^120,228 even ostrich¹³³ and kangaroo¹⁵⁶ pericardium have been proposed for use in BHVs, but the relatively low availability of such materials and the risk of unexpected immune responses has raised concern and prevented these options from being evaluated further.

Engineered Tissue Approaches

Tissue-engineered heart valves (TEHVs) present a beneficial alternative as they have the potential to eliminate the immune response, offer native like characteristics of ECM remodeling and repair, and ideally, dismiss the need for subsequent valve replacement surgeries. The latter is particularly important in pediatric patients where a TEHV could accommodate somatic growth, especially when used to treat congenital heart valve diseases. The ultimate goal for TEHVs is to create a non-thrombogenic living tissue substitute that can grow, repair, and remodel and be fully integrated into the patient. The most common approach in creating TEHVs is to seed autologous cells onto a biodegradable scaffold and allow the cells to produce ECM. This process generates a living tissue-like valve construct for implantation into the body. There have been several promising studies that have successfully demonstrated in vivo functionality of TEHVs: (i) Hoerstrup and co-workers²³² implanted TEHVs in a ovine model that demonstrated functionality without stenosis, thrombus, or aneurysm for up to 20 weeks and histological data and ECM quantification showed ECM content comparable to native tissues; (ii) Stock et al.¹⁸⁹ formed pulmonary artery tissue similar to native; (iii) Sutherland et al.²⁰⁰ successfully implanted TEHVs that demonstrated substantial in vivo remodeling and remained functional for at least four months; and (iv) Rabkin et al.¹⁵⁷ reported the development of multi-layered TEHVs, with variations in ECM components in each layer. Much progress has been made in TEHVs, yet so far no patients have benefited from this nascent technology. While the results of these studies are indeed promising, TEHVs are still in early stages of development and have yet to become a truly viable heart valve replacement. As the body of knowledge surrounding TEHVs grows, it is important to fully understand the functional biomechanics of the engineered tissues and to compare their performance to their native counterparts to ensure a fully equivalent replacement tissue is generated. The current state of TEHVs and the engineering design and modeling principles that must be associated with future TEHV research has been extensively reviewed (cf. e.g., Sacks et al.¹⁶⁷).

MECHANICAL BEHAVIOR OF BIOPROSTHETIC HEART VALVE TISSUES

Mechanical testing typically involves applying some type of stimulus and measuring a response, and is generally achieved through imposing deformations on material—displacements/strains are specified and controlled and then the forces/stresses needed for such are measured or computed. The reciprocal approach, i.e., subjecting the material to a known force and recording its response, is also valid, although the former is more common. A constitutive model (or relation since it relates stress to strain) describes the gross behavior of the material to the applied loads under certain conditions of interest.⁹⁴ Only the specific form of the constitutive model is assumed, whereas its parameters are either measured or computed. Moreover, without accurate constitutive models, one clearly cannot establish a valid relationship between forces and displacements with predictive capabilities, and perform even the most elementary modeling and analyses. Furthermore, it must be stressed that no constitutive model will describe well all ranges of stress and strain, strain rate, loading cycles, temperature, humidity, etc. Rather, a constitutive model describes a material’s behavior under specific loading conditions that are of interest to a particular application. This rather intuitive statement is often overlooked—many discussions on the relative merits of different constitutive models often ignore that their intended uses are very different, and it is thus inappropriate to compare them. In general, in formulating a constitutive model for a material, one should “delineate general characteristics of the material, establish an appropriate theoretical framework, identify a specific functional (i.e., mathematical) form of the model, calculate values of the material parameters, and finally, evaluate the predictive capability of the final relation”.⁹⁴ It is first essential to stress the important distinction between experiments for material behavior characterization and experiments for model parameter identification.

Central to the framework of continuum mechanics is the concept of a material continuum and its applicability. The discrete composition of matter is ignored in the classical concept of a continuum—matter is uniformly distributed within each of the infinitesimal particles. However, real materials, particularly biological tissues, are inhomogeneous and a tolerable error must be accepted. Notwithstanding, if the tissue of interest possesses a length scale that is large enough with respect to the local structural details such that it is composed by a large enough number of infinitesimal particles, the material can be treated as a continuum. Heterograft tissues, e.g., bovine pericardium or valve leaflets, are highly hierarchically organized materials that have several orders of structural organization across multiple length-scales, such as fibrous networks and other large-scale structures, so that determining an appropriate continuum scale can be very difficult. Generally, the proper continuum scale of each structure (tissue, collagen network, cell) must be accessed and even with the inherent errors in utilizing a finite lower bound and disregarding lower scale features, the simplification in any analysis is enormous, but its practicality and applicability is crucial.

The framework of continuum mechanics is employed in the study of BHVs in two distinct but inter-related levels: (i) on one hand, valves function as a device, i.e., how in vivo loads affect valve leaflet deformation, is investigated at organ-level usually with the aid of finite element methods and is able to answer questions such as “what is the pressure differential that will cause valve prolapse?” or “how does the coaptation area changes with pressure?”; (ii) on the other hand, the framework or continuum mechanics is employed at tissue level, in association with systematic experiments such as uniaxial extension or biaxial extension, to determine the characteristic mechanical response of the valve material and to answer questions such as “what model should one employ to describe the response of the material?” or “how does the material moduli change with fixation treatments?”. In order to perform analyses of type (i) accurately, one needs to have sufficient confidence on models of type (ii) to be employed on them. However, additional modeling layers may be necessary to capture relevant biochemical and biological phenomena because these are complex and evolving tissues that interact with a living organism—these modeling layers could be included as coupled models at the cellular scale, or alternatively, incorporated ad hoc into the parameters of tissue-level models.

The formulation of constitutive frameworks to describe material behavior involves a two-pronged approach between theory and experiments. Initially, experiments are necessary to understand the response of the materials in question. The first step is to observe the many particular behaviors of interest, and then, by induction, delineate its general characteristics—this step is as critical as is difficult. The results of diverse exploratory experiments as well as pre-existing published results must be distilled to depict the underlying mechanisms or general characteristics of importance. Once this is accomplished, one then attempts to formulate general hypotheses or theoretical frameworks, which must be followed by more experiments to test their validity. These validating experiments are different in concept from the initial experiments—not only may these necessitate the design and construction of new experimental systems, but also they are driven by the predictions of the theory. Designed experiments are required for the determination of values of the material parameters and allow the evaluation of the predictive capability of the theoretical framework. Based on the experimental data, one will often need to refine the theory and perform additional experiments and data analysis for validation purposes. This iterative procedure continues until the associated model has predictive capability. Only then can one begin to answer the applied questions of interest, often via parametric studies with numerical simulations and ultimately resulting in animal and clinical trials.⁹⁴

There have been many studies to evaluate and characterize the mechanical properties of BHV tissues, however most of the available published data provides uniaxial tensile data only. Uniaxial data is fairly straightforward to obtain and allows for basic assessments of tissue mechanics. The studies and data presented herein exemplify a small portion of all available data, but allow for the comparison of multiple fixation chemistries and provide baseline material characterization data. Certainly these studies are not directly related to each other and they were not done in any systematic or concerted fashion, but significant conclusions can be obtained from their meta-analysis. The biaxial and flexural studies, in particular, have laid the framework for most computational models.

Uniaxial Tensile Mechanics

Uniaxial tensile testing is the most straightforward method used to evaluate very basic mechanical properties of biomaterials and cardiovascular tissues.^121,225 Usually, samples are placed in ambient phosphate buffered saline (PBS) and preconditioned using up to ten cycles of loading and unloading at 30-50% of the estimated failure stress to obtain reproducible results. Preconditioning is used to obtain a pseudoelastic response, in which separate but repeatable loading and unloading behaviors are observed. Then controlled uniaxial tension is applied to a sample until it fails. Values directly obtained from such testing include ultimate tensile strength (UTS) and maximum elongation, but reported data usually includes the stress–strain relationship, failure stress, and failure strain. Uniaxial tensile behavior of heterograft tissues is generally nonlinear, with the exponential behavior commonly observed in biological tissues and attributed to collagen fiber undulation, de-crimping, and engagement upon extension.^29,161 Simpler mechanical properties such as Young’s elastic modulus are not able to fully characterize this inherently nonlinear response, and most importantly, are not suited because they entail the application of the linearized theory of isotropic elasticity (with the restriction to infinitesimal strains) to biomaterials of BHVs undergoing large deformations not only during testing (for parameter determination) and but also during function (for subsequent mechanical analyses). However, it must be remarked that the Young’s modulus of the material is the slope of the stress vs. strain curve at the origin and can be used directly to compare performance at infinitesimal strains.

On the other hand, uniaxial tensile testing by itself is useful in the sense that it can be used to obtain insights into material characteristics based on method of failure. The specimen can exhibit fracture via crack development and propagation, creep due to slow increase in deformation, buckling, or even plastic deformation. These results provide information about the brittleness and ductility of the samples, as well as the uniaxial strength. Furthermore, although failure modeling is usually somewhat unreliable due to the currently underdeveloped state-of-the-art of theoretical models of material failure or even the physical understanding of its specific mechanisms, it is possible to ascertain trends and general failure characteristics by critical and rational comparison of ultimate tensile strength experiments of several materials, e.g., “material A fails at a higher stress than material B, and if material B is acceptable, then material A is acceptable”. Moreover, such characteristics can be correlated to other material characteristics, e.g., “if fatigue failure is assumed to be directly correlated with ultimate tensile strength, then material A will last higher number of cycles than material B”—however, caution must be taken when drawing conclusions from such inferences because one is implicitly assuming the direct correlation between both phenomena.

Multiple groups have evaluated the tensile strength of natural and chemically modified bovine pericardium.^36,122 The preferred fiber direction can usually be assigned to samples of carefully harvested fibrous pericardium. This tissue orientation direction is usually employed as a testing axis and subsequently, its orthogonal direction is defined as the cross-preferred direction. Collagen fibers contribute significantly to the mechanical response of the tissue, and tension needed to achieve similar extensions is significantly higher in the preferred direction than in the cross-preferred direction, corroborating the expected anisotropic response of the material. Uniaxial testing does not provide a great deal of information about the tissue, but it is a tool to perform simple characterization for comparative studies. Sung et al.¹⁹⁷ (among many others) have conducted uniaxial extension experiments of both native and fixed BP (Table 1). Sung et al¹⁹⁹ reported tangent modulus and have clearly observed the differences between the uniaxial characteristics for the PD and XD orientations, as well as the differences between multiple fixation chemistries including glutaraldehyde, epoxy and genipin, a naturally occurring crosslinking agent. Similar studies have been performed to characterize the uniaxial mechanical properties of porcine AV tissue.^20,124,115 Using a testing similar protocol, Sung et al.¹⁹⁸ reported uniaxial mechanical properties of fresh and fixed PAV (Table 1). On the other hand, published data on the human pulmonary valve mechanical and structural suitability as a long-term substitute for aortic valve are limited – Stradins et al.¹⁹⁰ compared aortic and pulmonary valve properties (Table 1).

TABLE 1.

Uniaxial mechanical properties of bovine pericardium, porcine AV, and human AV and PV, fresh and fixed (±SD). Adapted from Sung et al.^197,198 and Stradins et al.¹⁹⁰

Fixation method	Thickness (mm)	UTS (MPa)	Strain at fracture (%)	Tissue modulus (MPa)	Toughness (MPa)	Shrinkage (%)
Bovine pericardium
PD	n = 10	n = 5	n = 5	n = 5	n = 5	n = 5
Fresh	0.252 ± 0.027	25.6 ± 4.5	82.7 ± 4.7	69.6 ± 9.6	6.3 ± 0.7	N/A
Glutaraldehyde	0.448 ± 0.06	17.7 ± 3	120.6 ± 7.1	43.9 ± 10.6	5.7 ± 1.0	17.2 ± 0.5
Epoxy	0.376 ± 0.059	16.4 ± 3.4	114.7 ± 12.4	40.5 ± 4.7	6.5 ± 1.5	14.9 ± 2.7
Genipin	0.059 ± 0.08	21.3 ± 5.4	120.2 ± 10.9	42.5 ± 8.3	6.8 ± 2.4	17.1 ± 2.0
XD	n = 10	n = 5	n = 5	n = 5	n = 5	n = 5
Fresh	0.252 ± 0.027	12.7 ± 1.9	55.3 ± 4.6	48.8 ± 7.3	2.8 ± 0.7	N/A
Glutaraldehyde	0.448 ± 0.06	12.2 ± 3.5	103.6 ± 15.4	31.4 ± 8.1	3.8 ± 0.9	23.7 ± 3.5
Epoxy	0.376 ± 0.059	11.6 ± 1.9	103.9 ± 16.8	24.8 ± 1.8	4.3 ± 1.5	23.9 ± 4
Genipin	0.059 ± 0.08	21.7 ± 2.3	102.2 ± 9.8	41.0 ± 9.9	6.3 ± 1.6	23.2 ± 1.5
Porcine AV
PD	n = 12	n = 6	n = 6	n = 6	n = 6	n = 6
Fresh	0.261 ± 0.026	8.3 ± 0.9	48.7 ± 7.3	44.7 ± 5.3	1.8 ± 0.3	N/A
Glutaraldehyde	0.334 ± 0.043	8.3 ± 1.3	59.2 ± 7.6	32.1 ± 6.6	2 ± 0.1	6.7 ± 4.3
Genipin	0.397 ± 0.051	7.6 ± 0.7	69.8 ± 5.1	25.6 ± 4.8	2.3 ± 0.1	12.5 ± 4.3
XD	n = 12	n = 6	n = 6	n = 6	n = 6	n = 6
Fresh	0.261 ± 0.026	1.4 ± 0.2	134.8 ± 27.7	6.4 ± 0.9	0.8 ± 0.1	N/A
Glutaraldehyde	0.334 ± 0.043	1.2 ± 0.2	164.6 ± 17	5.3 ± 0.5	0.9 ± 0.0	11.3 ± 2.2
Genipin	0.397 ± 0.051	1.2 ± 0.3	177.3 ± 19.8	4.9 ± 0.5	1.0 ± 0.1	15.3 ± 6.4
Human valves	n = 11	n = 11	n = 11	n = 11
Pulmonary valve (circ)	0.397 ± 0.114	2.78 ± 1.05	19.40 ± 3.91	16.05 ± 2.02
Aortic valve (circ)	0.605 ± 0.196	1.74 ± 0.29	18.35 ± 7.61	15.34 ± 3.84
Pulmonary valve (rad)	0.397 ± 0.114	0.29 ± 0.06	29.67 ± 4.41	1.32 ± 0.93
Aortic valve (rad)	0.605 ± 0.196	0.32 ± 0.04	23.92 ± 3.94	1.98 ± 0.15

PD preferred direction, XD cross-preferred direction.

Planar Biaxial Tensile Mechanics

While uniaxial testing is useful for isotropic materials, biaxial tensile testing is necessary to properly characterize anisotropic materials. Biaxial loading testing allows one to obtain a tensorial relationship between stresses and strains. Most soft biological tissues exhibit significant anisotropy due to their fiber-oriented microstructure and thus their mechanical response is dependent on orientation. Biaxial tensile testing allows for a better understanding of the mechanical properties of the tissues under more complex loading conditions, more similar to those experienced in vivo. Additionally, the development and the employment of anisotropic constitutive models requires data obtained via biaxial testing. For biaxial mechanical tests, sutures are placed around the perimeter of rectangular shaped specimens and markers are placed in the center of the specimen. Similarly to uniaxial testing, specimens are placed in a bath of ambient PBS and undergo cyclic preconditioning up to 10 cycles. Then, controlled planar biaxial tension is applied to the sample. The displacement of the markers is recorded and is subsequently used to calculate the inplane strain tensor. Multiple test protocols are performed to fully characterize the sample under different loading states. Each protocol is stress- or strain-controlled and all protocols keep a constant ratio of stress or strain. Representative experimental data are a set of the stress vs. strain responses for multiple protocols (Fig. 7). Data from all protocols serves as input into a constitutive model, and a single stress vs. strain response to one particular protocol is meaningless—only when the entire set of experimental data is reduced into the parameters of the model of choice by regression, the constitutive model is able to describe the response of the material in general, and then, a few illustrative responses of the model are usually reported (e.g., equibiaxial response). For the sake of comparison, the responses of various tissues to one protocol and the models describing such responses can be paired and are frequently reported as a result.

FIGURE 7.

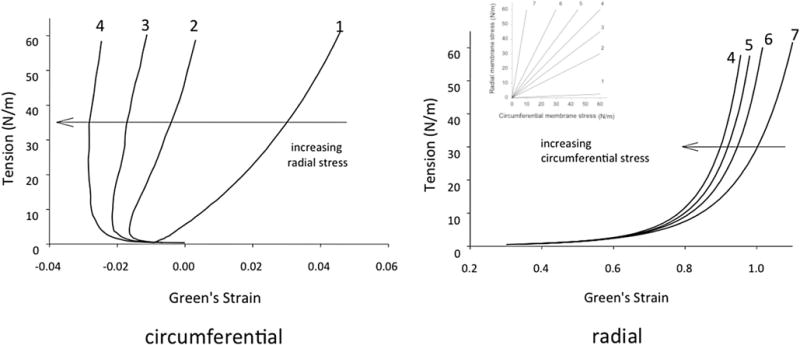
AV cuspal stress-strain data for the (a) circumferential and (b) radial directions for a GL treated cusp demonstrating the effects of transverse loading (in-plane coupling). Number adjacent to curves indicate biaxial test protocol number.⁷

Sacks and Chuong performed a series of biaxial tests to characterize fresh and fixed bovine pericardium (Table 2).¹⁶³ All chemically treated specimens were seen to exhibit mechanical anisotropy, with the pre-stretched tissues showing the most distinct anisotropic response, followed by the free-fixed and the control groups. The experimental data obtained in this study was then reduced to constants of a hyperelastic constitutive model. Christie and Barratt-Boyes performed the first porcine AV equibiaxial testing,²⁸ however it was determined that in order to develop a constitutive model more complete multiprotocol data was required. Billiar and Sacks⁷ were the first to compile comprehensive biaxial data for modeling the porcine aortic valve leaflet (Fig. 7; Table 3). It was determined that the optimal tissue selection site was from the lower-belly region of the valve leaflet, slightly off-center below the nodulus of Arantii. In light of the complex composition, curvature, and geometry of the aortic valve, this section of tissue has the most homogeneous strain field and fiber structure and the collagen alignment is primarily in the circumferential direction. Once again, data collected by Billiar and Sacks was reduced to constants of a structural constitutive model.⁸ Christie and Barratt-Boyes measured the biaxial properties of pulmonary and aortic leaflets in extension in the native and treated states (Table 4).⁷⁴ Additionally, Martin and Sun compared aortic valve tissues in humans and common animal models, namely porcine and ovine (Fig. 8).¹³⁶ Both ovine and porcine valvular tissues consistently show higher strain at 60 N/m membrane tension than human tissues, and this is an important consideration when developing preclinical models.

TABLE 2.

Biaxial data for native and fixed bovine pericardium.

Group	Strain at fixation	Max. strain	Thickness (μm)	Peak stress (kPa)		Max. tangent modulus (MPa)
				PD	XD	PD	XD
Control	N/A	0.16	343 ± 10	323.18 ± 22.56	107.12 ± 6.75	14.96 ± 2.77	2.8 ± 0.35
GLFF	Free	0.16	781 ± 114	168.73 ± 9.74	96.66 ± 8.09	3.27 ± 0.25	1.31 ± 0.18
GLPS	0.22	0.06	430 ± 81	429.47 ± 49.28	122.46 ± 5.00	39.89 ± 11.14	1.28 ± 0.2
POFF	Free	0.16	719 ± 77	66.17 ± 2.31	37.53 ± 5.16	1.22 ± 0.06	0.46 ± 0.1
POPS	0.22	0.16	512 ± 91	125.34 ± 11.29	43.57 ± 2.98	2.43 ± 0.31	0.42 ± 0.05

Thickness values are ± SD, peak stress and MTM are ± SEM.¹⁶³

TABLE 3.

Radial and circumferential extensibility for fresh and glutaraldehyde treated porcine aortic valve under equi-biaxial tension (± SEM). Adapted from Billiar and Sacks.⁷

	Width (mm)	Thickness (mm)	Green’s Strain at 1 N/m	Green’s Strain at 9 N/m	Green’s Strain at 60 N/m	Index of Isotropy	Shear angle α (deg)
Radial
Fresh	13.68 ± 0.46	0.466 ± 0.02	0.646 ± 0.035	0.913 ± 0.061	1.109 ± 0.075	0.247 ± 0.023	5.88 ± 1.326
Fixed	11.32 ± 0.27	0.457 ± 0.02	0.292 ± 0.028	0.619 ± 0.047	0.958 ± 0.07	0.022 ± 0.012	13.02 ± 1.58
Circumferential
Fresh	14.23 ± 0.42	0.466 ± 0.02	0.194 ± 0.012	0.244 ± 0.016	0.264 ± 0.017	0.247 ± 0.023	5.88 ± 1.326
Fixed	13 ± 0.19	0.457 ± 0.02	0.001 ± 0.006	0.01 ± 0.008	0.024 ± 0.012	0.022 ± 0.012	13.02 ± 1.58

TABLE 4.

Biaxial stretch for fresh and glutaraldehyde treated porcine pulmonary valve under equi-biaxial tension (± SEM). Adapted from Christie and Barratt-Boyes.⁷⁴

	Stretch at 60 N/m (percent)
	Radial	Circumferential
Aortic, natural	74.5 ± 7.8	12.4 ± 1.8
Pulmonary, natural	90.3 ± 5.7	10 ± 1.9
Aortic, GLUT	64.3 ± 5.8	9.5 ± 1.8
Pulmonary, GLUT	88.8 ± 2.6	13.5 ± 1.0

FIGURE 8.

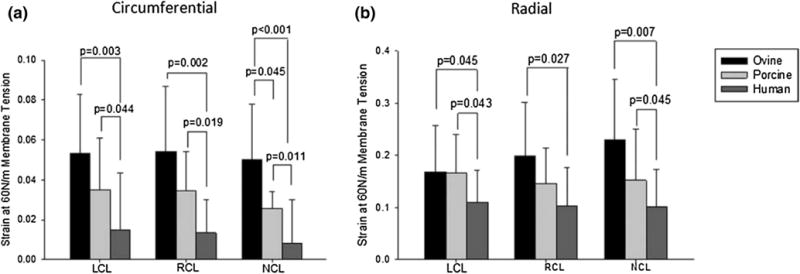
Green strain presented as a mean ± standard deviation at a membrane tension of 60 N/m in the (a) circumferential and (b) radial directions with all statistically significant differences indicated by the corresponding p value, with n = 10 for each species and leaflet type. Adapted from Martin and Sun.¹³⁶

Flexural Tensile Mechanics

Flexural mechanical testing is used to add further insight to tissue response, particularly when subjected to different modes of deformation that are not included in uniaxial and biaxial extension. In flexural analysis, different parts of the sample being tested are subjected to shear, tension, and compression. Flexure is vital for understanding the in-plane response of the material as this direction is not tested in uniaxial, strip-biaxial or multi-axis biaxial. Furthermore, flexural testing allows the determination of the effect of compressive forces on a tissue in a bent configuration, especially since this is considered to be a major deformation mode of the AV. Additionally, compressive stresses are believed to impact the degradation of bioprosthetic tissues,^213,224 and are thus critical to better understand in order to design improved BHVs. To test the flexural rigidity of a sample, an optical system is used to obtain curvature data and bending bar displacement, which are subsequently used to calculate the moment-curvature (M/I vs. Δκ) response (Fig. 9). Data obtained from flexural testing can then be used to calculate the effective modulus of a tissue using the Euler–Bernoulli relationship (detailed testing methodology and experimental results for various flexural mechanical responses can be found elsewhere^44,61,141).

FIGURE 9.

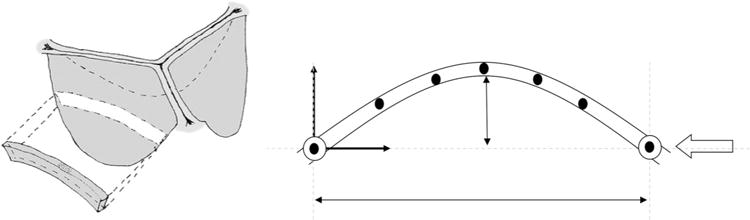
(a) Section of aortic valve used for flexural testing to capture unique interaction between transmural layers. (b) Schematic of the experimental determination of curvature with markers.

Flexural mechanical testing has been used to effectively study cellular and structural effects on the flexural stiffness of both pericardial biomaterials and the aortic valve leaflet. Mirnajafi et al.¹⁴¹ evaluated the effect of collagen fiber orientation on the flexural properties of pericardial heterograft tissues. When evaluated for flexural mechanics, native bovine pericardium produced a slightly non-linear moment-curvature response in both the visceral and epicardial directions of flexure (Fig. 10). Due to the non-linearity of the results, instantaneous effective stiffness is reported (Table 5).¹⁴¹ This contrasts to porcine aortic valve tissue, which presented a very linear moment–curvature response. As expected, chemical fixation by glutaraldehyde increased the stiffness for BP and porcine AV. Upon fixation, non-linearity is maintained for BP just as linearity is maintained for porcine AV. The flexural mechanics of the belly region of the native porcine AV were measured in a study looking at the effects of cellular contraction on stiffness by Merryman et al.¹³⁸ (Table 6). However, the complex geometry of the commissural region made it necessary to use a cantilever method to fully evaluate flexural mechanics of the porcine AV (Table 7).¹⁴⁰ Additionally, while it has previously been unknown as to how the layers of the AV interact, recent transmural flexural data has shown that the fibrosa, spongiosa, and ventricularis act as one bonded unit, rather than sliding as has previously been thought to occur.¹⁵ Flexural mechanical testing has also been used to evaluate the flexural stiffness of TEHV scaffolds and constructs.^44,45

FIGURE 10.

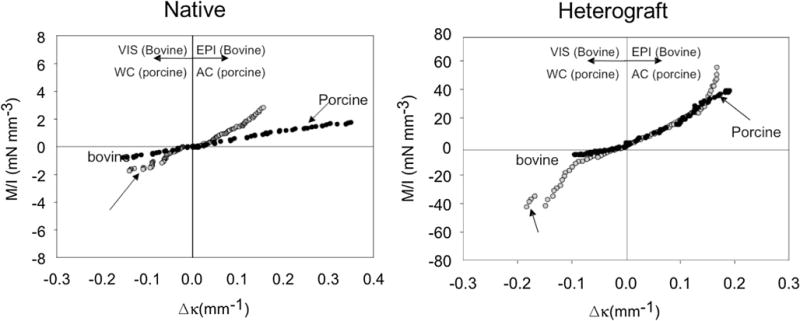
Representative moment-curvature data for both (a) natural and (b) heterograft bovine pericardium and porcine AV. Adapted from Mirnajafi.¹⁴¹

TABLE 5.

The dimensions of the specimens and the maximum moments applied to the specimens of native and fixed bovine pericardium (±SEM). Adapted from Mirnajafi.¹⁴¹

	Thickness (mm)	Width (mm)	I (mm4)	Max M VIS (mn-mm)
PD Native	0.35 ± 0.02	3.3 ± 0.1	0.0125 ± 0.0025	0.9049 ± 0.3753
XD Native	0.35 ± 0.02	3.9 ± 0.2	0.0147 ± 0.0024	0.7363 ± 0.1431
PD GLPB	0.67 ± 0.02	2.8 ± 0.31	0.0716 ± 0.0082	0.3691 ± 0.0828
XD GLPB	0.65 ± 0.95	2.55 ± 0.02	0.0624 ± 0.0479	0.5033 ± 0.0066
	Max M EPI (mn-mm)	Max Δκ VIS (mm−1)	Max Δκ EPI (mm−1)	Ē at Δκ = 0.02 mm−1
PD Native	0.6033 ± 0.1666	0.169 ± 0.0171	0.1853 ± 0.0412	0.128 ± 0.062
XD Native	0.6182 ± 0.093	0.1245 ± 0.0119	0.1102 ± 0.0157	0.391 ± 0.064
PD GLPB	0.4739 ± 0.1044	0.281 ± 0.0168	0.2369 ± 0.0162	0.7201 ± 0.1549
XD GLPB	0.5409 ± 0.0395	0.2535 ± 0.0687	0.2307 ± 0.017	1.2097 ± 0.1156

n = 8 for native, n = 10 for GLBP.

TABLE 6.

The dimensions of and the maximum moments applied to the specimens of native porcine AV. Adapted from Merryman et al.¹³⁸

	Thickness (mm)	l (mm4)	Max M (mN-mm)	Max Δκ (mm−1)	Eeff (kPa)
AC	0.38 ± 0.03	1.00E–02 ± 2.18E–03	1.529 ± 0.204	0.268 ± 0.025	703.05 ± 132.58
WC	0.43 ± 0.02	2.75E–02 ± 3.65E–03	1.701 ± 0.203	0.153 ± 0.018	491.69 ± 135.17

n = 9, ± SEM.

TABLE 7.

Cantilever method for porcine aortic valve tissue, n = 10, ± SEM. Adapted from Mirnajafi et al.¹⁴⁰

	Forward direction	Reverse direction
Effective modulus, E, at flexure angle of 30° (kPa)	42.73 ± 4.44	75.01 ± 14.53
dE/dϕ (kPa/°)	−2.24 ± 0.6	−1.9 ± 0.3

EFFECT OF EXOGENOUS CROSS-LINKING AS A MEANS FOR TISSUE PRESERVATION

Bioprosthetic heart valve tissue generated from heterograft tissues must be chemically fixed to preserve the tissue and to decrease potential in vivo structural degradation. The most commonly utilized crosslinking agent for bioprosthetic tissues is glutaraldehyde (GLUT). Glutaraldehyde fixation employs a Schiffbased aldehyde reaction to crosslink two amine groups, and is very effective at crosslinking collagen molecules. It is the current standard fixation method for bioprosthetic heterograft tissues, however glutaraldehyde significantly affects leaflet mechanics. Additionally, while tissues fixed by glutaraldehyde initially have no immune response, they are susceptible to eventual calcification, and using an aldehyde to fix implantable tissue has also raised concerns regarding cytotoxicity. Other fixation methods are being evaluated with the goal to reduce calcification potential, maintain mechanical properties similar to native valve tissues, and reduce cytotoxicity.

In a study on the effect of different fixation methods on bovine pericardium, polyglycidyl ether and glutaraldehyde caused substantial crosslinking, and changes in mechanical properties including a decreased stress relaxation and increased extensibility. Cyanimide (which crosslinks pure collagen) did not effectively crosslink tissue, heat-drying increased ultimate tensile strength and tissue modulus, and freeze-drying had no effect.¹⁵¹ Genipin, a naturally occurring crosslinking agent, and carbodiimide were found to be effective crosslinking agents but produce distinct crosslinking structures, which may in turn affect other properties of the fixed tissue (Table 5).¹⁹⁹ Mercuri et al.¹³⁷ looked into GAG-targeted fixation which allowed for higher retention of GAGs, but did not alter the calcification potential of the leaflets compared to conventional GLUT-treated tissue.

Zero-pressure GLUT-fixation has been shown to produce fixed tissue with minimal changes to functional biomechanics and produces a softer and more extensible tissue than one treated under even low pressure.²⁷ However, Wells and Sacks varied transvalvular fixation pressure and applied accelerated cyclic-loading tests and showed that zero pressure fixed porcine BHV demonstrated conformational changes under long-term cyclic loading and eventually decreased in extensibility to the level of the low-pressure fixed tissue.²²⁷

Sung et al.¹⁹⁹ performed a study to investigate the effect of different fixation chemistries on porcine pericardium and found that genipin and carbodiimide are indeed effective crosslinking agents for tissue fixation. The authors have also incorporated the use of Nhydroxysuccinimide to increase the number of crosslinks introduced (Table 8).

TABLE 8.

Mechanical properties of porcine pericardium tissues fixed with various methods. Adapted from Sung et al.¹⁹⁹

Fixation chemistry	Thickness (mm) n = 10, ±SD	Tensile strength (MPa) n = 5, ±SD	Strain at fracture (%) n = 5, ±SD
Fresh	0.095 ± 0.008	18.1 ± 1.6	55.6 ± 13.5
Genipin	0.167 ± 0.006	16 ± 1.2	81.9 ± 5.9
Carbodiimide	0.114 ± 0.004	13.1 ± 1	60 ± 10.9
Carbodiimide + NHS	0.119 ± 0.008	13.4 ± 0.6	60.5 ± 9.1
Genipin then Carbodiimide + NHS	0.154 ± 0.014	15.9 ± 1.4	84.1 ± 13.4
Carbodiimide + NHS then Genipin	0.168 ± 0.008	15.7 ± 0.9	85.3 ± 13.3

CONSTITUTIVE MODELS

Early attempts to describe valve tissue properties used the linear elastic model following the generalized Hooke’s law.²² Linear elastic models are appropriate when the stress-strain relationship is indeed linear, yet the linearized theory of elasticity is restricted to motions with relatively small displacement gradients. However, the stress-strain relationship of heterograft materials is grossly nonlinear, and valvular function typically involves finite large deformations. As a common computational mechanics alternative, Hamid et al.⁷⁹ and Li et al.¹²⁶ specified piece-wise linear tangent modulus to approximate non-linear material behavior, thus avoiding the numerical difficulties associated with full blown nonlinear material models. Nonetheless, the overwhelming disadvantage of the linearized elasticity framework lies in its inaccuracy dealing with finite deformations, thus prohibiting any realistic valve simulations. To overcome this challenge, hyperelastic models have been employed to describe biological tissue under finite deformations for simulation of the function of BHVs.^193,194 The most common hyperelastic material model is the exponential model proposed by Fung,²⁹ and has been utilized to date for characterizing the mechanical response of soft biological tissues, including skin,²¹⁵ pericardium,²⁵ epicardium,⁹⁷ visceral pleura,⁹⁸ and many others.

Phenomenological Hyperelastic Models

Glutaraldehyde-treated pericardium tissue under biaxial stretch is properly described with an orthotropic, Fung type hyperelastic model. The second Piola–Kirchhoff stress S can be computed by

$$\mathbf{S}=\frac{\partial W}{\partial \mathbf{E}}$$ (1)

where E is the Green-Lagrange strain tensor, and W is the stored energy function of the BHV material. Pericardial tissues and heart valve leaflets are thin membranes, therefore two-dimensional constitutive laws are often implicitly assumed. A Cartesian coordinate system (e₁, e₂, e₃) is employed with the 1- and 2-directions commonly in the plane and aligned along preferred and cross-preferred fiber directions respectively, and the 3-direction as the transversal direction. The in-plane bending response is neglected, and although pericardium and heart valve leaflets are not homogeneous membranes (i.e., there are observable variations across the thickness), the state of plane stress is commonly assumed (by definition, S₁₃ = S₂₃ = S₃₃ and consequently E₁₃ = E₂₃ = 0, but E₃₃ ≠ 0 and often overlooked experimentally). Notwithstanding, it is worth remarking that Sun et al.¹⁹⁶ have observed high in-plane shear stresses in GLBP generated with substantially asymmetric protocols (e.g., 1:0.1) while covering a wide range of the strain-stress space. Asymmetric protocols showed not only large shear response, but also lesser extensibility for the normal components, suggesting a substantial change in mechanical behavior under extreme T₁₁:T₂₂ ratios. In order to account for this difference, more general constitutive relations accounting for high inplane shear response or bending stresses can be obtained simply by complementing the 2D-plane stress tensor with additive higher order terms (cf. Sun et al.¹⁹⁶)—nevertheless, more general and capable constitutive models often imply additional constants to be determined, and mainly, multiprotocol experimental data to be made available. The generalized Fungtype elastic 2D-anisotropic model under the assumption of plane stress is

$$W=\frac{c}{2}(e^Q-1)$$ (2)

with

$$\begin{array}{l}Q=a_1{E}_{11}^2+a_2{E}_{22}^2+2a_3{E}_{11}{E}_{22}+a_4{E}_{12}^2+2a_5{E}_{11}{E}_{12}\\ +2a_6{E}_{12}{E}_{22}\end{array}$$ (3)

Constants c and a_i, i = 1,2,…6 are material constants, characterize the mechanical response of the material, and must be determined from experimental data reduction. Li and Sun performed biaxial mechanical testing on 25 mm × 25 mm squares of native and treated bovine and porcine pericardium,¹²⁷ have observed the usual anisotropy of these tissues, and identified the X₁ direction as the stiffer orientation of the material and X₂ direction along the less stiffer direction determined by the equibiaxial testing protocol. Conducting a systematic set of stress-controlled test protocols with different stress ratios on 10 samples of each type of tissue, the authors have determined a set of constants using the Marquardt-Levenberg nonlinear least squares method with a simultaneous fit of all the collected experimental data with a different testing protocols to reduce the effect of multiple collinearities (Table 9; Fig. 11).

TABLE 9.

Material constants of Fung-elastic model of glutaraldehyde-treated bovine and porcine pericardium (cf. Li and Sun¹²⁷).

	c (kPa)	a1	a2	a3	a4	a5	a6	r2
Bovine pericardium	16.24	66.73	34.52	1.29	24.09	0.77	0.53	0.99
Porcine pericardium	20.23	59.33	26.1	−2.68	24.04	−1.35	1.51	0.99

Material parameters were obtained by reducing biaxial testing experimental data. The specific form of stored energy function employed is given in Eqs. (2) and (3) and illustrative results comparing model predictions and experimental data is shown in Fig. 6.

FIGURE 11.

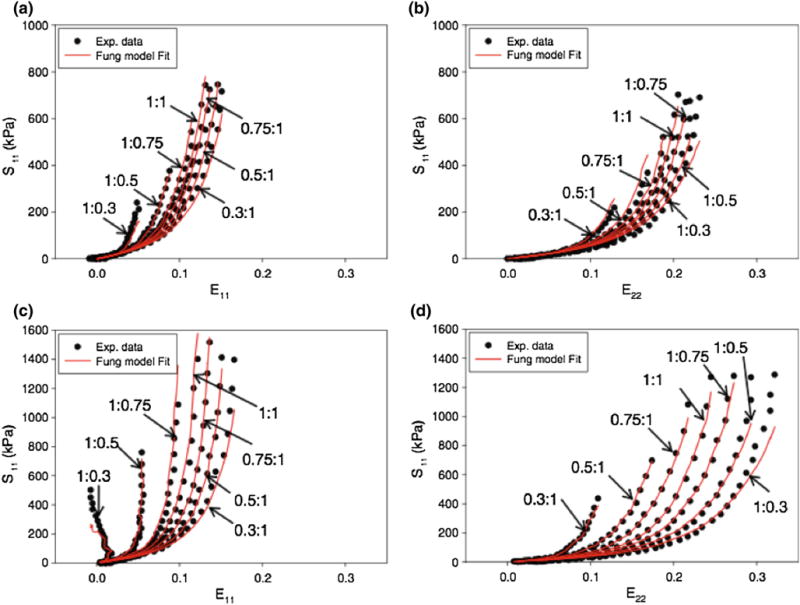
Representative biaxial test data and Fung model fitting curves [with Eq. (4)] of glutaraldehyde treated (a, b) bovine pericardium and (c, d) porcine pericardium for 7 strain protocols (from Li and Sun¹²⁷).

Sacks and Chuong¹⁶³ have employed a different orthotropic stored energy function of the form (adopted from Choi and Vito²⁶ proposed for canine pericardium):

$$W=b_0\left[\exp \left(\frac{1}{2}{b}_1{E}_{PD}^2\right)+\exp \left(\frac{1}{2}{b}_1{E}_{XD}^2\right)+\exp \left(b_3{E}_{PD}{E}_{XD}\right)-3\right]$$ (4)

where PD and XD are tissue directions aligned with preferred fiber direction and perpendicular to preferred fiber direction determined by SALS. Choi and Vito²⁶ and Sacks and Chuong¹⁶³ have both obtained good fits of experimental data obtained with biaxial testing for canine and bovine pericardium respectively (not shown), and the latter have conducted a study on the effects of different chemical treatments on the mechanical properties of the tissue (Table 10).

TABLE 10.

Material constants of orthotropic Fung-elastic model of bovine pericardium chemically treated with different protocols (cf. Sacks and Chuong¹⁶³).

Group	n	b0 (kPa)		b1 (kPa)		b2 (kPa)		b3 (kPa)		r2
		Specimen	Group	Specimen	Group	Specimen	Group	Specimen	Group	Specimen	Group
Control	7	0.243 ± 0.117	0.217	288.96 ± 45.88	256.3	154.01 ± 25.66	144.13	131.67 ± 24.74	113.01	0.933 ± 0.038	0.842
GLIFF	12	1.873 ± 0.153	1.738	106.93 ± 2.79	111.23	71.39 ± 6.04	74.16	45.52 ± 2.60	46.83	0.970 ± 0.003	0.723
POFF	11	0.838 ± 0.088	0.834	101.5 ± 4.00	100.80	63.29 ± 5.48	64.28	43.19 ± 0.79	42.09	0.990 ± 0.002	0.947
GLPS	9	3.677 ± 0.470	4.93	601.8 ± 57.78	517.47	107.29 ± 25.24	88.56	124.1 ± 7.30	88.55	0.982 ± 0.003	0.924
POPS	10	2.151 ± 0.439	1.55	99.36 ± 8.526	104.99	43.99 ± 5.57	44.98	33.64 ± 5.08	38.32	0.991 ± 0.002	0.881

The specific form of stored energy function employed to reduce the experimental data is given in Eq. (4).

Although the Fung model has been in the literature for many years, and systematic experiments to obtain its constants describing chemically treated multi-species pericardium have been conducted and published, its actual implementation into finite element formulations has been very limited—a major reason for this is the inherent numerical instability/convergence of the Fung model in numerical schemes due to its conditional convexity/elipticity²²⁹ and exponential behavior (making small changes in strain result in large changes of stress). One often overlooked aspect of the employment of phenomenlogically-based hyperelastic models (not only Fung’s model, but other models as well, e.g., such as Mooney-Rivlin’s W = μ₁ (I₁−3)+ μ₂ (I₂−3) where I₁ and I₂ are the principal invariants of the left Cauchy–Green stretch tensor C and μ₁ and μ₂ are material parameters) to fit experimental data is associated with the restrictions necessary to be enforced in the parameter space such that the second law of thermodynamics is not violated. The stored energy function must remain positive-definite, and best fit values of the material parameters must yield physically realistic results for all deformations within the range of interest—two ways of ensuring this are either (i) to restrict a priori the allowable ranges of parameters that the regression can choose, or (ii) to check a posteriori that one does in fact obtain reasonable predictions with the best-fit parameters. The former has been subject of extensive research: particularly related with biological materials, Humphrey et al.^95,96 performed biaxial testing on excised myocardium and has identified inequalities necessary to be satisfied by the best fit parameters, and Sun and Sacks¹⁹⁴ have restricted the parameter space of Eqs. (2) and (3) with the following inequalities

$$\begin{array}{l}c>0,\\ a_1>\left|a_3\right|,\\ a_2>\left|a_3\right|,\\ a_1{a}_2{a}_4+2a_3{a}_5{a}_6-a_2{a}_5^2-a_1{a}_6^2-a_4{a}_3^2>0\end{array}$$ (5)

and demonstrated that these numeric constraints need to be imposed in order to achieve computational stability and have presented the first valve simulation using the Fung elastic model.¹⁹⁴

Not much novelty in regard to material models has been employed in BHV simulations besides standard hyperelasticity, where the application of phenomenologically-reasoned exponential forms (as originally proposed by Fung) has dominated over the polynomial and the logarithmic forms in the accurate description of cardiovascular tissue in general. However, these models do not account for fiber orientation directly (but here, it must be stressed that anisotropic hyperelastic material models are in fact naturally able to account for tissue anisotropy originating due to fiber orientation), and fiber orientation and material inhomogeneity is a key aspect not only of native heart valves, but also of bovine pericardium (Fig. 12; Table 10). The impact of material inhomogeneity in BHVs is twofold: (i) Sacks and Chuong¹⁶³ used small angle light scattering (SALS) to quantify the collagen fiber architecture of the bovine pericardium sac and have observed large animal-to-animal variability in fiber architecture, precluding the use of an anatomic location as a simple guideline for selecting structurally consistent specimens, not only for material characterization but also for BHV fabrication; and (ii) tissue structure and collagen fiber architecture are major factors of the anisotropic response of the tissue, therefore in order to minimize difficulties with its intrinsic structural and mechanical variability, structurally uniform specimens must be selected from the BP sac for material characterization.^83,84 Only by conducting a two-step pre-sorting procedure with bovine pericardium examined with SALS, Sacks and Chuong¹⁶³ were able to collect biaxial test samples with a high degree of structural uniformity from regions of good structural consistency. The consistency of the samples was then reflected in the consistency of the mechanical properties and the small standard errors in the material constants for all specimens (Fig. 13; Table 10), and in the ability to combine all experimental data into a single data set and reduce it to group material constants representing the data reasonably well and showing predictive capability.

FIGURE 12.

Overview of two-tiered BP tissue sorting procedure with vector plots showing distribution of regional fiber preferred directions (from Sacks and Chuong¹⁶³). (a) A course small angle light scattering (SALS) scan of an anterior section of the BP sac showing where a 50 mm × 75 mm rectangular cutout regions were extracted, (b) a rescan of the cutout showing where the 25 mm × 25 mm biaxial testing specimen was selected, and (c) high spatial resolution scan of the biaxial test specimen overlaid on a gray scale OI values demonstrating high uniformity of both fiber preferred directions and OI, along with definition of the preferred and cross direction axes.

FIGURE 13.

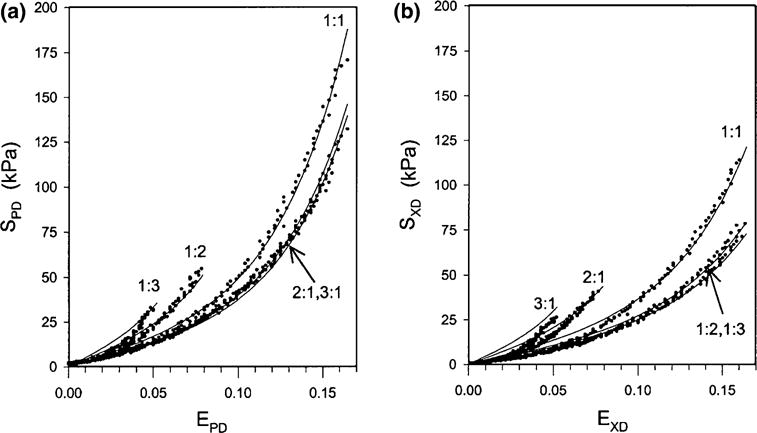
Biaxial mechanical behavior of glutaraldehyde treated bovine pericardium for five strain protocols (indicated beside each curve) for the (a) preferred direction (PD, 11 in the above nomenclature) and the (b) cross direction (CD, 22 in the current nomenclature). Also shown is the fit of the structural constitutive orthotropic model [cf. Eq. (4)], which demonstrated a very good fit to the data for all protocols (adapted from Sacks¹⁶¹).

Another important aspect is the inherent inability of phenomenologically-based hyperelastic models with parameters determined by fitting experimental data to obtain reliable predictions outside of the range of conditions tested. Although the determined parameters are reliable descriptors of the material behavior within the tested conditions (i.e., when one in interpolating material behavior from the experimental data), they fail considerably in ranges beyond the conditions tested. Phenomenologically-based hyperelastic models should not be used for extrapolating material behavior. Faced with such scenario, new datasets of material response under these new conditions of interest must be obtained, and new parameters must be fitted such that the hyperelastic model is once again able to interpolate material behavior. Overall, phenomenologically-based models are always hampered by the amount of experimental data that is or is not collected, and most importantly, the inherent need of multiprotocol data to capture effects that may not be observable within a certain experimental regime—indeed, only an infinite number of experiments is able to fully characterize an hyperelastic material. Finally, it is also generally perceived that these models encompass further disadvantages: they (i) require a large number of parameters to obtain accurate data fits, (ii) originate parameters without direct physically meaning, and (iii) possess a natural difficulty to account for regional differences in material behavior. These drawbacks have been responsible to drive the general preference to structurally-informed models where spatial dependent fiber orientation is explicitly incorporated in the constitutive model.^{86,117,161,162}

Structurally-Informed Hyperelastic Models

The ability to go beyond the tested conditions with at least some degree of confidence and robustness is the main reason why structurally-informed models, derived from critical reasoning of material structure and response, might be considered advantageous over their phenomenological counterparts. Over the last decade Sacks and co-workers have been developing and refining structural based constitutive models of planar soft tissues,^7,8,161,162 an approach based on the theoretical framework of Lanir.^117,118 Structural models rely on experimental data characterizing the tissue microstructure and a representative volume element (RVE), which is large enough to represent the processes associated with the microstructure of the material in some average sense (particularly, the collagen fiber architecture), but yet small compared to the characteristic length scale of the bulk tissue (i.e., the tissue thickness). The RVE is treated as a fiber-reinforced three-dimensional continuum and it is assumed that the stress in the material can be obtained from the stored energy function of a hyperelastic solid following Eq. (1).

Within the RVE, the following assumptions are made:

1. Pericardium can be idealized as a planar network of collagen fibers embedded in a compliant ground substance, i.e., the matrix. Since pericardium contains only a small amount of elastin,²¹⁷ its contribution is usually ignored. Further, the hydrostatic forces generated by the matrix are considered negligible compared to the fibers forces and are usually ignored (recently, Fata et al.⁴⁸ have proposed a 3 component structural model for pulmonary artery remodeling on which the effect of muscle and elastin were included because not only the mass fractions of each component were determined with biochemical assays, but also the effect of passive muscle and the elastin micro-structure was available using novel-biaxial mechanical-multiphoton microscopy).

2. Collagen fibers are undulated, and their undulation gradually disappears with stretch. The load required to straighten the collagen is negligible compared to the load transmitted by the stretched fibers. Hence, each collagen fiber transmits load only if stretched beyond the point when all its undulation has disappeared, and is assumed to be elastic.

3. The degree of fiber undulation can vary considerably. At the tissue level, the gradual straightening of the linear elastic collagen fibers with variable undulations produces the classical nonlinear stress-strain relationship of soft tissues.

4. Fiber strain can be computed from the tensorial transformation of the global strain tensor referenced to the fiber coordinate system (i.e., the affine transformation assumption).

5. The strain energy function of the tissue is the sum of the individual fiber strain energies.

Affine transformation from the bulk tissue to the collagen microstructure allows the determination of the uniaxial strain ε along each fiber from the global tissue strain state E

$$\epsilon =\mathbf{n}\cdot \mathbf{E}\mathbf{n}$$ (6)

where n is a unit vector aligned with the fiber orientation (n = cos θe₁ + sin θe₂, thus θ is the angle of the fiber with the tissue e₁ direction). The 2^nd Piola–Kirchhoff stress in the fiber is given as a function of the fiber strain, and because the fiber is only able to carry stress along its direction, results in

$$S^f=S^f(\epsilon )=S_{nn}^f(\epsilon )\mathbf{n}\otimes \mathbf{n}.$$ (7)

One component of the structural model is the fiber uniaxial stress-uniaxial strain law $S_{nn}^f(\epsilon )$, which can simply be given by

$$S_{nn}^f(\epsilon )=A[\exp (B\epsilon )-1]$$ (8)

with A and B positive constants.

The other component of the structural model is the tissue stress-strain relationship. The stored energy function of the fiber ensemble is the summation of the stored energies functions w(ε) of each individual fiber of the ensemble and is achieved with the integration along all fiber directions

$$W_f=c_f{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}R\left(\theta \right)w\left(\epsilon \right)d\theta }$$ (9)

where c_f is the fiber volume fraction. Fiber angular distribution function R(θ) is a key component of the structural model. Unlike in many man-made composites, the angular orientation of collagen fibers in tissues is not known a priori. This feature is measured experimentally with small angle light scattering (SALS). SALS principle relies on the fact that angular distribution of scattered light I(θ) is directly proportional to the angular distribution of fibers.¹⁶⁸

The tissue stored energy function, assuming an isotropic strain energy contribution due to the matrix and a volume fraction of fibers given by c_f, results in

$$W=c_f{W}_f+(1-c_f)W_m$$ (10)

with

$$W_m=\frac{c_0}{2}\exp [c_1(E_{11}^2+E_{22}^2+2E_{11}{E}_{22})]$$ (11)

where c₀ and c₁ are constants characterizing the isotropic mechanical response of the matrix. Finally, the stress-strain relationship,

$$\mathbf{S}=\frac{\partial W}{\partial \mathbf{E}}=c_f{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}R(\theta )}{S}_{nn}^f(\epsilon )\mathbf{n}\otimes \mathbf{n}d\theta +(1-c_f)\frac{\partial W_m}{\partial \mathbf{E}}$$ (12)

or, in component form along the tissue directions, is given by

$$\begin{array}{l}{S}_{11}=c_f{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}R(\theta )}{S}_{nn}^f(\epsilon ){\cos }^2\theta d\theta \\ +(1-c_f)c_0{c}_1(E_{11}+E_{22})[c_1(E_{11}^2+E_{22}^2+2E_{11}{E}_{22})]\\ S_{12}=c_f{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}R(\theta )}{S}_{nn}^f(\epsilon )\cos \theta \sin \theta d\theta \\ S_{22}=c_f{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}R(\theta )}{S}_{nn}^f(\epsilon ){\sin }^2\theta d\theta \\ +(1-c_f)c_0{c}_1(E_{11}+E_{22})[c_1(E_{11}^2+E_{22}^2+2E_{11}{E}_{22})]\end{array}$$ (13)

Sacks¹⁶¹ employed the structural model described above and obtained good agreement with experimental data and small variations on constants A, B, c₀ and c₁ in Eqs. (8) and (11) (Table 11). Fiber angular distribution R(θ) is experimentally determined by SALS, thus values of constants A and B can be determined by fitting the results obtained with the equibiaxial strain test protocol (E₁₁ = E₂₂ = E) on which the contribution of the isotropic matrix can be removed by considering the stress difference S₁₁ – S₂₂. Once A and B are determined, constants c₀ and c₁ could be found, while fiber volume fraction c_f was not known and was set at c_f = 0.5.

TABLE 11.

Fitted material constant results for Eq. (4) with GLBP treatment (cf. Sacks¹⁶¹).

	A (kPa)	B	c0	c1	r2
Bovine Pericardium, GLBP	10.9299	16.1559	2.3432	26.9825	0.9616

Alternatively, more complex structural models can be sought, particularly models incorporating a higher level of information of the microstructure, if available, and naturally able to describe the mechanisms of fiber recruitment and alignment upon deformation. This can be done in a structural sense starting from the mechanical response of individual fibers. However, as the number of fibers in a RVE can be one hundred or more, modeling individual fibers fully is not feasible. Therefore a stochastic approach is needed to derive a new ensemble stress-strain response using the mean fiber stress-strain response.

The structure of a collagen fiber network is composed of individually crimped fibers interwoven together. The crimping can be either sinusoidal in flat membrane like tissues¹⁴⁸ or helical in tendons.²³¹ Once straightened, these fibers appear to behave linearly in force vs. displacement ^{129,130,173,147} and this relation appears to hold valid for strains less than 0.35.¹⁶ The straightening behavior of the crimped phase, also unknown as the elastica effect, has been modeled by Freed et al.⁵⁰ and Garikipati et al.⁵⁵ However, the simulation using a finite element model and Garikipati et al. model shows no significant or impactful effect at the fiber ensemble scale (Fig. 14).

FIGURE 14.

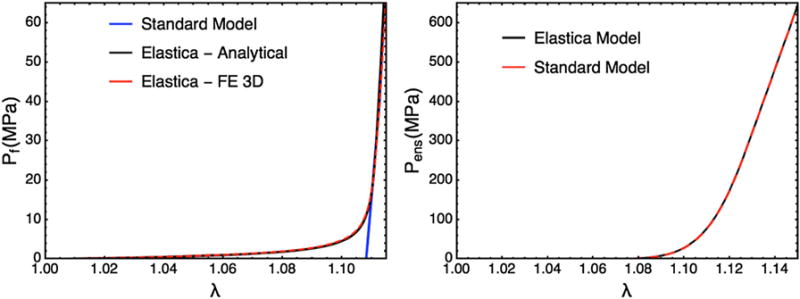
(a) The Elastic response of a single collagen fiber: comparing the standard model with no elastica effect, the analytical model based on Garikipati et al.,⁵⁵ and a FE simulation of 3D Neo Hookean fiber using the FEniCs project. (b) The simulated ensemble response of the Elastica model and the standard model shoes minimal difference.

Within the tissue composite, small angle X-ray scattering and second harmonic imaging results demonstrate that these fibers also appear to follow affine deformation in valvular tissue.¹²³ Therefore, the local fiber stretches can be determined from the stretch of the fiber ensemble and the fiber strain ε required to straight the fibers. The gradual recruitment of fibers can be emulated using a statistical distribution D(ε).^47,162 Physically, D(ε) represent the fraction of fibers fully straightened between ε and ε + Δε, and can be represented by e.g., a Beta distribution

$$D(\epsilon )=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}\frac{x^{\alpha -1}{(1-x)}^{\beta -1}}{UB-LB};x=\frac{\epsilon -LB}{UB-LB}$$ (14)

with α and β positive constants. Beta distributions are attractive in that the bounds of the distribution can be set, preventing unrealistic or even negative crimp values, and the parameters α and β can be expressed in terms of the mean and variance.

$$\alpha =-\mu \frac{({\sigma }^2+{\mu }^2-\mu )}{{\sigma }^2},\beta =(\mu -1)\frac{({\sigma }^2+{\mu }^2-\mu )}{{\sigma }^2}$$ (15)

Thus, an alternative to Eqs. (7) and (8) and assuming a mean elastic modulus K for the collagen fibers can be established. In previous literature, the stress strain relation that is linear in 2^nd Piola–Kirchhoff stress–Green–Lagrange strain common,^47,117,162 with the fiber stress–strain relationship

$$S_{nn}^f(\epsilon )=K{\displaystyle \underset{0}{\overset{\epsilon }{\int }}D(x)\frac{\epsilon -x}{{(2x+1)}^2}}dx$$ (16)

However, based on a linear force displacement relation, a stress-strain relation that is linear in 1^st Piola–Kirchhoff stress-stretch can also be used:

$$S_{nn}^f(\epsilon )=K{\displaystyle \underset{0}{\overset{\epsilon }{\int }}D(x)\frac{1}{2x+1}}\left(1-\frac{\sqrt{2x+1}}{\sqrt{2x-1}}\right)dx$$ (17)

For parameter estimation purposed, the two models behave with no observable difference. Due to the relatively small variations in crimped length of collagen fibers common is valvular and pericardial tissue, the collagen fibers extend by no more that 4–5% under physiological loading. Thus the two models, when integrated into an ensemble, are effectively the same; albeit the modulus estimated will be different.

In order to assess the improvements obtained with this better description of the microstructure and its inherent microstructural deformation mechanisms, Sacks¹⁶² employed and compared both models, the fiber recruitment model with the two parameter model, but without considering the effect of the matrix to describe biaxial testing experimental data of untreated bovine pericardium (Table 12). Although both models attempt to describe the same microstructural behavior (fiber reinforcement, recruitment and lengthening), the former shows certain advantages when compared to the later. One key difference resides in the different models of fiber response [Eqs. (8) and (16)] and results in an important characteristic that can be denominated terminal stiffness. Due to the simple exponential term present in Eq. (8), it can be easily observed that the stress on the fiber increases exponentially with strain, therefore fiber stiffness (slope of the stress vs. strain curve) increases as strain increases; on the other hand, Eq. (16) results in a linear increase of stress and a maximum fiber stiffness beyond a certain strain value, i.e., the terminal stiffness, which is observed experimentally. Overall, the advantage of the fiber recruitment structural model is its ability to provide insight into tissue function. In particular, the structural model allows for an explicit relationship between fiber straightening and recruitment and bulk tissue strain, and most importantly, allows for the formulation of hypothesis regarding tissue function at the microstructural level and their evaluation with parametric studies and sensitivity analyses, such as e.g., the influence of different degrees of collagen crimping on overall tissue response.¹⁶²

TABLE 12.

Fiber stress-strain model parameters for grouped specimens data for both fiber models (cf. Sacks¹⁶²).

	Two Parameter Model			Fiber Recruitment model
	A (kPa)	B	r2	K (kPa)	α	β	r2
Bovine Pericardium, untreated	0.336	44.921	0.913	58.73	5.6470	0.0428	0.899

An important feature of the current structural approach is that summing the two expressions for the normal stresses under equibiaxial strain conditions (E₁₁ = E₂₂, E₁₂ = 0, thus S₁₂ = 0), the fiber stress–strain law can be obtained directly from the experimental data using $S_{nn}^f=S_{11}+S_{22}$. Thus, the material parameters for $S_{nn}^f$ [A and B on Eq. (8) or K, α, and β in Eqs. (14)–(17)] are experimentally determined directly from the equibiaxial test data using the Marquardt–Levenberg nonlinear least squares method, which together with experimentally obtained fiber angular distribution R(θ) compose the entire set of material parameters of the fiber ensemble in the structural model. Once found, the matrix properties can then be determined with any of the non-equilibrated protocols. Other mechanical properties of other components of the stored energy function that could be accounted for, such as in plane bending stiffness, are determined afterwards with other experimental protocols.

Sacks et al.¹⁴² recently developed the first rigorous full structural model (i.e., incorporating various features of the collagen fiber architecture) for exogenously cross-linked soft tissues. This was made possible, inpart, with the use of native-cross-linked matched experimental dataset and an extension to the collagenous structural constitutive model so that the uncrosslinked collagen fiber responses could be mapped to the cross-linked configuration. This separated the effects of cross-linking from kinematic changes induced in the cross-linking process, which in turn allowed the nonfibrous tissue matrix component and the interaction effects to be identified. Native and cross-linked valvular tissues exhibit minimal time dependent effects.^43,75,76,188 Exogenous-cross-links induce fiber–fiber and fiber-matrix interactions that are mechanically significant. Sacks et al.¹⁷⁰ considered pericardial tissues to be composed only of collagen fibers and a matrix constituent that represents non-cross-linked and cross-linked components, and water. The contributions from elastin or other tissue components are ignored since they have either negligible mass or stiffness. In all previous structural models of soft tissues, interactions between components have been ignored and Sacks et al. utilized the following hyperelastic general form

$$\begin{array}{l}\psi (\mathbf{C})={\varphi }_c[{\psi }_c(\mathbf{C})+{\psi }_{\mathrm{int}}(\mathbf{C})]\\ +(1-{\varphi }_c){\psi }_m(\mathbf{C})+p(J-1)\end{array}$$ (18)

where ϕ_c is the mass fraction of the collagen fibers, ψ_c, ψ_m, ψ_int are the strain energy density functions of the collagen, matrix, and interaction terms, respectively, J = det(F), and p is the Lagrange multiplier to enforce incompressibility. The following final form of the constitutive model was used

$$\begin{array}{l}\mathbf{S}={\mathbf{S}}_c+{\mathbf{S}}_{\mathrm{int}}+{\mathbf{S}}_m\\ =\frac{{\varphi }_c{\eta }_c}{{ }_1^t\lambda }{\displaystyle {\int }_{{\theta }_1}{\mathrm{\Gamma }}_1[{\mu }_{\mathrm{\Gamma }},{\sigma }_{\mathrm{\Gamma }},{\theta }_1]}\\ \times \left\{{\displaystyle {\int }_1^{{ }_1^t\lambda }\frac{D_1({\mu }_0,{\sigma }_0{,}_0{\lambda }_{lb0}{\lambda }_{ub}{,}_0^1\lambda [{\theta }_0({\theta }_1)],x)}{x}\left(\frac{{ }_1^t\lambda }{x}-1\right)dx}\right\}\\ \times ({\mathbf{n}}_0\otimes {\mathbf{n}}_0)d{\theta }_1+{\varphi }_c{\displaystyle \underset{\alpha }{\int }{\displaystyle \underset{\beta }{\int }\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(}\beta )}\\ \times [d_0{d}_1({\lambda }_{\alpha }{\lambda }_{\beta }-1)e^{d_1{({\lambda }_{\alpha }{\lambda }_{\beta }-1)}^2}\\ \times \left[\frac{{\lambda }_{\beta }}{{\lambda }_{\alpha }}({\mathbf{n}}_0\otimes {\mathbf{n}}_0)+\frac{{\lambda }_{\alpha }}{{\lambda }_{\beta }}({\mathbf{m}}_0\otimes {\mathbf{m}}_0)\right]]d\alpha d\beta \\ +(1-{\varphi }_c)\left({\mu }_a{(I_1-3)}^{a-1}+{\mu }_b{(I_1-3)}^{b-1}\right)(\mathbf{I}-C_{33}{C}^{-1})\end{array}$$ (19)

It is understood that n₀ and m₀ are referred to β₁ and that the Lagrange multiplier was merged with the matrix by assuming a planar tissue to simplify the formulation. This final model parameters has eleven independent fitted parameters (η_c μ_Γ σ_Γ μ₀ σ₀, a, b, μ_a, μ_b, d₀, d₁) and three directly determined parameters (ϕ_c, ₀λ_lb, ₀λ_ub), all with a physical meaning.

While at first glance this appears to be a major nonlinear optimization undertaking with all the usual pitfalls, a sequence to make actual parameter estimation quite tractable was employed:

1. From the native tissue mechanical data, the collagen phase parameters (η_c, μ_Γ, σ_Γ, μ₀, σ₀) can be predicted using standard procedures.^49,233

2. From the pre-transition collagen recruitment portion of all of the EXL tissue mechanical data, the matrix parameters (a, b, μ_a, μ_b) can be determined.

3. Using the ${ }_1^t{\mathbf{S}}_c({\eta }_c,{\mu }_{\Gamma },{\sigma }_{\Gamma },{\mu }_0,{\sigma }_0)$ and S_m(a,b,μ_a,μ_b) responses, the interaction stress responses for all test protocols can be determined using ${\mathbf{S}}_{\mathrm{int}}=\mathbf{S}-\frac{1}{{\phi }_c}({\phi }_{c1}^t{\mathbf{S}}_c+(1-{\phi }_c){\mathbf{S}}_m)$.

4. Using the results of step 3, the final two parameters (d₀, d₁) can be determined by fitting Eq. (19) but only allowing them to vary while keeping the other terms to their above fitted values.

This basic sequence ensured a robust parameter set to be obtained, since the entire model is never fit at once. Moreover, this approach allowed the separation of the contributions to the stress of each of these mechanisms. The most novel findings were that (Fig. 15): (1) the effective collagen fiber modulus was unaffected by cross-linking, and (2) fiber-ensemble interactions played a large role in stress development, often dominating the total tissue response (depending on the stress component and loading path considered). An important utility of the present model is its ability to separate the effects of exogenous cross-linking on the fibers from changes due to the matrix. Applications of this approach include utilization in the design of novel chemical treatments that produce specific mechanical responses and the study of fatigue damage in BHV biomaterials.

FIGURE 15.

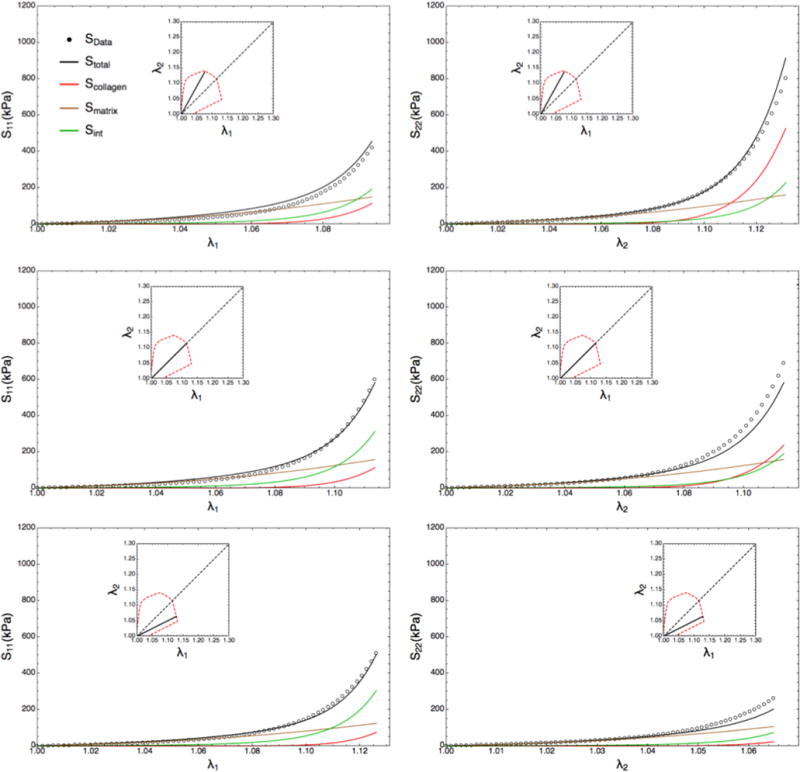
Complete EXL structural model results or the S₁₁ and S₂₂ stress components for three protocols. The interactions produced the largest contribution to S₁₁ followed by matrix and collagen fibers; however, the contributions towards S₂₂ are dependent on loading path, with collagen dominating when λ₁ λ₂ and matrix dominating when λ₂ λ₁. The contribution of the matrix was much less loading path sensitive, owing to its near-linear, isotropic behavior (from Sacks et al.¹⁷⁰).

BHV Critical Engineering: Modeling-Driven Experimentation and Experimentally-Based Modeling

Critical BHV engineering aims to ensure valve functionality for its clinical performance with a combination of hemodynamic, biomechanical and biological aspects, e.g., sufficient effective orifice area, transvalvular pressure gradient, good leaflet coaptation without regurgitation, among others, and to predict and extend as much as possible valve durability. Rational methodologies and a quantitative approach must be pursued to optimize the device at all stages of its design process. However, experimental testing for material characterization alone cannot provide a reasonable assurance for comparing different candidate heterograft materials, as it is inconsequential to compare two different BHVs solely based on values of the material properties of its leaflets. Rather, it is essential to integrate multiple tests to increase the knowledge about the tissue and to generate a predictive model of its behavior, and only then, try to analyze biomechanical function, and possibly predict durability and provide assistance against the failure of the valve. While leaflet tears are the main failure mode of porcine valves,²²³ these can be caused by many factors including mechanical stresses, calcification, or crosslink deterioration. The mechanisms of fatigue and valve deterioration are very complex and are currently not completely understood, and ultimately the durability of a tissue is most frequently estimated experimentally via the use of an accelerated wear tester, which attempts to mimic the valve in vivo function.

Material property data can easily be obtained from basic experimental tests, such uniaxial, biaxial, or flexural mechanical testing. However, all heterograft tissues are composite materials, are highly inhomogeneous, clearly show anisotropic behavior, and undergo large deformations. Experiments for material behavior characterization must be performed with the objective of motivating the choice of proper models, and once the suitable model is defined, subsequent experiments must be performed not only to infer the validity of the model chosen, but also to determine the constants that describe the behavior of the material accurately. Unfortunately, systematic experimental data of bovine pericardium, particularly, when subjected to biaxial test protocols, do not exist. To date, no material model is able to account in full for such complex observed microstructure and biological behavior, and the inclusion of such detailed information would certainly prove useful in extending the ability to better model and simulate the response of BHVs.

Nonetheless, (i) theoretical developments resulting in new and better models to describe the behavior of BHV tissues, and (ii) experimental advancements with novel techniques collecting data to understand and quantify such behavior, must proceed simultaneously and closely tied. With the objective of providing reliable experimental data for BHV simulation, Mirnajafi et al. conducted a systematic set of flexural experiments on native and glutaraldehyde-treated bovine pericardium and to date these seem to be the most employed set of material parameters describing these materials¹⁴¹ upon flexure. With the goal of improving the understanding of the micromechanical changes chemical modification induces in native tissues utilized in BHV, the authors have investigated the relation between collagen fiber preferred direction and the resulting flexural properties, and have concluded that the flexural properties are indeed dominated by interfiber cross-links as opposed to the stiffness of the collagen fibers themselves. Subsequently, Mirnajafi et al. conducted tests following similar experimental techniques on porcine BHV heterograft materials with the objective of characterizing the fatigue failure behavior occurring in these materials upon cyclic flexure.¹⁴²

Once a suitable initial model has been established, the choice of experiments to support the model must be carefully considered. The three main considerations are the (i) determination of the constitutive model form, (ii) determination of the material parameters, and (iii) constitutive model validation. All three tasks are interrelated. Perhaps the best and earliest example of using data to guide the form of the material model is by Humphrey et al.^95,96 Here, the invariants suitable for the material were established initially. The mechanical testing was controlled so that only a single invariant was allowed to vary at a time, thus deducing the dependency of the model on each. For more complex models, such as structurally informed models, this may not always be possible. However, certain kinematical state, i.e., equibiaxial strain, can be used to independently determine the contribution of the fiber ensemble response by summing the principal components.^49,162 Additional, the fiber and matrix contributions can be separated by subtraction.^49,162

Alternative testing methods can also be used as a way to valid the form of the model. For example, although uniaxial testing provide an incomplete description of the tissue mechanical behavior, when the fibers are highly aligned, uniaxial stretch along the preferred direction can be used as another way to estimate the ensemble behavior. In elastin rich tissues, low stress biaxial testing and flexural studies can be used to determine behavior of matrix and elastin separately from the behavior of the collagen fiber ensemble.⁴⁹ Imaging methods, such as small angle X-ray scattering, have been used in combination with mechanical testing to examine the form and modulus of the stress-strain relation of collagen fibrils. ^{129,130,173,174} Obviously, structural parameters are best measured directly rather than obtained through optimization. Given sufficient a priori information, the number of parameters in structural models that needed to be optimized can be drastically reduced. The remaining parameters should be optimized against a sufficient range of data relative to those needed for ultimately simulation purposes and then validated against different datasets. In cases where data such as the above cannot be acquired on a specimen to specimen basis, they may be measured separately and used as validation. Through the process, it is common to find the need to alter/refine the model assumptions based on unexpected/unpredictable experimental results. At this point, additional experiments for hypothesis formulation and subsequent parameter determination should be done—model development is an iterative process between experimentation, theoretical formulation, and validation of predictive capabilities.

The employment a proper constitutive model—not only the choice of its specific form, but also the correct determination of its parameters—gains relevance when the next step is to perform FE simulations of the entire BHV to compute leaflet strains and stresses. In reality, leaflet tissues will deform by the same amount in response to the same force independently of the choice of constitutive model one uses in the attempt to describe such behavior. The forces and displacements measured in the laboratory, and consequently, the strains and stresses experimentally determined, will not change if a different constitutive model is chosen to describe its response. However, the descriptive/predictive capabilities of any analysis conducted with a computational model and the underlying constitutive formulation necessary will depend dramatically on all modeling assumptions made. Crucial questions are “what is the impact of picking different constitutive models in the organ-level simulation of a BHV?”, “what difference do phenomenological or structurally-based constitutive models make?”, and “what difference does different experimental protocols to obtain material parameters have?”

The answers to these questions are not straightforward. First, one must understand that biological tissues have complex morphology and response; therefore a certain degree of approximation is always associated with the choice of a constitutive model. The choice of a constitutive model is not an easy task to undertake as it is highly subjective and dependent on the desired degree of complexity/effort/accuracy. Certainly some models are better than others, but on the other hand, there are certain kinds of behavior that can be disregarded outright for the sake of simplicity, and sufficiently accurate simulation can still be achieved. Simulations and sensitivity analyses have been conducted with different extents of simplifying assumptions, such as e.g., different choices between phenomenological or structurally-based models (e.g., de Hart et al.³⁸ and Driessen et al.⁴²), and on constitutive assumptions such as material homogeneity or non-homogeneity, isotropy or anisotropy, and elasticity or viscoelasticity. Experimental evidence and computational simulations by Burriesci et al.¹⁷ and Li et al.¹²⁶ have shown the impact of different choices of constitutive models to simulate valve function and have observed that the stress and strain distribution in the leaflets was severely impacted by the homogeneous/inhomogeneous and isotropic/anisotropic modeling choice. Sun et al.¹⁹³ have compared the effect of spatial inhomogeneity in the material parameters of the valves and have determined material properties of each leaflet individually and have observed significant differences between two simulations of the entire valve apparatus: (i) one simulation was conducted with material properties corresponding to each leaflet, whereas (ii) the second simulation employed properties of one leaflet in all three. The authors have observed substantial differences in the leaflet stress and strain distributions Experimental evidence by Stella et al.¹⁸⁸ showed strain rate indifference upon deformation of valvular tissues across several orders of magnitude of strain rates has demonstrated that the dissipative mechanisms for creep and stress relaxation are functionally independent and may indicate that the viscoelastic component is indeed negligible in valve physiology and in organ level simulations of valve function.

Notwithstanding, the simplifying assumptions described above were still employed successfully (to some extent) not only to critically aid BHV design, but also to improve the existing knowledge of the mechanisms of valve failure. Without pursuing the goal of complete comprehensiveness, typical state-of-the-art computational simulation of BHVs is reviewed below.

COMPUTATIONAL SIMULATIONS

Overview

The analysis of native and prosthetic valve mechanics has been extensively conduced in silico through computational simulations with the aid of the finite element method.^23,165 Although most studies have initially been conducted with simplified geometries and basic material models, and sometimes, with idealized physical settings, finite element modeling studies have been able to guide design and manufacturing techniques with relative success.^{9,18,19,67,80,90,114,119} Simply by changing leaflet shapes and frame mounting methods, the stress distribution pattern acting on the leaflets is altered—as illustrative examples, Hamid et al.⁸⁰ have predicted an increase of stresses on the closed leaflets as stent height is reduced, and Cacciola et al.^18,19 demonstrated that a stentless design could reduce stress peaks by up to 80% for a sinusoidal fiber reinforcement layout with respect to a stented valve with the same reinforcement. Through observations made from computational simulations and experimental data, Salgo et al.¹⁷¹ proposed a teleologic argument of the characteristic saddle shape of mammalian mitral valve leaflet as a configuration that confers a mechanical advantage by adding curvature and reducing stress. Each of these small pieces of knowledge, if seen individually, certainly may have had just slight impact on the modus operandi associated with the overall design process of BHV. On the other hand, if taken as a whole and over the course of the 30 years since the inception of BHV, one is able to perceive and quantify the huge impact on success rates of clinical interventions and on the feasibility of the technology achieved with dramatic improvement on the durability of BHVs and better chemical treatments for heterograft materials. Nonetheless, the field has reached a point of current stagnation and general lack of progress—durability issues continue to hamper BHVs and the range of 10–15 years has remained unchanged over the last decade. The continued lack of rigorous mechanistic knowledge of in vivo durability and means to simulate effectively xenograft biomaterial responses in new designs (besides heart valve replacement in large animal studies with their associated difficulties, cost, and experimental variability) has hampered the research and development of novel and better BHVs.

Continued progress requires a much more sophisticated level of understanding. Computational simulations, in conjunction with bench-top and large animal experimental studies, can help to define how evolving biomaterial biomechanical properties drive valve function and performance. Computational studies are certainly limited on their range of applicability, in particular when applied to complex mechanical problems such as in BHVs, but have had the ability to shed light into the clarification of possible mechanisms of valve failure and to quantify BHV design improvements, at least, indirectly. Regions of high stress concentration determined computationally, particularly high tensile and bending stresses, have so far been correlated successfully with regions of tearing in BHV observed in vivo^85,178—the adverse mechanical environment occurring within the leaflet can either directly accelerate tissue structural fatigue damage, or initiate calcification by causing structural disintegration and enabling multiple calcification pathways that lead to valve failure.^166,211 Although details of the process are unclear, it is widely and pragmatically accepted that valve designs that reduce leaflet stress are more likely to result in improved performance in longterm applications. Computational studies can be employed in a very cost effective and reliable manner to optimize such design process.

Even from a purely mechanical standpoint, computational simulations of functioning heart valves are not at all trivial.¹⁶⁵ The realistic geometry of a heart valve is quite complex, and in particular, leaflets are very thin (on the order a few hundred μm). The unpressurized geometry of a BHV can be carefully characterized at the bench, however upon implantation is deformed into place. Most importantly, substantial host-implant interactions and adaptations occur acutely, evolve over time, and the resultant in vivo geometry of a BHV is rather difficult to predict reliably. Segmentation of medical images is difficult to conduct for such thin and complex structures and there are always crude approximations whenever realistic geometries are attempted from stacks of microCT, ultrasound or MRI data. Moreover, not only the realistic geometry is taxing, but also can pose certain problems in regard to meshing due to its thinness. The heterograft material is highly inhomogeneous, being composed of collagen bundles aligned along preferred directions with multiple dispersions, and both parameters are highly dependent on spatial location within the leaflet. Leaflets are adjoined at the commissures, and a general lack of detail of the particularities of these junctions, e.g., local microstructural environment, still exists. Sliding contact with friction in between leaflets occurs in the co-aptation area upon closing, and inertial effects may be important due to the rapid dynamic motion of valve function. Heart valves function on a highly dynamic fluid environment and realistic boundary conditions are either difficult to specify (for example, assuming hydrostatic differential pressure, but disregarding shear tractions occurring due to blood flow), or difficult to compute with fluid–structure interaction techniques (a severely difficult meshing problem as the fluid domain changes topology with valve closing). All of the above challenges are related with mechanical aspects and modeling assumptions are usually made to either simplify the problem or tackle the difficulties—on top of those, the biological aspect must be somehow included, and here, the lack of fundamental understanding is even more pronounced. The purist desire to model rigorously and accurately every detail and phenomena involved in BHV function is clearly ill-posed and will not be certainly possible within the near-future—on the other hand, the approach should be pragmatic instead. Modeling efforts should focus on clinically-driven critical engineering with the sole objective of better informing design methods to achieve clinical improvements, mitigate valve dysfunction, and improve valve durability.

Numerous challenges are encountered in numerical simulations of native and BHV, including: (i) proper determination of a geometry, either idealized^67,80,90 or morphologically realistic obtained from ultrasound, computed tomography, or magnetic resonance imaging²³; (ii) challenges of rigorous fluid-structure interaction analyses^{23,115,134,184} and the role of mechanical forces in leaftlet coaptation^62,186 and valve dysfunction; (iii) inhomogeneous, nonlinear, and anisotropic leaflet mechanical properties^{7,126,163,196}; and lastly and quite often overlooked, (iv) the experimental validation of in silico simulations^9,17,114 or the lack of thereof.

The importance of experimental validation, in addition to accurate material models and simulation methodologies, cannot be overstated. However, experimental measurements of leaflet strain for validation are difficult to preform owing to practical limitations in obtaining measurements very close to the leaflets and valve housing. Thus, previous finite element studies offered no experimental validation (e.g.,^{9,78,80,90,126}), or simple validations that only demonstrate comparisons of gross leaflet geometric configurations with pulse duplicator images.^17,114 Gorman et al.⁶⁶ developed a sonomicrometry technique to track the three-dimensional geometry of native heart valves in vivo. The technique relies on the determination of the path of an array of sonocrystals placed in the leaflet and allows the calculation of the local strain field and the validation of computational simulations. Gorman et al.⁶⁶ imaged the ovine mitral valve, and Sacks et al.¹⁶⁴ employed the technique to determine the dynamic in vivo strain field of a functioning mitral valve anterior leaflet, which indicated large anisotropic strains and very high strain rates (Fig. 16). Sonomicrometry has been extensively used up to 16-weeks in vivo in native heart valves in the ovine model and has provided critical information to improve clinical interventions such as ring annuloplasty and mitral valve repair.^4,65 Nevertheless, it must be remarked that sonomicrometry is a limited technique and yet unproven in BHVs—although it has been shown that markers do not interfere with the biaxial mechanical properties of the tissues tested in vitro and the shape and motion of instrumented valves in vivo obtained with echocardiographic imaging, the limited size of markers arrays usually result in a poor resolution of the strain field. Moreover, the technique is not trivial and there are several difficulties associated with marker tracking, marker detachment, and data post-processing. Validation techniques should rely on the resolution of the motion during valve function, either in vivo or in vitro—several techniques have been developed, mostly relying in the tracing of implanted markers.^54,131,212 An alternative possible validation methodology employs the methodology of Iyengar et al.⁹⁹ of resolving leaflet motion using structural light projection. Their system features a structured laser-light projection technique, eliminates the need of markers, and allows imaging of the complete valve leaflet surface dynamically with high temporal and spatial resolutions.

FIGURE 16.

(a) A schematic of the nine sonocrystals placement on the mitral valve arterial leaflet surface, showing crystal positions in relation to valvular geometry. (b) Two three-dimensional reconstructed views of the nine sonocrystals in the unloaded reference state (t = 0 ms) and the fully coapted state (t = 500 ms). The evaluation of valve deformation is extremely difficult and, being crucial for simulation validation, still remains a significant challenge (from Sacks et al.¹⁶⁴).

Representative Biomechanical Modeling Results

Computational simulations have been used mainly with the purpose of determining the stress distribution on the leaflets, correlate regions of stress concentration with regions of leaflet calcification and/or leaflet tear in implanted valves, and guide the design process with such information. Rousseau et al.¹⁶⁰ incorporated fiber reinforcement and the viscoelastic properties of a porcine bioprosthetic valve leaflet in their FE analysis with time-varying pressure load on the leaflets and have found that regions of high fiber stress, located near the aortic ring, correlated with some common regions of valve failure. Grande-Allen et al.⁶⁸ have employed realistic geometries obtained with MR images of human valve specimens with higher order shell elements that incorporated anisotropic material behavior coinciding with the collagen fiber alignment. The authors were able to analyze the variations of stress across the valve and root, attributed such differences to inherent morphologic asymmetry and stress sharing, and claimed that bioprosthetic valves should be assembled using leaflets from three different porcine valves or from bovine pericardium with the objective of better replication the normal human valve asymmetry and human leaflet size arrangement. Subsequently, Grande-Allen and co-workers extended their computational analysis to study the effects of aging,⁶⁹ aortic root dilation,⁷⁰ valvular incompetence due to Marfan syndrome,⁷² and clinical procedures associated with valve sparing.^71,73 Overall, the geometries of the AV and of the aortic root play a substantial role in AV biomechanical function. Most importantly, the characteristics of the aortic root are very patient-specific, and are pivotal to optimize surgical procedures and could possibly inform bioprosthetic valve design. Through computational simulations with morphologically realistic aortic root obtained from MRI data, Conti et al.³³ has shown that anatomical differences between leaflet-sinus causes substantial differences in stress and strain patterns, specifically due to leaflet asymmetry. Labrosse et al.¹¹⁶ employed a comparable methodology from transesophageal echocardiography to obtain patient-specific geometric models of the AV and aortic sinus. The computational simulations demonstrated agreement in leaflet coaptation area with the medical images, and the authors were able to associate in a comparative sense regions with higher values of mechanical stress to regions of higher risk of tearing and/or development of calcification.

Sun et al.¹⁹³ presented a study of prosthetic valve deformation under quasi-static loading. In this study, quasi-static leaflet deformations under 40, 80, and 120 mmHg transvalvular pressures were simulated in a pericardial BHV (Fig. 17). A Fung-elastic material model utilizing material parameters derived from actual leaflet biaxial tests and measured leaflet collagen fiber structure axes obtained from physical leaflets were used (Fig. 18).^194,195 Rigorous experimental validation of the predicted leaflet strain field was used to validate the computational results of the simulations. An overall discrepancy of 2.36% strain between the FE model results and the experimental measurements was obtained, indicating excellent agreement between computed and measured principal strains. Results generally indicate that the peak stress always occurred in the vicinity of the commissures, with the lowest stress occurring near the free edges (Fig. 17). High stresses were also observed in the belly region in all three leaflets in similar locations on the aortic side. The free edge experienced the less amount of stress on the ventricular side surface, consistent with the stress levels determined at the free edge on the aortic side. This is most likely to be due to the contact of the leaflets that lead to compressive stress at the free edge. Sun et al.¹⁹³ extended the analysis to infer the effects of tissue anisotropy by conducting parametric studies utilizing the material parameter set from one leaflet for all three leaflets and noticed that a substantial variation in leaflet stress and strain distributions, and concluded the importance of using actual leaflet material properties and the profound impact of the degree of material anisotropy for accurate BHV FE simulations. Subsequently, Li and Sun extended the computational simulations to investigate the effects of pericardial tissue thickness and pericardial material orientation and have observed a general decrease of peak stresses with decreasing leaflet thickness and when the stiffer direction of the material is aligned with the circumferential direction of the leaflet.¹²⁷ This type of material orientation is indeed observed in native aortic leaflets, where the collagen bundles are predominantly aligned along the circumferential direction.⁹

FIGURE 17.

Maximum in-plane principal strain magnitude plotted using the same color fringe scale for pressure levels of 40, 80 and 120 mm Hg. It is interesting to note that the free edge of one leaflet was slightly higher than that of the other two leaflets at 120 mm Hg and this feature was captured by the FE model (from Sun et al.¹⁹³).

FIGURE 18.

Representative SALS data for three leaflets of an pericardial BHV. The vectors represent the local preferred fiber orientations, the color indicates the degree of collagen fiber orientation. Most leaflets have a ±45° preferred orientation and a fairly uniform degree of orientation throughout the leaflet (from Sun et al.¹⁹³).

Sun et al.¹⁹³ also conducted simulations to investigate the correlations between calculated stress distribution and common regions of failure in tissue valves. The failure phenomena of leaflets in valve prostheses basically may be divided into the following three types: (i) leaflet calcification, tearing and laceration;⁵² (ii) tears in the leaflets in the vicinity of the commissure;²¹⁶ and (iii) leaflet tears associated with suture attachments.^144,216 Sun et al. simulation results indicate that the highest tensile stresses occurred in the vicinity of the commissure region and in the belly region. It is possible that the tears and perforations that were observed in these regions are due to these high tensile stresses. Valves in the closed state also experience bending stress, especially at the co-aptation area. Negative values of the minimum principal stress are found in the co-aptation area and edges where the leaflets are attached to the stent. These compressive stresses, despite their minimal magnitude, may cause fiber wrinkling and lead to the flexure damage of collagen fibers and, consequently, damage leaflets.⁶¹

Kim et al.^111,112 proposed a new modeling approach for heart valve leaflets using the stress resultant shell theory—the point of departure is the employment of separately characterized constitute models for the inplane and flexure response of the leaflet tissue, the former characterized with biaxial in-plane material tests,¹⁹⁴ and the latter with three-point bending.⁴⁴ Kim et al. implemented the anisotropic models into the stress resultant, geometrically exact shell element developed by Simo et al.^180,181 Kim et al. performed dynamic analyses of a pericardial BHV during the opening and closing phases of a human complete cardiac cycle under physiological conditions and obtained results that compare favorably with in vitro dynamic simulation in a pulse duplicator. Wavy wrinkles were observed along the free edges during closing as the leaflet moved quickly inward due to the high pressure load on the aortic side, but disappeared when the free edge region reached the contact position (Fig. 19). Coaptation area was approximately 35% (clinical studies considered ideal co-aptation when 30–50% of cusp area is involved⁸⁷), hence Kim et al. result indicates that the dynamic simulation well-represented a healthy pericardial BHV at the fully closed position. Relatively high stresses first occurred near the belly and free edge region and then spread over both sides of the commissural attachment area during the opening phase. The highest stresses were then observed primarily in the vicinity of both sides of the cuspal commissure at the fully closed position, correlating properly with photographs and radiographs of calcified areas in the BHV reported in previous studies¹⁷⁸ and supporting the hypothesis that in-plane stress concentration within the leaflets induces calcification. Bending moment distribution demonstrated slight different patterns from the in-plane stress distribution, particularly during the closing phase. Relative high bending moments were observed near the center region of the co-aptation edge line where high curvature is induced, and this finding shows good agreement with the areas of mechanically damaged collagen fibers within BHV leaflets.¹⁸³ Similarly, regions of compressive stresses during the closing phase correlated with regions structural damage.¹⁶⁶ These results favor the hypothesis that collagen fiber structures are more vulnerable to in-plane compression rather than in-plane tension (the latter usually associated with calcification), and that dramatic curvature changes and even curvature reversal occurring during valve operation induces high flexural strain and damage by severe inter-laminar shearing, and consequently, out-of-plane bending stresses might be more hazardous for structural damage than in plane stresses after all.

FIGURE 19.

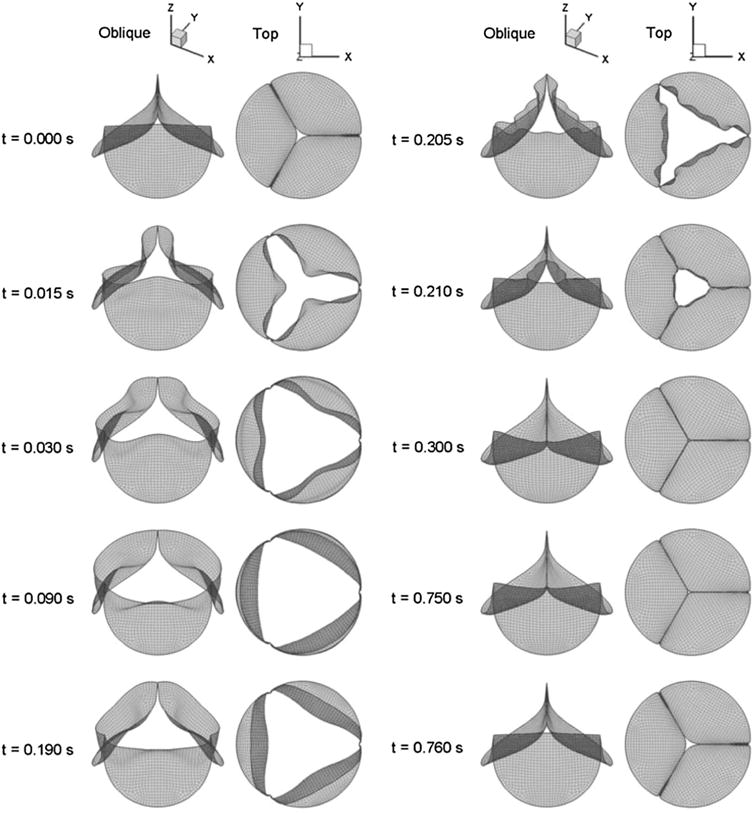
Sequence of displacement of the BHV resultant shell model during the complete cardiac 6 cycle (from Kim et al.¹¹²).

Challenges in the Computational Simulation BHV Function-Fluid Structure Interaction

BHVs operate in the vasculature: their mechanical environment includes the surrounding blood flow. The influence of blood flow on a closed valve may be modeled as a (quasi-) static pressure load, but insight into the dynamic opening and closing processes requires a more sophisticated modeling approach. These considerations motivate ongoing research on fluid-structure interaction (FSI) simulations of heart valves, which couple numerical methods for structural mechanics of valves to those for computational fluid dynamics (CFD) of the surrounding blood flow. FSI studies of BHVs are still nascent—as FSI techniques generally improve and the effects of blood flow are accounted in BHV simulations, their accuracy and relevance will certainly improve.

Native and prosthetic valves present a number of unique challenges for FSI analysis. Foremost among these is the fact that the heart valve leaflets contact one another, changing the topology of the fluid subdomain. Standard arbitrary Lagrangian–Eulerian (ALE)^40,41,93 or deforming-spatial-domain/space-time (DSD/ST)^207,208 numerical schemes, which continuously deform a mesh of fluid elements that is fitted to the moving fluid-structure interface, are no longer directly applicable. To salvage such methods, one must augment them with special techniques to handle extreme deformations like topology changes. One solution is re-meshing, i.e., generating a new mesh for the fluid sub domain whenever its deformation becomes too extreme.^102,104,206 This allows computations to proceed, but introduces additional computational cost and numerical errors associated with the projection of fluid solutions from old to new meshes. Recent work by Takizawa et al.²⁰² introduced the space-time with topology change (ST-TC) method, which extended the DSD/ST framework to allow topology changes without re-meshing. The ST-TC method was employed to resolve the fluid dynamics problem of a heart valve with prescribed leaflet motion,²⁰³ but the application of ST-TC to complex FSI with sliding and/or unpredictable structural self-contact remains an open problem. Makhijani et al.¹³⁴ reported a boundary-fitted BHV FSI simulation, but replaced true contact with inverse-square repulsive forces between leaflets and a symmetry plane. While the results were promising, no further analysis using this method was pursued.

In light of the difficulties encountered in boundary-fitted FSI analysis of heart valves, the overwhelming majority of work to-date on native and BHV FSI analysis has followed in the tradition of Peskin’s immersed boundary method.¹⁵³ While it is not a universal convention, this review follows references^143,185 in applying the term “immersed boundary method” liberally, to any numerical method in which the fluid and structure meshes are not required to match at the fluid-structure interface. Highly variable interpretations of the term “immersed boundary methods” do exist, and explicit clarification of its meaning is highly recommended. Immersed boundary methods greatly simplify the treatment of large structural deformations and structural self-contact, but add some disadvantages (relative to ALE and DSD/ST), specifically in capturing boundary layers near the FSI.²⁰⁵ Takizawa et al.²¹⁵ found that the resolution of such layers is essential to obtaining accurate interface shear stresses in hemodynamic analysis. A comprehensive overview of various immersed boundary methods, their properties, and diverse applications can be found in several review articles.^143,185 An even more radical departure from boundary-fitted FSI is to discretize the fluid using a mesh-free approach, such as smoothed-particle hydrodynamics (SPH).⁵⁹ SPH is not widely used in CFD or FSI areas of research, but has been applied to evaluate mechanical, bioprosthetic, and native mitral valve function.²¹⁴

Peskin originally introduced the immersed boundary concept in 1972 with a crude representation of the heart valve as a collection of markers connected by elastic fibers,¹⁵³ specifically to meet the demands of heart valve FSI analysis. In the early 2000s, de Hart et al.^37,38,39 and van Loon et al.^219–221 used the immersed boundary method re-introduced by Baaijens⁶ to couple finite element discretizations of heart valves and with computational fluid dynamics analyses of blood flow. This allowed for investigation of various constitutive models, but numerical instabilities prevented analysis at realistic Reynolds numbers and transvalvular pressure levels. Increasing availability of parallel computing resources in the last decade has led to higher resolution simulations of heart valves in recent years. Griffith⁷⁷ adapted Peskin’s original immersed boundary approach to modern distributed-memory architectures and included adaptive mesh refinement for the fluid sub problem to compute FSI of a native aortic valve throughout a full cardiac cycle, with physiological flow velocities and pressure differences. The highest resolution heart valve FSI simulation is due to Borazjani,¹² who applied the curvilinear immersed boundary (CURVIB) method^13,56 to simulate systolic ejection through a bioprosthetic aortic valve. The valve leaflet models of Griffith and Borazjani suffered from deficiencies; Griffith applied Peskin’s original connected markers; while Borazjani omitted bending stiffness. The CURVIB method was recently extended to include fluid-shell structure interaction by Gilmanov et al.,^57,58 but the efficacy of the approach has not yet been demonstrated for the portion of the cardiac cycle in which the leaflets are coapted and must support large transvalvular pressure differentials. Kamensky et al.^88–89,107 have modeled the valve leaflets as Kirchhoff–Love thin shell structures using isogeometric analysis (IGA)⁹² (cf. Kiendl et al.^108,109 for methodology details and Fig. 20 for representative results). Recent work by Kiendl et al.¹¹⁰ and Buganza-Tepole et al.²⁰⁴ has shown that IGA of Kirchhoff–Love shell structures can easily incorporate a wide variety of 3D constitutive models specifically suited for thin biological membranes with complex anistropic behavior. Morganti et al.¹⁴⁵ found that IGA greatly improved the representation of leaflet co-aptation in structural simulations of native aortic valves, with traditional finite element analysis requiring approximately 200 times as many nodes as IGA to compute a qualitatively-correct co-aptation region.

FIGURE 20.

Volume rendering of the velocity field at several points during a cardiac cycle. The immersogeometric fluid structure interaction methodology applied to BHV modeling and simulation grants higher levels of automation, robustness, and realism than its standalone structural dynamics counterpart (from Hsu et al.⁸⁹).

Current state-of-the-art immersed boundary FSI approaches have relied on academic research codes. However, the commercial software LS-DYNA have been used for FSI simulations of bioprosthetic and native aortic valves^{21,24,191,230} since the late 1990s with immersed boundary methods. The time-explicit procedures used by LS-DYNA result in severe Courant—Friedrichs—Lewy conditions that limit the maximum stable time step size in hemodynamic computations, because blood is nearly incompressible, rendering the problem effectively parabolic.^34,35 Sturla et al.¹⁹¹ circumvented this difficulty in an aortic valve simulation by artificially reducing the speed of sound in blood by a factor of 10, reporting that the fluid density variations introduced by this deliberate modeling error were negligible. The use of other commercial off-the-shelf analysis software for heart valve FSI analysis may be possible using so-called “black box”coupling algorithms¹¹ to connect independent finite element analysis and CFD programs without access to their internal details. Specialized methods are required for stable and efficient black box coupling of fluids to thin, light structures such as heart valve leaflets.^139,218 Astorino et al.⁵ applied a novel black box coupling algorithm to FSI analysis of an idealized aortic valve.

Current immersed boundary FSI techniques are able to incorporate both the physiological flow conditions and realistic solid constitutive models needed to produce estimates of bending and tensile stresses in heart valve leaflets. However, their weakness in resolving boundary layers prevents accurate predictions of shear stresses at the interfaces and phenomena associated with them such as hemolysis, thrombosis, or cavitation. The further development of boundary-fitted FSI analysis techniques therefore remains important to computational simulation of heart valves. Determining the range of applicability of any FSI model will depend ultimately on rigorous experimental validation, comparing computed leaflet deformations to quantitative in vitro measurements. Such measurements may be collected through techniques such as stereo photogrammetry^53,54 or structured light projection.^99,192 However, no such validation has ever been carried out.

Challenges in the Computational Simulation BHV Function—Geometry and Properties

Valve leaflets are thin-walled structures that have sometimes been modeled as membranes^22,78,160 or shells,^9,90 the key difference being the modeler’s choice to exclude (i.e., neglect) or include bending stiffness respectively. Even though each formulation has its own limitations, these are the most appropriate and realistic types to represent the characteristics of thin-walled leaflet structures. Modeling leaflets as tension-only membrane structures essentially eliminates bending effects. However, previous studies using shell elements did show that leaflets were subjected to bending, bending stresses are substantial in BHVs during the cardiac cycle due to the large deflections leaflets undergo,^90,99 and bending damage is one of the main causes of valve mechanical damage.⁶¹ Another alternative is the use of three-dimensional elements,¹¹⁴ however it was noticed that there are severe problems of modeling thin structures with brick elements.²⁰⁹ Moreover, three-dimensional FE formulations will necessitate a three-dimensional constitutive model, which requires the determination of tissue properties in the out-of-plane direction, or else, the addition of underlying assumptions or the expansion of two-dimensional experimental data into a three-dimensional constitutive law.^169,195,196 Enforcing material incompressibility is another aspect whose difficulty is rather simplified with a two-dimensional approach, realized by kinematic constraints for the plane stress assumption,¹⁹⁴ whereas the three dimensional approach requires a generalized penalty method.

The effects of using different material models has also been investigated by Patterson et al.,¹⁴⁹ who compared the effects of using linear and nonlinear isotropic elastic models of leaflets. The authors found that the nonlinear model was more responsive to time-varying pressure waves, and induced a lower compressive, but higher tensile stresses in leaflets. Burriesci et al.¹⁷ studied the effects of mechanical orthotropy of a pericardial heart valve and found that even a small amount of orthotropy can significantly affect the mechanical behavior of the simulated valve. Li et al.¹²⁶ modeled porcine heart valves as transversely isotropic material with fiber-reinforced composite based on uniaxial extension experiments and have observed significant changes in the stress patterns and in the location of the peak stress due to the nonlinear anisotropic behavior of the material model composing the leaflets. Moreover, even though native⁹ and bioprosthetic leaflet mechanical properties^163,196 have been demonstrated to be mechanically anisotropic, no studies yet have utilized leaflet mechanical properties, geometry, and fibrous structural information of actual BHV to assess the effect of inter-leaflet variability in the resulting leaflet stress.

The geometric characterization of a BHV and the translation of mechanical properties measured at the bench into in silico simulations is of crucial importance for accurate and rigorous BHV simulations. The unpressurized geometry of a BHV can be carefully determined at the bench before implantation; however, this configuration may not be free of residual/internal stresses originating from fixation/manufacturing processes. Subsequently, BHVs are implanted, interact and adapt acutely with the host tissue, and over time, long term evolution occurs in an unavoidable process that will eventually terminate in failure at the end-life of the implant. Evolution of the implant entails not only a progressive shift in the initially-considered “reference” configuration, but also on a substantial change in measurable mechanical properties. The most commonly used technique for determining the mechanical properties of heart valve leaflets is direct ex vivo experimentation; however, such techniques require explanation, preventing their usability in a clinical setting. Also, changes in tissue structure and shape as it is explanted (e.g., valve’s reference configuration⁴), leads to challenges in relating ex vivo measurements to its in vivo behavior. With the objective of avoiding the need for excision, inverse modeling approaches have been employed to determine accurately and reliably the mechanical properties of valve leaflets. Recent advancements in 3D ultrasound technology provide the opportunity to obtain patient specific valve images in vivo,¹⁵⁵ specifically the shape of the leaflets as they are loaded during the closing phase without the need to include physical markers that severely hamper the clinical applicability of the inversemodeling approach—these methods are certainly the only resort to characterize native leaflets non-invasively in vivo, but their direct translation to monitor the performance of BHVs over their service life could yield important data to improve insight on failure mechanisms and possibly aid the design of more durable heterograft tissues and better BHVs.

BHV leaflets are highly non-homogeneous materials, composed by collagenous bundles inside extracellular matrix composed of elastin, GAGs, and other traditional connective tissue components. Collagenous bundles have a preferred direction of alignment and some degree of dispersion, and most importantly, these parameters are spatially dependent within the leaflet and confer local anisotropy to the tissue. Material models accounting for such spatial distribution, which can nowadays be accurately resolved experimentally with, e.g., small angle light scattering,¹⁶⁸ are of the utmost importance for accurate computational simulations of the function of BHV. Material microstructure and their multiple length scales are usually dealt with two distinct strategies—on one hand, micromechanics and multiscale methods attempt to segment and describe the detailed microstructural topology of the material and the interaction in between constituents and their response, and with such, structurally informed models are built; on the other hand, homogenization techniques attempt to employ such information in a representative volume element to obtain homogenized constitutive models; nevertheless, the pivotal point is that both strategies should yield models able to describe the experimental data collected on the mechanical behavior of the material at the bulk level and be employed accurately in properly validated BHV simulations. Regardless, it is not presently possible to determine the fiber structure of native heart valve of BHV leaflets on per-patient basis without explanting them. While this is less of a problem in BHVs at implantation stage (where the materials employed to construct them are well defined and characterized), the determination of possible evolutions of fiber orientation after implantation requires either explantation followed by ex vivo material analysis and characterization, or alternatively, inverse modeling approaches with population averages to yield such measurements.^4,155

Current state-of-the-art in incorporating biological material inhomogeneity into computational models employs techniques based on population averages, structure templates, and three-dimensional mapping. Aggarwal et al.¹ have developed a spline fitting techniques to connect surface deformation with structure (Fig. 21). More generally, determining the biomechanical behavior of heart valve leaflet tissues in a noninvasive manner remains an important clinical goal. While advances in 3D imaging modalities have made in vivo valve geometric data available, optimal methods to exploit such information in order to obtain functional information remain to be established. Aggarwal et al.² developed a novel leaflet shape-based framework to estimate the biomechanical behavior of heart valves from surface deformations by exploiting tissue structure. The authors determined accuracy levels using an “ideal” in vitro dataset,^193,194 in which the leaflet geometry, strains, mechanical behavior, and fibrous structure were known to a high level of precision. By utilizing a simplified structural model for the leaflet mechanical behavior [cf. Eq. (8)], the number of parameters to be determined per leaflet were reduced to only two. This approach allowed dramatically reduced computational time and easily visualize the cost function to guide the minimization process. It was determined that the image resolution and the number of available imaging frames were important components in the accuracy of the framework. Furthermore, their results suggest that it is possible to detect differences in fiber structure, thus allowing an opportunity to diagnose asymptomatic valve diseases and begin treatment at their early stages. Lastly, good agreement of the final resulting stress-strain response was observed when an averaged fiber architecture was used. This suggests that population-averaged fiber structural data may be sufficient for the application to in vivo studies, although clearly much work remains to extend the present approach to in vivo problems.

FIGURE 21.

(a) Quadrilateral mesh used, (b) fiber structure of three leaflets measured experimentally with SALS and then mapped onto valve geometry using spline technique, and (c) another view of the final valve mesh with fiber structure (from Aggarwal and Sacks²).

Challenges in the Computational Simulation BHV Function—Modeling Material Evolution

Material models should indeed advance in the path of more complexity to improve their descriptive capability and accuracy, always with the aid of observations from systematic and carefully designed experiments. It is well know that biological tissues show a significant amount of viscoelastic effects, but to date only a few computational simulations have employed viscoelastic models, and at the same time, only a few experimental studies have attempted to fully characterize the viscoelastic behavior of BHV leaflets. Pre-existing stress is another key aspect for accurate biomechanical simulations,³⁰ and the same argument can be made in regard to it—not only it is usually neglected computationally, but also is often overlooked experimentally. Better and more critical experimental techniques are methodologies are certainly in need, not only to fully characterize the present state of the leaflet tissue, but also its evolution.

In fact, the highly dynamic motion of BHVs and its lifetime presents yet another challenge: BHV function occurs in cycles of approximately 1 Hz, with the valve undergoing a full cycle of opening and closing, but on the other hand, BHV dysfunction occurs in a much longer timescale, with its endpoint occurring at approximately 10–15 years after hundreds of millions of cycles. Bridging this huge temporal scale gap is certainly a challenge—it is ill-posed to conduct a complex and detailed simulation of one valve cycle for such high number of cycles, and simulation strategies must be developed to deal with this class of multi-timescale problems.

The ultimate goal of modeling and computational simulation of BHVs is the prediction of the progression of damage and their durability in response to dynamic in vivo biomechanical and biological environment. So far, most attention has been focused on the former, the mechanics, but the importance of the latter, the biology, is properly recognized yet much more difficult to tackle. BHVs function occurs in vivo; therefore its evolving biochemistry must be taken into account. Yet, most BHV biochemical research has focused almost exclusively on mitigation of calcification, which is puzzling as calcification affects less than half of failed BHV while tears due to structural degradation is the predominant mode of failure. Little attention has been paid to understanding the basic biological mechanisms of BHV tissue degeneration to improve long-term durability. Glutaraldehyde treatment forms stable crosslinks within and between extracellular matrix molecules providing resistance to enzymatic and chemical degradation. However, glutaraldehyde crosslinking does not stabilize elastin and GAGs originally present in valve tissue.^132,226 The alteration in the behavior of collagen fibers during valve function as well as the inability of the BHV tissue to remodel can result in abnormal leaflet motion. Damage accumulation has been shown to occur in the collagen microstructure, likely making it more prone to failure.²²⁶ Reduction in GAG content is also thought to be involved in this process, possibly resulting in tissue buckling and the reduction of the valve’s ability to sustain high compressive loads.¹³⁵ The loss of GAGs might also be responsible for the presence of interlaminar shearing, resulting in delamination and loss of collagen fibers from the functioning valve.

Long-term loss of these components may ultimately accelerate valve failure, so that development of models to describe and predict the evolution of these components could guide design better methods to preserve them and enhance BHV durability. Observed changes in BHV tissue shape and mechanical behavior can be a result of gross fiber structural changes (e.g., changes in fiber alignment and architecture), or the effective stiffness of the fibers themselves, or the loss of other tissue components such as elastic or GAGs.^182,183 Purely mechanical experiments alone are insufficient to characterize the evolution of the constituents of the valve leaflet tissue and its mechanical response, and the progression of damage over service life. A shift towards a biochemically driven modeling approach is clearly necessary to account for observable evolving quantities such as constituent mass fractions, GAG depletion, collagen fiber intrinsic stiffness, orientation, recruitment, and fiber-fiber interactions. Carefully designed critical experiments will then be needed to provide further insight into the mechanisms of BHV damage progression. Only with the aid of reliable models backed by observed experimental data, hypothesis formulation to guide BHV design and improve chemical treatment methods can subsequently be developed and tested. Ultimately, the ability to predict biomaterial durability will certainly result in a crucial simulation tool for bioprosthetic heterograft tissue and valve design.

FUTURE PERSPECTIVES

Replacement of diseased natural heart valves with prosthetic replacements has been a lifesaving procedure for millions of patients over the last 50 years and will certainly continue with ever increasing number of deployments, success, and safety. Since BHV do not require anticoagulant therapy, and exhibit good medium- to long-term durability, the heterograft alterative is currently the most favored heart valve substitute biomaterials. For at least the next 20–30 years, BHV fabricated from heterograft tissues will continue to be extensively used and will probably remain as the dominant valve design. Moreover, as developing countries continue to improve their medical delivery infrastructure, worldwide heart valve replacement will continue to rise. BHVs should not be dismissed as the “been there, done that” technology of the last decade—heterograft tissues for BHVs will continue to be extensively used, improved and refined. Rational and scientifically-based approaches to BHV biomaterial development and design can lead to significantly improved BHV over the coming decades, which will impact millions of patients worldwide with heart valve disease.

Durability of BHVs still is the major limitation of the current technology for most patients. Modest improvements in valve durability (e.g., an increase in average durability by 3–5 years) can have dramatic clinical impact. The improvement of the experimental and processing techniques, the accuracy of the assessment of material properties, and the advancement of methods for simulation of heart valve function reviewed here offer rational approaches to further improve the design and durability of BHVs.

Novel approaches to valve implantation, such as percutaneous valve technologies, offer new hope to patients in need of heart valve replacement who are unable to undergo valve replacement surgery. These heart valve designs require novel biomaterials that are substantially thinner than current heterograft tissues and can withstand collapse within a delivery catheter without suffering damage during valve deployment. In the long term, novel tissue sources or new approaches to manufacturing, such as genetically manipulated pigs or engineered tissue heart valves offer great promise for better heart valve prosthesis. Genetic manipulations of animal donors for xenotransplantation may prove to be extremely beneficial to hamper immune response and prevent calcification and structural deterioration. Tissue engineering approaches are particularly attractive for the pediatric population were accounting for somatic growth is paramount. Non-invasive techniques for BHV functional assessment, especially the degree of calcification and the evolution of leaflet mechanical properties (changing due to material fatigue, the major failure mechanism of the biomaterial), will be of considerable clinical use in determining when and where a prosthetic heart valve may be reaching the end of its functional life. Most importantly, the improvement of minimally-invasive assessment technologies will be crucial to provide critical experimental data for model development and computational simulation, which in turn may confer a higher degrees of rationality to the majorly empirical modus operandi of BHV research and development.

Over the last 20 years, the mechanical function of BHVs has been well defined and the mechanical requirements for functional performance carefully characterized. Similarly, methods and protocols for tissue fixation, processing, and BHV manufacturing have been extensively attempeed, tested, and developed, and may have been refined to optimal state. However, accelerated wear testing still is the one and only pass/fail test regarding durability and these neglect all the biochemical and biological aspects of BHV function. A push towards better understanding of the biological and biochemical events associated with valve function is definitely necessary. This knowledge, when framed into novel methods and frameworks rendering mechanical theories of valve function with critical biological aspects, will certainly lead to substantial advancements in BHV durability. Overall, rigorous modeling and simulation with the objective of complementing exploratory experimentation and technological invention will be crucial to BHV design and fabrication, in vivo biochemical and biological interactions post implantation, and the long-term fate of BHVs.

NOMENCLATURE

Abbreviations

AHA

American Heart Association

AV

Aortic valve

BHV

Bioprosthetic heart valve

BP

Bovine pericardium

ECM

Extracellular matrix

FE

Finite element

GAG

Glycosaminoglycan

GLBP

Glutaraldehyde bovine pericardium

GLUT

Gluraraldehyde treatment

LEHI

Linear elastic homogeneous incompressible

microCT

Micro X-ray computed tomography

MRi

Magnetic resonance images

MV

Mitral valve

PAV

Porcine aortic valve

PBS

Phosphate buffered saline

PD

Preferred direction

RVE

Representative volume element

SALS

Small angle light scattering

TEHV

Tissue-engineered heart valve

UTS

Ultimate tensile stregth

VEC

Valvular endothelial cell

ViC

Valvular interstitial cell

XD

Cross-preferred direction

List of symbols

ΔM

Infinitesimal mass

ΔV

Infinitesimal volume

ρ

Mass density

ε

Fiber uniaxial strain (in structural constitutive model)

θ

Fiber orientation angle (in structural constitutive model)

c_f

Volume fraction of fibers (in structural constitutive model)

C

Left Cauchy-Green stretch tensor

D(ε)

Fiber recruitment statistical distribution (in structural constitutive model)

E

Green–Lagrange strain tensor

E_ij

Components of the Green-Lagrange strain tensor

I(θ)

Angular distribution of scattered light (in SALS analysis)

R(θ)

Fiber angular distribution (in structural constitutive model)

S

Second Piola–Kirchhoff stress tensor

S_ij

Components of the second Piola–Kirchhoff stress tensor

S^f

Second Piola–Kirchhoff stress tensor in the fiber (in structural constitutive model)

$S\begin{array}{c}f\\ nn\end{array}$

Component of the Piola–Kirchhoff stress tensor in the fiber along fiber direction (in structural constitutive model)

W

Stored energy function

w(ε)

Stored energy function of fiber (in structural constitutive model)

W_f

Stored energy function of the fiber ensemble (in structural constitutive model)

W_m

Stored energy function of the matrix (in structural constitutive model)

I₁, I₂, I₃

Principal invariants of the left Cauchy-Green stretch tensor