Heat Equation Inversion Framework for Average SAR Calculation From Magnetic Resonance Thermal Imaging

Abstract

Deposition of radiofrequency (RF) energy can be quantified via electric field or temperature change measurements. Magnetic resonance imaging has been used as a tool to measure three dimensional small temperature changes associated with RF radiation exposure. When duration of RF exposure is long, conversion from temperature change to specific absorption rate (SAR) is nontrivial due to prominent heat-diffusion and conduction effects. In this work, we demonstrated a method for calculation of SAR via an inversion of the heat equation including heat-diffusion and conduction effects. This method utilizes high-resolution three dimensional magnetic resonance temperature images and measured thermal properties of the phantom to achieve accurate calculation of SAR. Accuracy of the proposed method was analyzed with respect to operating frequency of a dipole antenna and parameters used in heat equation inversion.

Introduction

Exposure to radiofrequency (RF) radiation results in increased heating of tissue via Joule and dielectric heating mechanisms [Juutilainen and De Seze, 1998]. In order to prevent deposition of excessive RF energy into the body, maximum allowed temperature increase during RF heating is regulated [ICNIRP, 2009] by means of measuring specific absorption rate (SAR), the rate at which energy is deposited inside the body. SAR is conventionally measured in the wireless industry using electric (E) field probes [Schmid et al., 1996] that are mechanically moved in a point-by-point, grid-like fashion in three dimensional (3D) space inside a phantom filled with a liquid mimicking electrical properties of human tissues. Okano and Shimoji have shown that RF energy exposure quantification can be conducted by measuring temperature increase due to RF exposure using highly sensitive temperature probes [Okano and Shimoji, 2012]. Gultekin and Moeller [2013] have shown that magnetic resonance (MR) methods can be used to measure temperature increase due to RF energy absorption, where the magnitude of temperature increase was a function of RF power and exposure time in brain equivalent gels and brain tissue [Gultekin and Moeller, 2013]. Recently, high-resolution MR thermal mapping has been utilized for assessment of RF energy absorption from handheld wireless devices [Alon et al., 2015] that output less than 1W of power.

In order to ensure RF safety regulations using SAR [IEC, 2010], temperature change measurements need to be converted to spatial-average 10 g average SAR by keeping the RF exposure duration short for capturing the initial slope of the temperature increase [IEC/IEEE, 2015]. In practice, however, the E fields produced by the antenna, maximum power capabilities of the RF amplifiers, and conductivity of the phantom can be limiting factors in keeping the duration of heating small, requiring longer RF exposure duration for accurate temperature measurements. In such cases, heat diffusion in the phantom cannot be ignored, and the conventional method fails to provide accurate results [Alon et al., 2014]; thus proper conversion of temperature change into spatially average SAR is required.

In this work, we introduce a generalized heat equation inversion (HEI) framework that takes into account heat-dissipation due to boundary conditions and heat-diffusion. A finite difference framework was used to model heat diffusion and conduction and calculate the point-wise SAR. Calculated point-wise SAR was later used as input for average SAR calculations by defining a spherical volume of 1 and 10 g around the voxel of interest. Fidelity of the inversion of the heat equation was investigated using Electromagnetic (EM) field simulations of dipole antennas operating at different frequencies, where true simulated SAR (which is not known in experiments) is recovered from temperature with realistic noise addition. HEI framework results are compared to the conventional method, which does not model heat convection and diffusion [Cline et al., 2004], using MR thermal measurements of different RF exposure durations. Experimental results demonstrate that combining the information provided by MR temperature mapping [Rieke and Butts-Pauly, 2008] with physical thermal measurements of the phantom enables inversion of the heat equation and accurate computation of the spatial average SAR distribution.

Materials And Methods

Theory-Heat Equation Inversion (HEI)

The heat equation with source term is a parabolic partial differential equation, which captures the behavior of temperature in spatial location, r, and time, t, when a body is exposed to an external energy source. The equation in non-perfused, homogeneous media is expressed as:

$$\rho (\mathit{r})C(\mathit{r})\frac{\mathit{\text{dT}}(\mathit{r},t)}{\mathit{\text{dt}}}=\nabla \cdot (k(\mathit{r})\nabla T(\mathit{r},t))+\text{SAR}(\mathit{r},t)\rho (\mathit{r})$$ (1)

where ρ, C, k, and SAR are tissue density (kg/m³), specific heat (J/kg/°C), thermal conductivity (W/m/°C), and SAR (W/kg), respectively. SAR—the driving force for temperature rise as a result of Joule/Dielectric heating mechanisms—is defined as:

$$\text{SAR}(\mathit{r},t)=\frac{\sigma {(\mathit{r}|\mathit{E}(\mathit{r},t)|)}^2}{\rho (\mathit{r})}$$ (2)

where E is induced electric field (V/m) due to RF exposure inside the body, and σ is electrical conductivity (S/m). When heating duration is short, heat diffusion terms in Eq. (1) can be neglected and Eq. (1) can be simplified to:

$$\text{SAR}(\mathit{r})=C(\mathit{r})\mathrm{\Delta }T(\mathit{r})/\mathrm{\Delta }t$$ (3)

where Δt is RF heating time-interval. Using MR temperature mapping measurements at each spatial location r and thermal property measurements of the homogeneous media, the unknown heat source term, SAR, at each location r can be calculated by solving the inverse problem associated to Eq. (1). There are several methods available to extract the source term from parabolic partial differential equations [Johansson and Lesnic, 2007; Taylor et al., 2010; Yan et al., 2012]. In the current implementation, a finite difference approximation to the heat equation is used [Collins et al., 2004]. Using the finite difference approximation with discretizing total heating time in N time samples, final temperature distribution at time NΔt, defined as T_N, can be written in the form of a linear polynomial equation from Eq. (1) for a time-invariant but spatially-changing SAR source, SAR(r):

$$T_N(\mathit{r})={(1-L)}^{N-1}{T}_1(\mathit{r})+\sum _{i=0}^{N-2}{(1+L)}^{i}f(\mathit{r})$$ (4)

where f is unknown source term defined as: f = SAR*Δt/C, T₁ is the initial temperature of the sample, and L is a linear Laplace operator, $L=\frac{\mathrm{\Delta }t}{\rho C}\ast \nabla \cdot (k\nabla )$, which accounts for possible tissue property variations in space. By discretizing space in M locations, Eq. (4) can be written as a linear matrix equation:

$$\mathit{A}\mathit{f}=\mathit{b}$$ (5)

where $\mathit{A}=\sum _{i=0}^{N-2}{(1+\mathit{L})}^i$ defines a MxM system matrix and b = T_N − (1 + L)^N−1 T₁ defines a Mx1 measurement vector. All terms in Eq. (5) except f are measurable quantities (k and C can be measured using a thermal probe, and ΔT = T_N − T₁ using MR temperature mapping). Unknown f can be calculated using the following L1 norm weighted least squares minimization, which has been shown to be robust with respect to noise for sparse representations [Candes et al., 2006; Donoho et al., 2009]:

$$\underset{f}{\text{argmin}}\{{\Vert \mathit{A}-\mathit{b}\Vert }_2+\mathrm{\lambda }{\Vert \mathit{f}\Vert }_1\}$$ (6)

where λ is regularization parameter. λ trades off sparsity of the solution with the error and ensures conditioning for the inverse problem. In the reconstruction, λ was normalized by total input energy (temperature change) in the system, since temperature change imposed a different weighting on the minimization function (‖Af−b‖₂). This normalization was performed such that a similar λ can be used for different heating durations and frequencies.

Evaluation of a Simplistic Approach for SAR Calculation From Temperature Difference Maps

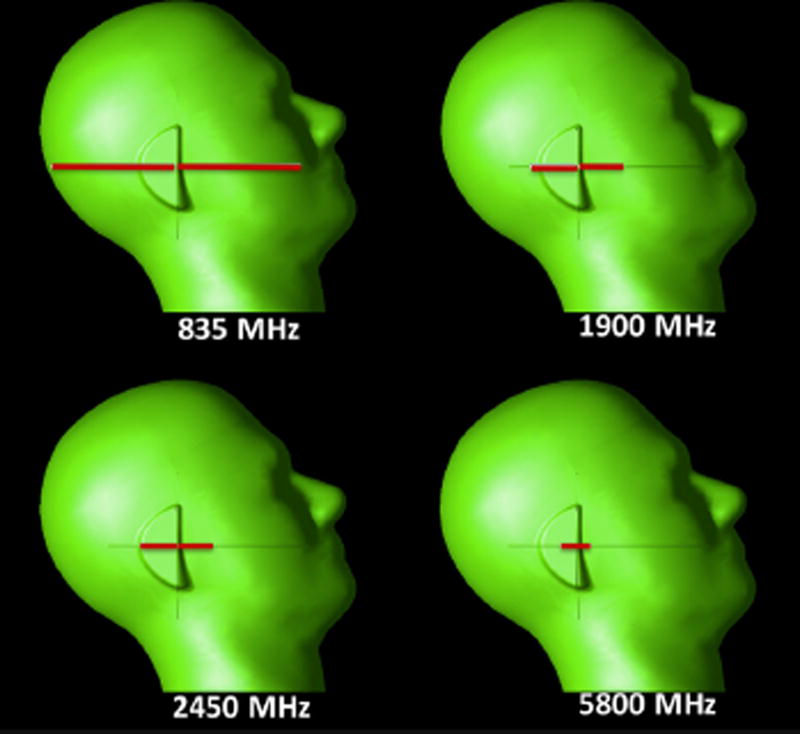
Equation (3) can be used to reconstruct SAR maps from temperature difference (ΔT) distributions [Cline et al., 2004]; however, in practice heating duration cannot be kept “sufficiently” small such that thermal convection and conduction inside the phantom and at the air-phantom interface have little effect on temperature rise. Due to the required sensitivity of temperature measurements, heating duration needs to be extended into a few minutes where thermal convection and conduction start to play an important role in safety assessment. The effect of heating time (6 and 15min) on reconstructed 1 and 10 g average SAR maps was analyzed in this section. Four half-wavelength dipole antennas were modeled using a commercially available finite difference time domain (FDTD) simulation solver (XFDTD version 7.3, Remcom, State College, PA). Dipole antennas were tuned to frequencies 838, 1900, 2450, and 5800 MHz by adjusting the length of the dipole arms, resulting in dipole lengths of 17.1, 7.5, 5.8, and 2.5 cm for each respective frequency. Each dipole antenna was placed adjacent to the specific anthropomorphic mannequin (SAM) head phantom (Fig. 1), the gold standard for compliance testing [IEEE Std. C95.1, 2003]. Electrical properties of material inside the SAM phantom were selected to match standard properties defined at the operating frequency of the antennas (Table 1) [Federal Commnunications Commission, 2005]. A port with unit voltage source was placed between the arms of the dipole antennas. For the excitation, a voltage source providing unit voltage was placed between the legs of the dipole antenna. Simulation mesh size was 170 × 126 × 336 and resolution was 2×2×2 mm³. A seven-layer perfectly matched layer (PML) absorbing boundary condition was applied at all outer boundaries, and convergence criterion was set to −50 dB. Upon convergence of the simulation, the match of antennas was <−15 dB, and net output power of each antenna was scaled to 100 mW of power. SAR distribution and thermal properties of the SAM phantom were exported to Matlab (version 8.5, MathWorks, Natick, MA), and 1 and 10 g average SAR distributions were computed. SAR and thermal properties of the phantom were used as input for a thermal solver [Wang et al., 2007], simulating RF heating for 6 and 15 min using a thermal solver with 4 s step size [Ozisik, 1994]. From the temperature difference maps, SAR was calculated (using Eq. [3]) and averaged over 1 and 10 g of tissue [IEEE Std. C95.3, 2002].

Fig. 1.

Dipole antenna of different sizes, tuned to four different frequencies, were placed next to SAM head model.

Table 1.

Dielectric and Thermal Properties of Phantoms in Reported Simulations/Experiments

Modality	Frequency (MHz)	εr	σ (S/m)	ρ (kg/m3)	K (W/m/°C)	C (J/kg/°C)
Simulation	835	41.5	0.9	1000	0.35	2940
	1900	40	1.4
	2450	39.2	1.8
	5800	35.3	5.3
Simulation	1960	36	1.5
Dipole experiments (SAM phantom)	1960	40	1.4
Magnetic loop experiments	275	71	1.0	1064	0.57	3660

Sensitivity Analysis of HEI Framework for Regularization Parameter Calibration

The regularization parameter, λ, plays an important role in conditioning the inversion problem and trading off the sparsity with reconstruction error. Dipole antenna simulations performed in the previous section were used to assess sensitivity of the HEI process to the regularization parameter, λ. Output power of simulations was scaled to 100 and 200 mW, and temperature maps for 6 and 15 min RF heating were computed using a thermal simulator [Wang et al., 2007] with 4s step size. This resulted in four simulations for each frequency band (100 mW–6 min, 100 mW–15 min, 200 mW–6 min, 200 mW–15 min). Gaussian noise with 0 mean and standard deviation of 0.035 °C was injected into temperature difference maps. Noise was chosen based on empirical noise figures in MR thermal mapping phantom data in MRI literature [Alon et al., 2015]. HEI reconstruction framework used simulated temperature maps to reconstruct SAR using different lambda values between 0 and 80 in a logarithmic scale. Overall, 1,280 reconstructions were conducted. Reconstruction of SAR distributions from 3D temperature maps was performed on a high performance computing cluster with 112 nodes, each with two Intel Xeon E-2690v2 3.0 GHz CPUs and 64 GB of memory. Using reconstructed SAR distributions, 1 and 10 g average SAR were reconstructed and compared to true simulated SAR distributions.

Experimental Validation of HEI Framework Using a Dipole Antenna Operating at 1.96 GHz

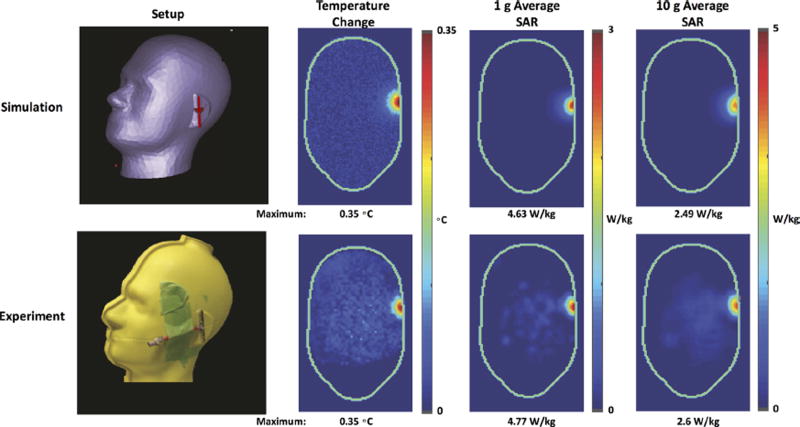
Validation of the HEI framework on a dipole antenna placed next to a SAM phantom was performed in simulations and experiments using the lambda parameter specified in the sensitivity analysis. EM field simulations were performed on the dipole antenna—SAM phantom (Fig. 5), in order to obtain SAR distribution induced by the dipole antenna inside the phantom and compare with SAR distribution obtained from experiments using HEI framework and MR temperature mapping. Commercial Microwave Studio software (CST, Framingham, MA) using finite integration technique (FIT) was used for simulations. Parameters used in FIT calculations were as follows: 2 mm isotropic cell size, mesh dimensions 112 × 111 × 111, feeding with a voltage source operating at 1.96 GHz. A 5 mm separation between the phantom and dipole antenna was used to simulate the physical setup in the scanner room. Simulated SAR distribution was used along with thermal properties of the phantom to model temperature distribution in the phantom numerically by solving the Heat equation (Eq. 1) (forward problem) as a result of 6.5 min of heating. Gaussian noise (similar in mean and standard deviation of measured MR temperature maps) with standard deviation of 0.035 °C was added to simulated temperature maps. Inversion of the heat equation was conducted using L1 weighted norm minimization (Eq. 6) in order to calculate the local SAR at each spatial location. The spatial-averaged 1 and 10 g average SAR, which is regulated for RF safety by international standard committees [IEC, 2010], was calculated [IEEE Std. C95.3, 2002] and plotted for a center axial slice at the middle of the SAM phantom. Maximal temperature change, reconstructed 1 and 10 g average SAR were reported.

Fig. 5.

Simulated temperature change, 1 and 10 g average SAR from a simulated dipole (top row). Experimental temperature measurement using MR thermal mapping alongside reconstructed 1 and 10 g average SAR maps using HEI method (bottom row).

For the experimental setup, a half wavelength dipole antenna was constructed to operate at 1.96 GHz and matched for maximum efficiency with S11 < −15 dB. The antenna was placed adjacent to the pinna of the SAM phantom, filled with gel having dielectric properties of σ = 1.4 S/m and ε_r = 40, respectively (Table 1). During the RF heating period, the antenna was operated in continuous wave mode for 6 min, and net injected RF power was monitored using a directional coupler (778D, Agilent Technologies, Santa Clara, CA) and a power sensor (NRP-Z11, Rhode & Schwarz, Munich, Germany). Net input power measured at the dipole antenna input port was 0.65 W. For experimental validation, RF heating was detected using a 3 T MR scanner and head and neck coil (Siemens Medical Solutions, Erlangen, Germany) with 20 receive elements. Multi-slice, interleaved, spoiled gradient-echo (GRE) images of the phantom before and after RF heating were acquired with the following parameters: repetition time (TR) = 244 ms, echo time (TE) = 17 ms, voxel dimension = 2.7 mm × 2.7 mm × 5 mm, number of slices = 11, and total acquisition time = 31 s. The fundamental phenomenon governing most MR-based temperature mapping is the Proton Resonance Frequency (PRF) shift, which linearly relates precession frequency of the spins of protons with temperature [Rieke and Butts-Pauly, 2008], enabling RF power deposition assessment via temperature measurements. The PRF shift method was used to convert multi-coil GRE phase measurements into a temperature difference map. Thermal properties of the phantom were measured using a KD2 Pro thermal property analyzer (Deacon Devices, Pullman, WA). SAR was then computed using the HEI method via inversion of the heat equation and spatially averaged over 1 and 10 g. The measured temperature change and reconstructed 1 and 10 g average SAR distributions were plotted for an axial slice of the SAM phantom. Maximal temperature change and reconstructed 1 and 10 g average SAR were reported.

Experiments with a Magnetic Loop Antenna Operating at 275 MHz

We performed loop antenna experiments with two different power levels in order to demonstrate the feasibility of extracting SAR using the heat inversion equation experimentally. A gelatin phantom was created to emulate electrical properties of human tissue by combining 500 ml of water, 115.4 g of Gelatin, 1 g NaCl, and 0.5 g of benzoic acid. The phantom’s electrical conductivity and relative permittivity were 1 S/m and 71, respectively, measured using a dielectric probe kit (Agilent 85070E, Agilent Technologies). The gel was placed inside a bottle measuring 7 cm in diameter and 16.5 cm in height. Thermal properties of the gel were measured using a KD2 Pro thermal property probe (Deacon Devices) and listed in Table 1. A simple loop antenna for heating was placed on top of the phantom (Fig. 6) and inside a 28-channel knee coil (Quality Electrodynamics, Mayfield Village, OH). The 6.5 × 6.5 cm² loop antenna was tuned to 275 MHz with S₁₁ <15dB inside the coil in a 7T MRI system (Siemens Medical Solutions). The 7T system was used due to its high sensitivity to thermal changes that was suitable for this experiment. Phantom was placed in the scanner room 24 h before the experiments such that the phantom’s temperature was stabilized to room temperature.

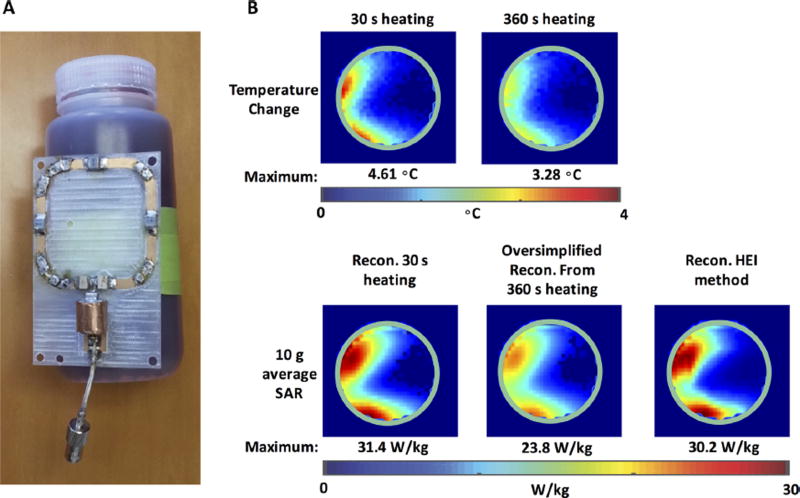
Fig. 6.

A: Illustration of magnetic loop antenna next to oil phantom setup. B: Reconstructed 10 g average SAR maps for a magnetic loop antenna using HEI method with λ = 0.075. A comparison between oversimplified and HEI reconstructions is illustrated in bottom row.

Two different RF heating experiments were conducted: (i) the loop antenna was connected to an RF amplifier (Kalmus, LA200UELP, Bothell, WA), delivering 7.9W of continuous power for 6 min. This long duration of heating time was used such that diffusion and boundary effects influence heat transfer in the phantom. (ii) 95 W of continuous power (12× relative to Experiment 1) was used to drive the antenna for a period of 30 s (12× time reduction compared to Experiment 1). In this short heating duration of 30 s, multiplying temperature change by the heat capacity of the phantom and dividing by heating duration can be used to calculate SAR (Eq. 3), with the assumption that initial slope of the temperature change curve due to RF exposure is captured. In each experiment, a pre-and post-heating image using MRI was acquired with the following parameters: TE=10 ms, TR= 184 ms, resolution = 2.5 × 2.5 × 5 mm³, acquisition time = 11.8 s. Pre- and post-heating images were used to reconstruct temperature change using the PRF shift method [Ishihara et al., 1995]. The temperature change map from Experiment 1 was fed into the HEI solver described in the Methods section to compute SAR distribution with λ = 0.075. Temperature change maps from Experiment 2 were multiplied by heat capacity of the phantom and divided by the time of heating to yield SAR. Results of the temperature change and 1 and 10 g average SAR calculation were analyzed and plotted for an axial center slice in the center of the phantom.

Results

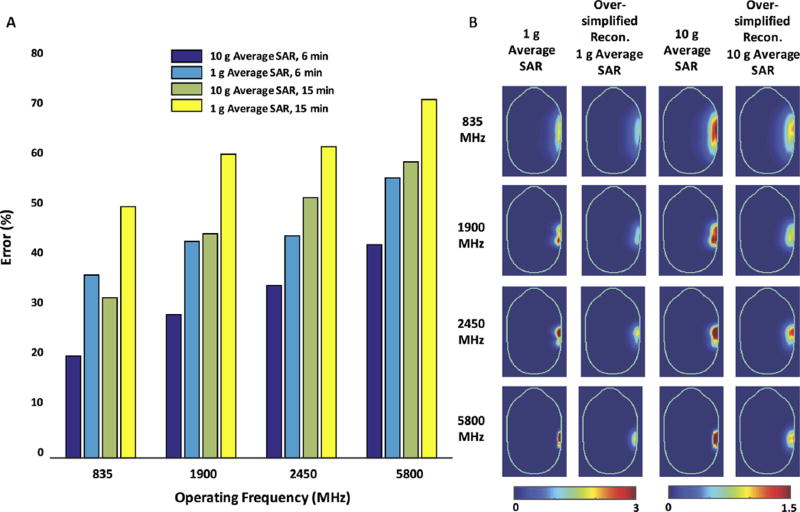
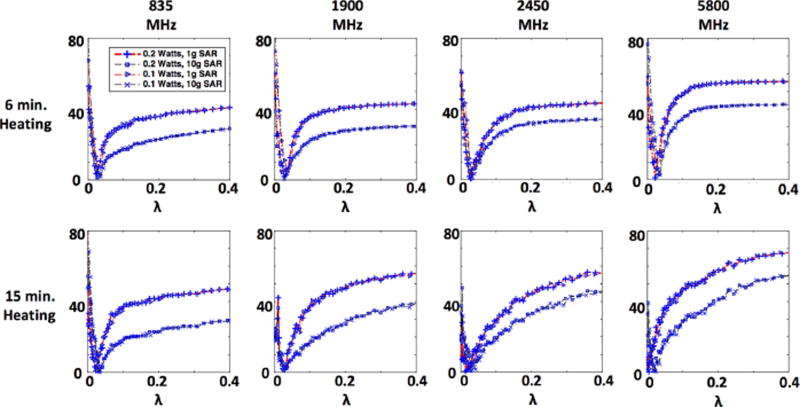
Challenges associated with estimation of average SAR distributions from temperature difference maps using Eq. (3) are summarized in Figure 2. Figure 2A plots the % error of the estimated over true 1 or 10 g average SAR computed using the simplistic approach (Eq. 3). A trend was observed where errors were exacerbated when the heating duration and operation frequency increased. Similarly, larger errors were observed when averaging volume decreased. The range of errors varies between 20% to 71%, where the minimum error occurs at 835 MHz for 10 g average SAR with 6 min heating, and maximum error occurs at 5800 MHz for 1 g average SAR with 15 min heating. This is consistent with the fact that the oversimplified inversion process does not take energy exchange into account, due to the phantom-air boundary as well as heat diffusion inside the SAM phantom. When the frequency of operation is increased, greater surface heating is observed which contributes to a larger heat exchange with air. Figure 2B illustrates average SAR distributions for an axial slice in the middle of the SAM phantom. Because the oversimplified reconstruction does not account for heat exchange, reconstructed average SAR distributions are consistently underestimated for all cases.

Fig. 2.

A: Maximum 1 or 10 g average SAR errors reconstructed using oversimplified reconstruction method for four simulations. B: Maps of true 1 and 10 g adjacent to oversimplified reconstructed 1 and 10 g average maps, illustrating underestimation of true SAR.

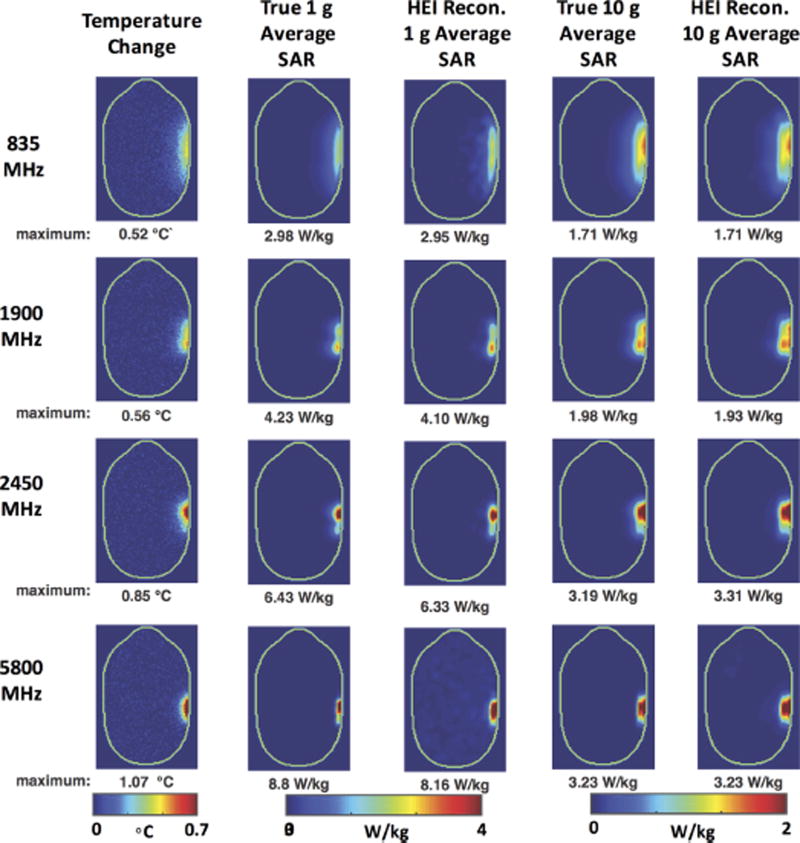
Sensitivity of the HEI process to the parameter l is illustrated in Figure 3, where the percent error in maximum 1 and 10 g average SAR is plotted versus the regularization parameter l. These errors were observed after injection of Gaussian noise into temperature maps that were used for the HEI reconstruction. Results remained consistent across different output power levels (100 and 200 mW) and heating durations (6 and 15 min). Temperature change and average SAR results with λ = 0.03, heating duration = 15 min, and output power = 100 mW are shown in Figure 4. For an axial slice in the center of the SAM phantom, true 1 and 10 g average SAR maps are juxtaposed next to HEI reconstructed average SAR maps. The largest error in the maximum was 7.3% and 3.8% for 1 g average SAR and 10 g average SAR, respectively. Reconstructed SAR maps are closely correlated with true average SAR maps in distribution and magnitude as opposed to average SAR results obtained with the oversimplified reconstruction (Fig. 2b).

Fig. 3.

Regularization parameter and its effect on HEI reconstruction. Maximum 1 and 10 g average SAR reconstruction error for 6 and 15 min with 100 or 200 mW of net input power is plotted.

Fig. 4.

Reconstructed 1 and 10 g average SAR maps using HEI method. Reconstruction was conducted from temperature difference maps due to 15 min of heating 100 mW of output power generated by antenna. Reconstruction results illustrate reconstructed maximum 1 or 10 g average SAR error of less than 7.3%.

After assessing sensitivity of the HEI reconstruction algorithm with respect to the λ parameter, experimental results illustrating HEI reconstruction are presented in Figure 5 for λ = 0.03. Experimental results are compared to EM field simulations in terms of distribution and maximum average SAR (Fig. 5, left). The maximum 1 and 10 g average SAR difference between the simulations and experiments were 3% and 4.4%, respectively. As illustrated in Figure 5, there was a good agreement in the thermal maps, while reconstructed 1 and 10 g average SAR in experiments and simulations were nearly identical in distribution in magnitude.

Further experimental validation of the HEI framework is shown in Figure 6, illustrating accurate 10 g average SAR reconstructed for a magnetic loop antenna when duration of heating was 6 min. The temperature change resulting from 30 s of heating with 95W of continuous power is shown in the top left where the maximum temperature change was 4.61 8C. Similarly, the temperature change resulting from 6 min of heating with 7.8 W of continuous power (12× reduction in power) is shown in the top right, where, because of boundary effects with air and heat diffusion, the maximum temperature change was lower at 3.28 °C. The bottom row shows results of two different methods for conversion of the temperature change to 10 g average SAR. On the left, 10 g average SAR was computed from the temperature change induced from 30 s of heating at 95 W, during which heat diffusion was minimal. Heat diffusivity of the phantom was measured as 0.146 mm²/s; therefore over a period of 30 s diffusion length was 2.96 mm. In the middle, oversimplified 10 g average SAR reconstruction is shown, where temperature change is scaled by heat capacity of the phantom and time of heating. Since heating duration is long, an underestimation of the maximum 10 g average SAR is shown in the bottom middle (23.8 vs. 31.4 W/kg, error of 24%). Using the HEI framework (Fig. 6b), the 10 g average SAR can be calculated accurately even when heating duration is long. The maximum 10 g average SAR error with respect to the 30 s of heating inversion was 3.8%.

Discussion

A generalized framework for computing average SAR from temperature change measurements is presented. The combination of high resolution MRI temperature mapping, acquired alongside thermal property measurements of the phantom, enabled accurate conversion of ΔT to average SAR using the HEI framework when heating durations were long (demonstrated for up to 15 min). The HEI method decreased the maximum average SAR error, compared to the over-simplified SAR calculation method, enabling the accurate safety assessment of low power wireless devices using thermal imaging. The authors designed the study such that the output power of the antennas (100 and 200 mW, respectively) were of the order of conventional handheld devices (<250 mW), and duration of heating (6 and 15 min, respectively) was equal to or lower than the time required to get a measureable temperature change using MR thermal mapping [Alon et al., 2015]. Similarly, the frequency of operation of the antennas was chosen to support most handheld technologies in today’s consumer market. By design the authors have decided to calibrate only a subset of exposure conditions, where in future studies, larger range of SAR distributions, power levels, and frequencies can be explored for the optimal value of λ. In this manuscript, we have tailored the HEI framework to work in conjunction with MR thermal mapping. MR thermal mapping was particularly advantageous for this framework as it provided high sensitivity to temperature changes with high spatial and temporal fidelity [Kickhefel et al., 2010; Yuan et al., 2012].

Knowledge of thermal properties of the phantom was key for creating the encoding matrix A (Eq. 6). Thermal parameters of gel phantom were measured prior to the experiments using a thermal property analyzer. These measurements were conducted outside the MRI scanner. Although external probes were used in the current study, thermal conduction, diffusion, and heat capacity can be measured accurately by using MRI while imaging an object during heating or cooling as demonstrated by Gultekin and Gore [2006, 2008, 2010, 2011]. In the future, these measurements alongside the HEI framework can possibly be combined as a sole MRI-based quantification of RF energy deposition.

In the dipole antenna simulations 2 mm³ resolution was used, which was sufficiently high for reconstruction of average SAR for wireless devices below 6 GHz. In order to allow proper convergence of conventional finite difference temperature simulations, a time step of 4 s was used. Time step in the HEI framework is the same as for the traditional forward finite difference forward solver [Ozisik, 1994] and can be analytically determined. The time step chosen in this work resulted in a stable HEI reconstruction. It is likely that resolutions that are finer than 2 mm³ are required when investigating RF exposure above 6 GHz since staircasing artifacts may occur if the resolution is not sufficiently high. In cases where higher spatial resolution is used, the time step required to ensure proper convergence would have to be shortened to uphold proper convergence. Here, we have defined the resolution and time step parameters required to ensure proper convergence for exposure conditions below 6GHz. Future investigation would be necessary for modification of this framework to encapsulate parameters such as resolution, time step, regularization parameter, etc. for frequencies above 6 GHz.

In the dipole experiments presented, a maximum temperature change of 0.35°C was measured with a standard deviation of noise level of 0.035. Temperature errors of the same magnitude have been demonstrated in various phantom studies [Gultekin and Moeller, 2013; Alon et al., 2015] with slightly higher errors for in vivo studies [Kickhefel et al., 2010]. At the reported standard deviation of the temperature measured here, proper reconstruction was conducted; however, average SAR reconstruction depends on the signal-to-noise of the measurement. In this study, we have investigated the maximum output of antennas equal or greater than 100 mW, while further investigation is needed to find limits of the reconstruction algorithm at power levels that yield significantly smaller temperature change. With these low power levels (below 100 mW), heating duration may have to be extended above 15 min in order to provide sufficient temperature-to-noise ratio. Furthermore, the thermal measurement modality used to capture temperature change can highly affect reconstruction by introducing different amounts of noise into the thermal image. In that respect, we have utilized traditional MR thermal imaging and phantoms for our acquisitions; however, in recent years there have been developments of more sensitive 3D temperature acquisitions and phantoms that can potentially improve the reconstruction [Zuo et al., 2001; Grissom et al., 2010; Yuan et al., 2012; Park et al., 2015].

The HEI framework was investigated in simulations and experiment for a dipole antenna as well as for a purely experimental magnetic loop antenna. The experiment shown in Figure 6 was possible, because of the high power amplifiers that were available to us at a frequency of 275 MHz. This enabled heating of the phantom by an appreciable amount very rapidly (30 s of heating). In these 30 s, heat diffusion and heat exchange with the air was small. During this time, thermal diffusion smoothed the temperature difference over a distance of $\sqrt{2\beta \mathrm{\Delta }t}$, where β is heat diffusivity. The value of β in our phantom gel was 0.146 cm²/s, and over a heating period of 30 s the characteristic temperature diffusion length was 0.3 cm [Cline et al., 2004]. When the output power delivered to the magnetic loop antenna was reduced 12-fold and duration of heating increased 12-fold (6 min), heat diffusion created a larger error in maximum average SAR estimation. This large error was reduced by accounting for heat diffusion and exchange as part of the HEI framework. In this manuscript, we have used conventional scanning protocols to acquire thermal maps. It is important to point out that with some MRI sequence optimization, rapid MRI scanning techniques can be used so that a thermal image is acquired as small as 2 s [Kickhefel et al., 2010; Yuan et al., 2012]. If these sequences are potentially used, errors resulting from the scan time can be virtually eliminated.

Furthermore, Moros and Pickard did important work on the assumption of negligible heat diffusion during thermal measurements [Moros and Pickard, 1999], studying at which time constants temperature change can be linearly converted to SAR. They demonstrated that the time window t_m, at which temperature variation associated with SAR is measured, should satisfy the following inequality:

$$t_m\le \frac{{\alpha }^2}{{\pi }^{2}D}$$

where α is characteristic length of the full width half max variation in SAR, and D is thermal diffusivity of the medium. In the context of this manuscript, thermal diffusivity of the phantom in dipole experiments was 0.119 mm²/s, and full width half max at the highest experimental frequency (1.9 GHz) was 8 mm (the smallest full width half max within the experiments). According to Moros and Pickard [1999], the measurement window at which temperature is measured should not exceed 44.3 s. As we have observed in this manuscript, heating durations of 6 and 15 min of heating, respectively, far exceed restrictions posed by Moros and Pickard [1999] and as a result, proper reconstruction of average SAR maps was not possible. These errors were greatly reduced using the HEI framework.

Conclusions

In this work, a HEI algorithm for 1 and 10 g average SAR reconstruction from high-resolution temperature difference maps, such as those acquired using MR thermal mapping, is presented. Stability of the algorithm was investigated in EM field simulations. Fidelity of the HEI algorithm was investigated using dipole antenna simulations and experiments, showing a good agreement between simulated and HEI algorithm-reconstructed SAR distributions.