Abstract
Most cancers evolve from a single founder cell through a series of clonal expansions that are driven by somatic mutations. These clonal expansions can lead to several coexisting subclones sharing subsets of mutations. Analysis of massively parallel sequencing data can infer a tumor’s subclonal composition through the identification of populations of cells with shared mutations. We describe the principles that underlie subclonal reconstruction through single nucleotide variants (SNVs) or copy number alterations (CNAs) from bulk or single-cell sequencing. These principles include estimating the fraction of tumor cells for SNVs and CNAs, performing clustering of SNVs from single- and multisample cases, and single-cell sequencing. The application of subclonal reconstruction methods is providing key insights into tumor evolution, identifying subclonal driver mutations, patterns of parallel evolution and differences in mutational signatures between cellular populations, and characterizing the mechanisms of therapy resistance, spread, and metastasis.
Massively parallel sequencing data (e.g., single nucleotide variants or copy number alterations) can be used to infer the subclonal composition—or the populations of cells with shared mutations—in a tumor.
Cancers evolve through the acquisition of changes in the genome and epigenome of their cells (Nowell 1976; Tabin et al. 1982). Some of these mutations provide the cell in which they occurred with an evolutionary advantage over other cells and are known as “driver” mutations, whereas other mutations (“passenger” mutations) are assumed to have a neutral effect (Stratton et al. 2009; Garraway and Lander 2013). A tumor cell with a selective advantage is better suited to its local microenvironment and can, therefore, proliferate quicker than other cells and generate more daughter cells. This process is called “clonal expansion” (Greaves and Maley 2012; Vogelstein et al. 2013). This interplay between mutation and selection allows a tumor to evolve and adapt to a changing environment.
Part of a tumor’s evolutionary story can be inferred through massively parallel sequencing of tumor samples (Fig. 1). Mutations that have occurred before the “most recent common ancestor” (MRCA) are carried by all tumor cells in a sample and can be used as markers of the clonal population (Campbell et al. 2008). As the tumor develops further, it continues to acquire more driver and passenger mutations. A tumor cell that acquires an additional driver mutation and embarks on a clonal expansion will generate a subpopulation of cells bearing mutations that are not shared by all cells in the tumor (Fig. 1A). Such a subclonal cell population can therefore be identified through a set of shared mutations.
Figure 1.
General overview of subclonal reconstruction. (A) During cancer evolution, a tumor acquires driver mutations (marked with a plus sign) that can initiate clonal expansions. (B) Over time, a number of these clonal expansions can occur, resulting in the increase of subpopulations of cells harboring distinct sets of mutations. Tumor samples typically consist of a mixture of tumor cells with mutations (solid lines) and normal cells without mutations (dashed lines). (C) Some mutations are carried by all tumor cells (marked with a square), whereas others are present in a subset of cells (triangle and circle). Using allele frequencies of mutations obtained from sequencing data and accounting for copy number aberrations, an estimate of the fraction of tumor cells carrying each mutation can be obtained. A set of mutations can then be used as a marker for a population of cells, allowing estimation of the fraction of tumor cells of the corresponding subclone. Clustering algorithms can be applied to obtain the cancer cell fractions (CCFs) of each subclone. (D and E) The relationship between subclones can be visualized as a tree. (D) Some methods perform this clustering in fraction of tumor cells space, and (E) others in the space of fraction of all cells.
Figure 1B shows a schematic example, in which the “square” mutations are carried by all tumor cells and are therefore clonal, and the “triangle” and “circle” mutations are present only in a subpopulation of tumor cells. A tumor sample usually also contains non-tumor cells, such as stromal cells, immune cells, and fibroblasts, that do not share any genomic mutations with the tumor clones. The fraction of tumor cells in a sequencing sample is known as the “purity” or “cellularity.”
For each of the somatic mutations, an associated “variant allele frequency” (VAF) can be calculated. Besides the tumor purity and the fraction of tumor cells carrying a mutation, the VAF also depends on copy number changes. For example, a mutation that has occurred before a gain is carried by two out of three chromosome copies, whereas a mutation that occurred after the gain is carried by one out of three chromosome copies. It is important to account for all these factors when using VAF values to infer a tumor’s subclonal architecture, as mutations from the same subclonal population may show different VAFs because of copy number changes.
Accounting for the factors above, it is useful to represent the propensity of mutations or mutation clusters through their “cellular prevalence” (CP, the fraction of cells carrying the mutation[s] in the sample), or their “cancer cell fraction” (CCF, the fraction of tumor cells carrying the mutation[s]). In Figure 1C, the CCF space is shown, where the clonal mutations (denoted by squares) now appear in a cluster around 1.0, as they are found in 100% of tumor cells, and the subpopulation denoted by triangles that consists of 33% of tumor cells now appears at 0.33. Subclonal reconstruction can be performed by clustering these mutations, here resulting in a “square” and a “triangle” cluster. A key underlying assumption is that each mutation has occurred only once during the lifetime of a tumor, which is referred to as the “infinite sites assumption” (Beerenwinkel et al. 2015). A tumor’s subclonal architecture can be represented by a phylogenetic tree (Fig 1D,E).
Here, we describe the principles of reconstructing the subclonal architecture of cancers from massively parallel sequencing data. Subclonal reconstruction methods build on the principles described above to reconstruct the subclonal architecture of tumors, starting from either single nucleotide variants (SNVs) or copy number alterations (CNAs), or both. We describe how CCFs can be calculated and outline the principles behind SNV- and CNA-based subclonal reconstruction methods, using data from single biopsies, multisampling and single-cell sequencing. Finally, we outline which biological insights have been obtained through these methods and outline future directions.
ESTIMATING CANCER CELL FRACTIONS
CCFs can be estimated from VAFs of SNVs. Massively parallel sequencing results in short reads, which can then be aligned to a reference genome, followed by SNV calling. Both the variant and reference alleles of an SNV are supported by a number of reads, rmut and rref, respectively. The VAF of SNV i, fi can straightforwardly be calculated as
| (1) |
However, mutation clustering to identify (sub)clonal populations, cannot be performed directly using VAFs, as copy number changes impact allele frequencies. Figure 2 shows four SNVs in a sequencing sample that consists of 80% tumor cells and 20% normal cells. SNV 1 is clonal and occurs in a region with a normal diploid copy number state. This mutation is therefore carried by approximately half the reads that represent tumor DNA. SNV 2 is subclonal and also occurs in a region of normal diploid copy number. As both copy number and normal cell contamination are equal for both SNV 1 and 2, their allele frequencies are directly comparable and proportionate to the fraction of tumor cells by which they are carried. SNV 3 falls into an area that was subclonally lost. As the subclonal loss here has occurred on the other allele, this SNVs VAF is increased compared with SNV 1. SNV 4 is clonal, falls into an area that is clonally gained and is on the gained allele. Its VAF is therefore higher than that of SNV 1. If these SNVs were clustered in VAF space, SNVs 3 and 4 would be mistaken for evidence of additional mutation clusters, while they in fact belong to the clonal cluster.
Figure 2.
Copy number alterations affect variant allele frequencies. Allele frequencies of single nucleotide variants (SNVs) must be transformed to cancer cell fractions (CCFs), accounting for copy number changes, before they can be clustered to identify subclonal populations. This illustration shows four SNVs in different (sub)clonal populations and in regions with different copy number states, to illustrate this principle. SNVs 1 and 2 are clonal and subclonal respectively and appear in a nonaberrated copy number state. SNV 3 coincides with a subclonal deletion, with the SNV falling on the retained allele (i.e., the other allele is subclonally deleted). SNV 4 has occurred before a gain and is therefore carried by two chromosome copies. Even though SNV 1, 3, and 4 are clonal, their allele frequencies differ because of copy number alterations (CNAs).
This example illustrates that the copy number state of an SNV, also called its “multiplicity,” is key to understanding VAF distributions of mutations. Estimating the multiplicity of an SNV is challenging, as it requires establishing the copy number state of a single base. Copy number callers often estimate copy number states for large stretches of DNA, which might not accurately represent the copy number state exactly at the base of the SNV. To assist with resolving this issue, it is helpful to consider the product of mutation multiplicity mi of a mutation i and its cancer cell fraction CCFi:
| (2) |
Let us consider the properties of ui. A clonal SNV will have a CCF of 1.0 (i.e., 100% of tumor cells) and in each cell the number of chromosome copies, mi, is an integer. It follows from the above equation that for clonal mutations ui ≥ 1. A subclonal mutation has a CCF less than 1.0 (for example, 0.4, or 40% of tumor cells) and can only be carried by a single chromosome copy (unless also affected by a subclonal CNA), therefore mi = 1. It follows that ui < 1 for subclonal mutations. We can use these observations to obtain mi from ui
| (3) |
Furthermore, ui can be written as a function of the fraction of tumor cells ρ with a total number of chromosome copies in tumor cells at locus i, ntot,n,i, and a fraction of normal cells 1−ρ with a total number of chromosome copies in normal cells at locus i, ntot,n,i
| (4) |
In the formula above, ρ and ntot,t,i can be obtained through copy number analysis, fi can be calculated from rmut and rref using Equation 1, and the ntot,t,i values are considered known (typically 2). Equation 4 therefore provides us with a way to calculate ui and by extension to obtain the multiplicity of the SNV.
SNV 1 in Figure 2, for example, is clonal and has four reads reporting the variant and six reporting the reference allele. The purity is 0.8 (80% of total cells are tumor cells) and the total copy number of both the tumor and normal cells is 2. Its ui, therefore, becomes
which translates into a CCF of 1.0 via Equation 3. Whereas for SNV 4, it yields
which also translates into a CCF of 1. SNV 4 illustrates that ui must be rounded to obtain the multiplicity of a clonal SNV. It differs slightly from the expected value 2 because of variability in the number of reads resulting from limited sequencing depth. A similar mutation with 12 variant-reads out of 20 would lead to an estimate of 2.100.
The accuracy of the multiplicity estimate in practice depends on the accuracy of the VAF and local copy number. Slight deviation of the VAF caused by read sampling can result in minor deviation of the multiplicity estimates, as illustrated in the example above. Incorrect copy number profiles may also result in large errors if, for example, the CNA profile has been called as diploid instead of tetraploid. Ambiguity in estimating whole-genome duplications is a difficult problem in copy number analysis. If a copy number profile is erroneously called as diploid, then SNVs carried by two chromosome copies will be estimated to have a multiplicity of 1, whereas SNVs on 1 chromosome copy will become subclonal as they appear to be on 0.5 copies (e.g., exactly half of tumor cells). The CCF space will therefore show an SNV cluster at exactly 0.5, while the copy number profile may also contain subclonal CNAs at exactly 50% of tumor cells. The uncertainty may be mitigated through the application of a key assumption: A CNA profile is thought to be in its normal state (diploid) unless substantial evidence of a whole-genome duplication is available (i.e., the most parsimonious diploid state is assumed unless there is evidence otherwise). However, in rare cases, when whole-genome duplications occur late and are not followed by other CNAs, they leave no traces in the data and it is mathematically impossible to infer from the data available that they occurred.
We now have obtained a series of formulas to calculate CCF from a VAF and copy number profile. First, we obtain ui through Equation 4 and then calculate the multiplicity and CCF using Equations 3 and 2, respectively. Some methods cluster SNVs as a fraction of all cells in the sample, including normal and tumor cells, and, therefore, need to make one more step
| (5) |
Finally, some methods adjust the multiplicity to address SNVs that may appear subclonal because of a subclonal deletion. In these cases, it is unknown whether the SNV occurred first and was then deleted in a fraction of cells, or the SNV occurred after the deletion. It is important to account for such subclonal deletions (e.g., by appropriately adjusting multiplicity estimates), and ensure that these subclonal deletions do not result in the inference of spurious subclonal populations.
SNV-BASED SUBCLONAL RECONSTRUCTION
SNV-based reconstruction methods cluster SNVs with a similar CCF or CP, derived from VAF values as described in the last section. However, the VAF of a SNV—and therefore also its CCF—can be a relatively coarse measure and is a function of local sequencing depth, which should be taken into account when clustering SNVs. For example, if the SNV falls in a region of diploid copy number with a depth of 20 reads in a sample with 50% tumor cells, its CCF changes by 0.2 when a variant read is added or removed (e.g., three mutant reads correspond to a CCF of 0.6, while four mutant reads correspond to a CCF of 0.8). If the same SNV is sequenced to 80× depth, one additional variant read would change the CCF by only 0.05. Tumors are often sequenced at 30× average coverage or higher, but this coverage is not constant across the genome. As a result of this, discrete sampling of mutant and nonmutant reads, and the variability of the sequencing depth, CCF estimates of mutations from specific (sub)clones will show a distribution of values. For example, clonal mutations will display a range of CCF values around 1.0 (Fig. 1C).
A suitable error model can account for this variability. The number of variant reads can be seen as the number of successes of N independent coin tosses, where N is the total read depth. The number of successes (variant reads) can therefore be modeled through a binomial distribution with ri the number of reads reporting the variant at location i, rtot,i the total depth at location i, and pi the probability of observing a mutant read
| (6) |
Both ri and rtot are observed in the data. pi can be considered the product of two factors: The proportion of reads one expects to see if the mutation is fully clonal, ζi, and the true fraction of tumor cells carrying the mutation πi
| (7) |
ζi can be calculated from the tumor purity and the copy number state of the locus, as detailed above. Take, for example, a clonal SNV in a balanced diploid copy number region in a sequencing sample consisting of 80% tumor cells. The SNV is heterozygous and therefore expected to be carried by half the reads that represent tumor DNA. The expected proportion of reads is therefore 0.5*0.8, that is, 0.4. If the region has three copies and the SNV is carried by two copies, one expects two-thirds of the reads representing tumor DNA to be carrying the variant allele, making the expected fraction 2*0.8/(3*0.8 + 2*0.2), that is, 0.57.
The key estimate in subclonal reconstruction is the true fraction of tumor cells that are carrying mutation i, πi. Many methods (Nik-Zainal et al. 2012; Landau et al. 2013; Jiao et al. 2014; Roth et al. 2014; Deshwar et al. 2015) use a Dirichlet process (DP), which models subclonal fractions as
| (8) |
where DP(αP0) is a DP with a given probability distribution P0 and a dispersion parameter α. A realization of a DP can be seen as a distribution over a (possibly) infinite sample space, or alternatively, as a sampling from an unknown number of unknown distributions (Dunson 2010). This approach allows coestimating both the number of contributing distributions n (the number of cellular populations) and their properties (fraction of tumor cells and number of mutations they contain). The observed sampling P0 represents n of the (possibly) infinite number of distributions and can be used to estimate n (i.e., cellular populations) through the stick-breaking representation (Sethuraman 1994). Stick-breaking implies that the real probability distribution P can be expressed as follows
| (9) |
where is a location in CCF space and ωh represents the probability weight of cluster h
| (10) |
with
| (11) |
The Vh represent parts of a unit length stick that are iteratively broken off from the remaining stick. The Vh becomes increasingly smaller as more parts are broken off, providing a discrete representation of an infinite space.
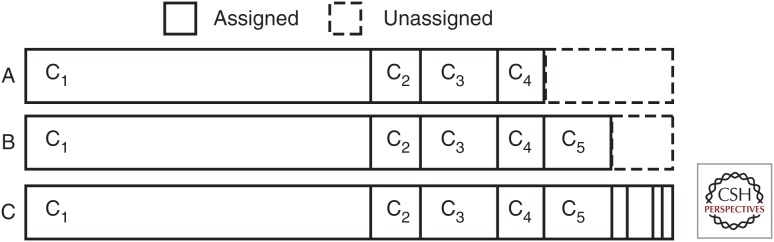
Figure 3 symbolizes the stick at various iterations of the stick-breaking procedure. Figure 3A,B show the stick after 4 and 5 breaks, respectively, whereas Figure 3C shows it after completion. Each substick represents a fraction of the total weight (number of SNVs) of a cluster and can be assigned a CCF through resampling using the assigned SNVs. Then, for each SNV and for each substick, a likelihood can be calculated representing the probability that that SNV is generated by that substick, taking the characteristics of the SNV, the stick location and its associated weight into account. After assigning all SNVs, the weights are updated such that they reflect the overall likelihood across SNVs.
Figure 3.
Stick-breaking schematic. The stick-breaking property of the Dirichlet process (DP) is used to estimate the number of mutation clusters in the data. For each mutation, a stick of arbitrary length is broken into randomly sized bits that represent a cluster. At point A, breaks have been introduced, corresponding to clusters c1-c4. B shows the stick after introducing break 5, whereas C shows the completed stick-breaking procedure. The size of each broken part represents the weight associated with a cluster and influences the mutation assignments, in which a high weight makes it more likely that a mutation is assigned to that cluster. These weights are updated after probabilities for each cluster have been obtained for each mutation, eventually converging on a solution.
The DP models an appropriate number of clusters because the assigned SNVs (influenced by the cluster weight) are used to resample the cluster CCF and the weight represents the fraction of total SNVs assigned to the cluster. By repeating this process over many iterations, the weight and SNV assignments will accumulate in certain locations that correspond to the estimated clusters. Therefore, the DP has the advantage that the number of clusters does not have to be specified a priori, making it ideally suited to this problem.
Subclonal reconstruction also depends on the ability to call subclonal SNVs in a sequenced tumor. The number of reads required to call a SNV depends on the properties of the SNV caller (outside the scope of this text), and on the sequencing error rate distribution. As a rough rule of thumb, three mutant reads are typically required to detect an SNV, and mutations present in small fractions of tumor cells may be missed. The coverage at which the tumor was sequenced, the admixture of tumor and normal cells in the sequencing sample and the total amount of DNA from each tumor cell all contribute to the ability to detect clonal and subclonal mutations. The following formula combines these three factors into a power metric
| (12) |
Here, cS is the sequencing coverage of the tumor sample, ρ is the tumor purity, and ψt and ψn are the ploidy of the tumor and normal cells respectively (the amount of genomic material per cell, expressed in number of haploid genome copies). pS is equivalent to the number of reads per chromosome copy and represents the expected number of reads reporting a clonal SNV. If, for example, pS equals 10 and an SNV can be detected when there are three mutant reads, then (as an approximation) mutations present in >30% subclones can be detected.
The DP provides a flexible framework that has a built-in mechanism that restricts it from creating a large number of clusters, can incorporate a suitable error model to address variability caused by read sampling and does not require specification of the number of clusters. Many methods are based on the above principles, including PyClone (Roth et al. 2014), PhyloSub (Jiao et al. 2014), and PhyloWGS, (Deshwar et al. 2015). Alternatively, SciClone uses a variational Bayesian mixture model that does not require a Markov chain Monte Carlo approach, but does require specification of the number of clusters (Miller et al. 2014). CloneHD is based on a hidden Markov model and couples SNV and CNA data to perform subclonal reconstruction (Fischer et al. 2014).
COPY NUMBER–BASED SUBCLONAL RECONSTRUCTION
Subclonal reconstruction can also be performed using copy number changes. Somatic copy number callers often use read depth and/or the imbalance in the number of the maternal and paternal alleles to estimate copy number aberrations (Van Loo et al. 2010; Carter et al. 2012; Nik-Zainal et al. 2012; Fischer et al. 2014; Ha et al. 2014). To observe allelic imbalances, it is helpful to look at the B-allele frequency (BAF) of a germline heterozygous SNP. For sequencing data the BAF can be calculated as
| (13) |
where rA,i and rB,i represent the total reads reporting allele A and B, respectively. Alternatively, the BAF can be expressed as a function of the number of chromosome copies of allele A and B (nA and nB, respectively)
| (14) |
A germline heterozygous SNP will have a BAF of ∼0.5 in the absence of any copy number changes. Deviations from 0.5 therefore can be used to detect somatic aberrations.
As tumors are often admixed with normal cells, establishing the copy number state of an aberration based on the deviation of BAF requires estimating the fraction of tumor cells in the sample (the tumor purity). The number of chromosome copies in the formula above should therefore be split into a contribution of ρ tumor cells and (1−ρ) normal cells
| (15) |
where ρ represents the tumor purity, nA,t and nB,t the number of chromosome copies in tumor cells, and nA,n and nB,n the number of chromosome copies in normal cells. Several methods have been developed to coestimate clonal copy number states and tumor purity based on these allele-specific signals (Van Loo et al. 2010; Carter et al. 2012; Ha et al. 2014).
Tumors that show much clonal genomic instability will show deviation of the BAF for large proportions of the genome. In such tumors, the BAF values show clear levels corresponding to different clonal states, which translates into more usable signal for methods that coestimate copy number states and tumor purity. However, genomes that show large amounts of subclonal genomic instability will show a range of different BAF values and will be more difficult to fit.
Figure 4 shows allele frequency values for a number of example cases that are affected by copy number changes and different normal cell admixtures. Panel A shows a region with no CNAs in a tumor that has no normal cell infiltration. One expects both alleles to be present in equal proportions, resulting in allele frequencies of 0.5. Panel B shows a region with a clonal gain. The bands representing allele A and B are clearly separated, with allele A representing two thirds of the total chromosome copies and allele B one third. Panel C contains a similar gain, but in a sample with 75% tumor purity, resulting in a smaller difference between the bands. Panel D shows the gain, again with 75% tumor cells, but now the coverage is reduced from 100X (as in panels A, B, and C) to 40×. The bands appear to be overlapping as lowering the depth increases the noise and widens the bands. Panel E shows an example in which the gain is subclonal in 60% of tumor cells resulting in further overlap of both bands. And finally panel F shows a subclonal loss in 40% of tumor cells.
Figure 4.
Coverage, purity, and alterations affect the B-allele frequency of SNPs. B-allele frequencies (BAF) of germline heterozygous SNPs can be used to identify copy number aberrations. A–F show that the BAF is noisy, and that it gets increasingly more difficult to separate the bands as the purity or coverage goes down and when the aberration is subclonal. To reduce the noise, SNPs can be phased to determine which allele is the B-allele. By combining the SNPs over longer stretches of DNA it becomes possible to detect subclonal aberrations.
Figure 4 shows that the allele frequencies of individual SNPs are subject to statistical variation and this noise increases with lower coverage. Combining SNPs into haplotype blocks through phasing can mitigate this effect (Carter et al. 2012; Nik-Zainal et al. 2012). Through haplotype phasing, information can be combined across multiple SNPs within a region of copy number change, by matching alleles across SNPs. For example, for SNP i, allele A may correspond to the maternal allele, whereas for SNP i+1, allele B may correspond to the maternal allele. If these are combined appropriately, smaller deviations of the BAF from the normal state can be detected, and higher precision copy number changes, including subclonal copy number changes, can be inferred.
Once exact allele frequencies of segments have been calculated after haplotype phasing, subclonal copy number changes can be detected. As a first step, for each segment, one can determine whether the BAF value of this segment can be explained by a clonal copy number change. Deviation of the observed exact allele frequency from the theoretical allele frequency can be used to identify a segment having a subclonal copy number state, that is, a combination of two or more populations of tumor cells with different copy number states, in addition to a population of normal cells.
When such a segment is fit with a clonal copy number state, the multiple subclonal states are combined into a single (integer) representation. For example, if the real copy number state of the segment is 2 + 1 (two copies of one parental allele and one copy of the other allele) in 80% and 1 + 1 in 20% of tumor cells (i.e., on average 1.8 + 1), its clonal fit will likely be 2 + 1 in 100% of tumor cells (1.8 + 1 rounded up). The observed allele frequency will therefore deviate from the frequency expected under the clonal copy number fit, allowing us to infer that the segment cannot be explained with a clonal copy number state.
Formally, given allele-specific copy number values nA and nB (integer if clonal, noninteger if subclonal), there are four options for the theoretical clonal allele frequency (assuming diploid copy number in the normal cell population):
Allele A and B are both rounded down
| (16) |
Allele A is rounded up and B is rounded up
| (17) |
Allele A is rounded down and B is rounded up
| (18) |
Allele A and B are both rounded up
| (19) |
Subclonal segments can be identified by testing the observed allele frequency hf against the theoretical values and accepting a segment as subclonal if the observed hf is significantly different from in all four scenarios.
After inferring that the data for a given segment cannot be explained by any realistic clonal copy number state and, therefore, this segment must be a combination of two or more subclonal populations with different copy number states, one can estimate the combination of subclonal copy number states for the segment. This depends on the different copy number states at the locus and their respective fractions of tumor cells. This problem has multiple solutions, as there can be any number of subclones with distinct subclonal copy number states. However, for any given segment, the most parsimonious assumption is that there are only two distinct copy number states, and that those copy number states differ at most by one chromosome copy (i.e., are separated by only one copy number event). Formally, if a fraction of tumor cells τ shows copy number state nA,1 + nB,1 and a fraction of tumor cells 1-τ shows copy number state nA,2 + nB,2, τ can be calculated as
| (20) |
The principles outlined above are implemented in the Battenberg algorithm (Nik-Zainal et al. 2012). Other BAF-based methods apply similar metrics to detect deviation from clonal copy number. There are two different approaches to establish these values: event-based or population-based. Event-based callers, such as the Battenberg algorithm, aim to establish these values for each segment individually (Carter et al. 2012; Nik-Zainal et al. 2012), whereas population-based callers aim to explain as many segments as possible with a single subclonal fraction (Fischer et al. 2014; Ha et al. 2014).
It is also possible to estimate total copy number from read depth alone by binning reads across the genome and comparing the relative differences between bins with a matched normal sample. The advantage of methods such as Battenberg that rely heavily on BAF values is that allele frequencies are less affected by various biases that affect read depth (such as wave bias related to GC content and/or replication timing [Diskin et al. 2008; Koren et al. 2012]), as these biases affect both alleles equally and will, therefore, be canceled out in the BAF calculation.
PRINCIPLES OF PHYLOGENETIC TREE RECONSTRUCTION
Evolutionary relationships between subclonal populations can be inferred as well. Phylogenetic trees are often constructed building on the “pigeonhole principle,” which states that if there are m containers (pigeonholes) and n items (pigeons) to be stored then there must be a container with more than one item if n>m. In subclonal reconstruction terms, the pigeonhole principle states that no sum of subpopulations can exceed the CCF or CP of their ancestor (Beerenwinkel et al. 2015). For example, consider a subclonal reconstruction with mutation clusters at 100%, 80% and 40% of tumor cells. The pigeonhole principle determines that as 100% + 80% > 100%, the 80% cluster must represent a cellular population that is a descendant of the 100% population. Furthermore, as 80% + 40% > 100%, the population at 40% must be a descendant of the population at 80%. Therefore, the pigeonhole principle dictates a linear phylogeny for this example. In contrast, if the second cluster was found to represent 50% of tumor cells instead of 80%, the population at 40% could either be a descendant of the 50% population, or a parallel population (directly descending from the 100% population), as 50% + 40% < 100%.
A corollary of the pigeonhole principle is that mutations in clusters with low CCF values are not necessarily part of the same subclone. For example, a tumor with two separate subclonal cell populations at 40% will appear to have only a single 40% subclone. Indeed, mutations that each of the founder cells of the subpopulations acquired at the start of the two separate clonal expansions will both appear at a CCF of 0.40. In such a scenario, all these mutations are clustered together and as there is no further information about the separate subclones are therefore (parsimoniously) assumed to represent a single cellular population. However, in such case, the pigeonhole principle does infer that there can be no more than two such subpopulations.
Both populations can however be separated through mutation phasing, or when a second sample is available. For example, when one of the two subclones has expanded into a metastasis, the metastasis sample will show these mutations at a CCF of 1.0, whereas the mutations in the other subclone are completely absent.
Mutation phasing can provide evidence for the existence of two separate cellular populations when a pair of mutations cannot have occurred in the same cell. For example, when a subclonal mutation is found on an allele that is lost in a specific subclone, one can infer that that mutation cannot be present in that subclonal lineage.
In general, to help resolve the tree topology, one could use SNVs that cannot have occurred in the same cell and therefore must be markers of distinct cellular lineages that correspond to branching evolution. One can phase SNVs against each other or against heterozygous SNPs and use fraction of tumor cells estimates to assess whether the aberrations can have occurred in the same lineage. Consider the phasing of two SNVs that are close enough to be spanned by a single read pair. If there are read pairs showing both variants, then the SNVs must belong to the same lineage (be part of the same node in the tree or show an ancestor–descendant relationship), as there must then be at least one cell that has both variant alleles (Fig. 5A).
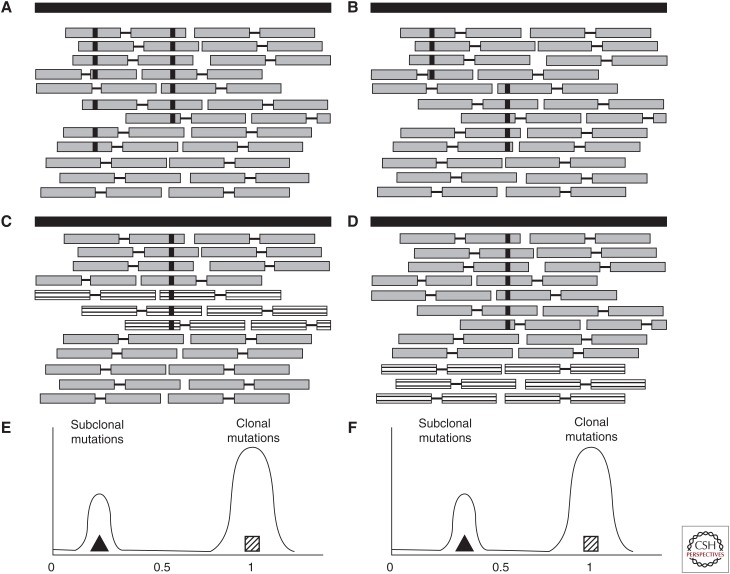
Figure 5.
Principles of SNV phasing. (A) A pair of single nucleotide variants (SNVs) that are close enough to be covered by a single read pair and that have occurred in the same lineage appear as read pairs that contain both variant alleles. (B) If the SNVs have originated in different lineages they appear in read pairs that contain the variant allele of one SNV and the wild type allele of the other. The variant allele frequency (VAF) of a subclonal SNV that has been subclonally deleted (as shown by the striped reads that represent the deleted copies in C) is “shifted” (E). An SNV that has occurred on the retained allele (i.e., the other allele is subclonally deleted, D) will not be shifted (F).
Using the same principle, one can also sometimes exclude that two mutations are on the same lineage, thereby showing that the tumor must have a branching phylogeny. Consider two SNVs (SNV 1 and 2) that are close enough to be spanned by a single read pair, in a region with only one chromosome copy in the tumor cells. If there are no read pairs reporting both variant alleles, but there are read pairs showing (1) SNV 1 and a wild-type allele of SNV 2, and (2) SNV 2 and a wild-type allele of SNV 1, then the SNVs must be part of different branches of the phylogenetic tree (Fig. 5B).
It is also possible to infer the phylogenetic relationship between subclones by phasing SNVs and copy number changes. This principle is based on the observation that, for linear phylogenies, clusters of subclonal mutations that occur on a deleted allele will show different (“shifted”) VAF values than clusters of subclonal mutations that occur on the other (retained) allele (illustrated in Fig. 5C,E). If the subclonal copy number change occurs in a different branch of the phylogenetic tree, no such shift should appear (Fig. 5D,F).
Nik-Zainal et al. (2012) first used phasing to create branched evolutionary stories, but, to date, there is no published method that can automatically leverage the potential of mutually exclusive mutations. In addition, it must be emphasized that with a haploid genome size of 3 Gb and typically a few thousand mutations per tumors, with current read lengths, mutation pairs that can be phased using the principles above are rare.
SINGLE-CELL-BASED APPROACHES
The advent of single-cell sequencing theoretically gives access to a more fine-scaled level of tumor heterogeneity than bulk sequencing data. By sequencing a large number of single cells, one can gain in-depth understanding of the diversity within a tumor sample. However, in contrast to bulk sequencing methods, single cells are often sequenced at a much lower coverage. Further, the data suffers from uneven coverage and allele dropouts, errors introduced during whole genome amplification resulting in false positive SNV calls, and in some cases two cells are inadvertently sequenced together (called “doublets”) (Hou et al. 2012; Zong et al. 2012; Voet et al. 2013; Van Loo and Voet 2014). Subclonal reconstruction methods therefore must account for missing values because of mutant alleles being missed owing to a lack of coverage or allelic dropout. A doublet effectively fuses two cells together and therefore contains mutations from both cells. A subclonal reconstruction method might take this as misleading evidence since separate cells each carry one of the sets of mutations, whereas a doublet contains both.
Various approaches have recently been published to estimate the tumor phylogeny from single cell data (Kim and Simon 2014; Yuan et al. 2015; Jahn et al. 2016; Ross and Markowetz 2016; Roth et al. 2016). Some methods infer phylogenies of cellular populations, in a similar manner to methods for bulk data. Others build mutation trees that instead show the order in which mutations have occurred without establishing cellular populations. These methods all start from a genotype matrix in which all mutations in all cells are represented. They (1) cocluster evidence from bulk sequencing and single cell data using a DP (Yuan et al. 2015), (2) construct mutation lineages by a pair-wise mutation ordering (Kim and Simon 2014), (3) use heuristics to find a basic tree topology followed by clustering of single cells and further refinement (Ross and Markowetz 2016), or (4) build mutation trees using a Markov chain Monte Carlo–based approach (Jahn et al. 2016). The recently developed single-cell genotypes (Roth et al. 2016) implement a robust feature allocation model to identify subclones with shared genotypes and to infer the genotype of each subclone. This method elegantly accounts for missing data because of single-cell sequencing limitations such as allelic dropout, as well as for the occurrence of doublets.
MULTI-SAMPLE-BASED APPROACHES
Obtaining multiple samples from the same donor allows for extraction of more detailed subclonal reconstructions. These datasets can consist of multiple tumors taken from different sites (e.g., multiple primary sites, primary and metastasis), multiple samples from the same tumor or multiple samples from the same cancer that represent different time points (e.g., primary and relapse).
Multiple sampling strategies provide a series of advantages. Consider a tumor that has two subclones that each comprise 20% of tumor cells. A single sample analysis will not be able to separate the two groups of mutations as both occur in 20% of tumor cells. But if the CCF of the two subclones is different in another sample, one can separate the two groups of mutations. In addition, having multiple samples may help resolve tree topologies. In single sample cases it is often not possible to resolve phylogeny, as more rare subclones may be placed in multiple positions in the tree. By applying the pigeonhole principle across the samples for each subclone, one can often rule out various configurations in which a subclone may fit in multiple places in one sample, but not the other. Finally, with multiple sampling strategies, mutations with low allele fractions in one sample can be confirmed (or detected) in another sample in which they have higher allele fractions owing to higher tumor purity or higher CCF.
Approaches based on a DP can be extended into multiple dimensions (Bolli et al. 2014). The read counts across n samples can be modeled as independent draws from n binomial distributions.
| (21) |
| (22) |
The stick-breaking procedure is performed across the samples in which a cluster has a single weight (representing the number of mutations), but a separate location in each of the samples. Posteriors are obtained across samples by calculating the total probability for each mutation for each cluster under consideration. Finally, the DP can be used to jointly perform clustering and infer phylogenetic relationships between the clusters by interleaving two stick-breaking procedures (Ghahramani et al. 2010).
Several methods for single sample analysis, including PyClone (Roth et al. 2014), SciClone (Miller et al. 2014), and CloneHD (Fischer et al. 2014), can be used to analyze multiple samples. Furthermore, automated tree inference has been implemented in PhyloSub (Jiao et al. 2014) and extended to include SNVs in copy number aberrant regions in PhyloWGS (Deshwar et al. 2015).
BIOLOGICAL INSIGHTS OBTAINED THROUGH SUBCLONAL ARCHITECTURE RECONSTRUCTION
Subclonal reconstruction analysis has recently been used to reveal insights into the complexities of tumor evolution in a number of cancer types. Various articles focused on a single cancer type report vast differences in heterogeneity between patients, in which known genes are mutated early in one case, but late in another (Yates et al. 2015) and that some tumors can show evidence of rapid evolution, while other tumors in the same cohort show a stable balance between subclones (Schuh et al. 2012).
The application of treatment can introduce a phase of rapid tumor evolution (Landau et al. 2013, 2015), in which mutations in known drivers are observed to be subclonal (Landau et al. 2013; Bolli et al. 2014; Gerlinger et al. 2014). Mechanisms of resistance can be acquired in parallel in different lesions (Gerlinger et al. 2014; Gundem et al. 2015), subclones can persist through treatment (Schuh et al. 2012) and the existence of a subclonal driver mutation can be an independent risk factor for disease progression (Landau et al. 2013).
A primary tumor can contain observable signs of metastatic and treatment resistance potential before onset (Yates et al. 2015) and in some cases can contain patterns that predict the evolutionary progression (Landau et al. 2015). Mutational processes can differ between clones and subclones through spatially (De Bruin et al. 2014) and temporally (Bolli et al. 2014) separated samples from the same cancer. Gundem et al. (2015) reported metastasis-to-metastasis seeding in a number of lethal metastatic prostate cancers and Cooper et al. (2015) observed clonal expansions in morphologically normal cells in multifocal prostate tumors.
These separate studies hint that intratumor heterogeneity is widespread and that tumors of the same cancer type can differ greatly. McGranahan et al. (2015) reported that subclonal mutations in known drivers are common across 2694 exome-sequenced tumors representing 9 cancer types from The Cancer Genome Atlas (TCGA). Andor et al. (2016) performed subclonal reconstruction on 1165 exome-sequenced tumors from TCGA and report that 86% of tumors across 12 cancer types contain at least one subclone. Larger studies as well as systematic pancancer studies are required to further our insight into whether there are distinguishable patterns of tumor evolution.
Through large-scale international efforts such as TCGA and the International Cancer Genome Consortium (ICGC), a wealth of whole-exome and whole-genome sequencing data has been generated, most of which presently has not been mined from the perspective of evolution. We expect that efforts such as the ICGC Pan-Cancer Analysis of Whole Genomes have the potential to significantly broaden our understanding of tumor’s subclonal architecture and evolutionary history. For subclonal inference, whole-genome sequences show clear advantages over exome sequences, as they allow detection of nearly two orders of magnitude more mutations, and more detailed (and subclonal) copy number changes can be inferred. We expect that large-scale multisampling whole-genome sequencing approaches across cancer types will lead to key evolutionary insights. However, the cost of sequencing is at present still a limiting factor.
There is also a need for smaller, more focused studies with the right data to further deepen our understanding of the factors that play a role in tumor progression, how they interact together and what that means for patient care. Subclonal reconstruction methods have already enabled important discoveries that are of direct clinical interest. We expect that these types of studies will play a key role in further advancing our understanding of tumor evolution.
ACKNOWLEDGMENTS
This work was supported by the Wellcome Trust (Grant No. WT098051) and by the Francis Crick Institute which receives its core funding from Cancer Research UK (FC001202), the UK Medical Research Council (FC001202), and the Wellcome Trust (FC001202). P.V.L. is a Winton Group Leader in recognition of the Winton Charitable Foundation's support toward the establishment of The Francis Crick Institute. D.C.W. is supported by the Li Ka Shing foundation.
Footnotes
Editors: Charles Swanton, Alberto Bardelli, Kornelia Polyak, Sohrab Shah, and Trevor A. Graham
Additional Perspectives on Cancer Evolution available at www.perspectivesinmedicine.org
REFERENCES
- Andor N, Graham TA, Jansen M, Xia LC, Aktipis CA, Petritsch C, Ji HP, Maley CC. 2016. Pan-cancer analysis of the extent and consequences of intratumor heterogeneity. Nat Med 22: 105–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beerenwinkel N, Schwarz RF, Gerstung M, Markowetz F. 2015. Cancer evolution: Mathematical models and computational inference. Syst Biol 64: e1–e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolli N, Avet-Loiseau H, Wedge DC, Van Loo P, Alexandrov LB, Martincorena I, Dawson KJ, Iorio F, Nik-Zainal S, Bignell GR, et al. 2014. Heterogeneity of genomic evolution and mutational profiles in multiple myeloma. Nat Commun 10.1038/ncomms3997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell PJ, Pleasance ED, Stephens PJ, Dicks E, Rance R, Goodhead I, Follows GA, Green AR, Futreal PA, Stratton MR. 2008. Subclonal phylogenetic structures in cancer revealed by ultra-deep sequencing. Proc Natl Acad Sci 105: 13081–13086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter SL, Cibulskis K, Helman E, McKenna A, Shen H, Zack T, Laird PW, Onofrio RC, Winckler W, Weir BA, et al. 2012. Absolute quantification of somatic DNA alterations in human cancer. Nat Biotechnol 30: 413–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper CS, Eeles R, Wedge DC, Van Loo P, Gundem G, Alexandrov LB, Kremeyer B, Butler A, Lynch AG, Camacho N, et al. 2015. Analysis of the genetic phylogeny of multifocal prostate cancer identifies multiple independent clonal expansions in neoplastic and morphologically normal prostate tissue. Nat Genet 47: 367–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Bruin EC, McGranahan N, Mitter R, Salm M, Wedge DC, Yates L, Jamal-Hanjani M, Shafi S, Murugaesu N, Rowan AJ, et al. 2014. Spatial and temporal diversity in genomic instability processes defines lung cancer evolution. Science 346: 251–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshwar AG, Vembu S, Yung CK, Jang GH, Stein L, Morris Q. 2015. PhyloWGS: Reconstructing subclonal composition and evolution from whole-genome sequencing of tumors. Genome Biol 16: 35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diskin SJ, Li M, Hou C, Yang S, Glessner J, Hakonarson H, Bucan M, Maris JM, Wang K. 2008. Adjustment of genomic waves in signal intensities from whole-genome SNP genotyping platforms. Nucleic Acids Res 36: e126–e126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunson DB. 2010. Nonparametric bayes applications to biostatistics. In Bayesian nonparametrics (ed. Hjort NL, Holmes C, Müller P, Walker S). Cambridge University Press, Cambridge. [Google Scholar]
- Fischer A, Vzquez-Garca I, Illingworth CR, Mustonen V. 2014. High-definition reconstruction of clonal composition in cancer. Cell Rep 7: 1740–1752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garraway L, Lander E. 2013. Lessons from the cancer genome. Cell 153: 17–37. [DOI] [PubMed] [Google Scholar]
- Gerlinger M, Horswell S, Larkin J, Rowan AJ, Salm MP, Varela I, Fisher R, McGranahan N, Matthews N, Santos CR, et al. 2014. Genomic architecture and evolution of clear cell renal cell carcinomas defined by multiregion sequencing. Nat Genet 46: 225–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghahramani Z, Jordan MI, Adams RP. 2010. Tree-structured stick breaking for hierarchical data. Adv Neural Inf Proc Syst 23: 19–27. [Google Scholar]
- Greaves M, Maley CC. 2012. Clonal evolution in cancer. Nature 481: 306–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gundem G, Van Loo P, Kremeyer B, Alexandrov LB, Tubio JMC, Papaemmanuil E, Brewer DS, Kallio HML, Högnäs G, Annala M, et al. 2015. The evolutionary history of lethal metastatic prostate cancer. Nature 520: 353–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ha G, Roth A, Khattra J, Ho J, Yap D, Prentice LM, Melnyk N, McPherson A, Bashashati A, Laks E, et al. 2014. TITAN: Inference of copy number architectures in clonal cell populations from tumor whole genome sequence data. Genome Res 24: 1881–1893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou Y, Song L, Zhu P, Zhang B, Tao Y, Xu X, Li F, Wu K, Liang J, Shao D, et al. 2012. Single-cell exome sequencing and monoclonal evolution of a JAK2-negative myeloproliferative neoplasm. Cell 148: 873–885. [DOI] [PubMed] [Google Scholar]
- Jahn K, Kuipers J, Beerenwinkel N. 2016. Tree inference for single-cell data. Genome Biol 17: 86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiao W, Vembu S, Deshwar AG, Stein L, Morris Q. 2014. Inferring clonal evolution of tumors from single nucleotide somatic mutations. BMC Bioinformatics 15: 35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim KI, Simon R. 2014. Using single cell sequencing data to model the evolutionary history of a tumor. BMC Bioinformatics 15: 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koren A, Polak P, Nemesh J, Michaelson JJ, Sebat J, Sunyaev SR, McCarroll SA. 2012. Differential relationship of DNA replication timing to different forms of human mutation and variation. Am J Hum Genet 91: 1033–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landau D, Carter S, Stojanov P, McKenna A, Stevenson K, Lawrence M, Sougnez C, Stewart C, Sivachenko A, Wang L, et al. 2013. Evolution and impact of subclonal mutations in chronic lymphocytic leukemia. Cell 152: 714–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landau DA, Tausch E, Taylor-Weiner AN, Stewart C, Reiter JG, Bahlo J, Kluth S, Bozic I, Lawrence M, Böttcher S, et al. 2015. Mutations driving CLL and their evolution in progression and relapse. Nature 526: 525–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGranahan N, Favero F, de Bruin EC, Birkbak NJ, Szallasi Z, Swanton C. 2015. Clonal status of actionable driver events and the timing of mutational processes in cancer evolution. Sci Transl Med 7: 283ra54–283ra54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller CA, White BS, Dees ND, Griffith M, Welch JS, Griffith OL, Vij R, Tomasson MH, Graubert TA, Walter MJ, et al. 2014. SciClone: Inferring clonal architecture and tracking the spatial and temporal patterns of tumor evolution. PLoS Comput Biol 10: e1003665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nik-Zainal S, Van Loo P, Wedge DC, Alexandrov LB, Greenman CD, Lau KW, Raine K, Jones D, Marshall J, Ramakrishna M, et al. 2012. The life history of 21 breast cancers. Cell 149: 994–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowell PC. 1976. The clonal evolution of tumor cell populations. Science 194: 23–28. [DOI] [PubMed] [Google Scholar]
- Ross EM, Markowetz F. 2016. OncoNEM: Inferring tumor evolution from single-cell sequencing data. Genome Biol 17: 69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth A, Khattra J, Yap D, Wan A, Laks E, Biele J, Ha G, Aparicio S, Bouchard-Côté A, Shah SP. 2014. PyClone: Statistical inference of clonal population structure in cancer. Nat Methods 11: 396–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth A, McPherson A, Laks E, Biele J, Yap D, Wan A, Smith MA, Nielsen CB, McAlpine JN, Aparicio S, et al. 2016. Clonal genotype and population structure inference from single-cell tumor sequencing. Nat Methods 10.1038/nmeth.3867. [DOI] [PubMed] [Google Scholar]
- Schuh A, Becq J, Humphray S, Alexa A, Burns A, Clifford R, Feller SM, Grocock R, Henderson S, Khrebtukova I, et al. 2012. Monitoring chronic lymphocytic leukemia progression by whole genome sequencing reveals heterogeneous clonal evolution patterns. Blood 120: 4191–4196. [DOI] [PubMed] [Google Scholar]
- Sethuraman J. 1994. A constructive definition of Dirichlet priors. Stat Sinica 4: 639–650. [Google Scholar]
- Stratton MR, Campbell PJ, Futreal PA. 2009. The cancer genome. Nature 458: 719–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tabin CJ, Bradley SM, Bargmann CI, Weinberg RA, Papageorge AG, Scolnick EM, Dhar R, Lowy DR, Chang EH. 1982. Mechanism of activation of a human oncogene. Nature 300: 143–149. [DOI] [PubMed] [Google Scholar]
- Van Loo P, Voet T. 2014. Single cell analysis of cancer genomes. Curr Opin Genet Dev 24: 82–91. [DOI] [PubMed] [Google Scholar]
- Van Loo P, Nordgard SH, Lingjærde OC, Russnes HG, Rye IH, Sun W, Weigman VJ, Marynen P, Zetterberg A, Naume B, et al. 2010. Allele-specific copy number analysis of tumors. Proc Natl Acad Sci 107: 16910–16915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voet T, Kumar P, Van Loo P, Cooke SL, Marshall J, Lin ML, Esteki MZ, Van der Aa N, Mateiu L, McBride DJ, et al. 2013. Single-cell paired-end genome sequencing reveals structural variation per cell cycle. Nucleic Acids Res 41: 6119–6138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogelstein B, Papadopoulos N, Velculescu VE, Zhou S, Diaz LA, Kinzler KW. 2013. Cancer genome landscapes. Science 339: 1546–1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yates LR, Gerstung M, Knappskog S, Desmedt C, Gundem G, Van Loo P, Aas T, Alexandrov LB, Larsimont D, Davies H, et al. 2015. Subclonal diversification of primary breast cancer revealed by multiregion sequencing. Nat Med 21: 751–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan K, Sakoparnig T, Markowetz F, Beerenwinkel N. 2015. BitPhylogeny: A probabilistic framework for reconstructing intra-tumor phylogenies. Genome Biol 16: 36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zong C, Lu S, Chapman AR, Xie XS. 2012. Genome-wide detection of single-nucleotide and copy-number variations of a single human cell. Science 338: 1622–1626. [DOI] [PMC free article] [PubMed] [Google Scholar]