Measurement of bacterial replication rates in microbial communities

Culture-independent microbiome studies have increased our understanding of the complexity and metabolic potential of microbial communities. However, to understand the contribution of individual microbiome members to community functions, it is important to determine which bacteria are actively replicating. We developed an algorithm, iRep, that uses draft-quality genome sequences and single time-point metagenome sequencing to infer microbial population replication rates. The algorithm calculates an index of replication (iRep) based on the sequencing coverage trend that results from bi-directional genome replication from a single origin of replication. We apply this method to show that microbial replication rates increase after antibiotic administration in human infants. We also show that uncultivated groundwater-associated Candidate Phyla Radiation bacteria only rarely replicate quickly in subsurface communities undergoing substantial changes in geochemistry. Our method can be applied in all genome-resolved microbiome studies to track organism responses to varying conditions, identify actively growing populations and measure replication rates for use in modeling studies.

Dividing cells in a natural population contain, on average, more than one copy of their genome (Fig. 1). In an unsynchronized population of growing bacteria, cells contain genomes that are replicated to different extents, resulting in a gradual reduction in the average genome copy number from the origin to the terminus of replication¹. This decrease can be detected by measuring changes in DNA sequencing coverage across complete genomes². Bacterial genome replication proceeds bi-directionally from a single origin of replication^3,4, therefore the origin and terminus of replication can be deduced based on this coverage pattern². GC skew^5–7 and genome coverage⁸ analyses of a wide variety of bacteria have shown that this replication mechanism is broadly applicable. Further, early studies of bacterial cultures revealed that cells can achieve faster division by simultaneously initiating multiple rounds of genome replication⁹, which results in an average of more than two genome copies in rapidly growing cells.

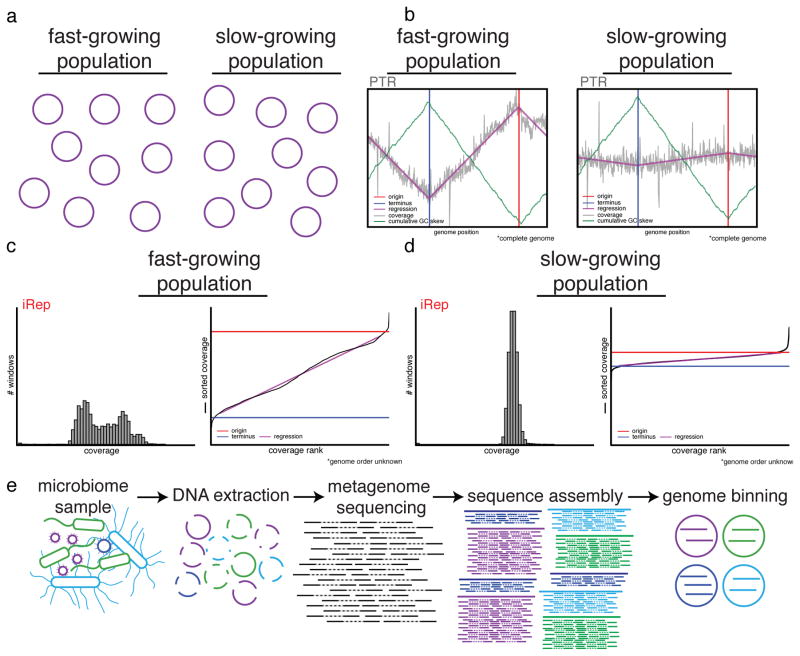
Figure 1. iRep determines replication rates for bacteria using genome-resolved metagenomics.

(a) Populations of bacteria undergoing rapid cell division differ from slowly growing populations in that the individual cells of a growing population are more actively in the process of replicating their genomes (purple circles). (b) Differences in genome copy number across a population of replicating cells can be determined based on sequencing read coverage over complete genome sequences. The ratio between the coverage at the origin (“peak”) and terminus (“trough”) of replication (PTR) relates to the growth rate of the population. The origin and terminus can be determined based on cumulative GC skew. (c–d) If no complete genome sequence is available, it is possible to calculate the replication rate based on the distribution of coverage values across a draft-quality genome using the iRep method. Coverage is first calculated across overlapping segments of genome fragments. Growing populations will have a wider distribution of coverage values compared with stable populations (histograms). These values are ordered from lowest to highest, and linear regression is used to evaluate the coverage distribution across the genome in order to determine the coverage values associated with the origin and terminus of replication. iRep is calculated as the ratio of these values. (e) Genome-resolved metagenomics involves DNA extraction from a microbiome sample followed by DNA sequencing, assembly, and genome binning. Binning is the grouping together of assembled genome fragments that originated from the same genome. This can be done based on shared characteristics of each fragment, such as sequence composition, taxonomic affiliation, or abundance.

Korem et al. used the ratio of sequencing coverage at the origin compared to the terminus of replication to measure replication rates for bacteria⁸. Because the origin and terminus correspond to coverage peaks and troughs, respectively, the authors named their method PTR (peak-to-trough ratio). They applied PTR to calculate replication rates for specific bacteria in the human microbiome, but the requirement for mapping sequencing reads to a complete, closed, circular reference genome for a bacterium of interest is a major limitation. The vast majority of bacteria remain uncultivated and lack reference genomes.

Metagenomics methods routinely generate draft genomes for bacteria and archaea that lack reference genomes^10–17 (Fig. 1 and Supplementary Fig. 1). Often these organisms are from little known microbial phyla, and are vastly different from organisms for which there are complete genomes in databases^15–21. It is sometimes possible to recover hundreds or thousands of draft or near-complete genomes from a single ecosystem. We introduce a method that can extend coverage-based replication rate analyses to enable measurements based on sequencing coverage trends for these draft genomes. The method works, despite the fact the order of the fragments is unknown. Unlike PTR, our approach can be applied in virtually any natural or engineered ecosystem, including complex systems such as soil, for which complete genomes for the vast majority of bacteria are unavailable.

RESULTS

The Index of Replication (iRep) metric

The method that we developed determines replication rates based on measuring the rate of the decrease in average sequence coverage from the origin to the terminus of replication. This rate of coverage change can be used to accurately estimate the ratio between the coverage at the origin and terminus of replication, which is proportional to replication rate. The values are comparable to PTR, but are derived differently so we named this method and metric iRep (Index of Replication). With PTR, the origin and terminus of replication must be identified and the calculation requires position-specific coverage values. In contrast, the iRep algorithm is distinct in that it makes use of the total change in coverage across all genome fragments.

iRep values are calculated by mapping metagenome sequencing reads to the collection of assembled sequences that represent a draft genome (Fig. 1 and Supplementary Fig. 1; Online Methods and Supplementary Code). The read coverage is evaluated at every nucleotide position across every scaffold. The series of coverage values for the scaffolds are then concatenated, and the average coverage values within 5 Kbp sliding windows are calculated (window slide length 100 bp; see Supplementary Fig. 2, Supplementary Table 1, and Online Methods for evaluation of sliding window methods). Then, a sequencing GC bias correction is applied (Supplementary Fig. 2; Online Methods). The average coverage values for each window are then ordered from lowest to highest to assess the coverage trend across the genome. Because coverage values for each window are re-arranged, the order of the fragments in the complete genome need not be known. Extreme high and low coverage windows are excluded (>8-fold difference compared to the median), as they are well known to correlate with highly conserved regions, strain variation, or integrated phage. Finally, the overall slope of coverage across the genome is used to calculate iRep, a measure of the average genome copy number across a population of cells. In a population in which most cells are replicating (making a single copy of their chromosome), iRep would be two. Since iRep is an average across the population, some organisms may not be replicating, but for that to be the case others would have to be in the process of conducting two, or more, simultaneous rounds of genome replication. An iRep value of 1.25 would indicate that, on average, only one quarter of the cells are replicating.

iRep is accurate for complete or draft genomes

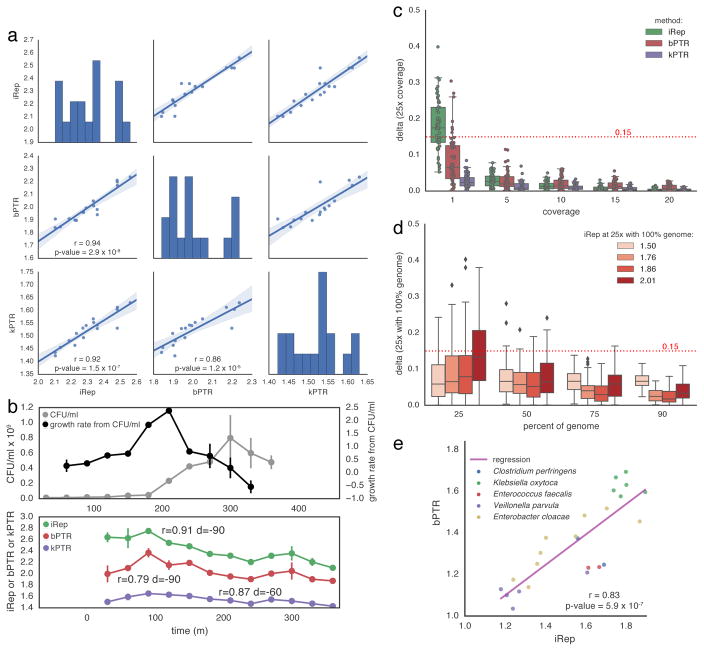
In order to evaluate the ability of iRep to measure replication rates, we compared iRep to PTR using 17 samples sequenced to sufficient depth from the growth rate experiments reported by Korem et al. as part of their validation of the PTR method⁸. As there is no open-source version of the PTR software, we re-implemented the PTR method, with some improvements that include an option to determine the origin and terminus positions based on GC skew²² (Online Methods; Supplementary Code). PTRs generated using the Korem et al. software (kPTRs) use a genome database of unknown composition that can be neither viewed nor modified, and no metrics for evaluating measurement reliability are provided. These limitations are addressed in our PTR implementation (named bPTR). kPTR and bPTR values for this dataset were highly correlated, and each was correlated with iRep (Fig. 2a and Supplementary Table 2). We used growth rates calculated using counts of colony forming units (CFU), as reported by Korem et al., to verify that iRep values correlate as well as PTRs (Fig. 2b). It should be noted that growth rates derived from CFU data are based on total population size, including cell death rates, and can be negative. iRep and PTR methods only measure replication, not death. Therefore, these metrics represent the physiological state of the cells independent of death rates.

Figure 2. iRep is an accurate measure of in situ replication rates.

(a) iRep, bPTR, and kPTR measurements made for cultured Lactobacillus gasseri⁸ were compared (r = Pearson’s r value), showing strong agreement between all methods. (b) Colony forming unit (CFU) counts were available for a subset of these samples⁸, and used to calculate growth rates (n = 2). All methods were highly correlated with CFU-derived rates after first accounting for the delay between start of genome replication and observable change in population size (as noted previously⁸). Replication rates from CFU data were adjusted by variable amounts before calculating correlations with sequencing-based rates (best correlation shown; d = time adjustment). CFU data are plotted with a −90 minute offset. (c) Using the L. gasseri data, minimum coverage requirements were determined for each method by first measuring the replication rate at 25× coverage, and then comparing to values calculated after simulating lower coverage. This shows that ≥5× coverage is required. (d) The minimum required genome fraction for iRep was determined by conducting 100 random fragmentations and subsets of the L. gasseri genome. Sequencing was subset to 5× coverage before calculating iRep to show the combined affect of low coverage and missing genomic information. With ≥75% of a genome sequence, most iRep measurements are accurate ±0.15. (e) iRep and bPTR measurements were calculated using five genome sequences assembled from premature infant metagenomes, showing that these methods are in agreement in the context of microbiome sequencing data.

We tested the minimum sequencing coverage requirements for iRep, kPTR and bPTR using sequencing data of cultured Lactobacillus gasseri from the Korem et al. study⁸. We first subsampled reads to achieve 25× coverage of the genome and then calculated replication rates to use as reference values. Then, the dataset was subsampled to lower coverage values and the replication rates re-calculated. Comparing these rates to the reference values enabled evaluation of the amount of noise introduced by increasingly lower coverage. Results show that all three methods are affected by coverage, and that although kPTR has the least amount of variation at 1× coverage, all methods are reliable when the coverage is ≥5× (Fig. 2c and Supplementary Table 3).

Because iRep does not require knowledge of the order of genome fragments, it can be used to obtain replication rates when only draft quality genomes are available. Therefore, we evaluated the minimum percentage of a genome that is required to obtain accurate results by conducting a random genome subsampling experiment (Fig. 2d, Supplementary Fig. 2, and Supplementary Table 1). iRep values were determined for L. gasseri cells sampled when growing at different rates⁸, and then compared with values determined from genomes at various decreasing levels of completeness. Our analysis revealed that ≥75% of the genome sequence is required for iRep to be accurate (difference from known value <0.15). Extensive genome fragmentation will introduce noise into iRep calculations; however, our analysis showed that only a moderate amount of noise is introduced for genomes with less than 175 scaffolds per Mbp of sequence (Supplementary Fig. 2 and Supplementary Table 1). Genome completeness and contamination can be estimated based on the presence and copy number of expected single copy genes (SCGs). Based on these findings, and to prevent inclusion of genomes with substantial levels of contamination, our analyses included genomes estimated to be ≥75% complete based on the presence of 51 SCGs with no more than two duplicate copies, and having fewer than 175 scaffolds per Mbp of sequence (see Methods). As shown below, these standards can be met for a significant number of genomes recovered from metagenomic datasets.

The human microbiome includes some bacteria with genomes that are sufficiently similar to reference genomes to enable ordering and orienting of draft genome fragments, making it possible to calculate both iRep and bPTR for comparison. We carried out an analysis using five genomes reconstructed in a metagenomics study of premature infants (GC range: 28–56%)²³. Importantly, unlike when using kPTR, the reads were mapped to the genome that was reconstructed from the infant gut metagenomes in order to achieve more robust results than would be achieved using a public database-derived reference genome, due to the fact that differences in gene content and gene order will perturb coverage trends. The correct ordering of the scaffolds in the reconstructed genome was confirmed based on both coverage patterns and cumulative GC skew (Supplementary Fig. 3). For all 24 comparisons involving populations with iRep values of 1.8–1.9, there was a strong correlation between iRep and bPTR values (Pearson’s r = 0.83, p-value = 5.9 × 10⁻⁷; Fig. 2e).

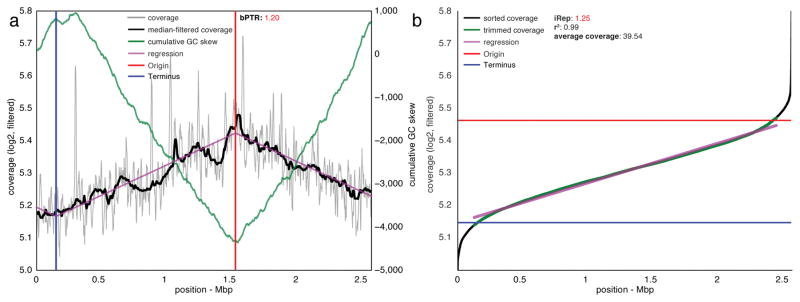
Although a few complete reference genomes were similar enough to reconstructed draft genomes to facilitate scaffold ordering, these reference genomes were from organisms relatively distantly related to those present in samples of interest. Specifically, for the five genomes with available similar reference genomes (average nucleotide identity 91–99%), as much as 19.5% of reference genomes was not represented by metagenome reads (min. = 1.6%, average = 13.5%), compared with essentially perfect mapping to reconstructed genomes (Supplementary Fig. 4 and Supplementary Table 4). This level of genome deviation compared to reference genomes would preclude accurate replication rate calculations due to perturbation of coverage trends, as noted above, and emphasizes the need to reconstruct genomes for organisms of interest. We also compared iRep and bPTR replication rate metrics for a large, manually curated genome scaffold ~2.5 Mbp in length that was reconstructed from a complex groundwater metagenome. Because the scaffold contains both the origin and terminus of replication, as identified both by coverage and cumulative GC skew (Fig. 3), it was possible to calculate both bPTR and iRep. For this single time point measurement, the bPTR value of 1.20 agrees with the iRep value of 1.25. Importantly, it would not have been possible to obtain this information based on mapping to complete reference genomes because this is the first sequence for an organism affiliated with a novel genus within the Deltaproteobacteria²⁴. This finding demonstrates the iRep method in the context of a very complex natural environment.

Figure 3. iRep and bPTR calculations agree for a novel Deltaproteobacterium sampled from groundwater.

(a) bPTR was calculated after determining the origin and terminus of replication based on regression to coverage calculated across the genome. Coverage was calculated for 10 Kbp windows sampled every 100 bp (see Online Methods). The ratio between the coverage at the origin and terminus was determined after applying a median filter. The cumulative GC skew pattern confirms the genome assembly and locations of the origin and terminus of replication. (b) iRep was determined by first calculating coverage over 5 Kbp windows sampled every 100 bp, and then the resulting values were sorted. High and low coverage windows were removed, and then the slope of the remaining (trimmed) values was determined and used to evaluate the coverage at the origin and terminus of replication: iRep was calculated as the ratio of these values. (r² was calculated between trimmed data and the linear regression).

Replication rates in environmental and human microbiomes

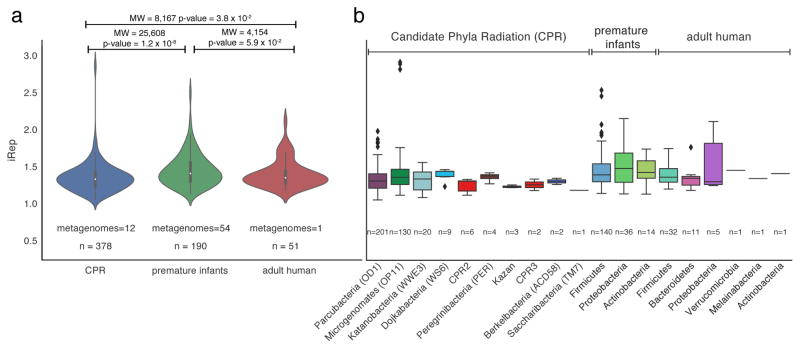
We obtained 241 iRep measurements using 152 genomes reconstructed as part of a study of premature human infant gut microbiomes²³, and 51 draft genomes that we reconstructed from an adult human microbiome dataset¹⁹ (Fig. 4a, Supplementary Tables 5–7, and see Data Availability). In infant microbiomes, members of the Firmicutes had the highest replication rates and Proteobacteria had the highest median replication rates (Fig. 4b). In the premature infant dataset, 63 iRep measurements were obtained for 8 species that could be matched to results from the kPTR program; however, there was no strong correlation between the values (Pearson’s r = 0.52, Supplementary Fig. 5, Supplementary Tables 5 and 8). Because of the strong correlation between these methods when the organisms were represented by reference genomes (Fig. 2a–b), we attribute this to measurement errors due to differences between the database reference genomes used by kPTR and the genomes of the organisms sampled (Supplementary Fig. 4).

Figure 4. Replication rates were determined for Candidate Phyla Radiation (CPR) and human microbiome-associated organisms.

iRep values were measured and compared across studies (a; MW = Mann-Whitney, n = number of measured replication rates), and compared based on taxonomic affiliation (b).

Using iRep, we obtained replication rates for 51 of the 54 organisms for which we had draft genomes (≥75% complete) from an adult human microbiome sample (see Methods; Fig. 4 and Supplementary Table 6). Due to a lack of overlap with reference genomes, the kPTR method returned only three values, none of which were credible because all were <1 (Supplementary Table 9). Similarly, we attempted to select complete reference genomes for bPTR, but were only able to do so in five cases (Supplementary Fig. 6). Even for these five cases, on average only 94% (min. = 88%, max. = 98%) of each complete reference genome was covered by metagenome sequences.

The Candidate Phyla Radiation (CPR) is a major subdivision within domain Bacteria known almost exclusively from genome sequencing¹⁵. Almost nothing is known about the growth rates of these enigmatic organisms. We measured 378 replication rates from CPR organisms using a time series of samples collected from an acetate amended aquifer near the Colorado River, and 99 different draft genome sequences reconstructed from those datasets¹⁵ (Supplementary Table 10). Only 33 of 378 iRep values were calculated using complete genome sequences. One member of the CPR superphylum Microgenomates (OP11) had iRep values amongst the highest observed across CPR and human gut associated microorganisms (Fig. 4b). However, only 16.1% of iRep values from CPR organisms were >1.5, compared with 35.8% of premature infant and 19.6% of adult human microbiome measurements. Median iRep values from CPR bacteria were significantly lower compared with those from premature infant microbiomes (Fig. 4a; CPR = 1.34, premature infant = 1.42, and adult = 1.37). Overall, the results show that CPR bacteria only rarely replicate quickly, and that iRep can be applied in communities with different levels of complexity.

Microbiome responses to antibiotic administration

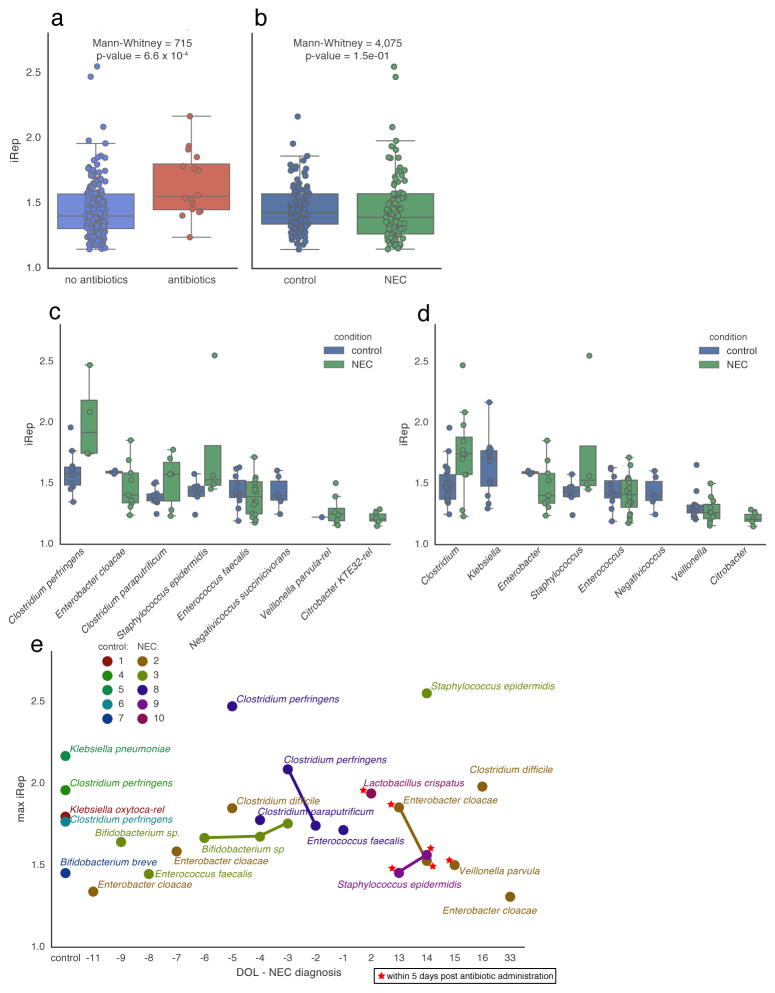
Twelve samples were collected during periods following antibiotic therapy for six of the ten infants²³ (Supplementary Fig. 7). To measure microbial responses to antibiotics, we compared iRep values from samples collected within five days after antibiotic administration to values from other time points. This showed that the median replication rate for organisms present after administration of antibiotics is higher compared to those present during periods without antibiotic treatment (Fig. 5a). Fast replicating organisms were from the genera Klebsiella, Lactobacillus, Escherichia, Enterobacter, Staphylococcus, and Enterococcus (iRep >1.5; Supplementary Table 5).

Figure 5. Elevated replication rates are associated with antibiotic administration and were detected prior to onset of necrotizing enterocolitis (NEC) in premature infants.

iRep distributions were compared (a) between samples collected during or within five days after antibiotic administration and samples from other time points, and (b) between samples collected from NEC and control infants. (c–d) Comparison of iRep values measured for different species (c) and genera (d) sampled from NEC and control infants (shown are taxa with ≥5 observations from either group). (e) iRep for the fastest growing organism observed for each control infant, and for the fastest growing organism from each day of life (DOL) sampled for each NEC infant, reported relative to NEC diagnosis. High replication rates for members of the genus Clostridium were detected in infants surveyed prior to NEC diagnosis.

iRep values for bacteria associated with premature infants

The premature infant dataset consisted of 55 metagenomes collected from ten co-hospitalized premature infants, half of whom developed necrotizing enterocolitis (NEC). There was no statistically significant difference between iRep values from NEC and control infant microbiomes (Fig. 5b), nor was there a statistically significant difference between values determined for the same species found in both infant groups (Fig. 5c). However, organisms from the genus Clostridium were replicating significantly faster in microbial communities associated with NEC versus control infants (Mann-Whitney p-value = 5.1 × 10⁻³; Fig. 5d). Although Klebsiella pneumoniae was found to replicate rapidly in control infant microbiomes, it was only infrequently detected in infants that developed NEC, and no iRep values could be determined. Intriguingly, high iRep values for Clostridium species were detected in two infants prior to development of NEC (Fig. 5e and Supplementary Fig. 7).

iRep documentation of community dynamics

Raveh-Sadka et al. measured absolute cell counts per gram of feces collected using droplet digital PCR (ddPCR) as part of a premature infant microbiome study²³. Using these measurements and metagenome-derived relative abundance calculations we were able to track absolute changes in the population sizes of 51 genotypes (Supplementary Table 5 and Supplementary Fig. 7). For nine of the ten infants in the study, iRep and both relative and absolute abundance values could be determined for the bacterial populations. Interestingly, despite fast replication rates of Clostridium species in two infants before NEC diagnosis, total observed cell counts were either very low or decreasing, emphasizing that populations of active organisms may not necessarily undergo large changes in population size (Supplementary Fig. 7).

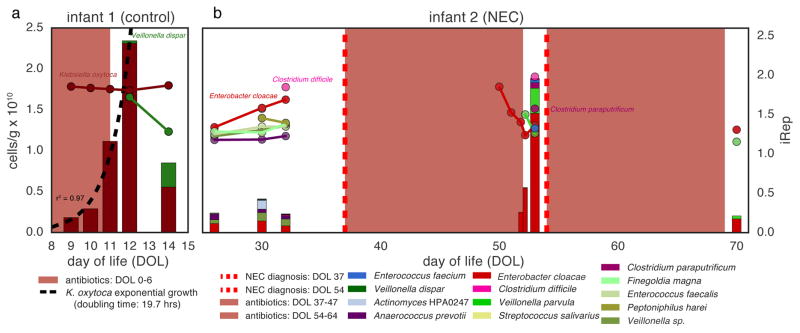
Doubling times are usually calculated for organisms growing in pure culture without resource limitation or host suppression. We used the absolute abundance of Klebsiella oxytoca following antibiotic administration to calculate an in situ doubling time of 19.7 hours across a four-day period starting three days after an infant was treated with antibiotics (Fig. 6a). iRep values for K. oxytoca during this period were consistently high (1.74–1.80), as required for the population growth that was well described by an exponential equation (r² = 0.97). Notably, K. oxytoca was essentially the only organism present during this time.

Figure 6. Absolute abundance (bars, left axis) and iRep (scatter plot, right axis) values for bacteria associated with two premature infants.

The five days following antibiotic administration are indicated using a color gradient. (a) Exponential growth was determined by regression to K. oxytoca absolute abundance values. (b) Infant 2 was diagnosed with two cases of necrotizing enterocolitis (NEC) during the study period.

In one infant, iRep values for Clostridium difficile and Enterobacter cloacae prior to the first NEC diagnosis were unusually high compared to values for organisms found in other infants. However, these organisms remained at low absolute abundance (Fig. 6b). Total cell counts were low following antibiotic treatment; however, this period was associated with high E. cloacae replication rates and a subsequent 2.7-fold increase in population size, as determined by ddPCR, prior to the second NEC diagnosis. Interestingly, low-abundance Clostridium paraputrificum and C. difficile were also replicating quickly before the second diagnosis.

A clear finding from analysis of replication rates for bacteria in multi-species consortia in the premature infant gut is the general lack of correlation between high iRep values and increased population size in the subsequently collected sample (Supplementary Fig. 7). Notably, iRep measures the instantaneous population-average replication rate, which provides insights into population dynamics at a physiological level and time scale that cannot be determined by abundance measurements, especially when more than a day separates sampling time points. Using cell counts alone as a metric for replication would miss key features of the ecosystem because the approach measures the cumulative effect of both cell replication and death rates over a specific time period.

Discussion

We developed a method named iRep that uses metagenome sequences and draft-quality genomes, which are routinely assembled in metagenomics analyses, to determine bacterial replication rates in situ. As long as accurate genome bins are obtained from the metagenomes of interest (see below), bacterial replication rates derived using iRep are more accurate than those obtained using PTR with complete reference genomes. Even when complete genomes are available, superior results can be obtained using iRep rather than PTR, owing to the potential for error when identifying the origin and terminus of replication (Online Methods). The combination of obtaining draft genomes from metagenomes and iRep measurements from read data from multiple samples from the same environment can provide a comprehensive view of microbiome membership, metabolic potential, and in situ activity.

Despite the premature infant gut microbiome having relatively consistent community composition over time, iRep analyses indicate that brief periods of rapid replication are common during colonization, possibly due to varying conditions in the infant gut. Even transitory levels of increased replication, especially for potential pathogens, could have phenotypic outcomes that affect clinical presentation since bacteria are known to produce different metabolites concordant with different growth rates²⁵. An important finding relates to the faster bacterial replication rates after antibiotic treatment, an observation that we attribute to high resource availability following elimination of antibiotic sensitive strains. Interestingly, rapid replication rates of several different but potentially pathogenic organisms from the genus Clostridium, including C. difficile, precede some NEC diagnoses, consistent with NEC being a multi-faceted disease. Further studies that include more samples and infants may establish a link between rapid cell division and NEC.

iRep measurements provide information about activity around the time of sampling. The approach could be used to probe the responses of specific bacteria to environmental stimuli. However, periods of fast bacterial replication may not lead to increased population size because other processes exert controls on absolute abundances (e.g., predation and immune responses). In a few cases where community complexity was low, fast replication rates did predict an increase in absolute cell numbers in subsequent samples (Fig. 6 and Supplementary Fig. 7). The fact that high replication rates do not necessarily predict increases in population size of bacteria growing in community context is unsurprising since iRep directly measures replication, which represents the physiological state of the organisms, but does not account for cell death rates. Replication rates and population size are distinct measurements, and both are important for studying microbial community dynamics.

An interesting question relates to how quickly organisms proliferate in the premature infant gut compared to the adult gut environment. Measurements in such environments are very challenging using alternative approaches such as isotope tracing²⁶. These studies typically target specific organisms, and such measurements have only recently been implemented in the human lung microbiome²⁶. Large-scale comparisons using PTR are not possible due to a lack of complete reference genomes. Using iRep, we found that bacteria from premature infant gut microbiomes had higher replication rates compared with those from a more complex adult gut consortium. If future studies confirm this finding, it might reflect greater levels of competition for resources or other factors related to gut development in adults compared to premature infants.

Candidate Phyla Radiation (CPR) organisms have been detected in a wide range of environments²⁷. Together, they make up considerably more than 15% of bacterial diversity^15,28, yet they are known almost exclusively from genomic sampling^{7,15,18,29–33}. Based on having small cells and genomes with only a few tens of ribosomes, it was inferred that these organisms grow slowly^27,34. Our analysis of CPR organisms sampled across a range of geochemical gradients¹⁵ directly demonstrated their slow replication rates. However, the analysis also showed that some CPR bacteria grow rapidly under certain conditions (Fig. 4). Symbiosis has been inferred as a general life strategy for these organisms^{7,15,18,29–33}, and has been demonstrated in a few cases^35–38. Rapid growth of CPR bacteria may require rapid growth of host cells. If CPR cells typically depend on a specific bacterial host, as is the case for some Saccharibacteria (TM7)³⁷, replication rate measurements may provide insights into possible host-symbiont relationships, paving the way for co-cultivation studies.

It is important to consider factors that could lead to erroneous results. For example, the presence of multiple strains that are similar enough that their conserved single copy genes co-assemble could introduce error. This usually results in draft genomes that are so fragmented that they do not meet the genome quality requirements for iRep. However, error can also be introduced if a user maps reads from a sample containing multiple closely related strains to a high-quality genome reconstructed from a different sample. If the latter approach is used, we recommend checking for evidence of strain variation by analysis of polymorphism frequencies in mapped reads.

An important objective for microbial community studies is the establishment of models that can accurately predict microbial community dynamics and functions under changing environmental conditions. Prior to the current study, these models could include growth rate information derived from laboratory experiments involving isolates, inferred from fixed genomic features such as 16S rRNA gene copy number or codon usage bias³⁹, or from in situ measurements such as PTR⁸. Further complicating matters, commonly used survey methods based on DNA sequencing cannot be used to track changes in the abundance of individual populations in microbial communities, and overall measurements of community composition can be confounded by the presence of DNA derived from dead cells⁴⁰. We used iRep to quantify replication rates for most bacteria in infant gut microbial communities and found that the rates can be highly variable (Fig. 5 and Supplementary Fig. 7). Such measurements could be used in models that seek to understand microbial ecosystem functioning, allowing incorporation of organism-specific behavior throughout the study period. Importantly, iRep can be applied to identify actively growing bacterial populations in any ecosystem, regardless of how distantly related they are to cultivated bacteria, and to track bacterial replication in response to changing conditions. The ability to make these measurements has the potential to improve our understanding of relationships between bacterial functions and biogeochemical processes or health and disease.

Data and Code Availability

DNA sequencing reads are available from the NCBI Sequence Read Archive for the groundwater¹⁵ (SRP050083), premature human infant²³ (SRP052967), and adult human¹⁹ (SRR3496379) microbiome projects. Genomes analyzed as part of this study are available from ggKbase for the groundwater¹⁵ (ggkbase.berkeley.edu/CPR-complete-draft/organisms), premature human infant (ggkbase.berkeley.edu/project_groups/necevent_samples), and adult human (ggkbase.berkeley.edu/LEY3/organisms) datasets, as well as for the curated novel Deltaproteobacterium (ggkbase.berkeley.edu/novel_delta_irep/organisms). CPR genomes (BioProject PRJNA273161) and adult human microbiome genomes (BioProject PRJNA321218) are available from NCBI GenBank, and the Deltaproteobacterium genome from DDBJ/ENA/GenBank under the accession LVEI00000000 (version LVEI02000000 described here; see Supplementary Tables 1–6 and 10 for additional accession numbers). iRep and bPTR software are maintained under github.com/christophertbrown/iRep (v1.10 used in this analysis: github.com/christophertbrown/iRep/releases/tag/v1.10; Supplementary Code).

Online Methods

Calculating bPTR for complete genomes

Our implementation of the PTR method (see Code Availability) differs from the method described by Korem et al.⁸ in several key respects. To distinguish between these two methods, we refer to our method as bPTR and the Korem et al. method as kPTR. Both methods involve mapping DNA sequencing reads to complete (or near-complete, in the case of bPTR) genome sequences in order to measure differences in sequencing coverage at the origin (Ori_cov) and terminus (Ter_cov) of replication.

$$\mathit{PTR}=\frac{{\mathit{Ori}}_{\mathit{cov}}}{{\mathit{Ter}}_{\mathit{cov}}}$$

kPTR makes use of a database of reference genome sequences, whereas bPTR is designed to be more flexible and can use mapping of reads to any genome sequence. For our bPTR analyses, we used Bowtie2⁴⁹ with default parameters for read mapping.Both bPTR and kPTR can determine the location of the origin and terminus of replication of growing cells by identifying coverage “peaks” and “troughs” associated with these positions. Identification of the origin and terminus of replication requires measuring changes in coverage along the genome sequence. This is accomplished by calculating the average coverage over 10 Kbp windows at positions along the genome separated by 100 bp. To increase the accuracy of results, a mapping quality threshold can be used in which both reads in a set of paired reads are required to map to the genome sequence with no more than a specified number of mismatches (this option is unique to bPTR). Since highly conserved regions, strain variation, or integrated phage can result in highly variable coverage, high and low coverage windows are filtered out of the analysis. Coverage windows are excluded if the values differ from the median by a factor greater than 8 (threshold also used by kPTR), or if the values differ from the average of 1,000 neighboring coverage windows by a factor greater than 1.5 (threshold unique to bPTR). If more than 40% of the windows are excluded, no bPTR value will be calculated (threshold also used by kPTR). The origin and terminus are identified by fitting a piecewise linear function to the filtered, log₂-transformed coverage values. Coverage values are log₂-transformed to improve fitting, but the transformation is reversed prior to calculating bPTR. Fitting is conducted as described by Korem et al. by non-linear least squares minimization using the Levenberg-Marquardt algorithm implemented by lmfit⁵⁰.

Piecewise linear function modified from Korem et al.⁸:

$$f(x)=\{\begin{array}{ll}\hfill -ax+y_1+a{x}_1,& x\le x_1\hfill \\ \hfill ax+y_1-a{x}_1,& x_1<x<x_2\hfill \\ \hfill -ax+y_2+a{x}_2,& x\ge x_2\hfill \end{array}$$

• $a=\frac{{\mathit{Ter}}_{\mathit{cov}}-{\mathit{Ori}}_{\mathit{cov}}}{{\mathit{Ter}}_{\mathit{loc}}-{\mathit{Ori}}_{\mathit{loc}}}$

• x₁ = min(Ter_loc, Ori_loc)

• $y_1=\{\begin{array}{llll}{\mathit{Ter}}_{\mathit{cov}}\hfill & if& x_1& ={\mathit{Ter}}_{\mathit{loc}}\\ {\mathit{Ori}}_{\mathit{cov}}\hfill & if& x_1& ={\mathit{Ori}}_{\mathit{loc}}\end{array}$

• x₂ = max(Ter_loc, Ori_loc)

• $y_2=\{\begin{array}{llll}{\mathit{Ter}}_{\mathit{cov}}\hfill & if& x_2& ={\mathit{Ter}}_{\mathit{loc}}\\ {\mathit{Ori}}_{\mathit{cov}}\hfill & if& x_2& ={\mathit{Ori}}_{\mathit{loc}}\end{array}$

Ori_loc and Ter_loc refer to the locations of the origin and terminus of replication, respectively, and Ori_cov and Ter_cov refer to log₂-transformed coverage at those positions. All x values refer to positions on the genome, and y values to log₂-transformed coverage values. The fitting is constrained such that Ori_loc and Ter_loc are separated by 45–55% of the genome length⁸. In order to reduce the amount of noise introduced by fluctuations in sequencing coverage, a median filter is applied to the coverage data before calculating bPTR. This smoothing operation replaces the coverage value at each position with the median of values sampled from the 1,000 neighboring windows. The log₂-transformed, median-filtered values corresponding with Ori_loc and Ter_loc (Ori_cov-med and Ter_cov-med, respectively) are used to calculate bPTR.

Since the values have been log₂-transformed, the final value is calculated as:

$$\mathit{bPTR}=\frac{2^{{\mathit{Ori}}_{\mathit{cov}-\mathit{med}}}}{2^{{\mathit{Ter}}_{\mathit{cov}-\mathit{med}}}}$$

Ori_loc and Ter_loc are determined based on sequencing from each available sample. In order to calculate bPTR using the same positions for all samples, consensus Ori_loc and Ter_loc positions are determined by finding the circular median of the positions determined from each individual sample (all Ori_loc and Ter_loc positions with bPTRs ≥1.1 are considered), as is done for kPTR⁸. Once these values are determined, all bPTR values are re-calculated using the coverage at the consensus positions. It is important to note that Ori_loc and Ter_loc may vary depending on what samples are analyzed, and that with bPTR this can be avoided by using GC skew to identify Ori_loc and Ter_loc (see below).

For bPTR we added the option to find Ori_loc and Ter_loc based on GC skew. GC skew is calculated over 1 Kbp windows at positions along the genome separated by 10 bp. Since Ori_loc and Ter_loc coincide with a transition in the sign (+/−) of GC skew, these positions can be identified as the transition point in a plot of the cumulative GC skew⁵¹ (for examples see Fig. 3, Supplementary Fig. 3, and Supplementary Fig. 6). These transition points are identified by finding extreme values in the cumulative GC skew data separated by 45–55% of the genome length. Once Ori_loc and Ter_loc are identified, bPTR is calculated from median-filtered log₂-transformed coverage values calculated over sliding windows as described above. bPTR provides visual representation of both coverage and GC skew patterns across genome sequences that enable verification of genome assemblies and predicted Ori_loc and Ter_loc positions (this visualization is not provided by kPTR).

Calculating the Index of Replication (iRep) for complete and draft-quality genomes

iRep (Supplementary Code) analyses are conducted by first mapping DNA sequencing reads to genome sequences with Bowtie2 (default parameters). For genomes in multiple pieces, the coverage values determined at each position along the fragments are combined, and then average coverage is calculated over 5 Kbp windows at positions along the concatenated genome that are separated by 100 bp (Supplementary Fig. 1; see Supplementary Fig. 2 and below for accuracy metrics related to sliding window calculations). As with bPTR, a mapping quality threshold can be used to increase the accuracy of results by ensuring that both reads in a set of paired reads mapped to the genome sequence with no more than a specified number of mismatches. Coverage values from the first and last 100 bp of each scaffold are excluded due to possible edge effects. Coverage windows are filtered out of the analysis if the values differ from the median by a factor greater than 8, and then GC sequencing bias is measured and corrected (see below). Coverage values are log₂-transformed and then sorted from lowest to highest coverage. Because the coverage windows are re-ordered in this step, it does not matter if the correct order of genome fragments is unknown. The lowest and highest 5% of sequences are excluded, and then the slope of the remaining coverage values is determined by linear regression. As with bPTR, log₂-transformations are conducted to improve regression analysis, but are removed before comparing coverage values. iRep, which is a measure of the ratio between Ori_cov and Ter_cov, can be determined based on the slope (m) and y-intercept (which is synonymous with Ter_cov, see Supplementary Fig. 1) of the regression line, and the total length of the genome sequence (l):

$$\mathit{iRep}=\frac{m\times l+{\mathit{Ter}}_{\mathit{cov}}}{{\mathit{Ter}}_{\mathit{cov}}}$$

However, since the values have been log₂-transformed, the final value is calculated as:

$$\mathit{iRep}=2^{m\times l}$$

Since partial genome sequences will include a random assortment of genome fragments, the coverage trend determined from the available sequence will be representative of the coverage trend across the complete genome. Several quality thresholds are used to ensure the accuracy of iRep measurements: i) coverage depth must be ≥5x, ii) ≥98% of the genome sequence must be included after filtering coverage windows, and iii) r² values calculated between the coverage trend and the linear regression must be ≥0.90. These criteria are important because they ensure that enough sequencing data is present to achieve accurate measurements, and that the genome sequence is appropriate for the analysis. The 98% genome sequence coverage threshold differs from the genome completeness requirement in that this is not a measure of the quality of the genome assembly, but rather a measure of the overlap between a genome sequence and the sequencing data. Low values would indicate that the genome used for mapping is not appropriately matched with an organism present in the system. Likewise, having a strong fit of the linear regression to the coverage data indicates that sequencing coverage calculations are not influenced by strain variation, choice of an inappropriate genome sequence, or other factors that may skew replication rate measurements.

Both PTR methods involve calculations based on only two data points (Ori_cov and Ter_cov). In contrast, iRep uses coverage trends determined across an entire genome sequence, and thus is less susceptible to noise in sequencing coverage or errors in the prediction of Ori_loc and Ter_loc. Further, since both PTR methods involve predicting Ori_loc and Ter_loc based on data from multiple samples, the same positions may not be chosen for different analyses. This makes it difficult to reproduce and compare results (an issue that can be avoided by predicting Ori_loc and Ter_loc using cumulative GC skew and bPTR). iRep calculations do not depend on analysis of multiple samples, and thus results will not change based on what samples are included in an analysis. Since the order of genome fragments need not be known when calculating iRep, the method is not affected by genome assembly errors, which are present even in some genome sequences reported to be complete (Supplementary Fig. 6).

Determining the minimum sequencing coverage required for iRep analysis

Lactobacillus gasseri data from the Korem et al.⁸ study was used to determine the minimum coverage required for iRep, bPTR, and kPTR. Reads from each sample were first mapped to the complete genome sequence, and then subsampled to 25× before calculating iRep, bPTR, and kPTR. Then, each mapping was further subsampled to lower coverage levels (20x, 15x, 10x, 5x, and 1x) and replication rates were re-calculated using each method. Comparison of these values to those determined at 25× coverage enable quantification of the amount of noise introduced by increasingly lower coverage (Fig. 2c and Supplementary Table 3).

Determining genome quality requirements for iRep analysis

The L. gasseri data from Korem et al.⁸ subsampled to 25× coverage was also used to test the minimum fraction of a genome required for obtaining accurate iRep measurements. Four samples representing iRep values between 1.50 and 2.01 were selected in order to test the effect of missing genomic information across a range of replication rates. Genome subsampling experiments were conducted on each sample in order to evaluate the amount of noise introduced by missing genomic information. For each tested genome fraction (90%, 75%, 50%, and 25%), iRep was calculated for 100 random genome subsamples. For each subsample, the genome was fragmented into pieces with lengths determined by selecting from a gamma distribution modeled after the size of genome fragments expected for draft-quality genome sequences (alpha = 0.1, beta = 21,000, minimum length = 5 Kbp, maximum length = 200 Kbp; Supplementary Fig. 2a). Once fragmented, the pieces were randomly sampled until the desired genome fraction was achieved. Partial fragments were included in order to prevent the desired genome fraction size from being exceeded. In order to ensure that the results were accurate even when sequencing coverage is low, iRep calculations were conducted after subsampling reads to 5× coverage. iRep values calculated after subsampling were compared to values determined at 25× coverage with the complete genome sequence in order to measure the combined affect of lower coverage and missing genome sequence information (Fig. 2d and Supplementary Table 3). In order to determine the effect of increased genome fragmentation on iRep calculations, additional genome fragmentation experiments were conducted in which the minimum and maximum allowed fragment lengths were varied in order to determine the effects of higher than normal levels of genome fragmentation (Supplementary Fig. 2b and Supplementary Table 1).

Evaluation of iRep sliding window calculation methods

The accuracy of iRep when implemented using different sliding window coverage calculation methods was determined based on additional random genome fragmentation experiments using the L. gasseri data from Korem et al.⁸ (Supplementary Fig. 2c–e and Supplementary Table 1). Three sliding window methods were tested: 1) the method implemented in iRep (described above and referred to as the “iRep” method), 2) as implemented in iRep, except for that the iRep value is taken as the median of ten iRep values each obtained after concatenating available genome fragments in different arrangements (referred to as the “median iRep” method), and 3) obtained after calculating coverage sliding windows for each fragment individually, and then combining the sliding window data (referred to as the “scaffold windows” method). The amount of noise in the iRep calculation using each method was determined based on comparing iRep values achieved with 5× sequencing coverage and varying levels of genome completeness (see above) to values determined based on the standard iRep method and the complete genome sequence with 25× sequencing coverage (Supplementary Fig. 2c). This was repeated using different sliding window sizes in order to determine the optimal method. Furthermore, the range of iRep values obtained for tests using the “median iRep” method was used to determine the amount of noise introduced when scaffold coverage data is concatenated in a random order prior to conducting sliding window calculations (Supplementary Fig. 2d). Because the standard iRep method with 5 Kbp windows was determined to be the best, a final test of this method was conducted in order to compare different window slide lengths (Supplementary Fig. 2e).

Correcting for GC sequencing bias

DNA sequencing platforms are biased towards sequences based on their GC content⁵². Because this bias can result in a difference in the sequencing coverage across a genome sequence, it could influence iRep results. To account for this, GC sequencing bias is measured and corrected independently for each genome and metagenome. This is accomplished by first determining the GC content of sliding windows across the genome sequence that correspond with the coverage measurements used for calculating iRep. Then, linear regression is conducted between the coverage and GC values determined for each sliding window. In order to get an accurate measurement, linear regression is conducted in two steps: first with the complete data set and then after removing the 1% of data points with the largest deviation from the initial regression analysis. Then, the results of the regression analysis are used to correct the coverage values for each sliding window. This method was used in the analyses of all metagenome data in this study, and is part of the iRep code (Code Availability). The GC sequencing bias correction resulted in better agreement between iRep and bPTR values determined using ordered and oriented genomes reconstructed from the premature infant dataset (Supplementary Fig. 2f).

Comparative analyses of replication rate methods

iRep, bPTR, and kPTR were calculated for all samples from the Korem et al.⁸ L. gasseri experiments (these were the only samples sequenced to a high enough depth to enable comparison with iRep; Supplementary Table 3). For a subset of these data, replication rates could also be calculated based on counts of colony forming units (CFU/ml)⁸ (Fig. 2b and Supplementary Table 2). Pearson’s correlations were calculated between replication rates based on CFU/ml data and iRep, bPTR, and kPTR, after first accounting for the time delay between start of genome replication and observable change in population size (as previously noted⁸). The time delay was determined independently for each method as the delay that resulted in the highest correlation.

iRep and bPTR values were compared for a novel Deltaproteobacterium after manually curating the draft genome sequence recently reported by Sharon et al.²⁴ (see below). Reads from the GWC2 sample from Brown et al.¹⁵ were used to conduct the analysis (Fig. 3). For this comparison, and all subsequent iRep and bPTR calculations, coverage was calculated based on reads that mapped to the genome fragment with no more than two mismatches (see above for details). Although enough of the genome sequence was assembled in order to calculate bPTR, the results could not be compared with kPTR because a complete reference genome sequence was not available.

In order to further compare iRep and bPTR in the context of microbial community sequencing data, bPTR values were calculated using genomes reconstructed from the premature infant dataset²³ that were ordered and oriented based on complete reference genome sequences (see below; Fig. 2e and Supplementary Table 4). Although these genomes were similar enough to reference genomes to facilitate ordering and orienting the sequences, the reference genomes themselves were too divergent to facilitate replication rate calculations (see Results; Supplementary Fig. 4), which prevented inclusion of kPTR in this analysis.

Manual curation of a Deltaproteobacterium genome

The genome sequence of a previously reported Deltaproteobacterium was manually curated. Unplaced or misplaced paired-read sequences were used to fill scaffolding gaps, correct local assembly errors, and extend scaffolds. Overlapping scaffolds were combined when the join was supported by paired read placements. The final assembled sequence was visualized to confirm that all errors had been corrected.

Ordering and orienting draft genomes based on complete reference genomes

Reference genomes similar to draft genomes were obtained from NCBI GenBank. Genomes with aberrant GC skew patterns were not used for ordering draft genomes as they likely contain assembly errors. The average nucleotide identities (ANI) between each draft genome and associated reference genomes were calculated using the ANIm method⁵³, and the reference genome with the highest ANI was chosen. Draft genome fragments were aligned to the reference genome using BLAST⁵⁴, and any fragment with less than 20% alignment coverage was discarded. The remaining sequence was then aligned to the reference genome using progressive Mauve⁵⁵, resulting in an ordered and oriented genome to be used for calculating bPTR. These genomes were manually inspected and curated based on cumulative GC skew and genome coverage patterns based on graphs generated by the bPTR script (Supplementary Fig. 3).

iRep measurements for premature infant metagenomes

Previously reconstructed genomes from the premature infant gut microbiome study²³ were included in the iRep analysis if they were estimated to be ≥75% complete based on analysis of universal single copy genes (SCGs), had no more than two duplicate SCGs, and had less than 175 fragments/Mbp of sequence. In order to maximize the number of iRep values that could be determined, custom read mapping databases were used for each metagenome. Each database was constructed by first including genomes reconstructed from the metagenome that passed the above thresholds, and then by adding additional draft-quality genomes reconstructed from other metagenomes from the same infant. This prioritizes genomes reconstructed from the metagenome used for mapping, but also attempts to include genomes from organisms that may have been present, but for which a genome sequence was not assembled.

Overlap in community membership across time-series studies results in the same genome sequence being reconstructed in multiple samples. Including highly similar or identical genome sequences in databases used for read mapping would lead to aberrant coverage calculations. This becomes a concern when including genomes reconstructed from additional samples in read mapping databases for iRep calculations. To prevent adding highly similar genomes to the databases, only the representatives of 98% ANI genome clusters (see below) were added to mapping databases, and only if a representative of the cluster was not already included. Consistent with clustering genomes based on sharing 98% ANI, iRep calculations were conducted based on coverage calculations determined from reads mapping to genomes with no more than two mismatches (see above for details; Supplementary Table 5).

Clustering genomes based on average nucleotide identity (ANI)

Average nucleotide identity was determined between all pairs of genome sequences using the Mash algorithm⁴⁸ (kmer set to 21). Clusters were defined by selecting groups of genomes connected by ≥98% ANI. Representatives of each cluster were chosen by selecting the longest genome with the largest number of single copy genes, and the fewest number of single copy gene duplicates that had less than 175 fragments/Mbp.

Comparison of iRep and kPTR measurements for premature infant gut metagenomes

The kPTR software from Korem et al.⁸ was run on the premature infant metagenomes²³ (Supplementary Table 8). Comparisons between iRep and kPTR were made when it was possible to link the name of the genome provided by kPTR with the taxonomy given to reconstructed genome sequences (Supplementary Table 5).

Genome binning and iRep measurements for adult human metagenomes

Genomes were binned from the adult human metagenome¹⁹ based on coverage, GC content, and taxonomic affiliation using ggKbase tools (ggkbase.berkeley.edu), as previously described^15,23. Genome completeness was evaluated based on the fraction of universal single copy genes^23,46 that could be identified (Supplementary Table 6). Genomes estimated to be ≥75% complete, with no more than two additional single copy genes, and no more than 175 fragments per Mbp of sequence, were used in the analysis. iRep was conducted using reads mapped to genomes with no more than two mismatches (Supplementary Table 7).

bPTR and kPTR measurements from the adult human metagenome

The kPTR software from Korem et al.⁸ was run on the adult human metagenome¹⁹ (Supplementary Table 9). bPTR calculations were conducted based on mapping metagenome reads to selected complete reference genomes (≤2 mismatches; Supplementary Fig. 6). Reference genomes for bPTR analysis were selected by searching scaffolds from reconstructed genome sequences against complete genomes from NCBI GenBank. The complete genome with the best BLAST hit to each reconstructed genome was selected for bPTR analysis.

iRep measurements for Candidate Phyla Radiation (CPR) organisms

CPR genomes identified by Brown et al.¹⁵ to be ≥75% complete, with no more than two additional single copy genes, and no more than 175 fragments per Mbp of sequence, were selected for iRep analysis. These genomes were reconstructed previously from multiple metagenomes spanning an acetate amendment time-series field experiment. Reads from each of 12 metagenomes sequenced from groundwater filtrates, collected from serial 0.2 and 0.1 μm filters at six time points, were mapped to the genome sequences for iRep calculations (≤2 mismatches; Supplementary Table 10).

Absolute abundance and doubling time determinations

Raveh-Sadka et al. determined the concentration of cells in each collected fecal sample using droplet-digital PCR²³. In this study, the population size of each species was determined by multiplying total cell counts by the fractional (relative) abundance calculated based on genome sequencing (Supplementary Fig. 7 and Supplementary Table 5). These values were used to calculate the doubling time for Klebsiella oxytoca (Fig. 6).

Supplementary Material

ST1. Supplementary Table 1 Analysis of the impact of genome completeness on iRep replication rate measurements.

iRep was first calculated using sequencing data from Lactobacillus gasseri (NC_008530) experiments⁸ with the complete genome at 25× coverage, and then compared with values calculated at 5× coverage after subsampling the genome 100 times for each targeted percent of the genome sequence (“delta”). This was conducted using different coverage sliding window methods (see Online Methods for descriptions), sliding window sizes, and window slide lengths. In order to test different levels of genome fragmentation, the minimum and maximum allowed fragment size was also varied. iRep range is the difference between the min. and max. iRep values determined when using the “median iRep” sliding window calculation method.

ST10. Supplementary Table 10 iRep measurements for Candidate Phyla Radiation (CPR) organisms.

iRep measurements were determined using genomes and metagenomes from the Brown et al. CPR dataset¹⁵.

ST2. Supplementary Table 2 Comparison of iRep, bPTR, and kPTR measurements.

The Korem et al.⁸ Lactobacillus gasseri (NC_008530) data was used to measure replication rates using iRep, bPTR, and kPTR. iRep % windows refers to the percent of coverage windows that passed the iRep filters, and iRep r^2 is the r² value calculated between the sequencing coverage trend and regression used for calculating iRep. Coverage is the average sequencing depth calculated across the genome sequence. Colony forming units per ml of culture (CFU/ml) was obtained from the Korem et al.⁸ study.

ST3. Supplementary Table 3 iRep, bPTR, and kPTR measurements for minimum genome sequencing coverage analyses.

Genome coverage tests were conducted using Lactobacillus gasseri (NC_008530) data from previously published experiments⁸. Target coverage is the level of coverage achieved after sub-sampling sequencing reads.

ST4. Supplementary Table 4 Comparison of iRep and bPTR measurements for draft-quality genomes ordered and oriented based on complete genome sequences.

Genomes reconstructed for organisms sampled as part of the Raveh-Sadka et al. premature infant dataset²³ were ordered based on complete reference genome sequences. iRep and bPTR values were calculated for all pairs of genomes and samples by mapping reads from the samples to the genome sequences. GC r^2 is the r² value from the linear regression between sequencing coverage and GC content that is used for correcting GC sequencing bias. GC bias is the GC r² value multiplied by the slope of the regression line, and is a measure of the magnitude and direction of GC sequencing bias. Un-filtered iRep values include iRep values that may not have passed the quality thresholds. Raw iRep values are iRep values determined without the GC sequencing bias correction. Fragments/Mbp is the number of genome fragments per Mbp of genome sequence. Coverage breadth is the percent of the genome covered by sequencing reads.

ST5. Supplementary Table 5 iRep measurements for organisms associated with premature infant microbiomes.

iRep measurements were determined using genomes and metagenomes from the Raveh-Sadka et al. premature infant dataset²³. DOL = day of life and NEC = necrotizing enterocolitis. The DOL – sample column indicates whether additional samples were collected on a particular day, the DOL – NEC diagnosis column includes day of life relative to NEC diagnosis, and condition indicates whether or not the infant was diagnosed with NEC. The antibiotics column indicates whether or not antibiotics were administered at, or within five days prior to, the time of sample collection. Relative abundance was calculated for each organism based on the number of sequencing reads mapped to the genome sequence as a percent of sequences mapped to all draft-quality genomes. Absolute abundance (cells/g) was determined for each organism based on relative abundance and previously published ddPCR measurements of total cells/g of feces²³. kPTR values are provided for cases where there was a clear match with results from the kPTR software⁸ (Supplementary Table 8).

ST6. Supplementary Table 6 Single copy gene inventory for genomes reconstructed from an adult human gut metagenome.

Genomes were binned as part of this study from a previously published metagenome dataset from Di Rienzi et al. (SAMN04978193)¹⁹. The number of single copy marker genes, which can be used as a proxy for genome completeness, was determined for each genome.

ST7. Supplementary Table 7 iRep measurements for organisms associated with an adult human microbiome.

iRep measurements were determined using the metagenome from Di Rienzi et al. (SAMN04978193)¹⁹ and the genomes reconstructed as part of this study.

ST8. Supplementary Table 8 kPTR values determined from the premature infant metagenomes.

The kPTR software⁸ was used to measure replication rates for organisms represented in the Raveh-Sadka et al. premature infant metagenomes²³.

ST9. Supplementary Table 9 kPTR values determined from the adult human metagenome.

The kPTR software⁸ was used to measure replication rates for organisms represented in the metagenome from Di Rienzi et al. (SAMN04978193)¹⁹.

SupplementalFigures

Supplementary Figure 1 Schematic showing steps involved in a genome-resolved metagenomics study that includes iRep analysis. Microbiome sample collection and DNA extraction methods should be determined on a per-project basis, and metagenome sequencing can be conducted on the Illumina, PacBio, or another sequencing platform. Sequencing reads are trimmed based on quality scores (e.g. using Sickle⁴¹) and filtered for contamination (e.g. removal of human genome sequences). High-quality reads are then assembled (e.g. using IDBA_UD⁴²), and the resulting scaffolds are binned either manually (e.g. based on GC content, taxonomic affiliation, coverage), and/or using a clustering algorithm such as ESOM^12,23,43) or using an automated binning program (e.g. MaxBin⁴⁴, CONCOCT⁴⁵, or ABAWACA¹⁵). Genome bins can then be assessed for completion and contamination based on inventory of expected single copy genes (SCGs), either based on identification of these genes from genome annotations (see^15,23,46), or using software such as CheckM⁴⁷. High-quality genomes are then compared with one another and grouped into clusters based on average nucleotide identity (ANI; e.g., based on sharing 98% ANI determined using Mash⁴⁸). A representative of each cluster should be included in a genome database that will be used for iRep analysis, along with genomes from other projects that may be appropriate for the analysis. Reads from each metagenome are then mapped to the genome database (e.g. using Bowtie2⁴⁹), and iRep is calculated from the read mapping data (see Online Methods).

Supplementary Figure 2 Evaluation of iRep method parameters. (a) Gamma distribution used to simulate genome fragmentation for genome completeness analyses. The frequency of genome fragment sizes from all genomes analyzed in this study are compared with genome fragment sizes simulated using a gamma distribution with parameters: alpha = 0.1, beta = 21,000, min. = 5,000, max. = 200,000. These parameters were first estimated by fitting to the genome data, and then manually adjusted. Similarity between the two distributions shows that this gamma distribution can be used to approximate the level of genome fragmentation expected for draft-quality genome sequences. (b) iRep was calculated from random genome fragmentation simulations in order to survey a range of fragmentation levels (Supplementary Table 1). The analysis was conducted for an L. gasseri sample from the Korem et al.⁸ study in which iRep was determined to be 2.01 using the complete genome with 25× sequencing coverage. This known iRep value was then compared with iRep values determined from each genome fragmentation simulation after subsampling to 75% of the genome and using only 5× sequencing coverage. This enabled analysis of the influence of fragmentation on iRep calculations at the completeness and coverage limits of the method. Results show that 91.8% of iRep values are within the expected range of 0.15 when genomes have fewer than 175 fragments/Mbp of genome sequence. (c) Four L. gasseri samples from the Korem et al.⁸ study that represent iRep values between 1.50 and 2.01 were selected in order to test different coverage sliding window calculation methods (see Online Methods for description of each method) and window sizes. For each sample, 100 random genome fragmentations and subsets were conducted in order to assess each method based on various levels of genome completion. The results show that the “iRep” and “median iRep” methods using 5 Kbp windows exhibited the least amount of variation. (d) Because the iRep method involves randomly combining coverage data from different genome fragments prior to calculating coverage sliding windows, some sliding windows will include coverage values from different locations on the complete genome sequence. In order to evaluate the variation introduced by the (random) order in which scaffolds are combined, iRep calculations were conducted for ten random orderings of 100 random genome fragmentations conducted using the sample set described in (c). Results show a very minimal amount of variation in iRep values as described by the difference between the lowest and highest values determined from each of the ten orderings (“iRep range”). Because of this, we chose not to implement the “median iRep” strategy. (e) Using the sample set described in (c), the iRep method was implemented using 5 Kbp windows using different window slide values in order to test whether or not the slide value would change the results. Because both 10 and 100 bp window slides produced similar results, we implemented the iRep method using a 100 bp window slide. (f) iRep is not as strongly correlated with bPTR without the GC sequencing bias correction for five genome sequences assembled from premature infant metagenomes (Supplementary Table 4; compare with GC corrected data in Fig. 2e).

Supplementary Figure 3 Coverage, GC skew patterns, and bPTR measurements for reconstructed genomes oriented and ordered based on complete reference genome sequences. (a–e) Read mapping was conducted using sequences from the sample used for genome recovery. bPTR was calculated after determining the origin and terminus of replication based on cumulative GC skew. Coverage was calculated for 10 Kbp windows calculated every 100 bp (extremely low and high coverage windows were filtered out; see Online Methods). bPTR was calculated as the ratio between the coverage at the origin and terminus after applying a median filter. Cumulative GC skew and coverage patterns confirm the ordering of genome fragments.

Supplementary Figure 4 Reference genomes are not representative of organisms surveyed in the premature infant microbiome study. Reads were mapped to both reconstructed genomes and closely related reference genomes (Supplementary Table 4), and the percent of each genome covered by sequencing reads is reported. Average nucleotide identity (ANI) is reported between each reconstructed genome and the paired reference genome. The large fractions of reference genomes not represented by metagenome sequencing show that extensive genomic variation is present between surveyed and reference genomes, despite high ANI values in some cases.

Supplementary Figure 5 Replication rates determined by iRep and kPTR are not in strong agreement for the premature infant study. iRep values were determined based on reconstructed genomes and kPTR values based on complete reference genomes (r = Pearson’s r value).

Supplementary Figure 6 Coverage, cumulative GC skew, and bPTR measurements for complete reference genomes with similarity to genomes from the adult human microbiome sample. (a–e) Reads from the adult human microbiome were mapped to complete reference genome sequences. Coverage was calculated for 10 Kbp windows every 100 bp (extremely low and high coverage windows were filtered out; see Online Methods). The origin and terminus of replication were determined based on coverage. bPTR was calculated as the ratio between the coverage at the origin and terminus after applying a median filter. Cumulative GC skew and coverage patterns suggest the presence of genomic variation or assembly errors for some genomes (b–c, e).

Supplementary Figure 7 Absolute abundance (bars, left axis) and iRep (scatter plot, right axis) for bacteria associated with premature infants. The five days following antibiotic administration are indicated using a color gradient (DOL = day of life).