Abstract
We have recently developed a novel computational methodology (termed RSF for Real-Space Fluctuations) to quantify the bending rigidity and tilt modulus of lipid membranes from real-space analysis of fluctuations in the tilt and splay degrees of freedom as sampled in molecular dynamics (MD) simulations. In this article, we present a comprehensive study that combines results from the application of the RSF method to a wide range of lipid bilayer systems that encompass membranes of different fluidities and sizes, including lipids with saturated and unsaturated lipid tails, single and multi-component lipid systems, as well as non-standard lipids such as the four-tailed cardiolipin. By comparing the material properties calculated with the RSF method to those obtained from experimental data and from other computational methodologies, we rigorously demonstrate the validity of our approach and show its robustness. This should allow for future applications of even more complex lipidic assemblies, whose material properties are not tractable by other computational techniques. In addition, we discuss the relationship between different definitions of the tilt modulus appearing in current literature to address some important unresolved discrepancies in the field.
Keywords: lipid splay, tilt modulus, bilayer bending rigidity, membrane deformations, elasticity, molecular dynamics
Graphical Abstract

INTRODUCTION
Among the various ways that the lipid environment can regulate the function and organization of membrane proteins, the material (elastic) properties of lipid membranes and their modulation have justifiably taken center stage [1, 2]. Dependent sensitively on lipid composition, these properties determine the extent of membrane resistance to different modes of deformation, including membrane curvature and lipid tilt. As such, lipid material properties can directly influence the energetics of membrane reshaping during many cellular processes that require partitioning of proteins in specialized functional lipid domains (e.g. fusion and endocytosis [1]). Once proteins enter these domains, their conformational dynamics can be further affected by the energetic cost associated with deformations of the local lipid environment, as the membrane responds to protein conformational transitions [3, 4].
Given the importance of the bilayer material properties to its biological function, several methodologies have been implemented to probe and follow them in vitro and in silico. The quantitative framework for these methodologies is most often based on the Helfrich-Canham-Evans theory of elasticity [5], which treats a lipid bilayer as a two-dimensional incompressible, continuum, elastic medium. Under these conditions, and assuming small deformations, the free energy contributions of various modes of membrane elasticity can be approximated by a quadratic function of the relevant deformation.
Membrane bending rigidity, in particular, has generated considerable interest due to the direct implications of bilayer curvature to protein-membrane interactions [4]. The two most common experimental techniques for measuring the bilayer’s rigidity, flicker spectroscopy [6–9] and micropipette aspiration [10–13], require the use of giant unilamellar vesicles (GUVs). Less frequently used are electrodeformation of GUVs [14, 15] and scattering techniques including low angle diffuse X-ray scattering from multibilayer stacks [16, 17] and neutron spin-echo (NSE) analysis of large unilamellar vesicles (LUVs) [18, 19]. Flicker spectroscopy involves analysis of Fourier modes of the fluctuation spectra measured at the GUV equator using video microscopy, and generally produces bending rigidity values that are higher in magnitude compared with other methods [20–22]. Micropipette aspiration and electrodeformation, on the other hand, quantify bending rigidity from the linear relationship between tension and area expansion of the GUVs in the low tension regime, where thermal undulations are smoothed by increasing tension [10, 20]. The difference between the two techniques is that in the former tension is applied to the GUV surface through suction pressure, while in the latter it is applied through electrostatic stresses induced by an external electric field. Information on bilayer thermal fluctuations is also encoded in the static scattering signature, or form factor, of oriented bilayer stacks measured with X-ray diffraction [16]. The corresponding analysis is model-based and produces bending rigidities similar to those obtained from GUV pipette aspiration [23]. An alternative dynamic technique, NSE, is characterized by correlation times and length scales that are very similar to those of membrane thermal fluctuations, and measures bending rigidity from neutron scattering as a function of Fourier time [24]. A detailed description of these experimental methods can be found in Ref. [25].
These experimental approaches have been recently complemented by computational methods, based on both mean-field level theory [26], and on atomistic (or coarse-grained) molecular dynamics (MD) simulations [27–33]. The quantitative framework for these computational methodologies is based on the generalized “Helfrich Hamiltonian” in which contributions associated with the free energy of bending (splay distortion) and Gaussian curvature from the original Helfrich formulation are supplemented by additional deformation modes, such as area compression/expansion, lipid tilt, and lipid twist. In the context of this work, we focus our discussion on two major contributions to the bilayer deformation free energy related to the tilt and bending deformations, and express them as:
| (1) |
| (2) |
In the above, ft and fb are the quadratic approximations for the free energies associated with monolayer tilt and bending, respectively. We represent the lipid tilt vector as t⃗, lipid splay is S, and n⃗ and N⃗ unit vectors denote, respectively, the local lipid director and the local normal to the lipid-water interface. In these relations, κt and KC are coefficients representing the thermodynamic tilt modulus and the bending rigidity, correspondingly, per unit area, the 〈 〉brackets denote a thermodynamic ensemble average, and 〈·〉2 in Eq. 1 represents the dot product. The full derivation of Eqs. 1–2 from the Hamiltonian of a monolayer under deformations can be found in Ref [34].
Using Eq. (1), κt was previously obtained based on mean field theory of lipid chain packing [26] by computing the mean-square fluctuations in lipid tilt. The approach suggested a range of values ~ 0.1–0.2 kBT/Å2 for a typical lipid monolayer (kB represents the Boltzmann constant, and T is temperature), equivalent to ~ 4.0–8.0 × 10−20 J/nm2 per monolayer at room temperature.
The extraction of the elastic moduli from atomistic MD simulations in recent decades has relied on sampling thermally excited fluctuations in the bilayer shape during the course of the MD trajectory (reviewed in [32]). These undulations are then Fourier transformed into reciprocal space using the two-dimensional reciprocal space vector, q⃗. Thus, the bending rigidity, for example, can be obtained from the spectral analysis in the limit of small-q modes. However, dependence on robust sampling of global bilayer undulations has restricted the spectral analysis method to relatively large membrane systems (~1000 lipids or larger). Yet, recent modifications of this approach to sample in reciprocal space the fluctuations in lipid tilt vectors instead of undulations of membrane shape have allowed the application of the method to rather small membrane patches (~400 lipids) [30]. In addition, the spectral analysis technique enabled determination of the so called theoretical tilt modulus, κt0, which is related, yet not identical, to the thermodynamic tilt modulus κt in Eq. 1 (see more below).
Importantly, thus far, results from the reciprocal space method have only been reported for single component fluid lipid bilayers where the method yields bending moduli values that are in good agreement with experiments [32]. However, the method is yet to be validated for mixtures of lipids, as well as for lipidic assemblies of different curvatures and different levels of fluidity and stiffness, such as cholesterol-enriched liquid ordered phases.
We have developed an alternative computational approach that is also based on analysis of MD simulations but which calculates the thermodynamic tilt modulus and bending rigidity by analyzing the fluctuations in the tilt and splay degrees of freedom as sampled in the MD trajectories in real space. As described in depth elsewhere [35–37] and highlighted below, this real-space fluctuation (RSF) analysis is local in nature, and therefore overcomes several limitations inherent in the Fourier space methodology. Thus, the RSF method typically only requires as input an MD trajectory of a rather small size lipid system (~100 lipids in the case of single-component bilayers), and has been extended to complex multi-component lipid bilayers, including liquid ordered membrane systems consisting of cholesterol in complex with several types of lipids (saturated or unsaturated). Importantly, a recent generalization of the methodology [35] (see below) not only enabled extensions to lipid assemblies with high curvatures (e.g. hexagonal phases), but also allowed a more accurate determination of the bending and tilt moduli for lamellar membrane systems.
In this article, we present a comprehensive study that combines results from the application of this generalized RSF method to a range of lipid bilayer systems, such as single-component membranes (containing saturated or unsaturated lipids, as well as hybrid lipids with combinations of saturated and unsaturated tails), mixtures of several lipids, including cholesterol-containing systems, and various size lipid membranes (from 128 to 1600 lipid-size patches). Where available, the material properties calculated with our method are compared to those obtained from experimental data and other computational methodologies. This comparison further allowed us to address some unresolved discrepancies related to the different definitions of the tilt modulus that appear in current literature. In the following, we first briefly summarize the theoretical aspects of the RSF method highlighting the recent enhancements to the approach (the full mathematical formulation of the RSF methodology can be found in [35]), and then describe recent results that emerge from implementing this methodology.
METHODS
Theoretical aspects of the RSF method
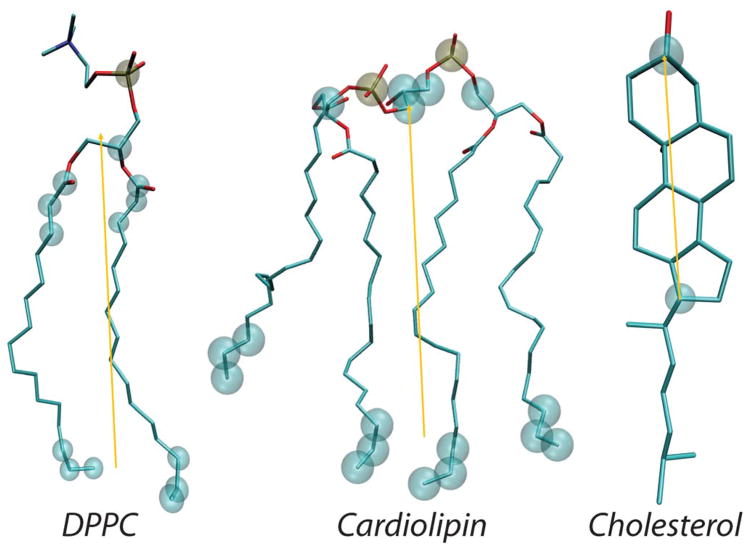
In the RSF analysis, the field of vectors normal to the membrane plane, N⃗, is first derived from the time-averaged shape of the lipid-water interface obtained from a well-equilibrated MD trajectory [35, 38, 39]. Then, fluctuations of tilt and splay degrees of freedom are sampled around this average shape. The director vector n⃗ for a lipid is defined as the vector pointing from the tail of the lipid to its head (the specific choice of the atoms for constructing n⃗ is dictated by the type of force-field used in the MD simulations to represent the lipid species, i.e. all-atom vs. coarse-grained, and the type of lipid, see Figure 1; also see Fig. 1B in Ref. [38, 39] and Fig. S2 in Ref. [35] for a visualization of the vector fields).
Figure 1.
Structures of all-atom DPPC lipid (left), cardiolipin (middle), and cholesterol (right) molecule highlighting positions of the atoms (in transparent spheres) used for definition of local director vector (yellow) definitions. For all-atom systems, the following set of atoms (in CHARMM36 force-field notations) are used: for standard two-tail phospholipids, the director vector connects the center of mass (COM) of the head-group region (defined by P, C2, C21, C22, C23, C31, C32, C33 atoms) to the COM of the last three terminal carbons in each lipid tail. For cardiolipin, the director vector joins the COM of the two phosphates (P1 and P3 atoms), the two carbon atoms attached to each of the PO4 moieties (C1, C3, C11, C31 atoms) and the central carbon atom connecting them (C2 atom), and the center of mass of the last three carbon atoms of all four chain. For cholesterol, the director vector connects C3 and C17 atoms on the ring.
Assuming independence of lipid tilt and splay degrees of freedom, we express the probabilities of lipid tilts and splays as Boltzmann distributions:
| (3) |
| (4) |
In the above, Al represents the area per lipid, and Ct and Cs are normalization constants. Eqs. (3–4) can be re-written as:
| (5) |
| (6) |
From the above, the thermodynamic tilt modulus κt and bending rigidity KC can be obtained by constructing the distributions of tilts and splays in the simulations and fitting a quadratic function to the left-hand side of Eqs. (5–6) in the regime of small splay and tilt angles. Thus κt and KC will emerge as the coefficients of the quadratic term of the best fit [35].
To proceed with the tilt modulus calculation, it is convenient, for numerical purposes, to assume the limit of small angle θ between the n⃗ and N⃗ unit vectors, so that (see also Eq. 1) [26, 40]:
Note that this limit is equivalent to the small-deformation limit, which is also the assumption that allows the neglect of higher order terms in Eq.1. Then, from Eq. (5) we can use P(θ) to write the probability of finding a lipid with its director vector at an angle θ with the local normal vector, as:
| (7) |
In the above, the sinθ factor accounts for the degeneracy of microstates for a particular value of θ [40] (i.e. the number of states accessible to a vector undergoing precession around an axis while maintaining constant polar angle θ with respect to this axis is equal to sinθ), and B is the normalization constant. Using Eq. (7), κt can be obtained from the P(θ) distribution by fitting the left-hand-side expression to a quadratic function. Note that this expression in Eq. (7) contains an additional factor of 2 in comparison to Eq. (5). This follows from the fact that for laterally isotropic systems (such as lipid monolayers in the liquid state) the tilt modulus is strictly a two-dimensional diagonal tensor with κt representing the diagonal contributions (along the x or y axes of the lateral plane) of this tensor, κt = κtxx = κyy [26]. Noting that the sum of two random variables each with Gaussian distribution of variance σ2 is a random variable with a Gaussian distribution with variance 2σ2 [35], the change in variables from t⃗2 to the scalar θ, therefore, leads to the additional factor that appears in Eq. (7).
Following a procedure similar to that described above for calculating the tilt modulus, one can obtain the bending rigidity KC from Eq. (6) by first approximating S by (∇ · α)2, where α is the angle formed by the directors of neighboring lipids, and then constructing probability distributions P(α) for all possible pairs of lipids in the system. As we discussed earlier [35], this formulation is only strictly valid in the regime of small tilt and splay angles, in the absence of lipid twist, and assuming, on average, the same distance between neighboring lipids. To overcome these restrictions, we have recently generalized the formulation to include a direct numerical calculation of the ∇(t⃗ − N⃗) divergence that appears in Eq. 6. To this end, we follow a procedure described in detail in Ref. [35] and introduce Si – the covariant derivative of the vector field t⃗ − N⃗ at point p⃗ on the membrane surface and along one direction on the membrane interface:
| (8) |
In the above, e⃗ is a unit vector tangent to the membrane, h is the distance between the lipids, and ni(p⃗) and Ni(p⃗) are the components of the lipid director and membrane normal vector fields, respectively, along e⃗.
It can then be shown [35] that the Si -s are independent variables, so that we can write their probability distributions as
| (9) |
from which we obtain
| (10) |
Therefore, the bending rigidity KC can be obtained from P(Si) by fitting a quadratic function to the left-hand-side of Eq. (10).
It must be noted that, according to Eqs. (1) and (2), κt and KC represent the monolayer tilt modulus and bending rigidity, respectively, for single-component lipid membranes where only one type of lipid can contribute to the tilt and splay degrees of freedom. For mixtures of lipids, the above formulation allows calculation of a tilt modulus for each lipid species and splay moduli for all possible (i,j) pairs of lipids. Then, κt and KC for the entire membrane can be obtained using the following empirical phenomenological expressions (see details in Ref. [37]):
| (11) |
| (12) |
where Ni denotes the number of lipids of type i, Ntot is the total number of lipids, ϕij represents the number of near neighbor (i,j) lipid pairs sampled in the MD trajectory (within the cutoff distance), and ϕtot is the number of all the lipid pairs sampled. The area per molecule, Al, for lipid mixtures is taken as the area of the unit simulation cell in the membrane plane divided by the total number of lipids per leaflet. Additional details of the RSF method and full derivations are presented in Ref. [35].
Molecular dynamics simulations
All-atomistic molecular dynamics (MD) simulations were carried out on a number of single and multi-component lipid membranes, as listed in Table 1. Two of the bilayers, POPC/POPS and POPC/POPS/Chol (see Table 1 caption for lipid definitions), have been described in Doktorova et al. (submitted manuscript). Those, as well as all other systems were built with the CHARMM-GUI web server [41–44] (see details in Table 1) and the majority of them were equilibrated using the standard multi-step equilibration protocol provided by CHARMM-GUI. The only exceptions were the large POPC, POPE/POPS and POPC/PSM bilayers which, after the initial bilayer construction were energy minimized for 10,000 steps, then simulated with a 1 fs time step for 500 ps. After these initial equilibration phases, all systems were subjected to long MD simulations (for simulation times see Table 1).
Table 1.
Lipid bilayer systems studied with atomistic MD simulations. Given are: composition of the membranes; temperature (T), total number of lipids in each system, number of water molecules per lipid, concentration of ionic solution; simulation times (total and analyzed trajectories per each system); area per lipid resulting from the simulations with corresponding standard errors calculated from consecutive 20 ns blocks; references for the corresponding experimentally determined areas per lipid compared to the simulation values in Figure 2.
| Bilayer | T (oC) | # of lipids | waters per lipid | salt (mM) | simulation time (ns) | (Å2) | References | |
|---|---|---|---|---|---|---|---|---|
| total | analysis | |||||||
| POPC a | 25 | 416 | 45 | - | 520 | 120 | 64.6±0.2 | [65, 66] |
| POPC b | 25 | 200 | 70 | 140 | 226 | 123 | 64.4±0.4 | |
| POPE | 55 | 200 | 45 | - | 190 | 102 | 60.9±0.2 | [67] |
| DLPC | 30 | 128 | 45 | - | 278 | 120 | 62.8±0.1 | [65, 68] |
| DPPC | 50 | 200 | 45 | - | 335 | 142 | 61.2±0.3 | [48, 65] |
| SOPC | 25 | 200 | 45 | - | 490 | 124 | 63.8±0.3 | [65, 69] |
| DOPC | 25 | 200 | 45 | - | 523 | 126 | 68±0.1 | [48, 70, 71] |
| DEPC | 25 | 200 | 45 | - | 680 | 92 | 64.4±0.2 | |
| TOCL | 30 | 100 | 60 | 140 | 310 | 150 | 130.3±0.3 | [52] |
| DMPC | 30 | 128 | 50 | 140 | 200 | 100 | 60.3±0.1 | [65, 68] |
| DLiPC | 25 | 200 | 45 | - | 278 | 140 | 70.3±0.1 | |
| DOPG | 25 | 200 | 60 | 140 | 246 | 122 | 71.4±0.2 | [72] |
| DPPC/Chol | 25 | 200 | 45 | - | 384 | 90 | 40.7±0.1 | |
| POPE/POPG 70:30 a | 37 | 1600 | 60 | - | 150 | 80 | 60.6±0.1 | |
| POPE/POPG 70:30 b | 37 | 200 | 60 | - | 280 | 117 | 61.1±0.3 | |
| POPC/POPS 70:30 | 20 | 140 | 45 | 50 | 191 | 100 | 60.9±0.1 | |
| POPC/POPS/Chol 34:30:36 | 20 | 200 | 45 | 50 | 270 | 180 | 43.5±0.2 | |
| POPE/POPS 70:30 a | 25 | 420 | 82 | - | 690 | 140 | 55.5±0.1 | |
| POPE/POPS 70:30 b | 25 | 200 | 70 | 140 | 208 | 129 | 55.6±0.3 | |
| POPC/PSM 70:30 a | 25 | 400 | 45 | - | 517 | 103 | 59.9±0.1 | |
| POPC/PSM 70:30 b | 25 | 200 | 70 | 140 | 229 | 126 | 59.6±0.1 | |
For several lipid compositions two independent simulations were carried out with different system sizes (denoted by superscripts “a” and “b”). Lipid name abbreviations used are as follows: POPC – 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine; POPE – 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine; DLPC – 1,2-dilauroyl-sn-glycero-3-phospho-choline; DPPC – 1,2-dipalmitoyl-sn-glycero-3-phosphocholine; SOPC – 1-stearoyl-2-oleoyl-sn-glycero-3-phosphocholine; DOPC – 1,2-dioleoyl-sn-glycero-3-phosphocholine; DEPC – 1,2-dielaidoyl-sn-glycero-3-phosphocholine; TOCL – 1′,3′-bis[1,2-dioleoyl-sn-glycero-3-phospho]-sn-glycerol (or tetraoleoyl cardiolipin); DMPC – 1,2-dimyristoyl-sn-glycero-3-phosphocholine; DLiPC – 1,2-dilinoleoyl-sn-glycero-3-phosphocholine; POPG – 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol); POPS – 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-L-serine; Chol – cholesterol; PSM – N-palmitoyl-D-erythro-sphingosyl-phosphorylcholine (or palmitoyl sphingomyelin).
All simulations were carried out with NAMD versions 2.7–2.10 [45] and using the CHARMM36 force field for lipids and ions [46]. The simulations implemented the rigidbonds all option allowing for 2 fs time step, vdwForceSwitching option, PME for electrostatic interactions, and were carried out in the NPT ensemble under semi-isotropic pressure coupling conditions, at temperatures listed in Table 1. The Nose-Hoover Langevin piston algorithm was used to control the target P = 1 atm pressure. For the POPE/POPG and DMPC bilayers, the LangevinPistonPeriod was set to 50 fs and LangevinPistonDecay was set to 25 fs. For all other bilayers LangevinPistonPeriod was set to 200 fs and LangevinPistonDecay was set to 50 fs. The van der Waals interactions were calculated by applying a cutoff distance of 12 Å and switching the potential from 10 Å. All simulations were performed on local computational resources as well as on the resources provided by XSEDE [47].
To build the DEPC bilayer, we first constructed a DOPC bilayer with CHARMM-GUI, then applied a home source tcl script to flip all double bonds between the C9 and C10 atoms on both chains of the lipids from cis to trans isomerization. The standard equilibration protocol provided from CHARMM-GUI was subsequently used by changing the constraint of the dihedral angle between the C8-C9–C10-C11 atoms to be 180 degrees (corresponding to cis isomerization), instead of 0 degrees (corresponding to trans isomerization).
Application of the RSF method to MD trajectories
For the RSF analysis we used a set of computational modules documented in detail in Refs. [38, 39] and freely available online at https://github.com/njohner/ost_pymodules/. This utility extracts P(θ) and P(S) distributions from MD simulations by first aligning the analyzed trajectories, and then generating normal N⃗ and director n⃗ vector fields using molecular definitions described earlier ([38, 39]). In particular, for all standard two-tail lipids, the director vector joins the center of mass of the last three carbon atoms of each chain to the center of mass of the phosphate and backbone carbon atoms (see Fig. 1). For cardiolipin, which possesses four hydrocarbon lipid chains, the director vector joins the center of mass of the two phosphates, the two carbon atoms attached to each of the PO4 moieties and the central carbon atom connecting them, and the center of mass of the last three carbon atoms of all four chains. The director vector for cholesterol (Chol) connects C3 and C17 atoms (see Fig. 1).
As described previously [35, 37], we restrict the calculation of splays to pairs of lipids that are near-neighbors, to maintain the validity of the numerical calculation of the lipid splay (Eq. 8) and to ensure that splays are independent. As before, we used h<10Å for the distance cut-off of all systems except for the cardiolipin membrane. Since this lipid is about twice as large as a typical phospholipid, we reasoned that 10Å cut-off would likely be too short for numerical accuracy of splay calculations. Thus, we evaluated the organization of cardiolipin molecules in the bilayer and compared it to that of DOPC lipids by means of their radial distribution functions (RDFs). The coordination number of DOPC calculated from the integral of the RDF at the default cut-off distance of 10Å was 3.6. The same coordination number for TOCL was reached at 14Å which was therefore set as the respective distance cut-off for the analysis of the cardiologic bilayer.
Once P(θ) and P(S) distributions were constructed, fitting of the quadratic functions was performed and κt and KC were obtained according to Eqs. (7) and (10). Note that, for the tilt modulus the software outputs 2κtAl or what could be described as the tilt modulus per bilayer, in units of kBT. KC is outputted per monolayer and has units of kBT.
RESULTS AND DISCUSSION
The all-atom lipid membrane systems for which bending rigidity and tilt modulus were calculated in the current work encompass membranes of different fluidities and sizes, include lipids with saturated and unsaturated lipid tails, single and multi-component lipid mixtures, as well as non-standard lipids such as cardiolipin which contains four hydrocarbon lipid tails. The wide range of physico-chemical properties represented in these membrane systems allows us to rigorously demonstrate the general applicability of the RSF method.
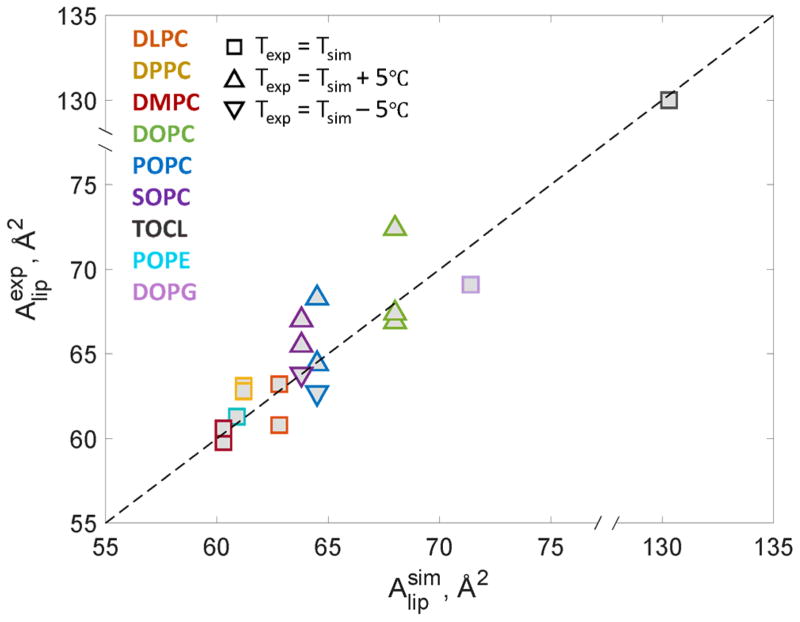
Since the RSF analysis requires well-equilibrated MD trajectories, we first confirmed that our simulations protocol, simulations times, and force-fields used produced well-behaved membranes by calculating the area per lipid ( in Table 1) for each system and comparing the values to experimentally determined reported in the literature. All experimental values come from scattering experiments and the variability among these can be attributed to differences in the underlying models used for data analysis (e.g. independent or joint analysis of neutron and X-ray scattering datasets [48]). As shown in Figure 2, experimentally and computationally derived areas are in excellent agreement, confirming that the lipid packing in the simulations was well converged.
Figure 2.
Experimentally measured area per lipid ( ) is plotted vs. area per lipid determined from the atomistic MD simulations ( ) for various single-component lipid membranes from Table 1. The data points follow near linear f(x)=x relationship (dashed line) indicating that the MD simulations are well-converged. For lipid abbreviations please see Table 1 caption and for literature references see Table 2.
In Tables 2 and 3 we report bending rigidity (KC) and thermodynamic tilt modulus (κt) values, respectively, from the RSF analysis obtained separately for each leaflet in all simulated membranes. The data shows that the bending rigidity and tilt modulus values are insensitive to the system size (e.g. KC and κt are the same, within uncertainty, for 200-lipid and 1600-lipid patches of 70:30 POPE/POPG membranes). Also, in general, the values obtained for the two bilayer leaflets are found to be within error bars. The only exceptions are several lipid mixtures, 70:30 binary POPC/POPS and POPC/PSM systems as well as 34:30:36 ternary mixture of POPC/POPS/Chol, for which we observe small, yet outside the statistical error, variations between the two leaflets. These differences are likely due to insufficient simulation times to allow for proper lipid mixing in these systems.
Table 2.
Bending rigidity (KC) values calculated from the RSF analysis of the MD simulations.
| Bilayer | KC (kBT) | ||
|---|---|---|---|
| top leaflet | bottom leaflet | bilayer | |
| POPC a | 12.3±0.5 | 12±0.4 | 24.3 |
| POPC b | 12.9±0.5 | 12.4±0.6 | 25.3 |
| POPE | 14.5±0.4 | 14.9±0.6 | 29.4 |
| DLPC | 13.4±0.6 | 12.4±0.5 | 25.8 |
| DPPC | 17.4±0.9 | 16.7±0.7 | 34.1 |
| SOPC | 13.2±0.5 | 13.2±0.5 | 26.4 |
| DOPC | 9.5±0.3 | 8.8±0.1 | 18.3 |
| DEPC | 12.1±0.4 | 12.1±0.4 | 24.2 |
| TOCL | 16.2±0.6 | 15.9±0.3 | 32.1 |
| DMPC | 17.4±0.9 | 17.3±0.8 | 34.7 |
| DLiPC | 7.9±0.1 | 8.4±0.3 | 16.3 |
| DOPG | 7.9±0.2 | 7.5±0.2 | 15.4 |
| DPPC/Chol | 66.1±2.1 | 63.9±1 | 130 |
| POPE/POPG 70:30 a | 14.1±0.3 | 14.5±0.4 | 28.6 |
| POPE/POPG 70:30 b | 14.7±0.4 | 14.2±0.3 | 28.9 |
| POPC/POPS 70:30 | 16.7±0.7 | 14±0.4 | 30.7 |
| POPC/POPS/Chol 34:30:36 | 28.6±0.4 | 33.5±0.5 | 62.1 |
| POPE/POPS 70:30 a | 20.8±0.5 | 19.7±0.4 | 40.5 |
| POPE/POPS 70:30 b | 20.2±0.5 | 20.6±0.5 | 40.8 |
| POPC/PSM 70:30 a | 15.7±0.3 | 16.8±0.5 | 32.5 |
| POPC/PSM 70:30 b | 17.3±0.6 | 16.9±0.5 | 34.2 |
Table 3.
Thermodynamic tilt modulus (κt) values calculated from the RSF analysis of the MD simulations.
| Bilayer | κt (×10−20 J/nm2) | ||
|---|---|---|---|
| top leaflet | bottom leaflet | bilayer | |
| POPC a | 4.07±0.032 | 4.07±0.032 | 8.15 |
| POPC b | 4.15±0.013 | 4.09±0.032 | 8.24 |
| POPE | 5.80±0.074 | 5.91±0.074 | 11.71 |
| DLPC | 4.13±0.067 | 4.13±0.067 | 8.26 |
| DPPC | 5.43±0.073 | 5.43±0.036 | 10.85 |
| SOPC | 4.35±0.064 | 4.29±0.032 | 8.64 |
| DOPC | 3.33±0.030 | 3.30±0.001 | 6.62 |
| DEPC | 4.05±0.032 | 4.02±0.032 | 8.08 |
| TOCL | 3.75±0.032 | 3.63±0.002 | 7.38 |
| DMPC | 4.85±0.035 | 4.85±0.001 | 9.71 |
| DLiPC | 3.04±0.003 | 3.13±0.029 | 6.17 |
| DOPG | 3.00±0.029 | 2.71±0.058 | 5.70 |
| DPPC/Chol | 13.79±0.202 | 11.17±0.606 | 24.96 |
| POPE/POPG 70:30 a | 5.22±0.035 | 5.19±0.035 | 10.41 |
| POPE/POPG 70:30 b | 5.36±0.070 | 5.29±0.035 | 10.64 |
| POPC/POPS 70:30 | 5.51±0.100 | 4.78±0.033 | 10.29 |
| POPC/POPS/Chol 34:30:36 | 12.41±0.139 | 13.20±0.139 | 25.61 |
| POPE/POPS 70:30 a | 7.26±0.074 | 7.19±0.037 | 14.45 |
| POPE/POPS 70:30 b | 7.58±0.111 | 7.66±0.074 | 15.24 |
| POPC/PSM 70:30 a | 5.53±0.069 | 5.36±0.103 | 10.88 |
| POPC/PSM 70:30 b | 5.66±0.069 | 5.76±0.104 | 11.42 |
Importantly, as we describe in the following, the material properties calculated with the RSF method are in close agreement with those obtained from experimental studies as well as from other computational approaches. We first discuss in depth the bending rigidity data followed by presentation of the tilt modulus results.
Bending rigidity from the RSF analysis
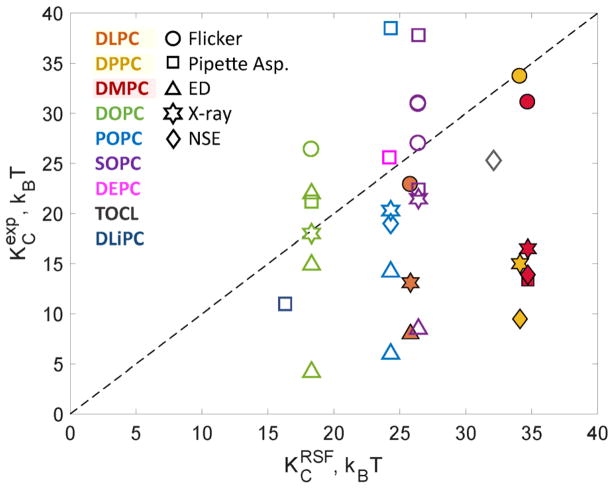
Fig. 3 compares KC values calculated from the RSF method to literature values obtained from various experimental techniques (see also Table 4). The best agreement for all simulated bilayers is with the flicker spectroscopy technique that measures rigidities by analysis of GUV shape fluctuations (denoted as circles in Fig. 3). The values obtained by electrodeformation are generally much lower and consequently deviate significantly from both the flicker and simulation results (triangles localized mostly at the bottom right of the 1-to-1 correlation line in Fig. 3). The KC values from micropipette aspiration (square symbols in Fig. 3) also correlate reasonably well with the simulation rigidities, with the exception of POPC and DMPC. It should be noted that the value for POPC was obtained by Henriksen et al. [12] after applying a modified algorithm for analyzing the micropipette aspiration data, which generally produced higher values than the ones initially reported by Rawicz et al. [11]. Indeed, the KC of SOPC reported by Henriksen et al. [13] is higher than those obtained by both Rawicz et al. and the RSF method (compare the two purple squares in Fig. 3). Regarding DMPC, Rawicz et al. measured a lower KC compared to the value obtained by the RSF analysis; yet note that micropipette aspiration measurements of KC are best performed at lower temperatures (e.g. 18 °C) that minimize evaporative loss from the sample chamber. Due to DMPC’s higher melting temperature (TM = 24°C) the measurement had to be performed at 29°C, subjecting the sample to potential hyperosmotic conditions and changes in the entrapped GUV volume.
Figure 3.
Bending rigidities per bilayer for selected systems from Table 2 determined from the atomistic MD simulations using the RSF analysis ( ) are plotted against corresponding values determined experimentally ( ). Dashed line represents f(x)=x function. Colors denote different lipids and symbols denote different experimental techniques used for measuring . Filled symbols denote all fully saturated lipids. For lipid abbreviations please see Table 1 caption and for literature references see Table 4.
Table 4.
Experimentally determined bilayer bending moduli from Figure 2 expressed as a percent difference from the simulation values, , and the corresponding literature references.
| Bilayer | Flicker | Pipette Asp. | ED | X-ray | NSE | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KC% | T | Ref. | KC% | T | Ref. | KC% | T | Ref. | KC% | T | Ref. | KC% | T | Ref. | |
| POPC | 57 | 25 | [12] | −76 −44 |
22 24 |
[14] [73] |
−19 | 30 | [66] | −23 | 22 | [19] | |||
| DLPC | −34 | 24 | [74] | −77 | 22 | [14] | −63 | 30 | [68] | ||||||
| DPPC | 0 | 50 | [74] | −56 | 50 | [75] | −71 | 60 | [18] | ||||||
| SOPC | 17 17 2 |
24 24 24 |
[9] [76] [76] |
17 44 |
18 25 |
[11] [13] |
−70 | 21 | [73] | −17 | 30 | [69] | |||
| DOPC | 42 | 23 | [15] | 15 | 18 | [11] | 20 −18 −78 |
23 23 21 |
[15] [73] [73] |
2 | 30 | [71] | |||
| DEPC | 7 | 18 | [11] | ||||||||||||
| TOCL | 25 | 30 | [52] | ||||||||||||
| DMPC | −11 | 30 | [74] | −63 | 29 | [11] | −51 | 30 | [68] | −60 | 28 | [18] | |||
| DLiPC | −33 | 18 | [11] | ||||||||||||
Shown also are the respective temperatures (T) of the experimental measurements in units of Celsius. Note that in the calculation all experimental values have been rounded from those reported in the original publications. The different techniques are designated as follows: Flicker – flicker spectroscopy; Pipette Asp. – pipette aspiration; ED – electrodeformation; X-ray – low angle diffuse X-ray scattering; NSE – neutron spin-echo.
It is interesting that the two scattering techniques, X-ray and NSE (denoted in Fig. 3 by stars and diamonds respectively), show general agreement with the simulation and flicker values for lipids possessing one or two unsaturated chains (i.e., DOPC, POPC, SOPC), but give smaller KC values for all lipids with fully saturated chains (i.e., DLPC, DMPC, DPPC). In contrast to the GUV experiments, scattering data is determined only by fluctuations at shorter (10–100Å) length scales. In this respect, it is informative to note recent work by Nagle and co-workers [49, 50] that brings into light the importance of considering lipid tilt-dependent corrections to the KC values in this dynamics regime. The importance of lipid tilt in this regime has been previously shown in silico [51] which has prompted current computational approaches based on Fourier space analysis to include this deformation mode in the derivation of the bending rigidity modulus (reviewed in [32]). Indeed, our results for κt (see below) indicate that fully saturated lipids have larger tilt moduli than the unsaturated ones, which could help explain the observed trends in the KC values determined from scattering experiments.
We also compared KC values for single-component systems obtained from the RSF analysis to bending rigidities reported from the alternative and most commonly used computational methodology based on sampling in the Fourier space of thermally excited fluctuations in the bilayer shape [32]. We found the two methods yielding consistent results for DPPC, POPE, and DMPC lipids (within 4%, 6%, and 15%, respectively). For the DOPC and POPC bilayers the discrepancies between the two approaches are larger, with the KC values obtained from the RSF method being 35% and 21% lower, respectively.
It is instructive to examine the complete data set of bending rigidities presented in Table 2 in view of the chemical structure and thermodynamic behavior of the respective lipids. First, increasing the degree of unsaturation (e.g. SOPC < DOPC < DLiPC) increases the area per lipid (63.8 < 68 < 70.3 Å2) and consequently decreases the bending rigidity (26.4 > 18.3 > 16.3 kBT) as expected. Changing the isomerization of the double bonds from cis to trans, e.g. DOPC vs. DEPC, increases KC from 18.3 to 24.2 kBT, consistent with the corresponding increase in the melting temperature from −17°C to 12°C and the subsequent decrease in area per lipid, from 68 to 64.4 Å2 at 25°C. Both DMPC and DPPC have similar bending rigidities (34.7 vs. 34.1 kBT) at 30 and 50°C, respectively, consistent with their similar reduced temperatures, τ = (T − TM)/TM, in the simulations (TM being the melting temperature). Indeed, τ for DMPC and DPPC systems were 0.22 and 0.25, respectively.
The detailed structure of tetraoleoyl cardiolipin (TOCL), a less commonly studied lipid present in the mitochondrial membrane, was recently reported from scattering experiments [52]. The area per lipid from our simulations performed under the same conditions as the experiments (i.e. at 30°C and at 140 mM NaCl), was 130.3 Å2, in excellent agreement with the experimental result of 129.8 Å2. The bending rigidity obtained with the RSF method was 32.1 kBT, about 27% higher than the KC measured with the NSE technique, which we found generally to underestimate KC for the other lipids as well when compared to the RSF values (see Fig. 3). Since TOCL has four oleoyl chains (i.e. 18 carbon long with one double bond), and two phosphate moieties connected by a single glycerol headgroup (see Fig. 1), it chemically resembles two linked DOPG lipids. Indeed, we found that while DOPG area per lipid was a little over half that of TOCL (71.4 vs 130.3 Å2), its KC was 15.4 kBT, exactly half the KC of TOCL.
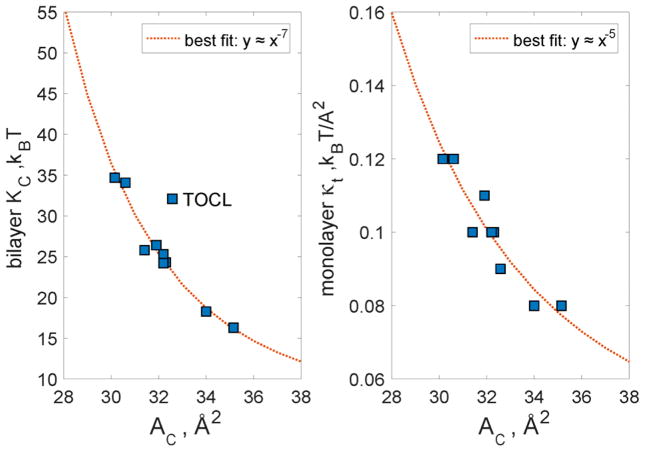
In addition to illustrating the relationship between experimental and simulation bending moduli, Fig. 3 also shows an interesting clustering of the RSF-based KC values in 3 groups with increasing average KC: 1) DOPC and DLiPC, 2) DLPC, DEPC, POPC and SOPC, and 3) DMPC and DPPC. While there are no apparent structural features (chain length, saturation) that connect the lipids within each of these groups, we reasoned that the observed clustering could be based on area per lipid. Indeed, as shown in Figure 4 (left panel), the grouping is very apparent when the KC values are plotted against area per lipid chain, AC (the area per lipid divided by the number of lipid chains). Importantly, when the data was fitted using a power law relation , the simulation values were best fit by the curve with α≈7 exponent, the exact scaling predicted between KC and AC by Szleifer et al from theoretical mean field calculations (Fig. 13c in Ref. [53]). This analysis indicates that the bilayer bending rigidity is influenced mostly by the packing of the lipid chains (or similarly, the area per lipid) and not by other generic lipid properties such as chain length and unsaturation.
Figure 4.
Values for KC (left panel) and κt (right panel) calculated from the RSF analysis plotted against the respective areas per chain (AC) for all lipid bilayers from Fig. 3. The data was fit using a power law form and the best fit is shown as a dotted line. For KC, the best fit parameters were: c1=1.972e+12, c2=6.904, and α=7.328; For κt we found the best fit with: c1=1.903e+06, c2=0.03802, and α=4.971. The apparent outlier, TOCL was excluded from the fitting procedure on the left panel. The optimal scaling parameters reported in the legends of the two panels match earlier predictions from computational mean field theory for the respective relationships [26, 53]. See text for details.
Our simulations also allow us to examine the effect of charged lipids on KC. Theoretical considerations predict an increase in bending rigidity in the presence of charged lipids due to stronger repulsion between the lipid headgroups [54–56] while experimental measurements are scarce and report conflicting trends [20, 57–60]. From our simulations, we find that DOPG in 140 mM NaCl has lower bending rigidity than DOPC (15.4 vs 18.3 kBT, respectively). While this observation does not correspond to the theoretically expected membrane stiffening, it does correlate well with the larger area per lipid of DOPG versus DOPC, suggesting that possibly membrane thinning could be a decisive consequence of headgroup charging that leads to the apparent softening of the charged membrane. At the same time, while POPE has a KC of 29.4 kBT at 55°C and is expected to have higher rigidity at lower temperatures, addition of 30 mol% POPG at 37°C slightly lowers the bilayer KC to 28.8 kBT. We must note however, that POPG has a lower melting temperature than POPE (−2°C vs 25°C, respectively) and the addition of a lower melting temperature lipid to a bilayer would naturally act to decrease KC. On the other hand, adding PS (which bears the same negative charge as PG) appears to increase somewhat the bending rigidity of the bilayer (compare POPC with POPC/POPS and POPE with POPE/POPS). In contrast to PG lipids, which have similar melting temperatures as their corresponding PC lipids with the same chains (e.g. DOPG and DOPC), PS lipids are characterized by melting temperatures that are higher from their PC counterparts (e.g. 14°C and −2°C for POPS and POPC, respectively). As a result, the lipid packing and consequently the surface charge density in PS-containing bilayer mixtures can be higher from those in PG-containing bilayers. Thus, the effect of charged lipids on bilayer KC is expected to depend not only on the amount of charge carried by the lipid headgroup (in addition to the salt concentration of the solvent) but also on the general chemical structure of the lipid, and can hardly be generalized to different lipid types.
The RSF method further quantifies the increase of KC upon addition of cholesterol and high melting lipids. Replacing 36 mol% of POPC in a POPC/POPS 0.7/0.3 bilayer with Chol increased the membrane rigidity two-fold, from 30.7 to 62.1 kBT. For comparison, a POPC bilayer with similar amounts of Chol was found to have KC in the range 27 – 86.8 kBT with different experimental techniques [12, 19]. Addition of 30 mol% of palmitoyl sphingomyelin (PSM) to a POPC bilayer also increased KC by 34%, as expected from the higher melting temperature of PSM relative to POPC (42 vs −2 °C).
Due to the local nature of the lipid splays calculations, the RSF method can also be applied to simulation trajectories of highly ordered lipid bilayers, whose global thermal fluctuations are suppressed on the time scale of the simulation, and thus are not tractable by the computational methods that seek to determine membrane elastic properties from Fourier-space analysis. Indeed, we have previously shown that the bending rigidity of liquid ordered bilayers calculated from the RSF method was in good agreement with the experimentally determined KC values [37]. Here, we report the bending modulus of a very ordered gel-like DPPC bilayer with 20 mol% Chol at 25°C. The resulting KC of 130 kBT, is much higher than the KC of any of the other examined bilayers and is comparable to the experimentally determined rigidities of SM:Chol mixtures [15] and liquid ordered phases [61, 62].
Collectively, these results demonstrate the direct applicability of the RSF method to a wide range of lipids and lipid mixtures as the calculated bending rigidities are in good agreement with experiments and successfully reproduce expected trends in bilayer mechanical properties based on considerations of the known physical and chemical characteristics of the lipids.
Thermodynamic tilt modulus from the RSF analysis
The thermodynamic tilt modulus κt was first introduced into Helfrich-Evans-Canham theory of elasticity by Kozlov and Hamm as a parameter that describes the extent of the resistance of a lipid monolayer to lipid tilt deformations [63] (see Eq. 1). In subsequent work ([26]), May et al. derived a simple relationship between the tilt modulus κt, and the tilt vector fluctuations:
| (13) |
Accordingly, κt was estimated using a molecular-level chain-packing mean field theory, from the probability distribution function of chain conformations in the monolayer. In the RSF analysis, we follow a somewhat similar methodology in that we determine κt from the probability distribution function of the lipid tilt degree of freedom sampled in MD simulations. The resulting values, presented in Table 3, are in general agreement with the 4.0–8.0 × 10−20 J/nm2 range of the thermodynamic tilt modulus per monolayer predicted from the chain-packing theory [26], and exhibit high correlation with the bending rigidity values from Table 2 (with Pearson correlation coefficient 0.8). Indeed, similar to the trends observed in bending rigidity, κt values are smallest for lipids with unsaturated tails, such as DOPC, DLiPC, and DOPG and increase in magnitude with increasing lipid tail saturation. Interestingly, for TOCL, which contains 4 unsaturated lipid tails, we find a relatively low κt, whereas the bending rigidity for TOCL was comparable to that of other saturated lipids, such as DPPC and DMPC.
To better evaluate the observed trends in κt, we plotted the thermodynamic tilt modulus against AC (area per lipid chain). Similar to the bending rigidity, we found a clear relation between the tilt modulus and AC (Fig. 4, right panel). Importantly, the data could be fitted by functional form with α ≈ 5 – a relationship very similar to that predicted by May et al from theoretical mean field calculations (Fig. 6 in Ref. [26]).
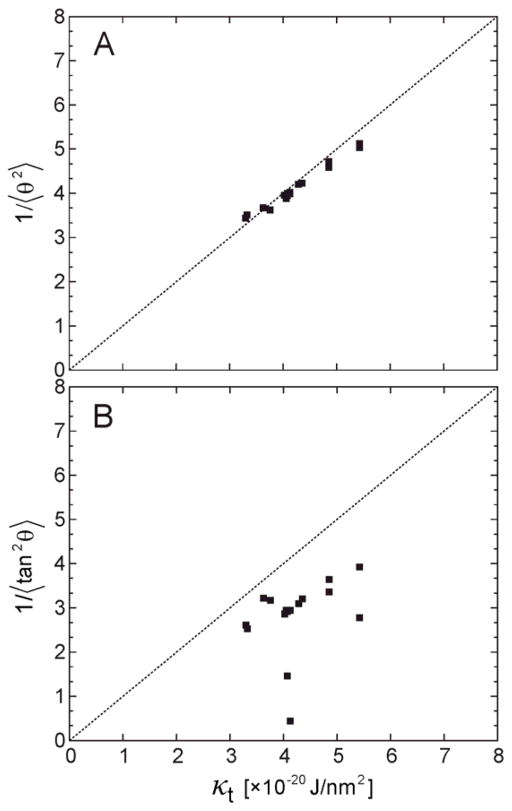
In order to further validate the κt values as obtained from the RSF analysis, we computed the thermodynamic tilt modulus in an alternative way, by directly using the equality in Eq. (13). To this end, we calculated the right-hand-side of Eq. (13) by first expressing t⃗2either by tan2 θ or by approximating it as θ2 (i.e., taking the small angle approximation), and then computed 1/〈tan2 θ〉 and 1/〈θ2〉 quantities from the P(θ) probability distributions using:
| (14) |
| (15) |
The results (converted to kBT/Al units using Eq. (13)) were then plotted against κt values from Table 3. As illustrated in Figure 5A, the κt values are nearly identical to 1/〈θ2〉 for all membrane systems tested. On the other hand, as shown in Fig. 5B, 1/〈tan2 θ〉 values are systematically lower than the tilt moduli values calculated from Eq. (7) (or compared to 1/〈θ2〉). This result is not surprising given the fundamental assumption of the underlying theory, which approximates free energy contribution of the lipid tilt as a quadratic function (see Eq. (1)), an assumption that is strictly valid only in the limit of small tilt angles where tanθ and θ are equivalent. Indeed, including sampling outside the small tilt regime, where tanθ function deviates strongly from θ, leads to inconsistent values for the tilt modulus. Altogether, the data in Fig. 5 provide additional support for the low-angle fitting procedure implemented in the RSF analysis for obtaining κt.
Figure 5.
Correlation between the thermodynamic tilt modulus (κt) determined from the RFS analysis and 1/〈θ2〉(A) and 1/〈tan2 θ〉 (B). All measures are per monolayer and given in the units of [×10−20 J/nm2]. Symbols represent data per each leaflet for all single component systems from Table 2. 〈θ2〉 and 〈tan2 θ〉 were obtained from the respective P(θ) distributions, see text. Dashed line represents f(x)=x function.
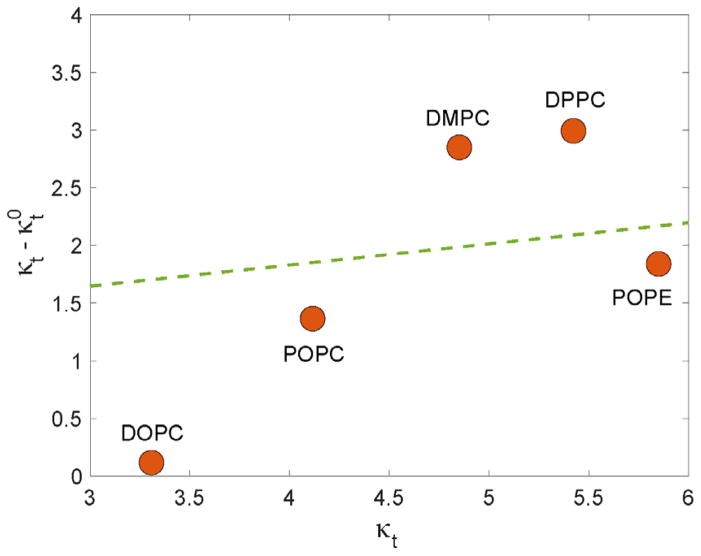
Next, we sought to compare κt values from the RSF method to the tilt moduli reported from computational studies based on the spectral analysis (SA) of MD simulations performed in the reciprocal space [32]. In this context, it is important to note that the SA approach derives a somewhat different tilt modulus parameter, sometimes termed the theoretical tilt modulus [21] (also referred to as the elastic contribution to the tilt modulus [26]), which we denote here by κt0 (following the notation in Ref. [26]). As described in Ref. [26] and extensively reviewed in Ref. [21], the two moduli κt and κt0 are inequivalent. According to Ref. [26], κt0 was interpreted as a contribution to the thermodynamic tilt modulus that arises from stretching of lipid chains when lipids are tilted and the following phenomenological expression was suggested to relate the two moduli:
| (16) |
where the second term on the right-hand side of Eq. (16) quantifies contributions from losses in the orientational entropy (OE) experienced by a tilted lipid chain. Using molecular level chain packing theory, May et al predicted [26] that for typical lipids (i.e. with area per lipid in the range of 60–70 Å2) the two contributions to the thermodynamic tilt modulus would be approximately equal, suggesting that κt0 is roughly half of κt since it was calculated in the model to be ~2×10−20 J/nm2 (assuming 60Å2 area per lipid in the expression κOE =3kBT/Al as proposed in Ref. [26] ). An alternative model was proposed by Nagle et al. [21], which argued that the difference between the two moduli should depend on the value of κt0 (or κt). Indeed, according to this model, the difference between the κt and κt0 moduli grows as the magnitude of the tilt modulus itself increases. This trend is illustrated in Figure 6 as a dashed line within the typical range of 3.0 – 6.0 ×10−20 J/nm2 of κt.
Figure 6.
Differences between the thermodynamic tilt modulus calculated from the RSF analysis (κt) and the theoretical tilt modulus obtained from the spectral analysis (κt0) as a function of κt for selected single component membrane systems. The dashed line corresponds to the model prediction by Nagle et al. (Ref. [21]). All reported values are per monolayer and given in units of [×10−20 J/nm2].
In order to compare the values of κt from Table 3 to published κt0 values obtained from the SA method (Ref. [32]), we calculated the differences between the two moduli, , as a function of the thermodynamic tilt modulus. It must be noted that the force fields as well as simulation protocol used in Ref. [32] and in the current work are practically identical, thereby allowing for direct comparison of the two sets of data (i.e. from the RSF and SA analyses). As shown in Fig. 6 (symbols) we find that Δκ strongly depends on the level of lipid saturation. Thus, Δκ decreases with the extent of chain saturation such that ΔκDPPC,DMPC > ΔκPOPC,POPE > ΔκDOPC. This progression is interesting considering Eq. (16) which suggests that Δκ differences presented in Fig. 6 should be closely related to the entropic losses of the orientational degrees of freedom as lipids are tilted. Indeed, a lipid directed on average along the normal to the surface has 2π to explore. A chain that is tilted is necessarily constrained because the average tilt angle is nonzero, so states with specific tilt should get more weight. Stated differently, any deviation from zero means a departure from the totally random configuration – so it necessarily entails entropic loss.
Thus, the data in Fig. 6 suggests that the loss in orientational entropy upon lipid tilt is the largest for lipids with saturated tails and decreases with the degree of unsaturation. This trend can be rationalized by the fact that the orientational entropy of unsaturated lipid tails is larger than that of the saturated lipids even in the conformations where lipid director vector on average remains aligned with the membrane normal. Therefore, a tilt of a saturated lipid molecule away from the normal will bring about larger losses in the orientational entropy than a tilt of an unsaturated lipid. Stated differently, the orientational entropic cost of tilting is lower for lipids with unsaturated chains than for lipids with saturated chains, potentially because this entropy was lower already in the untilted state due to the larger conformational constraints. A more quantitative exploration of this point would require additional computational analysis.
From Fig. 6, it is also apparent that for pairs of lipids with similar extent of chain saturation, such as DPPC and DMPC, or POPC and POPE, Δκ increases moderately with increasing κt. This observation is in general agreement with the trend in Δκ suggested by the model of Nagle et al. (see dashed line in Fig. 6), however from Fig. 6 it also follows that the ratio between the two moduli can take a wide range of values that depends sensitively on the lipid properties, most notably the degree of saturation. While it is yet unclear what is the exact link between the κt and κt0, from the above analysis as well as from the works by May et al. [26] and Nagle et al. [21], it is now apparent that not only is the relationship between κt and κt0 strongly dependent on the underlying model, but that the various methodologies report on distinctly different tilt moduli. While addressing this issue in depth goes beyond the scope of the current work, the analyses presented here provide an important framework to connect the tilt modulus obtained from the RSF approach to the tilt modulus calculated from alternative methodologies, as well as to the different free energy terms that contribute to it directly.
CONCLUSIONS
In conclusion, we have applied the RSF method to MD trajectories from a large set of lipid membranes encompassing a wide range of lipid types and biophysical properties. Moreover, we have rigorously demonstrated the applicability of the RSF approach to quantify elastic properties of lipid bilayers, such as the tilt modulus and bending rigidity, and discussed how different definitions of the tilt modulus appearing in the current literature could be related to each other. Due to the local nature of the analysis, the RSF method has already proven to be a unique computational tool to treat lipid mixtures or curved lipid assemblies. The method is now perfectly set to tackle future applications of even more complex systems that could include asymmetric membranes, phase-separated lipid mixtures [64], as well as protein-decorated membranes.
Acknowledgments
GK is supported by HRH Prince Alwaleed Bin Talal Bin Abdulaziz Alsaud Institute of Computational Biomedicine at Weill Medical College of Cornell University. MD is supported by NIH grant PO1DA012408. The Fritz Haber Research Center is supported by the Minerva Foundation, Munich, Germany. This work used the Extreme Science and Engineering Discovery Environment (XSEDE, accounts TG-MCB150040 and TG-MCB130010), which is supported by National Science Foundation grant number ACI-1053575. Some of the simulations and computational analysis have been carried out using computational resources of the David A. Cofrin Center for Biomedical Information in the HRH Prince Alwaleed Bin Talal Bin Abdulaziz Alsaud Institute for Computational Biomedicine at Weill Cornell Medical College.
References
- 1.Simunovic M, et al. When Physics Takes Over: BAR Proteins and Membrane Curvature. Trends in Cell Biology. 2015;25(12):780–792. doi: 10.1016/j.tcb.2015.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Phillips R, et al. Emerging roles for lipids in shaping membrane-protein function. Nature. 2009;459(7245):379–85. doi: 10.1038/nature08147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lundbaek JA, et al. Lipid bilayer regulation of membrane protein function: gramicidin channels as molecular force probes. J R Soc Interface. 2010;7(44):373–95. doi: 10.1098/rsif.2009.0443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mondal S, Khelashvili G, Weinstein H. Not Just an Oil Slick: How the Energetics of Protein-Membrane Interactions Impacts the Function and Organization of Transmembrane Proteins. Biophysical Journal. 2014;106(11):2305–2316. doi: 10.1016/j.bpj.2014.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z Naturforsch C. 1973;28(11):693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 6.Faucon JF, et al. Bending Elasticity and Thermal Fluctuations of Lipid-Membranes - Theoretical and Experimental Requirements. Journal De Physique. 1989;50(17):2389–2414. [Google Scholar]
- 7.Engelhardt H, Duwe HP, Sackmann E. Bilayer Bending Elasticity Measured by Fourier-Analysis of Thermally Excited Surface Undulations of Flaccid Vesicles. Journal De Physique Lettres. 1985;46(8):L395–L400. [Google Scholar]
- 8.Schneider MB, Jenkins JT, Webb WW. Thermal fluctuations of large cylindrical phospholipid vesicles. Biophys J. 1984;45(5):891–9. doi: 10.1016/S0006-3495(84)84235-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pecreaux J, et al. Refined contour analysis of giant unilamellar vesicles. Eur Phys J E Soft Matter. 2004;13(3):277–90. doi: 10.1140/epje/i2004-10001-9. [DOI] [PubMed] [Google Scholar]
- 10.Evans E, Rawicz W, Smith BA. Concluding remarks Back to the future: mechanics and thermodynamics of lipid biomembranes. Faraday Discussions. 2013;161:591–611. doi: 10.1039/c2fd20127e. [DOI] [PubMed] [Google Scholar]
- 11.Rawicz W, et al. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys J. 2000;79(1):328–39. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Henriksen J, Rowat AC, Ipsen JH. Vesicle fluctuation analysis of the effects of sterols on membrane bending rigidity. European Biophysics Journal with Biophysics Letters. 2004;33(8):732–741. doi: 10.1007/s00249-004-0420-5. [DOI] [PubMed] [Google Scholar]
- 13.Henriksen JR, Ipsen JH. Measurement of membrane elasticity by micro-pipette aspiration. European Physical Journal E. 2004;14(2):149–167. doi: 10.1140/epje/i2003-10146-y. [DOI] [PubMed] [Google Scholar]
- 14.Kummrow M, Helfrich W. Deformation of Giant Lipid Vesicles by Electric-Fields. Physical Review A. 1991;44(12):8356–8360. doi: 10.1103/physreva.44.8356. [DOI] [PubMed] [Google Scholar]
- 15.Gracia RS, et al. Effect of cholesterol on the rigidity of saturated and unsaturated membranes: fluctuation and electrodeformation analysis of giant vesicles. Soft Matter. 2010;6(7):1472–1482. [Google Scholar]
- 16.Lyatskaya Y, et al. Method for obtaining structure and interactions from oriented lipid bilayers. Phys Rev E Stat Nonlin Soft Matter Phys. 2001;63(1 Pt 1):011907. doi: 10.1103/PhysRevE.63.011907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu Y, Nagle JF. Diffuse scattering provides material parameters and electron density profiles of biomembranes. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;69(4 Pt 1):040901. doi: 10.1103/PhysRevE.69.040901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yi Z, Nagao M, Bossev DP. Bending elasticity of saturated and monounsaturated phospholipid membranes studied by the neutron spin echo technique. J Phys Condens Matter. 2009;21(15):155104. doi: 10.1088/0953-8984/21/15/155104. [DOI] [PubMed] [Google Scholar]
- 19.Arriaga LR, et al. Stiffening effect of cholesterol on disordered lipid phases: a combined neutron spin echo + dynamic light scattering analysis of the bending elasticity of large unilamellar vesicles. Biophys J. 2009;96(9):3629–37. doi: 10.1016/j.bpj.2009.01.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dimova R. Recent developments in the field of bending rigidity measurements on membranes. Adv Colloid Interface Sci. 2014;208:225–34. doi: 10.1016/j.cis.2014.03.003. [DOI] [PubMed] [Google Scholar]
- 21.Nagle JF, et al. What are the true values of the bending modulus of simple lipid bilayers? Chem Phys Lipids. 2015;185:3–10. doi: 10.1016/j.chemphyslip.2014.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Marsh D. Elastic curvature constants of lipid monolayers and bilayers. Chem Phys Lipids. 2006;144(2):146–59. doi: 10.1016/j.chemphyslip.2006.08.004. [DOI] [PubMed] [Google Scholar]
- 23.Nagle JF. Introductory lecture: basic quantities in model biomembranes. Faraday Discuss. 2013;161:11–29. doi: 10.1039/c2fd20121f. discussion 113–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mell M, et al. Bending stiffness of biological membranes: what can be measured by neutron spin echo? Eur Phys J E Soft Matter. 2013;36(7):75. doi: 10.1140/epje/i2013-13075-2. [DOI] [PubMed] [Google Scholar]
- 25.Bouvrais H. Bending Rigidities of Lipid Bilayers: Their Determination and Main Inputs in Biophysical Studies. Advances in Planar Lipid Bilayers and Liposomes. 2012;1515:1–75. [Google Scholar]
- 26.May S, et al. Tilt modulus of a lipid monolayer. Eur Phys J E Soft Matter. 2004;14(3):299–308. doi: 10.1140/epje/i2004-10019-y. [DOI] [PubMed] [Google Scholar]
- 27.Lindahl E, Edholm O. Mesoscopic undulations and thickness fluctuations in lipid bilayers from molecular dynamics simulations. Biophys J. 2000;79(1):426–33. doi: 10.1016/S0006-3495(00)76304-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hofsass C, Lindahl E, Edholm O. Molecular dynamics simulations of phospholipid bilayers with cholesterol. Biophys J. 2003;84(4):2192–206. doi: 10.1016/S0006-3495(03)75025-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Levine ZA, et al. Determination of biomembrane bending moduli in fully atomistic simulations. J Am Chem Soc. 2014;136(39):13582–5. doi: 10.1021/ja507910r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Watson MC, et al. Determining biomembrane bending rigidities from simulations of modest size. Phys Rev Lett. 2012;109(2):028102. doi: 10.1103/PhysRevLett.109.028102. [DOI] [PubMed] [Google Scholar]
- 31.Watson MC, et al. Thermal fluctuations in shape, thickness, and molecular orientation in lipid bilayers. J Chem Phys. 2011;135(24):244701. doi: 10.1063/1.3660673. [DOI] [PubMed] [Google Scholar]
- 32.Venable RM, Brown FL, Pastor RW. Mechanical properties of lipid bilayers from molecular dynamics simulation. Chem Phys Lipids. 2015;192:60–74. doi: 10.1016/j.chemphyslip.2015.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang X, Deserno M. Determining the Lipid Tilt Modulus by Simulating Membrane Buckles. J Phys Chem B. 2016;120(26):6061–73. doi: 10.1021/acs.jpcb.6b02016. [DOI] [PubMed] [Google Scholar]
- 34.Hamm M, Kozlov MM. Elastic energy of tilt and bending of fluid membranes. European Physical Journal E. 2000;3(4):323–335. [Google Scholar]
- 35.Johner N, Harries D, Khelashvili G. Curvature and Lipid Packing Modulate the Elastic Properties of Lipid Assemblies: Comparing HII and Lamellar Phases. J Phys Chem Lett. 2014;5(23):4201–6. doi: 10.1021/jz5022284. [DOI] [PubMed] [Google Scholar]
- 36.Khelashvili G, et al. Molecular origins of bending rigidity in lipids with isolated and conjugated double bonds: the effect of cholesterol. Chem Phys Lipids. 2014;178:18–26. doi: 10.1016/j.chemphyslip.2013.12.012. [DOI] [PubMed] [Google Scholar]
- 37.Khelashvili G, et al. Calculating the Bending Modulus for Multicomponent Lipid Membranes in Different Thermodynamic Phases. J Chem Theory Comput. 2013;9(9):3866–3871. doi: 10.1021/ct400492e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Johner N, Harries D, Khelashvili G. Erratum to: Implementation of a methodology for determining elastic properties of lipid assemblies from molecular dynamics simulations. BMC Bioinformatics. 2016;17(1):236. doi: 10.1186/s12859-016-1091-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Johner N, Harries D, Khelashvili G. Implementation of a methodology for determining elastic properties of lipid assemblies from molecular dynamics simulations. BMC Bioinformatics. 2016;17:161. doi: 10.1186/s12859-016-1003-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kessel A, Ben-Tal N, May S. Interactions of cholesterol with lipid bilayers: the preferred configuration and fluctuations. Biophys J. 2001;81(2):643–58. doi: 10.1016/S0006-3495(01)75729-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jo S, et al. CHARMM-GUI: a web-based graphical user interface for CHARMM. J Comput Chem. 2008;29(11):1859–65. doi: 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
- 42.Lee J, et al. CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field. J Chem Theory Comput. 2016;12(1):405–13. doi: 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wu EL, et al. CHARMM-GUI Membrane Builder toward realistic biological membrane simulations. J Comput Chem. 2014;35(27):1997–2004. doi: 10.1002/jcc.23702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jo S, et al. CHARMM-GUI Membrane Builder for mixed bilayers and its application to yeast membranes. Biophys J. 2009;97(1):50–8. doi: 10.1016/j.bpj.2009.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Phillips JC, et al. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26(16):1781–802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Klauda JB, et al. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J Phys Chem B. 2010;114(23):7830–43. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Towns J, et al. XSEDE: Accelerating Scientific Discovery. Computing in Science & Engineering. 2014;16(5):62–74. [Google Scholar]
- 48.Kucerka N, et al. Lipid bilayer structure determined by the simultaneous analysis of neutron and X-ray scattering data. Biophys J. 2008;95(5):2356–67. doi: 10.1529/biophysj.108.132662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jablin MS, Akabori K, Nagle JF. Experimental support for tilt-dependent theory of biomembrane mechanics. Phys Rev Lett. 2014;113(24):248102. doi: 10.1103/PhysRevLett.113.248102. [DOI] [PubMed] [Google Scholar]
- 50.Nagle JF, Jablin MS, Tristram-Nagle S. Sugar does not affect the bending and tilt moduli of simple lipid bilayers. Chem Phys Lipids. 2016;196:76–80. doi: 10.1016/j.chemphyslip.2016.01.003. [DOI] [PubMed] [Google Scholar]
- 51.May ER, Narang A, Kopelevich DI. Role of molecular tilt in thermal fluctuations of lipid membranes. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76(2 Pt 1):021913. doi: 10.1103/PhysRevE.76.021913. [DOI] [PubMed] [Google Scholar]
- 52.Pan J, et al. Structural and mechanical properties of cardiolipin lipid bilayers determined using neutron spin echo, small angle neutron and X-ray scattering, and molecular dynamics simulations. Soft Matter. 2015;11(1):130–8. doi: 10.1039/c4sm02227k. [DOI] [PubMed] [Google Scholar]
- 53.Szleifer I, et al. Molecular Theory of Curvature Elasticity in Surfactant Films. Journal of Chemical Physics. 1990;92(11):6800–6817. [Google Scholar]
- 54.Winterhalter M, Helfrich W. Bending Elasticity of Electrically Charged Bilayers - Coupled Monolayers, Neutral Surfaces, and Balancing Stresses. Journal of Physical Chemistry. 1992;96(1):327–330. [Google Scholar]
- 55.May S. Curvature elasticity and thermodynamic stability of electrically charged membranes. Journal of Chemical Physics. 1996;105(18):8314–8323. [Google Scholar]
- 56.Andelman D. Handbook of biological physics. Elsevier; 1995. Electrostatic properties of membranes: the Poisson-Boltzmann theory; pp. 603–642. [Google Scholar]
- 57.Mertins O, Dimova R. Insights on the interactions of chitosan with phospholipid vesicles. Part II: Membrane stiffening and pore formation. Langmuir. 2013;29(47):14552–9. doi: 10.1021/la4032199. [DOI] [PubMed] [Google Scholar]
- 58.Song J, Waugh RE. Bilayer membrane bending stiffness by tether formation from mixed PC-PS lipid vesicles. J Biomech Eng. 1990;112(3):235–40. doi: 10.1115/1.2891178. [DOI] [PubMed] [Google Scholar]
- 59.Meleard P, et al. Mechanical properties of model membranes studied from shape transformations of giant vesicles. Biochimie. 1998;80(5–6):401–13. doi: 10.1016/s0300-9084(00)80008-5. [DOI] [PubMed] [Google Scholar]
- 60.Vitkova V, et al. Surface charge effect on the bending elasticity of lipid bilayers. Comptes Rendus de l’Academie Bulgare des Sciences. 2004;57(11):11–25. [Google Scholar]
- 61.Semrau S, et al. Accurate determination of elastic parameters for multicomponent membranes. Phys Rev Lett. 2008;100(8):088101. doi: 10.1103/PhysRevLett.100.088101. [DOI] [PubMed] [Google Scholar]
- 62.Nickels JD, et al. Mechanical Properties of Nanoscopic Lipid Domains. J Am Chem Soc. 2015;137(50):15772–80. doi: 10.1021/jacs.5b08894. [DOI] [PubMed] [Google Scholar]
- 63.Hamm M, Kozlov MM. Tilt model of inverted amphiphilic mesophases. European Physical Journal B. 1998;6(4):519–528. [Google Scholar]
- 64.Rosetti CM, Montich GG, Pastorino C. Molecular Insight into the Line Tension of Bilayer Membranes Containing Hybrid Polyunsaturated Lipids. J Phys Chem B. 2017;121(7):1587–1600. doi: 10.1021/acs.jpcb.6b10836. [DOI] [PubMed] [Google Scholar]
- 65.Kucerka N, Nieh MP, Katsaras J. Fluid phase lipid areas and bilayer thicknesses of commonly used phosphatidylcholines as a function of temperature. Biochim Biophys Acta. 2011;1808(11):2761–71. doi: 10.1016/j.bbamem.2011.07.022. [DOI] [PubMed] [Google Scholar]
- 66.Kucerka N, Tristram-Nagle S, Nagle JF. Structure of fully hydrated fluid phase lipid bilayers with monounsaturated chains. J Membr Biol. 2005;208(3):193–202. doi: 10.1007/s00232-005-7006-8. [DOI] [PubMed] [Google Scholar]
- 67.Kucerka N, et al. Molecular structures of fluid phosphatidylethanolamine bilayers obtained from simulation-to-experiment comparisons and experimental scattering density profiles. J Phys Chem B. 2015;119(5):1947–56. doi: 10.1021/jp511159q. [DOI] [PubMed] [Google Scholar]
- 68.Kucerka N, et al. Structure of fully hydrated fluid phase DMPC and DLPC lipid bilayers using X-ray scattering from oriented multilamellar arrays and from unilamellar vesicles. Biophys J. 2005;88(4):2626–37. doi: 10.1529/biophysj.104.056606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Greenwood AI, et al. CRAC motif peptide of the HIV-1 gp41 protein thins SOPC membranes and interacts with cholesterol. Biochim Biophys Acta. 2008;1778(4):1120–30. doi: 10.1016/j.bbamem.2008.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Kucerka N, et al. Areas of monounsaturated diacylphosphatidylcholines. Biophys J. 2009;97(7):1926–32. doi: 10.1016/j.bpj.2009.06.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Pan J, et al. Temperature dependence of structure, bending rigidity, and bilayer interactions of dioleoylphosphatidylcholine bilayers. Biophys J. 2008;94(1):117–24. doi: 10.1529/biophysj.107.115691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Pan J, et al. Revisiting the bilayer structures of fluid phase phosphatidylglycerol lipids: Accounting for exchangeable hydrogens. Biochim Biophys Acta. 2014;1838(11):2966–9. doi: 10.1016/j.bbamem.2014.08.009. [DOI] [PubMed] [Google Scholar]
- 73.Niggemann G, Kummrow M, Helfrich W. The Bending Rigidity of Phosphatidylcholine Bilayers - Dependences on Experimental-Method, Sample Cell Sealing and Temperature. Journal De Physique Ii. 1995;5(3):413–425. [Google Scholar]
- 74.Fernandez-Puente L, et al. Temperature and Chain-Length Effects on Bending Elasticity of Phosphatidylcholine Bilayers. Europhysics Letters. 1994;28(3):181–186. [Google Scholar]
- 75.Guler SD, et al. Effects of ether vs. ester linkage on lipid bilayer structure and water permeability. Chem Phys Lipids. 2009;160(1):33–44. doi: 10.1016/j.chemphyslip.2009.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Vitkova V, et al. Sugars in the aqueous phase change the mechanical properties of lipid mono- and bilayers. Molecular Crystals and Liquid Crystals. 2006;449:95–106. [Google Scholar]