Eavesdropping and animal conflict

Abstract

Fights between pairs of animals frequently take place within a wider social context. The displays exchanged during conflict, and the outcome of an encounter, are often detectable by individuals who are not immediately involved. In at least some species, such bystanders are known to eavesdrop on contests between others, and to modify their behavior toward the contestants in response to the observed interaction. Here, I extend Maynard Smith's well known model of animal aggression, the Hawk–Dove game, to incorporate the possibility of eavesdroppers. I show that some eavesdropping is favored whenever the cost of losing an escalated fight exceeds the value of the contested resource, and that its equilibrium frequency is greatest when costs are relatively high. Eavesdropping reduces the risk of escalated conflict relative to that expected by chance, given the level of aggression in the population. However, it also promotes increased aggression, because it enhances the value of victory. The net result is that escalated conflicts are predicted to occur more frequently when eavesdropping is possible.

Evolutionary biologists interested in animal aggression typically focus on pairwise interactions (1). Yet such contests take place within a wider social environment. The agonistic displays exchanged during a fight, and the outcome of the encounter, are often detectable by neighbors who are not directly involved (2–13). Because fighting a dangerous opponent can entail substantial risks, we might expect selection to favor individuals who gather information from interactions between others. Eavesdropping, as this behavior has been called (4), allows an animal to assess the aggression and fighting ability of potential opponents before any direct contest. In this way, an eavesdropper may avoid escalated conflict with a dangerous enemy (3–5, 8, 11, 12).

Despite current interest in eavesdropping (5–13), and evidence from recent experimental studies that potential competitors do attend to contests between others (7–9), this possibility has yet to be incorporated in models of conflict behavior. Here, I extend Maynard Smith's classic, game-theoretical model of animal aggression, the Hawk–Dove game (14), to incorporate eavesdropping.

The basic Hawk–Dove game allows for two strategies or types of player, “hawk” and “dove.” Aggressive hawks do well when rare, because they defeat cautious doves when contesting a resource. Hawks do poorly when common, however, because two aggressive individuals who encounter one another become embroiled in an escalated and costly fight. If the cost of fighting is great enough, the game thus yields a mixed equilibrium featuring both strategies. In this context, it seems likely that selection will favor eavesdroppers who attend to the outcome of contests between others, because the information they have gathered may allow them to determine whether they face an aggressive or cautious opponent (and thereby avoid a costly, escalated fight). Below, I explore the conditions under which selection will favor eavesdropping in the Hawk–Dove game, and the consequences this tactic has for the evolution of aggressive behavior. The methods I adopt are similar to those used in recent analyses of cooperation that incorporate “image scoring” or “indirect reciprocity” (15, 16).

Eavesdropping in the Hawk–Dove Game

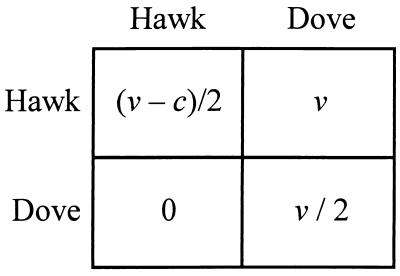
The model deals with repeated aggressive interactions among a population of individuals, over a large number of rounds. In every round, members of the population are paired at random, and each pair plays a single bout of the Hawk–Dove game: each individual must choose to play hawk (i.e., to escalate) or to play dove (i.e., to rely on ritualized display, and back down in the face of escalated aggression). The two then obtain the payoffs shown in Fig. 1. As indicated in the payoff matrix, the (additive) fitness value of victory is v, and the (additive) fitness cost of defeat in an escalated contest is c. An individual who plays hawk always defeats an opponent who plays dove, whereas contestants who adopt the same course of action are both equally likely to win (or to lose) the fight. I will assume that 0 < v < c, the condition for a mixed equilibrium in the basic Hawk–Dove game.

Figure 1.

Payoff matrix for the Hawk–Dove game (focal player's strategies are listed vertically down the left-hand side and opponent's are listed horizontally along the top).

I consider three possible strategies or types of player: hawks and doves always adopt the tactic for which they are named; eavesdroppers, by contrast, play hawk when facing an opponent who lost in the previous round and dove when facing an opponent who won (I thus assume that eavesdroppers have a “memory” of only one round and do not track the success of others over a longer time period).

Let f_H denote the frequency of hawks in the population, f_D the frequency of doves, and f_E the frequency of eavesdroppers (so that f_H + f_D + f_E = 1). Further, let p_H(n), p_D(n), and p_E(n) denote the proportion of hawks, doves, and eavesdroppers in the nth round who won their last fight. These proportions will change from one round to the next according to the following difference equations:

1a

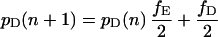1b

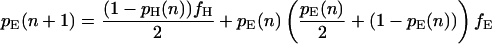1c

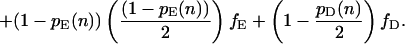Each difference equation is obtained by summing the probabilities of victory for an individual of the relevant type when facing all possible types of opponent, weighted according to the probability with which each is encountered (note that having obtained victory probabilities for any two of the three types in this way, the probability of victory for the remaining type may be derived from the requirement that the overall proportion of winners in any one round equals 0.5).

From Eq. 1 a–c, it follows that the proportions of the three types that were victorious in their last encounter rapidly converge to p_H, p_D, and p_E, given by

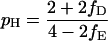2a

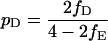2b

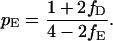2c

Consequently, the expected payoffs that individuals of the three types obtain in round n, denoted W_H(n), W_D(n), and W_E(n), converge to the values W_H, W_D, and W_E given by

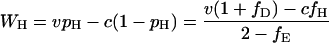3a

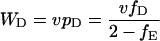3b

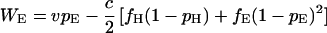3c

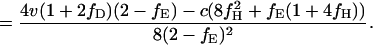The average payoff per round that hawks obtain, over the course of n rounds, is equal to (1/n)Σ W_H (n). As the number of rounds played increases, this average payoff also converges, although more slowly, to W_H (i.e., lim_n→∞(1/n)Σ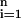 W_H(i) = W_H), and the equivalent is true for W_D and W_E. Consequently, assuming that a large number of rounds are played, we may take W_H, W_D, and W_E as the fitness of each of the three strategies.

By using Eq. 3 a–c, one can thus investigate the evolution of the frequencies of the three types under the influence of selection. To do so, I use the continuous replicator dynamics (17)

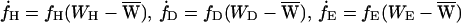4

on the simplex S₃ = {f = (f_H, f_D, f_E) ∈ ℛ³:f_x ≥ 0, Σf_x = 1}, where 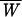(= f_HW_H + f_DW_D + f_EW_E) is the mean fitness of individuals in the population.

Under this dynamic (and given the assumption that 0 < v < c), there exists a unique fixed point f* = (f^*_H, f^*_D, f^*_E) in the interior of S₃ (i.e., at which all three types are present):

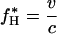5a

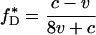5b

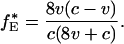5c

One can show that (f^*_H − f_H)W_H + (f^*_D − f_D)W_D + (f^*_E − f_E)W_E > 0 for (f_H, f_D, f_E) ≠ f*. From this, it follows that f^*_H log f_H + f^*_D log f_D + f^*_E log f_E is a monotonically increasing global Lyapunov function for the continuous replicator dynamic within the interior of S₃ (17). Consequently, f* represents a globally stable rest point within the interior of the simplex.

There are additional fixed points on the boundary of the simplex S₃ [three at the corners of the simplex that feature a single type; two on the edges f_E = 0 and f_D = 0 that feature a mixture of hawks and doves or of hawks and eavesdroppers; and for (v/c) < 0.25, one on the edge f_H = 0 that features a mixture of eavesdroppers and doves]; however, these fixed points are all unstable, because a population of a single type or a mixed equilibrium featuring two is always vulnerable to invasion by one or both of the remaining strategies. Allowing for occasional mutation, f* thus represents the only stable outcome of selection.

The model, as I have described it, assumes that eavesdroppers are informed perfectly as to the outcome of their opponent's last fight. In reality, however, there are likely to be constraints on the reliability of assessment, such as the difficulty of tracking and discriminating between many individuals in a large population, particularly when several interactions may be occurring at one time (4, 12). However, the analysis can be extended easily to consider imperfect eavesdropping. To do so, I assume that with probability m (where 0 ≤ m < 0.5), an eavesdropper adopts an inappropriate response to its opponent, i.e., plays dove against an individual that lost its last fight or hawk against an individual that won. I will not give the expressions for the equilibrium frequencies of the three strategies under these circumstances, because they are rather lengthy. However, the influence of error on the outcome of selection is illustrated graphically in the next section.

Results and Discussion

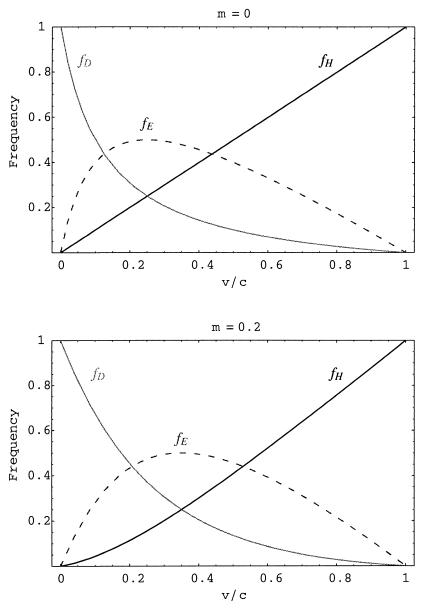
Fig. 2 shows the frequencies of hawks, doves, and eavesdroppers at the equilibrium f*, as a function of the value of victory (v) relative to the cost of losing (c), both for perfect and for imperfect eavesdropping. Comparing these values with the outcome of the basic Hawk–Dove game, when eavesdropping is perfect the frequency of hawks is unchanged (v/c), whereas eavesdroppers replace a certain fraction of the doves. The frequency of eavesdroppers reaches a peak of 0.5 when v/c = 0.25. When eavesdropping is imperfect, in this case when m = 0.2, the frequency of hawks is slightly reduced compared with the basic Hawk–Dove game, and the frequency of eavesdroppers peaks at a higher value of v/c = 0.35. Thus the model upholds suggestions that eavesdropping is most likely when the costs of fighting are relatively high (3, 8, 11), although the less reliable eavesdroppers are, the lower the cost of fighting at which they reach peak frequency.

Figure 2.

Equilibrium frequencies of hawks (f_H), doves (f_D), and eavesdroppers (f_E), as a function of the value of victory relative to the cost of losing an escalated fight (v/c), for perfect eavesdropping (i.e., m = 0; Upper) and for imperfect eavesdropping (m = 0.2; Lower).

Why is it that eavesdropping does not spread to fixation? When rare, eavesdroppers prosper because they are able to anticipate the behavior of their opponents. The behavior of hawks and doves is predictable (to some degree) on the basis of the outcome of their last fight, because they consistently use the same strategy in each round. Eavesdroppers themselves, however, do not behave consistently. Instead, the tactic that an eavesdropper adopts changes from one round to the next, according to whether each successive opponent it faces won or lost in the previous round. Consequently, one eavesdropper cannot anticipate the behavior of another. The spread of the eavesdropping strategy thus erodes the predictability on which its fitness advantage depends. The result is that eavesdropping will not spread to fixation. Rather, a mixed equilibrium is attained at which eavesdroppers coexist with hawks and doves. As can be seen in Fig. 2, the equilibrium frequency of eavesdroppers reaches a peak when the equilibrium frequencies of hawks and doves are equal to one another. Under these circumstances, eavesdropping yields the greatest amount of useful information.

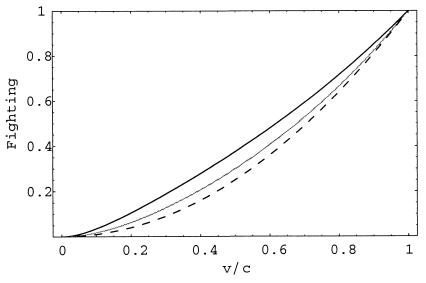
Discussions of eavesdropping have emphasized the opportunity they provide to assess the fighting ability and motivation of others, and thus to avoid conflict with a dangerous enemy (3–5, 8, 11, 12). In this light, we might expect eavesdropping to lead to a reduction in the risk of escalated conflict. However, as shown in Fig. 3, the frequency of escalated fighting (i.e., the frequency with which both opponents play hawk) is always higher in the present model than in the basic Hawk–Dove game. The lower the probability of error (i.e., the greater the accuracy and reliability of eavesdropping), the more pronounced the effect. How can we explain this surprising result?

Figure 3.

Equilibrium frequency of escalated fighting, as a function of the value of victory relative to the cost of losing an escalated fight (v/c), with error-free eavesdropping (m = 0, dark line), with imperfect eavesdropping (m = 0.2, pale line), and in the basic Hawk–Dove game without eavesdropping (dashed line).

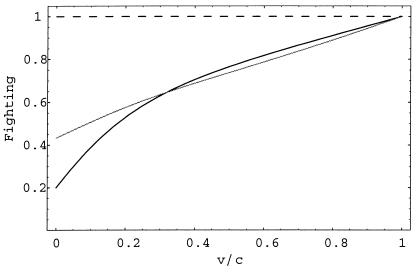
On the one hand, eavesdropping means that escalated conflict will occur less often than one would expect by chance, given the frequency of aggression. In the basic Hawk–Dove game, the probability with which two opponents both play hawk (leading to an escalated fight) is simply equal to the square of the probability that any one individual does so. When eavesdroppers are present in the population, however, the frequency of escalated fighting is lower than this value. The reason is that eavesdroppers are less likely than hawks are to play hawk against an aggressive opponent (who is more likely to have won in the previous round). This effect is illustrated in Fig. 4, which shows the frequency of costly fighting predicted by the present model relative to that expected under the assumption of random interaction (i.e., relative to the square of the probability of individual aggression).

Figure 4.

Equilibrium frequency of escalated fighting relative to random expectation (given the frequency of individual aggression), as a function of the value of victory relative to the cost of losing an escalated fight (v/c), for error-free eavesdropping (m = 0, dark line) and imperfect eavesdropping (m = 0.2, pale line) .

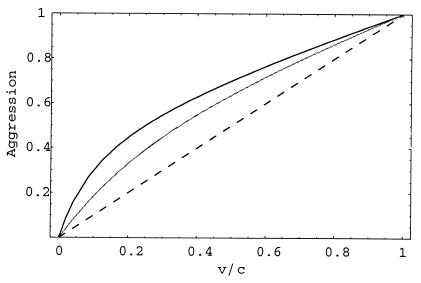
On the other hand, the model predicts that the overall frequency of individual aggression (i.e., the frequency with which individuals play hawk) will be greater in the presence of eavesdroppers, particularly when errors are rare, as shown in Fig. 5. This increase in the frequency of aggression outweighs the reduction in the risk of escalated fighting described above, giving rise to the higher frequencies of conflict illustrated in Fig. 3.

Figure 5.

Equilibrium frequency of individual aggression, as a function of the value of victory relative to the cost of losing an escalated fight (v/c), with error-free eavesdropping (m = 0, dark line), with imperfect eavesdropping (m = 0.2, pale line), and in the basic Hawk–Dove game without eavesdropping (dashed line).

Individual aggression is predicted to occur more frequently in the current model than in the basic Hawk–Dove game, because in the presence of eavesdroppers, there is an extra benefit to be gained by winning a contest. An individual that is victorious in one round is more likely to win in the next, because its opponent is less likely to mount an escalated challenge. This advantage of a positive “image” or “reputation” effectively adds to the value of the contested resource (v), and thus favors increased aggression. The effect is more pronounced when eavesdropping is more accurate—the lower the probability of error, the greater the advantage of a positive image.

As previously stated, the present model is similar in structure to recent analyses of cooperation that incorporate image scoring or indirect reciprocity (15, 16). In these analyses, “eavesdroppers” (although they are not named as such) observe potentially cooperative interactions between others, and are more likely to respond favorably to individuals who treat others favorably themselves. By contrast with eavesdropping in the present model, however, indirect reciprocity entails attending to the behavior of others rather than to the outcome of their interactions. Moreover, the effect of eavesdropping in that context is to promote cooperation and raise the mean fitness in the population.

That eavesdropping promotes conflict in the present model reflects the basic assumption of the Hawk–Dove game—the benefits of adopting aggressive tactics are lower when facing a more aggressive opponent. Under these circumstances, eavesdroppers will tend to refrain from such tactics more often when confronting the winner rather than the loser of a fight. Although this assumption is plausible (8), there are also situations in which the reverse might be true (9). In some contexts, an eavesdropper might be more aggressive to the winner than to the loser of a contest if the former poses a greater threat. The impact of eavesdropping on the evolution of aggression may therefore vary according to the use that eavesdroppers make of the information they acquire. Reduced aggression toward previously victorious opponents is likely when the costs of losing an escalated fight are high, as in the Hawk–Dove game, but this is not the only possibility.

The present model can be modified easily and extended in various ways. For example, as stated above, I have assumed that eavesdroppers attend to the outcome of interactions between others, rather than to their individual behavior. In other words, an eavesdropper will respond according to whether its opponent won or lost in the previous round, not according to whether its opponent played hawk or dove. This assumption is based on recent empirical studies, which suggest that animals respond to asymmetries in interactions between others, i.e., to whether an individual is more or less dominant than an opponent (8, 9). However, one can easily alter the model to consider the alternative possibility that eavesdroppers attend to the tactic their opponent adopted in the previous round. This is perhaps a purer form of eavesdropping, because it requires direct observation of the opponent's prior interaction (whereas it may sometimes be possible to determine whether an opponent won or lost without observing the fight, for instance by assessing the level of damage it has suffered). Attending directly to an opponent's previous action leads to greater levels of aggression and to a shift in the peak frequency of eavesdropping toward greater values of v/c, but to no qualitative change in the results.

As another instance, I have assumed that individuals differ in aggressiveness rather than in fighting ability. In reality, both kinds of variation are likely, and eavesdropping may yield information about a potential opponent's strength as well as its tendency to adopt aggressive tactics. Once again, one might extend the present model to allow for individual variation in fighting ability, or other aspects of condition; this modification would, however, yield a conditional, rather than a mixed equilibrium (18). Suppose, for instance, that the value of victory and/or the cost of losing an escalated fight vary among individuals. The model then yields a conditional equilibrium, in which individuals who suffer a high cost of losing (or enjoy a low payoff from victory) play dove, those who experience intermediate costs or benefits play eavesdropper, and those who suffer a low cost of losing (or enjoy a high payoff from victory) play hawk.

To conclude, although many modifications and extensions of the present model are possible (in addition to those discussed above, one might consider direct costs of eavesdropping or the possibility of keeping track of others' success over several encounters), it is sufficient to demonstrate that selection will often favor eavesdropping as a means to minimize the risk of escalated conflict with an aggressive opponent. Paradoxically, however, such eavesdropping may promote increased aggression and thus ultimately lead to a higher frequency of fighting. More generally, it is clear that one cannot consider pairwise contests in isolation; the tactics that opponents adopt in a fight are influenced by the wider social environment in which the fight takes place. Failure to consider this broader context can only impede our understanding of the evolution of aggression.