Control of standing posture requires fusion of multiple inputs including visual, vestibular, somatosensory, and other sensors, each having distinct dynamics. We propose that postural control also entails a shared neural integrator. To test this theory, we perturbed standing subjects with classic sensory stimuli (optokinetic and galvanic vestibular stimulation) and found that our proposed shared filter reproduces the dynamics of subjects’ postural responses.
Keywords: postural control, neural integrator, optokinetic, galvanic vestibular stimulus
Abstract
Control of standing posture requires fusion of multiple inputs including visual, vestibular, somatosensory, and other sensors, each having distinct dynamics. The semicircular canals, for example, have a unique high-pass filter response to angular velocity, quickly sensing a step change in head rotational velocity followed by a decay. To stabilize gaze direction despite this decay, the central nervous system supplies a neural “velocity storage” integrator, a filter that extends the angular velocity signal. Similar filtering might contribute temporal dynamics to posture control, as suggested by some state estimation models. However, such filtering has not been tested explicitly. We propose that posture control indeed entails a neural integrator for sensory inputs, and we test its behavior with classic sensory perturbations: a rotating optokinetic stimulus to the visual system and a galvanic vestibular stimulus to the vestibular system. A simple model illustrates how these two inputs and body tilt sensors might produce a postural tilt response in the frontal plane. The model integrates these signals through a direct weighted sum of inputs, with or without an indirect pathway containing a neural integrator. Comparison with experimental data from healthy adult subjects (N = 16) reveals that the direct weighting model alone is insufficient to explain resulting postural transients, as measured by lateral tilt of the trunk. In contrast, the neural integrator, shared by sensory signals, produces the dynamics of both optokinetic and galvanic vestibular responses. These results suggest that posture control may involve both direct and indirect pathways, which filter sensory signals and make them compatible for sensory fusion.
NEW & NOTEWORTHY Control of standing posture requires fusion of multiple inputs including visual, vestibular, somatosensory, and other sensors, each having distinct dynamics. We propose that postural control also entails a shared neural integrator. To test this theory, we perturbed standing subjects with classic sensory stimuli (optokinetic and galvanic vestibular stimulation) and found that our proposed shared filter reproduces the dynamics of subjects’ postural responses.
human posture control relies on a combination of visual, vestibular, somatosensory, and other sensory information (Young 1984). The combination of multiple inputs makes posture relatively robust to sensory and physical perturbations. For example, when a standing person is presented with a visual field (optokinetic stimulus) that rotates about the roll (naso-occipital) axis, he/she will usually begin to lean in the direction of rotation but stop short of falling over (Keshner and Kenyon 2000; Tanahashi et al. 2007). Other sensors provide additional references for body tilt that fuse with, and in part contradict, the visual input, so that the steady-state tilt appears to be a compromise between the various inputs. Another feature of the response is that it is gradual rather than immediate. A step change in the angular velocity of visual input initiates a change in body pose, which only reaches steady state after 10 or more seconds (Dichgans and Brandt 1978). This resembles a low-pass filter response, suggesting that the central nervous system (CNS) may filter incoming sensory signals. It is unknown, however, what form this filter might take, and whether it is even necessary to explain the behavior. Perhaps the dynamics of the sensors themselves are sufficient to explain the behavior without invoking a higher-order process. To resolve this question, we propose two models of sensory integration, with and without a filter. We compare model predictions to experimental data to determine whether filtering can explain how humans combine sensory information.
Evidence of CNS filtering is also observed in postural responses to a vestibular stimulus. Galvanic vestibular stimulation refers to a direct current applied to the mastoid processes that affects the vestibular nerve (e.g., Fitzpatrick and Day 2004; Nashner and Wolfson 1974). A step change in current produces a postural response somewhat complementary to that of optokinetic stimulus, such that the body immediately tilts to the side. If the step is prolonged, this is followed by a gradual return to upright stance (Fig. 1), again taking some tens of seconds (e.g., Fransson et al. 2003; Séverac Cauquil et al. 1998), reminiscent of the optokinetic response. This cannot be explained by the step stimulus, which is immediate, nor by the dynamics of vision and the somatosensors, which also have relatively faster dynamics and time delays (Young 1981, 1984). The semicircular canals do have slower, high-pass filter characteristics, where a step change in angular velocity causes a sudden response that decays with a time constant of ~7 s (Cohen et al. 1981; Robinson 1981). However, galvanic vestibular stimulation appears to act on the vestibular nerve rather than the canals (Goldberg et al. 1984), suggesting that the slow return here is attributable to the CNS rather than the dynamics of the semicircular canals.
Fig. 1.
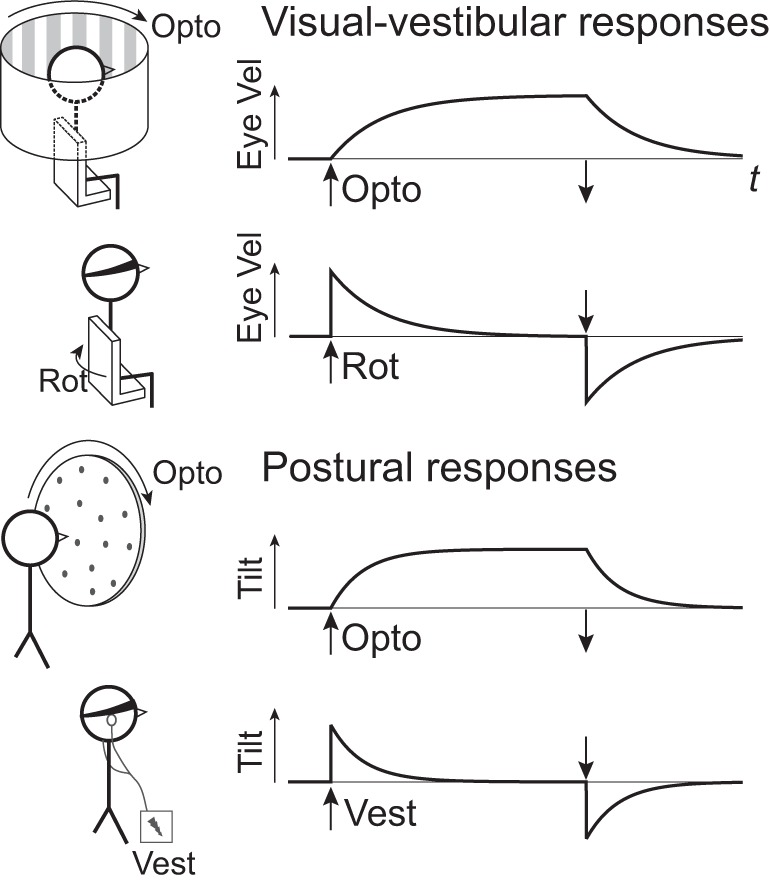
Conceptual comparison of visual-vestibular and postural responses to two types of sensory perturbations: optokinetic and vestibular perturbations (top and bottom of each pair, respectively). Visual-vestibular stimulus is a step in angular velocity about the yaw (vertical) axis, applied optokinetically (Opto) with a rotating visual field, or physically with a rotating (Rot) chair without vision. Response is angular velocity of compensatory eye movements (Eye vel) vs. time t, indicating gaze stabilization. Posture stimulus is a step in angular velocity of an optokinetic field about the roll axis, and a step in direct current of galvanic vestibular (Vest) stimulus without vision. Response is trunk tilt vs. time, here interpreted in terms of exponential time constants similar to visual-vestibular responses. Stimulus on and off times are denoted by vertical arrows.
Similar concepts of CNS filtering have long been applied to the stabilization of gaze (Fig. 1, visual-vestibular responses). Head rotations normally produce feedback from both visual and vestibular systems, which then drive compensatory eye movements. A step in rotational velocity of the visual field alone (optokinetic stimulus without head rotation) produces eye movements that only gradually match the stimulus velocity, similar to a low-pass filter with a time constant of ~20 s (Robinson 1981). A complementary behavior occurs in response to a step change in angular velocity of the head, without visual input (e.g., vestibular stimulus alone). The compensatory eye movements resemble a decaying exponential, similar to a high-pass filter with the same time constant as the optokinetic response (Raphan et al. 1979). Both responses are explained by a single model, where the eye velocity command is produced by visual and vestibular signals feeding through a direct pathway, which directly sums the signals, as well as an indirect pathway into a shared neural integrator, or velocity storage unit (Cohen et al. 1981). Both pathways converge to act as a filter (Robinson 1981), such that vestibular signals, especially sensitive to high-frequency information, are high-pass filtered, whereas visual signals are low-pass filtered. In the veridical case where both inputs are present, the two complementary responses sum to an almost immediate, steplike compensatory eye movement.
A number of theoretical frameworks predict such neural integration by the CNS. Velocity storage for gaze stabilization is predicted by optimal state estimation models, where an internal model of head and sensor dynamics is used to estimate head tilt and rotation with minimum error (Ormsby and Young 1977; Borah et al. 1988; Merfeld et al. 1999), subject to assumed noise distributions. These have since been extended to broader approaches such as Bayesian estimation (Green and Angelaki 2010), as well as computational approaches such as particle filters (Karmali and Merfeld 2012; Laurens and Droulez 2007; Paulin 2005) for arbitrary probability distributions. These may be considered generalizations of state estimation theory that can predict an even greater variety of behaviors.
It is conceivable that posture control could incorporate neural integration similar to visual-vestibular responses (Fig. 1, postural responses). Similar models of control and estimation (Goodworth and Peterka 2012; Kiemel et al. 2011; Kuo 1995, 2005) have long been applied to posture, and the associated CNS filtering suggests a need for neural integration analogous to the velocity storage integrator. However, postural responses have not typically been characterized in terms of simple time constants, and the models have yet to be tested in terms of such simple perturbations and responses. For posture control, only visual input is directly amenable to experimental perturbations (Keshner and Kenyon 2000; Nashner et al. 1989; Tarr and Warren 2002). Vestibular inputs may be perturbed with galvanic vestibular stimulation (Goldberg et al. 1984), and somatosensory inputs with vibration (Kavounoudias et al. 2001; Lee et al. 2012, 2013a, 2013b), but the physiological interpretation of such inputs is less certain. Further insight may require more complex inputs (e.g., a combination of inputs with sway-referencing). As a result, there is little evidence of neural integration in posture, in contrast to the well-documented velocity storage phenomenon observed in eye movements (Cannon and Robinson 1987; McFarland and Fuchs 1992; Yokota et al. 1992).
The present study examines the fusion of sensory information for posture control, with and without a hypothesized neural integrator circuit. The simplest means of fusion would be to form a direct weighted sum of the inputs from the sensory systems to produce a body tilt response without filtering. This is contrasted with an indirect pathway through a shared integrator, which affords the ability to perform low- and high-pass filtering, not unlike the integrator for gaze stabilization. Here we compare these alternatives, using simple models of the sensory system dynamics, including vision, the semicircular canals, and combined tilt information from somatosensors, otoliths, and other modalities. To test the model, we perform an experiment where stimuli are applied to the visual and vestibular systems, and the resulting body tilt responses are examined. We thus seek to test whether posture control shows evidence for shared neural integration analogous to that long observed in visual-vestibular responses.
MODEL
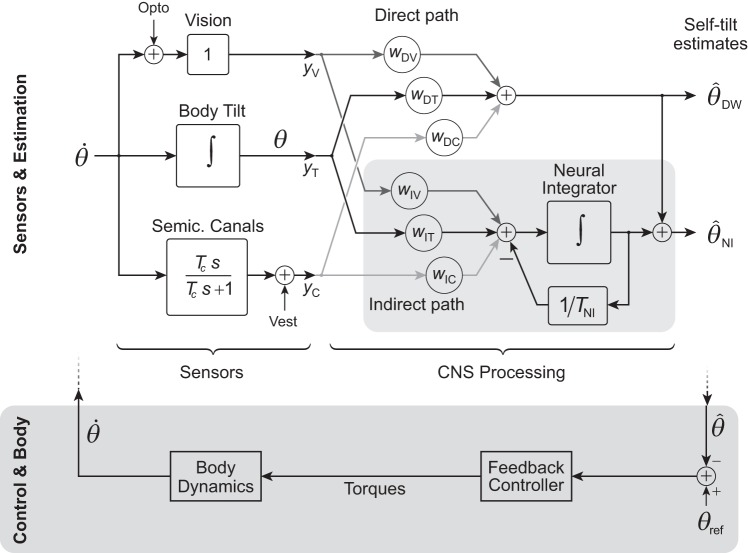
We propose two alternative models for CNS processing of sensory information (Fig. 2): a neural integrator (NI) model and a direct weighting (DW) model. The first feeds the afferent signals through two pathways, termed direct and indirect, each forming a weighted sum (linear combination) of inputs, but with the latter also passing through a neural integrator. Both pathways converge and add together to produce the tilt estimate. The DW is a simpler alternative, dispensing with the indirect pathway and integrator. Both models receive input from three sensory modalities—vision, semicircular canals, and body tilt sensors—each modeled with very simple dynamics (Fig. 2), so that sensor and CNS processing together determine the overall behavior. We examine these behaviors in the context of two types of stimuli, optokinetic and galvanic vestibular stimulation. The two models are used to determine the simplest possible system that can explain the observed postural behaviors.
Fig. 2.
Simple model of sensors and sensory processing for posture control. Angular velocity of the body is transduced by vision, body tilt sensors (comprising somatosensors, otoliths, and other graviceptors), and semicircular (semic.) canals, each with linear dynamics. These afferents pass through CNS processing to estimate self-tilt, to be used for control of balance (dark shaded area at bottom; treated as fast relative to semicircular canal dynamics). Sensory processing is modeled with two pathways, denoted Direct and Indirect paths. The Direct path is a weighted sum of the sensory data, whereas the Indirect path (shaded area) augments a weighted sum with a neural integrator (NI) using negative feedback to retain only the recent past. The tilt estimate is produced from the sum of both direct and indirect paths. A simpler alternative direct weighting (DW) model uses only the Direct path to yield its tilt estimate . Vision and canals are subject to external perturbations, Opto and Vest, respectively.
We model the sensors with linearized dynamics. We treat vision as having proportional sensitivity to the angular velocity of the visual field (Cohen et al. 1981; Dichgans et al. 1972; Young 1984) and the semicircular canals as having first-order high-pass filter characteristics with an approximate time constant Tc = 7 s (Cohen et al. 1981; Robinson 1981). Tilt refers to sensors such as somatosensors and otoliths, which contribute sensitivity to the vertical through reference to ground or gravity (e.g., Burgess and Perl 1973; Peterka and Benolken 1995). We treat the dynamics of such sensors as much faster than the observed postural response (Agarwal and Gottlieb 1984; Young and Meiry 1968) and therefore lump them into a composite tilt sensor with constant gain.
The sensory outputs feed into the CNS processing model to produce a tilt estimate. This refers to a hypothesized internal CNS representation of the body’s tilt, which is not directly measurable but rather indirectly revealed by the body’s actual tilt θ, in an attempt to align the body with vertical. The actual body motion results from CNS control (not modeled explicitly; see Fig. 2, bottom shaded area), acting on the internal tilt estimate. For simplicity, we ignore the closed-loop control dynamics, with the reasoning that the body can be controlled at much higher bandwidth than the postural responses resulting from the relatively slow dynamics of the semicircular canals and sensory processing. This is analogous to the approach for eye movements, which often treat the control and eye dynamics as fast, relative to these same sensory/processing dynamics (e.g., Raphan et al. 1979; Robinson 1981). [As a simple indication of body bandwidth, we asked subjects to actively sway their bodies quickly from side to side, and we observed a closed-loop natural frequency of 0.85 ± 0.38 Hz (mean ± SD, N = 16), at least 20 times faster than the sensory processing bandwidth examined here.] We also presume that control actions feed an efference copy into the sensory processing system, so that self-generated movements do not themselves cause self-opposing postural responses. Another simplification is that we define a sign convention such that the angular motion of the visual field (e.g., clockwise direction), the internal estimate of body tilt (e.g., counterclockwise direction), and the actual body tilt (e.g., clockwise direction) all have positive signs during the optokinetic response.
We next consider the tilt estimates that arise from the two models. For each model, there are four stimuli of interest: optokinetic step input (Opto-Step), galvanic vestibular stimulation with a step change in current (Vest-Step), galvanic vestibular with an exponential decay (Vest-Decay), and veridical tilt shift. Stimulus Opto-Step refers to a step change in the visual field angular velocity, which results in a gradual (low-pass filter) shift in tilt. Stimulus Vest-Step (Fig. 3) refers to a step change in direct current applied to the vestibular nerve, which appears to act on the primary afferents, bypassing the canal dynamics (Goldberg et al. 1984). Stimulus Vest-Decay is a variation on the traditional step waveform, where the stimulus is applied with an exponential decay with time constant Tc. The rationale is that the standard constant-current galvanic stimulus might be considered nonphysiological, because it corresponds to a physical stimulus of sustained angular acceleration, rarely encountered on earth. Thus Vest-Decay is intended to crudely model the equivalent of a step change in angular velocity (Cohen et al. 1981), for which the canal afferents would normally produce an exponentially decaying response. Finally, veridical shift refers to a step change in body tilt that affects all three sensory systems together, as might occur with a physical rather than purely sensory perturbation. The present experiment does not apply such a perturbation, but it is expected that humans should rapidly and correctly sense self-tilt in the absence of any sensory conflict.
Fig. 3.
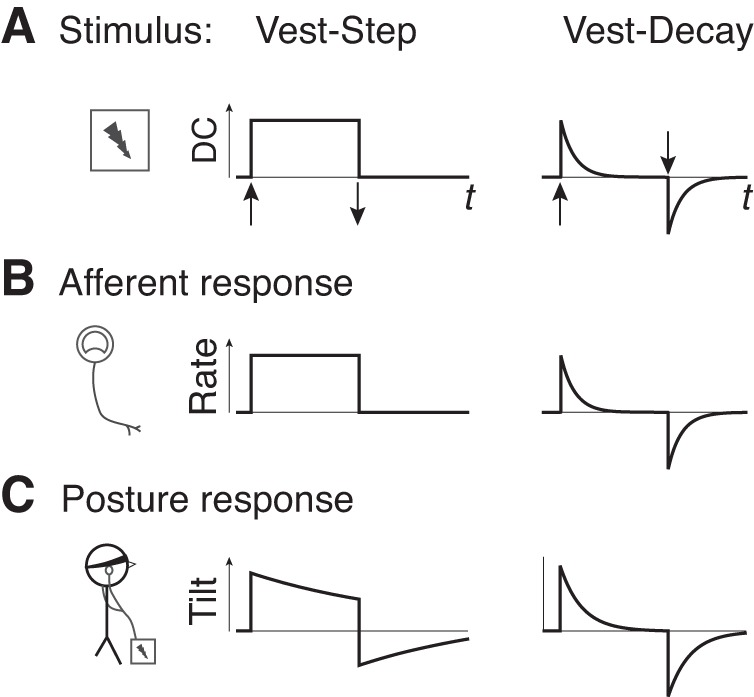
Hypothetical comparison of two galvanic vestibular stimuli. A: step in direct current (DC) (denoted Vest-Step) and decaying exponential (Vest-Decay). Galvanic vestibular stimulus acts on vestibular afferents (B), with effect similar to a rotary acceleration on the semicircular canals. Due to canal dynamics, the equivalent to a step in rotational angular velocity should be induced by a decaying exponential stimulus. C: postural responses produced by the two stimuli are expected to differ in time course, with Vest-Decay more similar to a step in angular velocity. Stimulus on and off times are denoted by vertical arrows.
Application of these stimuli to the models reveals several key features (Table 1). The Neural Integrator (NI) model only requires indirect pathways for vision and canal inputs to produce tilt responses that roughly approximate the expected experimental responses: an exponentially decaying shape for Opto-Step and Vest-Step inputs (which can each increase or decrease depending on separate weights), an additional exponential (with the time constant Tc) for Vest-Decay, and a faster, steplike shift for veridical shift. The corresponding direct weights (wDV and wDC) are therefore treated as zero in the NI model henceforth as they only serve to offset responses. In contrast, the DW model cannot reproduce the observed optokinetic response dynamics. In response to an Opto-Step stimulus the DW model yields a step change in tilt and cannot possibly reproduce the low-pass filter response of humans. In addition, the veridical stimulus produces a shift in tilt in the model, but with a relatively slow exponential decay due to the canal time constant, whereas the human veridical response is expected to be quite fast. The direct pathways for semicircular canals and visual input are particularly problematic, because nonzero weightings imply an unrealistically impulsive shift. Both models, particularly the NI model, produce the expected high-pass filter response for galvanic stimulus. These observations are independent of parameter values, which are determined from experimental data to further test the models.
Table 1.
Predicted tilt responses from neural integrator and direct weighting models
| Stimulus | Input | Tilt Response |
|---|---|---|
| Neural Integrator | ||
| Opto-Step | ||
| Vest-Step | ||
| Vest-Decay | ||
| Veridical shift | ||
| Direct Weighting | ||
| Opto-Step | ||
| Vest-Step | ||
| Vest-Decay | ||
| Veridical shift | ||
Responses are for four possible stimuli: a step in angular velocity of optokinetic field (Opto-Step), a step in galvanic vestibular input (Vest-Step), as well as a decaying galvanic waveform (Vest-Decay) that models a step in angular velocity applied to the semicircular canals. The final stimulus is equivalent to a veridical positional shift in the body, detected by all sensors. All stimuli are applied with the body initially at rest in an upright position (θ = 0) at stimulus onset t = 0. The ideal impulse function is denoted by δ(t). NI, neural integrator model; DW, direct weighting model.
EXPERIMENTAL METHODS
To test the models, we measured human postural tilt responses in the frontal plane evoked by three types of experimental stimuli. These included an optokinetic stimulus with a step change in visual field roll velocity (Opto-Step), galvanic stimulus with a step change in current (Vest-Step), as well as galvanic stimulus with an exponential decay in current (Vest-Decay) that was meant to mimic the dynamics of the canals (with an assumed time constant Tc = 7 s; see model section for details). The postural responses were quantified in terms of the angular tilt of the trunk laterally from undisturbed quiet stance, as measured by motion capture markers at the base of the neck (near C7 vertebra) and at the pelvis (near L5). As an additional comparison measure, we also recorded lateral excursion of the center of pressure (COP). The time trajectories of trunk tilt were then used to determine best-fit parameter values for the models, with the resulting model trajectories compared against human responses.
Sixteen healthy young adults (22.8 ± 2.8 yr old, 4 men, 12 women) were recruited for this study. The protocol was approved by the University of Michigan Institutional Review Board, and subjects provided written, informed consent. Subjects were excluded if they reported difficulty with standing, walking or balance, vision problems despite correction, or a diagnosed neurological disorder, or if they had used medication or drugs that might impair balance. Subjects stood without shoes with their feet together (Romberg stance) and arms crossed. Kinematic data were recorded at 100 Hz using a passive motion tracking system (Vicon Motion Systems). For comparison with body tilt, center of pressure of ground reaction forces was recorded at 1,000 Hz from an in-ground force plate (OR6–7, Advanced Mechanical Technology), with signals low-pass filtered with a 5-Hz cutoff frequency.
The optokinetic stimulus consisted of a computer-generated field of random dots displayed on a large projection screen in an otherwise dark room. The screen was curved to wrap around the subjects (O’Connor and Kuo 2009), who stood ~0.6 m from its front, so that the field of view extended nearly 180° in the horizontal plane, with the intention of reducing visual cues regarding vertical. Step changes in angular velocity were applied at speeds of 15 and 30°/s and in clockwise or counterclockwise directions (all randomly selected). Each trial was 80 s long: 20 s prestimulus (no rotation, baseline) and 60 s per-stimulus (rotation). Each subject performed three repetitions of each trial type as well as three separate control trials with no stimulus.
Bilateral bipolar galvanic vestibular stimulation was applied to subjects standing with eyes closed in the dark room. Electrodes were placed on the mastoid processes to apply a direct current stimulus (Johansson et al. 1995; St George et al. 2011; Wardman et al. 2003). Four trial types were defined based on the amplitude (0.25, 0.5, or 1.0 mA) and waveform (Vest-Step and Vest-Decay) of the current. However, only two current amplitudes were used for each subject. Default values were 1.0 and 0.5 mA, which were briefly applied as a pretest. If a subject reported discomfort with 1 mA, then 0.5 and 0.25 mA were applied instead (for 6 of the 16 subjects). Each subject performed three repetitions of each trial type (12 experimental trials) as well as three control trials with no stimulus, for a total of 15 trials. The order of trial presentation and the direction of current (positive or negative) were randomized. These trials were 60 s long: 20 s prestimulus (no current), and 40 s per-stimulus (current).
The three repetitions for each trial type were averaged together and fit with exponential curves for comparison with the models. The trunk tilt trajectory of each trial was first normalized for stimulus direction, by negating the data of the negative-stimulus trials. The mean of the prestimulus trunk tilt was also subtracted from the trial data as a baseline.
All model predictions were tested by least squares fitting to generic equations resembling the predicted waveforms (t) (Table 1) according to one or more terms of a sum of exponentials
| (1) |
with fitting parameters A1, A2, τ1, τ2, c, and time delay τd relative to stimulus onset at t = 0 and upright position θ = 0 [please note, (t) = 0 for t < τd]. Only the terms relevant to a particular combination of model and stimulus were included. For example, only a constant term c was predicted for the DW model’s Opto-Step response. A single exponential (one time constant and a constant term) was predicted for NI Opto-Step and Vest-Step, and DW Vest-Decay. Only the NI Vest-Decay response included all of the terms above. Some fits yielded much longer time constants than the trials themselves, and those exceeding 100 s were considered extraneous and excluded from further statistical tests; 13 of the 192 fits performed (16 subjects × 6 trial types × 2 models) were removed for this reason. In addition, we also observed some cases (9 trials) of a resetting behavior for Opto-Step, similar to a periodic resetting reported previously for long stimulation durations (Dichgans and Brandt 1978), but too small to warrant modeling its effect. These trials were not removed. The minimum mean-square error and residual sum-squared error were determined by nonlinear optimization (MATLAB “fmincon,” MathWorks, Natick, MA), and the Bayesian Information Criterion (BIC) was used to quantitatively compare the two models, with a difference of at least 10 considered strong evidence for a superior fit (Schwarz 1978).
RESULTS
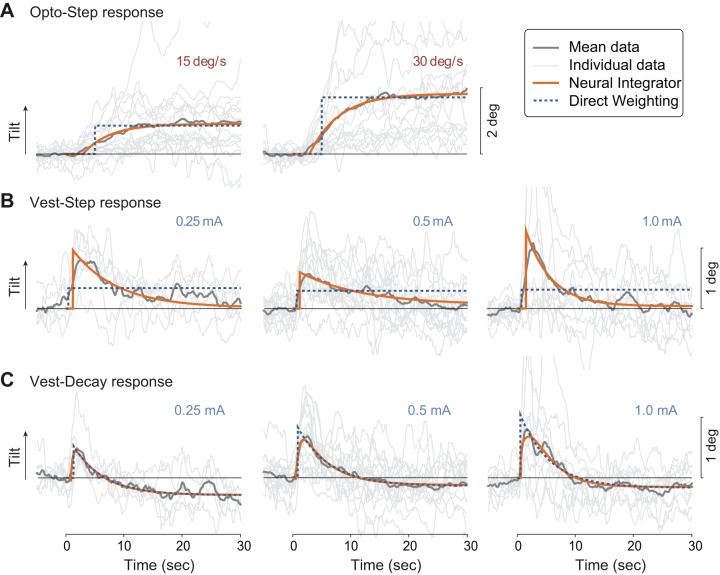
Subjects responded to the stimuli with postural responses that generally met expectations (Fig. 4). Specifically, the Opto-Step response was a slow tilt of the trunk to a steady-state angle, like a low-pass filter. The Vest-Step response was a fast shift (toward the anode) followed by an exponential decay returning toward upright. The Vest-Decay response was similar, except with a somewhat faster decay. Individual curve fits were also performed for each subject’s data, summarized in Table 2. As another indicator, we found the COP trajectories, expressed as lateral shift divided by leg length, to correlate well with trunk tilt θ; the correlation coefficient averaged 0.76 across all visual inputs, and 0.74 across all galvanic vestibular inputs. The COP data were not used to test any hypotheses, and therefore subsequent analyses concern only trunk tilt θ.
Fig. 4.
Experimental responses and model fits for three stimuli: optokinetic step (Opto-Step; A), galvanic vestibular step (Vest-Step; B) in current, and galvanic decaying exponential (Vest-Decay; C). Experimental trajectories are trunk tilt in the lateral direction vs. time (initiation of stimulus at time zero), averaged across all subjects (“Mean data,” darker gray); also shown are each individual’s responses averaged across trials (“Individual data,” lighter gray). Model fits for NI (solid lines) and DW (dashed lines) are also shown, fitted to mean data. Positive direction for tilt is defined along optokinetic stimulus direction or anode side for galvanic stimulus. Quantitative fits were also computed for each individual, based on each subject’s mean response across trials, for each condition (Table 2).
Table 2.
Curve fit parameters for experimental data, for neural integrator and direct weighting models with three stimuli: Opto-Step, Vest-Step, Vest-Decay
| τ1, s |
A1,° |
τ2, s |
A2,° |
td, s |
c,° |
MSE |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stimulus | Amplitude | mean | SD | mean | SD | mean | SD | mean | SD | mean | SD | mean | SD | ( × 103) | BIC |
| Neural Integrator | |||||||||||||||
| Opto-Step | 15°/s | 6.79 | 5.65 | −0.99 | 0.83 | 2.52 | 1.85 | 0.99 | 0.83 | 80.78 | −8,131 | ||||
| 30°/s | 9.70 | 9.01 | −2.09 | 1.58 | 2.99 | 1.90 | 2.09 | 1.58 | 185.06 | −6,965 | |||||
| Vest-Step | 0.25 mA | 9.63 | 7.28 | 1.10 | 0.55 | 1.62 | 1.85 | −0.12 | 0.31 | 58.72 | −5,152 | ||||
| 0.50 mA | 6.13 | 6.64 | 0.73 | 0.69 | 0.99 | 0.65 | 0.11 | 0.46 | 65.49 | −5,156 | |||||
| 1.00 mA | 7.85 | 7.17 | 1.51 | 1.60 | 2.55 | 1.63 | −0.06 | 0.34 | 137.46 | −4,798 | |||||
| Vest-Decay | 0.25 mA | 5.78 | 4.50 | 1.91 | 1.14 | 1.76 | 2.26 | −1.49 | 1.32 | 0.51 | 0.42 | −0.34 | 0.21 | 36.94 | −5,773 |
| 0.50 mA | 3.75 | 3.16 | 2.55 | 2.07 | 0.77 | 0.40 | −2.33 | 2.11 | 0.59 | 0.33 | −0.10 | 0.26 | 36.17 | −5,960 | |
| 1.00 mA | 3.55 | 2.79 | 3.53 | 2.20 | 1.30 | 1.11 | −3.03 | 2.02 | 0.67 | 0.24 | −0.26 | 0.40 | 85.76 | −5,403 | |
| Direct Weighting | |||||||||||||||
| Opto-Step | 15°/s | 4.32 | 0.99 | 0.79 | 0.65 | 120.77 | −6772 | ||||||||
| 30°/s | 4.84 | 0.45 | 1.76 | 1.20 | 296.50 | −4,290 | |||||||||
| Vest-Step | 0.25 mA | 0.38 | 0.33 | 0.40 | 0.33 | 173.41 | −3,888 | ||||||||
| 0.50 mA | 0.70 | 0.34 | 0.35 | 0.32 | 115.57 | −4,512 | |||||||||
| 1.00 mA | 0.67 | 0.31 | 0.38 | 0.49 | 282.43 | −3,435 | |||||||||
| Vest-Decay | 0.25 mA | 5.80 | 5.44 | 1.02 | 0.43 | 1.07 | 0.81 | −0.29 | 0.13 | 38.86 | −5,687 | ||||
| 0.50 mA | 3.38 | 1.56 | 1.20 | 0.58 | 1.37 | 0.71 | −0.10 | 0.27 | 48.99 | −5,629 | |||||
| 1.00 mA | 5.36 | 3.58 | 1.09 | 0.71 | 0.94 | 0.84 | −0.18 | 0.22 | 65.95 | −5,429 | |||||
Parameters were fit with nonlinear least squares to reveal time constants (τ1 and τ2), amplitudes (A1 and A2), offset (c), and time delay (td). One fit was performed for each subject’s data per condition, with mean (SD) reported, as well as overall mean-square error (MSE) and Bayesian information criterion (BIC; more negative is better). Six of 16 subjects performed trials with the 0.25 and 0.5 mA stimulus amplitudes, while the others performed trials with the 0.5 and 1.00 mA stimulus amplitudes.
The models differed considerably from each other in their ability to reproduce the observed responses (Table 2). For optokinetic inputs, the NI model’s slow time constant of several seconds was necessary to capture the gradual postural shift exhibited by subjects (compare exponential decaying terms of subject data and NI model for Opto-Step in Fig. 4A; see also estimated values of τ1 for Opto-Step in Table 2, top). In contrast, the DW model only includes an instantaneous tilt (compare subject data to DW model’s step change in tilt in Fig. 4A; see also offset c with no exponential terms, Table 2, bottom), and therefore could not reproduce the transient dynamics at all. The NI model also yielded considerably lower BIC values than DW (e.g., −8,131 vs. −6772 for 15°/s visual stimuli), signifying a better fit while accounting for model parameters.
For galvanic vestibular inputs, the NI model also better reproduced observed responses. In particular, its Vest‐Step response exhibited an immediate tilt followed by a gradual return to upright with a relatively slow time constant, similar to the experimental findings (Vest-Step exponential decay for both human and NI model, Fig. 4B; see also τ1 for Vest-Step in Table 2, top). This response is not reproducible by the DW model, which again only produces an instantaneous step change in tilt (DW model in Fig. 4B; offset c in Table 2, bottom). The Vest-Step input also caused some subjects to exhibit a lingering trunk tilt for the duration of the stimulus (see offset c in Table 2), as also expected by the NI model (constant wDC for Vest-Step in Table 1, top). For the Vest-Decay input similarly reproduced the experimental response, because both models include at least one exponential, which was the gross feature dominating the observed human behavior. Some subjects also appeared to exhibit a lingering tilt in the opposite direction (offset c in Table 2, NI and DW Vest-Decay), which was not expected for either model (Table 1, DW and NI Vest-Decay). As with visual stimuli, the NI model yielded considerably lower BIC values than DW, for five of the six cases (e.g., −5,156 vs. −4,512 for 0.5 mA Vest-Step).
Our model proposes that a single integrator could explain the responses to both visual and vestibular inputs. To illustrate the consequences of a shared neural integrator and to further test our hypothesis that Vest-Decay would complement Opto-Step, we also conducted an additional fit to the data, where both visual and vestibular responses (Opto-Step and Vest-Decay) were constrained to a single time constant (Fig. 5). The fit included the same mathematical structure as above, but with the restriction that a single time constant τ1 was shared across conditions. A single fit to the mean data—averaged across all subjects and trials for each condition (30°/s Opto-Step and 0.5 mA Vest-Decay)—yielded a shared time constant of 5.2 s (mean-square error 0.0082, residual sum-squared error 32.8). We also compared the fitted τ1 time constants from all subjects for the same Opto-Step and Vest-Decay conditions and found no significant difference (P = 0.13, paired t-test). We chose to fit only a single stimulus amplitude for each condition to include all subjects in the analysis (as mentioned previously, all subjects performed both amplitudes of the optokinetic stimulus but the only galvanic vestibular stimulus amplitude used for all subjects was 0.5 mA).
Fig. 5.
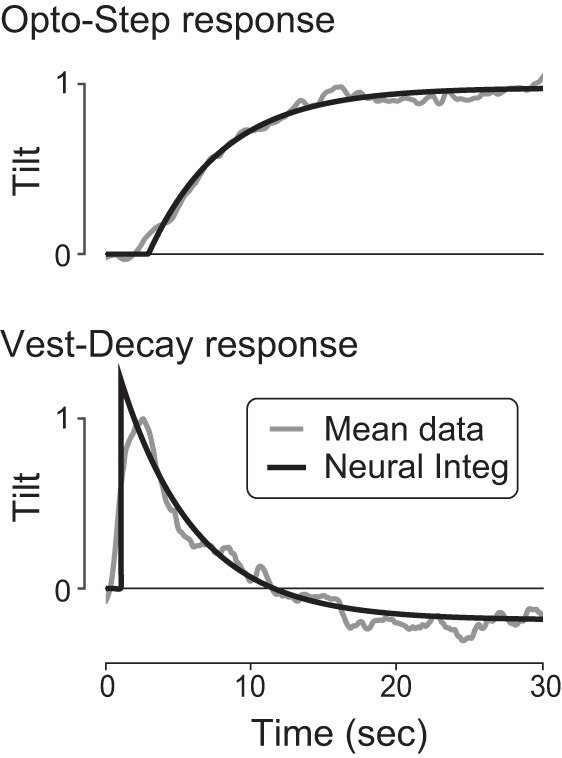
Illustration of NI fit with a shared time constant, compared with mean experimental data. Experimental responses to optokinetic and galvanic vestibular decaying exponential inputs (Opto-Step and Vest-Decay) are fit with the proposed neural integrator (Neural Integ) response, constrained with a single time constant (τ1 = 5.2 s). Tilt data were normalized to unit amplitude; stimulus initiated at time zero.
DISCUSSION
The goal of this study was to test how the CNS combines sensory information during standing balance. We characterized human responses to optokinetic and galvanic vestibular stimuli, specifically the exponential rise during Opto-Step stimulus and the exponential decay during both Vest-Step and Vest-Decay stimuli. We found that the NI could reproduce all responses (Fig. 4), as well as the fast hypothetical response expected for a veridical position shift. In contrast, the DW model was unable to reproduce the time course of the Opto-Step and Vest-Step responses, as evidenced by substantially poorer fits (differences in BIC greater than 10; Table 2). Moreover, there was no significant difference between the separate time constants determined from visual or vestibular stimuli, and forcing the fitted responses to share a single time constant yielded a reasonable match to mean data (Fig. 5). We interpret our findings to suggest that a neural integrator may play an important role in posture stabilization.
The neural integrator concept was inspired by the velocity storage integrator (Cohen et al. 1981; Robinson 1981) governing many eye movements. Although long linked to the semicircular canal dynamics, such integration has not similarly been applied to posture control, despite the need to integrate similar sensory information. In our model, the integrator’s role is not to store velocity, but instead to filter disparate sensory inputs to estimate the body’s angular tilt. Here, gravity contributes to estimation of self-motion, unlike the classic yaw-rotations of visual-vestibular interactions, where gravitational cues do not conflict with the induced sensation. In contrast, roll rotation entails a changing gravitational vector that must be reconciled with graviceptor input such as from the otoliths and somatosensors (Dichgans and Brandt 1978; Merfeld et al. 1999). The additional input from these sensors inhibits circular vection and instead produces a sensation of tilt, as well as a rotation of subjective visual vertical (Dichgans et al. 1972). The neural integrator for posture could thus be thought of as a position storage integrator.
Accordingly, the neural integrator is important to the general processing of sensory signals for perception and motor control. The dynamics of any sensor would be expected to require some degree of filtering, which implies temporal dynamics within the CNS. Such filtering can be predicted by state estimation theory, which has long been applied to both visual-vestibular interactions (Borah et al. 1988; Merfeld et al. 1999; Green and Angelaki 2010) and posture control (Kuo 1995, 2005). A state estimator uses an internal model of body and sensory dynamics that predicts sensory signals, which are then corrected by comparison with actual afferent information to yield an estimate of spatial orientation. In fact, previously proposed estimators would be expected to generate the responses examined here (Borah et al. 1988; Goodworth and Peterka 2012; Klein et al. 2011; Kuo 2005). Such models are able to reproduce a variety of responses as well as explain why the observed filtering behavior might be optimal, as a consequence of the high-pass filter dynamics of the semicircular canals. Our intent was to perform an extreme simplification of a filtering behavior, to focus on basic characteristics that could potentially be tied to a neural substrate, analogous to the velocity storage integrator for gaze stabilization. We demonstrate how the same type of integrator may be applied to posture, and by extension how estimator and sensory reweighting dynamics proposed by others might be physiologically realized.
A secondary aim of this study was to examine the effect of galvanic vestibular stimuli. If it is equivalent to direct stimulation of the vestibular afferents (Goldberg et al. 1984; St George et al. 2011), then the NI model predicts that a step in galvanic current should resemble the canal response to angular acceleration, and thus produce an exponentially decaying response, plus a nonzero steady-state offset (Table 1). The subjects here appeared to respond with a relatively strong exponential decay and a weaker offset. This model also predicted that the Vest-Decay stimulus would be more similar to a step in head angular velocity and thus produce a fully decaying exponential, dominated by the relatively slow neural integrator time constant. Some subjects appeared to exhibit a negative steady-state offset not predicted by our model, which was perhaps indicative of yet another, still-slower time constant in the sensory processing dynamics, or even a nonlinear adaptation (discussed below). It is unclear whether subjects produced similar offsets to the model (nonzero for Vest-Step, and zero for Vest-Decay), but both of the galvanic vestibular responses did exhibit evidence of a neural integrator with time constants of several seconds. We also found that the amplitude of the response to the 0.25 mA stimulus was larger than the response to the 0.5 mA stimulus. However, the observed decrease in amplitude associated with the larger stimulus level may have been a small sample size effect (six of the 16 subjects performed trials with the 0.25 mA stimulus, while all 16 performed trials with the 0.5 mA stimulus).
Current practice often treats galvanic vestibular stimulus as a general means to stimulate the vestibular system, but without a specific real-world interpretation. This differs from the rotational (i.e., vestibular) stimuli that are often applied in a controlled manner for assessment and diagnosis of oculomotor and vestibular dysfunction (Dix and Hallpike 1952; Suzuki and Komatsuzaki 1962; Zee et al. 1976). It may therefore be helpful for posture assessments to apply interpretable vestibular signals, similar to the visual and support surface perturbations already available (Nashner and Peters 1990; Woollacott et al. 1986). We posited that the stimulus should ideally be a decaying exponential (Vest-Decay) to model a step in angular velocity of the body (Fitzpatrick et al. 2002, 2006). Although we did not prove that possibility, development of vestibular prostheses reveals that a high-pass filter of angular velocity, with a relatively long time constant, yields a galvanic stimulus that partially restores the normal velocity storage behavior (Merfeld et al. 2007). This suggests that head movements might indeed be emulated with a galvanic stimulus that models the dynamics of the semicircular canals, as was intended by our Vest-Decay input. In contrast, the Vest-Step stimulus hypothetically produces an unnatural afferent response of sustained angular acceleration (see Fig. 3). In the Vest-Step response, we also anecdotally observed that some subjects retained different steady offsets for head and trunk tilts. It is possible that this is due to different sensory information available to distinct body segments (Peterka and Benolken 1995; Kiemel et al. 2011; Goodworth and Peterka 2012), not considered here. Nevertheless, if galvanic stimulus acts on the vestibular afferents, we would expect a decaying stimulus to better mimic the effects of a physical rotation.
There have been other observations of slow dynamics in posture control. Unperturbed sway exhibits a very slow fluctuation in COP, which could be interpreted as a fluctuation of a reference signal (Dijkstra 2000; Zatsiorsky and Duarte 2000). Others have argued that the fluctuation is within the feedback loop, perhaps as a consequence of state estimation noise (Kiemel et al. 2002, 2006). Although we do not preclude the possibility of a fluctuating reference signal, the present results demonstrate slow dynamics specifically associated with sensory processing. We do not explore the origin of the slow time constant here, but we expect that a state estimator would introduce dynamics that are at least qualitatively similar to our observations, although that connection remains to be examined more closely.
There are a number of limitations to this study. We proposed a very simple model with a single neural integrator, whereas more complex models might better reproduce the empirical observations. We also measured trunk tilt as an indicator of the body, and did not consider the multisegmental kinematics of the entire body, and particularly its interaction with closed-loop, CNS feedback control (Hettich et al. 2014; Kuo 1995, 2005). Much of this control appears to be relatively fast, as exemplified by the fast rise in tilt at onset of galvanic vestibular stimulus (Fig. 4; τ2 in Table 2, top), far faster than the decaying exponential modeled here. We therefore presume feedback control dynamics to be considerably faster than the neural integrator time constant, which we consider indicative of state estimation. However, even considering state estimation alone, more sophisticated models typically entail more complex filtering (Goodworth and Peterka 2012; Kiemel et al. 2011; Kuo 2005), and therefore multiple, and in some cases, adaptable, neural integrators (Assländer and Peterka 2014; Borah et al. 1988; Klein et al. 2011). We also regard most of these as relatively fast, as the slowness of the position storage integrator is a consequence of the uniquely slow dynamics of the semicircular canals.
Our experiment also used extremely simple input functions for both visual and vestibular disturbances. An alternative to step functions and exponentially decaying inputs is to apply broadband input (e.g., Assländer and Peterka 2014) and perform system identification (e.g., Johansson et al. 1995, 2001). Such approaches are particularly apt for multiple inputs and outputs, and complex models with more degrees of freedom and states. However, our main purpose was to explicitly test a simple model to explain long-recognized responses to step stimuli, analogous to the classic experiments of visual-vestibular interactions (Robinson 1981). Despite being less sophisticated, simple yet specific models can be more appropriate for hypothesis testing.
Other limitations include our model’s ability to characterize longer‐term behaviors. The galvanic vestibular responses at times appeared to exhibit a steady-state offset that was more negative than expected, for both the step and decaying exponential stimuli. This could potentially be an indicator of long-term habituation or adaptation to tonic stimuli, included in some models as a very long time constant (e.g., Borah et al. 1988; Guedry and Lauver 1961; St George et al. 2011). It might also be reminiscent of a nonlinear, long-term adaptation reported by Johansson et al. (1995) resulting from broadband stimulus. Unfortunately, the present data are insufficient to confirm whether the lingering effect we observed is either linear or nonlinear; however, they at least superficially agree with the previous reports. For some of our subjects, the optokinetic responses also appeared to exhibit a very slow resetting behavior on the order of tens of seconds, resulting in wide variance in the steady-state offset. This might be interpreted as similar to long-reported periodic resetting of subjective vertical (Mauritz et al. 1977), or to periodic nystagmus of eye movements (Robinson 1981). We did not model or characterize this behavior, which might be separable as a basic behavior similar to the fast phase of eye movement nystagmus or might be due to conscious compensations performed by subjects.
Some of these issues might be resolved using more complete kinematic measurements and more sophisticated models. However, despite the simplicity of the present study, there does appear to be evidence in favor of a neural integrator for posture as opposed to direct weighting of sensory inputs. This could potentially inform how these sensory inputs might be tested in the clinic as well as how their functions might be restored using prosthetic devices (e.g., Merfeld et al. 2007).
GRANTS
This material is based on work supported by National Institute on Aging Claude D. Pepper Older Americans Independence Center (Grant no. AG024824), Department of Defense (W81XWH-09-2-0142 and NDSEG), Office of Naval Research (ETOWL), National Institutes of Health (AG0308), and Defense Advanced Research Projects Agency (M3 Atlas Program). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Institutes of Health, the Department of Defense, or the Office of Naval Research.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
S.E.H. and A.R.W. performed experiments; S.E.H. and A.R.W. analyzed data; S.E.H., A.R.W., K.H.S., and A.D.K. interpreted results of experiments; S.E.H. and A.R.W. prepared figures; S.E.H. drafted manuscript; S.E.H., A.R.W., K.H.S., and A.D.K. edited and revised manuscript; S.E.H., A.R.W., K.H.S., and A.D.K. approved final version of manuscript.
REFERENCES
- Agarwal GC, Gottlieb GL. Mathematical modeling and simulation of the postural control loop--Part II. Crit Rev Biomed Eng 11: 113–154, 1984. [PubMed] [Google Scholar]
- Assländer L, Peterka RJ. Sensory reweighting dynamics in human postural control. J Neurophysiol 111: 1852–1864, 2014. doi: 10.1152/jn.00669.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borah J, Young LR, Curry RE. Optimal estimator model for human spatial orientation. In: Representation of Three-Dimensional Space in the Vestibular, Oculomotor, and Visual Systems, edited by Cohen B, Henn V. New York: The New York Academy of Sciences, 1988, p. 51–73. [DOI] [PubMed] [Google Scholar]
- Burgess PR, Perl ER. Cutaneous mechanoreceptors and nociceptors. In: Somatosensory System, edited by Iggo A. Berlin: Springer, 1973, p. 29–78. doi: 10.1007/978-3-642-65438-1_3 [DOI] [Google Scholar]
- Cannon SC, Robinson DA. Loss of the neural integrator of the oculomotor system from brain stem lesions in monkey. J Neurophysiol 57: 1383–1409, 1987. [DOI] [PubMed] [Google Scholar]
- Cohen B, Henn V, Raphan T, Dennett D. Velocity storage, nystagmus, and visual-vestibular interactions in humans. Ann NY Acad Sci 374: 421–433, 1981. doi: 10.1111/j.1749-6632.1981.tb30888.x. [DOI] [PubMed] [Google Scholar]
- Dichgans J, Brandt T. Visual-vestibular interaction: effects on self-motion perception and postural control. In: Handbook of Sensory Physiology. Perception, edited by Held R, Leibowitz HW, Teuber HL. Berlin: Springer, 1978, vol. 8, p. 755–804. doi: 10.1007/978-3-642-46354-9_25 [DOI] [Google Scholar]
- Dichgans J, Held R, Young LR, Brandt T. Moving visual scenes influence the apparent direction of gravity. Science 178: 1217–1219, 1972. doi: 10.1126/science.178.4066.1217. [DOI] [PubMed] [Google Scholar]
- Dijkstra TMH. A gentle introduction to the dynamic set-point model of human postural control during perturbed stance. Hum Mov Sci 19: 567–595, 2000. doi: 10.1016/S0167-9457(00)00027-0. [DOI] [Google Scholar]
- Dix MR, Hallpike CS. The pathology symptomatology and diagnosis of certain common disorders of the vestibular system. Proc R Soc Med 45: 341–354, 1952. [PMC free article] [PubMed] [Google Scholar]
- Fitzpatrick RC, Butler JE, Day BL. Resolving head rotation for human bipedalism. Curr Biol 16: 1509–1514, 2006. doi: 10.1016/j.cub.2006.05.063. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick RC, Day BL. Probing the human vestibular system with galvanic stimulation. J Appl Physiol (1985) 96: 2301–2316, 2004. doi: 10.1152/japplphysiol.00008.2004. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick RC, Marsden J, Lord SR, Day BL. Galvanic vestibular stimulation evokes sensations of body rotation. Neuroreport 13: 2379–2383, 2002. doi: 10.1097/00001756-200212200-00001. [DOI] [PubMed] [Google Scholar]
- Fransson P-A, Hafström A, Karlberg M, Magnusson M, Tjäder A, Johansson R. Postural control adaptation during galvanic vestibular and vibratory proprioceptive stimulation. IEEE Trans Biomed Eng 50: 1310–1319, 2003. doi: 10.1109/TBME.2003.819851. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Smith CE, Fernández C. Relation between discharge regularity and responses to externally applied galvanic currents in vestibular nerve afferents of the squirrel monkey. J Neurophysiol 51: 1236–1256, 1984. [DOI] [PubMed] [Google Scholar]
- Goodworth AD, Peterka RJ. Sensorimotor integration for multisegmental frontal plane balance control in humans. J Neurophysiol 107: 12–28, 2012. doi: 10.1152/jn.00670.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green AM, Angelaki DE. Internal models and neural computation in the vestibular system. Exp Brain Res 200: 197–222, 2010. doi: 10.1007/s00221-009-2054-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guedry F, Lauver L. Vestibular reactions during prolonged constant angular acceleration. J Appl Physiol 16: 215–220, 1961. [Google Scholar]
- Hettich G, Assländer L, Gollhofer A, Mergner T. Human hip-ankle coordination emerging from multisensory feedback control. Hum Mov Sci 37: 123–146, 2014. doi: 10.1016/j.humov.2014.07.004. [DOI] [PubMed] [Google Scholar]
- Johansson R, Magnusson M, Fransson PA. Galvanic vestibular stimulation for analysis of postural adaptation and stability. IEEE Trans Biomed Eng 42: 282–292, 1995. doi: 10.1109/10.364515. [DOI] [PubMed] [Google Scholar]
- Johansson R, Magnusson M, Fransson PA, Karlberg M. Multi-stimulus multi-response posturography. Math Biosci 174: 41–59, 2001. doi: 10.1016/S0025-5564(01)00075-X. [DOI] [PubMed] [Google Scholar]
- Karmali F, Merfeld DM. A distributed, dynamic, parallel computational model: the role of noise in velocity storage. J Neurophysiol 108: 390–405, 2012. doi: 10.1152/jn.00883.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kavounoudias A, Roll R, Roll J-P. Foot sole and ankle muscle inputs contribute jointly to human erect posture regulation. J Physiol 532: 869–878, 2001. doi: 10.1111/j.1469-7793.2001.0869e.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keshner EA, Kenyon RV. The influence of an immersive virtual environment on the segmental organization of postural stabilizing responses. J Vestib Res 10: 207–219, 2000. [PubMed] [Google Scholar]
- Kiemel T, Oie KS, Jeka JJ. Multisensory fusion and the stochastic structure of postural sway. Biol Cybern 87: 262–277, 2002. doi: 10.1007/s00422-002-0333-2. [DOI] [PubMed] [Google Scholar]
- Kiemel T, Oie KS, Jeka JJ. Slow dynamics of postural sway are in the feedback loop. J Neurophysiol 95: 1410–1418, 2006. doi: 10.1152/jn.01144.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiemel T, Zhang Y, Jeka JJ. Visual flow is interpreted relative to multisegment postural control. J Mot Behav 43: 237–246, 2011. doi: 10.1080/00222895.2011.568991. [DOI] [PubMed] [Google Scholar]
- Klein TJ, Jeka J, Kiemel T, Lewis MA. Navigating sensory conflict in dynamic environments using adaptive state estimation. Biol Cybern 105: 291–304, 2011. doi: 10.1007/s00422-011-0466-2. [DOI] [PubMed] [Google Scholar]
- Kuo AD. An optimal control model for analyzing human postural balance. IEEE Trans Biomed Eng 42: 87–101, 1995. doi: 10.1109/10.362914. [DOI] [PubMed] [Google Scholar]
- Kuo AD. An optimal state estimation model of sensory integration in human postural balance. J Neural Eng 2: S235–S249, 2005. doi: 10.1088/1741-2560/2/3/S07. [DOI] [PubMed] [Google Scholar]
- Laurens J, Droulez J. Bayesian processing of vestibular information. Biol Cybern 96: 389–404, 2007. doi: 10.1007/s00422-006-0133-1. [DOI] [PubMed] [Google Scholar]
- Lee B-C, Martin BJ, Ho A, Sienko KH. Postural reorganization induced by torso cutaneous covibration. J Neurosci 33: 7870–7876, 2013a. doi: 10.1523/JNEUROSCI.4715-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee B-C, Martin BJ, Sienko KH. Directional postural responses induced by vibrotactile stimulations applied to the torso. Exp Brain Res 222: 471–482, 2012. doi: 10.1007/s00221-012-3233-2. [DOI] [PubMed] [Google Scholar]
- Lee B-C, Martin BJ, Sienko KH. The effects of actuator selection on non-volitional postural responses to torso-based vibrotactile stimulation. J Neuroeng Rehabil 10: 21, 2013b. doi: 10.1186/1743-0003-10-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauritz K, Dichgans J, Hufschmidt A. The angle of visual roll motion determines displacement of subjective visual vertical. Atten Percept Psychophys 22: 557–562, 1977. doi: 10.3758/BF03198763. [DOI] [Google Scholar]
- McFarland JL, Fuchs AF. Discharge patterns in nucleus prepositus hypoglossi and adjacent medial vestibular nucleus during horizontal eye movement in behaving macaques. J Neurophysiol 68: 319–332, 1992. [DOI] [PubMed] [Google Scholar]
- Merfeld DM, Haburcakova C, Gong W, Lewis RF. Chronic vestibulo-ocular reflexes evoked by a vestibular prosthesis. IEEE Trans Biomed Eng 54: 1005–1015, 2007. doi: 10.1109/TBME.2007.891943. [DOI] [PubMed] [Google Scholar]
- Merfeld DM, Zupan L, Peterka RJ. Humans use internal models to estimate gravity and linear acceleration. Nature 398: 615–618, 1999. doi: 10.1038/19303. [DOI] [PubMed] [Google Scholar]
- Nashner LM, Peters JF. Dynamic posturography in the diagnosis and management of dizziness and balance disorders. Neurol Clin 8: 331–349, 1990. [PubMed] [Google Scholar]
- Nashner LM, Shupert CL, Horak FB, Black FO. Organization of posture controls: an analysis of sensory and mechanical constraints. Prog Brain Res 80: 411–418, 1989. doi: 10.1016/S0079-6123(08)62237-2. [DOI] [PubMed] [Google Scholar]
- Nashner LM, Wolfson P. Influence of head position and proprioceptive cues on short latency postural reflexes evoked by galvanic stimulation of the human labyrinth. Brain Res 67: 255–268, 1974. doi: 10.1016/0006-8993(74)90276-5. [DOI] [PubMed] [Google Scholar]
- O’Connor SM, Kuo AD. Direction-dependent control of balance during walking and standing. J Neurophysiol 102: 1411–1419, 2009. doi: 10.1152/jn.00131.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ormsby CC, Young LR. Integration of semicircular canal and otolith information for multisensory orientation stimuli. Math Biosci 34: 1–21, 1977. doi: 10.1016/0025-5564(77)90032-3. [DOI] [Google Scholar]
- Paulin MG. Evolution of the cerebellum as a neuronal machine for Bayesian state estimation. J Neural Eng 2: S219–S234, 2005. doi: 10.1088/1741-2560/2/3/S06. [DOI] [PubMed] [Google Scholar]
- Peterka RJ, Benolken MS. Role of somatosensory and vestibular cues in attenuating visually induced human postural sway. Exp Brain Res 105: 101–110, 1995. doi: 10.1007/BF00242186. [DOI] [PubMed] [Google Scholar]
- Raphan T, Matsuo V, Cohen B. Velocity storage in the vestibulo-ocular reflex arc (VOR). Exp Brain Res 35: 229–248, 1979. doi: 10.1007/BF00236613. [DOI] [PubMed] [Google Scholar]
- Robinson DA. Control of eye movements. In: Handbook of Physiology. The Nervous System. Motor Control. Bethesda, MD: Am. Physiol. Soc, 1981, sect. 1, vol. II, pt. 2, chapt. 28, p. 1275–1320. [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann Stat 6: 461–464, 1978. doi: 10.1214/aos/1176344136. [DOI] [Google Scholar]
- Séverac Cauquil A, Gervet MF, Ouaknine M. Body response to binaural monopolar galvanic vestibular stimulation in humans. Neurosci Lett 245: 37–40, 1998. doi: 10.1016/S0304-3940(98)00161-X. [DOI] [PubMed] [Google Scholar]
- St George RJ, Day BL, Fitzpatrick RC. Adaptation of vestibular signals for self-motion perception. J Physiol 589: 843–853, 2011. doi: 10.1113/jphysiol.2010.197053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki J-I, Komatsuzaki A. Clinical application of optokinetic nystagmus. Optokinetic pattern test. Acta Otolaryngol 54: 49–55, 1962. doi: 10.3109/00016486209126922. [DOI] [PubMed] [Google Scholar]
- Tanahashi S, Ujike H, Kozawa R, Ukai K. Effects of visually simulated roll motion on vection and postural stabilization. J Neuroeng Rehabil 4: 39, 2007. doi: 10.1186/1743-0003-4-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarr MJ, Warren WH. Virtual reality in behavioral neuroscience and beyond. Nat Neurosci 5 Suppl: 1089–1092, 2002. doi: 10.1038/nn948. [DOI] [PubMed] [Google Scholar]
- Wardman DL, Day BL, Fitzpatrick RC. Position and velocity responses to galvanic vestibular stimulation in human subjects during standing. J Physiol 547: 293–299, 2003. doi: 10.1113/jphysiol.2002.030767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woollacott MH, Shumway-Cook A, Nashner LM. Aging and posture control: changes in sensory organization and muscular coordination. Int J Aging Hum Dev 23: 97–114, 1986. doi: 10.2190/VXN3-N3RT-54JB-X16X. [DOI] [PubMed] [Google Scholar]
- Yokota J, Reisine H, Cohen B. Nystagmus induced by electrical stimulation of the vestibular and prepositus hypoglossi nuclei in the monkey: evidence for site of induction of velocity storage. Exp Brain Res 92: 123–138, 1992. [DOI] [PubMed] [Google Scholar]
- Young LR. Visual and vestibular influences in human self-motion perception. In: The Vestibular System: Function and Morphology, edited by Gualtierotti T. New York: Springer, 1981, p. 393–424. doi: 10.1007/978-1-4612-5902-2_24. [DOI] [Google Scholar]
- Young LR. Perception of the body in space: mechanisms. In: Handbook of Physiology. The Nervous System. Motor Control. Bethesda, MD: Am. Physiol. Soc., 1984, sect. 1, vol. III, pt. 2, chapt. 22, p. 1023–1066. [Google Scholar]
- Young LR, Meiry JL. A revised dynamic otolith model. Aerosp Med 39: 606–608, 1968. [PubMed] [Google Scholar]
- Zatsiorsky VM, Duarte M. Rambling and trembling in quiet standing. Mot Contr 4: 185–200, 2000. doi: 10.1123/mcj.4.2.185. [DOI] [PubMed] [Google Scholar]
- Zee DS, Yee RD, Robinson DA. Optokinetic responses in labyrinthine-defective human beings. Brain Res 113: 423–428, 1976. doi: 10.1016/0006-8993(76)90955-0. [DOI] [PubMed] [Google Scholar]