Predicting the response of striatal spiny neurons to sinusoidal input

During repetitive firing, the timing of action potentials is determined by the interaction between the input and voltage-sensitive currents throughout the interspike interval. This interaction is encapsulated in the neuron’s phase-resetting curve. The phase-resetting curve predicted spike timing to small sinusoidal currents over a wide range of stimulus frequencies. Firing patterns were most sensitive to oscillatory components near the cell’s own firing rate, even in the presence of noise and other inputs.

Abstract

Spike-timing effects of small-amplitude sinusoidal currents were measured in mouse striatal spiny neurons firing repetitively. Spike-timing reliability varied with the stimulus frequency. For frequencies near the cell’s firing rate, the cells altered firing rate to match the stimulus and became phase locked to it. The stimulus phase of firing during lock depended on the stimulus frequency relative to the cell’s unperturbed firing rate. Interspike intervals during sinusoidal stimulation were predicted using an iterative map constructed from the cells’ phase-resetting curve. Variability of interspike intervals was reduced by stimulation at all frequencies higher than about half the cell’s unperturbed rate, and interspike intervals were accurately predicted by the map. Long sequences of spike times were predicted by iterating on the map. The accuracy of that prediction varied with frequency. Spike time predictability was highest near and during phase lock. The map predicted the phase of firing on the input and its dependence on stimulus frequency. Prediction errors, when they occurred, were of two kinds: unpredicted variation in interspike interval from intrinsic cell noise and accumulation of prediction errors from previous interspike intervals. Each type of prediction error arose from a different mechanism, and their impact was also predicted from the phase model. When two oscillatory input currents were presented simultaneously, striatal neurons responded selectively to only one of them, the one closest in frequency to the cell’s unperturbed firing rate. Their spike times encoded the frequency and phase of that single oscillatory input.

NEW & NOTEWORTHY During repetitive firing, the timing of action potentials is determined by the interaction between the input and voltage-sensitive currents throughout the interspike interval. This interaction is encapsulated in the neuron’s phase-resetting curve. The phase-resetting curve predicted spike timing to small sinusoidal currents over a wide range of stimulus frequencies. Firing patterns were most sensitive to oscillatory components near the cell’s own firing rate, even in the presence of noise and other inputs.

if the operating principle for a neuron is known, it should be possible to predict its output firing pattern in response to any input. For most neurons, this goal remains elusive. Attempts to predict spike times of real neurons are rare, because making a predictive model for a neuron is difficult. Electrical properties of neurons are controlled by numerous ion channels, whose maximal conductances and states of activation are needed to specify the state of the neuron at every instant. Channel expression and modulation vary among neurons, even among neurons of the same type (Taylor et al. 2009). Quantitative prediction of spike times for any individual neuron would seem to require a complete description of its unique ion channel expression pattern, which cannot normally be gathered in time to predict that same cell’s response to an input.

Perhaps quantitative spike-by-spike prediction of a single neuron’s response is impossible. Neurons or their synaptic circuits might generate noise sufficient to ensure that the spike-by-spike structure of a cell’s response is fundamentally unrepeatable and thus unpredictable. In that case, any signal conveyed by the neuron’s firing must be embedded in some lower-order feature, such as its firing rate averaged over a broader time window. Alternatively, spike timing may be repeatable (and predictable) for some noise-insensitive input patterns, but not for other more noise-sensitive ones. A predictive model of a pattern-selective neuron should explain the rules governing its selective predictability.

It is well known that responses of neurons driven by large-amplitude broadband current or conductance waveforms may be precise and repeatable, but rhythmic repetitive firing in response to constant current is not (e.g., Bryant and Segundo 1976; Hunter et al. 1998; Mainen and Sejnowski 1995). While firing under the influence of constant current, a cell resets its rhythm after every spike. Any variation in interspike interval will alter the starting time for all subsequent spikes, and so even a small degree of variability within each interval will accumulate over a period of a few spikes. Predictability of spike times thus decreases with time after the onset of rhythmic firing elicited by a current step (e.g., Segundo et al. 1968). In contrast, neurons excited by transient depolarizations from rest may only fire when specific events in the input waveform drive the membrane potential rapidly across threshold (e.g., Nowak et al. 1997; Rodriguez-Molina et al. 2007; Toups et al. 2012), producing very repeatable responses. Even when perturbed by inputs and no longer firing rhythmically, repetitively firing neurons obey very different sets of rules from those for neurons firing from rest (Schreiber et al. 2009; Wilson et al. 2014).

One may prefer to study cells excited from the rest state, on the assumption that many cells in vivo maintain a balance of background excitation and inhibition below spike threshold. However, there are also many cells for which that assumption does not hold. Among them are autonomous oscillators, neurons that fire even in the absence of any input. These cells have no resting potential, and their firing in the absence of synaptic inputs resembles that of cells responding to constant current. Other neurons receive prolonged synaptic currents that exceed rheobase and evoke more than one action potential, so that they fire repetitively (but not necessarily rhythmically) for brief periods. By analogy to cells firing repetitively in response to constant current, it might be concluded that in both of these cases the timing of action potentials cannot be reliable and the cells’ firing patterns cannot carry information about the fine temporal structure of the input. However, numerous studies show that repetitively firing neurons may fire very reliably when phase locked to a sinusoidal input signal (e.g., Hunter et al. 1998; Schreiber et al. 2009). At least for some input signals, repetitively firing neurons’ spike timing may be highly reliable, and so potentially predictable. These cells may be able to communicate information about the temporal structure of their input.

The striatal spiny projection (SP) neurons are often silent, but fire in episodes lasting on the order of seconds. These episodes of firing are associated with specific sensory, motor, or motivational events and so are considered to be the responses of the striatum to those events. During their responses, the cells may fire at high rates, up to 80–100 spikes/s (e.g., Kimura 1990; Opris et al. 2011). The firing rate changes of striatal neurons are thought to carry the messages conveyed by the cells onto their target neurons in globus pallidus and substantia nigra (e.g., Wichmann and DeLong 1996). However, striatal local field potentials show prominent behavior-related changes in oscillatory components at much higher frequencies (Courtemanche et al. 2003; Leventhal et al. 2012; van der Meer and Redish 2009). Moreover, firing of responding neurons can be phase locked to particular frequencies in the local field potential (Berke et al. 2004; Courtemanche et al. 2003; Sharott et al. 2009; van der Meer and Redish 2009). Groups of striatal neurons phase locked to a shared oscillatory input might deliver powerful coherent inhibition to neurons in the globus pallidus and substantia nigra. The feasibility of this idea depends on the reliability and predictability of responses of spiny neurons to low-amplitude oscillatory components in the input.

Predicting spike times of real neurons is difficult, but a predictive analysis of the responses of the integrate-and-fire model neuron to sinusoidal inputs was performed long ago by Keener et al. (1981). They constructed a map of spike phases (relative to an input sine wave) and used it to predict the phase of any spike on the input from the phase of the preceding spike. They could explain why phase locking occurs at some frequencies and not others, the phase at which the model cell locked, and the variation of locked phase with frequency. They also predicted the distribution of phases for any stimulus amplitude and frequency, including those that did not evoke phase locking. The creation of the map was possible because the authors had a closed solution for the evolution of state (intrinsic phase) in this very simple neuron model. For a real neuron, or even for a moderately simple conductance-based neuron model, this is still not possible, but it is possible to construct a similar map empirically for any repetitively firing neuron (Stiber et al. 1997). Here we employ the method used by Keener et al. (1981), but with an empirical map for the striatal SP neuron obtained experimentally from its phase-resetting curve during repetitive firing.

MATERIALS AND METHODS

Experiments were performed in accordance with the National Institutes of Health guidelines and were approved by the Institutional Animal Care and Use Committee of the University of Texas at San Antonio. For studies of spiny neurons of unidentified subtype, experiments were performed on 22 cells from striatal slices obtained from 17 C57BL/6 mice of both sexes, aged 27–72 days. Recordings from identified direct and indirect pathway neurons were done in 22 cells from striatal slices cut from 13 animals of both sexes, aged 60–114 days. These mice were the result of crossing B6.Cg-Tg(Drd1a-tdTomato)6Calak/J (stock no. 016204; The Jackson Laboratory) and Tg(Drd2-EGFP)S118Gsat/Mmnc (stock no. 000230-UNC; Mutant Mouse Resource and Research Center) and expressed tdTomato under the control of the promoter for the D1 dopamine receptor (D1R) and/or enhanced green fluorescent protein (EGFP) under the control of the promoter for the D2 dopamine receptor (D2R). In all cases, spiny neurons were identified by their somatic morphology and by the response to 1-s current steps over a range of amplitudes from −200 to +500 pA. Spiny neuron responses were characterized by their strong, fast inward rectification in response to hyperpolarizing current, depolarizing ramp voltage response, delayed firing near rheobase, and reverse spike frequency adaptation at low firing rates. Direct and indirect pathway spiny neurons were additionally identified by fluorescence associated with their specific dopamine receptor.

C57BL/6 mice were deeply anesthetized with isoflurane and perfused intracardially with sodium-free artificial cerebrospinal solution consisting of (in mM) 2.5 KCl, 1.25 NaH₂PO₄, 0.5 CaCl₂, 10 MgSO₄, 10 d-glucose, 26 NaHCO₃, and 202 sucrose, ice-cold, at pH 7.4. The brains were sectioned at 300 µm in the parasagittal plane and collected in artificial cerebrospinal fluid containing (in mM) 126 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, 2 MgSO₄, 10 d-glucose, 26 NaHCO₃, 0.005 l-glutathione, 1 Na-pyruvate, and 1 Na-ascorbate and bubbled with 95% O₂-5% CO₂. Slices were warmed to 35°C for 1 h after cutting and stored at room temperature until used.

D1R/D2R mice were deeply anesthetized with isoflurane, decapitated, and sectioned in the coronal plane at 300 µm, at 37°C, in a solution containing (in mM) 126 NaCl, 2.5 KCl, 1.25 NaH₂PO_4, 2 MgCl₂, 2 CaCl₂, 10 d-glucose, 25 NaHCO₃, 1.3 ascorbate, and 2.4 pyruvate and 2 µM kynurenic acid. Sections were collected in the same storage solution described above and stored at room temperature.

For recording, slices were superfused on the microscope stage with artificial cerebrospinal solution bubbled with 95% O₂-5% CO₂ and containing 5 µM 2,3-dihydroxy-6-nitro-7-sulfamoyl-benzo(f)quinoxaline-2,3-dione (NBQX), 5 µM (2-carboxypiperazin-4-yl)-propyl-1-phosphanoic acid (CPP), and 100 µM picrotoxin at 34°C. Perforated patch recordings were required to maintain constant-frequency repetitive firing in spiny neurons over the periods required for these recordings (30 min to 1 h). In whole cell recordings, firing rate gradually slowed and became irregular over the course of several minutes after rupture of the membrane. Electrodes for perforated patch recording were filled with a solution consisting of 140 mM Na-methylsulfate, 10 mM HEPES, and 7.5 mM NaCl. One milliliter of this solution was filtered, and 1 µl of a solution of 0.5 mg/ml gramicidin (Invitrogen) in DMSO was added and mixed thoroughly. Filled electrodes had resistances of 3–7 MΩ. After a seal was established, 10–30 min was allowed, to achieve access adequate for current-clamp recording (20–70 MΩ) using the active bridge circuit of an Axon Instruments Multiclamp 700B amplifier (Molecular Devices, Sunnyvale, CA). The output was filtered at 10 kHz and digitized at 20 kHz using a HEKA Instruments (Holliston, MA) ITC-18 analog-to-digital converter. Intracellular current command waveforms were made using custom software written using Igor Pro (WaveMetrics, Portland, OR). Access resistance was monitored carefully over the course of the experiment, and any sudden reduction was interpreted as rupture of the cell membrane. Recording was terminated at that point.

Data analysis was performed using software written with Mathematica (Wolfram Research, Champaign, IL). Estimates of the infinitesimal phase-resetting curves were generated using the method described by Wilson et al. (2014). Constant current was adjusted to at least 50 pA above rheobase, to obtain stable repetitive firing at 5–20 spikes/s. Spike times and injected-current waveforms were recorded in repetitively firing neurons during application of a contiguous series of 0.5-ms current pulses. The amplitude of each pulse was an independent draw from a Gaussian distribution with a mean of 0 pA and SD of 40 pA. Each interspike interval was divided into 50 equal-sized phase bins, and a phase was assigned to each by interpolation. The charge delivered in each phase bin was calculated by integrating the current injected over that period, and the resulting series of charges regressed against interspike interval using standard multiple linear regression. This yielded an estimate of the slope and the standard error of the slope estimate for each phase bin. Pulses were applied for 640 s, yielding samples ranging from ~3,000 to 14,000 spikes.

Entropy measurement.

The phase of each spike on the sinusoidal stimulus was measured, and histograms of spike phase were constructed for each stimulus amplitude and frequency. The deviation of each distribution of spike phases from a random distribution was quantified using entropy of the phase histograms, expressed as a proportion of the expected entropy for an identical-size sample drawn from a uniform distribution. The Shannon entropy for the histograms (H) was calculated in the usual way:

$$H=-{\displaystyle \sum }_{i=1}^N{p}_i\hspace{0.17em}{\text{log}}_2\left(p_i\right)$$

in which N is the number of bins in the histogram and p_i is the value of the ith bin normalized by the sample size. This entropy measure takes a value of 0 if all spikes occurred in the same phase bin. The maximal value of H, which is the expected value for a random (uniform) phase distribution E(H_uniform), depends on the number of bins and the number of spikes making up the histogram. A Monte Carlo method was used to determine the E(H_uniform) for each histogram. The entropy of the histogram was scaled by this value so that the values of entropy ranged from 0 to 1. All reported entropies are this measure.

$$H_{\text{corrected}}=\frac{-{\displaystyle \sum }_{i=1}^N{p}_i{\text{log}}_2\left(p_i\right)}{E\left(H_{\text{uniform}}\right)}$$

Firing-time predictions.

The measured phase-resetting curve was fit with a fourth-order polynomial, and the resulting function Z(φ) was used in the phase equation

$$\frac{\text{dφ}}{\text{d}t}=F_{\text{Cell}}+I_{\text{Stim}}\left(t\right)Z\left(\text{φ}\right)$$

in which φ is the intrinsic phase of the neuron, evolving from 0 to 1 during the interspike interval, F_Cell is the cell’s unperturbed firing rate, and I_Stim(t) is the stimulus current, which was the sinusoidal stimulus or combination of sinusoids. Constant current used to set the cells’ firing rates was not included in I_Stim, as its influence was embedded in the value of F_Cell. The phase equation was integrated using the Mathematica NDSolve function, resetting φ to 0 and registering the occurrence of a spike whenever φ ≥ 1. The function Z(φ) is an approximation of the response of the neuron to relatively weak injected currents (Oprisan 2012).

Iterative map of phase.

This map provided the predicted stimulus phase at which a spike will occur (θ_i+1) as a function of the stimulus phase for the previous spike (θ_i) for a given stimulus frequency and amplitude. The map was constructed by running the phase model 1,000 times, starting each simulation at φ = 0 (i.e., the beginning of the interspike interval) at 1,000 values of θ_i from 0 to 0.999.

Lyapunov exponent.

The Lyapunov exponent (LE) was used to predict the propagation of error in long series of spike times. It was calculated by integrating the phase equation for 1,000 cycles and averaging the log of the absolute value of the slope of the iterative map (dθ_i+1/dθ_i) at each phase visited during the 1,000 spikes.

$$\text{LE}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\text{ln}\left(\left|\frac{{\text{dθ}}_{i+1}}{{\text{dθ}}_i}\right|\right)$$

RESULTS

Rate modulation, entrainment, and phase locking.

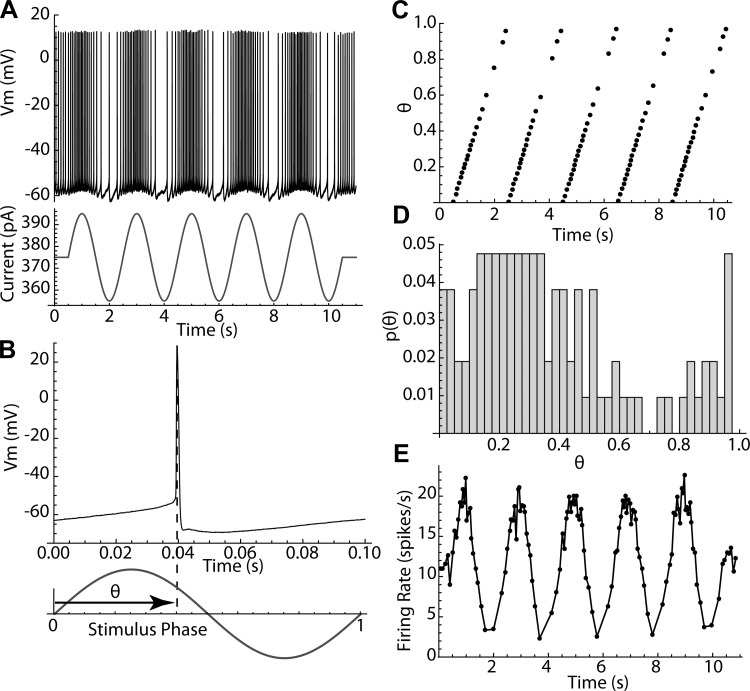
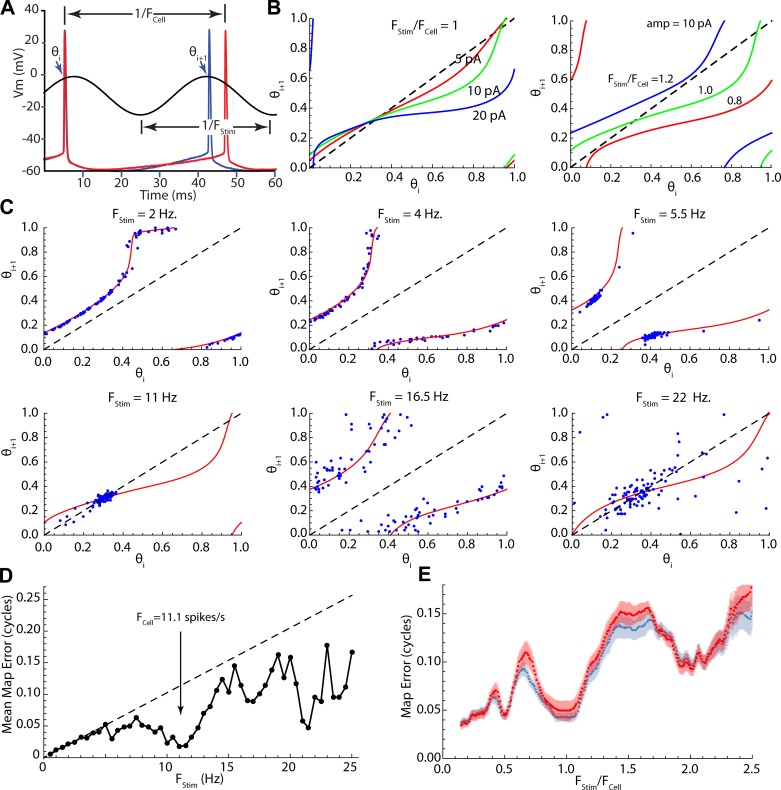
Even small (10–30 pA) sinusoidal currents produced substantial changes in the firing patterns of striatal spiny neurons firing repetitively by concurrent application of a much stronger (150–550 pA) constant depolarizing current. The constant current was adjusted to be at least 50 pA above the minimum required to sustain repetitive firing (rheobase), to ensure that even at the minimum of the sinusoidal current, total current would never fall below rheobase. Cells recorded in perforated patch configuration sustained constant firing at a consistent rate for 1–2 h without adjustment of injected current. Current was set to produce a firing rate within the range from 5 to 20 spikes/s. Ten-second episodes of sinusoidal current modulation were superimposed on the constant current as shown in Fig. 1A, with amplitudes of 10–30 pA and frequencies covering the range from 0.5 to 25 Hz, at 0.5-Hz increments. Each such episode contained 50–200 action potentials, whose phases were measured relative to the stimulus sinusoid. Phase on the stimulus was measured on a scale ranging from 0 to 1, as shown in Fig. 1B, and a sequence of stimulus phases was calculated for each episode, as shown in Fig. 1C. Phase histograms such as the one in Fig. 1D were constructed to measure entrainment of firing to the sinusoidal current.

Fig. 1.

Measurement of the phases of action potentials. A: basics of the experiment; an 11-s trace of a repetitively firing spiny neuron has a 10-s, 20-pA, 0.5-Hz sinusoidal modulation superimposed. Vm, membrane potential. B: each action potential has a phase θ defined relative to the sinusoidal current. Phase varies from 0 to 1. C: graph of the phases of every spike in the trace shown in A. D: histogram of phases for the same trace. E: modulation of instantaneous firing rate for the same trace.

The phase histograms were sometimes multimodal, so the deviation of the histogram from a uniform distribution was calculated using entropy. The entropy of a histogram varies from zero (if all counts are in a single bin) to a positive maximal value expected for a sample from a uniform distribution. The maximal value depends on the number of bins and the sample size (number of action potentials). As used here, corrected entropy is entropy expressed as a proportion of that expected from histograms generated by samples of the same size from a uniform probability distribution (see materials and methods). In this measure, an entropy of 1 indicates a random phase distribution, and lower entropies indicate increasingly structured firing relative to the phase of the stimulus.

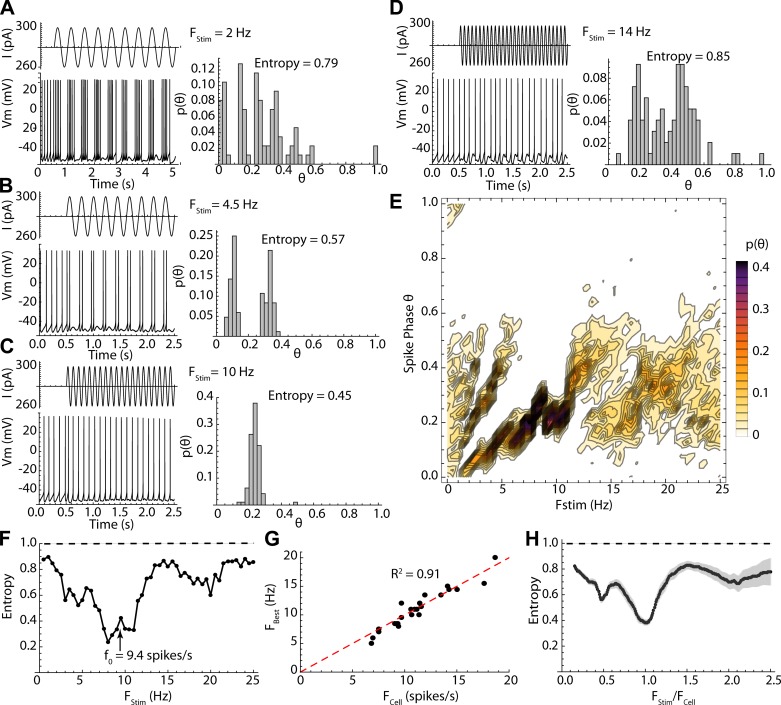
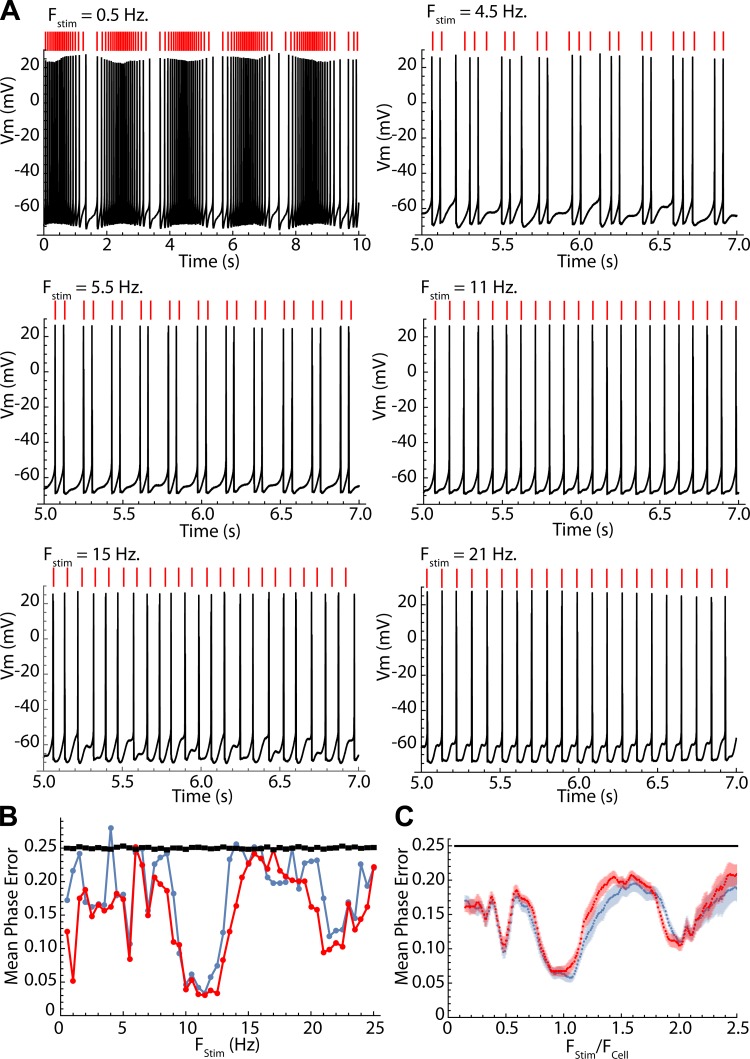
The sinusoidal current modulations delivered no net average charge to the cell and so had only small effects on the average firing rate, but they exerted a powerful influence on the timing of action potentials. The effect of a sinusoidal modulation depended on its frequency. At very low stimulus frequencies (e.g., 0.5 Hz), firing rate was modulated sinusoidally (Fig. 1E), but spikes did not occur at fixed phases on the stimulus. At higher frequencies, action potentials occurred at the same phase on each cycle (e.g., Fig. 2, A and B). Over some range of stimulus frequencies only one action potential was elicited on each cycle of the stimulus, and it occurred at a fixed phase (1:1, Fig. 2C), whereas at still higher stimulus frequencies, one or fewer action potentials occurred per stimulus cycle, and these often were distributed over a wide range of stimulus phases (Fig. 2D). The overall distribution of phases for all stimulus frequencies is shown for the example in Fig. 2E. The phase of firing for 1:1 locking started at ~0.2 and increased with stimulus frequency to ~0.4, after which phase locking was lost. Fixed-phase spike doublets (2:1) occurred at a narrower frequency range in this example centered on 5 Hz, and the phases of both spikes increased with frequency. At high frequencies, the cells fired preferentially at phases between 0.1 and 0.6 but were much less reliable. The stimulus frequencies over which sinusoidal currents evoked this sequence of firing patterns were strictly dependent on a cell’s unperturbed firing rate (i.e., its firing rate in the absence of sinusoidal current). This dependence is shown in Fig. 2, F–H. The low point in entropy (most reliable pattern of firing) corresponded to 1:1 phase locking when the stimulus frequency was near the frequency of unperturbed firing, as shown in Fig. 2C. This is shown for all cells in Fig. 2G, in which the stimulus frequency for minimum entropy (F_Best) is plotted against unperturbed firing rate (F_Cell) for each cell. Additional low points in entropy and fixed-phase firing also occurred at frequencies twice the cell’s unperturbed rate (1:2 phase locking) and one-half the rate (2:1 phase locking). In some cells an additional entropy minimum was observed at one-third of the cell’s firing rate. This pattern was evident in the entropy vs. frequency profile for the entire sample of 24 cells studied in this way, when stimulus frequency was normalized by each cell’s unperturbed firing rate as shown in Fig. 2H. The most disordered firing patterns occurred between the regions of 1:1 and 2:1 phase locking, when the stimulus frequency was between 1.25 and 1.75 times the cells’ firing rates. Even when firing reliability was lowest, phases were not distributed randomly, but were mostly confined to the first half (the depolarizing component) of the stimulus current cycle, and so the corrected entropy was <1 for all stimulus frequencies.

Fig. 2.

Frequency dependence of firing patterns evoked by sinusoidal current. A–D: stimulus currents (traces at top left), neuronal responses (traces at bottom left), and spike phase distributions and their entropies (right) for selected stimulus frequencies in an example cell. E: combined spike phase distribution for all stimulus frequencies tested in the same cell. Each histogram is a column, and probability is in color. Note firing twice per cycle between 3 and 6 Hz and once per cycle from 7 to 11 Hz. In both cases the phase of entrainment increases with increasing stimulus frequency. F: entropy of the phase distribution for all frequencies tested in the same example cell, which had an unperturbed firing rate (f₀) of 9.4 spikes/s (arrow). The phase-locked frequency range was centered on the cell’s unperturbed rate. The entropy values expected if the stimulus intensity were zero are shown by the dashed line. G: relationship between frequency of best phase locking (lowest entropy) vs. unperturbed firing rate for the sample of 24 neurons. H: entropy vs. stimulus frequency (like that shown in F) but for the sample (standard error of estimates in gray). Frequency is normalized by each cell’s unperturbed firing rate to allow comparison across cells firing at different rates. Sine wave stimulation modulates firing pattern at all frequencies but is most effective at the cell’s unperturbed firing rate.

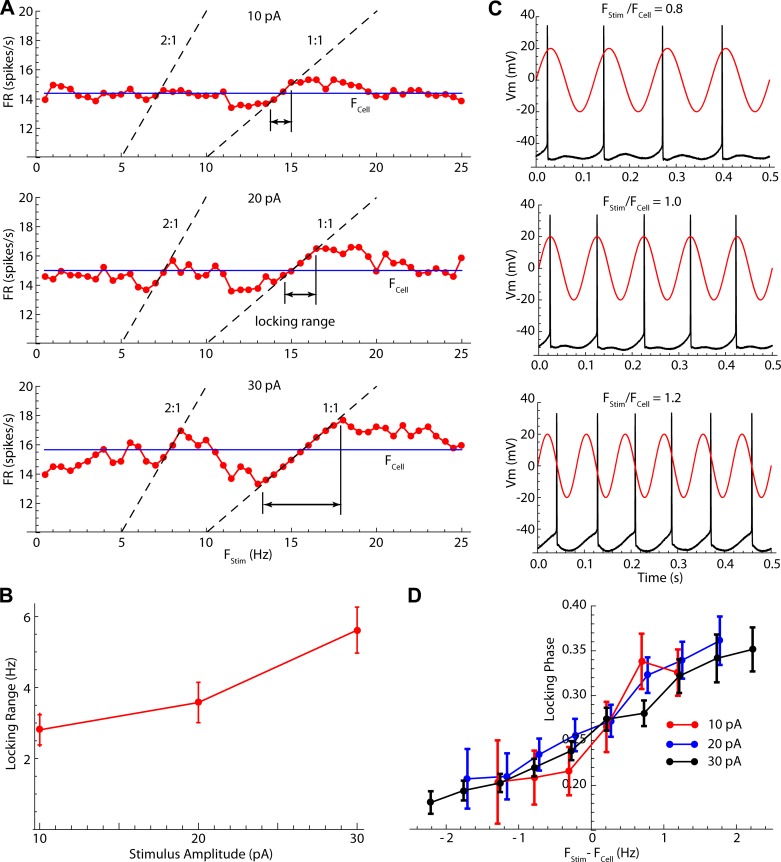
Cells established stable 1:1 phase locking with stimulus frequencies both lower and higher than their unperturbed firing rates, doing so by altering their firing rates to match the stimulus (Fig. 3A). The range of stimulus frequencies over which phase locking was maintained (the locking range) depended on stimulus intensity, with larger-amplitude stimuli producing phase lock over a larger range of stimulus frequencies (Fig. 3B). Firing rates tracking stimulus frequency were also seen near the 2:1 and 1:2 phase-locking frequencies, although the ranges there were much narrower. Changes in average firing rate produced by the stimuli were not confined to the locking range. Stimulus frequencies below the phase-locking range also produced small decreases in firing rate, whereas stimulus frequencies above the point at which locking failed increased firing rate (Fig. 3A). Very low or very high stimulus frequencies had little effect on average firing rates, although the firing patterns could still be altered by these stimuli.

Fig. 3.

Phase-locking frequencies and phases. A: example showing average firing rate (FR) over 10-s episodes of 10-, 20-, and 30-pA sinusoidal stimulation. Blue lines labeled F_Cell are the unperturbed firing rate. During phase lock, firing rate lies on the 1:1 line (firing rate equals stimulus frequency). Locking also occurs on the 2:1 line (2 spikes per stimulus cycle). The range of lock, defined as the frequency range over which there is <10% difference between firing rate and stimulus frequency, is shown. B: averages ± SE of the locking range vs. stimulus amplitude for the sample of 24 neurons (F = 28.65; df = 2,24; P < 0.01). C: in the locking range, the phase of firing depends on stimulus frequency relative to unperturbed rate, even though at that moment the cell is firing at the stimulus frequency. D: means ± SE of the firing phase at lock for 10-, 20-, and 30-pA sinusoidal stimulation. Locking range is defined relative to the cell’s unperturbed rate (F_Cell). The phase range (0.2–0.35) is the same for all amplitudes.

The highly reliable nature of the cell’s firing pattern in response to oscillatory input suggests that it might be possible to understand the rules governing the entrainment of firing and to predict the firing sequence of the cell, at least for some stimulus frequencies. What determines the frequency-specific firing patterns produced by these oscillating inputs? How can a symmetric input such as a sine wave produce changes in firing rate that force a cell to match its rate to the input frequency, as seen in and near the phase-locking range? What determines the phase of the stimulus at which the cell locks and the frequency-dependent sequence of phases seen in the locking range?

Phase model.

For neurons firing repetitively, the rules governing responses to inputs are different from those holding for even the same neurons when a momentary input excites them to fire from a rest state. The evolution in the cell’s state variables (voltage and the activation and inactivation states of all its ion channels) forms a closed loop between action potentials during repetitive firing, connecting each action potential to the ones before and after it. The multidimensional state-space of the neuron is thus reduced effectively to a circle (Oprisan 2012). A single time-varying quantity, phase, specifies the state of the cell as a position on that loop. Note that this kind of phase, the cell’s intrinsic phase (denoted φ), is distinct from the phase of the action potential on a sinusoidal stimulus (θ) described above. The intrinsic phase does not refer to any stimulus, but to the cell’s own progress from one action potential to the next. In the absence of any stimulus, intrinsic phase would advance at a constant rate, so that the cell completes one cycle in a fixed amount of time, its unperturbed period. Inputs acting on the cell perturb its intrinsic phase. All inputs, even continuous ones such as sinusoids, may be viewed as a dense sequence of asymptotically brief current pulses. The phase change produced by each pulse is retained after that input is complete and has the effect of shifting phase so that the cell will fire slightly earlier or later than it would have otherwise. The effects of multiple inputs occurring in the same interspike interval accumulate, so that the time of firing is determined by all the input currents arriving between two action potentials. Each interspike interval is assumed to be independent of the previous one, depending only on the inputs arriving within it. Of course, all of this is an approximation, and a phase model is not guaranteed to predict the firing accurately for any real neuron. However, there is reason to expect phase models to work well in some situations (Gutkin et al. 2005; Smeal et al. 2010; Stiefel and Ermentrout 2016), and they have been shown to predict firing statistics and interspike intervals for subthalamic neurons firing irregularly during dense current noise (Wilson et al. 2014).

The phase evolution of a repetitively firing neuron with baseline frequency F_Cell is determined by

$$\frac{\text{dφ}}{\text{d}t}=F_{\text{Cell}}+I_{\text{Stim}}\left(t\right)Z\left(\text{φ}\right)$$

in which φ is the intrinsic phase of the neuron, progressing from 0 to 1 over each interspike interval, I_Stim(t) is the time-varying input current, and Z(φ) is the phase-resetting curve (PRC), which represents the phase change produced by a unit charge applied instantaneously at phase φ (Kuramoto 1984). The PRC contains an implicit description of the set of cell properties that determine its response to inputs. The dependence of phase resetting on intrinsic phase reflects the fact that the effect of a stimulus depends on the timing of the stimulus within the interspike interval. For example, in many cells, currents applied immediately after an action potential (when the after-hyperpolarization conductance is large) are relatively ineffective at changing the timing of the next action potential, so the value of Z at early phases may be low. Similarly, the changes in sensitivity to inputs throughout the interspike interval reflect the changes in activation of all the ion channels that are driving the cell’s repetitive firing (e.g., Farries and Wilson 2012). For the experiments described here, the constant current stimulus controls F_Cell, whereas I_Stim(t) is the sinusoidal time-varying modulation of current, which has an amplitude (a), frequency (F_Stim), and starting stimulus phase θ₀. For these stimuli,

$$\frac{\text{dφ}}{\text{d}t}=F_{\text{Cell}}+a\hspace{0.17em}\text{sin}\left[2\pi \hspace{0.17em}\left(F_{\text{Stim}}t+{\text{θ}}_0\right)\right]Z\left(\text{φ}\right)$$

To determine any interspike interval, φ is set to 0 at the time of an action potential, and the phase equation is integrated numerically until the time of the next action potential (which happens when φ is 1). The interspike interval (ISI) is the elapsed time.

Measuring the phase-resetting curves of spiny neurons.

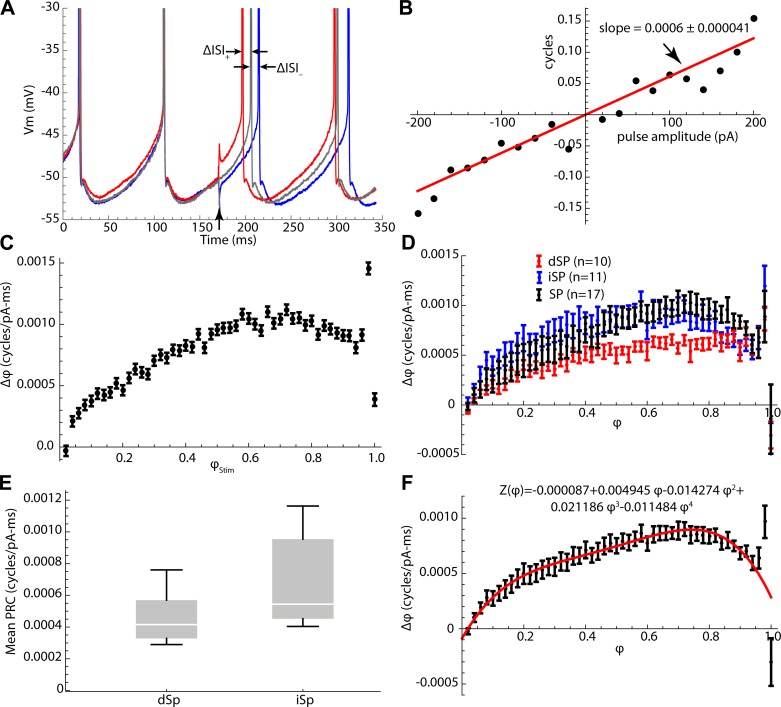
There are many ways to measure the PRC, but the simplest is to apply a single, brief current pulse at time t_s during the interspike interval and measure the resulting change in timing of the next spike. With no other stimulus current present, there is nothing to alter the cell’s phase in the portion of the interspike interval preceding the stimulus, so the phase of a stimulus at time t_s can be estimated accurately as t_s × F_Cell and the change in phase produced by the stimulus pulse can be measured as ΔISI × F_Cell. By applying pulses over a range of amplitudes, one expects to obtain a linear relationship between pulse amplitude and the resulting phase change, as shown in Fig. 4A. The slope of this line (scaled by the duration of the current pulse) is the value of the PRC at phase t_s × F_Cell. Repeating this process over the entire range of interspike times would eventually describe the entire curve. There is some intrinsic variability of the unperturbed interspike intervals, because of intrinsic membrane current noise (e.g., the stochastic opening of ion channels), and this produces variability in the change in phase for a given stimulus phase and amplitude, as seen in Fig. 4B. The resulting uncertainty in the slope of the stimulus charge vs. phase change relationship is quantified by the standard error of the estimate of slope. The values of the slopes and their standard errors at each stimulus phase become the values and standard errors of estimation of the phase response curve. Although simple, this method is inefficient. To speed it up, the PRC was measured using a variant of the method employing dense random noise pulses (Wilson et al. 2014). Current pulses with 0.5-ms duration were applied every 0.5 ms for 640 s. Current pulse amplitudes were selected as individual draws from a normal distribution with a mean of 0 pA and SD of 40 pA, so that the average current was zero, and the average firing rate was not changed. The individual contributions of pulses applied at any one phase were extracted by multiple regression to get the slopes and standard errors of the phase-resetting curve over the entire range of phases (Fig. 4C).

Fig. 4.

Measuring the phase-resetting curve for SP neurons. A: effect of ±180-pA, 0.5-ms current pulses on the membrane potential trajectory and firing time of a spiny striatal neuron during repetitive firing at ~10 spikes/s. B: change in phase (ΔISI × F_Cell) for a variety of pulse amplitudes applied at the same time point. The slope of the line indicates the sensitivity of the cell to applied charge at that point in the interspike interval. C: a phase-resetting curve (PRC) constructed for a striatal spiny neuron by calculating the slopes at times covering the entire range of the interspike interval. Stimulus time (on the abscissa) is normalized to intrinsic phase. D: phase-resetting curves for three groups of cells, identified direct pathway neurons (dSP), indirect pathway neurons (iSP), and a sample of spiny cells of unidentified pathway (SP). E: comparison of the average amplitude of the PRC for dSP and iSP neurons. F: average PRC for all neurons in the sample, and fourth-order polynomial fit used for predicting spiny cell responses (red line and equation).

PRCs were constructed for 38 SP neurons, including 10 direct pathway (dSP) neurons, 11 indirect pathway (iSP) neurons, and 17 not identified by pathway. dSP and iSP neurons were identified by tdTomato or EGFP expressed under the D1R or D2R promoter, respectively (see materials and methods). PRCs of SP neurons in all three groups strongly resembled each other in shape, although they differed in size. The size, or average amplitude, of the phase-resetting curve is a measure of the overall sensitivity of the cell. It has previously been shown that direct and indirect pathway cells differ in their sensitivity of firing rate to the amplitude of constant current pulses (Gertler et al. 2008; Kreitzer and Malenka 2007). The phase-resetting curves for direct and indirect pathway neurons and for the group of unidentified spiny neurons were compared, as shown in Fig. 4D. As expected, the distributions of average amplitudes of dSP and iSP neurons were highly overlapping (Fig. 4E), but the average PRC size was higher for the indirect pathway neurons than for direct pathway neurons [t = 2.3, degrees of freedom (df) = 19, P < 0.05]. When scaled to have the same average amplitude, the average PRCs for the three groups of cells were very similar. Over the range of firing rates studied, there was no systematic variation in PRC shape or size with changes in firing rate. For purposes of predicting the responses of spiny neurons, a fourth-order polynomial was fit to the PRC of individual cells or to the average PRC for the entire sample of spiny cells, and for each cell the fitted PRC waveform (Fig. 4F) was scaled to the average amplitude of the PRC for that individual cell.

Iterative map of phase.

The first step in predicting the responses of neurons from the PRC is to use the stimulus phase of one spike (θ_i) to predict the next (θ_i+1). This is equivalent to predicting single interspike intervals in the presence of the stimulus, as illustrated in Fig. 5A. The predictions were performed by numerically integrating the phase model for many (1,000) values of the starting phase θ_i. This produces a series of phase pairs that can be joined to make a continuous map showing the predicted outcome θ_i+1 for all starting phases θ_i. The features of the map depend on the phase-resetting curve and the amplitude and frequency of the sinusoid. As shown in Fig. 5B, each stimulus amplitude and frequency generate a unique map. Increasing stimulus amplitude increases the curvature of the map (deviation from the diagonal line), whereas changes in stimulus frequency shift the map’s position. It should be noted that phase is circular, so that what appear to be discontinuities are only the map wrapping around the 0-1 phase boundary.

Fig. 5.

Iterative maps of spike phase on sine wave stimuli. A: measurement of phase pairs. The phases of the ith and (i+1)th action potentials on the stimulus (blue trace) and the trajectory of an unperturbed interspike interval (red trace). B: stimulus frequency and amplitude (amp) dependence of the phase map. Increasing stimulus intensity increases the deviation of the map from the diagonal, whereas changes in stimulus frequency translate the map. C: comparing the maps, based on the phase model, with actual stimulus phases of spike pairs in an example spiny neuron. D: phase map error for the example shown in C. Dashed line indicates expected error for a zero-amplitude stimulus. Note especially accurate predictions for the map near the cell’s unperturbed firing rate (arrow) and at twice that frequency. E: averages ± SE of map prediction errors for the entire sample. Prediction errors were calculated twice, once (blue curve) using each cell’s individual PRC and once (red curve) using the average PRC for striatal spiny neurons. Stimulus frequency is normalized to each cell’s unperturbed firing rate to allow comparison across neurons.

The effectiveness of the phase map at predicting interspike intervals throughout the stimulus was tested by superimposing its prediction on the actual phase pairs from a spiny neuron collected at the same stimulus frequency and intensity. For these comparisons, we used the map calculated using the average phase-resetting curve for spiny neurons (Fig. 4E). An example comparing the phase map (red lines) with the phase pairs from an example neuron (blue points) is shown for selected stimulus frequencies in Fig. 5C. The mean absolute value of the prediction error of the map was measured for each frequency, as shown in the example in Fig. 5D. There is an overall increase in error with increased frequency. This is expected, even in the absence of an effective stimulus, because the same small variations in spike timing produce small phase errors at low stimulus frequencies (for which stimulus phase changes slowly) but make larger phase errors at high stimulus frequency (for which stimulus phase changes rapidly). This expectation is shown by the dashed line in Fig. 4D, which represents the phase error for a stimulus of vanishing amplitude. In this example, the mean interspike interval was 91 ms, and the mean absolute deviation of interspike intervals during unperturbed firing was 10 ms. At a stimulus frequency of 1 Hz this translates into a mean prediction error of 0.01, but at 20 Hz it would produce a prediction error of 0.2. Downward deviations of the error from the dashed line in Fig. 5D represent increases in the accuracy of prediction better than that expected from the variance of interspike intervals during unperturbed firing. Note that predictions are better than expected for all frequencies above ~5 Hz and predictions improve greatly in the phase-locking ranges near the cell’s unperturbed firing rate and twice the firing rate. The average map error for all the neurons in the sample is in Fig. 5E and shows the same trend. For this measurement, stimulus frequency was normalized to each cell’s unperturbed firing rate, so that curves from cells going at different rates could be averaged. There was no improvement in the average quality of the prediction when the cell’s own PRC was used to make the prediction instead of the mean PRC, consistent with the strong similarity of the PRCs across spiny neurons.

Sequences of spikes.

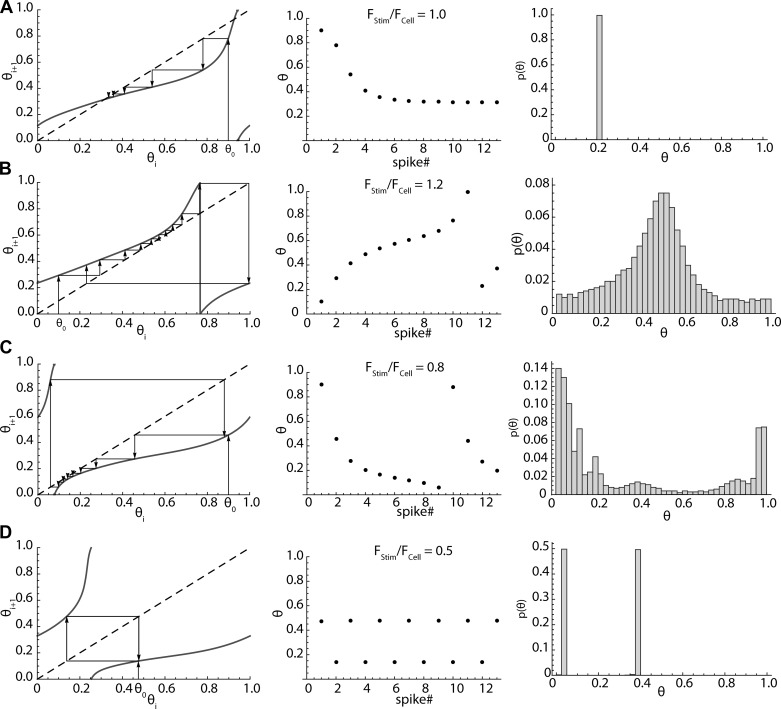
The phase map provides a means of predicting phase sequences of arbitrary length, as well as single phase pairs. Predicted 10-s sequences were compared with those obtained in striatal spiny neurons during sinusoidal stimulation. A starting stimulus phase θ₀ was determined by the time of the first spike after onset of the sinusoidal stimulus. The map was used to find the next phase, and this was repeated. The identity line is useful as a graphical aid for iterating on the map, as shown in Fig. 6. The sequences of phases predicted in this manner were used to calculate the distributions of phase expected in a noise-free model striatal spiny cell characterized by its firing rate and PRC, while applying a stimulus of specified frequency and amplitude.

Fig. 6.

Predicting phase sequences and histograms by map iteration. The order of phases in the sequence is indicated by arrows. A: fixed points in the map (left) arise when the map (solid line) crosses the identity line (dashed line). One of the crossings will be stable, and phase sequences (middle) approach that point. This is phase lock. The steady-state phase distribution (right) consists of only that point, the phase at lock. B: at sufficiently high stimulus frequency there is no longer a fixed point, but a sequence of stimulus phases. Phases associated with the closest approach of the map to the identity line occur more than others, because the stimulus causes the cell to speed up at these phases, reducing the difference between the stimulus frequency and the firing rate. C: at stimulus frequencies too slow to have a fixed point in the map, the closest approach of the map to the identity line occurs at earlier phases, at which the stimulus is most effective at slowing the cell’s firing. The cell fires faster at other parts of the sequence. D: when the stimulus frequency is half the cell’s firing rate, the cell fires twice on each stimulus cycle. Each of the two stimulus phases at which the cell fires maps onto the other.

At some stimulus frequencies, the phase map for SP neurons crosses the identity line (the line for which θ_i = θ_i+1) at two places (e.g., Fig. 6A). These are fixed points, at which the map predicts no change in stimulus phase from one spike to the next. One fixed point is stable, and one is unstable, as apparent from the sequences of spike phases formed in their vicinities. Upon iteration, the stimulus phase of spiking in these sequences approaches a constant value at the stable fixed points, as shown in Fig. 6A. If the map for some combination of stimulus frequency and amplitude contains a stable fixed point, the steady-state distribution of phases will be narrow and centered on the phase of the fixed point. There is a stable fixed point when the stimulus phase matches the cell’s firing rate, and this corresponds to 1:1 phase locking between the cell and stimulus. The shape of the phase-resetting curve determines the value of stimulus phase at the fixed point. For maps made using the striatal spiny neuron PRC, fixed points occurred at phases between 0.2 and 0.35. Increases in stimulus frequency shift the map up, causing the intersection with the identity line to shift to higher phases, whereas decreases in stimulus frequency shift the map down and decrease the cell’s stimulus phase during lock, which explains the results obtained in spiny neuron recordings (Fig. 3).

Not all combinations of stimulus amplitude and frequency make maps with fixed points. Even so, many key features of the response of the neuron to sinusoidal stimulation can be understood by examination of the phase map. At frequencies just above and below the range of phase lock, the intersection between the map and the identity line is lost, and firing occurs as a sequence of stimulus phases rather than approaching a fixed value (Fig. 6, B and C). The frequency range of lock is determined by the stimulus amplitude and the shape of the phase map, being broader for high amplitudes, as observed empirically (Fig. 3).

The cause of changes in firing rate in and near phase lock is also evident from the map. The cell fires at some stimulus phases much more often than others (as seen in the histograms in Fig. 6, B and C), and each stimulus phase aligns the stimulus differently with respect to the cell’s PRC. For example, when the cell is phase locked but the stimulus frequency is lower than the cell’s unperturbed firing rate, the depolarizing half of the stimulus waveform is aligned with the low-sensitivity early part of the cell’s PRC, whereas the hyperpolarizing part of the stimulus is aligned with the higher-sensitivity later part. The net effect is to slow firing. Likewise, when the stimulus rate is higher than the cell’s unperturbed firing rate, the depolarizing part of the stimulus is aligned with the most sensitive region of the PRC. This effect is responsible for the frequency changes that happen over the entire locking range of stimulus frequencies, but it also happens at other nearby frequencies (e.g., Fig. 6, B and C). Although not phase locked, the cell lingers at some phases, changing slowly, and then changes rapidly at others. In this situation as well, when the stimulus frequency is higher than the cell’s unperturbed rate, the most sensitive part of the cell’s interspike interval occurs more often during the depolarizing phase of the stimulus, and thus the net impact of the stimulus is to shorten intervals (increase rate). These map features explain the stimulus frequency-dependent rate changes shown in Fig. 3A.

Although the map does not represent the effects of cellular spike time variability, the features associated with phase lock remain even in the presence of phase perturbations caused by the cell’s noise or by other stimulation occurring at the same time as the sinusoidal oscillation, because they are governed by the attractive nature of the map and the shape of the PRC. The effect of a singular stimulus or noise that could transiently disrupt phase lock with the stimulus would dissipate over time rather than propagating to future spikes. Thus, for cells responding to periodic inputs, predictability does not necessarily decay over time, and the prediction of phase of firing on the stimulus far in the future may be as good as that for the next action potential.

Predicting phase.

The accuracy of the phase model in predicting spike timing over entire sequences was measured by integrating the phase equation to predict spike times over the entire 10-s sequences of sine wave stimulation, using only the phase of the first action potential in the sequence as the starting point, θ₀. Example results are shown in Fig. 7A, where it is evident that the prediction accuracy is frequency dependent. To quantify the accuracy of the prediction, the absolute values of the differences between the phase of every spike in the predicted sequence and that of the corresponding neuronal spike were averaged to get a mean phase error. Phase is circular and varies from 0 to 1, so the maximum error possible is 0.5 and the expected value for a uniform distribution is 0.25. The average phase error may thus vary between 0 and 0.25, the expected value for a random spike train. Neuronal spikes were compared with the predicted spike strictly by order in the sequence (not by proximity in time). Unlike the predictions for single phase pairs or interspike intervals, this prediction is very sensitive to accumulated errors. Mean phase errors for every stimulus frequency for the example in Fig. 7A are shown in Fig. 7B. Also shown in Fig. 7B are the expected values and standard errors for a random spike train of the same length. The prediction was done twice, once using the cell’s own PRC and once using the average PRC for spiny neurons scaled to have the same mean value (overall sensitivity to input) as the cell’s PRC. This tests whether heterogeneity among neurons in the shape of phase-resetting curves might impact the prediction. In this example and in all neurons, the predictions obtained with the average PRC were as good as or better than those for the cell’s own PRC. The average prediction error for the sample of 24 neurons is shown in Fig. 7C. Note that prediction was better than chance over all frequencies but was especially good at frequencies for which the cell’s firing was phase locked to the stimulus.

Fig. 7.

Testing the phase model predictions of full firing sequences. Predictions were made by iterating the map as in Fig. 6, from a starting phase measured from the first spike in the sequence. A: predicted spike times and actual spike times for an example neuron at selected frequencies. Predicted spike times are shown as red lines above each trace. The lowest frequency (0.5 Hz) shows an entire trace; the rest are 2 s of data taken halfway through the trace, to allow spike-by-spike comparison. Predictions are very good at some frequencies (e.g., 11 and 21 Hz) and poor at others (e.g., 4.5 and 15 Hz). B: mean prediction error at all stimulus frequencies for the example cell shown in A, calculated as the mean absolute value of the difference in stimulus phase of every spike and its corresponding prediction. Two error estimates were calculated, one using the cell’s own PRC (blue) and one using the average PRC for the sample of striatal spiny neurons (red). The black line is the expected value and standard error for a zero-amplitude stimulus (uniform stimulus phase distribution). C: averages ± SE of prediction error for the entire sample of striatal spiny neurons, calculated using each cell’s own PRC (blue) or the average for the sample (red). Chance performance is indicated by the black line.

Predicting predictability.

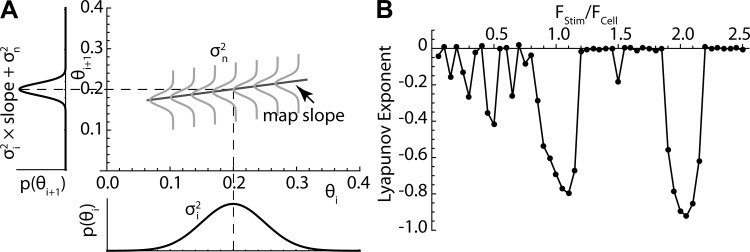
The phase model predicts the behavior of a noise-free cell. The difference between the model prediction and the cell is attributable to the intrinsic irregularity of the cell’s firing. Thus the frequencies for which prediction is accurate must be those at which the cell is insensitive to disruption by noise and other inputs. What controls the sensitivity to noise? It is useful to divide variability into two components. The first is the influence of noise on individual interspike intervals. During the interspike interval, noise is effectively an input current that acts through the PRC to alter phase. If the noise is symmetrical (its overall average is zero), it has little effect on mean rate but produces variation from one interspike interval to the next and is responsible for the nonzero variance of the interspike interval histogram (Ermentrout et al. 2011; Wilson et al. 2014). A second component of variability is the accumulated error from the previous intervals. For purposes of any one iteration on the phase map, this second part can be represented as a probability distribution surrounding the value of θ_i. For a stable fixed point on the map, at which the expected value of θ_i is constant from interval to interval and the uncertainty in θ_i is symmetrical around that point, as shown in Fig. 8A, the propagation of previous errors to the next interval can be seen to depend on the slope of the phase map. A distribution of phases on the abscissa (θ_i) will be converted by the map to a predicted distribution on the ordinate (θ_i+1), and this determines what proportion of the variance of phases on the ith cycle is propagated to the (i+1)th cycle. For a Gaussian distribution on the ith cycle, the proportion of its variance propagated to the (i+1)th cycle is the map slope. If the map slope is 1, as happens when the stimulus intensity is zero, then all of the variance on each cycle propagates to the next. New variance is inserted on each interspike interval because the cell is exposed to noise in the time between spikes. The phase variance of the (i+1)th cycle will be the proportion propagated from the previous cycle plus the variance inserted by the new noise. The shallower the slope of the map at the fixed point, the less errors will propagate and the more noise insensitive the cell will be. If the slope of the map at the fixed point were zero, then there would be no propagation of the effects of noise from one spike to the next. The phase model not only predicts the sequence of spike times but also sets limits on the predictability (and reliability) of spike times as a function of frequency and amplitude of a single sinusoidal input, in the presence of noise.

Fig. 8.

Slope of the iterative map determines accumulation of error. A: at phase lock in the presence of noise, the phase of the ith spike is described as a probability distribution with variance σ_i². During the interspike interval, exposure to noise introduces additional variability with variance σ_n². If the slope of the map is larger than zero, some of the variance of the ith interspike interval will propagate to the next, and errors will accumulate. The rate of accumulation is equal to the slope of the map. B: the Lyapunov exponent is the mean value of log of the slopes of all visited points on the map. It predicts the frequencies at which errors will accumulate, with a value of zero meaning summation of errors over time and with negative values associated with small values of slope and frequencies at which error accumulation will be minimal. Note the similarity between the graph in B and the mean errors shown in Fig. 7.

The slope of the map predicts the propagation of noise at all stimulus frequencies, not only at phase lock. Sequences of firing when the cell is not phase locked visit many locations on the map, and so the slopes at each of these points contribute to the average accumulated error of prediction. By calculating the slope at each visited phase on the map and averaging those slopes in proportion to how often they are visited over a long sequence of firing, it is possible to predict the propagation of prediction error for any stimulus frequency and amplitude. The standard measure is the Lyapunov exponent of the map, which is the average of the logs of the slopes visited in an infinitely long sequence of spikes (Galán et al. 2008). A Lyapunov exponent of zero corresponds to an average map slope of 1 and indicates that all variation in spike time accrued on each interval will on average be propagated to the next interval. This is the case during unperturbed firing, when stimulus amplitude is zero, and spike time prediction decays rapidly over time because of accumulated error. Very negative values represent slopes approaching zero and are associated with improved reliability and predictability. The Lyapunov exponent was estimated by iterating the map for 10,000 spikes and averaging the log of the slopes at visited points. Figure 8B shows the values for the spiny cell example in Fig. 7 with a stimulus amplitude of 20 pA. Note that regions of negative Lyapunov exponents correspond closely to the frequencies of maximum predictability.

It should be noted that for cells receiving sinusoidal stimuli, the spike time variance caused by noise exposure during single interspike intervals is also dependent on stimulus frequency. This occurs because the sinusoidal stimulus alters the shape of the cell’s intrinsic phase trajectory, φ(t). For example, at the fixed point at F_Stim/F_Cell = 1, the cell’s intrinsic phase trajectory increases slowly at first, under the influence of the hyperpolarizing part of the sinusoidal stimulus, causing the cell to linger at phases for which the value of the PRC is low, making the cell insensitive to its intrinsic noise. When the depolarizing part of the stimulus arrives, it accelerates the cell’s intrinsic phase rapidly to the firing point, so the cell spends a short time in the noise-sensitive late phase of its trajectory. The noise insensitivity at phase locking is caused by the combination of two effects: 1) reduced noise sensitivity during each interspike interval and 2) reduced error propagation from one interval to the next. These effects account for the improvement of interspike interval prediction caused by the stimulus, shown in Fig. 4, D and E.

Striatal neurons select frequency components in their input.

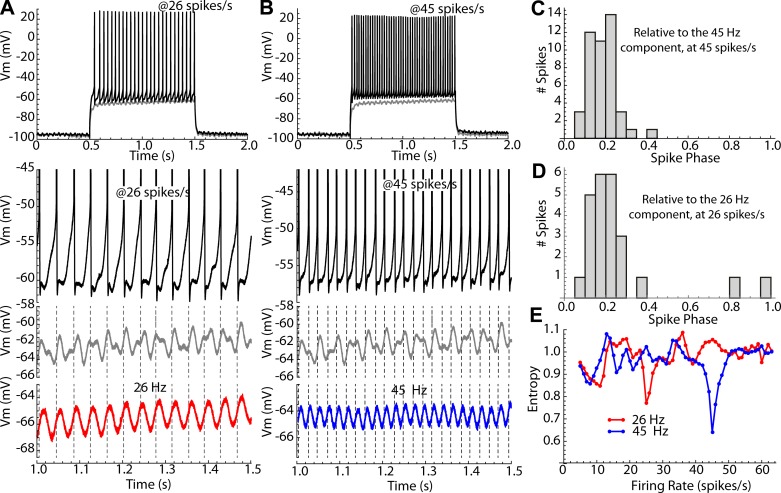
Striatal neurons receive periodic input signals of more than one frequency arising from circuits in the cerebral cortex and striatum (e.g., Sharott et al. 2009). Moreover, the firing rates of striatal spiny neurons are not constant, as in the experiments above, but alternate between periods of relative silence and episodes of firing. In behaving animals, the episodes of activity may be correlated with specific sensory, motor, or cognitive states. To better reflect the effects of periodic input to spiny neurons under natural circumstances, two different frequencies of small-amplitude (20 pA) sinusoidal currents were applied simultaneously, and the firing rate of the spiny neurons was manipulated by injection of 1-s current pulses. The amplitudes of the current pulses were varied systematically to evoke episodes of repetitive firing over a wide range of rates comparable to the range seen in vivo. The two oscillatory inputs were selected to be of incommensurable frequency, so that there would be no overlap in the frequency ranges of firing at which they might evoke phase locking in the neurons. One oscillatory input was in the gamma range (45 Hz), and the other was in the beta range (26 Hz), both rates at which it was easy to drive spiny neurons’ firing. Upon establishing a perforated patch recording, the cell’s sensitivity to current pulses (frequency-intensity curve) was characterized using constant current pulses. The cell was then tested over a firing rate range of 10 to at least 50 Hz in the presence of both the 26- and 45-Hz oscillating inputs, and with the 26- or 45-Hz input alone.

Figure 9 illustrates the experiment. The frequency-intensity curve for the cell was constructed using 1-s constant current pulses. This was then repeated with the addition of the 26- and 45-Hz sinusoids or with each sinusoid alone (Fig. 9, A and B). The effect of the sinusoidal currents on membrane potential was assessed in the subthreshold range by superimposing them on a subthreshold current pulse (Fig. 9, A and B). This allowed a visual comparison of spike times relative to the subthreshold membrane potential waveforms. One might expect that action potentials would occur at times when there were peaks in the subthreshold membrane potential waveform, but this was never observed. During repetitive firing, the spike-related currents dominated the membrane potential trajectory, obscuring the direct membrane response to the sinusoidal input current. Over most of the range of firing rates, the small sinusoidal currents had only a weak influence on the firing pattern. When the firing rate approached the frequency of one of the sinusoidal currents, firing of the neuron became phase locked to that sinusoidal component, with no apparent relation to the other component. This could be seen by comparing the subthreshold membrane potential waveform in response to one of these components alone with the subthreshold response when both components were present (note that both components were present when the cell was firing). To quantify the effect of the small sinusoidal currents on repetitive firing at all rates, phase histograms were created, and their entropies were calculated, as described above. For each current step, the phases relative to the 26-Hz oscillation and those relative to the 45-Hz oscillation were determined, and their entropies were calculated. An example is shown in Fig. 9, C–E. Phase entropy relative to each of the two stimulus frequencies showed a minimum when the cell’s firing rate corresponded to that stimulus frequency, and there was very little effect of the sinusoidal currents at other firing rates.

Fig. 9.

Two-frequency stimulation of an example SP neuron. A and B: constant current pulses were used to evoke episodes of repetitive firing at 5–75 spikes/s, and two different 20-pA sine wave currents were superimposed, one at 26 Hz and one at 45 Hz, either alone or together. A: with the cell firing at ~26 spikes/s the interspike voltage trajectory is dominated by spike currents, and the influence of the sine wave stimulus is detectable but not clearly related to firing. With the constant current reduced just enough to not evoke firing (gray trace), the influence of the two sine wave stimuli on the membrane potential is apparent. The timing of action potentials (dashed lines) does not correspond with peaks in the subthreshold membrane potential waveform. However, the spikes are phase locked to the subthreshold membrane response to the 26-Hz sine wave component, as is apparent when it is presented alone (red trace). B: similarly, when the cell is firing at ~45 spikes/s, action potentials are phase locked to the membrane response to the 45-Hz component (shown alone in blue), even though the spiking trace is recorded in the presence of both sine waves. C–E: quantification of phase locking to the individual sine wave components. C: phase distribution of firing at 45 spikes/s on the 45-Hz component of the stimulus current waveform. D: phase distribution of firing at 26 spikes/s on the 26-Hz sine wave component. E: entropy of the phase distributions of firing on the 26-Hz (red) and 45-Hz (blue) components at all firing rates.

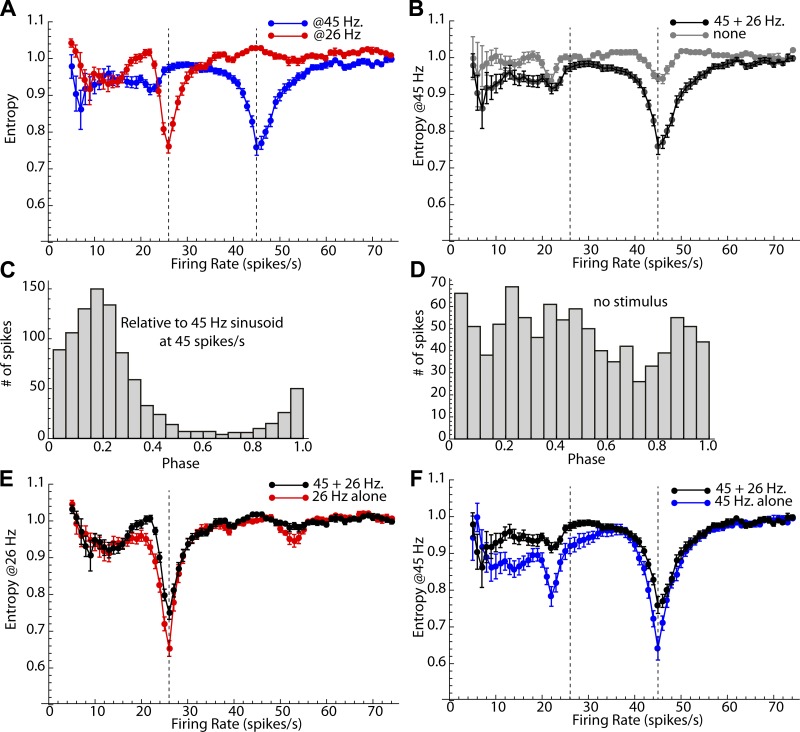
Entropy measurements for the sample of cells showed the same result (Fig. 10A). When the constant current pulse caused the cells to fire at or near 26 Hz, firing became phase locked to the small 26-Hz sine wave input. Likewise, the 45-Hz sine wave did not structure firing of spiny cells except when they were firing at a rate close to 45 Hz. Of course, two uncoupled oscillators (e.g., the sine wave and the neuron) running at the same frequency may show a spurious phase locking merely because they are at the same frequency. To rule out such effects, the sinusoidal stimulus was calculated but not applied to the cell. The entropy measurements for the 20- and 0-pA stimuli are compared for the sample at each firing rate (Fig. 10B). Although there is a small effect of rate similarity, little of the entropy effect can be attributed to this artifact. Moreover, when oscillators with identical frequency are spuriously phase locked, their relative phases are determined by the starting phase. The starting phase varied from cell to cell, so the phase of any spurious phase locking will be random across cells. The combined distributions of phase for all neurons in the sample are shown in Fig. 10, C and D. When the cell was firing at 45 spikes/s and phase locked to the 45-Hz component of the two-frequency signal, firing phase on the sine wave was preferentially near 0.2 for all cells in the sample (Fig. 10C), as predicted by the iterative map for SP neurons. When the stimulus was not applied to the neuron, there was some remaining reduction of entropy at the corresponding frequency, but the average phase distribution was approximately uniform.

Fig. 10.

Average 2-frequency stimulation results for the sample of 17 neurons. A: averages ± SE of entropy for the histograms of phase at 26 Hz (red) and 45 Hz (blue) at firing rates from 5 to 75 spikes/s. Dashed lines indicate the frequencies of the stimulus sine waves. The small sinusoidal currents were effective at structuring the firing of the neurons, when cells were firing at rates near the stimulus frequency. B: entropy changes in A are not caused by spurious coherence due to rate similarity. The entropy of the phase distribution obtained with a zero-amplitude stimulus showed a much smaller effect. C and D: comparison of the combined phase distribution for all cells shows a strong entrainment near 0.2, as expected for phase locking when the sine wave stimulus is present (C) but not when it is absent (D). E and F: there is little interference between the effects of the two sine wave stimuli. E: the entropy profile for the simultaneous 26- and 45-Hz stimulus is similar to the profile for a 26-Hz stimulus alone at most firing rates. There is only a small increase in entropy (decrease in the effectiveness of the 26-Hz component) when the 45-Hz component is present. F: a similar comparison for the 45-Hz component. The presence of the 26-Hz stimulus slightly reduces phase locking to the 45-Hz component, especially at firing rates <45 spikes/s.

It is possible that although a neuron’s firing pattern is not strongly structured by a sine wave input, that input might disturb the structure generated by another input component. If the cell is entrained by a 45-Hz sine wave input, would that entrainment be disrupted by the presence of the 26-Hz sine wave? To answer this question, entrainment was compared for the combined sine wave stimuli and for each of the sine waves given alone. The results are shown in Fig. 10, E and F. The degree of entrainment (measured using entropy) when both 26- and 45-Hz sine waves were present was similar to that when the 26-Hz sine wave was given alone (Fig. 10E). Similarly, the entropy profiles observed with the combined sine wave stimulus and the 45-Hz sine wave were similar (Fig. 10F). At the frequencies of best entrainment (26 and 45 Hz, respectively), there was a small but statistically significant increase in entropy (reduction of entrainment) in both cases (t = 2.94, df = 15, P < 0.01 for 45 Hz and t = 4.28, df = 15, P < 0.01 for 45 Hz, comparing for 16 neurons for which data were available for all conditions, Bonferroni corrected for 2 comparisons). Thus the presence of the other sine wave did disrupt entrainment, but only slightly. Thus, when two different small sine wave currents were applied, the firing patterns of striatal spiny cells were influenced by the sinusoidal stimuli only when one of the components was near its own firing rate, but not otherwise. When firing was affected by the composite stimulus, it fired to the pair of sine waves almost as if it were only one. The cells selected the frequency component in their input that matched the cell’s own rate, locked to it, and largely ignored the other.

This experiment illustrates the failure of our standard intuition to explain spike timing in repetitively firing neurons. An intuitive view of the neuron based on the notion of subthreshold membrane potential fluctuations and a constant threshold would predict that when the neuron is firing repetitively, action potentials would occur on the peaks of the same membrane potential fluctuations that we can see when the cell is not firing. Perhaps this could have occurred in these experiments if the constant current were adjusted with great precision, so that it remained below threshold except for brief moments at the peaks of the sine wave components. It was impossible to adjust the constant current with sufficient precision to test this intuitive prediction. With the small-amplitude sine wave currents used in the present study, too little constant current gave no spiking, whereas a slight increase in depolarization drove the cell into repetitive firing. Beyond that point, action potential timing was not predictable from the location of the peaks of the membrane potential below threshold. Instead, the much larger ionic currents generated by repetitive firing interacted with the oscillatory inputs to produce the observed firing pattern.

DISCUSSION

Striatal neurons receive oscillatory synaptic input in vivo.

Each striatal spiny neuron receives synaptic input from ~10,000 different presynaptic neurons (Zheng and Wilson 2002), most of which are spontaneously active in vivo (Stern et al. 1997). The synaptic currents delivered to the soma from all of these sources produce a continuously varying membrane potential waveform, in which individual synaptic components cannot be distinguished, each being obscured by the effects of thousands of others. This continuous waveform is reflected in the local field potential recorded in the striatum, which is generated locally (DeCoteau et al. 2007a) and mostly composed of synaptic currents generated in striatal neurons. The striatal field potential often shows pronounced spectral peaks indicating the presence of periodic components and may be dominated by components at specific frequency ranges at particular moments during behavior (Courtemanche et al. 2003). The firing of some striatal SP neurons becomes phase locked to the dominant frequency components of the field potential, indicating that periodic components of the input can drive firing in SP cells (e.g., Courtemanche et al. 2003; Leventhal et al. 2012). These periodic components in the striatal synaptic barrage are the neurophysiological signatures of specific behavioral states. For example, periods of theta (7–11 Hz) in the local field potential are seen in rat striatum at characteristic times while running a T-maze (DeCoteau et al. 2007a, 2007b). Likewise, beta (13–30 Hz) periodic components are seen at specific times during performance of a cued-choice task (Leventhal et al. 2012). Synchronous gamma (>30 Hz) oscillations are prominent in the ventral striatum during specific points in performance of a learned spatial decision task (van der Meer and Redish 2009). In all cases, the oscillations can be seen directly in the raw field potential recordings as well as by spectral analysis. In sleep and anesthesia, input to striatal neurons has been seen in intracellular recordings to oscillate in the delta (<4 Hz) frequency range (Stern et al. 1997). All the oscillations are probably produced by coordinated changes in both excitation and inhibition (Wilson 2009) and, at the spike initiation site, produce periodic currents similar to those used in this study. Periodic continuous synaptic input is, of course, not restricted to striatal spiny neurons, but is seen in the neurons of many brain structures, including cortical pyramidal neurons that project to striatal SP cells (Cowan and Wilson 1994; Stern et al. 1997). Oscillations in membrane potential are often superimposed on longer-lasting periods of depolarization during neuronal responses that produce episodes of repetitive firing.

Spike statistics cannot reveal whether a cell is firing repetitively.

Repetitive firing is usually rhythmic in the absence of synaptic input, but it may be highly irregular when inputs are present. This change does not imply that the cells have quit firing repetitively. For example, repetitively firing neurons densely perturbed by noise may show no repetitive peaks in their autocorrelations, and so appear to be firing randomly. Although it appears random, this firing is very deterministic and reflects the fine structure of the noise input (Wilson et al. 2014). It appears random only because the input is random. More structured inputs, such as the sine wave currents used here, produce more complex patterns that can have coefficients of variation well above 1, without ever taking the cell out of repetitive firing. Repetitively firing neurons cannot be identified by the regularity of their firing, unless all fast synaptic perturbations are blocked (e.g., Kita et al. 2004). During unperturbed firing (e.g., firing in slices in the absence of input), the intrinsic variability of firing can be treated as a noisy current input acting through the same phase-resetting mechanism responsible for the response to extrinsic inputs (Ermentrout et al. 2011; Wilson et al. 2014). The effect of noise on the variance of phase accumulates during the interspike interval, so that slowly firing neurons are more variable than more rapidly firing ones. Noise occurring during phases of the interspike interval for which the cell is relatively insensitive (the phase-resetting curve’s value is small) has less effect on spike time variability than noise applied at the more sensitive portion of the cell’s cycle. During unperturbed firing, the cell’s phase progresses approximately linearly through time, so the overall effect of intrinsic noise scales with the integral of the square of the phase-resetting curve (Ermentrout et al. 2011). During sinusoidal driving, the evolution of the cell’s phase during the interspike interval is altered by the driving stimulus. Thus the effect of noise on the neuron and the variability of the interspike interval may deviate greatly from that seen for unperturbed firing. In findings reported here, the intrinsic variability of interspike intervals during sinusoidal driving was much smaller than during unperturbed firing, except at the lowest frequencies (e.g., Fig. 5, D and E). Thus estimates of cellular reliability based on the variance of interspike intervals during unperturbed firing are not applicable during driven firing.

Phase model predicts spike trains of repetitively firing neurons.

The phase model is only an approximation, based on the assumption that no matter how perturbed it is by input, the cell remains near its oscillatory trajectory. There is no guarantee that this will remain so, especially for inputs that alter firing rate, such as the ones used here. It is an empirical question whether a phase model can predict the firing of a repetitively firing neuron, as such models embody the assumption that the cell’s behavior is still governed by the dynamics along its limit cycle and that each interspike interval is independent of previous ones. Neither of these assumptions can be true in the strictest sense, but the phase model did successfully predict interspike intervals of subthalamic neurons whose firing was strongly perturbed by current noise (Wilson et al. 2014), and it was very effective at predicting both the frequency dependence of spike-timing reliability and the specifics of spike timing of striatal spiny neurons in the present study. It should be noted, however, that both subthalamic neurons and striatal spiny neurons exhibit features that make them especially suited to spike-timing prediction by this model. These include absence of membrane impedance resonance (Beatty et al. 2015), relatively brief spike after-hyperpolarization currents that do not accumulate during repetitive firing, and strong persistent sodium currents that produce a small net negative slope conductance over most of the interspike interval (Farries and Wilson 2012).

A phase model built for individual neurons or a set of neurons based on their phase-resetting curves can predict firing patterns evoked by arbitrary input on a spike-by-spike basis. If the phase model is applicable, the prediction is limited only by the degree to which the input is known and by the cell's intrinsic noise. The phase model also predicts the quality of its own prediction. That is, some inputs produce more predictable firing than others, and this difference is explained by the phase model. For broadband current noise, prediction of interspike intervals is accurate (Wilson et al. 2014); however, errors of prediction accumulate, and so, long sequences of spike times cannot be predicted accurately. Errors of prediction also accumulate in response to sinusoidal stimuli at very slow frequencies (those at which the cell fires several times on the depolarizing phase of each cycle), and for the same reason. At other frequencies, prediction is excellent, even for long sequences of spike times. It has been shown here that in both cases the extent to which errors accumulate is evident (and predictable) from an analysis of the slopes of the iterative map of firing on stimulus phase. The statistic that predicts accumulation of errors is the Lyapunov exponent of the map, which is the aggregate measure of map slope for the set of locations visited by the cell during repetitive firing. This statistic and its relationship to reliability of firing for the phase model have previously been described by Galán et al. (2008).

Very small periodic inputs can shape firing.

During repetitive firing, a very small, continuously varying input can have a large influence on firing pattern. This is because the repetitively firing neuron integrates inputs throughout the interspike interval but does not do so uniformly. In cells excited from rest, inputs that do not contribute to a threshold crossing within a narrow window of integration are effectively forgotten, as their charge dissipates through the resting membrane conductance. In repetitive firing, spike threshold and the time constant of charge dissipation are no longer the issues; the cell will cross threshold regardless of input. Input currents arriving at all times between spikes are effectively incorporated into the cell's oscillation and influence the time of the next action potential. For periodic inputs the frequency of the input is so critical because all times during the interspike interval do not matter equally (i.e., the PRC is not flat; the cell is not a perfect integrator). A periodic input whose depolarizing phase is consistently aligned with the most sensitive part of the PRC during an interspike interval will make the cell fire earlier (speed up firing), and one aligned in the opposite way will delay firing (slow it down). This makes frequencies near the cell's intrinsic oscillation rate the most effective, because the cell’s rate can adjust to maintain a consistent alignment between a periodic input and the cell’s PRC from interval to interval.

Striatal spiny neurons may encode the phase of oscillations.

We previously reported that SP neurons subjected to a broadband barrage of synaptic-like currents or conductance transients fire coherently with frequency components at or near their unperturbed firing rate (Beatty et al. 2015). This was strictly a feature of repetitive firing because the preferred input frequency band shifted with the cell’s firing rate and because the same neurons showed no corresponding subthreshold resonance. In those experiments, the input waveform contained a flat spectrum over the frequency range of interest, and the frequency components to which the cells responded could not be identified by eye. It appeared that the cells were doing a spectral analysis of their input and responding only to components near their firing rates. Here, we have shown that this is a general feature of repetitive firing and can be predicted using phase-resetting methods.

It is possible to divide the influence of periodic inputs into two categories: those that modulate rate and those that structure spike timing. Both work through the PRC, and the responses to each can be predicted by the phase model; however, they differ in how they affect the postsynaptic spike train. Slow input frequencies, less than about half of the cell's own firing rate, did not produce consistent spike-timing sequences, but did effectively and predictably modulate the instantaneous firing rate of the cell. In contrast, oscillating inputs with frequencies above about half of the cell’s firing rate produced little or no modulation of firing rate. Instead, these inputs had a powerful effect on the fine structure of the temporal sequence of spikes. It is remarkable how sensitive the neurons were to these small (20–40 pA) sinusoidal currents at frequencies between 5 and 50 Hz. The sinusoidal currents were usually <10% of the current required to evoke repetitive firing. For comparison, the peak current generated by miniature glutamatergic excitatory postsynaptic currents in striatal neurons is ~10–15 pA (Tang and Lovinger 2000). These small current modulations could induce phase lock in striatal projection neurons that were firing near the input frequency and effectively disrupted rhythmic firing at most other frequencies. Slower periodic components, by changing the firing rate, could control the frequency selectivity of the cell to higher-frequency components, effectively tuning the neuron to fire coherently with higher-frequency inputs in a different range.

Striatal SP neurons exist in two forms, one (iSP) projecting specifically to the external segment of globus pallidus and one (dSP) that projects to both pallidal segments and to the substantia nigra (Chang et al. 1981; Kawaguchi et al. 1990). These two cell types are very similar in somatodendritic morphology and intrinsic physiological properties but have been shown to differ in input resistance and excitability. On average, iSP cells have a higher input resistance and excitability than dSP cells, although the distributions of these measures in the two cell groups are highly overlapping (Gertler et al. 2008; Kreitzer and Malenka 2007). Our results confirm the difference in sensitivity of these neuron types, seen as the integral of their phase-resetting curves. The shapes of the phase-resetting curves for these two cell types were similar and statistically indistinguishable in our sample. The shape of the phase-resetting curve reflects the constellation of ion channels active during the interspike interval (Farries and Wilson 2012), and so this similarity confirms the previously held view that the cells have similar ion channel expression patterns. It also suggests that the cells may not have fundamentally different styles of synaptic integration and may differ more in the source of their synaptic inputs than in the way that they process their inputs. Likewise, striatal SP neurons had very similar phase-resetting curves, and their spike timing was as well predicted by a scaled version of the phase-resetting curve averaged across neurons as it was using each cell’s own curve. This is in strong contrast to results from other brain structures, such as the subthalamic nucleus (Wilson et al. 2014) and olfactory bulb (Burton et al. 2012), which show much greater cellular heterogeneity. In the subthalamic nucleus, prediction of interspike intervals was much more accurate when made using the cell’s own phase-resetting curve, rather than the average for all cells. The results presented here show that differences in the shape of the phase-resetting curve would translate to differences in the phase at which cells would lock to a periodic input near their own firing rate. The uniformity of striatal SP neuron phase-resetting curves suggests a more uniform mode of synaptic integration in striatal SP cells and a tendency for cells receiving a common periodic input component to lock at the same phase and so to fire more synchronously.

The striatal SP neuron in vivo exhibits periods of very low rate (<1 spike/s) firing interrupted by periods of firing at a much higher rate, driven by cortical and thalamic excitation—the responses seen in experiments on awake animals (e.g., Kimura 1990). The timing of responses and the behavioral conditions that trigger them have been studied extensively. Responses vary greatly in size (i.e., firing rate during the response) across neurons. Our results suggest that during these responses, the timing of action potentials may carry information about the phase of oscillatory activity in striatal afferents and interneurons. If this is correct, the firing rate of the cells during the response would determine the frequency band to which an individual spiny neuron is tuned. Spike timing in that cell would reflect oscillatory components of the input over a range of nearby frequencies. Cells responding but firing at different rates would have spikes locked to oscillatory components at different frequencies. It is well known that spiny neurons do not show strong spike-timing correlations, even when responding to stimuli (e.g., Bakhurin et al. 2016; Jaeger et al. 1995). Our results suggest that cells firing at the same rate (responding with the same strength) to the same stimulus might be locked to oscillatory components with the same frequency and so be highly correlated, whereas those responding to the same stimulus but firing at different rates would be uncorrelated, as they are locked to different oscillatory components.

GRANTS

This study was supported by National Institute of Neurological Disorders and Stroke Grants 72197 and 97185.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author.

AUTHOR CONTRIBUTIONS

C.J.W. conceived and designed research; C.J.W. performed experiments; C.J.W. analyzed data; C.J.W. interpreted results of experiments; C.J.W. prepared figures; C.J.W. drafted manuscript; C.J.W. edited and revised manuscript; C.J.W. approved final version of manuscript.