Rapid accumulation of inhibition accounts for saccades curved away from distractors

In this research article, we propose a novel, noninvasive approach to behaviorally model the time course of competitive oculomotor processing. Our results highly resembled those from previously published neurophysiological experiments utilizing similar oculomotor processing contexts, thus validating our approach. Furthermore, this methodology provided new insights into the underlying neural mechanism subserving oculomotor processing given that we applied it to a context with which the neural mechanism is more contentious, and the results clearly favored one view.

Abstract

Saccades curved toward a distractor are accompanied by a burst of neuronal activation at the distractor locus in the intermediate layers of the superior colliculus (SCi) ~30 ms before the initiation of a saccade. Although saccades curve away from inactivated SCi loci, whether inhibition is restricted to a similar critical epoch for saccades curved away from a distractor remains unclear. We examined this possibility by modeling human saccade curvature as a function of the time between onset of a task irrelevant luminance- or color-modulated distractor and initiation of an impending saccade, referred to as saccade distractor onset asynchrony (SDOA). Our results demonstrated that 70 ms of luminance-modulated distractor processing or 90 ms of color-modulated distractor processing was required to modulate saccade trajectories. As these behavioral, feature-based differences were temporally consistent with the cortically mediated neurophysiological differences in visual onset latencies between luminance and color stimuli observed in the oculomotor and visual system, this method provides a noninvasive means to estimate the timing of peak activation in the oculomotor system. As such, we modeled SDOA functions separately for saccades curved toward and away from distractors and observed that a similar temporal process determined the magnitude of saccade curvatures in both contexts, suggesting that saccades deviate away from a distractor due to a rapid accumulation of inhibition in the critical epoch before saccade initiation.

NEW & NOTEWORTHY In this research article, we propose a novel, noninvasive approach to behaviorally model the time course of competitive oculomotor processing. Our results highly resembled those from previously published neurophysiological experiments utilizing similar oculomotor processing contexts, thus validating our approach. Furthermore, this methodology provided new insights into the underlying neural mechanism subserving oculomotor processing given that we applied it to a context with which the neural mechanism is more contentious, and the results clearly favored one view.

interest in using saccade curvatures to examine competitive oculomotor processing of potential saccade goals has increased in the last several decades. This interest is likely due in part to the striking correlation between the neurophysiology and behavioral output of the oculomotor system: potential oculomotor movement goals are represented in the intermediate layers of the superior colliculus (SCi), a midbrain structure with a highly ordered movement map (Robinson 1972; Wurtz and Goldberg 1972) that projects directly to the brain stem saccade pulse generators (Moschovakis et al. 1988) and contributes to target selection for both pursuit (Basso et al. 2000; Carello and Krauzlis 2004; Krauzlis and Dill 2002; Krauzlis 2003, 2005) and saccadic eye movements (Basso and Wurtz 1997, 1998; Horwitz and Newsome 2001; McPeek and Keller 2002, 2004). Activity on the motor map is spatially averaged whereby saccade vectors curve toward an area with excitation (McPeek et al. 2003; Port and Wurtz 2003) or away from an inactivated area (Aizawa and Wurtz 1998). In addition to spatial factors, saccade curvatures are also affected by robust temporal factors.

McPeek et al. (2003) reported that saccades that landed near a target but curved toward a distractor were accompanied by a neuronal burst at the SCi locus encoding the distractor, which occurred ~30 ms before the motor burst at the SCi locus encoding the target. This was then causally demonstrated whereby subthreshold microstimulation administered to the distractor locus with the same spatiotemporal profile elicited a saccade curved toward the distractor. A subsequent study reported that these curved saccade trajectories conform to a vector average model weighted by the activity levels of the neuronal populations encoding vectors to the target and distractor (Port and Wurtz 2003). The spatiotemporal factors that relate SCi excitation to saccades curved toward distractors are well understood. However, these factors are more controversial for linking SCi inhibition to saccades curved away from distractors (White et al. 2012).

Neurophysiological experiments have demonstrated that inhibition of potential saccade goals (e.g., a distractor stimulus) slowly accumulates over time (McPeek and Keller 2002). This is also reflected in behavioral studies given that saccade curvatures are generally curved toward a distractor at early saccadic reaction times (SRTs) but begin to curve away from the distractor after ~200 ms (McSorley et al. 2006, 2009; Walker et al. 2006). Interested in examining the temporal factors that cause saccades to curve away from distractors, White et al. (2012) examined the activity of SCi neurons encoding the distractor vector during a saccade task specifically on trials with saccades curved away from the distractor. They observed that the magnitude of these saccade curvatures only correlated with distractor-related neuronal activity in the epoch between −22 and 0 ms before saccade initiation and argued that this was too brief to reflect a slow accumulation of top-down inhibition. However, this critical epoch in which SCi inhibition correlated with the magnitude of saccade curvature away from distractors is entirely consistent with the epoch in which distractor-related excitation correlates with the magnitude of saccade curvature toward distractors (McPeek et al. 2003; Port and Wurtz 2003). Given that spatially specific inhibition is tonically projected onto SCi at a quick temporal frequency of 50–100 Hz by the oculomotor control system of the basal ganglia (Hikosaka et al. 2000), then as acknowledged by White et al. (2012), it is possible that saccades curve away from a distractor when inhibition rapidly accumulates at the distractor locus in SCi in this critical epoch.

This possibility was examined in the current study by comparing the accumulation of excitation and inhibition in the oculomotor system during saccadic target selection. One method to examine the accumulation of oculomotor excitation and inhibition is to systematically measure the influence of an irrelevant distractor across time while a saccade is concurrently being planned. Therefore, we noninvasively measured saccade curvatures while human participants completed a simple saccade task, and we modeled these saccade curvatures as a function of the time between saccade initiation and the presentation of a transient luminance- or color-modulated distractor. Because saccade curvatures toward and away from distractors reflect excitation (McPeek et al. 2003; Port and Wurtz 2003) and inhibition (Aizawa and Wurtz 1998) in the oculomotor system, respectively, then by analyzing saccade curvature separately for saccades curved toward and away from the distractor, we could compare the accumulation of excitation and inhibition in the oculomotor system during target selection.

We refer to the time between saccade initiation and the intervening stimulus as saccade-distractor onset asynchrony (SDOA), which was manipulated by utilizing various distractor-target onset asynchronies (DTOAs) and subtracting them from SRT. Because we observed in a pilot study that SRTs cluster around 200 ms for this saccade task, we utilized DTOAs of 50, 100, 150, 200, and 250 ms to probe a wide range of the SRT distribution and consequently capture a wide SDOA range. We modeled saccade curvature as a function of SDOA using Gaussian and logistic models for three reasons: 1) these models are defined with slope and midpoint parameters, which allowed us to examine potential temporal processing differences between post hoc conditions; 2) by including a floor parameter, we could examine when saccade curvatures were above baseline by comparing mean curvature at various SDOA time points to the floor of the function; and 3) determining which of these models better fits the data will provide insight into whether distractor-related saccade vector modulation decays over time (Gaussian) or is sustained over time (logistic).

We tested three predictions directly related to the temporal effects of processing an irrelevant distractor during oculomotor planning. Fist, various behavioral studies have provided converging evidence that a minimum of 60–80 ms is required for visual stimulation to modulate various characteristics of an impending saccade, such as amplitude and direction (Becker and Jürgens 1979; Findlay and Harris 1984; Ludwig et al. 2007) or SRT (Reingold and Stampe 2002). Such results are usually interpreted as reflecting the additive delays of afferent and efferent signals processed by the oculomotor system. Because saccade curvature should also be constrained by these temporal delays, we predicted that a distractor must onset between 60 and 80 ms before saccade initiation to elicit saccade curvature.

Second, a recent investigation of SCi neuronal responses to visual onsets found that burst latencies for isoluminant color stimuli were ~35 ms longer than for maximum contrast luminance stimuli (White et al. 2009). Given that direct retinotectal projections to the SCi are colorblind (Schiller et al. 1979), such color differences suggest that the visual input was cortical in origin (White et al. 2009). To examine whether the excitatory or inhibitory distractor representations in the current experiment originated cortically, we compared the minimum SDOA required to elicit curved saccades for color- and luminance-modulated Gabor patches while controlling for spatial frequency and orientation. Given the results of White et al. (2009), we predicted that color distractors should require an additional ~35 ms of processing to elicit curved saccades.

Finally, we examined whether a single spatiotemporal oculomotor mechanism can account for saccades curved away from and toward distractors. Oculomotor excitation that elicits saccades curved toward distractors is restricted to a critical epoch ~30 ms before saccade initiation (McPeek et al. 2003; Port and Wurtz 2003). As such, a parsimonious account of saccade curvature requires that the inhibition that elicits saccades curved away from distractors (Aizawa and Wurtz 1998) be restricted to this critical epoch also. Because there is at least preliminary evidence for this account (White et al. 2012), we predicted that the slope parameters for saccade curvature as a function of SDOA on trials with saccades curved away from the distractor should be similar to those on trials with saccades curved toward the distractor, consistent with oculomotor inhibition and excitation accumulating at the same rate.

METHODS

Participants.

Twenty-two York University undergraduate students (18–28 yr old, 11 men) participated in the experiment for course credit. Participants had normal or corrected-to-normal visual acuity, had normal red-green color vision as assessed by Ishihara color plates (Ishihara 2006), and were naive to the purpose and design of the experiment. Informed consent was obtained before participation. All research was approved by York University’s Human Participants Review Committee.

Stimuli.

The saccade target was a white (x = 0.29, y = 0.30, L = 122.70 cd/m², where L is luminance) square that subtended 0.6° × 0.6° and was located 12° above or below central fixation. We replicated the Gabor patches utilized by Burr and Morrone (1993) as our distractors because they allowed us to investigate potential differences in the timing of luminance and color signals in the oculomotor system while controlling for other visual features such as contrast, spatial frequency, and orientation. We created these stimuli offline using MATLAB (The MathWorks, Natick, MA) by superimposing equiluminant red (peak intensity: x = 0.63, y = 0.33, L = 7.58 cd/m²) and green (peak intensity: x = 0.29, y = 0.58, L = 7.57 cd/m²) sinusoidal waves with a spatial frequency of 1 deg/cycle, an orientation of 180°, and a phase shift of either 1 (luminance modulation) or 0.5 (color modulation) and then convolving them with a two-dimensional (2D) Gaussian filter (σ = 1.5°). Stimuli were embedded in a gray (x = 0.28, y = 0.30, L = 7.51 cd/m²) background. Distractors faded to gray by weighting the blue color channel with the inverse of the 2D Gaussian filter. The stimuli were displayed on a 21-in. CRT monitor (85 Hz, 1024 × 768 pixels). Participants viewed stimuli in a dimly lit room from a viewing distance of 57 cm with a headrest stabilizing their head position.

Apparatus and measurement.

Stimulus presentation was controlled using a computer running Presentation software (Neurobehavioral Systems, Berkeley, CA). Eye position was recorded using infrared eye tracking (500 Hz, EyeLink II; SR Research, Mississauga, ON, Canada). The eye tracker was calibrated at the beginning and halfway point of each experimental session, and as needed.

Task procedure.

Trials were initiated by maintaining fixation (1.89° square window) to a white, central fixation cross (0.4° × 0.4°) for 200 ms, after which the fixation cross offset and the target onset 12° above or below fixation (Fig. 1). Participants were instructed to fixate the target as soon as it appeared. After an interval of 50, 100, 150, 200, or 250 ms, the luminance- or color-modulated distractor onset to the left or right of the target at an eccentricity of 12° with an angular separation of 45° to the target. This interval is subsequently referred to as the distractor-target onset asynchrony (DTOA). The trial ended when a saccade was made to the target or 500 ms had elapsed (time-out). Time-out trials were randomly replaced back into the block and were signified with an error tone and message. Trials were separated by a 1,000-ms intertrial interval (ITI) with a blank, gray display.

Fig. 1.

Example trial sequence. After viewing fixation for 200 ms, the target onset above or below fixation until it was fixated or the trial timed out (500 ms). The luminance- or color-modulated distractor appeared to the left or right of the target 50, 100, 150, 200, or 250 ms after target onset (DTOA).

Participants completed 1 session with 10 blocks of 78 trials for a total of 780 trials. For half of the participants (determined by the order in which they appeared in the laboratory), we utilized DTOAs of 50, 100, and 150 ms (short group). For the remaining half, we utilized DTOAs of 150, 200, and 250 ms (long group). On each trial, the target location, distractor location, distractor feature, and DTOA were randomized. This design contained a total of 24 (2 × 2 × 2 × 3) experimental conditions. Baseline trials with targets at both target locations and no distractors were randomly interleaved into the blocks and increased the number of conditions to 26. There were an equal proportion of trials from all 26 conditions on every block.

Saccade detection and analysis.

Saccades were detected, visualized, filtered, and analyzed offline using customized MATLAB algorithms. Saccades were defined as a velocity exceeding 20 deg/s for at least 8 ms and a peak velocity exceeding 50 deg/s. Trials that contained blinks (1.10%), corrective saccades (0.42%), saccade amplitudes <1° (0.54%), end-point deviations >3° from the center of the target (8.90%), fixation drifts >0.5° during the presaccadic latency period (1.88%), or an SRT <100 ms (3.25%) were excluded from further analysis, leaving 83.91% of the data remaining. The data from two participants were not analyzed because over 50% of trials were removed using these criteria.

To analyze saccade curvatures, saccade start points were translated back to the origin and then trigonometrically rotated so that the end point was aligned to the positive y-axis. The following metrics were then used to quantify saccade curvatures: 1) sum deviation, the sum of all x deviations along the length of the saccade, and 2) max deviation, the maximum x deviation along the length of the saccade. Baseline saccade curvatures for each participant at each target location were subtracted from the data to reduce inherent, idiosyncratic curvature. The curvature metrics were then recoded so that positive deviations correspond to deviations toward a distractor, whereas negative deviations correspond to deviations away from a distractor.

We calculated the saccade distractor onset asynchrony (SDOA) by subtracting SRTs from DTOA such that SDOA = DTOA − SRT. Thus this metric indicates how much time the distractor has been displayed for relative to saccade initiation, where a negative value indicates how long before saccade initiation the distractor onset. SDOA values greater than zero were not analyzed because this indicates that the distractor appeared after the initiation of the saccade. We binned the SDOA data such that each bin contained data from a 20-ms SDOA interval aligned to an SDOA of zero. We herein refer to each individual bin by its center (e.g., bin −10 contains the SDOA data between −20 and 0 ms). We performed regression analyses on the average sum curvature and max curvature as a function of bin center for every bin that contained ≥20 trials. Because there was an uneven SDOA distribution across subjects, we averaged saccade curvatures across subjects in each bin. By using a customized MATLAB implementation of the maximum likelihood estimation (MLE) method, the mean absolute saccade curvature as a function of SDOA bin center was fit to the following two functions: 1) Gaussian:

$${\text{ƒ}}_{\text{G}}\left(x\right)=\left(\alpha -\delta \right)\cdot e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}+\delta$$

where α is the height of the function, μ is the midpoint of function, σ is the slope of the function, and δ is the floor of the function, and 2) logistic:

$${ƒ}_{\text{L}}\left(x\right)=\frac{L-\delta }{1+e^{k\left(x-x_0\right)}}+\delta$$

where L is the height of the function, x₀ is the midpoint of the function, k is the slope of the function, and δ is the floor of the function.

Using the same method, the mean signed saccade curvature as a function of SDOA was also fit using the first-order partial derivative of the Gaussian function:

$${\text{ƒ}}_{\text{G}\prime }{}^{}\left(x\right)=\frac{\alpha \left(\mu -x\right)}{\sigma e^{-\frac{1}{2}}}\cdot e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}+\delta$$

where α is the height of the maxima/minima with respect to the vertical midpoint, μ is the horizontal midpoint of the function, σ is the distance of the maxima/minima from the horizontal midpoint, and δ is the vertical midpoint of the function.

RESULTS

Trials were removed if the sum curvature was 3 SD above or below the mean in each SDOA bin. Trials were categorized as having curved toward or away from the distractor. Saccades that could not be classified according to this dichotomy (i.e., so-called “cubic” saccades; Ludwig and Gilchrist 2002) were also omitted from subsequent analyses. Because we were interested in determining how much distractor processing time is sufficient for saccade vector modulation by the distractor, we calculated the unsigned magnitude of saccade curvatures in each SDOA bin (regressed using bin centers) by averaging the absolute mean saccade curvature for each subject. Furthermore, to determine when saccade curvatures had significantly deviated from baseline, we compared the absolute subject means in each SDOA bin with the fitted floor parameter (δ) from the regression analysis using a two-tailed, paired-samples t-test and a Bonferroni multiplicity adjustment. We assessed whether each function accounted for a significant proportion of the variance by using an F-test regression analysis. If both models significantly fit the data, we assessed whether the Gaussian or logistic model provided a statistically better fit to the data by using an F-test performed on the ratio of the sum-of-squared model residuals with N − k degrees of freedom. Similarly, the goodness of fit of each function to the data was evaluated by calculating the coefficient of determination (R²).

Saccadic response time and amplitude.

We compared saccadic response times (SRTs) and saccade amplitudes between the distractor feature conditions (i.e., luminance modulated, color modulated, and baseline) to determine whether subsequent potential saccade curvature differences between distractor features are more simply explained by non-curvature-related saccade parameters. We examined potential mean differences using multiple paired-samples t-tests with Bonferroni multiplicity adjustments.

SRTs in the baseline condition (194.61 ± 4.57 ms; mean ± SE) were significantly shorter than in both the luminance condition [202.90 ± 4.55 ms; t(19) = 5.17, P < 0.001, d = 1.16] and the color condition [203.14 ± 4.73 ms; t(19) = 6.85, P < 0.001, d = 1.53]. Critically, there was no difference between the luminance and color conditions [t(19) = 0.33, P = 1, d = 0.07]. Saccade amplitudes in the baseline condition (12.44 ± 0.10°) were significantly longer than in both the luminance condition [12.28 ± 0.08°; t(19) = 3.31, P = 0.011, d = 0.74] and the color condition [12.29 ± 0.09°; t(19) = 3.61, P = 0.006, d = 0.81]. Critically, there was no difference between the luminance and color conditions [t(19) = 0.31, P = 1, d = 0.07]. Saccades were more accurate but took longer to execute when a distractor was present. Critically, these results demonstrate that any potential saccade curvature differences between luminance- and color-modulated distractors would be independent of SRT and saccade amplitude.

Overall SDOA functions.

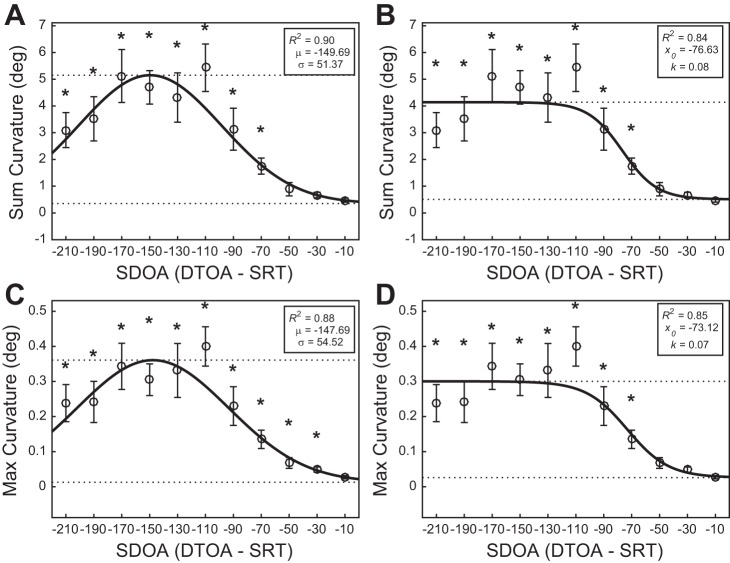
The overall sum curvature data was significantly fit by the Gaussian [F(3,7) = 21.34, P < 0.001, R² = 0.90; Fig. 2A] and logistic models [F(3,7) = 11.35, P = 0.004, R² = 0.84; Fig. 2B]. Neither model provided a statistically better fit of the data (F < 1). However, a comparison of the R² values and a visual inspection of the fit suggested that the Gaussian model provides a better mathematical description of the distractor integration process. As such, the Gaussian model demonstrated that sum curvatures significantly deviated from baseline for SDOA bins centered to an SDOA of less than or equal to −70 ms, suggesting that ~70 ms of distractor processing time is required for saccade vector modulation.

Fig. 2.

Gaussian and logistic models fitted to the overall mean sum and max curvatures as a function of SDOA bin center. Data points (open circles) represent mean saccade curvature. Error bars represent SE. Broken lines depict fitted floor and ceiling parameters. Asterisks denote significant (P < 0.05) curvature deviations from baseline. A: Gaussian model fitted to the overall sum curvature data. B: logistic model fitted to the overall sum curvature data. C: Gaussian model fitted to the overall max curvature data. D: logistic model fitted to the overall max curvature data.

The overall max curvature data were also significantly fit by the Gaussian [F(3,7) = 17.63, P = 0.001, R² = 0.88; Fig. 2C] and logistic models [F(3,7) = 11.85, P = 0.004, R² = 0.85; Fig. 2D]. Neither model provided a statistically better fit of the data (F < 1). A similar inspection as before suggested that the Gaussian model provides a better mathematical description of the distractor integration process. According to the Gaussian model, max curvatures significantly deviated from baseline for SDOA bins centered to an SDOA of less than or equal to −30 ms. This result conflicts with the estimate from the sum curvature data for the minimum distractor processing time required for saccade vector modulation. However, given that the mean and SD of the fitted Gaussian models for the sum and max curvature data are quite similar (μ_sum = −149.69 ms, σ_sum = 51.37 ms; μ_max = −147.69 ms, σ_max = 54.52 ms, respectively), the sum and max curvature appear to reflect the same process. Furthermore, the logistic model demonstrated that max curvatures significantly deviated from baseline for SDOA bins centered to an SDOA of less than or equal to −70 ms (see Fig. 2D), consistent with the sum curvatures. Taken together, these results suggest that the max curvature bins centered to an SDOA of −50 and −30 ms likely significantly deviated above baseline due to extremely low variability in these bins and a small fitted floor parameter by the Gaussian model. We maintain that our data show that ~70 ms of distractor processing time is required for saccade vector modulation.

Distractor feature differences.

To examine potential feature differences in the sum and max saccade curvatures, we split the data into trials with a luminance-modulated distractor and a color-modulated distractor (Fig. 3). The Gaussian model significantly fit the sum curvature data from luminance trials [F(3,7) = 13.61, P = 0.003, R² = 0.86] and color trials [F(3,7) = 12.16, P = 0.004, R² = 0.79; Fig. 3A]. The logistic model also significantly fit the data from luminance trials [F(3,7) = 8.74, P = 0.009, R² = 0.80] and color trials [F(3,7) = 34.60, P < 0.001, R² = 0.94; as in Fig. 3B]. Neither model was a statistically better fit to the luminance data (F < 1). However, the logistic model provided a marginally better fit to the color data [F(7,7) = 3.25, P = 0.072, η² = 0.76]. On the basis of a comparison of the R² and a subjective evaluation, it appears as though the Gaussian model provided a better description of luminance-modulated distractor processing, whereas the logistic model provided a better description of color-modulated distractor processing with marginal, yet unreliable, statistical evidence for this conclusion. The Gaussian model indicated that the sum curvatures measured on trials with luminance-modulated distractors deviated from baseline in SDOA bins centered to an SDOA of less than or equal to −70 ms as with the overall data. However, the logistic model indicated that the sum curvatures measured on trials with color-modulated distractors deviated from baseline in SDOA bins centered to an SDOA of less than or equal to −90 ms. This result indicates that the minimum distractor processing time necessary for saccade vector modulation is 20 ± 10 ms longer for color than for luminance. This is further corroborated by a comparison of the midpoint parameters from both models (Gaussian: μ₂ − μ₁ = 10.81 ms; logistic: k₂ − k₁ = 13.51 ms), and these differences exist despite similar slope parameters (Gaussian: σ₁ = 52.73 ms, σ₂ = 46.40 ms; logistic: k₁ = 0.10 ms, k₂ = 0.09 ms).

Fig. 3.

Gaussian and logistic models fitted to mean sum and max curvatures as a function of SDOA bin centers split into trials with a luminance-modulated distractor (blue) and color-modulated distractors (red). Data points (open circles) represent mean saccade curvature. Error bars represent SE. Broken lines depict fitted floor and ceiling parameters. Asterisks denote significant (P < 0.05) curvature deviations from baseline. A: Gaussian model fitted to the sum curvature data. B: logistic model fitted to the sum curvature data. C: Gaussian model fitted to the max curvature. D: logistic model fitted to max curvature data.

We repeated the above analyses for the max curvature metric, which provided consistent results (Fig. 3). The Gaussian model significantly fit the max curvature data for luminance trials [F(3,7) = 14.56, P = 0.002, R² = 0.87] and color trials [F(3,7) = 9.59, P = 0.007, R² = 0.81; Fig. 3C]. The logistic model also significantly fit the data for luminance trials [F(3,7) = 7.78, P = 0.012, R² = 0.78] and color trials [F(3,7) = 23.32, P < 0.001, R² = 0.92; Fig. 3D]. Consistent with the sum curvature data, neither model was a statistically better fit to the luminance data (F < 1). Furthermore, the logistic model was not a statistically better fit to the color data [F(7,7) = 2.29, P = 0.148, η² = 0.70]. However, on the basis of a comparison of the R² and a subjective evaluation, it appears as though the Gaussian model provided a better description of luminance-modulated distractor processing, whereas the logistic model provided a better description of color-modulated distractor processing. Consistent with the sum curvature data, the Gaussian model indicated that the max curvatures measured on trials with luminance-modulated distractors deviated from baseline in SDOA bins centered to an SDOA of less than or equal to −70 ms, whereas the logistic model indicated that the max curvatures measured on trials with color-modulated distractors deviated from baseline in SDOA bins centered to an SDOA of less than or equal to −90 ms. Once again, this difference of 20 ± 10 ms between color and luminance is corroborated by a comparison of the midpoint parameters from both models (Gaussian: μ₂ − μ₁ = 22.90 ms; logistic: k₂ − k₁ = 14.71 ms) despite similar slope parameters (Gaussian: σ₁ = 54.81 ms, σ₂ = 58.30 ms; logistic: k₁ = 0.09 ms, k₂ = 0.10 ms).

Directional differences.

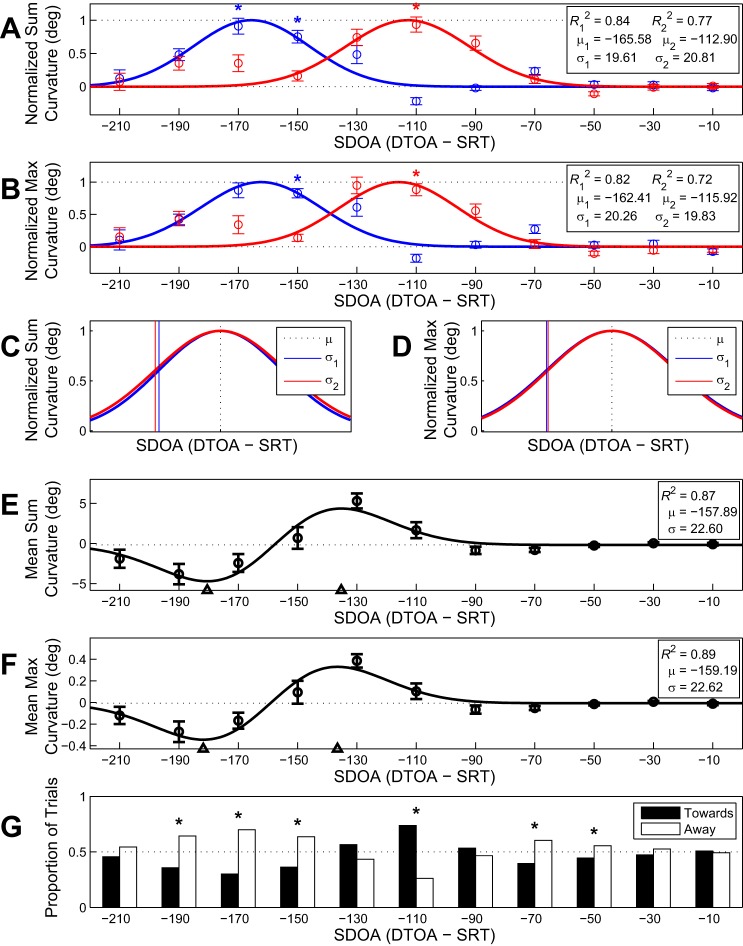
Because we were interested in examining potential differences in saccade curvature as a function of SDOA when saccades curved toward or away from the distractor, we split the data into trials on which saccades curved toward the distractor and trials on which saccades curved away from the distractor (Fig. 4). For the sum curvature data, the Gaussian model significantly fit the data for trials with saccades curved toward distractors [F(3,7) = 10.97, P = 0.005, R² = 0.77] and away from distractors [F(3,7) = 13.63, P = 0.003, R² = 0.84; Fig. 4A]. Conversely, the logistic model did not provide a significant fit to the data for trials with saccades curved toward distractors [F(3,7) = 1.93, P = 0.213, R² = 0.474] and provided an unreliable, yet marginal, fit for trials with saccades curved away from distractors [F(3,7) = 3.93, P = 0.062, R² = 0.64]. The fitted Gaussian model demonstrated that sum curvatures toward distractors deviated from baseline in SDOA bin −110, whereas the sum curvatures away from distractors deviated from baseline in the SDOA bins −170 and −150. These deviations from baseline coincide closely with the midpoint parameters from each respective Gaussian model as can be seen in Fig. 4A. Furthermore, the functions fits for trials with saccades curved toward and away from distractors have nearly identical slope parameters but are shifted along the abscissa as indicated by the midpoint parameters. By removing this offset and overlapping these normalized functions (Fig. 4C), it becomes apparent that the accumulations of excitation and inhibition follow a very similar time course.

Fig. 4.

Accumulation models for excitation and inhibition. A and B: normalized Gaussian models fitted to the absolute sum (A) and max (B) curvatures as a function of SDOA bin split into trials with a saccade curved away from the distractor (blue) and toward the distractor (red). Data points (open circles) represent absolute mean saccade curvature. Error bars represent SE. Broken lines depict fitted floor and ceiling parameters. Asterisks denote significant (P < 0.05) curvature deviations from baseline. C and D: from A and B, the normalized Gaussian models for absolute mean sum (C) and max (D) curvature as a function of SDOA adjusted so that the fitted functions for trials with saccades curved away (blue) and toward (red) distractors are overlapped. The broken vertical black line represents the overlapped midpoints (μ = μ₁ = μ₂), and the solid vertical blue and red lines depict μ − σ for away and toward trials, respectively. E and F: fitted first-order Gaussian derivative models for signed mean sum (E) and max (F) curvature as a function of SDOA. Broken line depicts the vertical midpoint of the function, and open triangles on the abscissa represent μ ± σ, which correspond to the function maxima and minima and depict the time point of peak excitation and inhibition, on average. G: proportion of trials with a saccade curved toward (filled bars) or away from (open bars) a distractor in each SDOA bin. Asterisks denote significant (P < 0.05) deviations from a random distribution of trials with saccades curved toward or away from distractors.

For the max curvature data, the Gaussian model significantly fit the data for trials with a saccade curved toward distractors [F(3,7) = 7.49, P = 0.014, R² = 0.72] and away from distractors [F(3,7) = 11.74, P = 0.004, R² = 0.82; Fig. 4B]. The logistic model did not significantly fit the data for trials with a saccade curved toward distractors [F(3,7) = 2.37, P = 0.156, R² = 0.53] but did fit the data for trials with a saccade curved away from distractors [F(3,7) = 4.43, P = 0.048, R² = 0.61], and neither model was statistically better fit to the data (F < 1). However, a comparison of the R² and a subjective evaluation suggested that the Gaussian model provided a better description of inhibitory influences on distractor processing. Consistent with the sum curvature data, the fitted Gaussian model demonstrated that max curvatures toward distractors deviated from baseline in SDOA bin −110 and marginally in bin −130 (P = 0.067), whereas the max curvatures away from distractors deviated from baseline in SDOA bin −150 bin and marginally in bin −170 (P = 0.093). As with sum curvature, these deviations from baseline coincide closely with the midpoint parameters from the Gaussian models, and both functions have nearly identical slope parameters but are shifted along the abscissa as indicated by the midpoint parameters (Fig. 4B). We have removed this offset and overlapped the normalized functions in Fig. 4D, which demonstrates that the accumulations of excitation and inhibition follow a very similar time course.

One critical question that remains is whether distractor processing during target selection involves two separate processes. Resting on this assumption is whether the data can be meaningfully parsed into two distinct distributions (i.e., trials toward and away from the distractor). Evidence for our assumption that distractor processing involves two distinct processes, and thus partial validation of our analytic technique, could be provided by demonstrating that there is an SDOA time period in which saccades, on average, curve toward the distractor, followed by an SDOA time period in which saccades, on average, curve away from the distractor. Therefore, to examine this assumption, we analyzed the signed mean curvature data in which a positive curvature corresponds to a deviation toward the distractor and a negative curvature corresponds to a deviation away from the distractor. If oculomotor excitatory processing transitions into inhibitory processing of a distractor, there should be a positive inflection of signed mean saccade curvatures followed by a negative inflection as a function of SDOA. We therefore fit the signed mean curvature data as a function of SDOA with the first-order partial derivative of the Gaussian function.

For the signed mean sum curvature data, the first-order Gaussian derivative significantly fit the data [F(3,7) = 18.54, P < 0.001, R² = 0.87; Fig. 4E]. This was corroborated by the signed mean max curvature data, which were also significantly fit by the first-order Gaussian derivative [F(3,7) = 21.97, P < 0.001, R² = 0.89; Fig. 4F]. These fits clearly demonstrate that 1) consistent with sequential excitatory and inhibitory distractor processing, there is a time period in which saccades, on average, curve toward the distractor and a subsequent time period in which saccades, on average, curve away from the distractor; 2) these periods extend approximately equal intervals in time, because the Gaussian derivative fit functions are symmetrical about the horizontal midpoints (μ), which is therefore also consistent with the nearly equal slope parameters observed previously for the separately fitted Gaussian functions for saccades curved toward and away from distractors; and 3) critically, the time between positive and negative peaks is 45.20 ms for the sum curvature data and 45.24 ms for the max curvature data because (μ_sum + σ_sum) − (μ_sum − σ_sum) = 45.20 ms and (μ_max + σ_max) − (μ_max − σ_max) = 45.24 ms, which closely resembles the differences in peak activity for saccades toward and away from distractors estimated using the dual Gaussian model approach for absolute mean sum (μ₁ − μ₂ = 52.68 ms) and max curvature (μ₁ − μ₂ = 46.49 ms) (Fig. 4, A and B).

Analyzing the proportion of saccades curved toward and away from the distractor in each SDOA bin could provide further evidence of two distinct distributions for saccades curved toward and away from a distractor. A χ² goodness-of-fit analysis demonstrated that there was a higher probability of saccades curved away from distractors than saccades curved toward distractors [χ²(1, N = 6,792) = 12.04, P < 0.001, ϕ_c = 0.04]. Similarly, a subsequent χ² test-of-independence analysis demonstrated that the frequency distribution of saccades across SDOA bins was related to the directionality of saccades [χ²(10, N = 6,792) = 241.33, P < 0.001, ϕ_c = 0.19]. As such, we analyzed the proportion of saccades that curved toward and away from distractors in each SDOA bin using χ² goodness-of-fit analyses weighted using the Bonferroni multiplicity adjustment (Fig. 4G). This analysis demonstrated that the SDOA time point of peak saccade curvature toward a distractor corresponded to a higher probability of saccades curved toward distractors. Similarly, the SDOA time point of peak saccade curvature away from a distractor corresponded to a higher probability of saccades curved away from distractors.

A potential issue with aggregating the data from the short and long DTOA groups (see methods, Task procedure) for our analysis of saccade curvature as a function of SDOA is that the short and long groups could have been systematically sampling from different SDOA ranges. Therefore, the two groups could potentially have saccade curvature SDOA distributions that occupy different restricted ranges of the total SDOA range, which means that the data in the away and toward distributions could potentially have been generated from different groups. If such group differences were driving our effects, this would suggest that 1) the midpoint, and perhaps shape, of the fitted functions for overall saccade curvature as a function of SDOA should differ between groups, with one group having a “toward” peak and the other having an “away” peak; 2) if one group has a “toward” peak and the other has an “away” peak, the signed mean saccade curvature should differ between groups, with one group being predominately positive (toward) and one predominately negative (away); and 3) there should be between-group differences of mean absolute saccade curvature across SDOA bins.

First, for the absolute mean sum curvature data, the Gaussian model significantly fit the data from the short group [F(3,7) = 7.69, P = 0.013, R² = 0.74] and the long group [F(3,7) = 25.82, P < 0.001, R² = 0.92]. However, the shapes of the SDOA functions were similar between groups as demonstrated by the midpoints (μ₁ = −153.68 ms; μ₂ = −150.70 ms) and slopes (σ₁ = 46.82 ms; σ₂ = 51.94 ms). Similarly, for the absolute mean max curvature data, the Gaussian model significantly fit the data from the short group [F(3,7) = 7.46, P = 0.014, R² = 0.74] and the long group [F(3,7) = 14.47, P = 0.002, R² = 0.86]. The shapes of the SDOA functions were also similar between groups, as demonstrated by the midpoint (μ₁ = −146.39 ms; μ₂ = −151.52 ms) and slope parameters (σ₁ = 48.63 ms; σ₂ = 55.61 ms). Second, for signed mean sum curvature, there was no mean difference between the short group (−0.12 ± 0.16°) and the long group [−0.47 ± 0.15°; t(18) = 1.58, P = 0.132]. Similarly, for signed mean max curvature, there was no mean difference between the short group (−0.01 ± 0.01°) and the long group [−0.03 ± 0.01°; t(18) = 1.44, P = 0.166]. Third, as determined by Mann-Whitney U-tests with Bonferroni multiplicity corrections, there were no group differences between any consecutive pair of SDOA bins for absolute mean sum and max curvature (all P ≥ 0.476). The results of these three analyses demonstrate that both DTOA groups of participants elicited a similar overall pattern of results across the full range of SDOA values. Therefore, it is unlikely that the SDOA distributions were generated from different groups of participants. Thus potential DTOA group differences in SDOA distributions are inadequate to explain our results suggesting that oculomotor excitation and inhibition accumulate at a similar rate.

DISCUSSION

We examined the time course of competitive oculomotor processing by analyzing saccade curvatures as a function of the time between distractor onset and initiation of an impending saccade (SDOA). We performed two analyses to validate this methodological approach to modeling the time course of competitive oculomotor processing. The first analysis demonstrated that a minimum of 70 ms of distractor processing time was required to modulate saccade vectors, which is consistent with converging evidence from various other behavioral paradigms (Becker and Jürgens 1979; Findlay and Harris 1984; Ludwig et al. 2007; Reingold and Stampe 2002). The second analysis demonstrated that the minimum distractor processing time for saccade vector modulation was ~20 ms longer for color-modulated distractors than for luminance-modulated distractors and suggested that excitatory and inhibitory processing in the oculomotor system was performed on cortical input to the oculomotor system. This result provided the human behavioral sequelae to a recent neurophysiological experiment that demonstrated SCi neuronal visual onset latencies for luminance and color onsets offset by ~35 ms (White et al. 2009), although we note that these timings may decrease if weaker distractor stimuli are used, such as lower contrast, or near threshold. Finally, we analyzed SDOA functions separately for saccades curved toward and away from distractors. This analysis suggested that oculomotor inhibition and excitation accumulate at the same rate and are offset in time, because the fitted Gaussian models were nearly identical in shape and shifted along the abscissa. We now discuss each of these main findings and their implications and then turn our attention to a putative neural mechanism that can potentially link the current behavioral data to the neurophysiological behavior of SCi visuomotor (VM) neurons.

Saccade curvature timing.

Our analysis of the overall sum curvature data as a function of SDOA demonstrated that saccade curvatures significantly deviated from baseline when the oculomotor system received distractor input at least 70 ± 10 ms before the initiation of an impending saccade. This result suggests that there is a point of no return for modulating saccade trajectories and is thus consistent with a ballistic account of saccade generation (Becker 1989) as opposed to an adaptive control account (Chen-Harris et al. 2008). Various other behavioral methodologies have provided evidence for a point of no return for an impending saccade, which has been estimated between 60 and 80 ms before saccadic initiation (Becker and Jürgens 1979; Findlay and Harris 1984; Ludwig et al. 2007; Reingold and Stampe 2002; cf. Buonocore et al. 2016) and referred to as saccadic dead time (SDT; Ludwig et al. 2007). When we conducted the overall saccade curvature analysis for the max curvature metric, we observed that the SDT estimate generated by the Gaussian function dropped to 30 ms. However, we reasoned that this estimate is likely due to a small fitted floor parameter and extremely small variability in bins −50 and −30, because the SDOA distribution contained a high number of observations in these bins. Three additional observations supported this reasoning: 1) the logistic fit to the overall max curvature data suggested that the SDT is indeed 70 ms; 2) subsequent fits to the both the sum and max curvature data for luminance- and color-modulated distractors suggested that more than 30 ms are required for saccade vector modulation; and 3) the fitted slope and midpoint parameters were nearly identical between the sum and max curvature data for both fit models, suggesting that both metrics reflect the same underlying process and should have provided similar estimates. Therefore, despite this caveat, our overall data set is consistent with the body of evidence suggesting that to interfere with an impending saccade, an intervening stimulus must onset a minimum of 70 ms before the initiation of the movement.

Our methodology is similar to those previously utilized to examine SDT in that we presented an intervening stimulus before saccade initiation. However, it differs in two important ways. First, certain SDT experiments involve presenting an intervening flash (e.g., Buonocore et al. 2016; Reingold and Stampe 2002), which does not present a competing saccade vector and therefore cannot examine saccade vector averaging as a function of time. A second category of SDT experiments involves double-stepping targets (Becker and Jürgens 1979; Findlay and Harris 1984; Ludwig et al. 2007). Because the intervening stimulus in these experiments is a transient shift of the target location, this stimulus is always task relevant and suprathreshold for eliciting saccades. Therefore, the current methodology differs from previous experimental techniques for estimating SDT, because the intervening stimulus was a sustained competing saccade vector that is also task irrelevant and subthreshold for eliciting a saccade. This uniquely allows for the examination of sustained competition between a suprathreshold target and a subthreshold distractor as a function of time.

Distractor feature differences in saccade curvature timing.

A recent neurophysiological investigation by White et al. (2009) discovered SCi VM neurons with color “sensitivities” (as supposed to selectivities due to their very broad tuning) and observed that the transient onset related burst latencies for these neurons were 35 ms slower in response to isoluminant color saccade targets than to maximum contrast luminance saccade targets. Because the distractors utilized in the current experiment had similar visual properties as the targets utilized by White et al., and because SDT likely reflects the afferent delay of visual input into the oculomotor system (Becker and Jürgens 1979), we predicted that SDT would be ~35 ms longer for color distractors than luminance distractors. Qualitatively consistent with this prediction, our data demonstrated that the SDT for color-modulated distractors was longer than that for luminance-modulated distractors. However, this difference was only 20 ± 10 ms, because saccade curvatures deviated from baseline in SDOA bin −90 for color-modulated distractors and deviated from baseline in SDOA bin −70 for luminance-modulated distractors. This was consistent across sum and max curvature metrics and across fit functions, and was also corroborated by the fitted midpoint parameters, which estimated the SDT difference to be between 10.81 and 22.90 ms.

These featural differences in SDT very likely arose as a result of cortical processing, because the alternative retinotectal visual pathway is colorblind (Schiller et al. 1979) and rapidly projects to the subcortical oculomotor substrates on timescales of 11–27 ms (Schiller and Malpeli 1977), which should reduce the SDT estimates well below 70 ms. This suggestion of cortically projected visual representations into the oculomotor system eliciting saccade curvatures also offers several possible explanations for the discrepancy between our color and luminance SDT difference of 20 ms and the 35-ms difference observed by White et al. (2009). One explanation is that color is processed considerably faster in human cortex than in monkeys; however, this is unlikely given the close correspondence between human and monkey early visual cortical processing (Self et al. 2016). More likely is that the Gabor patches utilized in the current study offered additional featural processing of spatial frequency and orientation, and because these features are processed earlier than color but not earlier than luminance, this additional processing could have speeded the projection of color-modulated distractor representations from cortex to the oculomotor system but offered no such advantage for luminance-modulated distractors. This explanation suggests that this effect of distractor feature can be attributed to early cortical processing differences and is therefore consistent with the observation that visual onset latencies are 23 ms shorter in the dorsal stream layers of both V1 and V2 than in the ventral stream layers (Schmolesky et al. 1998). In any case, these SDT differences cannot be attributed to practice effects (see Gilbert et al. 2001 for a review), because participants observed an equal number of luminance and color distractors, and the presentation and location of these features were not predictable. Similarly, although saccade curvatures vary as a function of SRT generally (McSorley et al. 2006, 2009; Walker et al. 2006), and sum curvature is intrinsically related to saccade amplitude, we found no differences in SRT or amplitude based on the type of distractor, suggesting that SDT differences between color and luminance distractors could not be attributed to differences in SRT or amplitude.

An inspection of goodness of fit suggested that the Gaussian model provided a better description of luminance-modulated distractor processing, whereas the logistic model provided a better description of color-modulated distractor processing. These results suggest that irrelevant color representations are maintained ≥200 ms after onset while the oculomotor system is concurrently planning a saccade to a task-relevant target. Conversely, under the same task conditions, irrelevant luminance representations begin to decay ~140 ms (based on the Gaussian midpoint parameters) after onset. If these results simply reflected the transient onset differences indexed by SDT, one would expect that color decays ~20 ms after luminance, which would be ~160 ms after onset. Given that the logistic modeling suggested that color representations do not decay for at least 200 ms after onset, these results may therefore reflect a fundamental representational difference between luminance and color in the oculomotor system, and perhaps more generally in the visual system. Because our distractor feature analysis suggested that distractor representations were likely projected from cortex, such differences could arise due to dorsal stream attentional circuits processing luminance-modulated distractors and disengaging after target discrimination, and ventral stream perceptual circuits processing the color-modulated distractors and sustaining object representations.

Directional differences on saccade curvature timing.

The current analysis of directional differences demonstrated that the processing responsible for eliciting saccades curved toward a target occurs before the processing responsible for eliciting saccades curved away from distractors, because the Gaussian functions for each of these trial types were offset by ~50 ms along the SDOA axis. This result is consistent with previous behavioral studies that have examined saccade deviations as a function of SRT on trials with synchronous distractor and target onsets and found that saccades curve toward distractors at short latencies between 150 and 200 ms, but then begin to curve away from distractors after latencies of ~200 ms (McSorley et al. 2006, 2009; Walker et al. 2006). This transition from saccades curving toward and then away from distractors has been interpreted as reflecting fast excitatory activation of the distractor saccade vector followed by slow(er), monotonically accumulating, and sustained inhibition of this vector (McSorley et al. 2006, 2009; Walker et al. 2006). However, our data provide novel evidence inconsistent with this conceptualization of oculomotor inhibition, because we observed that saccade curvatures away from a distractor increased and decayed according to a Gaussian function of SDOA. This result seems to suggest that, on the current task, when the oculomotor system inhibited the competing distractor saccade vector to ensure that an accurate saccade was made to the target, this inhibitory response actually pushed the distractor vector representation below the level that would be expected if no distractor were present (i.e., baseline). Over time, however, this overshoot normalized, and the distractor vector representation returned to baseline. Critically, because the slope parameters were nearly identical between SDOA functions for saccades curved toward and away from distractors, the rates of accumulation and decay for both excitation and inhibition were very similar. Given that fast, transient, excitatory activity occurring immediately before the initiation of a saccade causes saccades curved toward a distractor (McPeek et al. 2003), the most parsimonious account of our data is that a fast, transient, inhibitory response elicited saccades curved away from distractors.

This account of the spatiotemporal factors that elicit saccades curved away from distractors is also supported by a recent neurophysiological experiment. White et al. (2012) analyzed SCi neuronal activity specifically on trials on which saccades curved away from a distractor. They observed that the magnitude of saccade curvatures only correlated with distractor-related neuronal activity in the epoch between −22 and 0 ms before the initiation of a saccade. This result is also inconsistent with the elicitation of saccade curvatures by a slow, sustained, accumulating inhibitory response during competitive oculomotor processing and instead suggests that a transient shift of distractor-related inhibition in the critical epoch elicited saccade curvatures.

Putative neural mechanisms.

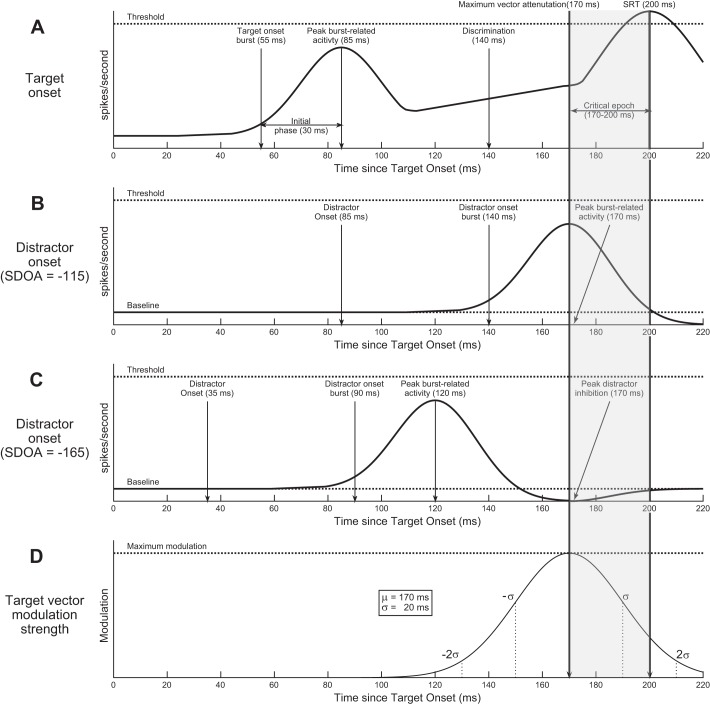
Our explanation of how the current data are related to neural processing is based on the very robust neurophysiological time course of collicular neurons observed during oculomotor target selection (Fig. 5A). In a thorough examination of this time course, McPeek and Keller (2002) observed that target and distractor transient onsets elicited equal bursts of activity in SCi VM “prelude” neurons with a latency of ~55 ms and an initial phase of ~30 ms. After this burst, target-related activity steadily increased, whereas distractor-related activity remained constant or decreased. Eventually, a target could be reliably discriminated from a distractor ~140 ms after stimulus onset, and this discrimination latency was independent of SRT for approximately half of the neurons. Target-related activity continued to increase until a secondary movement-related burst of activity was observed around the time of saccade initiation. A simulation of this neurophysiological time course for a correct trial with a target in the receptive field of the neuron and an arbitrarily chosen SRT of 200 ms is displayed in Fig. 5A.

Fig. 5.

Schematic diagram of putative neural mechanism for target vector modulation by a transient distractor. All subplots depict a correct trial with an SRT of 200 ms observed on the current saccade task. Arrows indicate critical temporal events during target selection. All temporal values were reported by McPeek and Keller (2002) with the exception of peak distractor inhibition (C), which is inferred from the current data. A: simulated firing rates as a function of time from target onset for a typical SCi prelude/build-up neuron with a target in the receptive field. B: simulated firing rates as a function of time from target onset for a typical SCi prelude/build-up neuron with a distractor in the receptive field on a trial with an SDOA of −115 ms. C: simulated firing rates as a function of time from target onset for a typical SCi prelude/build-up neuron with a distractor in the receptive field on a trial with an SDOA of −165 ms. D: a hypothetical model of saccade target vector modulation strength as a function of time, where the point of maximum modulation (μ) is aligned to the critical epoch 30 ms before saccade initiation and the rate of decay (σ) is based on the fitted slope parameters for the saccade curvature SDOA functions for saccades curved toward and away from the target.

A critical component of our proposed neural mechanism is the causal demonstration by McPeek et al. (2003) that saccade curvature toward a distractor is elicited by subthreshold excitation at the SCi distractor locus ~30 ms before the initiation of a saccade (see “Critical epoch” in Fig. 5). Furthermore, subthreshold excitation elicited by a competing distractor stimulus during oculomotor target selection is sufficient to elicit these saccade curvatures (McPeek et al. 2003; Port and Wurtz 2003). Given this robust critical epoch and the predictable timing of visual onset bursts in SCi VM neurons in response to transient visual onsets (Boehnke and Munoz 2008), by analyzing the data as a function of relative time between distractor transient onset and saccade initiation (i.e., SDOA), we postulated that we could indirectly measure the effect of this onset burst on the impending saccade trajectory at various time points relative to saccade onset. Consistent with this reasoning, we determined that the maximum vector modulation for saccades curved toward the distractor was at an SDOA of −115 ms, which indicates trials on which the distractor onset occurred 115 ms before the saccade initiated. As can be seen in Fig. 5B, if we add to this SDOA value 55 ms to account for the onset burst latency (Boehnke and Munoz 2008) and an additional 30 ms to account for the initial phase of the onset burst (McPeek and Keller 2002), this situates the peak level of activity associated with the onset burst at 30 ms before the initiation of the saccade (i.e., −115 + 55 + 30 = −30), which aligns exactly to the critical epoch (McPeek et al. 2003). Interestingly, the Gaussian shape of our SDOA functions suggested that saccade target vector modulation also gradually decreased when this theoretical onset burst was before or after the critical epoch.

Given the above observations, we therefore propose a Gaussian model of saccade target vector modulation by a competing saccade vector as a function of time relative to the initiation of the saccade (Fig. 5D). For this model, the point of maximum modulation (μ) corresponds to the critical epoch and is therefore determined by the SRT on any particular trial (for Fig. 5, an SRT of 200 ms was arbitrarily chosen). The modulatory strength of the competing vector gradually and continuously decreases in either direction about this time point at a particular rate (σ). This constant reflects the spatiotemporal interactions of subthreshold competing vectors in the oculomotor system and was estimated by using an approximation of the fitted slope parameter for the SDOA functions robustly observed across saccade curvature metrics and directions (i.e., 20 ms).

Interestingly, there are two possible interpretations of the Gaussian shape of the SDOA functions. The first is that the spatiotemporal interaction between the competing vectors is binary: if the competing activity aligns with the critical epoch, there is vector modulation, and otherwise, there is not. Under such circumstances, a Gaussian-shaped SDOA function could still emerge if the exact latency of the distractor-related onset burst stochastically varies trial to trial according to a Gaussian distribution with an SD of ~20 ms. However, this interpretation is unlikely given that it predicts that the total observed range of visual onset burst times should be between ~55 ± 40 ms (i.e., mean onset time ± 2 SD), which is inconsistent with the actual observed range of these onset bursts: 40–70 ms (reviewed by Boehnke and Munoz 2008). The second interpretation is that the spatiotemporal interaction between competing saccade vectors varies continuously over time. This entails that the latency of the distractor-related onset burst is consistent across trials, but the modulatory effect of this burst on the impending saccade target vector varies as a function of the relative time between the critical epoch and the competing vector. Support for this interpretation is provided by the seminal work of Robinson (1972), who thoroughly investigated suprathreshold spatiotemporal interactions between competing saccade vectors using double stimulation. He reported that when suprathreshold stimulation was delivered to two separate locations in SCi, if there was a sufficiently large temporal interval between the pulses (>75 ms), two distinct saccades were elicited to their corresponding locations. However, as this temporal interval decreased below 75 ms, the second saccade mechanically interfered with and replaced a portion of the first saccade. Critically, the attenuated portion of the first saccade increased as the temporal interval between pulses decreased, until the interval was sufficiently short (<30 ms) and the second saccade entirely replaced the first. Finally, when both vectors were stimulated simultaneously, this elicited a saccade that was the average of the two vectors weighted by the strength of the current delivered to each location. These observations therefore demonstrated that saccade vector modulation by a competing vector varies continuously as a function of the relative time between saccade initiation and the competing activity. Furthermore, a more recent neurophysiological experiment has generalized these observations to circumstances involving subthreshold activity encoding the competing saccade vector, where Port and Wurtz (2003) observed that curved saccades were associated with sequential neuronal activity at distractor and target loci offset by ~20 ms. Conversely, when this activity occurred simultaneously, this was associated with straight saccades that landed between stimuli.

The putative neural mechanism outlined above provides an explanation for saccade curvature toward the distractor with a high degree of temporal consistency to the thoroughly examined neurophysiological time course of oculomotor target selection processing. Critically, this mechanism can also account for saccade curvature away from the distractor. Because our results suggest that saccade target vector modulation varies continuously as a function of relative time between the critical epoch and activity related to a competing vector, then given that our data for saccades curved away from the distractor conformed to a very similar SDOA function, this suggests that 1) there was a time point of maximum inhibition relative to the transient onset of the distractor that was relatively stable across trials, and 2) this inhibition accumulated and decayed at a similar rate as the initial onset burst given the almost identical fitted-slope parameters of the SDOA functions between saccade directions. The maximum saccade curvature away from the distractor was observed at an SDOA of −165 ms, indicating trials on which the distractor onset 165 ms before saccade initiation. If the critical epoch is situated 30 ms before saccade initiation, then we can estimate the time of maximum distractor-related inhibition after distractor onset with the subtraction 165 – 30 = 135 ms. This is depicted in Fig. 5C: a distractor onset initially elicits a burst of activity reaching a peak ~85 ms after onset and subsequently elicits an inhibitory “burst” that reaches a trough ~135 ms after onset. On trials with an SDOA of 165 ms, this trough is aligned with the critical epoch. However, as the SDOA varies in either direction about this value, the modulatory effect on the saccade target vector decreases according to the model discussed above in detail and illustrated in Fig. 5D.

This speculative inhibitory “burst” may be explained by the predictable irrelevance of the distractor because the target and distractor always appeared at different locations, were visually very dissimilar, and always appeared in the same temporal order. Stimulus predictability has a systematic effect on saccade curvature (McSorley et al. 2009; Walker et al. 2006), as well as the activity levels of SCi VM neurons whereby the magnitude of onset-related bursts decrease proportionally to the unlikelihood that the stimulus in the receptive field of the neuron is a saccade target (Basso and Wurtz 1997, 1998). This validates the plausibility of two critical features of the above speculative inhibitory burst: temporal contingency to the preceding onset burst and temporal independence to saccade initiation. Furthermore, this may explain why the current results differ from those of other behavioral studies that have clearly demonstrated a slower, more gradual increase in saccade curvature away from a distractor (e.g., McSorley et al. 2006, 2009; Walker et al. 2006). Given the top-down nature of stimulus predictability, it seems more likely that this inhibition is mediated by the inhibitory oculomotor control system of the basal ganglia (see Hikosaka et al. 2000) than local lateral inhibitory circuits in SCi (Munoz and Istvan 1998).

Although a neurophysiological experiment has demonstrated that saccades curved away from distractors are caused by inactivation at the distractor locus in SCi (Aizawa and Wurtz 1998), the temporal mechanics of these saccades curved away from distractors remain disputed (White et al. 2012). By analyzing saccade curvature as a function of SDOA, we observed that the maximum modulation of an impending saccade vector by a competing vector occurs when the competitive activity occurs in the critical epoch of ~30 ms before saccade initiation. Furthermore, the strength of this modulation decreases in either direction of the critical epoch according to a Gaussian function with σ ≈ 20 ms. Because saccades curved toward a distractor are elicited by a rapid, transient shift of activation at the distractor locus in this critical epoch (McPeek et al. 2003), then given the similar shape of the Gaussian functions for saccades curved toward and away from distractors, we conclude that saccades curved away from distractors were caused by a rapid accumulation of inhibition at the distractor locus.

Conclusion.

With the use of a novel methodological technique, the current experiment demonstrated that a minimum of 70 ms is required for saccade vector modulation by a distractor. This replicated the results from previous behavioral studies employing various other methodologies and analytic techniques (Becker and Jürgens 1979; Findlay and Harris 1984; Ludwig et al. 2007; Reingold and Stampe 2002; cf. Buonocore et al. 2016). We also observed that the time course of saccade vector modulation was affected by the visual features constituting the distractor, because color distractors required an additional ~20 ms of processing time compared with luminance distractors to modulate saccade vectors. These behavioral, feature-based temporal differences are consistent with differences observed in the neurophysiological response times of neurons in the oculomotor (White et al. 2009) and visual systems (Schmolesky et al. 1998) mediated through cortical visual processing and therefore suggest a possible underlying neural mechanism for this result. Finally, we modeled saccade curvature as a function of the relative time between distractor onset and saccade initiation (saccade-distractor onset asynchrony; SDOA) separately for saccades curved toward and away from a distractor to examine the spatiotemporal interaction of competing saccade vectors. We observed that these function fits had nearly identical slope parameters. Critically, because saccades curved toward distractors are elicited by a rapid, transient accumulation of excitatory activity encoding a distractor vector (McPeek et al. 2003; Port and Wurtz 2003), this result suggests that saccades curved away from distractors are elicited by a rapid, transient accumulation of inhibition.

GRANTS

This work was funded by a National Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant (to M. Fallah) and NSERC Canada Graduate Scholarships-Master’s Program and Ontario Graduate Scholarships (to D. H. Kehoe).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

D.H.K. and M.F. conceived and designed research; D.H.K. performed experiments; D.H.K. analyzed data; D.H.K. and M.F. interpreted results of experiments; D.H.K. prepared figures; D.H.K. drafted manuscript; D.H.K. and M.F. edited and revised manuscript; M.F. approved final version of manuscript.