Hierarchical differences in population coding within auditory cortex

Prevailing models of population coding of sensory information are based on a limited subset of neural structures. An important and under-explored question in neuroscience is how distinct areas of sensory cortex differ in their population coding strategies. In this study, we compared population coding between primary and secondary auditory cortex. Our findings demonstrate striking differences between the two areas and highlight the importance of considering the diversity of neural structures as we develop models of population coding.

Abstract

Most models of auditory cortical (AC) population coding have focused on primary auditory cortex (A1). Thus our understanding of how neural coding for sounds progresses along the cortical hierarchy remains obscure. To illuminate this, we recorded from two AC fields: A1 and middle lateral belt (ML) of rhesus macaques. We presented amplitude-modulated (AM) noise during both passive listening and while the animals performed an AM detection task (“active” condition). In both fields, neurons exhibit monotonic AM-depth tuning, with A1 neurons mostly exhibiting increasing rate-depth functions and ML neurons approximately evenly distributed between increasing and decreasing functions. We measured noise correlation (r_noise) between simultaneously recorded neurons and found that whereas engagement decreased average r_noise in A1, engagement increased average r_noise in ML. This finding surprised us, because attentive states are commonly reported to decrease average r_noise. We analyzed the effect of r_noise on AM coding in both A1 and ML and found that whereas engagement-related shifts in r_noise in A1 enhance AM coding, r_noise shifts in ML have little effect. These results imply that the effect of r_noise differs between sensory areas, based on the distribution of tuning properties among the neurons within each population. A possible explanation of this is that higher areas need to encode nonsensory variables (e.g., attention, choice, and motor preparation), which impart common noise, thus increasing r_noise. Therefore, the hierarchical emergence of r_noise-robust population coding (e.g., as we observed in ML) enhances the ability of sensory cortex to integrate cognitive and sensory information without a loss of sensory fidelity.

NEW & NOTEWORTHY Prevailing models of population coding of sensory information are based on a limited subset of neural structures. An important and under-explored question in neuroscience is how distinct areas of sensory cortex differ in their population coding strategies. In this study, we compared population coding between primary and secondary auditory cortex. Our findings demonstrate striking differences between the two areas and highlight the importance of considering the diversity of neural structures as we develop models of population coding.

though many basic principles of sensory coding at the single neuron level have been discovered, much is still unknown about how this relates to populations of neurons encoding stimuli. Population coding allows for higher complexity of sensory representation than single-neuron coding, due to an exponential increase in the dimensionality of the population response space as the size of the population increases (Cunningham and Yu 2014; Fusi et al. 2016; Pang et al. 2016; Panzeri et al. 2015). Neural populations exhibit high heterogeneity both within and across structures, leading to a vast number of possible ways that populations can encode information (Lehky and Sereno 2011; Zhang and Sejnowski 1999; Zohary 1992). Theoretical models of neural populations have been of tremendous use in discerning some of the principles that govern population coding, but these models have mainly focused on a subset of the possible types of neural populations and have generally assumed that single neurons within a population are homogeneous (Ecker et al. 2011; Fusi et al. 2016). Thus a key task in pursuing general models of population coding is to integrate findings across diverse neural structures, accounting for single-neuron heterogeneity both within and across areas. In doing so, we may also shed light on how population coding is transformed along the sensory hierarchy.

In the auditory system, most of researchers’ efforts have been directed toward understanding coding in only a few structures, including primary auditory cortex (A1). However, prevailing models suggest at least 10 cortical fields in primates (Hackett 2011). Recently, more work has been done to study the properties of neurons outside of A1, but models of how populations encode information in these fields are still few (Carruthers et al. 2015; Miller and Recanzone 2009; Noda and Takahashi 2015; Recanzone et al. 2011). Based on the differences in single-neuron response properties between A1 and higher fields (Bendor and Wang 2008; Camalier et al. 2012; Kuśmierek et al. 2012; Niwa et al. 2013, 2015; Rauschecker et al. 1995; Recanzone et al. 2000; Scott et al. 2011; Tian et al. 2001), it stands to reason that diverse population coding strategies emerge along the auditory cortical hierarchy.

A commonly studied variable in population coding is noise correlation (r_noise) (Cohen and Kohn 2011; Gawne and Richmond 1993; Kohn et al. 2016; Zohary et al. 1994). Noise correlations arise when trial-by-trial fluctuations in neural activity are correlated between the neurons in a population. Theoretical studies suggest that r_noise affects coding differently depending on many aspects of the structure of the neural population, including globally correlated single-neuron tuning (Abbott and Dayan 1999; Averbeck et al. 2006; Ecker et al. 2011; Oram et al. 1998), differential correlations (Moreno-Bote et al. 2014), heterogeneity of single-neuron tuning (Ecker et al. 2011), the magnitude of correlations (Hu et al. 2014), and stimulus dependence (Zylberberg et al. 2016). Furthermore, it appears that observed changes in r_noise in response to changes in behavioral state are diverse and depend on specific task demands (summarized in Doiron et al. 2016). Thus measuring r_noise across diverse neural structures under diverse behavioral conditions can provide critical insights toward the development of general models of population coding.

We recorded from both A1 and a secondary auditory cortical field, middle lateral belt (ML), while we presented amplitude-modulated (AM) noise during both task engagement and passive listening. In both fields, neurons exhibit monotonic tuning to AM depth, with A1 neurons mostly exhibiting increasing rate-depth functions and ML neurons evenly distributed between increasing and decreasing functions (Niwa et al. 2015). We measured r_noise between simultaneously recorded neurons and found that whereas engagement decreased average r_noise in A1 (previously reported in Downer et al. 2015), engagement increased average r_noise in ML. We constructed models of both A1 and ML and varied r_noise across multiple iterations of these artificial populations, and we used two different decoding methods to determine the consequences of r_noise in each field. Whereas A1 population performance exhibits sensitivity to r_noise, ML performance is quite robust to changes in r_noise. Our results support diverse effects of r_noise across neural structures and show that r_noise can be differently shifted by task demands in adjacent cortical fields.

MATERIALS AND METHODS

All data have been presented previously (Downer et al. 2015; Niwa et al. 2013, 2015) and have been reanalyzed for the purpose of comparing A1 and ML population coding properties.

Subjects

Subjects were three adult rhesus macaques (2 female, 1 male; 6–11 kg). We recorded the activity of single units from primary auditory cortex (A1) and middle lateral belt (ML) from the right hemisphere. All procedures were approved by the University of California, Davis animal care and use committee and met the requirements of the United States Public Health Service policy on experimental animal care.

Stimuli

Each recording session consisted of the presentation of eight unique stimuli: an unmodulated broadband (white) noise as well as sinusoidal amplitude-modulated (AM) broadband noise at seven modulation depths (6, 16, 28, 40, 60, 80, and 100% depth). The unmodulated broadband noise can be described as having 0% AM depth. Across recording sessions, we varied the frequency of the AM, from 2.5 to 1,000 Hz. The frequency selected for a given session was picked on the basis of the response of the multiunit (MU) activity of the selected recording site (see Physiology). All stimuli were 800 ms in duration and were calibrated to be 63 dB at the outer ear (model 2231 sound level meter; Bruel and Kjaer). We generated stimuli using a custom MATLAB program and then passed these signals through a digital-to-analog converter (Power 1401; Cambridge Electronic Design). These analog signals were then attenuated (PA5 and Leader LAT-45; TDT Systems), amplified (MPA-200; RadioShack), and presented from a speaker (PA-110; RadioShack or Pro-7AV; Optimus) positioned 0.8 or 1.5 m in front of the subject and placed in the middle of the interaural axis. Sounds were generated at a 100-kHz sampling rate and cosine-ramped at the onset and offset (5 ms).

Task

The behavioral paradigm is the same used by Niwa et al. (2012) and Downer et al. (2015). We recorded single-unit activity from A1 and ML of rhesus macaque auditory cortex during each of two conditions: 1) active engagement and 2) passive presentation. During the active condition, animals engaged in an AM detection task. During the passive condition, we presented the same stimuli while they sat quiet and awake.

Active engagement.

Animals indicated whether a sound was AM in a Go/No-Go paradigm. Animals completed a single a trial by 1) waiting for a cue light to prompt trial initiation, 2) depressing a lever to initiate a trial, 3) listening to two successive sounds, S1, which was always the 0% AM-depth stimulus, and S2, which could either be the 0% AM-depth stimulus (nontarget) or AM noise (target), and 4) indicating detection of target (AM depth of 6–100%) by releasing the lever within 800 ms after S2 offset, or indicating the second sound was a nontarget (AM depth of 0%) by keeping the lever depressed for 800 ms after S2 offset. S1 and S2 were both 800 ms and were separated by 400 ms of silence. Animals were rewarded with liquid (juice or water) for both hits (correctly releasing the lever after target presentation) and correct rejections (correctly withholding lever release after nontarget presentation). Animals were informed of both misses (failure to release lever after AM) and false alarms (inappropriate lever release after nontargets) via flashing LED and received a penalty (15- to 60-s timeout in which a new trial could not be initiated) for false alarms. After correct trials, there was a minimum 2-s intertrial interval. Multiple stimuli (16, 28, and 40% AM depth) were near animals’ AM detection thresholds (O’Connor et al. 2000, 2011).

Passive presentation.

During passive blocks, animals sat quietly while we presented the same stimulus set as in the active condition. Stimulus presentation differed from the active condition in that we presented no S1 during passive blocks. Animals received randomly timed liquid rewards between stimulus presentations. During a recording, animals participated in one passive and one active block, each consisting of ~450 trials (roughly 50 repetitions per stimulus, with 100 repeats of the 0% AM stimulus). Animals were cued to begin an active block by a cue light. For two animals, we counterbalanced which condition, passive or active, came first. For the other animal, the active condition was always followed by the passive condition. The order of the behavioral condition did not significantly affect our results.

Physiology

Surgery.

After each animal learned the task, we performed a surgery to place a recording cylinder and head post to allow for daily recordings from auditory cortex (AC). For the cylinder, we first performed a craniotomy over the right parietal lobe and then placed a CILUX recording cylinder over the craniotomy. We placed a titanium head post behind the brow ridge along the midline of the skull. Both the cylinder and the head post were held in place using bone screws and dental acrylic. After recovery from surgery, the animal was retrained on the task, and then we began recording.

Recording procedures.

During all recordings, animals sat head-restrained in an acoustically transparent chair in a sound-attenuated booth. On each recording day, we advanced a tungsten microelectrode (FHC, 1–4 MΩ; Alpha-Omega, 0.5–1 MΩ) through the parietal lobe to the superior temporal plane to record from AC. To allow for precise and stable placement of the electrode, we fastened a plastic grid over the top of the recording cylinder. This grid contains holes that snugly fit 27-gauge hypodermic tubing. These holes are arranged linearly in the caudal-rostral and medial-lateral axes, and spaced 1 mm apart along each axis. After the grid was attached to the recording cylinder, we inserted a 27-gauge hypodermic “guide tube” to penetrate the dura mater. We then inserted the electrode through the guide tube to access the brain. The vertical position of the electrode was controlled via a manual hydraulic drive (Stoelting).

Signals from the electrode were amplified (AM Systems model 1800), bandpass filtered between 0.3 and 10 kHz (Krohn-Hite 3382), and then digitized at a 50-kHz sampling rate (Power 1401; Cambridge Electronic Design). The electrode was advanced to the superior temporal plane while we presented the animals a range of sounds, including AM noise. When we reached a location where neural activity appeared strongly responsive to AM, we stopped advancing the electrode and then determined the AM-response properties of the aggregate neural activity (MU activity) at that site.

We determined which AM frequency to present during the session by finding the best modulation frequency (BMF) of the MU activity at each site. MU activity was defined as any clear spiking activity well above the background noise level of the recording. After an AM-responsive site was found, we presented 800-ms AM stimuli across a range of frequencies, all at 100% depth, as well as 800-ms unmodulated stimuli. We measured MU firing rate and vector strength (phase-projected vector strength, VSpp; Yin et al. 2011) over the entire 800-ms stimulus period in response to each stimulus. We then used the distribution of neural activity in response to each stimulus to calculate the area under the receiver operating characteristic (ROC area) of the MU for each AM frequency. This analysis quantifies how well an ideal observer could estimate what stimulus had been presented on a given trial on the basis of the MU response alone. In this case, we are measuring how well the MU activity responds differently to 100% depth AM stimuli compared with the unmodulated broadband noise. For two completely nonoverlapping MU activity distributions, ROC area will be 1.0 (or 0), and for identical distributions, ROC area will be 0.5, meaning an ideal observer is at chance level at guessing which stimulus was just presented. The AM frequency at which ROC area was highest (farthest from 0.5) was that MU’s BMF.

We calculated both firing rate and VSpp on each trial; thus we derived two separate BMFs at each recording site. Sometimes, the rate-based BMF (BMF_FR) differed from the vector strength-based BMF (BMF_VS). In these cases, we alternated which BMF was used such that we used the BMF_FR if we used BMF_VS the last time the issue arose, and vice versa.

Single-neuron contributions to the MU signal were determined offline. We sorted spikes using template-based sorting algorithm functions in Spike2 (v.6; Cambridge Electronic Design) to create single-unit template waveforms and then matched spiking events to those templates. We then used principal components analysis to visually confirm that events assigned to separate single units formed separable clusters in principal component space. Thresholds for determining spiking activity above background noise were determined visually by the experimenters with the aid of Spike2’s automatic trigger-setting algorithm. Spiking activity was generally four to five times the background noise level. Fewer than 0.2% of spike events assigned to single-neuron clusters fell within a 1-ms refractory period window.

To determine the cortical field from which we recorded on a given day, we used both physiological measures (Rauschecker et al. 1995; Tian and Rauschecker 2004) and stereotactic coordinates (Martin and Bowden 1996). In one animal, we anatomically confirmed our recording locations (described below); for another animal, tissue has not yet been analyzed; the final animal is still serving as a research subject. We used stereotactic coordinates to target AC and used physiological response properties during recording to differentiate between A1 and ML. We presented pure tone stimuli at a range of frequencies and intensities, as well as bandpass noise stimuli at a range of frequencies, intensities, and bandwidths, to assess frequency tuning. Stimuli were 100 ms in duration and varied across frequency and intensity (and bandwidth for bandpass noise stimuli), with at least 3 repetitions for each frequency/intensity/bandwidth combination. This allowed us to measure each unit’s frequency-response area by finding the contour line for frequency/intensity combinations that evoked firing rates at least 2SD above the spontaneous firing rate (determined in a 75-ms window before stimulus presentation). Thus we could measure each unit’s characteristic frequency (CF) and sharpness of tuning, i.e., bandwidth (BW). In each animal, we mapped CF and BW to determine the topographic distribution of each.

Using the topographic distribution of CF, we established a tonotopic gradient wherein, in both A1 and ML, CF is highest at its most caudal extent and lowest at its most rostral extent. Borders between adjacent fields in either direction were drawn when the gradient reversed direction. We used the topographic distribution of BW, spike latency, and robustness of response to pure tones to determine the border between A1 and ML. Whereas both A1 and ML exhibit a similar tonotopic map, A1 exhibits narrower frequency-response functions than ML and responds more strongly and quickly to pure tones (Niwa et al. 2015). We drew the border between A1 and ML on the basis of the gradients of cells’ BW, pure-tone response latency. and overall robustness in response to tones, as measured by firing rate.

In one animal, we confirmed our stereotactic and physiological assignments by performing postmortem histological analyses. On termination of recording, we inserted biotinylated dextran amine to the rostral, middle, and caudal regions of physiologically determined A1 at the border between A1 and middle medial belt (MM). The animal was then given an overdose of pentobarbital sodium and perfused using 4% paraformaldehyde in 0.1 M phosphate buffer. The brain was removed, blocked, and sliced into 50-μm sections, and slices were stained in alternation with 1) mouse anti-parvalbumin → biotinylated horse anti-mouse secondary → acetyl-avidin-biotinylated peroxidase complex (ABC) → diaminobenzadine (DAB); 2) Nissl substance; and 3) Nissl substance → ABC → DAB. This histology was previously shown by O’Connor et al. (2010), and our physiologically determined A1 borders were validated with anatomical evidence, e.g., dense parvalbumin staining in the area within the biotinylated dextran amine markers.

Data Analysis

Selection of single neurons for analysis.

Although in a previous study using some of these data we limited analyses to neurons with a significant change in firing rate in response to sounds (Downer et al. 2015), recent work provides evidence that stimuli can affect the r_noise of pairs even when the stimuli do not elicit changes in firing rate (Snyder et al. 2014). Thus we are including in the present analysis all recorded neurons from each field, provided that they were well isolated throughout an entire block. Noise correlation measures were only calculated between pairs of neurons recorded from the same electrode. We analyzed 268 A1 pairs (246 active, 167 passive, 145 both conditions) and 94 ML pairs (84 active, 56 passive, 46 both conditions).

Tuning correlation and noise correlation.

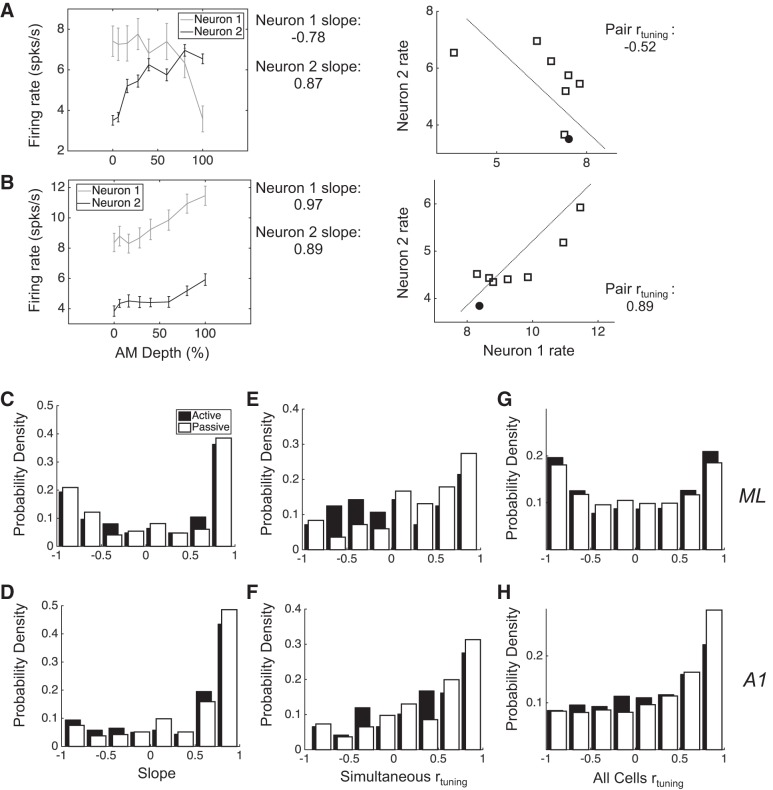
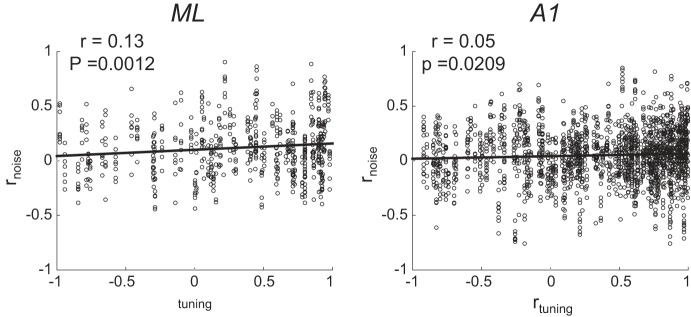
Conceptually, noise correlation (r_noise) and tuning correlation (r_tuning) describe joint neural response distributions in much the same way that variance and mean describe single-neuron response distributions. The joint non-stimulus-related variance between neurons is measured by r_noise, and the joint stimulus tuning is measure by r_tuning. We calculate both r_tuning and r_noise in all simultaneously recorded pairs, separately in each condition. We calculated r_noise by computing the Pearson correlation coefficient between vectors of trial-by-trial firing rates of individual neurons. Firing rates were calculated over the entire 800-ms stimulus presentation window. We calculate r_noise within each stimulus. For some analyses, we want to collapse across stimuli, so we first z-score firing rates within each stimulus, create a large vector of normalized trial-by-trial firing rates that includes responses to all stimuli, and then compute the Pearson’s correlation as above. Collapsing across stimuli in this manner produces nearly identical results as if we simply averaged the r_noise across all stimuli. We obtained as many stimulus repetitions as we could within a recording session while maintaining isolation of neurons. To include the active condition of a recording session for analysis, the animal had to have completed at least 450 trials, although they often did more. To include a recorded neuron for analysis within a given condition, the cell had to have been well isolated for at least 25 repetitions per stimulus. The minimum number of repetitions of a given stimulus was 27, the maximum was 71, and the average was 50.5. We calculate r_tuning by computing the Pearson correlation between the neurons’ mean firing rates across all eight unique stimuli. Whereas r_noise measures shared variability between neurons, r_tuning quantifies the shared signal between neurons. Figure 1, A and B, illustrates how single-neuron AM tuning relates to r_tuning. Namely, when both neurons exhibit similar firing rate vs. AM depth functions, their r_tuning tends to be positive (Fig. 1B), and when the functions are dissimilar, r_tuning tends to be negative (Fig. 1A). Note that neurons do not need to have been simultaneously recorded for us to measure r_tuning (e.g., Fig. 1, C and D, far right). We used Pearson’s correlation in all analyses in the present study but have confirmed the robustness of our results by also calculating Spearman’s correlation. All analyses and interpretations thereof are consistent across these two calculation methods.

Fig. 1.

Different AM tuning properties in A1 and ML lead to different r_tuning distributions. A, left: shown are the firing rates along the range of tested AM depths for 2 simultaneously recorded ML neurons, with their rate-depth slopes noted at right. Right panel shows their joint mean firing rate distribution and the r_tuning value between them. This value is negative because as the mean firing rate of neuron 1 decreases, the mean firing rate of neuron 2 increases. B: same as in A but for a pair with positive r_tuning. C and D: the distribution of slopes in ML has 2 peaks, corresponding to distinct populations of neurons with increasing and decreasing rate-depth slopes, respectively, whereas the distribution in A1 has 1 peak and favors increasing slopes. E and F: the r_tuning of simultaneously recorded pairs in ML and A1 (simultaneous r_tuning) reveals a greater proportion of pairs with negative r_tuning in ML. G and H: r_tuning is calculated between all recorded neurons (all cells r_tuning), showing that the r_tuning distribution has 2 peaks in ML and 1 positive peak in A1. Error bars are SE.

Measuring sensory performance of pairs.

We measure the effect of r_noise on neural coding by measuring the performance at two different levels: 1) we measure the performance of simultaneously recorded pairs of neurons, and 2) we measure the performance of larger populations, via simulations. To measure neural coding, we measured how well target sounds (6–100% AM depth) can be discriminated from nontarget sounds (0% AM depth) on the basis of neural activity. For pairs, we use binomial logistic regression to classify stimuli as AM or not, as in Downer et al. (2015) and Jeanne et al. (2013). The binomial logistic regression model takes as inputs two firing rate vectors (one for each neuron in the pair), coded for whether or not the firing rates were in response to a target or nontarget sound (0 or 1). A set of coefficients is fit to a subset of the data (half of the trials), and then a holdout data set (the other half of the trials) is used to test the performance. The model outputs a single classification prediction value for each trial, between 0 (0% likely to be classified as target) and 1 (100% likely to be classified as target). The percentage of correct classifications for a target stimulus (neural hit rate) was simply the mean prediction classification value. The neural false-alarm rate was the proportion of classifications of nontarget stimuli as targets. Therefore, the percentage of correct classifications for the nontarget stimulus was simply (1 − neural false alarm rate). The overall percentage of correct classifications for each pair at each AM depth was the weighted mean of these two values such that

$$\text{\%correct= [(no. target trials)}·\text{(neural hit rate) + (no. nontarget trials)}·\text{(1}-\text{neural false alarm rate)]/}\left(\text{no. target trials + no. nontarget trials}\right)$$

We used the MATLAB function glmfit with a logistic link function to fit the regression. The link function assigns coefficients to joint firing rates using the equation

$$\ln [y/(1-y)]=b1(X1)+b2(X2)+a$$

where X1 and X2 are the vectors of trial-by-trial firing rates for neuron 1 and neuron 2, respectively, and y is the estimated stimulus category (target or nontarget). The glmfit function assigns the coefficients b1 and b2 and intercept a using maximum likelihood estimation. We used MATLAB’s glmval command to obtain the classification prediction values.

Modeling Larger Populations

We used single electrodes in these recordings; thus the number of simultaneously recorded neurons we obtained in a given session is very low (2–4) relative to the number of neurons in each area that may comprise the perceptually relevant population (assuming weak pairwise correlations; Britten et al. 1992; Cohen and Newsome 2009). Therefore, to address the question of how r_noise may impact both A1 and ML populations, we used resampling methods from our recorded data to model larger populations.

We modeled each population as an array of filters, tuned to AM depth. In this way, neurons with positive rate-depth slopes can be thought of as high-pass filters, and neurons with negative rate-depth slopes can be thought of as low-pass filters. The minority of cells with nonmonotonic AM tuning are thus thought of as bandpass filters. We order neurons by their rate-depth slopes, from most negative to most positive. For each simulation, neurons are added to the population via random selection with replacement until the desired population size is reached. After neurons have been selected and ordered, we normalize each neuron’s mean responses across all eight stimuli to the response of that neuron’s best stimulus (stimulus with the maximum mean firing rate). Thus each modeled neuron’s maximum normalized mean response is 1, and its minimum is 0. Trial-by-trial responses are also normalized to the maximum mean firing rate and thus can go above 1. Finally, we reshape each within-stimulus distribution to ensure that its Fano factor (variance/mean) is maintained when transformed in this way. Otherwise, variance would be underestimated, and responses to stimuli with high firing rates would end up with disproportionately wider response distributions relative to stimuli with lower mean firing rates.

To measure trial-by-trial performance, we simulated trials by drawing randomly from the response distributions of the modeled neurons and used a least-squares error method to classify stimuli as either targets or nontargets. On a given simulated trial, we randomly drew one firing rate from each neuron’s normalized distribution of responses to a single stimulus. This single-trial population response vector was then projected into the same space as the mean responses. We then calculated the mean square error (MSE) of this single-trial response vector from the least-squares curves (3rd-order polynomial fit) of both the actual stimulus being tested and the nontarget. For instance, if we were to test a single-trial response to 100% AM, we would draw a single trial from each of the modeled neurons’ normalized 100% AM-response distributions and then calculate the distance (MSE) of that single-trial population response from both the 100% (target) fit and the 0% (nontarget) fit. The stimulus fit to which the population response was closest (lowest MSE) was the classified stimulus. This was done 400 times for each stimulus, including the nontarget. For the nontarget stimulus, we repeated this process for every stimulus to obtain a measure of how often the population response to nontargets would be classified as a target. Correct classifications of target stimuli as targets were scored as “hits,” and incorrect classifications of nontarget stimuli as targets were scored as “false alarms.” For each stimulus, we quantified population performance as d′, a signal detection theory metric that measures bias-corrected sensitivity.

Simulating r_noise

To analyze the sensory consequences of different r_noise values, we artificially manipulated r_noise in modeled populations, both at the level of pairs and in the larger modeled populations. We used methods developed by Shadlen and colleagues, which are described in detail in (Shadlen et al. 1996). Briefly, we can roughly determine pairwise r_noise values by entering desired r_noise values into a matrix (Q), which constitutes an approximation of the matrix square root of the correlation matrix (C) of the neurons in the population. The matrix Q can be used to impose correlations in a matrix of random numbers, z. For the purposes of this article, the random numbers in z are drawn from a Poisson distribution with mean 1. The size of z is determined by the desired number of trials (400; rows) and neurons in the population (which we varied from 2 to 500; columns). The matrix of correlated response distributions, y, is thus created:

$$y=\mathrm{Qz}$$

We then recovered the original firing rates and Fano factors of the simulated neurons by 1) subtracting the mean from each row of y to obtain distributions with mean of 0; 2) multiplying each element of y by the square root of the neuron’s observed variance, and then 3) adding the neuron’s mean firing rate. The success of this procedure was verified by comparing the observed and the simulated firing rate distributions using a Kolmogorov-Smirnoff test. Only matrices for which the simulated distribution of the neurons did not differ significantly (P > 0.05) from the observed distributions were analyzed further; otherwise we simply recreated y.

As we and others have shown, r_noise between a pair depends on many factors, including r_tuning and joint firing rate. We took this into account when we imposed r_noise between any pair. The r_noise between a pair was determined by the following equation:

$$r_{\text{noise}}={\mu }_{\text{desired}}+m(\mathrm{rate})+n(r_{\text{tuning}})$$

where µ_desired is the desired mean r_noise across the modeled population, rate is the pairwise firing rate (geometric metric of each neuron’s rate), m is the coefficient transforming pairwise rate to r_noise, r_tuning is the pair’s tuning correlation, and n is the coefficient transforming r_tuning to r_noise.

RESULTS

Amplitude Modulation Coding Differs Between A1 and ML

Our laboratory has previously reported some of the single-neuron AM tuning properties in A1 compared with ML (Niwa et al. 2013, 2015). Whereas both fields encode AM depth with firing rate (and with phase-locked spikes), A1 neurons tend to monotonically increase firing rate with increasing AM depth, whereas ML neurons either increase or decrease firing rate with roughly equal proportions across the population. Figure 1, A and B, demonstrates AM-depth tuning in examples of pairs of simultaneously recorded neurons from ML. In 1B, both neurons have increasing slopes. In cases where both neurons’ slopes are the same sign, r_tuning tends to be positive (Fig. 1B, right). In Fig. 1A, one neuron has an increasing slope and the other a decreasing slope. In cases where the slopes of the two neurons of the pair have opposite signs, r_tuning tends to be negative (Fig. 1A, right).

We calculated the slope of AM-depth response functions across all analyzed neurons by first normalizing each neuron’s mean firing rate distribution so that the means vary between 0 (lowest mean firing rate) and 1 (highest mean firing rate). Transforming firing rates in this way before calculating slope provides a means of normalizing slopes for comparison across neurons. The slope was calculated as the linear best-fit line (least squares) across the mean responses to all eight stimuli. In ML, the distribution of slopes across recorded neurons exhibits peaks at both ends, with the vast majority of cells having either very positive or very negative slopes (Fig. 1C). In A1, on the other hand, the distribution shows that A1 neurons are relatively homogeneously tuned to AM, mainly exhibiting positive slopes (Fig. 1D). These differences hold across both active (open bars) and passive (solid bars) conditions (Kolmogorov-Smirnoff test, P < 0.001, active; P = 0.023, passive).

We calculated r_tuning both in simultaneously recorded pairs (Fig. 1, E and F, simultaneous r_tuning) and between all recorded neurons (Fig. 1, G and H, all cells r_tuning). The r_tuning between simultaneously recorded pairs is quite similar between ML and A1, with a slight increase in pairs with negative r_tuning in ML during the passive condition (Fig. 1, E and F; Kolmogorov-Smirnoff test, P = 0.039). However, when we consider all possible r_tuning values, A1 and ML differ strikingly across conditions (Fig. 1, G and H; Kolmogorov-Smirnoff test, P < 0.001, active; P < 0.001, passive). Whereas A1 exhibits primarily positive r_tuning, the r_tuning in ML is roughly evenly distributed between positive and negative values. Such differences in both single-neuron tuning and pairwise correlation properties between ML and A1 suggest distinct population coding strategies between these areas.

Effects of Task Engagement on r_noise

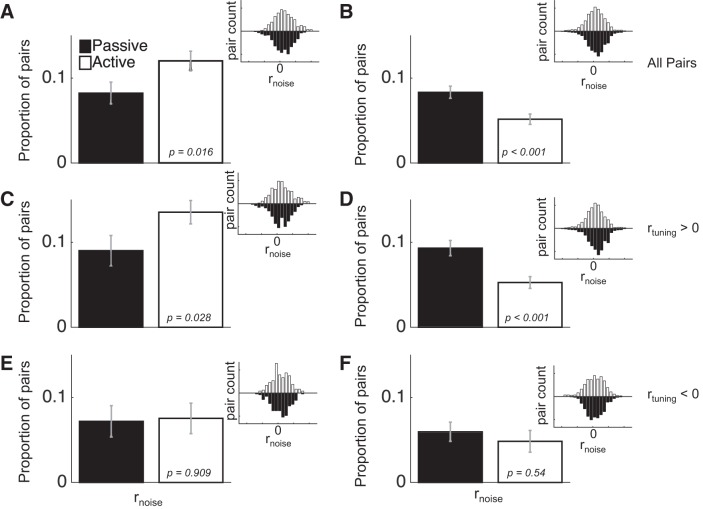
We have previously reported that task engagement reduces r_noise in A1, and also provided evidence that this effect provides a unique contribution to improving AM coding performance during task engagement (Downer et al. 2015). The effect of engagement on r_noise in A1 is presented again in this report to allow for comparisons with ML (Fig. 2). To briefly summarize the A1 findings, during task engagement we observed a decrease in the average r_noise in A1 [Fig. 2B; F_(1,7,403) = 14.92, P < 0.001]. When we further analyzed the data for mediating effects of r_tuning (Fig. 2, D and F), we found that this engagement-related decrease in r_noise was only present in pairs with positive r_tuning [Fig. 2D; F_(1,7,291) = 17.97, P < 0.001], and not in pairs with negative r_tuning [Fig. 2F; F_(1,7,112) = 0.37, P = 0.54]. According the “sign rule” (SR) theory of r_noise, r_noise hampers neural coding when it is the same sign as r_tuning and aids coding when it is the opposite sign (Hu et al. 2014). Therefore, such a selective decrease in r_noise between pairs with positive r_tuning may enhance sensory coding by ameliorating harmful r_noise and leaving beneficial r_noise intact.

Fig. 2.

Task engagement differentially affects r_noise in ML and A1. A and B: during task engagement (active; open bars), r_noise on average goes up in ML (A) but goes down in A1 (B). These effects, in both A1 and ML, hold primarily for pairs with positive r_tuning (C and D), whereas task engagement does not significantly impact r_noise in pairs with negative r_tuning (E and F). Inset histograms show the distribution of r_noise values across the pairs used for each comparison. Error bars are SE.

In contrast, in ML, we found that engagement increased average r_noise [Fig. 2A; F_(1,7,130) = 5.8, P = 0.016]. When we analyzed the mediating effect of r_tuning, we found that pairs with positive r_tuning (Fig. 2C) are driving the overall increase in r_noise observed across all pairs, in that there was an average increase in r_noise among these pairs [F_(1,7,85) = 4.84, P = 0.028]. On the other hand, pairs with negative r_tuning exhibited no effect of engagement on r_noise [Fig. 2E; F_(1,7,45) = 0.01, P = 0.909]. According to the SR, this result may yield an overall decrease in coding performance in ML, since increasing r_noise among pairs with positive r_tuning will diminish population coding accuracy. Such a result seems counterintuitive, considering that, during task engagement, the need to detect stimuli is greater than in the passive condition.

We therefore measured AM detection performance by pairs in both passive and active conditions via binomial logistic regression (see materials and methods). We found that, in both A1 and ML, engagement enhances pairs’ ability to detect AM relative to the passive condition, as revealed by a two-way ANOVA [Fig. 3, A and B; ML: F_(1,6,131) = 4.68; P = 0.031; A1: F_(1,6,404) = 6.03; P = 0.014], although the overall performance of ML pairs is lower than that of A1 pairs [F_(1,6,535) = 97.14; P < 0.001]. This led us to more deeply analyze to what extent r_noise affects coding in both ML and A1.

Fig. 3.

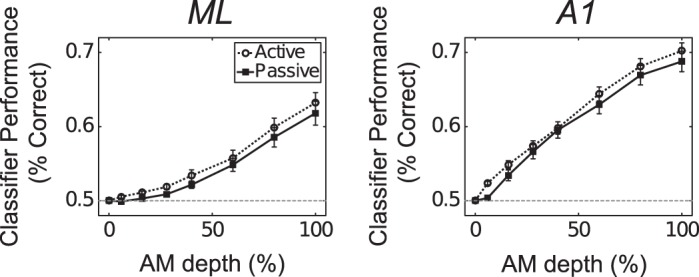
In both ML (A) and A1 (B), pairs classify sounds better in the active condition (open circles) relative to the passive condition (filled squares).

Relationship Between r_noise and Pairs’ Ability to Detect AM

We began by directly analyzing the relationship between r_noise and AM detection in pairs, by parametrically simulating a range of r_noise values and calculating pairs’ performance at each simulated r_noise value. We varied r_noise between −1 and 1 in increments of 0.005, for a total of 401 simulated r_noise values. Figure 4 shows the relationship between r_noise and the performance of the binomial logistic classifier across all simulated r_noise values for three example pairs. The pair in Fig. 4A exhibits a nonmonotonic relationship between r_noise and classifier performance. The vertical black line shows the r_noise value at which this pair’s performance is lowest (approximately −0.4). The pair in Fig. 4C also displays a nonmonotonic relationship between r_noise and classifier performance, whereas the pair in Fig. 4B exhibits a monotonic relationship.

Fig. 4.

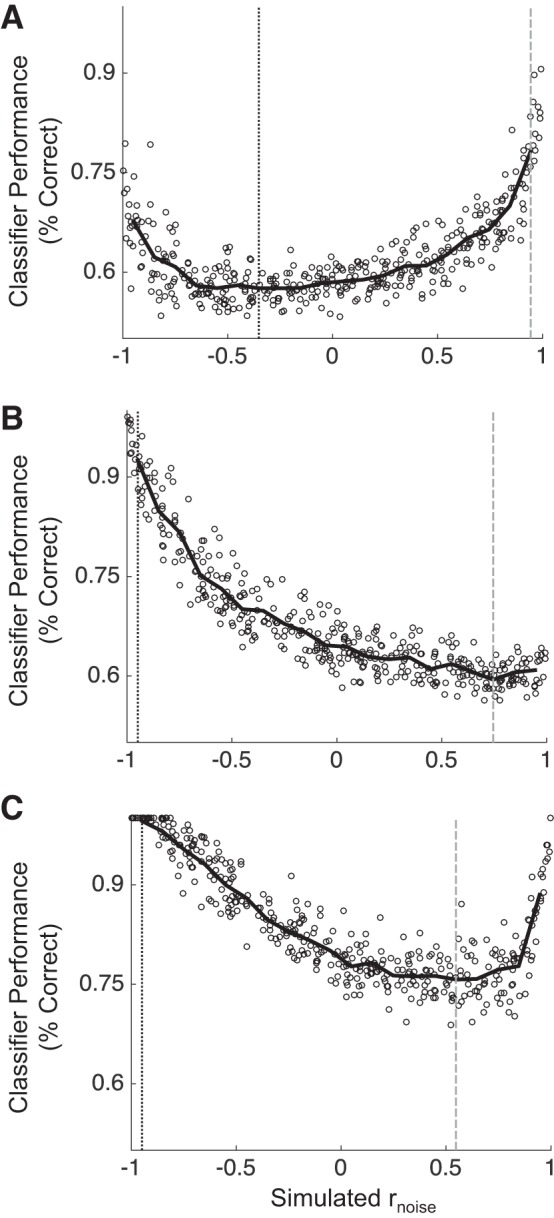
Classifier performance in 3 example pairs over a range of simulated r_noise values. r_noise was varied from −1 to 1 measure classifier performance for each simulation. The pairs in A and C show striking nonmonotonicity in their relationships between r_noise and classifier performance. The pair in B, on the other hand, shows a monotonic relationship. Gray vertical lines show r_noise at maximum performance, and black vertical lines show r_noise at minimum performance.

This nonmonotonicity violates the SR: the SR predicts that sensory performance should monotonically increase as the sign of r_noise changes from being the same sign as r_tuning to the opposite sign. Hu et al. (2014), however, showed performance can increase when r_noise and r_tuning have the same sign when the magnitude of r_noise is very large. In our simulations, we found that many pairs do not violate the SR (e.g., Fig. 4B), but that many pairs do (e.g., Fig. 4, A and C). We hypothesized that pairs in ML could be more likely to exhibit a nonmonotonic relationship between r_noise and coding performance than pairs in A1, and that this difference could explain why engagement increases r_noise in ML in pairs with positive r_tuning. For instance, if many pairs with positive r_tuning in ML perform best when r_noise is very positive, perhaps increasing r_noise across these pairs enhances neural sensitivity in ML.

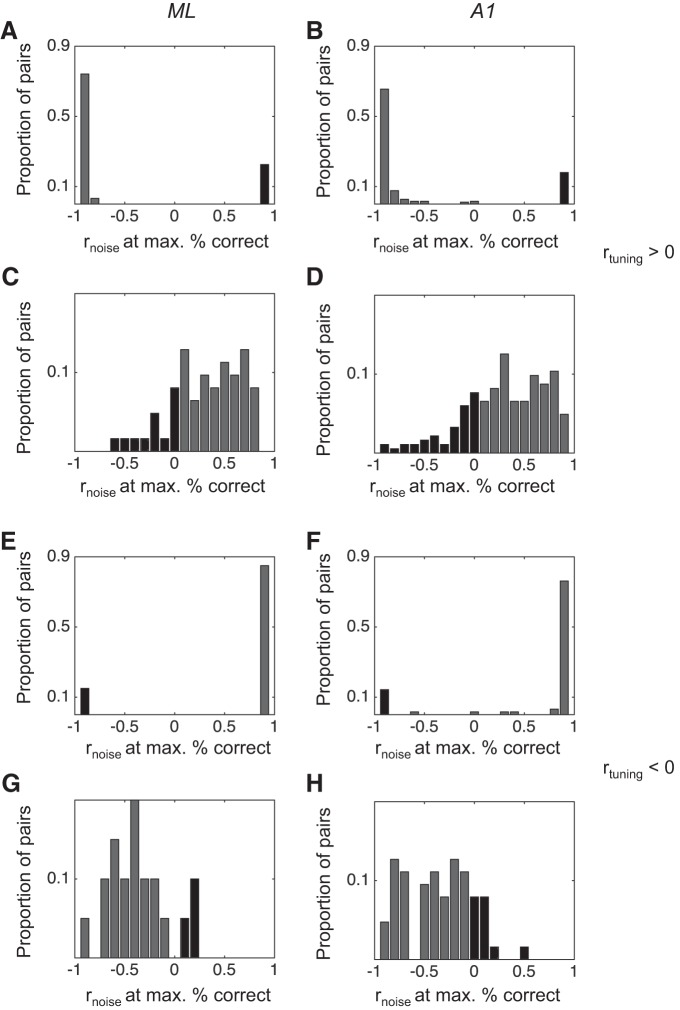
For each pair, we calculated the r_noise at both maximum and minimum performance across all simulated r_noise values. For pairs that violate the SR, performance at maximum (vertical gray lines in Fig. 4) should often be at r_noise values that are the same sign as r_tuning. Likewise, if the r_noise at minimum performance (vertical black lines) is the opposite sign as r_tuning, these count as violations of the SR. We then compared the distributions of r_noise at maximum performance and r_noise at minimum performance between A1 and ML. Our prediction was that a higher proportion of pairs in ML than in A1 would exhibit violations of the SR, particularly for pairs with positive r_tuning. We summarize these analyses in Fig. 5.

Fig. 5.

Distributions of r_noise values corresponding to pairs’ best (max) and worst (min) classifier performance in ML and A1. For pairs that violate the SR, r_noise at maximum performance will be at a value that is the same sign as the r_tuning value, and/or r_noise at minimum will have the opposite sign as r_tuning. These distributions are not distinct between ML and A1, suggesting that pairwise violations of the SR do not contribute to a different role for r_noise in sensory coding between ML and A1. Dark shaded bars indicate pairs that violate the SR.

In Fig. 5 we show the distributions of r_noise at maximum performance and r_noise at minimum performance, broken down into r_tuning sign (positive, Fig. 5, A–D and negative, Fig. 5, E–H) and cortical field (ML, Fig. 5, A, C, E, G, and A1, Fig. 5, B, D, F, H). We found that many pairs violate the SR according to these measures, as evidenced by r_noise at maximum values that are the same sign as r_tuning and r_noise at minimum values that are the opposite sign of r_tuning. However, when we compared each distribution between ML and A1, we found no significant difference (Kolmogorov-Smirnoff test, P > 0.05 in each case). Thus we cannot explain the increase in r_noise with task engagement in ML as a beneficial modulation due to pairwise violations of the SR.

We next focused directly on the potential impact of the observed shifts in r_noise between active and passive conditions. We did this to assess the unique contribution of r_noise shifts on the increase in classifier performance that we observed in the active relative to passive condition in both ML and A1 (Fig. 3). To do this, we first imposed the r_noise value observed in a pair during the passive condition (“simulated passive r_noise”) on the matrix of firing rates observed in the active condition. We then calculated the performance of the pair with simulated passive r_noise and compared this performance against the performance of the pair with its observed active r_noise intact. Because the only difference between these two firing rate distributions values is r_noise, we can attribute any differences in performance to shifts in r_noise. We performed this procedure across all pairs recorded in both conditions (n = 145 in A1, n = 46 in ML). By taking this approach, we can uncover any changes in the performance of pairs in ML that might be attributable to increased r_noise but which are not predicted by the SR. These analyses are summarized in Fig. 6.

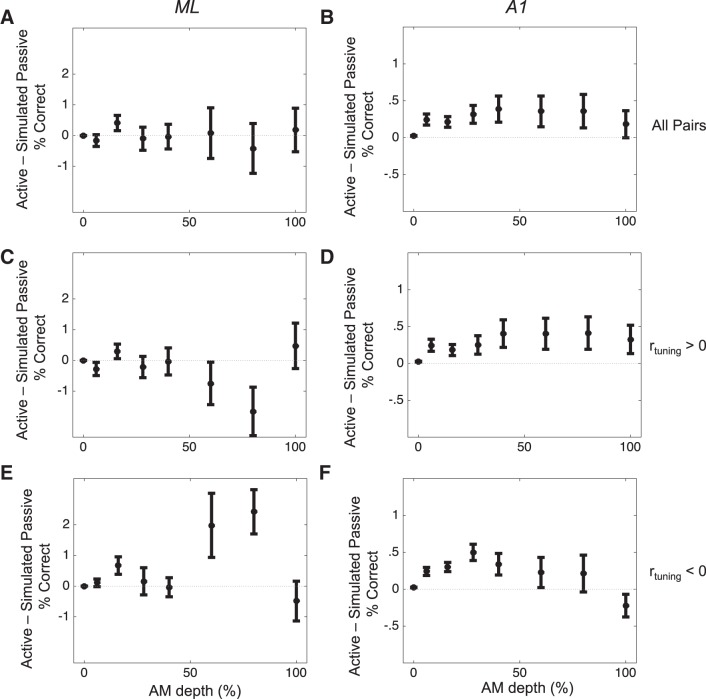
Fig. 6.

Task-related changes in r_noise enhance coding in A1, not in ML. Values above 0 indicate that r_noise in the active condition uniquely brings about an improvement in pairwise performance. r_noise changes in ML (A) do not uniquely contribute to the observed increase in pairwise performance shown in Fig. 3. However, in A1 (B), r_noise does make a contribution to increased coding accuracy. In ML (C and E), task-related r_noise effects do not contribute to average performance differences in either the positive (C) or negative (E) r_tuning groups. However, at AM depths of 60 and 80%, r_noise contributes to decreased (C) or increased (E) performance, in pairs with positive or negative r_tuning, respectively. In A1 (D and F), task-related r_noise effects appear to enhance sensory coding across both r_tuning categories.

In Fig. 6, we plot the performance of the classifier using the r_noise from the active condition minus the performance of the classifier using the r_noise from the passive condition. We show these analyses in all pairs (Fig. 6, A and B), as well as broken down by r_tuning sign (Fig. 6, C–F), in both ML (Fig. 6, A, C, E) and A1 (Fig. 6, B, D, F). Across all pairs, task-related changes in r_noise yield no significant difference in average coding performance in ML [Fig. 6A; 2-way ANOVA, F_(1,6,37) = 0.29, P = 0.942]. In A1, however, the performance of pairs with the r_noise observed in the active condition was consistently higher than with the simulated passive r_noise (Fig. 6B; 2-way ANOVA, F_(1,6,136) = 22.89, P < 0.001]. Directly comparing A1 and ML revealed this interaction to be nearly significant, trending toward a greater effect of r_noise on pairs’ performance in A1 [F_(1,1,6,181) = 3.48, P = 0.062].

We then analyzed these effects separately for pairs with positive and negative r_tuning (Fig. 6, C–F). For pairs with positive r_tuning, there was no significant main effect of task-related r_noise in ML [F_(1,6,17) = 0.74, P = 0.84], although for two of the stimulus conditions (AM = 60 and 80%) there was a significant effect for engagement-related r_noise shifts to decrease performance [Fig. 6C; Tukey’s honestly significant difference (HSD), P < 0.05]. For pairs with negative r_tuning in ML, engagement-related shifts in r_noise also exert no overall change in classifier performance (Fig. 6E). Similarly to pairs with positive r_tuning, there was no significant omnibus effect, yet there was a significant engagement-related increase in performance attributable to r_noise at AM values of 60 and 80%. Taken together, these analyses suggest that the engagement-related r_noise effects we observed in ML do not contribute to either increasing or decreasing sensory performance. Thus the increase in sensory performance during engagement in ML is not due to changes in r_noise.

For pairs with positive r_tuning in A1, engagement-related shifts in r_noise yield an overall increase in performance [F_(1,6,98) = 12.74, P < 0.001]. Post hoc tests reveal this increase to be significant for four stimulus conditions: AM depths of 6, 16, 28, and 40% (Tukey’s HSD, P < 0.05). We also found a significant main effect for engagement-related r_noise to increase classifier performance between pairs with negative r_tuning in A1 [F_(1,6,38) = 4.02, P = 0.046], and post hoc tests for each stimulus condition reveal a significant increase for an AM depth of 28% only. These results support the argument that engagement enhances sensory coding in A1 in part by shifting r_noise.

Relationship Between r_noise and AM Detection Performance in Larger Populations

Our final analysis of differences between ML and A1 population coding, and the impact of r_noise thereon, focused on larger populations of cells in each area. Because we did not obtain simultaneous recordings from across large populations in either area, we did this by modeling population activity. We first measured two key relationships among our simultaneously recorded pairs to inform our models. First, we measured the relationship between r_tuning and r_noise across pairs, because this relationship is argued to affect coding (Averbeck et al. 2006). Figure 7 shows that, across ML and A1, r_noise and r_tuning exhibit a weakly positive relationship. This relationship is consistent with what others have found across many studies (see Cohen and Kohn 2011 for review). Second, we measured the relationship between pairwise firing rate (geometric mean between each neuron’s firing rate) and r_noise (Fig. 8). This relationship has been shown to be positive across in many studies (de la Rocha et al. 2007; Franke et al. 2016; Kohn and Smith 2005) and has been argued to impact coding (Zylberberg et al. 2016). In contrast to what others have reported, we found a negative relationship between r_noise and firing rate. When we modeled populations in ML and A1, we constructed them to be faithful to the observed relationships between r_noise and r_tuning, and r_noise and firing rate.

Fig. 7.

In both ML and A1, r_tuning and r_noise are positively correlated. We incorporate this relationship in our simulations of r_noise across modeled neural populations. Note that each pair contributes 8 points to the plot (1 point per stimulus condition).

Fig. 8.

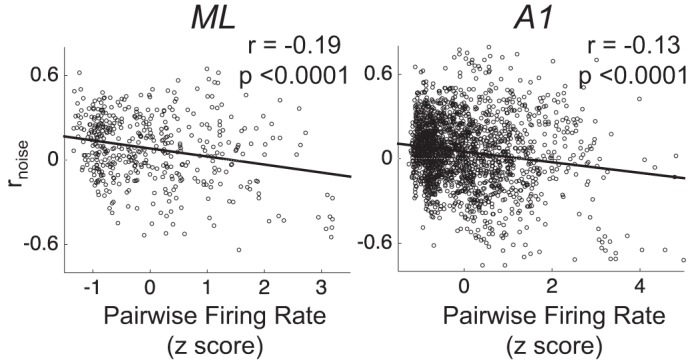
In both ML and A1, pairwise firing rate and r_noise are negatively correlated. As in Fig. 7, each pair contributes 8 points (1 per stimulus condition) to this plot. Firing rates are z-scored within each pair, across stimulus conditions. We also incorporate this relationship in our simulations of r_noise across modeled neural populations.

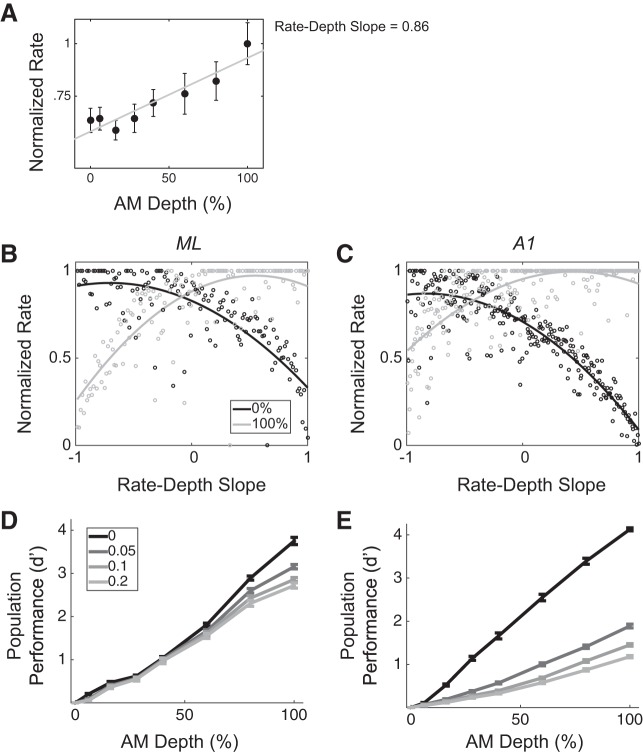
We modeled each population as an array of tuned filters in which each element represents a neuron whose AM tuning (rate-depth function) provides the details of the filter (e.g., whether high pass, low pass, or bandpass, as well as the cutoffs). We show an example neuron in Fig. 9A. This neuron has a positive rate-depth slope and can thus be thought of as a high-pass filter for AM depth; neurons like this one are arranged to the right on the x-axis, whereas neurons with negative rate-depth slopes are arranged on the left (Fig. 9, B and C). Arranging neurons according to their slope leads to population responses that are distinct for each AM depth. For instance, in Fig. 9A, an instantiation of an ML population is shown, with each point of a given color representing each neuron’s mean response to a given stimulus. We show the population mean response to two stimuli, 0% (black) and 100% depth (gray), and it can be seen that the scatter of points differs between stimuli. Thus an ideal observer could decode the scatter of points to estimate the stimulus. For each realization of a simulated population, we fit this scatter with the best-fit (least squares) 3rd-order polynomial function. The solid curve passing through each scatter of points in Fig. 9, B and C, shows this function.

Fig. 9.

ML and A1 modeled populations are differentially affected by r_noise. A: an example neuron’s normalized firing rate and slope. B and C: 2 example instantiations of modeled populations of size n = 100 neurons. Populations are modeled as arrays of tuned filters, with neurons arranged according to AM slope (from most negative to most positive). Population mean responses to each stimulus are fit with 3rd-order polynomial least-squares curves (solid lines). Each data point represent the mean (maximum normalized) response of one neuron to one stimulus (black for 0% AM and gray for 100% AM). D and E: in populations of n = 100 neurons, across 400 simulated trials per simulated r_noise, average classifier performance was obtained at each AM depth in ML and A1. Whereas ML is modestly affected by r_noise, and only at higher AM depths, A1 performance is dramatically reduced for weakly positive r_noise values at each depth other than 6%.

We simulated various r_noise values across the population and measured the population’s ability to detect AM across AM depths for each simulated r_noise value. We measured detection on a trial-by-trial basis, as described in materials and methods, for 400 trials at each stimulus condition for each simulated r_noise value. Figure 9D shows population AM detection performance in ML, at each stimulus condition, for each of the four simulated r_noise values. We found an overall effect of r_noise to decrease performance in ML populations [F_(3,6,131) = 53.58, P < 0.001]. However, at lower AM depths, r_noise exerts no effect on ML’s coding accuracy (depths 6, 16, 28, and 40%; Tukey’s HSD, P > 0.05). On the other hand, coding accuracy is slightly degraded with r_noise at higher depths (60, 80, and 100%; Tukey’s HSD, P < 0.05). In A1, population coding is dramatically affected by r_noise at all depths other than 6% [Fig. 9E; F_(3,6,404) = 53.58, P < 0.001]. Directly comparing ML and A1 showed their detection performance is similar when average r_noise across the populations is ~0, although performance is slightly higher for A1 (Fig. 9, D and E, solid black lines), but population coding performance in ML is higher than that in A1 at all other average r_noise values [Fig. 9, D and E, gray lines; F_(1,6,535) = 349.48, P < 0.001]. Thus, for this particular model of population coding of AM, ML and A1 diverge dramatically in terms of their coding of AM stimuli under conditions of weakly positive r_noise. Whereas A1 exhibits large decreases in performance as r_noise values increase, ML performance stays relatively constant.

DISCUSSION

The distribution of single-neuron tuning properties in a population of neurons has been argued to affect the coding capacity of a population of neurons, including how r_noise affects coding (Butts and Goldman 2006; Ecker et al. 2011; Fiscella et al. 2015; Lehky and Sereno 2011; Zhang and Sejnowski 1999). We therefore compared both the single-neuron properties and the emergent population properties between two adjacent auditory cortical fields to explore hierarchical differences in population coding. Specifically, we compared AM encoding properties between primary auditory cortex (A1) and a secondary field (ML) and found multiple compelling differences: 1) ML exhibits greater heterogeneity than A1 in terms of how single neurons encode sounds; 2) joint tuning (i.e., tuning correlation, or r_tuning) is also more heterogeneous in ML than in A1; 3) correlated variability (r_noise) between neurons is differently affected by task engagement in the two areas, with ML increasing average r_noise during engagement and A1 decreasing average r_noise; and 4) whereas r_noise appears not to affect encoding accuracy in ML, r_noise has a strong impact in A1. Taken together, these results provide insights into a number of open questions in neuroscience, including how sounds are encoded at the population level and how population codes are transformed along the sensory hierarchy, as well as how different neural populations are affected by r_noise.

Potential Causes of Increased r_noise

One confusing aspect of what we find is that r_noise increases in ML with task engagement, yet this increase appears to confer no sensory advantage. This result is particularly conspicuous given that most studies of behavioral effects on r_noise within a cortical areas have shown that contexts in which sensory demand is heightened, r_noise decreases (Cohen and Maunsell 2009, 2011; Ecker et al. 2014; Herrero et al. 2013; Issa and Wang 2013; Mitchell et al. 2009; Nandy et al. 2017; Ruff and Cohen 2014a; Vinck et al. 2015). However, other studies have shown increases in r_noise alongside decreases in r_noise, in distinct subsets of neural populations (Downer et al. 2017; Jeanne et al. 2013; Ruff and Cohen 2014b), but in these studies observed increases in r_noise are predicted to enhance coding according to the SR. There is debate as to the sensory consequences of r_noise, but studies showing attention-related decreases in r_noise lend credence to the notion that reducing r_noise enhances coding accuracy in those contexts. We tested the effect of varying r_noise on coding accuracy in ML, both at the level of pairs and in a larger population model, and found that, according to these analyses, r_noise exerts little effect on coding performance in ML. Why, then, should task engagement increase r_noise across the population? In a recent study, Gu et al. (2011) similarly reported a behavioral modulation of r_noise in visual cortex (area MSTd) that resulted in no net effect on coding accuracy. In their study, they measured r_noise before and after animals underwent a perceptual learning period. They found that learning decreased average r_noise across the population, but because r_noise was equally reduced between pairs with positive and negative r_tuning, this reduction provided no apparent benefit to coding accuracy. They interpret their observed learning-related reduction in r_noise as a collateral effect of changes in neural circuitry, resulting from a reduction in either shared feedforward or feedback connections between neurons. In such a case, a shift in r_noise is not causally related to the increased sensory sensitivity associated with perceptual learning. The task-related changes in r_noise in ML that we observe likely also are not causally related to any increase in sensory sensitivity to AM that comes with task engagement. On the other hand, we have previously provided evidence that the task-related changes we observe in A1 do support enhanced AM detection (Downer et al. 2015).

Another possibility is that the increase in r_noise that we observe in ML during task engagement reflects processes similar to what Cohen and Newsome (2008) previously reported in visual cortex (area MT) when animals switched between different motion detection tasks. They designed the experiment so that during one task, two simultaneously recorded neurons provided evidence for the same perceptual decision, and during another task, those same two neurons provided evidence for opposite perceptual decisions. They found that when the neurons provided evidence for the same decision, r_noise was increased relative to when the neurons provided evidence for different decisions. They interpreted this effect as shared fluctuations in feature-based attentional gain, inspired by the findings of Martinez-Trujillo and Treue (2004). In this scenario, attending toward the feature for which the two neurons provide the same evidence (equivalent to positive r_tuning) results in trial-by-trial fluctuations in attention being shared by the two neurons, resulting in increased r_noise. It may be that, in the passive state, neurons in ML receive less shared feature-based gain input than during task engagement; then, during task engagement, attention increases the gain of AM-tuned neurons, and fluctuations in this gain would be shared across neurons and result in higher r_noise. Many other studies have suggested that increased r_noise values can result from fluctuations in attention (Ecker et al. 2016; Scholnivk et al. 2015; Vinck et al. 2015) and shared choice-related activity (Cumming and Nienborg 2016). This explanation suggests that A1 and ML are differentially affected by modulatory and/or top-down input during this task, possibly related to a greater role for ML in cognitive aspects of hearing than A1. Differences in attention-related modulatory input between sensory areas is a topic for further research and is guided by anatomical studies of the differences in cortico-cortical connections between core and belt auditory areas (Hackett et al. 1999; Hackett and de la Mothe 2014; Kaas and Hackett 2000).

Difference Between ML and A1 in the Sensory Consequences of r_noise

On the basis of two sets of analyses, we argue that r_noise carries very different sensory consequences in A1 than in ML. In A1, r_noise appears to reduce coding performance, whereas ML coding performance is quite robust to r_noise. This type of effect has been observed in both the somatosensory cortex (Romo et al. 2003) and the visual cortex (Poort and Roelfsema 2009). In both of these studies, r_noise is on average positive between all pairs, including those with dissimilar tuning. According to the SR, r_noise has opposite effects on pairs with similar and dissimilar tuning, so, across the population, the effect of r_noise on coding is negligible. This can certainly explain differences in the effect of r_noise on coding in A1 and ML, particularly for our larger population model. When we analyzed the distribution of r_tuning in A1 and ML, we found a preponderance of similarly tuned pairs in A1, whereas ML pairs were roughly as likely to be similarly tuned as dissimilarly tuned (Fig. 1, G and H).

This difference can be intuitively understood by considering a single-trial response to 100% AM, in the presence of positive r_noise, modeled in the larger population (Fig. 9, B and C). With positive r_noise, neurons in the population tend to either fire above or below their means at the same time. On trials in which the neurons all tend to fire above their mean, the offset (y-intercept) of the single-trial population-response function would be higher than that of the mean 100% AM population-response function. If the stimulus were modulated, this effect would simultaneously bring the segment of the population with decreasing slopes (“low-pass filter” neurons) closer to the mean 0% AM population-response function, and farther from the 100% AM population mean response. For a decoder that considers only this segment of the population, this trial would be more likely to result in a :miss” than if there were no r_noise. However, for the segment of the population with increasing slopes (“high-pass filter” neurons), the single-trial population response would be less likely to be decoded incorrectly. Since the whole population is being read out in our model, these effects could average out, if and only if the decreasing segment and the increasing segment make roughly equal contributions to the population. This is the case in ML, but not in A1.

Transformation of Sensory Codes Along the Auditory Cortical Hierarchy

A paucity of data exists on cortical fields beyond A1, but a picture is emerging that suggests that neural codes proceed from more sensory-based to choice-based moving from A1 to higher fields. Many have previously shown that choice-related activity is evident in both A1 and secondary AC (Bizley et al. 2013; Niwa et al. 2012, 2013), although others have presented null results for choice-related activity in early auditory cortex (Lemus et al. 2009). However, whereas one might expect choice-related activity to increase along the hierarchy, previous results suggest that A1 and ML carry similar choice-related activity and that the main transformation between A1 and ML is in the types of cells exhibiting task-related effects, as well as the timing of effects (Niwa et al. 2013, 2015). Similarly, results from area AL (the anterolateral belt, rostral to and putatively higher than ML) suggest that choice-related activity is not remarkably different from that observed in A1 (Tsunada et al. 2011). At the level of prefrontal cortex, however, cells begin to exhibit very clear activity related to animals’ perceptual categorization of sounds, rather than the sensory elements themselves (Russ et al. 2008). How and where this transformation takes place remains an open question, although a recent study has shown that microstimulation of AL, but not ML, biases animals’ decisions. They hypothesize that this is due to AL’s role in categorizing sounds (Tsunada et al. 2016). Thus ML may lie between A1 and AL in the pathway along which sound representations are abstracted from sensory based to meaning based.

Our present results agree with much previous work that the role of A1 is to analyze sensory aspects of hearing tasks, whereas higher areas such as ML gradually represent more integrated, abstract aspects of hearing tasks, potentially diverging into distinct processing “streams” (Rauschecker and Scott 2009; Recanzone and Cohen 2010). However, recordings in behaving animals from auditory cortical areas beyond A1 are still too few in number to create a clear picture of how sound representations progress as acoustic information is processed throughout the brain. Future work is necessary to discover the myriad auditory and nonauditory variables represented at successive stages of auditory processing. Such work will shed light on the neural mechanisms that give rise to auditory perception.

Limitations of the Proposed Population Coding Models

Whereas we report differences between ML and A1 in their population performance, the models we use for these analyses (pairwise linear coding and population filterbank) represent two of many potential coding strategies. Most obviously, we have omitted spike-timing information (phase-locked spikes) from our analyses. In both A1 and ML, phase-locked spikes carry information about AM above and beyond what firing rate provides (Liang et al. 2002; Malone et al. 2007, 2010; Niwa et al. 2013, 2015; Overton and Recanzone 2016; Scott et al. 2011; Yin et al. 2011). The present work focuses primarily on the differential impact of firing rate r_noise on coding performance, but it is unknown to what extent r_noise affects phase-locking codes. Considering the evidence that firing rate and phase-locking provide complementary codes for AM (Yin et al. 2011) and previous findings that only firing rate (and not phase-locking) correlates with subjects’ perceptual reports during AM detection (Niwa et al. 2012; 2013), we argue that the results of our analyses present a meaningful aspect of AM coding across auditory cortex. Future work is necessary to understand the relationships between firing rate variability and phase-locking variability in auditory cortex, as well as the joint correlation structure of both codes across the population.

We would also like to the issue of the effect of cortical distance on r_noise. In the present report, we only record from pairs of neurons recorded at the same site, likely within ~100 µm of each other. However, previous studies in both auditory cortex (Rothschild et al. 2010) and visual cortex (Smith and Kohn 2008) show that r_noise decreases as a function of distance between neurons. Therefore, it is possible that our results are most trenchant when population coding is considered on a more local scale, as opposed to globally across the entire cortical field. On the other hand, factors besides physical distance predict r_noise between pairs, including tuning similarity (Smith and Kohn 2008), and r_noise in auditory cortex commonly has significant non-zero magnitude across distances of ~300–400 µm between pairs recorded on different electrodes (Downer et al. 2017). Thus, although our results may be most applicable to small populations, the principles governing the effect of r_noise on AM coding likely scale to larger populations across the entire cortical field.

GRANTS

This work was funded by National Institute on Deafness and Other Communication Disorders Grant DC002514 (to M. L. Sutter), National Research Service Award Fellowship F31 DC008935 (to M. Niwa), and National Science Foundation Graduate Research Fellowship Program Fellowship 1148897 (to J. D. Downer).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

ENDNOTE

At the request of the author(s), readers are herein alerted to the fact that additional materials related to this manuscript may be found at the institutional website of one of the authors, which at the time of publication they indicate is: https://github.com/joshddowner/pop_code_aud_ctx. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

AUTHOR CONTRIBUTIONS

J.D.D., M.N., and M.L.S. conceived and designed research; M.N. performed experiments; J.D.D. analyzed data; J.D.D. and M.L.S. interpreted results of experiments; J.D.D. prepared figures; J.D.D. and M.L.S. drafted manuscript; J.D.D. and M.L.S. edited and revised manuscript; J.D.D., M.N., and M.L.S. approved final version of manuscript.