Abstract
Genetic encoding provides a generic construction scheme for biomolecular functions. This paper addresses the key problem of coevolution and exploitation of the multiple components necessary to implement a replicable genetic encoding scheme. Extending earlier results on multicomponent replication, the necessity of spatial structure for the evolutionary stabilization of the genetic coding system is established. An individual-based stochastic model of interacting molecules in three-dimensional space is presented that allows the evolution of genetic coding to be analyzed explicitly. A massively parallel configurable computer (NGEN) is used to implement the model, on the time scale of millions of generations, directly in electronic hardware. The spatial correlations between components of the genetic coding system are analyzed and found to be essential for evolutionary stability.
The genetic code, as a wonder of ancient biological engineering, has excited much recent study (1). Its structure, origin, uniqueness, and information-processing capabilities have been the focus of biochemical and theoretical analysis. Its emergence has often been identified (2) with the origin of life itself in the long-standing debate as to whether genes or proteins came first. Genetic coding of function remains a central issue in an RNA world, in which RNA catalysts could act singly or jointly as polymerases to replicate other RNA as genes. It has long been realized that some form of effective compartmentation is necessary to allow the selection of the functional multicomponent replicable systems needed to implement a genetic code, and this has added an additional complexity to models of the evolution of such systems. Possibly for this reason, there have been few explicit models of the evolution of genetic coding. In this paper, we show that a multicomponent replication–translation system can evolve a stable genetic code in a continuous medium with no explicit compartmentation or control thereof.
The model framework is simple and abstract, compared with our detailed understanding of the cellular translation process. However, it appears to capture the essential organizational problem associated with the simultaneous evolution of a generic coding mechanism and self-replicating entities. The basic assumptions of the model are:
- (i)
Two distinct combinatorial families of chain molecules (catalysts and templates) are formed at a slow rate by random synthesis.
- (ii)
Catalytic molecules (like proteins) are mostly not capable of self replication, whereas template molecules (like RNA) can be transcribed (or replicated) and translated generically.
- (iii)
At least one rare polymer sequence exists that catalyzes the replication of templates; no recognition of specific template sequences is assumed.
- (iv)
Rare polymer sequences exist that catalyze the translation of templates to potentially catalytic molecules according to one of a number of “conflicting” codes; no specific recognition of template sequences is assumed.
- (v)
Molecular reactions are limited by diffusion in a three-dimensional medium.
The basic structure of the model is then given by two reaction mechanisms:
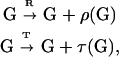 |
1 |
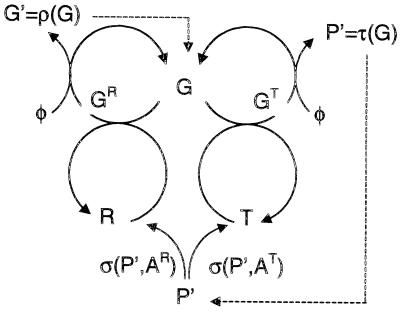
where G stands for a “genetic” template, R for a replicase catalyst, and T for a catalyst of translation. The product templates ρ(G) and translation-derived polymers (potential catalysts) τ(G) depend on the mappings (encodings) ρ and τ that are implemented by the catalysts R and T, respectively, which in turn are a function of their polymer sequences. We must emphasize that the two types of reactions in Eq. 1 are considered separately for each member of a large combinatorial family of templates G ∈ {Gi} with different sequences, giving rise to a wide range of products via the mappings ρ() and τ(), in particular R = τ(GR) and T = τ(GT).
A number of less fundamental assumptions are made for modeling convenience: sequences have a constant length; catalytic activity of translation-derived sequences falls off exponentially with the number of mutations (hamming distance) from a specified catalytic center in the polymeric sequence space; the fidelity of copying and translation is assumed to be a constant property of the catalytic sequence; and the molecular population is treated on an individual basis in three-dimensional space with a single common diffusion coefficient.
In a spatially homogeneous system, even the simplest cases of generic functionality are exploited to extinction. This fact has been established in the simpler gene and replicase system (3, 4) (which we refer to as GR). For the current gene-replicase-translatase (GRT) coding system, exploitation in the spatially homogeneous case is demonstrated in Appendix 1. Several authors have seen the solution to this type of problem in compartmentation. An alternative is pattern formation induced by finite diffusion. Boerljist and Hogeweg (5, 6) showed that a hypercycle with more than five catalysts and diffusion in two dimensions exhibited self-organization into spiral patterns that persist in the presence of exploiting parasites. (For a thorough discussion of hypercycles, see ref. 7.) A significantly simpler route to stable evolutionary multimolecular self-organization has been recognized (8, 9). It involves the self-replicating spot patterns that emerge (10) in systems that incorporate the Scott–Gray mechanism. Self-replicating spots may also provide exploitation-resistant evolution in three dimensions (11), but no demonstration of exploitation resistance for a multicomponent system such as translation has yet been forthcoming in any number of spatial dimensions. We have adopted three dimensions as arguably the most difficult and physically the most relevant case.
The simulation of the evolution of molecular functions entails a large number of different molecular sequences of which some species may occur only in single copies. These two features conspire to make an analysis in terms of concentrations (by partial differential equations) both misleading and unfeasible. Rather, molecular interactions have to be processed individually. Spatial effects can be simulated by placing the molecules on a finite grid and allowing only local reactions. The treatment of sequence-specific reactions of a million molecules over some millions of generations (which is necessary to capture evolutionary phenomena) is a computationally extremely time-consuming task. The custom-configurable discrete simulation computer NGEN (12, 13) (see also www.gmd.de/BIOMIP) was designed for the study of such systems. The machine is based on field-programmable gate arrays and is particularly suited for parallel and systolic computations.
Although the GRT system comprises only a minimal set of functions, it is potentially universal, because further functionality can be implemented simply by adding genetic sequences; the apparatus to express and replicate those sequences is already present. Consequently, this system, once established, can evolve without reorganizing its basic structure. The central feature that this model explores is distributed functionality (among different molecules). The basic problem is the generic exploitation of molecular catalysts by any “selfish” gene that does not contribute to their reconstruction.
Dyson (2) presented a stochastic model of the origin of replication and translation in which the problem was simplified to a one-dimensional (biased) random walk in the number of correctly placed monomers in chemical islands with limited size. This provocatively simple model is characterized by the manner in which the correct monomer placement increases towards full functionality. It does not account for the problem of exploitation correctly, nor for the influence of interchanges between island populations. These absent features are essential to a proper understanding of the emergence of coding, as we shall argue below. Our model corrects these deficiencies and is also spatially simpler in that no explicit island structure is necessary: the molecules self-organize, producing the local correlations necessary to stabilize the coding function.
Wills (14) formulated a more explicit model of the self-organization of proteins to form a translation system, assuming a constant set of genes. However, the code does not emerge by using random genes and is not stable if the correct genes are allowed to mutate during the process of self-organization. In this work, we simplify the translation process of Wills, which involved separate codon-assignment proteins (like amino-acyl transferases) by linking a set of codon assignments on a single catalyst, which we call a “translatase.” However, we allow conflicting sets of codon assignments to exist for different translatase sequences, so we do study the emergence of a coding system in the presence of interfering codes as Wills did, but now letting the genes evolve as well.
The paper is organized as follows. Methods deals with the details of the implementation and the relevant features of the customizable computer NGEN. Simulation results are presented in Results and analyzed by using correlation functions. The paper concludes with a discussion of the significance of these results.
Methods
Individual Molecule Implementation in Configurable Hardware.
To capture evolutionary time-scales and to obtain statistically significant results, it is necessary to trace diverse and large spatially distributed populations. We observed about one million individuals over several million generations, using the reconfigurable computer NGEN (12, 13). Biochemical reactions on chain molecules (especially transcription and translation) can be understood as bit serial processes, so the choice of a systolic architecture, as on NGEN (15), is both conceptually appropriate and efficient. In contrast, cellular automata (even probabilistic ones) are much less suited to describing the complex processing of the large-state spaces demanded in any representation of an evolving complex chemistry.
All the reactions of the model can be separated into unimolecular and bimolecular steps. Bimolecular reactions are simple functions of the two sequences involved, and the unimolecular reaction steps may depend on external reference sequences, which define the centers of catalytic reactivity in the sequence space of translation products. In this way, both reaction types can be handled uniformly as binary reactions, which is also of technical advantage when using a computing device based on field-programmable gate arrays. Likewise, diffusion can be modeled as a binary interchange reaction, and we integrated this one step further, as in the two-dimensional Margolus algorithm (16), using local rotations to implement diffusion in three dimensions.
Reformulated as a uniformly bimolecular scheme with the introduction of destruction processes and resources (voids) Φ, the elements of the sequence-dependent mechanism of the model represented by Eq. 1 are given in Table 1 and Fig. 1.
Table 1.
Uniformly bimolecular reaction scheme for coding system
| Reaction | Kinetic equation |
|---|---|
| Replication complex formation and replica release | G + R→GR + R |
| GR + Φ→G + ρ(GR) | |
| Translation complex formation and translate release | G + Ti→GTi + Ti |
| GTi + Φ→G + τ(GTi) | |
| Recognition as a catalyst | 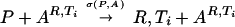 |
| Destruction of translated-polymers, templates, and complexes | P,R,Ti + DP→Φ + DP |
G, GR, 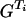 + DG → Φ + DG + DG → Φ + DG
|
Figure 1.
Flow chart of the reaction network given in Table 1. The unimolecular decay processes are not shown.
Different possible genetic codes are executed by alternative translatases Ti, ATi, and AR, being the central catalytic sequences for translation (via Ti with code i) and replication (via R), with G representing either GP, GR, or GTi. A superscript on G denotes the formation of the gene-replicase or gene-translatase complex, GR or GTi. The first two pairs of reactions describe rapid transcription or translation of the template, followed by a slow release of product. The function ρ(GR) stands for the newly produced gene sequence and includes all details, such as errors in the replication process. Analogously, τ(GTi) denotes the result of a translation process and may be regarded as an as-yet-inactive (unfolded) protein P. DG,P mediate the destruction of catalysts and templates with stochastic rate coefficients.
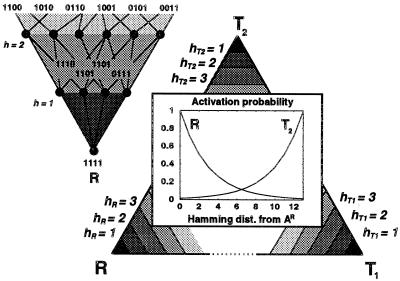
Recognition of a translation product as a catalyst reflects the sequence-dependent folding process determined by the physical chemistry of the macromolecules in a specific chemical context (such as pH, temperature, and ligands). We assume it is sufficient to model the complex sequence dependence of the recognition function σ(P,A) by a single peak landscape, which involves a multiplicative reduction (by a constant factor 2−a) for each monomer difference between P and the central catalytic sequence A and may be implemented by a simple systolic algorithm. Moreover, we do take into account that the genetic proximity of translation systems (translatases) implementing conflicting codes may affect their independent evolvability (see Fig. 2). Following Wills (14), this sequence dependence is determined by the positioning of the catalytic centers for the different encodings in sequence space. Only non-neutral sequence positions are considered in this analysis (see ref. 17) for proteins. Note that any given catalytic sequence has nonzero probability for folding to each of the possible catalytic functions. More complex sequence dependencies will affect the emergence times (see below) more than the evolutionary stability, which is the key issue here.
Figure 2.
Catalytic centers in sequence space. (Upper Left) The catalytic center in sequence space for R is given by the sequence 1111 (in practice, longer sequences are used). Assuming a sequence length n, the n!/r!(n − r)! sequences with hamming distance r from the catalytic center have a probability 2−ar of being activated into a R. The Lower Right stresses the fact that any sequence has a nonvanishing probability of being activated into any function represented by a catalytic center in the sequence space: replication, R, or one of two different translation schemes; direct, T1, and bit inversion, T2. The triangle is equilateral, implying that the hamming distances between all catalytic centers are equal. This is not exactly the case, but the hamming distances and α are big enough to make any difference negligible.
In the basic version of the model analyzed here, catalytic centers for three conflicting codes are assumed. The self-organization and stability of a code can be investigated with a single code, but interference between alternative codes is potentially a significant barrier to self-organization. The first set of codon assignments, T1, is direct (protein monomer corresponding to gene monomer), whereas in the complementary code, T2, translation results in a sequence of protein monomers complementary to the genetic sequence. Finally, T0 executes a random assignment.
In summary, the model is implemented with a total of eight parameters that can be grouped in three classes. First, activation and decay are controlled via the numbers of the different reference and decay sequences, resulting in stochastic rate coefficients aR,Ti and dG,P. Activation is reduced exponentially, with parameter α, according to the Hamming distance from a catalytic center. Second, the diffusion rate determines the scale of spatial correlations that stabilize the system. Third, the stability of the system depends on the fidelity of the copying process, specified by a mutation rate.
Results
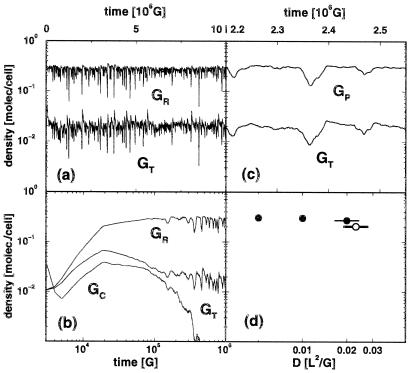
The main problem this article addresses is the evolutionary stability of spatially resolved genetic replication and translation. The model was simulated by distributing individual molecular sequences in a three-dimensional space with periodic boundary conditions. In Fig. 3 a–c, the typical temporal evolution of three classes of genetic molecules is portrayed: those coding for replicase, translatase T1, and nonfunctional proteins. A randomly distributed initial population of genes and proteins with random sequence was seeded with a small region composed of functional proteins (replicase and translatase T1) and the genes encoding them. Four time domains may be distinguished: (i) initial nonfunctional decay, (ii) spread of the code to saturation, (iii) wide-spread exploitation, and (iv) spatially heterogeneous cycles of expansion and exploitation. This sequence of evolutionary phases was observed repeatedly over a range of parameters. For all results presented, time is measured in population updates (G), meaning one stochastic reaction trial for every molecule in the population. Length is measured in units of the lattice spacing (L).
Figure 3.
Time evolution of relevant gene population in the GRT model. The molecules are enclosed in a pool with 88 × 88 × 128 cells. The y axis shows normalized gene densities. The sequences have a length of 26 bits. As parameters, we set: diffusion rate D = 0.02, mutation rate m = 2−9 (per bit), and decay rates for genes and proteins dG = dP = 0.001 (per generation). Both decay rates are equal; this means that the decay may as well be understood as outflow. The probability of accepting a wrong bit in the activation process is set to p = 2−4, and the activation rate of translatases and replicases is α = 0.01 (per generation). All activation and independently all decay rates are set equal, despite the fact that the translatase population could be stabilized at a higher value by tuning these parameters individually. (a) The long-time behavior of the genes coding for replicases (GR) and translatases (GT). (b) A double-logarithmic plot of the same curves showing the four time domains defined in the text. The fate of a subpopulation GC of nonfunctional genes is also shown. (c) The time evolution of genes coding for general nonfunctional proteins (GP) and translatases is given in higher time resolution. (d) The average number of genes coding for replicases as function of the diffusion constant D. Filled circles indicate populations that persist in all calculations (at least 15 million generations). Open symbols stand for populations that may attain a fully reproducing state of organization over several million generations but eventually become extinct. One standard deviation of the average replicase gene number is given by the error bars for D = 0.02 and D = 0.023.
The variation in the number of active proteins and the genes coding them in the fourth time domain suggests that the translation system may be evolutionarily stable. However, population stability might in principle be simply the result of sequence longevity caused by slow neutral drift in the absence of selection for functionality. To check that this was not the case, and to quantify the extent of genetic turnover, special marker sequences were introduced that could be copied but were nonfunctional. The comparatively rapid decay of these marker sequences demonstrates the selective advantage of the genes coding for functional proteins (Fig. 3b). The rapid extinction of GC proves that nonfunctional sequences do have a selective disadvantage. Although they are amplified with the other sequences in the expansion phase (time domain ii), they are eliminated in later phases by selection. On the other hand, genes coding for replicases or translatases persist despite decay and mutation (Fig. 3a).
The behavior of the model differs fundamentally in kinetics from the quasispecies theory of macromolecular self-organization (7). As in hypercycle theory, the deterministic form of the model exhibits unbounded growth for finite times in the absence of saturation effects (see Appendix 2). However, the selection is not “once forever” (preventing further optimization) because of the generic character of gene recognition by replicases and translatases.
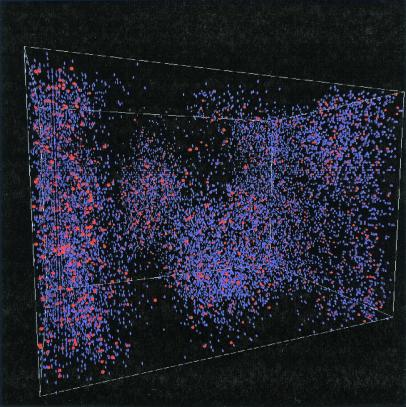
The persistence of the gene population, together with the impossibility of homogeneous solutions (see Appendix 1), indicates the crucial role of spatial heterogeneity for the stabilization of the translation system. This claim is supported by Fig. 4, where a three-dimensional plot of the active proteins is shown at a time point during the final phase (iv) when there is a comparably low concentration of active molecules (Fig. 3c at t = 2.3 × 106 G). Chemical activity is indeed concentrated in clusters. Some of these clusters survive periods of general decay and eventually spawn new clusters of functional molecules, ensuring system survival. These dynamics are analyzed further below. Whether cluster formation can stabilize the code depends on the diffusion constant, D. A series of simulations with increasing diffusion coefficients were performed for a period of several million generations. For D > 0.02, stabilization of the code is no longer possible, and the system dies out (Fig. 3d).
Figure 4.
Three-dimensional plot of the replicase (blue) and translatase (red) distribution in the spatially resolved simulation. Simulation parameters were as in Fig. 2. The image was taken after 2.3 × 106 G during the time domain iv after allowing initial transients to subside. The clustering shown is generic to this time domain.
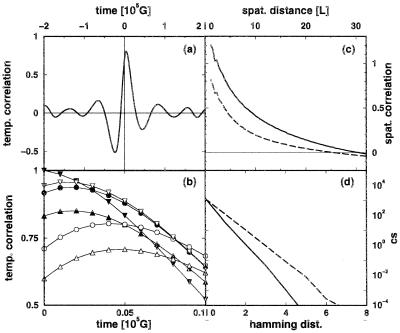
How is the spatially inhomogeneous coding system regulated? Fig. 4 shows an image of the spatially clustered population taken in time domain iv, demonstrating the generic feature of population clusters of active replicases and translatases. In Fig. 3c, a detailed view of the time evolution of two gene populations is shown. A clear synchrony is apparent between these densities; however, a more detailed analysis, based on the calculation of the time correlation functions, exhibits phase shifts that shed light on the underlying dynamics (Fig. 5, a and b). A variation in the translatase density is tracked 2,000 G later by a corresponding variation of the densities of replicases, nonfunctional proteins, and genes coding for translatases, and 3,000 G later by the variation in densities of genes coding for replicases and nonfunctional proteins. The local density of translatase is crucial to coding system stability, because the density of translatase is smaller by at least one order of magnitude than that of the replicase or those of the various genes. Consequently, the translation functionality in the coding system is more vulnerable to statistical fluctuations than replication. However, the ratio between translatases and replicases is not dictated by any exterior condition but is adjusted by the system itself. That translatase or replicase may diffuse between clusters ensures an efficient utilization of genetic resources, but at the risk of exploitation.
Figure 5.
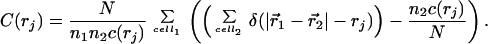 |
The question then arises whether the translatase fluctuations are a purely temporal phenomenon, acting to return the whole system to abundant resources (voids), or whether the structures of the clusters themselves give rise to the variations in (local) translatase density. Spatial correlation functions are tools well suited for analyzing this, as shown in Fig. 5c. The autocorrelation functions are averaged over two different sets of sample times in the fourth time domain: when the number of translatases nTi is increasing and decreasing, respectively. During periods of growth, the correlation is significantly stronger, so the fluctuations in nTi (see Fig. 3) are connected with the loss and re-establishment of spatial translatase correlations. Although the difference between the two curves might be caused by different population sizes, this is unlikely, because the average translatase numbers for the two curves differ by only 2% and are higher in the case of decreasing populations. The slight shoulder for low distances is caused by finite size effects of the grid. We emphasize that a global increase in translatases nTi does not imply ubiquitous growth; it just means that the effect of growing clusters is stronger than that of shrinking ones. Nevertheless, for the finite system size here, periods of average decrease or increase retain a significant difference in the globally averaged correlation functions, reflecting stronger differences at the level of individual clusters.
Because different codes may emerge in different regions, competing translation schemes pose a potential threat to stability. In a competition between the codes T0 − T1,2, the proliferative advantage of spatial regions with GT1,2 and T1,2 predominating ultimately leads to the extinction of T0 and its gene. Note that T0 and R alone cannot form a stable system; a T0 translation scheme could persist only as a parasite of T1,2. For interference between T1 − T2, the situation is different, because both schemes may operate independently. In all simulations, regions containing clusters built up from molecules belonging to one translation scheme merged together. No persistent coexistence of different translation schemes in the same region was observed. Regions or super clusters containing different schemes were separated by layers of low chemical activity. Eventually, one translation system always died out completely. This behavior was observed for α = 4 (the value taken for the results given in Figs. 2–5c) as well as for α = 1. Fig. 5d shows the spread of the active proteins in sequence space for these two values of α.
For the sake of completeness, an analysis of the probability of emergence in the current model is presented in Appendix 3.
Conclusion
The above results demonstrate that it is possible to evolve a stable coded construction system in free space, despite the formidable obstacles posed by the exploitability of such a system. We have deliberately specified the basic functions of the model to be generically utilizable, as this allows ongoing evolution and the generic acquisition of new functions simply by adding new genes. We have focused on the simplest case of sequence-dependent functionality (single-peak landscapes) and collected the various components necessary for translation into a single translatase complex. A physical rescaling of the model in time, density, and population size is necessary to match conditions available physically at the origin of life. However, the model does demonstrate that it is possible to simulate such complex evolution at the basic level of individual molecules. In contrast with Wills' earlier results on the self-organization (14) of the genetic code, the current model does not require the genes to be fixed at their correct sequences. Computationally, it turns out that the problem of evolutionary stabilization as investigated here is the harder part of the problem. In future, the results will be extended to include more realistic sequence dependencies, the consequences of codon assignment embeddings in sequence space (see ref. 18), separate molecules for codon assignments (splitting the translatase into subcomponents), the acquisition of novel genes, and a seamless simulation of the entire process of emergence.
Spatial structure, stability, selectivity, and exploitation are closely related, and therein lies a major difference between our approach and Dyson's mean-field assumption (2). Dyson's model seriously underestimates the importance of proliferation and exploitation at the origin of life, which can be understood only in a spatially resolved multicomponent context. For example, Dyson's conclusion about genetic and protein alphabet sizes is not correct, because proliferation and exploitation have been neglected. A binary–binary code is possible as the current work shows [extension to larger alphabets has been discussed previously (18)] and probably advantageous at the origin (see ref. 19). The difference between high-dimensional simplex and three-dimensional space is perhaps not so critical (20), but Dyson also ignores the exchange of molecules between islands and thus interisland proliferation and exploitation. In contrast, in the current model, a region that has been degraded has a finite probability of becoming repopulated again by migration, and this is important for viability and stability.
Although the model prescribes certain sequences as the centers of functional activity, this is purely for modeling transparency and could be replaced in the simulation by the solution of any combinatorial optimization problem for which the solution is not known in advance. Given a suitable such description of diverse protein functional activities impacting on chemical kinetics, the model should allow the study of open-ended evolution with the acquisition of new functions. As such, the solution of the coding problem does take us over the threshold toward more realistic models of life, because the mechanism of proliferation is ensured for arbitrary gene-encoded catalysts.
The evolution of a genetically coded system in three dimensions is of relevance not only because of possible insights into problems connected with the origin of life. The advances of supramolecular chemistry open ways toward truly molecular machinery (for a review, see ref. 21) that operate on the borderline between chemical reaction and mechanical manipulation. The stability of evolving multicomponent molecular machines faces issues similar to those addressed here. Mechanisms for proliferating nonreplicable components, maintaining correlations between evolving functional parts, and limits to the amount of information that can be assembled are consequently of present technological interest.
Acknowledgments
We thank P. R. Wills especially for his influential collaboration on an earlier more complex model (still to be solved), and S. Altmeyer and U. Tangen for constructive debate and substantial technical help. This work was partially supported by the Swiss National Science Foundation and by the German National Government (BMBF #01SF9952).
Abbreviations
- GR
gene and replicase system
- GRT
gene-replicase-translatase
No Stable Coding System for the Homogenous Model
Here we demonstrate that the GRT model is unstable in the deterministic well mixed case. In the simplest case with only one type of translatase, three classes of genes are considered: GR coding for a replicase R, GT coding for a translatase T, and GP coding for inactive translation products P (parasites). The results may readily be generalized. There are many more sequences of type GP than the special types GR and GT, so back mutations from GP to GR,T can be neglected. For future reference, reactions conserve the total number of molecules through utilization of a resource species Φ, which may be regarded as a vacancy and so is also the product of all decay reactions. The GRT coding system reactions are:
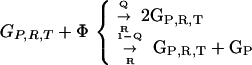 |
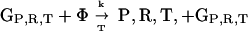 |
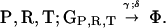 |
Replication takes place with a quality factor Q < 1. Time is rescaled so that the rate coefficient for replication is 1, and the total concentration is normalized to 1. The commas separate corresponding reactants and products for similar reactions. These reactions then lead to the system of equations:
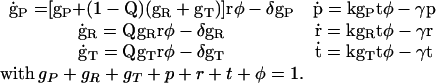 |
We are interested in the existence of a stationary state with t ≠ 0. Stationarity demands kgTφ = γ, which implies gT ≠ 0 and φ ≠ 0 for a nonzero death-rate coefficient γ. Furthermore, gR = γr/ktφ = rgT/t ≠ 0, and so factoring out gR from the second equation gives rφ = δ/Q, which after rearranging the first equation implies gP + gR + gT = 0, contradicting gT ≠ 0 above, because all concentrations must be non-negative. Thus no nontrivial stationary solution exists.
Hyperexponential Growth at Low Concentrations
The low-concentration behavior of the GRT system describes the initial growth of unsaturated spots. The formalism given in Appendix 1 is used, with vacancy density φ set to a constant, and parasitic proteins p and their genes gP ignored. Furthermore, because the equations for ġR and ġT are identical, gR() and gT() differ only by a constant factor, say c. Then
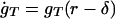 |
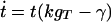 |
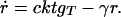 |
These equations set a lower limit for the local densities: if r < δ, gT < γ/k, and t < γr/(ckgT), no growth is possible. Further neglecting decay and solving the phase plane ordinary differential equations dr/dt = c and dgT/dt = c/k, a singularity for finite time occurs, indicating faster than exponential growth.
Random Emergence of a Coding System
The coding system GRT is stable once it is established, but the question remains whether it will self-organize from random initial conditions. In this appendix, analytical estimates are derived for the formation of critical clusters. More precisely, we calculate the probability that minimal clusters arise by chance, then that they lead to a critical density of local activity, and finally check that this nucleates a proliferating coding system with high probability (under conditions reported above for which the coding system is stable).
(i) A cluster of three molecules with appropriate sequences is sufficient in principle to nucleate the coding system. A protein activated as translatase together with genes that code for translatase and replicase activity is all that is required.
(ii) If pA is the small probability that a random protein is functional (or its gene leads to such a protein), then the probability of an active triple cluster in a small volume V = 4π/3R3 is (pAΨV)3. The steady-state site occupation probability Ψ of random genes and proteins prior to emergence is Ψ = κ/δ for random synthesis (at rate κ) and uniform decay (at rate δ). For the simple sequence dependence of our model:
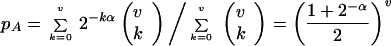 |
(iii) For a region to support growth, it needs a certain density of active molecules. The net production rate coefficient of active molecules inside a ball must be greater than the losses caused by destruction and surface outflux by diffusion. Simulations of cluster growth from balls of radius R = 3–8 showed growth to a stable translation system with a significant probability (several percent) if ρ is above a critical value (∼15 genes of each type for R = 3). The critical concentration agrees well with a simple analytical estimate based on nucleation theory xc = δ + 3D/R, for the kinetics of the model (Appendix 1).
(iv) A single translatase will translate a neighboring replicase gene with high probability. We need to calculate the probability p(x) of attaining a large enough clone of x genes before the replicase is lost. Given continued replication, a simple birth and death process (for example, see refs. 22 and 23) with rates μ and λ, respectively, gives x copies at time t with probability
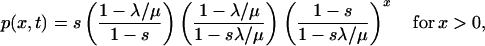 |
where s = e−t(μ−λ). Without further translation, the probability of a gene cluster of size x occurring before translatase loss is
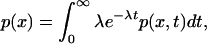 |
where λ is the total death rate (including outflux of genes). For values of δ = 0.005, R = 3 and x = 30 as above, this gives p(30) = 3∗10−18, 3∗10−9, and 10−5 for nR = 1–3 replicases produced by translation, and replication rate μ = nR/nV (where nV is the number of cells in V).
(v) Combining these results, we obtain the probability for emergence
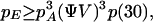 |
giving values of ∼10−24 (i.e., reciprocal Avogadro's number) for the parameters of the model. For lower δ and α, the probability increases sharply, and future calculations will address stability in this domain where emergence should be accessible to direct simulation.
References
- 1.Knight R D, Landweber L F. Cell. 2000;101:569–572. doi: 10.1016/s0092-8674(00)80866-1. [DOI] [PubMed] [Google Scholar]
- 2.Dyson F J. J Mol Evol. 1982;18:344–350. doi: 10.1007/BF01733901. [DOI] [PubMed] [Google Scholar]
- 3.Maynard Smith J. Nature (London) 1979;280:445–446. [Google Scholar]
- 4.Bresch C, Niesert U, Harnasch D. J Theor Biol. 1980;85:399–405. doi: 10.1016/0022-5193(80)90314-8. [DOI] [PubMed] [Google Scholar]
- 5.Boerljist M C, Hogeweg P. Physica D. 1991;48:17–28. [Google Scholar]
- 6.Boerljist M C, Hogeweg P. Physica D. 1995;88:29–39. [Google Scholar]
- 7.Eigen M, Schuster P. Naturwissenschaften. 1977;64:541–565. doi: 10.1007/BF00450633. [DOI] [PubMed] [Google Scholar]
- 8.McCaskill J S. Inaugural Lecture at the Friedrich Schiller University, Jena, Germany: Ursprünge der molekularen Kooperation: Theorie und Experiment. Jena, Germany: IMB Press; 1994. [Google Scholar]
- 9.Cronhjort M B, Blomberg C. Physica D. 1997;101:289–298. [Google Scholar]
- 10.Pearson J E. Science. 1993;261:189–192. doi: 10.1126/science.261.5118.189. [DOI] [PubMed] [Google Scholar]
- 11.Cronhjort M. Ph.D. thesis. Stockholm: Kunigla Tekniska Högskolan; 1995. [Google Scholar]
- 12.McCaskill J S, Tangen U, Ackermann J. In: Proceedings of the 4th European Conference on Artificial Life. Husbands P, Harvey I, editors. Cambridge, MA: MIT Press/Bradford Books; 1997. pp. 398–406. [Google Scholar]
- 13.McCaskill J S, Maeke T, Gemm U, Schulte L, Tangen U. Lect. Notes Comp. Sci. 1997. 1259, pp. 260–276. [Google Scholar]
- 14.Wills P R. J Theor Biol. 1993;162:267–287. doi: 10.1006/jtbi.1993.1087. [DOI] [PubMed] [Google Scholar]
- 15.Breyer J. Ph.D. thesis. Jena, Germany: Friedrich Schiller University; 1998. [Google Scholar]
- 16.Toffoli T, Margolus N. Cellular Automata Machines. Cambridge, MA: MIT Press; 1987. pp. 119–139. [Google Scholar]
- 17.Plückthun A, Pack P. Immunotechnology. 1997;3:83–106. doi: 10.1016/s1380-2933(97)00067-5. [DOI] [PubMed] [Google Scholar]
- 18.Nieselt-Struwe K, Wills P R. J Theor Biol. 1997;187:1–14. doi: 10.1006/jtbi.1997.0404. [DOI] [PubMed] [Google Scholar]
- 19.Eigen M, Winkler-Oswatitsch R. Naturwissenschaften. 1981;68:217–282. doi: 10.1007/BF01047470. [DOI] [PubMed] [Google Scholar]
- 20.Altmeyer S A, McCaskill J S. Phys Rev Lett. 2001;86:5819–5822. doi: 10.1103/PhysRevLett.86.5819. [DOI] [PubMed] [Google Scholar]
- 21.Gale P A. Philos Trans R Soc London A. 2000;358:431–453. [Google Scholar]
- 22.Darvey I G, Ninham B W, Staff P J. J Chem Phys. 1966;45:2145–2155. [Google Scholar]
- 23.McCaskill J S. Biol Cybernet. 1984;50:63–73. [Google Scholar]
- 24.Grassberger P, Procaccia I. Phys Rev Lett. 1983;50:346–349. [Google Scholar]
- 25.Füchslin, R. M., Shen, Y. & Meier, P. F. (2001) Phys. Lett. A, in press.