Tinker-OpenMM : Absolute and Relative Alchemical Free Energies using AMOEBA on GPUs

Abstract

The capabilities of the polarizable force fields for alchemical free energy calculations have been limited by the high computational cost and complexity of the underlying potential energy functions. In this work, we present a GPU based general alchemical free energy simulation platform for polarizable potential AMOEBA. Tinker-OpenMM, the OpenMM implementation of the AMOEBA simulation engine has been modified to enable both absolute and relative alchemical simulations on GPUs, which leads to a ~200-fold improvement in simulation speed over a single CPU core. We show that free energy values calculated using this platform agree with the results of Tinker simulations for the hydration of organic compounds and binding of host-guest systems within the statistical errors. In addition to absolute binding, we designed a relative alchemical approach for computing relative binding affinities of ligands to the same host, where a special path was applied to avoid numerical instability due to polarization between the different ligands that bind to the same site. This scheme is general and does not require ligands to have similar scaffolds. We show that relative hydration and binding free energy calculated using this approach match those computed from the absolute free energy approach.

Graphical Abstract

We have developed Tinker-OpenMM, a computational platform for the calculation of free energies on Graphics Processing Units. This allows for free energy simulations to be run 200 times faster than is possible on a single CPU core. In addition, we have developed a platform for the calculation of relative free energies.

INTRODUCTION

Free energy is the driving force for spontaneous molecular processes and accurate alchemical free energy calculations can benefit a broad range of chemical and biomedical applications^1–5. The accurate prediction of the binding affinities for ligands to their target proteins has been a great challenge in the computational drug development process⁶. Today, it is common to utilize empirical docking algorithms in the identification of potential lead compounds^7–11. However, in order to screen large ligand libraries in a short amount of time, empirical docking typically relies on incomplete physics models¹², and only account for limited system dynamics (such as loop flexibility) when predicting ligand affinity¹³. These limitations result in a lack of the accuracy necessary for lead optimization^14,15. The calculation of ligand binding free energies from elaborated molecular simulations has also been limited by a combination of underlying force fields and sampling algorithms^16,17.

One pathway for the calculation of binding free energies is the double decoupling approach. In this approach, one includes a parameter (lambda) that controls the interaction of a ligand with its environment. When transitioning from lambda=1 (full ligand intermolecular interaction) to lambda=0 (no ligand intermolecular interaction), a ligand’s interaction with its environment is evaluated. Simulations of the system are conducted with the solvated ligand and the protein-ligand complex, and the binding free energy is calculated as the complexation energy minus the solvation energy, plus standard state and other corrections¹⁸. In this methodology restraints¹⁹ are often used to keep the ligand bound to the protein complex throughout the decoupling process. The magnitude of this restraint term is then analytically corrected for.

Another major class of approaches of binding free energy involve the calculation of the potential of mean force. In these approaches, pioneered by the Roux lab²⁰, one calculates the average force needed to maintain a system in a given configuration (e.g. the distance and orientation between a ligand and the active site). Free energy is then calculated by calculating the work integral from the starting to ending distances. In order to obtain energy data on all relevant distances, a biasing process such as steered MD^21,22 or umbrella sampling^20,23 is often used. The advantage of this technique is that it allows for the collection of free energy profiles, including information about the energy barriers to binding. The main challenge of this approach is the difficulty in defining an appropriate reaction coordinate for the biasing process. Therefore, this technique has been mostly applied to systems such as channel proteins^24,25 that have an obvious pulling dimension. However, this technique can also be applied to general protein-ligand binding^26–28.

The free energy between the bound and unbound states in either approach can be sampled by using various techniques such as free energy perturbation (FEP)³, thermodynamic integration (TI)²⁹, metadynamics^30–32 or Orthogonal Space Random Walk (OSRW)^33,34. A common method for calculating the free energy between neighboring states in alchemical perturbation is the Bennett acceptance ratio (BAR)³⁵. The free energy of binding can then be calculated as the difference between the ligand-host interaction energy and the ligand-water interaction energy. In thermodynamic integration, one utilizes lambda much like in setting up a simulation for BAR and calculate the numerical integration of <∂H/∂λ)>_λ from lambda=0 to lambda=1²⁹. Compared to BAR, it can be difficult to determine which discrete values of lambda should be used, as convergence can be difficult in regions of high curvature of <∂H/∂λ)>_λ. Due to this, comparison studies³⁶ have suggested that TI simulations may require more states than BAR to reach converged free energies. However, TI simulations require less post-simulation processing than BAR based approaches.

The second ingredient of free energy simulations is the choice of force field. Popular force fields include CHARMM^37–40 and AMBER^41–44. More recent advances have resulted in the development of force fields with more complex electrostatics models, particularly incorporation of polarization. General polarizable force fields include polarizable multipole based AMOEBA,^45–47 polarizable OPLS^48–50, fluctuating charge^51,52 and Drude-Oscillator^53–55 based CHARMM force fields. The defining feature of the AMOEBA force field we have been developing is its electrostatic model based on permanent atomic multipoles, as well as many-body polarization through induced dipoles. These added terms, while computationally expensive, allow for a more rigorous modeling of ligand-protein interaction, particularly at short range, than is possible using a fixed-charge based force field.

Previous work using AMOEBA force field has shown an accurate recapitulation of experimental free energies in small molecules hydration,^56,57–59 metal ion hydration^60–62, as well as ligand binding in synthetic hosts⁶³, and protein systems^64–70. The inclusion of a complex electrostatic force leads to increasing computational cost, so that potential it can benefit even more from parallel computing of protein-scale systems consisting of tens of thousands of atoms. Earlier implementations of AMOEBA in Tinker have utilized OpenMP⁷¹, which allows for limited parallelism on commercially available CPUs. Massively parallel computation using AMOEBA is possible on supercomputers using the Tinker-HP package^72–74. In addition, AMOEBA has been previously implemented in OpenMM, enabling massively parallel molecular dynamics simulations on GPUs^75,76. In order to enable alchemical free energy calculations in OpenMM, we have incorporated “lambda” into force and energy calculation via a soft-core approach,⁷⁷ which is necessary to remove the singularities in van der Waals (vdW) interactions that occurs when atoms are in close contacts.⁷⁸ In addition, we modified the tinker-OpenMM interface to allow for perturbation of the electrostatic force via the scaling of electrostatic parameters. Another feature of OpenMM that is now supported by the Tinker-OpenMM interface is the addition of support for the CustomCentroidBondForce. This addition enables the coupling of a two groups of atoms (such as a ligand and its binding site).

Compared to the state of CPU alchemical free energy calculations, GPU alchemical free energy calculations is still in its infancy. It is possible to perform MD simulations on GPUs using a few software, including AMBER⁷⁹, NAMD⁸⁰, and OpenMM⁷⁵. However, very few GPU platforms have yet supported alchemical simulations. In addition to the work with OpenMM-AMOEBA described here, the YANK package⁸¹ for the use of OpenMM to simulate AMBER force fields is currently in development. Therefore, the AMOEBA on GPU implementation described here(Tinker-OpenMM) constitutes the first available platform for free energy perturbation simulations on GPUs using a polarizable force field.

It is not always necessary to compute the absolute alchemical free energy, and binding or solvation energies relative to a reference ligand are sufficient. In those cases, it may be advantageous to calculate relative energies instead of absolute energies. Many previous relative binding free energy calculation use a “dummy atom” single topology approach^82–86 where a pair of ligands are simulated as a common core of atoms connected to a set of atoms sufficient to describe both desired molecules. This dummy atom approach has been used to calculate a number of molecular properties, including binding free energies^83–87 Previous work with the AMOEBA force fields on CPUs have accurately calculated the relative binding free energies of ligands to trypsin using a single topology approach^66,67,69. The weakness of this scheme is that it is not general; it is more suitable for pairs of molecules with significant chemical similarity. A different approach is that of dual topology free energy calculation, where two ligands are always present in the binding pocket. Relative complexation free energy is calculated via a path starting in a state with fully ligand 1-environmental interaction, and ending at a state of fully ligand 2- environmental interaction. Dual topology free energy calculations have been possible in CHARMM since the late 80’s⁸⁸ and have more recently been implemented in AMBER⁷⁹. However, this dual topology scheme is more difficult to implement in a polarizable force field due to the complexity of the electrostatics making it difficult to selectively “scale” the polarization between two ligands. By utilizing a pathway where only one ligand is charged during any perturbation step, we were able to avoid this complication.

Currently, the ability to perform GPU based platform alchemical simulations, particularly for polarizable force fields, has been limited. In this work, we created Tinker-OpenMM, an OpenMM implementation of AMOEBA that enables alchemical free energy calculations on GPUs, while also adding the capability to perform dual topology simulations to both the Tinker⁸⁹ and OpenMM^75,76 platforms. We then proceed to test the GPU based free energy calculations for hydration free energies of aromatic systems⁹⁰, absolute and relative binding free energies of the sampl4 host-guest systems⁹¹.

IMPLEMENTATION DETAILS

Tinker-OpenMM interface

Tinker-OpenMM is built using an interface to pass tinker coordinates and parameters to OpenMM. Tinker reads in the input key and coordinate files, and passes the relevant variables in to a C++ script. This script then uses the OpenMM C API to create the relevant OpenMM parameters and forces, and initiates GPU Molecular Dynamics simulation. Coordinate saving is then managed by occasionally transferring atomic coordinates and velocities from the GPU to main system memory. Tinker then saves these outputs in Tinker coordinate and velocity files, enabling post-processing by Tinker commands (eg. BAR). This interface was originally created by Mark Friedrichs, Lee-Ping Wang, Kailong Mao, and Chao Lu.

Absolute binding free energy

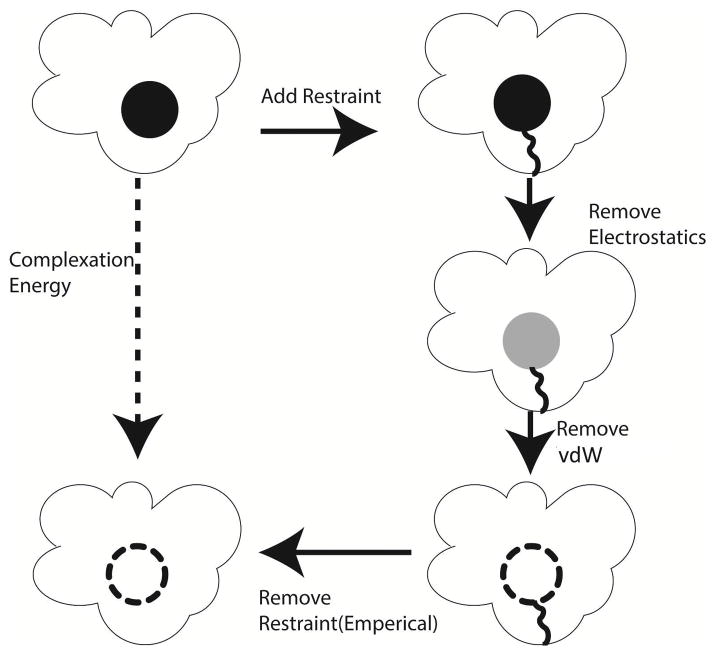
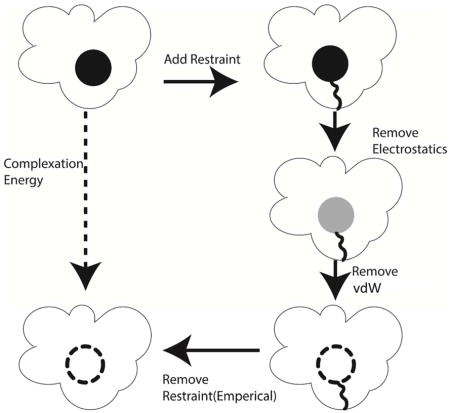
In this work, we employ double-decoupling and alchemical perturbation to compute free energy of binding. First, the electrostatic interactions between the ligand and its environment (water or protein/water) are scaled from 0 to 100% in a series of simulations. With no electrostatic interaction between ligand and surroundings, a series of simulations are run where the (softcore) vdW interactions between ligand and environment are scaled. The path utilized for absolute complexation simulations is shown in Figure 1. This process is also repeated in an aqueous environment to account for hydration free energy.

Figure 1.

Thermodynamic path used to calculate the absolute complexation energy of a ligand using a double-decoupling approach.

After running these simulations, the Bennett Acceptance Ratio (BAR) method is used to calculate the free energy difference between each pair of neighboring states. Since energy is a state function, we can calculate the total complexation energy as the sum of many small perturbations in ligand-environmental interaction strengths. The binding energy is calculated as the complexation free energy, minus the hydration free energy, with the addition of several corrections explained below.

When conducting alchemical perturbation, it is necessary to denote which atoms belong to the ligand. In the simulation system, the ligand atom indices are identified by using the ligand keyword in the key file (e.g. “ligand −1 14” denotes that atoms 1 through 14 belong to a ligand).

Alteration of the electrostatic interactions between the ligand and its environment is accomplished via the scaling of the electrostatic parameters passed from the Tinker interface to OpenMM. The atomic charge, dipole, quadrupole, and polarizability of all ligand atoms are each multiplied by the current simulation electrostatic lambda value (between 0 and 1), which is denoted by the ele-lambda keyword. This results in no electrostatic interaction between the ligand and its environment when ele-lambda=0, and full interaction strength when ele-lambda=1. This methodology also “turns off” the intra-ligand electrostatic interactions. When calculating hydration free energy, the intra-ligand/solute electrostatic contributions are added back by “growing” the electrostatic parameters for ligand alone (in gas phase). However, when calculating binding free energy, this contribution is exactly canceled by an equal omission in the ligand-solvent interaction.

When conducting alchemical perturbation simulations, the change in energy and structure that results from each perturbation needs to be relatively small. To avoid the numerical instability of the standard vdW function when the ligand-environment interaction approaches zero, a softcore buffered 14-7 vdW (energy equation shown below) has been used to calculate the forces and energies.⁶⁹

$$U_{\text{ij}}^{\text{vdw}}={\lambda }_{ij}^5{\epsilon }_{ij}\frac{{1.07}^7}{0.7{(1-{\lambda }_{ij})}^2+{({\rho }_{ij}+0.07)}^2}\left(\frac{1.12}{0.7\ast {(1-{\lambda }_{ij})}^2+{\rho }_{ij}^7+0.12}-2\right)$$ (1)

Here ε_ij is the well depth, and ρ_ij represents the current interatomic distance divided by r_min, the interatomic distance that results in the lowest vdW energy. In order to use this softcore vdW force, we need to assign the appropriate value of the lambda parameter λ_ij. In this implementation, each ligand atom is assigned a lambda value equal to the vdW-lambda keyword value in the simulation input key file. Each non-ligand atom is assigned a lambda value of 1. When calculating a pairwise vdW interaction, it is necessary to have a set of combining rules to convert two atomic vdW lambdas into a combined, λ_ij. For a pair of atom i and j, λ_ij is determined as the lesser of λ_i and λ_j. If the two lambda values are identical (as is the case in an intra-ligand or water-water interaction), λ_ij = 1.

In order to ensure that the ligand stays in the binding pocket even when intramolecular interactions are weak, a distance restraint (k(r − r₀)²) is applied between the centers of mass of the ligand and the center of the binding pocket. The bias introduced by the restraint is corrected for at the start and end of our thermodynamic path. The restraint correction at the end of simulation where no intermolecular interaction between ligand and environment is given by⁹²

$$\mathrm{\Delta }{G}_{\mathit{restraint}}=\mathit{RTln}\left[C^0{\left(\frac{\pi RT}{k}\right)}^{\frac{3}{2}}\right]$$ (2)

Here C⁰ represents standard state concentration (1 mol/L). In this work, we use a force constant (k) of 15 kcal/mol/Ų, and this correction amounts to 6.25 kcal/mol.

In order to remove the ligand restraint from the system with full ligand-protein interaction, we repeat the simulation but with the restraint off. The free energy difference between the two simulations is then calculated using BAR. Alternatively, one could also gradually turn off the restraint while the interaction strength between ligand and protein increases so that no additional correction is needed.

Dual-topology based relative free energy

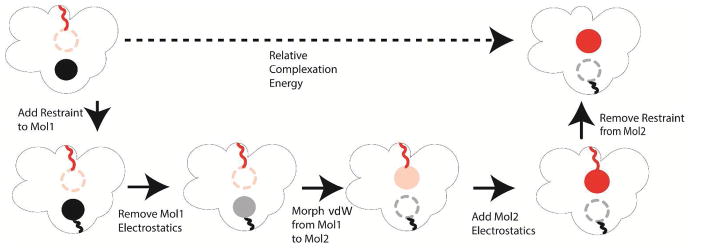
Relative binding free energy can potentially be calculated more reliably as it avoids simulation of the non-ligand bound form of the protein. In this implementation of the calculation of relative binding free energies, we take a thermodynamic path where we first reduce ligand 1’s electrostatic parameters to zero magnitude. We then proceed to reduce the vdW interactions between ligand 1 and environment, while simultaneously increasing the vdW interactions between ligand 2 and environment. Finally, we increase ligand 2’s electrostatic parameters from zero to full. The path we used to calculate relative complexation energy (ligand binding to receptor in water) is shown in Figure 2. Since the two ligands are never charged at the same perturbation step, ligand 1 and 2 never interact with each other (the vdW interactions are also turned off via the soft-core formula), which requires minimal changes to the electrostatic force in the existing OpenMM code.

Figure 2.

Path used to determine the relative complexation interaction energy of two ligands using a dual topological approach.

In order to run the simulations in our thermodynamic path, we require independent (ligand1 and ligand2) keywords to denote the indices of ligand 1 and ligand 2, respectively. The electrostatic perturbation segments of our path require that we independently control the electrostatic interaction of ligand 1 and ligand2. This is accomplished by having two electrostatic lambda keywords (ele-lambda1 and ele-lambda2, respectively). The charge, dipole, quadrupole and polarizability of each ligand is multiplied by the appropriate ele-lambda variable.

When perturbing the vdW force, we need to assign each ligand atom the correct lambda value. The vdW-lambda of all ligand 1 atoms is equal to the value specified by the vdW-lambda keyword, and vdW-lambda of all ligand 2 atoms is equal to 1 minus vdW-lambda. Therefore, changing the vdw-lambda keyword from 1.0 to 0.0 results in removing all ligand1-environment interactions while setting all ligand2 atoms to full vdW interaction with the environment.

When conducting relative binding simulations or BAR energy calculations, we need to ensure that the two ligands do not interact via the vdW force. Therefore, we need a way for our vdW force and energy calculations kernels to know which ligand each atom belongs to. This is accomplished by adding an internal variable to the vdW force used to designate which ligand (if any) an atom belongs to. This variable is equal to 0 for environmental (non-ligand) atoms, 1 for ligand 1, and 2 for ligand 2. Each pairwise vdW interaction is checked to ensure that ligand1- ligand2 interactions are omitted.

The relative binding free energy is calculated as the relative complexation energy minus the relative hydration energy. Note that if one uses the same force constant for ligand-receptor restraint for all simulations, the restraint correction discussed above is identical for both ligands and drops out in the relative binding free energy.

METHODS

Simulation setup

Prior to all simulation, the system energy was minimized to 1 kcal/mol/Å in order to avoid close atomic contacts. All simulations were run under OpenMM mixed precision mode. Ewald cutoff was set to 7.0 Å, with a 12 Å vdW cutoff in both simulations. All simulations converge the induced dipole moments between iterations to <0.00001 D. Sampl4 and aromatic simulations use a cubic box of 40 Å an Ewald grid of 48 × 48 × 48, while the larger bench7 dataset uses an Ewald grid of 64 × 64 × 64 and a cubic box of 62.23 Å. Example Tinker key files are included in the Supplementary Materials.

Molecular dynamics

Perturbation steps for absolute binding and solvation simulations were conducted with a stepwise reduction of the ele-lambda keyword, followed by a stepwise reduction of the vdw-lambda keyword at 0 ele-lambda. MD used a RESPA integrator, and a BUSSI thermostat. Information on what perturbation steps were used is included in the Supplementary Materials.

Relative binding and solvation simulations were conducting starting with the ele-lambda1 and vdw-lambda keywords at 1.0, and the ele-lambda2 keyword at 0.0. In a series of simulations, the ele-lambda1 keyword is then gradually reduced to 0.0. This is followed by simulations with a stepwise reduction of vdw-lambda1 to 0.0, then a stepwise increase of ele-lambda2 to 1.0.

All CPU simulations were conducted using Tinker dynamic.x for 1ns with a 2fs time step and snapshots saved every 1ps. Each GPU perturbation simulation was conducted using dynamic_omm for 5ns, with a 2fs time-step and snapshots saved every 2ps (except for relative free energy simulations, which had snapshots saved every 1ps). All simulations were conducted at 298K.

Bennett Acceptance Ratio

Bar was computed using Tinker’s BAR program. This program iterates between the two equations below until convergence:

$$\begin{array}{c}{e}^{-\beta \mathit{\Delta }F}=\frac{{\langle f(\beta (U_2-U_1-C))\rangle }_1}{{\langle f(\beta (U_1-U_2+C))\rangle }_2}\\ C=\mathit{\Delta }F\\ f(x)=\frac{1}{1+e^x}\end{array}$$ (3)

For all CPU based trajectories, BAR used frames 400 to 1000 for calculation, with the initial 400ps equilibration discarded. For absolute free energy trajectories generated on the GPU, BAR used frames 1 to 2500(0–5ns) for calculation. For the relative free energy trajectories generated on the GPU, BAR used frames 1 to 5000(0–5ns) due to more frequently saved snapshots.

Hydration of aromatic compounds

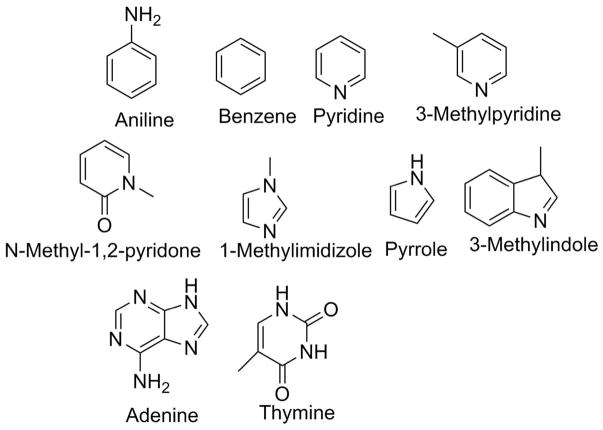
Parameters for the aromatic molecules were previously generated.⁹⁰ Structures of the 10 compounds are shown in Figure 3. Initial simulation systems were generated by solvating each ligand in water boxes using the Tinker commands solvate and crystal. Initial structures for relative HFE simulations were generated by concatenating ligand 2’s coordinates to the solvated ligand 1 pose.

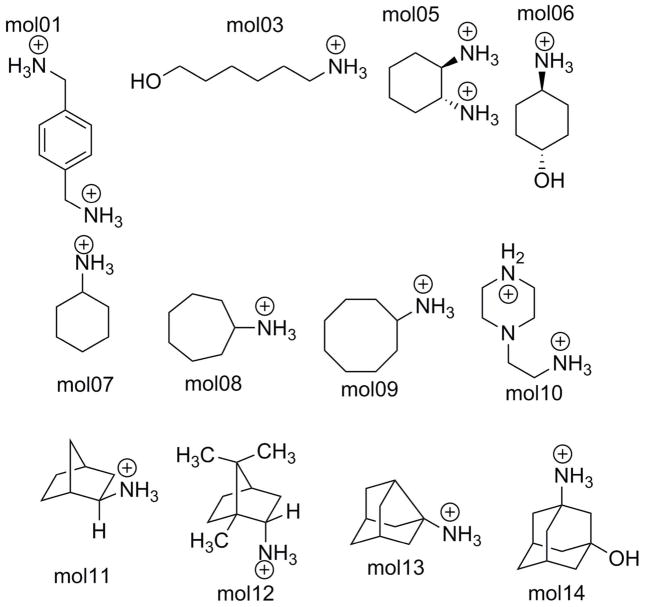
Figure 3.

Structures of the 12 sampl4 molecules utilized in this study.

In order to calculate the absolute hydration free energy, it is necessary to correct for the contribution of intramolecular electrostatics as we scale the solute electrostatic parameters in “disappearing” or “growing” the solute molecule. The intra-solute electrostatic energy was calculated by running simulations on CPU (this same value was used for both the CPU and GPU simulations). Each molecule was simulated alone in a non-periodic system at ele-lambda values of 0, 0.1, … and 1.0. Simulations were run for 1ns using a time step of 0.1 fs, with structures saved every 0.5 ps at constant volume of 40.0 Å with temperature at 298K. The intra-solute electrostatic energy was then calculated using BAR.

Sampl4 binding simulations

Parameters and starting poses for 12 molecules of the sampl4 dataset were generated as described previously⁶³. Structures of the sampl4 ligands utilized in this study are shown in Figure 4. Relative binding poses were generated as in the relative aromatic simulations.

Figure 4.

Structures of the 10 aromatic compounds used in this study.

The final absolute binding energy was calculated as ΔG of complexation (from no interaction to full interaction) − ΔG of solvation (from no interaction to full interaction) + ΔG of going from no restraint to full restraint at 0 interaction lambda + ΔG of removing the restraint at full interaction energy.

The latest version of Tinker is available at https://github.com/jayponder/tinker. Tinker-OpenMM is available at https://github.com/pren/tinker-openmm. Note that Tinker only works using the modified Tinker-OpenMM, not the main OpenMM release.

RESULTS

Force agreement

Correct simulation of molecular systems requires an accurate calculation of both force and energy. However, since energy is only utilized by Tinker in the BAR process, and isn’t used during OpenMM molecular dynamics, we focused our initial analysis of Tinker-OpenMM on agreement of OpenMM forces with those of Tinker. To ensure that lambda was working in the Tinker-OpenMM implementation, we tested molecule 1 of the sampl4 dataset bound to the host at a range of lambda values, and compared the resulting static forces to those of Tinker. The Tinker-OpenMM platform was able to closely match that of Tinker for all tested lambda values, with a root mean squared error of approximately 8.6*10⁻⁴ kcal/mol/Å, and a maximal atomic force deviation of approximately 4.7*10⁻³ kcal/mol/Å (Table 1). These degrees of deviation are negligible when considering that the RMS force is 31 kcal/mol/Å. The force deviation is partially due to the single precision used in GPU force evaluation.

Table 1.

Force comparison between the Tinker-AMOEBA CPU and Tinker-OpenMM-AMOEBA GPU platforms for Sampl4 molecule 1 at a range of lambda values.

VDW lambda/ele-lambda	RMSE force (10− 4 kcal/mol/Å)	Max force deviation (10− 3 kcal/mol/Å)
1/1	8.58	4.69
1/0.5	8.59	4.66
1/0.0	8.58	4.71
0.5/0.0	8.58	4.72
0.0/0.0	8.58	4.72

Computational efficiency

In order to test the speed and scalability of the Tinker-OpenMM platform, we ran 1000 steps of MD on sampl4 molecule 1 (6417 atoms), and the bench7 test case distributed with Tinker (a protein system of 23,558 atoms). For both test systems, the NVidia GTX1070 and GTX 970 were approximately 66-fold and 40-fold faster than an 8 core CPU simulation, respectively (Table 2). A single CPU core is approximately 200-fold slower than simulation on a GTX1070 due to the poor core scalability of Tinker utilizing OpenMP. The GPU platform shows better than linear scaling with respect to system size, with a 3.7-fold increase in particle number resulting in a 2.4-fold or 2.5-fold decrease in speed on the GTX1070 and GTX970 platforms, respectively. This better then linear scaling is likely a result of the smaller sampl4 systems being unable to saturate GPU core utilization, as verified by profiling GPU core utilization during simulations. The change of the vdW force to the softcore 14-7 force resulted in no observable difference in speed compared to the kernel used in OpenMM. This was confirmed by running simulations using a version of Tinker-OpenMM that had been modified to utilize a standard, non-softcore 14-7 vdW force without the presence of the lambda parameter in the codebase.

Table 2.

Performance of Tinker-OpenMM on Nvidia GTX1070 and GTX970 GPUs without the relative binding calculations compared to Tinker CPU running on 8 OpenMP threads (4X of single CPU speed). Values are in nanoseconds/day

	GTX1070	GTX970	CPU
mol01(6417 atoms)	20.0	12.2	0.3
bench7(23558 atoms)	8.3	4.8	0.16

In order to test the cost of utilization of relative vdW, tests were run on bench7 with the relative VDW activated by using two waters (atoms 9000–9002 and 9003–9005) as “ligands” for the alchemical dual topology process. Both of these waters had their ele-lambda values set at 0.0, with a utilized vdW-lambda of 1.0. This allowed for the activation of dual topology kernels without introducing extra costs. This system was minimized, and a speed test was run as above. This resulted in a speed of 4.68 ns/day on a GTX 970, an approximately 2.5% speed reduction when compared to the absolute simulations. This small cost is only present when doing relative free energy calculations; when no ligand2 parameter is set, the cheaper absolute vdW kernel is used for force and energy calculation.

Tinker-OpenMM defaults to a utilizing a “mixed” precision mode in all calculations. This mixed precision mode uses 32-bit floating point calculation for all forces, and integrates using 64-bit floating point precision. Due to the poor double floating point calculation of the consumer GeForce line of graphics cards, the use of double precision for both integration and force calculation results in an 18.1-fold reduction in performance on a GTX 970.

GPU/CPU absolute free energy agreement

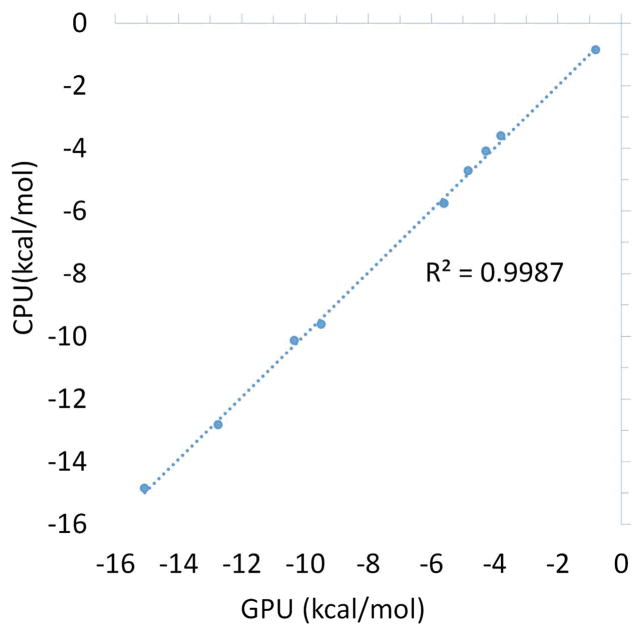
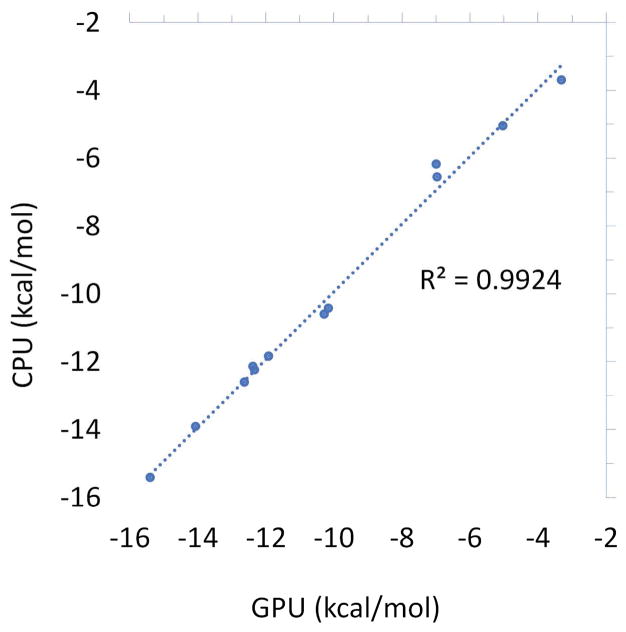
As a test of the ability of the Tinker-OpenMM platform to reproduce the results of the Tinker CPU implementation, we performed hydration free energy calculation on a dataset of 10 aromatic compounds, as well as binding free energies on 12 ligands of the sampl4 dataset (9). Both the solvation (Figure 5) and sampl4 datasets (Figure 6) show agreement within the uncertainty of BAR, with R² values of (0.9924) and (0.9987), respectively. This, along with the static force calculations provides strong evidence that the GPU and CPU implementations of the AMOEBA force field produce comparable results. The fact that a high degree of agreement is possible despite the fact that the GPU simulations were run for 5 times longer (5ns vs 1ns at each perturbation step) is an indication that the tested systems converge relatively rapidly.

Figure 5.

Comparison between the sampl4 binding free energies of 12 sampl4 compounds computed by the Tinker-OpenMM GPU and Tinker CPU platforms. GPU simulations were run for 5ns at each perturbation step, while CPU simulations were run for 1ns.

Figure 6.

Comparison between the calculated solvation free energies for the 10 molecule aromatic compound dataset on the Tinker-OpenMM GPU and Tinker CPU platforms.

GPU/CPU relative free energy agreement

We then proceeded to test the capability of the dual-topology based relative free energy platform by computing the relative solvation values for the aromatic dataset. For all tested aromatic pairs, the relative hydration free energy values computed from the dual-topology approach and the absolute HFE showed an agreement within 0.3 kcal/mol, with an R² value of 0.999 (Table 3). The observed deviation is likely a result of random, non-systematic statistical error.

Table 3.

Comparison between the Tinker-OpenMM absolute and relative platform calculation of the solvation energy between pairs of aromatic compounds. Values are in kcal/mol.

	Relative from Dual-Topology	Difference by Absolute
Aniline/Benzene	4.2±0.1	4.0±0.1
Adenine/Pyrrole	11.4±0.1	11.3±0.1
Aniline/Adenine	−10.2±0.1	−10.2±0.1
Benzene/3-Methylimidizole	−9.0±0.1	−8.7±0.1
3-Methylpytidine/pyridine	−0.1±0.1	0.0±0.1

Finally, we tested the relative binding prediction of two pairs of sampl4 compounds. The first set of compounds, mol05 and mol06 share similar scaffolds, and show agreement in both complexation and solvation to within the uncertainty of BAR(Table 4).

Table 4.

Comparison between the Tinker-OpenMM absolute and relative platform calculations of the relative binding free energy between pairs of sampl4 compounds. Values are in kcal/mol.

	mol05-mol06		mol09-mol10
	Relative from absolute GPU	Relative from dual topology	Relative from absolute GPU	Relative from dual topology
Complexation energy	44.3±0.1	44.3±0.1	−56.3±0.1	−56.0±0.1
solvation energy	47.3±0.1	47.3±0.1	−68.0±0.1	−68.0±0.1
total ΔΔG	−2.9±0.1	−2.9±0.1	10.4±0.2	10.7±0.1

The relative binding between molecules 9 and 10 constitutes a more challenging case that cannot be handled using the dummy atom based approach due to the lack of a shared scaffold. In addition, this dissimilarity between the ligands may theoretically make convergence more difficult in the intermediate vdW transitions. Nonetheless, the relative binding platform was still able to agree with the absolute platform to within 0.3 kcal/mol, demonstrating the advantage of dual-topology platform.

DISCUSSION AND CONCLUSIONS

This work reports a GPU implementation of alchemical free energy simulation for polarizable force field AMOEBA. The enhanced speed of GPU over CPU will be valuable for applications such as lead optimization. We have shown that the Tinker-OpenMM GPU platform is capable of reproducing the results of Tinker CPU platform, with an approximately 200-fold improvement in computational performance over what is possible on a single CPU core. This usage of GPU computation greatly improved sampling, which should allow for accounting for slow dynamics such as induced fit effects and other local changes in protein structure. Therefore, we expect the better sampling afforded by the GPU based platform will potentially lead to improved accuracy in ligand binding free energy prediction.

In addition to raw performance, one of the biggest challenges facing the free energy calculation field is the application of techniques to improve sampling of flexible systems to enable convergence with lesser simulation times. One methodology to achieve this increase in sampling efficiency is the calculation of relative binding free energies. Unlike previously utilized dummy atom based approaches ^82–86, the framework presented here is general and doesn’t require a shared set of atoms to be utilized effectively. A special path has been designed to avoid unstable ligand-ligand polarization in the dual-topology approach. We expect that for flexible protein systems, the dual-topology approach will be more efficient and reduce the time needed for convergence in comparison with absolute free energy approaches.