Mottness at finite doping and charge-instabilities in cuprates

Abstract

The influence of the Mott physics on the doping-temperature phase diagram of copper oxides represents a major issue that is subject of intense theoretical and experimental effort. Here, we investigate the ultrafast electron dynamics in prototypical single-layer Bi-based cuprates at the energy scale of the O-2p→Cu-3d charge-transfer (CT) process. We demonstrate a clear evolution of the CT excitations from incoherent and localized, as in a Mott insulator, to coherent and delocalized, as in a conventional metal. This reorganization of the high-energy degrees of freedom occurs at the critical doping p_cr ≈0.16 irrespective of the temperature, and it can be well described by dynamical mean field theory calculations. We argue that the onset of the low-temperature charge instabilities is the low-energy manifestation of the underlying Mottness that characterizes the p < p_cr region of the phase diagram. This discovery sets a new framework for theories of charge order and low-temperature phases in underdoped copper oxides.

When charge carriers are chemically doped into a Mott or charge-transfer insulator, the system progressively evolves into a metal whose electronic properties are strongly reminiscent of the on-site electronic correlations¹. In the case of copper oxides, the complexity of the problem has roots in the intertwining between the high energy scale of the Mott physics² (several electronvolts) and the low-energy phenomena that typically emerge in the low temperature/doping region of the phase diagram^3–6. For example, the vicinity to the Mott insulating phase at zero doping (p=0) has been advocated^7–9 as the main mechanism that drives the freezing of the charge carriers within the CuO₂ unit cell and the reduction of their kinetic energy, thus facilitating the low-temperature formation of charge-ordered states and other forms of order that spontaneously break the translational symmetry of the underlying crystal. In fact, the universal tendency to develop short-ranged incommensurate charge density waves (CDW) in the underdoped region of the phase diagram and below a characteristic temperature has been recently reported in both hole- and electron-doped copper oxides by X-ray diffraction^10–16, tunneling microscopy^{17, 18} and nuclear magnetic resonance¹⁹. More in general, the breaking of the rotational symmetry from C₄ to C₂ (nematicity) has been argued from X-ray and neutron scattering experiments^20–22 and directly imaged by scanning tunneling microscopy (STM)²³. The signature of intra-unit-cell magnetic order has been observed by neutron scattering²⁴ and Kerr effect measurements²⁵.

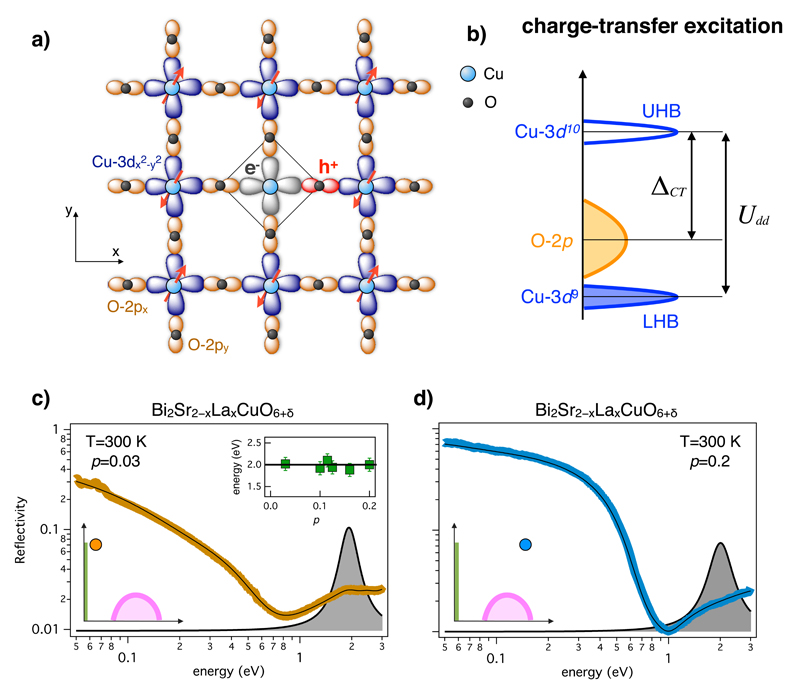
The ubiquitous instability towards ordered states raises the fundamental question whether these phenomena hide a common and profound origin connected to the existence of an elusive correlated metallic state^{2, 26, 27} that emanates from the Mott insulator and extends up to the critical hole doping level, p_cr ~0.16, at which the symmetry-broken orders vanish. In charge-transfer systems, such as cuprates, the oxygen bands play a fundamental role in renormalizing the energy scale at which this possible Mott physics can be studied. Considering the simplest case of the parent insulator (p=0), the valence fluctuations of Cu-3d⁹ are suppressed by the strong Coulomb repulsion (U_dd ~ 10 eV) between two electrons occupying the same Cu orbital. The lowest-energy excitation is thus the charge-transfer (CT) of a localized Cu-3d_x²−y² hole to its neighbouring O-2p_x,y orbitals (see Fig. 1a,b), with an energy cost Δ_CT ~2 eV< U_dd. In the optical conductivity, this process is revealed by a typical CT edge at ħω=Δ_CT, which corresponds to the onset of optical absorption by particle-hole excitations in the complete absence of a Drude response²⁸.

Figure 1. Charge-transfer excitation and optical properties of cuprates.

a,b) A sketch of the generic charge-transfer process in the Cu-O layer of copper oxides is shown. The upper (UHB) and lower (LHB) Hubbard bands, corresponding to the Cu-3d¹⁰ and Cu-3d⁹ configurations, are indicated c) The reflectivity curve, R(ω), of the underdoped sample is reported (yellow dots, taken from Refs. ²⁹, ³⁰). The black line is the fit to the data obtained from a model dielectric function which contains an extended-Drude term and three Lorentz oscillators that account for the high-energy transitions. The contribution of the first interband oscillator (ω_CT), attributed to the charge-transfer process, to the total dielectric function is reported as a grey region. The inset displays ω_CT as a function of the hole concentration. The left-bottom inset shows the position of the sample in the p-T phase diagram. The pink line represents the superconducting dome, while the green line indicates the CT insulating region. d) The panel displays the R(ω) of the overdoped sample (blue dots, taken from Refs. ²⁹, ³⁰). The black line is the fit of the model dielectric function to the data. The grey area represents the contribution of the CT oscillator to the dielectric function. The left-bottom inset shows the position of the sample in the p-T phase diagram.

Here we shed new light on the nature of the electronic excitations at the Δ_CT energy scale by adopting a non-equilibrium approach. The high temporal resolution (~10 fs) of the time-resolved technique employed in this work allows us to access the ultrafast dynamics of the CT excitations before complete thermalization is achieved. We performed experiments on the single-layer Bi₂Sr_2−xLa_xCuO_6+δ (La-Bi2201) cuprate family (see Methods), in which the hole doping concentration can be accurately controlled by La substitution and can span a broad doping region (0.03< p <0.2) across the critical doping p_cr=0.16. The ultrafast dynamics of the CT excitations is directly compared to the CDW amplitude, that has been measured on the same samples by resonant soft X-ray scattering (RXS) at low temperature¹⁷. These results, supported by dynamical-mean-field-theory (DMFT) calculations, unveil a temperature-independent crossover of the CT dynamics at p_cr ~0.16 and suggest that the high-temperature Mott-like state at p < p_cr is the necessary precursor of the low-temperature instabilities.

In Figure 1c,d we report the reflectivity curves, R(ω), for the most underdoped (p=0.03, non-superconducting) and the most overdoped (p=0.2, T_c/T_c,max=0.57) samples^{29, 30}. Considering the deeply underdoped sample, the first high-energy optical transition is found at Δ_CT =2 eV and hence can be safely ascribed to the charge-transfer process. When the doping concentration is increased, the energy of this optical transition remains constant (see the inset of Fig. 1c), while its spectral weight progressively decreases. Furthermore, the low-energy region develops a pronounced metallic plasma edge at ħω ~1 eV.

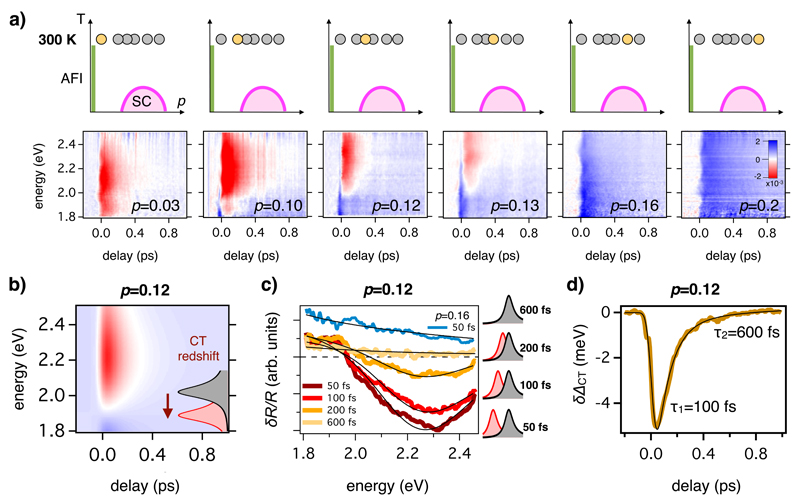
Fig. 2a reports the ultrafast dynamics of the CT transition at T =300 K in the 1.8-2.5 eV energy range. The dynamics is triggered by pump pulses whose frequency content (1.35 eV central energy with 0.3 eV bandwidth, see Methods) guarantees a significant overlap with the CT transition (≈1 eV full-width-half-maximum, see Fig. 1c,d) as well as the temporal resolution necessary for the experiment. Similar results were obtained with 1.6 eV and 2.1 eV pump photon energies (see figures S3, S4). The measured sub-ps dynamics exhibits a clear doping dependence: while the reflectivity variation (δR(ω)/R) measured on the underdoped samples is characterized by a pronounced negative (red) signal for ħω > 2 eV, it progressively evolves toward a featureless positive (blue) signal for p ≥ 0.16. The negative δR(ω)/R measured in underdoped samples at ħω ~ Δ_CT cannot be explained by simply assuming a variation of the total scattering rate of the conduction electrons^{31, 32}, since this would lead to a flat and positive signal over the entire probed frequency range (see Supplementary). In contrast, the δR(ω)/R signal can be perfectly reproduced by assuming a pump-induced redshift of the CT transition (see Supplementary), which results in a reflectivity variation proportional to the derivative of the peak shape. In Fig. 2b we report the δR(ω,t)/R signal calculated by introducing a redshift of the CT peak in the equilibrium dielectric function of the intermediately doped sample (p=0.12) and by assuming an exponential decay of the signal. The main features of the experimental transient reflectivity map are qualitatively reproduced by this simple assumption. For a quantitative analysis of the ultrafast dynamics, we report in Fig. 2c the fit to the δR(ω,t)/R spectra for the p=0.12 sample at fixed delays (t=50, 100, 200, 600 fs), from which we can extract the time evolution of the CT redshift (δΔ_CT). For all the under-doped samples, the δΔ_CT dynamics (see Fig. 2d) is similar and is characterized by two exponential recovery times, τ₁ ≃100 fs and τ₂ ≃600 fs. These timescales are compatible with the coupling to the optical buckling and breathing phonons and, subsequently, to the rest of the lattice vibrations³¹, while the coupling of the local charge excitations to short-range antiferromagnetic fluctuations is expected to be effective on the 10 fs timescale³². The maximum δΔ_CT is estimated by considering the value extracted from the fitting procedure at t=50 fs. Considering the p=0.12 sample, we obtain δΔ_CT=-5±1 meV at the excitation density of 7 J/cm³. With this excitation density the maximum value of the CT redshift, i.e., δΔ_CT =-10±2 meV, is measured at p=0.10 hole doping.

Figure 2. Ultrafast optical spectroscopy on La-Bi2201.

a) The top row shows the position of the measured samples in the p-T phase diagram. In the bottom row we report the δR(ω,t)/R maps measured by ultrafast optical spectroscopy on La-Bi2201. The colour scale is reported in the inset. b) Simulation of the δR(ω,t)/R signal for the p=0.12 sample. A transient redshift of the CT oscillator, described by an exponential decay, is assumed. The colour scale is the same than that in panel a). c) δR(ω)/R spectra at different time delays for the p=0.12 sample. The black line is the fit to the data obtained by red-shifting the position of the CT oscillator. For comparison, we report δR(ω)/R for the p=0.16 sample (blue line), along with the best fit obtained by increasing the scattering rate in the Drude model. d) Dynamics of δΔ_CT for the p=0.12 sample. The black line is the fit to the data of a double-exponential decay convoluted with a step function.

The measured CT redshift discloses important information about the nature of the charge-transfer transition. This process can be easily rationalized starting from the CT insulator (p=0), in which the completely localized picture provides a good description of the fundamental electronic excitations. In this framework, the energy necessary to move a localized hole from the Cu-3d_x²−y² to the O-2p_x,y orbitals is renormalized by the Coulomb interatomic potential (U_pd) between the excess Cu-3d electron and the holes residing on the nearest neighbouring oxygen sites. In simple terms, U_pd provides a binding energy for the local Cu-3d_x²−y²–O-2p_x,y exciton. Within this local picture, we can sit on a spin-up polarized Cu atom (see Fig. 1a) and assume that the effect of the pump pulse is to transfer to that atom a fraction of spin-down electrons, δϵ_↓, from the oxygens within the same CuO₂ cell. The excess of positive charges on the oxygen atoms leads to an increase of the binding energy of the additional excitons that can be created on the neighbouring cells by the following probe pulse. This process can be revealed as a decrease of the effective CT energy measured by the probe. Quantitatively, the pump-induced redshift of Δ_CT can be estimated by a simple mean field calculation (see Methods):

$$\delta {\Delta }_{CT}=-\left(2U_{pd}-\frac{5}{24}{U}_{pp}\right)|\delta {ϵ}_{\downarrow }|,$$ (1)

where U_pp is the Coulomb repulsion between two charges occupying the same O-2p orbital. Considering the realistic values U_pp ~5 eV and U_pd ~2 eV (Ref. ³³) and the photodoping δϵ_↓ ~0.3% (see Methods), we estimate δΔ_CT ~-9 meV, which is in very good quantitative agreement with the measured pump-induced redshift in underdoped samples.

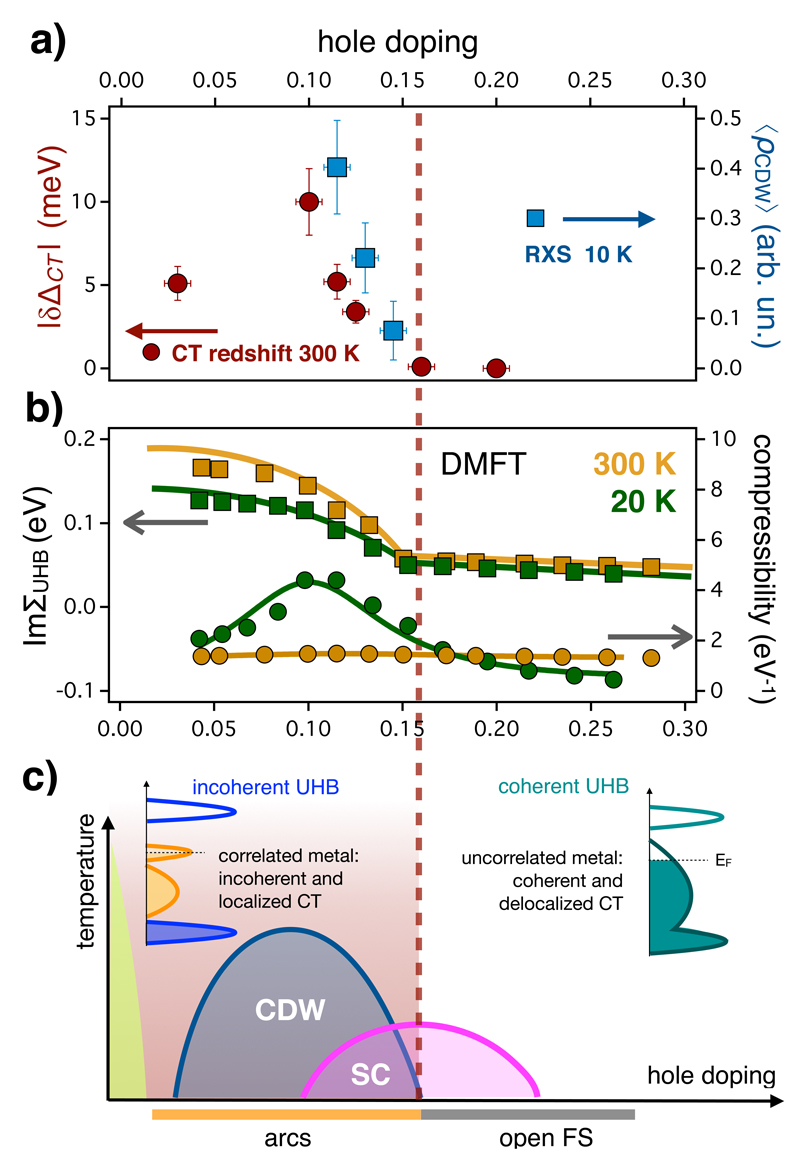
Interestingly, the δΔ_CT measured in the experiments progressively decreases as the hole doping increases until the p_cr ≃ 0.16 critical doping concentration is reached (see Figure 3a). The δR(ω,t)/R signal measured on the optimally (p=0.16) and over-doped (p=0.2) samples does not show any evidence of a CT redshift, while it can be easily reproduced (see Figure 2c) by assuming an average increase of the electron-boson scattering in the Drude component of the dielectric function, in agreement with the results reported in Refs. ^{31, 32}. These results are independent of the base temperature of the sample, as evidenced by the temperature-dependent broadband measurements reported in the Supplementary Material. The picture emerging from these results can be summarized as follows: for p < p_cr, the photoexcitation induces a redshift of the CT transition, which is qualitatively and quantitatively similar to what expected for a CT insulator^{34, 35}; for p > p_cr the ultrafast dynamics can be explained by an increase of the scattering rate of the charge carriers, as expected for a metal. We thus conclude that p_cr discriminates, already at high temperature, an underdoped region in which the CT transition is a spatially localized process, as in a Mott insulator, from an overdoped region in which the CT excitation involves wavefunctions spread over many sites, as in more conventional band metals. We note that this localized-delocalized transition of the CT excitation is clearly distinct from the onset of the pseudogap physics, which occurs at a temperature evolving from T* ~250 K at very low doping to T*=90-150 K at p=0.16 and T* ~50 K at p=0.2, as observed by Knight-shift measurements³⁶ and confirmed by single-colour pump-probe measurements on the same samples (see Supplementary Information). A similar T*(p) line has been recently observed by monitoring the p-T dependence of the scattering rate of the Drude peak via non-equilibrium infrared spectroscopy in the 0.5-2 eV energy range³⁷. Notably, no transition at p_cr is observed when we analyse the δR(ω)/R traces extracted at t >600 fs (Fig. 2c), i.e., when the excess energy is dissipated in low-energy excitations and converted into heat. This demonstrates that the effect reported here for doped cuprates remains inaccessible to equilibrium techniques, in which only the charge-fluctuations at k_BT are activated.

Figure 3. The high-energy phase diagram of cuprates.

a) The values of the room-temperature CT redshift (δΔ_CT, red dots, left axis) and the intensity of the low-temperature CDW signal (〈ρ_CDW〉, blue dots, right axis) are reported as a function of the hole concentration of the La-Bi2201 samples. The excitation fluence of the pump beam has been tuned in order to maintain a constant absorbed energy density of 7 J/cm³ for the different dopings (see Supplementary). The error bars correspond to the uncertainty of the excitation fluence. 〈ρ_CDW〉 has been obtained by integrating the difference between the RXS signals measured at the temperatures of 20 K and 300 K at the CDW wavevector¹⁷. The error bars represent the standard deviation of the total number of counts in the integration area. The result has been normalized to the total RXS signal at 300 K. Both δΔ_CT and 〈ρ_CDW〉 vanish at the critical doping p_cr =0.16±0.01. The uncertainty in the doping concentration represents the maximum and minimum values compatible with the nominal La concentration (x) and the experimental critical temperature, following the procedure described in Ref 53. b) The imaginary part of the electronic self-energy of the UHB (colored squares) is calculated by DMFT and is reported as a function of the doping concentration for different temperatures (300K dark yellow; 20 K green). The calculated electronic compressibility is indicated by colored circles. The full lines are guides to the eye. c) A sketch of the non-equilibrium p-T phase diagram of copper oxides is reported. The pink, blue and green areas delimit the superconducting (SC) dome, the charge-ordered (CDW) state and the antiferromagnetic insulator, respectively.

The crucial idea that drives the present work is that the Mott-like nature of the electronic states, that we probe at the energy scale Δ_CT, is the fundamental prerequisite for the development of low-temperature instabilities. A possible link between the high- and low-energy physics is that a correlated metal in proximity of the Mott insulating phase is characterized by a reduced mobility of the charge carriers confined into a narrow band at the Fermi level. Upon small variations of the chemical potential µ, the density of states at the Fermi level is expected to dramatically change, thus possibly leading to a very high electronic compressibility^{38, 39}, K ∝ ∂_n/∂_µ. At low temperatures the additional freezing of the thermal excitations renders the system naturally prone to phase separation, in which strong charge inhomogeneities (δ_n) can coexist at the same chemical potential. DMFT calculations provide a solid support to this naive picture in the case of a realistic three-band model with interaction terms among the O-2p_x,y and Cu-d_x²–y² orbitals similar to those used in Eq. 1 (see Methods). In particular, we focus on the doping-dependence of the upper Hubbard band (UHB), that corresponds to the double occupation of the Cu-3d_x²−y² levels, i.e., the final state of the CT process. In Figure 3b we plot the imaginary part of the electronic self energy, that corresponds to the inverse lifetime, of the UHB (ImΣ_UHB). At temperatures as high as 300 K the large value of the inverse lifetime, typical of local incoherent excitations in the vicinity of the Mott insulating state, progressively decreases until the p_cr doping is reached. Above this value, ImΣ_UHB shows a smaller and almost constant value that indicates the transition to delocalized and coherent excitations, similar to what expected for conventional interband transitions in uncorrelated solids. In the three-band model considered, the onset of coherence of the CT excitations at p_cr coincides with the merging of the quasiparticle peak at the Fermi level with the broad conduction band of mixed p-d character, characteristic of the doping-driven Mott transition in DMFT ⁴⁰. As expected, the computed high-temperature compressibility is a smooth function of doping and does not evidence any tendency to charge-separation (Figure 3b). The picture dramatically changes at low temperature, when the additional freezing of the charge carriers in the correlated states close to µ cooperates in increasing K in the underdoped region of the phase diagram. As shown in Figure 3b, while the high-energy ImΣ_UHB transition is almost unaffected by temperature, the compressibility shows at low temperatures a pronounced maximum for p < p_cr that suggests the tendency to develop charge inhomogeneities. Even though the emergence of CDW at a specific wavevector is the result of more complex ingredients, such as the long-range Coulomb interactions⁸ and the topology of the Fermi surface, our results suggest that the proximity to the Mott-state is the prerequisite for the low-temperature development of charge-order instabilities.

The validity of this picture is further corroborated by the outcome of RXS measurements at T=10 K on the same samples, as previously measured in Ref. 17. The spontaneous breaking of the translational symmetry of the charge distribution within the CuO₂ planes is detected as a resonance in the RXS signal at a specific exchanged parallel wavevector (see Supplementary Information). While the width of the RXS peaks indicates a CDW correlation length of the order of 2-3 nm, the momentum-integrated signal can be taken as proportional to the average amplitude of the charge-density modulation. Fig. 3a reports the CDW amplitude, 〈ρ_CDW〉, on La-Bi2201 at different hole doping concentrations, obtained by integrating the RXS signal measured at the proper CDW wavevector. The CDW amplitude progressively decreases until 〈ρ_CDW〉 → 0 at p_cr=0.16±0.01, that is the same doping concentration at which the δΔ_CT signal vanishes. This observation undoubtedly demonstrates that the development of short-ranged CDW at low temperature takes place only in the doping region p < p_cr, that is characterized, already at room temperature, by the Mottness of the UHB.

Taken together, these observations consistently show that the phase diagram of copper oxides is characterized by a temperature-independent transition from a correlated to a more conventional metal at p_cr ≃0.16. This phenomenon, that involves energy scales as high as Δ_CT, can be observed already at room temperature via non-equilibrium experiments. Our observations impact on many aspects of the physics of copper oxides: i) charge-order emerges as the low-energy manifestation of a correlated ground state in the p < p_cr region of the phase diagram; ii) while low-energy models, which take into account the details of the electronic interactions at the Fermi level, are necessary to correctly predict the CDW wavevector, symmetry and onset temperature, the value p_cr at which the charge order vanishes is the consequence of a high-energy phenomenon; iii) any theory for the charge-order phenomenon should rely on the correlated nature of the electronic states at the Fermi level, which is reflected in the quenching of the O-2p→Cu-3d charge fluctuations at the energy scale Δ_CT and in the freezing of the charge carriers that drives the upturn of the electronic compressibility at p < p_cr.

More in general, we note that the critical doping p_cr is a turning point for many low-temperature properties of copper oxides, such as the momentum space topology^{41, 42}, the ARPES quasiparticle strength⁴³, the superconductivity-induced kinetic energy change^{44, 45}, the time-reversal symmetry breaking⁴⁶, the change of the in-plane resistivity curvature⁴⁷, the transition from p to 1 + p charge carrier density^48–50 and the strong increase of the quasiparticle effective mass⁵¹. Our results suggest a novel intriguing scenario, in which the crossover at p_cr between the physics of a doped Mott insulator to that of a more coherent metal is at the origin of the low-temperature phenomenology. In this framework, the reduced mobility of the charge carriers associated with the Mottness for p < p_cr constitutes the fertile ground for the onset of lower-symmetry instabilities which are commonly claimed to fan out from a putative zero-temperature quantum critical point hidden by the superconducting state.

Methods

Experiments

A Ti:sapphire amplifier (Clark-MXR model CPA-1) delivers a train of pulses at 1 kHz repetition rate with 150-fs duration at 780 nm central wavelength and is used to simultaneously drive two Non-collinear Optical Parametric Amplifiers (NOPAs) operating in different frequency intervals. All NOPAs are seeded by white light continuum (WLC) generated in a sapphire plate. The first NOPA (NOPA1) is pumped by the second harmonic and amplifies in a beta-barium borate (BBO) crystal pulses with a spectral content between 820 nm (1.5 eV) and 1050 nm (1.2 eV), which are compressed to nearly transform-limited 13-fs duration by a couple of fused silica prisms. This NOPA serves to trigger the dynamics and it is synchronized with a second NOPA (NOPA2), pumped by the second harmonic and using BBO, which is used to probe the reflectivity variation of the system. The spectrum of NOPA2 spans a frequency range between 510 nm (2.4 eV) and 700 nm (1.8 eV) and it is compressed to 7 fs duration by multiple bounces on a pair of chirped mirrors, making the overall temporal resolution of the pump-probe setup below 15 fs. The time delay between pump and probe is adjusted by a motorized delay stage and both the beams are focused on the sample by a spherical mirror in a quasi-collinear geometry. The reflected probe spectrum is detected by a Si spectrometer working at the full 1 kHz laser repetition rate. By recording the reflected probe spectrum at different temporal delays t with and without pump excitation, we measure the differential reflectivity: δR(ω, t)/R(ω)=[R(ω, t)-R_eq(ω)]/R_eq(ω). The pump fluence used for the experiments is 500 µJ/cm². The density of CT excitations can be estimated starting from the pump penetration length (l_pen) at a specific doping (see Supplementary Information). For example, assuming l_pen ~700 nm for ħω=1.4 eV and p=0.10 we obtain an absorbed energy of ~7 J/cm³, which corresponds to a density of Δ_CT =2 eV excitations of about 2x10¹⁹ cm⁻³. Considering that the density of Cu atoms is ~6x10²¹ cm⁻³, we obtain that the fraction of holes transferred from the Cu atoms is δϵ_↓ ~3x10⁻³. The La-Bi2201 crystals were grown using the floating-zone technique, and characterized as described in Ref. 52. The doping has been determined following Ref. 53.

Differential analysis of the transient reflectivity

The analysis of the time-resolved data has been carried out starting from the equilibrium dielectric function of the samples that has been measured elsewhere ²⁹. The best fitting to the complex optical conductivity has been obtained by combining a Drude model ^{31, 32} and high-energy Lorentz oscillators:

$$\sigma \left(\omega \right)=\frac{1}{4\pi }\frac{{\omega }_{pD}^2}{1/{\tau }_D-i\omega }+\frac{\omega }{4\pi }{\displaystyle \sum _j\frac{{\omega }_{pj}^2}{\omega /{\tau }_j-i\left({\omega }^2-{\omega }_j^2\right)}}$$

The first term refers to the relaxation of the free charge carriers with the scattering rate γ = 1/τ_D; the second term is a sum of Lorentz oscillators - characterized by the central frequency ω_j, the strength of the oscillator ${\omega }_{\mathit{\text{pj}}}^2$ and the scattering rate γ_j = 1/τ_j - that describe the response of bound charges.

The underlying idea of the differential model is to find the minimum number of parameters in the equilibrium dielectric function which have to be modified to reproduce the reflectivity variation, i.e., δR(ω, τ)/R, measured at a given time delay τ. As discussed in Refs. ³¹ and ³², the δR(ω, τ)/R signal measured on optimally and overdoped copper oxides can be interpreted, already after ~40 fs, as a transient increase of the electron-boson scattering rate. The increase of the scattering rate induces a broadening of the Drude plasma edge across the plasma frequency at ω_D =~1 eV. The δR(ω, τ)/R detected at probe frequencies ω > ω_D results in a positive and featureless signal, which monotonically decreases at high frequencies. This behaviour, that is confirmed in the measurements on La-Bi2201 for hole concentrations p ≥0.16 , clearly contrasts with the δR(ω, τ)/R signal observed at p < 0.16 and for τ <600 fs (see Fig. 2). As an example, we report in the Supplementary Figure S4 the signal δR(ω,50 fs)/R measured on the underdoped La-Bi2201 sample with p=0.12. Clearly, the negative reflectivity variation at ω > Δ_CT ≃2 eV cannot be attributed to a change of the electron-boson scattering rate. On the other hand, the δR(ω, τ)/R signal is perfectly reproduced simply by assuming a redshift of the CT oscillator alone. For completeness, we also show that a change in the spectral weight of the CT oscillator does not account for the measured δR(ω, τ)/R.

Mean-field calculation of the CT redshift

In the fully atomic picture (half-filling), the hamiltonian governing the physics of the CuO₂ plane can be written as:

$$\begin{array}{l}H={ϵ}_{\text{Cu}}{n}_d+{ϵ}_{\text{O}}\left(n_{{\text{O}}_1}+n_{{\text{O}}_2}\right)+\frac{U_{dd}}{2}{\left(n_d-1\right)}^2+\frac{U_{pp}}{2}{\displaystyle \sum _{i=1,2}{\left(n_{{\text{O}}_i}-6\right)}^2}\\ +U_{pd}\left(n_d-1\right){\displaystyle \sum _{i=1,2}\left(n_{{\text{O}}_i}-6\right)}\end{array}$$

in order to minimize the interaction when one electron sits on the Cu atom and both the oxygens (labeled by i) are fully occupied, i.e., 〈n_d + n_O1 + n_O2〉=13. As a crude approximation, we assume a localized spin (up) on the Cu atom through the following parametrization: 〈n_d↑〉=1 − ϵ_↑,, 〈n_d↓〉=−ϵ_↓, and $\langle n_{{\text{O}}_{1\uparrow (\downarrow )}}\rangle =\langle n_{{\text{O}}_{2\uparrow (\downarrow )}}\rangle =3+\frac{ϵ}{2},$ where 2ϵ = ϵ_↑ + ϵ_↓ is the total photoinduced change of the occupation of the Cu_↑ and Cu_↓ sites.

The mean-field calculation of the mean value of the Cu and O levels, i.e., µ_Cu,σ and µ_O,σ, result to be:

$$\begin{array}{c}{\mu }_{\text{Cu},\uparrow (\downarrow )}={ϵ}_{\text{Cu}}-U_{dd}\left({ϵ}_{\downarrow (\uparrow )}+(-)1/2\right)+2U_{pd}ϵ\\ {\mu }_O={ϵ}_{\text{O}}+\frac{5}{24}{U}_{pp}\left(2ϵ-\frac{72}{5}\right)-2U_{pd}ϵ.\end{array}$$

In the simplest case of a single band model, the difference between the empty and occupied Cu levels, i.e., µ_Cu,↓ – µ_Cu,↑=U_dd, results independent of the photoinduced occupation, since intrinsically ϵ_↑=ϵ_↓. This result suggests that in the single-band Mott insulator, the density of states of the upper- (UHB) and lower-Hubbard bands (LHB) decreases upon photoexcitation, while the gap value remains constant.

The scenario is qualitatively different for a charge-transfer insulator, in which the electrons are transferred from the Cu to the O atoms and the ϵ_↑=ϵ_↓ symmetry is broken. If we sit on the spin up Cu site, the effect of the pump excitation is to transfer a certain amount of electrons from the oxygen to the Cu spin down state, i.e., δϵ_↓ < 0 while δϵ_↑ = 0. Therefore, the change of the charge-transfer gap measured by the probe pulse is given by:

$$\delta \left({\mu }_{\text{Cu},\downarrow }-{\mu }_{\text{O}}\right)=-\left(2U_{pd}-\frac{5}{24}{U}_{pp}\right)|\delta {ϵ}_{\downarrow }|,$$ (2)

Mean field theory calculations

We consider a model including copper d_x²–y² orbitals and oxygen p_x and p_y orbitals with the same interaction terms as in the Hartree-Fock calculation and near neighbor hopping between copper and oxygen and oxygen-oxygen. The parameters are U_dd=10 eV, U_pp=5 eV, U_pd=2 eV, Δ_CT=2 eV, t_pd=0.3 eV, t_pp=0.1 eV. We solve the model using single-site DMFT treating both the copper-oxygen and oxygen-oxygen repulsions at the Hartree-Fock level, while the copper-copper interaction is included without approximations. The impurity model is solved using exact diagonalization at finite temperature with 8 levels in the bath (N s=9) and keeping ⁵⁰ states in the calculation of the trace. We have verified that the results for statical observables are converged in both truncation parameters.