Fairy circle landscapes under the sea

We derive a model explaining the formation of fairy circles and patterns in seagrasses along the Mediterranean coast.

Abstract

Short-scale interactions yield large-scale vegetation patterns that, in turn, shape ecosystem function across landscapes. Fairy circles, which are circular patches bare of vegetation within otherwise continuous landscapes, are characteristic features of semiarid grasslands. We report the occurrence of submarine fairy circle seascapes in seagrass meadows and propose a simple model that reproduces the diversity of seascapes observed in these ecosystems as emerging from plant interactions within the meadow. These seascapes include two extreme cases, a continuous meadow and a bare landscape, along with intermediate states that range from the occurrence of persistent but isolated fairy circles, or solitons, to seascapes with multiple fairy circles, banded vegetation, and “leopard skin” patterns consisting of bare seascapes dotted with plant patches. The model predicts that these intermediate seascapes extending across kilometers emerge as a consequence of local demographic imbalances along with facilitative and competitive interactions among the plants with a characteristic spatial scale of 20 to 30 m, consistent with known drivers of seagrass performance. The model, which can be extended to clonal growth plants in other landscapes showing fairy rings, reveals that the different seascapes observed hold diagnostic power as to the proximity of seagrass meadows to extinction points that can be used to identify ecosystems at risks.

INTRODUCTION

The spatial organization of vegetation landscapes is a key factor in assessment of ecosystem health and functioning (1–4). Spatial configurations of vegetation landscapes act as potential indicators of climatic or human forcing affecting the ecosystem (2) and determine energy and material budgets and feedbacks across space (2, 4–6). In addition, although vegetation tends to cover all available ground under favorable conditions, plant distributions can spontaneously develop spatial inhomogeneities under resource limitation, acting as ecosystem engineers that modify the fluxes of nutrients and water to improve their growth conditions (4, 7). Hence, the spatial organization of vegetation landscapes provides an indicator of the existence of stressing factors and the proximity of critical thresholds leading to irreversible losses (4, 8).

The processes conducive to different dynamics of vegetation landscapes have been assessed in habitats ranging from arid ecosystems and savannahs to forests and wetlands (1, 2, 4). The most striking patterns have been reported in drylands, where competition for water leads to self-organized vegetation patchiness (9–13), including the appearance of the so-called fairy circles, whose origin has stirred significant controversy (12, 14–17). These are bare circular patches surrounded by grass, which appear, for example, in regions of the grassy deserts of Namibia (14) and Australia (16) and have been used as a basis to formulate a theory of self-organization of vegetation landscapes in water-limited ecosystems.

Although self-organized patchiness and pattern formation are well documented in terrestrial ecosystems, their occurrence in marine environments has attracted much less attention. Fairy circle–like structures have been reported in seagrass meadows, such as Mediterranean Posidonia oceanica (18, 19) and Zostera marina in the Danish Kattegat (20). Complex landscapes, such as bare seascapes dotted with plant patches, termed “leopard skin” (21), and striped vegetation patterns (22, 23), have also been studied. However, inspection of satellite images and side-scan cartography reveals that complex seascapes are abundant in meadows of P. oceanica, suggesting that self-organized submarine vegetation patterns may be prevalent but have remained thus far largely hidden under the sea. Obviously, the mechanisms responsible for the formation of these submarine fairy circle landscapes must be necessarily different than those operating in water-limited ecosystems on land (12, 14, 16). Although there are some hypotheses of possible mechanisms in several marine ecosystems (23–26), there is only a partial understanding of the phenomenon in P. oceanica meadows.

With a global distribution along the shorelines of all continents except Antarctica, seagrass meadows are valuable ecosystems that provide valuable ecosystem services (27); but they rank among the most threatened ecosystems globally (28). P. oceanica is the dominant seagrass in the Mediterranean Sea, where it forms underwater meadows that support great biodiversity, are a site of intense CO₂ sequestration, and offer shoreline protection (29, 30). Unfortunately, this ecosystem is affected by multiple anthropogenic impacts, including reduced water quality and physical impacts, that have led to a loss of 6.9% per year over the past 50 years (30). Although P. oceanica is a strongly clonal plant propagating through rhizome growth, its very slow horizontal spread of a few centimeters per year implies that losses are essentially irreversible over managerial time scales (30).

Here, we report that inspection of side-scan sonar cartography of seagrass meadows (P. oceanica and Cymodocea nodosa) in Mallorca Island (Western Mediterranean) reveals that vegetation patterns of holes and spots spanning over many kilometers are prevalent along the coastline of the Balearic Islands (see Fig. 1A) (31). We also present a simple, parsimonious model of clonal plant growth yielding self-organized submarine vegetation patterns that encompass the diversity of seascapes observed.

Fig. 1. Examples of fairy circles and spatial patterns in Mediterranean seagrass meadows.

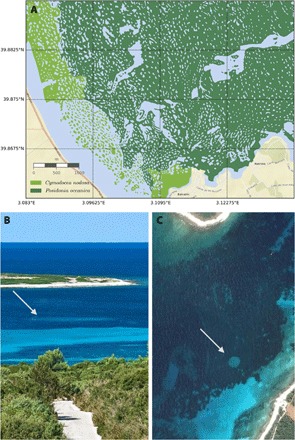
(A) Side-scan image of a seagrass meadow in Pollença bay (Mallorca Island, Western Mediterranean) from LIFE Posidonia (31) showing different patterns in meadows of P. oceanica and C. nodosa. Other examples are shown in figs. S9 to S11. (B) Image of a fairy circle in a P. oceanica meadow in the Adriatic Sea as seen from the coast. Photography by Zvaqan is available in Google Street View and (C) the same fairy circle in a satellite image of Google maps (44°05′37.5″N, 14°55′37.6″E). Other fairy circles can be found at the following locations: 44°04′01.8″N, 14°57′53.3″E and 39°08′48.2″N, 2°56′07.1″E.

RESULTS

Sintes et al. (32, 33) developed a model, based on a limited set of simple rules underpinning clonal growth, successfully reproducing seagrass growth: First, the growing apex of seagrass rhizomes elongates in a fixed horizontal direction with a velocity ν, leaving new shoots behind, which are separated along the rhizome by a typical distance ρ. Second, the growing apex develops new branches at a rate ω_b, with these branches elongating into a horizontal direction at an angle φ_b from the original rhizome. Living shoots have a typical lifetime, depending on external factors and the presence of neighboring shoots, resulting in a per capita mortality rate ω_d. If ω_d < ω_b at a given position, the density of shoots will increase locally. The typical value of each parameter is a characteristic feature of each species with some variability driven by genetic and environmental conditions (32).

We have scaled up this model (originally conceived to describe patch development) to landscape scale by coarse-graining it to describe the dynamics of the shoot, n_s, and apex, n_a, densities. Total shoot density n_t, is calculated as the sum of shoots and apices growing in all directions. This model, which we call the “Advection-Branching-Death” (ABD) model, includes rhizome growth in different directions, contributions from rhizome branching, and shoot death. Shoot mortality rates are density-dependent as well as dependent on environmental factors (for example, resource availability). More specifically, three terms contribute to the total mortality

$${\mathrm{\omega }}_{\mathrm{d}}[{\mathit{n}}_{\mathrm{t}}(\overrightarrow{\mathit{r}},\mathit{t})]={\mathrm{\omega }}_{\mathrm{d}0}+\mathit{b}{\mathit{n}}_{\mathrm{t}}^2+{\displaystyle \int }{\displaystyle \int }\mathcal{K}(\overrightarrow{\mathit{r}}-{\overrightarrow{\mathit{r}}}^{\prime })(1-{\mathit{e}}^{-\mathit{a}{\mathit{n}}_{\mathrm{t}}({\overrightarrow{\mathit{r}}}^{\prime })})\mathit{d}{\overrightarrow{\mathit{r}}}^{\prime }$$ (1)

On the one hand, the intrinsic mortality rate, ω_d0 > 0, of an individual shoot at a particular position in the landscape depends on environmental factors, and on the other hand, on two density-dependent terms: local saturation and nonlocal interaction. The saturation term $\mathit{b}{\mathit{n}}_{\mathrm{t}}^2$ is nonlinear and prevents an unlimited growth, increasing mortality locally when the density increases excessively. The strength b of this density-dependent term reflects the environmental carrying capacity, determining the maximum density in the meadow. Nonlocal interactions are included through an integral term accounting for the interaction of shoots at position $\vec{\mathit{r}}$ with those in a neighborhood weighted by the kernel $\mathcal{K}$$(\vec{\mathit{r}}-{\vec{\mathit{r}}}^{\prime })$. Through nonlocal interactions, the abundance of shoots in a place can affect the growth in a neighborhood. The model therefore includes two essential components to yield self-organization: nonlinearity and spatial interaction.

The three terms in Eq. 1 are consistent with the current functional understanding of seagrass meadows. The intrinsic mortality rate of individual shoots, determining ω_d0, depends on external factors such as temperature and irradiance regimes (34). Local density dependence results from self-shading, determining the maximum density of shoots for a given plant size (35) and the general decline in seagrass density and biomass with depth (36), as well as local depletion of other resources, such as CO₂, which is depleted during daytime in dense meadows (37). Nonlocal interactions integrate a number of facilitative and competitive mechanisms. Facilitative interactions arise, for instance, in the form of stress amelioration, when the presence of neighboring plants dissipates wave energy, which may prevent shoot removal from scouring of waves within the meadow (38) and contributes to stabilize and trap sediments (39). Facilitation has been argued to play a role in shaping seagrass landscapes (40, 41). Negative interactions appear, for instance, as a result of anaerobic microbial decomposition in dense meadows, which leads to diffusing sulfide fronts that spread mortality, leading to the appearance of fairy rings (20). Competition can arise also from depletion of nutrients from the flow by plants up-current (42) or of other diffusing resources, such as CO₂.

Hence, existing evidence suggests intraspecific facilitation and competitive nonlocal interaction whose precise ranges are difficult to determine. As a result of these interactions, the meadow can self-organize enhancing facilitative effects and diminishing competition, altering the environment to yield more favorable growth conditions.

We consider a kernel $\mathcal{K}$ with two terms of Gaussian shape

$$\mathcal{K}(\overrightarrow{\mathit{r}})=\mathrm{\kappa }\mathcal{G}({\mathrm{\sigma }}_{\mathrm{\kappa }},\overrightarrow{\mathit{r}})-\mathrm{\mu }\mathcal{G}({\mathrm{\sigma }}_{\mathrm{\mu }},\overrightarrow{\mathit{r}})$$ (2)

where κ > 0 is the strength of the competitive interaction with width σ_κ, and μ > 0 is the strength of facilitation with width σ_μ, where the widths of the Gaussians correspond to the spatial extension of the interactions. Note that we should have μ ≤ ω_d0 to guarantee positive mortality. For simplicity, in the following, we take μ = ω_d0. As a result of the two Gaussians with different widths and signs, the kernel has the shape of an inverted Mexican hat, and the interaction is stronger at short distances, decaying very fast with $|\vec{\mathit{r}}|$.

Competition or facilitation may dominate at shorter or longer distances depending on the values of σ_κ and σ_μ. On general grounds, the main effect of facilitation is to permit the coexistence of the populated and unpopulated homogeneous states, whereas nonlocal competition is one of the mechanisms responsible for the spontaneous formation of regular patterns, either on itself (43) or acting together with the facilitative interaction (4). Thus, observation of spatial patterns suggests the existence of nonlocal competitive interactions. Selecting σ_κ > σ_μ results in a kernel that is weakly competitive at large distances, yielding to a suitable nonlocal interaction for pattern formation (see the Supplementary Materials) (4). The main nonlocal interaction terms (κ, σ_κ, μ, and σ_μ) can be inferred from the comparison of numerical simulations and observed patterns, whereas seagrass growth parameters are largely known [see the study by Sintes et al. (33) and references therein].

The ABD model yields a great diversity of complex spatial patterns emerging at different parameter regions, including nonlinear phenomena resulting in the coexistence of different solutions, which are shown in Fig. 2 for the case of constant ω_d0 and b. When mortality is high (ω_d0/ω_b > > 1), the only possible solution is bare soil, the unpopulated solution. Decreasing the mortality (or increasing branching rate), the unpopulated solutions become unstable at a threshold ω_d0/ω_b = 1. Below this mortality, any small nonzero density will grow to form a meadow. If mortality is much smaller than the branching rate, ω_d0/ω_b < < 1, the vegetation will uniformly cover all the available space. Thus, there are two extreme homogeneous stable states: a uniform, continuous meadow (ω_d0/ω_b < < 1) and bare seafloor, with no vegetation (ω_d0/ω_b > > 1), as it is shown in Fig. 2 (red solid lines). The parameter values that better reproduce the observed patterns of P. oceanica meadows correspond to a kernel $\mathcal{K}$ that, although competition extends farther, is overall facilitative. As a result, the transition (T) from bare soil to the populated solution is subcritical, so that there is a mortality range in which both populated and unpopulated solutions coexist (Fig. 2). Competition between shoots can destabilize the populated solution, leading to patterns, whereas the homogeneous states are the only possible solutions in the absence of nonlocal interactions. Therefore, the presence of fairy circle landscapes in seagrass meadows is indirect evidence of nonlocal negative interactions.

Fig. 2. Mean shoot density ${\overline{\mathit{n}}}_{\mathbf{t}}$ (that is, total number of shoots divided by the whole simulation area) as a function of normalized mortality ω_d0/ω_b for five different solutions of the ABD model for homogeneous ω_d0 and homogeneous b.

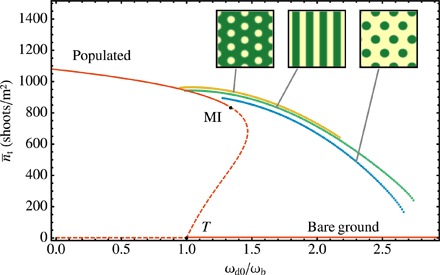
Homogeneous populated and unpopulated states are shown in red, hexagonal arrangement of fairy circles in yellow, stripes in green, and hexagonal arrangement of spots in blue. Solid (dashed) lines indicate stable (unstable) solutions. The insets show the vegetation patterns in the inhomogeneous cases. Only the stable part of the pattern branches is shown, as obtained from direct numerical simulations of the model. MI corresponds to the modulational instability of the populated state, and T corresponds to the transcritical bifurcation of the bare soil. We take parameter values in a range that reproduce patterns seen in side scans using typical values for P. oceanica for the parameters already known [see the study by Sintes et al. (33) and references therein]: ω_b = 0.06 year⁻¹, ν = 6.11 cm year⁻¹, ρ = 2.87 cm, φ_b = 45°, b = 1.25 cm⁴ year⁻¹, κ = 0.048 year⁻¹, σ_κ = 2851.4 cm, a = 27.38 cm², σ_μ = 203.7 cm, μ = ω_d0 (see the Supplementary Materials). The formation of the three patterned solutions (negative hexagons, stripes, and positive hexagons) is shown in movies S1, S2, and S3, respectively.

A linear stability analysis of the homogeneous populated solution reveals that it undergoes a finite wavelength instability, also known as Turing (4) or modulation instability (MI), at a critical value of mortality rate ${\mathrm{\omega }}_{\mathrm{d}0}={\mathrm{\omega }}_{\mathrm{d}0}^{\mathrm{c}}$ (in Fig. 2, ${\mathrm{\omega }}_{\mathrm{d}0}^{\mathrm{c}}/{\mathrm{\omega }}_{\mathrm{b}}=1.34$), leading to the emergence of complex spatial patterns. Above this mortality, any small perturbation to the homogeneous meadow is enough to trigger a feedback process driving the vegetation to form an inhomogeneous pattern. Different spatial structures are possible. As mortality rate increases, possible patterns shift from negative hexagons (holes arranged in a hexagonal pattern), to stripes, and to positive hexagons (spots of vegetation arranged in a hexagonal pattern), as expected from the general theory of pattern formation (44, 45). Each solution is stable in a different region of parameter space, and two different solutions can be simultaneously stable for the same value of the mortality, a coexistence between solutions that would give rise to hysteresis. In particular, negative hexagons coexist with the homogeneous populated solution in a mortality range below ${\mathrm{\omega }}_{\mathrm{d}0}^{\mathrm{c}}$. In part of this region, a single bare hole embedded in a dense meadow (Fig. 3), known as dissipative soliton (46), which is the submarine analog of a terrestrial fairy circle, can be stable (47, 48). Many of the bare circles visible in the coasts of Mallorca and the Adriatic Sea (Fig. 1) can be identified with dissipative solitons.

Fig. 3. Spatial distribution of the shoot density (high densities are represented in dark green and low ones in bright yellow) in a simulation of a P. oceanica meadow showing a stable fairy circle.

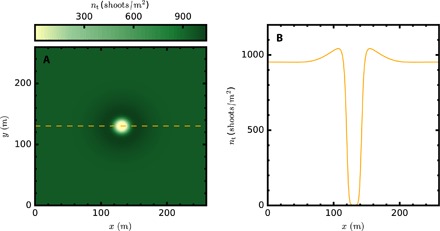
The fairy circle, or dissipative soliton, is clear in the density profile (B) along the transverse cut shown in (A) by a dashed line. Here, ω_d0 = 0.057 year⁻¹. Other parameters are the same as in Fig. 2.

Thus, our model is able to reproduce and to facilitate understanding of the nonlinear behavior, leading to the emergence of dynamic complex landscape patterns in seagrass meadows. The spatial scale of real patterns is mainly related to the range of the competing interaction σ_κ. An estimation of the length scale of the observed patterns can be obtained using the Fourier spectrum (see the Supplementary Materials) of images such as Fig. 1A. It is not always possible to obtain a precise estimate of this length scale, because often, patterns are not regular enough, although local hexagonal ordering can be appreciated in the more regular regions. In these regions, one can identify in the Fourier spectrum a typical periodicity of 62.9 ± 12.7 m (see the Supplementary Materials). Choosing σ_κ = 28.5 m, the critical wavelength at the MI threshold (see the Supplementary Materials) fits this observed characteristic length, and simultaneously, a typical hole size of about 30 m is also correctly reproduced. This result allows us to conjecture the existence of a competitive interaction with a range of around 20 to 30 m, whose specific nature is not yet known. In addition to their local contribution, the competition for natural resources (for example, dissolved inorganic nutrients or CO₂) and the interactions mediated by toxic compounds, such as sulfide, which is accumulated in the soil (20), are expected to contribute to nonlocal competitive interactions. Other hypotheses include interaction through hydrodynamics, which may modify the sedimentary delivery of nutrients.

The time scales for the landscape dynamics captured by the model are long, encompassing decades to millennia (movies S1 to S5 and the Supplementary Materials), depending on the characteristic demographic time scales of the species. For instance, P. oceanica clones are long-lived organisms, with clones living tens of thousands of years (49) and forming meadows over centuries to millennia (50, 51), whereas C. nodosa grows much faster and can form meadows over decades to centuries (50). Hence, the dynamics conducive to formation of complex landscape patterns and the transition between them are too slow to be observed empirically and can be grasped only through a modeling approach, such as the one developed here (movies S1 to S6), with parameter values properly constrained by present-day observations.

In addition to providing qualitative understanding of how demographic imbalances affect the spatial configuration of seagrass meadows, the model proposed provides a remarkable, given its parsimony, description of observed patterns in seagrass meadows (Fig. 4). Two additional model components are needed to reproduce observed density patterns: a decline in mortality rate, ω_d0, with the distance from the coast, x, and a spatial random noise term that mimics irregular spatial variability of the parameters. Simulations in small systems and under ideal conditions (that is, in the absence of noise) may yield perfectly periodic patterns (insets in Fig. 2), whereas simulations in large domains, including noise, better resemble observed patterns (Figs. 4 and 5, movies S4 to S6, and the Supplementary Materials).

Fig. 4. Comparison of numerical simulations with patterns observed in seagrass meadows.

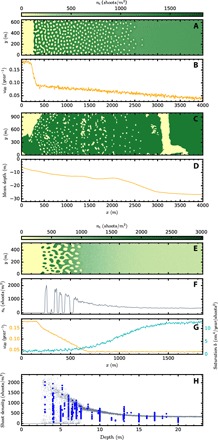
(A) Final spatial density distribution of shoots from a numerical simulation of the ABD model that uses the mortality profile plotted in (B). (C) Observed coverage (31) of P. oceanica from LIFE Posidonia side-scan cartography in the Balearic coast area limited by the following coordinates: 39°45′54.1″N, 3°09′49.5″E; 39°47′25.6″N, 3°11′48.7″E; 39°47′48.6″N, 3°11′19.0″E; and 39°46′17.1″N, 3°09′19.9″E. (D) Depth in that region averaged along the y direction. (E to H) Comparison of a numerical simulation with field density measures: (E) Spatial density distribution of P. oceanica as obtained from numerical simulations with a custom spatially dependent mortality [orange line in (G), left scale] and a profile of the saturation strength b(x, y) [blue line in (G), right scale]. (F) Cut of (E) at y = 102. (H) Observed P. oceanica density measured by scuba divers (in blue, data file S1) as function of the depth for different locations spread over the coastline of the Balearic Islands and the density in random locations of the numerical simulation shown in (E) (gray). Parameters are same as in Fig. 2. The time evolutions of the simulations are shown in movies S4 and S5.

Fig. 5. Comparison of numerical simulation with patterns observed by side-scan sonar (31) for a region of coexistence between holes and patches in a meadow of C. nodosa in Mallorca Island (Fig. 1).

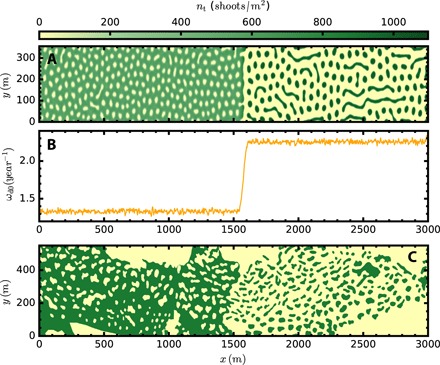
The set of model parameters for C. nodosa is ω_b = 2.3 year⁻¹, ν = 160 cm year⁻¹, ρ = 3.7 cm, φ_b = 45°, b = 112.71 cm⁴ year⁻¹, κ = 2.76 year⁻¹, σ_κ = 2226.1 cm, a = 21.0 cm², σ_μ = 139.1 cm, and μ = ω_d0, and the area modeled (a subset of that shown in Fig. 1A) is bounded by the coordinates 39°53′16.4″N, 3°05′12.7″E; 39°51′52.0″N, 3°06′15.7″E; 39°51′43.1″N, 3°05′55.6″E; and 39°53′07.5″N, 3°04′52.6″E (movie S6). (A) Final spatial density distribution of shoots from a numerical simulation of the ABD model using the mortality profile shown in (B). (C) Observed coverage (31) of C. Nodosa from LIFE Posidonia side-scan cartography in the Balearic coast.

The increase in area coverage from the shore toward moderate depths is characteristic of P. oceanica meadows (Fig. 4C) [as is also the its decrease and disappearance toward deep waters; (36)]. This indicates high mortality rates in shallow, nearshore waters, which could be attributed to scouring by waves, leading to the unpopulated model solution in waters shallower than the upslope limit of the seagrass, and low mortality rates in moderately deeper waters, allowing the formation of stable homogeneous meadows. A smooth decline in mortality with depth should then lead to complex spatial patterns at intermediate depths, where the homogeneous solution is unstable (see Fig. 2). Including such decline in mortality (Fig. 4B) with added noise (see the Supplementary Materials), the resulting patterns (Fig. 4A) accurately reproduce observed features in P. oceanica meadows (Fig. 4C), such as more elongated vegetation gaps near the shore and scattered gaps close to the homogeneous meadow. The transition from bare soil to patterns with elongated gaps signals that this region experiences a steep mortality decrease from very high to moderate values where hexagons begin to be unstable with respect to stripes. Scattered gaps are well reproduced close to the homogeneous meadow, in a mortality range where hexagonal gap patterns coexist with the homogeneous populated state (see Fig. 2) and dissipative solitons (fairy circles) can form. Further downslope, the homogeneous meadow prevails.

The model also reproduces the decline of shoot density and its variability with depth observed in meadows along the littoral of the Balearic Islands (Fig. 4H). Shoot density was measured by scuba divers at random positions in the meadows without previous knowledge of their spatial distribution. The results consistently showed low shoot density variability at depths >10 m compared to high variability at shallower depths (<10 m), ranging from close to 0 to 2000 shoots/m², a variability much larger than that in deeper regions (thick blue dots Fig. 4H). Our model suggests that high shoot density variability in shallow waters is a consequence of the presence of complex spatial patterns near the coast. Simulations using noisy and depth-dependent mortality and carrying capacity, b(x, y) (see Fig. 4G), account for the decrease in shoot density with depth and generate patterns of shoot density that capture the dispersion of the density close to the coast where patterns form (Fig. 4, E to H, and movie S5). The model also reproduces complex patterns in meadows of C. nodosa, such as the transition from holes to patches observed in one of the meadows (Figs. 1 and 5C). Because this transition occurs parallel to the coast, that is, at a uniform depth, we inferred this pattern to be derived from a sudden increase in the mortality rate along the shore (see Fig. 5B). The resulting simulated pattern (Fig. 5A) reproduces very well the observed features of the real meadow, further confirming that the complex seascape of fairy circle patterns observed in Mediterranean seagrass meadows can be reproduced parsimoniously as a consequence of variability in the seagrass demographic balance caused by spatial interaction and nonlinearity.

DISCUSSION

We have demonstrated that complex landscape patterns, such as those dotted by fairy circles characteristic of arid grasslands, are also common features of seagrass seascapes in the Mediterranean and have also been reported in seagrass meadows elsewhere (20–22, 27). The parsimonious model developed here demonstrates that fairy circle seascapes emerge as consequences of nonlinearity and spatial interactions in seagrass meadows at critical levels of demographic imbalances, typically met in relatively shallow nearshore areas of seagrass meadows. In contrast, comparatively low mortality rates in deeper areas lead to a prevalence of stable continuous meadows toward the deeper ranges of seagrass meadows. The model developed here, based on simple inherent growth traits of the seagrass species and variable mortality due to nonlocal interaction and nonlinearity, is able to reproduce the range of complex landscape configurations, including striped, hexagon, and soliton-dominated landscapes encountered between the bare sediments and continuous meadow end members for these landscapes. The model results are robust enough as to allow inferences on the demographic status of the meadows on the basis of observed landscape configurations. In particular, positive hexagons signal the proximity of tipping points where further increase in seagrass mortality relative to growth may lead to catastrophic loss of seagrass meadows (1, 52). Because seagrass ecosystems rank among the most threatened ecosystems globally (28), the capacity to diagnose the proximity of seagrass meadows to tipping points for catastrophic loss based on landscape configurations provides a tool to guide conservation measures aimed at preventing further losses.

MATERIALS AND METHODS

Derivation of the ABD model

Focusing on the three main mechanisms involved in the growth of clonal plants, namely, apices’ linear growth, branching, and death, we developed a set of partial differential equations (PDEs; or, more precisely, integro-differential equations) for the density of shoots and apices. These mechanisms were identified and implemented in a previous model, which focused on individual shoots (32, 33). Here, we formulated these mechanisms in terms of upscaled continuous densities, thus allowing for the description of much larger spatial and temporal scales. The spatial density of shoots at position $\vec{\mathit{r}}=(\mathit{x},\mathit{y})$ of the sea bottom at time t is ${\mathit{n}}_{\mathrm{s}}(\vec{\mathit{r}},\mathit{t})$, and the density of apices growing in the direction given by the angle φ is ${\mathit{n}}_{\mathrm{a}}(\vec{\mathit{r}},\mathrm{\phi },\mathit{t})$. Note that the magnitude of the apices’ growth velocity v is assumed constant, and a growth velocity vector can be written as $\vec{\mathit{v}}(\mathrm{\phi })=(\mathrm{\nu } \text{cos} \mathrm{\phi },\mathrm{\nu } \text{sin} \mathrm{\phi })$. The total density of shoots, n_t, considering for simplicity that an apex is carrying a shoot, is the sum of shoots n_s and apices n_a growing in all directions, ${\mathit{n}}_{\mathrm{t}}(\overrightarrow{\mathit{r}},\mathit{t})={\mathit{n}}_{\mathrm{s}}(\overrightarrow{\mathit{r}},\mathit{t})+{\displaystyle {\int }_0^{2\mathrm{\pi }}}{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})\mathit{d}\mathrm{\phi }$.

Two PDEs describing the evolution of the densities of shoots and apices can be derived in terms of the contributions of the three growth mechanisms to the number of shoots in an infinitesimal surface. First, the number of apices growing in direction φ at t + dt in an infinitesimal surface of area dxdy located at $\vec{\mathit{r}}$ will be the sum of two contributions: (i) the apices that remain alive coming from $\vec{\mathit{r}}-\vec{\mathit{v}}(\mathrm{\phi })\mathit{d}\mathit{t}$ because of rhizome elongation and (ii) new apices that appear because of branching from directions of growth φ + φ_b and φ − φ_b, which are the only directions contributing to the growth in direction φ. φ_b is the branching angle. Note that those apices that go away due to rhizome elongation are contributing to position $\vec{\mathit{r}}+\vec{\mathit{v}}(\mathrm{\phi })\mathit{d}\mathit{t}$. Then, we obtain

$${\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t}+\mathit{d}\mathit{t})\mathit{d}\mathit{x}\mathit{d}\mathit{y}=(1-{\mathrm{\omega }}_{\mathrm{d}}\mathit{d}\mathit{t}){\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}}-\overrightarrow{\mathit{v}}\mathit{d}\mathit{t},\mathrm{\phi },\mathit{t})\mathit{d}\mathit{x}\mathit{d}\mathit{y}+\frac{{\mathrm{\omega }}_{\mathrm{b}}\mathit{d}\mathit{t}}{2}({\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi }+{\mathrm{\phi }}_{\mathrm{b}},\mathit{t})+{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi }-{\mathrm{\phi }}_{\mathrm{b}},\mathit{t}))\mathit{d}\mathit{x}\mathit{d}\mathit{y}$$ (3)

where ω_b and ω_d are branching and death rates, respectively. Making a Taylor expansion of Eq. 3 and neglecting second-order terms and higher, we obtain

$${\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})+{\partial }_{\mathit{t}}{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})\mathit{d}\mathit{t}=(1-{\mathrm{\omega }}_{\mathrm{d}}\mathit{d}\mathit{t}){\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})-\overrightarrow{\mathit{v}}\mathit{d}\mathit{t}\cdot \overrightarrow{\nabla }{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})+\frac{{\mathrm{\omega }}_{\mathrm{b}}\mathit{d}\mathit{t}}{2}({\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi }+{\mathrm{\phi }}_{\mathit{b}},\mathit{t})+{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi }-{\mathrm{\phi }}_{\mathrm{b}},\mathit{t}))$$ (4)

Rewriting Eq. 4, we obtain the PDE that describes the growth of apices in the direction φ

$${\partial }_{\mathrm{t}}{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})=-{\mathrm{\omega }}_{\mathrm{d}}{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})-\overrightarrow{\mathit{v}}(\mathrm{\phi })\cdot \overrightarrow{\nabla }{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})+\frac{{\mathrm{\omega }}_{\mathrm{b}}}{2}({\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi }+{\mathrm{\phi }}_{\mathrm{b}},\mathit{t})+{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi }-{\mathrm{\phi }}_{\mathrm{b}},\mathit{t}))$$ (5)

where $\vec{\nabla }=({\partial }_{\mathrm{x}},{\partial }_{\mathrm{y}})$.

The same procedure can be used to obtain the equation for the shoot density. The first contribution is the shoots that remain alive at the same position, and the second contribution is due to the apices that survive and go away in any direction leaving a shoot behind

$${\mathit{n}}_{\mathrm{s}}(\overrightarrow{\mathit{r}},\mathit{t}+\mathit{d}\mathit{t})\mathit{d}\mathit{x}\mathit{d}\mathit{y}=(1-{\mathrm{\omega }}_{\mathrm{d}}\mathit{d}\mathit{t}){\mathit{n}}_{\mathrm{s}}(\overrightarrow{\mathit{r}},\mathit{t})\mathit{d}\mathit{x}\mathit{d}\mathit{y}+\frac{\mathrm{\nu }}{\mathrm{\rho }}\mathit{d}\mathit{t}(1-{\mathrm{\omega }}_{\mathrm{d}}\mathit{d}\mathit{t}){\displaystyle {\int }_0^{2\mathrm{\pi }}}{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})\mathit{d}\mathit{x}\mathit{d}\mathit{y}\mathit{d}\mathrm{\phi }$$ (6)

where ρ is the distance between shoots.

Using the Taylor expansion and keeping first-order terms only, we have

$${\mathit{n}}_{\mathrm{s}}(\overrightarrow{\mathit{r}},\mathit{t})+{\partial }_{\mathrm{t}}{\mathit{n}}_{\mathrm{s}}(\overrightarrow{\mathit{r}},\mathit{t})\mathit{d}\mathit{t}=(1-{\mathrm{\omega }}_{\mathrm{d}}\mathit{d}\mathit{t}){\mathit{n}}_{\mathrm{s}}(\overrightarrow{\mathit{r}},\mathit{t})+\frac{\mathrm{\nu }}{\mathrm{\rho }}\mathit{d}\mathit{t}{\displaystyle {\int }_0^{2\mathrm{\pi }}}{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})\mathit{d}\mathrm{\phi }$$ (7)

which leads to the PDE for the shoot population density

$${\partial }_{\mathrm{t}}{\mathit{n}}_{\mathrm{s}}(\overrightarrow{\mathit{r}},\mathit{t})=-{\mathrm{\omega }}_{\mathrm{d}}{\mathit{n}}_{\mathrm{s}}(\overrightarrow{\mathit{r}},\mathit{t})+\frac{\mathrm{\nu }}{\mathrm{\rho }}{\displaystyle {\int }_0^{2\mathrm{\pi }}}{\mathit{n}}_{\mathrm{a}}(\overrightarrow{\mathit{r}},\mathrm{\phi },\mathit{t})\mathit{d}\mathrm{\phi }$$ (8)

The time evolution of a meadow can then be described by two coupled PDEs, Eqs. 5 and 8, one for each population density. We name this set of two equations the ABD model.

The first term in Eqs. 5 and 8 corresponds to death of shoots and apices. The same death rate ω_d is considered. The second term in Eq. 5 is an advection in the direction of the elongation $\vec{\mathit{v}}(\mathrm{\phi })$ of the rhizome, describing the movement of the apices. The last term in Eq. 5 corresponds to the branching process. Finally, the second term in Eq. 8 accounts for the shoots left behind by the apices.

The death rate is given by

$${\mathrm{\omega }}_{\mathrm{d}}[{\mathit{n}}_{\mathrm{t}}(\overrightarrow{\mathit{r}},\mathit{t})]={\mathrm{\omega }}_{\mathrm{d}0}+\mathit{b}{\mathit{n}}_{\mathrm{t}}^2+{\displaystyle \int }{\displaystyle \int }\mathcal{K}(\overrightarrow{\mathit{r}}-{\overrightarrow{\mathit{r}}}^{\prime })(1-{\mathit{e}}^{-\mathit{a}{\mathit{n}}_{\mathrm{t}}({\overrightarrow{\mathit{r}}}^{\prime })})\mathit{d}{\overrightarrow{\mathit{r}}}^{\prime }$$ (9)

$$\mathcal{K}(\overrightarrow{\mathit{r}})=\mathrm{\kappa }\mathcal{G}({\mathrm{\sigma }}_{\mathrm{\kappa }},\overrightarrow{\mathit{r}})-\mathrm{\mu }\mathcal{G}({\mathrm{\sigma }}_{\mathrm{\mu }},\overrightarrow{\mathit{r}})$$ (10)

where μ = ω_d0 for simplicity and ω_d0 > 0. Both interaction terms in Eq. 10 are considered to have a Gaussian shape $\mathcal{G}(\mathrm{\sigma },\overrightarrow{\mathit{r}})={\mathit{e}}^{-{\mathit{r}}^2/(2{\mathrm{\sigma }}^2)}/({\mathrm{\sigma }}^{2}2\mathrm{\pi })$, where r² = x² + y². Other kernels have been considered in the literature in different contexts (53), although qualitatively, the pattern formation feature does not depend strongly on the precise shape of the kernel (54, 55), provided it decays faster or equal than exponential (56). Figure S5 shows the form of the kernel used in this work.

Thus, the interaction is stronger for short distances and decreases exponentially fast with r². Because $\mathcal{G}$ is normalized to 1, if κ > ω_d0 (κ < ω_d0), then the interaction is overall competitive (facilitative). Depending on the values of σ_κ and σ_μ, competition or facilitation may dominate at short or long distances. The term $(1-{\mathit{e}}^{-\mathit{a}{\mathit{n}}_{\mathrm{t}}})$ can be expanded for low densities as $(1-{\mathit{e}}^{-\mathit{a}{\mathit{n}}_{\mathrm{t}}})\simeq \mathit{a}{\mathit{n}}_{\mathrm{t}}$, leading to the usual nonlocal term in Lotka-Volterra–like models (57). The exponential has been introduced to saturate the interaction strength for high densities, such that the mortality rate ω_d cannot become negative because of the facilitative interaction leading to the local creation of plants, which is unreal because a new shoot can be created only through the growth of the rhizomes or a branching event. For low densities, then, parameter a multiplies the strength of the nonlocal interaction. However, the larger the parameter a, the faster the saturation of the interaction as the density grows. Varying a and κ, one can change the relative strength between competition and facilitation. Here, we chose a kernel that is facilitative at short ranges and competitive at larger scales (fig. S5).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/8/e1603262/DC1

Materials and Methods

fig. S1. Mean shoot density ${\overline{\mathit{n}}}_{\mathrm{t}}$ (that is, total number of shoots divided by the whole simulation area) as a function of normalized mortality ω_d0/ω_b for the supercritical case.

fig. S2. Growth rate of perturbation with wave number (q_x, q_y = 0) close to the MI.

fig. S3. Phase diagram of the ABD model for P. oceanica.

fig. S4. Wavelength of the maximum growth rate as function of the competition range σ_κ for five different values of the intrinsic mortality ω_d0.

fig. S5. Shape of the kernel $\mathcal{K}$$(\vec{\mathit{r}})$ in real space (left) and Fourier space (right).

fig. S6. Comparison of numerical simulations with patterns in real meadows in the absence of noise in the profile corresponding to the same conditions as those in Fig. 4 (A to D).

fig. S7. Example of noise distribution used in the numerical simulations.

fig. S8. Fourier transform of a side-scan cartography image of a rectangular region of a meadow of P. oceanica.

fig. S9. Side-scan cartography of Pollença and Alcúdia bays (Mallorca Island, Western Mediterranean).

fig. S10. Side-scan cartography of Llevant coast (Mallorca Island, Western Mediterranean).

fig. S11. Side-scan cartograhpy of Cap Enderrocat (Mallorca Island, Western Mediterranean).

table S1. Coordinates of analyzed regions.

table S2. Measured wavelength of the patterns.

movie S1. Formation of negative hexagons.

movie S2. Formation of stripes.

movie S3. Formation of positive hexagons.

movie S4. Temporal evolution of Fig. 4A.

movie S5. Temporal evolution of Fig. 4 (E, F, and H).

movie S6. Temporal evolution of Fig. 5A.

data file S1. P. oceanica density as function of the depth for different locations spread over the coastline of the Balearic Islands.

Reference (58)