Improving graph-based OCT segmentation for severe pathology in Retinitis Pigmentosa patients

Abstract

Three dimensional segmentation of macular optical coherence tomography (OCT) data of subjects with retinitis pigmentosa (RP) is a challenging problem due to the disappearance of the photoreceptor layers, which causes algorithms developed for segmentation of healthy data to perform poorly on RP patients. In this work, we present enhancements to a previously developed graph-based OCT segmentation pipeline to enable processing of RP data. The algorithm segments eight retinal layers in RP data by relaxing constraints on the thickness and smoothness of each layer learned from healthy data. Following from prior work, a random forest classifier is first trained on the RP data to estimate boundary probabilities, which are used by a graph search algorithm to find the optimal set of nine surfaces that fit the data. Due to the intensity disparity between normal layers of healthy controls and layers in various stages of degeneration in RP patients, an additional intensity normalization step is introduced. Leave-one-out validation on data acquired from nine subjects showed an average overall boundary error of 4.22 μm as compared to 6.02 μm using the original algorithm.

1. INTRODUCTION

Many algorithms have been developed to segment the retinal layers in optical coherence tomography (OCT) images;^1–5 however, most of these algorithms were specifically designed to find the layers in either healthy subjects or those with relatively benign pathological changes, such as glaucoma or multiple sclerosis.^6,7 Pathological data having large scale changes due to edema, retinal detachments, cystoid spaces, or atrophy, among other changes, often presents a challenge which cannot be handled by existing algorithms. To account for specific physiological changes that occur as a result of certain diseases, either existing algorithms need to be adapted or new algorithms need to be developed. Examples of diseases requiring adaptation of previously developed methods include age related macular degeneration,⁸ diabetic macular edema,⁹ and retinitis pigmentosa (RP).¹⁰ Unfortunately, these methods were developed to only find a few specific layers within the retina.

Retinitis pigmentosa (RP) is a hereditary degenerative disease which results in a loss of vision due to degeneration of the photoreceptor (PR) layers in the outer retina. Using OCT, the severity of RP can be quantified and tracked over time by measuring the thickness of the outer layers.¹¹ By looking at full two dimensional fundus maps of these thicknesses, we can explore the spatial changes that occur in specific areas of the retina. While the outer retina is the primary target for the disease, the inner retina has also been shown to undergo changes.¹² Thus, it is important to be able to accurately measure thicknesses for all of the layers in the retina to better understand the disease characteristics and progression. Example OCT images from three different RP subjects are shown in Fig. 1, where the variability in this data is clearly seen.

Figure 1.

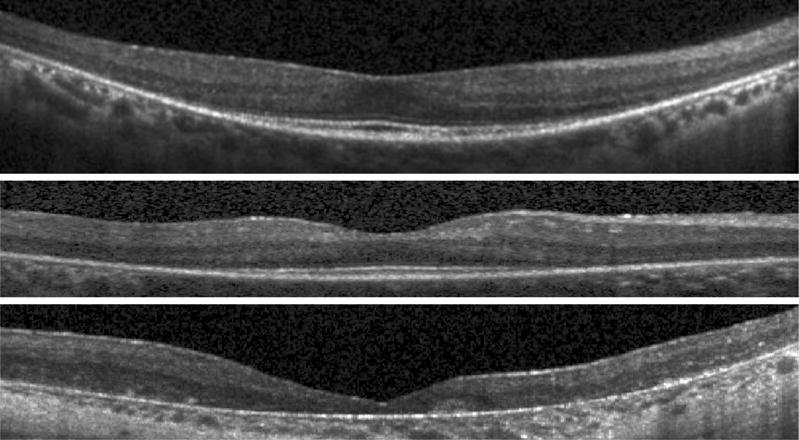
B-scan images from three RP subjects.

The difficulty in segmentation of RP data is the degeneration of the outer layers as these scans often have poor quality, making inner boundaries difficult to distinguish as well. Few methods have been previously developed for automated RP segmentation.^10,13 In Ref.¹⁰, a dynamic programming approach was used to estimate four boundaries in the retina, finding only two layers along with the total retina thickness. In Ref.¹³, a Gaussian mixture model was used to define both the position of and the number of visible layers (up to four) in the outer retina. The delineated boundaries were not continuous, however. Overall, the problem of finding all of the retinal layers remains open to be explored. In this work, we present an algorithm for segmentation of eight layers in macular RP data. The method follows the same framework as our previous work combining machine learning with a graph search algorithm to find the boundaries.⁷ By using a classifier to do a pixel-wise prediction trained from manually segmented data, we learn where the boundaries are likely to be. This information is then used by the graph search with additional constraints on layer thickness and smoothness to produce a final segmentation.

2. METHODS

To segment the RP data, we follow the same steps as the RF+GC method detailed in our prior work.⁷ In brief, these steps are: 1) estimation of the inner and outer retinal boundaries, 2) flattening to the outer boundary, 3) intensity normalization, 4) generation of boundary probabilities using a random forest classifier, and 5) refinement of the final boundary positions using an optimal graph search algorithm. With the exception of the second step, the remaining four steps required some adaptation to improve the segmentation performance on RP data, better capturing the increased variability. These changes are outlined below.

2.1 Retinal boundary estimation

The initial step of the algorithm is to estimate the inner and outer retinal boundaries, the inner limiting membrane (ILM) and Bruch’s membrane (BrM), respectively. As in the prior work,⁷ these boundaries are initially estimated using the smallest and largest vertical gradients in each B-scan image after Gaussian smoothing. Outlier points are detected and removed using a median filter, and the final surfaces are then produced after additional Gaussian smoothing of the boundary positions. For the RP data, the only change made was to use a larger kernel size (σ = 200 μm) in the final smoothing step. Note that due to the reduced contrast between the BrM and the choroid, the BrM surface is not as accurately estimated in the RP subjects at this stage. As a result, the subsequent flattening of the data will not be as smooth. However, the boundary classification step is largely insensitive to this inaccuracy, provided the result is not extremely poor.

2.2 Intensity normalization

Before running the data through the classifier, the intensities are normalized to provide a more consistent feature response. This step is particularly important for the RP data as the OCT scans from these patients have a varying appearance due to the loss of the PR layers. Previously,⁷ every B-scan image was normalized by rescaling the intensity range of each image by a fixed amount based on a robust estimate of the maximum intensity in each image. For the RP data, which often have varying intensities laterally in an image, the normalization step rescales the intensity range of every A-scan in the data. Specifically, this step has been changed to produce images where the top and bottom layers (the RNFL and RPE, respectively) have approximately uniform intensity distributions, with a value near 1. To do this, we generate a 3D gain field, B(x, y, z), that produces an intensity corrected volume as Î(x, y, z) = I(x, y, z)/B(x, y, z). The x, y, and z directions are in the lateral, through plane, and axial directions, respectively.

To create B(x, y, z), we first estimate the intensity of the RNFL and RPE layers for every A-scan as I_RNFL(x, y) and I_RPE(x, y). Each of these estimates are generated in two parts, with one part varying smoothly over the entire volume (in x and y) and one part varying smoothly within each B-scan (along x only). An initial, noisy estimate of the intensities in the respective layers is found using the maximum value within 80 μm of the inner and outer retinal boundaries. The volumetric component of the gain field is estimated by fitting a bivariate tensor cubic smoothing spline to this map of intensity values for each of the RNFL and RPE. A fixed value of 0.9 was used for the regularization weight of the spline, which removes higher frequency variations. Finally, a per-B-scan component is estimated using a robust linear regression fit to the intensity profile of the A-scans in each B-scan. A bisquare weighting function was used in the robust fitting. The resulting intensity estimate for each A-scan is found by multiplying the two components together.

The final 3D gain field, B(x, y, z), is computed from the linear fit along each A-scan between the two gain fields as

$$B\left(x,y,z\right)=m\left(x,y\right)\ast z+b\left(x,y\right)$$

where

$$m\left(x,y\right)=\frac{I_{\text{RNFL}}\left(x,y\right)-I_{\text{RPE}}\left(x,y\right)}{S_{\text{ILM}}\left(x,y\right)-S_{\text{BrM}}\left(x,y\right)}$$

is the slope term,

$$b\left(x,y\right)=I_{\text{RNFL}}\left(x,y\right)-m\left(x,y\right)\ast I_{\text{RPE}}\left(x,y\right),$$

is the intercept, and S_ILM and S_BrM are the estimated ILM and BrM boundary surfaces. An example of how this gain field correction works for an individual A-scan is shown in Fig. 2(a) with the red line showing how the gain field changes linearly between the two retinal surfaces. An example B-scan before and after normalization is shown in Figs. 2(b) and (c), respectively.

Figure 2.

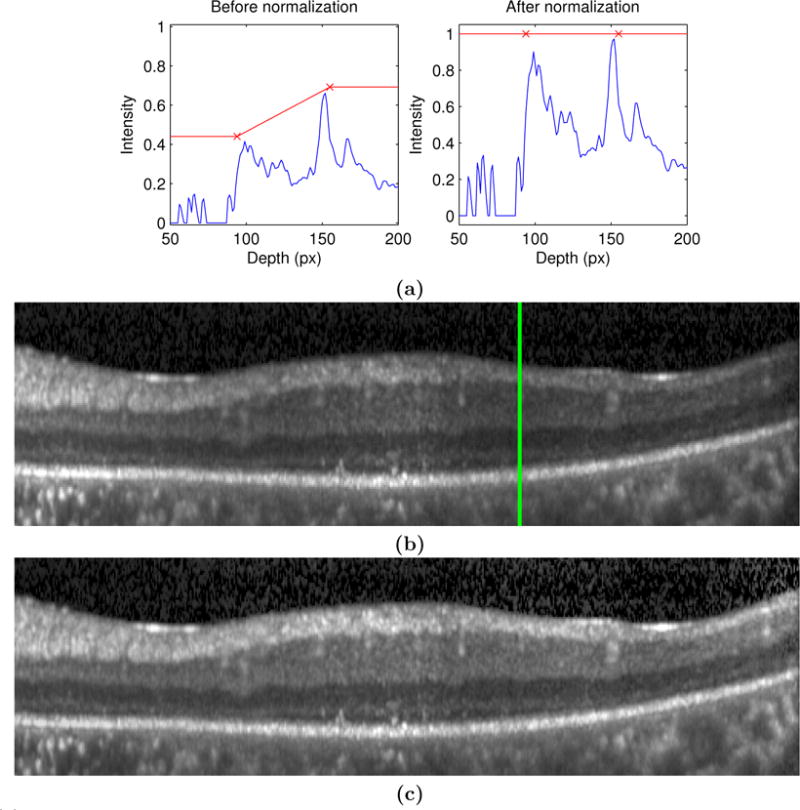
(a) On the left and right are A-scan profiles before and after normalization, respectively. The red ×’s show the estimated intensity values for the ILM and BrM. B-scan images before and after normalization are shown in (b) and (c) (respectively), where the green line represents the A-scan shown in (a).

2.3 Boundary learning

As an initial step in segmenting the retinal boundaries, a random forest classifier (RFC)¹⁴ is used to produce probabilities for each boundary at every voxel. In our previous work, a total of 27 features were used by the RFC to learn the boundary appearance in healthy data.⁷ To better capture the wider variability in shape and intensity of the RP data, we have augmented the previous feature set to produce a total of 44 features. Many of these features are unchanged, including the spatial features consisting of the distance to the fovea in the x and y directions, as well as the relative vertical distance within the retina. The remaining features are intensity-based; contextual features provide the average intensity and gradient within a 20 μm area from 90 to 90 μm away from each pixel in the vertical direction, in increments of 20 μm. Instead of using oriented Gaussian – first and second derivative features, as used previously, we included isotropic Gaussian first and second derivative kernels at 6 scales: σ = 1, 2, 5, 10, 15, and 20 μm. Also, as used previously, the final nine features are simply the intensity values in a 3 × 3 neighborhood around each pixel. The removal of the oriented filtering, as well as the use of more filter scales, appear to have the largest impact on improving the performance on RP data. By filtering at only three orientations before, we were restricting the shape of the boundaries, which have a much higher variability in RP due to the layer atrophy.

The RFC was trained on manual segmentation data from eight subjects. Nine boundaries were delineated on seven B-scan images for each subject, with three of the B-scans selected near the fovea. All boundary points were used for training with half of the background pixels used, reducing the class imbalance and the computation time. Background pixels were sampled proportionally to the number of points within each layer.

2.4 Optimal graph segmentation

The final segmentation is produced using a graph search algorithm^1,15 designed to simultaneously find the surfaces which maximize the total boundary probability given by the output of the RFC. Spatially varying constraints are incorporated into the graph through infinity weighted edges which cannot be cut. Two different types of constraints are used. First, the thickness of each layer is constrained to lie within a fixed range. Second, the amount that each surface can change in the lateral and through plane directions is also constrained to lie within a fixed range. For this work, these constraints are learned from a cohort of healthy subjects. Specifically, the minimum and maximum values for a given constraint were set to lie within 2.6 standard deviations of the mean value. The resulting values were subsequently smoothed spatially using a 100 μm Gaussian kernel.

Since the constraints were learned on healthy data, and to account for differences in the retina due to RP, we modified the constraints in the following ways. The smoothness constraints are increased by 3 times for the first five boundaries and by 1.5 times more for the last four. This change handles the increased variability added by the degeneration of the PR layers. Next, the maximum thickness of the first three layers is allowed to be 50% larger to account for increased thickness values sometimes found in these layers. Finally, the minimum thicknesses of the outer five layers were reduced by 75% of the learned values. Due to the discrete nature of the graph, this minimum often took a value of zero due to rounding.

The final change to the graph construction is that the first four layers are constrained to have zero thickness at the fovea. This constraint locks in the position of layers at the fovea where the RF sometimes produces a weaker response due to the disappearance of these layers. This constraint was included by changing the minimum and maximum thickness to zero within a 75 μm radius around the fovea. The location of the fovea was estimated using the total retina thickness by template matching to maximize the cross correlation with a template of the fovea generated from a healthy population.

3. EXPERIMENTS AND RESULTS

Macular OCT scans from nine subjects with RP were acquired using a Heidelberg Spectralis scanner (Heidelberg Engineering, Heidelberg, Germany). Scans were acquired in a 6 × 6 mm area with 512 A-scans and a variable number of B-scans ranging from 19 to 49. Therefore, the data was highly anisotropic with large inter-B-scan distances. The axial resolution was smaller at 3.9 μm with a depth of 2 mm. Manual segmentations were carried out on each of the scans. In some areas, the boundaries between layers could not be delineated due to poor scan quality. In these cases, the boundaries were traced based on the typical location found in other scans. In places where the PR layers showed significant degradation, the boundaries were placed arbitrarily close together, but not necessarily to have zero thickness.

A leave one out cross validation scheme was used to evaluate the segmentation results. The RFC was trained on eight scans with the evaluation done on the ninth scan. The average boundary errors across all subjects are presented in Table 1, with average layer thickness errors in Table 2. Figure 3 shows example results on three subjects. The boundaries with the two largest errors were the RNFL-GCL and OPL-ONL interfaces. In some of the scans, the RNFL and GCL are difficult to distinguish, partially due to scan quality and partially due to the lack of context provided by the missing layers. Figure 3(c) shows an example of this type of error. The errors at the OPL-ONL boundary were due to similar problems, in addition to the disparity of visual appearance due to Henle’s fiber layer (e.g., Fig. 3(b)).

Table 1.

Mean (std. dev.) of the boundary errors over all subjects.

Boundary	Signed Error	Absolute Error
ILM	0.12(±1.69)	2.52(±0.69)
RNFL-GCL	1.82(±1.76)	6.25(±3.39)
IPL-INL	−2.70(±2.88)	4.83(±2.27)
INL-OPL	−1.65(±2.90)	5.47(±2.27)
OPL-ONL	−3.77(±3.19)	6.43(±2.86)
ELM	−1.19(±2.76)	4.39(±1.58)
IS-OS	−0.65(±1.78)	3.23(±1.33)
OS-RPE	0.02(±1.14)	2.68(±0.67)
BrM	−0.13(±0.79)	2.20(±0.58)
Mean	−0.90(±2.65)	4.22(±2.44)

Table 2.

Mean (std. dev.) of the layer thickness errors over all subjects.

Layer name	Signed Error	Absolute Error
RNFL	1.70(±1.66)	6.59(±2.80)
GCL+IPL	−4.52(±3.84)	8.10(±3.66)
INL	1.05(±2.66)	6.04(±1.81)
OPL	−2.12(±1.97)	4.63(±1.17)
ONL	2.58(±4.51)	6.59(±2.37)
IS	0.54(±1.35)	2.78(±0.49)
OS	0.67(±1.94)	2.98(±1.09)
RPE	−0.15(±1.72)	3.39(±0.67)
Mean	−0.03(±3.33)	5.14(±2.69)

Figure 3.

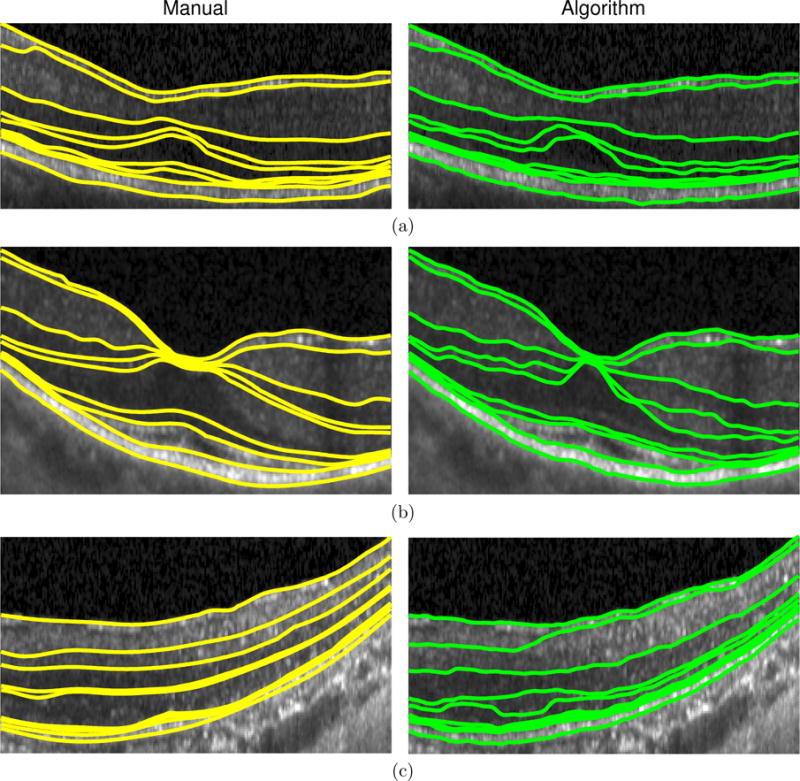
A comparison of the manual delineation (left) and algorithm (right) result for three RP patients.

To show the importance of the intensity normalization and the spatial constraints in the graph, we ran the algorithm without those elements. The average absolute thickness errors over all layers was 5.80 μm without the intensity normalization, 5.82 μm without the spatial constraints, and 7.14 μm without either of these steps, which are all much worse than the errors with the improvements (5.14 μm). Note that layer ordering was still enforced for the graph without constraints. The setup missing both steps was most similar to our previous work,⁷ which was shown to perform well on healthy data. Most of the improvement when the constraints were included was in the first four layers where the average errors decreased by more than 1 μm per layer.

One subject with particularly poor image quality, where the layers were more difficult to manually delineate, showed larger errors than the rest of the subjects (boundary error = 7.56 μm). An example delineated image from this subject is shown in Fig. 3(c). Upon removing this subject from the analysis, the mean absolute boundary and layer errors decrease to 3.84 μm and 4.72 μm, respectively.

4. CONCLUSIONS

In this work, we modified a previously developed segmentation algorithm for use with RP data, a disease where the outer retinal layers degenerate, especially in the peripheral regions. A graph search algorithm was used to segment the data using constraints modified to accommodate the increased or decreased retinal thicknesses and intensities found in RP patients. The performance of the algorithm was generally good for all of the layers with the average absolute boundary error of 4.22 μm comparing favorably with the average error of 3.38 μm reported on healthy data in our previous work.⁷ In fact, many of the changes to the algorithm including modification of the RFC features, intensity normalization, and the zero thickness constraint at the fovea are expected to be beneficial if applied on the healthy data as well. Future work includes learning RP specific constraints to specifically model the changes of the disease, as well as exploration of the spatial changes in each layer to better understand the disease and how it progresses.