Removing inter-subject technical variability in magnetic resonance imaging studies

Abstract

Magnetic resonance imaging (MRI) intensities are acquired in arbitrary units, making scans non-comparable across sites and between subjects. Intensity normalization is a first step for the improvement of comparability of the images across subjects. However, we show that unwanted inter-scan variability associated with imaging site, scanner effect and other technical artifacts is still present after standard intensity normalization in large multi-site neuroimaging studies. We propose RAVEL (Removal of Artificial Voxel Effect by Linear regression), a tool to remove residual technical variability after intensity normalization. As proposed by SVA and RUV [Leek and Storey, 2007, 2008, Gagnon-Bartsch and Speed, 2012], two batch effect correction tools largely used in genomics, we decompose the voxel intensities of images registered to a template into a biological component and an unwanted variation component. The unwanted variation component is estimated from a control region obtained from the cerebrospinal fluid (CSF), where intensities are known to be unassociated with disease status and other clinical covariates. We perform a singular value decomposition (SVD) of the control voxels to estimate factors of unwanted variation. We then estimate the unwanted factors using linear regression for every voxel of the brain and take the residuals as the RAVEL-corrected intensities. We assess the performance of RAVEL using T1-weighted (T1-w) images from more than 900 subjects with Alzheimer’s disease (AD) and mild cognitive impairment (MCI), as well as healthy controls from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database. We compare RAVEL to two intensity-normalization-only methods: histogram matching and White Stripe. We show that RAVEL performs best at improving the replicability of the brain regions that are empirically found to be most associated with AD, and that these regions are significantly more present in structures impacted by AD (hippocampus, amygdala, parahippocampal gyrus, enthorinal area and fornix stria terminals). In addition, we show that the RAVEL-corrected intensities have the best performance in distinguishing between MCI subjects and healthy subjects using the mean hippocampal intensity (AUC=67%), a marked improvement compared to results from intensity normalization alone (AUC=63% and 59% for histogram matching and White Stripe, respectively). RAVEL is promising for many other imaging modalities.

1 Introduction

In recent years, there has been an increase in the number of multi-site neuroimaging studies, including the Human Connectome Project (HCP), the Alzheimer’s Disease Neuroimaging Initiative (ADNI) and the Australian Imaging, Biomarkers and Lifestyle Flagship Study of Aging (AIBL). In structural magnetic resonance imaging (MRI) studies, larger samples of subjects yield more power to detect structural variations in different subgroups, for example changes in the hippocampal volume associated with Alzheimer’s disease (AD) and mild cognitive impairment (MCI). However, because MRI intensities are acquired in arbitrary units, it has often been found that the differences in MRI intensities between scanning parameters and studies are larger than the biological differences observed in these images. For instance, Shinohara et al. [2014] shows that in the ADNI and AIBL studies, which have highly standardized protocols, striking differences in the raw intensities are observed between imaging sites.

Since the raw image intensities are non-comparable across sites and between subjects, intensity normalization is paramount before performing between-subject intensity comparisons at the voxel level. While intensity normalization is not as important in other applications such as morphometry and brain volumetrics [Ashburner and Friston, 2000, Jovicich et al., 2013], it is essential for analyzing change in intensities within a MRI volume over time [Sweeney et al., 2016, Ghassemi et al., 2015a], developing intensity-based biomarkers [Chong and Lim, 2009, Vardhan et al., 2014, Meier et al., 2007] and for regression analyses at the voxel level [Hartung et al., 2014, Smith et al., 2004]. The challenge of intensity normalization has been largely addressed in the literature [Nyúl and Udupa, 1999, Nyúl et al., 2000, Weisenfeld and Warfield, 2004, Jager et al., 2006, Madabhushi et al., 2006, Leung et al., 2010, Shinohara et al., 2011, Shinohara et al., 2014], with several methods reviewed in [Shah et al., 2011]. Recently, a novel intensity normalization method, called White Stripe [Shinohara et al., 2014], was developed to bring raw image intensities to a biologically interpretable intensity scale. The method applies a z-score transformation to the whole brain using parameters estimated from a latent subdistribution of normal-appearing white matter (NAWM). The use of NAWM for normalization makes the method suitable for many studies of brain abnormalities, as in the case of multiple sclerosis (MS) lesions. While the method has been shown to make the white matter (WM) comparable across subjects, it was noted that residual across-subject variability was still present in the grey matter (GM).

In this work, we investigate between-scan technical variability that is left uncorrected by intensity normalization. We show that while common intensity normalization methods successfully correct for global intensity shifts associated with scanner site, substantial between-scan technical variation remains. This technical variation can be due to scanning parameters, scanner manufacturers, scanner field strength, and other factors. We refer to any post-normalization inter-scan variation that is not biological in nature as a “scan effect”.

To correct for scan effects, we propose Removal of Artificial Voxel Effect by Linear regression (RAVEL). RAVEL is a tool for removing unwanted variation present after intensity normalization. RAVEL is inspired by the batch effect correction tools SVA [Leek and Storey, 2007, 2008] and RUV [Gagnon-Bartsch and Speed, 2012] used broadly in genomics. In the analysis of gene expression and other genomic data, residual noise after intensity normalization is referred to as batch effects, because experiments are often performed in batches run on different dates. If not accounted for, batch effects have been shown to lead to spurious associations [Leek et al., 2010]. To make a parallel with brain imaging studies, batch effects are comparable to scan effects, where a single scan plays the role of a batch.

We use the linear model introduced in [Leek and Storey, 2007] to decompose the variation of the normalized intensities into a biological component of interest (variation associated with clinical covariates) and an unknown, unwanted variation component to be estimated from the data. The unwanted variation component encapsulates both technical variation and biological variation that is not of interest in the study. We register the different scans to a common template to allow the use of voxel-wise linear models, and estimate the unwanted variation component from regions of the brain that are not expected to be associated with the clinical covariates of interest. This follows the methodology of the RUV batch effect correction tool [Gagnon-Bartsch and Speed, 2012] which was later discussed in [Leek, 2014] for RNA sequencing. Unlike intensity-normalization methods, RAVEL utilizes all images in the study to leverage information about unwanted variability. Here, we use voxels that are consistently labelled as cerebrospinal fluid (CSF) across subjects as a control region; these voxels are not expected to be associated with disease [Luoma et al., 1993].

We evaluate the performance of RAVEL using a large subset of the ADNI database consisting of more than 900 subjects. We demonstrate our method by using the T1-weighted (T1-w) images from subjects with AD and MCI, as well as healthy controls. We follow the work of Fortin et al. [2014] to benchmark RAVEL against two intensity normalization procedures without any scan effect correction: the popular histogram matching algorithm and White Stripe. We focus on showing that RAVEL improves the replicability of the biological findings. Critically, we show that a reduction of technical variation does not result in removing biological variability. Namely, making intensity densities more similar does not necessarily improve sensitivity to biological changes; on the contrary, overmatching of distributions can result in the removal of biologically relevant signal. To show improvement in terms of biological findings, we first demonstrate that the top voxels associated with AD in the RAVEL-corrected dataset are more replicable across independent subsets of subjects. We measure the replicability of the results by randomly splitting the ADNI dataset into discovery and validation cohorts multiple times. Then, we show that the top voxels associated with AD after RAVEL correction are more enriched for brain regions known to undergo structural changes in AD. Finally, we show that the average hippocampal intensity after RAVEL correction performs better than intensity-normalized-only images in discriminating between AD patients and healthy controls, and between MCI patients and healthy controls. This shows that RAVEL-corrected T1-w intensities are more biologically meaningful than intensity-normalized-only images for group comparisons, and also potentially promising for the development of biomarkers.

Although we apply RAVEL in the context of T1-w MRI of the brain, our method is promising for many other imaging modalities. Furthermore, the flexibility in the choice of the control voxels makes RAVEL applicable to other diseases and pathologies.

2 Materials and methods

2.1 Study population

Our dataset consists of a subset of 917 subjects downloaded from the ADNI database (adni.loni.usc.edu). For each subject, we selected a study visit at random. We obtained 506, 184 and 227 subjects from the ADNI, ADNI-2 and ADNI-GO phases, respectively. We present summary statistics of the study population in Table 1. The selected scans were acquired at 83 different imaging sites, with a median number of 10 patients per site. The scans are also well-balanced for disease status across sites. The different scanning parameters are presented in Table A.1.

Table 1.

Summary statistics of the ADNI sample

		Healthy	MCI	AD
	n	261	439	217
	% Female	48	36	47
	Median Age [Q1, Q3]	76 [72–79]	75 [70–80]	76 [71–81]
Manufacturer	% GE	42	45	47
	% Philips	11	10	14
	% Siemens	47	45	39
Field Strength	% 1.5T	85	88	88
	% 3T	15	12	12

2.2 Imaging sequences and preprocessing

We considered T1-w imaging acquired on T1.5 and T3 scanners according to the ADNI standardized protocol [Jack et al., 2008]. The analysis was performed in R [R Core Team, 2014], using the packages oro.nifti [Whitcher et al., 2011], fslr [Muschelli et al., 2015], ANTsR [Avants et al., 2015] and WhiteStripe [Shinohara and Muschelli, 2015].

We applied the N4 inhomogeneity correction algorithm [Tustison et al., 2010] to each image. We nonlinearly registered all T1-w images to a high-resolution T1-w image atlas [Oishi et al., 2009], using the symmetric diffeomorphic image registration algorithm [Avants et al., 2008] implemented in the ANTs suite. We used non-linear registration in order to define a brain control region aligned across subjects and to find spatially coherent nuisance patterns for removal. Compared to the population-level atlases, the advantage of using a single-subject atlas is that it contains sharp definitions of anatomical structures, many of which are highly variable across individuals and cannot be easily delineated in population atlases. We emphasize that all of the techniques proposed here can be applied directly to data in either multi- or single-subject template spaces. To remove extra-cerebral tissue from each scan, we first created a brain mask on the template using the skull-stripping algorithm FSL BET [Smith, 2002] using the fslr package and subsequently applied this resulting brain mask to all N4-corrected and registered images. The preprocessing pipeline is summarized at the top of Figure 1.

Figure 1.

Schematic showing the RAVEL pipeline. The steps shown in the blue region are standard preprocessing steps that can be run in parallel. The green region shows the RAVEL algorithm.

In addition to the template brain segmentation, we performed a 3-class tissue segmentation by running the FSL FAST segmentation algorithm [Zhang et al., 2001] on the N4-corrected, registered and skull-stripped images, for each subject separately.

2.3 RAVEL methodology

The RAVEL correction procedure adapts the linear model introduced in SVA [Leek and Storey, 2007, 2008] to intensity-normalized MRI images. The method removes unwanted variation in the normalized intensities by modeling the residual unwanted variation across subjects. For the optimal performance of RAVEL, we use intensities normalized with White Stripe (see Figure A.1a). We model the m × n matrix V^WS of registered and White Stripe-normalized voxel intensities, for m voxels and n subjects, as a decomposition of a biological component of interest and an unwanted component as follows:

$${\mathbf{V}}^{WS}=\alpha {\mathbf{1}}^T+\beta {\mathbf{X}}^T+\gamma {\mathbf{Z}}^T+\mathbf{R}.$$ (1)

where α1^T represents the average scan in the sample, βX^T accounts for the known clinical covariates of interest (e.g. AD status, age, gender), and γZ^T accounts for unknown, unwanted factors. We refer to V^WS as the m × n matrix of intensities, α as the m × 1 vector of baseline intensities, X as the n × p matrix of clinical covariates, β as the m × p coefficient matrix associated with X, Z as the n × b matrix of unwanted factors, γ as the m × b coefficient matrix associated with Z, and R as the m × n matrix of residuals. In this model, α, β, γ and Z are unknown parameters that are estimated from the data. In the case the unwanted factors Z are known, the problem is reduced to simple linear regression models fit at each voxel separately.

Similar to RUV [Gagnon-Bartsch and Speed, 2012], we use a subset of the voxels not associated with disease to estimate the unwanted factors Z^T. We refer to such voxels as “control voxels”. An association between CSF intensities and disease status is highly unlikely [Luoma et al., 1993], and therefore CSF voxels are good candidates for inferring Z^T. We perform a subject-specific tissue segmentation of the T1-w image and choose control voxels as voxels classified as CSF for all subjects in the study. We denote by ${\mathbf{V}}_c^{WS}$ the subset of V^WS confined to the control voxels, and let m_c be the total number of control voxels. In addition, let ${\mathbf{V}}_c^{\ast }={\mathbf{V}}_c^{WS}-{\overline{\mathbf{v}}}_c{\mathbf{1}}^T$ be the matrix of intensities centered by row. For ${\mathbf{V}}_c^{\ast }$, Equation 1 simplifies to

$${\mathbf{V}}_c^{\ast }={\gamma }_c{\mathbf{Z}}^T+{\mathbf{R}}_c$$ (2)

as a result of the centering (α_c = 0) and the absence of association between the control voxels and the clinical covariates (β_c = 0). An estimate of Z^T can be obtained by performing a factor analysis on ${\mathbf{V}}_c^{\ast }$. More specifically, we first perform a singular value decomposition (SVD) of ${\mathbf{V}}_c^{\ast }$ as follows

$${\mathbf{V}}_c^{\ast }={\mathbf{UDW}}^T$$ (3)

where U is the m_c × n matrix of left-singular vectors, D is the n × n diagonal matrix of singular values, and W is the n × n matrix of right-singular vectors. Denoting b ≤ n as the true rank of $V_c^{\ast }$, we can rewrite Equation 2 as

$${\mathbf{V}}_c^{\ast }={\mathbf{U}}_b{\mathbf{D}}_b{\mathbf{W}}_b^T+{\mathbf{R}}_c$$ (4)

where ${\mathbf{U}}_b{\mathbf{D}}_b{\mathbf{W}}_b^T$ is the truncated SVD of rank b for ${\mathbf{V}}_c^{\ast }$, that is U_b and W_b contain only the first b columns of U and W respectively, and D_b contains only the first b diagonal elements of D. The first b right-singular vectors {w₁, w₂, …, w_b}of W, that is W_b, form a linear basis of unwanted factors for ${\mathbf{V}}_c^{\ast }$. Therefore, we use W_b as the estimate Ẑ in Equation 1. In practice, the rank b is not known. We discuss in Section 2.5 how b can be chosen to maximize the replicability of the voxels associated with the outcome of interest. Note that for b = 1, the estimator Ẑ will closely estimate the average CSF intensity at each subject. We obtain the estimates γ̂_i in Equation 1 by performing a linear regression at each voxel separately, using our estimate of Z^T in the equation. We define the RAVEL-corrected voxel i for subject j as

$$v_{ij}^{\text{RAVEL}}=v_{ij}^{WS}-{\widehat{\gamma }}_i{\widehat{\mathbf{Z}}}^T$$

where $v_{ij}^{WS}$ is the White Stripe-normalized intensity for the i-th voxel and for the j-th subject. In summary, RAVEL aims to identify patterns of variation in the control voxels across subjects, and then assess the degree to which this variation explains the brain-wide intensity distributions. In practice, this works well if the space spanned by the unwanted factors estimated from the control voxels also spans the unwanted variation space for all voxels. A schematic of the RAVEL method is presented in Figure 1.

2.4 Evaluation framework

We compare RAVEL to two intensity normalization procedures without scan effect correction: White Stripe, as implemented in Shinohara and Muschelli [2015], and the popular histogram matching method proposed by Nyúl and Udupa [1999] and further refined in Shah et al. [2011]. The histogram matching method matches the histograms of each subject to a reference population histogram using a piecewise linear transformation. We implemented the algorithm in R and we made the code available at https://github.com/Jfortin1/RAVEL/blob/master/R/hm.R. For better performance, we removed the background voxels before running the histogram matching algorithm. We used healthy subjects to form a reference population histogram distribution, as described in Shinohara et al. [2014].

To measure the association of the T1-w intensities with the disease status, we perform at each voxel a multiple linear regression analysis of the intensities on the disease status, adjusting for age and gender. We consider the standard Wald t-statistic for the disease status covariate to quantify the strength of association. We thus obtain a t-statistic for each of the m voxels, that is a list {t₁, t₂, …, t_m}, and we rank the t-statistics in a decreasing order to get a list of rank indices {r₁, r₂, …, r_m} where r_j is such that t_rj = t_(m−j), the latter being (m − j)-th order statistic. For a given integer k, we refer to the top k elements of the list {r₁, r₂, …, r_m} as the “top k voxels associated with AD”. For the rest of the paper, we will investigate the performance of the different normalization methods at replicating the top k voxels associated with AD. We do not fix the value of k in order to avoid an arbitrary choice. Instead, we have devised different evaluation metrics that use curves to represent the results for a large spectrum of values of k. The evaluation criteria are presented below.

Evaluation criterion 1: replicability of the voxels associated with AD

As a first evaluation criterion, we estimate the replicability of the biological findings, that is the chance that an independent experiment will produce consistent results [Leek and Peng, 2015]. We devised a discovery-validation cohorts scheme inspired by [Fortin et al., 2014]. We randomly split the full dataset into two equally sized subsets that we call discovery and validation cohorts, assigning AD and healthy patients equally between the two cohorts. For each of the two cohorts separately, we perform a differential analysis, described above, to obtain two lists of ranked voxels using the differential t-statistics: ${\mathbf{r}}^{\mathit{Dis}}=\{r_1^{\mathit{Dis}},r_2^{\mathit{Dis}},\dots ,r_m^{\mathit{Dis}}\}$ and ${\mathbf{r}}^{\mathit{Val}}=\{r_1^{\mathit{Val}},r_2^{\mathit{Val}},\dots ,r_m^{\mathit{Val}}\}$, for the discovery and validation cohorts respectively. The agreement between the two lists r^Dis and r^Val serves as a measure of replicability. More specifically, we are interested in the agreement of the top k ranked voxels, for different values of k. Those voxels are likely more relevant and more representative of a true biological signal. For a given integer k, the proportion of overlap for the top k voxels can be written as

$$O(k)=\frac{\mid \{r_1^{\mathit{Dis}},r_2^{\mathit{Dis}},\dots ,r_k^{\mathit{Dis}}\}\cap \{r_1^{\mathit{Val}},r_2^{\mathit{Val}},\dots ,r_k^{\mathit{Val}}\}\mid }{k}.$$

A concordance at the top (CAT) plot [Irizarry et al., 2005] is a plot showing O(k) for several values of k. To quantify uncertainty of the overlap measure O(k), we repeat the random discovery-validation cohort splitting one hundred times, and present the mean curve along with a 95% confidence band.

Evaluation criterion 2: enrichment of the top k voxels with brain structures known to be associated with AD

As a second evaluation criterion, we use pseudo-ROC curves [Bourgon, 2006] and enrichment curves to assess the biological validity of the top voxels associated with AD. In several neuroimaging studies, prior information about a specific disease allows us to expect a set of voxels to be associated with disease. In the case of AD and MCI, it is known that a large proportion of the hippocampus and parahippocampal voxels are associated with the progression of the disease (see Table 2 for references). In the absence of a gold standard, these voxels can play the role of a proxy for a gold standard. We refer to these voxels as a silver standard, that is a gold standard with some contamination.

Table 2.

Brain regions previously reported to undergo a structural change in the progression of AD.

Brain region	References
Hippocampus	Fox et al. [1996], Mori et al. [1997], Jack et al. [1999] Visser et al. [1999], Jack et al. [2000], Xu et al. [2000] Callen et al. [2001], Du et al. [2001], Bottino et al. [2002] Chételat et al. [2002], Pennanen et al. [2004], Wolf et al. [2004] Chételat et al. [2005], Ridha et al. [2006], Farrow et al. [2007] Whitwell et al. [2007], Poulin et al. [2011]
Amygdala	Scott et al. [1991, 1992], Vereecken et al. [1994] Mori et al. [1997], Callen et al. [2001], Bottino et al. [2002] Horínek et al. [2006], Farrow et al. [2007], Whitwell et al. [2007] Poulin et al. [2011], Miller et al. [2015]
Parahippocampal gyrus	Mori et al. [1997], Visser et al. [1999], Callen et al. [2001] Bottino et al. [2002], Chételat et al. [2005], Khan et al. [2014]
Enthorinal region	Gómez-Isla et al. [1996], Xu et al. [2000], Du et al. [2001] Pennanen et al. [2004], Whitwell et al. [2007] Braak and Del Tredici [2012], Khan et al. [2014]
Fornix and S. Terminalis	Callen et al. [2001], Mielke et al. [2009], Liu et al. [2011]

Bourgon [2006] show that receiver operating characteristic (ROC) curves based on a silver standard, called “pseudo-ROC curves”, preserve the relative ranking of different classification methods with respect to ROC curves based on a gold standard. A sufficient condition for the validity of the pseudo-ROC curves ranking is that the contamination of the silver standard, with respect to the gold standard, occurs independently of the misclassification errors of the different methods compared. In the Results section, we use the t-statistics measuring the association of the voxel intensities with AD to classify voxels as either associated with AD or not. To estimate the sensitivity and specificity of each normalization method, we use voxels from 5 regions known to be associated with AD from an extensive search of the literature (see Table 2) as a silver standard.

A second approach to benchmark different normalization/scan effect correction methods is to count the number of candidate voxels that fall into the list of the top k voxels associated with disease. We refer to a curve that depicts the counts for different values of k as an “enrichment curve”.

2.5 Estimation of the number of unwanted factors

To select the optimal number of unwanted factors b to include in Equation 1, we choose the value of b that maximizes the discovery-validation replication rate introduced in section 2.4. Normalized intensities for which the top voxels associated with disease have better replication between independent experiments are more robust to technical artifacts, like site effect and differences in protocol.

Other approaches have been proposed to select b. Among others, Gagnon-Bartsch and Speed [2012] use voxels that are known to be associated with a clinical outcome to optimize b, called “positive control voxels”. These authors perform a sensitivity analysis for the parameter b, and b is chosen to optimize the number of positive control voxels that fall into the top voxels associated with the outcome. The downside of using this approach is that positive controls must be identified in advance, which is not possible for discovery studies.

Alternatively, the estimation of b could be done in an unsupervised manner by thresholding the percentage of variance explained by the first b singular vectors. This approach, which is agnostic of the outcome, can potentially provide additional safeguards against overfitting, but could also decrease the performance of RAVEL by adding noise.

3 Results

We compared RAVEL to three normalization strategies: raw image intensities (no normalization), White Stripe [Shinohara et al., 2014], and histogram matching [Shah et al., 2011].

3.1 RAVEL reduces inter-subject variability

We used a subset of the CSF intensities as control voxels to estimate factors of unwanted variation in the RAVEL model. We obtained 9869 CSF control voxels; we recall that a voxel is qualified as a CSF control if it is classified as CSF for all subjects. As expected, the CSF control voxels were located primarily in the center of the ventricles (Figure 2a). Maximizing the discovery-validation replication rate, we only kept the first singular vector as the unwanted factor term Z^T in Equation 1, that is we chose b = 1 (see Figure A.1b). Unsurprisingly, the singular vector was highly correlated with the mean CSF intensity for each subject (correlation of 95.7%). In order to investigate potential partial volume contamination, we eroded the CSF control region using a box kernel of size 3 [Muschelli et al., 2015]. The resulting eroded control region was reduced to 1419 voxels. The singular vector obtained from the eroded control region was correlated at 99% with the singular vector obtained from the original control region, showing the robustness of our estimated control region.

Figure 2. Estimation of technical variability using CSF control voxels.

(a) The voxels selected in the RAVEL model as control voxels for CSF are shown in blue overlaid on the template; the control voxels were selected as voxels classified as CSF for every subject. (b) Heatmap of the RAVEL coefficient γ̂ from Equation 1 depicted on the template, using b = 1 in Equation 1. The coefficient depends on the brain tissue, with a high coefficient for voxels in CSF (yellow regions), a moderate coefficient in GM (orange and lighter red) and a low coefficient for WM (darker red).

In Figure 2b, we depict the coefficient γ̂ at each voxel. We notice that the distribution of γ̂ varies across brain tissues, for instance darker red in WM (coefficient values close to 0) and yellow in CSF (high positive coefficient values). This is not surprising as the White Stripe normalization is designed to remove technical variability in the WM and performs best in that tissue class. Therefore, RAVEL does not need to perform any additional correction in the WM tissue. On the other hand, it is known that White Stripe leaves residual across-subject variability in the GM and CSF [Shinohara et al., 2014]. Consequently, RAVEL removes more variability in those two tissue classes (higher γ coefficient). This shows that the RAVEL method allows a spatially varying gamma coefficient and does not overcorrect for already-corrected voxels, which is in this case the WM.

In Figure 3, we show the histograms of intensities for the different normalization methods and RAVEL. In accordance with the findings of Shinohara et al. [2014], the White Stripe-normalized images show good comparability of the WM across subjects; this can be seen by the similar WM densities centered around zero (Figure 3 second row, third column). However, for GM, the White Stripe densities are less clustered and show more variability, which is even more exaggerated for the CSF intensities. This shows that scaling and centering using a NAWM stripe is not enough to make GM and CSF intensities comparable across subjects. This could be explained by differential WM to GM and WM to CSF contrast ratios across images and protocols. One can observe that RAVEL substantially corrects for that extra variability in CSF and GM intensities, in addition to preserving the good comparability of the WM intensities. The histograms for each tissue class cluster together well and show similar characteristics (mean, scale and range). As expected, the histograms for Histogram matching also show good comparability for all three tissues. However, we will show in the subsequent sections that Histogram matching does not perform as well as RAVEL at finding voxels truly associated with AD. This is consistent with the idea that Histogram matching can remove biological variation in addition to unwanted technical variation.

Figure 3. Effect of RAVEL on the histograms of intensities.

Rows correspond to different preprocessing steps, and columns to different brain tissues. Each curve represents the histogram of intensities for one subject.

The main source of variation in the unnormalized images is from scanning site. At each voxel, we calculated the percentage of variation in the intensities explained by the scanning site variable (R²) using an ANOVA model. We averaged the R² values across voxels and obtained an average R² value of 67.8%. Interestingly, we observed much less variation explained by scanning site for both intensity-normalized datasets (18% for both White Stripe and histogram matching) and for RAVEL (18%). We randomly permuted the scanning site variable 100 times and obtained a null distribution of the average R² with range of [16.1%, 16.5%]. This implies that after intensity normalization alone, the variability between different sites is close to the within-site variability. However, as shown in Figure 3, RAVEL removes additional technical variability in comparison to intensity normalization alone.

3.2 RAVEL improves replicability of large MRI studies

The study of large epigenetic data has shown that the ability to reduce technical variation does not necessarily lead to a better detection of features associated with the outcome of interest [Fortin et al., 2014, Dedeurwaerder et al., 2014]. A good normalization method should both reduce technical variability and enhance the replicability and robustness of biological findings. Here, we evaluate the performance of RAVEL in terms of estimating brain regions associated with AD.

We randomly split the ADNI dataset into discovery and validation cohorts one hundred times, and we present in Figure 4b the mean CAT curves with 95% confidence bands. As expected, the raw images intensities show very poor replication of the results (maximum of 0.18), while RAVEL improves replication of the findings substantially (up to 0.67) upon intensity normalization methods alone. We also investigated whether or not including explicitly known technical covariates (field strength, scanner manufacturer, and scanning site) in the regression model improves the replicability of the results. While correcting for field strength and scanner manufacturer did not substantially change the results (see Figure A.2a), additionally correcting for scanner site markedly decreased the replicability of the voxels associated with AD (Figure A.2b) for all methods except modeling the raw data. This shows that correcting the raw data explicitly for known technical covariates is insufficient at removing unwanted variation in comparison to RAVEL. This is not surprising, however, due to the substantial unwanted within-site variability is left uncorrected by such model.

Figure 4. RAVEL improves replicability of voxels associated with AD.

(a) In template space, we depict in yellow the voxels that are replicated across all random splittings, from the list of the top 50,000 associated with AD. (b) Mean CAT curves for association with AD with 95% confidence bands. (c) Number of voxels replicated for each method in (a). RAVEL shows excellent performance at replicating the discovery of regions of the brain associated with AD.

The replicated voxels fall into regions that are known to be associated with AD. In Figure 4a, we show voxels associated with AD that were replicated among the top 50,000 voxels for all random splittings. No normalization led to zero voxels replicated across splittings. This is not surprising since raw image intensities are expressed in arbitrary units. White Stripe replicated 1557 voxels, while histogram matching and RAVEL replicated 4026 and 5128 voxels respectively (Figure 4c). In addition, RAVEL is the most powerful method for finding replicated voxels in the hippocampus and amygdala, two structures known to be associated with AD. The number of replicated voxels for the hippocampus are the following: 0 for no normalization, 324 for White Stripe, 1775 for histogram matching and 2501 for RAVEL. For the amygdala, we obtained the following counts: 0 for no normalization, 321 for White Stripe, 369 for histogram matching and 514 for RAVEL.

White Stripe and histogram matching, by correcting for inter-subject variability in the white matter, substantially increased the number of replicated voxels associated with AD in comparison to no normalization. RAVEL led to a 3-fold increase in the number of replicated voxels with respect to White Stripe. This was achieved by additionally modeling brain-wide unwanted variability using a CSF control region. This is consistent with the idea that while CSF is not interesting on its own with respect to disease, it can be used powerfully to distinguish signal from noise in the entire brain. Interestingly, performing the RAVEL correction on the histogram matching-normalized intensities did not lead to better performance (see Figure A.1a). The superior performance of White Stripe combined with RAVEL can be explained by the following: the White Stripe normalization corrects for WM intensities, and RAVEL additionally corrects for the residual variability in the GM and CSF intensities, as seen in the histograms presented in Figure 3. This results in a powerful additive effect that removes most of the technical variability for all tissues. On the other hand, the Histogram matching normalization aggressively removes a substantial part of the between-subject variability that can be biological in nature. Because most of the variation is already removed, this leaves little room for improvement by additionally applying a scan-effect removal tool like RAVEL.

3.3 RAVEL uncovers known regions associated with AD

The discovery-validation scheme allowed us to evaluate the replicability of the top voxels associated with AD. In the current section, we aim to evaluate the validity of the results by comparing the top voxels to brain regions known to undergo a structural change in the progression of AD. Those structural changes include, among others, GM and WM atrophy, neuronal loss, amyloid senile plaques, loss of fiber tract integrity and tau lesions. In the context of AD, these changes have been described in the hippocampal formation and several parahippocampal structures. The list includes, but is not limited to, the hippocampus, the amygdala, the enthorinal cortex, the fornix, the stria terminalis and the parahippocampal gyrus. Table 2 lists several studies that have reported structural changes in these regions.

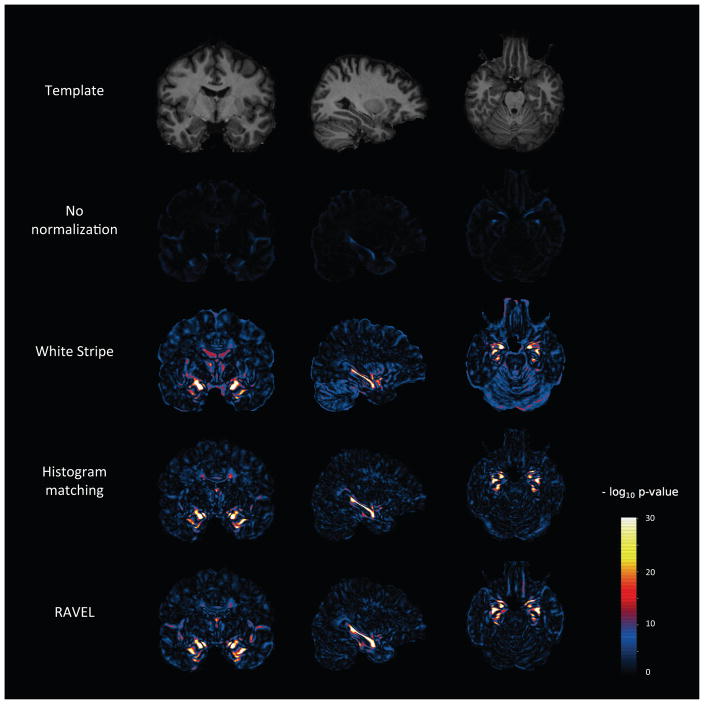
Using the template parcellation map [Oishi et al., 2009], we considered 67,983 voxels that are part of the regions listed in Table 2. These voxels represent 3.5% of the template and are candidates for association with AD. We use these voxels as a silver standard to evaluate the performance of the different normalization methods and RAVEL. For different values of k, we count the number of the top k voxels associated with AD that are part of the silver standard, which are said to be enriched for the truth. The enrichment curves, depicted in Figure 5a (solid lines), show the number of enriched voxels for different values of k, for each normalization method. The dotted line at the bottom represents the number of voxels expected by chance only. To account for variability in the enrichment curves, we nonparametrically bootstrapped with replacement by subject to recalculate the top voxels associated with AD and recompute the curves. The shaded regions of Figure 5 represent bootstrapped 95% confidence bands. We observe that RAVEL discovers significantly more voxels that are truly associated with AD than the competing methods. The top voxels associated with RAVEL are also more stable than other methods, as measured by narrower 95% confidence bands. Notably, RAVEL offers a substantial improvement with respect to intensity normalization with White Stripe alone. We also calculated the number of significant voxels falling into the silver standard, defined as voxels with a p-value ≤ 0.05 after correcting for multiple comparison using Bonferroni correction. We obtained 0, 2488, 3265 and 4560 such voxels for the raw, White Stripe-normalized, Histogram Matching-normalized and RAVEL-corrected intensities respectively. In Figure A.3, we show in template space the negative log p-value at each voxel for association between the intensities and AD status.

Figure 5. The top voxels associated with AD are enriched for the hippocampus and parahippocampal regions.

(a) For the top k voxels associated with AD (x-axis), the solid lines display the number of voxels out of the k voxels falling into five structures known to be associated with the progression of AD: the hippocampus, amygdala, enthorinal cortex, fornix and stria terminalis and parahippocampal gyrus. The dotted line represents the number of voxels expected by chance only. The shaded areas represent 95% confidence bands computed using 100 bootstrapped samples. (b) From the t-statistics measuring the association of the voxel intensities with AD, we present the pseudo-ROC curves for classifying a voxel as a member of the five regions described in (a). RAVEL shows significantly better sensitivity and specificity than the other methods for detecting hippocampus and parahippocampal changes associated with AD.

Next, we obtained pseudo-ROC curves to measure the specificity and sensitivity of RAVEL for detecting a true association between voxel intensities and AD. In Figure 5b, we present the pseudo-ROC curves for classifying voxels as associated with AD or not, using the differential analysis (voxel-wise) t-statistics as a measure of association. The voxels from the regions listed in Table 2 are used as a silver standard. As with the enrichment curves, we present bootstrapped 95% confidence bands. RAVEL outperforms histogram matching, White Stripe and raw image intensities for the full range of specificity.

We note that the number of false positives, defined as the number of top voxels that are not part of the silver standard, is high for all methods for all values of k (Figure A.4). This it not unexpected when using a silver standard. We note nonetheless that RAVEL is the method with the smallest number of false positives. Interestingly, most of the false positives are located near the hippocampal and parahippocampal structures (voxels shown for RAVEL in Figure A.5), indicating that the high number of false positives is a consequence of the choice of silver standard, and not the methods themselves. Among others, voxels within the cingulum, which is not part of our silver standard, were consistently found by all four methods. This is reassuring, as the cingulum has been previously reported as a region of interest implicated in AD [Delano-Wood et al., 2012].

3.4 RAVEL-corrected intensities improve prediction of AD and MCI

We investigated the potential use of T1-w RAVEL-corrected intensities as biomarkers for disease identification and progression. We first compared the average hippocampal intensity between AD patients and healthy controls. We used the template parcellation map to identify 9847 voxels labelled as hippocampus. Using the mean intensity of the hippocampus as a score, we classified each subject as either having AD or being healthy, thresholding the scores at different levels. The corresponding ROC curves are presented in Figure 6a. We obtained an area under the curve (AUC) of 81.7% for RAVEL (95% CI [77.6, 85.4]), as opposed to 74.9% for histogram matching ([70.4, 79.2]), 64.4% for White Stripe ([58.9, 69.0]), and 57.0% for no normalization ([52.1, 62.0]). We obtained the 95% confidence intervals by bootstrapping the samples with replacement 1000 times. Similarly, we used the average hippocampal intensity to distinguish between MCI patients and healthy controls; the corresponding ROC curves are presented in Figure 6b. We obtained an AUC of 67.3% for RAVEL (95% CI [63.1, 71.3]), as opposed to 63.4% for histogram matching ([59.6, 67.7]), 59.0% for White Stripe ([54.8, 63.4]), and 52.9% for no normalization ([48.4, 57.3]).

Figure 6. RAVEL improves the prediction of AD and MCI.

(a) The mean hippocampus intensity was used to predict AD. The AUC is 81.7 % for RAVEL, 74.9% for histogram matching, 64.4% for White Stripe and 57.0% for no normalization, with 95% CIs [77.6, 85.4], [70.4, 79.2], [58.9, 69.0] and [52.1, 62.0] respectively. (b) The mean hippocampus intensity was used to predict MCI. The AUC is 67.3% for RAVEL, 63.4% for histogram matching, 59.0% for White Stripe and 52.9% for no normalization with 95% CIs [63.1, 71.3], [59.6, 67.7], [54.8, 63.4] and [48.4, 57.3] respectively.

While normalized intensities are not as predictive of AD as other brain features, such as hippocampal volume and cortical thickness [Wolz et al., 2011], this nevertheless shows that RAVEL-corrected intensities are more representative of true biological variation than intensity-normalized intensities alone. While there are limitations to the development of biomarkers using the quantitative information of conventional MRI intensities, previous studies have shown that a great deal of quantitative information in the MRI intensities can be harnessed to study disease [Sweeney et al., 2016, Reich et al., 2015, Ghassemi et al., 2015b, Mejia et al., 2015, Meier et al., 2007]. The present results show that the development of biomarkers using MRI studies in many neurological and psychiatric disorders could benefit from the RAVEL scan-effect correction tool.

4 Discussion

In this work, we have presented the scan effect correction tool RAVEL, to correct for inter-scan unwanted variability in MRI studies that is present after intensity normalization. We have shown that RAVEL, applied after normalizing the intensities with White Stripe, substantially improves the replicability of the regions of the brain found to be the most associated with AD. RAVEL, inspired by the batch effect correction tools SVA and RUV, infers the unwanted variation in the images by using regions of the brain that are not associated with disease. After registering all images to a common template, we used voxels that were labelled as CSF for all images as control voxels. We used a linear regression model at each voxel to regress out the variation in the intensities explained by variation in the control CSF voxels intensities. We used an SVD to reduce the dimensionality of the control voxels, and selected the number of components to include in the regression models by maximizing the replication rate of biological findings between independent subsets of the data.

We have shown that while common intensity normalizations remove a large part of the unwanted site effects for T1-w imaging, significant unwanted variation remains uncorrected. We encapsulated this post-normalization residual variability using the term scan effect. We have shown that the scan effect correction tool RAVEL successfully improves the comparability of the images in a large subset of the ADNI database by removing this extra variability. We measured the performance of RAVEL and other methods by estimating the replicability of the top voxels associated with AD in independent subsets of the ADNI dataset. To do so, we randomly divided the ADNI dataset into discovery and validation cohorts several times, and computed the top-replicated voxels for each random split. We have also shown that the top voxels associated with AD in our analysis and replicated in the discovery-validation division are more enriched for brain regions known to be associated with AD than those found using intensity-normalized data only. This shows that RAVEL is a potent method for improving the discovery of brain regions associated with disease. Finally, we have also shown that the RAVEL correction improves the prediction of AD and MCI compared to healthy controls, using the mean hippocampal intensity as a predictor. This suggests that RAVEL is a promising method that may facilitate the development of biomarkers using MRI intensities. Furthermore, with the recent emphasis on multivariate pattern analysis for biomarker development [Davatzikos et al., 2005, De Martino et al., 2008, Vemuri et al., 2008, Craddock et al., 2009, Davatzikos et al., 2011, Gaonkar and Davatzikos, 2013], RAVEL promises to produce more generalizable biomarkers that are less susceptible to biases associated with scanner and site imbalances.

The idea of using a control region of the brain which is not associated with disease is not new. In Pujol et al. [1992], Bakshi et al. [2002], Tjoa et al. [2005], Brass et al. [2006], Neema et al. [2009], the regions of interest were divided by the mean signal intensity of a CSF region to correct for potential inter-subject variation. Shinohara et al. [2014] used a NAWM stripe to estimate a scaling and shifting parameter in their z-score normalization method. In Mejia et al. [2015], in the context of estimating quantitative T₁ maps (qT₁) from conventional MRI, the authors proposed an adaptation of the z-score normalization method by using a combination of NAWM and cerebellar gray matter (CBGM), where the NAWM was used for the scaling parameter and the CBGM was used for the shifting parameter. In Ghassemi et al. [2015b], the authors used the median GM intensity for the shifting parameter, and the difference between the median intraconal orbital fat intensity and the median GM intensity for the scaling parameter. In Sweeney et al. [2013], the authors use the whole brain to estimate the scale and shift parameters. We note that the different versions of the z-score transformation used in Shinohara et al. [2014], Sweeney et al. [2013], Mejia et al. [2015], Ghassemi et al. [2015b] only leave room for the choice of two control regions at maximum, corresponding to the mean and scale parameters. While this improves comparability between subjects in comparison to the unnormalized intensities, as shown in Figure 4b, we have shown that RAVEL improves dramatically upon a z-score transformation only.

There are several limitations to our method. If control regions are misspecified, i.e. the regions do not carry any information about the technical variability across subjects, or worse yet, if the control regions are inadvertently associated with the outcome of interest, the RAVEL correction may remove biological signals of interest. In both cases, however, cross-validation using the concordance curves from the discovery-validation scheme allows the user to estimate directly the performance of RAVEL on their dataset.

Another limitation is the use of nonlinear registration to align voxels across subjects. The registration step is necessary to apply the voxel-wise linear models from Equation 1. Because patients with AD and MCI have different volumes of WM, GM and CSF in comparison with healthy controls, misregistration error might be associated with the outcome of interest. However, this is a problem inherent to any cross-subject voxel analysis, and remains an active subject of research in image analysis. While voxels that are associated with disease can be a consequence of differential misregistration, this does not change the results of the present work, as misregistered voxels should be detected by intensity normalization method, after scan effect correction. It may also be possible to approximate RAVEL corrections using mean values in reference regions; indeed, in the ADNI dataset, the mean T1-w intensity in CSF after White Stripe correction was highly correlated with the first RAVEL factor. Thus, in the case of the well-controlled ADNI protocol, adjusting by regression on the mean in CSF would yield similar results. In cases where there is more heterogeneity in acquisitions, and in imaging modalities that are more difficult to calibrate, additional RAVEL factors are likely and using the mean in the reference region may not perform well.

A first extension of the presented methodology is to precede the RAVEL correction tool by a variant of the White Stripe intensity normalization method. For instance, as used in Sweeney et al. [2013], a whole-brain z-transformation might be used instead, where the mean and scaling parameters are estimating using all brain intensities. Subsequently, the RAVEL correction model can be applied using additional control regions. A second extension is to implement a mixed-effect model using scan-rescan pairs into the RAVEL framework to improve the estimation of the unwanted variation component. Such approaches have been shown to be successful in the context of technical replicates in genomic studies [Jacob et al., 2013].

Although we have shown the performance of RAVEL in the context of T1-w MRI of the brain, RAVEL is a promising scan effect correction tool for other imaging modalities. The RAVEL software can be found at https://github.com/Jfortin1/RAVEL.

Highlights.

• Between---scan unwanted variation is still present after intensity normalization

• We propose a scan---effect removal tool for removing post---normalization artifacts.

• We model the unwanted variability between MRI T1---w scans using CSF region.

• We use a large subset of the ADNI database to showcase our method.

• We show that our method improves replicability of the voxels associated with AD.

• MRI intensities corrected by our method improves prediction of AD and MCI.

Abbreviations

AD

Alzheimer’s disease

ADNI

Alzheimer’s Disease Neuroimaging Initiative

ANTs

Advanced Normalization Tools

AUC

area under the curve

BET

Brain Extraction Tool

CAT

concordance at the top

CBGM

cerebellar gray matter

CSF

cerebrospinal fluid

DTI

diffusion tensor imaging

FAST

FMRIB’s Automated Segmentation Tool

FMRIB

Oxford Centre for Functional MRI of the Brain

FSL

FMRIB Software Library

GM

grey matter

MCI

mild cognitive impairment

MRI

magnetic resonance imaging

NAWM

normal-appearing white matter

NIFTI

The Neuroimaging Informatics Technology Initiative

RAVEL

Removal of Artificial Voxel Effect by Linear regression

ROC

receiver operating characteristic

RUV

removing unwanted variation

SVA

surrogate variable analysis

SVD

singular value decomposition

T1-w

T1-weighted

WM

white matter

WMPM

white matter parcellation map

Appendix A

Figure A.1. CAT plots with additional methods.

(a) Like Figure 4b, but distinguish between RAVEL run on intensities normalized by White Stripe (default) and RAVEL run on intensities normalized by histogram matching. (b) Like Figure 4b, but for different numbers of unwanted factors in the RAVEL model. The pink line is for RAVEL with 2 factors, and the grey lines represent RAVEL with 3 to 15 factors. We can observe that the choice of 1 or 2 factors in the RAVEL model optimizes the replication of the voxels associated with AD.

Table A.1. Scanning parameters for the ADNI data subset.

We report the different scanning parameters of the ADNI dataset for the images used in our analysis. The different scanning parameters are flip angle in degrees (FA), inversion time in milliseconds (TI), repetition time in milliseconds (TR) and echo time in milliseconds (TE). We report the range of the parameters if more than one value was reported across subjects. For each scanner configuration (row of the table), we report the number of healthy controls (Cont), the number of patients with AD (AD) and the number of patients with MCI (MCI) that we included in our subset of the ADNI database.

Manufacturer	Field (T)	Model	Sequence	Coil	FA (°)	TI (ms)	TR (ms)	TE (ms)	Cont	AD	MCI
GE	1.5	GENESIS SIGNA	MPRAGE	HEAD	8	1000	(10.2,10.4)	4.1	15	15	38
GE	1.5	SIGNA EXCITE	MPRAGE	8HRBRAIN	8	1000	(8.6,9.2)	(3.8,4.1)	71	57	107
GE	1.5	SIGNA EXCITE	MPRAGE	8NVHEAD A	8	1000	9	3.9	1	0	0
GE	1.5	SIGNA EXCITE	MPRAGE	HEAD	8	(1000,1043)	(9,11)	(3.9,5)	10	13	19
GE	1.5	SIGNA HDx	MPRAGE	8HRBRAIN	8	1000	(8.6,9.2)	(3.8,4.1)	2	8	13
GE	1.5	SIGNA HDx	MPRAGE	HEAD	8	1000	8.6	3.8	0	0	2
GE	1.5	Signa HDxt	IR-SPGR	8HRBRAIN	8	600	9.2	3.9	2	0	6
GE	3	DISCOVERY MR750	IR-SPGR	8HRBRAIN	11	400	7.3	3	0	2	4
GE	3	SIGNA EXCITE	MPRAGE	8HRBRAIN	8	900	7	3	1	0	3
GE	3	Signa HDxt	IR-SPGR	8HRBRAIN	11	400	(7,7.2)	(2.8,3)	7	7	4
Philips	1.5	Achieva	MPRAGE	SENSE-Head-8	8	0	8.6	4	3	4	10
Philips	1.5	Gyroscan Intera	MPRAGE	HEAD	8	0	8.6	4	3	4	2
Philips	1.5	Gyroscan Intera	MPRAGE	SENSE-Head	8	0	8.6	4	2	0	1
Philips	1.5	Intera	MPRAGE	HEAD	8	0	8.6	4	5	4	6
Philips	1.5	Intera	MPRAGE	SENSE-Head	(8,90)	0	(8.5,3000)	(4,12)	13	13	22
Philips	1.5	Intera	MPRAGE	SENSE-Head-6	8	0	8.6	4	1	1	1
Philips	1.5	Intera Achieva	MPRAGE	SENSE-Head-8	8	0	8.6	4	1	0	0
Philips	3	Ingenia	MPRAGE	MULTI COIL	9	0	6.8	3.2	0	3	0
Philips	3	Ingenia	MPRAGE	SENSE-Head	9	0	6.8	3.2	0	1	0
Philips	3	Intera	MPRAGE	SENSE-Head	8	0	6.8	3.2	1	0	0
Philips	3	Intera	MPRAGE	SENSE-Head-8	(8,9)	0	6.8	3.2	0	1	2
Siemens	1.5	Avanto	MPRAGE	PA	8	1000	2400	3.5	24	13	31
Siemens	1.5	Sonata	MPRAGE	HE	8	1000	(2400,3000)	3.5	15	15	28
Siemens	1.5	Sonata	MPRAGE	PA	8	1000	(2400,3000)	3.5	7	8	22
Siemens	1.5	SonataVision	MPRAGE	PA	8	1000	2400	3.5	1	1	5
Siemens	1.5	Symphony	MPRAGE	HE	8	1000	3000	(3.6,3.9)	8	9	18
Siemens	1.5	Symphony	MPRAGE	PA	(2,8)	(0,1000)	(3.9,3000)	(1.3,3.7)	38	25	57
Siemens	3	TrioTim	MPRAGE	PA	9	900	2300	3	25	9	32
Siemens	3	Verio	MPRAGE	PA	9	900	2300	3	5	4	6

Figure A.2. CAT plots with explicit correction for technical covariates.

(a) The solid lines correspond to the CAT curves described in Figure 4b. The dotted lines correspond to the CAT curves for the data corrected by each of the normalization method and corrected for the following technical covariates: field strength (1.5T or 3T) and scanner manufacturer (Siemens, GE, or Philips). The correction was made by adjusting for the technical covariates in the multiple linear model analysis framework. (b) is similar to (a), but also adjusting for scanner site.

Figure A.3. Voxel-level p-value maps from AD vs. healthy patient differential analysis.

At each voxel, we computed a t-statistic for testing a difference in intensities between AD and healthy patients. For each normalization method, we report the negative log p-values from the t-test. We include at the top of the figure the template for anatomical reference.

Figure A.4. Number of false positives for each method.

(a) Number of false positives (voxels that do not fall into the silver standard) for a range of values of k ≤ 10, 000.

Figure A.5.

Location of the false positives for the RAVEL-corrected intensities, for the top k=10,000 voxels associated with AD.