Exploring the high-dimensional structure of muscle redundancy via subject-specific and generic musculoskeletal models

Abstract

Subject-specific and generic musculoskeletal models are the computational instantiation of hypotheses, and stochastic techniques help explore their validity. We present two such examples to explore the hypothesis of muscle redundancy. The first addresses the effect of anatomical variability on static force capabilities for three individual cat hindlimbs, each with seven kinematic degrees of freedom (DoFs) and 31 muscles. We present novel methods to characterize the structure of the 31-dimensional set of feasible muscle activations for static force production in every 3-D direction. We find that task requirements strongly define the set of feasible muscle activations and limb forces, with few differences comparing individual vs. species-average results. Moreover, muscle activity is not smoothly distributed across 3-D directions. The second example explores parameter uncertainty during a flying disc throwing motion, by using a generic human arm with five DoFs and 17 muscles to predict muscle fiber velocities. We show that the measured joint kinematics fully constrain the eccentric and concentric fiber velocities of all muscles via their moment arms. Thus muscle activation for limb movements is likely not redundant: there is little, if any, latitude in synchronizing alpha-gamma motoneuron excitation-inhibition for muscles to adhere to the time-critical fiber velocities dictated by joint kinematics. Importantly, several muscles inevitably exhibit fiber velocities higher than thought tenable, even for conservative throwing speeds. These techniques and results, respectively, enable and compel us to continue to revise the classical notion of muscle redundancy for increasingly more realistic models and tasks.

Introduction

This invited paper has the dual purpose of being didactic about computational methods to test neuromechanical hypotheses in the context of high-dimensional subject-specific and generic models; and applying these methods to explore the classical notion of muscle redundancy, a central tenet in our field. This is made possible by computational geometry and stochastic techniques we have been developing to understand the interactions among (i) model topology (the number and type of and connectivity among the elements of the model); (ii) parameters values (the individual and specific numerical values assigned to each model parameter); and (iii) the requirements of real-world tasks for tendon-driven biomechanical systems with numerous kinematic degrees of freedom and muscles.

The notion of computational models as instantiations of specific hypotheses, the stochastic exploration of model capabilities to test these hypotheses, and the relationship between generic vs. subject-specific models has been addressed elsewhere [3–7]. However, increasing the physiological realism and utility of these techniques requires extending them to ever higher dimensions (i.e., larger numbers of muscles and kinematic degrees-of-freedom, DoFs), and to real-world tasks involving the production of static forces and fast motions—while limiting computational cost. But working with ever-greater numbers of muscles and DoFs inevitably challenges our ability to visualize the complex and high-dimensional structure of the set of feasible muscle activation patterns. It also significantly challenges our ability to find unique solutions (if they even exist) to these computational problems, or defend their optimality/uniqueness.

We have found these stochastic modeling techniques particularly useful to test the classical notion of muscle redundancy, which has often been called the central problem of motor control [8]. The classical notion of muscle redundancy is thought to arise by virtue of having (many) more muscles than DoFs. With many muscles acting upon the same number or fewer joints, some argue that the central nervous system (CNS) must solve an optimization problem to select and implement specific muscle activation patterns from a theoretically infinite set of possibilities [9, 10]; while others argue for near- or sub-optimal solutions being good enough [11, 12]. If fewer muscles actuated a limb, the arguments go, feasible forces and motions could be produced without significant need for such optimizations.

Several of us have argued that this classical interpretation of the number of muscles in vertebrate limbs is paradoxical with respect to evolutionary biology, and the clinical reality of motor dysfunction: extant vertebrates tend to have many more muscles than DoFs, even though it is energetically expensive to develop and maintain muscle mass—and injury to even a few muscles can cause dysfunction. Using the same argument of energetic efficiency invoked for optimization in motor control—but at the scale of evolutionary time—we, and others, have argued that we likely have barely enough muscles for versatile real-world behavior [13–17]. This view is closely aligned with the computational neuroethology approach [18–20] that argues that perhaps we need all our muscles because of the sheer variety of tasks—each distinguished by the type and number of constraints they must meet—over the course of a day/week/lifespan. Put differently, if we have too many muscles in our limbs, which ones would you like to donate or paralyze? Therefore, it is important that our research into muscle redundancy work toward reconciling these different views.

Still, for most tasks in healthy individuals, some redundancy is bound to remain; regions of feasible activation solutions that are not a single point will consist of a neighborhood or subspace that naturally contains an infinite number of solutions (i.e., points). The nervous system is still confronted with the need to choose a specific solution to implement at any point in time; however, that collection of feasible solutions remains highly structured due to both the mechanics of the limb and the constraints of the task [2, 16, 17, 21–23]. The purpose of this work, therefore, is to begin to address the need posed by us [16, 17, 21], and others [2, 14, 22], to improve computational methods for understanding and visualizing the dimensionality and structure of feasible solutions sets for limbs with large numbers of muscles performing tasks with realistic constraints. Here we do so for 3-D musculoskeletal models of a cat hindlimb and a human arm with 31 and 17 muscles, respectively, using MATLAB (v2013b, The Mathworks, Natick MA).

Cat hindlimb model: Methods

The purpose of this cat hindlimb model is to present a novel way to visualize the structure of the set of all feasible muscle activations to produce maximal and submaximal static paw forces in every 3-D direction. In addition, we compare solutions among three subject-specific models to explore the effect of between-subject anatomical variability on muscle activation. The models consist of three feline (Felis catus) hindlimbs, each with 31 muscles actuating 7 kinematic DoFs from the hip to the ankle. We used the bone lengths and moment arms for the cat hindlimbs originally presented by McKay and Ting in 2008 [24], and modified by Sohn et al. 2013 [2], that were graciously shared with us by the authors. The species average model for the cat hindlimb is shown in Figure 1.

Figure 1.

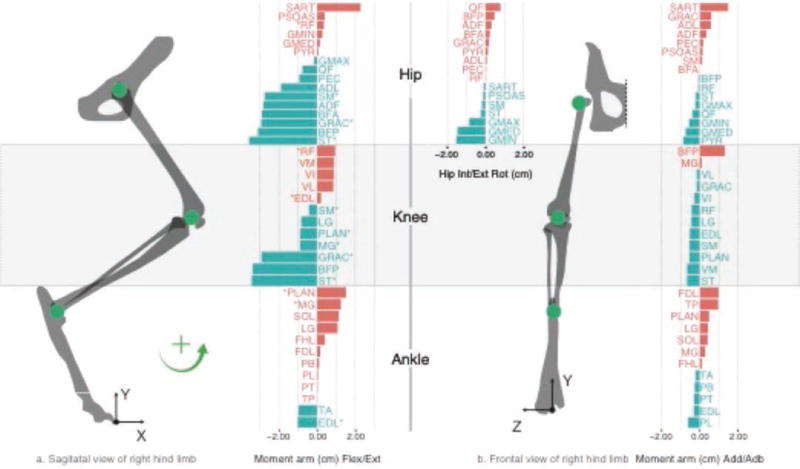
Bone lengths, joint axes of rotation, and moment arm matrix for the species average cat hindlimb model, in cm. Positive values are shown in red and negative values in blue, as per the right-hand-rule.

Feasible force and feasible activation sets for cat hindlimb model

As described in detail elsewhere (e.g., [21, 25, 26]), a feasible force set (FFS) describes the set of all static forces that can be produced at the endpoint of a limb. Briefly, the feasible mechanical output of the endpoint of a limb is 6-dimensional: 3 forces (the FFS) and 3 torques (the feasible output torque set)—which arises from the fact that a rigid body (i.e., the endpoint of a limb) has six degrees of freedom, three displacements and three rotations. Together they form a 6-dimensional feasible output wrench [27]. In the robotics literature [28], feasible force and torque outputs are plotted separately as they have different units. Thus the FFS can be at most 3-D, and is a subset of the feasible wrench set. For the task of producing pure output force as in this model, we enforce the constraint that the endpoint produce no output torques [21]. Thus the FFS is the complete representation of the maximal mechanical output of the limb. For limb models constrained to move on a plane, the FFS is a convex 2-D polygon (Figure 2, Left). For models that can move in 3-D space, the FFS is a convex 3-D polyhedron (Figure 2, Center) with its origin at the endpoint of the limb [21, 26].

Figure 2.

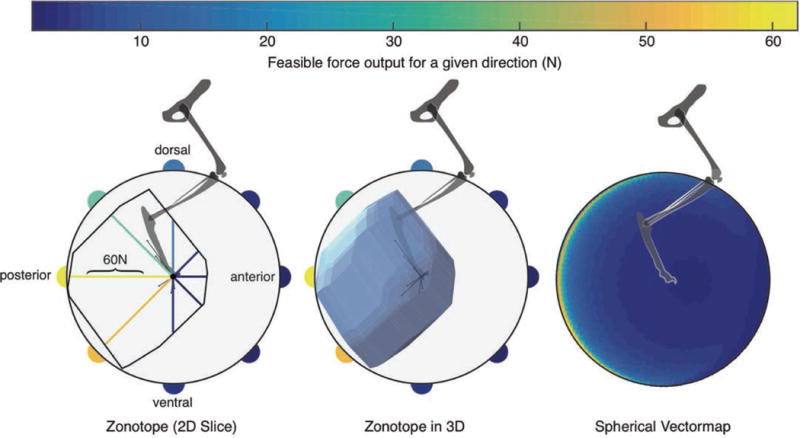
Left: The polygon of the 2-D feasible force set in the sagittal plane. The color-coded vectormapping of radial lines indicate the magnitude of the maximal feasible force along that direction, then vectormapped onto the perimeter of the circle surrounding the FFS. The very thin lines emanating from the origin are the lines of action of each of the 31 muscles. Center: the polyhedron of the 3-D FFS, again with the vectormapping of force magnitude values onto a circle in the sagittal plane. Right: The color-coded vectormapping onto the surface of a sphere indicating the maximal feasible force in every direction in 3-D. Note the FFS is rather flat on the sagittal plane, but elongated towards the posterior direction. All data are for the cat called Birdy in [2]. For 3-D views see [[[add Elsevier URL]]].

Importantly, as described elsewhere [21, 25, 26, 29], the FFS is produced by the feasible activation set (FAS)—the set of all muscle activations that meet the constraints of the task. For linear constraints as in this case, the FAS is a convex polytope in n-dimensional space, where n is the number of independently controlled muscles acting on the limb. The FAS is at the center of studies of muscle redundancy because it contains an infinite number of points. Sometimes this subspace is called the nullspace of the task as any point in it can, by construction, meet its constraints [30]. But it is nevertheless a highly structured subset of n-dimensional space. A critical result of our work is that we present a means to visualize and characterize the FFS by examining one muscle at a time.

Vector mapping of the feasible force set

It is challenging to understand and visualize a 3-D FFS, as it is an irregularly shaped convex polyhedron (Figure 2, Center). Likewise, those difficulties are exacerbated for the FAS as it is also an irregularly shaped polytope, but in high dimensions. As mentioned in the Introduction, it is critical to understand the structure of the FFS and FAS as they lie at the heart of many debates about muscle redundancy, muscle synergies, disability, rehabilitation, motor learning, etc. One approach to connect the structure of the FFS and the FAS is by computing their bounding boxes (i.e., the extreme points in every dimension [2, 16, 31]). However, this overestimates both their size and volume, and ignores the complexity of their structure. Another possibility is to find the largest sphere the polytope can encase [31], but this underestimates their size and volume, and assumes a uniform structure. We now propose an alternate method that helps us visualize the structure of the FFS, in a ‘vectormap’. After identifying the maximum feasible force in a given direction (Figure 2, Left), we assign that value of force to a 3-D point, where color denotes the force intensity. A spherical heatmap is formed with all of the computed directions and respective maximum forces; Figure 2 (Right) shows the vectormap representation of the FFS.

Traditionally, polyhedra like the FFS cannot be combined or compared quantitatively because the vertices do not align across different individual musculoskeletal models. As vectormaps are composed of consistent unit vectors for force output (or muscle activation, see next section), they can be averaged and compared. For example, they can be compared across individuals of a species to identify regions that have higher variability within a population. The color on the surface of the sphere can then be used to represent the mean or standard deviation of maximal output force or muscle activation (Figure 3).

Figure 3.

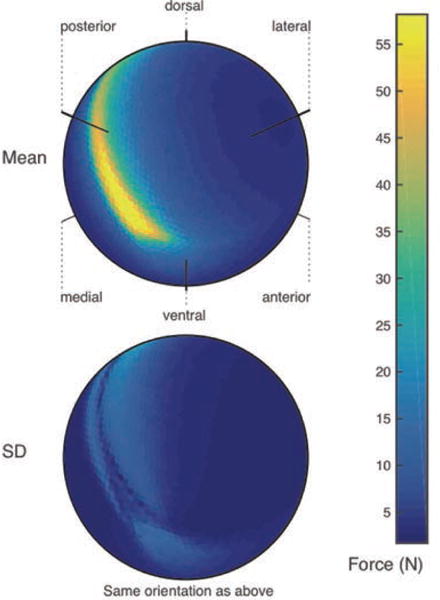
Top: Vectormap of the average of maximal feasible force across all sampled output vectors in three feline hindlimbs. Bottom: A vectormap displaying regions of the feasible force space that have higher standard deviation across three cat hindlimbs. Force in Newtons represented by color scale.

Vectormapping of the feasible activation set

We present a way to visualize the structure of the FAS, a convex polytope in n-dimensional space, on a muscle-by-muscle basis. For each muscle we can generate activation vectormaps where color represents its unique activation level for every point on the surface of the FFS (Figure 4). This is possible because any point on the surface of the FFS (i.e., the maximal force in every direction) is generated by a unique muscle activation pattern [21]. This unique activation pattern assigns the color to that point on the vectormap of each muscle. In the case of the cat hindlimb there are 31 muscles, and therefore, 31 vectormaps of unique muscle activations.

Figure 4.

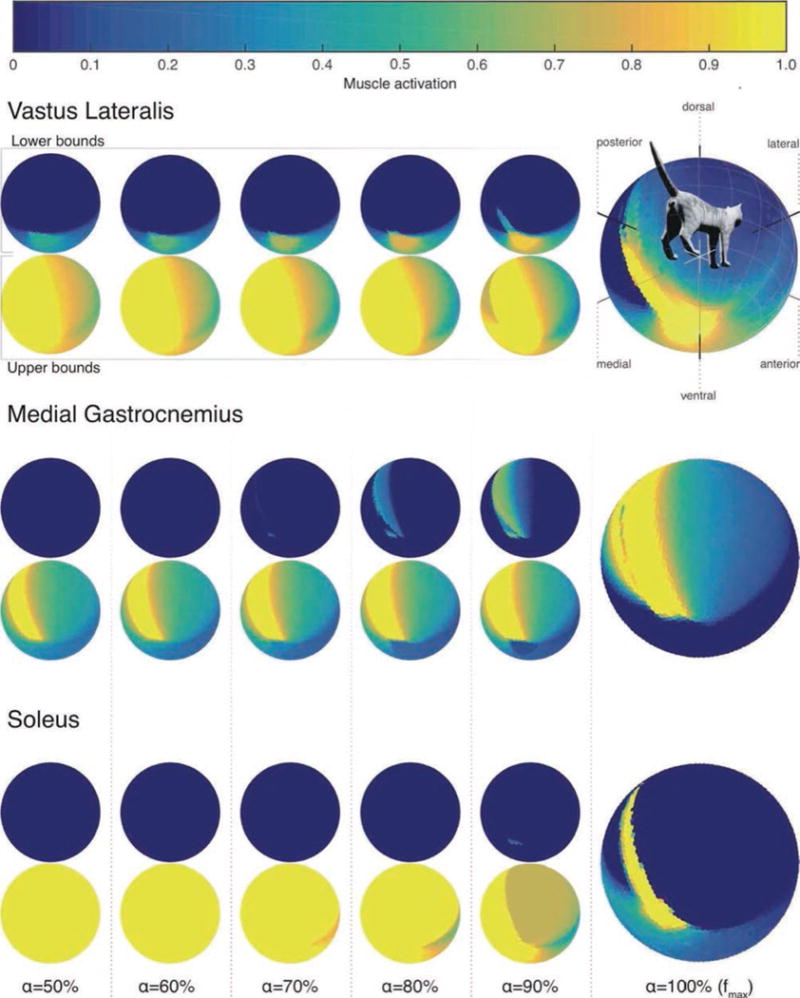
Structure of the feasible activation set for three muscles. The large vectormaps on the far Right show their unique activation level for maximal force output in every 3-D direction. Because multiple activation levels can produce submaximal forces, the small vectormaps to the Left show the lower and upper bounds of those feasible activation levels for force magnitudes (a) gradually increasing from 50% of maximal in every 3-D

Importantly, submaximal forces in each 3-D direction (i.e., points within the FFS) can be produced by an infinite number of solutions [21, 30]. The structure of those solutions can be approximated by the bounding box approach in [2, 16]. We extend that prior work by creating vectormaps of the lower and upper bounds of activation for each muscle, for all directions in 3-D (Figure 4).

Cat hindlimb model: Results

Intra-species differences in the feasible force set

With one FFS per cat, we find that force capability distributions for the three cats can differ in specific 3-D directions. Figure 3 shows between-cat comparisons: a species average (top), and standard deviation (bottom) plots across the three FFSs. We see that species average and individual FFSs are of the same general shape (c.f. Figure 2, Right and Figure 3, Top) with maximal force magnitudes remaining in the same general direction (towards the posterior direction) and of similar magnitude (c. 60 N) as for the individual cat in Figure 2. However, the standard deviation among the FFSs of the three cats can show important differences in the range of 20 N in those same directions as the maximal magnitude. But in most other 3-D directions the differences remain below 5 N.

Structure of feasible activation sets

Figure 4 shows what to our knowledge is the first portrayal of the structure of the FAS for force production in every 3-D direction. For the sake of brevity, we only show the results for three muscles. The plots for all 31 muscles are available at [[[Insert Elsevier URL here]]]. The vectormaps on the far right show the unique level of activation for maximal feasible forces in all directions. While in several 3-D directions that activity of a muscle can remain unchanged, we also see discontinuities where muscle activity is not smoothly distributed across 3-D directions as, for example, the ‘fingers’ of higher activations penetrating into areas of lower activations for vastus lateralis.

To extend prior work [2, 16], we also found the lower and upper bound vectormaps for all muscles for submaximal forces in all 3-D directions. This is the bounding box approach in [2, 16], but extended to every direction in 3-D. These plots provide a detailed view of the structure of the 31-dimensional FAS for different force magnitudes, viewing one muscle at a time. The smaller vectormaps to the left in Figure 4 show the lower and upper bounds as one increases force magnitude in all directions in 10% steps, starting at 50% of maximal force. The lower and upper bounds naturally converge for maximal output, but they converge at different rates across muscles and directions of force output—sometimes towards the upper bound, and sometimes towards the lower bound. These vectormaps of the FAS enable us to understand the rate at which redundancy is ‘lost,’ or not for every direction of force production. They also enable future studies where, say, the loss of the soleus muscles, or its hypertonia, are simulated by driving its activation to the lower or upper bound, respectively, to visualize the feasible range of compensations by other muscles.

Human arm model: Methods

The purpose of this human arm model is to understand the constraints imposed on time varying muscle activation during the kinematics of a high-speed athletic movement. Specifically, our model predicts muscle fiber lengths and velocities during a specific athletic activity—in this case throwing a flying disc with a backhand motion, like throwing a Frisbee^®. A five-DoF, 17-muscle arm model of the right arm was modeled after [1], and consisted of three joints (shoulder, elbow, and wrist) articulating three limb segments (upper arm, lower arm, and hand) with lengths of 0.35m, 0.27m, and 0.11m, respectively (Figure 5). The three DoFs at the shoulder included internal/external rotation, abduction/adduction, and horizontal abduction/adduction, and the DoF at both the elbow and wrist is flexion/extension. We note that our simplified model does not consider all DoFs at the elbow and wrist. This limitation affects the calculation of joint angles and fiber velocities, but likely does not challenge our results as in some cases fiber velocity would be somewhat lower, but also somewhat higher. We added 17 muscles/muscle groups with resting fiber length and moment arm data from various sources [32–35]. The moment arm data are shown in Figure 5.

Figure 5.

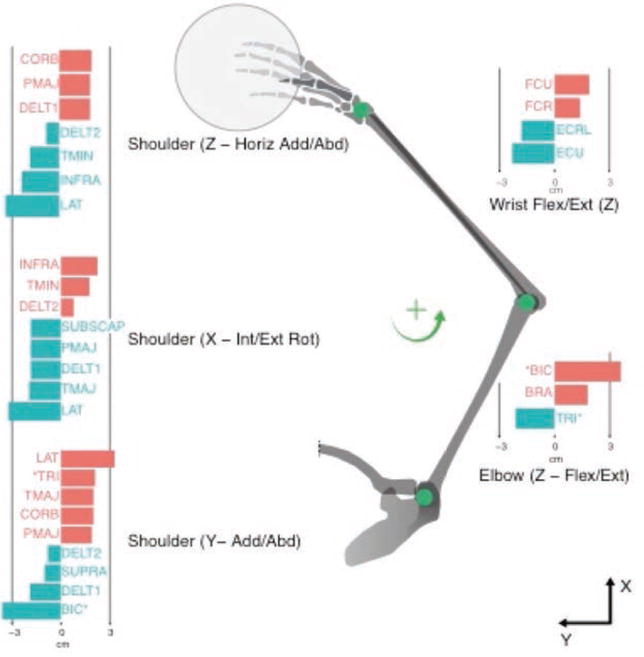
Moment arm values for human arm model. The moment arms from the 17 muscles considered in this model and their associations with the five DoFs are illustrated, in cm. The moment arms are grouped by DoF and are shown below the associated joint. Positive values are shown in red and negative values in blue.

Kinematics of throwing a flying disc and resulting muscle fiber velocities

The time-history of joint angles of the throwing motion were also obtained from [1]. We considered the initiation of forward motion, release, and follow-through portions of the throw to last, conservatively, 450ms; and approximated it as 45 unique postures at 10ms time steps, as illustrated in Figure 6. We combined measured limb kinematics with moment arm values to predict the instantaneous normalized muscle fiber velocity throughout the throw (Fig. 5).

Figure 6.

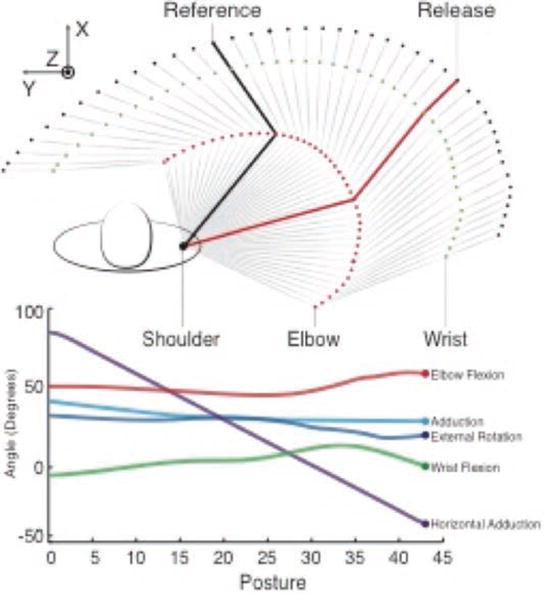
Top view of the 3-D human arm model. This figure illustrates the initiation of forward motion through follow-through of the flying disc throw. The reference posture is shown in black and the release point in the throw is shown in red. The interpolated joint angles for the 45 postures describing this motion, obtained from [1], are shown in the bottom panel.

Consider a tendon-driven limb with n muscles (17 in this case) and m joints (or DoFs, five in this case), and a limb posture defined by joint angles θ = [θ₁ … θ_m]^T. The moment arm matrix R(θ)^mxn can be defined for this tendon-driven system, having entries consisting of the moment arms r(θ)_i,j: i = 1, …, m, j = 1, …, n, at the i^th joint and j^th muscle [36]:

$$\mathbf{R}(\mathit{\theta })=\left(\begin{array}{ccccc}r{(\mathit{\theta })}_{1,1}& r{(\mathit{\theta })}_{1,2}& r{(\mathit{\theta })}_{1,3}& \cdots & r{(\mathit{\theta })}_{1,n}\\ r{(\mathit{\theta })}_{2,1}& r{(\mathit{\theta })}_{2,2}& r{(\mathit{\theta })}_{2,3}& \cdots & r{(\mathit{\theta })}_{2,n}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ r{(\mathit{\theta })}_{m,1}& r{(\mathit{\theta })}_{m,2}& r{(\mathit{\theta })}_{m,3}& \cdots & r{(\mathit{\theta })}_{m,n}\end{array}\right)$$ (Eq. 1)

As per the right-hand-rule, r(θ)_i,j is positive when pulling j^th tendon induces a counterclockwise rotation at the i^th joint, and negative otherwise. A postural change is a rotation of joints from a reference limb posture θ₀ = [θ₀₁ … θ_0m]^T to a new limb posture θ₀ = [θ₁ … θ_m]^T and is denoted Δθ = θ − θ₀ = [Δθ₁ … Δθ_m]^T. This fully determines the excursions Δs of all n muscles [36], where negative and positive excursion values correspond to eccentric and concentric contractions, respectively:

In this case we obtain the over-determined system where the changes of angles of a few variables (the joint angles) specify the excursions of all the many muscles.

$$\Delta \mathbf{s}=-{\mathbf{R}}^{\mathbf{T}}(\mathit{\theta })\Delta \mathit{\theta }=-\left(\begin{array}{cccc}r{(\mathit{\theta })}_{1,1}& r{(\mathit{\theta })}_{2,1}& \cdots & r{(\mathit{\theta })}_{5,1}\\ r{(\mathit{\theta })}_{1,2}& r{(\mathit{\theta })}_{2,2}& \cdots & r{(\mathit{\theta })}_{5,2}\\ r{(\mathit{\theta })}_{1,3}& r{(\mathit{\theta })}_{2,3}& \cdots & r{(\mathit{\theta })}_{5,3}\\ ⋮& ⋮& ⋮& ⋮\\ r{(\mathit{\theta })}_{1,17}& r{(\mathit{\theta })}_{2,17}& \cdots & r{(\mathit{\theta })}_{5,17}\end{array}\right)\Delta \mathit{\theta }$$ (Eq. 2)

To be clear, this is the very opposite of redundancy.

When the interval between postures is allotted a given amount of time, the instantaneous velocity of the muscle fibers is

$$\mathit{\nu }=\frac{\Delta \mathit{s}}{\Delta t}$$ (Eq. 3)

Please note that the velocity of the muscle fibers is not necessarily the velocity of the musculotendon. Muscle fiber pennation angle and tendon elasticity can both contribute to this [37]. For the sake of simplicity, and without loss of generality, we assume muscle fibers span the length of the whole muscle and have a small pennation angle so that we can consider them to be equivalent. A recent modeling study [38] also suggests that ‘paradoxical’ contractions—where the extreme case of muscle fibers shortening while the musculotendon as a whole is lengthening due to tendon stretch—are brief events limited mostly to large eccentric contractions to reverse movement direction. Due to these reasons, we assumed the velocities of the muscle fibers and tendons were mostly equivalent during the midsection of the uni-directional throwing motion we consider in our analysis. As is customary, we calculated the normalized muscle fiber length velocities by dividing fiber velocities by the resting muscle fiber length (l_o) of each muscle [37].

$$\overline{\mathit{\nu }}=\frac{\mathit{\nu }}{{\mathit{l}}_o}$$ (Eq. 4)

Human arm model: Results

Muscle fiber velocities for flying disc throw

Figure 7 shows the normalized muscle fiber velocities for all muscles during a 450ms flying disc-throwing motion. Notice that multiple muscles have normalized muscle fiber velocities exceeding ±5 fiber lengths/s (deep blue and deep red in Figure 7 Top, respectively). Because these high velocities are considered to be unrealistically fast [37, 39], we used Monte Carlo simulations to explore the robustness of our findings (Figure 7, Bottom).

Figure 7.

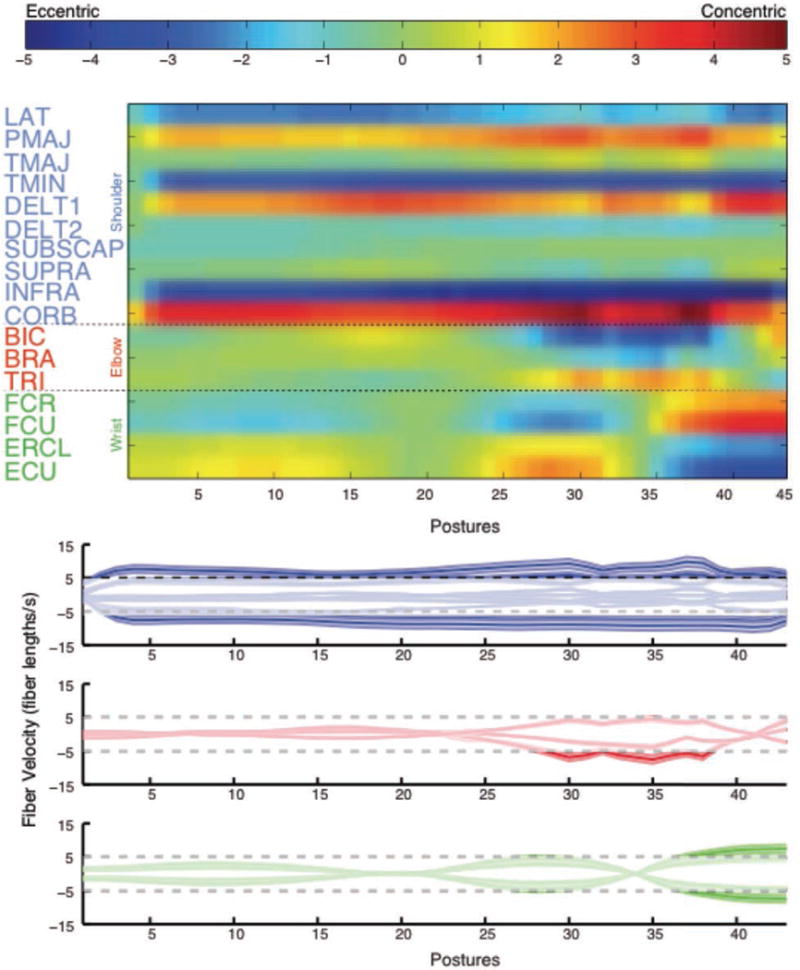
Normalized instantaneous fiber velocities during the throw for the nominal model. Top: The muscles are listed on the y-axis and the 45 postures making up the throw are shown on the x-axis. Excessive muscle velocities are shown in red (shortening) and blue (lengthening). Bottom: The same data are illustrated with individual traces for each muscle that show the fiber velocity. Muscles controlling the shoulder, elbow, and wrist are illustrated in blue, red, and green, respectively. Instantaneous fiber velocity is given on the y-axis and the postures during the throw are on the x-axis. Regions of the traces outside of the horizontal dashed lines indicate excessive muscle velocities. In both figures, the release point of the throw is indicated with a vertical dashed line.

As is often done in musculoskeletal modeling [3], we explored the effect of modeling uncertainty by iteratively running our model while sampling parameter values from uniform distributions spanning ±25% of the nominal moment arm values. Given that the joint kinematics and segment lengths come from direct measurements, our stochastic approach focused in the uncertainty of moment arm values obtained from the literature as they may or may not be appropriate for the arm of the subject who performed the flying disc throw. Note we fixed the duration of the motion to 450ms because, although slow in comparison to competitive athletes, it provides a conservative estimate of muscle fiber velocities and thus a more reasonable and defensible set of results. We guaranteed convergence of the Monte Carlo simulation by testing the variability of the running mean of normalized fiber velocity of the infraspinatus [3]. This muscle experienced the largest lengthening velocities, and as such, was at the greatest risk for injury. Only twelve iterations sufficed for the running mean of the maximal infraspinatus normalized fiber velocity to vary less than 2%. Running the Monte Carlo simulation for more iterations unnecessarily increases processing time without refining the results of maximal fiber velocities for this task. The results of our Monte Carlo simulation (Figure 7, Bottom) provide confidence in the assertion that the task of throwing a flying disc using a stroke that lasts 450ms will induce multiple muscles to exhibit normalized fiber velocities exceeding ±5 fiber lengths per second.

Discussion

In this invited methods-driven paper, we present two examples of computational methods to test neuromechanical hypotheses in the context of subject-specific and generic models, and apply these methods to explore different aspects of the classical notion of muscle redundancy. In the first example, three individual models of a cat hindlimb with 31 muscles allowed us to investigate the intra-species variation in maximal force production. This was made possible by novel computational and visualization techniques to complement a computational geometry approach to the control of tendon-driven limbs. The results presented in this manuscript, and supplemental results online at [[[add Elsevier URL]]], allows us to, for the first time, describe detailed features of intra-species differences in maximal force production, and of the structure of the 31-dimensional feasible set of muscle activation patterns for submaximal and maximal forces in all 3-D directions. In the second example, we used stochastic Monte Carlo methods to demonstrate that the kinematics of the everyday recreational and sports task of throwing a flying disc inevitably leads to unexpectedly fast eccentric and concentric muscle fiber velocities. These two examples challenge different aspects of the classical notion of muscle redundancy, and lead to specific new testable hypotheses to move our field forward.

It is useful to first mention that the analytical support for the perspective that musculature is not as redundant as we have come to believe comes from examining the set of feasible muscle activations that gives rise to the set of feasible limb outputs [21, 29]. This is the counterpart to using an optimization approach to find a single unique and optimal solution to that task [15, 21]. Rather, it seeks to find the set of all feasible muscle activation strategies that, naturally and by construction, are a well-defined region in the high-dimensional space formed by the intersection of all operating mechanical constraints of the task, given the anatomy of the limb. Therefore, the number of constraints that define the task is as important as the number of muscles in the limb—where more muscles allow meeting a greater variety and number of functional constraints [13, 14, 40].

Thus an argument against the classical notion of muscle redundancy is that the number of muscles in vertebrate limbs has evolved under functional constraints of versatile real-world behavior [13–17, 21]. We can perform ‘complex’ tasks (complexity defined as satisfying many constraints simultaneously or sequentially [14]) because we have many muscles—and muscle redundancy is most prominently seen in laboratory tasks that are too simple, and not equivalent to tasks in the natural environment [20]. This view is compatible with the above reasoning that a task is defined by the type and number of constraints that must be met. The geometric approach to define feasible outputs and their associated feasible neural inputs (FFS and FAS, respectively) provides a rigorous computational approach to the concept of muscle redundancy. Thus muscle redundancy is really more a feature of the task than of the limb [13, 14, 40].

Structure of the feasible activation and feasible force sets of the cat hindlimb

We present the vectormap as an innovative way to visualize and analyze the structure of the irregular FFS polyhedra and FAS polytopes that result from the interaction of the biomechanics of the limb and the constraints of the task. This allows us not only to interpret individual feasible sets, but also provide a coordinate system (i.e., the surface of the sphere) to combine or compare feasible sets. This differs from prior approaches that have compared their relative volume, shape, or bounding box, as described above. Figure 3 identifies the specific 3-D directions and regions of feasible force generation that exhibit the highest variability across three individuals of a species. This has applications to, for example, understanding how phenotypical (i.e., anatomical) changes lead to behavioral changes in feasible force and activation on which evolutionary selection may act.

It is of critical interest to the field of neural control to understand why extant vertebrates have ‘so many’ muscles—yet we previously lacked means to visualize the structure of the set of feasible muscle activations for a given task. The main difficulty is that selecting a given muscle activation pattern necessitates selecting a point from within the set of all feasible activations determined by the mechanics of the limb and the constraints of the task [17, 21, 22]. As described above, prior work approximated the structure of feasible activations for force production in a given direction by their bounding box [2, 16, 17]. In Figure 4 we present how it is now possible to visualize the lower and upper bounds of feasible levels of activation for each and every muscle when producing submaximal force in every 3-D direction. It can be quite striking that even for very near maximal activation (i.e., at 90%), the range in between these upper and lower bounds can be exceptionally wide, as in Figure 4. This had been reported in a single direction of force production by [2], but here we can show the rate of convergence to the unique solution for maximal force for every direction of force production.

The wide (or narrow) latitudes in allowable coordination patterns for submaximal force seem to very clearly demonstrate that trying to find and justify a ‘unique’ solution to these types of problems is highly dependent on the task and the cost function chosen. Note that in other muscles and/or directions this rate of loss of redundancy can proceed at different rates, directly affecting the latitude the nervous system has to select a given coordination strategy—and the necessary correlations in activations among muscles [16, 17].

The structure of the solution space, the latitude it affords, and the necessary correlations in muscle activations are all at the root of the study of muscle redundancy, muscle synergies, learning and adaptation, uncontrolled manifolds, etc. Importantly, these vectormaps of feasible activation ranges for submaximal forces motivate EMG studies to understand whether and how vertebrates actually make use of them (e.g. during learning and adaptation). This ties into the spatiotemporal exploration-exploitation of the null-space of a task. As discussed in detail elsewhere ([41] and references therein), traversing the solution manifold is likely an active spatio-temporal process where the neural controller can choose to inhabit a particular region or subset of the solution space to meet the requirements of the task. Thus, the nature of motor control may be more related to exploring and learning the feasible set of activations, and using memory and improvements via fast and slow gradients, than the current thinking emphasizing optimization to find unique solutions. A subtle point is that muscle synergies will naturally be detected from such explorations-exploitations of a well-structured feasible activation space. Our hope is that these techniques may help the evolution of this [17, 22, 23, 42] and other debates in motor control.

While questions remain about which muscles are necessary or optional to produce submaximal force output for a given set of constraints and why [2], they can only be answered as we begin to add all spatio-temporal constraints [41, 43] for natural behavior in the real world [13, 14]—as opposed to tasks in the laboratory setting. But for now, we at least demonstrate that we have the tools to visualize and compare changes in the structure of the FAS. In fact, for the case of maximal force output for which the activation levels are unique, we can already glean important lessons that motivate testable hypotheses (Figure 4, far Right).

An example that comes to mind looking at the three muscles shown (and more available online), is that the interaction between limb mechanics and task constraints leads to irregular and complex levels of activation across 3-D directions of force production. This counters the widespread view that muscles are engaged in a manner consistent with spatially smooth cosine tuning functions [44]. Therefore, these tools begin to address the need for computational tools pointed out in [2, 17, 23] to characterize and explore the extent to which mechanical considerations determine the neural control of numerous muscles.

Muscle activation for fast everyday recreational and sports tasks

The velocities of individual muscle fibers, and how they are determined by the kinematics of a task, are a particular example of task constraints that have often been overlooked. We find the common recreational task of throwing a flying disc (and reasonably other similar tasks such as throwing a ball, etc.) invariably leads to muscle fiber velocities greater than c. 5 muscle fiber lengths per second (Figure 7). Such high concentric and eccentric muscle fiber velocities are thought to incapacitate active force production or lead to tearing injuries, respectively [37, 39]. We employed a process of elimination to systematically investigate our model and its parameters to give us confidence in our interpretation of the results. Intuitively, we can assume that the bone (segment lengths) and joint kinematics were obtained experimentally and are physiologically reasonable. The muscle fiber lengths and moment arms we considered in our study were obtained from published data [32–35]. Due to the between subject variability, we applied a Monte Carlo analysis to consider a range of moment arm values for each muscle and still find high fiber velocities (Figure 7, bottom). While we do not show them, we find similar results in a Monte Carlo analysis of the muscle fiber lengths. Moreover, even though our model is limited in that it did not include the acceleration and deceleration phases of the movement, adding them could only increase muscle fiber velocities we report. Likewise, assuming a less conservative total time for the movement would only exacerbate the high velocities we find. Despite this systematic Monte Carlo analysis, we still find muscle fiber velocities greater than 5 fiber lengths per second. Thus we are compelled to challenge the traditional understanding of the force-velocity properties of muscles and motivate future research in muscle mechanics: somehow, such high fiber velocities are likely present in everyday tasks do not lead a complete loss of force production capabilities in the concentric phase, or injury in the eccentric phase. This is not the first time we question the functional role of the force-velocity properties of muscles for everyday tasks [13].

Another fundamental result from these simulations is that they emphasize the need to study the temporal structure of muscle activation in the context of muscle redundancy [41, 43]. Consider Eq. 2 defining the over-determined physical relationship between changes in joint angles and tendon excursions that drive changes in muscle fiber lengths. This relationship defines the obligatory correlations among tendon excursions where a sequence of (a few) joint angles uniquely and completely determines the excursions of all (numerous) musculotendons. This is the opposite of muscle redundancy as there is a single and unique set of tendon excursions that can satisfy the kinematics of a given movement. This begs the question of how the nervous system coordinates eccentric and concentric contractions to produce such fast movements. If, for any reason, any muscle fails to lengthen (i.e., contract eccentrically) to satisfy the rotations of the joints it crosses, the desired motion will, at best, be disrupted, or at worst, the limb will freeze.

What inhibits stretch reflexes to allow such coordinated eccentric contractions? Alpha-gamma co-activation, reciprocal-inhibition, and gating of spindle afferent information are some of neural interactions thought to be necessary to modulate/inhibit stretch reflexes [45]. Thus the nervous system must issue neural commands, coordinated throughout the entire duration of the movement, to (i) alpha-motoneurons to produce the necessary joint torques as per the standard force-sharing motor control problem (e.g., [9, 30]); (ii) coordinate reciprocal-inhibition of alpha-motoneuron pools across shortening and lengthening muscles (e.g., [46]); (iii) inhibit the stretch reflex in muscles needing to undergo eccentric contractions (e.g., [47]); while (iv) satisfying the time constants of muscle excitation-contraction dynamics [37] to ensure the continuity of these neural commands as the motion progresses. This compounding of multiple spatial and temporal constraints naturally leads to a shrinking of the set of feasible motor commands for natural movements (see above discussion and [13]). In fact, clinicians have long been aware of how disorders of reflexes or the neural circuits of ‘afferented muscles’ lead to disruptions or failures of movements (for an overview see [48, 49]. We now propose that these so-called dystonias may in fact be a natural consequence of the nervous system failing to meet the stringent temporal demands on alpha-gamma neural drive for the eccentric and concentric contractions essential to smooth limb movement. This again supports the view that extant vertebrates have barely enough neural degrees of freedom for versatile real-world behavior [13–17] as the muscle activations to produce smooth movements is likely not redundant, or at the very least not as redundant as currently thought.

One last comment is on the over-determined nature of producing the necessary muscle excursions for a limb movement. As mentioned above, over-determined systems either have one unique solution (if it exists), or no solution at all. When no solution exists, a practical alternative is found by violating some or all constraints as in the method of least squares for a set of equations in which there are more equations than unknowns. This may actually begin to explain why muscles and tendons have non-trivial amounts of passive elasticity—to provide tolerance to errors in the neural control of their excursions when eccentric and concentric contractions are not controlled accurately enough by the CNS. From the engineering perspective, such elasticity complicates control as it adds delays and internal actuator dynamics, and reduces actuator bandwidth. But in the case of biological tendon-driven limbs, this built-in tolerance to excursion errors may be a critical compliment to, and enabler of, the neural control of smooth movements.