Abstract
Purpose
Segmentation of the prostate on MR images has many applications in prostate cancer management. In this work, we propose a supervoxel‐based segmentation method for prostate MR images.
Methods
A supervoxel is a set of pixels that have similar intensities, locations, and textures in a 3D image volume. The prostate segmentation problem is considered as assigning a binary label to each supervoxel, which is either the prostate or background. A supervoxel‐based energy function with data and smoothness terms is used to model the label. The data term estimates the likelihood of a supervoxel belonging to the prostate by using a supervoxel‐based shape feature. The geometric relationship between two neighboring supervoxels is used to build the smoothness term. The 3D graph cut is used to minimize the energy function to get the labels of the supervoxels, which yields the prostate segmentation. A 3D active contour model is then used to get a smooth surface by using the output of the graph cut as an initialization. The performance of the proposed algorithm was evaluated on 30 in‐house MR image data and PROMISE12 dataset.
Results
The mean Dice similarity coefficients are 87.2 ± 2.3% and 88.2 ± 2.8% for our 30 in‐house MR volumes and the PROMISE12 dataset, respectively. The proposed segmentation method yields a satisfactory result for prostate MR images.
Conclusion
The proposed supervoxel‐based method can accurately segment prostate MR images and can have a variety of application in prostate cancer diagnosis and therapy.
Keywords: magnetic resonance image, prostate, segmentation, supervoxel
1. Introduction and Purpose
Prostate cancer is the second leading cause of cancer mortality in American men.1 It was estimated that in 2016 there were 180,890 new cases of prostate cancer, and 26,120 deaths from prostate cancer in the United States.1 Magnetic resonance imaging (MRI) has become one of the most promising methods for prostate cancer diagnosis and MR images has also been used for targeted biopsy of the prostate. Segmentation of the prostate on MR images has many applications in the management of this disease.2, 3, 4 Registration between transrectal ultrasound (TRUS) and MRI can provide an overlay of MRI and TRUS images for targeted biopsy of the prostate.5, 6
There are extensive studies on prostate MR image segmentation.3, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 Among these methods, active contour model (ACM)‐based methods have been widely used due to their good performance.11, 17, 18 This method aims to evolve a curve, subject to constraints from a given image, in order to detect objects in that image. Kass19 proposed an active contour model that depends on the gradient of the image in order to stop the evolving curve on the boundary of the object. Chan and Vese17 proposed a level set formulation of the piecewise constant variant of the Mumford–Shah model20 for image segmentation. Their model can detect an object whose boundary is not necessarily defined by image gradient. Tsai18 presented a shape‐based method for curve evolution to segment medical images. A parametric model for an implicit representation of the curve is derived by applying the principal component analysis to a collection of signed distance representations of the training data. The parameters are then manipulated to minimize an objective function in order to get the segmentations. Qiu11 proposed an improved ACM method incorporated into a rotational slice‐based 3D prostate segmentation to decrease the accumulated segmentation errors generated by the slice‐by‐slice method. A modified distance regularization level set algorithm was used to extract the prostate. Shape constraint and local region‐based energies were imposed to avoid the evolved curve to leak in regions with weak edges. Given a good initialization, ACM could yield a good segmentation result. However, it is a nontrivial task to get a good initialization. Therefore, ACM is difficult to get a global minimum of the energy function.
Another popular method for segmenting prostate segmentation is graph cut‐based algorithm. Graph cut (GC)21, 22 is a global optimization tool, which gains more attentions due to its efficiency. Egger12 proposed a graph‐based approach to automatically segment the prostate central glands based on a spherical template. The rays travel through the surface points of a polyhedron to sample the graph nodes. The minimal cost on the graph was optimized by graph cut, which results in the segmentation of prostate boundaries and surface. Mahapatra and Buhmann13 proposed a fully automated method for prostate segmentation using random forests and graph cuts. The probability map of the prostate was generated by using image features and random forests classifier. The negative log‐likelihood of the probability maps was considered as the penalty cost in a second‐order Markov random field (MRF) cost function, which was optimized by graph cuts to get the final prostate segmentation. However, graph cut tends to leak at weak boundary. Fig. 1 shows the limitations of the graph cuts and the active contour model.
Figure 1.
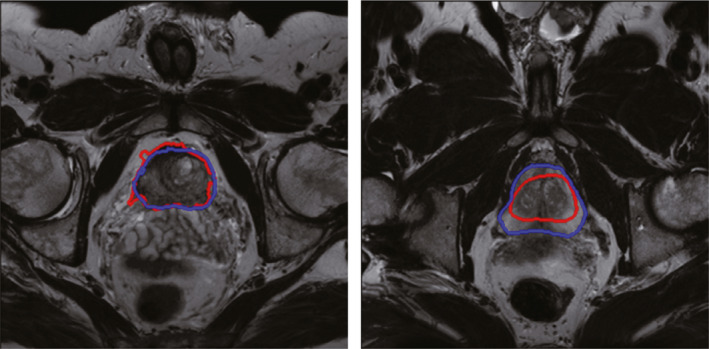
Limitations of the graph cut method and the active contour model‐based method for prostate segmentation. Blue curve is the ground truth from manual segmentation by a radiologist, while the red curves are the segmented contours by the computer algorithms. Left figure is the segmentation result obtained by graph cuts, while the right figure is the segmentation result obtained by active contour model. The graph cut method tends to leak at the location with low image contrast, while the active contour model‐based method may fall at local minima based on an inaccurate initialization. [Color figure can be viewed at wileyonlinelibrary.com]
Combination of ACM and graph cut is a straightforward method to overcome the drawbacks of both methods. The graph cut‐based active contour method23, 24 has been proven effective for object segmentation in the computer vision field. They showed that the combination of graph cut and active contour can alleviate the disadvantages of both algorithms. Zhang et al.25 proposed a graph cut‐based active contour model for kidney extraction in CT images. The experiments showed that the algorithm takes the advantages of graph cut and active contour for kidney CT segmentation. In our method, we combine graph cut and active contour in a cascade manner, which could yield better performance compared to an individual algorithm.
In this work, we propose a hybrid method, which combines graph cut and active contour model. This hybrid method takes the advantages from both GC and ACM, while it alleviates the effect from both disadvantages. The proposed prostate segmentation method is different from the aforementioned methods in the following aspects: i) a 3D graph cuts and a 3D active contour model are combined in a cascade manner, which can yield accurate segmentation results. ii) The shape model is obtained based on each MR volume individually, which further improve the performance. This patient‐specific shape model makes our method more robust across different prostate MR image datasets. iii) To the best of our knowledge, there is no report on 3D supervoxel‐based graph cuts segmentation for the prostate in MR images.
The remainder of the paper is organized as follows. In Section 2, supervoxel‐based prostate segmentation framework is introduced, which is followed by the details for each part of the proposed method. In Section 3, we show the experimental results. We conclude this paper in Section 4.
2. Method
2.A. Framework of the proposed method
Figure 2 shows the framework of the proposed method that consists of three parts: supervoxel generation, graph cuts, and 3D active contour model. The first part is the supervoxel generation, which is the basic processing unit in our method. After getting the supervoxels, a neighborhood system is built by connecting supervoxel to each other. The second part is the supervoxel‐based graph cuts. The supervoxel labeling problem is considered as a minimization of an energy function by using graph cuts. A supervoxel‐based shape data term and a supervoxel‐based smoothness term are computed to construct energy function. The segmentation result obtained by graph cuts tends to leak at the location with low image contrast. Therefore, a 3D active contour model is introduced to refine the segmentation obtained from graph cuts as the third part of the proposed method.
Figure 2.
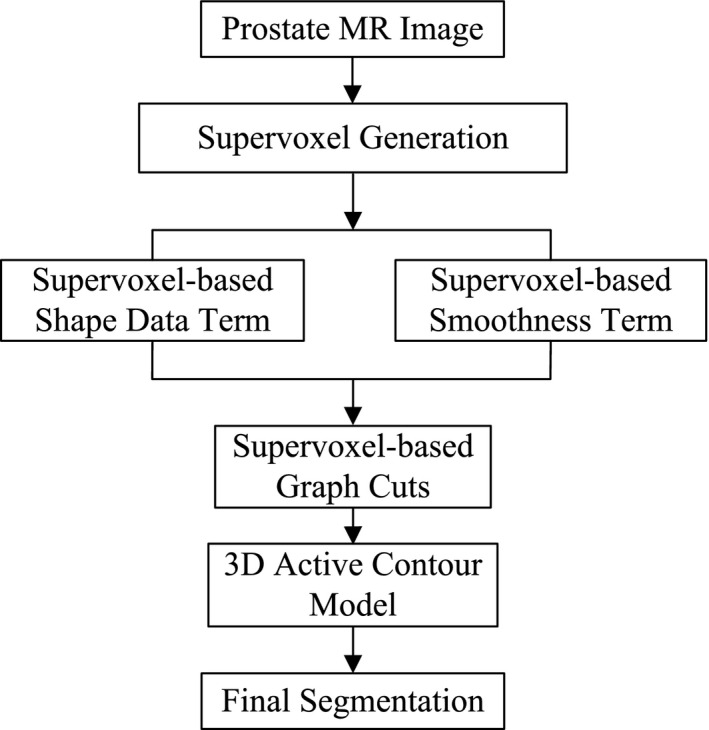
The framework of the proposed method.
2.B. Supervoxel
In this work, we consider each point in an MR slice as a pixel instead of a voxel. A set of pixels, which have similar intensities, locations, and textures in a slice, are called superpixel. Meanwhile, a set of pixels have similar intensities, locations, and textures in an MR volume are considered as supervoxel, which represents a 3D tube.
Ideally, superpixels with similar intensities, locations, and textures across image sequence should have same labels. However, most superpixel methods do not meet this requirement. To solve this problem, supervoxel is proposed to segment image slices into 3D tubes which can yield consistent image segmentation through the whole image volume. Xu and Corso26 studied five supervoxel algorithms and measured the performance of these methods, which provides the details on the generation of supervoxels.
There are two advantages of using supervoxel for the proposed method. First, the supervoxel captures the local redundancy in the 3D medical image, which yields a small number of supervoxels. The small number of superpixels reduces the computational cost of the proposed algorithm significantly, e.g., for a 3D prostate MR image with a size of 320 × 320 × 100, the number of voxels is over 10 million, while the number of supervoxels is only about 20,000 in our method. Second, a supervoxel containing more voxels makes the supervoxel‐based feature more reliable, which can minimize the risk of assigning wrong labels to the supervoxels.
Figure 3 shows the supervoxel and their geometric relationships. In this work, supervoxel is defined as follows.
| (1) |
where K is the number of the supervoxels in an MRI volume. is the number of slices contained in supervoxel i. is an intersection between supervoxel and slice j. In the MRI volume, different supervoxels may have different beginning slices and ending slices, which result in a different life span.
Figure 3.
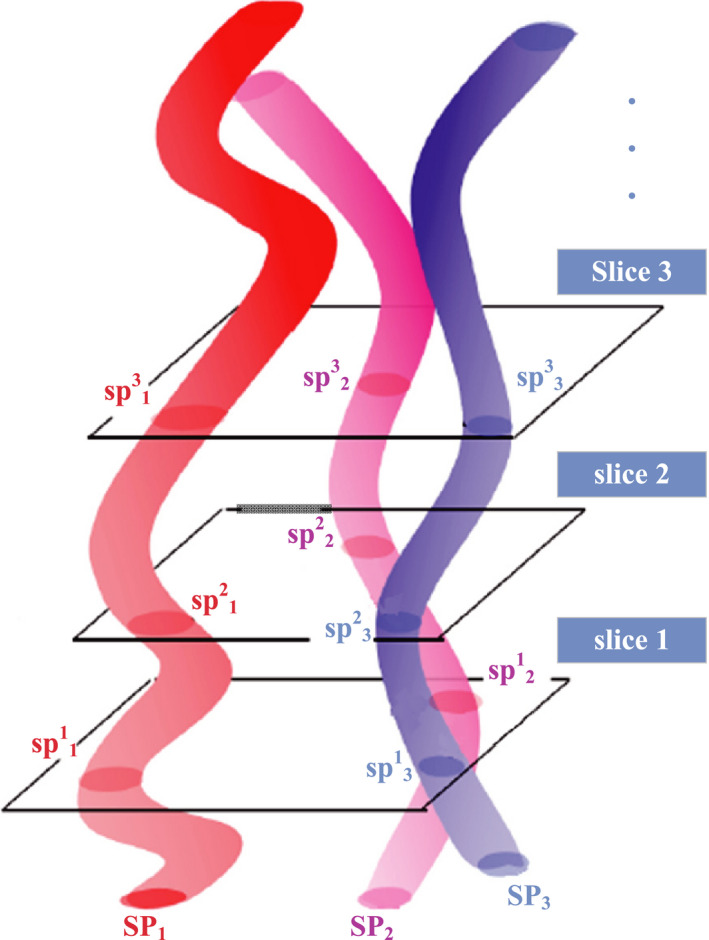
Supervoxels and their geometric relationships. Different colored 3D tubes represent three supervoxels in the slice sequence. [Color figure can be viewed at wileyonlinelibrary.com]
As supervoxel is the basic processing unit of our method, it should satisfy two requirements. First, it should be efficient. Second, the number of supervoxels or the size of each supervoxel should be adjustable. Based on the requirements, simple linear iterative clustering (SLIC)27 algorithm is adopted to obtain the supervoxel. Figure 4 shows an example of supervoxel map of an MR volume.
Figure 4.

Top: Four consecutive slices from a typical MR volume. Middle: The corresponding supervoxel maps. The second row shows the boundaries of supervoxels. Bottom: The colored supervoxel maps, while same color through four slices means the same supervoxel. [Color figure can be viewed at wileyonlinelibrary.com]
Instead of generating 2D regions and reconnecting in the third dimension, the supervoxels are directly generated in a 3D manner at one time. Here we give a brief introduction of the 3D supervoxel generation. First, k initial cluster centers are chosen on a 3D regular grid at the intervals of length in all three dimensions. Second, the centers are moved to the lowest gradient position in a small local region. Third, the SLIC assigns each voxel to the new center based on spatial proximity and intensity. Then the algorithm iteratively computes the new centers and assigns the voxels. The iteration will stop after n iterations or until the distance between the new centers and previous one is small enough. As SLIC does not guarantee that the supervoxel are fully connected, which means some isolated voxels are not assigned to any supervoxels. Therefore, a postprocessing step enforces connectivity by reassigning these voxels to nearby supervoxels.
2.C. Graph cut
For graph cuts, it seeks a labeling that minimizes the energy function as described below:
| (2) |
The data term evaluates the penalty for assigning a particular pixel to the object or background according to the prior knowledge; while the smoothness term evaluates the penalty for assigning two neighboring pixels different labels in term of the given image data. In general, the data term is formulated as , where evaluates how well the label fits the pixel i given the observed data. The choice of smoothness term is an important issue. Ideally, it should make labels smooth in the interior of the object and preserve discontinuity at the boundary of the object. Once the energy is defined, the graph cuts algorithm can be used to find a global minimum efficiently.
In our work, the prostate segmentation is considered as a labeling problem, where each supervoxel in the MR volume will be assigned a label . Label 1 represents the prostate, while Label 0 corresponds to the background. The labels can be obtained by minimizing the energy function defined on an undirected graph G = (V,E). V is a set of vertices correspond to supervoxels, and the edge E connects neighboring superpixels in a 3D neighborhood system, which will be introduced later. Our supervoxel‐based energy function is formulated as follows:
| (3) |
where SP is a set of supervoxels, N represents the 3D neighborhood system, {p,q} stands for two neighboring supervoxels in the 3D neighborhood system. The data term D quantifies the distance of each supervoxel to a proposed shape model. The smoothness term V quantifies how likely two supervoxels have the same labels. The parameter γ balances the weight between the data term and the smoothness term. The graph cut method was implemented by using the public library “maxflow‐v3.01".28 The default weight parameter is fixed to γ = 0.2 in all of our experiments. Empirically, this weight is found to provide good results for all MR images.
2.C.1. Shape model‐based data term
To build the data term, a shape model is proposed to obtain the supervoxel‐based shape feature. The basic idea is that the supervoxel is close to shape model will have a high probability to be labeled as the prostate. The shape model of the prostate is obtained based on user intervention, which could capture the shape variability more accurately for an individual prostate. However, the automatic methods use population information to train a model to capture a statistical shape of the prostate on MR images. For segmenting the prostate on a new MR image, the patient‐specific shape model plays more important role than statistical shape to guide the algorithm to segment the prostate. Therefore, the patient‐specific shape model makes our method more robust across different datasets. In addition, it can obtain more consistent segmentation results than other automatic methods that are based on population information.
There are three steps to get the shape model. First, three key slices are selected from a 3D MR image, which are from the apex, base, and middle regions of the prostate. Second, four points are marked by the user for each of these three key slices. For each key slice, the four points are located at the boundary of the prostate. An initial prostate contour in one key slice can be determined through these four points. Therefore, three contours are obtained for the apex slice, based slice, and middle slice, respectively. Third, two semiellipsoids are fitted based on these three contours. One is toward to the apex slice based on the contours in the apex and middle slices, the other is toward to the base slice based on contours in the base and middle slices. Note that these two fitted surfaces of semiellipsoids are not accurate for the prostate, but it is good enough to be used for computing the shape feature.
Once the semiellipsoids are obtained, the prostate and background shape data terms can be defined as follows.
| (4) |
where represents the mean value of shape feature of a supervoxel. and are calculated by using a distance transform based on the fitted semiellipsoids as follows.
| (5) |
where d is the distance of a voxel to the surface of the fitted semiellipsoids, which computed by a fast implementation.29 κ controls the contrast between the inside and outside of the shape model. ε controls the fatness of the shape model. In our experiments, the parameters κ and ε are set as 20 and 0.1 for all images, respectively.
The distance‐based shape model is difficult to find the accurate boundaries between the prostate and the background by using voxels. Because the voxels on the both close sides of the prostate contour have a very similar distance to the fitted ellipsoids, it is difficult to separate these voxels based on the distance from the shape model. In contrast to voxels, supervoxels on the both close sides of prostate contour have distinguishing distance. Therefore, supervoxel is needed by shape model for segmenting prostate in our method.
In the proposed method, the shape feature is used to represent the supervoxels. Based on the feature of each supervoxel, the similarity of two neighboring supervoxels can be measured, which is smoothness term of the energy function in the GC method. In addition, the shape model can also describe the likelihood of each supervoxel belonging to the prostate or background, which is the data term of the energy function. Figure 5 shows the supervoxel‐based data term computed based on the shape model.
Figure 5.

The supervoxel‐based data term. The first image is one original image slice of the prostate MR. The second image is the corresponding supervoxel map. The third image is the foreground shape data term. If the supervoxels are assigned as the foreground, the penalties of the shape model are shown in color. Darker region represents a low penalty, while brighter region represents a high penalty. The fourth image is the background shape data term. The color has same meaning with the foreground shape data term. [Color figure can be viewed at wileyonlinelibrary.com]
2.C.2. Smoothness term
The affinity of two neighboring supervoxels and are used to build the smoothness term. Therefore, the smoothness term is defined as follows.
| (6) |
where and are the number of slices of supervoxels and , respectively. represents the number of common slices between two neighboring supervoxels. The smoothness term encourages that supervoxels have similar affinities and share more common slices to be labeled as same labels.
2.D. 3D Active contour model
The graph cut algorithm is an efficient method. However, the output of graph cut may be not satisfactory when the supervoxel algorithm cannot find the boundary of the prostate accurately. Because the supervoxel algorithm only uses local information in a small region to cluster voxels into a 3D supervoxel, it is hard to find the prostate boundary accurately, especially when the background has similar intensities and textures to that of the prostate. To solve this problem, the segmentation result obtained from the graph cut should be refined. In our method, 3D ACM is adopted to refine the prostate surface. Before presenting the 3D active contour model, a 2D active contour is reviewed first.
Let Ω denote the image domain, where . Considering an image I contains two regions, the object region to be segmented is denoted ω, the other is background region. The following model is proposed:
| (7) |
The last regularizing term ∂ω represents the curve C weighted by a constant μ, and is the average value of I inside of ω, while is the average value of I outside of ω. Chan and Vese simplified the Mumford–Shah function as the following energy function:
| (8) |
where H is the Heaviside function. Φ is a level set function, whose zero level set C = {x,y:Φ(x,y) = 0} segments the image into two regions, the object region {Φ(x,y) > 0} and the background region {Φ(x,y) < 0}. The minimization of the energy is achieved by finding the level set function Φ and the constants and .
For 3D segmentation, the energy function is defined as follows:
| (9) |
Now, ∂ω represents the surface S weighted by a constant μ. Following 2D simplification, the functional is simplified as the following energy function:
| (10) |
Based on this model, the 3D active contour model could get smooth surface of the prostate, which can cover the shortage of the graph cut.
The work of Zhang et al.30 was used in our method, which integrates edge and region‐based segmentation in a simple equation as follows.
| (11) |
Φ is a signed distance function, I is the image to be segmented, g = g(¦∇I¦) is boundary feature map related to the image gradient. α and β are predefined parameters to balance these two terms. 3D ACM is implemented by using a 2D/3D image segmentation toolbox.31 The parameters used in the toolbox are set as α = 1e−6 and β = 1 for all of our experiments.
Instead of dealing with the entire MR volume, ACM only considers an inner and outer region on both sides (15 voxels) from the fitted surfaces for detection of prostate. The number of iterations of 3D ACM is set as five in our experiment. If there is no change on the surface between two iterations, the algorithm will stop early. The local evolution and small number of iterations guarantee that the ACM only smooths the segmented contour without changing the segmented contours in a major way.
2.E. Segmentation evaluation
The proposed method was evaluated based on four quantitative metrics, which are Dice similarity coefficient (DSC),32, 33 relative volume difference (RVD), Hausdorff distance (HD), and average surface distance (ASD).9, 34 The DSC is calculated as follows:
| (12) |
where is the number of pixels of the prostate from the ground truth and is the number of pixels of the prostate from the segmentation of our method.
The relative volume difference is computed as follows:
| (13) |
The RVD evaluates the algorithm whether tends to oversegment or undersegment the prostate. RVD is positive, if the algorithm undersegments the prostate and vice versa. To compute the HD and ASD, a distance from a pixel x to a surface Y is first defined as:
| (14) |
The HD between two surfaces X and Y is calculated by:
| (15) |
The ASD is defined as:
| (16) |
where ¦X¦ and ¦Y¦ represent the number of pixels in the surface X and Y, respectively.
3. Experimental results
3.A. Data
3.A.1. Our own dataset
The proposed method was evaluated on our in‐house prostate MR dataset, which consists of 30 T2‐weighted MR volumes. Transverse images were used in the experiments. The voxel sizes of the volumes are from 0.875 mm to 1 mm. The field of view varies from 200 × 200 mm to 333 × 500 mm. No endorectal coil was used for our data acquisition. Each slice was manually segmented three times by two experienced radiologists. Majority voting is used to obtain the final ground truth from the six ground truths.
3.A.2. PROMISE12 dataset
In addition, the PROMISE12 challenge dataset35 is used in our experiment, which has 50 training and 30 test MR images. The dataset is transversal T2‐weighted and from multicenter and multivendor. The MR images are acquired under different acquisition protocols, such as slice thickness and image size. The size of MR image is 512 × 512 (voxel size is 0.4 × 0.4 × 3.3 mm) or 320 × 320 (voxel size is 0.6 × 0.6 × 3.6 mm).
3.A.3. ISBI dataset
The National Cancer Institute (NCI) Cancer Imaging Program in collaboration with the International Society for Biomedical Imaging (ISBI)36 has launched a grand challenge involving 60 prostate MR images for training. The training dataset consists of axial scans with half obtained at 1.5 T with endorectal coil and other half at 3 T without endorectal coil. The T2‐weighted MR sequences were acquired with 4 mm or 3 mm thickness, while the voxel size varies from 0.4 mm to 0.625 mm. The image size is from 320 × 320 to 400 × 400.
3.B. Implementation details
The proposed method was implemented in MATLAB codes and C++ codes. The algorithm runs on an Ubuntu 14.04 desktop with an Intel Xeon CPU (3.4GHz) and 96 GB memory. Our code is not optimized and does not use parallel programming or multithread. The segmentation time is about 40 seconds for one 3D prostate MR image.
The user interaction time for manual segmentation varies between an experienced radiologist and a technician. The selection of the key slices and the initial points requires less than 30 seconds for a radiologist and about 1 minute for the trained technician.
3.C. Qualitative results
The qualitative results on our in‐house MR images and the PROMISE12 MR images are shown in Fig. 6. Blue curves are ground truths from manually segmentations, while the red curves are the segmentations of the proposed method.
Figure 6.
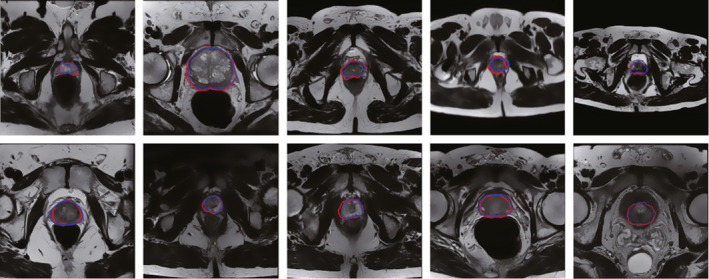
The qualitative results on two datasets. Top: Segmentation results on our in‐house MR images. Bottom: Segmentation results on the PROMISE12 MR images. [Color figure can be viewed at wileyonlinelibrary.com]
These images have different voxel sizes and image sizes, which shows the robustness of our method for different MR images. The qualitative results on our dataset and PROMISE12 dataset show that the supervoxel‐based method is able to obtain satisfactory segmentation results.
3.D. Quantitative results
3.D.1. Our own dataset
The quantitative evaluation results on our in‐house 30 MR image volumes are shown in Table 1. The values of four metrics, which are DSC, RVD, HD, and ASD, are posted in the table.
Table 1.
Quantitative results of the proposed method using our own dataset
| PT# | DSC | RVD | HD | ASD |
|---|---|---|---|---|
| Avg. | 87.19 | −4.58 | 9.92 | 2.07 |
| Std. | 2.34 | 7.59 | 1.84 | 0.35 |
| Max | 90.95 | 12.99 | 13.75 | 2.68 |
| Min | 82.77 | −16.75 | 6.93 | 1.28 |
(DSC(%), RVD(%), HD(mm), and ASD(mm))
The proposed method yields a DSC of 87.19 ± 2.34%, while it varies from 82.77% to 90.95%. It shows that the proposed method has a high accuracy and robustness. The mean RVD is negative, which shows that the proposed method tends to yield an oversegmented prostate. However, the value of mean RVD is −4.58%, which is very close to zero. This small RVD shows that the proposed method has a good balance between oversegmentation and undersegmentation. The value of HD measures the maximum distance between two surfaces, which is 9.92 ± 1.84 mm. The ASD is 2.07 ± 0.35 mm, which shows that the proposed method is able to segment the prostate with a relative small average surface distance.
3.D.2. PROMISE12 dataset
Table 2 shows the segmentation results by the proposed method on PROMISE12 dataset,35 which consists of 50 MR volumes. The proposed approach yielded a DSC of 88.15 ± 2.80%, while the maximum is 92.92% and minimum is 81.80%. The RVD is 2.82 ± 9.56%, while HD is 5.81 ± 2.01 mm, and ASD is 2.72 ± 0.77 mm. Details of the results are listed in Table 2.
Table 2.
Quantitative results on PROMISE12 dataset
| DSC | RVD | HD | ASD | |
|---|---|---|---|---|
| Avg. | 88.15 | 2.82 | 5.81 | 2.72 |
| Std. | 2.80 | 9.56 | 2.01 | 0.77 |
| Max | 92.92 | 20.68 | 11.40 | 4.43 |
| Min | 81.80 | −15.96 | 1.25 | 1.62 |
3.E. Comparison between supervoxel‐based and voxel‐based methods
To evaluate the advantage of using supervoxels compared with that of using voxels, we performed an experiment using our in‐house dataset. The DSC was used to evaluate the comparison results. In the experiment, both methods use the same framework of the proposed method. The DSC of the supervoxel‐based method is 87.2 ± 2.3%. For the voxel‐based method, the DSC is 75.3 ± 3.7%. Because the segmentation result of the voxel‐based graph cut method is not good enough to be the initialization of ACM, the final result is worse than the supervoxel‐based method.
3.F. Comparison with other methods and automatic version of the proposed method
The PROMISE12 dataset is used for comparing our method with other prostate segmentation methods. Eight methods are used for the comparison, which are Imorphics,37 ScrAutoProstate,38 SBIA,39 grislies,40 Robarts,41 ICProstateSeg,42 Utwente,43 and the automatic version of the proposed method.
The proposed method can be implemented in a fully automatic version. The straightforward way is that an automatic method is applied to substitute the user intervention to obtain the initialization for graph cuts. Milletari et al.43 proposed a convolutional neural network‐based method for automatically segmenting the prostate on MR images. Therefore, the segmentation result of Milletari's method was selected as an initialization for the shape model of graph cuts in the proposed method. The implementation of this method is publicly available.44 We used the default parameters of Milletari's method.
Table 3 shows the comparison results in terms of DSC and HD. The results were shown as mean ± standard deviation. DSC is available for all the methods, while HD are not available for all. Therefore, the hyphen is used in the table, which means that the corresponding measures are not reported in the papers. The proposed method gives the second higher DSC and the second lower standard deviation among all the methods. ScrAutoProstate38 has the highest DSC of 90%, and very low standard deviation of 1.1%. For the HD, our method is at the second place. Although, ScrAutoProstate method has the highest DSC and Imorphics method has the lowest HD, our method has a relative good performances in terms of both DSC and HD at the same time.
Table 3.
Comparison with seven other prostate MR segmentation methods and with automatic version of our method using the PROMISE12 dataset
| Ours | grislies | ScrAutoPro | Utwente | Imorphics | Robarts | ICProSeg | SBIA | Ours+Auto | |
|---|---|---|---|---|---|---|---|---|---|
| DSC | 88.2 ± 2.8 | 86 ± 6 | 90 ± 1.1 | 81 ± 12 | 88 ± 3 | 85 ± 5 | 84.6 ± 4.3 | 85 ± 4.4 | 87.8 ± 2.9 |
| HD | 5.8 ± 2.0 | 9.5 ± 2.7 | – | 7.3 ± 4.9 | 4.1 ± 1.4 | 6.4 ± 4.2 | – | – | 6.2 ± 2.5 |
3.G. Effect of the supervoxel size
Different supervoxel sizes have different performances. Bigger supervoxels contain more pixels to calculate features, which makes the supervoxel‐based features more robust. But they may contain multiple classes, which may not be representative of one class. Smaller supervoxels contains less pixels, which are more homogeneous and the extracted features are representative of a single class. However, they may not always provide a sufficient number of voxels to calculate robust features.
For the SLIC method, the third dimension (z direction) of the 3D supervoxel must be same as the first dimension (x direction) and the second dimension (y direction) of the 3D supervoxel. This constraint leads to a poor quality of the 3D supervoxel. Therefore, the size of supervoxel on the xy‐plane and z‐plane is set separately, instead of using the same step size.
To evaluate the effect of supervoxel size on segmentation performance, our dataset is used in this experiment. Figure 7 shows the performance for different supervoxel sizes in terms of DSC(%) and HD(mm). This experiment shows that a good performance is achieved when the supervoxel size on the xy‐plane is around 150.
Figure 7.
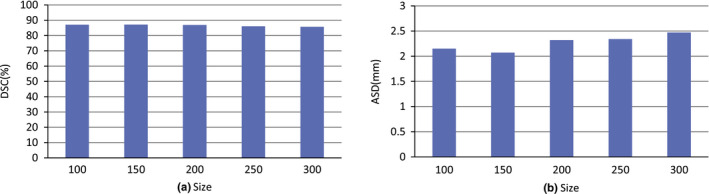
The effect of the supervoxel size on the xy‐plane. [Color figure can be viewed at wileyonlinelibrary.com]
3.H. The effect of the manual initialization
To evaluate the influence of the manual initialization, we performed two experiments using our in‐house dataset. The first experiment is evaluated the number of the points marked by the user on each key slice. The second experiment is to evaluate the effect of selecting three key slices, which are apex, base, and middle key slices. DSC is used as the metric to evaluate the influences.
For the first experiment, different numbers of the points marked by the user are chosen for performing the experiment. Figure 8 is the evaluation result, which indicates that the proposed method is not sensitive to the number of points marked by the user.
Figure 8.
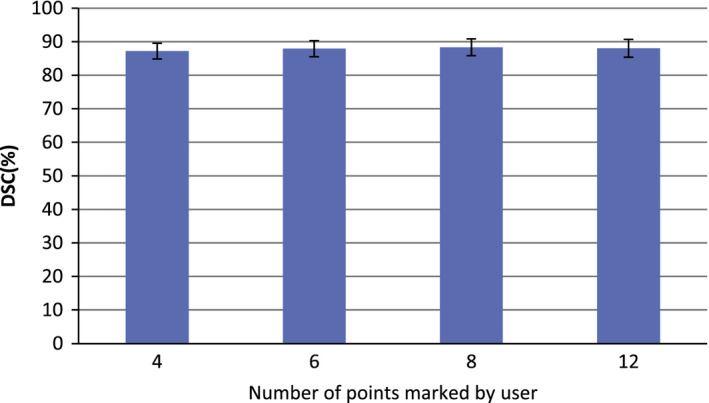
The effect of the number of initial points on segmentation performance. [Color figure can be viewed at wileyonlinelibrary.com]
For the second experiment, the user selects three key slices for the ellipsoid fitting. To individually evaluate the effect of selecting each key slice, two slices around each key slice are selected to run the algorithm, e.g., for evaluating the apex key slice Apex(i), two slices Apex(i‐1) and Apex(i+1) are individually selected as the apex key slice to run the algorithm, where i presents the index of the slice. Fig. 9 shows the evaluation result, which indicates that the proposed method is not sensitive to the selection of the three key slices.
Figure 9.

The influences of selecting three key slices on the final results. [Color figure can be viewed at wileyonlinelibrary.com]
3.I. The effect of combining GC and ACM
To evaluate the performances of the supervoxel‐based GC method and the ACM without supervoxel‐based GC, we performed a segmentation experiment using PROMISE12 dataset. Figure 10 shows the performances of the supervoxel‐based GC algorithm, ACM algorithm without supervoxel‐based GC, and the proposed hybrid method. For the ACM algorithm without supervoxel‐based graph cut, the semiellipsoids, which are fitted based on manual alignment, are used as the initialization. For the supervoxel‐based GC method, the segmentation results are directly evaluated, which is not processed by the ACM algorithm.
Figure 10.
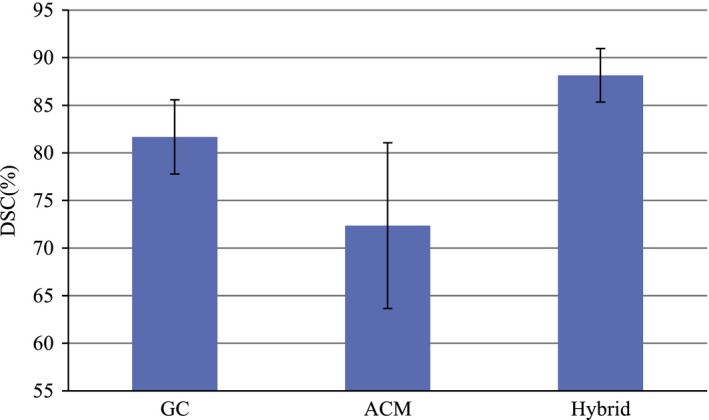
Comparison of three segmentation methods: GC only, ACM only, and the proposed hybrid method. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 10 shows the average DSC of these two methods and our hybrid method. The DSC of the ACM without supervoxel‐based GC is 72.35%, which is not satisfactory. This is because the initialization obtained without supervoxel‐based GC is not good for ACM. For the supervoxel‐based GC algorithm, the DSC is 81.67%, which is still not ideal. For the proposed hybrid method with both supervoxel‐based GC and ACM, the performance is improved significantly, which is increased to 88.15%.
Figure 11 shows the segmentation result of GC and the final segmentation result improved by using ACM.
Figure 11.
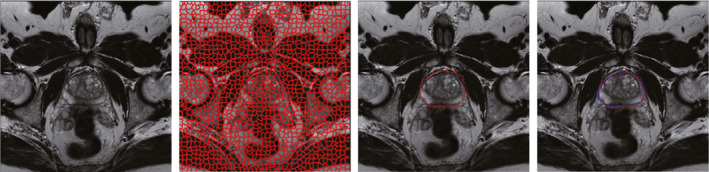
The first image is one original slice of prostate MR. The second image is the corresponding supervoxel map. The third image is the segmentation result of GC. The fourth image is the final segmentation result improved by using AC. The darker contour is the ground truth, while the brighter contour is the final segmentation result. [Color figure can be viewed at wileyonlinelibrary.com]
3.J. The robustness comparison
To compare the robustness of our semiautomatic method with the automatic segmentation methods, a comparison experiment was performed. The implementations of most automatic methods in the PROMISE12 challenge are not available. Therefore, we chose a public available method called V‐net43, 44 for the robustness comparison, which is an automatic method with a comparable performance to our method and the top two methods of the PROMISE12 challenge on PROMISE12 dataset.
Three datasets are used to compare the robustness of our semiautomatic method and the automatic V‐net method. The data include our in‐house dataset with 43 MR images, the PROMISE12 dataset with 50 MR images, and the ISBI dataset with 60 MR images. The DSC is selected as the metric to evaluate the robustness. The segmentation results of two methods on three datasets are listed in Table 4.
Table 4.
Robustness of V‐net method and our method: average of means ± average of standard deviations of DSC across three different datasets
| In‐house | PROMISE12 | ISBI | |
|---|---|---|---|
| V‐net | 81.47 ± 4.49 | 87.12 ± 4.22 | 83.12 ± 5.22 |
| Ours | 87.19 ± 2.34 | 88.15 ± 2.80 | 88.23 ± 2.45 |
The DSC of our semiautomatic method varies from 87.19 to 88.23 on three datasets, while the DSC of V‐net is from 81.47 to 87.12. It shows that our method is more robust than the V‐net method, which yields more consistent segmentation results. Our method has user intervention for initialization, and could capture the shape variability more accurately across different datasets for an individual MR image. For segmenting prostate on a new MR image, our patient‐specific shape model plays an important role to guide the algorithm to segment the prostate accurately.
4. Conclusion
We proposed a supervoxel‐based segmentation method for prostate MR images. The experiments on our own dataset and public dataset showed that the proposed method is able to accurately segment the prostate in MR volumes. Compared with a pixel‐based method, the proposed supervoxel‐based algorithm significantly reduces the number of the computing points for MR volume segmentation. Meanwhile, the proposed method makes the graph cuts algorithm to be competent for handling big 3D medical data. The framework of the proposed method can be applied to segment other organs.
Experimental results on three different MR image datasets, including 30 in‐house patient data, 50 PROMISE12 data, and 60 ISBI MR Images, with different acquisition protocols from multiple centers and multiple vendors, showed that the proposed method can segment the prostate accurately in terms of four quantitative metrics. In addition, the proposed method generated low inter‐observer variability introduced by manual initialization in term of DSC, which shows a high reproducibility. Another advantage of the proposed method is that it generated consistent segmentation result across three different datasets. This is important to deploy our method for image‐guided biopsy in multiple centers. The experimental results of the proposed method shows that it has a potential to be used for image guided prostate interventions.
The automatic methods depend on the population information, which cannot cover all kinds of prostate shapes on MR images. Although, the public dataset PROMISE12 collected from different centers with different protocols, the diversity of this dataset is still not enough. We use patient‐specific shape information obtained from user intervention, which could alleviate the drawback of these automatic methods. In addition, the models trained by the automated methods on a specific dataset do not work well on the other new datasets that are not seen before. For a new dataset, automated methods need to be trained on the new dataset, which makes the deployment of these methods difficult. In contrast, our semiautomated method has a high reproducibility across different datasets, which is easy to be deployed in multiple centers.
The segmentation time of the ScrAutoProstate method is 1.1 second based on C++ implementation with parallelization. The computing time of the proposed method can be reduced by using C/C++ implementation of shape feature extraction and active contour instead of current MATLAB codes. Furthermore, parallel computing can be used on multiple CPU processors to accelerate the proposed method.
Conflict of Interest
The authors have no relevant conflicts of interests to disclose.
Acknowledgments
This research is supported in part by NIH grants R01CA156775 and R21CA176684, NSFC Project 61273252, Georgia Cancer Coalition Distinguished Clinicians and Scientists Award, and the Emory Molecular and Translational Imaging Center (NIH P50CA128301).
References
- 1. Siegel RL, Miller KD, Jemal A. Cancer statistics, 2016. CA Cancer J Clin 2016;66:7–30. [DOI] [PubMed] [Google Scholar]
- 2. Wu Y, Liu G, Huang M, et al. Prostate segmentation based on variant scale patch and local independent projection. IEEE Transactions Med Imaging 2014;33:1290–1303. [DOI] [PubMed] [Google Scholar]
- 3. Litjens G, Debats O, Barentsz J, Karssemeijer N, Huisman H. Computer‐aided detection of prostate cancer in mri. IEEE Trans Med Imaging 2014;33:1083–1092. [DOI] [PubMed] [Google Scholar]
- 4. Akbari H, Fei BW. 3D ultrasound image segmentation using wavelet support vector machines. Med Phys 2012;39:2972–2984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Hu Y, Ahmed HU, Taylor Z, et al. Mr to ultrasound registration for image‐guided prostate interventions. Med Image Anal 2012;16:687–703. [DOI] [PubMed] [Google Scholar]
- 6. Fei BW, Nieh PT, Schuster DM, Master VA. PET‐directed, 3D ultrasound‐guided prostate biopsy. Diagn Imaging Eur 2013;29:12–15. [PMC free article] [PubMed] [Google Scholar]
- 7. Qiu W, Yuan J, Ukwatta E, Sun Y, Rajchl M, Fenster A. Fast globally optimal segmentation of 3d prostate mri with axial symmetry prior. Med Image Comput Comput‐assist Interv: MICCAI 2013;16:198–205. [DOI] [PubMed] [Google Scholar]
- 8. Toth R, Madabhushi A. Multifeature landmark‐free active appearance models: application to prostate mri segmentation. IEEE Trans Med Imaging 2012;31:1638–1650. [DOI] [PubMed] [Google Scholar]
- 9. Qiu W, Yuan J, Ukwatta E, Sun Y, Rajchl M, Fenster A. Prostate segmentation: an efficient convex optimization approach with axial symmetry using 3‐d trus and mr images. IEEE Trans Med Imaging 2014;33:947–960. [DOI] [PubMed] [Google Scholar]
- 10. Gao Y, Sandhu R, Fichtinger G, Tannenbaum AR. A coupled global registration and segmentation framework with application to magnetic resonance prostate imagery. IEEE Trans Med Imaging 2010;29:1781–1794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Qiu W, Yuan J, Ukwatta E, Tessier D, Fenster A. Three‐dimensional prostate segmentation using level set with shape constraint based on rotational slices for 3d end‐firing trus guided biopsy. Med Phys 2013;40:072903. [DOI] [PubMed] [Google Scholar]
- 12. Egger J. Pcg‐cut: graph driven segmentation of the prostate central gland. PloS One 2013;8:e76645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Mahapatra D, Buhmann JM. Prostate mri segmentation using learned semantic knowledge and graph cuts. IEEE Trans Biomed Eng 2014;61:756–764. [DOI] [PubMed] [Google Scholar]
- 14. Tian Z, Liu L, Fei BW. A supervoxel‐based segmentation for prostate mr images. Proc SPIE Med Imaging 2015;9413:941318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Tian Z, Liu L, Zhang Z, Fei B. Superpixel‐based segmentation for 3d prostate mr images. IEEE Trans Med Imaging 2016;35:791–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Tian Z, Liu L, Fei BW. A fully automatic multi‐atlas based segmentation method for prostate mr images. In: Proc. SPIE Med Imaging. SPIE; 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Chan TF, Vese LA. Active contours without edges. IEEE Trans Image Process 2001;10:266–277. [DOI] [PubMed] [Google Scholar]
- 18. Tsai A, Yezzi A Jr, Wells W, et al. A shape‐based approach to the segmentation of medical imagery using level sets. IEEE Trans Med Imaging 2003;22:137–154. [DOI] [PubMed] [Google Scholar]
- 19. Kass M, Witkin A, Terzopoulos D. Snakes: active contour models. Int J Comput vision 1988;1:321–331. [Google Scholar]
- 20. Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational problems. Commun Pure Appl Math 1989;42:577–685. [Google Scholar]
- 21. Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. IEEE Trans Pattern Anal Mach Intell 2001;23:1222–1239. [Google Scholar]
- 22. Boykov YY, Jolly MP. Interactive graph cuts for optimal boundary & region segmentation of objects in nd images. In: Werner B, ed. Computer Vision, 2001. ICCV 2001. Proceedings Eighth IEEE International Conference on, Vol. 1 Los Alamitos, CA: IEEE; 2001: 105–112. [Google Scholar]
- 23. Xu N, Ahuja N, Bansal R. Object segmentation using graph cuts based active contours. Comput Vis Image Underst 2007;107:210–224. [Google Scholar]
- 24. Kim JS, Hong KS. A new graph cut‐based multiple active contour algorithm without initial contours and seed points. Mach Vis Appl 2008;19:181–193. [Google Scholar]
- 25. Zhang P, Liang Y, Chang S, Fan H. Kidney segmentation in ct sequences using graph cuts based active contours model and contextual continuity. Med Phys 2013;40:081905. [DOI] [PubMed] [Google Scholar]
- 26. Xu C, Corso JJ. Evaluation of super‐voxel methods for early video processing. In: Mortensen E, ed. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Washington, DC: IEEE; 2012:1202–1209. [Google Scholar]
- 27. Achanta R, Shaji A, Smith K, Lucchi A, Fua P, Susstrunk S. Slic superpixels compared to state‐of‐the‐art superpixel methods. IEEE Trans Pattern Anal Mach Intell 2012;34:2274–2282. [DOI] [PubMed] [Google Scholar]
- 28. Boykov Y, Vladimir K. Max‐flow/min‐cut . http://vision.csd.uwo.ca/code/.
- 29. Felzenszwalb PF, Huttenlocher DP. Distance transforms of sampled functions. Theory Comput 2012;8:415–428. [Google Scholar]
- 30. Zhang Y, Matuszewski BJ, Shark LK, Moore CJ. Medical image segmentation using new hybrid level‐set method. In: Moore C, ed. Fifth International Conference BioMedical Visualization. IEEE; 2008:71–76. [Google Scholar]
- 31. Zhang Y. 2D/3D image segmentation toolbox . http://www.mathworks.com/matlabcentral/profile/authors/1930065-yan-zhang.
- 32. Fei BW, Yang X, Nye JA, et al. Mr/pet quantification tools: registration, segmentation, classification, and mr‐based attenuation correction. Med Phys 2012;39:6443–6454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Yang X, Wu S, Sechopoulos I, Fei B. Cupping artifact correction and automated classification for high‐resolution dedicated breast ct images. Med Phys 2012;39:6397–6406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Garnier C, Bellanger JJ, Wu K, et al. Prostate segmentation in hifu therapy. IEEE Trans Med Imaging 2011;30:792–803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Litjens G, Toth R, van de Ven W, et al. Evaluation of prostate segmentation algorithms for mri: the promise12 challenge. Medical Image Anal 2014;18:359–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Bloch N, Madabhushi A, Huisman H, et al. Nci‐isbi 2013 challenge: automated segmentation of prostate structures. 10.7937/K9/TCIA.2015.zF0vlOPv. [DOI]
- 37. Guillard G, Vincent G, Bowes M. Fully automatic segmentation of the prostate using active appearance models. In: Ayache N, ed. MICCAI Grand Challenge: Prostate MR Image Segmentation. Berlin: Springer: 2012. [Google Scholar]
- 38. Birkbeck N, Zhang J, Requardt M, Kiefer B, Gall P, Kevin Zhou S. Region‐specific hierarchical segmentation of mr prostate using discriminative learning. In: Ayache N, ed. MICCAI Grand Challenge: Prostate MR Image Segmentation. Berlin: Springer; 2012. [Google Scholar]
- 39. Erus G, Ou Y, Doshi J, Davatzikos C. Multi‐atlas segmentation of the prostate: a zooming process with robust registration and atlas selection. In: Ayache N, ed. MICCAI Grand Challenge: Prostate MR Image Segmentation. Berlin: Springer; 2012. [Google Scholar]
- 40. Jung F, Kirschner M, Wesarg S. Automatic prostate segmentation in mr images with a probabilistic active shape model. In: Ayache N, ed. MICCAI Grand Challenge: Prostate MR Image Segmentation. Berlin: Springer; 2012. [Google Scholar]
- 41. Yuan J, Qiu W, Ukwatta E, Rajchl M, Sun Y, Fenster A. An effcient convex optimization approach to 3d prostate mri segmentation with generic star shape prior. In: Ayache N, ed. MICCAI Grand Challenge: Prostate MR Image Segmentation. Berlin: Springer; 2012. [Google Scholar]
- 42. Rueckert D, Gao Q, Edwards P. An automatic multi‐atlas based prostate segmentation using local appearance‐specific atlases and patch‐based voxel weighting. In: Ayache N, ed. MIC‐ CAI Grand Challenge: Prostate MR Image Segmentation. Berlin: Springer; 2012. [Google Scholar]
- 43. Milletari F, Navab N, Ahmadi SA. V‐net: fully convolutional neural networks for volumetric medical image segmentation. In: Bilof R, ed. 2016 Fourth International Conference on 3D Vision (3DV). Los Alamitos, CA: IEEE; 2016;565–571. arXiv preprint arXiv:1606.04797. [Google Scholar]
- 44. Milletari F. VNet software . https://github.com/faustomilletari/VNet.


