Photoacoustic-based sO₂ estimation through excised bovine prostate tissue with interstitial light delivery

Abstract

Photoacoustic (PA) imaging is capable of probing blood oxygen saturation (sO₂), which has been shown to correlate with tissue hypoxia, a promising cancer biomarker. However, wavelength-dependent local fluence changes can compromise sO₂ estimation accuracy in tissue. This work investigates using PA imaging with interstitial irradiation and local fluence correction to assess precision and accuracy of sO₂ estimation of blood samples through ex vivo bovine prostate tissue ranging from 14% to 100% sO₂. Study results for bovine blood samples at distances up to 20 mm from the irradiation source show that local fluence correction improved average sO₂ estimation error from 16.8% to 3.2% and maintained an average precision of 2.3% when compared to matched CO-oximeter sO₂ measurements. This work demonstrates the potential for future clinical translation of using fluence-corrected and interstitially driven PA imaging to accurately and precisely assess sO₂ at depth in tissue with high resolution.

1. Background

Cell hypoxia, or areas of low oxygen concentration in tissue, can result from a multitude of factors, including reduced arterial oxygen partial pressure (pO₂), reduced tissue perfusion, increased oxygen diffusion distances, and an inability of cells to use oxygen [1]. Studies have shown that 50–60% of locally advanced solid tumors may present with heterogonous hypoxic and/or anoxic regions within a tumor mass [2]. The existence of a hypoxic tumor microenvironment has also been shown to correlate with malignant progression, tumor aggressiveness, and resistance to therapy (e.g., radiotherapy and chemotherapy) [3], [4]. In particular, prostate cancer patients displaying increased hypoxia factors (i.e., HIF-1α and VEGF) have shown significantly worse response to treatment than those displaying normal levels of the same factors [5].

Due to the prognostic nature of hypoxia, providing a physician with a quantitative, real-time assessment of intratumoral hypoxia during conventional diagnostic or therapeutic interventional procedures could improve patient outcomes during cancer treatment. The current standard of care calls for these interventional procedures to be performed with only anatomical image guidance, providing no clear method to assess hypoxia or other clinically relevant tumor markers. Integrating a method to image local hypoxia during such procedures, however, has the potential to improve clinical care by directing the physician to higher-risk regions within the tissue of interest. In particular, providing a method of evaluating tissue hypoxia during biopsy procedures may allow the physician to sample the highest-risk regions within an organ, while embolization procedures could be targeted more specifically to regions of hypoxia to prevent over-treatment of healthy tissue.

Current imaging methods tend to lack the hypoxia-assessment capability needed for maximal clinical effectiveness and translation as they tend to either rely on exogenous contrast agents or have limited spatiotemporal resolution [6], [7], [8]. The most direct method currently used to determine tissue hypoxia is the measurement of pO₂ through the use of either optical fluorescence measurements or polarographic electrodes. These techniques provide a direct measure of pO₂ at the probe insertion site, but they have several disadvantages as they are limited to time-averaged point measurements [9], [10].

One promising technique being investigated for the assessment of in vivo oxygenation status during an interventional procedure is photoacoustic (PA) imaging in conjunction with interstitial irradiation (i.e., providing an irradiation source within the tissue via an optical fiber) [11], [12], [13], [14], [15]. While this approach does not eliminate the invasiveness of electrode sampling, it is capable of interrogating tissue volumes at clinically relevant depths with good spatial resolution. Given their minimally invasive nature, interventional procedures are prime candidates for such an approach as the introduction of an interstitial source could be achieved with minimal disruption to clinical workflow.

PA imaging utilizes a narrow-pulse-width laser to interrogate the optical properties within a tissue of interest with improved spatial resolution at depth when compared to common optical imaging techniques. As the laser light passes through tissue, it is absorbed and converted to heat, leading to thermal expansion and the generation of an acoustic signal that is dependent on the local light fluence (or local energy density per area), optical absorption properties of the tissue, and thermally dependent material properties; the acoustic signal can be imaged using an ultrasound (US) transducer [16], [17]. The initial pressure of the acoustic wave generated by the PA effect is described by

$$p_{\text{o}}\left(r,\lambda \right)=\frac{\beta c^2}{c_{\text{p}}}{\mu }_{\text{a}}\Phi =\Gamma *{\mu }_{\text{a}}\left(r,\lambda \right)*\Phi \left(r,\lambda \right),$$ (1)

where p_o [Pa] is the initial pressure, β [K⁻¹] is the thermal coefficient of volume expansion, c [m s⁻¹] is the speed of sound through tissue, c_p [K kg⁻¹] is the heat capacity at constant pressure, μ_a [cm⁻¹] is the optical absorption coefficient, Φ [J cm⁻²] is the local laser energy fluence, and Γ is the unitless Grüneisen coefficient, which varies with material composition but is often assumed to be spatially invariant within biological tissue due to similarities in tissue composition [18]. Although such an assumption is not always valid, Γ will be assumed constant for the purpose of this work. Given that PA imaging is often limited by the optical fluence reaching the imaging field, the use of an interstitial optical source during appropriate procedures (i.e., minimally invasive interventional procedures) helps alleviate this concern by decreasing the light propagation distance, thereby decreasing optical attenuation.

The amplitude of the initial PA signal (p_o) varies with wavelength (λ) and location (r) due, in part, to the heterogeneous distribution of photoabsorbers (e.g., hemoglobin and lipid) that have unique spectral absorption properties [19]. Within the body, the dominant endogenous photoabsorber in the near-infrared (NIR) range is hemoglobin, which is found in red blood cells and can be either saturated with oxygen (i.e., oxyhemoglobin [HbO₂]) or not (i.e., deoxyhemoglobin [HHb]). Due to the known spectroscopic absorption differences in HbO₂ and HHb, which affect the generated PA signal (Eq. (1)), the relative concentration of each hemoglobin species can be determined by linear unmixing of spectroscopic PA (sPA) data, which are acquired at multiple wavelengths of light [20], [21], [22], [23], [24]. Once unmixed, the percentage of hemoglobin molecules saturated with oxygen is referred to as blood oxygen saturation (sO₂)

$$\mathrm{s}{\mathrm{O}}_2=\frac{C_{{\text{HbO}}_2}}{C_{{\text{HbO}}_2}+C_{\text{HHb}}}\text{,}$$ (2)

where $c_{{\text{HbO}}_2}$ is the concentration of HbO₂ and C_HHb is the concentration of HHb [25]. Within an imaging voxel that lacks major vessels, PA-based methods tend to estimate the average sO₂ across capillary junctions. Although sO₂ does not directly measure cellular hypoxia, as hemoglobin tends to be limited to the intravascular space, it has shown to be correlated to pO₂ in the extracellular space proximal to capillaries [26].

PA imaging requires sufficient fluence to generate an image, and the significant optical attenuation inherent to most tissue can complicate pixel-based unmixing techniques by resulting in poor signal at depth and a heterogeneous fluence distribution. However, when these issues are mitigated, sPA imaging can be used to quantify sO₂ and indirectly assess local hypoxia [26], [27], [28], [29], [30]. Although PA estimation of sO₂ has been demonstrated in vivo, the accuracy of the measurements is not well validated [28], [29], [31], [32], [33]. As shown in a study of prostate cancer patients, average sO₂ can vary spatially as little as 2% across a prostate, as measured by invasive time-resolved spectroscopy [34]. Thus, it is critical to achieve estimates with high spatiotemporal resolution and accuracy when using PA-based sO₂ estimation in order to evaluate its clinical potential.

Unknown changes in local fluence (i.e., photon flux at a particular point in the imaging field) can significantly affect PA-based sO₂ assessment accuracy. Local fluence at depth is conventionally assumed to be related to surface fluence (or more exactly, laser-pulse energy) by a wavelength-dependent but spatially independent correction factor. After application of this correction factor, and if analysis is limited to a fixed point in space, the fluence term in Eq. (1) drops out such that a PA signal is assumed to be directly proportional to the absorption coefficient for a given imaging voxel (again, assuming a constant Grüneisen coefficient). The estimation of sO₂ values based on surface fluence correction results have been shown to be accurate provided that the irradiation experiences minimal wavelength-dependent attenuation between the optical source and the region of interest (ROI) [25]. However, tissue presents an environment with significant wavelength-dependent attenuation in the low-NIR range [35], [36]. Therefore, while the assumptions used to justify application of just surface-fluence correction simplify acquisition and analysis, they typically fail to produce an accurate measurement of sO₂ when imaging at depths beyond the ballistic regime due to wavelength-dependent attenuation, the effects of which increase with photon propagation distance [19].

Wavelength-dependent attenuation can be represented by absorption and scattering terms, where μ_a accounts for the fraction of incident energy absorbed by tissue per distance, and wavelength-dependent scattering can be represented, assuming such scattering occurs over multiple scattering agents, by a reduced scattering coefficient (μ_s′) defined as

$${\mu }_{\text{s}}^{\text{'}}={\mu }_{\text{s}}\left(1-g\right)\text{,}$$ (3)

where μ_s is the scattering coefficient, or the fraction of energy scattered by tissue per distance, and g is the anisotropy factor, or the cosine of the angle of scatter, which provides a measure of scatter over several scattering agents [19].

Because the PA signal is proportional to fluence at the site of absorption, it becomes necessary to account for local fluence in order to improve spectroscopic assessment accuracy [37]. While local fluence estimation techniques using Monte Carlo modeling, finite-element/finite-volume modeling, light tagging, and diffuse optical tomography have previously been proposed to provide accurate assessment of local fluence for PA imaging, all tend to be either computationally intensive or require specialized equipment; these aspects may not be ideal for real-time clinical imaging [37], [38], [39], [40], [41]. Additionally, a recent study investigated eigenspectra-based correction for improved PA-based sO₂ assessment [42]. Although this method was shown to provide significant sO₂ estimation improvement at depths less than 1 cm, it requires computation of an ill-posed minimization problem that must be properly regularized to ensure it converges to a correct solution.

An alternative approach to these complex fluence correction techniques is to use a simple and fast calculation method with an appropriate balance between sO₂ estimation accuracy and speed, while potentially sacrificing some accuracy of optical component reconstruction. To this end, a simple fluence estimation model based on the P1 diffusion approximation for light transport used in conjunction with methods to reduce the light path length, such as interstitial irradiation, could enable greater sO₂ estimation accuracy than conventional unmixing techniques used in combination with external-beam irradiation, while providing real-time feedback to physicians during procedures [12]. The P1 diffusion approximation model represents light transport through a scattering medium as diffusion from high to low concentration and is a valid model for many tissue types [43]. The use of interstitial irradiation yields an improvement in the signal-to-noise ratio (SNR) and contrast-to-noise ratio (CNR) at increased depth (away from the skin surface and US array) because of the reduced optical path length to the ROI [12]. Additionally, by utilizing an optical fiber, accurate sO₂ estimates (i.e., estimates before significant spectral shifts) can be made proximal to the fiber tip as an input parameter for a tissue’s assumed optical absorption, thereby allowing for adaptive modeling. Preclinical work has shown that PA-based interstitial irradiation could be implemented during minimally invasive clinical interventional radiology procedures involving a needle biopsy and/or the introduction of a catheter [12], [14], [15].

In general, this work investigates the use of interstitial irradiation in conjunction with a transrectal ultrasound (TRUS) probe to assess the accuracy of sO₂ estimation in a phantom comprised of excised bovine prostate containing blood targets at varied distances and sO₂ percentages. A photon diffusion model was then implemented to correct for local fluence change over the ROI. Finally, 2- and 6-wavelength linear unmixing was then applied to assess sO₂ estimation accuracy and precision when compared to gold-standard CO-oximeter measurements.

2. Methods

2.1. Imaging setup

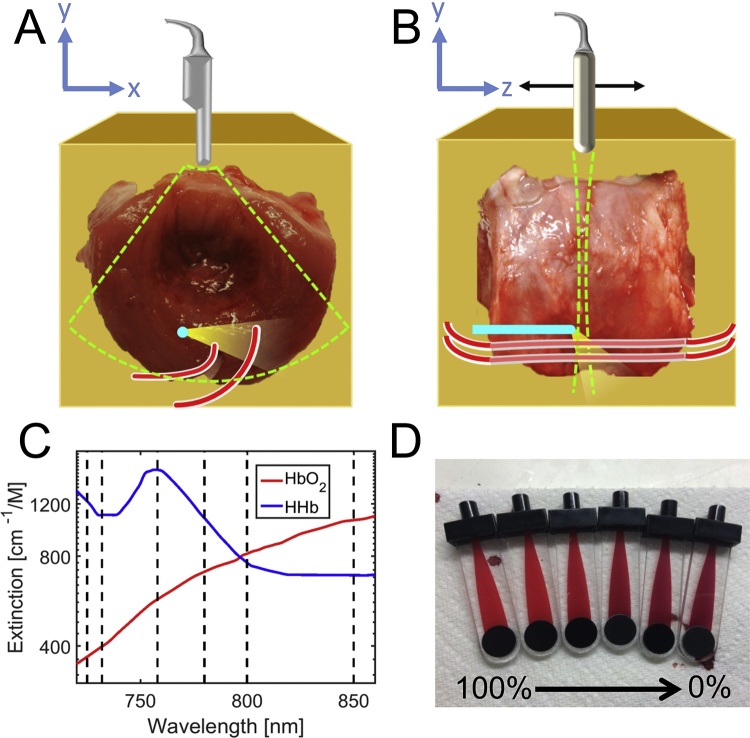
The imaging setup used for all experiments consisted of a Quanta-Ray^® Pro 270 pulsed Nd:YAG laser with a 10-Hz repetition rate coupled into a GWU versaScan tunable optical parametric oscillator (OPO; Newport Corp., Irvine, CA). After leaving the OPO, the beam was coupled into a clinically approved, side-fire optical fiber (Pioneer Optics, Bloomfield, CT) [44]. The optical fiber used in this work has a 1.5-mm outer diameter, which was chosen so that it could easily be incorporated into clinical procedures using 16-gauge biopsy needles or into more common 18-gauge needles with minimal additional effort [44], [45], [46]. The distal end of the fiber was inserted into the phantom to provide a local irradiation source. The generated PA signal was detected using a Vantage 128 US system (Verasonics Inc., Redmond, WA) with a C9-5 transrectal array (Royal Phillips, Amsterdam, Netherlands) operating at a 7.8-MHz center frequency with nominal lateral and axial resolutions of 0.1 and 0.2 mm, respectively (Fig. 1A and B). PA acquisitions were triggered by the Q-switch of the laser to ensure coincident timing.

Fig. 1.

A) Schematic representing the imaging plane (lime dashed lines), including the optical fiber (blue), PE tubing (red), & direction of light (yellow cone). B) Schematic representing a side view of the imaging setup, with the direction of transducer translation shown with a black arrow. C) Molar absorption coefficient spectra of HHb and HbO₂ (red, blue) from 720 to 860 nm, with dashed lines denoting wavelengths used in this work. D) Blood samples in CO-oximeter cuvettes; blood oxygenation decreases from left to right.

Energy output of the laser was measured during imaging by splitting the beam into a PE25-V2 detector connected to a Nova II meter (Ophir Optronics Solutions Ltd., Jerusalem, Israel). Energy output of the fiber tip was measured prior to imaging with a PE50-DIF-ER-V2 detector (Ophir Optronics Solutions Ltd.); these measurements were used to generate a table of wavelength-dependent ratios of input energy (as measured during imaging with the PE25-V2 sensor) and fiber output energy. All imaging in this study was performed using six wavelengths (725, 732, 758, 780, 800, and 850 nm) in order to best characterize the optical absorption profiles of hemoglobin in the low-NIR range (Fig. 1C) [30]. These wavelengths were selected, in part, to obtain samples at the local minimum and maximum of the HHb extinction spectrum in the low-NIR range. Pulse energy at the distal tip of the interstitial fiber ranged from 7.5 mJ at 725 nm to a maximum of 12 mJ at 800 nm, producing estimated incident fluence values ranging from 58 to 92 mJ/cm², respectively, at the surface of the quartz cap surrounding the optical fiber tip [13].

The imaging process was automated with a custom LabVIEW GUI (National Instruments Corporation, Austin, TX) that triggered co-registered PA and B-mode US data acquisition. Volumetric imaging was made possible via RS-232 serial communication to the OPO to control laser wavelength and to a motor-driven translational stage (Velmex Inc., Bloomfield, NY) to sweep the elevational position of the US transducer.

2.2. Phantom setup

All phantoms used in this investigation were created with freshly excised bovine prostate tissue (Animal Technologies Inc., Tyler, TX) embedded in a mixture of 8% (wt%) gelatin (Sigma-Aldrich Corp., St. Louis, MO), 0.1% glutaraldehyde (Sigma-Aldrich Corp., St. Louis, MO), and 91.9% deionized water (Fig. 1A and B) to prevent tissue motion during imaging; the gelatin sample was surrounded by a deionized water bath to provide acoustic coupling. For all studies, a guide needle was used to insert an optical fiber, which provided a local optical source. Additionally, strands of polyethylene (PE) tubing (OD: 1 mm; ID: 0.38 mm) were introduced into the prostate tissue to provide a contained volume for blood injection as an imaging target at set distances from the optical fiber. All blood targets were comprised of freshly excised and heparinized bovine blood (Animal Technologies Inc., Tyler, TX). To prepare samples with the sO₂ percentages listed in Table 1, two flasks containing fresh bovine blood were prepared with an inlet in each, allowing bubbling gas (pure oxygen or pure nitrogen) to mix with and fully oxygenate or deoxygenate blood in the respective flasks. Specific ratios of the aforementioned HbO₂ and HHb batch preparations were then pipetted into an Eppendorf tube based on the desired sO₂, mixed, and then stored in a 1-mL syringe. sO₂ for each sample was measured with spectrophotometry using a Gem OPL CO-oximeter (Instrumentation Laboratory, Bedford, MA; Fig. 1D) that has a reported error of 1.5%. Based on longitudinal PA imaging, it was determined that blood mixtures could be refrigerated at 4 °C for three hours without measurable changes in sO₂. Blood samples were returned to room temperature and injected into PE tubing within the prostate tissue for imaging, where longitudinal PA imaging showed less than 3% change in measured sO₂ for up to 30 min.

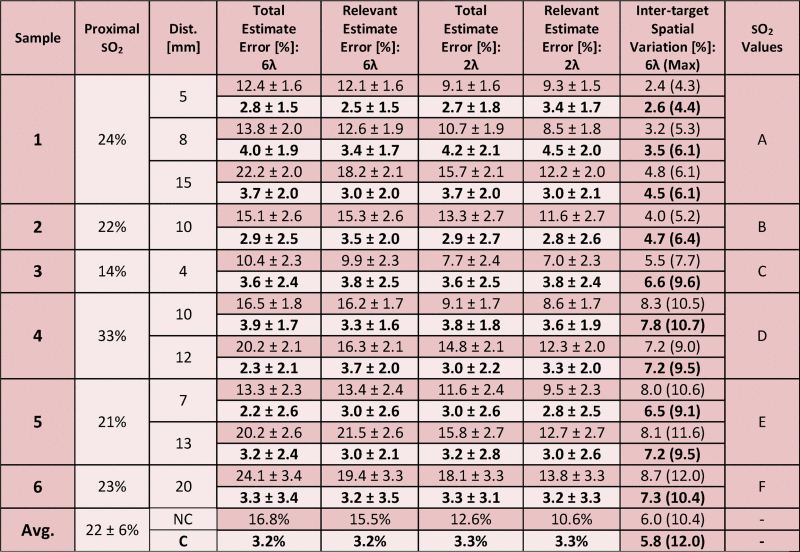
Table 1.

Mean variation of each target from known CO-oximeter reading across all sO₂ values tested. Unless stated otherwise, values are average error across the varying sO₂ values ± average value of the standard deviation across the ten samples at each sO₂ value. Top row of each prostate/distance combination represents data before fluence normalization (dark shading), while bottom row represents data after local fluence correction (light shading). The unmixing columns represent data from 6-wavelength linear unmixing, while the 2-wavelength columns represent data from 2-wavelength unmixing. “Total” estimate inaccuracy reports the estimation accuracy of all sO₂ values, while “relevant” estimate inaccuracy reports only accuracy of sO₂ values greater than 50%. The letter in the final column codifies the sequence of sO₂ values used for each target, as defined by the following: A = 100%, 82%, 66%, 57%, 52%, 36%, 14%; B = 95%, 85%, 72%, 62%, 48%, 20%; C = 99%, 86%, 70%, 55%, 48%, 34%, 19%; D = 100%, 89%, 71%, 63%, 57%, 41%; E = 100%, 90%, 81%, 65%, 58%, 48%, 34%; F = 100%, 90%, 64%, 59%, 48%, 35%.

2.3. sO₂ local fluence correction

Local fluence correction was based on a photon diffusion approximation, which requires that scattering in the tissue account for significantly more attenuation than absorption processes [47]. While literature values regarding the true value of μ_a and μ_s′ within prostate tissue vary, all of these studies report that scattering dominates for both in vivo and ex vivo prostate at any given wavelength; therefore, the diffusion approximation is assumed to be a valid approximation for this application [19], [34], [48]. This approximation allows for the application of an analytic solution to estimate the fluence at any point based on μ_a, μ_s′, the relative fluence at the source, and the distance from the fluence source as

$$\varphi \left(r,\lambda \right)={\varphi }_{\text{o}}*\frac{3*{\mu }_{\text{tr}}\left(\lambda \right)*e^{\left(-{\mu }_{\text{eff}}\left(\lambda \right)*D\right)}}{4*\pi *D},$$ (4)

where Φ(r,λ) [mJ cm⁻²] is the optical fluence varying with wavelength at any given position, Φ_o [mJ cm⁻²] is the initial optical fluence at the light source, μ_eff (λ) = $\sqrt{3*{\mu }_{\text{a}}*{\mu }_{\text{tr}}}$ [cm⁻¹], where μ_tr (λ) = μ_a + μ_s′ [cm⁻¹], and D (cm) is the distance from an optical source to a given point in the field. The location of the optical source, which was approximated as a superposition of multiple point sources, was determined based on the location of the optical fiber in B-mode US imaging for the purpose of distance measurement.

To estimate the local fluence, this work assumes spatially invariant μ_a and μ_s′ values throughout ROIs in the prostate; however, both parameters are assumed to have wavelength dependence. The assumed μ_s′ spectrum for all prostates was calculated using the wavelength-dependent reduced scattering relationship presented in the literature by Jacques [19]. A μ_a spectrum was calculated for each prostate based on literature values for hemoglobin/water concentrations in prostate tissue and sPA-derived sO₂ data proximal to the fiber for a given prostate to determine the ratio of HbO₂ to total hemoglobin [19]. The sO₂ data provided prostate-specific input to allow the assumed μ_a spectrum to adapt to the specific tissue environment and was assumed to be constant throughout the tissue. Hemoglobin and water were both assumed to result in optical absorption, while only hemoglobin was assumed to generate PA signal.

These absorption and scattering spectra for the initial prostate were then multiplied by a range of scaling values in order to provide a relevant range for parameter optimization. The tested values encompassed values ranging from 20% to 250% of the limits reported in the literature for ex vivo prostate for both μa and μs′ [19], [34], [48]. Scaling factors were optimized using least-squares minimization in which the μa and μs′ scaling factors were allowed to vary independently from one another. During the optimization procedure, fluence maps were calculated for all combinations of μ_s′ and μ_a scaling values on the initial prostate sample; each scaled combination was used to estimate local fluence for improved PA-based sO₂ estimation. The μa and μs′ scaling factors that minimized the least-squares difference between PA-estimated and CO-oximeter measured sO₂ in the first prostate were then prospectively applied to all future prostates. Additionally, for all subsequent prostates, the μ_a spectrum was adapted based on the prostate-specific PA-based sO₂ estimate.

2.4. Imaging procedure

PE tubes within the prostate were injected with blood of the same sO₂ level, imaged, flushed with saline, and then re-injected with blood of a different sO₂ until all available blood mixtures were imaged (Fig. 1A and B). For each wavelength, ten independent image acquisitions were performed, each containing ten frames. An imaging plane was established by translating the transducer along the surface of the phantom in the elevation direction (Fig. 1B, black arrow) until a peak PA signal could be observed in a PE tube, which was identified using B-mode US. PA imaging was collected at all six wavelengths at the slice containing the peak signal.

The PA images were then cropped to exclude the fiber signal, and unmixed after normalization for just surface fluence (‘uncorrected’) or for local fluence (‘corrected’). In order to ensure its exclusion, the optical fiber was localized within the PA image using 3D cross-correlation across all wavelengths imaged comparing the PA spectrum at each point in the image to the PA spectrum generated within the optical fiber in the initial data set with a correlation coefficient cut-off of 0.95. The centroid of the largest contiguous region above the cut-off was assumed to be the center of the fiber. Following this, a circular region with a 2-mm diameter surrounding the centroid was excluded from unmixed images to prevent the fiber signal from being mistaken for blood upon unmixing. Both 6-wavelength and 2-wavelength (i.e., 732 and 850 nm) linear unmixing was applied to each imaging data set after application of a 3 × 3-pixel spatial averaging kernel. For both techniques, it was assumed that only HbO₂ and HHb absorbers contributed to PA signal generation.

2.5. Bleeding in the fiber track

An additional experiment investigated the effect of blood in the fiber track on sO₂ estimation accuracy. In contrast with the primary experiment, the prostate phantom was coupled with US gel to ensure injected blood remained within the fiber track and did not leak into the surrounding water bath. Baseline imaging data from one target prior to fiber-track blood injection were first taken for all seven blood samples at the same six wavelengths used previously. To increase its viscosity, 60% sO₂ blood was mixed with US gel (30% by volume) to a volume of 0.15 mL and then injected into the fiber track from the contralateral side of the prostate. The injection needle was monitored using B-mode US to ensure the blood was injected into the track along with the fiber; accumulation of this blood-gel mixture was visible under B-mode US. After introduction of blood, all imaging performed during baseline acquisitions was repeated to provide a matched comparison. Due to geometrical constraints, only one target was placed in this sample. Images were then processed in the same manner as described in Sections 2.3 and 2.4.

2.6. 3D image acquisition

The final experiment investigated the feasibility of performing a 3D image acquisition to simulate a clinical prostate biopsy procedure. Two PE tubes were placed into an ex vivo prostate and filled with blood at an sO₂ level of 81%. Co-registered photoacoustic-ultrasound (PAUS) images were acquired at 20 slices across a 2-cm extent in the elevational dimension with a 1-mm step size (Fig. 1B, black arrow). The image stacks were then loaded into Amira image analysis software (FEI Company, Hillsboro, OR), and the margins of the prostate were manually segmented to generate 3D-rendered PAUS data, while the fiber was automatically masked prior to spectral unmixing.

2.7. Statistical considerations

Accuracy and precision of the sO₂ estimates were calculated for each acquisition (n = 10). For analysis, an ROI was manually assigned around each PE tube inclusion based on B-mode US images, and the mean estimated sO₂ value was calculated within this ROI. The absolute value of the difference between these mean sO₂ values and the matched CO-oximeter sO₂ was then averaged across all ten samples for each sO₂ value to provide the reported accuracy values. Precision values for each blood sample were determined by calculating the standard deviation between the ten mean sO₂ estimates for a given distance and sO₂ value. Spatial variation within the ROIs was also assessed by calculating the standard deviation of sO₂ estimates within a given ROI; the values reported in Table 1 offer the average and maximum spatial variation within an ROI for a given distance.

3. Results

3.1. Uncorrected accuracy and precision

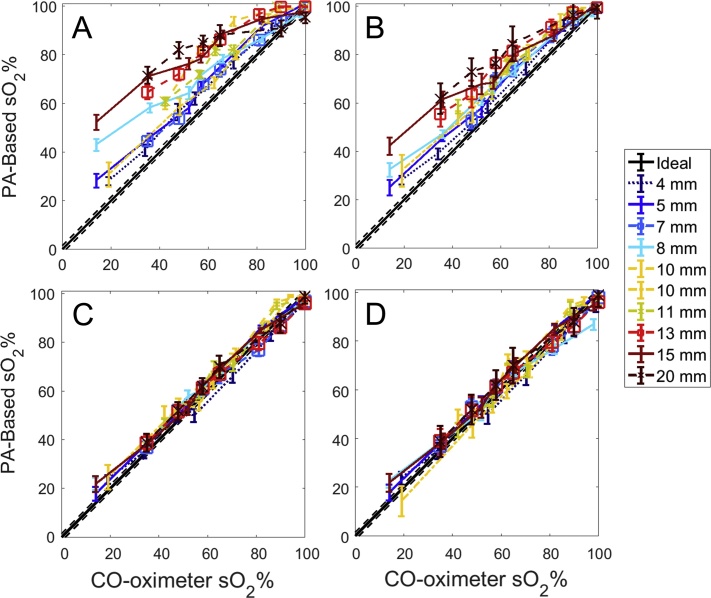
Across six bovine prostates, ten targets were photoacoustically imaged using interstitial irradiation at six wavelengths. The mean error in sO₂ estimation using 6-wavelength unmixing without local fluence correction is 16.8% sO₂, while the mean error is 12.6% when 2-wavelength unmixing was applied. Within a physiologically relevant range of sO₂ (i.e., greater than 50%), 6-wavelength unmixing provides a mean error of 15.5%, while mean error is 10.6% when using a 2-wavelength method. The maximum mean error for a specific target across all sO₂ values acquired occurs at the farthest target from the optical fiber, with a mean estimate error of 24.1% when unmixing with six wavelengths (maximum error 34.4%), and a mean estimate error of 18.1% when unmixing with two wavelengths (maximum error 28.4%). The mean precision value for both 6-wavelength and 2-wavelength unmixing across all sO₂ values is 2.3%. A graphical depiction of these results can be found in Fig. 2, while tabulation can be found in Table 1. Prior to fluence correction, the maximum variation within an ROI across all distances and sO₂ values is 12.0%, while the average variation is 6.0%.

Fig. 2.

Estimated vs. measured sO₂ data from (A) 6-wavelength & (B) 2-wavelength unmixing with surface fluence correction only and (C) 6-wavelength & (D) 2-wavelength unmixing with local fluence correction in 6 prostates at 10 distances; each line style represents a unique prostate, while the black line is the CO-oximeter measurement. Precision of the CO-oximeter is displayed as dashed lines.

3.2. Fluence-corrected accuracy and precision

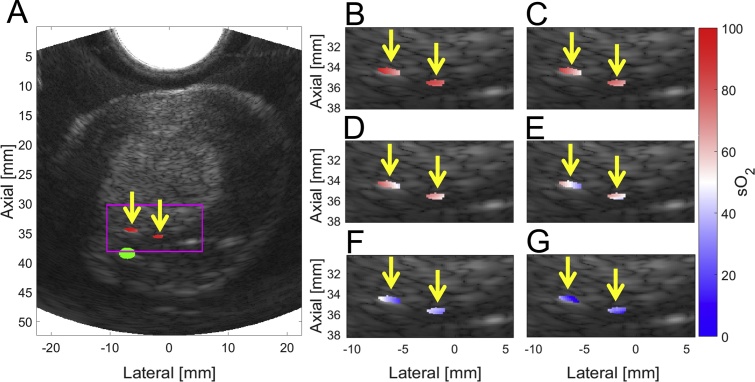
The μ_a and μ_s′ values at 732 nm of 1.3 cm⁻¹ and 33.8 cm⁻¹, respectively, yielded the least-squares sum minimum during optimization on the initial prostate; assumed absolute optical scattering and absorption parameters were based on these values for all subsequent prostates. After applying local fluence correction, the mean error in sO₂ estimation using 6-wavelength unmixing is 3.2% sO₂, while it is 3.3% when unmixing with two wavelengths across both the full range of sO₂ values tested as well as the physiologically relevant ranges. The maximum mean error for a specific target across all sO₂ values no longer occurs at the farthest target from the optical fiber; rather 6-wavelength unmixing provides a maximum mean error at 8 mm from the fiber tip of 4.0% (maximum error of 8.1% across all distances and sO₂ values), while unmixing at two wavelengths again provides maximum error at 8 mm from the fiber tip, with a mean error of 4.2% (maximum error of 8.2% across all distances and sO₂ values). Mean precision for 6-wavelength unmixing across all sO₂ values is 2.3%, while mean precision for 2-wavelength unmixing is 2.4%. A visualization of this data can be seen in Fig. 2, tabulation can be seen in Table 1, while representative images showing estimated sO₂ overlaid B-mode images can be found in Fig. 3. After fluence correction, the maximum variation within an ROI across all distances and sO₂ values is 12%, while the average variation is 5.8%.

Fig. 3.

Local fluence-corrected sO₂ 6-wavelength estimates overlaid B-mode US data. A) PA-based sO₂ estimates of 100% blood overlaid B-mode US image of prostate; magenta box depicts area of sO₂ unmixing for all acquisitions, green circle identifies automatically identified fiber location, and yellow arrows identify PE tube ROIs. PA-based sO₂ estimates overlaid B-mode US (within magenta box) for (B) 82%, (C) 66%, (D) 57%, (E) 52%, (F) 36%, and (G) 14% sO₂ blood targets.

3.3. Effect of bleeding in the fiber track

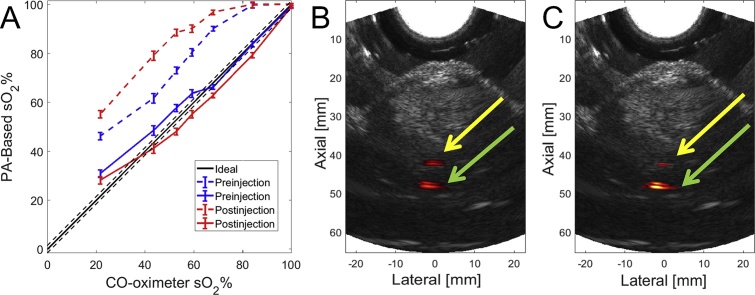
Experiment 2.5 investigated the impact of bleeding on sO₂ estimation using local fluence correction. As seen in Fig. 4A, the sO₂ estimate before fluence normalization becomes less accurate after injecting blood into the fiber track, yielding a mean error of 17.4% when unmixed with six wavelengths before blood injection and 25.8% after injection. The 2-wavelength unmixing data follows a similar trend, with a mean error of 14.9% before the introduction of the inter-track blood and 22.6% after injection. After applying local fluence correction using the μ_a and μ_s′ values determined in Section 3.2, the sO₂ estimates are similar to previous tests without blood in the insertion track, with 6-wavelength unmixing providing 3.8% mean error before and 4.0% mean error after blood injection, as seen in Fig. 4A. Additionally, 2-wavelength unmixing provides 3.1% mean error before blood injection and 3.6% mean error after injection. PA images (at 800 nm) overlaid with matched B-mode US data are provided in Fig. 4B and C to show the effect of the added blood on the PA image. After injection of blood, an 18% increase in signal was observed in the ROI surrounding the optical fiber at 800 nm, while a corresponding 32% decrease in PA signal was observed in a kernel surrounding the blood-filled PE tube (Fig. 4B and C).

Fig. 4.

Results from blood injection in fiber track. A) Estimated vs. measured sO₂ prior to (dashed) and following (solid) fluence correction of blood contained in a PE tube both before (blue) and after (red) blood injection. Overlaid PA and B-mode image data at 800 nm of 68% sO₂ blood target (yellow arrow) (B) prior to and (C) following blood injection around optical fiber (green arrow).

3.4. 3D image acquisition

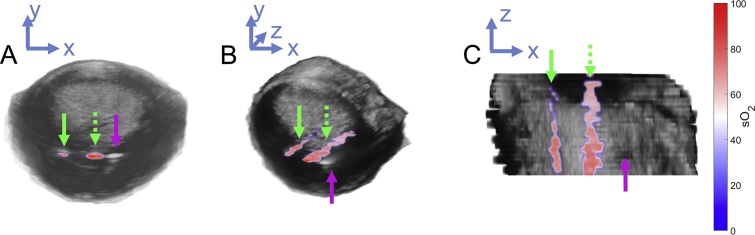
Experiment 2.6 investigated the feasibility of 3D PAUS imaging of the whole prostate gland. As seen in Fig. 5, PA-based sO₂ estimates consistent with the injected 81% sample are present throughout the elevational extent of the prostate when using a stationary optical fiber. The optical fiber is the rightmost region of signal US contrast, while the other two regions of signal represent the unmixed sO₂ estimation from the blood-filled PE tubes after local fluence correction. The signal from the more distant PE tube appears much fainter than the tube immediately next to the optical fiber, indicating that the PA signal falls off as distance from the irradiation source increases.

Fig. 5.

3D rendering of PA-based sO₂ estimates throughout the prostate. Green arrows identify blood-filled PE tubing, while magenta arrow indicates location of optical fiber. A) Axial, (B) off-axis, and (C) coronal 3D renderings of PAUS imaging data of prostate with embedded blood targets.

4. Discussion

In this work, we show that PA-based sO₂ estimation without local fluence correction through excised prostate tissue results in a mean error of 16.8% across all distances and sO₂ values tested, with up to 24.1% error at distant blood targets. To address this issue, we also demonstrate that a simple fluence correction method in conjunction with interstitial irradiation is capable of improving the accuracy of sO₂ estimates through tissue to within 3.2% error for all sO₂ levels. Neither the standard deviation within a given imaging kernel at each acquisition (i.e., spatial variation), nor the standard deviation between kernels across the ten matched acquisitions (i.e., precision) are significantly impacted by this fluence correction technique.

The fluence normalization model in this work accounts, in part, for the wavelength-dependent optical attenuation as light passes through the tissue. Due to the monotonic decrease observed in μ_s′ across the wavelengths used, the fluence reaching a given ROI at higher wavelengths tends to be higher than that at lower wavelengths; thus, surface-fluence-based correction models tend to underestimate fluence at higher wavelengths [19]. As can be observed in Fig. 2, such a fluence underestimation results in an overestimation in sO₂ percentage and the proportion of HbO₂, which has strong absorption – and produces an increased PA signal – at these higher wavelengths. By normalizing each PA frame by local fluence, however, the wavelength-dependent fluence term in Eq. (1) is effectively normalized, providing a more direct relationship between PA signal amplitude and μ_a as a function of wavelength for a fixed point in space. As a result, we improved the spectral fidelity of the PA signal (as it relates to the μ_a of hemoglobin), and thus sO₂ estimation accuracy is likewise improved, as seen in Fig. 2, Fig. 3. The modest improvement seen with 2-wavelength unmixing could be due to increased bias introduced when the local 758-nm HHb absorption maximum (Fig. 1C) is included in spectral unmixing in the 6-wavelength case. Presence of HHb upstream will cause fluence around this local maximum to be further reduced, which could introduce a disproportional bias when unmixing with this wavelength if such wavelength-dependent fluence variations are not properly considered.

Although a significant improvement in the accuracy of mean sO₂ (i.e., within a PE tube ROI) was achieved, spatial variation of this parameter was observed within many of the blood targets (denoted with yellow arrows in Fig. 3B–G), which were assumed to be homogeneous. Given that the fluence modeling assumes spatially uniform optical parameters, results from such correction can introduce artefactual spatial variation within ROIs that have optical parameters (e.g., increased hemoglobin absorption and minimal scattering) that vary substantially from the assumed modeling parameters. The impact of this effect becomes more significant as the size of such ROIs increases and the modeling assumptions of gross homogeneity become less valid. In an effort to mitigate such an effect in the future, an iterative model that incorporates local absorption information based on sPA data could be implemented [40], [49].

Fig. 4 shows the results of introducing blood into the optical fiber track, which would occur during in vivo fiber insertion. As seen in Fig. 4A, introduction of blood in the fiber track results in a significant decrease in estimation accuracy in the absence of local fluence correction. However, when the PA signal is corrected for local fluence, the sO₂ estimates again become far more accurate, demonstrating that these effects also can be mitigated by a fluence correction scheme. Fig. 5 offers results of sO₂ estimation from a 3D PAUS acquisition, where we achieved good visualization of both inserted PE tubes on PA and B-mode US images. However, the optical fiber does not appear within the PA data in the figure as it was intentionally excluded for unmixing and display. For actual clinical implementation, this acquisition approach would likely need to be improved by implementing a simultaneous pull-back approach (of both the optical fiber and transducer) or use of a 2D US transducer array [15]. As the PA spectrum of the fiber itself did not change after the application of the surrounding blood, the automated fiber segmentation technique described previously should still perform adequately to mask the fiber signal in the presence of active bleeding.

By assuming a homogeneous tissue sample, it is possible to easily and quickly calculate the relative fluence at each point in the image based on the diffusion approximation for light propagation. This assumption of a spatially homogeneous medium is possible, in part, due to the use of interstitial irradiation as an optical source. While tissue is generally not homogeneous in nature, the assumption of homogeneity is more valid if light propagation distances are reduced and can be limited to a single tissue type. On the other hand, conventional external irradiation requires light passage through skin (or the rectal wall) as well as any tissues between the irradiation surface and the ROI, thereby increasing propagation distance and introducing multiple tissue interfaces that tend to violate this homogeneity assumption. Additionally, by utilizing interstitial irradiation, the optical source is more likely to move with the tissue of interest, providing the potential for a more consistent frame-to-frame optical path length, thereby mitigating one aspect of the challenges inherent to motion.

While the fluence correction method presented in this work provides a significant increase in sO₂ estimation accuracy, it suffers from inherent limitations. Most obviously, the use of interstitial irradiation would be too invasive for many general-use situations; however, such an approach could still be employed during minimally invasive interventional radiology procedures such as biopsy or embolization. Steps taken to simplify the fluence normalization model will also ultimately provide some limitations to this technique. The optical fiber was modeled as a superposition of point sources within the same slice in elevation during analysis. However, the center of the fiber tip was often not located in the frame of analysis, which resulted in distance-measurement error and likely could account, in part, for selection of optimum μ_a and μ_s′ values slightly greater than previously reported in the literature for ex vivo prostate. Additionally, the diffusion approximation of photon propagation is only valid at a distance greater than ∼0.3 mm from the source for the μ_a and μ_s′ values used in this work and requires that scattering be the dominant attenuation mechanism, which has also been shown to be true for in vivo tissue [34], [35], [50]. No targets were imaged within this distance in this study, so this assumption did not impact the results; however, it should be considered for future work with superficial imaging targets [49].

Although prostate tissue is certainly not perfectly homogeneous, the employed fluence model assumed an average reduced scattering value, which provided reasonable estimates for attenuation experienced over the tested light propagation distance. A proximal sPA acquisition then provided a prostate-specific average absorption spectrum as a model input. The variation in proximal sO₂ estimates across the six prostates – ranging from 14 to 33% – was likely due to variations in prostate-sample temperature (e.g., longer to warm after being removed from the refrigerator), which will influence oxygen-hemoglobin dissociation [51]. Such an issue was not a concern, however, for blood samples as independent CO-oximeter measurements (which could not be acquired on prostate tissue) were obtained just prior to PA imaging. Additionally, while the assumption of perfectly homogeneous sO₂ within the prostate is not true, it can be modeled as such due to the method’s relatively short light propagation distances through only one tissue type as opposed to conventional irradiation which would require light to pass through multiple tissue types.

Future in vivo implementation of this approach would encounter a significantly different optical absorption environment due to the drastically increased levels of HbO₂ inherent to viable tissue. However, proximal sPA sampling could similarly provide a more accurate (i.e., prostate-specific) gross absorption estimate. Reduced scattering, on the other hand, is not expected to change solely based on the tissue’s viability state, and it similarly may be accurately estimated with an average μ_s′ value if an ROI is kept within the organ of interest and does not extend across tissue boundaries. Additionally, while fluence levels at the tip of the optical fiber do exceed ANSI limitations for skin exposure at all wavelengths, this fluence is not applied to skin but is instead introduced directly into the prostate tissue, which has no specified regulatory limit at this time. It will be important in the future to establish safety guidelines for pulsed irradiation through organ types other than skin, which generally do not contain melanin and can vary drastically in hemoglobin concentration (e.g., liver vs. prostate) [52], [53]. Although no observable tissue changes were noted following imaging at the presented fluence levels, light-diffusing fiber tips could be utilized to reduce peak fluence levels in vivo.

One application for the imaging approach presented herein could be monitoring sO₂ during clinical prostate biopsy procedures. As a study of prostate cancer patients has shown, average time-resolved spectroscopy-based sO₂ levels within human prostates have a mean of 76% with spatial variance as low as 2% across some prostates [34]. The sO₂ estimation error of only 3% achieved in this study begins to approach this observed intra-prostate variability. Preliminary studies of PA-based sO₂ estimates often rely on relative sO₂ changes – over time or due to varied oxygen inhalation conditions – as opposed to comparison of absolute sO₂ values [21], [54]. Having an imaging technique with the accuracy and precision demonstrated in this work could improve the clinical usefulness of sO₂ estimation, particularly if longitudinal acquisitions are not permitted for relative comparisons. Ultimately, more work will have to be conducted in correlating absolute and/or relative sO₂ changes to relevant pathology or treatment outcomes. To this end, it will be critical to achieve sO₂ estimates with high accuracy and spatiotemporal resolution to allow for comparisons with histopathological results and known clinical outcomes.

5. Conclusion

This work demonstrates the feasibility of using transrectal ultrasound, interstitial irradiation, and local fluence correction to improve sO₂ estimation of blood targets in excised prostate tissue. Mean sO₂ estimation error was shown to improve from 16.8% to 3.2% for 6-wavelength unmixing between surface-fluence and local-fluence correction methods, respectively, while estimation precision consistently remained at 2.3% for ten target distances ranging from 4 to 20 mm. Similar techniques could be implemented clinically to provide real-time feedback during needle biopsies or a catheter-based procedure. As demonstrated by the results of this study, application of local fluence correction with interstitial irradiation significantly improves PA-based sO₂ estimation accuracy, which may allow PA imaging to play a greater role in future interventional clinical procedures.

Conflict of interest statement

The authors declare that there are no conflicts of interest with this work.

Biographies

Trevor Mitcham received his B.S. degree in Bioengineering at Rice University in 2012. He is currently a graduate student in Medical Physics at The University of Texas MD Anderson Cancer Center UTHealth Graduate School of Biomedical Sciences in Houston, Texas. His research interests include preclinical and clinical photoacoustic imaging for diagnostics and image-guided therapy.

Houra Tagahvi received her B.B. degree in Electrical Engineering from Azad University, Iran and M.S. degree in Biomedical Engineering at Texas A&M University in 2013. She is currently a researcher at the University of Texas MD Anderson Cancer center in Houston, Texas, and her research interests include integrated ultrasound and photoacoustic imaging and nanoparticle contrast agents in photoacoustic imaging.

James Long is currently an undergraduate student at Rice University, where he is pursuing a B.S. degree in Bioengineering. His research interests include preclinical and clinical photoacoustic-ultrasonic imaging for diagnostics and therapeutics.

Cayla Wood received her B.S. degree in Engineering Physics in 2014 and her M.S. degree in Applied Physics in 2015, both from Colorado School of Mines. She is currently a graduate student in Medical Physics at The University of Texas MD Anderson Cancer Center UTHealth Graduate School of Biomedical Sciences in Houston, Texas. Her research interests include preclinical and clinical photoacoustic imaging for diagnostics and therapy guidance.

David Fuentes received his B.S. degree in Aerospace Engineering from The University of Texas at Austin in 2002 and received his Ph.D. degree in Computational and Applied mathematics from The University of Texas at Austin in 2008. He completed a postdoctoral fellowship in the Image-guided Interventional Laboratory at MD Anderson Cancer Center in 2010. Dr. Fuentes is currently an Assistant Professor in the Department of Imaging Physics at the University of Texas MD Anderson Cancer Center. His research interests include image analysis for image guided interventions.

Wolfgang Stefan received a Diplom (Univ.) in Technical Mathematics at the Technical University in Munich, Germany, in 2003 and received a PhD in Mathematics at the Arizona State University in Tempe, AZ. He completed a post-doctoral fellowship at the Rice University in Houston, TX. He is currently conducting research in the Department of Imaging Physics at the University of Texas MD Anderson Cancer Center. His research interests are ill posed inverse problems and image processing.

John Ward is Associate Professor of Surgery, Department of Urology, at the University of Texas M.D. Anderson Cancer Center in Houston, TX. He received his BS in Biology at the University of Notre Dame and his MD at Georgetown University in Washington, DC. Postgraduate training includes a clinical residency in urology at the Naval Medical Center in San Diego, CA, and a clinical fellowship in urologic-oncology at the Mayo Clinic in Rochester, MN. Dr. Ward is a member of the American Board of Urology, the recipient of numerous awards, and the author of dozens of peer-reviewed publications.

Richard R Bouchard received his B.S. degree in Biomedical and Electrical engineering and Cultural Anthropology from Duke University in 2004 and received his Ph.D. degree in Biomedical engineering from Duke University in 2010. He completed a postdoctoral fellowship in the Ultrasound Imaging and Therapeutics Research Laboratory at the University of Texas at Austin in 2012. Dr. Bouchard is currently an Assistant Professor in the Department of Imaging Physics at the University of Texas MD Anderson Cancer Center. His research interests include preclinical and clinical photoacoustic-ultrasonic imaging and ultrasound-based elasticity imaging.