Not all sex ratios are equal: the Fisher condition, parental care and sexual selection

Abstract

The term ‘sex roles’ encapsulates male–female differences in mate searching, competitive traits that increase mating/fertilization opportunities, choosiness about mates and parental care. Theoretical models suggest that biased sex ratios drive the evolution of sex roles. To model sex role evolution, it is essential to note that in most sexually reproducing species (haplodiploid insects are an exception), each offspring has one father and one mother. Consequently, the total number of offspring produced by each sex is identical, so the mean number of offspring produced by individuals of each sex depends on the sex ratio (Fisher condition). Similarly, the total number of heterosexual matings is identical for each sex. On average, neither sex can mate nor breed more often when the sex ratio is even. But equally common in which sex ratio? The Fisher condition only applies to some reproductive measures (e.g. lifetime offspring production or matings) for certain sex ratios (e.g. operational or adult sex ratio; OSR, ASR). Here, we review recent models that clarify whether a biased OSR, ASR or sex ratio at maturation (MSR) have a causal or correlational relationship with the evolution of sex differences in parental care and competitive traits—two key components of sex roles. We suggest that it is more fruitful to understand the combined effect of the MSR and mortality rates while caring and competing than that of the ASR itself. In short, we argue that the ASR does not have a causal role in the evolution of parental care. We point out, however, that the ASR can be a cue for adaptive phenotypic plasticity in how each sex invests in parental care.

This article is part of the themed issue ‘Adult sex ratios and reproductive decisions: a critical re-examination of sex differences in human and animal societies’.

1. Introduction

Women are not going to be equal outside the home until men are equal in it.

— Widely attributed to Gloria Steinem (neatly, albeit inadvertently, summarizes how parental care affects the operational sex ratio)

Biologists and anthropologists are fascinated by male–female differences in ornamentation or aggressiveness, the propensity to search for mates, the willingness to mate and parenting (in combination often called ‘sex roles’; reviews: [1,2]). Sex roles are partly due to stronger sexual selection on one sex, usually males (reviews: [3,4]). Given the existence of trade-offs, greater investment into sexually selected traits reduces the resources that are allocated to naturally selected traits, such as parental care or immune system defence. In turn, changes in the allocation of resources, interactions between traits that affect the costs/benefits of different activities (e.g. an ornamental trait might reduce the efficiency of parental care) and variation in subsequent mate availability due to sex-specific rates of mortality and/or time spent in other activities generates sex-specific natural selection on life-history traits (see Box 1 in [5]). In short, both sexual and natural selection drive sex role divergence. But why does production of either eggs or sperm (anisogamy) lead to the consistent directional trends in sexual divergence seen in so many taxa (reviews: [6–8])? Why do females tend to care, and males to compete [9]?

Standard sex allocation theory dictates that sex ratios at birth are usually close to even [10–12]. Afterwards, however, sex ratios can become biased due to sex-specific factors. Various post-birth sex ratio biases are regularly invoked to explain sex roles [13] (table 1). Traditionally, theoreticians have argued that the operational sex ratio (OSR) in the mating pool plays the central role because of stronger sexual selection on the more common sex due to greater competition for mates ([6,20]; review: [21]), although the actual relationship is less straightforward than once assumed ([19,22,23]; but see [24]). More recently, others have noted that the adult sex ratio (ASR) is influential, not just because it affects the OSR, but because it determines the reproductive rate (offspring production per time unit) and reproductive value (i.e. expected lifetime offspring production) of each sex, which then affects key life-history decisions, such as whether to extend parental care or seek out another mate [9,25,26]. Other researchers suggest, however, that the sex ratio at maturation (MSR) is more relevant [14]. Initial emphasis on the ASR, MSR or OSR when explaining sex roles depends on whether the focus is on: (i) a biased MSR or ASR generating selection that drives sex differences in parental investment; these then increase sexual selection on the sex that returns to the mating pool sooner due to a biased OSR, or (ii) a biased OSR selecting for investment into more competitive traits in the more common sex, which favours less parental care due to trade-offs between caring and competing. Given that parental care and sexually selected traits both evolve and affect each other, a model for the origin of divergence in one trait can be initiated by a small sex difference in the other trait. In general, it has proved conceptually fruitful to treat parental care as the lynchpin to explain other components of sex roles. This is mainly because care affects mate availability, and mate availability alters both the costs of being choosy (i.e. of rejecting a potential mate; e.g. [27]) and the value of sexually selected traits that elevate mating rates (see §5). We therefore mainly take that approach in this review.

Table 1.

Implications of the Fisher condition, which formally states that when some average quantity x_f, measured for a set of females, is logically linked to the corresponding male quantity x_m due to heterosexual interactions, then r = x_f/x_m is the relevant male : female sex ratio. Each entry states whether the Fisher condition applies to the sex ratio for a given quantity. Notable evolutionary implications are given as footnotes. The sex ratio at maturation (MSR) is the ratio of males to females in a cohort that reach maturation. The ASR is the ratio of adult males to females that are currently alive. The operational sex ratio (OSR) is the ratio of males to females that are in the mating pool seeking mates. The effective sex ratio (ESR) is the ratio of males to females that mate at least once.

	sex ratio
quantity measured	primary	at end of parental investment	maturation (MSR)	effective (ESR)	adult (ASR)	operational (OSR)
lifetime matings	yes	yes	yes	yes	no	no
lifetime offspring production	yesa	yesb	yesc	yesd	no	no
mate encounter rate (per time unit in the mating pool)	no	no	no	no	no	yesf,g
mating rate (per time unit in the mating pool)	no	no	no	no	no	yesh
mating rate (per time unit alive)	no	no	no	no	yes	no
reproductive rate (offspring per time unit alive)	no	no	no	no	yese	no

^aIf sons and daughters are equally costly to produce (and there is no sex-specific population structure, such as local mate competition), parents should produce a 1 : 1 primary sex ratio.

^bIf offspring of one sex are costlier to produce, where the cost = [total investment in sex i]/[surviving offspring of sex i at the end of parental investment], parents should produce fewer offspring of this sex to equalize total investment in offspring of each sex (but see [12]).

^cIndividuals of the rarer sex should provide less parental care as they have a higher mean reproductive value (at least at maturation). They should be less willing to risk their more valuable lives for a given set of offspring [14].

^dA male-biased ESR is a precondition for the evolution of a male monogamy strategy (seen in some spiders, insects, crustaceans and fish), whereby males commit themselves (e.g. die) to mate with only a single female [15].

^eIn the special case where mortality does not differ between activities, reproductive rate is an appropriate fitness measure. The rarer sex should then provide less care, because a given fitness return from caring (i.e. rearing x extra offspring per time unit) is less profitable compared with a high reproductive rate (of the rare sex) versus a low reproductive rate (of the common sex). In the more general case where mortality can differ between caring and competing, the source of ASR bias determines its relationship with the proportion of care by each sex.

^fThe more common sex is predicted to be less choosy because it typically has a higher ‘relative searching time’ (proportion of lifetime spent in the mating pool), which increases the fitness costs of rejecting a proportion of mates [16,17].

^gIndividuals of the more common sex may be expected to face stronger sexual selection, such that a smaller proportion ‘qualify to mate’ [18].

^hIndividuals of the more common sex are predicted to invest more in traits that elevate their mating rate, because they typically have greater ‘scope for competitive investment’ (i.e. fitness increases more steeply with mating rate; [19]).

The existence of sex roles has prompted four main types of mathematical models of sex role evolution to explain why one sex is more likely to: (i) search for mates (e.g. [28–30]), (ii) be choosy and reject prospective mates (e.g. [17,31–34]), (iii) invest in competitive traits to improve mating opportunities (e.g. [8,19,35]; for a review of models for traits that elevate fertilization success, see [7,36]); (iv) care for offspring (e.g. [9,14,26,37–39]). Biologists frequently emphasize that the trend in many taxa is for males to search for mates and invest in weaponry and attractive ornaments, while females are choosier about mating and more likely to care for offspring. This constellation of sex differences is often used to designate species with ‘classical’ sex roles (see also [40]). Taxa like fish, where male-only care is common [41], are then seen as anomalous (for healthy debate on the advantages and pitfalls of this approach, see [5,42–44]).

Here we first describe how theoretical models of sex role evolution are built (see §2) and why the correct use of the Fisher Condition is essential (see §3). We then describe specific models that ask how various sex ratios affect the evolution of parental care (see §4) and, because of the resultant differences in the availability of each sex in the mating pool (OSR), how this affects the evolution of sexual competitiveness (see §5). (For recent models of the two other key components of sex roles, namely, mate choice and mate searching, see [17,30], respectively). When reviewing models of parental care, we pay special attention to the role of the ASR because models differ in whether or not they predict that this ratio will directly affect sex roles (see §6). In addition, recent phylogenetic comparative analyses in shorebirds show that the ASR is correlated with breeding system evolution [45], divorce rates [46] and sex differences in parental care [47]; and studies of humans link the ASR to mating competition, dispersal patterns and parental care (e.g. [48–52]). Finally, we ask what data we need to test sex role models (see §7).

2. Modelling sex role evolution

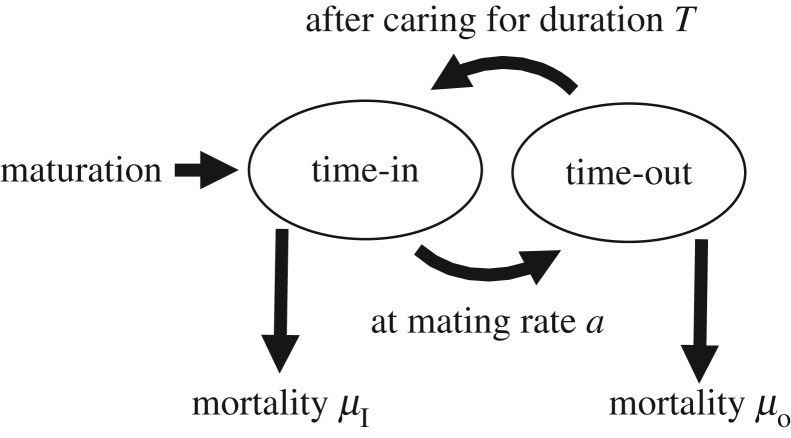
Most models assume a time-based trade-off between caring and competing. This is readily seen in the continuous breeding, ‘time in/out’ models pioneered by Clutton-Brock & Parker [35]. To begin, an individual is in the mating pool seeking mates (time in). As soon as it mates it leaves the mating pool to produce offspring, replenish gametes and care for offspring (‘time out’, T or 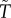for females and males respectively; note: the sperm-like tilde (∼) designates a male variable here and elsewhere; figure 1). Owing to this strict temporal trade-off an individual cannot simultaneously acquire mates and care for offspring. Of course, in many fish, frogs, birds and mammals (including humans), a male can obtain a new mate while caring for offspring. So too can females if they use stored sperm to fertilize their next clutch or litter. There is, however, variation in the extent to which species violate the trade-off assumption. For example, in many fish, territorial males guard nests that contain fertilized eggs (i.e. males care for offspring). Guarding males readily acquire new mates because females are willing, and even prefer, to spawn in nests already containing another female's eggs (e.g. [53]). By contrast, in socially monogamous birds that feed nestlings, a caring parent has less time available to acquire a new mate than does an unpaired bird. As a further complication, ‘time out’ after mating might depend on whether a mating is with a male's social partner or an extra-pair female: males rarely care for their offspring from extra-pair matings. ‘Time in/out’ models represent one end of the biological continuum between a perfect trade-off and no trade-off between caring and competing. In all cases, however, the models assume that the duration of care (T or 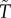) determines offspring survival. Survival is a positive function of either the sum (additive) or the product (synergistic) of the time spent caring by each parent. The benefit to each parent is, however, weighted by its mean relatedness to the offspring it cares for, which depends on how many males (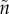) and females (n) participate per mating event and therefore share parentage.

Figure 1.

Schematic of the life-cycle envisaged in many models of mating system evolution. Upon mating individuals enter a ‘time-out’ period where they care for the resultant offspring and/or replenish their resources for the next breeding attempt. This applies to both sexes, whose mating rates are linked by the OSR via the Fisher condition (table 1).

A crucial life-history trait that affects the outcome of sex role models is the risk of dying while caring during ‘time out’ (μ_O and 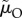), or while competing during ‘time in’ (μ_I and 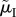). This can result in very biased ASRs, and these biases are often associated with predictions of differences in the amount of care each sex will provide when a population reaches evolutionary equilibrium. One reason populations can differ in their ASR is because they also vary in their MSR. Modellers can therefore manipulate the MSR to generate a specified level of bias in the ASR. Even with a 1 : 1 MSR, however, a biased ASR can still arise due to sex-specific adult mortality. For example, the sexes may have different mortality rates when performing the same activity (e.g. 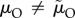). This possibility is of little interest when attempting to explain from first principles why anisogamy leads to greater female care. Far more intriguing is a situation where the sexes differ in how much time they spend caring (because of, say, lower benefits to caring when 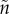≠ n, so that one parent is less closely related to a set of offspring) and, even without sex-specific mortality rates, mortality rates differ when caring and competing (i.e. 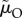= μ_O ≠ μ_I = 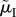). This will bias the ASR towards the sex that spends more time engaged in the less risky activity. The main point we wish to emphasize is that the same ASR can be generated in different ways. If the ASR is correlated with the sex roles seen at evolutionary equilibrium in a model, it is tempting to attribute a causal role to the ASR. For this to be a productive line of reasoning the route by which a biased ASR emerges should not matter. If it does matter then, perhaps, the factors that affect the ASR (i.e. the MSR and/or mortality rates that we have just described) should themselves be treated as the cause of the sex roles. As an aside, it is worth noting that when individuals enter a permanent post-reproductive phase (i.e. menopause), they should be excluded from empirical measures of the ASR. If not, empiricists will misrepresent the selective pressures faced by reproductively active individuals arising from competition for mates.

There are two ways in which sexual selection is incorporated into parental care models. Some models specify that only 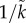of males and 1/k of females are ‘qualified’ to mate (i.e. male–male mating competition is greater when is larger) (e.g. [26]). The use of 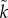or k has the limitation that the level of sexual competition remains the same even when the duration of parental care evolves such that the OSR changes. In other models, individuals have a sexually selected trait that, depending on its level of expression relative to rivals, affects their mating rate and determines how long they spend in the mating pool (e.g. [14]). These sexually selected traits elevate mortality, but how this cost is exacted can vary. At one extreme, it affects all adult life-history stages equally. This represents a trait that is continually present so that the risk of attracting a predator is always elevated (e.g. bright plumage): this is modelled as a uniform increase in mortality during ‘time in’ and ‘time out’ (e.g. [19]). At the other extreme, a sexually selected trait might only be expressed when seeking a mate, such as an advertisement call that attracts predators. Between these extremes there is ‘carry over’ of mortality costs between life-history stages (e.g. [30]).

In §§4 and 5, we present specific ‘time in/out’ sex role models that focus on the relationships between sex differences and various sex ratios. Before doing so, it is worth noting that Lehtonen et al. [8] recently proposed a concise model to explain the initial evolution of sex roles that is based purely on sex differences in the return from investment into traits that increase fertilization rates. Their model does not explicitly deal with ‘time in/out’. Their starting premise is that the sexes are identical, except in gamete size. Lehtonen et al. made a minimal assumption: the sexes initially invest identically into gamete production. If so, sperm vastly outnumber eggs due to their smaller size because there is a 1 : 1 ASR. The ASR is even because the sexes are identical so there is initially no sex-biased mortality and the primary sex ratio is even [11]. Given the high sperm to egg ratio, all eggs will be fertilized. If true, females cannot gain from investing in traits that increase their fertilization rate: such investment will only lower egg production. By contrast, males will benefit from investing some proportion (r) of their reproductive investment into competitive traits that increase the per-sperm likelihood of fertilizing an egg (e.g. weapons, ornaments, manipulating female sperm usage and seeking out mates) if this compensates for producing fewer sperm.

An obvious criticism of Lehtonen et al.'s model is that once males divert resources away from gamete production, the assumption that all eggs are fertilized fails. There is, however, still a sexual asymmetry in the fitness gained by increasing r even if females become sperm-limited. The marginal returns per additional investment in gametes are lower for a male because his sperm compete more intensely with each other for eggs than do a female's eggs for sperm. Owing to local gamete competition, selection still favours greater male investment into traits that elevate the fertilization rate per gamete. Even if the ASR becomes heavily female-biased (e.g. because sexually selected traits elevate male mortality), this is unlikely to be so extreme that eggs will ever be more numerous than sperm for a given breeding event.

3. Sex ratios and the Fisher condition

Before we present specific sex role models, we need to explain the Fisher condition. In diploid, sexually reproducing species, each offspring has one father and one mother. Consequently, the total number of offspring produced or matings by each sex is identical and the mean contribution per male or per female depends on the relevant sex ratio (table 1). This is the ‘Fisher condition’ that cannot be violated in an internally consistent model (review: [54]). Unfortunately, several influential models violated the Fisher condition or have drawn erroneous conclusions from it, including sex role models of parental care (e.g. [37,55–57]) and mate searching (e.g. [29,30]).

When applying the Fisher condition to link lifetime averages (or expectations) of success, the sex ratio must include all individuals over whose lives these averages are calculated (table 1). When applying the Fisher condition to link success rates per time unit, the sex ratio must include those individuals who are considered as potential recipients of success at any given time. A crucial measure of success is the expected lifetime number of offspring, because this is the measure of fitness in most models. Expected offspring production is closely related to the life-history concept of reproductive value (RV), which determines optimal life-history decisions. For example, when RV is high, individuals are less willing to engage in costly acts that increase their risk of mortality because they have more to gain by staying alive [58]. Whether males and females differ in their RV has major implications for the extent to which they engage in parental care: the more ‘valuable’ sex should value its life more highly compared with the life of a brood, hence it should be less willing to provide care at a risk to its own survival.

The primary sex ratio (at conception), the secondary sex ratio (at birth) and the MSR all link each sex's lifetime expectations of matings and offspring via the Fisher condition. It is tempting to add the ASR and the OSR to the list of ratios, but this would be a mistake. To see why, consider the example of a demographically stable population with a 1 : 1 MSR (regardless of the resultant ASR and OSR): in this population, a maturing individual of either sex must on average produce exactly two (maturing) offspring during its lifetime: one daughter and one son. If it produced a different number of daughters, the population would grow or shrink; and if it produced a different number of sons, the MSR would change. By contrast, the ASR is not a suitable predictor of lifetime success because it can become biased due to sex-specific adult mortality, which has counteracting effects on lifespan and reproductive rate (the sex with higher survival and a longer lifespan must have a lower reproductive rate if the MSR is 1 : 1). In other words: the average lifetime success of each sex must match as long as there are equal numbers of lives to account for, even if one sex lives longer and the ASR is consequently biased. (Note: the Fisher condition does apply to the OSR, but only for the rate of mating or encountering mates while in the mating pool. Likewise, the Fisher condition applies to the ASR for mean mating or offspring production rate of adults per unit time alive).

We belabor the appropriate use of the Fisher condition because one of us (MDJ) has implicitly linked the OSR to fitness (i.e. lifetime offspring production) when trying to explain in seminars why the null model of Kokko & Jennions [26] led to egalitarian parental care by the sexes (an incorrect result; see §4). This misapplication of the Fisher condition always went unnoticed. The more general point is that explanations as to why the sexes differ in how much they, say, care or invest in being sexually competitive often invoke the Fisher condition. If the wrong ratio is used, the explanation—no matter how appealing—is flawed.

4. Models for the evolution of sex differences in parental care

Kokko & Jennions [26] produced a continuous breeding, ‘time in/out’ model to investigate the evolution of sex roles for parental care: that is, T and 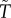could evolve under selection. (It is implicit that they evolve due to a change in the time spent caring rather than in the time taken to replenish gametes or other resources needed to breed.) In each scenario modelled, they fixed the parameters for: sex-specific mortality rates, the mean number of males and females per breeding event, variation in sexual selection on each sex (k and 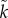), and the MSR. They assumed that parental care had an additive effect on offspring survival. In the null model, where the only initial difference between the sexes was the duration of care, they reported stabilizing selection so that the equilibrium state was equal care by both sexes. Unfortunately, this finding was incorrect, because the cost–benefit calculations did not equate to maximizing fitness [14]. Nonetheless, it was an intriguing result that had to be explained at the time, but how (see §6)? In an extension of the null model, Kokko & Jennions [26] then showed that female-only care is more likely when males are less related to the brood ( 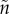> n, which is biologically likely given that sperm greatly outnumber eggs). Lower relatedness reduces the benefit of care as the increase in offspring survival has to be discounted by relatedness. 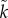They also showed that female-only care is more likely when there is stronger sexual selection on males ( > k; for why this is likely see the description of Lehtonen et al. [8] in §2). These findings, while tainted by concerns about how fitness was calculated, agreed with elegant, earlier arguments of Queller [9] as to why females care more than males.

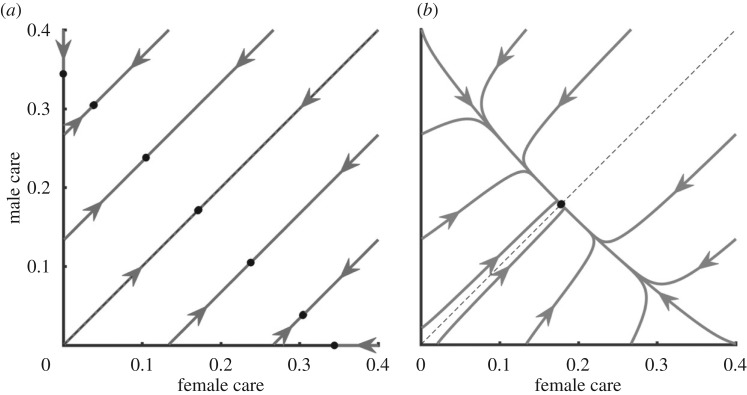
Fromhage & Jennions [14] recently revised Kokko & Jennions [26]'s models, finding that a key result of the original null model did not hold up: there was, in fact, no stabilizing selection on sex roles for parental care. Instead, selection merely stabilized the total duration of care provided, regardless of the relative contribution of each sex. This result can be visualized as a line of equilibria (figure 2a), on which each point corresponds to a combination of sex-specific care durations that add up to the appropriate total duration. We defer our explanation as to why this occurs to §6. To investigate the effect of changes in other parameters, Fromhage & Jennions [14] then examined a model where the benefits of care are synergistic (i.e. offspring survival is a function of T * 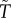). In this case, the model resulted in an equilibrium with equal care by both sexes (figure 2b). This confirmed Queller's prediction that female-only care is more likely when males are less related to the brood ( 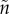> n), and when there is stronger sexual selection on males (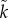 > k). If fewer males than females ‘qualify’ to mate, qualified males (which includes all caring males) have a higher RV (i.e. expected future fitness gain) due to their rarity, in the same way as an MSR bias increases the RV of the rarer sex (Fisher condition). (Note: In our model, the RV of surviving males is not higher when the ASR is female-biased due to male mortality, because past survival does not imply future survival (i.e. survival rates are a constant), and RV reflects the expected future, not the past. In the real world, however, in some species adult mortality rates change with age so that RV varies over time (e.g. due to a period of high mortality as a young adult or due to senescence). To account for age-dependent mortality would, however, require a less generalizable model with age-dependent parental decisions. We do not believe this would change the main message of the model though).

Figure 2.

Evolution of care durations of both sexes, assuming the sexes are identical in all respects other than care duration. (a) Care is additive, such that it makes no difference for the offspring how a given total care duration is divided between parents. This leads to a line of equilibria connecting all combinations that sum to the same total duration. (b) Care durations are synergistic, such that the same total care duration becomes more valuable if divided more evenly between parents. Arrows indicate evolutionary trajectories from arbitrary starting points, based on selection gradients. Black dots indicate stable end points. Dashed lines indicate equal caring by both sexes. Based on the model by Fromhage & Jennions [14], with parameter values: k = n = M = r = 1; 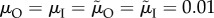; α = 0.1; synergy coefficient γ = 0 (in a), γ = 0.1 (in b).

Fromhage & Jennions [14] next produced a ‘two-trait’ sex role model for the evolution of both the time spent caring (T, 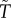) and investment in a sexually selected trait (x, 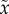) that causes the bearer to mate more rapidly upon entering the mating pool. The cost of the sexual trait was uniformly higher mortality when competing or caring. The result was clear: evolution of a sexually selected trait promotes care by only one sex. If sex A cares even slightly more than sex B (e.g. because 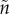≠ n), there is a relatively greater fitness benefit to B of decreasing the time spent waiting to mate because they are more common in the OSR ([19]; see §5). B therefore invests in the sexual trait. This, however, increases their mortality while caring. Natural selection therefore favours less care by B (as there is no concomitant fitness gain of trait x when caring). This selects for a compensatory increase in care by A, so B is under even stronger sexual selection. Positive feedback ensues until A alone cares. Females are likely to initially care slightly more than males (e.g. because 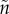> n) so positive feedback will select for still greater care by females than males. McNamara & Wolf [39] have similarly shown that coevolution of care effort and care ability promotes sex role divergence.

In sum, these initial models provide us with a basic understanding of when males will care more than females in different species (or different populations if they evolve independently). We can then ask whether the ASR affects which sex cares more, and why. More specifically, does it matter whether the ASR varies due to changes in the MSR, or mortality during ‘time in’ or ‘time out’? The answers are provided in §6.

5. The evolution of competitive sexual traits

It was long argued that a biased OSR favours greater investment in sexual traits by the more common sex [6,20]. If true, sex role divergence in competitiveness is readily explained by the propensity for males to care less than females. If males return to the mating pool sooner, this creates a male-biased OSR. The problem with this argument is that it conflates the intensity of competition for mates with the response. Evidence that the argument is incomplete comes from a very simple model by Jennions et al. [59]: the selection differential on a sexually selected trait was unchanged as the OSR shifted from 2 : 1 to 1 : 2. To clarify the circumstances that favour a sexually selected trait, Kokko et al. [19] built a ‘time in/out’ model in which ‘time out’ for each sex was fixed. They calculated the minimum increase in mating rate needed for selection to favour a sexually selected trait that uniformly increases mortality. The lower the requisite increase in mating rate for a given reduction in lifespan, the higher the ‘scope for competitive investment’. They showed that, the greater the proportion of an individual's life that is spent in the mating pool, the larger the scope for competitive investment. In general, the major determinants of time spent in the mating pool are the relative ‘time out’ of each sex and the ASR (which depends on both the MSR and adult mortality). Individuals of the sex with the longer ‘time out’ are rarer in the OSR, mate more quickly and spend less of their life in the mating pool. They therefore gain proportionately less by mating faster, so only small mortality costs are tolerable. Reassuringly, this implies that the OSR (insofar as it reflects differences in ‘time out’) does predict which sex will invest more into competitive traits. But there is a subtle caveat. If one sex has a very short ‘time out’ then the scope for competitive investment for this sex remains high, irrespective of the OSR.

6. How do sex ratios explain the outcome of sex role models for parental care?

How do the ASR, MSR and activity-specific mortality affect the evolution of parental care? Kokko & Jennions [26] reported that male care is higher when the ASR is male-biased, regardless of whether this is due to a male-biased MSR, or to a sex difference in adult mortality. This generated the intriguing claim that higher mortality of adults when caring will result in the evolution of increased male care if it leads to a male-biased ASR (i.e. because females were initially providing more care), even though this means that males then evolve to spend more time engaged in a risky activity. Kokko & Jennions [26] concluded that the ASR has a causal role in the evolution of sex roles for parental care. This appeared to confirm earlier work in which the ASR was modelled as an input parameter, while leaving its source of variation unspecified [60,61].

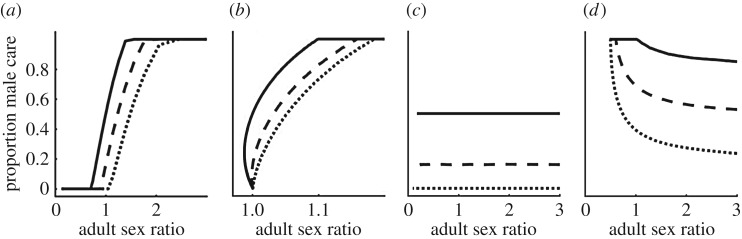
More recently, Fromhage & Jennions [14] have queried this view because the route by which the ASR becomes biased seems to matter. Specifically, they showed that males provide more care than females if the ASR is male-biased because of (i) a male-biased MSR or (ii) uniformly lower male than female adult mortality (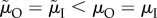). However, the proportion of care provided by males does not change if the male-biased ASR arises solely (i.e. the MSR is 1 : 1) because of lower male mortality while competing, which can be (iii) sex-specific (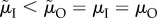) (figure 3) or (iv) non-sex-specific (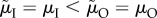) when males initially care less (i.e. when 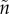> n). (While the above arguments are phrased in terms mortality differences that create a male-biased ASR, they apply in an analogous fashion to differences that create a female-biased ASR.)

Figure 3.

The proportion of male care (of the total care provided by both sexes) as a function of the ASR (males per female), when (a) the ASR is manipulated by changing the maturation sex ratio MSR or (yielding identical results) when the ASR is manipulated by simultaneously changing male mortality in both states (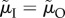); or (b) when the ASR is manipulated by changing male mortality only during time-out (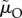); (c) when the ASR is manipulated by changing male mortality only during time-in (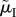); or (d) when the ASR is manipulated mostly by changing male mortality during time-in ( 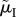ranges from 0.08 on the left to 0.0025 on the right side of the graph) while male mortality during time-out varies in the opposite direction ( 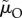ranges from 0.00025 on the left to 0.008 on the right side of the graph). Based on the model by Fromhage & Jennions [14], with parameter values: solid line: 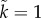, 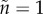; dashed: 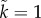, 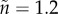; dotted: 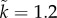, . Default parameter values: k = n = M = r = 1; 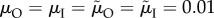; α = γ = 0.1.

We suggest that, generalizing from the insights gleaned from the models of Koko & Jennions [26] and Fromhage & Jennions [14], the ASR is not a causal factor driving obligate (i.e. non-context-dependent) sex differences in parental care behaviour. We explore scenarios (i–iv) above to understand how care evolved, and note that we do not need to invoke any effect of the ASR itself. In scenario (i) when the MSR is male-biased, the Fisher condition implies that, on average, males at maturity have a lower lifetime reproductive output, hence lower RV, than females. RV determines the ‘cost of caring’ for each sex (i.e. how much fitness they stand to lose if they die while caring, which depends on 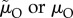). The MSR therefore predicts the proportion of care provided by each sex. If the MSR is male-biased, males have a lower RV and pay a lower cost to care. One line of reasoning as to why the ASR does not have a causal role in the model is to understand that adult mortality that changes the ASR does not affect the relative RV of each sex. For example, in scenario (iii) when males have lower mortality than females in the mating pool (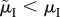) the resultant male-bias in the ASR decreases the mating rate of the surviving males. This, however, is perfectly offset by their longer lifespan so that male RV (relative to female RV) stays the same (figure 3c; which always follows from the Fisher condition). The same logic applies in scenario (iv) when the sexes have the same mortality rate in the mating pool () but initially differ in the time spent caring: despite a change in the ASR, the proportion of care given by males remains the same. Finally, in scenario (ii), disentangling the underlying mortalities shows that the positive relationship between the ASR and male care was driven entirely by 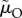(i.e. the cost of caring; figure 3b), and not at all by 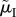(whose counteracting effects on lifespan versus reproductive rate cancel out; figure 3c). Using this insight, we can even construct a scenario in which the relationship between the ASR and the proportion of male care is reversed: males care less as the ASR becomes more male-biased (figure 3d). Here, a change in 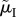changes the ASR without affecting care, while a weak counteracting change in 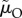drives the pattern of care. It is worth noting that the underlying model assumes no senescence, so all individuals in the mating pool are indistinguishable from (and have the same RV as) newly matured individuals.

In our view, none of the above justifies the claim that the ASR has an independent causal effect on the proportion of male care. That said, the claim is defensible if we make a rather strong simplifying assumption (even by the yardstick of modelling!). Specifically, what about earlier models [60,61] that appeared to show a general effect of the ASR on care decisions? Were they wrong? No, but their conclusions reflect a technical limitation of their mathematical framework: they are ‘rate-maximization models', built on the strong assumption that individuals cannot influence their lifespan, so maximization of their rate of reproduction maximizes their fitness (following [55] model 3; [35,62]). Within this framework, selection for caring can be described in a simple way, analogous with intake-maximization in foraging theory [63]: the optimal point at which to cease caring is when the marginal rate of return falls below the average rate of return (i.e. the reproductive rate) for this type of individual. This focus on reproductive rates imputes a pivotal role to the ASR via the Fisher condition, as (males alive) × (male reproductive rate) = (females alive) × (female reproductive rate). If males are y times more common than females in the ASR, their average reproductive rate (hence their required marginal value of caring) is lower by 1/y. As this holds regardless of the source of ASR variation, the ASR appears to determine the evolution of sex roles [60,61]. This is not a general finding though as its validity rests on the restrictive assumption that mortality does not differ between activities, so that (as in scenarios (i) and (ii)) individuals cannot influence their lifespan. But this is often not the case: whenever mortality differs between caring and competing, then care decisions affect lifespan (scenarios (iii) and (iv)) and selection favours individuals that maximize their lifetime offspring production or RV [64] (see also [65]) and not necessarily their reproductive rate.

What then is the role of the OSR in the evolution of sex roles of parental care? It is possible to read Kokko & Jennions [26] as arguing that individuals of the more common sex in the OSR are selected to provide more care, because they are ‘unprofitably’ waiting in the mating pool. This reading is tempting because of the need to explain the (erroneous) result of stabilizing selection for equal parental care in their null model (where the MSR, hence ASR, was 1 : 1). When the MSR and ASR are 1 : 1, then (all else equal) the OSR is biased towards sex A if sex B provides more care (i.e. longer ‘time out’). Sex A will then spend longer in ‘time in’. However, this does not select for greater care by sex A because both sexes nevertheless have identical incentives to care or desert: both benefit equally from each extra offspring that survives in the current brood, and both face the same expectation of future reproduction after deserting. In rate-maximization terms (see above), both sexes have identical reproductive rates, hence require the same benefit of caring (in terms of additional surviving offspring per time unit) to make caring worthwhile. Because these arguments apply regardless of current care durations, Fromhage & Jennions' [14] corrected null model revealed a line of equilibrium for care: as long as the total amount of care is appropriate given its effect on offspring survival, it does not matter for selection which sex provides more care.

7. Empirical tests of how sex ratios affect sex roles

(a). Adaptive plasticity and evolved responses

Most empirical studies that test evolutionary sex role models look for phenotypically plastic responses to changes in the ASR or OSR (review: [66]). This is based on the problematic assumption that adaptive plasticity acts in the same direction as a trait will evolve under selection. Kahn et al. [12] provide an instructive counter-example. They show that mothers should initially produce more sons than daughters if individual males are less costly because they die during the period of care and free up resources. However, when mothers have access to local cues that indicate their sons are more likely to die than their daughters (e.g. sons require more resources and the mother is on a low-quality territory) the adaptive response is to produce fewer sons. This is the opposite trend to that predicted by the evolutionary model.

The appropriate way to test predictions from evolutionary sex role models is to show that traits evolve in the predicted fashion. We see two main approaches when it comes to the effect of sex ratios. First, establish experimental evolution lines in which the MSR is manipulated (e.g. [67]). One should, however, bear in mind what other factors might then change. For example, a male-biased MSR is predicted to increase male care but, prior to any evolution of care duration, this MSR will create a more male-biased OSR. This OSR could elevate polyandry and reduce the benefit of male care due to lower relatedness to a set of offspring. Putting these concerns aside, a critical test would be to compare the evolution of care when the ASR is manipulated either by changing the MSR or male mortality in the mating pool: sex role models predict different outcomes (figure 3).

Second, use comparative analyses to test for the predicted causal relationship between the MSR and sex roles for parental care and, given coevolution, mating competitiveness. Note, however, that the ASR might still prove a better predictor, as it can become correlated with sex roles through more than one mechanism (figure 3a,b). Which sex ratio predicts sex roles better should depend on the extent to which different mechanisms contribute to empirically observed ASR variation. If ASR variation reflects mostly MSR and time-in mortality, the MSR should be a better predictor; if it reflects mostly general mortality (not limited to time-in), then the ASR should be a better predictor. So far, comparative analyses have only considered the ASR in this context (e.g. [45,46]). This is a reasonable first step, but it falls short of revealing the underlying evolutionary mechanism: there is more to be learned by relating sex roles directly to the causes of ASR variation. Given the challenges of estimating sex ratios [68], researchers might seek out traits that are plausibly correlated with the MSR to see whether they predict sex roles for parental care (e.g. sex-biased juvenile dispersal biases the MSR because dispersal tends to elevate mortality).

(b). Population- versus individual-level responses

The use of appropriate baseline expectations is crucial to test how the ASR affects behaviour. Consider a study asking whether the ASR affects the propensity of males to try to copulate. For simplicity, assume a population of 1000 individuals with an even ASR (males, m = females, f = 0.5), where individuals encounter each other at random. Whenever a male encounters a female there is a 60% chance that he tries to copulate. For every 1000 encounters, there are 500 male–female encounters (proportion = f² + 2fm + m²) and, of these, 300 involve a copulation attempt. The population-level rate is 300 copulation attempts per 1000 individuals, while the rate per male is 0.60 (=300/500). If the ASR then shifts to 90% male, there are 180 male–female encounters and 108 copulation attempts. The population rate now drops to 108 attempts per 1000 individuals, and 0.12 attempts per male (=108/900).

Using the population rate (300 versus 108) to test whether the ASR affects males is clearly inappropriate: it includes females and we are only interested in a male's propensity. But using the rate of occurrence per male is also misleading. It suggests that males are less sexually eager: given a more male-biased ASR the rate fell from 0.60 to 0.12. However, a male's propensity to try to copulate upon encountering a female stayed constant at 60%. Researchers have to consider carefully how changes in the ASR affect interactions between the sexes if their focus is on individual-level responses, which is usually required to test evolutionary models. The point we make is not novel, but it is worth reiterating: some researchers still use the equivalent of collecting data from 1000 encounters (i.e. rates from a fixed sampling duration) to infer male behavioural propensities.

8. Future considerations

We now have models that individually investigate each component of sex roles. These models usually fix the value of non-focal components to investigate how extrinsic factors (e.g. mortality rates of different activities) affect the evolution of the focal component. For example, Kokko et al. [19] model the evolution of sexually competitive traits while holding constant the time each sex spends providing parental care. But external factors might change, often in predictable ways, if other sex role components evolved. For example, what if greater investment into competitive traits alters selection on parental care? Competitive traits might increase mortality while caring or reduce the efficiency of caring. If so, coevolution of care and competitiveness could lead to a different outcome (e.g. [14]; see §4). It is prudent to remember this limitation when one interprets the results of single component models. Feedback can cause traits to coevolve. The caveat ‘all else being equal’ really matters. Empiricists crave sex role models that cover the evolution of all aspects of sex differences, but such models are generally analytically intractable. What then should we do? A pragmatic step is to produce models where pairs of components evolve. Some such models exist (e.g. care and choosiness [69]); or care effort and care ability [39]; or care and competing [14]) but more are needed so that we can better understand if, and how, selection for greater expression of one component facilitates or retards the evolution of other components.

Empiricists are often disappointed when models exclude biological realities. There are some features missing from the current models that might concern empiricists, and should be born in mind when testing them. First, trade-offs for a trait between life-history stages are often ignored. Specifically, a trait that elevates the mating rate could reduce the efficiency of parental care or vice versa. This could be a direct result of the expression of the trait at both life-history stages (e.g. ornaments hinder feeding offspring), or due to allocation of limited resources (e.g. energetic courtship reduces the resources available to care effectively). Second, the sex ratios could directly alter the benefits of prolonged care. For example, the ASR or OSR might affect the risk of infanticide, because there are more potential predators per offspring [70]. Third, the sex ratio could directly affect the likelihood of mortality in the mating pool (e.g. more fights or elevation of courtship to out-signal rivals could increase the rate of mortality; i.e. OSR affects ‘time in’ mortality). Fourth, higher mortality rates could affect other model parameters. For example, even if mortality is not sex-specific such that sex ratios stay the same, a uniformly higher mortality rate will lower population density. A reduced mate encounter rate decreases mate choice because the time cost of rejecting a potential mate is higher [31], and the cost of choosiness is related to the proportion of the lifetime that is spent searching or waiting to mate [16,17]. Less choosiness might then reduce the strength of sexual selection (e.g. more males ‘qualify’ to mate as 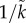is larger), which, in turn, will affect the evolution of sex differences in parental care (see §4). Fifth, sex ratios could affect the likelihood of multiple mating. With a more male-biased OSR, it seems likely that, unless females are fully in control of mating [71], polyandry will increase, which reduces the benefit of male care (see §4). More generally, current sex role models ignore the trade-off between allocation into traits that increase mating success versus those that elevate fertilization success (for a single-sex model, see [72]; review: [73]). Finally, in many species there is a finite breeding season but the sex role models we have described all assume continuous breeding with overlapping generations and constant sex ratios. Models with breeding seasons that allow for more than one breeding attempt can predict more complex, time-dependent patterns of parental care, e.g. reflecting seasonal variation in mate availability [37,74].

In sum, the so-called classical sex roles are commonplace in nature, and it is likely that parental care models that predict greater parental care by females will show that this asymmetry promotes the coevolution of stronger female choosiness, lower female competitiveness ([14]; two-trait model) and less mate searching by females. However, it remains to be seen what additional factors explain the evolution of ‘role reversed’ species, or those with unusual sex-specific combinations of choosiness, competitiveness and care (e.g. [75]). Encouragingly though, comparative evidence that the ASR predicts breeding systems, at least in shorebirds [45], suggests that attention to factors that affect the ASR or MSR is a profitable way forward for both empiricists and modellers.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

This paper was written while M.D.J. was a fellow at the Wissenschaftskolleg zu Berlin, and a EURIAS fellow. L.F. was funded by the Academy of Finland.