The potential pitfalls of studying adult sex ratios at aggregate levels in humans

Abstract

Human adult sex ratios have been studied extensively across the biological and social sciences. While several studies have examined adult sex ratio effects in a multilevel perspective, many studies have focused on effects at an aggregated level only. In this paper, we review some key issues relating to such analyses. We address not only nation-level analyses, but also aggregation at lower levels, to investigate whether these issues extend to lower levels of aggregation. We illustrate these issues with novel databases covering a broad range of variables. Specifically, we discuss distributional issues with aggregated measures of adult sex ratio, significance testing, and statistical non-independence when using aggregate data. Firstly, we show that there are severe distributional issues with national adult sex ratio, such as extreme cases. Secondly, we demonstrate that many ‘meaningless’ variables are significantly correlated with adult sex ratio (e.g. the max. elevation level correlates with sex ratio at US state level). Finally, we re-examine associations between adult sex ratios and teenage fertility and find no robust evidence for an association at the aggregate level. Our review highlights the potential issues of using aggregate data on adult sex ratios to test hypotheses from an evolutionary perspective in humans.

This article is part of the themed issue ‘Adult sex ratios and reproductive decisions: a critical re-examination of sex differences in human and animal societies’.

1. Introduction

(a). Adult sex ratios effects on human behaviour

Adult sex ratios (ASRs) have long been studied not just in evolutionary biology (e.g. [1–6]), but also in the social sciences (e.g. [7–10]). However, following the seminal book by Guttentag & Secord, entitled ‘Too Many Women? The sex ratio question’ [11], there has been a resurgence in the study of the influence of ASR on human behaviour. Since its publication in 1983, there has been a growing literature across a broad range of disciplines, including epidemiology, political science, criminology, sociology, economics and demography, dealing with the role of ASR for behaviour (e.g. [12–18]), such as marriage patterns (‘The marriage squeeze’: e.g. [17,19]) and crime (e.g. [20]). Pedersen [21] reframed Guttentag & Secord's work into a sexual selection framework, based on Bateman [22] and Trivers [23], and also tied it to evolutionary psychology [24,25]. Individuals are predicted to alter their decisions and behaviour in response to local sex ratios in an adaptive fashion [26]. Local ‘market dynamics’ should influence individual behaviour in line with predictions from sexual selection theory. For example, marital stability is predicted to be lower as the ‘availability of a pool of young sexually active women means that men who marry are closing off a reproductive opportunity’ ([27]: 260). Similarly, teenage pregnancy and fertility rates are expected to be higher when there is an oversupply of women.

Currently, there is a broad range of empirical studies examining the effect of ASR by using outcomes at the individual level (e.g. [28–34]) or by mathematical modelling (e.g. [35]). Some psychological studies have also used vignettes to describe imbalances in ASR (e.g. [36–38]) or manipulated cues to sex ratios [39] and examining how individuals respond. Table 1 gives an incomplete list of examples of the levels at which ASR have been studied. Table 1 shows that there are also many papers relying solely on analyses with aggregate data (e.g. [21,40,41]). Here we focus on those papers relying (exclusively) on aggregate data. By aggregate data, we refer to data pooled to some group or area level, such as nations, wards, provinces, districts or cities. These analyses on aggregate data are routinely used to support the argument that ASR influence human behaviour (e.g. [42–46,56,57]). The majority of studies with aggregate data rely on national level data, but some rely on smaller spatial units [47–50,58–60], such as states, regions, counties, wards, cities, metropolitan areas or even hunter–gatherer societies [51]. We focus on how known problems with country-level data affect the conclusions we can draw about the effect of ASR on human behaviour. Importantly, we extend this analysis to aggregation at lower levels such as US states and counties, and demonstrate that these problems exist in the same way for data aggregated at these lower levels. Finally, we provide new analyses on the relationship between ASR and teenage fertility. Before we proceed, we will review some of the findings on ASR and human behaviour derived from analyses on aggregate data.

Table 1.

Some examples of work on ASRs, the topic and the level of outcome and the level of ASR.

reference no.	year	topic	outcome level	sex ratio level
[16]	2010	sexual behaviour and risk	individual	county or equivalent (China)
[21]	1991	family behaviour	country (USA)	country (USA)
[30]	2015	mating strategies (sociosexuality)	individual	community (Guyana)
[32]	2010	romantic relationships/sexual behaviour	individual	university campus (USA)
[36]	2012	career aspiration	individual	individual (perception in vignette)
[40]	2000	violent crime	country	country
[41]	2009	violent crime	country	country
[42]	2003	single parenthood	country	country
[43]	2009	sociosexuality, sex drive, height	country	country
[44]	2013	premature gestation/birth weight	county (USA)	county (USA)
[45]	2014	assault rates	census tract (USA)	census tract (USA)
[46]	2017	violence against women	societies (standard cross-cultural sample)	societies (standard cross-cultural sample)
[47]	2015	violence and crime	county (USA)	county (USA)
[48]	2015	preventable death	individual	ward (Northern-Ireland)
[49]	2009	marriage	metropolitan statistical areas (USA)	metropolitan statistical areas (USA)
[50]	2013	birth rate	ward (UK)	ward (UK)
[51]	2012	mate competition	hunter–gatherer populations	hunter–gatherer populations
[52]	2008	homicide	country	country
[53]	2008	marriage	individual	state (USA)
[54]	2015	sociosexuality	individual	state (USA)
[55]	2016	mating	individual	individual (perception in vignette)

(b). Aggregate-level analyses of adult sex ratio

Several studies have now investigated the role of ASR at the national level with a range of psychological and behavioural variables, mostly in a cross-sectional design. Perhaps the most extensively studied relationship, not just in evolutionary psychology, is the relationship between ASR and various indicators of violent crime, such as homicide [40,41,61] and rape [62]. Surprisingly, ASR have been claimed to be positively and negatively related to crime (reviews in [60,63]). Hudson & den Boer [20] argued for a positive relationship between ASR and crime via use of case studies covering Asia. However, the majority of studies have actually suggested negative associations between ASR and crime at the national level [40,41,52,64–66] (reviews in [63,67]). For example, using a sample of a 100 countries, Antonaccio & Tittle [68] reported r = −0.32 between homicide (logged) and ASR (logged). More importantly, a meta-analysis covering all analyses on ASR and crime at the national level found no noteworthy relationship [69]. This meta-analysis also highlighted that substantial heterogeneity exists in the effect of ASR. Such heterogeneity could be partially due to the extensive methodological differences between studies. Firstly, the sample sizes vary considerably between studies, with some using samples of around 30 countries (e.g. [66]), while others used 100 or more (e.g. [68]). Secondly, the meta-analysis also indicated that the source of the data could contribute to the heterogeneity, even to the extent that the sign of the sex ratio effect could be reversed depending on the source of data used (WHO: negative, UN and Interpol: positive). Finally, there is considerable variation in analytical choices across these papers (also see [63,67]). For example, some authors chose to transform the homicide data but not ASR (e.g. [70]), others transform both the homicide data and ASR (e.g. [67]), others weigh the data (e.g. [71]), or perform weighted least-squares analysis [52]. Even within studies analytical decisions can matter. To illustrate: one study reported a positive but non-significant zero-order correlation (r = 0.094) between the natural logarithm of homicide and ASR, but found a negative and significant association in a weighted least-squares analysis when controlling for other factors (e.g. the Human Development Index) [70]. Analytical decisions such as the choice of technique, the sample, or the inclusion of covariates thus matter dramatically for the conclusions one draws.

Evolutionary psychologists have predominantly studied ASR and variables relating to mate preferences, such as sociosexuality [72], the degree to which individuals are willing to engage in sexual activities without being committed to a relationship (e.g. [56,73]). However, other research in this area suggested that national ASR are not significantly related to sociosexuality and sex differences therein [43]. Some studies moved beyond mate preferences and related national ASR to indices more directly relevant to behaviour, in particular marriage and fertility. In line with Pedersen's predictions [21], Barber showed that ASR were related to teenage pregnancies, indices of single parenthood and non-marital fertility [27,40,42].

Theoretically, the reasoning is that when one sex is scarcer, it will be driving ‘the demand’ for certain traits (e.g. [2,11,53,65,74]). For example, if there is an oversupply of men, a market logic would suggest that women would desire higher status in potential marriage partners. Conversely, following Guttentag & Secord [11], a low sex ratio, i.e. relatively more women, would lead to a decline in marital stability, such as higher divorce rates and greater non-marital fertility [21,27,56]. Barber extended this logic and in a series of studies showed that teenage fertility rates were negatively associated with ASR in aggregated cross-national analyses [27,56]. He argued that a low ASR, i.e. relatively more women, is associated with a ‘certain level of social disintegration’, and would be associated with higher teenage pregnancy rates. While he employed several statistical controls (e.g. latitude), the analyses did not account for spatial clustering of countries within regions (e.g. [75]). In this paper, we will present analyses that do control for clustering of countries. If the relationship between ASR and teenage fertility is substantially altered after accounting for such a spatial dependence, then the dynamics attributed to ASR are probably an artefact of broader regional dynamics (or unmeasured confounds). We elaborate on this point below. We revisit the relationship between sex ratio and teenage fertility and perform analyses at cross-national, US state, and county levels to illustrate the potential issues with such aggregate-level analyses.

While some research in this area has relied on multilevel models [54] or has presented both aggregated and multilevel analyses (e.g. [48]), analyses based exclusively on aggregate levels remain fairly common, at least in evolutionary psychology (e.g. [44,57,76–78]). Importantly, such findings based on aggregated data then form the basis for experimental studies [37,55] and theorizing [26,79,80]. More recent analyses have sometimes used a lower level of aggregated analysis (such as states or metropolitan areas). One aim of this paper is to investigate whether problems with nation-level analyses also apply to aggregated analyses at a lower level of aggregation (US states), or whether these analyses avoid such problems.

(c). Issues with aggregated, cross-cultural data

Before moving on to our analyses on ASR we discuss some other well-established issues with cross-cultural analyses [75,81–85]. These issues concern, but are not limited to, reversal-like phenomena after data pooling and cross-cultural measurement (equivalency). Several of the points we argue for below do not solely apply to ASR but are broader issues [81]. Nonetheless it is worthwhile reviewing them again here.

(i). Data pooling

One issue is that pooling data to aggregate levels can completely change relations between variables. It is well-established that reversal-like phenomena can occur when pooling data (e.g. [81,86–91]): a statistical relationship is found to be reversed when analysed at an aggregate instead of at a disaggregated level. A famous example demonstrated that one could find negative associations between the proportion of immigrants and illiteracy rates at US state level: states with higher proportions of immigrants had lower levels of illiteracy [87] (also see [92,93]). However, at the individual level the relationship was reversed: immigrants were more likely to be illiterate than ‘native borns’. If we were to infer based on the aggregated data that a similar relationship would exist at a lower level, we would commit ‘the ecological fallacy’ [75,81,87,94]. The key point, as demonstrated multiple times across a variety of disciplines (e.g. [90,95–98]), is that a pattern observed at a lower analytical level can run opposite to that of a higher analytical level (or vice versa).

This issue straightforwardly applies to analyses on ASR at an aggregate level: there appears to be a fundamental mismatch between the level of statistical analysis and the level of inference based on theory. Note that while ASR is an aggregated area-level variable, seldom the variable of theoretical interest that we want to relate to ASR is an aggregate. Researchers typically have predictions based on how individuals modify their decisions or behaviour in response to ASR shifts (e.g. [27]), not necessarily about how country-level indices modify in response to sex ratio shifts. Rather the changes in a country's measure are seen as reflective of changes at the individual level in line with the proposed theory. As a case in point, some researchers have argued for a positive association between measures of aggression and ASR at a national level (e.g. [20]). However, the theoretical arguments for such a relationship seem to have been largely based on individual-level data: given that men are primarily the aggressors [60,99], we could expect that this relationship would extend to cities, districts, states, provinces and nations. Thus, given the existence of the relationship at an individual level, we might therefore assume that at aggregated levels (such as the national level) a similar positive relationship should exist, with more men equalling more violence, as some authors have indeed done (e.g. [20], review in [63]). However, much evidence shows that one should not generalize from the individual to aggregate level and that the relationship could be different at different levels of analysis. For example, while some studies at state level found a positive relationship between ASRs and violence (in India: [100]), a study by Schacht and colleagues found a negative relationship at county level [47]. This would run counter a ‘more men, more violence’ explanation (e.g. [20]), which is derived at the individual level.

In order to fully understand the impact of ASR on behaviour at the individual level, researchers thus truly need a multilevel approach, incorporating data that matches the level at which theories are formulated. If a researcher is primarily interested in behaviour of individuals, e.g. how does a surplus of men influence mate preferences (e.g. [73]) or reproductive timing (e.g. [27]), then this analytical level should be present in the data analysis. Perhaps for some questions even longitudinal data within individuals are required [81,101]. For example, if we theorize that shifting sex ratios should lead to changes in psychological variables relating to mate preferences, then country-level associations, as they are based on aggregates, are less informative than a design that tests intra-individual change [75,101].

(ii). Measurement issues

When conducting any study across cultures, issues with cross-cultural measurement should be considered [82,102–104]. Is the variable measured in the same way across these cultures? Intuitively, it might seem that an ‘objective’ measure such as ASR should not be substantially influenced by cross-cultural differences in measurement. Yet, it is possible that even in ‘objective’ government data one sex is consistently underreported in a country's vital statistics. For example, systematic deviations in sex ratio at birth statistics have been observed in some former U.S.S.R. countries following its collapse [105,106]. Importantly, if there is a systematic deviation in registration of births/deaths and this is related to another variable of interest, say for example, life expectancy [107], then this could lead to a spurious association between ASR and that variable. In short, even in ‘objective’ data, such as vital statistics, there could be profound and systematic measurement issues.

In this paper, we demonstrate further potential issues with analysing aggregate-level data, specifically applied to the case of ASR. We present analyses at the national level but importantly also present US state-level and county-level data in order to investigate whether at these lower levels similar issues exist as at the national level. The issues we examined were the following. Firstly, we examine the distribution of the ASR variable and the existence of extreme values in ASR. Next, we explore the benchmark of statistical significance often employed in this research. Specifically, we examine how many statistical associations would be significant if we naively correlated ASR with a large number of other variables at national and US state level. Finally, we revisit a previously studied variable, teenage fertility rates and present results that challenge previous findings.

2. Methods

Our analyses consist of secondary analyses of country- and state- level databases.

(a). Country-level database

We compiled a database with a broad range of variables measured at country level. These measures are as diverse as for example: CO₂ emissions, number of McDonalds restaurants, the number of Olympic medals won, the number of psychiatrists per 100 000 people, the percentage of households with a fixed telephone line, the percentage uptake of contraception among women (15–49), the number of endangered mammals, the number of people incarcerated per 100 000 citizens, the percentage of Christians, when the country officially started, et cetera. These 110 variables are summarized in electronic supplementary material, table S1. The variables in our dataset were compiled from various sources, as we explicitly wanted to collect a diverse range of variables. The dataset we used is far from perfect, but its imperfections reflect those found in the kind of data used in published papers in this field. For example, several of our variables have a large number of missing cases, and some are measured at different time points or are collapsed across periods. These issues are common in the field (e.g. [27,40,66]).

The key variable of interest is the ASR and is derived from the CIA World Factbook 2012 [108], though we also included two 2016 sex ratio measures in our database. In a previous version of this paper, we used the sex ratio measure as based on the CIA's definition at the time, using a 15–64 age cut-off, with 1 being an equal ratio and a higher score indicating more men than women. This variable is fairly complete in the 2012 Factbook and is temporally close to most of the variables in our set, which is why we preferred it to the more recent measures. However, such ratio measures tend to have peculiar statistical properties [109,110], such as right skew and leptokurtosis. We therefore calculated the sex ratio as a proportion (N_men/(N_men + N_women)), as recommended by Ancona et al. in this issue [110] (15–64 year olds). This was calculated based on the population measures reported in [108].

For the additional analyses on teenage fertility, we also examined the effect of sex ratio (15–17) on teenage fertility (15–19) from the United Nations World Population Prospects (2010–2015) [111], as proportions. Note however that these measures are less complete than the 2012 CIA measure and are based on (estimated) averages for 2010–2015. The methodology is described at length in [112].

(b). State-level database and county level database for United States

We also compiled a database with a broad range of variables measured at US state level. As with the country-level data, we aimed for a diverse set, and our set has variables as diverse as, for example, the number of rollercoasters per state, the maximum elevation level, the number of Amish, and the number of building permits. The 50 variables and their sources are listed in electronic supplementary material. ASR (15–64) were calculated based on the US Census of 2010 [113], as described above [110]. The county level database was composed to specifically examine the relationship between ASR and teenage fertility.

(c). Analyses

All analyses were run in R v. 3.3.1 [114] and we included both the data and script with our paper (electronic supplementary material). The key analyses consist of Pearson correlations and a series of OLS regressions, as these are the analyses commonly used with these aggregate data (e.g. [27,77,78]). The purpose of these analyses is to illustrate multiple limitations of such analyses on ASR. Previously use of p value testing with aggregate data has been criticized [115]. We are fully aware of the limits of a null hypothesis significance testing approach (also see [116]). However, for the purpose of our paper, we will report p values as they remain commonly reported in this research area, and we want to empirically examine how ‘easy’ it is to obtain statistically significant results when analysing ASR at national and state level.

3. Results

(a). Distributional issues: adult sex ratios at the national level have issues

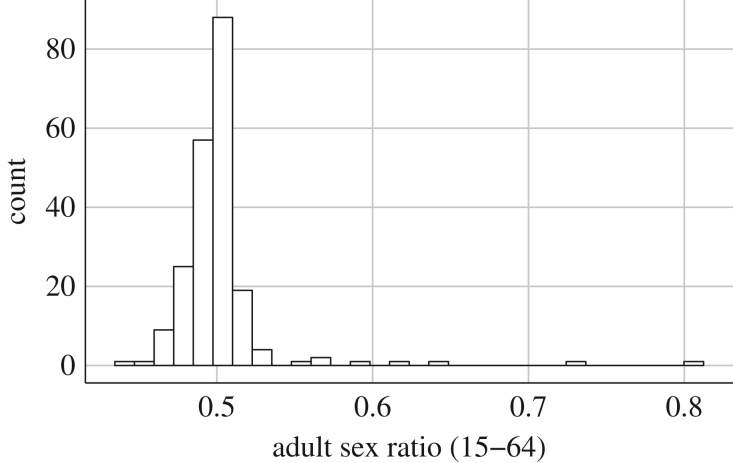
Figure 1 shows the histogram for ASR at country level. We find evidence for deviations in skew and kurtosis (5.58 and 44.59) and thus non-normality (Shapiro–Wilk W = 0.52, p < 0.00001; Jarque–Bera test = 16372, p < 0.00001). While several authors do not transform the data (e.g. [43]), some authors have suggested to take the natural logarithm (e.g. [40,41]) to combat these issues. However, there is still evidence for substantial deviations from normality after such a transformation (skewness: 4.53, kurtosis: 33.21; Shapiro–Wilk W = 0.61, p < 0.00001; Jarque–Bera test = 8785.3, p < 0.00001). At US state level, there are only limited deviations from normality in ASR (skew and kurtosis: 0.55 and 4.27; Shapiro–Wilk W = 0.964, p = 0.13; Jarque–Bera test = 6.05, p = 0.049). The degree to which distributional issues matter could thus be dependent on the level at which aggregation occurs.

Figure 1.

Histogram for adult sex ratio (15–64) at national level (CIA World Factbook data 2012).

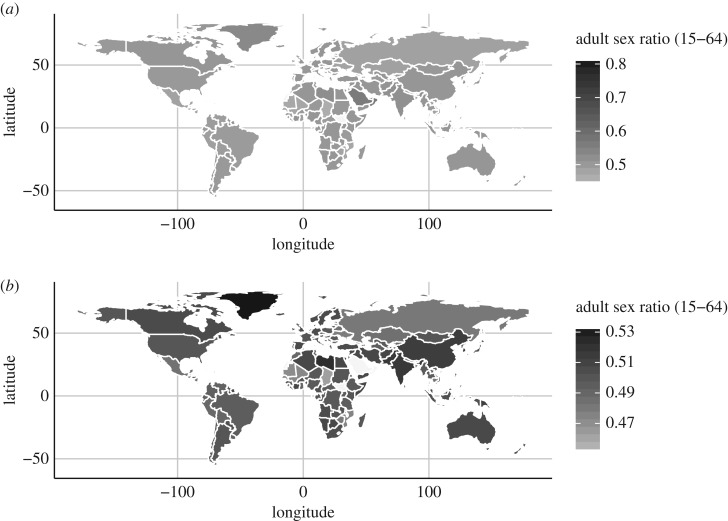
Next to deviations from a normal distribution, outliers could influence any statistical conclusions we draw. We examined the distribution of ASR using Tukey's approach [117], relying on the interquartile range (IQR), with outliers defined according to the 1.5 * IQR rule and extreme values defined via the 3 * IQR rule. We found six outliers on the left side of the distribution (Antigua and Barbuda, Chad, Curaçao, Djibouti, Northern Mariana Islands, and the Virgin Islands (US) and 10 outliers on the right of the distribution (Bahrain, Faeroe Islands, Greenland, Kuwait, Maldives, Oman, Palau, Qatar, Saudi Arabia and the United Arab Emirates). Nine of these 16 outliers were also extreme values, eight on the right side of the distribution (Bahrain, Kuwait, Maldives, Oman, Palau, Qatar, Saudi Arabia and the United Arab Emirates) and one on the left side of the distribution (Djibouti). The two most extreme cases, Qatar and the United Arab Emirates, were respectively 9.03 and 6.86 standard deviations away from the mean. Note that if we systematically deleted extreme cases, this would be distinctly non-random and we would then remove several ‘oil states’ in the Middle East. Any inclusion or exclusion thus has severe consequences on how representative the data are. Figure 2a,b illustrates the dramatic effect of excluding these extreme values on the global distribution of ASR. We will therefore report analyses on national ASR with and without these 9 extreme values. The dataset with US states showed two outliers in ASR with the 1.5 * IQR rule (Alaska (ASR: 0.53) and the District of Columbia (ASR: 0.48)). However, there were no extreme cases at US state level with the 3 * IQR rule.

Figure 2.

(a) Adult sex ratio (15–64) across the world (CIA World Factbook data 2012) (see electronic supplementary material for further description). (b) Adult sex ratio (15–64) across the world (CIA World Factbook data 2012) (after exclusion of extreme values, >3IQR rule) (see electronic supplementary material for further description).

(b). It is easy to find aggregate-level correlations with ASR

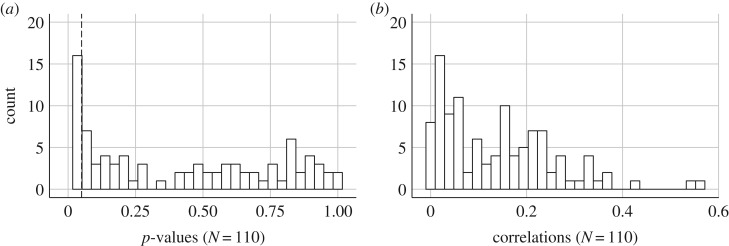
We correlated all variables in our national database with ASR, and then calculated the absolute median correlation and all p values (see figure 3). The (absolute) median correlation with ASR was 0.13. More importantly, 39 correlations out of 110 were statistically significant at p = 0.05 (35.45% of tests significant). This would imply that if we are conservative, we should not pay too much attention to statistical significance because there are many such statistically significant correlations. Moreover, this suggests that any correlation with ASR roughly below 0.13 in absolute strength does not necessarily warrant our attention: many such correlations will exist. If we exclude the extreme values, we obtain qualitatively similar results (median (absolute) r = 0.09, 28 out of 110 correlations statistically significant at p = 0.05).

Figure 3.

(a) p-Values of 110 Pearson correlations with adult sex ratio at national level, all data (dashed line at 0.05). (b) Absolute value of 110 Pearson correlations with adult sex ratio at national level, all data.

The top five correlations in terms of (absolute) strength were: CO₂ production in 2010, Oil use in 2011, Chocolate consumption in 2004, Military spending (% GDP) in 2013, and Population aged between 15 and 64 in 2013. However, exclusion of extreme values (3*IQR rule) gives a rather different top 5: Chocolate consumption in 2004, Contraception prevalence in 2010, Research & development expenditure in 2010, the % of malnutrition in 2010, and the % of teenage mothers in 2012. The fact that this top five looks quite different, points to the importance of outliers in ASR and exemplifies how volatile these statistical relationships are. For example, Military spending, ranked fourth without exclusion of extreme values, is now ranked 98th in terms of strength when excluding extreme values.

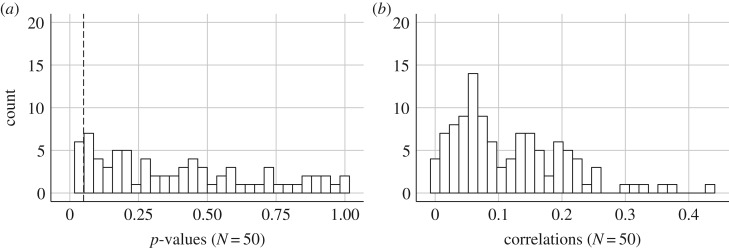
We repeated this exercise at US state level (see figure 4). The median (absolute) correlation with sex ratio was 0.22. Seventeen out of 50 correlations with sex ratio were statistically significant (34%). The top five correlations in terms of (absolute) strength were: Date of statehood, the Gini Coefficient (2010), mean travel time to work (2009–2013), the maximum level of elevation, and the land area of a state. Again, this suggests that many correlations with ASR will be statistically significant.

Figure 4.

(a) p-Values of 110 Pearson correlations with adult sex ratio at state level, all data (dashed line at 0.05). (b) Absolute value of 50 Pearson correlations with adult sex ratio at state level, all data.

(c). Revisiting the link between adult sex ratios and teenage fertility at national level

Previous research has found a negative relationship between adult sex ratio and teenage fertility [27,56]. We focus here on teenage fertility, as another relevant variable, teenage pregnancy variable (from the World Bank) in our dataset only has data available on 14 countries. The teenage fertility variable we used is part of the World Development Indicators and is defined as the number of births per 1000 women ages 15–19. Teenage fertility was ranked 35th out of 110 and 25th out of 110 correlations, depending on inclusion or exclusion of extreme values. There is thus a wide range of variables showing stronger associations with ASR than teenage fertility did.

Our OLS regression results including all available data suggest a significant negative effect of ASR on teenage fertility (table 2: Model 1; F_1,190 = 7.347, p = 0.007). The effect is upheld when extreme values are excluded (table 2: Model 3; F_1,182 = 7.034, p = 0.009). However, after adding a crude control variable for spatial clustering (continent) there is no evidence for an effect (p-values for ASR greater than 0.11; table 2: Model 2 and 4).

Table 2.

The effect of adult sex ratio (15–64) on teenage fertility in OLS regression models. Model 1 contains all available data, Model 2 controls for continent. Model 3, excludes extreme values in adult sex ratio (>3IQR rule) and Model 4 further controls for continent. Reference category for continent is Europe.

	teenage fertility
	Model 1	Model 2	Model 3	Model 4
sex ratio (15–64)	−228.356	−93.707	−643.956	−273.621
	(84.249)	(61.548)	(242.804)	(173.628)
	p = 0.008	p = 0.130	p = 0.009	p = 0.117
North America		6.684		7.342
		(20.404)		(20.302)
		p = 0.744		p = 0.719
Latin America		44.668		43.509
		(6.516)		(6.565)
		p < 0.001		p < 0.001
Africa		78.555		79.388
		(5.968)		(5.986)
		p < 0.001		p < 0.001
Asia		18.612		19.391
		(6.135)		(6.190)
		p = 0.003		p = 0.003
Oceania		19.397		20.489
		(9.020)		(9.025)
		p = 0.033		p = 0.025
constant	164.551	61.080	371.403	150.822
	(42.391)	(31.030)	(120.677)	(86.723)
	p = 0.0002	p = 0.051	p = 0.003	p = 0.084
N	192	192	184	184
R2	0.037	0.545	0.037	0.555
adjusted R2	0.032	0.531	0.032	0.540
residual std. error	40.403 (d.f. = 190)	28.141 (d.f. = 185)	40.598 (d.f. = 182)	27.988 (d.f. = 177)
F statistic	7.347** (d.f. = 1; 190)	36.970*** (d.f. = 6; 185)	7.034** (d.f. = 1; 182)	36.789*** (d.f. = 6; 177)

*p < 0.05; **p < 0.01; ***p < 0.001.

The above analyses are based on ASR with a range of 15–64 years old, while the range of teenage fertility are based on those aged 15–19. Therefore, following the suggestion of a reviewer, we also analysed data from the UN (table 3). We tested the effect of sex ratios (15–17) on teenage fertility (15–19). While there was a strong association in a base model, there was again little suggestion of an association after accounting for continent (table 3; model 1–2). After excluding extreme values in sex ratios (3 * IQR rule), we obtained similar results (table 3; model 3–4). Using sex ratio based on an age range of 15–24, leads to similar conclusions (see electronic supplementary material). In sum, accounting for spatial clustering, even if in a very crude way, renders the association between sex ratio and teenage fertility non-significant. This means that the statistical relationship between teenage fertility and ASR is probably due to mechanisms at a higher level (regions or continents) or to unmeasured confounding variables.

Table 3.

The effect of sex ratio (15–17) on teenage fertility in OLS regression models. Model 1 contains all available data, Model 2 controls for continent. Model 3, excludes extreme values in adult sex ratio (>3IQR rule) and Model 4 further controls for continent. Reference category for continent is Africa.

	teenage fertility (2010–2015)
	Model 1	Model 2	Model 3	Model 4
sex ratio (15–17)	−1309.521	−257.612	−1452.711	−281.114
	(296.264)	(227.266)	(321.356)	(250.403)
	p = 0.00002	p = 0.259	p = 0.00002	p = 0.264
Asia		−60.750		−61.174
		(5.673)		(5.775)
		p < 0.001		p < 0.001
Europe		−77.145		−77.137
		(6.147)		(6.276)
		p < 0.001		p < 0.001
Latin America		−33.077		−33.193
		(6.134)		(6.210)
		p < 0.001		p < 0.001
North America		−70.223		−70.175
		(20.364)		(20.545)
		p = 0.001		p = 0.001
Oceania		−57.449		−57.376
		(9.029)		(9.183)
		p < 0.001		p < 0.001
constant	715.502	223.143	787.874	235.160
	(150.555)	(114.512)	(163.217)	(126.135)
	p = 0.00001	p = 0.053	p = 0.00001	p = 0.064
N	194	194	191	191
R2	0.092	0.550	0.098	0.548
adjusted R2	0.088	0.535	0.093	0.533
residual std. error	39.393 (d.f. = 192)	28.112 (d.f. = 187)	39.487 (d.f. = 189)	28.316 (d.f. = 184)
F statistic	19.537*** (d.f. = 1; 192)	38.061*** (d.f. = 6; 187)	20.436*** (d.f. = 1; 189)	37.215*** (d.f. = 6; 184)

*p < 0.05; **p < 0.01; ***p < 0.001.

(d). ASR and teenage fertility at US state and county level

State level analyses showed that there is no evidence for a significant association between sex ratio and teenage fertility in a base model (p = 0.838; table 4: Model 1). County level analyses also showed no evidence of an association between sex ratio and teenage fertility in a base model (p = 0.109; table 4: Model 2). There is thus no evidence that sex ratios (15–19) are related to teenage fertility at either the state or county level in OLS regressions (both p > 0.1). Interestingly, the effects in the respective base models, i.e. state and county, are opposite in sign. While the state-level analyses were in the same direction as the pattern in cross-national analysis, a negative relationship between sex ratio and teenage fertility, the county-level analyses showed the opposite, a positive relationship. Depending on the level of analysis, one would thus reach opposing conclusions on the direction of the effect of sex ratio. We also ran a multilevel model where counties were nested in states via a random intercept model fitted with Restricted Maximum Likelihood (lme4 [118]), but this also did not support a robust effect for ASR (95% CI based on 10 000 replicates in a percentile bootstrap: −7.85 to 95.39; electronic supplementary material, R script for further details).

Table 4.

The effect of sex ratio (15–19) on teenage fertility in OLS regression models for US states (Model 1) and for US counties (Model 2).

	teenage fertility
	Model 1	Model 2
sex ratio (15–19)	−39.090	42.885
	(189.666)	(26.760)
	p = 0.838	p = 0.110
constant	47.588	9.714
	(97.113)	(13.934)
	p = 0.627	p = 0.486
N	51	3138
R2	0.001	0.001
adjusted R2	−0.020	0.0005
residual std. error	8.559 (d.f. = 49)	41.318 (d.f. = 3136)
F statistic	0.042 (d.f. = 1; 49)	2.568 (d.f. = 1; 3136)

*p < 0.05; **p < 0.01; ***p < 0.001.

4. Discussion

In this paper, we discussed and illustrated some pitfalls to analysing ASR at aggregated levels and drawing inferences from such analyses. Firstly, we showed that, at least at the national level, ASR have a very peculiar non-normal distribution. Even after a logarithmic transformation the data would remain distinctly non-normal. There were also many extreme cases, with for example some countries being an order of magnitude more male biased (for example, the United Arabic Emirates was around 7 s.d. away from the mean). The inclusion or exclusion of such extreme cases can have profound effects on any analysis and even a single extreme case could overturn a statistical relationship. Our recommendation is to report the results both with and without those extreme cases. For the US state level, there were no severe issues and therefore distributional issues should be reviewed on a case-by-case basis.

Second, our correlational analyses suggested that we should be wary of relationships between aggregated variables, as many variables might correlate with ASR without implying any substantive, theoretically meaningful relationship. For example, the level of elevation correlates significantly with ASR at US state level. Around a quarter to a third of the variables in our datasets had significant associations with ASR at national level. Importantly, also at the much smaller level of US states we found around a third of our variables to be associated with ASR. This means that problems with nation-level analyses are not necessarily resolved by moving to a lower level of aggregation. Therefore, we suggest that any finding of an association with ASR at an aggregate level should be treated with great caution.

Third, we argue that a reason for why we find many significant associations is probably due to the substantial (spatial) clustering in aggregated data. Such clustering violates the statistical assumption of non-independence of data points. Analytical units such as countries, states and counties are non-independent data points and this fact is often not fully appreciated [75]. Such clustering is often not (fully) accounted for (e.g. [40,72,73,77]). We illustrated the importance of clustering by controlling for region (continent) in an analysis of the relation between sex ratio and teenage fertility. While the analyses of country-level UN data suggest a statistically significant association between sex ratios (15–17) and teenage fertility, after controlling for region we no longer found any evidence for such a significant association. It is important to indicate here that we are not claiming that the dummy covariate approach used here is novel (e.g. [71,119]), or that is the optimal way for dealing with spatial clustering. In fact, many analytical options exist, such as, for example, multilevel modelling [120–122] or a phylogenetic approach [123–125]. What this dummy approach demonstrates is that, if controlling for clustering, even in a very crude way by using a division into continents, substantially reduces the effect we should be wary of the conclusions we can draw. In our case, the effects were strongly reduced and no longer statistically significant after accounting for clustering. Without accounting for clustering, we are ignoring that a statistical relationship could be (partially) driven by non-independence. The acknowledgement of clustering based on geography/history also has profound implications for theory formation based on aggregate data. In the context of national data, it implies that at least part of the observed variation is not due to differences in national-level sex ratios, but rather differences in broader geographical units (or confounds at that level) [75].

Finally, we briefly revisited the relationship between ASR and teenage fertility rates at the national, US state and US county level. Across all levels, we found little evidence for a substantive association. While some of the associations at the national level could be seen as suggestive, once we controlled for continent, there no longer was any indication of a significant association. At US state level, there was no effect of ASR on teenage fertility in a regression model. At US county level, there was also no robust evidence for an ASR effect. Interestingly, the sign at county level was positive and thus at odds with previous findings. There could be multiple reasons for the discrepancy between our findings and the literature. For example, it could be due to the measures we used, or it could be that the relationship no longer holds 10 years later. For now, we conclude that aggregate analyses offer no substantial support for predictions on sex ratios and teenage fertility, as derived in evolutionary psychology (e.g. [27,56]). Moreover, if anything, the data at a lower, county level suggest the opposite pattern. Rather than a low sex ratio, ‘too many women’, being positively associated with teenage fertility rates, the overall pattern was that high sex ratios were associated with high teenage fertility rates at US county level.

The analyses we presented have many limitations. Firstly, there are different ways to operationalize ASRs and age cut-offs in the calculation of sex ratios could matter a great deal [126]. We used an age range of 15–64 for the sex ratio variable from the CIA Factbook which has been previously used (e.g. [43,77]) for most of our analyses, but other operationalizations are perhaps somewhat narrower (e.g. 15–45 as used in [47] or 15–49 in [72]) and better map on to ‘operational sex ratio’. Worrisome for this area of research is that sex ratios might only correlate moderately with each other when using different age cut-offs (see [126] for a discussion with US census data). The recommendation, albeit based on US census data, is to use broader rather than narrower measures [126]. Therefore, we opted for the 15–64 cut-off, at least for most of our analyses. However, many of the points we illustrated should similarly apply to other cut-offs or operationalizations of sex ratios. Finally, it is also important to reiterate that we focused on certain issues with analyses on aggregated ASR and did not illustrate other issues, such as cross-cultural measurement. This does not imply that we believe that these issues are of lesser importance and should therefore be ignored. Instead, we argue that issues such as cross-cultural equivalency in measurement further compound the issues we outlined here.

Our results add to existing knowledge that associations found at an aggregated level need not correspond to associations at a lower level [81]. We have demonstrated this with the analyses on teenage fertility: while across nations and across US states there is a negative association between sex ratio and teenage fertility, the relationship is entirely reversed and positive at county level. Our recommendation is that researchers pay close attention to the analytical level their theory is most relevant to and analyse the data at that level, avoiding inferences to other levels. For researchers in the field of evolution and human behaviour, it would seem that the individual level, or within-individual level, should be of more interest than aggregate units, such as nations [81,101]. We believe it could be time to abandon aggregate analyses on sex ratios altogether, in favour of multilevel analyses (e.g. [28,30,33,34,54]). Furthermore, in this context it is important to highlight that the purported effect of local sex ratio might be heavily influenced by perception, and that this perception could be of greater importance than the actual sex ratio (e.g. [36,39]). Interestingly, a recent study showed that there was no correspondence between actual neighbourhood sex ratio and perceived neighbourhood sex ratio [127]. A challenge for the future will be to examine the psychological mechanism via which sex ratio effects occur and whether these are more or less important than other cues in one's local ecology.

In conclusion, we put forward that for researchers interested in how ASRs influence human behaviour, analyses on aggregate levels are not very informative. We therefore argue that at best these analyses on aggregates might be indicative of a relationship but ultimately these relationships are neither informative, nor do they allow for adequate tests of evolutionary theories on effects of sex ratios. Given the many serious issues with aggregate analyses on ASRs, some of which we illustrated here, we conclude that the study of ASRs exclusively at the aggregate level probably does not generate reliable findings for the field.

Ethics

This paper relies solely on secondary data analysis, which is exempt from ethical review procedures at the corresponding author's host institution when the data were collected.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material.

Authors' contributions

T.V.P. drafted a first version; T.K. and A.H.S. provided extensive feedback and revised the manuscript. A.H.S. compiled the majority of the country-level database, with help of T.K. and T.V.P. T.V.P. and T.K. generated the state and county databases. T.V.P. performed the analyses, with feedback from T.K.

Competing interests

We have no competing interests, other than that we have previously published on related topics.

Funding

T.V.P. was supported by a NIAS-KNAW fellowship.