Assessing the influence of rater and subject characteristics on measures of agreement for ordinal ratings

Abstract

Widespread inconsistencies are commonly observed between physicians’ ordinal classifications in screening tests results such as mammography. These discrepancies have motivated large-scale agreement studies where many raters contribute ratings. The primary goal of these studies is to identify factors related to physicians and patients’ test results which may lead to stronger consistency between raters’ classifications. While ordered categorical scales are frequently used to classify screening test results, very few statistical approaches exist to model agreement between multiple raters. Here we develop a flexible and comprehensive approach to assess the influence of rater and subject characteristics on agreement between multiple raters’ ordinal classifications in large-scale agreement studies. Our approach is based upon the class of generalized linear mixed models. Novel summary model-based measures are proposed to assess agreement between all, or a subgroup of raters, such as experienced physicians. Hypothesis tests are described to formally identify factors such as physicians’ level of experience that play an important role in improving consistency of ratings between raters. We demonstrate how unique characteristics of individual raters can be assessed via conditional modes generated during the modeling process. Simulation studies are presented to demonstrate the performance of the proposed methods and summary measure of agreement. The methods are applied to a large-scale mammography agreement study to investigate the effects of rater and patient characteristics on the strength of agreement between radiologists.

1. Introduction

Diagnostic and screening tests are used in a broad range of medical settings to assess patients’ disease status. The accuracy of these procedures depend on subjective interpretation of test results by radiologists. However, substantial discrepancies between radiologists’ classifications are often reported in breast cancer screening and many other settings [1–6] providing strong incentives to search for accurate and consistent classification procedures. Efforts to improve the effectiveness of screening tests have led to the implementation of large-scale agreement studies with the important goal of identifying characteristics of the raters and subjects, such as rater training and experience or patient age, that may contribute to variability between raters’ classifications of test results [2,4,7–9]. Large-scale agreement studies incorporate the classifications of many raters each independently grading a sample of patients’ test results, or some subset thereof.

Ordered categorical scales are commonly used to classify screening and diagnostic test results. For example, breast density is rated on mammograms using to an ordinal four-category BIRADS scale (fatty, scattered areas, heterogeneously dense, extremely dense) [10], and prostate cancer biopsies are classified according to a five-point Gleason grading scale [4,8]. However, assessing consistency between raters in agreement studies when an ordinal scale is used for classification purposes can be challenging. Further issues arise when multiple raters (more than two or three) contribute ratings. Some existing summary measures are commonly used to provide informative single number summaries of agreement between many raters’ ordinal classifications. These include Fleiss’ kappa for multiple raters which requires all subjects have an equal number of ratings [11], the intraclass correlation coefficient (ICC) which is equivalent to a weighted Cohen’s kappa in the case of two raters [12], Kraemer’s kappa coefficient [13], an AC2 statistic [14] and versions of Cohen’s weighted kappa [15–17]. However, these simple summary measures are not able to incorporate information on rater and patient characteristics that may impact agreement, and furthermore, some are sensitive to similar prevalence and marginal distribution issues as the original Cohen’s kappa [18–20].

Some modeling approaches also exist to investigate the effects of rater and item characteristics on agreement between ordinal classifications of multiple raters. Williamson et al [21] and Gonin et al [22] describe methods based upon generalized estimating equations which can incorporate rater and item characteristics to assess their impact on agreement [18,21] and association [22] respectively, and can accommodate unbalanced data. Again, similar to existing summary measures, both approaches rely on Cohen’s kappa-like statistics, and are prone to the well-known flaws of Cohen’s kappa measures, including a dependency on the underlying prevalence of disease [18–20]. Hsaio et al [23] developed a Bayesian hierarchical model for binary classifications with a nested random effects structure using ICC measures to describe correlation between classifications instead of kappa agreement measures. In many agreement studies, patients’ test results are classified by a small fixed number of raters, for example, two or three. The aforementioned methods including fixed terms for each rater can be used to appropriately describe the strength of agreement between raters in these smaller-scale studies. Some of these methods may potentially be extended to assess agreement in larger-scale studies with many raters by incorporating random effects. In this current paper we focus on large-scale agreement studies where classifications by several raters (usually more than three) who may be randomly sampled from their population of typical raters can be incorporated, allowing for statistical inference at the population level. A further Bayesian hierarchical modeling approach [24] incorporates a nested random effect structure and patient-level covariates but provides no summary agreement measures. Log-linear models [25,26] can also be used to assess the impact of rater and patient characteristics on agreement between a small number of raters, say two or three at most, for categorical classifications.

Our proposed methods fill a gap in the current agreement literature to provide a flexible modeling approach and summary measure to assess the impact of rater and subject characteristics on agreement between multiple raters. Our approach, based upon the class of generalized linear mixed models (GLMMs) [27,28] flexibly incorporates rater and subject characteristics to identify key factors impacting consistency between experts. Novel model-based summary measures are developed to assess and compare the strength of agreement between all raters, or between subgroups of raters (for example, experienced and inexperienced raters) and subjects (for example, mammograms of older versus younger patients). Our proposed summary measures of agreement are appealing in their simplicity of interpretation, adjust appropriately for chance agreement, and eliminate many biases observed in the use of Cohen’s kappa statistics. Unlike Cohen’s kappa statistic and its extensions, the proposed measures are unaffected by the underlying disease prevalence [28]. In contrast to other approaches, any number of subjects and raters’ classifications can be incorporated without increasing the complexity of the modeling process. An important strength is that conclusions can be generalized to the underlying populations of raters and items when raters and study participants are randomly sampled from their respective populations. It is assumed each rater independently classifies the same sample of subjects’ test results using to an ordinal classification scale, although missing and unbalanced data can be accommodated [29].

The remainder of the paper proceeds as follows. In the next section we describe the model-based agreement approach incorporating rater and subject characteristics. We demonstrate how to fit the proposed model and obtain parameter estimates for an agreement dataset using the statistical software package R [30]. In Section Three summary measures of agreement for assessing the effects of rater and subject characteristics are developed, while in Section Four, simulation studies are reported to establish the properties and behavior of the proposed methods and summary measure of agreement. Section Five discusses hypothesis tests to formally test the strength of agreement between subgroups of raters and for assessing the impact of factors on agreement. Following in Section Six we explain how unique characteristics of individual raters and patients in the study can be evaluated through conditional modes generated as part of the modeling process. The proposed methods are applied to a large-scale breast cancer agreement study in Section Seven, concluding with a brief discussion in Section Eight.

2. Models of Agreement

2.1. Ordinal agreement model incorporating rater and patient factors

An ordinal GLMM with fixed and random effects provides a flexible framework to assess effects of rater and item characteristics on agreement between multiple raters in a population-based setting. It is assumed a random sample of J raters each independently classifies the same random sample of I items using an ordinal classification scale with C categories. A classification provided by the jth rater for the ith item is denoted as Y_ij = c (i = 1,…, I; j = 1,…, J; c = 1,…, C). The ordinal GLMM model with a probit link function $\mathrm{\Phi }(\cdot )$ models an unobserved continuous latent variable W_ij associated with the true underlying disease severity of the ith patient, and is linked to the jth rater’s ordinal classification Y_ij via a series of strictly increasing threshold values ${\alpha }_0,{\alpha }_1,\dots ,{\alpha }_C$ that separates the real line into C+1 categories, with ${\alpha }_0=-\infty$ and ${\alpha }_C=+\infty$ ( ${\alpha }_0\le {\alpha }_1\le \dots \le {\alpha }_C$). A rater’s classification of an item, Y_ij, falls into category c when the latent variable W_ij takes a value between ${\alpha }_{c-1}$ and ${\alpha }_c$. For identification purposes, wlog, the intercept term ${\beta }_0$ is set to 0 in the GLMM [31]. The ordinal GLMM model takes the form:

$${\mathrm{\Phi }}^{-1}(\mathit{P}({\mathit{Y}}_{ij}\le \mathit{c}|{\mathit{u}}_i,{\mathit{v}}_j,{\mathit{x}}_i,{\mathit{x}}_j)={\mathit{\alpha }}_{\mathit{c}}-({{\mathit{\beta }}^{\prime }}_1{\mathit{x}}_i+{{\mathit{\beta }}^{\prime }}_2{\mathit{x}}_j+{{\mathit{z}}^{\prime }}_1{\mathit{u}}_i+{{\mathit{z}}^{\prime }}_2{\mathit{v}}_j)$$ (1)

where item and rater random effect vectors for the ith item and jth rater are u_i = (u_i0, u_i1,…, u_ip) and v_j = (v_j0, v_j1,…, v_jq) respectively. Crossed random effects for each item and rater, u_i0 and v_j0 (i = 1,…, I; j = 1,…, J) are always included in (1) to account for the dependency induced by the study design where each rater views every item. Additional random terms may be included for rater and item characteristics to examine their effects on the agreement between raters, for example, rater’s experience. Vectors z₁ of size (p+1) × 1 and z₂ of size (q+1) × 1 represent design structures of the random effect vectors. Rater and item random effect vectors are assumed to follow multivariate normal distributions with covariance matrices Σ_u and Σ_v of dimensions (p+1) × (p+1) and (q+1) × (q+1) respectively with u_i ~ MVN(0, Σ_u) and v_j ~ MVN(0, Σ_v) where

$${\sum }_u=\left[\begin{array}{cccc}{\sigma }_{u_0}^2& {\rho }_{u_{01}}{\sigma }_{u_0}{\sigma }_{u_1}& \dots & {\rho }_{u_{0p}}{\sigma }_{u_0}{\sigma }_{u_p}\\ {\rho }_{u_{01}}{\sigma }_{u_0}{\sigma }_{u_1}& {\sigma }_{u_1}^2& & \\ ⋮& & \ddots & {\rho }_{u_{p-1,p}}{\sigma }_{u_{p-1}}{\sigma }_{u_p}\\ {\rho }_{u_{0p}}{\sigma }_{u_0}{\sigma }_{u_p}& \dots & & {\sigma }_{u_p}^2\end{array}\right]\text{and}{\sum }_v=\left[\begin{array}{cccc}{\sigma }_{v_0}^2& {\rho }_{v_{01}}{\sigma }_{v_0}{\sigma }_{v_1}& \dots & {\rho }_{v_{0q}}{\sigma }_{v_0}{\sigma }_{v_q}\\ {\rho }_{v_{01}}{\sigma }_{v_0}{\sigma }_{v_1}& {\sigma }_{v_1}^2& & \\ ⋮& & \ddots & {\rho }_{v_{q-1,q}}{\sigma }_{v_{q-1}}{\sigma }_{v_q}\\ {\rho }_{v_{0q}}{\sigma }_{v_0}{\sigma }_{v_q}& \dots & & {\sigma }_{v_q}^2\end{array}\right]$$

For simplicity, we denote linear combinations of the random effects for items and raters as $u_i^{\ast }={z^{\prime }}_1{u}_i$ and $v_j^{\ast }={z^{\prime }}_2{v}_j$ with corresponding variances ${\sigma }_{u_i^{\ast }}^2=\mathrm{var}({z^{\prime }}_1{u}_i)={z^{\prime }}_1{\sum }_u{z}_1$ and ${\sigma }_{v_j^{\ast }}^2=\mathrm{var}({z^{\prime }}_2{v}_j)={z^{\prime }}_2{\sum }_v{z}_2$. Variance components for item random effects can be interpreted as follows: a large value of ${\sigma }_{u_0}^2$ denotes test results which vary substantially with regard to distinguishability of disease status; for example, cancer is clearly visible on some mammograms, while on others it is less obvious. Low or moderate-valued item variance components indicate less variability in distinguishability of disease status in test items. Large rater effect variance components reflect a population of raters who vary widely in the way they classify subjects, with some very conservative raters (i.e. not assigning many high score ratings), while other raters are very liberal, assigning higher score ratings. A rater variance component close to 0 indicates a population of raters who classify subjects very similarly. More complex random effect structures can be incorporated if desired, though a richer dataset with more raters and subjects will be required as the random effect structure increases in complexity.

Characteristics of raters and items can also be incorporated as fixed terms ${{\mathit{\beta }}^{\prime }}_1{\mathit{x}}_i+{{\mathit{\beta }}^{\prime }}_2{\mathit{x}}_j$ into the GLMM model (1) where x_i = (x_i1, x_i2,…, x_ir) and x_j = (x_j1, x_j2,…, x_js) refer to vectors of item and rater characteristics for the ith item and jth rater respectively. Vectors β₁ and β₂ refer to corresponding fixed coefficients vectors for items and raters. A fixed effect for a rater or item may be informative if that characteristic is linked with the underlying disease prevalence, reflected by the distribution of classifications across the ordered categories. For example, if older patients experience an increased prevalence of breast cancer, patient age can be included as a fixed effect to adjust overall cutoff thresholds ${\alpha }_1,\dots ,{\alpha }_{C-1}$ to reflect the higher probability of an elevated score. Examples are provided in Sections 4 and 5 for further clarification.

2.2. Fitting the Ordinal Generalized Linear Mixed Model

The ordinal GLMM in (1) is fitted quickly and efficiently using the ordinal package in R to estimate the parameter vector of interest, $\mathit{\theta }$ = $({\alpha }_1,\dots ,{\alpha }_{C-1},{\beta }_1,{\beta }_2,{\sum }_u,{\sum }_v)$. These parameter estimates form an important component of the summary measures of agreement developed in the next section.

The ordinal R package uses an approximate maximum likelihood procedure, multivariate Laplacian approximation for estimation purposes, yielding $\widehat{\mathit{\theta }}$ = $({\widehat{\alpha }}_1,\dots ,{\widehat{\alpha }}_{C-1},{\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\sum }}_u,{\widehat{\sum }}_v)$ [30]. Due to the presence of high-dimensional integrals in the marginal likelihood function with a crossed random effect structure, no closed-form solution is available, and adaptive quadrature fitting approaches which are commonly used for fitting GLMMs becomes infeasible in this setting [32–34]. The form of the marginal likelihood function for the ordinal GLMM in (1) is:

$$L(\theta ;Y)={\displaystyle \underset{u,v}{\int }L(\theta ;u,v,y)dudv=}{\displaystyle \underset{u,v}{\int }{f}_{Y|u,v}(y;u,v)f_u(u;{\sum }_u)}{f}_v(v;{\sum }_v)dudv$$

$$\begin{array}{l}={\displaystyle \underset{u}{\int }{\displaystyle \underset{v}{\int }\left[\underset{i=1}{\overset{I}{{\displaystyle \mathrm{\Pi }}}}\underset{j=1}{\overset{J}{{\displaystyle \mathrm{\Pi }}}}\underset{c=1}{\overset{C}{{\displaystyle \mathrm{\Pi }}}}{[\mathrm{\Phi }({\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j))-\mathrm{\Phi }({\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j))]}^{d_{\mathit{ijc}}}\right]\times }}\\ \left[\frac{1}{{(2\pi )}^{p/2}{\sum }_u^{1/2}}{e}^{-\frac{1}{2}{u}^{\prime }{\sum }_{u}u}\right]\left[\frac{1}{{(2\pi )}^{q/2}{\sum }_v^{1/2}}{e}^{-\frac{1}{2}{v}^{\prime }{\sum }_{v}v}\right]dudv\end{array}$$

where indicator function $d_{\mathit{ijc}}=1$ if $y_{ij}=c$ and 0 otherwise. Let $H={\partial }^{2}l(\theta ;u,v,y)/\partial \theta \partial {\theta }^t$ be the second-order derivative of the log-likelihood function l(θ; u, v, y) evaluated at the approximate maximum likelihood estimates of θ. The matrix H is generated during the model-fitting process and large-sample approximate standard errors for parameter estimates are estimated by taking the square-roots of the diagonals of H, $se(\widehat{\mathit{\theta }})=\sqrt{\text{diag}[-{\left\{H\right(\widehat{\mathit{\theta }})\}}^{-1}]}$. Parameter estimation of the fixed coefficient vectors β₁ and β₂ and standard errors se(β₁) and se(β₂) are routinely output from the ordinal package in R, providing an assessment of whether rater and item characteristics provide a significant adjustment to threshold estimates ${\widehat{\alpha }}_1,\dots ,{\widehat{\alpha }}_{C-1}$.

3. A Population-Based Measure of Agreement

Agreement measures for ordinal classifications provide a useful summary of exact agreement between raters, i.e. how much of the time experts classify a patient’s test result into the same category. When experts and patients are randomly sampled from their respective populations, a population-based measure of agreement describes how often an expert’s classification of a subject agrees with what other experts would have typically reported (inter-rater reliability), after correcting for chance agreement [35].

In this section we focus on developing summary measures for assessing agreement between raters based upon the ordinal GLMM in (1). In a study with a diverse range of radiologists, it is often of interest to study the strength of agreement between groups of raters or items. For example, we may be interested in whether raters provide more consistent classifications of test results of older patients compared with those of younger patients. We can incorporate these characteristics as additional random effects into the ordinal GLMM. To examine overall agreement between all raters, a GLMM without any additional fixed or random effect terms can be used [28].

We now define two important concepts, observed and chance agreement, which form the basis for the proposed model-based measure of agreement.

3.1. Observed and Chance Agreement in the Model-Based Setting

A population-based measure of observed agreement, p₀, is the uncorrected long-run proportion of time that raters j and j′ (j ≠ j′) classify patients into the same category. When raters are randomly selected, classifications made by the jth and j′th raters on a subject are interchangeable, and any pair of raters’ classifications has a distribution that is invariant under permutations of the experts [35]. In the population-based setting, this is written as

$$p_0={\displaystyle \sum _{c=1}^C[P(Y_{ij}=c\cap Y_{ij\text{'}}=c)]}$$

where raters j and j′ (j ≠ j′) share the same or a different set of characteristics, and both raters classify the same ith item. Under the GLMM framework, observed agreement is (derivations are in Appendix A):

$$\begin{array}{l}{p}_0={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\{{\displaystyle \sum _{c=1}^C\left[\mathrm{\Phi }\left(\frac{({\alpha }_c-k)/{\sigma }_T-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{({\alpha }_{c-1}-k)/{\sigma }_T-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]}}\times \\ \left[\mathrm{\Phi }\left(\frac{({\alpha }_c-k\prime )/{\sigma }_{T^{\prime }}-z\sqrt{\rho \prime }}{\sqrt{1-\rho \prime }}\right)-\mathrm{\Phi }\left(\frac{({\alpha }_{c-1}-k\prime )/{\sigma }_{T^{\prime }}-z\sqrt{\rho \prime }}{\sqrt{1-\rho \prime }}\right)\right]\}\varphi \left(z\right)dz\end{array}$$ (2)

where k and k′ denote the constant terms ${{\mathit{\beta }}^{\prime }}_1{\mathit{x}}_i+{{\mathit{\beta }}^{\prime }}_2{\mathit{x}}_j$ and ${{\mathit{\beta }}^{\prime }}_1{\mathit{x}}_i+{{\mathit{\beta }}^{\prime }}_2{\mathit{x}}_{j^{\prime }}$ and total variances are ${\sigma }_T^2={\sigma }_{u\ast }^2+{\sigma }_{v_j^{\ast }}^2+1$ and ${\sigma }_{T^{\prime }}^2={\sigma }_{u\ast }^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2+1$. Terms $\rho ={\sigma }_{u\ast }^2/{\sigma }_T^2$ and $\rho \prime ={\sigma }_{u\ast }^2/{\sigma }_{T^{\prime }}^2$ are natural measures of variability taking values between 0 and 1 which increase in value when variability amongst items is large relative to variability between raters. The random variable z is a $N(0,1)$variable. When raters j and j′ (j ≠ j′) share the same characteristic of interest (such as experience level), $x_j=x_{j^{\prime }}$. Chance agreement p_c is the probability that two different raters j and j′ (j ≠ j′) classify two different items i and i′ (i ≠ i′) into the same category simply by coincidence. Generally, raw agreement rates such as p₀ are inflated when chance agreement is high; therefore we seek a model-based chance-corrected measure of agreement in Section 3.2. In order to do so, we first provide an expression for chance agreement in the population-based setting:

$$\begin{array}{l}{p}_c={\displaystyle \sum _{c=1}^C[P(Y_{ij}=c)\times P(Y_{i\text{'}j\text{'}}=c)]}\\ ={\displaystyle \sum _{c=1}^C\left[\mathrm{\Phi }\left(\frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)}{\sqrt{1+{\sigma }_{u_i^{\ast }}^2+{\sigma }_{v_j^{\ast }}^2}}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)}{\sqrt{1+{\sigma }_{u_i^{\ast }}^2+{\sigma }_{v_j^{\ast }}^2}}\right)\right]}\times \\ \left[\mathrm{\Phi }\left(\frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_{i^{\prime }}+{{\beta }^{\prime }}_2{x}_{j^{\prime }})}{\sqrt{1+{\sigma }_{u_{i^{\prime }}^{\ast }}^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2}}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_{i^{\prime }}+{{\beta }^{\prime }}_2{x}_{j^{\prime }})}{\sqrt{1+{\sigma }_{u_{i^{\prime }}^{\ast }}^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2}}\right)\right].\end{array}$$ (3)

3.2. A Model-Based Measure of Agreement

A model-based chance-corrected measure of agreement ${\kappa }_m$ based on the ordinal GLMM in (1) can be used to assess levels of agreement between a subgroup of raters or items. The summary measure ${\kappa }_m$ is a linear function of observed agreement p₀ in (2) and adjusted to minimize the effects of chance agreement p_c in (3). The minimum value of chance agreement, $p_{cmin}$, is obtained by finding threshold values ${\alpha }_1,\dots ,{\alpha }_{C-1}$ ( ${\alpha }_0=-\infty$and ${\alpha }_C=+\infty$) which minimize the expression for chance agreement p_c in (3). When raters j and j′ (j ≠ j′) come from the same group of raters, the minimum value for p_c is 1/C (see Appendix C for proof). This is achieved when the thresholds take values ${\alpha }_{cmin}={\mathrm{\Phi }}^{-1}(c/C)\sqrt{{\sigma }_{u\ast }^2+{\sigma }_{v_j^{\ast }}^2+1}+({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)$ for c=1,…,C−1. These threshold values $({\alpha }_{min,1},{\alpha }_{min,2},\dots ,{\alpha }_{min,C-1})$ are then incorporated into the expression for ${\kappa }_m$ in (4). The measure is scaled to lie between 0 and 1, and takes the following form:

$$\begin{array}{l}{\kappa }_m=\left(\frac{1}{1-p_{cmin}}\right){\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\displaystyle \sum _{c=1}^C\left[\mathrm{\Phi }\left(\frac{({\alpha }_{cmin}-k)/{\sigma }_T-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{({\alpha }_{c-1min}-k)/{\sigma }_T-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]}}\ast \\ \left[\mathrm{\Phi }\left(\frac{({\alpha }_{cmin}-k\prime )/{\sigma }_{T^{\prime }}-z\sqrt{\rho \prime }}{\sqrt{1-\rho \prime }}\right)-\mathrm{\Phi }\left(\frac{({\alpha }_{c-1min}-k\prime )/{\sigma }_{T^{\prime }}-z\sqrt{\rho \prime }}{\sqrt{1-\rho \prime }}\right)\right]\varphi \left(z\right)dz-\left(\frac{p_{cmin}}{1-p_{cmin}}\right)\end{array}$$ (4)

where $\rho ={\sigma }_{u\ast }^2/{\sigma }_T^2$ and $\rho \prime ={\sigma }_{u\ast }^2/{\sigma }_{T^{\prime }}^2$, $k={\beta }_1{x}_i+{\beta }_2{x}_j$ and $k\prime ={\beta }_1{x}_i+{\beta }_2{x}_{j^{\prime }}$. For category c = 1 the second term in brackets is set to 0, and the first term in brackets for category c = C is set to 1. The proposed measure ${\kappa }_m$ takes values between 0 and 1 and is easily interpreted in a similar manner to Cohen’s kappa and Fleiss’ kappa [11, 15]. A value close to 1 suggests strong chance-corrected agreement while a value close to 0 indicates no to weak chance-corrected agreement between raters in the population. Landis and Koch [36] present a table that provides a suitable guide for interpreting the proposed measure of agreement. The summary measure, estimated as ${\widehat{\kappa }}_m$using the parameter estimate GLMM vector $\widehat{\mathit{\theta }}$ in Section 2.2 avoids some of the weaknesses observed in Cohen’s kappa including being robust to the underlying prevalence of disease and differing marginal distributions of raters.

The variance of the estimated summary measure ${\kappa }_m$, $\mathrm{var}({\widehat{\kappa }}_m)$ is derived using the multivariate delta method. As ${\kappa }_m$ is a function of $\theta =({\beta }_1,{\beta }_2,{\sigma }_{u\ast }^2,{\sigma }_{v_j\ast }^2,{\sigma }_{{v^{\prime }}_j\ast }^2)$ with ${\sum }_{\theta }$ the covariance matrix for $\mathit{\theta }$, $\mathrm{var}({\widehat{\kappa }}_m)$can be written as:

$$\mathrm{var}({\widehat{\kappa }}_m)=\left(\frac{\partial {\kappa }_m}{{\beta }_1},\frac{\partial {\kappa }_m}{{\beta }_2},\frac{\partial {\kappa }_m}{{\sigma }_{u\ast }^2},\frac{\partial {\kappa }_m}{{\sigma }_{v_j\ast }^2},\frac{\partial {\kappa }_m}{{\sigma }_{{v^{\prime }}_j\ast }^2}\right){\sum }_{\theta }{\left(\frac{\partial {\kappa }_m}{{\beta }_1},\frac{\partial {\kappa }_m}{{\beta }_2},\frac{\partial {\kappa }_m}{{\sigma }_{u\ast }^2},\frac{\partial {\kappa }_m}{{\sigma }_{v_j\ast }^2},\frac{\partial {\kappa }_m}{{\sigma }_{{v^{\prime }}_j\ast }^2}\right)}^{\prime }=\left(\frac{\partial {\kappa }_m}{\partial \theta }\right){\sum }_{\theta }{\left(\frac{\partial {\kappa }_m}{\partial \theta }\right)}^{\prime }.$$

For estimation purposes, the matrix H generated during the GLMM model-fitting process described in Section 2.2 provides approximate estimates of ${\sum }_{\theta }$. A sample dataset and R code is provided by the authors in the Supplementary materials to demonstrate how to use the proposed methods for an agreement dataset.

4. Simulation Studies

Extensive simulation studies were conducted to assess parameter estimation for the GLMM and to examine properties of the proposed model-based measure of agreement. We examined effects of increasing sample size (numbers of raters and items) and varying values and characteristics of rater and item variance components on the resulting bias and standard errors of the ordinal GLMM parameter estimates and properties of the proposed summary agreement measure.

4.1. Generating the Simulated Datasets

For each simulation scenario, one thousand datasets were randomly generated according to the ordinal GLMM in (1) by first calculating the true probabilities of being classified into each category c = 1,…,C, with the number of categories C = 5 where

$$P(Y_{ij}=c)=\mathrm{\Phi }({\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j))-\mathrm{\Phi }({\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j)).$$ (5)

Random effect vectors u_i ~ MVN(0, Σ_u) and v_j ~ MVN(0, Σ_v) (i = 1,…, I; j = 1,…, J) were randomly generated using the mvrnorm function in R using specified values of the variance components. The rmultinom function in R was then used to randomly generate n = I*J (I ratings per expert) observations Y_ij = c using the multivariate normal probabilities in (5). Each dataset was then fitted using the clmm function in the R ordinal package. The proposed summary measures and standard errors were then estimated using these GLMM parameter estimates. Simulation studies were conducted for each of the following three ordinal GLMM models, with rater and item characteristics incorporated in varying ways into each model. We also include results for an overall summary measure ${\kappa }_m$ modeling agreement between all J raters and I subjects (with no covariates or additional random effects) for each set of simulations.

1. $\mathrm{Pr}(Y_{ij}\le c)={\alpha }_c-(u_{0i}+v_{0j}+x_j\ast v_{1j})$ with $u_{0i}~N(0,{\sigma }_{u_0}^2)$ and

   $$(v_{0j},v_{1j})~\mathit{BVN}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],{\sum }_v=\left[\begin{array}{cc}{\sigma }_{v_0}^2& {\rho }_{v_{01}}{\sigma }_{v_0}{\sigma }_{v_1}\\ {\rho }_{v_{01}}{\sigma }_{v_0}{\sigma }_{v_1}& {\sigma }_{v_1}^2\end{array}\right]\right)$$
2. $\mathrm{Pr}(Y_{ij}\le c)={\alpha }_c-({\beta }_1\ast x_i+u_{0i}+x_i\ast u_{1i}+v_{0j})$ with $v_{0j}~N(0,{\sigma }_{v_0}^2)$ and

   $$(u_{0j},u_{1j})~\mathit{BVN}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],{\sum }_u=\left[\begin{array}{cc}{\sigma }_{u_0}^2& {\rho }_{u_{01}}{\sigma }_{u_0}{\sigma }_{u_1}\\ {\rho }_{u_{01}}{\sigma }_{u_0}{\sigma }_{u_1}& {\sigma }_{u_1}^2\end{array}\right]\right)$$
3. $\mathrm{Pr}(Y_{ij}\le c)={\alpha }_c-({\beta }_1\ast x_i+{\beta }_2\ast x_j+u_{0i}+x_i\ast u_{1i}+v_{0j}+x_j\ast v_{1j})$

   $$\text{with}(u_{0j},u_{1j})~\mathit{BVN}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],{\sum }_u=\left[\begin{array}{cc}{\sigma }_{u_0}^2& {\rho }_{u_{01}}{\sigma }_{u_0}{\sigma }_{u_1}\\ {\rho }_{u_{01}}{\sigma }_{u_0}{\sigma }_{u_1}& {\sigma }_{u_1}^2\end{array}\right]\right)\text{and}$$

   $$(v_{0j},v_{1j})~\mathit{BVN}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],{\sum }_v=\left[\begin{array}{cc}{\sigma }_{v_0}^2& {\rho }_{v_{01}}{\sigma }_{v_0}{\sigma }_{v_1}\\ {\rho }_{v_{01}}{\sigma }_{v_0}{\sigma }_{v_1}& {\sigma }_{v_1}^2\end{array}\right]\right)$$

Here, the binary rater covariate x_j, representing, for example, level of rater experience, was included in models (a) and (c) and generated using rbinom(J, 0.5). Similarly a binary item covariate x_i which could indicate, for example, age of patient (young or old), was included in models (b) and (c) and generated using rbinom(I, 0.5).

Simulation scenarios and parameters were chosen to reflect values that may be present in real agreement studies. Fixed parameters ${\beta }_1$ and ${\beta }_2$ were set at 1 in models (b) and (c). Variance components were set at $({\sigma }_{u_0}^2=1,{\sigma }_{v_0}^2=5,{\sigma }_{v1}^2=0.5)$ and $({\sigma }_{u_0}^2=5,{\sigma }_{v_0}^2=1,{\sigma }_{v1}^2=0.5)$. Parameters describing correlation between the random effects, ${\rho }_{u0u1}$ and ${\rho }_{v0v1}$ were set at (−0.25, 0, 0.25).

4.2. Results of Simulation Studies

Simulations results are presented in Tables 1(a) and (b) and Supplementary Tables 1(c) to (f) and 2(a) to (f). (Supplementary Tables can be found in the Supplementary Materials online). Tables 1(a) to (f) present summary results for the proposed model-based kappa ${\widehat{\kappa }}_m$ including estimates of ${\widehat{\kappa }}_m$ for subgroups of raters and items for all simulation studies. Tables 2(a) to (f) present summaries of the estimation of the ordinal GLMM parameter vector $\widehat{\theta }$ and proposed model-based kappa estimates ${\widehat{\kappa }}_m$ for each simulation study. Estimated standard errors (est S.E.) for each parameter is reported as the mean of the standard error estimates from each of the one thousand simulated datasets. The standard deviation of the observed one thousand estimates (obs S.E.) is also presented for each parameter. {Tables 1(a), (b) here}

Table 1.

(a) – (b). Results from six simulation studies in each table for the proposed measure of agreement ${\kappa }_m$ and its standard error $se({\widehat{\kappa }}_m)$. Each simulation study is based upon 1000 simulated datasets with C = 5 categories. Two sample sizes are examined (I = 100, J = 10) and (I = 250, J = 100) and random effect parameters in (a) ${\sigma }_{u_0}^2=1,{\sigma }_{v_0}^2=5,{\rho }_{v0v1}=0$and in (b) ${\sigma }_{u_0}^2=5,{\sigma }_{v_0}^2=1,{\rho }_{v0v1}=0.$

(a). Number of Categories C = 5; True parameters ( ${\sigma }_{u_0}^2=1,{\sigma }_{v_0}^2=5,{\rho }_{u0u1}={\rho }_{v0v1}=0$)
Model	True ${\kappa }_m$	I = 100 J = 10	I = 250 J = 100
		Mean ${\widehat{\kappa }}_m$ (S.E.)	Mean ${\widehat{\kappa }}_m$ (S.E.)
Overall	0.035	0.036 (0.007)	0.036 (0.005)
Model (a)
xj = 0	0.035	0.037 (0.007)	0.035 (0.004)
xj = 1	0.032	0.034 (0.006)	0.032 (0.004)
xj = 0, xj′ = 1	0.033	0.036 (0.006)	0.032 (0.004)
Model (b)
xi = 0	0.035	0.035 (0.004)	0.035 (0.004)
xi = 1	0.050	0.051 (0.006)	0.050 (0.006)
Model (c)
xi = 0, xj = 0	0.035	0.037 (0.006)	0.035 (0.004)
xi = 0, xj = 1	0.032	0.034 (0.006)	0.032 (0.004)
xi = 1, xj = 0	0.050	0.052 (0.009)	0.050 (0.006)
xi = 1, xj = 1	0.046	0.049 (0.008)	0.046 (0.006)

(b). Number of Categories C = 5; True parameters ( ${\sigma }_{u_0}^2=5,{\sigma }_{v_0}^2=1,{\rho }_{u0u1}={\rho }_{v0v1}=0$)
Model	True ${\kappa }_m$	I = 100 J = 10	I = 250 J = 100
		Mean ${\widehat{\kappa }}_m$ (S.E.)	Mean ${\widehat{\kappa }}_m$ (S.E.)
Overall	0.264	0.262 (0.022)	0.262 (0.015)
Model (a)
xj = 0	0.264	0.261 (0.026)	0.263 (0.018)
xj = 1	0.233	0.232 (0.027)	0.233 (0.018)
xj = 0, xj′ = 1	0.248	0.260 (0.027)	0.262 (0.017)
Model (b)
xi = 0	0.264	0.261 (0.017)	0.261 (0.017)
xi = 1	0.277	0.275 (0.017)	0.275 (0.017)
Model (c)
xi = 0, xj = 0	0.264	0.263 (0.026)	0.263 (0.017)
xi = 0, xj = 1	0.233	0.234 (0.026)	0.233 (0.017)
xi = 1, xj = 0	0.277	0.276 (0.026)	0.277 (0.017)
xi = 1, xj = 1	0.246	0.247 (0.026)	0.247 (0.017)

Table 2.

Results for five ordinal GLMM models fitted to Beam et al’s mammography study [2]. Each ordinal GLMM varies with regards to inclusion of rater and subject characteristics, including patient’s age (young = 0, old = 1) and rater inexperience (experienced = 0, inexperienced = 1).

		Model (i)	Model (ii)	Model (iii)	Model (iv)	Model (v)
Parameter	Symbol	Estimate (se)	Estimate (se)	Estimate (se)	Estimate (se)	Estimate (se)
Ordinal GLMM:
Thresholds: ( ${\alpha }_0=-\infty ,{\alpha }_5=+\infty$)
Between categories 1 and 2	${\alpha }_1$	−0.897 (0.135)	−0.902 (0.135)	−0.827 (0.138)	1.095 (0.666)	1.133 (0.670)
Between categories 2 and 3	${\alpha }_2$	−0.197 (0.135)	−0.201 (0.135)	−0.127 (0.138)	1.795 (0.666)	1.833 (0.670)
Between categories 3 and 4	${\alpha }_3$	0.761 (0.135)	0.757 (0.135)	0.831 (0.138)	2.753 (0.667)	2.791 (0.670)
Between categories 4 and 5	${\alpha }_4$	2.539 (0.137)	2.535 (0.137)	2.610 (0.140)	4.531 (0.667)	4.569 (0.671)
Fixed Coefficients:
Subject’s age	${\beta }_1$				0.034 (0.012)	0.034 (0.012)
Rater Experience (inexp =1)	${\beta }_2$					0.055 (0.094)
Random Effects Variance Components:
Subject intercept	${\sigma }_{u0}^2$	2.442 (0.288)	2.442 (0.104)	4.615 (0.543)	0.687 (0.081)	0.687 (0.079)
Subject’s age slope	${\sigma }_{u1}^2$			0.00145 (0.0002)	0.00014 (0.00002)	0.00014 (0.00002)
Rater intercept	${\sigma }_{v0}^2$	0.158 (0.023)	0.135 (0.019)	0.158 (0.023)	0.158 (0.023)	0.135 (0.019)
Rater’s inexperience slope (inexp=1)	${\sigma }_{v1}^2$		0.218 (0.030)			0.159 (0.022)
Fleiss’ kappa for multiple raters	κF	0.297 (0.001)

4.2.1. Estimation of Fixed Parameters

Fixed effects parameters in models (a) to (c) were consistently estimated with minimal or no bias in all simulation studies. Mean estimated standard errors of the fixed effects (est S.E.) for each set of simulations took very similar values to the observed standard errors (obs S.E.) thus for the fixed effects we display only the mean estimated standard errors.

4.2.2. Estimation of Random Components

Similar to the fixed effects, item and rater intercept variance components ${\sigma }_{u0}^2$ and ${\sigma }_{v0}^2$ were estimated with minimal or no bias throughout all simulation settings. The additional item variance component ${\sigma }_{u1}^2$ in models (b) and (c) (reflecting variability attributed to the binary covariate x_i =1) was slightly overestimated on average in each simulation scenario when overall rater variability was high relative to variability amongst items. Overestimation of ${\sigma }_{u1}^2$ was also observed in smaller samples when overall item variability was high relative to variability amongst raters, with substantial improvement for larger sample sizes. The additional rater variance component ${\sigma }_{v1}^2$ was also generally overestimated in simulation scenarios for smaller sample sizes with some underestimation for larger sample sizes. The correlation coefficient representing the strength of association between the item random effects ${\rho }_{u0u1}$ was consistently underestimated where variability amongst raters was larger than the variability between items, with some improvement observed in larger sample sizes. When variability amongst items was larger compared to rater variability, ${\rho }_{u0u1}$ was slightly underestimated in smaller sample sizes with little or no positive bias observed in larger sample sizes. Estimation of the rater correlation coefficient ${\rho }_{v0v1}$ representing the strength of association between rater random effects v_0j and v_1j in models (a) and (c) was slightly to moderately biased in the simulation scenarios. When variability amongst raters was larger compared to variability amongst items, ${\rho }_{v0v1}$ tended to be underestimated in the smaller sample sizes with some overestimation in larger sample sizes. When variability amongst items was relatively larger than the rater variability, ${\rho }_{v0v1}$ was again underestimated in smaller sample sizes with some improvement observed in larger sample sizes.

Estimation of variance components in GLMMs can be challenging due to the analytical intractability of the model, where the high dimensionality of the likelihood function has no closed form [34]. Approximate likelihood procedures for fitting a GLMM and parameter estimation such as a Laplacian approximation method are then often used [27, 34, 37], where the Laplacian approximation approach is considered a viable approach with good properties in many settings [34]. It has been demonstrated in prior research studies that underestimation and bias of variance components may occur in the use of approximate maximum likelihood approaches such as the Laplacian approximation, as we observed in our simulation studies, particularly in our estimation of the additional rater random effect ${\sigma }_{v1}^2$ and correlation coefficients ${\rho }_{v0v1}$ and ${\rho }_{u0u1}$.

Observed standard errors for all variance components were often a little larger than their mean estimated standard errors, with some improvement noted with increasing sample sizes. In general, ordinal GLMMs incorporating increasing numbers of random effects exhibited slightly more bias in the estimation of random effect parameters. This suggests that richer datasets incorporating more raters and items are required when many rater and item characteristics are included in the ordinal GLMM for reasonable parameter estimation.

4.2.3. Estimation of the Proposed Summary Measure of Agreement

Despite some biases observed in the estimation of additional random effects components, estimation of the proposed measure of agreement ${\kappa }_m$ proved to be consistently very stable and unbiased in all the simulation scenarios examined with only negligible bias at most, as displayed in Tables 2(a) − (f). Corresponding standard errors $se({\widehat{\kappa }}_m)$ for each simulation scenario were also very stable, with observed standard errors (calculated as the standard deviation of the 1000 ${\widehat{\kappa }}_m$’s) sometimes slightly larger. {Tables 2(a) – (b) here}

Histograms of the one thousand estimated kappa measures, ${\widehat{\kappa }}_m$, for each simulation scenario demonstrate that the distribution of ${\kappa }_m$ is reasonably well-approximated by a normal distribution in each case. Some slight bias and slight right-tailed skewness was observed in some of the distributions of ${\kappa }_m$ under models (b) and (c) which may be attributed to the approximate nature of the multivariate Laplacian estimation procedure used.

To evaluate whether 95% confidence intervals for ${\kappa }_m$ calculated as [ ${\widehat{\kappa }}_m$− 1.96×se( ${\widehat{\kappa }}_m$), ${\widehat{\kappa }}_m$ + 1.96×se( ${\widehat{\kappa }}_m$)] achieved the nominal level of coverage, we calculated the percent of the one thousand simulated datasets whose confidence intervals contained the true value of ${\kappa }_m$ in the simulation scenarios for the overall kappa and model (b). These results are presented in Supplementary Table 3 (in Supplementary materials online). The overall ${\kappa }_m$ for the simplest model with no covariates yielded coverage probabilities a little below or close to 95%, while in model (b) with a patient characteristic, the coverage probabilities were more conservative due to some slight bias and slight right-tailed skewness in the corresponding histograms of the estimates of ${\kappa }_m$ as observed in the histograms.

4.2.4. Estimation using the Bayesian MCMCglmm Package

The Bayesian MCMCglmm package in R provides an alternative approach for fitting the ordinal GLMM in (1). Simulation studies demonstrated that this method generally yielded reasonably unbiased estimates of the fixed effects, however markedly more severely biased variance components were observed for the MCMCglmm approach, especially for the additional rater random effect ${\sigma }_{v1}^2$ and correlation coefficient ${\rho }_{v0v1}$ in small and large sample sizes when compared with the ordinal package, thus we focused on using the ordinal package for our estimation.

5. Application to a Large-Scale Breast Cancer Agreement Study

A large-scale mammography study was recently conducted by Beam et al [2]. Each of 104 U.S. radiologists classified a sample of 148 mammograms according to a modified BIRADS ordinal scale five-point scale (C = 5) (1 = normal to 5 = probably malignant). Several radiologist and patient characteristics, including each radiologist’s number of years of experience, recent volume of mammograms (number read annually), gender, and patient’s age were collected in the study. The goal of our study is to investigate whether these factors have a significant impact on agreement using the proposed models and measures of agreement. Hypothesis tests are then described to formally test whether these characteristics significantly impact agreement between radiologists.

To demonstrate that our approach can flexibly be applied to address a broad range of clinical questions, we fit six agreement models to this breast cancer dataset using the ordinal package in R. Results are presented in Tables 2 and 3 and Figure 1. Models ranged from a simple ordinal GLMM with no covariates modeling agreement between all raters (model (i) in Table 2), to an agreement model incorporating several rater and item characteristics (Table 3). Models (ii) to (v) reflect the ordinal GLMMs described in simulation studies in Section 4. Rater and item characteristics include a binary indicator of level of inexperience of radiologist (x_j = 0 is 10 or more years’ experience, x_j = 1 is less than ten years’ experience), annual volume of mammography reading (x_j = 0 for <2500 mammograms; x_j = 1 for ≥2500 mammograms read per year on average), radiologist gender (1 = male, 2 = female) and the age of the patient (x_i = 0 for patients aged less than 60 years, x_i = 1 for patients aged 60+ years). Proposed measures of agreement ${\kappa }_m$ were calculated for each scenario, incorporating rater and item characteristics.

Table 3.

Results for the Beam et al mammography study [2] for an ordinal GLMM with several characteristics including patient’s age (young = 0, old = 1), rater experience (experienced = 0, inexperienced = 1), rater’s annual volume of reading mammograms (<2500 mammograms = 0, ≥2500 mammograms = 1) and rater gender (1= male, 2 = female).

Parameter	Symbol	Estimate	S.E.	Z-value
Ordinal GLMM parameters:
Thresholds: ( ${\alpha }_0=-\infty ,{\alpha }_5=+\infty$)
Between categories 1 and 2	${\alpha }_1$	−0.621	0.170	−3.657
Between categories 2 and 3	${\alpha }_2$	0.079	0.170	0.467
Between categories 3 and 4	${\alpha }_3$	1.037	0.170	6.103
Between categories 4 and 5	${\alpha }_4$	2.816	0.171	16.425
Fixed Coefficients:
Subject’s age (Older)	${\beta }_{11}$	0.549	0.258	2.130
Rater Inexperience (Inexperienced=1)	${\beta }_{21}$	−0.063	0.099	−0.635
Rater Volume (Higher)	${\beta }_{22}$	0.134	0.079	1.700
Rater Gender (Female)	${\beta }_{23}$	0.008	0.120	0.063
Random Effect Variance Components:
Subject intercept	${\sigma }_{u0}^2$	2.746	0.324
Subject’s age slope	${\sigma }_{u1}^2$	0.719	0.084
Subject correlation coefficient	${\rho }_{u_0{u}_1}$	−0.505	0.062
Rater intercept	${\sigma }_{v0}^2$	0.154	0.022
Rater’s inexperience slope	${\sigma }_{v1}^2$	0.142	0.019
Rater’s volume slope	${\sigma }_{v2}^2$	0.089	0.012
Rater’s gender slope	${\sigma }_{v3}^2$	0.009	0.001
Rater correlation coefficient	${\rho }_{v_0{v}_1}$	−0.126	0.097
Agreement Measures:
Experienced male radiologists with a high volume rating younger patients:
- GLMM Observed Agreement	p0	0.470
- Model-based Kappa	κm	0.306	0.016
Inexperienced male radiologists with a low volume rating older patients:
- GLMM Observed Agreement	p0	0.462
- Model-based Kappa	κm	0.254	0.019

Fig. 1.

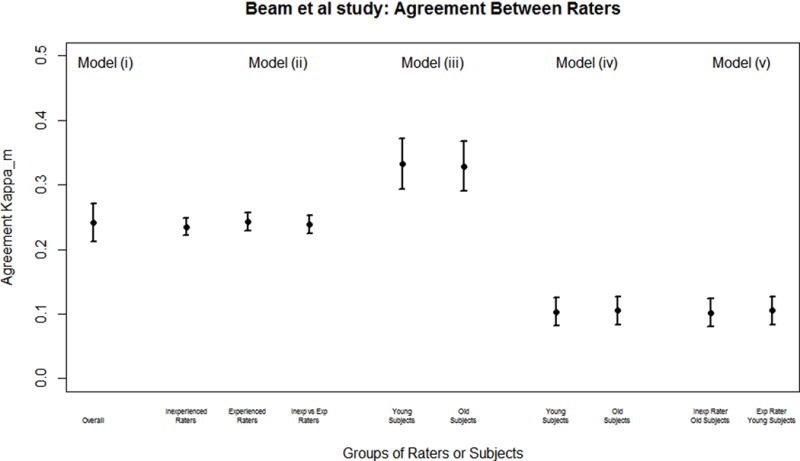
In the simplest model (i), the estimated variance component describing overall variability between mammograms is ${\widehat{\sigma }}_{u0}^2$ = 2.442, while the variance component for raters is ${\widehat{\sigma }}_{v0}^2$ = 0.158 hence $\widehat{\rho }=0.678$. This indicates that across all raters and mammograms, variability attributed to the distinguishability of disease on mammograms is much greater compared to variability amongst radiologists. In model (ii) we focused on assessing the effects of rater inexperience on agreement. Model-based measures of agreement for experienced and inexperienced radiologists are estimated as ${\widehat{\kappa }}_{m,\exp }$= 0.243 (s.e. = 0.012) and ${\widehat{\kappa }}_{m,\text{inexp}}$= 0.235 (s.e. = 0.012) respectively. These indicate only weak to moderate chance-corrected agreement between each group of radiologists, with experienced radiologists associated with a mild and insignificant increase in agreement. Agreement between radiologists when assessing mammograms of younger patients in model (iii) is similar for each agegroup of patients with ${\widehat{\kappa }}_{m,\text{young}}$ = 0.333 (s.e. = 0.020) and ${\widehat{\kappa }}_{m,\text{old}}$= 0.329 (s.e. = 0.020), suggesting that patient age does not significantly impact levels of agreement between radiologists.

Model (iv) explored agreement between small groups of raters and patients, for example, when younger patients are graded by inexperienced radiologists, and when older patients are graded by experienced radiologists. Fixed terms were also incorporated for rater’s inexperience (x_j = 0 or 1) and patient’s age (x_i = 0 or 1). Patient age was found to have a significant association with severity of disease ( ${\widehat{\beta }}_1$ = 0.034 (0.012), p = 0.003), where older patients were more likely to be more highly classified using the BIRADS ordinal scale. In contrast, radiologist’s experience level was not significantly linked with the BIRADS rating ( ${\widehat{\beta }}_2$ = −0.055 (0.092), p = 0.556). Only small differences were observed between the estimated measures of agreement when younger patients were graded by inexperienced radiologists ( ${\widehat{\kappa }}_{m,\text{young},\text{inexp}}$ = 0.100 (s.e. = 0.010)) and when older patients were graded by experienced radiologists ( ${\widehat{\kappa }}_{m,\text{old},\text{exp}}$ = 0.107 (s.e. = 0.013)) in both cases yielding low chance-corrected levels of agreement between radiologists.

Table 3 presents a full analysis of the Beam mammography study with several rater and patient characteristics included to assess their impact on agreement. Variability between subjects’ mammograms ( ${\widehat{\sigma }}_{u0}^2$ = 2.746) is higher than between radiologists, with subject’s age contributing only a small amount to the overall variability among classifications ( ${\widehat{\sigma }}_{u1}^2$ = 0.719). Overall variability amongst raters remained small ( ${\widehat{\sigma }}_{v0}^2$= 0.154) with rater characteristics of experience, volume and gender each contributing small amounts to the overall variability observed. We observed a higher level of agreement amongst experienced male radiologists with a high reading volume ( ${\widehat{\kappa }}_{m,\text{male},\text{exp},\text{high vol}}$ = 0.306 (s.e. = 0.016)) compared with inexperienced male radiologists with a low reading volume ( ${\widehat{\kappa }}_{m,\text{male},\text{inexp},\text{low vol}}$ = 0.254 (s.e. = 0.019)).

5.1. Hypothesis Testing of Rater and Item Characteristics

Hypothesis tests are described for formally testing whether rater and item characteristics of interest have an important role in determining the levels of agreement between radiologists. Factors identified as important will help to raise awareness regarding where improvements can be made in training of radiologists which may lead to stronger consistency between raters. Variance components of the random effects play a central role in these hypothesis tests since they break down overall variability between all classifications into specific components which impact agreement. We base our hypothesis testing on methods described in Molenberghs and Verbeke [38], and recommended likelihood ratio tests rather than Wald or Score tests which may be less stable in this setting [38, 39].

We first tested whether variability between raters’ classifications contributes significantly to the overall variability observed between all classifications by testing whether the rater random intercept variance component is 0, i.e. we wish to test H₀: ${\sigma }_{v0}^2$ = 0 in the simplest model (i) with no covariates. Boundary issues arise when testing variance components due to the requirement that variances must take non-negative values [38,40]. We conduct a one-sided likelihood ratio test comparing model (i) to a simpler model with only an item random effect term. The null distribution of the test statistic is a weighted sum of chi-squared distributions and has a 0.5*( ${\chi }_0^2$ + ${\chi }_1^2$) distribution [38]. The corresponding p-value is calculated by averaging the p-values of obtaining the likelihood ratio test (LRT) statistic from comparing the two GLMM models based upon the chi-squared distributions with 0 and 1 degrees of freedom. For the Beam mammography study, the LRT test-statistic = 1303.1 obtained from the anova test in R, and p-value < 0.001. This hypothesis test provides evidence that the rater variance intercept ${\sigma }_{v0}^2$ is an important component of the model, and that variability exists between the raters’ classifications.

To examine whether the level of rater experience (x_j = 0 or 1) contributes to the variability between raters’ classifications, and thus the agreement between raters, we conducted a hypothesis test H₀: ${\sigma }_{v1}^2={\rho }_{v0v1}$ = 0, where ${\sigma }_{v1}^2$ is the variance between raters that can be attributed to raters’ level of experience and ${\rho }_{v0v1}$ is the correlation between the two rater variance components ${\sigma }_{v0}^2$ and ${\sigma }_{v1}^2$. We thus compared our models (i) and (ii) for the Beam study from Table (3). Using the methods of Molenberghs and Verbeke, we obtained a LRT statistic of 1.905 which was tested against the null distribution 0.5*( ${\chi }_1^2$ + ${\chi }_2^2$) to yield a p-value of 0.277, indicating that the level of rater experience was not a significant factor in describing the variability between raters’ classifications. This result is supported by the estimated model-based kappas for experienced and inexperienced raters respectively which were fairly close in value with ${\widehat{\kappa }}_{m,\exp }$ = 0.235 (s.e. = 0.015) and ${\widehat{\kappa }}_{m,\text{inexp}}$ = 0.243 (s.e. = 0.015).

We also conducted a hypothesis test to examine the influence of the level of experience of radiologists (inexperienced versus experienced) when classifying the mammograms of older patients only (model iv) in Table 4. This entailed testing the hypothesis H₀: ${\sigma }_{v1}^2={\rho }_{v0v1}$ = 0 using the ordinal GLMM model (iv) which includes fixed and random effects terms for patient age, which we set as x_i = 1 for older patients, where patient’s age is also included as a fixed effect to adjust for the effects of increased prevalence of breast cancer for older patients. Comparing models (iv) and (v) we obtained a LRT statistic of 1.858 which was tested against the null distribution 0.5*( ${\chi }_1^2$

+ ${\chi }_2^2$) to yield a p-value of 0.284, indicating no significant influence of the level of rater experience when classifying the mammograms of older patients.

In summary, the above scenarios demonstrate the flexibility of the proposed approach for conducting a broad range of hypothesis tests depending upon the clinical questions of interest.

6. Traits of Individual Raters

The accuracy of a patient’s test result depends upon subjective interpretation by a radiologist, and as noted, there is often substantial variability amongst radiologists. For example, some radiologists may liberally assign higher scores indicating more severe disease status, while others are more conservative and rarely assign higher scores to patients. The ordinal GLMM in (1) provides a valuable opportunity to evaluate the performance of individual raters in a study. This is achieved by examining the random effects of individual raters, $v_j^{\ast }={z^{\prime }}_2{v}_j$ $(j=1,\dots ,J)$. Predictions of rater estimated effects ${\widehat{v}}_j^{\ast }={z^{\prime }}_2{\widehat{v}}_j$ are generated as part of the modeling process as conditional modes (also known as posterior Bayesian modes) in the ordinal package clmm using a Newton-Raphson algorithm, which are the modes of the distributions for the random effects given the observed data and estimated model parameters. A corresponding measure of uncertainty for each estimated effect, the conditional variance, is computed from second order derivatives of the conditional distribution of the random effects.

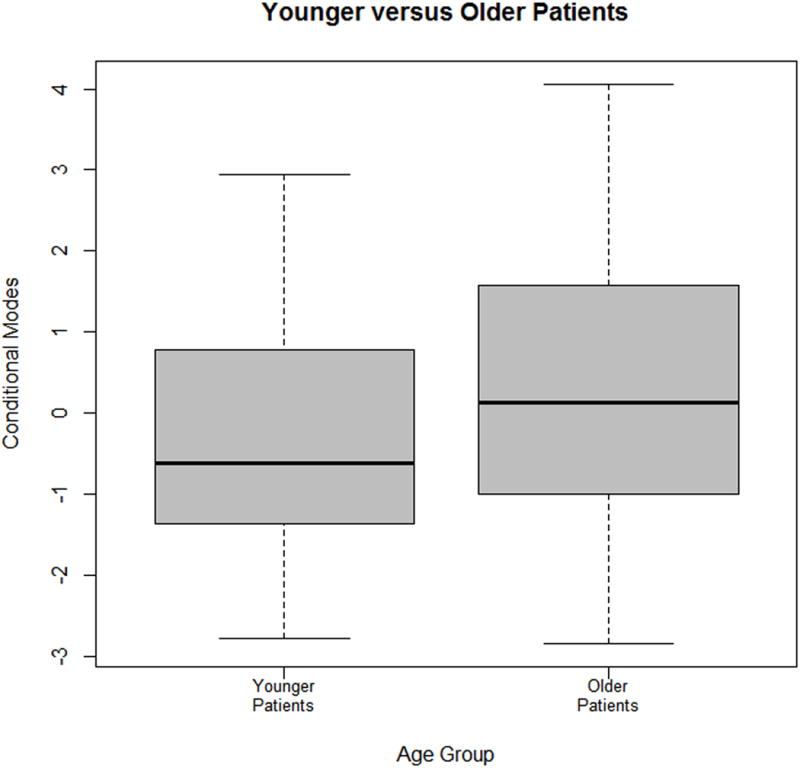
Figure 2 presents boxplots comparing the conditional modes of experienced versus inexperienced radiologists in the Beam mammography study [2]. Thirty-two inexperienced and seventy-two experienced raters were included in the study. The plots demonstrate that inexperienced raters had a broader range of conditional modes than experienced raters, leading to lower consistency amongst inexperienced raters. The conditional modes of individual raters ${\widehat{v}}_j^{\ast }$ $(j=1,\dots ,J)$ can also be used to identify individual raters in the study who are liberal or conservative in their ratings relative to other raters. In the Beam study, all raters displayed modest behavior in their classifications. Further boxplots of conditional modes ${\widehat{u}}_i^{\ast }$ $(i=1,\dots ,I)$ for older and younger patients are presented in Figure 3. These plots show that younger patients are classified with less overall variability than older patients, and have a lower probability of being classified into a higher BIRADS category.

Fig. 2.

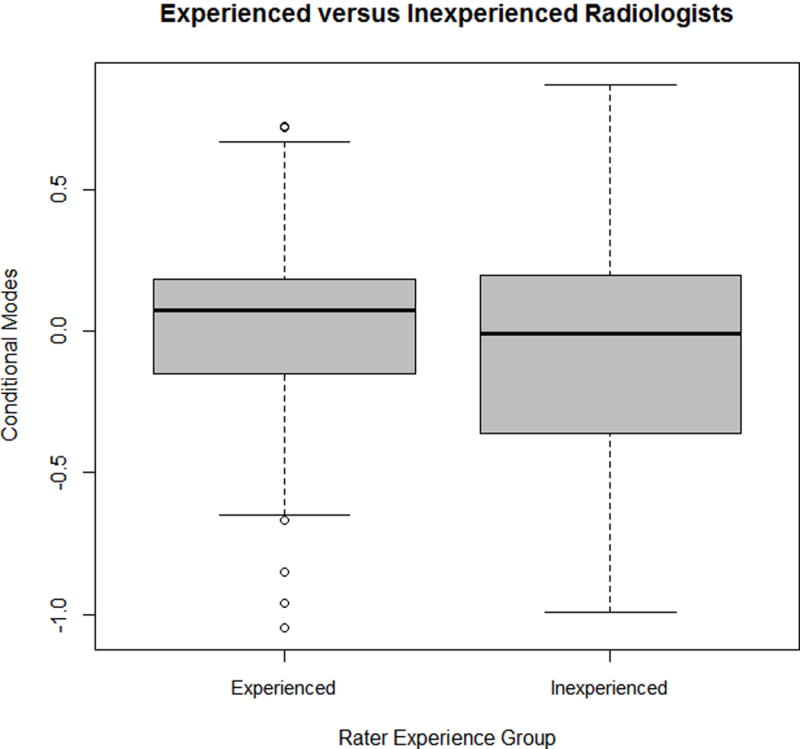
Fig. 3.

7. Discussion

With large-scale agreement studies becoming increasingly widespread in clinical settings, there is a necessity for the development of statistical methods for assessing levels of consistency between raters and to examine the impact of factors on agreement. Identification of influential factors in common screening tests provides valuable insight into how the reliability of these procedures might be improved. However, investigating the effects of rater and patient characteristics on agreement between multiple raters’ ordinal classifications is challenging in large-scale agreement studies. This is due in part to the dependency that arises when many raters contribute ratings on the same set of patients’ test results, and to the ordinal nature of the classification scale.

Currently, very few statistical approaches currently exist for modeling these types of ordered classifications in population-based studies and for assessing whether characteristics such as rater training or experience exert an important influence on the consistency between raters. Due to a lack of available methods to study effects of rater and subject characteristics on agreement, many research studies instead have elected to report several pairwise kappa measures for selected subgroups of interest, leading to a loss of power and efficiency and complexity in interpretation. Our approach models all classifications simultaneously in a unified manner, leading to a more powerful study.

In this paper we proposed a comprehensive and flexible model-based approach to address these issues, where raters can classify all or a subset of the patients’ test results. Novel summary measures of agreement are described to assess consistency amongst all raters in the study, or between raters in a specified group, such as those who are experienced at reading mammograms. Unbalanced or incomplete study design data can also be accommodated. In contrast to other approaches, increasing the number of raters and items does not add complexity to the modeling process. Our proposed summary measures are appealing in their simplicity of interpretation, adjust appropriately for chance agreement, and eliminate many biases observed in the use of Cohen’s kappa and its extensions, a commonly reported measure of agreement. Simulation studies demonstrated that the proposed summary measures are estimated with little or no bias under a range of scenarios including varying sample sizes and variance components. Results can also be generalized to the underlying populations of raters and patients if the raters and study participants are randomly sampled from their respective populations.

The proposed approach and summary measures have also been applied to a variety of other agreement studies with varying features, including smaller sample sizes of patients and raters and sparse classifications. For example, the Gonin and Lipsitz study [22] includes just 12 raters and 38 patients, where patients each received between 1 and 9 ratings in total, and also in datasets where each rater classified only a subset of the patients [6]. We found that our approach can flexibly accommodate the smaller sample sizes and unbalanced data in these settings. Ibrahim notes that GLMMs can accommodate unbalanced data [29]. However, it is important that at least three raters are included to ensure that the variance components can be estimated, and that as more patient and rater characteristics are incorporated into the model, it is ideal to have a larger dataset to ensure stability of the model estimation of the variance components in particular and model convergence using multivariate Laplacian approximation.

The proposed approach successfully accounts for the dependencies between the observations that arise due to the same sample of test results being classified by each rater by incorporating a crossed random effects structure for items and raters. We demonstrate how rater and patient characteristics can be incorporated into the models under study to assess their individual effects on agreement between raters. The proposed model incorporates rater and item effects as fixed or random terms or both. Interactions between item and rater effects can be examined by including additional terms into the GLMM in (1). While fixed interaction terms are easily incorporated, random interactive terms are a topic of future research.

Hypothesis tests are described for formally testing the significance of rater and patient characteristics which may be influential in the determining the strength of agreement between raters. The class of ordinal GLMMs also provides a valuable opportunity to gain insight into the unique characteristics of individual raters and patients through examination of the conditional modes generated as part of the modeling process, for instance, comparing experienced raters to inexperienced raters.

Measures of agreement and association are often reported in conjunction with each other in agreement studies of ordered categorical classifications. These single number summaries provide different insights into the consistency between raters’ classifications, with measures of agreement (described in this paper) providing information about the levels of exact agreement between raters. On the other hand, measures of association also provide valuable insight regarding the extent of disagreement between raters, where disagreement occurs when two raters provide different categorical classifications to the same patient’s test result. Developing a measure of association in the setting for multiple raters classifying patients’ test results using an ordered classification scale will be a topic of future research. The proposed methods in this paper can also be used in a broader setting to any study where a group of raters each assesses a collection of results defined according to an ordered categorical scale.

Appendix A - Derivation of Observed Agreement

Under the GLMM framework, observed agreement, p₀, is derived as:

$$\begin{array}{l}{p}_0={\displaystyle \sum _{c=1}^C[P(Y_{ij}=c\cap Y_{i{j}^{\prime }}=c)]}\\ ={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\{{\displaystyle \sum _{c=1}^C[P(Q\le {\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j))-}P(Q\le {\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j))]\times }\\ [P(Q\text{'}\le {\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_{j^{\prime }}))-P(Q\text{'}\le {\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_{j^{\prime }}))]\}f(u\ast )du\ast \\ ={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\{{\displaystyle \sum _{c=1}^C\left[P\left(\frac{Q-{z^{\prime }}_2{v}_j}{{\sigma }_{u\ast }}\le \frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+u\ast )}{{\sigma }_{u\ast }}\right)-P\left(\frac{Q-{z^{\prime }}_2{v}_j}{{\sigma }_{u\ast }}\le \frac{{\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+u\ast )}{{\sigma }_{u\ast }}\right)\right]}}\times \\ \left[P\left(\frac{Q-{z^{\prime }}_2{v}_{j^{\prime }}}{{\sigma }_{u\ast }}\le \frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}+u\ast )}{{\sigma }_{u\ast }}\right)-P\left(\frac{Q-{z^{\prime }}_2{v}_{j^{\prime }}}{{\sigma }_{u\ast }}\le \frac{{\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}+u\ast )}{{\sigma }_{u\ast }}\right)\right]\}f\left(\frac{u\ast }{{\sigma }_{u\ast }}\right)\frac{1}{{\sigma }_{u\ast }}du\ast \\ ={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\{{\displaystyle \sum _{c=1}^C\left[\mathrm{\Phi }\left(\frac{({\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j))/{\sigma }_{u\ast }-z}{\sqrt{(1+{\sigma }_{v_j\ast }^2)/{\sigma }_{u\ast }^2}}\right)-\mathrm{\Phi }\left(\frac{({\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j))/{\sigma }_{u\ast }-z}{\sqrt{(1+{\sigma }_{v_j\ast }^2)/{\sigma }_{u\ast }^2}}\right)\right]}}\times \\ \left[\mathrm{\Phi }\left(\frac{({\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}))/{\sigma }_{u\ast }-z}{\sqrt{(1+{\sigma }_{v_{j^{\prime }}\ast }^2)/{\sigma }_{u\ast }^2}}\right)-\mathrm{\Phi }\left(\frac{({\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}))/{\sigma }_{u\ast }-z}{\sqrt{(1+{\sigma }_{v_{j^{\prime }}\ast }^2)/{\sigma }_{u\ast }^2}}\right)\right]\}\varphi \left(z\right)dz\\ ={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\{{\displaystyle \sum _{c=1}^C\left[\mathrm{\Phi }\left(\frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)}{\sqrt{1+{\sigma }_{v_j\ast }^2}}-\frac{z\sqrt{{\sigma }_{u\ast }^2}}{\sqrt{(1+{\sigma }_{v_{j^{\prime }}\ast }^2)}}\right)-\mathrm{\Phi }\left(\frac{({\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)}{\sqrt{1+{\sigma }_{v_j\ast }^2}}-\frac{z\sqrt{{\sigma }_{u\ast }^2}}{\sqrt{(1+{\sigma }_{v_{j^{\prime }}\ast }^2)}}\right)\right]}}\times \\ \left[\mathrm{\Phi }\left(\frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }})}{\sqrt{1+{\sigma }_{v_{j^{\prime }}\ast }^2}}-\frac{z\sqrt{{\sigma }_{u\ast }^2}}{\sqrt{(1+{\sigma }_{v_{j^{\prime }}\ast }^2)}}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }})}{\sqrt{1+{\sigma }_{v_{j^{\prime }}\ast }^2}}-\frac{z\sqrt{{\sigma }_{u\ast }^2}}{\sqrt{(1+{\sigma }_{v_{j^{\prime }}\ast }^2)}}\right)\right]\}\varphi \left(z\right)dz\\ ={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\{{\displaystyle \sum _{c=1}^C\left[\mathrm{\Phi }\left(\frac{({\alpha }_c-k)/{\sigma }_T-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{({\alpha }_{c-1}-k)/{\sigma }_T-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]}}\times \\ \left[\mathrm{\Phi }\left(\frac{({\alpha }_c-k\prime )/{\sigma }_{T^{\prime }}-z\sqrt{\rho \prime }}{\sqrt{1-\rho \prime }}\right)-\mathrm{\Phi }\left(\frac{({\alpha }_{c-1}-k\prime )/{\sigma }_{T^{\prime }}-z\sqrt{\rho \prime }}{\sqrt{1-\rho \prime }}\right)\right]\}\varphi \left(z\right)dz\end{array}$$

where k and k′ denote the constant terms ${{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j$ and ${{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}$respectively and the total variances are ${\sigma }_T^2={\sigma }_{u\ast }^2+{\sigma }_{v_j^{\ast }}^2+1$ and ${\sigma }_{T^{\prime }}^2={\sigma }_{u\ast }^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2+1$.

Appendix B - Derivation of Chance Agreement

Under the GLMM framework, observed agreement p_C is derived as:

$$\begin{array}{l}{p}_c={\displaystyle \sum _{c=1}^C[P(Y_{ij}=c)\times P(Y_{i\text{'}j\text{'}}=c)]}\\ ={\displaystyle \sum _{c=1}^C\{\left[P(Q\le {\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j))-P(Q\le {\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j))\right]}\times \\ \left[P(Q\le {\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}+{z^{\prime }}_1{u}_{i^{\prime }}+{z^{\prime }}_2{v}_{j^{\prime }}))-P(Q\le {\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}+{z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_{j^{\prime }}))\right]\}\\ ={\displaystyle \sum _{c=1}^C\{\left[P(Q-({z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j)\le {\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j))-P(Q-({z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j)\le {\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j))\right]}\times \\ \left[P(Q-({z^{\prime }}_1{u}_{i^{\prime }}+{z^{\prime }}_2{v}_{j^{\prime }})\le {\alpha }_c-({{\beta }^{\prime }}_1{x}_{i^{\prime }}+{{\beta }^{\prime }}_2{x}_{j^{\prime }}))-P(Q-({z^{\prime }}_1{u}_{i^{\prime }}+{z^{\prime }}_2{v}_{j^{\prime }})\le {\alpha }_c-({{\beta }^{\prime }}_1{x}_{i^{\prime }}+{{\beta }^{\prime }}_2{x}_{j^{\prime }}))\right]\}\\ ={\displaystyle \sum _{c=1}^C\{\left[P\left(\frac{Q-({z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j)}{\sqrt{1+{\sigma }_{u_i^{\ast }}^2+{\sigma }_{v_j^{\ast }}^2}}\le \frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)}{\sqrt{1+{\sigma }_{u_i^{\ast }}^2+{\sigma }_{v_j^{\ast }}^2}}\right)-P\left(\frac{Q-({z^{\prime }}_1{u}_i+{z^{\prime }}_2{v}_j)}{\sqrt{1+{\sigma }_{u_i^{\ast }}^2+{\sigma }_{v_j^{\ast }}^2}}\le \frac{{\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)}{\sqrt{1+{\sigma }_{u_i^{\ast }}^2+{\sigma }_{v_j^{\ast }}^2}}\right)\right]}\times \\ \left[P\left(\frac{Q-({z^{\prime }}_1{u}_{i^{\prime }}+{z^{\prime }}_2{v}_{j^{\prime }})}{\sqrt{1+{\sigma }_{u_{i^{\prime }}^{\ast }}^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2}}\le \frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_{i^{\prime }}+{{\beta }^{\prime }}_2{x}_{j^{\prime }})}{\sqrt{1+{\sigma }_{u_{i^{\prime }}^{\ast }}^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2}}\right)-P\left(\frac{Q-({z^{\prime }}_1{u}_{i^{\prime }}+{z^{\prime }}_2{v}_{j^{\prime }})}{\sqrt{1+{\sigma }_{u_{i^{\prime }}^{\ast }}^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2}}\le \frac{{\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_{i^{\prime }}+{{\beta }^{\prime }}_2{x}_{j^{\prime }})}{\sqrt{1+{\sigma }_{u_{i^{\prime }}^{\ast }}^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2}}\right)\right]\}\\ ={\displaystyle \sum _{c=1}^C\left[\mathrm{\Phi }\left(\frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)}{\sqrt{1+{\sigma }_{u_i^{\ast }}^2+{\sigma }_{v_j^{\ast }}^2}}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)}{\sqrt{1+{\sigma }_{u_i^{\ast }}^2+{\sigma }_{v_j^{\ast }}^2}}\right)\right]}\times \\ \left[\mathrm{\Phi }\left(\frac{{\alpha }_c-({{\beta }^{\prime }}_1{x}_{i^{\prime }}+{{\beta }^{\prime }}_2{x}_{j^{\prime }})}{\sqrt{1+{\sigma }_{u_{i^{\prime }}^{\ast }}^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2}}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{c-1}-({{\beta }^{\prime }}_1{x}_{i^{\prime }}+{{\beta }^{\prime }}_2{x}_{j^{\prime }})}{\sqrt{1+{\sigma }_{u_{i^{\prime }}^{\ast }}^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2}}\right)\right]\end{array}$$

Appendix C - Minimizing Chance Agreement

We are interested in determining the threshold values ${\alpha }_0,{\alpha }_1,\dots ,{\alpha }_C$ with ${\alpha }_0=-\infty$ and ${\alpha }_C=+\infty$ ( ${\alpha }_0\le {\alpha }_1\le \dots \le {\alpha }_C$) that minimize the expression for chance agreement in equation (3) when raters j and j′ (j ≠ j′) come from the same group so that k = k′ and ${\sigma }_T^2={\sigma }_{T^{\prime }}^2$. Based upon the ordinal GLMM in equation (1), we define “gap” probabilities as:

$$g_c=P(Y_{ij}=c)=\mathrm{\Phi }\left(\frac{{\alpha }_c-k}{\sqrt{{\sigma }_T^2}}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{c-1}-k}{\sqrt{{\sigma }_T^2}}\right)\text{for}c=1,\dots ,C.$$

Then chance agreement p_c can be written as

$$\begin{array}{l}{p}_c={\displaystyle \sum _{c=1}^C[P(Y_{ij}=c)\times P(Y_{i\text{'}j\text{'}}=c)]}\\ ={\displaystyle \sum _{c=1}^C\left[\mathrm{\Phi }\left(\frac{{\mathit{\alpha }}_c-k}{\sqrt{{\mathit{\sigma }}_T^2}}\right)-\mathrm{\Phi }\left(\frac{{\mathit{\alpha }}_{c-1}-k}{\sqrt{{\mathit{\sigma }}_T^2}}\right)\right]}\times \left[\mathrm{\Phi }\left(\frac{{\mathit{\alpha }}_c-k\prime }{\sqrt{{\mathit{\sigma }}_{T^{\prime }}^2}}\right)-\mathrm{\Phi }\left(\frac{{\mathit{\alpha }}_{c-1}-k\prime }{\sqrt{{\mathit{\sigma }}_{T^{\prime }}^2}}\right)\right]\\ ={\displaystyle \sum _{c=1}^C{g}_c^2=g^{\prime }Ig}\end{array}$$

where k and k′ denote constant terms ${{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j$ and ${{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_{j^{\prime }}$ and total variances are ${\sigma }_T^2={\sigma }_{u\ast }^2+{\sigma }_{v_j^{\ast }}^2+1$ and ${\sigma }_{T^{\prime }}^2={\sigma }_{u\ast }^2+{\sigma }_{v_{j^{\prime }}^{\ast }}^2+1$. Vector $g=(g_1,g_2,\dots ,g_C)$ and matrix I is the C × C identity matrix. So our goal is to minimize $g^{\prime }Ig$subject to ${\displaystyle \sum _{c=1}^C{g}_c=1}$.

We can apply the LaGrangian approach here, such that $Q={\displaystyle \sum _{c=1}^C{g}_c^2}+\lambda \left({\displaystyle \sum _{c=1}^C{g}_c}-1\right)$ and $\frac{\partial Q}{\partial g_c}=2g_c+\lambda =0$, c = 1,…,C. The only solution to these equations has all probabilities g_c equal, hence g_c ≡ 1/C. Under this configuration, the minimum value of $p_c={\displaystyle \sum _{c=1}^C{g}_c^2={\displaystyle \sum _{c=1}^C{\left(\frac{1}{C}\right)}^2=\frac{1}{C}}}$. The threshold values that satisfy this condition of g_c ≡ 1/C are derived as follows:

For c = 1: $g_1=\mathrm{\Phi }\left(\frac{{\alpha }_1-k}{\sqrt{{\sigma }_T^2}}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_0-k}{\sqrt{{\sigma }_T^2}}\right)=\frac{1}{C}\Rightarrow$ ${\alpha }_{1min}=\sqrt{{\sigma }_T^2}{\mathrm{\Phi }}^{-1}\left(1/C\right)+k$. This process can be repeated for each c to obtain ${\alpha }_{cmin}={\mathrm{\Phi }}^{-1}(c/C)\sqrt{{\sigma }_{u_{\ast }}^2+{\sigma }_{v_j^{\ast }}^2+1}+({{\beta }^{\prime }}_1{x}_i+{{\beta }^{\prime }}_2{x}_j)$, c = 1,…., C−1.