Determining Atomistic SAXS Models of Tri-Ubiquitin Chains from Bayesian Analysis of Accelerated Molecular Dynamics Simulations

Abstract

Small-angle X-ray scattering (SAXS) has become an increasingly popular technique for characterizing the solution ensemble of flexible biomolecules. However, data resulting from SAXS is typically low-dimensional and is therefore difficult to interpret without additional structural knowledge. In theory, molecular dynamics (MD) trajectories can provide this information, but conventional simulations rarely sample the complete ensemble. Here, we demonstrate that accelerated MD simulations can be used to produce higher quality models in shorter time scales than standard simulations, and we present an iterative Bayesian Monte Carlo method that is able to identify multistate ensembles without overfitting. This methodology is applied to several ubiquitin trimers to demonstrate the effect of linkage type on the solution states of the signaling protein. We observe that the linkage site directly affects the solution flexibility of the trimer and theorize that this difference in plasticity contributes to their disparate roles in vivo.

Graphical abstract

1. INTRODUCTION

Characterizing the inherent flexibility of biomolecular complexes remains one of the key challenges in modern biophysics research.¹ Over the years, a wealth of both experimental and computational techniques have been developed that can explore the solution dynamics of proteins on a vast range of time and length scales. One particularly useful method for studying these properties is small-angle X-ray scattering (SAXS).^2,3 Unlike X-ray crystallography, which requires cohesive repeats of a singular representative structure in nonnative conditions, SAXS experiments probe the entire ensemble of a protein in physiologically relevant environments. SAXS experiments are relatively easy to perform and produce data that represent an ensemble average of all states at room temperature with results that are not influenced by factors such as lattice packing forces. Nevertheless, these advantages come at a cost: the primary data resulting from SAXS experiments, the scattering curve, is of low dimensions and can be difficult to interpret.² As a result, the analysis of SAXS data typically requires ancillary structural information provided by complementary methods, such as crystallography or spectroscopy,^4–7 which possess their own limitations with regard to system size and intrinsic disorder.^8,9

In principle, the conformational ensemble of a system can be fully characterized with molecular dynamics (MD) simulations. However, in practice MD is limited by both the amount of sampling that can be performed as well as the accuracy of the underlying models. Recent advances in computing power and enhanced sampling techniques have opened the door to MD-based methods that can probe biomolecular dynamics that occur on the μs-ms time scale.^10–18 For example, in replica exchange methods, multiple copies of the same system are simulated at either different temperatures or with different Hamiltonians, and a Markov Chain Monte Carlo algorithm is used to transfer information between neighboring replicas.^11,12 Metadynamics provides an alternative enhancement method in which the potential energy landscape underlying a system is smoothed through a history-dependent bias, thereby reducing the amount of sampling time required to escape local minima and increasing the conformational space sampled in a simulation.^17,18 Accelerated molecular dynamics (aMD) speeds sampling through the introduction of a “boost” potential that reduces the depths of energy wells and thus increases the rate of barrier crossings.^10,19 Unlike methods such as Hamiltonian replica exchange or metadynamics, aMD does not require the definition of a reaction coordinate along which to bias, and acceleration can be achieved without performing multiple concurrent simulations. On the other hand, aMD does disturb the Boltzmann distribution of states observed in a simulation and calculating the physically relevant populations of states from an aMD simulation can be difficult, especially for large biomolecular complexes.

The relative strengths and weaknesses of SAXS and enhanced sampling methods make them a natural complement to one another.²⁰ Indeed, several tools have been developed to directly use the high-resolution structures from enhanced sampling simulations to produce an ensemble-based interpretation of low-resolution SAXS data. For example, the SASSIE Web server conducts Monte Carlo samplings of molecular torsions and subsequently evaluates scattering states in a single interface.^21–24 In the BILBOMD protocol, multiple timestepping algorithms are coupled with high temperatures, and observed structures are subsequently reweighted using a genetic algorithm.²⁵ In another approach, collective modes gathered from an elastic network model of a protein are amplified during MD simulations, and representative structures are fit by the genetic algorithm implemented in the Ensemble Optimization Method of the ATSAS package.^26,27 A fourth method, BSS-SAXS, utilizes coarse-grained simulations to form a scattering basis and then distributes the ensemble population through a Bayesian Monte Carlo reweighting scheme.²⁸

These methods are particularly useful for flexible molecules where a single conformation cannot sufficiently describe the observed profiles. However, further conversation is required with regard to overfitting multistate models. That is to say, the parameters of an ensemble model can create arbitrarily strong goodness-of-fit values through the introduction of too many subpopulations. This can be viewed as a violation of Occam’s Razor,²⁹ where the addition of extra scattering states corresponds to an overly complicated model that contains irrelevant components. Therefore, an accurate model ensemble must resist this overfitting tendency and instead report the minimum number of states required to achieve good agreement with experimental scattering data.

Ubiquitin chains represent prototypical examples of highly flexible systems that are difficult to characterize through SAXS or MD methods alone. Within these oligomers, ubiquitin units are linked to one another through an isopeptide bond that forms between the C-terminus of one monomer and the ε-amino group of one of seven ubiquitin lysines (K6, K11, K27, K29, K33, K48, and K63; see Figure 1) or the N-terminus (M1). The dogma is that chain linkages dictate biological function. For example, K48-linked chains are typically involved in proteasomal degradation,³⁰ whereas K63-linked chains act as scaffolds for the formation of multiprotein complexes.^31,32 In vitro, ubiquitin subunits may be connected to one another through non-native linkages, such as with thiol–ene coupling, to quickly and robustly generate libraries of diverse chain linkages.^33,34 These non-native linkages generally have similar structural properties as those of native isopeptide bonds; however, they can be significantly easier to produce.³⁵

Figure 1.

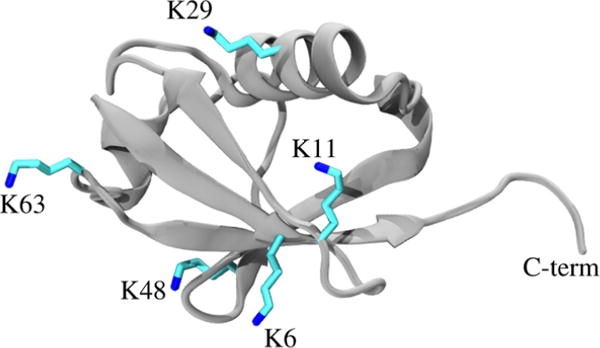
Crystal structure of ubiquitin monomer (PDB: 1UBQ).³⁶ Shown in sticks are the five lysine sites presented in this study. Other potential linkage sites exist but are not shown (M1, K27, and K33). The C-terminus (“C-term”) of one ubiquitin monomer forms an isopeptide or thiolene linkage with the amino group at one of these sites.

Here, we used SAXS experiments along with enhanced sampling MD simulations to characterize the conformational ensemble of seven ubiquitin chains. To do this, we developed a modified BSS-SAXS approach in which cMD and aMD simulations are combined with an iterative Bayesian population reweighting approach to rapidly model SAXS data. Our methods place an emphasis on determining ensembles that simultaneously minimize goodness-of-fit while resisting overfitting of the data. Results are compared for both conventional MD (cMD) and aMD simulations, and it was found that cMD simulations never outperformed the aMD trajectories in model quality or convergence speed. In fact, some aMD simulations produced better models up to an order of magnitude faster than cMD simulations of the same system. In all, these systems show that aMD enhanced sampling provides a straightforward method for quickly producing robust all-atom models from SAXS experiments.

2. METHODS

2.1. Experimental Details

2.1.1. Expression and Purification of Ubiquitin Variants

Lysine to cysteine mutations were introduced at specified sites in the DNA sequence of ubiquitin (Ub 1–76) using splice overlap extension. Primers containing the TGC mutation were inserted at the desired codon position. A codon extending the C-terminus of ubiquitin with D77 was introduced using reverse primer to afford all five constructs (UbKxC-D77, where x represents the position of the native lysine residue that was replaced), and then they were ligated into a pET22b vector (Novagen). Wild-type ubiquitin and its variants were expressed and purified from Rosetta 2(DE3)pLysS cells (Novagen) as previously described.^33,35

2.1.2. Generation of Native and Non-Native Ubiquitin Trimers

As previously described, the yeast C-terminal hydrolase Yuh1 was used to append allylamine (AA) to the C-terminus of ubiquitin to afford UbKxC-AA variants.³³ Irradiation of UbKxC-AA (2 mM) lithium acyl phosphinate (LAP) (0.5 mM) in 250 mM NaOAc pH 5 for 30 min at 4 °C yielded UbKxC oligomers with non-native thiol–ene-derived linkages.^33,35 All ubiquitin trimers were purified using size exclusion chromatography (Hiload 26/600 Superdex 75 pg, GE Healthcare).

2.1.3. SEC-SAXS Measurements and Data Processing

Size-exclusion chromatography small-angle X-ray scattering (SEC-SAXS)³⁷ experiments were performed at BioCAT (beamline 18-ID, Advanced Photon Source at Argonne National Laboratories). The camera included a focused 12 keV (1.03 Å) X-ray beam, a 1.5 mm quartz capillary sample cell, and a Pilatus 1 M detector (Switzerland). The q-range sampled was ~0.0045–0.35 Å⁻¹. To ensure sample monodispersity, we used an in-line SEC setup, which included an AKTA-pure FPLC unit and a Superdex-75 10/300 GL column (GE Healthcare Life Sciences). The column was run at 0.8 mL/min, and the outlet was directly connected to the SAXS sample cell. One second exposures were collected every two seconds during the gel-filtration chromatography run. Samples were analyzed at room temperature in 50 mM HEPES pH 7.5, 50 mM KCl, 5 mM MgCl₂, and 1 mM TCEP. Exposures before and after the elution of the sample were averaged and used as the buffer blank curve, and the exposures during elution (coincident with the UV peak on the chromatogram) were treated as protein plus buffer curves. Data were corrected for background scattering by subtracting the buffer blank curve from protein plus buffer curves. The radius of gyration (R_g) for each system was determined with the aid of PRIMUS,³⁸ and the resulting R_g values obeyed the limitation q_max·R_g < 1.3. To minimize the impact of low-q beamstop effects on model quality, experimental data were filtered such that all low-q points with a signal-to-noise ratio of 10.0 or below were manually removed and not used in the fitting protocol. Data were also truncated at q = 0.2 Å⁻¹ due to the inherent limitation of implicit hydration layer SAXS calculations.³⁹

2.2. Simulation Details

2.2.1. Construction of the Triubiquitin Systems

Initial structures were obtained from the Protein Data Bank for monoubiquitin (PDB: 1UBQ³⁶), K11-linked diubiquitin (PDB: 3NOB⁴⁰), K6-linked diubiquitin (PDB: 2XK5⁴¹), K29-linked diubiquitin (PDB: 4S22⁴²), K48-linked diubiquitin extracted from K48-linked cyclic tetraubiquitin (PDB: 3ALB⁴³), and K63-linked tetraubiquitin (PDB: 3HM3⁴⁴). Any missing or mutated residues in these structures were corrected by comparison with the 1UBQ structure of monoubiquitin with missing coordinates taken by aligning 1UBQ with the monomer of interest. K63-linked triubiquitin was constructed by removing one monomer from the tetraubiquitin crystal structure. The K6-, K29-, and K48-linked systems were constructed by overlapping two copies of the corresponding diubiquitin structures and then removing the overlapped monomer. Finally, the K11-linked triubiquitin was constructed by adding the monoubiquitin structure to the K11-linked diubiquitin crystal structure. Table S1 provides an overview of the PDB structures used to construct each system.

To match the prepared ubiquitin samples, all five linkage types were simulated with a non-native thiolene linkage between monomers instead of the native isopeptide bond (Figure 2). Additionally, two of the systems, K48 and K63, were also simulated with native isopeptide linkage to determine how linkage chemistry affects molecule dynamics and the solution ensemble. Both sets of linkage parameters were generated with GAFF with partial charges derived from a restrained electrostatic potential (RESP) fit to the electrostatic potential computed at the HF/6-31G* level using Gaussian 09.⁴⁵ Each system was solvated in a box of TIP3P water⁴⁶ with 12 Å of padding in each dimension; then, sodium and chloride ions were added to a 0.15 M concentration. The Amber force field ff14SB was used⁴⁷ along with the isopeptide and thiolene modifications described above.

Figure 2.

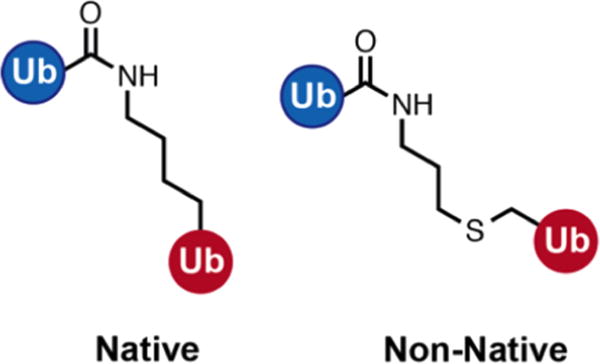
Depiction of the native isopeptide linkage between ubiquitin monomers (left) and the non-native thiolene linkage used in this study (right).

2.2.2. Conventional Molecular Dynamics

Initial equilibration was performed at constant temperature in both the constant volume and constant pressure ensembles with a 2 fs time step. Before the equilibration phase, the solvent was energy minimized using both the steepest descent and conjugate gradient algorithms. In the equilibration phase, the system was first heated in the NVT ensemble to 310 K over 50 ps with restraints on all non-hydrogen atoms of the solute. Next, the systems were simulated for 500 ps in the NPT ensemble with restraints on all non-hydrogen atoms of the solute to allow the density of the solvent to equilibrate. Finally, the restraints were slowly relaxed over 3 ns. No restraints were applied during the production phase, which was carried out for 500 ns in the NPT ensemble. Frames were saved every 5 ps during the production phase.

The temperature of the system was maintained at 310 K using Langevin dynamics with a collision frequency of 1.0 ps⁻¹. The pressure was maintained at 1.0 bar by means of isotropic coordinate scaling utilizing the Berendsen barostat and a relaxation time of 1.0 ps.⁴⁸ All hydrogen bonds were constrained using SHAKE.⁴⁹ A cutoff of 10.0 Å was used for direct nonbonded interactions, and long-range electrostatics were treated with the particle mesh Ewald (PME) method with a 1 Å grid spacing.⁵⁰ All simulations were performed with the gpu-accelerated version of pmemd in Amber 14,^13,51 and R_g time series were calculated using cpptraj.⁵²

2.2.3. Accelerated Molecular Dynamics

Following the minimization and equilibration phase simulations, each system was also simulated in the NPT ensemble using accelerated molecular dynamics (aMD).¹⁰ The aMD simulations were performed using the dual-boost variant¹⁹ in which a boost potential is applied to the whole potential with an extra boost to the torsions. The boost is defined by four aMD parameters, E_d, α_d, E_p, and α_p, where E_p/d defines the energy threshold below which the boost should be supplied and α_p/d is the acceleration factor that controls the shape of the modified potential. Values for E_d, α_d, E_p, and α_p were calculated individually for each system based on the number of atoms, dihedrals, and average energies from the first 50 ns of the cMD simulations (see Table S1).⁵³ For K6-linked triubiquitin, these parameters were insufficient to attain the desired sampling level (see section S4 for further discussion), so E_p and E_d were each incremented by the value of the corresponding α. All aMD simulations were carried out for 150 ns using the same simulation parameters as described above. Lastly, aMD ensembles were not reweighted according to the Boltzmann weight of the applied boosts, as populations of states were extracted directly from fitting to SAXS data after the simulation was completed.

2.3. Bayesian Modeling of SAXS Data

We developed and utilized an iterative Bayesian reweighting scheme to determine the ensemble of structures from our simulations that best represented the solution SAXS measurements (Figure 3). In summary, MD trajectories were subjected to two rounds of clustering: one based on their structures and another based on their theoretical scatting profiles. Structural clustering allowed us to focus on atomic scale structures that were sufficiently unique from one another, and the scattering clustering step allowed us to only consider structures that were experimentally distinguishable from one another. Ensembles of increasing size of theoretical scattering curves were then considered with a Bayesian Monte Carlo algorithm until overfitting was observed, at which point the statistically best-fit model was chosen.

Figure 3.

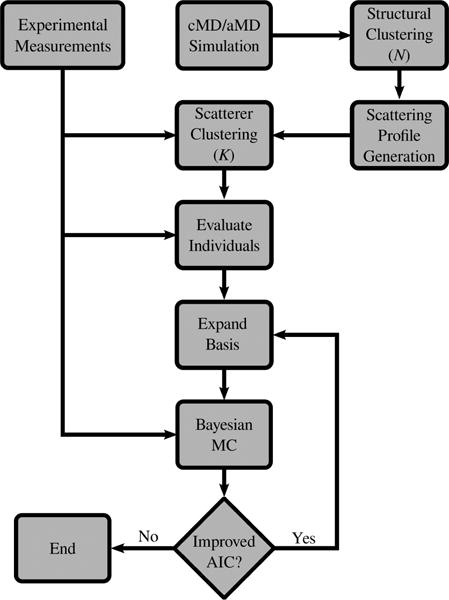
Schematic of the iterative Bayesian ensemble refinement workflow. MD trajectories were first clustered into similar structures that were subsequently clustered based on their scattering patterns. The full permutation of iteratively increasing subset sizes were then used to produce models through a Bayesian Monte Carlo until overfitting was observed.

2.3.1. Creation of Scattering Clusters

For decorrelating the configurations sampled in our MD simulations, N structural states were isolated using an agglomerative clustering algorithm.^54,55 For each structural state, a theoretical SAXS scattering profile was calculated by multipole expansion.⁵⁶ For the K nonredundant and experimentally distinguishable SAXS profiles from these N scattering curves to be determined, another agglomerative clustering was then utilized with the distance between scattering profiles metric defined as

$$S_{i,j}=\frac{1}{n_s}{\displaystyle \sum _{q\epsilon N_s}{\left(\frac{I_i(q)-I_j(q)}{\sigma (q)}\right)}^2}$$ (1)

where I_i(q) and I_j(q) are the scattering intensities of profiles i and j at momentum transfer q, σ(q) is the experimental scattering error, and N_s is the number of data points. The summation was subsampled based on the Nyquist–Shannon sampling theorem to ensure that data points in the scattering profiles were decorrelated from one another.⁵⁷ In this metric, an S_i,j of 1 suggests that two profiles are indistinguishable within the experimentally observed noise. In this way, the 2σ approach to signal recognition corresponds to clustering the similarity scores to a value of S_i,j = 2.

2.3.2. Bayesian-Based Population Estimates

The theoretical scattering profile for the ensemble of K scattering states is calculated as the population weighted average of the individual states^27,28

$$I_t(q)=\langle I(q)\rangle ={\displaystyle \sum _{i=1}^K{w}_i{I}_i(q)}$$ (2)

where I_i(q) is the scattering profile of state i and w_i is its fraction of the total population. Although multiple well-established techniques have been developed to calculate I_i(q) from atomic coordinates,^56,58–60 determining the population of states w_i is a nontrivial task. Here, we employed a modified and iterative implementation of the BSS-SAXS²⁸ approach to determine the population of states.

The posterior distribution of Bayes’ theorem is defined as⁶¹

$$p(\theta |X)=\frac{p(X|\theta )p(\theta )}{p(X)}$$ (3)

where X represents the experimental scattering profile (I(q)), θ is the set of population weights ({w_i}), p(X) is the marginal likelihood of the data, p(θ) is the prior distribution (probability distribution for the set of population weights {w_i}), p(X|θ) is the likelihood function (the probability that the set of weights {w_i} can reproduce the experimental scattering profile), and p(θ|X) is the posterior distribution from which the set of weights {w_i} that best models the experimental data are extracted. The likelihood function $\text{exp}(-{\chi }_{\text{free}}^2/2)$ is employed because experimental SAXS errors are approximately Gaussian,^62–64 but model qualities are reported as reduced ${\chi }_{\text{free}}^2$ values, as this is the colloquial value used when reporting SAXS models. The ${\chi }_{\text{free}}^2$ metric is used in place of the standard χ² as it is a more accurate measure of model quality and less prone to overfitting (section S2).⁶³ A reduced ${\chi }_{\text{free}}^2$ can be calculated analogously to the reduced χ² metric, but the nonreduced form was used in the likelihood function. In theory, a prior distribution with many features could be calculated from the MD trajectory. However, the sampling of the simulations presented here was sufficient to explore a variety of conformations but insufficient to discern their relative populations of states. Therefore, the prior distribution of population weights was assumed to be uniform.

A Baysian Monte Carlo algorithm was used to explore the θ parameter space and subsequently map the posterior distribution. For overfitting through an excessive number of possible scattering states to be avoided, an iterative “bottom-up” method was employed to determine the minimal number of structures required. First, the goodness-of-fit for each individual scattering state was determined, along with an associated Akaike information criterion (AIC)⁶⁵

$$\text{AIC}=2\nu -2\text{ln}(\widehat{L})$$ (4)

where ν is the number of model parameters and $\widehat{L}$ is the maximum observed likelihood (i.e., the minimum observed ${\chi }_{\text{free}}^2$). The AIC penalizes a model’s goodness-of-fit from arbitrarily increasing the number of model parameters (see section S1 of the Supporting Information for more details). Following the inspection of all single states, all permutations of ensembles that contained two states were considered. This procedure was repeated with incrementally increasing basis set sizes until the model AIC was not improved. Following these permutations, the minimum AIC model was reported as the one that best fits the experimental data.

2.3.3. Implementation

Initially, the MD ensembles from each simulation were structurally grouped using the hierarchical clustering protocol implemented in cpptraj.⁵² Coordinates from every 20 ps of simulation were least-squares fit according to their backbone atoms, and distances between members were defined using the RMSD of Cα atoms. To determine the effect of structural clustering on the final number of scattering states, several different structural bases were produced by defining the total number of clusters (N) to be 25, 50, 100, 200, 300, and 500. For each structural basis, the central member of each cluster was selected as the representative state, and the scattering profile of each representative was calculated using Crysol.⁵⁶ Structural clusters were then further grouped into scattering states separated by a similarity score of S_i,j = 2. Most systems did not display a large deviation in scattering numbers when more than 300 initial structures were considered, so N = 300 initial structural clusters was chosen for all systems (see below). For the sampling convergence calculations, if the total number of frames was less than or equal to 300, then no structural clustering was conducted, and the K scattering states were clustered from the theoretical profiles of every frame.

The number of Shannon channels for determining ${\chi }_{\text{free}}^2$ was defined using the SHANUM program of the ATSAS suite.⁶⁶ For each basis subset permutation, ten randomly initiated Monte Carlo searches were conducted for a total of 10,000 steps, and the last 9,000 steps of each run were combined and normalized to create the observed posterior distribution. The population of state i was defined as the average of the marginal posterior in w_i, and the uncertainty was defined as the standard deviation.

3. RESULTS

3.1. SAXS Experiments

Experimental data were gathered for seven different triubiquitin systems, five of which contained non-native thiolene linkages (K6, K11, K29, K48, and K63) and two of which contained native isopeptide bonds (nK48 and nK63). Beam smearing effects were observed at low q, but the SAXS intensity was otherwise well-resolved for each system (Figure S2). Differences in both the scattering curves and R_g values suggest these systems adopt a range of shapes and sizes, and differences in the values of each system suggest varying shapes and sizes based on linkage type (Table 1) with K11 linkages being the most compact and K63 the most extended.

Table 1.

R_g for Each System As Determined from a Guinier Analysis of the Experimental Data, Analysis of the cMD and aMD Trajectories, and from the Bayesian Ensemble Fitting Protocol^a

system	experiment (Å)	cMD (Å)	aMD (Å)	ensemble (Å)
K6	22.9 ± 0.1	19.0 ± 0.1	19.3 ± 0.2	21.8 ± 0.1
K11	21.4 ± 0.1	20.5 ± 0.1	19.5 ± 0.1	21.7 ± 0.6
K29	23.3 ± 0.3	24.6 ± 0.1	20.3 ± 0.2	24.9 ± 1.5
K48	22.3 ± 0.1	23.6 ± 0.3	21.3 ± 0.3	22.4 ± 0.3
nK48	23.7 ± 0.1	22.4 ± 1.0	23.4 ± 0.2	24.1 ± 0.6
K63	28.0 ± 0.1	25.0 ± 0.2	22.5 ± 0.2	28.3 ± 0.3
nK63	27.0 ± 0.2	25.6 ± 0.3	21.1 ± 0.5	28.6 ± 1.1

^aThe R_g of a ubiquitin trimer appears to be directly related to the geometry of the linkage. Furthermore, ensemble reweighting produces better agreement with experimental values than the raw MD trajectories. nK48 and nK63 denote trimers with the native isopeptide linkage.

3.2. aMD and cMD Sampling Inefficiencies

The inefficacy of the aMD and cMD simulations to accurately sample the experimental ensemble without reweighting the population of states can be established by comparing the R_g values of each trajectory (columns two and three of Table 1) with experimental measurements. The cMD-based R_g calculations are too compact in five systems (K6, K11, nK48, K63, and nK63), and only the R_g value of the K11-linked trimer is within 1.0 Å of the experimental value. In contrast, the aMD-based predictions are undervalued for every system. Indeed, both simulations are close to being within the error of predicting the R_g of one system: the nK48-linked trimer. However, the R_g predictions of our ensemble-based approach (discussed in detail below) are able to capture nearly every R_g value within the error.

3.3. Identifying Scattering Clusters

For the appropriate method for forming scattering clusters to be determined, the full 150 ns aMD trajectories were analyzed. Each simulation was structurally grouped into a range of total numbers of clusters (N), and then each set of structural representatives was subsequently clustered according to similarity values (S_i,j) of 1, 2, and 3 (Figure 4 and Figure S10). At each number of structural states, the most scattering states were identified when a similarity score of 1 was enforced, and the fewest number of scattering states were identified for a similarity score of 3. A similarity restriction of 2 was selected because it identified an intermediate number of scattering states and is analogous to a 2σ result in identifying one profile from another. In most simulations, the number of identified scattering states increased with the number of initial structural clusters until N = 300, after which there was little change. To test if a larger basis set N would affect our results, the non-native K63-linked system was also clustered according to the scattering profiles of all N = 7,500 frames and showed the same number of scattering states (K = 14) for 7,500 frames as for N = 300 structural states.

Figure 4.

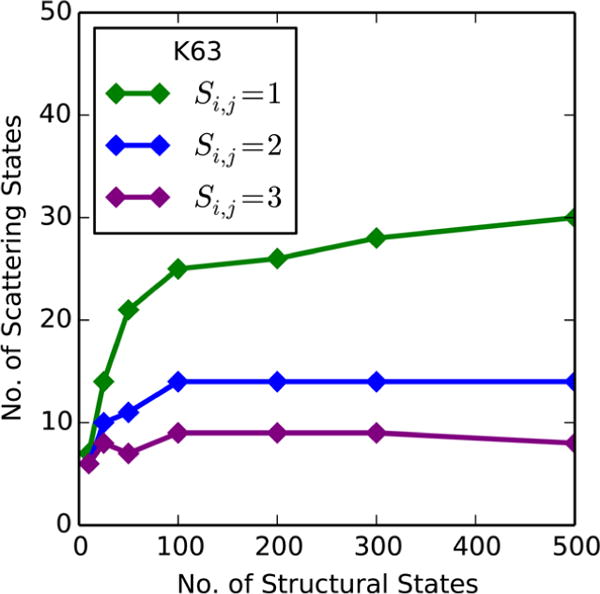
Number of identified scattering states vs the number of initial structural clusters from the K63 triubiquitin aMD simulation. At a similarity restriction of S_i,j = 2, the number of unique scattering states is unaltered when considering more than 100 structural states.

3.4. Preventing Overfitting with Iterative Inclusion

One inherent difficulty in producing multimember models is the potential of overfitting to experimental data. To demonstrate that our iterative Bayesian approach avoids overfitting, the full basis fitting of the non-native K63 aMD simulation is presented in detail. Initially, the full ensemble of all 14 scattering states was reweighted using a Bayesian Monte Carlo approach (Figure 5). This produced a model with a reduced ${\chi }_{\text{free}}^2$ value of 1.12, significantly better than any single scattering state. Although all 14 members were considered in the Monte Carlo, only clusters 2 and 3 contributed more than 0.1 of the population individually and combined for a net 39% of the total ensemble. As a result, the remaining 61% of the population was spread in small amounts throughout the other 12 clusters. This could be the result of overfitting through a large number of model parameters, or it could be the effect of the Monte Carlo sampling along a 14-dimensional hypersurface pooling small amounts of the population to unfavorable states.

Figure 5.

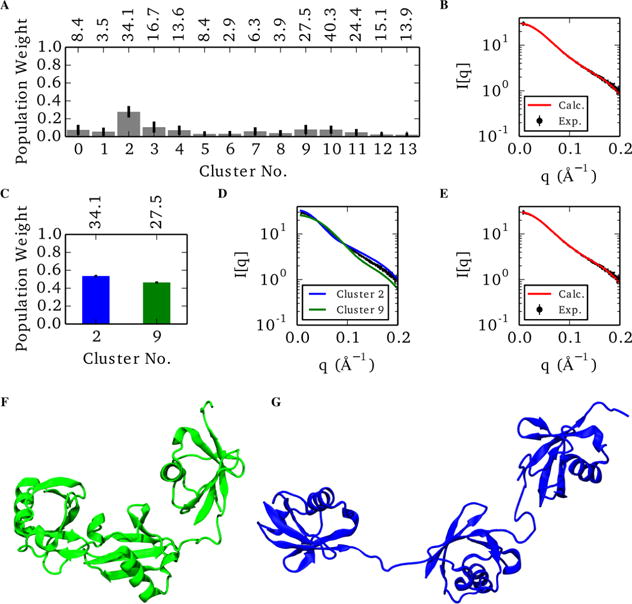
Representative ensemble of the non-native K63 aMD model using the full 14-member scattering basis (A,B) and the best two-state model (C-G). (A) Populations of the individual states of the 14-member model, where error bars indicate the standard deviation of each marginal posterior distribution. Individual goodness-of-fit values are denoted above the corresponding population bar. (B) Comparison of the ensemble averaged scattering profile (red) against the experimental data (black). (C) Relative populations of the best two-state combination with individual ${\chi }_{\text{free}}^2$ values above the plot. (D) Individual scattering profiles of each state. (E) Ensemble-averaged scattering of the two-state model compared with experimental data. (F) Representative member of the compacted cluster. (G) Representative member of the extended cluster.

For the minimal basis size that best fits the experimental data to be determined, all combinations of basis subsets were considered, and the best-fit model qualities from each subset size were compared (Figure 6). The best single-state model had a modest fit to the experimental data with ${\chi }_{\text{free}}^2$ of 2.9. The inclusion of a second conformation drastically improved the fit of our model, lowering the best observed ${\chi }_{\text{free}}^2$ to 0.96 for the combination of clusters 2 and 9. This improved goodness-of-fit was met with a decrease in the AIC value from 14.9 in the single-state to 6.5 in the two-state model, justifying the increase in model parameters. In contrast, the optimum three-state model modestly improved the goodness-of-fit $({\chi }_{\text{free}}^2=0.88)$ but also increased the AIC value to 8.4, suggesting that the benefit of a three-state model in place of the two-state is outweighed by the increase in the number of model parameters. All subsequent basis sizes displayed a consistent increase in AIC value, which suggests that the extra parameters have no beneficial effect on ${\chi }_{\text{free}}^2$ reduction and indicates a substantial degree of overfitting.

Figure 6.

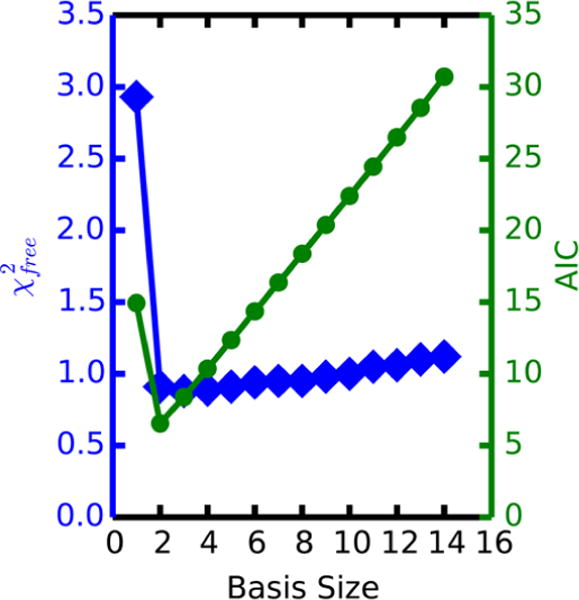
Lowest observed reduced ${\chi }_{\text{free}}^2$ goodness-of-fit (blue) and the corresponding AIC value (green) for each basis subset size in the non-native K63 aMD model. Although the ${\chi }_{\text{free}}^2$ value of a 3-state ensemble is a modest improvement over the 2-state model, the increased AIC value suggests that this is a result of increased overfitting by the 3-state case.

Surprisingly, clusters 2 and 3, the two most populated members in the full basis ensemble, are not the same combination that form the best two-state model. In fact, a two-state fit using only clusters 2 and 3 resulted in a distribution of nearly the entire population into cluster 3 (reduced ${\chi }_{\text{free}}^2=16.7$), which is significantly worse than the best individual scattering state (reduced ${\chi }_{\text{free}}^2=2.9$), the best two-state model (reduced ${\chi }_{\text{free}}^2=1.0$), and the full 14-member model (reduced ${\chi }_{\text{free}}^2=1.12$). Therefore, the 14-state model appears to represent a drastic overfitting of a poor choice in which two states are most important to the net scattering profile.

3.5. aMD Enhances Model Convergence Relative to that of cMD

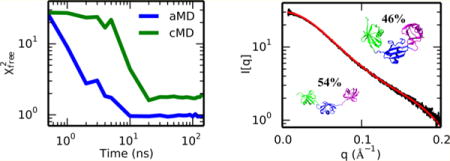
Comparisons of aMD and cMD simulations demonstrate that models generated from the accelerated simulations generally converge to lower ${\chi }_{\text{free}}^2$ values quicker than their corresponding conventional simulations (Figure 7 and Figure S11). In two cases, K11 and K29, the convergence speed and quality of the aMD models are comparable to those produced by cMD. However, these systems also had the best initial fits $({\chi }_{\text{free}}^2\le 2.5)$, suggesting the comparable performance may be due to the overall quality of the initial conformations.

Figure 7.

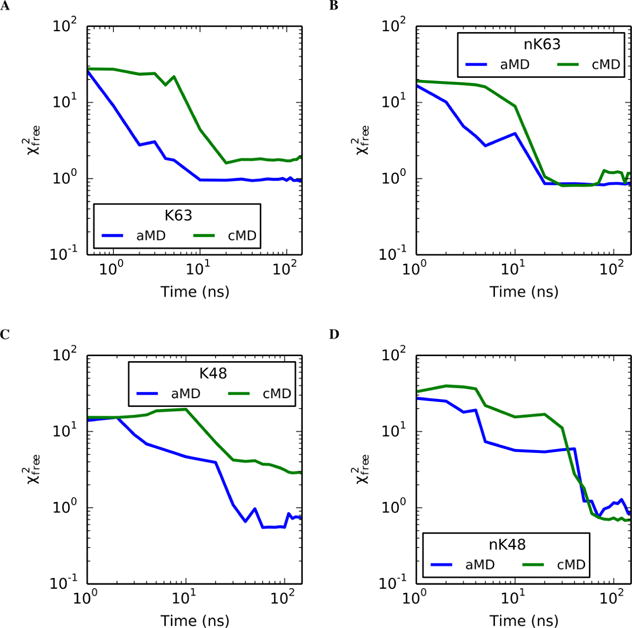
Reduced ${\chi }_{\text{free}}^2$ goodness-of-fit of identified ensembles vs sampling time for aMD (blue) and cMD (green) simulations of (a) non-native K63, (b) native K63, (c) non-native K48, and (d) native K48 linkages. Remaining systems can be found in Figure S11. In the systems presented above, the aMD simulations are the quickest to escape poor initial models, as shown by the more rapid initial decrease in ${\chi }_{\text{free}}^2$ in comparison to the cMD models.

In contrast, the initial K6 model was quite poor $({\chi }_{\text{free}}^2~8)$, and the cMD simulation never converged to an acceptable goodness-of-fit even after 500 ns of simulation (data not shown). However, the aMD simulation converged to an acceptable model $({\chi }_{\text{free}}^2\approx 2.5)$ within roughly 70 ns. Combined with the larger deviations in backbone RMSD values in this regime (Figure S3), this system highlights the ability of aMD to sample a wider variety of conformations. Similarly, the nonnative K48 linkage had a large discrepancy between aMD and cMD models (reduced ${\chi }_{\text{free}}^2$ of 0.7 and 2.8, respectively). The cMD trajectory identified a single state that is more extended (R_g = 24.3 Å) than is suggested by the experimental data (R_g = 22.3 Å). In contrast, the aMD model accurately predicts the molecular size (R_g = 22.4 Å). Given the trend of the convergence time series (Figure 7), the cMD simulation would likely reach an acceptable solution if the simulation times were significantly extended.

Furthermore, SAXS data were gathered for both native and non-native linkages of K48- and K63-linked trimers. In all four systems, the aMD simulations experienced the best initial improvements to the goodness-of-fit, but the native cMD simulations of both linkage sites eventually converged to the best model in the same time scale as their aMD counterparts. On the other hand, the non-native aMD models outperformed the cMD simulations at all time scales. This disparity between native and non-native convergence is likely due to performing a single simulation of each system and not due to any inherent difference between native and non-native linkages.

3.6. Triubiquitin Ensembles Depend on Linkage Type

Models for all seven triubiquitin systems were produced using both aMD (Table 2 and Figures S12–S17) and cMD (Table S2) simulations. Acceptable models $({\chi }_{\text{free}}^2\approx 1.0)$ were found for most systems with the K6-linked cMD simulation having the largest deviation from experimental results at a reduced ${\chi }_{\text{free}}^2$ value of 8.7. Additionally, for all but two systems, model ensemble R_g values were within 1 Å of the experimentally determined R_g values (Table 1). Four of the seven systems were best represented by two-state ensembles, whereas the other three were identified as one-state models.

Table 2.

Summary of the aMD Models for Each System^a

system	weight	Rg (Å)	sep. dist. (Å)	sep. angle (deg)	${\chi }_{\text{free}}^2$
K6	1.00	21.8 ± 0.1	33.4 ± 1.0	79.8 ± 4.8	2.4
K11	0.47	20.7 ± 0.2	27.4 ± 1.1	61.9 ± 3.6	1.8
	0.53	22.5 ± 0.6	35.9 ± 2.9	78.4 ± 8.2	1.8
	1.00	21.7 ± 0.6	31.9 ± 3.1	70.6 ± 8.9	0.7
K29	1.00	24.9 ± 1.5	44.6 ± 5.8	93.4 ± 12.1	0.9
K48	1.00	22.4 ± 0.3	37.1 ± 1.8	86.1 ± 8.9	0.7
nK48	0.11	29.8 ± 0.5	62.7 ± 1.8	130.9 ± 6.0	39.1
	0.89	23.4 ± 0.2	43.3 ± 0.8	111.1 ± 4.2	1.4
	1.00	24.1 ± 0.6	45.3 ± 2.0	113.2 ± 7.3	0.9
K63	0.54	32.6 ± 0.2	68.9 ± 0.4	120.4 ± 0.1	34.1
	0.46	23.3 ± 0.3	41.0 ± 1.5	97.0 ± 8.3	27.5
	1.00	28.3 ± 0.3	56.0 ± 1.6	109.6 ± 8.3	1.0
nK63	0.46	31.7 ± 1.0	69.8 ± 2.8	149.3 ± 8.3	3.5
	0.54	25.8 ± 0.5	51.2 ± 1.9	121.4 ± 4.8	2.3
	1.00	28.6 ± 1.1	59.8 ± 3.4	134.4 ± 9.7	0.9

^aSeparation distances and angles are measured between the centers of masses of the distal groups and using the center of mass of the central member as the vertex. For the K48 and K63 systems, “nK48” and “nK63” denote the trimers with the native isopeptide linkage. cMD models can be found in Table S2.

In the two-state models (K11, nK48, K63, and nK63), the final ensemble is generally composed of an open and compact state with the geometry of each varying based on the linkage. The difference between open and closed conformations is significant in the K63, nK63, and nK48 systems with the closed states possessing R_g of ~25 Å and the open states possessing R_g values between 27 and 32 Å. This range in R_g is a direct result of the separation between distal members with the distal groups separated up to 69 Å in the extended states and compacted as low as 27 Å in the closed state. In the K11 system, the difference between open and compact is more subtle with the open and compact states possessing R_g values of 22.5 and 20.7 Å, respectively. Similarly, the distal groups are separated by 35.9 Å in the open and 27.4 Å in the compact states.

The one-state models show a wide variety of geometries based on linkage type. In K6, the best fitting model possessed an R_g of 21.8 Å and a separation distance of 33.4 Å between distal units. In contrast, the molecular size of the K29-linked system was noticeably larger at an R_g of ~25 Å and distal separation of 44.6 Å.

The non-native K48 linkage was also identified as a single state with an R_g of 22.4 Å and a distal separation of 37.1 Å. As previously mentioned, the native K48 linkage was identified as a two-state model, and both the native and non-native K63 linkages were two-state models as well. A comparison of the experimental SAXS profiles from native and non-native K63 shows nearly identical profiles, whereas the non-native K48 is significantly different from its native counterpart, leading to the differences in identified computational models. Together, these results suggest that the solution ensemble of ubiquitin oligomers may be more affected by non-native linkages at some sites than at others.

4. DISCUSSION

Here, we have developed and applied an ensemble fitting method that utilizes MD simulations to fit experimental SAXS data. One critique of ensemble fitting is the potential of overfitting, where a large number of possible states leads to a better goodness-of-fit primarily by increasing the number of model parameters. However, our iterative Bayesian approach avoids this by not assuming the necessity of a particular population size but instead considering the full permutation of increasing subset sizes. By evaluating the AIC value of each ensemble, models that benefit solely from an increasing parameter space are correctly rejected in favor of smaller population sets, as is shown in the analysis of K63-linked triubiquitin (Figure 6). This ability to consider multistate models is in better agreement with the current understanding of solution ensembles than forcing a single representative fit.

Although this AIC protocol is functional in practice, it is important to note that the identified states are not necessarily representative of the full ensemble. Because of the inherently low resolution of SAXS data, increasing subset sizes may be routinely dismissed as long as the average shape and size of the ensemble is modeled by a combination of fewer members. In the future, the addition of further structural information, such as from FRET or NMR experiments, could be incorporated into the Bayesian likelihood function, and this higher resolution data may better differentiate between essential and trivial additional states.^67–71

This study presents, to our knowledge, the first example of using aMD simulations to rapidly produce atomistic models of experimental SAXS data. In each ubiquitin trimer, the aMD trajectories produced models equal to or better than their cMD counterparts in up to a magnitude less simulation time. This is rooted in the fact that aMD typically supplies not only larger maximum variations in structural RMSDs but also reduces the correlation time by significantly lowering energy barriers between states. However, a wide variety of other possible enhancement methods could be employed to the same end.^{11,12,17,18,72} Nonetheless, many of these methods may require producing multiple copies of the same system that must all be simulated simultaneously or performing simulations over a period of time to compute a history-dependent bias, potentially creating large computational overhead. In contrast, aMD requires no additional system replicas and is straightforward to apply with minimal computational cost.^73,74 Therefore, aMD may act as a user-friendly method for those interested in atomistic SAXS modeling without access to high-performance computing resources.

Our protocol was applied to simulations of seven ubiquitin trimers with varying linkage types. Regardless of one- or two-state models, both aMD and cMD results agree with previous studies that K63-linked oligomers adopt extended conformations in solution in contrast to the typically compacted state of K48-linked polyubiquitin chains.^75–78 In addition, our results for the so-called atypical chains reveal that K6 and K11 trimers favor more compact states,⁷⁹ whereas K29 trimers favor a more open/intermediate state. The biological functions of these atypical chains are not well-characterized, and it has been suggested that there is a built-in redundancy in the recognition and/or signaling of ubiquitin chains.⁸⁰ For example, K48-linked ubiquitin chains are the canonical proteasomal degradative signal, but K11-linked ubiquitin chains can also target substrates to the proteasome in the context of cell cycle progression.⁸¹ As another example, K6- and K63-linked chains are both involved in DNA damage response.⁸² Lastly, K29-linked chains are thought to have roles in both proteasomal degradation signaling and regulation of mRNA stability.^83,84 Thus, it appears that a compact structure does not always lead to one biological function and an open structure to another; thus, there is currently no simple correlation between oligomer compaction and cellular response.

Specific to the role of polyubiquitin chains as proteasomal degradation signals, it has been previously theorized that the tight compaction of K48-linked chains might allow for the formation of octamers that could bridge the ~90 Å distance from ubiquitin receptors Rpn10 to Rpn13 of the 26S proteasome.^85,86 Interestingly, our two-state model of K11-linked trimers identified a state with the same globular size as that of the K48-linked trimer, suggesting that it is possible for homotypical K11-linked octamers to satisfy a similar spatial ensemble as that of the K48 octamer. However, proteasomes are able to distinguish between these two modes of polyubiquitin linkage.⁸⁷ In our K48-linked trimer models, the hydrophobic patch is packaged around the I44 residue of the central and proximal monomers (Figure 8), and the alternative hydrophobic binding site of the I36 patch is exposed.⁸⁸ The opposite scenario is true in one state of our K11-linked model, and the fully compact state of K11 trimers buries all three I36 patch residues while simultaneously exposing all three I44 patch residues. Indeed, domains have been observed to bind selectively with these two sites,⁸⁹ and their differing levels of exposure likely contribute to the disparate modes of interactions between K11- and K48-linked polyubiquitin chains and the proteasome.

Figure 8.

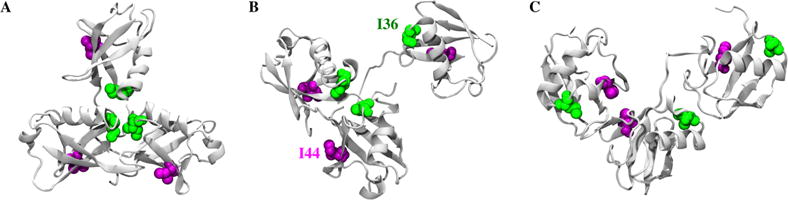
Orientations of I36 (green) and I44 (purple) hydrophobic residues in the (a) closed K11-trimer state, (b) open K11-trimer state, and (c) K48-linked trimer model. Although both the open K11 and K48 configurations display similar levels of compaction according to R_g, they expose different access to the hydrophobic patch: I44 in K11 and I36 in K48. Furthermore, the highly compacted K11 state buries all three I36 moieties into the same region, thus exposing all three I44 moieties. The deviations in modes of hydrophobic exposure may contribute to the binding disparities of K11- and K48-linked polyubiquitin chains with both proteasomes and deubiquitinating enzymes.

The overall varying degree of flexibility associated with each different linkage is also likely the major contributing factor to their biological roles.^80,87,90,91 The dynamic nature of ubiquitin chains that can allow their recognition by numerous protein partners is perhaps dictated by the linkage position. Comparison of our models of native isopeptide and non-native thiolene linkages suggest that certain positions (i.e., K48) may be significantly more affected by the local chemistry of the linkage than others (i.e., K63). Some of these effects may be more apparent in trimers than dimers,³⁵ and these differences may propagate in longer polyubiquitin chains into effects that are significant enough to be discerned by the relatively low-resolution SAXS observations. The methodology developed in this study is primed for investigating longer ubiquitin chains as well as more complex ubiquitin systems including ubiquitin chains bound to receptor proteins, mixed chains, and branched chains, among others, in an effort to better understand the complex role of ubiquitin chain function in cells.