Optimization of digital breast tomosynthesis (DBT) acquisition parameters for human observers: effect of reconstruction algorithms

Abstract

We showed in our earlier work that the choice of reconstruction methods does not affect the optimization of DBT acquisition parameters (angular span and number of views) using simulated breast phantom images in detecting lesions with a channelized Hotelling observer (CHO). In this work we investigate whether the model-observer based conclusion is valid when using humans to interpret images. We used previously generated DBT breast phantom images and recruited human readers to find the optimal geometry settings associated with two reconstruction algorithms, filtered back projection (FBP) and simultaneous algebraic reconstruction technique (SART). The human reader results show that image quality trends as a function of the acquisition parameters are consistent between FBP and SART reconstructions. The consistent trends confirm that the optimization of DBT system geometry is insensitive to the choice of reconstruction algorithm. The results also show that humans perform better in SART reconstructed images than in FBP reconstructed images. In addition, we applied CHOs with three commonly used channel models, Laguerre–Gauss (LG) channels, square (SQR) channels and sparse difference-of-Gaussian (sDOG) channels. We found that LG channels predict human performance trends better than SQR and sDOG channel models for the task of detecting lesions in tomosynthesis backgrounds. Overall, this work confirms that the choice of reconstruction algorithm is not critical for optimizing DBT system acquisition parameters.

1. Introduction

DBT is an x-ray breast imaging modality with limited angular span and number of views (Baker and Lo 2011, Sechopoulos 2013a, Sechopoulos 2013b). The design of the system acquisition geometry determines the system's ability to transfer information in the scanned object to the data, fundamentally determining system performance. Efforts to optimize system acquisition geometry for diagnostic image quality of the reconstructed DBT images have been reported (Chawla et al 2009, Reiser and Nishikawa 2010, Lu et al 2011, Young 2012, Mitchell et al 2014, Chan et al 2014). As various reconstruction algorithms have been developed for DBT, it is desirable to know whether the use of a different reconstruction algorithm would alter the optimal geometry associated with the current algorithm. We have previously investigated this problem by conducting an in silico imaging trial with digital breast phantoms, simulated DBT system with various reconstruction algorithms, and a computational model observer for image quality evaluation (Zeng et al 2015). System optimization was based on lesion detectability in a location-known task for a Laguerre–Gauss (LG) channelized model observer (CHO). The major finding was that the performance trends as a function of acquisition parameters were consistent among the reconstruction algorithms being investigated, indicating that the choice of reconstruction algorithm was not critical for system acquisition optimization. This finding suggests that optimization of system geometry and reconstruction algorithm can be done separately, which can be helpful to developers in that geometry optimization does not have to be repeated for a different reconstruction algorithm or for each update to a reconstruction algorithm.

It is important to note that the previous finding was based on LG-CHO, known to be an efficient model observer under certain assumptions. In other words, this observer utilizes all information in an image to determine the lesion probability score. When a human observer reads an image, not all the information may be effectively utilized toward the decision making process, such as the low- and high-frequency components not well perceived by humans. In current clinical practice DBT images are mainly interpreted by radiologists. It is therefore desirable to validate whether the model observer finding of our previous work predicts the results for the same study if it were performed with human readers. The goal of this study is for such a validation. Particularly, we use the previously generated DBT images with varying geometry settings in conjunction with two reconstruction algorithms and ask readers to score the images based on a lesion detection task. Lesion detectability under each imaging condition is calculated from the scores. The detectability curves as a function of the acquisition parameters are compared between the reconstruction algorithms to study whether the performance trends are consistent, similar to those found in our previous work.

In addition, we are interested in comparing performance trends of human readers with CHO making use of LG channels and two other commonly used anthropomorphic channels. Research in the literature has shown good ability by CHOs for predicting human performance in detecting round signals in lumpy backgrounds or uniform CT backgrounds (Abbey and Barrett 2001, Gallas and Barrett 2003, Leng et al 2013, Yu et al 2013, Yi et al 2014, Eck et al 2015). However, evidence on how well these CHOs predict human performance in breast tomosynthesis backgrounds is lacking. As the potential for greater reliance on in silico clinical imaging trials with model observers as a major component increases, developing confidence on the use of model observers in such studies is needed. The work we present in this paper will constitute another step toward the acceptance and increased use of computational reader models for the evaluation of DBT systems (Ikejimba et al 2016, Gifford et al 2016).

2. Methods and materials

2.1. DBT images

We used previously generated DBT images (Zeng et al 2015). Here we give a brief description of how the DBT phantom images were obtained. First, compressed breasts with a thickness of 5 cm were simulated using the breast phantom creation software developed by Bakic et al (2011). The phantoms contained basic breast anatomy components including skin, adipose tissue, glandular tissue and Cooper's ligaments with randomized internal structure for each realization. Lesion-present breast phantoms were simulated by inserting 8 spheres of 4 mm diameter. A total of 30 lesion-present and 30 lesion-absent breast phantoms were created. Second, the breast phantoms were passed to a virtual DBT scanner to generate projection images. Settings of varying angular span and number of projection views were used to create data to support four optimization scenarios: optimizing angular span for 5 views, optimizing angular span for 9 views, optimizing number of views for angular span of 20° and optimizing number of views for angular span of 50°. For the scenario of optimizing angular span, the angular span ranged from 10° to 70° with an increment of 10°. For the scenario of optimizing the number of views, the number of views ranged from 3 to 15 with an increment of 2. The total exposure was kept constant among the varying geometry settings. Finally, the projection views were reconstructed into DBT image slices with several reconstruction methods, including FBP, SART, maximum likelihood reconstruction (ML), and total-variation regularized reconstruction (TV). The reconstructed DBT volumes had a voxel size of 125 micron × 125 micron × 1 mm. See figure 1 for some sample slices.

Figure 1.

Examples of DBT volumes reconstructed with (a) FBP and (b) SART.

The major goal of this study is to determine whether the choice of reconstruction algorithm affects the optimization outcome differently for human readers than for models found in our previous study. It is not a significant challenge for a model observer to evaluate the image quality for all those imaging settings, but for human readers a study of this size is difficult because of the large number of images to read for each system geometry and reconstruction algorithm combination. Therefore we selected two optimization scenarios for the reader study for demonstration purpose: one for optimizing the angular span at 9 views and one for optimizing the number of views at 20° angular span. We further decreased the amount of data by half by considering the angular spans of (10°, 30°, 50°, 70°) for the 9-view scenario and the number of views of (3, 7, 11, 15) views for the 20°-span scenario. This decrease of system parameter values preserved our ability to compare the model and human performance trends as we still had sufficient samples in the performance space for this purpose. Although originally there was data from four types of reconstruction algorithms, we selected only two, FBP and SART, to represent the analytical and the iterative types exhibiting the largest difference in image appearance.

In summary, DBT phantom images from 8 geometrical settings and 2 reconstruction algorithms, totaling 16 imaging conditions, were used in the human reader study. There were 30 lesion-present and 30 lesion-absent phantom DBT images for each condition, each containing 8 ROIs for the purpose of reader scoring.

2.2. Reader study

2.2.1. Image preparation: removal of extremely easy ROIs

Regions of interest (ROI) of size 241 × 241 pixels (30 mm × 30 mm) were cropped from each phantom volume corresponding to the locations where lesions were placed. Eight ROIs were cropped from each breast phantom volume for a total of 240 pairs of lesion-present and lesion-absent ROIs. Among the 240 pairs, the extremely easy ROIs were not used to save reading time and improve study power—these cases would not contribute to differentiating the lesion detectability for the various geometry settings. ‘Easy cases’ refer to locations surrounded mostly by adipose tissue where a lesion would be easily detected due to the good contrast between lesion and adipose tissue. Alternatively, a lesion would be harder to detect if surrounded by a large amount of glandular tissue because the intensity values between lesion and glandular are very similar. Therefore, case difficulty level is correlated with local glandular density, i.e. the amount of glandular tissue in the background around the location. Local glandular density can be estimated as the sum of intensity values of voxels within a small volume around the location in the object space (the digital phantom before being imaged). We used a volume that was 4 mm wide in-plane and 2 mm thick around a location for computing this quantity. The images in figure 2 illustrate that the visibility of lesions decreases with the sum-of-intensity values of the VOI surrounding its center location. After an ascending ordering of the difficulty level, the 90 lesion-present ROIs with levels in the range (151:240) and the 100 lesion-absent ROIs in (141:240) were included in the study.

Figure 2.

Images of lesion-present ROIs extracted from reconstructed DBT slices. Case difficulty level increases from left to right according to the sum-of-intensity values. All the images were from a scanning geometry of 20° and 3 views, which had the least number of views and the narrowest angular span, representing the worst scan geometry of those simulated in this study.

2.2.2. Reader scoring

The reader's task was to determine on each trial whether there was a lesion at the center of an ROI and to provide a score (0–6) of the confidence level for lesion presence. A score of 0 corresponded to the lowest and 6 the highest confidence of a lesion at the center of the image. We are aware that this simplified detection task design may not necessarily represent how the DBT images are used by radiologist, since a clinical task can be more complicated involving an exploration of multiple slices around the lesion focal slice and may be combined with the reading of a mammography image or a synthetic 2D mammographic view. However, the main purpose for this study is to examine the effect of the choice of reconstruction algorithm on DBT system optimization. We believe that such a simplified task that is well established in the literature is suitable to use to measure the image quality for our study purpose.

Before scoring the selected images, readers were instructed to use the contrast and edge features to help with their scoring decision. Readers were trained with 30 images (different from those selected in the reader study) to get familiarized with the lesion appearance and the scoring interface. The scoring interface included a 3-step decision-making process to help readers to start from a rough decision and then further refine their decision to arrive at a final score. As illustrated in figure 3, at Step 1, if the reader was very sure of lesion-absent or lesion-present, he/she clicked the corresponding buttons and completed the image scoring process; otherwise, he/she clicked the ‘Less sure’ button and proceeded to Step 2. At Step 2, the reader was asked whether his/her decision tended toward ‘YES’ or ‘NO’ of a lesion being present, clicking either button leading to Step 3. At this last step, the reader was asked to further refine the corresponding confidence levels of this uncertainty: 3 levels for ‘toward YES’ and 2 levels for ‘toward NO’. We believe that the use of such a step-wise scoring strategy helps readers to be more consistent when assigning scores to the images.

Figure 3.

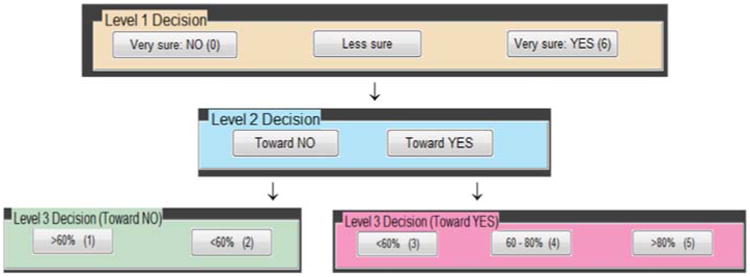
The 3-step scoring interface.

All the reading sessions were conducted in a dedicated display evaluation laboratory. An R31 calibrated monitor (RadiForce R31, EIZO, Cypress, California) was used in DICOM GSDF mode. Indirect ambient lighting was less than 10 lux at the front of the display device. Readers were not able to adjust the image display window/level, which was predetermined based on the overall intensity range of the image set in the corresponding modality.

We recruited 9 readers. None of the readers were radiologists since this was a relatively simple detection task using simulated images. The study was performed in two stages. First, 3 readers performed 16 reading sessions corresponding to the entire 16 imaging and reconstruction conditions. Each session included 90 signal-present images and 50 signal-absent images with the highest difficulty level. After the first 3 readers completed their readings, we realized that the workload of 16 sessions was demanding. Therefore, for the 6 readers we recruited for the second stage, we asked them to perform 8 reading sessions covering one optimization scenario with the two reconstruction algorithms. However, 50 more signal-absent images were included in each session for this stage. The signal-present images were kept the same. Therefore, we have 6 sets of reader scores for each optimization scenario. Table 1 summarizes the reader-session arrangement for the 9 readers. The session order was random for each reader. Readers read at most two sessions in one week.

Table 1.

Reader-session table for the two optimization scenarios: (a) optimizing angular span at 9 projection views; (b) optimizing number of projection views at 20° angular span.

(a) Scenario 1: optimizing angular span	9 projection views, FBP				9 projection views, SART
	10°	30°	50°	70°	10°	30°	50°	70°
Readers	R1, R2, R3, R4, R5, R6				R1, R2, R3, R4, R5, R6
(b) Scenario 2: optimizing number of views	20° angular span, FBP				20° angular span, SART
3 views	7 views	11 views	15 views	3 views	7 views	11 views	15 views
Readers	R1, R2, R3, R7, R8, R9				R1, R2, R3, R7, R8, R9

2.3. Model observers

Channelized model observers (CHO) with three types of channels were selected for this study: Laguerre–Gauss (LG) channels (Gallas and Barrett 2003), square (SQR) channels and sparse difference-of-Gaussian (sDOG) channels (Abbey and Barrett 2001). The LG-CHO represents efficient channels for this detection task while the other two represent anthropomorphic channels. The expressions of the three channel functions are given below in table 2. The parameters for each of the channel function were as follows. For the LG channels, the width parameter was 2 mm (matching the radius of the signal) and the number of channels was 6. These parameter values were found to be optimal in our previous study (Zeng et al 2015). For the SQR and sDOG channels, there are parameters that control the starting frequency and the frequency bandwidth for each channel. These parameters were slightly tuned starting from the values used in Abbey and Barrett (2001) to have similar detectability as human readers at one particular imaging condition (9 view and 10° span, SART reconstruction). Specifically, a₀ = 0.0103 and a = 2.1 for the SQR channels. a₀ = 0.011, a = 1.67 and Q = 1.67 for the sDOG channel. Definitions of the channel function parameters are described in table 2.

Table 2.

Expressions of the three channel functions.

Channel name	Expressions of the channel function
Laguerre-Gauss (LG)	$U_j(r|a)=\frac{\sqrt{2}}{a}{\mathrm{e}}^{-\frac{\pi r^2}{a^2}}{L}_j(\frac{2\pi r^2}{a^2}),$, with the Laguerre polynomial function $L_j(x)={\sum }_{i=0}^j{(-1)}^i\left(\begin{array}{c}j\\ i\end{array}\right)\frac{x^i}{i!}$
Square (SQR)	$C_j(\rho )=\{\begin{array}{cc}0& \text{for}\rho \le {\rho }_0{a}^{j-1}\\ 1& \text{for}{\rho }_0{a}^{j-1}<\rho \le {\rho }_0{a}^j\\ 0& \text{for}\rho >{\rho }_0{a}^j\end{array}$
Sparse difference of Gaussian (sDOG)	$C_j(\rho )={\mathrm{e}}^{-\frac{1}{2}{\left(\frac{\rho }{Q{a}_j}\right)}^2}-{\mathrm{e}}^{-\frac{1}{2}{\left(\frac{\rho }{a_j}\right)}^2}\text{with}{a}_j=a_0{a}^j$

Each model observer was trained with 85 pairs of signal-present and signal-absent ROIs to obtain estimates of the signal mean and data covariance. Recall that as described in section 2.2.1 easier ROIs (150 signal-present and 140 signal-absent ROIs) were discarded for the reader study because they would not contribute to the differentiation of the geometries being tested. However, these ROIs were used to train the model observers. After training, the model observers were applied to the same image sets included in the human reader study to obtain a probability score for each image.

2.4. Data analysis

2.4.1. ROC Data analysis

For human and model observers, AUC was calculated based on their scores for the images included in each session. Mean and variance of AUC were also evaluated. For human AUC, the mean and variance were estimated from 6 readings provided by the 6 available readers, as listed in table 1. For model observers, the mean and variance was estimated from 10 different training sets, each containing randomly selected ROIs from the entire training data. Sub-data ROC analysis was conducted on the human readings to check the impact of case difficulty on system optimization. This analysis was done by re-computing an AUC using scores of the most difficult 50 signal-present cases together with all the scores of the signal-absent cases in each reading session.

2.4.2. Correlation analysis

Since this work focuses on the agreement in performance trends between reconstruction algorithms rather than on absolute performance levels, we used Spearman's rank order correlation to analyze agreement. The value of this metric ranges in (−1, +1), with −1 indicating fully opposite rank and +1 indicating identical rank between the two sets of performance values being compared. The final metric was the averaged correlation coefficient value over the two optimization scenarios considered in this study.

Similarly, we analyzed the agreement between model and human observer results to quantify which models better predicted human performance trends. Since there were four combinations of optimization scenario and reconstruction algorithm, the final metric was an average over four correlation coefficient values.

3. Results

3.1. Human reader performance

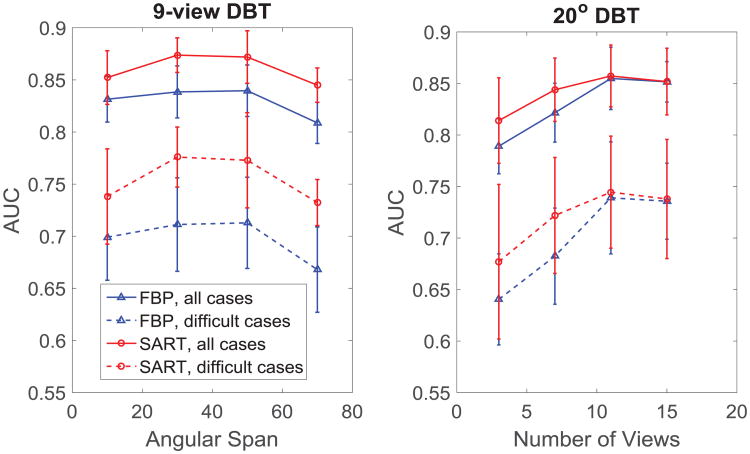
Figure 4 shows the readers' average AUC curves for the two optimization scenarios associated with FBP and SART reconstruction. Overall, the detectability is higher for SART than for FBP, indicating that SART was better at presenting perceptual information for the human visual system. However, when comparing optimization curves' trends, the use of FBP and SART reached similar optimal operating points. For example, for the simulated 9-view DBT system the optimal angular span is between 30° and 50° to detect the simulated lesions and for the 20° DBT system the optimal number of projection views is between 12 and 16.

Figure 4.

Reader performance curves for optimizing the 9-view DBT and the 20° DBT systems using the FBP and SART reconstructed images. The performance trends are similar between the two reconstruction algorithms in both optimization scenarios.

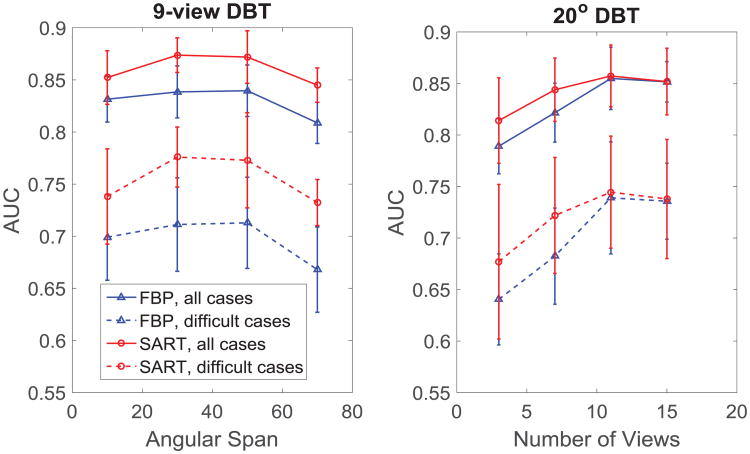
Figure 5 shows the sub-data ROC analysis results related to case difficulty. As expected, AUC decreases when difficult cases were used. However, the performance trend was not affected by case difficulty. Notice that the performance gap between SART and FBP curves became larger with case difficulty. However, in terms of system geometry optimization, the two reconstruction methods reached similar optimal operating points irrespective of case difficulty.

Figure 5.

The effect of Case difficulty on reader's performance. The increase of case difficulty decreases the performance however the performance trends did not change.

3.2. Model observer performance

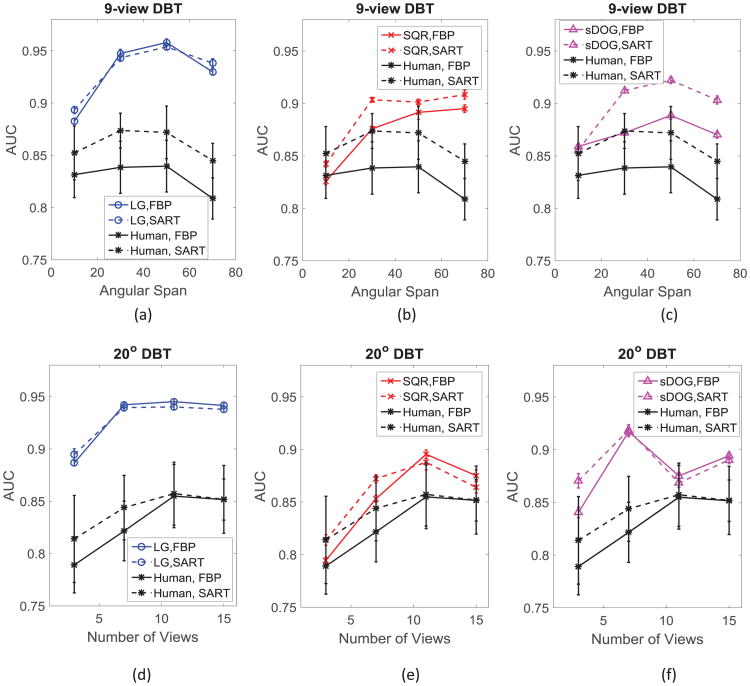
Figure 6 shows the performance curves of the three types of model observers (LG, SQR, sDOG) along with the human results. The performance trends appear to be different among the three types of models, but in general the AUCs in these curves start low, then climb up and end with a drop or a saturated level as the angular span or the number of views increases. The up-and-down of AUC as a function of the acquisition parameters refects the image resolution and noise tradeoff associated with the change of scan geometry. For example, when the number of views is fixed, increasing the angular span can lower anatomical noise, i.e. reduces the overlap of anatomical structures from the adjacent slices, but as the angular span becomes too large the in-plane resolution will be sacrificed. Therefore, there exists an optimal angular span associated with a certain number of views. Similarly, when the angular span is fixed, increasing the number of views improves the in-plane resolution but at the same time the images will contain higher quantum noise under the condition of constant total exposure. We notice in figure 6(f) that the AUC of sDOG CHO drops after 7 views, earlier than the other two channel models and human readers, resulting in a different ranking of the number of views. A possible reason for this earlier drop of AUC is that the selected sDOG CHO does not effectively utilize the relatively higher frequency information in the data that is transferred to the DBT images by the use of a larger number of views as the other observers do.

Figure 6.

Performance curves as a function of angular span (upper row) and as a function of number of views (bottom row) of the three model observers: LG (a) and (d), SQR (b) and (e), and sDOG (c) and (f). The corresponding human's performance curves are showed in each plot for easy comparison.

Although differences exist among the performance trends of the three model observers, when comparing the FBP and SART reconstruction algorithms within each individual type of model observer, the performance trends as a function of angular span or number of views are consistent, confirming that optimization of the acquisition geometry is insensitive to the choice of reconstruction method for this task. It can be seen from figures 6(a) and (d) that the AUCs associated with the LG-CHO are very close between FBP and SART. However, when using SQR and sDOG, the AUC differences between the two reconstruction algorithms for the same geometry setting are larger, similar to the magnitudes of differences in human readings, as seen in figures 6(b)–(e) and (f). In general, both human and anthropomorphic CHO (SQR and sDOG) performed better with SART than with FBP. For LG-CHO, there was no significant difference in performance with reconstruction algorithm as the curves associated with the two reconstructions are similar.

3.3. Spearman's rank order correlation analysis

Table 3 reports Spearman's rank order correlation coefficient between FBP and SART reconstructions. High correlations (none smaller than 0.9) were found between the performance associated with FBP and SART for all observers. The analysis confirms that the choice of reconstruction algorithm is not critical for optimizing DBT acquisition parameters.

Table 3.

Spearman's rank order correlation coefficients between the performance curves associated with FBP and SART reconstruction.

Observers	Human	LG	SQR	sDOG
Correlation between FBP and SART	0.9	1	0.9	0.9

Table 4 reports Spearman's rank order correlation between model and human observers. The correlations are 0.75, 0.35, and 0.3 for the LG, SQR and sDOG respectively. This indicates that the performance of the LG-CHO correlates with human's performance better than SQR and sDOG for this lesion detection task.

Table 4.

Spearman's rank order correlation coefficients between the model observers and human readers.

Observers	LG	SQR	sDOG
Human readers	0.75	0.35	0.3

4. Discussion

In silico clinical trials are attracting increasing attention in the biomedical field (Viceconti et al 2016). The AAPM task group TG234 on virtual tools for the evaluation of new 3D/4D x-ray breast imaging systems (Bakic et al 2013) and TG195 on Monte Carlo reference data for imaging research (Sechopoulos 2015) are two efforts that promote the advancement of tools and consensus on virtual clinical trials in medical imaging. The Food and Drug Administration also initiated the medical device development tools (MDDT) program to qualify tools that medical device manufacturers can in turn use in generating evidence for the regulatory evaluation of medical devices (C.f.D.a.R.D. US Food and Drug Administration 2013). Well-designed simulation studies together with validated modeling tools are essential aspects for an in silico imaging trial to yield reliable and useful conclusions on the device properties and to provide guidance to the planning of efficient and cost-effective clinical studies.

Our previous study using simulated DBT images and an LG-CHO model observer to test the impact of reconstruction algorithms on system optimization (Zeng et al 2015) falls in the in silico clinical trial framework. In this work, we conducted a human reader study to validate the model observer results in the previous study. We selected a subset of the images in the previous study and recruited nine human readers to score the images based on a location-known lesion detection task. The results show that the ranking of system geometry settings is consistent between the two different reconstruction algorithms, FBP and SART, confirming the findings of our previous LG-CHO based study. In addition, we applied two other types of anthropomorphic CHOs with SQR and sDOG. The use of SQR and sDOG CHOs also demonstrates the consistency of performance trends as a function of acquisition parameters between FBP and SART reconstructions. However, we should be aware that the lesion-detection task in this study mainly tests the system performance for lower frequencies. As we have discussed in the previous study (Zeng et al 2015), for high-frequency related tasks like micro-calcifcation detection and shape discrimination, the optimal system settings may be different and the effect of reconstruction algorithms may need to be re-evaluated.

There are some interesting observations to be made from a comparison of the three CHOs with human readers. First, in terms of performance trends as a function of acquisition parameters, the LG-CHO best agrees with human performance trends. Along the x-axis in our performance plots, both noise and resolution properties of the imaging systems are changing. The LG-CHO adapts for such changes in an efficient way enabled by two aspects. One is the capability of the LG basis function to efficiently model the features in the simulated signal and background. The other is the mechanism of CHO to maximize the signal detectability by optimally utilizing the first- and second-order image statistics (Barrett and Myers 2004, ch14). Our data indicate that in a similar way, humans adjust for changes in noise and signal appearance since human results are highly correlated with LG-CHO results. This may serve as supporting evidence for the utilization of this efficient model observer in optimizing DBT acquisition geometry for similar tasks in which the signal is approximately rotationally symmetric and the background texture has no orientation preference. Second, in terms of the performance differences between reconstruction algorithms, the LG-CHO performs equally with FBP and SART reconstructed images. However, the SQR and sDOG CHOs perform better with SART images than with FBP images, which agree with the difference of performance presented in human readers with the two reconstruction algorithms. This finding suggests that to optimize DBT reconstruction algorithms for human perception, using anthropomorphic CHOs may facilitate the differentiation among algorithms. However, this does not imply that LG-CHO is not suitable for evaluating reconstruction algorithms. The main reason that the LG-CHO did not show a difference between reconstruction algorithms could be attributed to the fact that the task was easy for the LG-CHO (AUC values approximately or above 0.9). We believe that for more difficult tasks either with weakened signal strength or by changing to a location-unknown task, LG-CHO may also differentiate the performance of the two reconstruction algorithms, as shown in He et al (2016).

How to choose the parameter values of channel functions is an important component in model observers. LG channels are an efficient type of channels. The LG-CHO channel parameters in this work were chosen to provide optimal detectability. The Width parameter was selected to match the signal size and the number of channels was such that using more channels would not further improve detectability. We determined the LG parameters this way in our previous study (Zeng et al 2015) and used the same parameter values in this work. The SQR and sDOG CHO make use of anthropomorphic channel types. Their channel parameters are supposed to determine a performance that approximates that of humans. We started with the parameter values used in Abbey and Barrett (2001), tuned the values to match the human detectability at one particular imaging condition and then fixed the parameter values for all other conditions. The condition we used to tune the SQR and sDOG was the 9-view 10°-span geometry with SART reconstruction, as can be seen from the relatively well matched points between human and model observers in figures 6(b) and (c).

In Abbey and Barrett (2001), the parameters for SQR were a₀ = 0.015 and a = 2.0, and for sDOG were a₀ = 0.015, a = 2.0 and Q = 2.0. In addition, internal noise was added to bring performance down to match that of humans. In our case, if we had used the values in Abbey and Barrett (2001), the detectabilities would be substantially lower than those of human readers. Therefore, we tuned the channel's starting frequency and the frequency bandwidth parameters to increase detectability without adding internal noise. We arrived at parameter values for SQR a₀ = 0.0103 and a = 2.1, and for sDOG a₀ = 0.011, a = 1.67 and Q = 1.67. We found that we needed to move the starting frequency closer to 0 to achieve similar detectability as that of humans for the condition we chose to match. The task in Abbey and Barrett (2001) was to detect a Gaussian signal in a lumpy background while the task in our work is to detect reconstructed spherical lesions in breast tomosynthesis backgrounds. Different parameter values had to be used in these two tasks to match the level of human performance, indicating that there are no universal parameter values for SQR and sDOG channels to model human detect-ability in different tasks. The anthropomorphic channel parameters need to be tuned again for detecting lesions in a different type of background to match human performance. Furthermore, the choice of which human data point we tune the model observer to may impact the overall performance curve for the model observer; it is not known whether the model observer performance curve will shift up or down uniformly or transform in some fashion. Further research is needed to better understand the impact of the anthropomorphic channel tuning process on model observer performance trends with imaging and reconstruction parameters as they change the noise and resolution properties of the imaging system. All this means that the tuning of anthropomorphic channel parameters is not trivial. In contrast, the process of determining efficient channel parameters can be purely based on the signal and image data. Moreover, efficient channels like LG usually provide relatively stable performance and good correlation with human performance trends as shown in this work and others (Ikejimba 2016). Therefore, we believe that model observers with efficient channel types are a reasonable and attractive choice in virtual DBT imaging trials over anthropomorphic channel types.

5. Conclusion

The main purpose of this work was to validate our earlier finding that the choice of reconstruction algorithm has minimal impact on the optimization of DBT system geometry. In our previous work, an LG-CHO model observer was used to optimize the system in terms of detecting a 4 mm lesion in simulated breast tomosynthesis backgrounds. In this paper, we conducted a human reader study for optimizing the DBT acquisition parameters (number of views and angular span) associated with two different reconstruction algorithms (FBP and SART). Our results show that the optimal geometry settings for humans agree between the two different reconstruction algorithms, as found in the previous study for the LG-CHO model observer. In addition, a comparison of the performance trend based on Spearman's rank order correlation indicates that the LG-CHO better predicts human reader performance trends compared to SQR and sDOG CHOs for detecting lesions in simulated breast tomosynthesis backgrounds. Most importantly, this work provides additional confidence to performing optimization of system geometry settings independently of the choice of DBT reconstruction algorithm.