Abstract
We investigated how kinematic redundancy interacts with the neurophysiological control mechanisms required for smooth and accurate, rapid limb movements. Biomechanically speaking, tendon excursions are over-determined because the rotation of few joints determines the lengths and velocities of many muscles. But how different are the muscle velocity profiles induced by various, equally valid hand trajectories? We used an 18-muscle sagittal-plane arm model to calculate 100,000 feasible shoulder, elbow, and wrist joint rotations that produced valid basketball free throws with different hand trajectories, but identical initial and final hand positions and velocities. We found large differences in the eccentric and concentric muscle velocity profiles across many trajectories; even among similar trajectories. These differences have important consequences to their neural control because each trajectory will require unique, time-sensitive reflex modulation strategies. As Sherrington mentioned a century ago, failure to appropriately silence the stretch reflex of any one eccentrically contracting muscle will disrupt movement. Thus, trajectories that produce faster or more variable eccentric contractions will require more precise timing of reflex modulation across motoneuron pools; resulting in higher sensitivity to time delays, muscle mechanics, excitation/contraction dynamics, noise, errors and perturbations. By combining fundamental concepts of biomechanics and neuroscience, we propose that kinematic and muscle redundancy are, in fact, severely limited by the need to regulate reflex mechanisms in a task-specific and time-critical way. This in turn has important consequences to the learning and execution of accurate, smooth and repeatable movements—and to the rehabilitation of everyday limb movements in developmental and neurological conditions, and stroke.
Keywords: kinematic redundancy, eccentric contractions, muscle mechanics, movement, limb kinematics
Introduction
The pursuit of, say, the perfect basketball free throw relies heavily on practice. Yet only those of us capable of consistently accurate throws can be paid millions of dollars as elite athletes. But why is it that practice or mimicry alone do not suffice to accomplish a professional level of accuracy and repeatability? In recent work, we re-emphasized that the neural control of limb movements is in fact over-determined, where the rotations of a few joints determine length changes in many muscles (Valero-Cuevas, 2015; Valero-Cuevas et al., 2015). While some muscles that are shortening during the movement can, of course, become lax, those that are lengthening must all do so by a prescribed amount.
As pointed out by Sir Charles Sherrington (Sherrington, 1913), movement can be disrupted if even one muscle undergoing eccentric contraction fails to silence its stretch reflex appropriately. Sherrington spoke of reflex inhibition being an important factor in the coordination of movement and posture, where the inhibitory process is no less capable of delicate quantitative adjustment than the excitatory process (Sherrington, 1932). This idea was later refined by a cohort of scientists (for overviews see Loeb (1984) and Prochazka et al. (1985)) as the explicit and context-dependent regulation of the fusimotor, or γ, system to control muscle spindle sensitivity independently of α-motoneuron drive. For a few decades now, it has been well accepted that the modulation of spinal reflexes, including the inhibition of stretch reflexes, is an intrinsic and necessary feature of the neural control of force, posture, and movement; and often a neurophysiological mechanism responsible for pathological disruptions such as spasticity and clonus (Zehr and Stein, 1999; Hultborn, 2006; Hidler and Rymer, 1999; Sanger et al., 2010). But the question remains: how accurately must spinal reflexes be modulated in natural movement?
Here we investigate the neuromechanical relationships between kinematic redundancy and muscle contraction velocities—and explore its consequences to muscle afferentation. Specifically, given that tendon excursions are over-determined, we calculate the different muscle velocity profiles induced by different, but equally valid, hand trajectories for a basketball free throw. This serves as the neuromechanical foundation to discuss how kinematic and muscle redundancy are, in fact, severely limited by the need to regulate reflex mechanisms in a task-specific and time-critical way. We conclude by discussing how these fundamental neuromechanical concepts have important neurophysiological consequences to the learning and execution of accurate, smooth, and repeatable athletic movements—and to the disruption and rehabilitation of everyday movements in neurological conditions and stroke.
Methods
The goal of our study was to determine whether and how different movement trajectories that meet the initial and final conditions for a successful free throw produce differences in muscle contraction velocities.
0.1. Arm kinematic model
We used an 18-muscle sagittal-plane arm model with 3 degrees of freedom (DOF; shoulder, elbow, and wrist joints) to calculate a family of 100,000 valid basketball free throws with different hand trajectories—but identical initial and final hand positions and velocities. The free throw motion is approximated by a planar 3-DOF model. While studies have shown that basketball players typically keep the ball, wrist, elbow, and shoulder in plane with the basket (Knudson, 1993), this purely kinematic model does not include the neuromuscular control needed to produce such planar movement. Anthropometry was used to estimate physiologically-reasonable upper-limb segment lengths for a hypothetical 183 cm tall (6 ft) basketball player throwing from the free throw line (Winter, 2009) and the forward kinematic (i.e., geometric) model of the arm was defined as
| (1) |
where the vector θ⃗ = (θ1, θ2, θ3)T contains the three arm joint angles for sagittal-plane shoulder rotation (θ1), elbow flexion/extension (θ2), and wrist flexion/extension (θ3)1. The upper-arm, forearm, and hand segments are denoted by link lengths l1, l2, and l3, respectively. This full geometric model of the limb in the sagittal plane specifies the horizontal (Gx) and vertical (Gy) position of the endpoint of the hand with respect to the shoulder joint, as well as the sum of all angles relative to rest (Gα) (Valero-Cuevas, 2015). This is because a rigid body (i.e., the hand) has three degrees of freedom on the sagittal plane: two positions, Gx and Gy, and one orientation, Gα.
0.2. Definition of initial and final arm postures, and hand positions and velocities
Initial and final arm postures for the model, θ⃗i and θ⃗f, were set to equal the averaged measurements from three sample free throw motions. Passing these joint angles through Eq. 1 generate initial and final hand endpoint positions, and As free throws begin from rest, the initial endpoint velocity is zero. Free throws are simple ballistic shots, and therefore the final endpoint velocity, v⃗f = (vx, vy)T, was set to the release velocity vector of the basketball necessary for a successful throw (See Figure 2 for detailed formulation). Illustrated in Figure 3(a), the initial and final arm positions and velocities are therefore defined as:
| (2) |
| (3) |
| (4) |
| (5) |
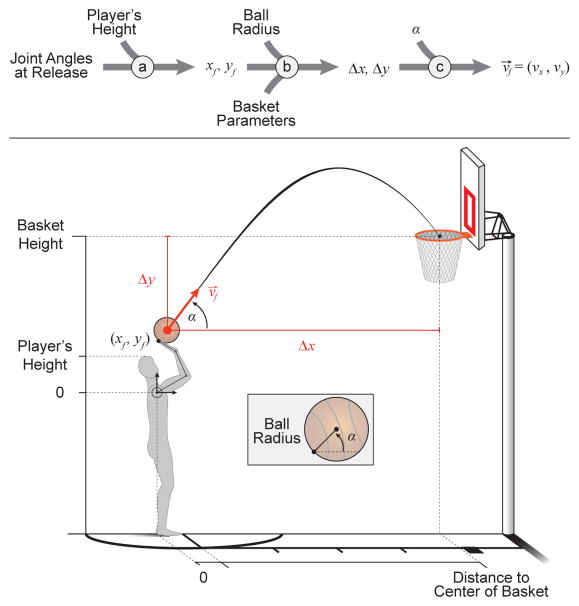
Figure 2.
Calculation of the final hand endpoint velocity vector (v⃗f ) necessary for a successful free throw. As this throw is well modeled as a ballistic problem, the independent variables are the angle of release (α) and the distance of the ball’s center from the basket’s center (Δx, Δy). (a) Utilizing the anthropometric geometric model described in Eq. 1, a player’s height and the joint angles at the point of release are utilized to find the position of the hand endpoint relative to the shoulder joint (designated here as the origin). (b) The radius of the ball and the parameters of the basket (i.e. height of the basket and horizontal distance of the shoulder joint to the basket’s center) are incorporated to find the necessary displacement parameters (Δx, Δy). (c) Utilizing these displacements and the angle of release (α), ballistics equations are rearranged and used to solve for the necessary release velocity vector for a successful free throw.
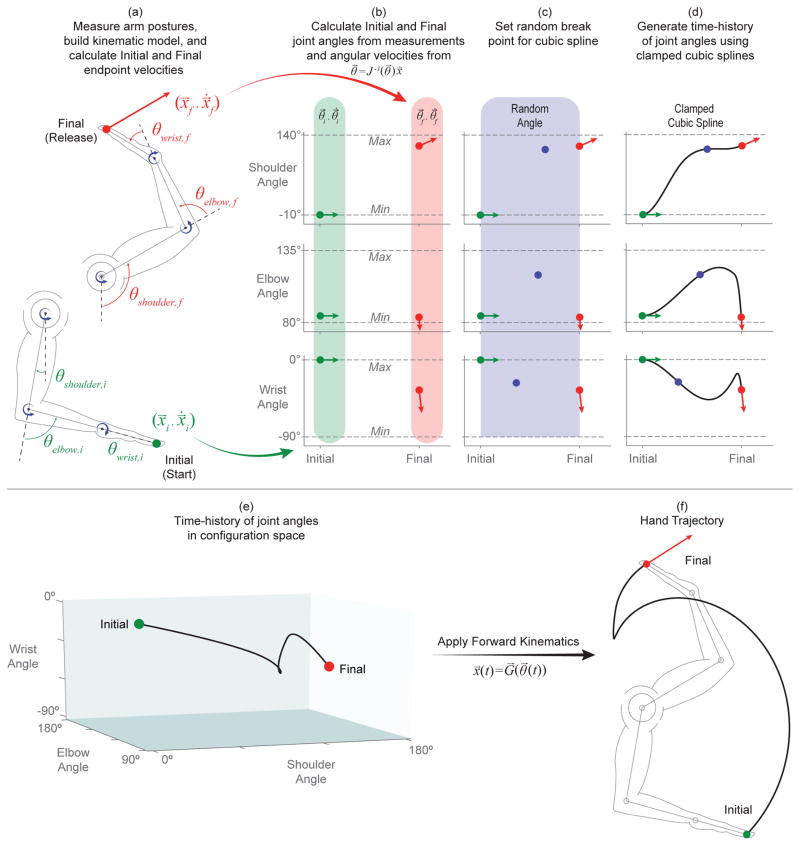
Figure 3.
Overview of trajectory generation technique. (a) Initial and final arm postures (taken from averaged, sample measurements) were passed through the kinematic model to find the initial and final hand endpoint positions (x⃗i and x⃗f) and twists ( and ) (See Figure 2 for overview of ballistics). (b) Initial and final angular velocities ( and ) were calculated from their relationship to endpoint twists by the inverse Jacobian matrix (J−1(θ⃗)) evaluated at their respective joint angles (θ⃗i and θ⃗f). (c) A random break point (i.e. knot or seed) was generated for each joint angle by uniformly sampling from the joint’s range of motion as well as from the time between initial and final postures (0–550 ms). (d) Time histories for each joint angle were generated through the use of clamped cubic splines to create smooth, piece-wise polynomial trajectories with proper initial and final conditions. Steps (c)–(d) were repeated if a resulting trajectory exceeded the joint’s range of motion or if undesirable (and unrealistic) rotations or velocities were encountered. (e) Combining joint angle time histories resulted in angle-angle-angle trajectories in configuration space. (f) Passing these combined angle time histories through the geometric model (i.e. the forward kinematic model) generated a hand endpoint trajectory with appropriate initial and final positions and velocities.
Note the final velocity of the hand as a rigid body, , is a twist that contains the linear velocity of the hand endpoint as the release velocity for the basketball, accompanied by zero net angular velocity (Valero-Cuevas, 2015).
Initial and final joint angular velocities ( and ) were calculated from their relationship with endpoint twists and the Jacobian of the limb evaluated at each respective posture (Eqs. 6 – 8; Valero-Cuevas, 2015), and is illustrated in Figure 3(b).
| (6) |
| (7) |
| (8) |
0.3. Generation of multiple valid hand trajectories
We used clamped cubic splines to generate the time histories of individual joint angles which, when combined, produced valid hand trajectories, allowing us to fix the appropriate initial and final hand positions and velocities across trials while exploring multiple valid trajectories between them. This process is discussed and illustrated in Figure 3(c)–(f). In brief, to produce a joint angle trajectory, a random break point (i.e., knot) was found by uniformly sampling the joints range of motion and the time between initial and final postures (assumed to have a conservative 550 ms movement duration chosen from observation) (Figure 3(c)). These three points (initial, knot, and final) were connected by two piece-wise cubic polynomials that produced a smooth, continuous trajectory with proper initial and final conditions (See Figure 3(d)). A trajectory was rejected if, at any point, it exceeded the joint’s defined range of motion. Additionally, shoulder or elbow angle trajectories were rejected if they produced initially negative angular velocities as this initial joint extension is not typically seen (i.e., players initially flex both the shoulder and elbow to bring the ball up from rest at the initial posture). Steps (c)–(d) in Figure 3 were repeated until these criteria were met for each joint angle.
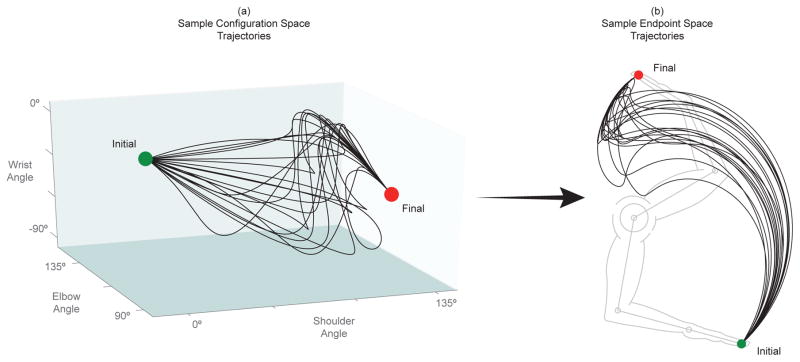
These joint angle trajectories were then combined to produce a trajectory in configuration space (Figure 3(e)) and this time-history of joint angles can then be passed through Eq. 1 to generate the resulting hand trajectory (Figure 3(f)). Steps (c)–(f) were then repeated until 100,000 feasible joint rotations were properly generated for the shoulder, elbow, and wrist joints that produced equally many joint angle time-histories in the configuration space and realistic hand trajectories in the endpoint space. Figure 4 shows 20 such random trajectories in configuration space and the corresponding endpoint space trajectories.
Figure 4.
20 trajectories in (a) configuration space and (b) endpoint space from a uniformly sampled solution space. These trajectories serve as examples of the solution space while individual trajectories will be explored further later in the analysis.
0.4. Calculation of normalized muscle velocities
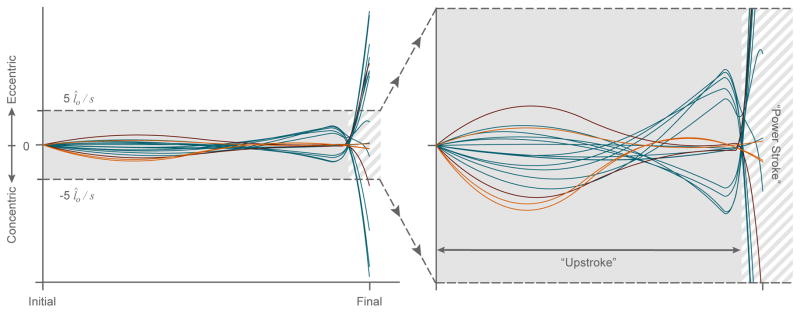
Existing literature was utilized to construct a posture-dependent moment arm matrix (R(θ⃗) in Eq. 9) (Valero-Cuevas, 2015; Ramsay et al., 2009; Holzbaur et al., 2005). The moment arms of these muscles at any particular joint configuration (θ⃗) can be used to calculate the changes in tendon excursions (δs⃗) associated with changes in joint angles (δθ⃗) (Eq. 10, An et al., 1983; Valero-Cuevas, 2015). Assuming stiff tendons, we can estimate muscle velocities for each of the 18 muscles included in our model (v⃗m) as the tendon excursion time derivative ( ) (Eq. 11). For ease of comparison across muscles, muscle velocities were normalized by their respective optimal muscle fiber lengths (Zajac, 1989). Figure 5 illustrates the normalized muscle velocity profile for a random trial.
Figure 5.
Normalized muscle velocities vs. time for a randomly selected free throw attempt both in its entirety (left) and bounded by ±5 muscle lengths per second (l̂0/s) (right) to highlight the upstroke phase. Muscles that only cross the shoulder are shown in orange, while the biceps and triceps muscles are shown in maroon. The remaining muscles that cross the elbow and/or wrist are shown in blue. Note that there exist two major zeros crossings during which many of the muscles change the direction of their contractions. The first instance occurs during the upstroke where the wrist extends as elbow flexes with similar but opposite angular velocities–while the shoulder continues to rotate upwards causing the net excursion time derivative for the bi-articulating muscles of the elbow and wrist to offset each other. The second instance defines the start of the power stroke phase where either the angular velocities of the elbow and/or wrist create a net zero tendon excursion time derivative or the muscles of the shoulder change the direction of their contractions (if they do at all). The muscles that only cross the shoulder do not exhibit this first zero crossing as they typically experience contraction throughout the entire upstroke without a change in direction (i.e. constant upward rotation about the shoulder joint), but will often exhibit the second zero crossing as a result of the cubic spline algorithm and the local extrema generated in the shoulder angle trajectory. As the biceps and triceps muscles cross over both the shoulder and elbow joints, they do not experience a zero crossing during the upstroke phase (i.e. the direction of both rotations are consistent and nonzero during this phase), but they do, however, exhibit typical zero crossings at the start of power stroke phase brought on by a major change in the direction of elbow rotation.
| (9) |
| (10) |
| (11) |
| (12) |
It is important to note that Eq. 12 represents an over-determined system of equations because v⃗m ∈ ℝ18 (an 18-dimensional vector), (a three-dimensional vector), and R(θ⃗)T ∈ ℝ18 × 3 (18 equations with three variables). Therefore, the values of three angular velocities determine the values of 18 muscle velocities. Given that a limb movement is a sequence of joint angular velocities, a given limb movement is only possible if all muscles are able to adopt their required muscle velocities as the movement progresses. For muscles undergoing concentric (i.e., shortening) contractions, it is possible for some of them to become lax and still allow the limb movement. But if any muscle that is lengthening (through either eccentric contraction or passive stretch) fails to do so at any time during the movements (e.g., because of failure or inability to regulate or silence its stretch reflex; Loeb, 1984; Prochazka et al., 1985), the movement will be disrupted (Sherrington, 1913; Valero-Cuevas, 2015)2.
0.5. Definition of movement phases
We considered each throw to have three phases: the upstroke, the power stroke, and the follow-through (Figure 5). The upstroke is the initial phase of the throw where the ball is brought from rest at the initial posture upwards towards a cocked position (i.e., when the velocities of the muscles that cross the elbow and/or wrist changed from eccentric to concentric contraction, or vice versa). As most muscles will undergo this change in the direction of their contraction velocity at different times (as dictated by their unique relationships between joint angles and moment arm values described in Eqs. 9–12), the upstroke is uniquely defined for each muscle during each trajectory. In the rare cases where none of the muscles of the shoulder exhibits this change in sign of contraction velocities, the upstroke is defined as the initial 520 ms of the motion. The power stroke is defined as the phase of the throw immediately following the upstroke. And lastly, the follow-through starts once the final endpoint velocity has been achieved. Here the wrist flexes as the ball is released. As stated previously, we do not consider this last phase as we only consider purely ballistic throws, and the mechanics of ball release and possible backspin are tangential to this study. Figure 5, therefore, only shows the two main phases of interest for our study.
0.6. Calculation of eccentric and concentric contraction velocity costs
Each trajectory was assigned cost values for eccentric and concentric contraction velocity magnitudes separately. Given that all trajectories had similarly large contraction velocities during the power stroke phase, we categorized trajectories as per their contraction velocities during the upstroke phase only. These cost values were defined as the Euclidean norms of the maximal eccentric (Eq. 13) and concentric (Eq. 14) contraction velocities for each muscles during that phase:
| (13) |
| (14) |
Results
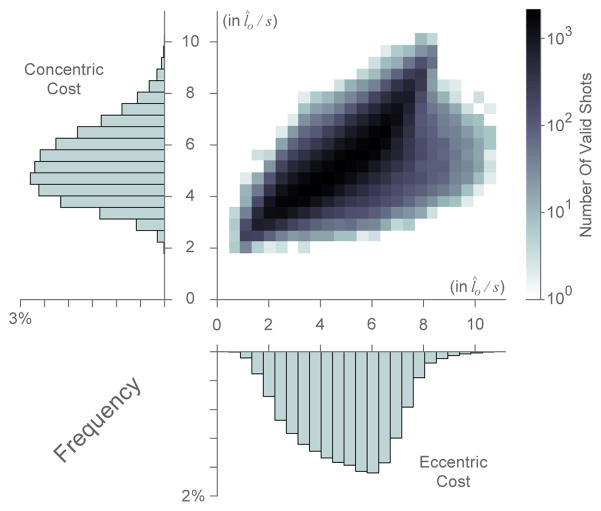
Using the computational method described above, we generated 100,000 realistic throwing motions that can achieve successful free throw hand trajectories. Surprisingly, we found that although the trajectories all clustered around a stereotypical path (Figure 4), there was a large distribution in both eccentric and concentric contraction velocity costs across them. Figure 6 shows both the histograms for eccentric and concentric costs separately, and a heat map of their joint distribution. This demonstrates that there exists a wide range of trajectories with very different eccentric and concentric costs that are capable of accomplishing the final hand position velocity for a valid throw.
Figure 6.
Two dimensional histogram of the eccentric and concentric costs of all trajectories as defined by equations 13 and 14, respectively (in normalized units l̂o/s (Zajac, 1989)) with one dimensional histogram axes overlays.
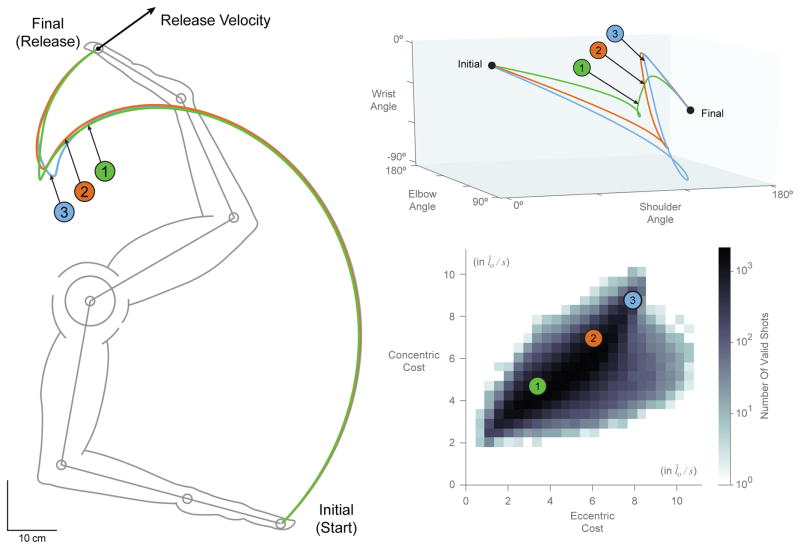
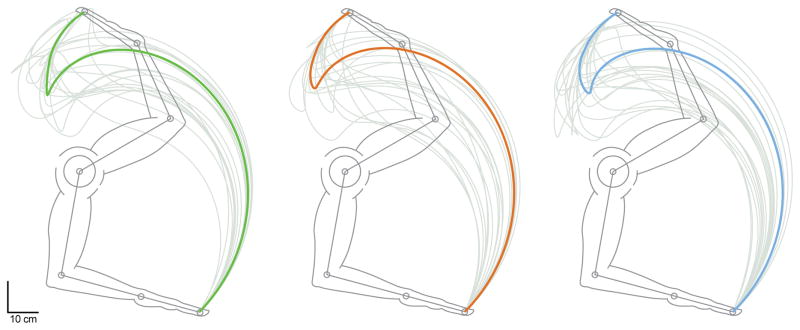
Furthermore, when sampling from these valid trajectories, we find cases where even kinematically similar basketball free throws have different contraction velocity costs (see sample trajectories 1, 2, and 3 in Figures 7). That is, the trajectory of the endpoint of the hand can be very similar across these three sample trajectories, but their paths in configuration space can be very different, as are their eccentric/concentric muscle velocity costs which can differ by a factor of 3. Conversely, we find that trajectories can also vary in endpoint space while incurring similar costs. Figure 8 demonstrates this observation by showing the 20 most similar trajectories to our sample trajectories in terms of cost values.
Figure 7.
Two dimensional histogram of the eccentric and concentric costs of all trajectories as defined by equations 13 and 14, respectively (in normalized units l̂o/s) (bottom right) with sample trajectories 1, 2 and 3 plotted in configuration space (top right) and endpoint space (left).
Figure 8.
Endpoint space plots of sample trajectories 1, 2, and 3, overlaid with their 20 most similar trajectories, respectively, as per eccentric and concentric cost values (gray).
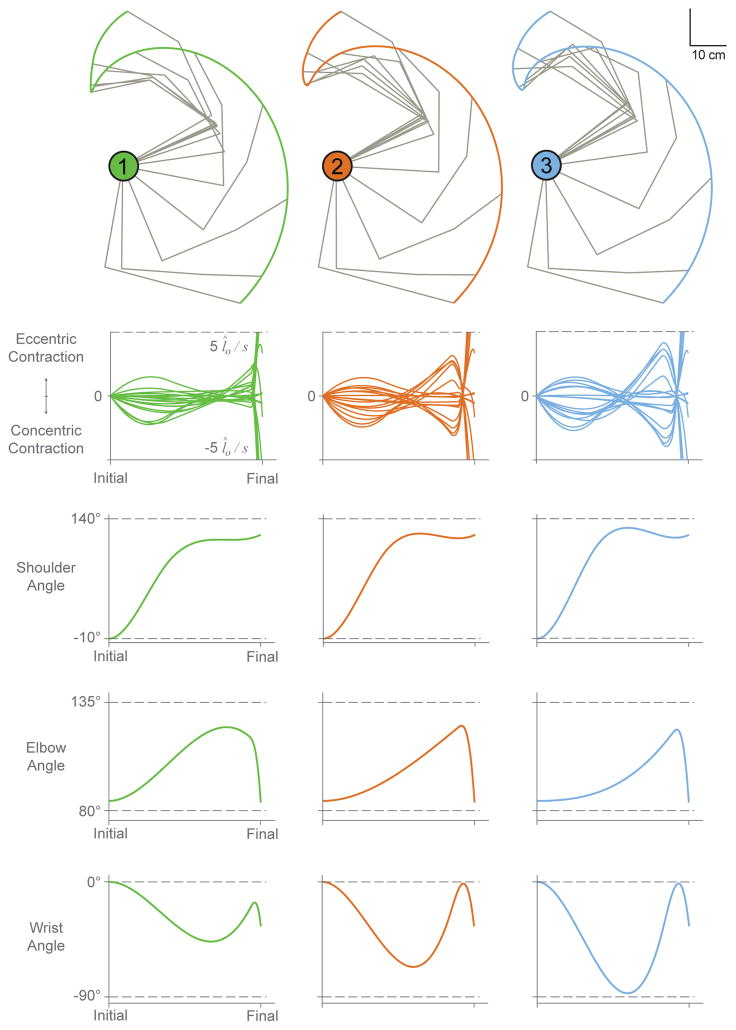
As seen in the bottom three rows of Figure 9, these three similar sample trajectories follow similar trends, but also exhibit subtle differences in individual angular trajectories (see stick figures at top and angle plots at bottom). Specifically, shoulder angle trajectories vary little in ranges or slopes, elbow angle trajectories have similar ranges with different slopes, and wrist angle trajectories have increasingly larger ranges and slope magnitudes (cf. across columns). Given that muscle velocities are related to joint angular velocities, changes in the slopes of joint angles across trajectories have large effects on contraction velocities as seen in Figure 9. Across these three sample trajectories, angle slopes vary little during the first third of the upstroke phase and, as a result, the magnitudes of muscle contractions are similar during that early period. Increasing slope values for both the elbow and wrist angles appear to heavily influence the magnitudes of contraction velocities, as seen by the remainder of the upstroke phase for sample trajectories 1, 2, and 3.
Figure 9.
Sample trajectories 1, 2, and 3 shown in endpoint space (top) with their corresponding normalized muscle velocity profiles and joint angle trajectories (bottom 3 rows). Note that the dotted lines in the velocity plots indicate ±5 l̂o/s, while dotted lines in the joint angle plots indicate the allowable range of motion for each joint.
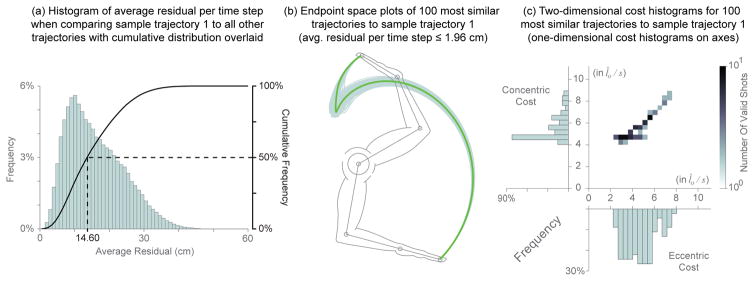
We quantified how similar the 100,000 trajectories were by measuring how well they followed a given valid path. We took the sample trajectory 1 shown in Figures 7–9 as the reference trajectory, and calculated the average residual per time step (i.e., Euclidean distance in the sagittal plane) between it and each of the remaining 99,999 trajectories. The frequency and cumulative histograms of these residuals are shown in Figure 10(a). We find that 50% of them have mean residuals ≤ 14.60 cm, with a median of 11 cm. By comparison, the sample trajectories 2 and 3 had mean residuals of 2.18 cm and 5.14 cm, corresponding to the 0.165% and 4.465% cumulative percentiles, respectively. Interestingly, even though sample trajectories 2 and 3 are among the 5% most similar to sample trajectory 1, their eccentric and concentric velocity costs differ greatly as show in Figure 7. In fact, even the 100 most similar trajectories to sample trajectory 1 (with average residual error per time step values ≤ 1.96 cm) have a fairly wide distribution in both eccentric and concentric costs with nearly four-and two-fold increases in cost ranges, respectively, as seen in Figure 10(b)–(c).
Figure 10.
(a) Histogram of the average residual per time step generated when comparing sample trajectory 1 to all remaining trajectories with cumulative distribution (solid black line) overlaid. Half of the trajectories had average residual values ≤ 14.60 cm while the mode of this distribution was 11 cm. (b) Endpoint space plot of the 100 most similar trajectories compared to sample trajectory 1 (green) as determined by the average residual per time step (≤ 1.96 cm). (c) The individual distributions (axes overlays) and the joint distribution of these most similar trajectories (in normalized units l̂o/s).
Discussion
It is, of course, undeniable that there are many ways in which one can coordinate joint rotations to smoothly and accurately produce a given trajectory of the endpoint of a limb (in this case, the hand during a basketball free throw). A first important result from this work is that the time histories of muscle lengths and velocities are not necessarily obvious for the multi-joint, multi-muscle limb— and that a given muscle can exhibit both eccentric and concentric contractions during a smooth and continuous hand trajectory such as the basketball free throw. The muscle length changes and velocities are, in fact, specified by the over-determined multi-dimensional matrix-vector Eqs. 9 – 12 that are a function of joint angles and angular velocities, moments arms, and link lengths. These multi-dimensional relationships are shown graphically in Figures 4, 5, 7, and 9.
We selected a few hand trajectories to explore, in detail, the relationships among joint angles and angular velocities, muscle velocity profiles, and hand trajectories. In particular, we selected sample hand trajectories 1, 2, and 3 (Figures 7, 8, 9, and 10) to make the point that there exist hand trajectories that are similar to each other, yet have very different muscle contraction velocities (Figure 7). Conversely, having similar muscle contraction velocities does not imply that the hand trajectories will be similar (Figure 8). The former point is explored further in Figure 10 by using sample trajectory 1 as a reference. Figure 10(a) shows how sample trajectory 1 is not an outlier because the median of the residual difference to all other 99,999 trajectories is lower than the mean of that difference. We then show the 100 most similar trajectories to it (Figure 10(b)) exhibit a large spread in muscle contraction velocities. While we could repeat this analysis with other trajectories as a reference, Figures 7–10 suffice as clear counterexamples to the notion that similarity in hand trajectory implies similarity in muscle contraction velocities, and vice versa.
To produce a given movement trajectory, all muscle activations must be appropriately coordinated, and afferent feedback from lengthening muscles must be appropriately tuned. Given muscle redundancy to produce joint torques, the efferent (outgoing) motor signals producing a limb movement may vary without changing the limb trajectory. But there is no such redundant relationship between limb kinematics and afferent (incoming) sensory signals. As per the over-determined nature of Eq. 12, a given limb movement fully determines the time history of muscle lengths and velocities and, therefore, the muscle proprioceptive signals that affect stretch reflexes. Thus, any muscle that fails to appropriately lengthen (either by failure to modulate or silence the stretch reflex, or by inappropriate activation) will disrupt the movement trajectory in some way (Sherrington, 1913; Loeb, 1984; Prochazka et al., 1985; Valero-Cuevas, 2015; Valero-Cuevas et al., 2015). Some muscles undergoing concentric contractions could, in principle, go slack so long as other muscles contribute to drive the limb (Valero-Cuevas et al., 2015). But the timely and appropriate modulation of force and afferent sensitivity in muscles which are lengthening is critically necessary. Therefore, each movement trajectory will require distinct and time-sensitive neural strategies. Here we present a detailed analysis of kinematic redundancy in light of its consequences on muscle lengths and velocities, and by inference, on neural control.
First, we reiterate that there are different valid hand trajectories (Figure 4) that produce a successful basketball free throw. What is less intuitive, and lacked characterization in prior literature, is that each valid trajectory is associated with quite different muscle velocity profiles—which has unavoidable physiological consequences to muscle mechanics and muscle afferentation. Muscle afferentation is the physiological term used to describe proprioception that is specific to muscles. This involves the afferent (i.e., from the periphery inwards) sensory flow from muscle mechanoreceptors to spinal, subcortical and cortical circuitry, as discussed further below. Our reasonable quantification of these consequences via eccentric and concentric costs (Eqs. 13 and 14) shows that valid trajectories are widely distributed and can differ by up to an order of magnitude in this cost lansdcape (Figure 6).
This result alone suffices to revisit our understanding of kinematic redundancy. Kinematic redundancy is considered a learning and decision-making challenge for the nervous system, which must select a particular time history of joint angles and angular velocities from among the many possible ones. At first, Bernstein proposed that the problem of kinematic redundancy is solved via a 3-stage approach, where initially some kinematic degrees of freedom are ‘frozen’ and then gradually released as the nervous system learns to control all degrees of freedom (Bernstein, 1967). More recently others have appropriately pointed out that kinematic redundancy must be evaluated with respect to the dimensionality of the task itself, and not just the number of kinematic degrees of freedom of the limb (e.g., Newell and Vaillancourt, 2001; Ko et al., 2003). Along similar lines, others propose that, given the dimensionality of a desired task, kinematic redundancy allows for ‘task-irrelevant’ joint angle changes and therefore gives rise to a nullspace or uncontrolled manifold for the task (e.g., Scholz and Schöner, 1999; Li et al., 2004). Moreover, the over-determined nature of muscle lengths and velocities has been implicated in the dimensionality reduction often seen in the control of limb function (Kutch and Valero-Cuevas, 2012; Brock and Valero-Cuevas, 2016). Along more computational lines, others propose that the decision-making challenge inherent to kinematic redundancy is addressed by the nervous system as an optimization problem (e.g., Loeb et al., 1990; Todorov and Jordan, 2002)—where the fitness of each possible movement solution is evaluated via a user-specified (and often debatable (Prilutsky, 2000)) cost function (e.g., energy expenditure (Crowninshield and Brand, 1981), jerk (Flash and Hogan, 1985), speed-accuracy tradeoff (Fitts, 1954)).
Our results, however, reveal an important Sherringtonian feature of kinematic redundancy by showing that valid trajectories are not intrinsically equivalent. Rather, they are intrinsically distinct in their muscle velocity profiles. This has physiologiocal consequences to muscle mechanics and afferentation, and therefore require distinct and time-sensitive neural reflex modulation strategies for their accurate, smooth, and repeatable execution (Sherrington, 1913, 1932; Loeb, 1984; Prochazka et al., 1985)—independently of any additional metabolic, state-dependent, or task-related cost function(s) the user may prefer to consider. In fact, we find that even very similar trajectories can have different muscle velocity profiles (Figures 7 and 9)3.
Where does the need for distinct and time-sensitive neural strategies come from? Three papers (Loeb, 1984; Prochazka et al., 1985; Duchateau and Enoka, 2016) review the nature of muscle afferentation and its role during functional tasks. Briefly, separate neural commands control the bulk of the muscle (i.e., α-motoneurons), muscle spindle gains (i.e., γ-motoneurons), and stretch reflex pathways gains. The stretch reflexes resist muscle lengthening in a velocity-dependent way. Given that a movement trajectory fully determines the speeds at which muscles must lengthen, stretch reflexes must be modulated or silenced to allow such lengthening. Failure to modulate or silence the stretch reflex will prevent the desired joint rotations—and thus disrupt the movement trajectory unless other joint rotations compensate the disruption. Thus, different muscle eccentric contraction velocities (i.e., movement trajectories) will require distinct reflex modulation strategies; and faster muscle velocities will require appropriately faster and more time-critical reflex modulation strategies (Valero-Cuevas, 2015; Valero-Cuevas et al., 2015; Duchateau and Enoka, 2016). The different concentric contraction velocities may also require distinct and time-sensitive strategies to ensure that muscles do not go slack and cease to produce force, and to ensure that the work loops of all muscles contribute appropriately to accomplish the task well (Tobalske et al., 2003). The distinct muscle velocity profiles for each valid trajectory reinforce the need for strict spatio-temporal constraints on the time-history of muscle coordination (Rácz and Valero-Cuevas, 2013; Dingwell et al., 2010). Thus, trajectories that produce faster or more variable contraction velocities (i.e., higher costs, Figure 6) will likely require more precise timing of reflex modulation across motoneuron pools; resulting in higher sensitivity to time delays, force-length and force-velocity properties, short-range stiffness, excitation/contraction dynamics, noise, errors, perturbations, etc.
This work justifies and enables future research directions by combining the Sherringtonian perspective with experimental (An et al., 1983) and analytical (Valero-Cuevas et al., 2015; Valero-Cuevas, 2015) demonstrations of the over-determined nature of muscle contraction velocities. This neo-Sherringtonian perspective towards kinematic redundancy has profound implications to the learning, execution, and rehabilitation of natural movements. For example, it leads to testable hypotheses of why learning to produce accurate, smooth, and repeatable movements takes immense amounts of practice, even in typically developing children (Adolph et al., 2012), why so few of us can become elite musicians or athletes (Gladwell, 2008), and why rehabilitation requires mass practice (Lohse et al., 2014). Future experiments and computational simulations can also begin to tie neural plasticity and learning rates to the specific characteristics of a smooth movement. For example, do humans favor trajectories producing lower and less variable contraction velocities? By extension, such an approach can help us understand how disruption of reflex mechanisms could lead to pathological movements such as spasticity, tremor and clonus (Zehr and Stein, 1999; Hultborn, 2006; Hidler and Rymer, 1999; Laine et al., 2016) in neurological conditions including cerebral palsy, stroke, Parkinsons disease and spinal cord injury (Sanger et al., 2010; de Vlugt et al., 2016; Phadke et al., 2016; Agapaki et al., 2016). Similarly, perhaps one can design arm movement trajectories that are more effective for rehabilitation because they require less time-critical modulation of stretch reflexes.
We conclude that moving smoothly, repeatedly, and well is neither a redundant nor a forgiving problem. It requires confronting and overcoming the over-determined problem of appropriately regulating α- and γ-motoneuron activity in a task-specific and time-critical way across all muscles in the context of the nonlinearities of neurons, muscles, proprioceptors, and limb mechanics.
Figure 1.
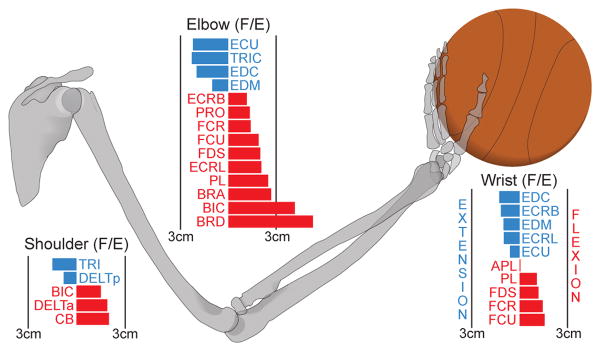
18 Muscle, 3 DOF Model. Model considers sagittal-plane Shoulder Flexion/Extension (F/E), Elbow Flexion/Extension and Wrist Flexion/Extension only. Forearm Pronation/Supination and Radial-Ulnar Deviation were excluded from our model as studies have shown player’s to typically keep the shoulder, elbow, wrist, and ball in the same plane as the basket (Knudson, 1993). For an overview of the muscles used and their posture-dependent moment arm functions see Valero-Cuevas (2015), Ramsay et al. (2009), and Holzbaur et al. (2005).
Acknowledgments
We thank the University of Southern California for facilities provided during the course BME/BKN 504, Steven Caja and Suraj Chakravarthi Raja for their help building the preliminary model, Brian Cohn for his help with the illustrations, and Dr. Emily Lawrence for sharing her arm model from Valero-Cuevas et al. (2015).
Research reported in this publication was supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health under awards number R01AR052345 and R01AR050520 to F.V-C. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Due to the full pronation of the forearm, the sign convention for wrist flexion/extension has been flipped in order to consistently associate positive angular velocity with flexion throughout the model.
The distinction between the underdetermined nature of the control of joint torques (with many solutions) vs. the over-determined nature of the control of joint rotations (with at most one solution) is often lost in the biomechanics and neural control literature (Valero-Cuevas, 2015). When controlling individual afferented muscles, the neural control of limb force is fundamentally different from that of limb movement. Not only are the governing equations for force and motion control different (Yoshikawa, 1990; Valero-Cuevas, 2015), but the former requires combining muscle forces to produce specific net joint torques, whereas the latter requires coordinating muscle forces while regulating reflexes to allow eccentric/concentric contractions compatible with the desired joint angles and angular velocities (Sherrington, 1913; Loeb, 1984; Prochazka et al., 1985; Mah and Mussa-Ivaldi, 2003; Venkadesan and Valero-Cuevas, 2008; Valero-Cuevas, 2015)
Strictly speaking, the endpoint trajectories of the hand are very similar while their hand orientations, which are not plotted, may differ given that the hand as a rigid body has three degrees of freedom in the sagittal plane. Nevertheless, by construction, all trajectories strictly meet the initial and final conditions for hand position and orientation to produce a successful basketball free throw, as is the case in Bernstein’s hammering example (Bernstein, 1967), see Figure 3.
Conflict of Interest
The authors have no conflict of interest related to the content of this manuscript.
All authors were fully involved in the study and preparation of this manuscript and the material within has not been and will not be submitted for publication elsewhere.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adolph KE, Cole WG, Komati M, Garciaguirre JS, Badaly D, Lingeman JM, Chan GL, Sotsky RB. How do you learn to walk? thousands of steps and dozens of falls per day. Psychological science. 2012;23:1387–1394. doi: 10.1177/0956797612446346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agapaki OM, Anastasopoulos D, Erimaki S, Christakos CN. Interaction of stretch reflex loop with descending b-oscillations and the generation of tremor in parkinson’s disease: A study of motor unit firing synchrony and patterns (p5. 369) Neurology. 2016;86:P5–369. [Google Scholar]
- An KN, Ueba Y, Chao E, Cooney W, Linscheid R. Tendon excursion and moment arm of index finger muscles. Journal of biomechanics. 1983;16:419–425. doi: 10.1016/0021-9290(83)90074-x. [DOI] [PubMed] [Google Scholar]
- Bernstein N. The co-ordination and regulation of movements. 1967. [Google Scholar]
- Brock O, Valero-Cuevas F. Transferring synergies from neuroscience to robotics: Comment on hand synergies: Integration of robotics and neuroscience for understanding the control of biological and artificial hands by m. santello et al. Physics of life reviews. 2016 doi: 10.1016/j.plrev.2016.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crowninshield R, Brand R. A physiologically based criterion of muscle force prediction in locomotion. Journal of Biomechanics. 1981;14:793–801. doi: 10.1016/0021-9290(81)90035-x. [DOI] [PubMed] [Google Scholar]
- Dingwell JB, John J, Cusumano JP. Do humans optimally exploit redundancy to control step variability in walking? PLoS Comput Biol. 2010;6:e1000856. doi: 10.1371/journal.pcbi.1000856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duchateau J, Enoka RM. Neural control of lengthening contractions. Journal of Experimental Biology. 2016;219:197–204. doi: 10.1242/jeb.123158. [DOI] [PubMed] [Google Scholar]
- Fitts PM. The information capacity of the human motor system in controlling the amplitude of movement. Journal of experimental psychology. 1954;47:381. [PubMed] [Google Scholar]
- Flash T, Hogan N. The coordination of arm movements: an experimentally confirmed mathematical model. Journal of neuroscience. 1985;5:1688–1703. doi: 10.1523/JNEUROSCI.05-07-01688.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gladwell M. Outliers: The story of success. Hachette UK: 2008. [Google Scholar]
- Hidler JM, Rymer WZ. A simulation study of reflex instability in spasticity: origins of clonus. IEEE Transactions on Rehabilitation Engineering. 1999;7:327–340. doi: 10.1109/86.788469. [DOI] [PubMed] [Google Scholar]
- Holzbaur KR, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Annals of biomedical engineering. 2005;33:829–840. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
- Hultborn H. Spinal reflexes, mechanisms and concepts: from eccles to lundberg and beyond. Progress in neurobiology. 2006;78:215–232. doi: 10.1016/j.pneurobio.2006.04.001. [DOI] [PubMed] [Google Scholar]
- Knudson D. Biomechanics of the basketball jump shotsix key teaching points. Journal of Physical Education, Recreation & Dance. 1993;64:67–73. [Google Scholar]
- Ko YG, Challis JH, Newell KM. Learning to coordinate redundant degrees of freedom in a dynamic balance task. Human Movement Science. 2003;22:47–66. doi: 10.1016/s0167-9457(02)00177-x. [DOI] [PubMed] [Google Scholar]
- Kutch JJ, Valero-Cuevas FJ. Challenges and new approaches to proving the existence of muscle synergies of neural origin. PLoS Comput Biol. 2012;8:e1002434. doi: 10.1371/journal.pcbi.1002434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laine CM, Nagamori A, Valero-Cuevas FJ. The dynamics of voluntary force production in afferented muscle influence involuntary tremor. Frontiers in Computational Neuroscience. 2016:10. doi: 10.3389/fncom.2016.00086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Todorov E, Pan X. Hierarchical optimal control of redundant biomechanical systems, in: Engineering in Medicine and Biology Society, 2004. IEMBS’04. 26th Annual International Conference of the IEEE; IEEE; 2004. pp. 4618–4621. [DOI] [PubMed] [Google Scholar]
- Loeb G, Levine W, He J. Cold Spring Harbor symposia on quantitative biology. Cold Spring Harbor Laboratory Press; 1990. Understanding sensorimotor feedback through optimal control; pp. 791–803. [DOI] [PubMed] [Google Scholar]
- Loeb GE. The control and responses of mammalian muscle spindles during normally executed motor tasks. Exercise and sport sciences reviews. 1984;12:157–204. [PubMed] [Google Scholar]
- Lohse KR, Lang CE, Boyd LA. Is more better? using metadata to explore dose–response relationships in stroke rehabilitation. Stroke. 2014;45:2053–2058. doi: 10.1161/STROKEAHA.114.004695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mah CD, Mussa-Ivaldi FA. Evidence for a specific internal representation of motion–force relationships during object manipulation. Biological cybernetics. 2003;88:60–72. doi: 10.1007/s00422-002-0347-9. [DOI] [PubMed] [Google Scholar]
- Newell KM, Vaillancourt DE. Dimensional change in motor learning. Human Movement Science. 2001;20:695–715. doi: 10.1016/s0167-9457(01)00073-2. [DOI] [PubMed] [Google Scholar]
- Phadke CP, Flynn S, Kukulka C, Thompson FJ, Behrman AL. Comparison of soleus h-reflexes in two groups of individuals with motor incomplete spinal cord injury walking with and without a walker. Topics in Spinal Cord Injury Rehabilitation. 2016;22:158–163. doi: 10.1310/sci2016-0007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prilutsky BI. Muscle coordination: the discussion continues. MOTOR CONTROL-CHAMPAIGN- 2000;4:97–116. doi: 10.1123/mcj.4.1.97. [DOI] [PubMed] [Google Scholar]
- Prochazka A, Hulliger M, Zangger P, Appenteng K. fusimotor set: new evidence for α-independent control of γ-motoneurones during movement in the awake cat. Brain research. 1985;339:136–140. doi: 10.1016/0006-8993(85)90632-8. [DOI] [PubMed] [Google Scholar]
- Rácz K, Valero-Cuevas F. Spatiotemporal analysis reveals active control of both task-relevant and task-irrelevant variables. Frontiers in computational neuroscience. 2013;7:155. doi: 10.3389/fncom.2013.00155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay JW, Hunter BV, Gonzalez RV. Muscle moment arm and normalized moment contributions as reference data for musculoskeletal elbow and wrist joint models. Journal of biomechanics. 2009;42:463–473. doi: 10.1016/j.jbiomech.2008.11.035. [DOI] [PubMed] [Google Scholar]
- Sanger TD, Chen D, Fehlings DL, Hallett M, Lang AE, Mink JW, Singer HS, Alter K, Ben-Pazi H, Butler EE, et al. Definition and classification of hyperkinetic movements in childhood. Movement Disorders. 2010;25:1538–1549. doi: 10.1002/mds.23088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Sherrington CS. Reflex inhibition as a factor in the co-ordination of movements and postures. Quarterly Journal of Experimental Physiology. 1913;6:251–310. [Google Scholar]
- Sherrington CS. Foundation N, editor. Nobel Lectures, Physiology and Medicine. 1932. Inhibition as a coordinative factor; pp. 278–289. [Google Scholar]
- Tobalske B, Hedrick TL, Dial K, Biewener A. Comparative power curves in bird flight. Nature. 2003;421:363–366. doi: 10.1038/nature01284. [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan M. Optimal feedback control as a theory of motor coordination. Nature Neuroscience. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas F, Cohn B, Yngvason H, Lawrence E. Exploring the high-dimensional structure of muscle redundancy via subject-specific and generic musculoskeletal models. Journal of biomechanics. 2015;48:2887–2896. doi: 10.1016/j.jbiomech.2015.04.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valero-Cuevas FJ. Fundamentals of neuromechanics. Vol. 8. Springer; 2015. [Google Scholar]
- Venkadesan M, Valero-Cuevas FJ. Neural control of motion-to-force transitions with the fingertip. The journal of Neuroscience. 2008;28:1366–1373. doi: 10.1523/JNEUROSCI.4993-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Vlugt E, van der Krogt HJ, Helgadóttir Á, Arendzen JH, Meskers CG, de Groot JH, et al. Estimation of tissue stiffness, reflex activity, optimal muscle length and slack length in stroke patients using an electromyography driven antagonistic wrist model. Clinical Biomechanics. 2016;35:93–101. doi: 10.1016/j.clinbiomech.2016.03.012. [DOI] [PubMed] [Google Scholar]
- Winter DA. Biomechanics and motor control of human movement. John Wiley & Sons; 2009. [Google Scholar]
- Yoshikawa T. Foundations of robotics: analysis and control. MIT press; 1990. [Google Scholar]
- Zajac FE. Muscle and tendon properties models scaling and application to biomechanics and motor. Critical reviews in biomedical engineering. 1989;17:359–411. [PubMed] [Google Scholar]
- Zehr EP, Stein RB. What functions do reflexes serve during human locomotion? Progress in neurobiology. 1999;58:185–205. doi: 10.1016/s0301-0082(98)00081-1. [DOI] [PubMed] [Google Scholar]