Rapid convergence of optimal control in NMR using numerically-constructed toggling frames

Abstract

We present a numerical method for rapidly solving the Bloch equation for an arbitrary time-varying spin-1/2 Hamiltonian. The method relies on fast, vectorized computations such as summation and quaternion multiplication, rather than slow computations such as matrix exponentiation. A toggling frame is constructed in which the Hamiltonian is time-invariant, and therefore has a simple analytical solution. The key insight is that constructing this frame is faster than solving the system dynamics in the original frame. Rapidly solving the Bloch equations for an arbitrary Hamiltonian is particularly useful in the context of NMR optimal control. Optimal control theory can be used to design pulse shapes for a range of tasks in NMR spectroscopy. However, it requires multiple simulations of the Bloch equations at each stage of the algorithm, and for each relevant set of parameters (e.g. chemical shift frequencies). This is typically time consuming. We demonstrate that by working in an appropriate toggling frame, optimal control pulses can be generated much faster. We present a new alternative to the well-known GRAPE algorithm to continuously update the toggling-frame as the optimal pulse is generated, and demonstrate that this approach is extremely fast. The use and benefit of rapid optimal pulse generation is demonstrated for 19F fragment screening experiments.

1. Introduction

Optimal control theory can be used to design pulses suitable for specific tasks in NMR spectroscopy, such as broadband excitation or inversion, decoupling, coherence transfer, and Hadamard encoding [1,2]. In particular, the gradient ascent pulse engineering (GRAPE) algorithm, based on the Pontraygin maximum principle [3,4], can generate a pulse sequence which steers spins to a desired final state. The pulse can be generated such that it functions correctly in the presence of a range of parameters such as chemical shifts, RF inhomogeneities, and couplings. Part of the power of this approach is that NMR experiments can be highly tailored to the specific system (i.e. set of chemical shifts) of interest. The GRAPE procedure requires repeated solutions to the spin dynamics for each set of parameters. These solutions must be generated both forwards and backwards in time. This gives the forward and backward trajectories of the density matrix in the presence of the pulse, and these jointly determine a correction to the pulse shape. The algorithm is then iterated, and generally converges to a pulse shape which produces the desired density matrix evolution.

Optimal control was originally applied to magnetic resonance in the context in MRI [5–7], and was later rediscovered and developed further for applications in NMR spectroscopy [8–13] and quantum computing [14,15]. However, the GRAPE algorithm has so far seen fairly limited use for highly tailored experiments of small molecules and simple mixtures, e.g. pulses designed to work for a particular sample. The GRAPE approach does not fit easily into rapid NMR workflows, such as fragment screening or small molecule NMR, since pulse generation takes from ~30 min up to several hours [16,13].

Rapid generation of optimal control pulses will extend their applicability to situations where pulse generation is required at the spectrometer, tailored to a sample, in an automation setup. For example, in 19F fragment screening there are typically 15–30 resonances spread over about 100 kHz of spectral bandwidth (in each of up to several hundred samples). General broadband excitation pulses wastefully target many empty spectral regions. Furthermore, these generally have long pulse durations and require high RF power levels. These pulse properties lead to relaxation losses and prohibit experiments such as CPMG that require repeated rapid refocusing for milliseconds. It would be useful to generate optimal excitation, inversion, and refocusing pulses tailored to each sample. The pulse can ignore unpopulated spectral regions, and focus on the specific resonances actually present. Therefore, such sample-specific optimal control pulses have shorter durations, lower RF power, and better performance. Generating all the optimal control pulses for a practical 19F fragment library is a formidable computational task, largely due to the fact that the density matrix trajectories need to be calculated many times.

Transforming the Hamiltonian to a different frame of reference can greatly simplify NMR calculations. Examples include the standard transformation from the laboratory frame to the rotating frame [17], as well as more intricate procedures such as the Magnus expansion [18,19] and other coherent averaging techniques [20–24]. Similarly, there have been a number of attempts to use frame transformations to simplify spin dynamics without completely removing time-dependence, and this has been useful for various pulse design schemes [25–27]. It is important to note that frame transformations do not only affect the complexity of analytical calculations, but also the computational effort required for numerical simulations. Since GRAPE is computationally intensive, it makes sense to ask if well-chosen frame transformations can simplify and accelerate the optimization procedure.

Here, we show that the forwards and backwards density matrix trajectories can be rapidly determined using repeated construction of appropriate toggling frames. A toggling frame is a generalization of the familiar rotating frame of reference, in which the new frame’s motion with respect to the original frame can be more intricate than a simple precession [28,23]. The procedure is as follows: The time-varying part of the Hamiltonian is reduced using a numerically-constructed toggling frame. This construction requires an integration (i.e. cumulative sum of a digital signal), a subtraction, and a rotation of the Hamiltonian—all of which are fast, vectorizable numerical operations. With iteration, the original time-varying Hamiltonian quickly converges to a time-invariant Hamiltonian, i.e. an average or equivalent Hamiltonian. Since the average Hamiltonian is time-invariant, it has a simple analytical solution, and the corresponding density matrix trajectory is easily extracted (both forwards and backwards in time). These trajectories are then re-expressed in the original frame of reference via a rotation operation, and the GRAPE correction to the pulse is calculated. In contrast, solving the Bloch equations in the original frame of reference, in which the Hamiltonian is time-varying, requires repeated matrix exponentiation, which is computationally slow [29,30].

We demonstrate that the toggling-frame method of generating the trajectories is about two orders of magnitude faster than working in the original frame of reference.

Moreover, this framework provides additional speedup opportunities. Suppose we have a time-varying Hamiltonian and have extracted the corresponding toggling frame and average Hamiltonian. We now add a small perturbation to the Hamiltonian; for example, we apply a correction based on the GRAPE algorithm. The same toggling-frame will now leave the new Hamiltonian very nearly time-invariant, since the Hamiltonian has only changed a little. In this case the toggling frame can be adjusted to remove the small additional time-variation, without having to start over from the original frame. The GRAPE algorithm requires a sequence of small directed changes to the pulse shape, so this method can be used to rapidly complete the GRAPE algorithm using only a few fast calculations at each step. This is significantly faster than using a full simulation of the Bloch equation at each step.

As a demonstration, we apply the toggling-frame method to the problem of in-phase excitation and refocusing of an arbitrary set of 19F resonances. These are sampled from a large spectral bandwidth. The optimal pulse shape is generated using GRAPE (in the toggling frame) in around 10 s. We show that this is much faster than what would be possible without the use of toggling frames. The performance of the optimal tailored pulse is, as one would expect, a significant improvement over more general broadband methods. The main point is the speed with which the optimal pulse is created by running GRAPE in the toggling frame.

2. Solution of the Bloch equation by toggling frames

In this section we briefly review the dynamics of spin-1/2 nuclei. We then explain how to use numerically constructed toggling frames to rapidly solve the system dynamics for arbitrary time-dependent Hamiltonians.

2.1. Dynamics of spin-1/2

The state of an isolated nuclear spin-1/2 is described using a basis of Pauli spin operators, I_x, I_y, and I_z, obeying the commutation relation [I_x, I_y] = iħI_z and cyclic permutations. A state ρ(t) = m_x(t)I_x + m_y(t)I_y + m_z(t)I_z can be thought of as a classical unit vector m⃗(t) evolving on the Bloch sphere. The Hamiltonian is also expressed in this basis. Since the Hamiltonian encodes the potential energy of each state, it determines the evolution of the system. Both the density matrix and Hamiltonian are, in general, time-varying. According to quantum mechanics the evolution of the density matrix is given by the von Neumann equation

$$\frac{d}{dt}\rho (t)=-i[H(t),\rho (t)]$$ (1)

where the Hamiltonian H(t) is expressed in frequency units. In the case of uncoupled spins, this is usually referred to as the Bloch equation. This can be integrated from any initial time t = t₁ to final time t = t₂ to form a unitary transition matrix V(t₂, t₁),

$$\rho (t_2)=V(t_2,t_1)\rho (t_1)V^{†}(t_2,t_1)$$ (2)

where

$$\frac{d}{dt}V(t,t_1)=-iH(t)V(t,t_1)$$ (3)

Since V(t₂, t₁) does not depend on the density matrix it can be calculated directly from the Hamiltonian and applied to any initial state ρ(t₁). The unitary transition matrix corresponds to a (nonunique) effective or average time-invariant Hamiltonian

$$V(t_2,t_1)=exp(-i{H}_{\text{eff}}(t_2-t_1))$$ (4)

Clearly, when the Hamiltonian is time-invariant, i.e. H(t) = H_eff, the unitary solution to the von Neumann equation V(t₂, t₁) is given in closed form by a matrix exponential. For time-varying Hamiltonians, the solution can be found by discretization of the time-axis between t₁ and t₂ into n small intervals dt over which H(t) ≈ H_k is approximately constant. Then

$$\begin{array}{l}{V}_k=exp(-i{H}_{k}dt)\\ V(t_2,t_1)=V_n{V}_{n-1}\dots V_2{V}_1\end{array}$$

For long and temporally-intricate pulse sequences, this can be a time-consuming calculation.

The Hamiltonian and density matrix can also be expressed in a different frame of reference, for example a rotating frame, encoded by a unitary transform U(t). If we transform the density matrix into a new frame by ρ₁(t) = U(t)ρ(t)U^†(t), then the equivalent Hamiltonian is

$$H_1(t)=U(t)H(t)U^{†}(t)+i\stackrel{.}{U}(t)U^{†}(t)$$ (5)

One common strategy for finding the solution V(t₂, t₁) is to find a frame U(t) that removes the time-dependence from the Hamiltonian. This can sometimes be done analytically. However, for sufficiently complicated Hamiltonians, finding a closed form U(t) is prohibitively difficult. The toggling-frame algorithm constructs U(t) and H_eff numerically.

2.2. Toggling frame solution

Next we describe the toggling-frame method for finding the solution to the von Neuman equation for an isolated spin-1/2. Consider an arbitrary time-varying Hamiltonian on t ∈ [0, T] of the form

$$H(t)=h_z(t)I_z+h_x(t)I_x+h_y(t)I_y$$ (6)

Suppose we wish to remove the time-dependence of the z-component. We separate h_z(t) into the direct-current (average) part $h_z^{dc}$ and the zero-mean oscillating part $h_z^{\mathit{osc}}(t)$. Note that h_z(t) can be expressed as a Fourier series with fundamental frequency f = 2π/T, so that $h_z^{\mathit{osc}}(t)$ comprises sinusoids at frequencies nf for positive integers n. We integrate the oscillating part to form

$$\begin{array}{l}{h}_z(t)=h_z^{dc}+h_z^{\mathit{osc}}(t)\\ P(t)={\int }_0^t{h}_z^{\mathit{osc}}(t)dt\end{array}$$

Next set up a unitary change of frames, i.e. a toggling frame,

$$\begin{array}{ll}\hfill {\rho }_1(t)& =U(t)\rho (t)U^{†}(t)\hfill \\ \hfill U(t)& =exp(-iP(t)I_z)\hfill \\ \hfill H_1(t)& =(h_z(t)-h_z^{\mathit{osc}}(t))I_z+(cos(P)h_x(t)+sin(P)h_y(t))I_x+(cos(P)h_y(t)-sin(P)h_x(t))I_y\hfill \end{array}$$ (7)

That is, the time-variation has been removed from the z-component of H(t). The remaining two axes of the Hamiltonian have been rotated. Crucially, P(0) = P(T) = 0, so that U(0) = U(T) is the identity; the toggling frame aligns with the original frame at the beginning and end of the pulse duration.

For sufficiently low-amplitude and/or rapidly oscillating $h_z^{\mathit{osc}}(t)$, it is clear that P(t) ≈ 0, so that the x and y components of the Hamiltonian are essentially unchanged. On the other hand, when P(t) is not close to zero, the rotation of the x and y components will be more significant, and potentially introduce new time-varying and/or constant terms along these axes, depending on the frequency profile of h_x(t), h_y(t), and P(t).

Next we repeat the procedure, cycling the axes. That is, we generate a second toggling frame which subtracts out the time-varying part of the x-axis, and rotates the y and z axes. We then do the same for the y-axis. By now, there might be some time-variation reintroduced along the z-axis, so we repeat the whole procedure. Any time that the rotation P(t) is small, we successfully remove time-variation from the Hamiltonian without reintroducing it anywhere else. Similarly, whenever the other two axes contain frequency components in common with P(t), these will resolve into additional constant (direct-current) terms.

We repeat this until H_tog, the Hamiltonian expressed in the toggling frame, has negligible time-dependence (the convergence of the process is derived below). Then the density matrix trajectory, expressed in the toggling frame, has a simple analytical form based on the matrix exponential function

$${\rho }_{\mathit{tog}}(t)=exp(-i{H}_{\mathit{tog}}t)\rho (0)exp(i{H}_{\mathit{tog}}t)$$ (8)

where the subscript tog indicates the toggling frame. ρ(0) has no subscript since it is the same in any frame; the toggling frame aligns with the original frame at times 0 and T. Note that calculation of ρ_tog(t) for each increment in a discretized time axis requires at most one matrix exponential calculation, since each incremental propagator over time dt is the same.

It is computationally simple to keep track of the overall toggling frame. Each U(t) is a rotation about either the x, y, or z axis, which can be encoded by a time-varying quaternion vector p⃗(t). The overall toggling-frame is the product of every frame change in this procedure. It can be adjusted by quaternion multiplication. This means only one set of quaternions, q⃗(t), needs to be stored, and each time we subtract a time-varying component we update it using quaternion multiplication (denoted by *)

$$\overrightarrow{q}(t)\to \overrightarrow{p}(t)\ast \overrightarrow{q}(t)$$ (9)

The initial value of q⃗(t), corresponding to the original frame of reference, is the quaternion identity q⃗(t) = [1, 0, 0, 0]. This represents no rotation at all. When we subtract out the time-dependent part of e.g. h_z(t), we must adjust the toggling frame by the quaternion p⃗(t) = [cos(P(t)/2), 0, 0, sin(P(t)/2)]. This is the quaternion representation of a rotation by angle P(t) about the z-axis.

A density matrix trajectory can be expressed as a 3D vector, which correspond to a ‘pure’ quaternion. These trajectories can be moved in or out of the toggling frame using the quaternion rotation formula, for example

$$\begin{array}{l}{\overrightarrow{\rho }}_{\mathit{tog}}(t)=\overrightarrow{q}(t)\ast {\overrightarrow{\rho }}_{\mathit{org}}(t)\ast {\overrightarrow{q}}^{†}(t)\\ {\overrightarrow{\rho }}_{\mathit{org}}(t)={\overrightarrow{q}}^{†}(t)\ast {\overrightarrow{\rho }}_{\mathit{tog}}(t)\ast \overrightarrow{q}(t)\end{array}$$ (10)

Here, ρ⃗_log(t) is the vector of density matrix I_x, I_y, and I_z components in the toggling frame, and ρ⃗_org(t) is the same vector expressed in the original frame.

In total, each step of this procedure requires extraction of the oscillating part of a signal, integration/summation, rotation of the other two Hamiltonian components, and a quaternion multiplication to keep track of the toggling frame. These are all vectorizable operations, and are fast compared with matrix exponentiation of each time-increment. The matrix exponential is defined by an infinite series, and numerical calculation of a matrix exponential requires a time-consuming calculation [29,30].

In Section 4 we demonstrate that the speedup, compared to solving the dynamics in the original frame, is substantial. Moreover, in cases where the Hamiltonian undergoes a series of small changes, for example in the GRAPE algorithm, there is no need to start over from the original frame each time. We can run the GRAPE algorithm in a continuously updated toggling frame, in which the Hamiltonian remains time-invariant. The solution (i.e. density matrix trajectory) can be rapidly extracted and then expressed in the original frame, and the correction to the pulse sequence can be calculated.

2.3. Convergence of the toggling frame procedure

In this subsection we show that the toggling frame procedure is guaranteed to converge to a time-invariant average Hamiltonian. Define the total squared-amplitude of the Hamiltonian:

$$\begin{array}{l}J={\int }_0^T{h}_z{(t)}^2+h_x{(t)}^2+h_y{(t)}^{2}dt\\ ={\int }_0^T{(h_z^{dc})}^2+h_z^{\mathit{osc}}{(t)}^2+h_x{(t)}^2+h_y{(t)}^{2}dt\end{array}$$

Such a term is known as the signal-energy (distinct from the physical energy of the system). The second line follows because any cross-terms between the two parts of h_z(t) will average out to zero over the duration of the integral.

The toggling frame algorithm removes $h_z^{\mathit{osc}}(t)$ entirely, does not affect $h_z^{dc}$, and rotates h_x(t) and h_y(t). Note that a rotation cannot change the length of the vector [h_x(t), h_y(t)], so the total squared-amplitude along the x and y axes is unchanged. Of course, there may be some exchange of amplitude between these two axes (x and y), and between DC and oscillating terms, depending on the frequency profile of the various terms, but the total signal-energy along these two axes is preserved exactly. After removing the oscillation along the z-axis using (7), J is reduced by the integral of $h_z^{\mathit{osc}}{(t)}^2$. That is, the total signal-energy is reduced by exactly the total squared-amplitude of the removed oscillations. The same argument applies when removing time-varying terms along any axis (z, x, or y), so J is strictly non-increasing under the toggling frame procedure. In fact, if there are any non-zero oscillations in the Hamiltonian, then J is decreasing over a set of three applications of (7) - one along each axis. This is because we will necessarily reduce J by the total squared-amplitude of any time-varying terms.

Obviously, J is bounded from below by zero, which guarantees convergence of this approach. However, the algorithm can terminate with J > 0 once all the squared-amplitude is confined to DC (time-invariant) terms.

3. GRAPE with toggling frames

In this section we first review the GRAPE algorithm. We then translate it into the toggling frame, and show that the additional calculations required to solve for the density matrix trajectory at each step can be very simple and fast.

3.1. Introduction to the GRAPE algorithm

The grape algorithm has been extensively studied, for ensembles of isolated spins as well as ensembles of coupled spin systems. More rigorous derivations are available in the literature [1,2]. Here, we present a simple derivation which captures the essential intuition. Recall that V(t₂, t₁) is the unitary solution to (3) from t = t₁ to t = t₂.

Suppose we wish to design a pulse to drive the density matrix from initial state ρ(0) to target final state λ(T). That is, we want the dynamics to be such that ρ(T) = V(T, 0)ρ(0)V^†(T, 0) = λ(T). The reason for including a time-dependence in the target state λ will become apparent below. We can measure the performance of a candidate pulse sequence via the figure of merit Φ:

$$\mathit{\Phi }=\text{tr}(\lambda (T)\rho (T))=\text{tr}(\lambda (T)V(T,0)\rho (0)V^{†}(T,0))$$

Clearly, Φ is maximized when the desired transition is achieved. Φ depends on the applied controls (pulse sequence). In order to improve Φ, we would like to know how to change the shape of the applied pulse. The GRAPE algorithm applies gradient ascent to this problem. We can calculate $\frac{d\mathit{\Phi }}{d{u}_k(t)}$, where u_k(t) is the amplitude of the k^th available control variable at time t. For an ensemble of isolated spins, there are two available controls, the x and y components of the B₁ field. Changing u_k(t) in the direction indicated by this gradient increases Φ so that it can be driven towards a local maximum.

We first express the Hamiltonian as a fixed drift part, and a part that can be freely chosen (within practical limits) by setting the control amplitudes u_k(t)

$$H(t)=H_d(t)+\sum _k{u}_k(t)H_k$$ (11)

Typically in solution-state NMR, the drift H_d is not time-dependent; however, for the GRAPE formalism this is not essential. We factor the unitary transition matrix into the part up to an arbitrary time t₁, and the part from t₁ to T:

$$V(T,0)=V(T,t_1)V(t_1,0)$$

That is to say, V(t₁, 0) accounts for the dynamics up to t₁, and then V(T, t₁) accounts for the dynamics from then until the pulse sequence is finished at time T. Taking the derivative with respect to u_k(t₁) gives

$$\frac{dV(T,0)}{d{u}_k(t_1)}=-V(T,t_1)i{H}_{k}V(t_1,0)dt$$

One way of seeing this is to consider a small duration dt beginning at t = t₁. For sufficiently small dt, H(t) remain constant and the evolution during dt is given analytically by a matrix exponential,

$$\begin{array}{l}V(T,0)=V(T,t_1+dt)V(t_1+dt,t_1)V(t_1,0)\\ =V(T,t_1+dt)exp(-iH(t_1)dt)V(t_1,0)\end{array}$$

from which the derivative of V(T, 0) with respect to the control amplitude u_k(t₁) follows. We can now use this to calculate the gradient of Φ with respect to the control amplitude:

$$\frac{d\mathit{\Phi }}{d{u}_k(t_1)}=-i.dt\text{.tr}(\lambda (T)V(T,t_1)H_{k}V(t_1,0)\rho (0)V^{†}(t_1,0)V^{†}(T,t_1)-\lambda (T)V(T,t_1)V(t_1,0)\rho (0)V^{†}(t_1,0)H_k{V}^{†}(T,t_1))$$

By the cyclic property of the trace, the term V^†(T, t₁) can move in front of λ(T). Then observe that V(t₁, 0)ρ(0)V^†(t₁, 0) is the initial state evolved under the Bloch equation up to time t₁, i.e. ρ(t₁). Moreover, V^†(T, t₁)λ(T)V(T, t₁) is the desired final state evolved backwards in time via the Bloch equation from time T to time t₁, i.e. λ(t₁). This simplifies the previous expression considerably,

$$\begin{array}{l}\frac{d\mathit{\Phi }}{d{u}_k(t)}=-i.dt\text{.tr}(\lambda (t_1)H_k\rho (t_1)-\lambda (t_1)\rho (t_1)H_k)\\ =-dt\text{.tr}(i[\rho (t_1),\lambda (t_1)]H_k)\end{array}$$ (12)

This is the component of [ρ, λ] that aligns with H_k. For example, in the typical case where we can choose the B₁ field in the x and y directions, and apply the control Hamiltonian

$$H_c(t_1)=u_1(t_1)I_x+u_2(t_1)I_y$$

then the gradient for u₁(t₁) is the x-component of i[ρ(t₁), λ(t₁)], and the gradient for u₂(t₁) is the y-component of i[ρ(t₁), λ(t₁)].

Crucially, the argument so far applies for any value of t₁. We only need to evaluate the trajectory ρ forwards in time, and the trajectory λ backwards in time from the target state, and we can retrieve the gradient for the control amplitudes simultaneously at every time t ∈ [0, T]. Depending on how the time axis is discretized, this could amount to many thousands of independent parameters—the values of the B₁ field at each time increment—all being optimized in concert. Note that for an isolated spin-1/2, (12) has stationary points only when ρ(t) = ±λ(t). For multi-spin systems or ensembles, more stationary points are possible.

To apply the GRAPE algorithm we adjust the control amplitudes by a small step in the direction indicated by the gradient. We then recalculate ρ(t) and λ(t) under the new, adjusted Hamiltonian. This, in turn, updates the gradient. Proceeding in this way, we can find a local maximum of Φ, which for reasonable tasks typically corresponds to extremely good performance [1].

Note that an alternative to calculating the trajectories ρ(t) and λ(t) separately is to evolve only the correction term, i.e.

$$i[\rho (t),\lambda (t)]=iV(t,0)[\rho (0),\lambda (0)]V^{†}(t,0)$$

However, this still requires two simulations of the Bloch equations, forward and backward in time, since we need to know λ(0) before evolving the correction term.

For an ensemble of spins with different parameters (such as chemical shifts and RF inhomogeneity factors), we can sum our figure of merit Φ over all parameterizations. We can weight the sum to emphasize certain parameterizations over others, for example to match a probability density of RF inhomogeneities. In this case, it is clear that the gradient, and therefore the correction at each time, sums in the same way. Therefore, we need to calculate the forwards and backwards solution to the Bloch equation for each parameterization to derive an overall gradient for the ensemble. For a reasonable sampling of parameters, this is a time-consuming calculation.

3.2. GRAPE in the toggling frame

In this section, we show that repeatedly calculating i[ρ(t), λ(t)], the therefore the GRAPE correction to the pulse shape, can be achieved rapidly using the toggling frame approach. We note that both ρ and λ can be moved in and out of the toggling frame using the quaternion rotation formula (10). Recall that the toggling frame transform is a time-dependent unitary U(t). Then

$$\begin{array}{l}[\rho (t),\lambda (t)]=U^{†}(t)[U(t)\rho (t)U^{†}(t),U(t)\lambda (t)U^{†}(t)]U(t)\\ =U^{†}(t)[{\rho }_{\mathit{tog}}(t),{\lambda }_{\mathit{tog}}(t)]U(t)\end{array}$$

In the toggling frame, the Hamiltonian is time-invariant, and therefore the trajectories of ρ_tog and λ_tog can be calculated along a discretized time axis with at most one matrix exponential calculation. Specifically, for time-step dt which divides the time axis into n points,

$$\begin{array}{l}A=exp(-i{H}_{\mathit{tog}}dt)\\ {\rho }_{\mathit{tog}}(k.dt)=A^k\rho (0)A^{k†}\\ {\lambda }_{\mathit{tog}}(k.dt)=A^{(n-k)†}\lambda (T)A^{n-k}\end{array}$$

This can be calculated considerably faster than with many matrix exponentials in the original frame. In fact, we can save further time by using a very coarse discretization of the time axis for this calculation, since any rapid modulations in H_org(t) are not present in H_tog. We can then interpolate this trajectory onto the more finely discretized time axis on which H_org(t) and U(t) were defined.

The accessible control fields are typically limited to the x and y components of the applied B₁ field (defined in the original frame of reference). The pulse may also be subject to other constraints, for example on maximum or peak amplitude, or on smoothness. Moreover, if we are treating an ensemble of spins with different parameters, the gradient terms must be summed, and this must occur in a common frame. Therefore, we need to convert the gradient term [ρ_tog(t), λ_tog(t)] back into the original frame of reference before proceeding. In practice, this can be achieved very fast using quaternion rotation.

We now show that after calculating the correction to the pulse shape, the corrected Hamiltonian should be transformed again, putting in back into the toggling frame. Specifically, we consider two Hamiltonians, H(t) and H(t) + ΔH(t), where the GRAPE gradient was extracted from H(t) and used to generate the correction term ΔH(t). In the toggling frame given by U(t), H_tog is time-invariant:

$$H_{\mathit{tog}}=U(t)H(t)U^{†}(t)+i\stackrel{.}{U}(t)U^{†}(t)$$

When H(t) + ΔH(t) is placed in the same toggling frame U(t),

$$U(t)(H(t)+\mathrm{\Delta }H(t))U^{†}(t)+i\stackrel{.}{U}(t)U^{†}(t)=H_{\mathit{tog}}+U(t)\mathrm{\Delta }H(t)U^{†}(t)$$

so that when the correction Hamiltonian is rotated into the toggling frame it can be added to time-invariant effective Hamiltonian from the previous iteration of the GRAPE algorithm. The key insight it that since this is a gradient ascent setting, the correction ΔH(t) is typically small, especially near the end of the GRAPE procedure. Therefore, the updated Hamiltonian, expressed in the toggling frame, has only low-amplitude time-varying terms. The toggling frame algorithm does not need to begin over from the original frame, potentially dealing again with high-amplitude modulations found in H(t). Rather, a small number of iterations of the toggling frame approach can remove any additional time-dependence introduced by U(t)ΔH(t)U^†(t). The toggling frame is updated, leaving the Hamiltonian, once again, time-invariant.

In the computational section below, we demonstrate that as GRAPE converges the number of iterations of the toggling frame algorithm—that is, the effort required to extract the forward and backward trajectories—is dramatically reduced.

4. Numerical implementation and speed analysis

4.1. Simulation of one Hamiltonian

Firstly, we provide a simple concrete example to clarify the ideas presented so far. We test the toggling frame method to solve a time-varying Hamiltonian. Our example Hamiltonian contains multiple high-amplitude oscillations and a range of frequency components. This Hamiltonian is difficult to solve analytically and must be simulated numerically. We compare the result to the standard simulation method (a product of unitary propagators, each of which captures the evolution over a small time interval dt). The Hamiltonian is

$$\begin{array}{l}u(t)=0.5+cos(4t)+sin(10t)+sin(14t)-0.4sin(16t)\\ v(t)=sin(4t)+cos(8t)+sin(12t)+2cos(16t)\\ H=u(t)I_x+v(t)I_y\end{array}$$ (13)

with t ∈ [0,π]. Since the duration is T = π (in arbitrary units) any u(t) and v(t) have a fundamental frequency f = 2π/T = 2 in the sense of Fourier series analysis, and therefore could be expressed using only even-integer frequencies. To keep this example simple, we have chosen to include only a few such modulations.

A discretization time must be chosen. For both methods, the choice of dt affects both the computation-time and the faithfulness with which high-frequency components are synthesized; to capture the effects of rapid oscillations dt has to be fairly small. In this case, we test a range of values of dt.

For practical implementation of the toggling frame method, the algorithm is considered to have converged to a time-independent average Hamiltonian when the maximum amplitude of the time-dependent part is less than one ten-thousandth of the inverse pulse duration. For our example Hamiltonian, the toggling frame method returns the average Hamiltonian after 12 iterations (4 along each axis), irrespective of dt. In fact, in this case the overall effect of the Hamiltonian is a very high fidelity x-phase excitation pulse, which steers the magnetization from ρ(0) = I_z to ρ(π) ≈ −I_y. Interestingly, in this case any Bloch–Siegert shifts, and other off-resonance effects, seem to have been removed/refocused by the end of the duration.

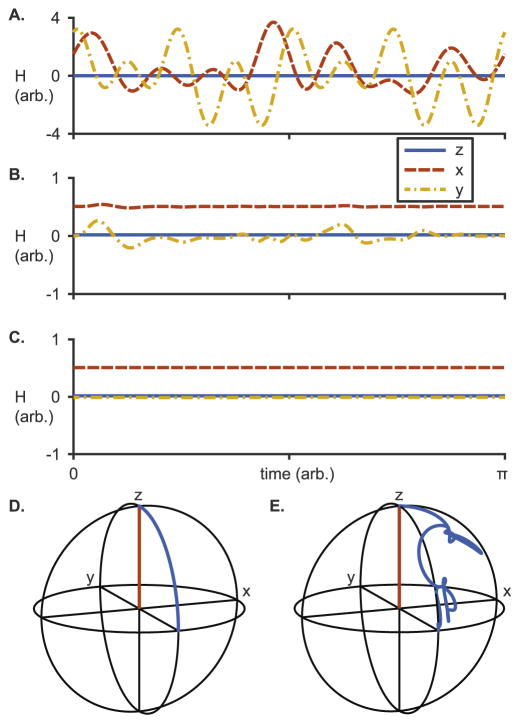
Fig. 1 shows the Hamiltonian H(t) expressed in successive toggling frames, after 0, 3, and 9 iterations of the toggling frame algorithm. This corresponds to 0, 1, and 3 iterations about each of the three axes. After one more iteration about each axis, the maximum amplitude of the oscillating part has become negligible and the algorithm terminates. The density matrix trajectory was then straightforwardly extracted from the average Hamiltonian, and converted back into the original frame of reference using (10). Fig. 1E shows the x, y, and z components of the density matrix expressed in the original frame.

Fig. 1.

Systematic removal of time-dependence by toggling frames. A: The Hamiltonian (13) expressed in the original frame of reference. B: The Hamiltonian after 3 iterations of the toggling frame algorithm (i.e. 1 iteration about each axis). C: The Hamiltonian after 9 iterations of the toggling frame algorithm (i.e. 3 iteration about each axis). The time variation is mostly removed, and the average Hamiltonian is clearly near H(t) ≈ 0.5I_x. Equilibrium magnetization ρ(0) = I_z would be excited to the transverse plane at ρ(π) = −I_y by this Hamiltonian. D: The magnetization trajectory expressed in the toggling frame, depicted on the Bloch sphere. E: The magnetization trajectory expressed in the original frame of reference, found by applying the quaternion rotation formula (10) to the trajectory in D.

The standard simulation method of calculating the unitary propagator for each dt and multiplying these all together takes considerably longer, especially for small dt. Table 1 summarizes the computational time for various values of dt. These were measured using the Matlab function timeit, which runs the code multiple times and calculates an estimate of the average run-time. Clearly, the toggling frame method is much faster, especially for finely discretized pulse shapes. The computational time using matrix exponentiation appears to grow linearly with the number of time points, whereas the time grows sub-linearly for the toggling frame method, at least up until around ~2¹⁵ time-points (incidentally, this is around the maximum number of points in a shaped pulse that can be loaded into a spectrometer). This means that for a wide range of relevant dt values, the toggling frame approach is 1–2 orders of magnitude faster than solving the dynamics in the original frame of reference.

Table 1.

Computational time for simulating H(t) (given by (13)) using the toggling frame method versus the matrix exponential method. The time axis is discretized into n equally sized increments, and ρ(t) for t ∈ [0, T] is extracted. The Matlab function timeit was used to estimate the running time. For the toggling frame method, the reported time includes constructing the toggling frame and average Hamiltonian, calculating the trajectory of the state in the toggling frame, and converting this back to the original frame. For the matrix exponential method, the time includes calculating the incremental propagator at each time using a matrix exponential. We also report the final state y component, showing that a discretization of at least ~ 1000 points is needed to adequately capture the highly oscillatory dynamics. 12 iterations of the toggling frame algorithm are needed to find the average Hamiltonian, regardless of the discretization. The last column is the multiple by which the toggling frame method is faster, which is up to two orders of magnitude for a very fine discretization. We used a regular personal computer.

n	Toggling frame			Matrix exponential		Speedup
	Time (ms)	2tr(Iyρ(T))	Num. togg.	Time (ms)	2tr(Iyρ(T))
25	1.06	−0.984	12	3.56	−0.980	3.35
26	1.13	−0.995	12	7.11	−0.994	6.31
27	1.20	−0.998	12	13.98	−0.998	11.63
28	1.48	−0.999	12	28.26	−0.999	19.10
29	1.95	−0.999	12	56.27	−0.999	28.87
210	2.35	−1.0	12	110.6	−1.0	47.17
211	3.66	−1.0	12	224.2	−1.0	61.24
212	5.28	−1.0	12	443.9	−1.0	84.09
213	10.68	−1.0	12	888.1	−1.0	103.27
214	15.40	−1.0	12	1783	−1.0	115.82
215	32.73	−1.0	12	3587	−1.0	109.61
216	70.12	−1.0	12	7113	−1.0	101.45

Finally, note that very small values of dt are often needed in order to analyze the effects of high-frequency terms. We explored this by adding a fast modulation to our test Hamiltonian, i.e. H(t) + 15 cos(300t)I_x + 15 sin(300t)I_y. This introduces a large Bloch–Siegert shift, and so the pulse no longer performs an x-phase excitation. Moreover, it requires a reasonably small dt to capture these oscillations (around 2¹³ time points are needed). The toggling frame algorithm now takes 15 iterations (5 per axis) to converge. However, the speedup compared to the standard product-of-unitaries method is maintained; the toggling frame approach is around 90 times faster. We have tested the toggling frame and exponentiation speeds on many different time varying Hamiltonians, and the qualitative conclusions of this section do not depend on the specific choice of H(t).

4.2. Heuristic explanation of the toggling frame method

A simple thought experiment can help explain why the toggling frame method can solve the dynamics more quickly than standard approaches. Suppose we set out to simulate a simple on-resonance hard pulse, but that we were working in the laboratory frame instead of the rotating frame. In this case, we would have to deal with oscillations in the Hamiltonian of hundreds of MHz. Therefore, we would require a very fine discretization of the time axis; we would need to calculate the incremental propagator for many short intervals to capture the resonant effect of the rapidly oscillating B1 field. In contrast, a transformation to the rotating frame simplifies matters considerably. The Hamiltonian becomes time invariant, and the solution is easily found in closed-form [17]. Crucially, the effort required to change the frame is surprisingly little - in practice it involves multiplying together a few sinusoids which resolve into constant terms. Yet this foundational idea makes it possible to understand and calculate spin dynamics very easily, and indeed, quickly. This is why NMR simulations are never constructed in the laboratory frame.

The toggling frame method applies the same logic to arbitrary time-varying Hamiltonians. Rapid oscillations require finely discretized time axes to track accurately in simulation. However, rapid oscillations are in fact the terms that are most easily removed by frame transformations. Therefore, just as for the familiar rotating frame, constructing a new frame in which the Hamiltonian is time-invariant is surprisingly easy.

4.3. GRAPE in the toggling frame for broadband 19F control

In this section, we use the GRAPE algorithm implemented in the toggling frame in a practical pulse-design problem. Recall that the toggling frame does not need to be recalculated from scratch at each step of the GRAPE algorithm. Rather, we convert the forwards and backwards density matrix trajectories into the original frame to calculate the pulse correction, and then apply constraints on the pulse. We then convert the correction into the toggling frame. If the correction is small, the Hamiltonian remains very nearly time-invariant in the toggling frame, reducing the number of calculations required to solve for the density matrix trajectories of the new Hamiltonian.

Near convergence of GRAPE, the size of the correction ΔH(t) tends to zero, and so the pulse and Hamiltonian are not changing much. Therefore, a traditional simulation using matrix exponentials is essentially repeating the same calculation at each additional epoch of the GRAPE algorithm. In contrast, the toggling frame method has already made this Hamiltonian time-invariant by appropriate frame construction, and is not repeating this process each epoch. Instead, the Hamiltonian is being expressed in the same toggling frame as in the previous epoch of GRAPE. Therefore, near convergence, we expect GRAPE in the toggling frame to be extremely efficient.

We use 15 different Hamiltonians: this corresponds to the chemical shift frequencies we observe in a mixture of fluorinated small molecules used in our fragment screening operations. We initialize the GRAPE algorithm with a random starting point. We choose an excitation time of 150 μs, a maximum RF amplitude of 13.5 kHz, and discretize the time axis into 2¹⁰ points. Within about 10 s, GRAPE in the toggling frame has produced a pulse shape which is at least 99% efficient at exciting these 15 spins to the y-axis.

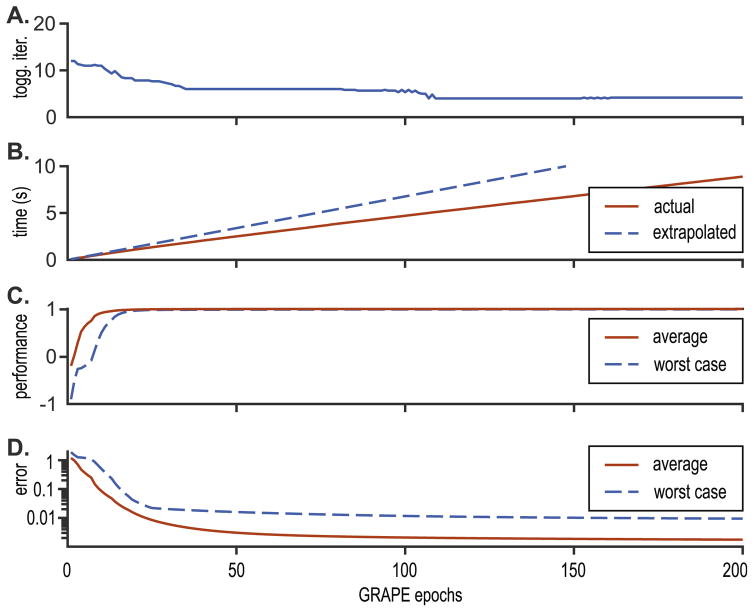
Fig. 2A shows the average number of iterations for toggling frame, which decreases near convergence. Fig. 2B shows the time taken to complete the GRAPE algorithm. We also show a rough extrapolation (dashed line) from the first few epochs. This shows how long the procedure might take if the toggling frame algorithm were starting over from the original frame each epoch. However, the toggling frame algorithm does not begin each epoch from the original frame (which would mean repeating a lot of calculations). Instead, it begins from the time-invariant effective Hamiltonian from the previous GRAPE epoch, and adds a low amplitude correction. This correction tends to zero near convergence of GRAPE. In total, there are two speedups at play: firstly, the togging frame method avoids matrix exponentiation and therefore has the speedups cataloged in Table 1. Secondly, the toggling frame method does not repeat the same calculations over and over near convergence, and therefore has the speedup depicted in Fig. 2B.

Fig. 2.

Grape in the toggling frame. A: The number of iterations of the toggling frame method that are needed to solve for the magnetization trajectory at each epoch of the GRAPE algorithm. This is the averaged over the 15 resonances in the computation. Clearly, near convergence, less computational effort is required. Note that only one toggling frame, q⃗(t), is stored for each of the 15 Hamiltonians, and it is being updated to remove time-varying terms introduced by Hamiltonian corrections. B: The time taken to find the pulse in terms of the number of epochs of GRAPE. If we extrapolate from the first few time points (dashed line) then the algorithm would take considerably longer. C: The performance metric ϕ converges to 1, both on average and for the worst performing resonance. D: The difference between ϕ and its theoretical maximum 1 tends towards zero, and all resonances are at least 99% aligned with the target state.

Fig. 2C and D show the figure of merit converging to one, both on average and for the worst-performing spin. We chose to terminate the GRAPE algorithm when the worst-case spin is at least 99% aligned with the y-axis at the final time.

5. Materials and methods

The experiments were performed on a Bruker 500 MHz spectrometer equipped with an Avance III HD console and a C/F-H triple resonance probe. The CPMG experiment was a modification of the 1H CPMG pulse sequence “cmpg1d” which is a part of the standard Bruker package. The CMPG times used ranged from 50 to 500 ms. The hard pulse was at 18.5 μs. The optimal control pulse had length of 150 μs at the same average RF power levels.

We used two samples in this manuscript. The first was ca. 5 mg of 5-F-Tryptophan dissolved in DMSO-d6. This gives a single 19F peak. The other sample was a mixture of 15 fluorinated compounds used in fragment screening experiments.

6. Experimental demonstration

In this section, we apply two different rapidly-generated optimal pulses to two samples, to demonstrate that these pulses function correctly in practice.

6.1. Simple excitation of three resonances

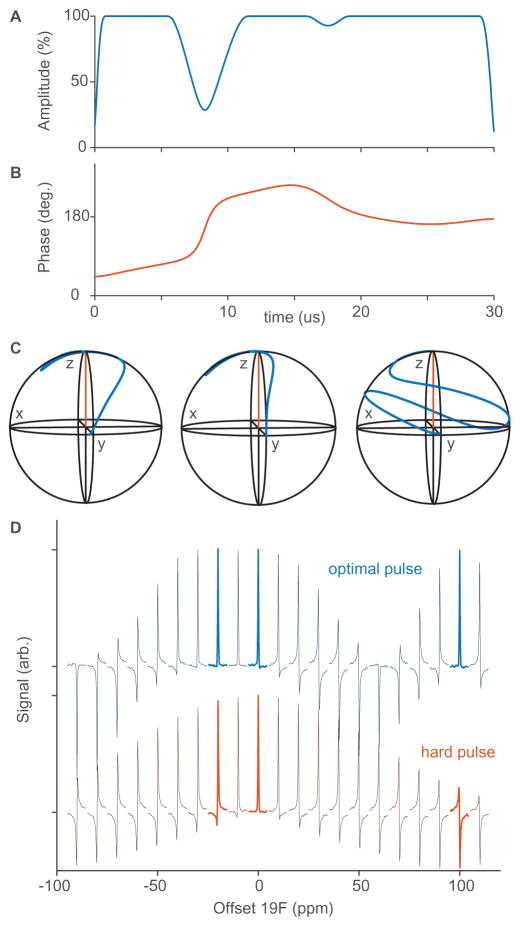
As a first demonstration, we consider a hypothetical sample that contains three resonances, at −20, 0, and 100 ppm on the fluorine channel of a 500 MHz (1H Larmor frequency) spectrometer. These three values were chosen so that there would be small and large unpopulated spaces between resonances, and so that the distribution of resonances would be asymmetric. The initial state is I_z, and we wish to excite the spins to I_y. The optimal control pulse duration was set to 30 μs, and the maximum amplitude was set to 20 kHz. The pulse shown in Fig. 3A and B was returned in about 3 s using the toggling frame algorithm. It excites all three resonances to at least 0.997I_y.

Fig. 3.

An example of excitation tailored to three specific resonances. A and B: The pulse shape, optimized in under 3 s using the toggling frame method. C: Simulated magnetization trajectories for resonances at −20, 0, and 100 ppm, respectively. All three trajectories end up with a y-component of at least 0.997. D: Experimental spectra obtained by moving the carrier frequency around the single resonance of 5-F-Tryptophan. The upper spectra were recorded with the optimal control pulse, and the lower used a hard pulse at the same maximum RF field strength (20 kHz). All processing settings, in particular phase and display settings, are the same for all spectra. The optimal control pulse is clearly more suited to simultaneous in-phase excitation of these three resonances.

Simulated trajectories offer some insight into how this pulse operates. Fig. 3C shows that the two nearby resonances (−20 and 0 ppm) follow fairly similar paths to the target state. In contrast, the far off-resonance spin (100 ppm) circumnavigates the Bloch sphere during the pulse. This is strikingly similar to how analytically designed dual-band pulses work [25,31,32]. That is, the optimization procedure has found a fairly intuitive solution to the problem of widely separated resonances, while also optimizing the fine details of the pulse shape to make sure the specific spins of interest end up in exactly the right place. Often, optimal control pulses are highly intricate and unintuitive (e.g. with highly erratic amplitude and phase profiles). However, in this simple case the algorithm has produced a smooth shape that is fairly easy to understand.

Fig. 3D shows experimental spectra with hard-pulse excitation (lower) and optimal pulse excitation (upper). These were found by moving the carrier frequency offset around a single isolated 19F peak. For the three values of interest, the maximum signal amplitude is 1.009, 1.002, and 0.994 respectively (with the hard pulse on resonance value normalized to 1, and the noise standard deviation is ~0.01). All processing settings, in particular phase and display settings, are the same for all spectra.

6.2. CPMG-based screening of 19F libraries—refocusing of a 19F mixture

Fluorine based fragment screening has become one of the more successful NMR based methods in drug discovery [33]. The 19F NMR spectra of these fragments typically contain one single resonance in a range that spans over 100 ppm, allowing the combination of up to 30 compounds in one screening sample. The CPMG experiment, for measuring T2 relaxation, is widely used in 1H detected fragment screens. Since binding events slow the molecular tumbling of ligands, pronounced changes in T2 in the presence of a target protein are indicative of binding. The 19F signal shows a marked dependence of chemical shift and T2 relaxation on binding, so the 19F CMPG experiment is the ideal method for screening. However, CPMG is not typically used in 19F fragment screening [34]. This is because is it difficult to rapidly and repeatedly refocus the fluorine bandwidth—available pulses typically have long durations and high RF power. Traditionally 19F screening use dynamic line broadening (DLB), or CMPG only on pools of compounds that have a narrow bandwidth of resonances. Neither of these methods are optimal. From 1H screening efforts, we know that DLB does not capture all binding events. Also, pooling compounds whose resonances occur only in a narrow spectral space is not optimal for deconvolution (identification) of a hit.

Here, we demonstrate that the simple optimal pulse tailored to the 15 peaks in the sample is sufficient to perform the CPMG experiment. Since this pulse was generated in seconds, it is feasible to include CPMG in large scale fragment screens. A new refocusing pulse would be generated for each mixture, tailored to peaks actually present. The idea is too take a 1D spectrum and automatically extract peak locations, which are the input to the optimal control algorithm. An optimized refocusing pulse is then generated on the fly; prior knowledge of chemical shift locations in not required.

The first step is to generate a refocusing pulse, starting with an in-phase excitation pulse. Specifically, the optimal control pulse is a point-to-point excitation, where as we require a universal rotation to refocus the spins. The refocusing pulse is extremely simple to generate, provided that the point-to-point excitation leaves all spins in phase. It can be shown that repeating the pulse twice, while performing certain symmetry operations on the x and y components of the B1 field during the second application, produces a new pulse with twice the flip angle (π instead of π/2) and a fixed rotation axis, i.e. a refocusing pulse. The appropriate symmetry operations can be derived by consideration of the toggling frame algorithm in the case that the x- and y-components are even and odd respectively (though the details are beyond the scope of this paper). An alternative derivation can be found in the literature [35]. In short, we concatenate two copies of the excitation pulse, we then time-reverse the second half’s x part, and time-reverse and negate the second half’s y part.

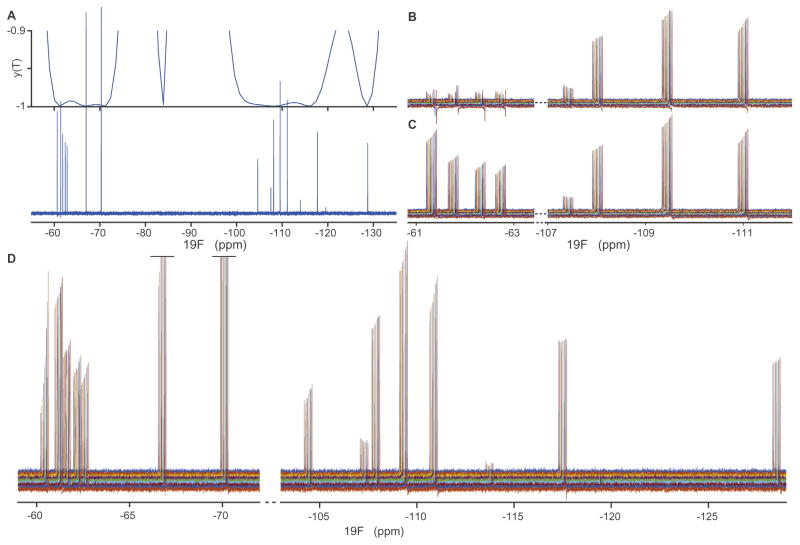
Fig. 4A shows the refocusing profile overlayed with the original spectrum. This shows that the y component of magnetization is being inverted for all spins. Additional simulations confirm that the z component is also being inverted, while the x-component is being preserved. Clearly, high fidelity refocusing is achieved at exactly the populated frequencies. Fig. 4B shows what happens if hard-pulse refocusing is used for refocusing in the CPMG. Far off resonance, the refocusing fails and signal is lost and/or dephased. However, using the optimal refocusing pulse we can refocus all spins (Fig. 4C). We observe smooth T2 decays, as expected from CPMG theory. Fig. 4D shows the complete CPMG data for the whole 19F spectrum, confirming that the CPMG effect is seen in all peaks.

Fig. 4.

Experimental test of sample-specific 19F refocusing pulse. A: The spectrum of the mixture of 19F labeled fragments (lower), overlayed with the simulated y-magnetization after application of the pulse from an initial ρ(0) = I_y (upper). Clearly, the y part of the magnetization is being inverted for the specific spins in the sample. Further simulations (not shown) confirm that the z-component is also inverted, and the x-component is not inverted; that is, the pulse functions as a refocusing pulse for this set of resonances. B: CPMG experiment using a hard pulse for refocusing. The hard pulse works well near its carrier frequency, but we observe loss of signal and dephasing far off resonance, e.g. near −62 ppm. C: In contrast, the optimal pulse refocuses all spins. D: The full CPMG spectrum using the optimal refocusing pulse. All 15 resonances show smooth CPMG decays.

7. Conclusion

The von-Neuman equation for an arbitrary time-varying Hamiltonian can be solved using numerically constructed toggling frames. Moreover, we demonstrated that this is a much faster way to simulate a temporally intricate Hamiltonian than the standard method of using matrix exponentials. The speedup is even more pronounced when the Hamiltonian being simulated is only slightly different from one that has already been simulated. This is exactly what happens in successive steps of the GRAPE algorithm; therefore, we have re-framed the GRAPE procedure so that these computations take place in a continually updated toggling frame. A rapidly generated optimal pulse was shown to perform very well in the context of NMR 19F fragment screening.

We aim to expand this research in two main directions. Firstly, to generalize the toggling frame approach to multi-spin systems. This will allow rapid generation of e.g. optimal pulses for magnetization transfer. Secondly, we will explore further applications in which rapid on-line generation of optimal pulses can be included in NMR work flows, especially in fragment screening, small molecule analysis, and metabolomics.