Selection of reference channels based on mutual information for frequency dependent subtraction method applied to fetal biomagnetic signals

Abstract

Fetal magnetoencephalography (fMEG) recordings are measured in the presence of maternal (mMCG) and fetal (fMCG) magnetocardiograms, and other biological and environmental interferences. MCG interferences can be attenuated by the frequency dependent subtraction (SUBTR) method which uses a set of reference channels and performs subtraction of interference in the frequency domain. We propose a method that uses minimal redundancy and maximal relevance (mRMR) based on mutual information (MI) as criteria to automatically select references. We measured the performance of SUBTR at removing mMCG and fMCG signals in two steps for different number of references in 38 real datasets. The evaluation was based on MCG amplitude reduction. We compared the performance of the mRMR approach with random selection of references. Significant differences in interference removal were found when a distinct number of references were chosen by mRMR compared to random selection. mRMR provides an effective tool to automatically select a set of featured references.

I. Introduction

Fetal brain activity recorded through fetal magnetoencephalography (fMEG) [1], [2], [3] is contaminated by interfering signals such as maternal (mMCG) and fetal (fMCG) magnetocardiograms as well as other biological and environmental signals [4]. After higher order gradiometers are used to attenuate environmental noise, the dominant signals are the fMCG and mMCG signals which can attain amplitudes between 10 to 100 pT [5], [6]. To separate the fMEG signals from noise and interference, frequency-dependent coherence-based methods have been proposed that include the frequency dependent subtraction (SUBTR) method [7]. SUBTR is based on a general input-output model [8], and uses a set of reference channels to perform subtraction of the interferences in the frequency domain. SUBTR has an advantage over other methods such as orthogonal projection (OP) [9] at removing cardiac interferences as well as other biological interference without causing signal redistribution. To perform the subtraction when signal of interest is fMEG, it is essential that reference channels are selected from a sensor region that is sufficiently distant from the fetal head; otherwise, the detected fMEG signals would be reduced. Thus, we can use all sensors outside of the area close to the fetal head (exclusion area), as references to perform the SUBTR method. Unfortunately a high computational effort is needed, especially when using a large array of MEG sensors. A method proposed by Vrba et al. [7] to reduce computational load was based on an initial supposition of reference channels with additional references added in the process that were outside of the exclusion zone and within 10 cm of the channel that has maximum fMCG amplitude. The SUBTR method was executed by selecting different numbers of reference sensors comprising 11, 13, 16, 18, and 33 channels from data corresponding to spontaneous fMEG activity. However with this approach, the user is required to select good initial references, and usually a visual inspection is necessary to assure that desirable reference channels are chosen. In this paper, our goal was to establish a more objective method to choose reference channels for the application of the SUBTR method.

Electrode selection strategies have been used to choose fetal electrocardiogram (ECG) channels [10] by rejecting the ones corresponding to the maternal ECG using the criterion of minimizing the mutual information (MI) between different electrodes and a set of template channels reflecting the pure maternal ECG. However, the pure maternal ECG signals (or fetal) are not unique to the sensors, and choosing channels by only minimizing the MI between the different electrodes and template channels may not be sufficient. In a study from Sameni et al. [11], the channel selection strategy reported in [10] was modified by using two criteria of minimizing and maximizing MI at the same time. The channels are selected by preserving the ones that have the lowest MI with the associated maternal ECG and the highest MI with the fetal ECG to avoid selecting highly noisy signals. Furthermore, they used a criterion for minimizing the MI with the associated maternal ECG, which assures that the selected channels contain the most independent features and are not redundant similar to min-redundancy and max-relevance (mRMR) method [12].

We apply a feature selection algorithm that uses the mRMR criterion to select automatically the MCG reference sensors to be used by SUBTR. Performance of SUBTR at removing mMCG and fMCG interferences in two steps was quantified. This will be helpful for clinical use when only fetal cardiac signals are needed, where a good mMCG attenuation is required. To evaluate the attenuation of the cardiac signals at each step, we calculated the percentage of attenuation as the ratio of the amplitude envelope before and after the SUBTR method was applied using time-averaged signals.

II. Methods

A. SUBTR

Consider y_m(t) to be the measurements obtained from an array of m = 1, 2,…, M MEG sensors at t = 1, 2,…, N time samples. Assume that y(t) is the i-th signal of y_m(t) containing the superposition of the signal of interest, which in most of our investigations is either fMEG or fMCG, and noise signals, denoted as b(t) and c(t), respectively. Thus, y(t) can be written as

$$y(t)=b(t)+c(t).$$ (1)

Moreover, c(t) contains the interferences, and can be described as a linear combination of a set of n = 1,…, N_ref reference signals that do not contain the signal of interest. Estimation of c(t) takes place in the frequency domain as

$$\widehat{C}(f)=\sum _{n=1}^{N_{\mathit{ref}}}{H}_n(f)X_n(f),$$ (2)

where X_n(f) is the finite Fourier transform of the measured reference signals x_n(t), and H_n(f) are frequency dependent transfer functions between x_n(t) and y(t). Note that uppercase letters denote finite Fourier transforms, and lowercase letters denote the associated time-domain signals. Therefore, estimation of the signal of interest in i-th channel

$$\widehat{B}(f)=Y(f)-\widehat{C}(f)=Y(f)-\sum _{n=1}^{N_{\mathit{ref}}}{H}_n(f)X_n(f),$$ (3)

where Y (f) is the Fourier transform of y(t). Note that H_n(f) are needed to be calculated separately for each i-th channel. Equation (3) can be re-written in matrix notation. Let X and Y be column vectors representing the Fourier transforms of x_n(t) and y(t), respectively. Hence, (3) can be expressed as

$$\widehat{\mathit{B}}=\mathit{Y}(f)-{\mathit{H}}^T(f)\mathit{X}(f).$$ (4)

Optimum estimate of H(f) for reduction of interference in B̂ can be attained by ordering and conditioning the reference signals in the frequency domain using the ordinary coherence calculated as follows

$${\mathit{\gamma }}_{ni}^2(f)=\frac{{\mid {\mathit{G}}_{ni}(f)\mid }^2}{{\mathit{G}}_{nn}(f){\mathit{G}}_{ii}(f)},$$ (5)

where G_ni (f), G_nn (f) and G_ii (f) are the corresponding cross-spectral density matrices between the x_n(t) and y(t). Once the references signals are ordered and conditioned, transfer functions [8] can be obtained as

$$\mathit{H}(f)={\mathit{G}}_{xx}^{-1}(f){\mathit{G}}_{xy}(f),$$ (6)

where G_xx (f) is the cross-spectral density matrix of references and G_xy(f) is the cross-spectral density vector between x_n(t) and y(t). Time series of b(t) are calculated by applying the inverse Fourier transform of (3). To accurately estimate of cross-spectral density functions, data is divided into trials L with overlap and shaped by a cosine window to avoid spectral leakage. L is computed using a desirable frequency resolution f_res which should match with the frequency corner f_o of the high-pass filter applied to raw data. The matching condition is $L\ge \frac{f_s}{f_o}$ or f_res ≤ f_o, where f_s is the sample rate of the data.

In this work, we are considering that the signal of interest is the fMEG signal, then mMCG/fMCG traces are the interferences that are needed to be remove with SUBTR method from the measured data.

B. Reference channels selection using mRMR method

MI measures the amount of information that one random variable contains about another, and it has been proposed for use in feature selection algorithms [13], [14]. If we consider a pair of MCG-signal channels as a realization of two random variables, then MI is a measure of the level of similarity between them. In terms of MI, mRMR framework allows to select promising features. Considering the MCG time series as continuous random variables, calculation of the MI is often difficult based on limited number of samples. Thus, a discretization pre-processing step is needed [15]. Allowing discrete variables, let S denote the subset of features that we are seeking and Ω the set of all candidate features {f_i}. The minimum redundancy condition is

$$\underset{S\subset \mathrm{\Omega }}{min}\frac{1}{{\mid S\mid }^2}\sum _{i,j\epsilon S}I(f_i,f_j),$$ (7)

where |S| is the number of features in S and I(f_i, f_j) is the MI between f_i and f_j given by

$$I(f_i,f_j)=\sum _{f_i,f_j}p(f_i,f_j)\mathit{log}\frac{p(f_i,f_j)}{p(f_i)p(f_j)},$$ (8)

where p(f_i, f_j) is the joint probability distribution between f_i and f_j, and p(f_i) and p(f_j) are the respective marginal probabilities.

The maximum relevance condition is to maximize the total relevance of all features in S. To do so, MI is calculated between the target class c ε {c₁,…, c_d} and the feature f_i to quantify the relevance of f_i using the following expression:

$$\underset{S\subset \mathrm{\Omega }}{max}\frac{1}{{\mid S\mid }^2}\sum _{i\epsilon S}I(c,f_i).$$ (9)

The criterion combining conditions (7) and (9) is called mRMR. These conditions can be optimized simultaneously by using the following expression:

$$\underset{S\subset \mathrm{\Omega }}{max}\left\{I(c,f_i)-\frac{1}{{\mid S\mid }^2}\sum _{i,j\epsilon S}I(f_i,f_j)\right\}.$$ (10)

The solution of (10) can be computed efficiently in O(|S| · P) using an incremental algorithm, with P being the total number of features in Ω. Thus for the first iteration of the incremental algorithm, a feature f₁ that shares the largest MI with the class attribute c is selected to the subset S, and additional features f₂,…, f_|S| from the set Ω_S = Ω − S are chosen in an incremental way by using (10).

We assume that all features of the cardiac signals for a specific dataset are covered from channels outside of the exclusion area. We decided to choose channels spatially separated in the SARA sensor array as target class c (see Fig. 1) for calculation of (10). Hence, the MI approach based on these target signals will determine the most adequate references based on the mRMR criterion. This approach has the restriction that information about target signals c is needed a-priori, but we fixed this channels list for all datasets so that no user intervention would be required.

Fig. 1.

mMCG (circles) and fMCG (squares) target channels over SARA sensor array used for mRMR method.

In this study, MI was calculated with the method described in [16], which proposed the feature selection problem with a conditional likelihood approach. Computer programs are freely available in FEAST toolbox at http://www.cs.man.ac.uk/~gbrown/fstoolbox/. The MCG signals were linearly scaled on a set of discrete values and the probability density functions were computed with histograms. Target signals were combined into a single feature vector by merging the array into a joint state [13].

To select references, the proposed approach consists of the following steps: first, mRMR is calculated between all channels and mMCG target channels (circles in Fig. 1), and the top |S_mMCG| mRMR-selected channels which do not belong to the exclusion area are used as references for applying SUBTR to obtain SUBTR-mMCG signals. For the second step, the fMCG signal dominates, hence mRMR is calculated between all channels of SUBTR-mMCG data and corresponding fMCG target signals (squares in Fig. 1). Last, the top |S_fMCG| mRMR-selected channels which do not belong to the exclusion area are used as references to perform SUBTR and obtain the SUBTR-mMCG-fMCG traces.

C. Recordings and data processing

Data was collected using the 151 channel SARA (SQUID Array for Reproductive Assessment) system installed at University of Arkansas for Medical Sciences (UAMS), Little Rock, USA. The duration of a recording was typically around 30 minutes. Subjects with normal pregnancies were recruited with informed consent, and measurement protocols were approved by the UAMS Institutional Review Board. Prior to the SARA recording, the location of the fetal head was identified using ultrasound image, and a marker coil was positioned on the skin of the maternal abdomen roughly over the fetal head. Once the subject is seated on SARA, fetal head location was reconfirmed with a portable ultrasound [17]. Therefore, sensors in the vicinity of the fetal head coil are marked as the exclusion area. Spontaneous data was recorded with sample rate f_s = 312.5 Hz, and highpass filtered with f_o = 0.5 Hz using a 4-th order Butterworth filter. Sensor noise density was $5fT/\sqrt{Hz}$. Data was divided into trials having overlap of 50% that were shaped by a cosine window. We used f_res = 0.4 Hz. Hence, cross-spectral density was estimated by averaging over the trials. The SUBTR method was performed in two steps by selecting references as described in Section II-B.

D. Attenuation percentage

We measured the attenuation of MCG interferences using the mean envelope of the time-averaged signals to the mMCG/fMCG markers before and after applying SUBTR. Thus, signals were lowpass filtered with f_o = 40 Hz. The R peaks of the MCG traces were obtained via a peak-detection algorithm [18], and were used to get the time-averaged signal from raw, SUBTR-mMCG, and SUBTR-mMCG-fMCG data. Next, envelopes for each channel over the sensor array’s exclusion area were calculated via Hilbert transform, and amplitudes were used to measure the percentage of attenuation. For the case of maternal attenuation, we used the envelopes of the time-averaged signals to mMCG markers of raw and SUBTR-mMCG signals. The attenuation percentage was calculated as

$${\tau }_{{\mathit{mMCG}}_1}=100-\left(\frac{A_{\mathit{SUBTR}-\mathit{mMCG}}}{A_{{\mathit{raw}}_{\mathit{mMCG}}}}\right)\ast 100,$$ (11)

where A_{·} denotes the maximum value of the amplitude of the mean envelope of the corresponding time-averaged signal. Note that, after the second step, mMCG signals could be reduced more if the references chosen for SUBTR still contained information of the mMCG traces. Thus, attenuation percentages can be calculated in same way as (11) using the time-averaged signal to mMCG markers of SUBTR-mMCG-fMCG instead of SUBTR-mMCG signals.

For fetal attenuation, we used the envelopes of the time-averaged signal to fMCG markers using raw and SUBTR-mMCG-fMCG data, as follows:

$${\tau }_{\mathit{fMCG}}=100-\left(\frac{A_{\mathit{SUBTR}-\mathit{mMCG}-\mathit{fMCG}}}{A_{{\mathit{raw}}_{\mathit{fMCG}}}}\right)\ast 100.$$ (12)

Note that we used the time-averaged signals of raw data because they provide a rough initial amplitude of the mMCG and fMCG signals. As described in Section II-B, the references found with the mRMR method are ranked by the highest to lowest featured channels; then a certain number of top channels needs to be predefined. Thus, we evaluated the attenuation percentage of the signals in SUBTR process for different numbers of maternal and fetal reference channels. Moreover, a test for monotone trend of the attenuation percentage with the number of sensors was performed by employing a subject-stratified version of Spearman correlation analysis that uses a generalized Cochran-Mantel-Haenszel (CMH) test with rank scores [19] to adjust for the expected dependency among different percent attenuations from the same dataset.

E. Comparison of mRMR and random selection of references

We evaluated mRMR-based method’s performance in selecting MCG references by comparing it to results from references selected randomly. Hence, for the first step of the SUBTR process, we selected random mMCG references within the upper area of sensors (from Q to L row of the SARA sensor array, see Fig. 1) whereas for the second step of SUBTR, bottom sensors were selected (from K to A row of SARA sensor array, see Fig. 1). To evaluate results statistically, the SUBTR method was applied each time after independent random selection of references was used 20 times on each dataset. We calculated the percentage of attenuation of MCG signals when different number of random maternal and fetal reference channels were used. The 20 values per condition were averaged together, and the resulting average attenuation percentages were compared via Wilcoxon signed-rank test with those obtained via the mRMR method.

III. Results and discussion

We processed 38 datasets from pregnant women whose gestational ages ranged from 27 weeks to a maximum of 38 weeks at time of the SARA measurement. We determined the exclusion area by selecting channels within a radius of 10 cm of the fetal head coil. The mRMR method was used to select mMCG/fMCG reference sensors and SUBTR was applied. We compared our approach with random selection of references. The inset plot in Fig. 2 shows an example of the SARA sensor array for a subject displaying the fetal head coil (triangle around LK3 sensor) and exclusion area (asterisks). Corresponding values of the mRMR score are shown in Figs. 2a and b, when maternal or fetal templates were used. For this example, we show the top 12 mMCG (circles) and 18 fMCG (squares) mRMR-selected reference sensors that obtain mRMR score values above 0.3 (Fig. 2a) and 0.8 (Fig. 2b), respectively. We observed that the mRMR calculation chose references with highest values even inside of the exclusion area (asterisks with high mRMR value in Fig. 2b) for the case of fMCG selection. However those sensors were only used to give further information to the mRMR method, which is helpful when there is large overlap between the exclusion area and cardiac signal area. These overlap sensors were not used as references when SUBTR was applied in the second step. Fig. 3a shows a time segment of raw data from sensors in the exclusion area where mMCG (with a period of about 0.8 s) and fMCG (with period of about 0.4 s) signals are visible. Fig. 3b and c show the corresponding time series after SUBTR was performed when the mRMR approach was applied. It can be observed that fMCG is visible after the first step (Fig. 3b) of the SUBTR process, whereas there is no residual visible in the time course after the second step (Fig. 3c). Furthermore, we calculated the averaged power spectrum density (PSD) for each step of the process (Fig. 3d), and it is observed that SUBTR removed other interferences such as power line noise (60 Hz).

Fig. 2.

Scores of mRMR when maternal or fetal templates were used for subject lr11_34w. Circles and squares are the top 12 mMCG and 18 fMCG mRMR-selected references. Inset plot shows: exclusion area (asterisks) selecting within 10 cm around the fetal head coil location (triangle).

Fig. 3.

Time series from sensors in the exclusion area for subject lr11_34w. a) Raw data. b) and c) Time traces after removing mMCG and fMCG interferences, respectively. d) PSD of the SUBTR process.

A. Attenuation for different number of references

We measured the percent of the attenuation of the MCG interferences for the 38 datasets as described in Section II-D. All results that we show below correspond to the attenuation of the MCG interferences in the exclusion zone. Fig. 4 is an example of the time-averaged signals of the SUBTR procedure for one subject when 12-mRMR and 18-mRMR mMCG and fMCG references, respectively, were used. The original time-averaged signal to mMCG markers (see Fig. 4a) is around 13 pT. After applying the first step of SUBTR, the signal is attenuated to around 8 fT (see Fig. 4b). After the second step, the mMCG signal (Fig. 4c) is attenuated to around 5 fT (which is in the range of SARA sensor noise), whereas for the time-averaged signal to fMCG markers, the signal is attenuated to around 4 fT from the original amplitude (1 pT). In the same way, Fig. 5 shows the time-averaged signals when random selection of references was utilized for the same dataset. This example shows more mMCG (Fig. 5b–c) and fMCG (Fig. 5e) residual compared to when the mRMR approach was applied.

Fig. 4.

Time-averaged signals when mRMR approach was used for reference selection. Traces are from exclusion area for subject lr11_34w for 12 and 18 mMCG and fMCG references. a) Time-averaged signal to mMCG markers of the raw data. b) Time-averaged signal to mMCG markers of SUBTR-mMCG data. c) Time-averaged signal to mMCG markers of SUBTR-mMCG-fMCG data. d) Time-averaged signal to fMCG markers of the raw data. f) Time-averaged signal to fMCG markers of SUBTR-mMCG-fMCG data.

Fig. 5.

Time-averaged signals when random selection of references was used. Traces are from exclusion area for subject lr11_34w for 12 and 18 mMCG and fMCG references. a) Time-averaged signal to mMCG markers of the raw data. b) Time-averaged signal to mMCG markers of SUBTR-mMCG data. c) Time-averaged signal to mMCG markers of SUBTR-mMCG-fMCG data. d) Time-averaged signal to fMCG markers of the raw data. f) Time-averaged signal to fMCG markers of SUBTR-mMCG-fMCG data.

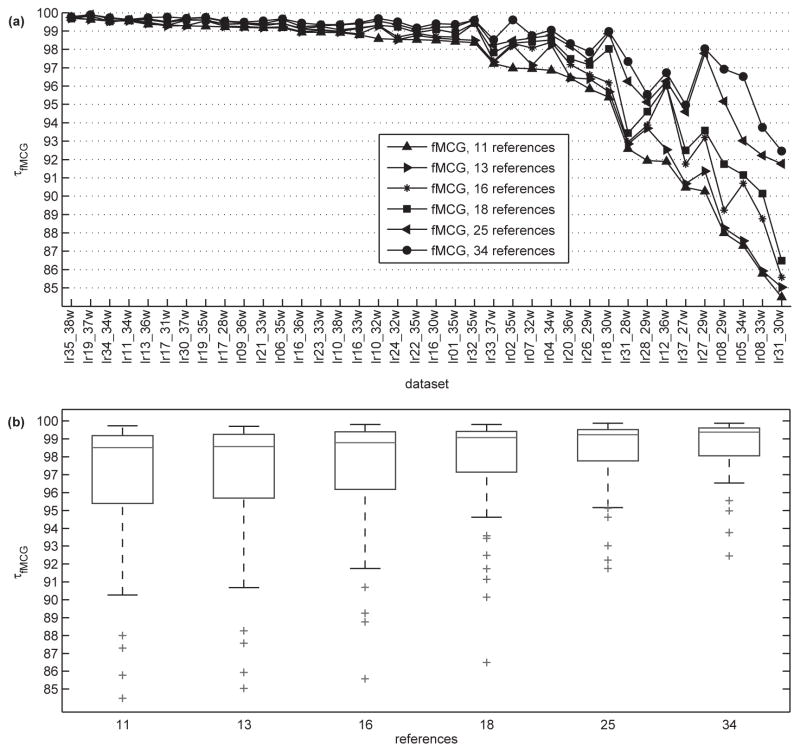
After processing all datasets, we found that mMCG can be completely cancelled by using 12 mRMR-selected references obtaining attenuation percentages of 99.26±1.4 (mean ± SD) and 99.86 ± 0.12 (mean ± SD), respectively, after first and second steps of the SUBTR process. However, for the case of fMCG, successful removal required more references. Thus, SUBTR procedure was performed with different sets of mRMR-selected references comprising 11, 13, 16, 18, and 34 channels. To accomplish this we found the top 34 mRMR-selected references, and removed the less featured channels from this set to get the 18, 16, 13, 11 references. After applying SUBTR, fMCG amplitudes of the time-averaged signals were generally close to or well below 20 fT with median amplitudes of 10.51, 10.13, 7.26, 6.72, 4.63, 4.13 fT for 11, 13, 16, 18, 25 and 34 references, respectively, and median percentage attenuation values of 98.51, 98.57, 98.78, 99.07, 99.23, 99.38, respectively (Fig. 6a). As we expected, more attenuation of the fMCG signals was observed with the increase in number of references. At the same time the attenuation percentage might not be significant for each additional reference sensor for a specific data set, or occasionally there could be fluctuation of attenuation percentages. Fig. 6a shows the results of the attenuation percentage per subject ranging between 99% − 95% of attenuation for 29 datasets using either 11 or 34 mRMR-selected references. For the remaining 9 datasets, we get the poorest rate of attenuation of 85% and around 92%−95% using 25 and 34 mRMR-selected references, respectively. Moreover, the percent attenuations displayed a significant monotone trend with the number of sensors (Fig. 6b), as demonstrated by a Spearman correlation between them of 95% (CMH chi-square=171.61, DF=1; p = 3.3 × 10⁻³⁸). Our results show that with the discretization preprocessing step, density estimation works well for discrete MI calculation. However, different approaches could be used [20] for calculation of MI between continuous variables to enhance the performance of the mRMR framework to select reference channels.

Fig. 6.

Attenuation percentages of fMCG signals using mRMR approach. a) Per datasets which were sorted from highest to lowest attenuation. b) Per number of references. Solid horizontal line inside the box corresponds to median, the edges of the box are the 25th and 75th percentiles, the whiskers extensions are the most extreme data points, and ”+” markers correspond to the outliers. Monotone trend was found with χ² = 171.61, df = 1 and p-value = 3.3 × 10⁻³⁸ with a value of 95% for the Spearman correlation between percent attenuation and the number of mRMR-selected references.

B. Comparison between mRMR and random selection of references

We systematically selected 26 datasets from Fig. 6a by excluding every third dataset from the analysis. For the case of mMCG removal, we used 12 randomly selected references, obtaining a percentage attenuation of mMCG signal for the 26 datasets of 99.5 ± 0.55 (mean ± SD) and 99.9 ± 0.09 (mean ± SD) after the first and second steps, respectively, of SUBTR. At each step, the corresponding values for the mRMR method of the 26 datasets were: 99.5 ± 0.50 (mean ± SD) and 99.9 ± 0.08 (mean ± SD). Hence, no significant difference was found when 12 references with random channel selection versus mRMR approach was used. However, with random selection, a visual inspection task might be performed to assure good attenuation of mMCG signals such as the example displayed in Fig. 5b and c where maternal residual is still visible. For fMCG removal, we tested SUBTR when 11, 13, 16, 18, and 34 references were randomly chosen. To this end, we performed random permutations by generating integers of the corresponding channels of the bottom area of SARA array that were outside of the exclusion area. We used different seeds for the pseudo-random number generator. For each dataset, we applied SUBTR for each condition of the number of fMCG references, repeating this 20 times with independent selection of references. Percentage attenuation in the sensors corresponding to the exclusion area was calculated using (12), and an average of the 20 repetitions was obtained for each dataset and condition. Furthermore, Wilcoxon-signed rank tests were used for statistical comparisons at the 5% significance level. Fig. 7a shows the ratio of attenuation percentages between mRMR and the random selection approach for the 26 selected datasets, which are displayed in the same order as in Fig. 6a. We found that the mRMR-selected references perform better for 24 datasets compared to references chosen by random selection. For these 24 datasets, the percent attenuation was higher when the mRMR method was used for each and every condition of the number of references chosen. For all such conditions, the difference between mRMR and random selection was statistically significant (see Fig. 7b).

Fig. 7.

Ratio of attenuation percentages of fMCG signals when references were selected with mRMR and random approach. a) Per datasets. b) Per number of references. Solid horizontal line inside the box corresponds to median, the edges of the box are the 25th and 75th percentiles, the whiskers extensions are the most extreme data points, and “+” markers correspond to the outliers. Statistical analysis was done using Wilcoxon signed-rank test.

IV. Conclusion

This study explored the use of the mRMR criterion for selecting references for the SUBTR method. Our experiments were tested with different datasets in which both mRMR and random selection were used. The results demonstrated that mRMR method provides an effective tool to select featured reference channels. Significant differences in fMCG removal were found when a distinct number of references were chosen by mRMR compared to random selection. mRMR method may be applied with a short window-segments approach where different references are chosen over time, this might improve the results of the SUBTR method when data is non-stationary. Sensor selection based on the mRMR method may be applied to sensor array data from other applications. Also, we are considering application of these methods for event-related fMEG signals.