AUTOMATED LEVEL SET SEGMENTATION OF HISTOPATHOLOGIC CELLS WITH SPARSE SHAPE PRIOR SUPPORT AND DYNAMIC OCCLUSION CONSTRAINT

Abstract

In this paper, we propose a novel segmentation method for cells in histopathologic images based on a sparse shape prior guided variational level set framework. We automate the cell contour initialization by detecting seeds and deform contours by minimizing a new energy functional that incorporates a shape term involving sparse shape priors, an adaptive contour occlusion penalty term, and a boundary term encouraging contours to converge to strong edges. As a result, our approach is able to accommodate mutual occlusions and detect contours of multiple intersected cells. We apply our algorithm to a set of whole-slide histopathologic images of brain tumor sections. The proposed method is compared with other popular methods, and demonstrates good accuracy for cell segmentation by quantitative measures, suggesting its promise to support biomedical image-based investigations.

1. INTRODUCTION

Image segmentation is a fundamental problem in computer vision and image analysis. In this community, level set-based approaches are important tools, because they are able to handle cell shapes with complex topological variations [1, 2, 3, 4]. However, this set of methods still faces several challenges. 1) It is difficult to segment cells without appropriate cell initializations. 2) Methods using shape prior models take as a reference a predefined set including shape priors insufficient to represent shape variations in most cases. 3) Segmentation of mutually occluded cells remains challenging. To address these problems, we propose a variational level set model to segment multiple cells with mutual occlusion and demonstrate its efficacy with application to pathologic images of brain tumor tissues. Although overlapped cells may take a small fraction of the cell population of interest, the absolute number is large in a whole-slide microscopy image where the total cell number is commonly on the scale of million [5]. Additionally, some tumor regions tend to have very high tumor cell density, presenting much more overlapped cells of interest than other regions. Thus, it would lead to too much information loss if we excluded such overlapped cells from clinically meaningful tissue areas for morphometry analysis [6]. The main contributions of this work are summarized as follows: 1) We propose a two-stage framework to effectively detect seeds and segment cells. 2) A sparse representation based shape term is introduced to better incorporate shape prior information. 3) We introduce a dynamic cell occlusion term to deal with occlusion events involving a variable number of cells. 4) Our approach is successfully applied to brain histopathological images for cell segmentation task. Our framework, as shown in Figure 1, consists of a seed detection algorithm for cell contour initialization and an integrated contour deformable model that incorporates region, shape and boundary information.

Fig. 1.

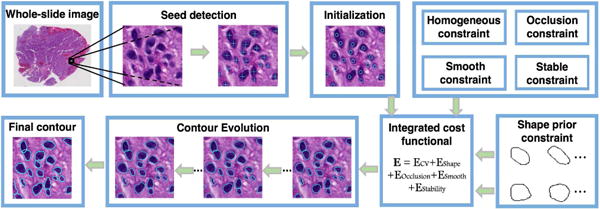
Schema of our developed cell segmentation method applied to histopathologic images.

2. METHOD

2.1. Shape representation

We locate cells and initialize cell contours by a previously developed seed detection algorithm that utilizes joint information of spatial connectivity, distance constraint, image edge map, and a shape-based voting map derived from eigenvalue analysis of Hessian matrix across multiple scales [7]. Given an image with detected seeds of N cells ${\mathcal{O}}_1$, ${\mathcal{O}}_2$, …, ${\mathcal{O}}_N$, we initialize each cell ${\mathcal{O}}_i$ as a small circle centered at a seed. Each cell contour is a closed and bounded shape contour $\partial {\mathcal{O}}_i$ in image domain $\mathrm{\Omega }\subset {ℝ}^2$. The level set framework implicitly represents $\partial {\mathcal{O}}_i$ as a zero level set of a Lipschitz function ${\varphi }_i:\mathrm{\Omega }\to ℝ$ where ϕ_i(x) has positive and negative value when x is inside and outside ${\mathcal{O}}_i$, respectively. A distance map function Γ(ϕ_i(x)) represents the shortest distance $d(\mathit{x},\partial {\mathcal{O}}_i)$ from a current pixel x in the image domain Ω to a given cell contour $\partial {\mathcal{O}}_i=\{\mathit{x}|{\varphi }_i(\mathit{x})=0,\forall \mathit{x}\in \mathrm{\Omega }\}$. In this way, we can represent N cells in a image as N distance map functions. Instead of partitioning an image into disjoint regions, we allow an image pixel to be associated with multiple cells with intersecting contours.

We use a set of 27,000 shape priors to cover the complex shape variation observed in most histopathology images. Shape priors are annotated manually and aligned by the generalized Procrustes analysis first [8]. Next, they are clustered with spectral clustering algorithm into M clusters and the average shape of each resulting cluster is computed [9]. We denote Ψ = {ψ₁, ψ₂, …, ψ_M} as the set of two-dimensional distance maps derived from average shape priors with unit Frobenius norm. We align the cell contour $\partial {\mathcal{O}}_i$ to shape priors Ψ by the similarity transformation: ${\stackrel{\sim }{\mathit{x}}}_i=T(\mathit{x};s_i,{\theta }_i,{\mathit{t}}_i)$, where x = [x₁, x₂]^T and ${\stackrel{\sim }{\mathit{x}}}_i$ are a pixel location before and after alignment; {s_i}, {θ_i}, and {t_i = [t_i1, t_i2]^T} are scale, rotation and translation coefficient, respectively. As our shape priors Ψ have nearly same scales, we set s_i = 1, ∀_i to achieve better computational efficiency.

After mapping the i-th cell to the shape prior set, we assume that a cell ${\mathcal{O}}_i$ with the associated distance map function Γ(ϕ_i(x)) can be approximately represented as a linear composition of aligned sparse shape priors in $\mathrm{\Psi }({\stackrel{\sim }{\mathit{x}}}_i)$. We vectorize two dimensional distance maps and denote vectorized distance map of ${\mathcal{O}}_i$ as $\overline{\mathrm{\Gamma }}({\varphi }_i(\mathit{x}))$. Additionally, we compose the mapped shape prior matrix with vectorized shape prior distance maps by column and denote it as $\overline{\mathrm{\Psi }}({\stackrel{\sim }{\mathit{x}}}_i)$. Note that each column has a unit ${ℒ}_2$ norm. By the linearity assumption, we have $\overline{\mathrm{\Gamma }}({\varphi }_i(\mathit{x}))=\overline{\mathrm{\Psi }}({\stackrel{\sim }{\mathit{x}}}_i){\mathit{\alpha }}_i+{\mathit{e}}_i$, where α_i is a coefficient vector representing the weights of shape priors in shape reconstruction and e_i is the error vector.

Given a large enough training set, a test shape can be sufficiently represented by a small number of shape priors [10][11]. Dissimilar prior shapes are suppressed due to large penalty measured by the reconstruction error. To ensure sparsity and solvability, we apply the relaxed ${ℒ}_1$ norm regularization in the formulation [12]. Moreover, we reduce $\overline{\mathrm{\Gamma }}$ dimensionality to accommodate computational cost using a non-zero projection matrix R ∈ ℝ^d×m, d ≪ m with entries randomly generated from standard Gaussian distribution and subject to unit length for all rows. Note the choice of matrix R does not critically affect the ability to find the optimal sparse solution by ${ℒ}_1$-minimization [10]. The resulting sparse representation problem is formulated as:

$${\widehat{\mathit{\alpha }}}_i=\underset{{\stackrel{\vee }{\mathit{\alpha }}}_i}{\text{arg}min}{\Vert \stackrel{\vee }{\mathrm{\Gamma }}({\varphi }_i)-B{\stackrel{\vee }{\mathit{\alpha }}}_i\Vert }_2^2+\mathrm{\lambda }{\Vert {\stackrel{\vee }{\mathit{\alpha }}}_i\Vert }_1$$ (1)

where $\stackrel{\vee }{\mathrm{\Gamma }}({\varphi }_i)=R-\overline{\mathrm{\Gamma }}({\varphi }_i)$, $B=[\stackrel{\vee }{\mathrm{\Psi }}({\stackrel{\sim }{\mathit{x}}}_i);I]$, $\stackrel{\vee }{\mathrm{\Psi }}=R\overline{\mathrm{\Psi }}$, ${\stackrel{\vee }{\mathit{\alpha }}}_i=[{\mathit{\alpha }}_i,{\stackrel{\vee }{\mathit{e}}}_i]$, and ${\stackrel{\vee }{\mathit{e}}}_i=R{\mathit{e}}_{i\cdot }{I}^{d\times d}$ is an identity matrix.

2.2. Level set functional formulation

Distance map Γ(ϕ_i) can be encoded as a sparse linear superposition of shape priors, with coefficients ${\widehat{\mathit{\alpha }}}_i$ obtained by optimizing equation (1). Thus, we define a shape term for the fitting shape error between individual deformable contours and linear combination of sparsely selected shape priors:

$$E_1={\displaystyle \sum _{i=1}^N{\displaystyle {\int }_{\mathrm{\Omega }}{(\mathrm{\Gamma }({\varphi }_i)-{\displaystyle \sum _{j=1}^M{\psi }_j{\widehat{\alpha }}_{ij}})}^{2}d\mathit{x}}}$$ (2)

where ${\widehat{\alpha }}_{ij}$ is the j-th entry of ${\widehat{\mathit{\alpha }}}_i$. With minimization of this term, the distance map function Γ(ϕ_i) best fits to the feature space defined by the shape priors. Note when λ is sufficiently large, the sparse shape term is determined by a single shape prior and our model is, therefore, degenerated to a single shape prior segmentation.

In two dimensional (2D) histopathologic images, it is common to have mutually occluded cells since 2D images represent projections of objects in 3D space. It is a challenging task to segment mutually occluded cells and identify separating boundaries. To address this problem, we introduce an adaptive occlusion penalty term to dynamically suppress cell intersection events. This occlusion penalty is designed to depend on the number of cells that are overlapped:

$$E_2={\displaystyle {\int }_{\mathrm{\Omega }}{\displaystyle \sum _{i=1}^{N}H({\varphi }_i)-[1-{\displaystyle \prod _{k=1}^N(1-H({\varphi }_k))}]}d\mathit{x}}$$ (3)

where H(·) is the Heaviside function. The first term in E₂ is a superposition of the Heaviside functions of all cells and the second term is a binary function indicating inside of any cell/outside of all cells. This term represents a dynamic occlusion penalty adaptive to the number of intersecting cells.

We solve cell segmentation problem by minimizing the following functional within a variational level set framework:

$$\begin{gathered} E(\mathrm{\Phi },C,\mathrm{\Theta },T)={\mathrm{\lambda }}_0{\displaystyle \sum _{i=1}^N{\displaystyle {\int }_{\mathrm{\Omega }}{\left(I-c_i\right)}^{2}H({\varphi }_i)d\mathit{x}}}+{\mathrm{\lambda }}_b{\displaystyle {\int }_{\mathrm{\Omega }}{\left(I-c_b\right)}^2{\displaystyle \prod _{i=1}^N(1-H({\varphi }_i))d\mathit{x}}+\nu E_1+\omega E_2+\mu {\displaystyle \sum _{i=1}^N{\displaystyle {\int }_{\mathrm{\Omega }}Q(I(\mathit{x}))|\nabla H({\varphi }_i)|d\mathit{x}}}} \\ +\xi {\displaystyle \sum _{i=1}^N{\displaystyle {\int }_{\mathrm{\Omega }}R(|\nabla {\varphi }_i|d\mathit{x})}} \end{gathered}$$ (4)

where c_i and c_b are scalars that define the average pixel intensities in cell regions and background, respectively. $Q(I(\mathit{x}))=\text{exp}(-\frac{{\left|\nabla I(\mathit{x})\right|}^2}{2{\sigma }^2})$ is an exponential function monotonously decreasing as the magnitude of gradient of x increases. R(·) is defined as a double-well potential function [13]. |∇H(ϕ_i)| is non-zero only on cell boundaries. We denote Φ = {ϕ_i}, C = {c_i, c_b}, Θ = {θ_i} and T = {t_i1, t_i2}, i = 1, 2, …, N as sets of variables of the energy functional. Parameters {λ_o, λ_b, μ, ξ, ω, ν} are weights of different terms. The last two terms in equation (4) are used to encourage contours to converge to strong boundaries and retain signed distance property for stable level set function computation respectively.

2.3. Numerical computations

We optimize the established functional iteratively by updating functions Φ and variables {C, Θ, T} alternatively. Parameterizing iteration as an artificial time variable t > 0, we minimize the functional by solving Euler-Lagrange equation:

$$\frac{\partial {\varphi }_i}{\partial t}=-{\mathrm{\lambda }}_o{\left(I-c_i\right)}^2\delta ({\varphi }_i)+{\mathrm{\lambda }}_b{\left(I-c_b\right)}^2{\displaystyle \prod _{k=1,k\ne i}^N(1-H({\varphi }_k))\delta ({\varphi }_i)}-2\nu (\mathrm{\Gamma }({\varphi }_i)-{\displaystyle \sum _{j=1}^M{\psi }_j{\widehat{\alpha }}_{ij}})-\omega \delta ({\varphi }_i)(1-{\displaystyle \prod _{k=1,k\ne i}^N(1-H({\varphi }_k)))}+\mu \delta ({\varphi }_i)(\nabla Q(I(\mathit{x}))\cdot \frac{\nabla {\varphi }_i}{\left|{\varphi }_i\right|}+Q(I(\mathit{x}))\mathit{div}(\frac{\nabla {\varphi }_i}{\left|\nabla {\varphi }_i\right|}))+\xi \mathit{div}(\frac{R^{\prime }(\left|\nabla {\varphi }_i\right|)}{\left|\nabla {\varphi }_i\right|}\nabla {\varphi }_i)$$ (5)

where δ(·) denotes the Dirac delta function.

Next, we fix Φ and update transformation parameters. We derive updating equations for transformation parameters by computing gradient descent of functional E(Θ, T):

$$\frac{\partial {\theta }_i}{\partial t}=2\nu {\displaystyle {\int }_{\mathrm{\Omega }}(\mathrm{\Gamma }({\varphi }_i)-{\displaystyle \sum _{j=1}^M{\psi }_j{\widehat{\alpha }}_{ij}})({\displaystyle \sum _{j=1}^M({\nabla }_{{\stackrel{\sim }{x}}_i}{\psi }_j\cdot {\nabla }_{{\theta }_i}{\stackrel{\sim }{\mathit{x}}}_i){\widehat{\alpha }}_{ij}})}d\mathrm{x}$$ (6)

$$\frac{\partial t_{ik}}{\partial t}=2\nu {\displaystyle {\int }_{\mathrm{\Omega }}(\mathrm{\Gamma }({\varphi }_i)-{\displaystyle \sum _{j=1}^M{\psi }_j{\widehat{\alpha }}_{ij}})({\displaystyle \sum _{j=1}^M({\nabla }_{{\stackrel{\sim }{x}}_i}{\psi }_j\cdot {\nabla }_{t_{ik}}{\stackrel{\sim }{\mathit{x}}}_i){\widehat{\alpha }}_{ij}})}d\mathrm{x}$$ (7)

where k = 1, 2. Finally, we fix Φ, and {Θ, T}, and update c_i and c_b.

$$\frac{\partial E(c_i,c_b)}{\partial c_i}=0\Rightarrow c_i=\frac{{\displaystyle {\int }_{\mathrm{\Omega }}IH({\varphi }_i)dx}}{{\displaystyle {\int }_{\mathrm{\Omega }}H({\varphi }_i)dx}}$$ (8)

$$\frac{\partial E(c_i,c_b)}{\partial c_b}=0\Rightarrow c_b=\frac{{\displaystyle {\int }_{\mathrm{\Omega }}I{\displaystyle {\prod }_{i=1}^N(1-H({\varphi }_i(x)))}dx}}{{\displaystyle {\int }_{\mathrm{\Omega }}{\displaystyle {\prod }_{i=1}^N(1-H({\varphi }_i(x)))}dx}}$$ (9)

3. EXPERIMENTAL RESULTS

We verify our algorithm with whole-slide histopathologic images of brain tumors. For computational efficiency, 512×512 pixel image patches are used for test, containing 1857 cells in aggregation. We set parameters empirically as follows: λ_o = λ_b = 1, μ = 5000, ξ = 2, ω = 2000, ν = 3000.

We cluster the shape priors into 100 groups by spectral clustering and use group mean shapes to construct the shape prior dictionary. Next, we apply the seed detection algorithm to search for seed points [7]. We present a typical cell seed detection result in Figure 2(a), where cyan circles are used to represent detected cell seeds. We solve the cell segmentation problem by the variational level set framework. The level set functions do not stop evolving until they either reach convergence or exceed iteration number limit. We present the evolution results of zero level sets at iteration 10, 20, and 30 in Figure 2 where the detected cell shapes are well defined. Notably, those overlapping cells are also correctly segmented, with occluded boundaries recovered. It is also observed that most zero level sets can rapidly converge to true cell boundaries within 10 iterations. After that, zero level sets fine tune themselves to better fit to cell contour details. This is especially noticeable for those overlapped cells.

Fig. 2.

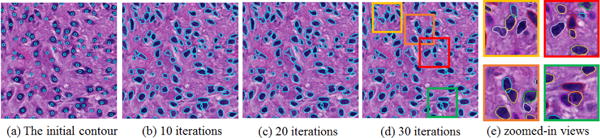
Cell contour deformation: initial zero level set and that after 10, 20, 30 evolving iterations, respectively. Overlapping cells are well separated, as shown in close-up views.

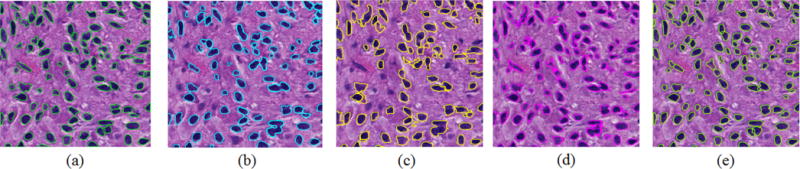
We also investigate the segmentation contribution from distinct terms in our variational model by comparing their associated segmentation results. The segmentation result with our default parameter setting is shown in Figure 3(a). When ν = 0, the shape prior fitting term E₁ does not take effect in the contour deformation process. The resulting segmentation outcome is presented in Figure 3(b), where finalized cell contours are less regulated. Similarly, we can remove the occlusion penalty term E₂ from the variational model by setting ω = 0. The associated result is illustrated in Figure 3(c). Under this setting, the detected cells present a strong inclination to overlap with each other. When the shape prior fitting term E₁, the dynamic occlusion penalty term E₂, and the evolutionary stability term are all removed (ν = ω = ξ = 0), the resulting cell contours become significantly degraded as shown in Figure 3(d). Note that shapes appear to be less regulated in Figure 3(b–d) without one or more terms in the variational model. In addition to the final results with only a subset of terms in Figure 3(b–d), we also investigate the sensitivity of parameters to final results. Our investigations with parameter deviation from our proposed value set suggest that results remain similar even when we change μ by 22% (μ = 3900), 10% (μ = 4500), and ν by 67% (ν = 5000), as presented in Figure 3(e–g). Figure 3(h) presents results when μ and ν are simultaneously changed by 22% and 67%. Overall, a larger μ leads to a better contour convergence to true cell boundary; A larger ν forces contours to look more similar to the reconstructed sparse shape priors by E₁; A larger ω tends to prevent cells more from overlapping with each other by E₂. The other three parameters, i.e. λ_o = λ_b = 1, ξ = 2, do not need to be tuned in general. As a result, this method can be applied to other datasets without much parameter tuning.

Fig. 3.

Segmented cells with distinct parameter settings: (a) μ = 5000, ξ = 2, ω = 2000, ν = 3000; (b) same as (a) except ν = 0; (c) same as (a) except ω = 0; (d) same as (a) except ξ = 0, ω = 0, ν = 0; (e) same as (a) except μ = 3900; (f) same as (a) except μ = 4500; (g) same as (a) except ν = 5000; (h) same as (a) except μ = 3900 and ν = 5000.

To assess our method quantitatively, we collect human expert annotations on testing images and use human annotations as ground truth. By comparing the experimental result B with ground truth annotation A, we evaluate our method with multiple metrics[17, 18]: Jaccard coefficient J(A, B), precision rate P(A, B), recall rate R(A, B), F1 score F₁(A, B) and Hausdorff distance H(A, B). We present in Table 1 performances of the proposed method and three other popular methods, including MS [14], ISO [15], and SBGFRLS [16]. A qualitative method performance comparison is shown in Figure 4. Note our proposed method is able to capture cell boundaries better. In particular, only our method can recover boundaries of overlapped cells by comparisons. This property makes our method superior to the other methods when analytics of occluded cells is crucial in investigations.

Table 1.

The performance comparison of different cell segmentation methods.

Methods	J		P		R		F1		H
	Mean	Std Dev	Mean	Std Dev	Mean	Std Dev	Mean	Std Dev	Mean	Std Dev
MS [14]	0.49	0.25	0.61	0.32	0.80	0.17	0.62	0.25	27.97	30.07
ISO [15]	0.69	0.22	0.82	0.27	0.83	0.14	0.79	0.21	12.77	24.39
SBGFRLS [16]	0.75	0.12	0.91	0.15	0.82	0.09	0.85	0.10	6.84	8.46
Ours	0.76	0.11	0.93	0.11	0.82	0.11	0.86	0.09	4.96	4.76

Fig. 4.

Segmentation results obtained by (a) ground truth; (b) MS; (c) ISO; (d) SBGFRLS; and (e) our proposed method.

4. CONCLUSION

We propose a new cell segmentation method based on the level set framework, aiming to identify contours of multiple cells with mutual occlusion in histopathologic images. For cell contour deformation, we construct a shape dictionary including typical cell prior shapes by spectral clustering. An adaptive cell occlusion penalty term is designed to dynamically penalize cell contour occlusion based on the number of overlapped cells. Experiments on brain tumor images produce promising results as compared with other methods, suggesting the effectiveness of our approach on cell segmentation for histopathologic images.