A Generic Approach to Pathological Lung Segmentation

Abstract

Accurate segmentation of pathological lungs from computed tomography (CT) scans remains unsolved because available methods fail to provide a reliable generic solution for a wide spectrum of lung abnormalities. In this study, we propose a novel pathological lung segmentation method that takes into account neighbor prior constraints and a novel pathology recognition system. Our proposed framework has two stages; during stage one, we adapted the fuzzy connectedness (FC) image segmentation algorithm to perform initial lung parenchyma extraction. In parallel, we estimate the lung volume using rib-cage information without explicitly delineating lungs. This rudimentary, but intelligent lung volume estimation system allows comparison of volume differences between rib cage and FC based lung volume measurements. Significant volume difference indicates the presence of pathology, which invokes the second stage of the proposed framework for the refinement of segmented lung. In stage two, texture-based features are utilized to detect abnormal imaging patterns (consolidations, ground glass, interstitial thickening, tree-inbud, honeycombing, nodules, and micro-nodules) that might have been missed during the first stage of the algorithm. This refinement stage is further completed by a novel neighboring anatomy-guided segmentation approach to include abnormalities with weak textures, and pleura regions. We evaluated the accuracy and efficiency of the proposed method on more than 400 CT scans with the presence of a wide spectrum of abnormalities. To our best of knowledge, this is the first study to evaluate all abnormal imaging patterns in a single segmentation framework. The quantitative results show that our pathological lung segmentation method improves on current standards because of its high sensitivity and specificity and may have considerable potential to enhance the performance of routine clinical tasks.

I. Introduction

Pulmonary diseases and disorders are one of the major causes of deaths and hospitalization around the world. The American Lung Association estimates that about 400,000 deaths occur per year in the United States from lung diseases [1]. For non-invasive detection and diagnosis of lung diseases, quantification of the disease severity, and therapy/surgery planning, radiological imaging techniques, particularly computed tomography (CT), are the current standard in the routine clinics. In parallel to the technological advances in imaging, automated computer analysis and decision support systems are often sought by clinicians and radiologists to further assist their diagnostic tasks. Specific to radiological quantification of lung diseases, efficient and robust image analysis tools are required for extracting information pertaining to lung pathology and morphology in a reliable and efficient way. The lung volume of interest containing abnormalities is often the subject of further analysis and; therefore, precise lung segmentation is a precursor to the deployment of such tools for pulmonary image analysis.

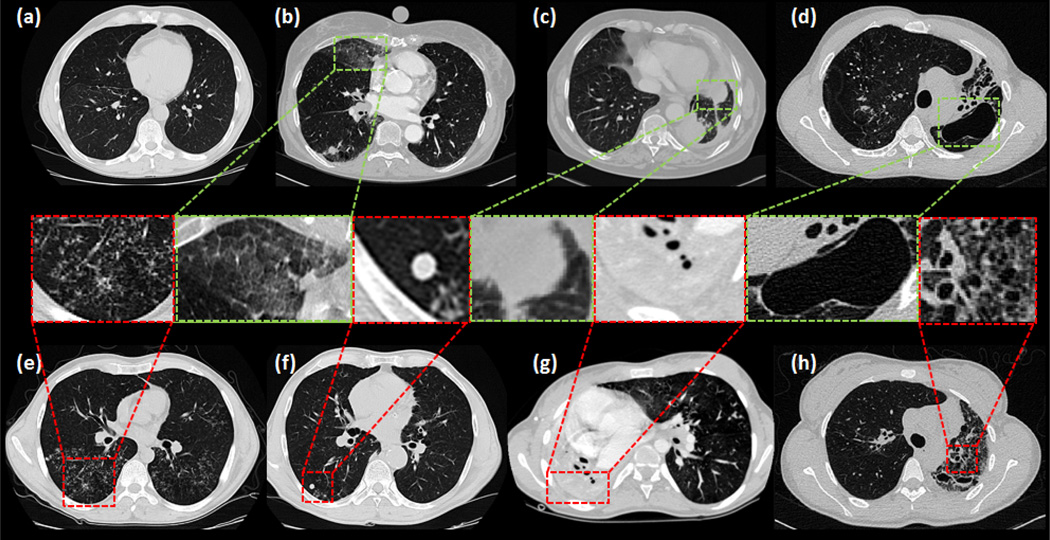
Although current state-of-the-art lung segmentation algorithms work well for certain lung pathologies present in moderate amounts, they fail to perform when dense pathologies exist. Accurate segmentation of the pathological lung is challenging since lung pathologies hold appearances different from the normal lung tissue. Fig. 1 highlights common abnormal imaging patterns and pleura pertaining to different lung diseases. CT scans of patients with severe lung diseases often include diverse imaging patterns. Thus, it is difficult to adapt the current state-of-the-art lung segmentation methods due to their limited ability to be applied to diverse imaging patterns with dense pathologies. Our aim in this work is to target this challenge, and provide a generic solution for lung segmentation from CT scans.

Fig. 1.

Different imaging patterns in pulmonary CT are shown: (a) normal lung (b) ground-glass opacity (GGO) (c) consolidation (d) cavity (e) tree-in-bud and micro nodules (f) nodules (g) pleural effusion (h) honeycomb.

A. Related work

Most methods reported in the literature evaluated a subset of pathologies when segmenting lungs. Therefore, a generic solution that can work in routine clinical environment for a wide range of pathologies without expert assistance is not available.

Threshold-based methods [2], [3] are often used for their efficiency. However, such methods have limited applicability as they fail to consider the intensity variations due to pathologies or even under normal conditions. Region-based methods, such as region growing [4]–[6], watershed transform [7], [8], graph search [9], [10], and FC [11], [12], are found useful in catering for the intensity changes. However, with the presence of dense pathology in the lung field, the intensity alone is not enough for successful delineation. As an example, Fig. 1 (c) and (d) show substantially different intensity values of consolidation and cavity regions from normal lung parenchyma. Therefore, these areas are often falsely excluded by thresholding–based lung segmentation methods.

For more advanced methods, the use of prior models has been found to be beneficial for cases with moderate amount of abnormality. For instance, anatomical shape models have been used in [13]–[18]. Basically, these methods fit a statistical shape model of an anatomical structure to the image of interest using an optimization procedure. However, as commonly known, the primary drawbacks of the model-based approaches are the requirement of large training data with high variations and accurate anatomical correspondences among the shape instances.

Atlas-based methods, on the other hand, transfer a priori object information from a reference image to the target image through image registration. They have been widely used in abnormal segmentation of organs including lungs [5], [19]–[21], abdomen [22], and brain [23]. Although atlas-based methods show promising results in lung segmentation, a representative atlas is often difficult to create due to high shape and intensity variability of the lung pathologies. Furthermore, atlas-based methods may fail to accommodate small details if registration is not designed to handle local variations.

Recently, machine learning approaches have gained growing interest in segmenting abnormal organs due to their strong abilities to exploit intensity, shape, and anatomy information. These approaches mostly focus on extracting suitable features (shape and/or texture) for a pre-defined classifier such as support vector machines, random forests, neural networks etc. Extracted features vary depending on the imaging modality and the body region. A number of feature sets for classification of lung pathologies have been proposed: 3D adaptive multiple feature method (AMFM) [24], texton-based approach [25], intensity-based features [26], gray level co-occurrence matrix (GLCM) [27], wavelet and Gabor transform [28], shape and context-based attributes [29], [30], local binary patterns (LBP) [31], and histogram of gradients (HOG) [29]. The most challenging aspect of these approaches is the selection of feature set appropriate for the task at hand, which is still an active area of research, however.

B. Our contributions

In this paper, we present a novel approach that, to the best of our knowledge, is the first fully automated pathological lung segmentation method spanning almost the entire spectrum of commonly encountered pathologies in pulmonary CT scans. Moreover, the study has been performed on the largest data set (> 400 CT scans) so far reported in the literature from diverse sources that contain different amounts and types of abnormalities. We developed a rough but intelligent pathology recognition system that automatically switches into the refinement step of the proposed framework when certain type of dense abnormalities are identified. Not only this switching system between the two stages of the proposed framework decreases the computational time, but it also allows users to be aware of the context of the pathologies in a similar fashion to most CAD (computer-aided detection) systems. The performance of our generic pathological lung segmentation (PLS) method was evaluated through: (i) submission to lung segmentation challenge for evaluation against the current state-of-the-art approaches on an unbiased platform, where the results were provided by organizers; and (ii) surrogate truths obtained by expert observers’ manual segmentations. The performance analysis was further divided into 4 categories: normal controls (no pathologies), minimum, medium, and large amount of pathologies. Note that all image sets were divided into subgroups based on the severity of cases, read and evaluated by participating expert radiologists prior to computer-based evaluation. We evaluated the accuracy of the algorithm separately for each category to demonstrate the robustness of the proposed system.

The remainder of manuscript describes and discusses the details of the PLS method and its performance. Section II gives a glossary of the abnormalities present in pulmonary CT scans and explains basic principles of the FC image segmentation algorithm. Section III introduces different modules of the proposed PLS technique. The results are presented in Section IV. Section V discusses performance aspects and future directions followed by a conclusion in Section VI.

II. Background

A. Fuzzy connectedness image segmentation

FC defines the “hanging togetherness” between any two voxels p and q within an image [32]. A binary adjacency relationship (µ_α) determines adjacent voxels in α-adjacency. Then, a path π between p and q can be identified as a sequence of adjacent voxels π = 〈p₀ = p, p₁, …, p_l = q〉. For any two adjacent voxels p_i and p_i+1, their local hanging togetherness is defined using an affinity function µ_k (p_i, p_i+1). The greater the affinity is, the more closely related the two voxels are. Then, for an arbitrary path π, the strength of the path is defined as the minimum affinity along the path:

$$\mu (\pi )=\underset{0\le i\le l}{\text{min}}{\mu }_k(p_i,p_{i+1}).$$ (1)

If 𝒫 (p,q) is the set of all possible paths between p and q, then FC between them is the strength of the strongest path:

$${\mu }_{\kappa }(p,q)=\underset{\pi \in 𝒫(p,q)}{\text{max}}\mu (\pi ).$$ (2)

The affinity function for two adjacent voxels under µ_α is the essential part of FC computation. Commonly, it consists of three components: distance-based affinity µ_d, homogeneity-based affinity (µ_ψ), and object-based affinity (µ_ϕ) as:

$${\mu }_k(p_i,p_{i+1})={\mu }_d(p_i,p_{i+1})\sqrt{{\mu }_{\psi }(p_i,p_{i+1}){\mu }_{\varphi }(p_i,p_{i+1})}.$$ (3)

A wide range of mathematical functions can be used for affinities [33], [34]. Here, we use Euclidean distance for µ_d, and adopt the following form of µ_ψ and µ_ϕ:

$${\mu }_{\psi }(p_i,p_{i+1})=\text{exp}(-\frac{{|f(p_i)-f(p_{i+1})|}^2}{2{\sigma }_{\psi }^2}),$$ (4)

and

$${\mu }_{\varphi }(p_i,p_{i+1})=\text{min}\left(\text{exp}\right(-\frac{{|f(p_i)-m|}^2}{2{\sigma }_{\psi }^2}),\text{exp}(-\frac{{|f(p_{i+1})-m|}^2}{2{\sigma }_{\psi }^2}\left)\right),$$ (5)

where σ_ψ and σ_ϕ control the variation, and m controls the expected mean intensity of the target object.

FC segmentation is obtained by generating a fuzzy object 𝓞 with regard to a set of seed points s ∈ 𝓢 The fuzzy object membership value at a voxel p is determined by the maximum FC value to all seed points as:

$${\mu }_{𝒮}(p)=\underset{S\in 𝒮}{\text{max}}{\mu }_{\kappa }(p,S).$$ (6)

The final object is obtained by thresholding over the fuzzy object 𝓞 for strength of connectedness.

B. Glossary of abnormal CT imaging patterns in pulmonary diseases

Visual patterns associated with abnormal lung anatomy in CT images carry valuable information for improving diagnostic confidence and consistency [35]. Commonly observed abnormal imaging patterns associated with lung diseases can be analyzed based on shape, texture, and attenuation information derived from CT images. The presence of more than one type of abnormality in the same region of interest can cause difficulty in understanding and quantifying the nature and extent of the disease. To enlist the common imaging patterns pertaining to different lung diseases, Table I provides a glossary of those patterns with short descriptions. Readers are encouraged to refer to [36] for further details from a clinical perspective.

TABLE I.

Glossary of common abnormalities in pulmonary CT scans.

Lung disease	Notes
Bronchocele	A Y- or V-shaped branching structure. For bronchial atresia, the surrounding lung parenchyma may be of decreased CT attenuation.
Crazy-paving pattern	Thickened intralobular lines superimposed on ground-glass opacity.
Consolidation	Homogenous increase in attenuation in lung parenchyma, obscuring the margins of airways and walls.
Ground-glass opacity (GGO)	Hazy lung opacity. Margins of vessels may be indistinct. GGO is less opaque than consolidation.
Halo-sign	GGO surrounding a nodule or a mass.
Honeycomb	Closely approximated textured ring shadows that resemble honeycomb.
Micronodules	Discrete small, round focal opacity. The term is often limited to nodules with less than 3 mm in diameter.
Mycetoma	Sponge-like pattern and a foci of calcification.
Beaded septum	Irregular and nodular thickening of inter-lobular septa that appears like a row of beads.
Perilymplatic distribution	Abnormalities along or adjacent to lymphatic vessels in the lung.
Bleb	Small air-containing space within the visceral pleura (not larger than 1 cm in diameter).
Bulla	Visceral pleura (not less than 1 cm in diameter).
Cavity	Air-filled space within pulmonary consolidation, mass, or nodule.
Pulmonary infarction	Triangular or dome-shaped with base containing pleura and apex directed toward hilum.
Pleural plaque	Areas of pleural thickening often with calcification.
Pleural effusion	Excess of fluid that accumulates between the two pleural layers.

III. Methods

The PLS method consists of two primary stages: (i) the initial FC segmentation step for normal lung parenchyma, and (ii) the refinement stage triggered by automatic pathology identification.

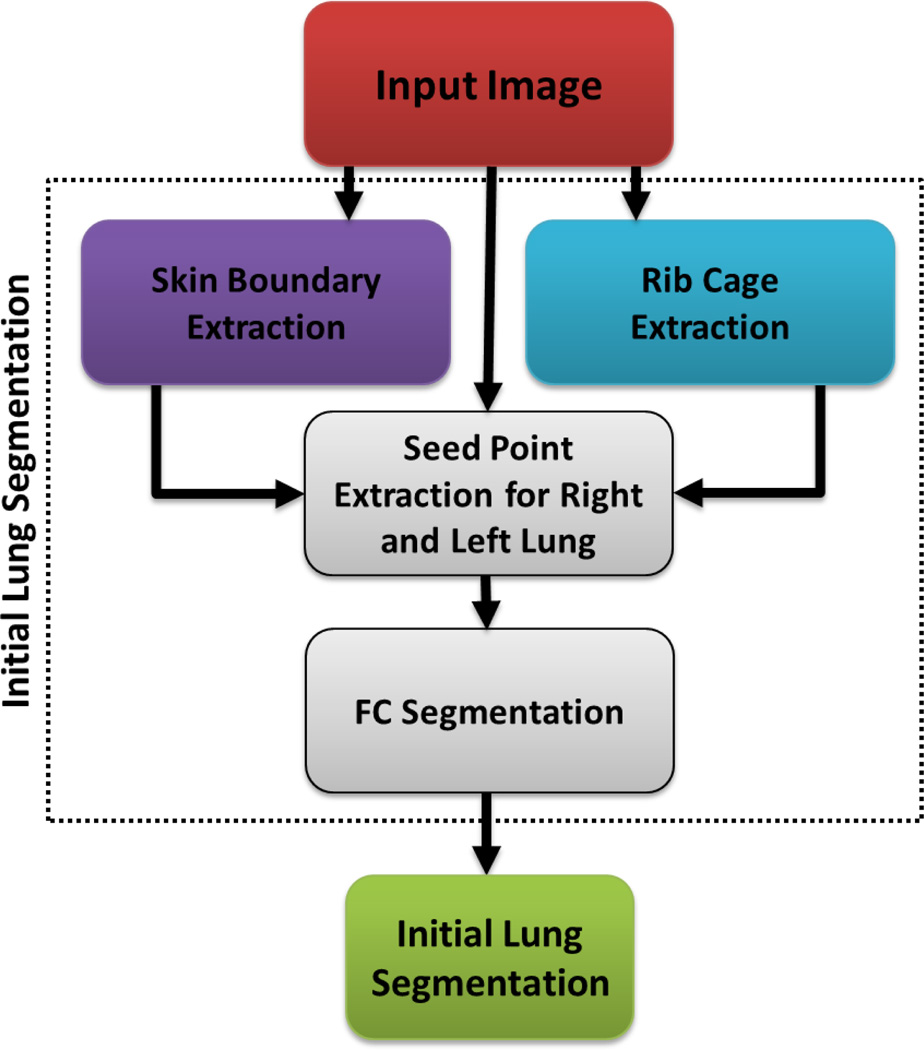
A. Seed selection and FC segmentation

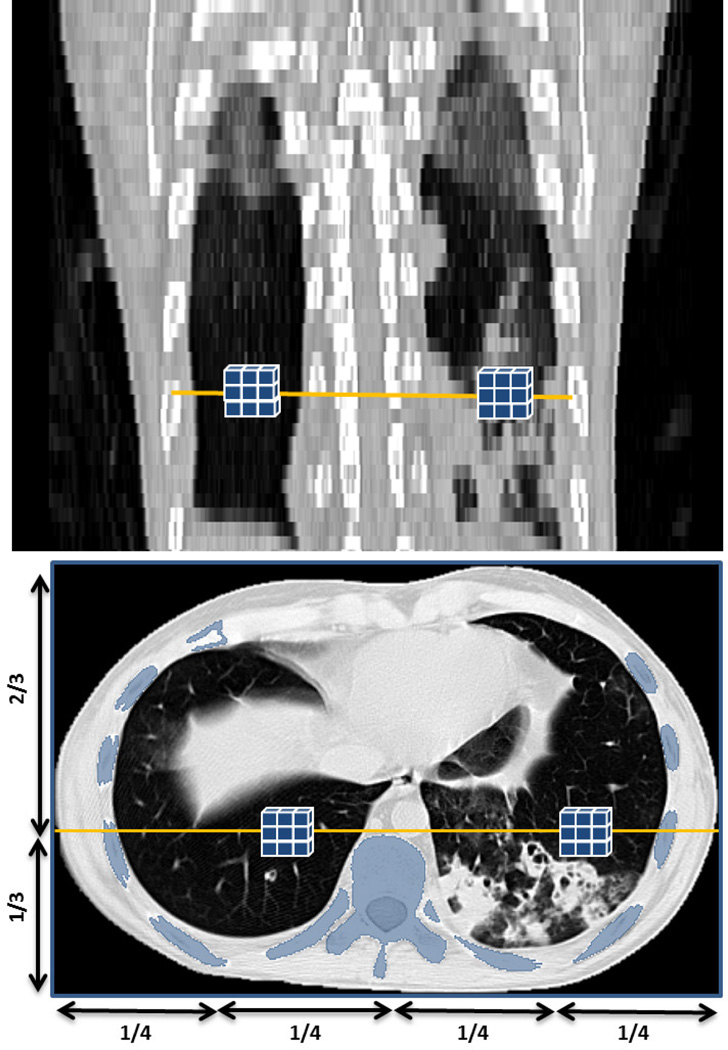
Fig. 2 summarizes the initial lung segmentation process using FC. For this process, FC requires two seed points: s_l, s_r, located within the left and right lungs, respectively. In our design, we automatically set seed locations through a pre-processing step, we then sampled a set of seeds from the regions obtained after strict thresholding. That is, for any given CT image I, we use a thresholding operation 𝒯 using CT attenuation values for normal lung parenchyma (Hounsfield Units (HU): −700 through −400, mean ≈ −550 HU). Thus, I^𝒯 = 𝒯{I}_{− 550HU}. Finally, we set the seed locations s_l and s_r after randomly sampling a few seed candidates, i.e., 3×3×3 seed window (not the physical size), for each lung from I^𝓢 and select the voxels with minimum HU value as seeds:

$$s_l\leftarrow 𝓛(\underset{\text{min}}{\overset{\mathit{\text{HU}}}{}}{\mathit{\text{ROI}}}_{\mathit{\text{random}}}^{3\times 3\times 3})\in I_{\mathit{\text{left}}}^{𝒯},s_r\leftarrow 𝓛(\underset{\text{min}}{\overset{\mathit{\text{HU}}}{}}{\mathit{\text{ROI}}}_{\mathit{\text{random}}}^{3\times 3\times 3})\in I_{\mathit{\text{right}}}^{𝒯}.$$ (7)

where 𝓛 denotes the location of the voxel(s), and $I^{𝒯}=I_{\mathit{\text{left}}}^{𝒯}\cup I_{\mathit{\text{right}}}^{𝒯}$. Fig. 3 demonstrates the approximate lung regions where we sample candidate seeds. Note that we carry out seed sampling over the extracted normal lung parenchyma, not the original CT image.

Fig. 2.

Flowchart explaining the initial segmentation using FC.

Fig. 3.

Automatic seed selection for initial FC segmentation based on voxel intensity and geometrical knowledge, i.e., the rib cage.

Apart from seeds, FC algorithm also requires approximate mean m and the standard deviation σ_ψ and σ_ϕ of the lung region to be used in affinity functions. These values were empirically set to normal lung parenchyma as m = −550 HU, σ_ψ = σ_ϕ = 150 HU after analyzing hundreds of CT images. Once seeds and affinity parameters for FC are set, delineation is performed. The output of the FC segmentation is a binary mask of the lung fields containing both the external airways (trachea and bronchi) and the left/right lungs. The extent of how well the initial FC segmentation performs depends on the amount and the kind of abnormality present in the target image. Fig. 4 illustrates how the performance of FC may deteriorate with an increase in the extent of pathology. It should be noted that although FC is more robust than region growing, graph-cut, and other region-based segmentation methods [37], further refinement is often inevitable for cases with dense pathologies.

Fig. 4.

Images with different pathologies along with overlaid with the respective initial FC segmentation.

B. Pathology presence test

The goal of the pathology presence test was to check the quality of initial segmentation and to determine whether any pathological areas were present in the target lung that need to be further included in the final lung volumes. The test consisted of two constraints: (i) the smoothness of the boundary pertaining to the initially segmented lung volume, and (ii) the difference between segmented and lung volumes estimated from rib cage information. Since the rib cage tightly bounds the lung field inside the body region, it can give an approximate value for expected lung volume. In other words, we used the pathology presence test to understand if the mild or severe amount of pathology present in the scan so then advanced machine learning methods can be used for voxel-based classification as a further step. It is important to note here that there is no “explicit” volume or spatial information involved in this test. Once this pathology recognition system reveals that the advanced machine-learning is necessary, then the next stage of our proposed framework is conducted. The details of those two constraints are explained in the following.

(i) Smoothness test

This test is based on the observation that the area per slice of a normal lung has a smooth transition along the z-axis; whereas in scans with moderate/dense abnormalities the 2D areas change abruptly due to the fact that abnormal imaging areas are not captured by the conventional segmentation algorithms. Since segmented lung areas may change irregularly between slices with the presence of abnormalities, we can track the abnormal changes in the lung surfaces by conducting a smoothness test. Let A(i) denotes the lung area on a given axial slice i, then the change in segmented area in the direction orthogonal to the slice plane can be monitored by C(i) = A(i+1) − A(i), for i = 1 … N − 1.

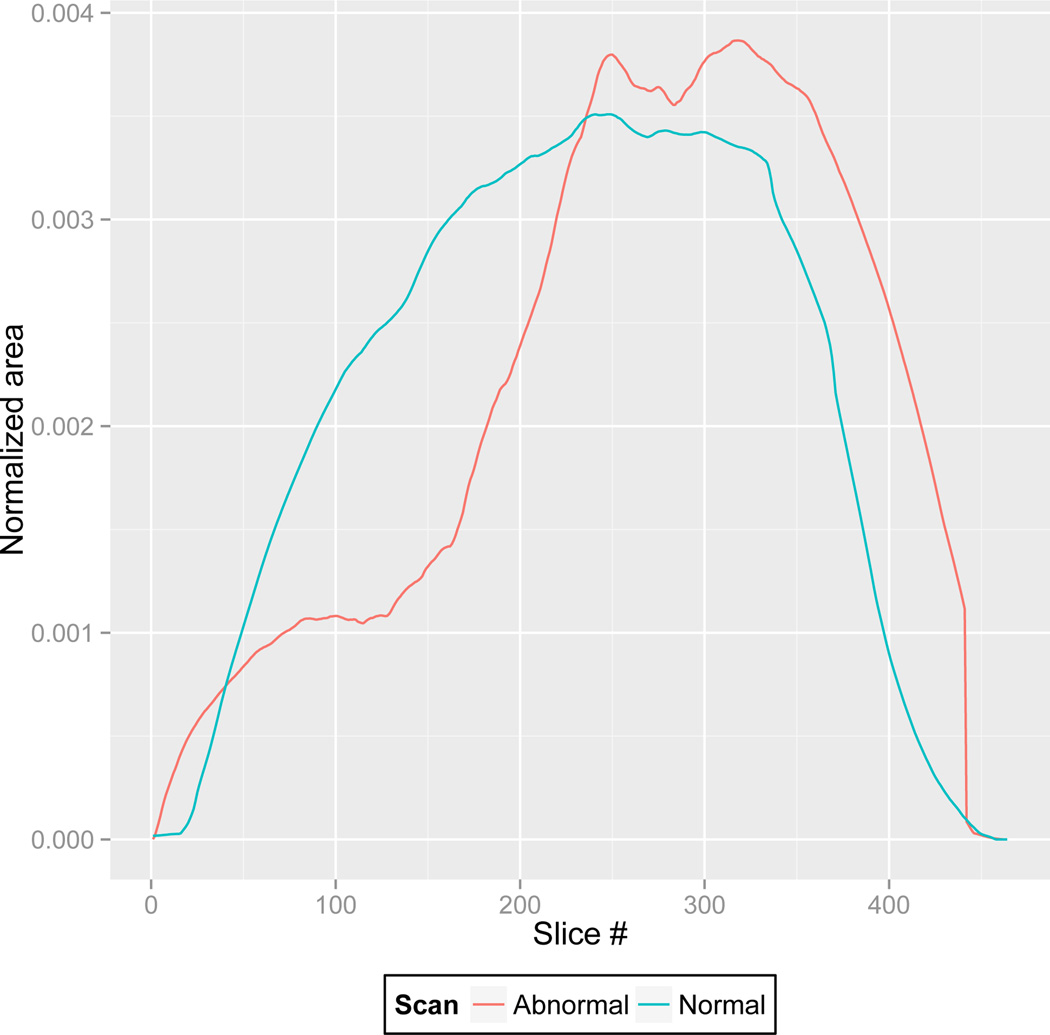
To quantify how segmented regions change when minimal or no pathology exists in the CT images, we selected a set of M control images $C_{\text{ref}}^j,j=1,2,\dots ,M$, and calculated the maximal variation for each control image: $K=\underset{j}{\text{max}}(\mathit{\text{VAR}}(C_{\text{ref}}^j))$, where VAR indicates variation. Note that the control images were lung scans of healthy subjects containing minimal or no abnormalities. Based on the smoothness assumption, any abrupt change in the segmented area C(i) > K indicated the presence of a potential abnormality which triggers the refinement stage. As an example, Fig. 5 shows a general trend in the area per slice along the axial plane for a normal lung scan, compared with the area per slice of a scan with moderate amount of pathology. As can be seen, abrupt change in the 2-D areas of lung regions may help detecting presence of mild/severe amount of pathology.

Fig. 5.

The plot shows the change in the normalized 2D segmented area (per slice) along the axial planes.

(ii) Volume difference test

Estimated lung volume is used as an additional constraint for the existence of pathology. The volume of the lung is estimated based on a regression analysis that was performed on training scans without abnormalities. First, the approximate ribcage volume for the training data was estimated by fitting a 2D convex hull on the ribcage. Second, a linear regression analysis was performed. Based on this regressed lung volume information from the ribcage volume, one may easily conduct a volume difference test using the estimated lung volume from the initial segmented lung volume determined by the FC.

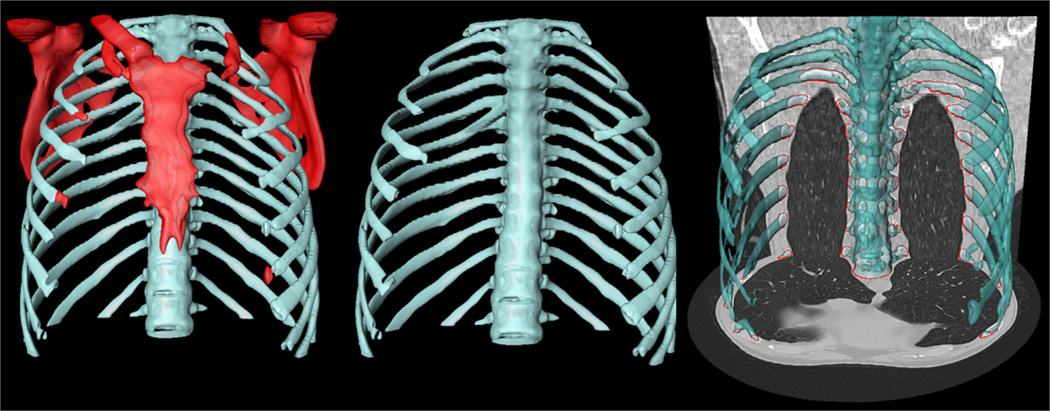
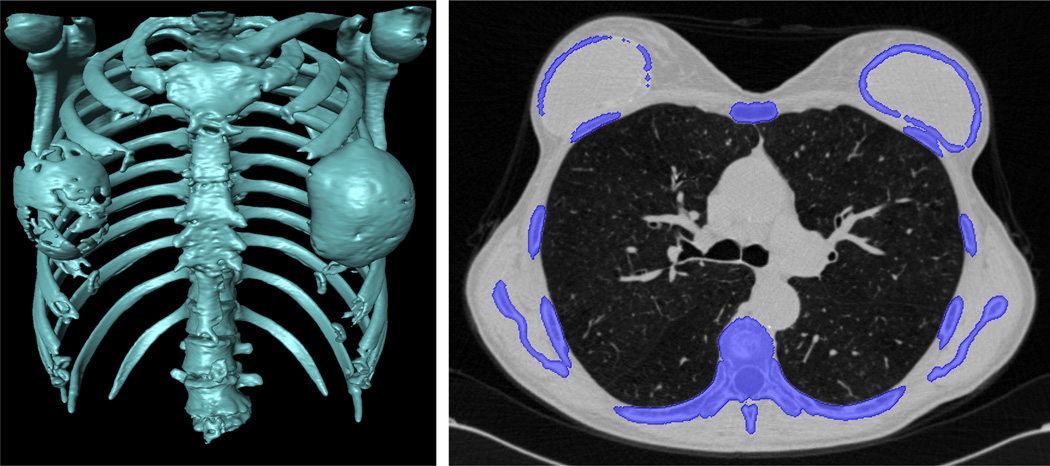
A number of approaches in the literature have used ribcage information to estimate the location of lung parenchyma [38]–[42]). We used a convex-hull that fit around the rib cage for a rough lung volume estimation. As observed from Fig. 6, the rib cage can be used as an anchor to estimate enclosed volume that is closely associated with lung volume when no or minor pathology exists.

Fig. 6.

The rib cage (blue) is separated (middle) from the adjacent bones (red) (left) for volume estimation. Lung fields are enclosed by rib cage (right).

Fitting a convex-hull to the rib cage structures requires the rib bony structures to be extracted. Since bone has relatively high contrast compared to surrounding tissues, thresholding allows identification of bonee structures. We chose the commonly used thresholding parameter of 300 HU for including all bone structures. Thresholding was followed by a connected component analysis in order to retain the largest component and remove noise. Although this process provided rib cage, some of the other bone structures including sternum and spine may also be often included. However, the scapula should not be included in our convex-hull fitting around the rib cage because scapula will falsely increase the estimated volume (Fig. 7). In order to remove the scapula, we used shape information of the bones – ribs have a tubular geometry while scapula is plate-like. Based on this distinguishing information, we utilized Hessian analysis to extract shape features. As shown in [43], analyzing the second-order information (Hessian) of a Gaussian convolved image provides local information of the structure. Specifically, eigenvalue decomposition was performed over the Hessian matrix and the resulting ordered eigenvalues, i.e., (|λ₁ ≤ |λ₂ ≤ |λ₃|), were examined. For tubular structures, it was expected that λ₁ was small and the other two were large and of equal sign; while for plate structures, it was expected that both λ₁ and λ₂ were small and λ₃ was large. Explicitly, for a bright structure on a dark background, ribness can be formulated as

$$V_{\sigma }=\{\begin{array}{ll}0,\text{\hspace{1em}\hspace{1em}if}{\lambda }_2>0\text{or}{\lambda }_3>0;\hfill & \hfill \\ (1-e^{-\frac{R_A^2}{2{\alpha }^2}})e^{-\frac{R_B^2}{2{\beta }^2}}(1-e^{-\frac{S^2}{2{\gamma }^2}}),\hfill & \text{otherwise},\hfill \end{array}$$ (8)

where R_A = |λ₂|/|λ₃|, $R_B=|{\lambda }_1|/\sqrt{|{\lambda }_2{\lambda }_3|}$ and $S=\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}$; and plateness can be formulated as

$$P_{\sigma }=\{\begin{array}{ll}0,\text{\hspace{1em}\hspace{1em}if}{\lambda }_3>0;\hfill & \hfill \\ e^{-\frac{R_B^2}{2{\beta }^2}}(1-e^{-\frac{S^2}{2{\gamma }^2}}),\hfill & \text{otherwise},\hfill \end{array}$$ (9)

where R_B = |λ₂|/|λ₃|, and $S=\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}$;

Fig. 7.

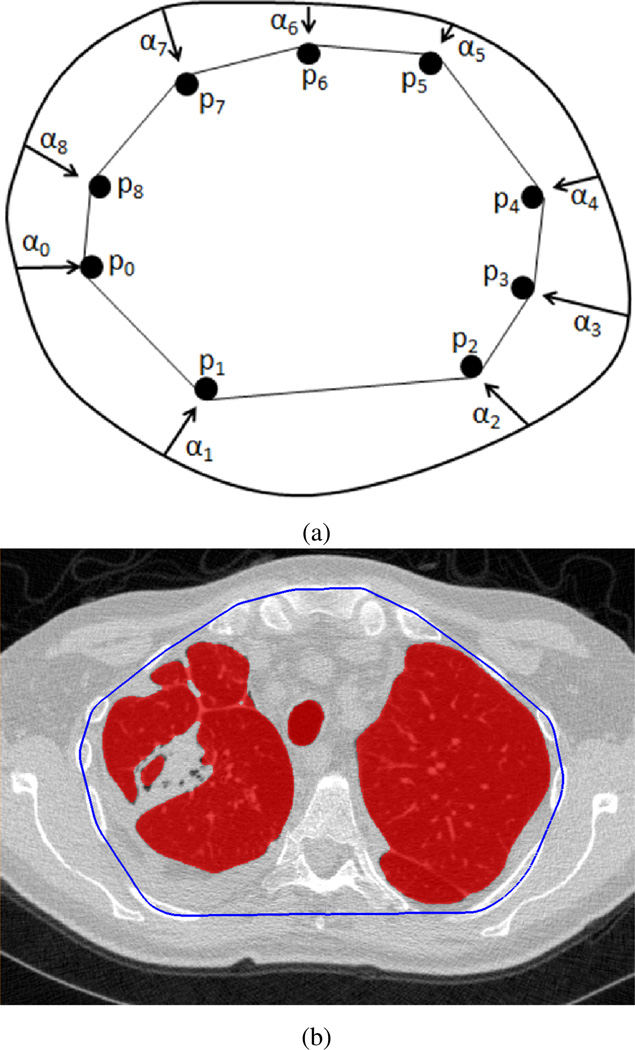
2D convex-hull (shown in blue) fitting in axial plane for pathology presence test of the segmentation.

The ribness and plateness measurements (V and P) above were calculated at different scales (σ) and the maximum response was achieved at a scale that matches the size of the structure. Therefore, by using a multi-scale approach which covers a range of structure widths and finding the maximum value V = max(V_σ), P = max(P_σ), σ_min ≤ σ ≤ σ_max, we enhanced the local tubular and plate structures.

Let S denote the scapula to be excluded and S̄ denote the bones useful for lung volume estimation such that B = S ∪ S̄. S can be characterized by high P and low V responses, while S̄ features high V and moderate P values. Therefore, thresholding was applied to extract candidate scapula voxels Sd_S ∈ S and rib voxels Sd_S̄ ∈ S̄. Since Sd_S and Sd_S̄ usually cover only part of the entire rib and scapula, these points were used as seed points to initiate a geodesic distance transform (GDT) within the initial bone segmentation B using a fast-marching algorithm [44]. The final step was to detach the scapula S from whole bone segmentation B based on the distance map, all voxels satisfying GDT(Sd_S) > GDT(Sd_S̄) were excluded from convex-hull generation.

Once the rib cage was segmented, a 2D convex-hull was fitted over the rib cage along the axial axis to estimate the lung volume. Let S̄(i) denote the set of all candidate voxels on slice i and hull(i) denote its convex-hull. From a boundary perspective, hull(i) can be regarded as the inside of the polygon formed by deforming a contour, which initially encloses S̄(i), so that the deformation simulates that of a rubber band contraction until it becomes taut by the outermost anchor points (Fig. 7). That is, hull(i) consists of all possible linear combinations of p_j ∈ S̄(i) as

$$\mathit{\text{hull}}(i)=\left\{\sum _j{\alpha }_j{p}_j\right\},$$ (10)

for all possible linear combination weighting scheme α_j such that ∀j, α_j ≥ 0 and $\sum _j{\alpha }_j=1$.

After rib cage segmentation and convex-hull fitting, the volume enclosing the convex-hull was estimated. In the refinement step, when indicated by the pathology presence test, the PLS method used the random forest classification algorithm at the voxel level. Furthermore, the method has additional modules for segmenting cavities and pleural diseases due to their unique appearances. In the following subsections, we describe the refinement process of the PLS method with its specific modules: FC based cavity segmentation, random forest-based pathology identification, and neighboring anatomy guided pleural effusion detection.

It is important to mention here that the parameters in both the smoothness test and volume difference test are chosen to minimize the type-II error, i.e. the probability of rejecting to proceed to the refinement stage when the target scan needs one at the expense of the type-I error.

C. Cavity detection and segmentation

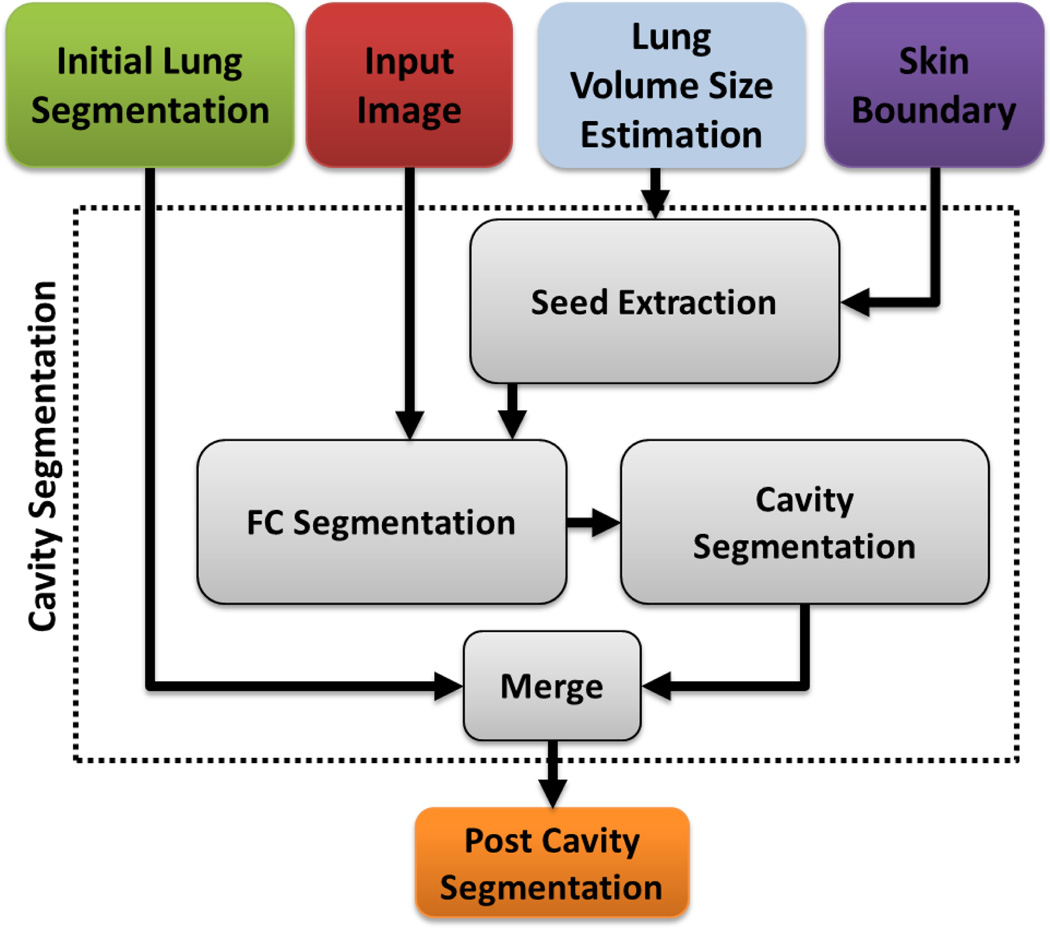
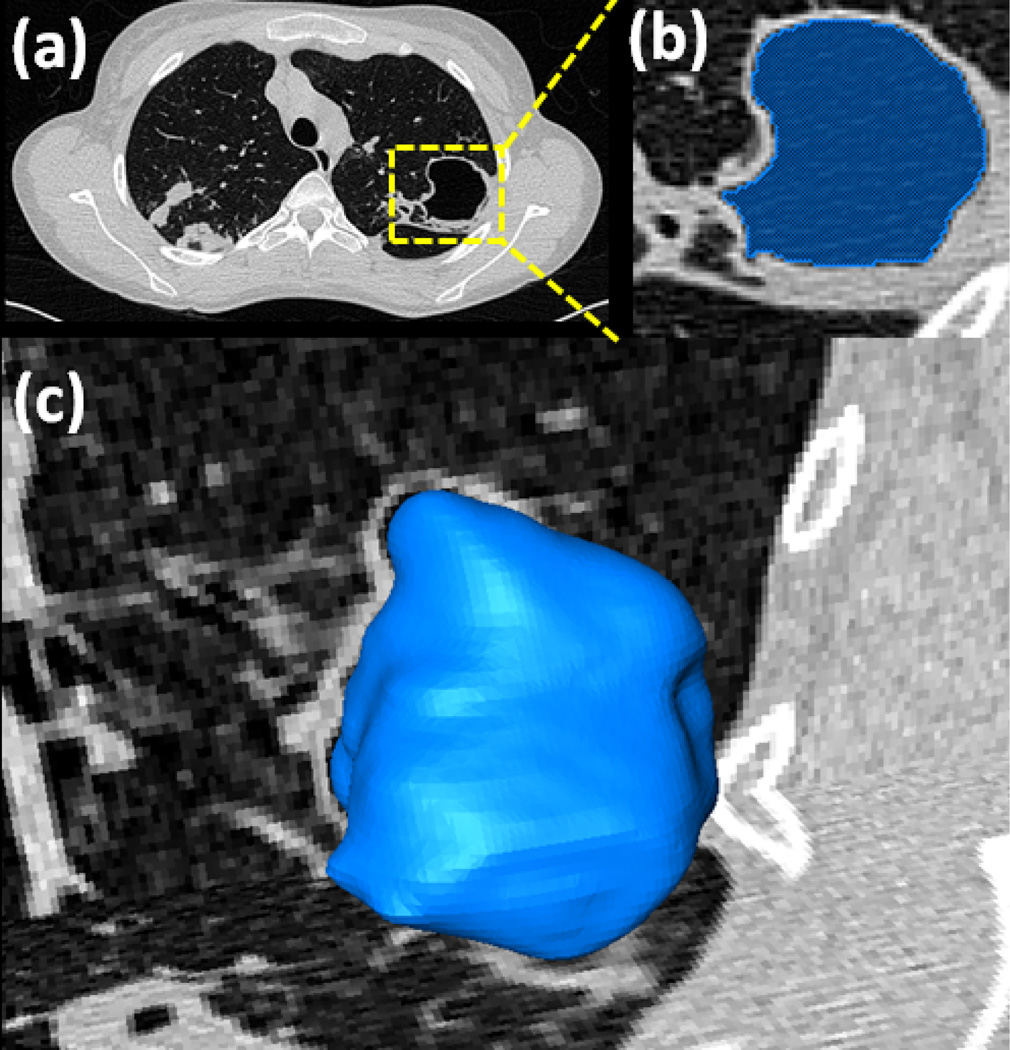
Cavities occur in multiple lung diseases and are a primary marker of tuberculosis (TB) infection [45], [46]. Severe cavities and blebs have a high contrast boundary separating them from the surrounding lung parenchyma (for a reference see Table I) and are therefore usually not captured within the initial FC segmentation phase. A separate mechanism has been put in place in the PLS method to ensure that the cavities are detected and included in the final segmentation. Fig. 8 provides an overview of the automatic cavity segmentation technique used in the PLS method. Briefly, we automatically search the candidate cavity regions by applying thresholding operation with strict HU level (< −990 HU) denoting gas-filled regions within the lung parenchyma. Our search was confine to the regions enclosed by convex-hull thus eliminating gas-filled regions. Next, amongst all the regions detected as cavities within the convex-hull, we select the voxels that had minimum HU values as seeds with which we initiated the FC segmentation. Fig. 9 shows a detected cavity region in (a), its FC segmentation in (b), and 3-D surface rendering in (c).

Fig. 8.

A flow diagram explaining the automatic cavity segmentation process.

Fig. 9.

Detected cavity (a), its FC segmentation (b), and surface rendition (c) are given.

D. Pathology detection via random forest classification

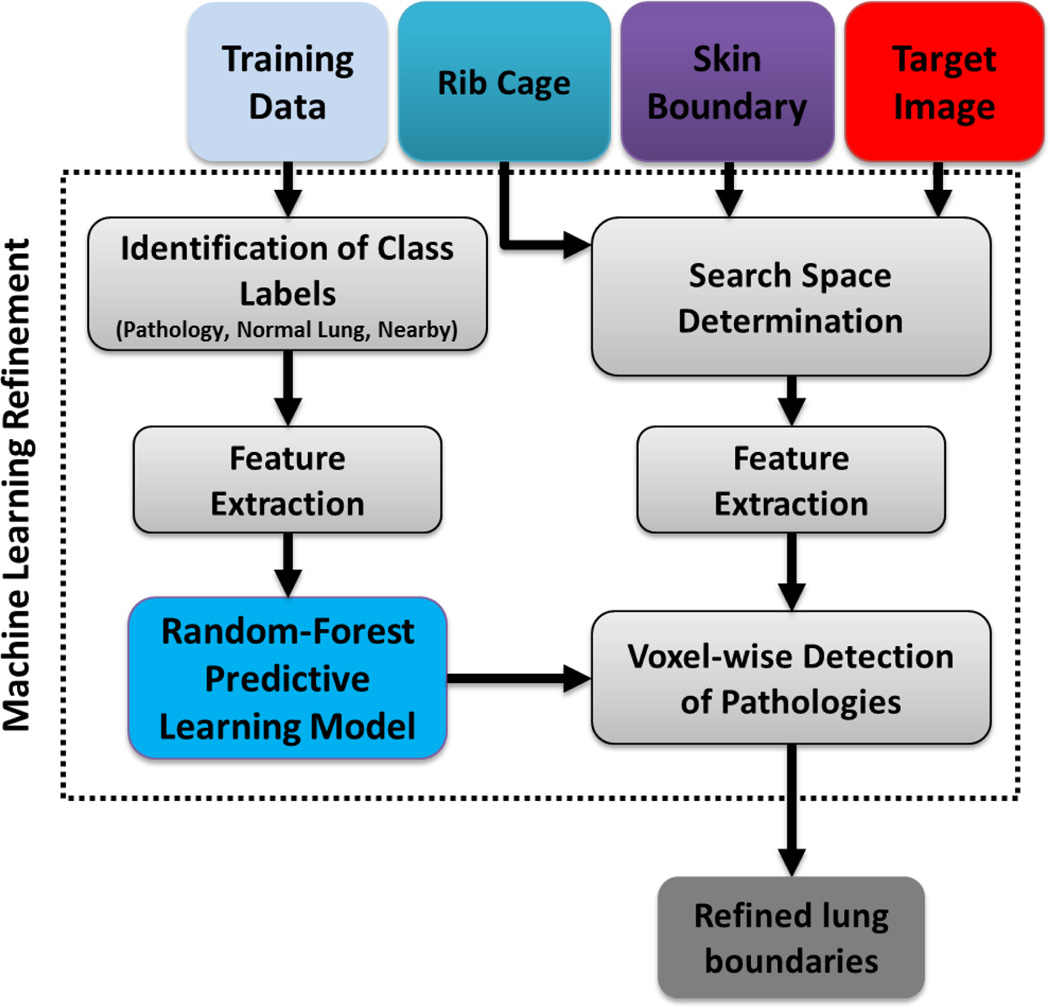
Following cavity detection, the pathology presence test was repeated. If the resulting smoothness and volume difference tests still indicated the existence of pathologies, the random forest classification of lung tissues at the voxel level was conducted. With voxel-wise classification, it is possible to determine different abnormal imaging patterns within the lungs. Fig. 10 illustrates the second module of the PLS method in which we recognize the general abnormal imaging patterns pertaining to the lung diseases other than pleural and cavity patterns.

Fig. 10.

Schematic diagram showing texture classification-based refinement, highlighting both predictive model learning for RF and the pathology classification in the target image based on the learned predictive model.

Although machine learning classification methods are very useful for detecting pathology, it is not trivial to extract discriminative feature sets to drive the detection process. Moreover, assessing every voxel’s class dependency may be computationally expensive. To address these two challenges, we integrated rib cage extraction and convex-hull fitting processes into the random forest classification algorithm in order to restrict the search space to rib cage area only. For random forest voxel classification of lung tissues, we employ feature sets commonly used in various lung CAD systems: gray-level run length matrix (GLRLM), gray-level co-occurrence matrix (GLCM), and histogram features. Justification of the use of GLCM, GLRLM, and histogram features is based on the visual analysis of CT lung pathologies [47]. Various studies have shown that texture, intensity, and gradient are the key discriminative features for automatically detecting abnormal imaging patterns. Thus we designed a patch-wise feature set encompassing texture, intensity, and gradient for our study.

Briefly, GLCM and GLRLM were calculated using 4-orientations (0°, 45°, 90°, 135°), and for 8,16,32,64,128 bins [48]. For every voxel within the search region, we extract the features considering a patch (i.e., ROI) around that voxel with 7×7×7 neighborhood. The complete list of 24 distinct features is shown in Table II

TABLE II.

Extracted features for voxel-wise classification of lung tissues.

GLCM	Energy (f1)
	Entropy (f2)
	Correlation (f3)
	Inverse Difference Moment (IDM) (f4)
	Inertia (f5)
	Cluster Shade (CS) (f6)
	Cluster Prominence (CP) (f7)
GLRL	Short Run Emphasis (SRE) (f8)
	Long Run Emphasis (LRE) (f9)
	Gray-Level Non-uniformity (GLN) (f10)
	Run Length Non-uniformity (RLN) (f11)
	Run Percentage (RP) (f12)
	Low Gray-Level Run Emphasis (LGRE) (f13)
	High Gray-Level Run Emphasis (HGRE) (f14)
	Short Run Low Gray-Level Emphasis (SRLGE) (f15)
	Short Run High Gray-Level Emphasis (SRHGE) (f16)
	Long Run Low Gray-Level Emphasis (LRLGE) (f17)
	Long Run High Gray-Level Emphasis (LRHGE) (f18)
Hist	Mean (f19)	Variance (f20)	Skewness (f21)
	Kurtosis (f22)	Min. (f23)	Max. (f24)

Since, our aim in this study was to segment pathological lungs, we considered all pathological regions as a single label (i.e., T_p) rather than sub-categorization of the abnormality types such as consolidation, GGO, etc. Assuming FC segmented the normal lung parenchyma in the initial delineation (ℛ_nlp), and cavities and pleural effusion regions are indicated by ℛ_cavities and ℛ_pe (segmentation of pleural effusion regions is discussed in the next section), respectively, then the pathological regions ℛ_rf which require voxel classification via random forest method can be defined as ℛ_rf = ℛ_hull \ (ℛ_cavities ∪ ℛ_pe ∪ ℛ_nlp). All the voxels belonging to ℛ_rf were classified into two classes: pathological (T_p) or non-pathological (T_n) regions. In particular, neighboring structures of the lung were considered as non-lung and/or non-pathological structures and labeled as T_n.

Any machine learning algorithm with the ability to separate normal lung parenchyma and neighboring anatomical structures from known abnormal imaging patterns of lung disease can be used in the refinement process. However, random forest has been shown to be powerful for this kind of classification tasks due to its high accuracy, efficiency, and robustness. In training a random forest classifier, two experienced observers annotated various pathology patterns from randomly selected CT scans (21 CT scans from different subjects). A total of 997 non-overlapping ROIs were extracted from those annotations such that 507 observations belong to T_p while 490 observations belong to T_n. A random forest classification model was constructed using those observations with the corresponding labels. Table III summarizes the set of parameters used for feature extraction and random forest classifier training.

TABLE III.

Parameter settings for random forest classification method in pathology detection.

GLCM	# of bins per axis = 16
	# of directions = 4
	Offset = 2
	Pixel intensity dynamic range = 16 bits
Rnd. fst	# of trees in a forest = 70
	% of training set used to build individual trees = 0.6
GLRLM	# of directions = 4
	# of levels = 8
Misc.	ROI dynamic-range = 16-bits
	ROI window = 7 × 7

E. Neighboring anatomy-guided pleural effusion detection

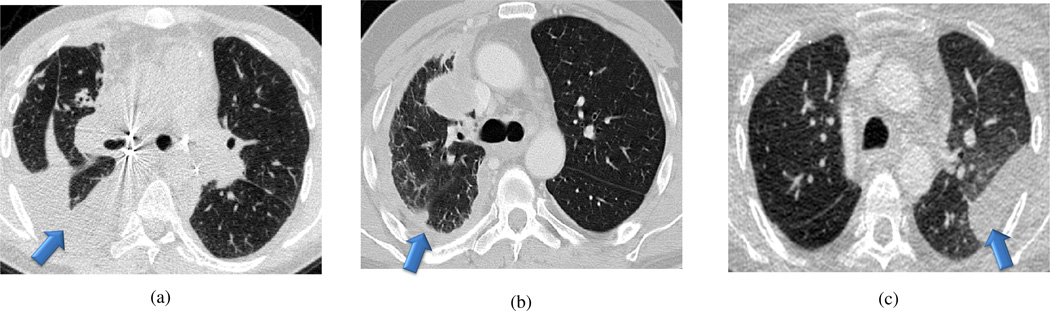
The final module of the proposed PLS method was the detection of pleural abnormalities. Pleural effusion is an accumulation of fluid in the pleural cavity. Similar to cavity formation, we considered the existence of pleural effusions as a separate detection problem due to its unique challenges. For example, pleural fluids usually has similar textural and intensity properties with the surrounding soft tissues (see Fig. 11 for pleural effusion and plaque examples). Recent studies [49], [50] on the discriminative role of CT intensity values in characterizing the pleural fluid concluded that the CT numbers of pleural effusions do not hold enough discriminative information to accurately detect/delineate pleural effusions. Existing attempts such as [51] do not solve the lung segmentation problem because, detection of the pleural effusion using the existing methods paradoxically requires a complete lung segmentation prior to its detection. In contrast, we would like to detect pleural effusion as a part of pathological lung segmentation.

Fig. 11.

Examples showing different cases highlighting the lung scans with pleural effusion (a–b) and the pleural plaque (c).

To address the challenge of pleural fluid detection, we used neighboring anatomy information of the pleural region as a stable marker for lung boundary. For neighboring anatomy, ribs, heart, and liver can also be used as potential markers. Hence, we extracted the feature sets from the anatomical location of these organs and their relative positioning information. Note that the heart, liver, and other neighboring structures are not segmented but rather considered as a single unit. Their relative spatial location in normal (healthy) scans were annotated by participating expert observers using the ROIs in the training step. in contrast to the pathology classification module, the feature set here consists of the relative position of the neighboring organs in ℝ³ rather than the textural features.

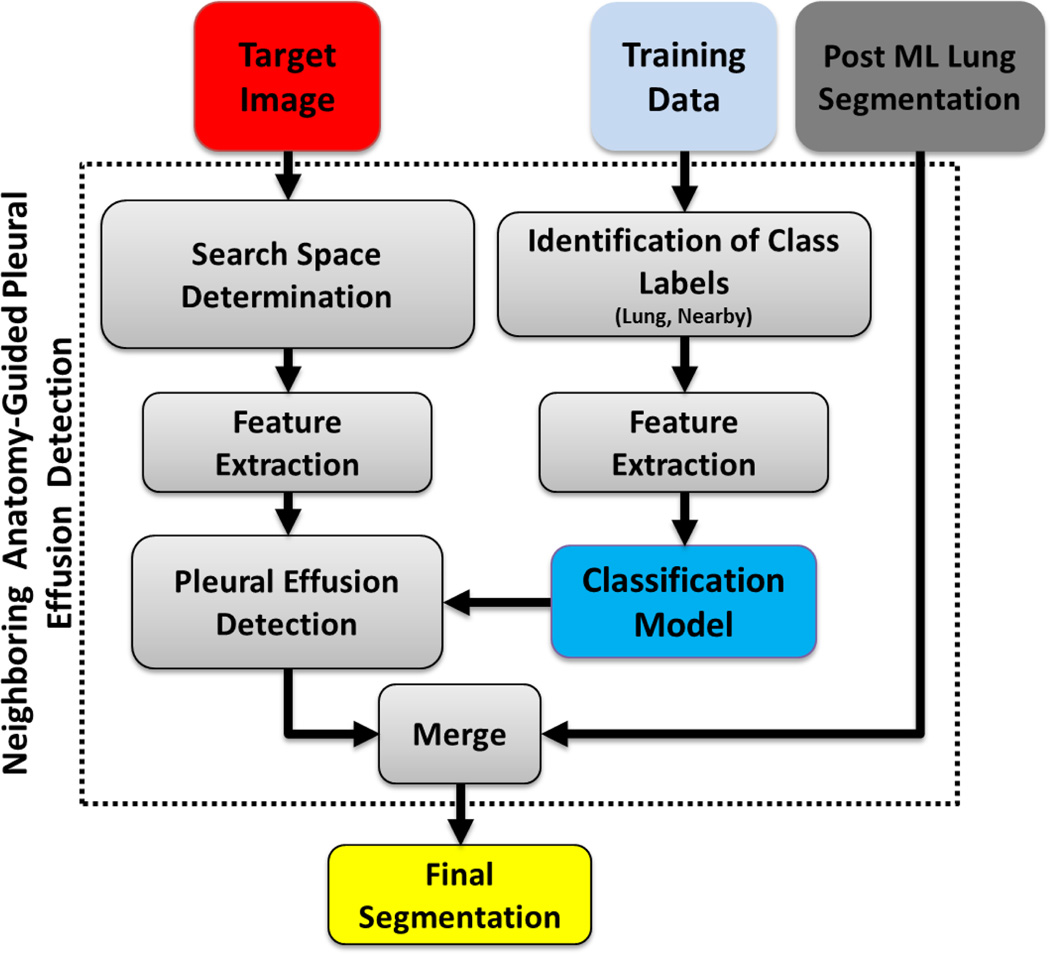
In other words, for neighboring anatomy-guided classification to detect pleural regions, we use normalized spatial coordinates as feature set. Normalized spatial coordinates in our method were obtained by dividing the spatial coordinates by the estimated total rib cage volume, the latter obtained by using the convex-hull method. The random-forest algorithm was used to classify the target region ℛ_p̂e = ℛ_hull \ (ℛ_cavities ∪ ℛ_rf ∪ ℛ_nlp)) into two classes: pleura (T_pe and neighboring-anatomy (T_na)). In training the classifier, two expert observers annotated lung-field and neighboring organs from randomly selected CT scans (27 CT scans from different data sets) and a random-forest classifier was constructed using the training data with the corresponding labels. Based solely on the knowledge of anatomical location, the method divides the region ℛ_p̂e into T_pe and T_na. The proposed framework for detecting pleural effusion is summarized in Fig. 12.

Fig. 12.

Flow chart explaining the neighboring anatomy-guided segmentation for difficult cases.

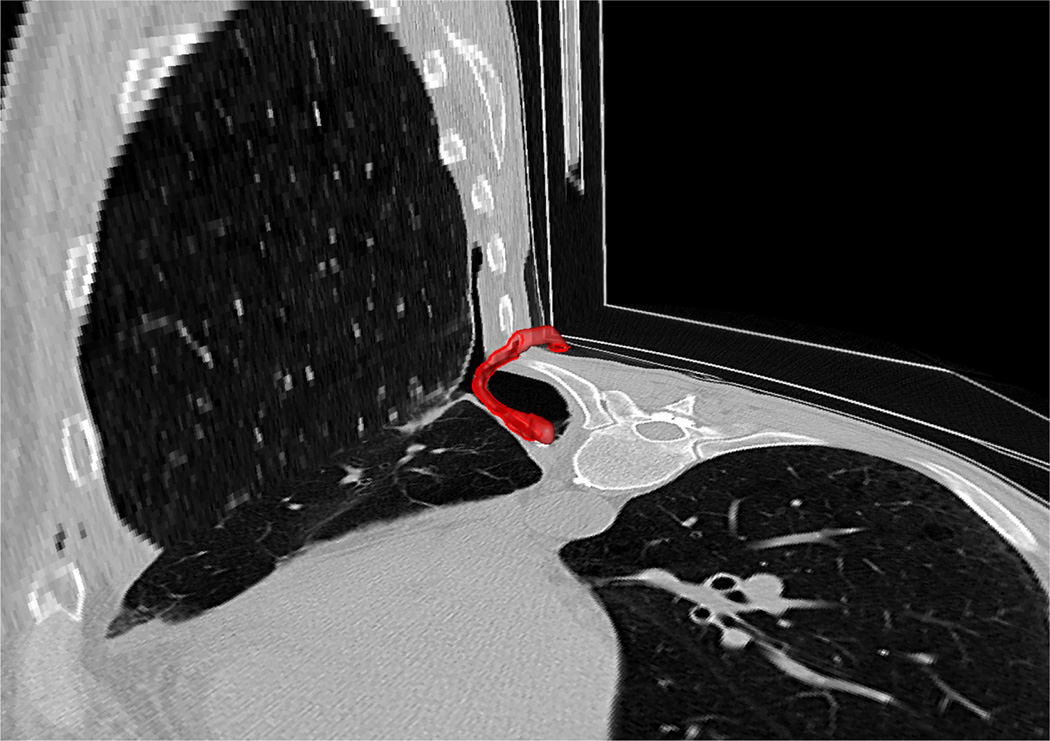
F. Automatic trachea extraction

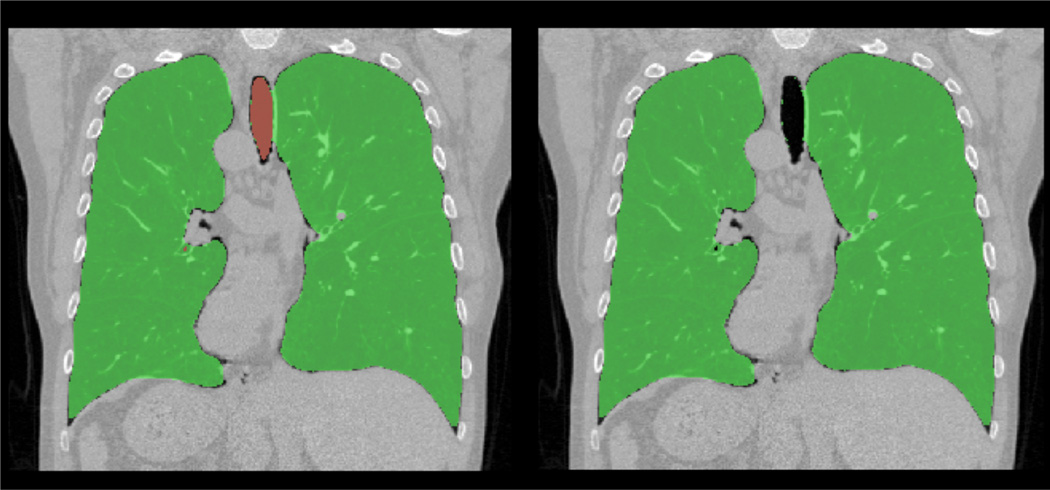
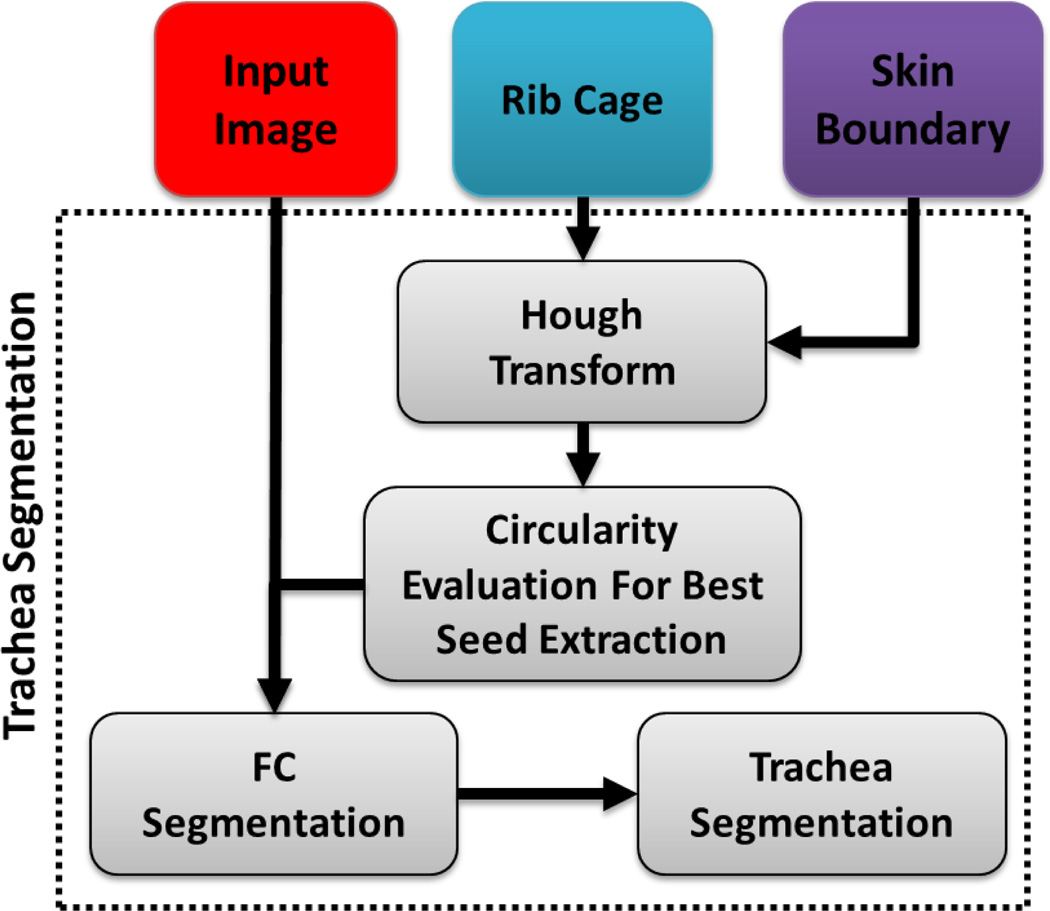
Since the trachea is contiguous with the lung, it is also included in the lung segmentation procedure. However, trachea and airways are typically evaluated separately from the lung parenchyma routinely in clinical practice. Hence, it is of interest to remove the trachea from the segmented lungs. This procedure can be performed simultaneously with lung segmentation, or as an alternative final step once the segmentation has been conducted. In our study, instead of increasing the complexity of lung segmentation, we preferred to keep trachea removal as an optional tool for users at the end of the final lung segmentation. To remove the trachea, we first used 2D Hough transform along the axial plane to detect the tracheal region (i.e., a circular region in the top slices of the CT scan) followed by conventional FC segmentation that accepts the voxels inside the circular region as initial seed points. Meanwhile, the orientation information for identifying the seed point location was extracted from the DICOM header, followed by a smoothing filter and 2-D Hough transform. Once, the seeding was done, we used FC to finalize trachea segmentation. Next, we started estimating trachea volume from the first axial slice that we found the trachea region with the Hough transform. Expected maximum capacity of trachea (i.e., < 30 cm³) [52] and the rate of change of the volume were used to determine the stopping criteria for trachea inclusion/exclusion in the final segmentation. Note that main bronchi were not removed due to the capacity constraint feature of the trachea removal tool. Fig. 13 illustrates example slices where the removed trachea was shown in red. A block diagram explaining the proposed automatic trachea extraction method is provided in Fig. 14 and the corresponding pseudo-code is given in Algorithm 1.

Algorithm 1.

Automatic trachea extraction algorithm

Require: 𝒯 MinRadius, MaxRadius. {𝒯 = Empirically determined thresh-old on the rate of change of volume per unit step. MinRadius/ MaxRa dius = Empirically determined minimum/maximum expected radius of the trachea region along the axial axis.}

1: for i = 1 to # of slices along axial plane do

2:   circles=HoughTranform(slice(i))

3:   for j = 1 to # of circles do

4:     if radius(circles(j))>MinRadius and radius(circles(j))<MaxRadius then

5:       TracheaRegion = circles(j)

6:       BREAK

7:     end if

8:   end for

9: end for

10: FCMap = DoFC(TracheaRegion)

11: τ=max(FCMap)

12: repeat

13:   TracheaSeg=Threshold(FCMap, τ)

14:   if Volume(TracheaSeg)> 30cm3 or (Volume(TracheaSeg)-Volume(PrevTracheaSeg))> 𝒯 then

15:     return PrevTracheaSeg

16:   else

17:     PrevTracheaSeg = TracheaSeg

18:     τ––

19:   end if

20: until τ > 0

Fig. 13.

An example for automatic trachea extraction (left) and trachea removal (b) is shown.

Fig. 14.

A flow diagram explaining the proposed automatic trachea segmentation method.

G. Left/right lung separation

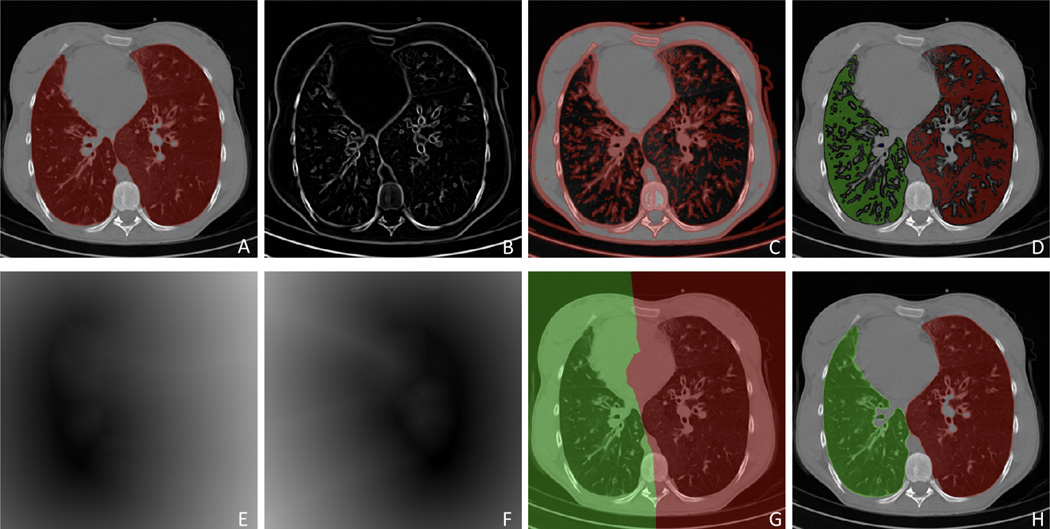
Lung separation was performed using a hysteresis approach which utilizes prior information from original lung segmentation as well as the background gaps [53]. First, Hessian-filtered original segmentation was bifurcated by subtracting gaps between potential left and right lungs. Second, a 2D separation manifold in 3D image space was estimated based on the information from the distance transform. Finally, the separation manifold was projected back to the origin space where segmented object was relabeled as left and right lungs. Fig. 15 illustrates this operation step by step.

Fig. 15.

Flow diagram explaining the hysteresis lung separation approach. (A) Original CT with binary lung segmentation, (B) Hessian analysis enhancing bright plate-like structures, (C) enhanced plate structure, (D) point groups from separated left and right lung regions by subtracting the dilated plate structures from original segmentation, (E–F) distance transform from the two point groups, (G) 2D separation manifold determined by distance transform, and (H) final separation result

IV. Experimental Results

A. Data and reference standards

To evaluate the performance of our PLS method, we used both publicly available and in-house acquired data sets. All in-house images were acquired at our institute using 64-detector row Phillips Brilliance 64 or GE Medical Systems Light Speed Ultra. Scans were performed at end-inspiration with 1.0 or 2.0 collimation and obtained at 10 or 20 mm intervals from the base of the neck to upper abdomen. After obtaining Institutional Review Board (IRB) approval, retrospective cases of human para-influenza (HPIV), necrotic tuberculosis (NTB), diffuse alveolar hemorrhage (DAH), influenza A (H1N1) were collected from May 2005 through September 2012. Table IV summarizes the data sets used in our study.

TABLE IV.

Data Description of the CT scans used in our experiments.

	Source	# of patients	# of scans	Slice Thickness	Median Age± SD (years)	Gender	Notes
HPIV	NIH	40	56	5 mm	39.98 ±17.54	M=18, F=22	Low-resolution scans of patients with human para- influenza virus. Scans include cases of heavy consolidation, various other pathologies, and effusion.
NTB	NIH	30	71	5 mm	42.4±15.4	M=17, F=13	Patient scans with neurotic tuberculosis. Scans include cases of heavy consolidation, and cavities.
DAH	NIH	26	68	5 mm	39.23 ±18.21	M=14, F=12	Low-resolution scans of patients with diffuse alveolar hemorrhage. Scans include cases of heavy consolidation, and effusion.
TB	Public	80	93	2.5 mm	41.5 ±17.26	M=49, F=31	Patient scans with pulmonary tuberculosis. The data contains various pathologies prominently: consolidation, GGO, cavity, bleb, and pleural effusion. (http://tuberculosis.by/).
H1N1	NIH	4	6	5 mm	50±12.8	M=3, F=l	Patient with influenza H1N1 pneumonia. The scans show blood clot and various pathologies such as GGO, micronodules, and consolidation.
LOLA Challenge Data	Public	55	55	< 1.5 mm	n/a‡	US+=55	Data set designed as part of the lung segmentation challenge (MICAII 2011). The pathologies in lung scans range from mild to severe. (http://lola11.com).
EXACT Challenge Data	Public	40	40	1 mm	45.67 ±32.92	M=19, F=14, US+=7	High-resolution scans with mild pathologies (consolidation, and effusion). (http://image.diku.dk/exact).
Control	NIH	14	14	2 mm	50±17.11	M=5, F=9	High resolution lung scans of healthy individual. The lung scans does not show any abnormality.
Total	—	288	403	—	41.91 ±20.72	M=124, F=100, US†=61

^†unspecified.

^‡data anonymized.

When biopsy images are not available, manual segmentation by experts is often accepted as the gold standard. For segmentation evaluation of in-house CT data, reference standards were provided by two experienced observers through manual segmentation. The left and right lungs were labeled separately in order to evaluate each lung individually. Dice similarity coefficient (DSC) [54], Hausdorff distance (HD) [54], specificity, and sensitivity evaluation metrics were used for quantitative analysis. Table V summarizes the quantitative evaluation of all 8 data sets segmented with the PLS algorithm. An average overlap score of more than 95% was obtained in our analysis of over 400 CT scans.

TABLE V.

Overall performance of the proposed lung segmentation approach averaged over different data sets and averaged overall. Mean and standard deviation (std) is provided for each index.

Data set		DSC		HD (mm)		Sensitivity		Specificity
		Observer-I	Observer-II	Observer-I	Observer-II	Observer-I	Observer-II	Observer-I	Observer-II
HPIV	mean	0.9542	0.9647	33.5875	17.8705	0.9978	0.8688	0.9427	0.9661
	std	0.0121	0.0241	7.0262	7.5309	0.0010	0.1966	0.0422	0.0338
NTB	mean	0.9728	0.9714	15.7875	14.0238	0.9886	0.9991	0.9779	0.9362
	std	0.0086	0.0107	10.8789	10.8513	0.0240	0.0019	0.0230	0.0404
DAH	mean	0.9102	0.9091	15.8562	14.6573	0.9592	0.9954	0.8943	0.9027
	std	0.0519	0.5794	8.2817	9.3531	0.0195	0.0039	0.1045	0.1264
TB Data	mean	0.9681	0.9767	21.6639	18.4931	0.9324	0.9874	0.9012	0.8884
	std	0.0274	0.0055	18.3700	12.5297	0.0195	0.0143	0.1054	0.0831
H1N1	mean	0.9222	0.9191	15.8562	12.2321	0.9556	0.9923	0.9018	0.9038
	std	0.0432	0.0082	8.2817	9.3131	0.0112	0.0011	0.1267	0.1323
Exact	mean	0.9897	0.9878	20.5478	21.740	0.9972	0.9987	0.9890	0.9667
	std	0.0040	0.0068	17.8197	17.6766	0.0024	0.0181	0.0066	0.0392
Control	mean	0.9903	0.9911	8.3671	7.5691	0.999	0.9981	0.9884	0.9898
	std	0.0018	0.0021	6.1891	7.2151	0.0037	0.0023	0.0066	0.0032
Total	mean	0.9595	0.9627	19.6467	18.0054	0.9684	0.9728	0.9297	0.9234
	std	0.0034	0.1058	12.8448	12.0798	0.0163	0.0475	0.0068	0.0667

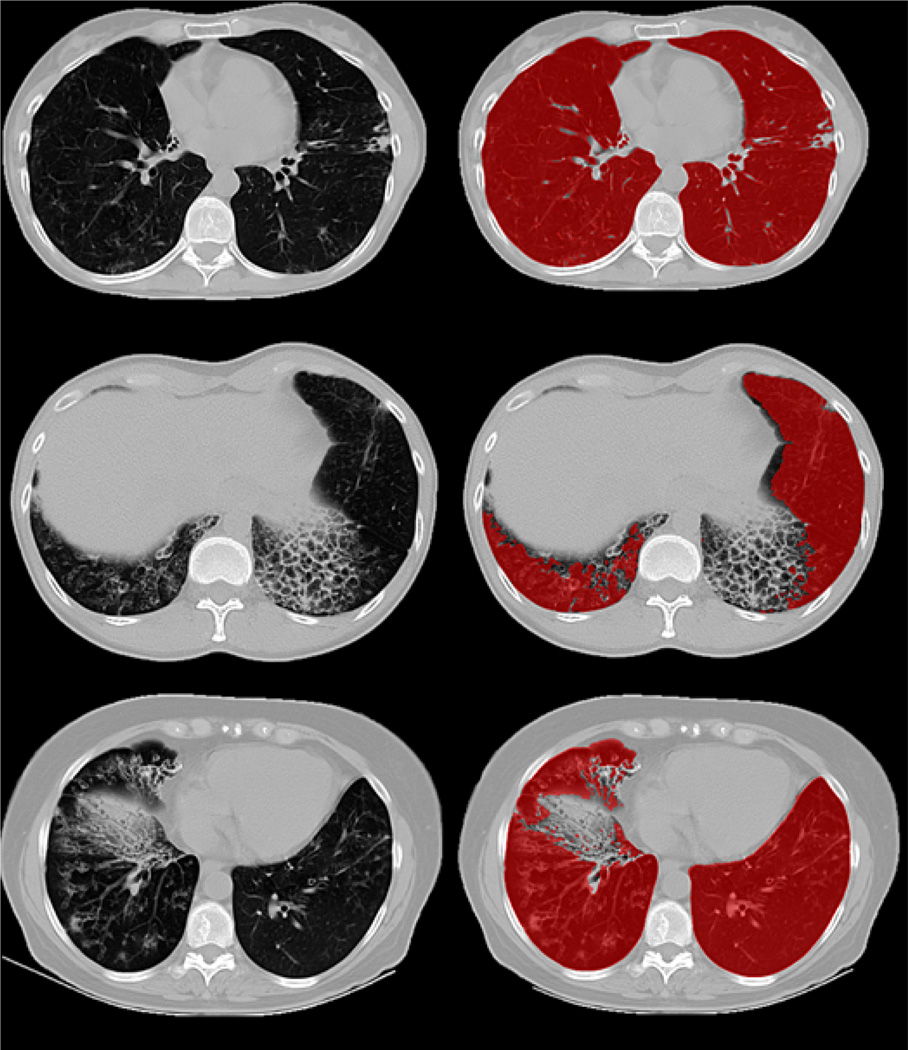
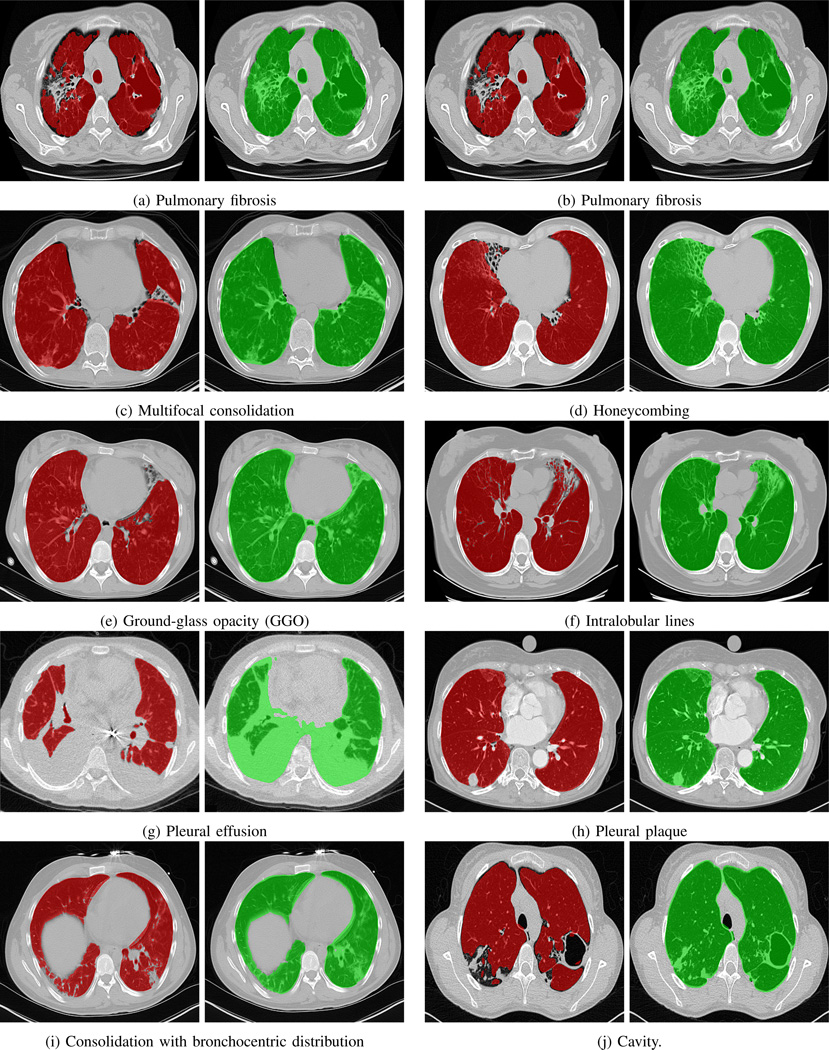
For qualitative evaluation, Fig. 16 indicates the initial FC segmentation of the lungs (shown in red) with various pathologies, and our proposed method (shown in green). Results obtained for different abnormal imaging patterns consistently indicate the superior performance of the PLS method. For a clinical reference, a summary of how various pathologies are handled inside our proposed framework is provided in Table VI. The table clearly demonstrates the effectiveness of the proposed technique in dealing with most commonly encountered pathologies.

Fig. 16.

Example axial slices of segmentation results on HRCT lung scans with different pathologies. Red segmentation shows the results using the FC while the corresponding green segmentation shows results using our proposed method.

TABLE VI.

Summary of the pathologies (along with normal lung parenchyma) segmented by different modules of the algorithm.

FC (initial)	Beaded Septum
	Varicose Bronchietiss
	Bronchocele
	Interstitial Emphysema
	Perilymplatic Distribution
	Micronodules
	Tree-in-bud (TIB)
FC (cavity)	Bleb
	Bulla
	Cavity
	Cyst
Texture classification	Interstitial pneumonia
	Air-filled bronchietasis
	Pulmonary fibrosis
	Consolidation
	Centrilobular emphysema
	Crazy paving pattern
	Ground glass opacity (GGO)
	Honey combing
	Halo sign
	Mycetoma
	Reverse Halo
Ngbr-guided	Infarction
	Pleural effusion
	Pleural plaque

B. Statistical comparison and inter- and intra-observer agreements

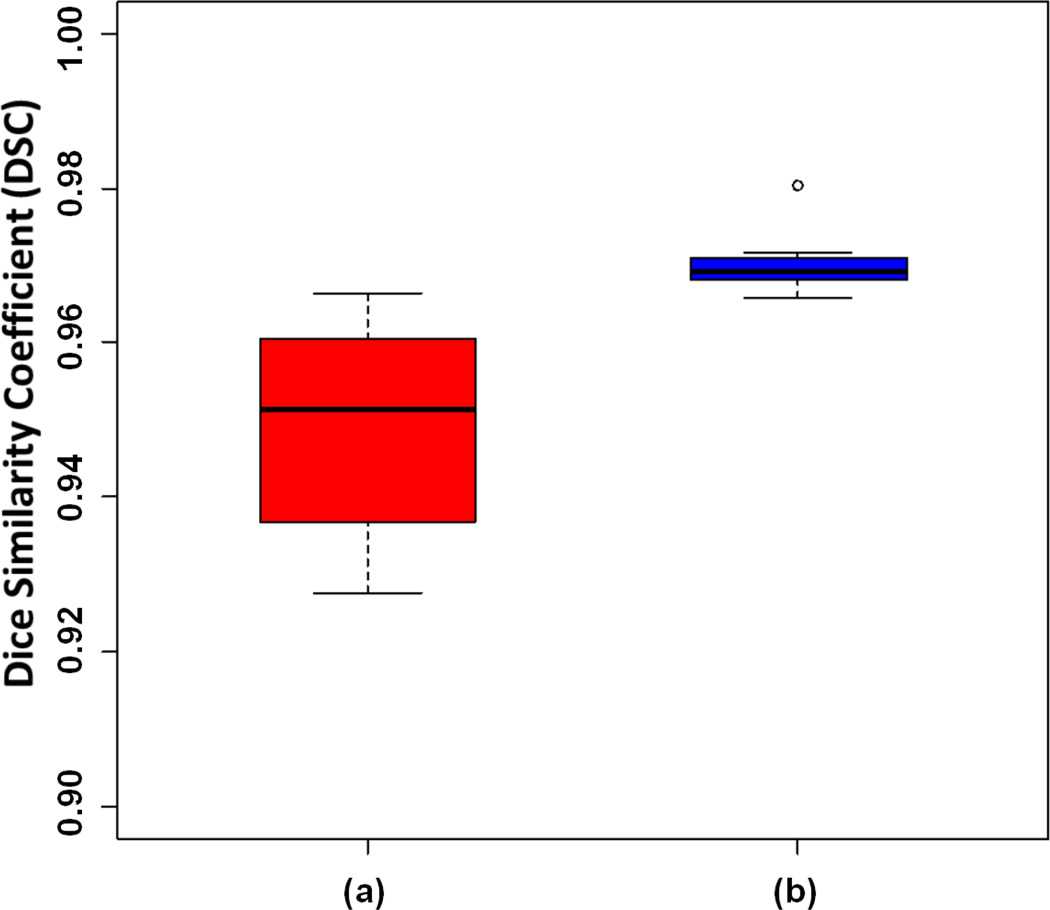
Compared to the initial FC segmentation, we observed significant improvement in the overlap score with the PLS method when applied to the HPIV data set which contained the widest range of abnormalities compared with other data sets. The statistically significant (p = 0.018) improvement with the use of the PLS method was observed in the data set (see Fig. 17).

Fig. 17.

DSC of the segmentation evaluation of HPIV data set through (a) initial FC segmentation, and (b) the proposed PLS method.

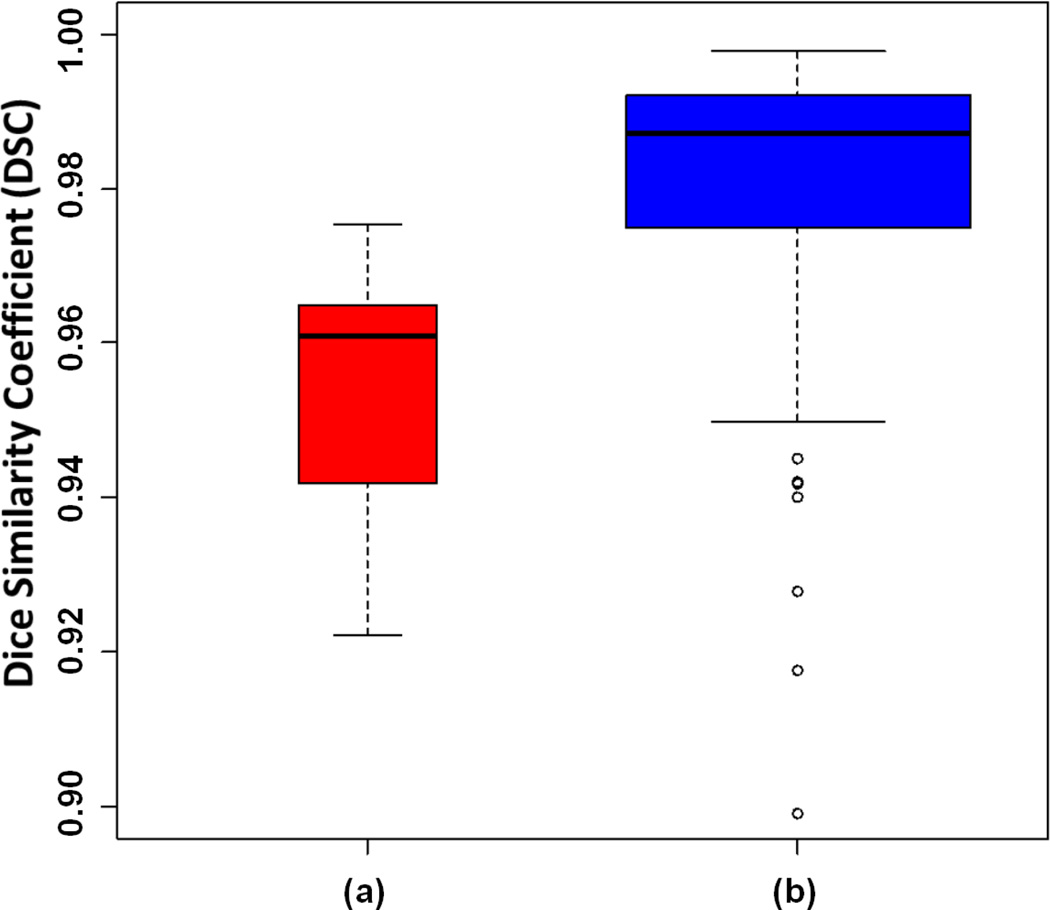
To quantify the inter- and intra-observer agreements, we compared the DSC values of the manually delineated CT scans. Fig. 18 shows the box-plots for intra-observer (a) and inter-observer (b) agreements. For intra-observer agreements, both observers were asked to repeat the manual segmentation of randomly chosen CT scans after a week of initial delineation, and segmentation variations were computed through DSC values. These results demonstrate that the difference between the overlap scores obtained using the PLS method compared to the manual segmentation are not statistically significant and, large intra- and inter-observer differences increase in the presence of heavy abnormalities. Automatic delineation methods such as the PLS method can be very useful in obtaining precise results in such cases.

Fig. 18.

Box-plots of dice coefficients for intra-observer (a) and inter-observer (b) agreement are demonstrated.

C. Comparison to the state-of-the-art methods

To analyze the effectiveness of the PLS method and for an independent evaluation and direct comparison of the proposed PLS method with other state-of-the-art techniques, we tested our algorithm using the publicly available LObe and Lung Analysis 2011 (LOLA11) Challenge data set http://lola11.com/. Submitted results were evaluated against a reference standard using overlap measures by the organizers and published online. The results were reported in terms of minimum, mean, median, and maximum overlap over the 55 scans for left and right lung separately. The final score was the mean over all scans. The evaluation provided for our algorithm was reproduced in Table VII. For comparison purpose, scores of other algorithms that joined the segmentation challenge are presented in Table VIII with a short description of each method. Further details of the methods can be found on the challenge website.

TABLE VII.

Overlap scores for the Automated Lung Segmentation for the 55 scans in LOLA11.

obj	mean	std	mm	Q1	median	Q3	max
Left lung	0.957	0.137	0.034	0.979	0.987	0.995	0.999
Right lung	0.952	0.151	0.000	0.984	0.990	0.997	0.999
score	0.955
(a) Pleural fluid included inside the lung field.
obj	mean	std	mm	Q1	median	Q3	max
Left lung	0.968	0.097	0.316	0.979	0.987	0.995	0.999
Right lung	0.968	0.134	0.000	0.984	0.990	0.997	0.999
score	0.968
(b) Pleural fluid excluded from the lung field.

TABLE VIII.

LOLA11 Segmentation Challenge results with a short description of the submitted methods.

Team Name	Score	Summary	Further Reading
Fraunhofer ME VIS	0.973	Region-based segmentation initiated by automatically detected seed points followed by morphological closing	[55]
yacta	0.97	Segmentation of trachea-bronchial tree. Landmark determination in left and right lung. Threshold based region growing. Filling of holes in axial slices.	[56]
NIH	0.968	Fully automated PLS method with- out considering pleural fluid as part of lung field.
SmartPaint	0.969	Interactive segmentation	[57]
UCLA Historic	0.963	Threshold-based 3D region growing followed by 6-neighborhood connected component analysis.	[2]
DIAG	0.962	Initial segmentation is performed using a conventional region growing and morphological smoothing. Next, automatic error detection (using shape analysis) is applied. The scans that are likely to contain errors are then segmented by a multi- atlas segmentation.	[58]
GE Research Niskayuna NY	0.952	Context Selective Decision Forests classification.	[59]
MCVGL	0.949	Rib cage detection followed by a robust active shape model for rough segmentation of lung field, and optimal surface finding approach for final refinement.	[60]
Barcelona	0.949	Sequential classifiers using pixel appearance and multiscale analysis of neighbors class likelihood.
CREATIS CLB Lyon	0.948	Region-growing followed by morphological operations.

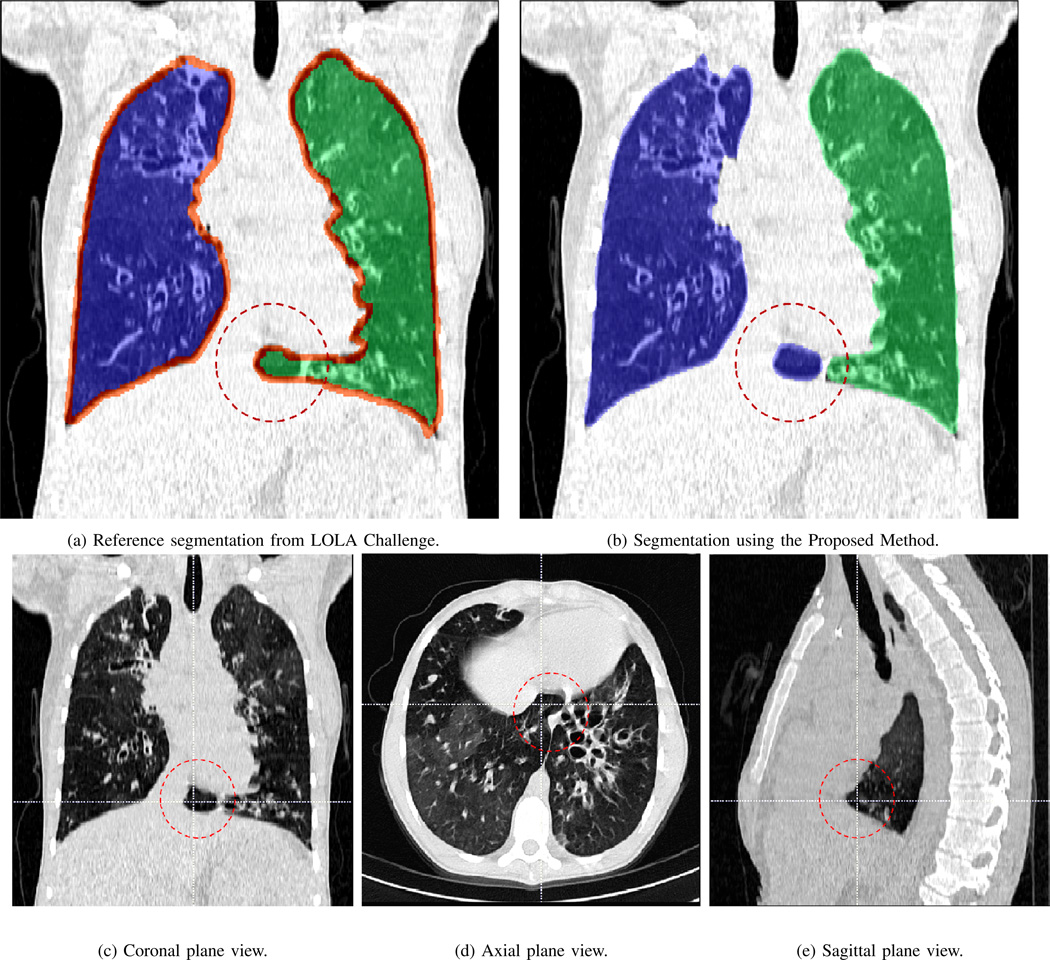
Since the medical imaging community lacks consensus on whether pleural fluid should be considered as a part of lung field or not, we segmented the LOLA data set including pleural field as a part of lung (Table VII (a), a score of 0.968 was obtained) and excluding the pleural field as an additional experiment in which we obtained a score of 0.955. Although not all segmentations evaluations were available on LOLA11’s website, a few available screenshots revealed that there were some inconsistency in creating ground truth by the organizers and this may eventually affect the ranking of the methods. For instance, screenshots of the LOLA image #37 from the website was reproduced in Fig. 19. The figure shows a reference ground truth and our method’s segmentation such that the areas marked by circle are falsely included in the wrong lung (i.e., left lung were falsely labeled as right lung) while the same region was correctly labeled with our algorithm (b). Fig. 19(c), (d), and (e) indicated the incorrect label assignment of LOLA data set, as also confirmed by our participant radiologists. As a result, computed overlap measures for this particular CT scan was lower than what we expected because of the false calculation of the overlap measure.

Fig. 19.

Reference segmentation from the LOLA challenge (a) and segmentation using our proposed method (b) is shown along with the coronal (c), axial (d), and sagittal (e) plane views of the segmented image (lola11-37). The part of right lung mistakenly included in the left in reference segmentation by LOLA is marked in coronal, axial, and sagittal planes.

D. Evaluation of the pathology presence test

Regarding the successful detection rate for minimal, mild, and severe cases, we first divided the whole data sets into three different groups by expert scores: none/minimal (# of scans=53), mild (# of scans=268), and severe (# of scans=87). In all severe cases, our pathology recognition system decides to switch into the machine learning classification phase (i.e. 100% detection rate). In evaluation of 268 mild cases, our algorithm only missed 4 scans to be evaluated in the machine learning phase; therefore, a successful detection rate of 98% was observed. Among 53 cases with none/minimal pathology, our algorithm has chosen 12 scans to be analyzed in the machine learning step, although the next step was not necessary. This additional selection was due to the fact that we tuned our pathology recognition system to have a tendency to switch into machine learning step when estimated volume and initial lung volume difference lies in the decision border. Note that with the expense of type II error only contributes to an increase in the computational cost (i.e., inclusion of machine learning step for cases which do not really need this step), we reduced the type I error considerably. It should be also emphasized that some inconsistencies in machine learning classification phase might occur when CT images are low resolution or poor quality and as a result of this, extracted texture features can be less effective in finding the correct class labels for the voxels. In such cases, our complementary third step (i.e., neighboring anatomy guided refinement) diminishes inconsistencies.

E. Computational efficiency

A switch named pathology-presence test has been put in place to assess if the target scan requires further refinement. One of the primary purposes of the switch is to make the segmentation platform computationally efficient by avoiding unnecessary steps. Therefore, the amount of time required to segment a particular scan depends largely on the amount of abnormality present inside the scan as well as the size the scan. For our workstation (Intel(R) Xeon(R) 3.10 GHz, 128 GB ram), the amount of time ranges from less than a minute (512×512×71 normal scan) to 15 minutes on average (512× 512 × 792, severe parenchymal pathology and the presence of pleural pathology). A recent study to explore the use of supervoxel based near optimal key-point sampling to further reduce the computational cost of the PLS method is presented in [?].

V. Discussion

For CAD applications such as detection, classification, and quantification, accurate lung segmentation is an extremely important pre-processing step. Conventional techniques in lung segmentation rely only on contrast differences between the lung field and the surrounding tissues thus failing to segment areas with pathologies. Notably, lung scans containing significant amount of pathologies and other abnormalities are much more prevalent in daily clinical environment than ones without pathologies. Therefore, expert manual segmentation is still considered to be the most reliable option for pathological lungs. Additionally, with improvement in quality and affordability, the use of non-invasive imaging methods will become more common in routine clinical practice, generating a significant amount of data will be impractical to evaluate manually.

Our pathological lung segmentation technique has been tested on over 400 CT scans, completed on more than 280 patients with a variety of comorbidities and demographic backgrounds (Table IV). By testing on versatile data, we made our best effort to cover the most prevalent cases in the routine clinical environment. We also believe that due to the fully automated nature of our technique, additional pre-/post-processing steps may be necessary for certain scan types. For instance, noise induced variabilities needs to be investigated further and rare cases of extreme noise may demand that denoising steps be performed prior to delineation.

Since our proposed technique assumes certain characteristic structure to the ribs for volume estimation and seed selection, patients without fully developed bones such as in children and patients with an abnormal or fractured rib cage may require some parameter adjustments in the proposed method’s pipeline. Issues such as these will be examined in our future work.

The PLS has other limitations and there are cases where different modules of the proposed system may fail. For instance, excessive noise, external objects, and very rare clinical cases may cause the PLS to perform poorly. Some of failures cases are described and illustrated below.

Excessive noise

The PLS does not have a denoising mechanism built into it. Although our method is robust to a vast range of streaking and noise artifacts, excessive ranges of these artifacts may affect the performance of our method. Nevertheless, one may readily pre-process images prior to delineation step with the PLS.

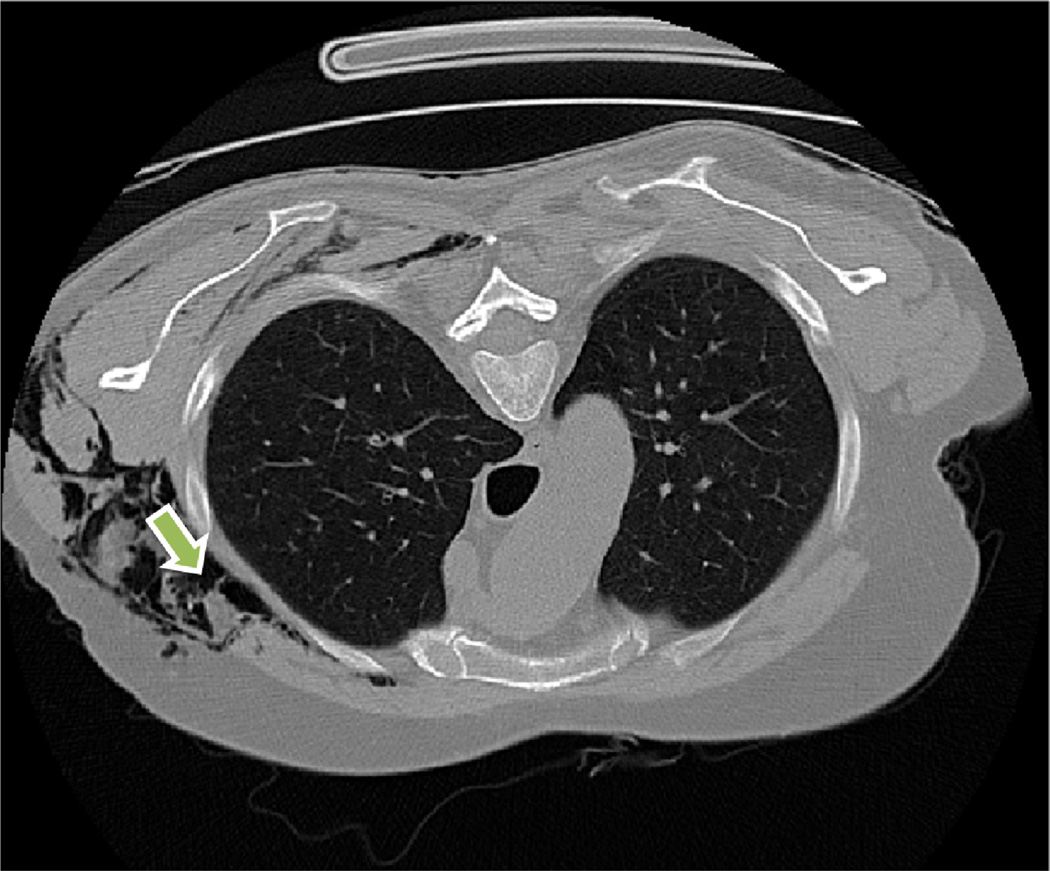
External objects

External objects such as tubes and medical implants may effect the performance of the method as illustrated in Fig. 20 (breast implants), and Fig. 21 (tube).

Fig. 20.

Artificial objects such as breast implants may affect the accurate ribcage extraction and manual interaction can be necessary for correcting the failure of pathology presence test.

Fig. 21.

Air and fluid-containing tubes and other cavity-like artificial objects such as the one shown may affect the performance of the PLS system.

Rare clinical cases

Subcutaneous emphysema occurs when gas or air is present in the subcutaneous layer of the skin (Fig. 22). The rare cases of CT scan with subcutaneous emphysema may result in the leakage of segmentation by the initial FC stage to air pockets within the subcutaneous layer.

Fig. 22.

An abdominal CT scan of a patient with subcutaneous emphysema (shown by an arrow).

In this article, we are not developing new feature sets or novel machine learning algorithms. Instead, we are developing and testing the complete pathological lung segmentation system on a large variety of cases with novel infrastructure. Nevertheless, our system can be further strengthened with more powerful machine learning classifiers and/or more discriminating higher order textural features. In its current form, the PLS is a promising tool to be used in routine clinics for pathological lung volume assessment as well as pathology recognition.

VI. Conclusion

We present a novel method for fully automated lung segmentation with and without abnormalities. To the best of our knowledge, the proposed method is the first fully automated-generic technique covering a wide range of pathologies and pleura without any human assistance. The core of our method is the FC initial segmentation. Our method is equipped with multiple refinement stages including machine-learning classification to handle pathologies; further, a novel neighboring anatomy-guided learning mechanism to handle extreme cases such as pleural effusion was introduced. The robustness and the effectiveness of our proposed method was tested on more than 400 lung scans acquired through various sources containing a wide range of abnormalities. The results obtained using the proposed method are tested in the most rigorous way possible, obtaining the overlap score of greater than 95%. The exhaustive testing confirm the accuracy and the effectiveness of the presented method.