Exact Confidence Intervals for Channelized Hotelling Observer Performance in Image Quality Studies

Abstract

Task-based assessments of image quality constitute a rigorous, principled approach to the evaluation of imaging system performance. To conduct such assessments, it has been recognized that mathematical model observers are very useful, particularly for purposes of imaging system development and optimization. One type of model observer that has been widely applied in the medical imaging community is the channelized Hotelling observer (CHO), which is well-suited to known-location discrimination tasks. In the present work, we address the need for reliable confidence interval estimators of CHO performance. Specifically, we show that the bias associated with point estimates of CHO performance can be overcome by using confidence intervals proposed by Reiser for the Mahalanobis distance. In addition, we find that these intervals are well-defined with theoretically-exact coverage probabilities, which is a new result not proved by Reiser. The confidence intervals are tested with Monte Carlo simulation and demonstrated with two examples comparing X-ray CT reconstruction strategies. Moreover, commonly-used training/testing approaches are discussed and compared to the exact confidence intervals. MATLAB software implementing the estimators described in this work is publicly available at http://code.google.com/p/iqmodelo/.

I. Introduction

Objective, task-based image quality assessments with mathematical model observers are a valuable tool for medical imaging system development, optimization, and characterization [1]–[3]. One type of model observer that has drawn considerable interest in the medical imaging community is the channelized Hotelling observer (CHO) [1]–[3], which is well-suited to known-location binary discrimination tasks. The CHO is the population equivalent of the classical Fisher linear discriminant function used in multivariate statistics and pattern recognition [4], [5] applied to a vector of image features, called channel outputs in the medical imaging and vision literature. Through various choices of channels, which determine relevant features and are used for dimensionality reduction, CHOs have been shown to track both human [6]–[11] and ideal linear [12] observer performance for known-location discrimination tasks. As a consequence, CHO methodology has been widely employed in medical imaging research, e.g., [13]–[25].

In some settings, CHO performance can be calculated accurately from analytical models [13], [15], [21]. However, due to complexities in the physics of data acquisition and in image formation, this approach is usually not feasible, and most practical evaluations instead estimate CHO performance from a finite set of images. Furthermore, the number of images available is typically limited for both real and simulated data sets by the available resources (acquisition time, computational cost, etc.), so that statistical variability in performance estimates cannot be neglected when making inferences.

One way to assess statistical variability in experimental results is through the use of confidence intervals. In contrast to traditional hypothesis testing, which is limited to only testing statistical significance, confidence intervals communicate statistical precision and effect size, in addition to statistical significance. These virtues make confidence intervals an attractive option for the presentation of experimental findings.

Typically, confidence intervals are constructed by starting with a point estimate. Two general approaches can be used to obtain point estimates of CHO performance from a set of images. In the first approach, all images are used to directly estimate the figure of merit by substituting sample estimates for population parameters [1, p. 972]. In the second approach, the images are split into two subsets, where one subset is used to estimate the observer template (i.e., train the observer), and the second subset is used to estimate performance of the trained observer (i.e., test the observer) [1, p. 973]. For the goal of estimating the performance of a CHO defined by population parameters (i.e., infinitely-trained), both approaches result in biased estimates. In this work, we adopt the first (direct) approach, and demonstrate how the point estimate bias can be overcome to obtain accurate confidence intervals for CHO performance. Later, we present a comparison of our confidence intervals with estimators based on training and testing.

This paper addresses the need for reliable confidence interval estimators for CHO performance. Specifically, we find that an approach introduced by Reiser [26] for interval estimation of the Mahalanobis distance can be applied to obtain confidence intervals for CHO performance. In addition, we prove that these intervals have theoretically-exact coverage probabilities, which is a new result not given by Reiser [26]. The exact confidence intervals are further evaluated with Monte Carlo simulation and are found to be superior to conventional Wald-style intervals [27, p. 499]. The application of the exact confidence intervals is demonstrated with examples comparing X-ray CT reconstruction strategies.

Our theoretical results rely on two assumptions: 1) the channel outputs follow a multivariate normal distribution for each image class, and 2) the covariance matrices for the channel outputs are the same for each class. These assumptions are typically well-justified for fixed-location discrimination tasks involving either a flat or a normally-distributed, variable background. Likewise, they can be employed when the measurement noise depends on the object and the mean difference between the two classes is small; in this case, the covariance matrices can be assumed to be the same.

More specifically, the first assumption is generally satisfied for reconstructed tomographic images, which are often approximately multivariate normal. Additionally, even for images that are not normally distributed, the central limit theorem implies that the channel outputs will tend to be normally distributed. For nuclear medicine applications, a strong argument justifying the normality assumption was provided by Khurd and Gindi [28]. In X-ray CT, the normality assumption was supported by Zeng et al. [29] with histogram plots, and by Wunderlich et al. in [30] using a univariate test and in [31] with a multivariate test. An argument in support of the second assumption for nuclear medicine was given by Barrett and Myers [1, p. 1209], and a quantitative analysis was presented by Wunderlich and Noo [30] in the context of X-ray CT.

In previous publications, we have presented related estimators for performance of linear observers [30], [32] and CHOs [33], [34]. To put the present work into proper perspective, it is helpful to clarify its relationship with these previous investigations. First, the estimators given in [30], [32] are designed for any linear observer defined by a fixed, known template, i.e., a classifier that is ready to be used in practice. Consequently, the estimators in [30], [32] are suitable for evaluations of finitely-trained observer performance when the template is determined by a fixed training set, or when the template is prespecified. By contrast, in this work and in [33], [34], the aim is to estimate performance of a CHO, which has a template that depends on unknown population parameters. Compared to [33], [34], in which the difference of class means is assumed to be known, the present work does not assume that any population parameters are known. Hence, the results given here can be seen as a complementary piece of a larger theory of model observer performance estimation. Further discussion of the relationships between the present work and other approaches is given at the end of the paper.

II. Background

In this section, we establish our notation by reviewing channelized Hotelling observers and associated performance measures.

One important component of a CHO is a set of channels. Channels are often used by model observers to reduce high-dimensional image data to a smaller number of relevant features. Each channel is itself an image that corresponds to a feature, and the scalar product of a channel with an image yields a channel output. We write the image as a q × 1 column vector, g, and denote the number of channels by p, where p is typically much smaller than q. The weights defining each channel are collected into a column of a q × p channel matrix, U, which is applied to each image to obtain a p × 1 channel output vector, v, where v = U^Tg. General considerations regarding the choice of channels are beyond the scope of this paper. The reader is referred to [1, pp. 936–937] and [3] for surveys of the literature on different channel models. In Section V, we present two CHO examples using Gabor channels, and provide an explanation of their essential characteristics. Note that if no channels are used, then U is equal to the identity matrix, i.e., U = I with p = q.

A CHO is designed for a binary discrimination task in which the goal is to classify each image as belonging to one of two classes, denoted as class 1 and class 2. For example, in the case of lesion detection, the two classes correspond to lesion-absent and lesion-present, respectively. To classify an image with a corresponding channel output vector v, a CHO starts by generating a rating statistic, t = w^Tv, where w is the p × 1 CHO template (defined below). Next, the rating statistic is compared to a threshold, c. If t ≥ c, then the image is classified as belonging to class 2, otherwise, the image is classified as belonging to class 1 [1].

We denote the means of the channel output vector, v, for classes 1 and 2 as μ₁ and μ₂, respectively, and their difference as Δμ = μ₂ − μ₁. In addition, let the (nonsingular) covariance matrices of v for class 1 and class 2 be Σ₁ and Σ₂, respectively, and write their average as Σ̅ = (Σ₁ + Σ₂)/2. In this notation, the template for a CHO is defined as w = Σ̅⁻¹Δμ [1]. Throughout this paper, it is assumed that Σ₁ = Σ₂ = Σ, so that the CHO template takes the simplified form w = Σ⁻¹Δμ.

For a binary classification task, an observer's performance is completely characterized by its receiver operating characteristic (ROC) curve, which plots true positive fraction (TPF) versus false positive fraction (FPF) over all decision thresholds [1], [35]. (In the medical literature, TPF and 1 − FPF are known as sensitivity and specificity, respectively.) A commonly used summary figure of merit for observer performance is the area under the ROC curve, denoted as AUC. If the observer's rating statistic, t, is normally distributed for each image class, then AUC can be expressed as $\text{AUC}=\mathrm{\Phi }(\text{SNR}/\sqrt{2})$, where Φ(x) is the cumulative distribution function (cdf) for the standard normal distribution, and SNR is the observer signal-to-noise ratio, defined as the difference of class means for t divided by the pooled standard deviation [1, p. 819], [35, pp. 83–84]. Above, because SNR and AUC are linked by a monotonic transformation, SNR is also useful as a figure of merit for observer performance [1, p. 819].

As discussed in the introduction, this work assumes that the channel output vector has a multivariate normal distribution for each class with a common covariance matrix. To express this assumption symbolically, we introduce the following notation. Let a p × 1 random vector x ∈ ℝ^p that follows a nondegenerate, multivariate normal distribution with mean, μ, and positive-definite covariance matrix, Σ, be denoted as x ~ 𝒩_p(μ, Σ). Writing the channel output vectors for classes 1 and 2 as v⁽¹⁾ and v⁽²⁾, respectively, our distributional assumptions can be expressed compactly as v⁽¹⁾ ~ 𝒩_p(μ₁, Σ) and v⁽²⁾ ~ 𝒩_p(μ₂, Σ).

The above distributional assumptions have three important implications. First, the CHO is optimal among all observers that operate on the channel output vector, in the sense that it maximizes SNR². In fact, if no channels are used, then the resulting observer coincides with the so-called “ideal observer” [1, p. 851]. Second, the observer rating statistic, t, is normally distributed under each class, so that $\text{AUC}=\mathrm{\Phi }(\text{SNR}/\sqrt{2})$, i.e., SNR and AUC are linked by a monotonic transformation. Third, the expression for observer SNR² simplifies to SNR² = Δμ^TΣ⁻¹Δμ [1, p. 967]. This last formula is our starting point in the next section. In the statistics literature, $\text{SNR}=\sqrt{\mathrm{\Delta }{\mathit{\mu }}^T{\sum }^{-1}\mathrm{\Delta }\mathit{\mu }}$ is also known as the Mahalanobis distance [4]. Note that since Σ is positive-definite, it follows that if Δμ is nonzero, which is generally true for image-quality evaluations, then SNR > 0 and 0.5 < AUC < 1.

III. Exact Confidence Intervals

Consider a random variable, X, with a distribution depending on a nonrandom parameter, θ. A random interval estimate [θ_L(X), θ_U(X)] for θ is said to be a 1 − α confidence interval [27] if for any θ in the parameter space, the probability that the interval covers θ is 1−α, i.e., P(θ ∈ [θ_L(X), θ_U(X)]) = 1−α. The value 1 − α is called the coverage probability for the confidence interval. A confidence interval is said to be exact if the coverage probability equation is exactly satisfied. Otherwise, a confidence interval is said to be approximate.

In this section, we construct exact SNR and AUC confidence intervals for a CHO. The construction is based on an approach first suggested by Reiser [26] for interval estimation of the Mahalanobis distance. Although Reiser stated that his intervals were approximate, we prove that they are, in fact, exact as long as SNR > 0, which is typically the case for image quality evaluations. We start by introducing an SNR² point estimator.

A. SNR² Point Estimation

Suppose that we are given m independent, identically distributed (i.i.d.) measurements of the class-1 channel output vector, ${\mathbf{v}}_1^{(1)},{\mathbf{v}}_2^{(1)},\dots ,{\mathbf{v}}_m^{(1)}$, and n i.i.d. measurements of the class-2 channel output vector, ${\mathbf{v}}_1^{(2)},{\mathbf{v}}_2^{(2)},\dots ,{\mathbf{v}}_n^{(2)}$. Write the sample means of the channel output vectors for classes 1 and 2 as ${\overline{\mathbf{v}}}_1=(1/m){\sum }_{i=1}^m{\mathbf{v}}_i^{(1)}$ and ${\overline{\mathbf{v}}}_2=(1/n){\sum }_{j=1}^n{\mathbf{v}}_j^{(2)}$, respectively, and their difference as Δv̅ = v̅₂ − v̅₁. Also, define a pooled estimate of the channel output covariance matrix, Σ, as

$$S=\frac{1}{m+n-2}\left[\sum _{i=1}^m\right({\mathbf{v}}_i^{(1)}-{\overline{\mathbf{v}}}_1){({\mathbf{v}}_i^{(1)}-{\overline{\mathbf{v}}}_1)}^T+\sum _{j=1}^n({\mathbf{v}}_j^{(2)}-{\overline{\mathbf{v}}}_2\left){({\mathbf{v}}_j^{(2)}-{\overline{\mathbf{v}}}_2)}^T\right].$$ (1)

Recall that under our distributional assumptions, SNR² = Δμ^TΣ⁻¹Δμ. Substituting the above sample estimates for Δμ and Σ into this formula results in a direct, plug-in point estimate given by θ̂_p = Δv̅^TS⁻¹Δv̅, where the subscript “p” stands for “plug-in.” Since S is nonsingular with probability one if m + n > p + 1 [4, Th. 3.1.4, p. 82], it follows that θ̂_p is well-defined as long as m + n > p + 1. Note that θ̂_p is equivalent to the maximum likelihood estimator (MLE) when multiplied by (m+n)/(m + n − 2).

It turns out that a multiplicative factor can be utilized to reduce the bias and variance of θ̂_p. Namely, let

$$\hat{\theta }=\gamma \mathrm{\Delta }{\overline{\mathbf{v}}}^T{S}^{-1}\mathrm{\Delta }\overline{\mathbf{v}}$$ (2)

where γ is a positive function of m, n, and p. Below, we derive an attractive choice for γ.

Under our distributional assumptions, the sampling distribution for θ̂ is closely related to the noncentral F-distribution, which arises as the ratio of a noncentral χ² random variable to an independent, central χ² random variable [4]. We denote a random variable, X, following a noncentral F-distribution with degrees of freedom ν₁ and ν₂, and noncentrality parameter, δ, with standard notation as $X~F_{{\nu }_1,{\nu }_2}^{\prime }(\delta )$. The following theorem characterizes the sampling distribution of θ̂.

Theorem 1

Suppose that ${\mathbf{v}}_i^{(1)}~{𝒩}_p({\mathit{\mu }}_1,\sum )$ for i = 1, 2, …, m and ${\mathbf{v}}_j^{(2)}~{𝒩}_p({\mathit{\mu }}_2,\sum )$ for j = 1, 2, …, n are independent. If m + n > p + 1 and γ is positive, then

$$\frac{(m+n-p-1)(\mathit{\text{mn}})}{p(m+n-2)(m+n)\gamma }\hat{\theta }~F_{{\nu }_1,{\nu }_2}^{\prime }(\delta )$$

with ν₁ = p, ν₂ = m+n−p−1, and δ = SNR²(mn)/(m + n).

Proof

The result follows from the distribution of the two-sample Hotelling T² statistic [4, Th. 3.2.13, p. 98].

We can draw three interesting observations from the above theorem that have implications for the confidence intervals presented in the next subsection. First, note that Theorem 1 holds independent of the choice of γ, since this factor also appears in θ̂ and cancels out of the quantity on the left side. Second, observe that the distribution of θ̂ depends on four parameters: m, n, p and SNR. Since m, n, and p are fixed for a given experiment, the only unknown parameter is SNR. Third, for fixed m and n, the noncentrality parameter, δ, is proportional to SNR². In the next subsection, this fact is utilized to construct confidence intervals for SNR.

Applying classical formulae for the mean and variance of the noncentral F-distribution [36], it is straightforward to obtain expressions for the mean and variance of θ̂. These expressions are collected in the corollary below.

Corollary 1

Suppose that the hypotheses of Theorem 1 are satisfied. If m + n > p + 5, then

$$\mathrm{E}[\hat{\theta }]=\gamma \left(\frac{m+n-2}{m+n-p-3}\right)\left[\right(\frac{m+n}{\mathit{\text{mn}}})p+{\text{SNR}}^2]$$

$$\text{Var}[\hat{\theta }]=2{\gamma }^2{\left(\frac{m+n-2}{m+n-p-3}\right)}^2{\left(\frac{m+n}{\mathit{\text{mn}}}\right)}^2\times \frac{1}{(m+n-p-5)}[{(p+\frac{\mathit{\text{mn}}}{m+n}{\text{SNR}}^2)}^2+(p+2\frac{\mathit{\text{mn}}}{m+n}{\text{SNR}}^2)(m+n-p-3)].$$

From the above expressions, it can be seen that by choosing

$$\gamma =\frac{m+n-p-3}{m+n-2},$$ (3)

the multiplicative bias is removed, and the overall bias is reduced, as compared to γ = 1. Namely, the bias, E[θ̂] − SNR², becomes (m + n)p/(mn), which increases with the number of channels, p, and decreases with the number of samples, m + n. Furthermore, the above choice of γ is seen to reduce the variance by a factor of [(m + n − p − 3)/(m + n − 2)]². Observe that since γ is strictly positive if m + n > p + 3, it follows that θ̂ is well-defined as long as m + n > p + 3. The multiplicative constant, γ, defined in (3) is an original contribution of this work; we use this definition throughout the remainder of the paper. However, the reader should note that since the distribution in Theorem 1 does not depend on γ, the exact confidence intervals defined in the next section are independent of γ.

Given the above observations, it is evident that an unbiased point estimate of SNR² can be obtained by subtracting the bias, (m + n)p/(mn), from θ̂ with γ given by (3). However, such bias subtraction is problematic, since it shifts the distribution of point estimates, and leads to potentially negative estimates of SNR². Because conversion of SNR² to SNR and AUC requires a square root operation, a negative SNR² estimate cannot be converted to a real-valued estimate of SNR or AUC, and its interpretation as a figure of merit is unclear. Moreover, truncation of a negative estimate at zero comes with another complication, since this operation will alter the statistical properties of the estimator and introduce a bias. This situation is similar to the possibility of negative estimates of variance components in the analysis of variance (ANOVA) when using unbiased estimators [37]. For the reasons mentioned above, we do not pursue an additional bias reduction through subtraction in our point estimates of SNR².

B. Reiser Intervals and Main Result

Under our assumptions on the channel output vector

$$X=\frac{(m+n-p-1)(\mathit{\text{mn}})}{p(m+n-2)(m+n)\gamma }\hat{\theta }$$ (4)

follows a noncentral F-distribution by Theorem 1. Moreover, the noncentrality parameter, δ, for this distribution is a strictly increasing function of SNR, and hence, AUC. As a result of these relationships, confidence intervals for SNR and AUC can be obtained from a confidence interval for the noncentrality parameter. To find a 1 − α confidence interval for δ, we use an approach suggested by Reiser [26], as described below.

Denote the cdf for X as F_X(x; ν₁, ν₂, δ) and suppose that α₁, α₂ ∈ (0, 1) are fixed numbers such that α₁ + α₂ = α for some α ∈ (0, 1). (For typical two-sided intervals, α₁ = α₂ = α/2.) Given an observation x of X, functions δ_L(x) and δ_U(x) are defined as follows, using the key property that the cdf for the noncentral F-distribution is a continuous, strictly decreasing function of δ; see Lemma 1 in the Appendix. First, if F_X(x; ν₁, ν₂, 0) > 1 − α₁, then δ_L(x) is defined as the implicit solution of the equation

$$F_X(x;{\nu }_1,{\nu }_2,{\delta }_L(x))=1-{\alpha }_1.$$ (5)

Otherwise, δ_L(x) is defined to be zero. Similarly, if F_X(x; ν₁, ν₂, 0) > α₂, then δ_U(x) is defined as the implicit solution of

$$F_X(x;{\nu }_1,{\nu }_2,{\delta }_U(x))={\alpha }_2.$$ (6)

Otherwise, δ_U(x) is defined to be zero.

From Lemma 1 in the Appendix, it follows that δ_L(x) and δ_U(x) are well-defined, which is a fact not proved by Reiser [26]. Because the noncentral F cdf is a built-in library function in many statistical software packages, δ_L(x) and δ_U(x) can be easily computed by iteratively solving the implicit equations in (5) and (6) with standard root-finding algorithms.

The functions δ_L(X) and δ_U(X) given above are the lower and upper endpoints, respectively, of a nominal 1−α confidence interval for the noncentrality parameter, δ. From its definition it can be observed that the confidence interval for δ can potentially be [0, 0] when θ̂ is very small. When this happens, the result should be interpreted to mean that zero is the best estimate of δ.

The interval [δ_L(X), δ_U(X)] for δ can be transformed into a confidence interval for SNR through the mapping given in Theorem 1. Namely, lower and upper endpoints for an SNR interval are given by ${\text{SNR}}_L(\hat{\theta })=\sqrt{{\delta }_L(X)(m+n)/(\mathit{\text{mn}})}$ and ${\text{SNR}}_U(\hat{\theta })=\sqrt{{\delta }_U(X)(m+n)/(\mathit{\text{mn}})}$, respectively. The functional dependence of SNR_L and SNR_U on θ̂ comes from the fact that X is a function of θ̂ (here, m, n, and p are fixed). Likewise, a confidence interval for AUC can be obtained by applying the transformation $\mathrm{\Phi }(\text{SNR}/\sqrt{2})$ to the SNR interval endpoints. We call the above confidence intervals for δ, SNR, and AUC Reiser intervals, since they were first defined in [26].

From heuristic reasoning and limited numerical evidence, Reiser [26] concluded that the confidence interval [δ_L(X), δ_U(X)] for δ has “essentially exact” coverage probability 1 − α. We have discovered that, in fact, this confidence interval has exact coverage probability 1 − α as long as δ > 0. Because the Reiser intervals for SNR and AUC are strictly increasing transformations of the interval for δ, they have the same coverage probability, and are thus exact under the condition that δ > 0, i.e., SNR > 0. Our findings are summarized below; see the Appendix for a proof.

Theorem 2

Suppose that the conditions of Theorem 1 are satisfied, and let SNR_L(θ̂) and SNR_U(θ̂) be defined as above for some α ∈ (0, 1). If SNR > 0, then [SNR_L(θ̂), SNR_U(θ̂)] and $[\mathrm{\Phi }({\text{SNR}}_L(\hat{\theta })/\sqrt{2}),\mathrm{\Phi }({\text{SNR}}_U(\hat{\theta })/\sqrt{2})]$ are exact 1−α confidence intervals for SNR and AUC, respectively.

The above theorem is the main theoretical result of this paper, and to our knowledge, is new. For readers interested in mathematical details, it is instructive to note that the proof given in the Appendix uses a different technique than the proofs in our previous papers on exact confidence intervals [30], [32], [34]. Specifically, the proofs in our previous papers relied on a standard theorem for pivoting a continuous cdf [27, Th. 9.2.12, p. 432], which does not apply in the present setting, because (5) and (6) do not have solutions for all observations x of X. To get around this difficulty, the proof of Theorem 2 (particularly Lemma 2), uses a slightly more general approach by returning to first principles.

As mentioned at the end of Section II, it is generally the case that for evaluations of image quality, which are the applications of interest in this paper, Δμ is nonzero, and hence, SNR > 0. Nevertheless, it is useful to note that when SNR = 0, the Reiser intervals are conservative. This fact was observed by Reiser [26], who gave an argument demonstrating that the coverage probability is 1 − α₁ in this case.

IV. Monte Carlo Evaluation

A Monte Carlo simulation study was carried out to evaluate the coverage probability of the Reiser confidence intervals given in the previous section. For purposes of comparison, the coverage of approximate Wald-type intervals based on a normality approximation was also assessed. The Wald-type intervals are described below.

Let V̂ be the point estimate of Var[θ̂] obtained by substituting the point estimate for θ̂ into the variance formula given in Corollary 1. Assuming that $(\hat{\theta }-{\text{SNR}}^2)/\sqrt{\hat{V}}$ approximately follows a standard normal distribution, a classical Wald-type confidence interval [27, p. 499] for SNR² with approximate coverage probability 1 − α is

$$[\hat{\theta }-z_{\alpha /2}\sqrt{\hat{V}},\hat{\theta }+z_{\alpha /2}\sqrt{\hat{V}}]$$ (7)

where z_α/2 = Φ⁻¹(1 − α/2) is the 1 − α/2 quantile for the standard normal distribution. Note that the lower bound of the Wald interval can possibly be negative. When the lower bound is positive, the above interval can be transformed into an SNR interval by taking the square root of the bounds, and into an AUC interval via the mapping $\mathrm{\Phi }(\text{SNR}/\sqrt{2})$.

For the simulation study, we used Monte Carlo simulation to test the coverage probabilities for the approximate Wald and exact Reiser confidence intervals. This was accomplished by simulating realizations of θ̂. For each estimate, we calculated the Reiser and Wald confidence intervals for SNR². Then we checked if the interval successfully covered the true value. The proportion of successes over many Monte Carlo trials then gave an estimate of the coverage probability, which ideally, should be 1−α. (Recall the definition of coverage probability stated at the beginning of Section III.)

For our evaluation, we took α = 0.05(α₁ = α₂ = 0.025), p = 5, 20, 50, AUC = 0.6, 0.75, 0.9, and (m, n) = (150, 50), (100, 100). The sampling distribution in Theorem 1 was used to generate 100 000 random deviates of θ̂, from which SNR² confidence intervals were obtained, and the coverage probabilities were estimated. Regarding the exact Reiser confidence intervals, note that since SNR and AUC are linked to SNR² through a strictly increasing transformation, the coverage probabilities for SNR and AUC intervals are the same. However, for the approximate Wald confidence intervals, the link between SNR², SNR and AUC is broken when the lower interval bound is negative.

The estimated coverage probabilities are listed in Table I. Since each entry is an estimate of a binomial proportion, the corresponding standard deviation is $\sqrt{\text{CP}(1-\text{CP})/N}$ [27], where CP is the true coverage probability and N is the number of Monte Carlo trials. For example, since the coverage probability of the Reiser intervals is 0.95, the standard deviation for a coverage probability estimate based on N = 100 000 trials is approximately 0.0007. For the Wald intervals, the true coverage probabilities are unknown, and the estimated coverage probability can be used in the above formula.

TABLE I.

Estimated Coverage Probabilities for 95% SNR² Confidence Intervals

p	AUC	m	n	CPWald	CPReiser
5	0.60	150	50	0.991	0.950
5	0.60	100	100	0.991	0.952
5	0.75	150	50	0.968	0.950
5	0.75	100	100	0.965	0.950
5	0.90	150	50	0.959	0.950
5	0.90	100	100	0.957	0.950
20	0.60	150	50	0.843	0.950
20	0.60	100	100	0.854	0.950
20	0.75	150	50	0.922	0.951
20	0.75	100	100	0.932	0.951
20	0.90	150	50	0.956	0.951
20	0.90	100	100	0.959	0.951
50	0.60	150	50	0.204	0.950
50	0.60	100	100	0.233	0.951
50	0.75	150	50	0.584	0.950
50	0.75	100	100	0.660	0.952
50	0.90	150	50	0.860	0.950
50	0.90	100	100	0.895	0.950

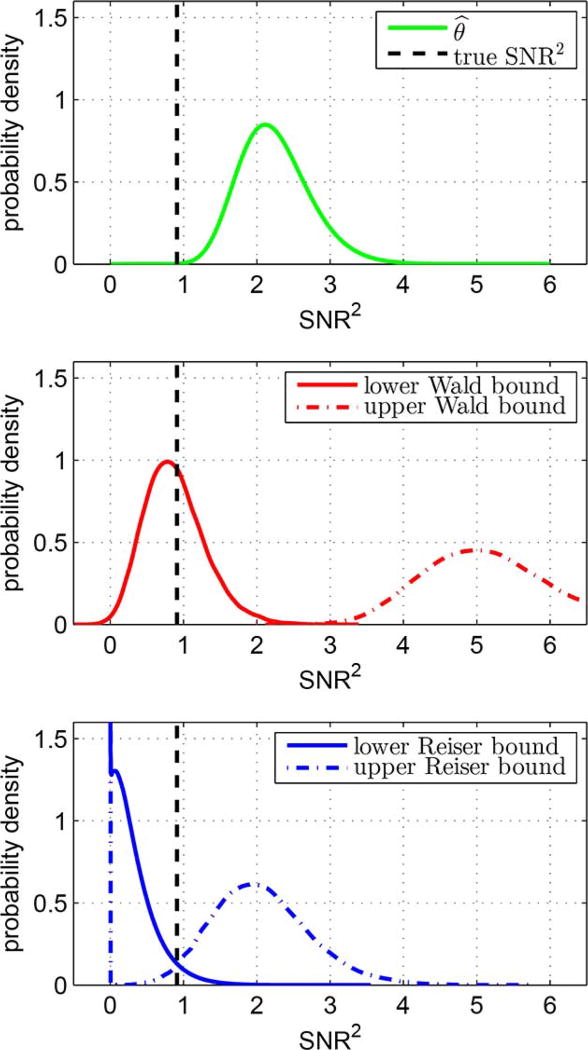
From Table I, it can be seen that the exact Reiser intervals have observed coverage probabilities very close to 95%, as expected. In contrast, the approximate Wald-style intervals are generally unreliable, especially for small AUC values and large numbers of channels. To better understand how the Wald intervals fail and the Reiser intervals succeed, plots of estimated probability density functions (pdfs) for the interval bounds (in the SNR² domain) are presented in Fig. 1 for the case p = 50, AUC = 0.75, and m = 150, n = 50, which is the fourth line from the bottom in Table I. The corresponding pdf for θ̂ is also plotted. In all plots, a dashed vertical line denoting the true SNR² value is given for reference. The estimated pdfs for the interval bounds are smoothed histogram estimates obtained with the kernel density method as offered in MATLAB, applied to the results of 50 000 Monte Carlo trials, whereas the pdf for θ̂ was obtained from the analytical expression in Theorem 1. From these plots, it can be seen that the distribution for θ̂ exhibits a positive bias, which strongly impacts the Wald interval bounds. On the other hand, the Reiser interval bounds are centered around the true SNR² value, and are not affected by the point estimation bias. Furthermore, it can be seen that the estimated pdfs for the lower and upper Reiser interval bounds both have spikes at SNR² = 0. This observation is expected, since the definition of the Reiser intervals implies that both the lower bound and the upper bound can be zero. In summary, the inaccuracy of the Wald intervals is largely a result of the positive bias of θ̂, whereas the Reiser intervals overcome this problem by using knowledge of the complete distribution for θ̂.

Fig. 1.

Estimated marginal distributions for Wald and Reiser SNR² confidence interval bounds with p = 50, AUC = 0.75(SNR² = 0.91), m = 150, and n = 50. (Top) pdf of θ̂, (Middle) estimated pdfs of upper and lower Wald bounds, (Bottom) estimated pdfs of upper and lower Reiser bounds. The true SNR² is denoted by the dashed vertical line.

V. Examples

To illustrate the exact CHO confidence intervals, we present two examples assessing image quality in X-ray computed tomography (CT). The first example uses simulated data of the XCAT phantom [38], and the second example is based on real CT scans of the QRM torso phantom.

Because noise in CT images is typically anisotropic due to its object-dependent nature, we implemented the CHOs in both examples with 18 Gabor channels centered on the location of interest. Gabor channels consist of a Gaussian modulated by a cosine function, and are circularly asymmetric and sensitive to image characteristics in different orientations. They have been used to model aspects of the human visual system [10], [39], and have been found to be yield higher detection performance than circularly symmetric channels in CT [40]. Mathematically, Gabor channels have the form [39]

$$G(x,y)=\text{exp}[-4(\text{ln }2)({(x-x_0)}^2+{(y-y_0)}^2)/w_s^2]\times \text{cos}[2\pi f_c((x-x_0)\text{ cos }\theta +(y-y_0)\text{ sin }\theta )+\xi ]$$ (8)

where f_c denotes the center frequency of the channel, w_s is the spatial width of the channel, the point (x₀, y₀) is the center of the channel, θ is the channel orientation, and ξ is a phase factor. The spatial width of the channel, w_s, is related to w_f, the full-width-at-half-maximum of the Fourier transform of the channel, through w_s = 4(ln 2)/(πw_f). We used three channel passbands, given by [1/32, 1/16], [1/16, 1/8], and [1/8,1/4] cycles/pixel, respectively; this choice of passbands is similar to those in [21], and was motivated by previous studies involving model observers [6], [7], [9]. The center frequencies for the passbands are f_c = 3/64, 3/32, and 3/16 cycles/pixel, with spatial channel widths of w_s = 28.24, 14.12, and 7.06 pixels, respectively. In addition, we used three orientations: θ = 0, π/3, and 2π/3 radians, and two phases: ξ = 0, π/2. Hence, there were 3 frequency bands × 3 orientations × 2 phases for a total of 18 channels.

A. Example 1

This example compares image quality for three fan-beam CT image reconstruction methods by using a known-location, background-variable classification task in which a CHO is applied to discriminate between two types of kidney stones. According to Kambadakone et al. [41], knowledge of kidney stone composition is an important factor influencing patient management. In particular, CT attenuation measurements have been found to be valuable for differentiation of uric acid stones from other stone types [41]. Motivated by this knowledge, we selected the task of discriminating between a uric acid stone (450 HU) and a struvite stone (600 HU) at a fixed location in the left kidney (recall that the left kidney is commonly displayed on the right side of transverse-plane CT images).

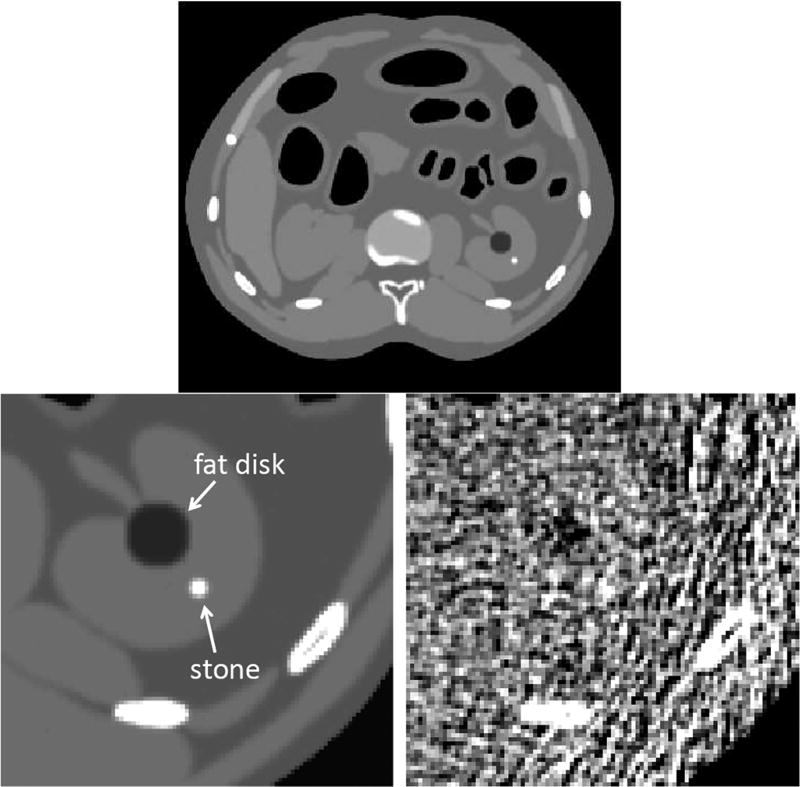
To generate images, we simulated CT data for the XCAT phantom [38] slice shown in Fig. 2. All images were reconstructed for a 96 × 96 region of interest (ROI) centered on the left kidney, with a pixel size of 1 mm × 1 mm. To simulate anatomical variations in the left kidney, we made two additions to the phantom, as follows. First, a circular disk of fat with a random radius between 5 mm and 10 mm was added to the kidney, near the ureter. Second, a random background was added to the kidney to simulate texture. This variable background was modeled as colored Gaussian noise following a power law model with an exponent of two [42], with an amplitude of ±6 HU. Last, a kidney stone of diameter 4 mm was added at a fixed location, with attenuation values of 450 HU for class 1 and 600 HU for class 2; see Fig. 2. Once a realization of the phantom was defined, fan-beam sinograms were computed, and Poisson noise with a photon level of 10 000 was added to the data with models for tube current modulation and a bowtie filter, as described in [21].

Fig. 2.

(Top) Slice of the XCAT phantom. (Lower Left) ROI centered on left kidney. (Lower Right) Noisy reconstruction. Grayscale: [−150, 250] HU.

We compared three fan-beam filtered backprojection (FBP) image reconstruction algorithms: A: Noo et al. [43] for full-scan data, B: Dennerlein et al. [44] for full-scan data, and C: Noo et al. [43] for short-scan data (240°). All algorithms were implemented so that resolution was matched near the field of view center. Algorithms A and B were expected to yield comparable CHO performance (since the kidney is fairly close to the field-of-view center), whereas algorithm C was anticipated to be worse since it uses less CT data.

To carry out the evaluation, 250 class-1 sinograms and 200 class-2 sinograms were generated. Next, every sinogram was reconstructed with the three algorithms to yield three sets of 450 images, i.e., one set for each reconstruction method. Finally, exact AUC confidence intervals describing CHO performance were estimated for each reconstruction algorithm.

Multivariate normality of the channel outputs was validated at the 10% significance level with the Henze–Zirkler normality test [45]. Since the confidence intervals were correlated, the coverage probability for each confidence interval was selected to be 96.67% so that the joint coverage probability for the three intervals was at least 90% by the Bonferroni inequality.¹ The results, given in Table II, indicate that Algorithms A and B were both better than Algorithm C with statistical significance. However, there was no statistically significant difference between Algorithms A and B, which was consistent with our expectations.

TABLE II.

Estimated 96.67% AUC Confidence Intervals for the Three Reconstruction Methods in Example 1

A:	[0.8044	0.8828]
B:	[0.7947	0.8754]
C:	[0.6892	0.7917]

B. Example 2

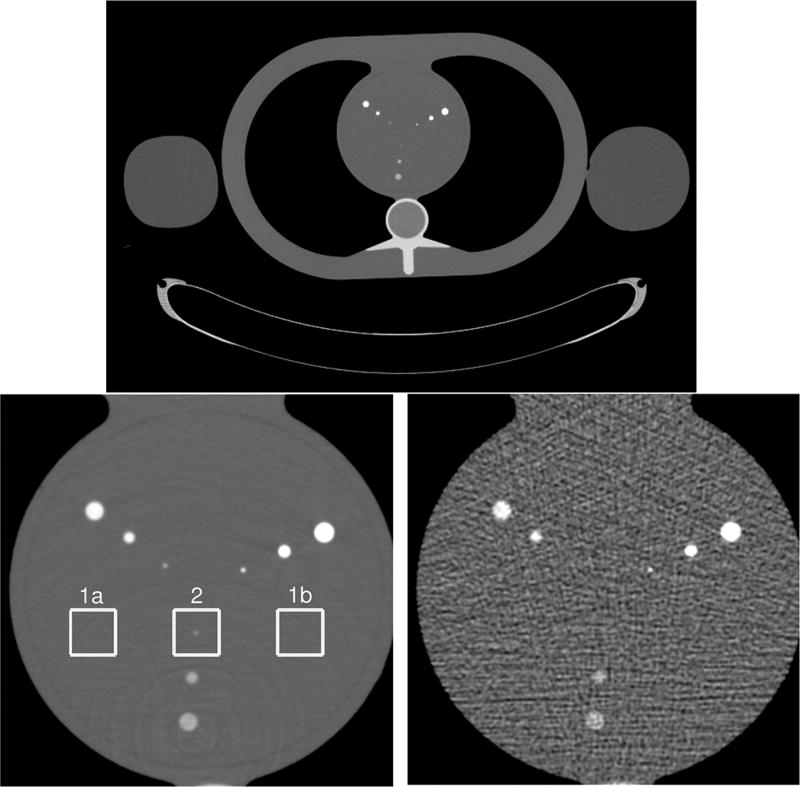
In this example, we evaluate image quality for two fan-beam CT image reconstruction methods applied to real CT data by using a CHO to detect a lesion at a known location in a torso phantom. Data was collected with a Siemens SOMATOM Sensation 64 CT scanner by repeatedly scanning a torso phantom 175 times over a circular source trajectory. The torso phantom, constructed by QRM (Möhrendorf, Germany), was used together with two water bottles placed on the sides to simulate arms. A mean image of the phantom estimated from all 175 scans is shown in Fig. 3. The scans were executed in thorax scan mode using a 2-slice acquisition with a slice thickness of 1 mm, a rotation speed of 3 rev/s, X-ray tube settings of 25 mAs and 120 kVp, and no tube current modulation. Fan-beam measurements for the first of the two slices over the 175 repeated scans were used for the evaluation.

Fig. 3.

(Top) Mean image of QRM torso phantom. (Lower Left) Mean image focused on the heart insert with ROIs marked by white boxes. (Lower Right) A noisy reconstruction of the heart insert. Grayscale: [−250, 500] HU.

The CT data was read with software provided by Siemens and then reconstructed using our implementation of the classical FBP algorithm for direct reconstruction from either short-scan or full-scan fan-beam data [21]. Short-scan reconstructions used data collected from 230° of the source trajectory. Images were reconstructed on a 550 × 550 grid centered on the heart insert, as shown in Fig. 3, with a pixel size of 0.2 mm × 0.2 mm.

For both short-scan and full-scan reconstructions, we considered a known-location lesion detection task in which the lesion was either absent or present at the center of a 64 × 64 region-of-interest (ROI). From each reconstructed image of the heart insert, we extracted three ROI images, labeled 1a, 1b, and 2 in Fig. 3. ROI-1a and ROI-1b were used for class-1 (lesion absent), and ROI-2 was used for class-2 (lesion-present). The lesion in ROI-2 had a diameter of 1 mm and a contrast of 210 HU with the background value of 40 HU. We assumed that the three ROIs obtained from a given CT image were statistically independent. This assumption was justified by a previous study of fan-beam FBP reconstruction from simulated CT data [21], which indicated that correlations between image pixels are negligible over the distance that separated the ROIs.

Since two class-1 ROIs and one class-2 ROI were extracted from each heart insert image, CHO performance for each reconstruction algorithm was estimated from a total of 350 class-1 and 175 class-2 ROI images. Multivariate normality of the channel outputs was checked with the Henze-Zirkler test [45]. As in Example 1, we found that the null hypothesis of multivariate normality was supported at the 10% significance level. Estimated 95% AUC confidence intervals for the short-scan and full-scan reconstructions are shown in Table III. By the Bonferroni inequality (see earlier footnote), the combined coverage probability of both intervals was at least 90%. The full-scan reconstruction was observed to be better than the short-scan reconstruction with statististical significance. This finding was consistent with the fact that the short-scan reconstruction used less data than the full-scan reconstruction.

TABLE III.

Estimated 95% AUC Confidence Intervals for the Two Reconstruction Methods in Example 2

short-scan	[0.8736	0.9267]
full-scan	[0.9282	0.9635]

VI. Comparison to Training/Testing Approaches

As mentioned in the introduction, CHO performance may also be estimated using a training/testing approach. In this approach, the CHO template is first estimated from a set of training images during the training phase. Second, during the testing phase, the estimated template is applied to a set of testing images to generate ratings, from which a performance estimate is obtained. Due to frequent use of training/testing in CHO performance evaluations, e.g., [11], [12], [14], [16]–[18], [20], [25], it is worthwhile to clarify the relationship between the approach of this paper and the training/testing paradigm.

The present work is concerned with performance estimation of a CHO that is defined by the template w = Σ⁻¹Δμ. Generally, the population quantities Δμ and Σ are unknown, and cannot be determined exactly from a finite sample of training images. Therefore, this work can be characterized in terms of training/testing terminology by saying that we aim to estimate infinitely-trained CHO performance, i.e., the performance that results from the true template. Alternatively, for a fixed number of training images, one can instead seek to estimate finitely-trained CHO performance, i.e., the performance that results from a template estimated with a finite training set. These contrasting goals are examined below.

Two strategies for training and testing are often employed in CHO evaluations. The first strategy, called the resubstitution method, uses the same images for training and testing. The second strategy, called the hold-out method, uses independent sets of images for training and testing. For the purpose of estimating the performance of an infinitely-trained CHO, it is well known from the pattern recognition literature that the resubstitution method yields point estimates with a positive bias, and that the hold-out method gives point estimates with a negative bias [46], [47].

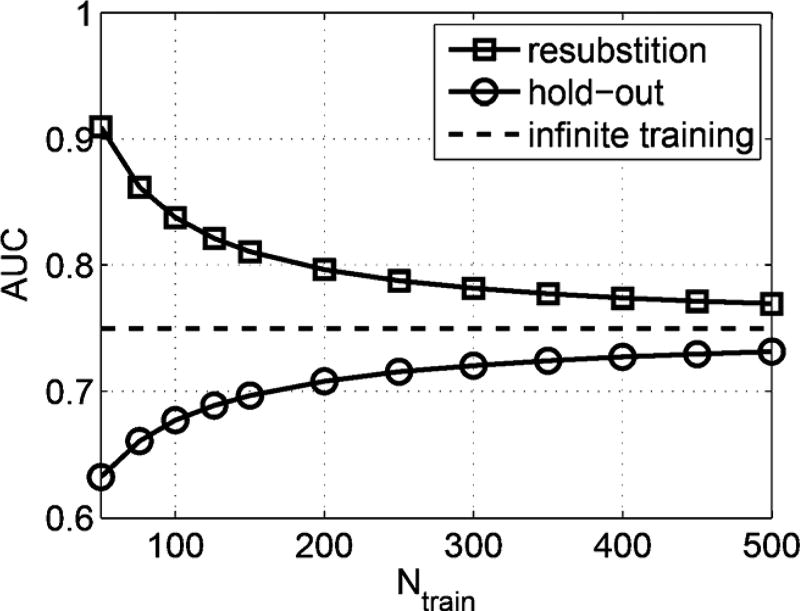
Fig. 4 illustrates these biases for a CHO with p = 18 channels when the channel output vector is multivariate normal under each class, and the class covariance matrices are equal. In this example, Σ was taken to be the identity matrix and Δμ was chosen so that AUC = 0.75. Specifically, the class means were taken to be μ₁ = 0, and μ₂ = 0.831ν, where ν was a p × 1 vector with entries increasing from 0.025 to 0.45 in increments of 0.025. For each point in Fig. 4, we generated 100 000 independent Monte Carlo trials with the number of training images equal to the number of testing images, N_train = N_test, and estimated AUC using the unbiased Mann-Whitney statistic [35]. The resulting mean AUC estimates are plotted as a function of N_train. As expected, the resubstitution and hold-out methods have positive and negative biases, respectively, which decrease with the number of training images.

Fig. 4.

Mean estimated AUC obtained from the resubstitution and hold-out methods as a function of the number of training images, for a CHO with AUC = 0.75 and p = 18 channels.

Two aspects regarding the biases described above deserve comment. First, the point estimator presented in Section III-A, like the resubstitution approach, utilizes all available images. In fact, it is straightforward to show that the resubstitution estimate of SNR² is equivalent to the plug-in estimator, θ̂_p, given in Section III-A, which as discussed earlier, has a positive bias. This observation is in agreement with the results given in Fig. 4 for the resubstitution estimator.

Second, although the hold-out method yields a negatively-biased estimate of infinitely-trained CHO performance, it gives an unbiased estimate of finitely-trained performance (if an unbiased performance estimator is used on the testing results), since the testing set is independent from the training set. This is the performance that is expected for a classifier that is applied in practice. The dependence of classifier performance on training is often depicted with a curve like the hold-out curve in Fig. 4, called a “learning curve” ([48, p. 215]). Learning curves are vital to understanding the effectiveness of training/testing approaches, as we will see next.

In addition to point estimates for CHO performance, training/testing methods can also be used to estimate confidence intervals. To illustrate the accuracy of confidence intervals obtained-with training and testing, and to compare such approaches with the Reiser intervals introduced in Section III, we carried out a Monte Carlo evaluation in which the channel output vectors were assumed to satisfy our distributional assumptions, i.e., multivariate normal under each class with equal class covariance matrices. Specifically, four types of bootstrap AUC confidence intervals were evaluated: 1) resubstitution with bootstrapping over testing cases only, 2) resubstitution with bootstrapping over both training and testing cases, 3) hold-out with bootstrapping over testing cases only, and 4) hold-out with bootstrapping over both training and testing cases. Bootstrap samples were obtained by sampling with replacement, and each confidence interval was estimated from 1000 bootstrap samples with the percentile method [49]. As above, p = 18 channels were used, Σ was taken to be the identity matrix, and Δμ was chosen so that AUC = 0.75. Coverage probabilities of confidence intervals were evaluated for N_train = 50, 100, 200, 500, and 1000 training images. The hold-out method was applied with an independent set of N_test = 200 testing images, while the resubstitution method utilized the same images for training and testing. In other words, letting N_tot denote the total number of images used, the Reiser and resubstitution methods utilized N_tot = N_train images, while the hold-out method was applied with N_tot = N_train + N_test = N_train + 200 images. Coverage probability estimates were obtained from 100 000 independent Monte Carlo trials, in which the channel output vectors were generated as random deviates from multivariate normal distributions with the previously specified parameters.

Estimated coverage probabilities of 95% AUC confidence intervals for infinitely-trained and finitely-trained CHO performance are listed in Tables IV and V, respectively. Here, the results for infinitely-trained performance assessed coverage of AUC = 0.75, whereas the results for finitely-trained performance assessed coverage of the mean AUC value obtained with the hold-out method, listed as the “target AUC” in the table, which was estimated from 100 000 Monte Carlo trials. From Table IV, we see that the Reiser intervals resulted in consistently accurate coverage for infinitely-trained performance. By contrast, the resubstitution method was not reliable, and the hold-out method was accurate only for a large number of training images. Given the learning curve in Fig. 4, this phenomenon is not surprising, since the biases of resubstitution and hold-out methods decrease with increasing numbers of training images. On the other hand, for the goal of estimating finitely-trained CHO performance, i.e., the value on the hold-out (learning) curve in Fig. 4, Table V illustrates that the hold-out method with bootstrapping over both training and testing sets gives conservative coverage, and that the hold-out method with bootstrapping over testing only is reliable for large numbers of training images. This latter result is consistent with the expectation that training variability becomes smaller as the number of training images increases. For both types of bootstrapping, the resubstitution method is seen to be unreliable, which is likely due to the positive bias of resubstitution (relative to the learning curve) as seen in Fig. 4. Last, as expected, the Reiser intervals were not as reliable for estimating finitely-trained performance, since they are not designed for this purpose.

TABLE IV.

Estimated Coverage Probabilities of 95% AUC Confidence Intervals for an Infinitely-Trained CHO With p = 18 and AUC = 0.75

Ntrain	target AUC	Reiser	resubstitution test bootstrap	resubstitution train/test bootstrap	hold-out test bootstrap	hold-out train/test bootstrap
50	0.75	0.951	0.153	0	0.213	0.124
100	0.75	0.951	0.453	0.007	0.510	0.419
200	0.75	0.951	0.683	0.172	0.781	0.725
500	0.75	0.950	0.842	0.560	0.921	0.912
1000	0.75	0.949	0.897	0.754	0.942	0.950

TABLE V.

Estimated Coverage Probabilities of 95% AUC Confidence Intervals for Mean Performance of a Finitely-Trained CHO With p = 18

Nrain	target AUC	Reiser	resubstitution test bootstrap	resubstitution train/test bootstrap	hold-out test bootstrap	hold-out train/test bootstrap
50	0.632	0.873	0.004	0	0.827	0.981
100	0.677	0.816	0.056	0	0.890	0.969
200	0.708	0.821	0.236	0.006	0.927	0.967
500	0.732	0.875	0.567	0.229	0.943	0.969
1000	0.741	0.908	0.748	0.518	0.946	0.966

In summary, the Reiser intervals were found to be well-suited for estimating infinitely-trained performance for all sample sizes. By contrast, the hold-out method, which uses independent training and testing sets, was observed to be best-suited for estimating finitely-trained performance, although it was also effective for estimation of infinitely-trained performance when the size of the training set was large. Lastly, the resubstitution method was not generally reliable for either purpose, although its accuracy improved as the number of training images increased.

It should be emphasized that the results presented above are for a limited number of examples, and that the channel output vector was taken to be multivariate normal under each class with equal class covariance matrices. A more thorough comparison of the Reiser intervals with methods based on training and testing is beyond the scope of the present work.

VII. DISCUSSION AND CONCLUSION

A widely-used approach for the characterization of medical image quality involves estimating the performance of a CHO applied to a known-location discrimination task. For the problem of estimating confidence intervals for CHO performance measures, we have shown that a method proposed by Reiser [26] can be used to obtain confidence intervals for SNR and AUC. In addition, we rigorously proved that these intervals are well-defined and exactly achieve the desired coverage probability, as long as SNR > 0, which is a new result not given in [26]. The coverage probability of the Reiser confidence intervals was verified with Monte Carlo simulation, and was found to be more robust than that for conventional Wald-style intervals based on a normality assumption. Application of the Reiser confidence intervals was demonstrated with two examples comparing reconstruction algorithms for fan-beam CT. Last, the relationship between the Reiser intervals and training/testing approaches was discussed and illustrated with examples based on Monte Carlo simulation.

To our knowledge, the Reiser intervals investigated here are presently the only known exact confidence intervals for CHO performance when both Σ and Δμ are unknown. As clarified in Section VI, these intervals are designed for estimation of infinitely-trained CHO performance, which is typically the goal of image quality studies aimed at imaging system optimization. On the other hand, if the goal is to estimate finitely-trained CHO performance, then approaches based on training and testing with independent data sets are preferable.

Our theoretical results assume that the channel output vector for a given class follows a multivariate normal distribution with equal covariance matrices for each class. As discussed in the introduction, these assumptions are often well-justified for image discrimination tasks involving a small lesion at a known location with either a flat or normally-distributed, variable background. Indeed, these assumptions are typically well-justified for tomographic imaging applications. To be sure of the applicability of the Reiser intervals in practice, it is generally desirable to check the aforementioned distributional assumptions; recall from the image quality evaluation examples in Section V, that multivariate normality was checked using the Henze-Zirkler normality test. We did not investigate robustness of the Reiser intervals to violations of the distributional assumptions. However, since the Reiser intervals are based on the two-sample Hotelling T² test statistic, which is invariant under nonsingular affine transformations of the channel output vector, it can be conjectured that the Reiser intervals possess robustness properties similar to those of the T² test [4]. Further research into this issue, both on theoretical grounds and with Monte Carlo studies, is a topic of high interest for future work.

It is useful to note that although our presentation concentrated on exact confidence intervals for SNR and AUC, exact confidence intervals can also be obtained for other figures of merit. In particular, because our distributional assumptions imply that the ROC curve is parameterized by only SNR, it follows that TPF at fixed FPF and partial AUC (pAUC) are strictly increasing functions of SNR. Consequently, Lemma 3 implies that exact confidence intervals for these figures of merit can be obtained through suitable transformations of an exact SNR interval; see [30], [34] for further details. Moreover, it turns out that the union of exact 1 − α TPF intervals over all FPF values is an exact, simultaneous 1 − α confidence band for the entire ROC curve in this setting [30].

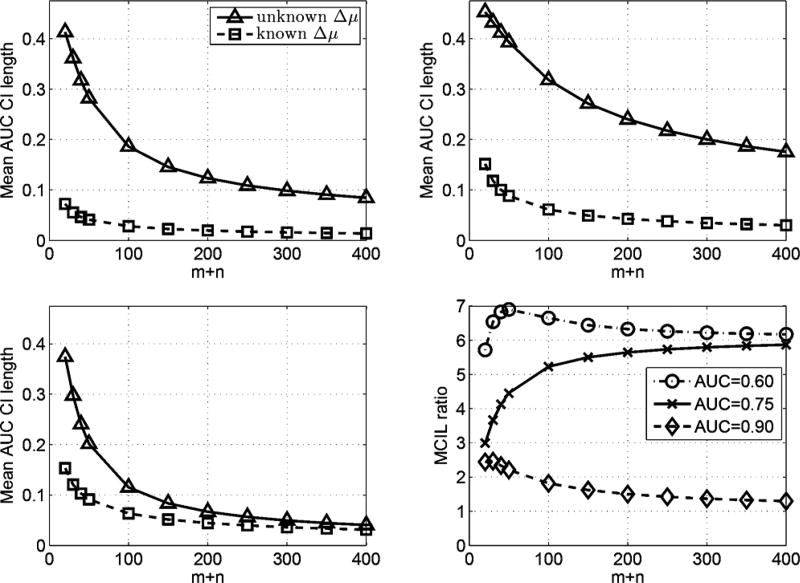
As one might intuitively expect, smaller confidence intervals can be obtained when prior knowledge is available. For example, in a recent paper [34], we have introduced exact intervals for situations when Δμ is known. To illustrate the advantage offered by prior knowledge of Δμ, Fig. 5 contains plots of mean confidence interval length (MCIL) for exact 95% AUC confidence intervals versus sample size. These plots compare the MCIL for the unknown-Δμ Reiser confidence intervals presented here to the known-Δμ confidence intervals given in [34]. Each point on these curves was calculated through a numerical integration as described in [34]. Note that in both cases, for given values of m, n, and p, the underlying statistical distributions depend only on AUC, and that the plots are valid for any choices of Δμ and Σ that yield the stated AUC value. From the plots in Fig. 5, it is evident that a large decrease in confidence interval length can be gained when Δμ is known, and that this decrease is larger as the nominal AUC value becomes smaller.

Fig. 5.

Mean confidence interval length (MCIL) for exact 95% AUC confidence intervals plotted versus sample size in the cases of unknown and known difference of class means, Δμ, for a CHO with p = 5 channels and m = n. Top Left: AUC = 0.6, Top Right: AUC = 0.75, Bottom Left: AUC = 0.9, Bottom Right: Ratio of MCIL for unknown Δμ to MCIL for known Δμ plotted versus sample size for AUC = 0.6, 0.75, and 0.9.

MATLAB software implementing the confidence interval estimators described in this work and in previous related publications [30], [32], [34] is publicly available at http://code.google.com/p/iqmodelo/.

Appendix

We prove Theorem 2 with the aid of three lemmas.

Lemma 1

The cdf of the noncentral F-distribution is a strictly-decreasing, continuous function of the noncentrality parameter.

Proof

Let $X~F_{{\nu }_1,{\nu }_2}^{\prime }(\delta )$. By the definition of the non-central-F distribution, X = U/V, where $U~{\chi }_{{\nu }_1}^{\prime 2}(\delta )$ and $V~{\chi }_{{\nu }_2}^2$ are independent random variables, i.e., U is a noncentral χ² random variable with ν₁ degrees of freedom and noncentrality parameter δ, and V is a central χ² random variable with ν₂ degrees of freedom. Denote the pdf's for U and V as f_U(u; ν₁, δ) and f_V(υ; ν₂), respectively, and denote the cdf of U as F_U(u; ν₁, δ). Since X = U/V, the cdf for X is F_X(x; ν₁, ν₂, δ) = P(X ≤ x) = P(U ≤ xV), and hence

$$F_X(x;{\nu }_1,{\nu }_2,\delta )={\int }_0^{\infty }{f}_V(\upsilon ;{\nu }_2)d\upsilon {\int }_0^{x\upsilon }{f}_U(u;{\nu }_1,\delta )\mathit{\text{du}}={\int }_0^{\infty }{F}_U(x\upsilon ;{\nu }_1,\delta )f_V(\upsilon ;{\nu }_2)d\upsilon .$$

Since F_U is differentiable with respect to δ [36, p. 442], we can differentiate under the integral sign to obtain

$$\frac{\partial F_X}{\partial \delta }={\int }_0^{\infty }\frac{\partial F_U}{\partial \delta }(x\upsilon ;{\nu }_1,\delta )f_V(\upsilon ;{\nu }_2)d\upsilon .$$ (9)

From (29.33e) in [36, p. 443], for any and u, ν₁ and δ, ∂F_U(u; ν₁, δ)/∂δ < 0. Combining this fact with (9), we see that ∂F_X(x; ν₁, ν₂, δ)/∂δ < 0.

Lemma 2

Let α₁, α₂ ∈ (0, 1) be fixed numbers such that α₁ + α₂ = α for some α ∈ (0, 1) and let $X~F_{{\nu }_1,{\nu }_2}^{\prime }(\delta )$, where ν₁, ν₂, and δ are fixed. Further, for each observation x of X, define the functions δ_L(x) and δ_U(x) as in Section III-B. If δ > 0, then the random interval [δ_L(X), δ_U(X)] is an exact 1 − α confidence interval for δ.

Proof

Denote the cdf of X by F_X(x; ν₁, ν₂, δ). We partition the sample space with the following three disjoint events:

$$A=\{X:F_X(X;{\nu }_1,{\nu }_2,\delta )>1-{\alpha }_1\}$$

$$B=\{X:{\alpha }_2\le F_X(X;{\nu }_1,{\nu }_2,\delta )\le 1-{\alpha }_1\}$$

$$C=\{X:F_X(X;{\nu }_1,{\nu }_2,\delta )<{\alpha }_2\}$$

By a standard theorem [27, Th. 2.1.10, p. 54], F_X(X; ν₁, ν₂, δ) is uniformly distributed. It then follows that P(A) = α₁, P(B) = 1 − α and P(C) = α₂. We will consider each of these events separately to determine their contribution to the overall coverage probability. Below, we repeatedly utilize the fact that F_X(x; ν₁, ν₂, δ) is a strictly decreasing function of δ, as stated by Lemma 1.

For X ∈ A, the definition of δ_L(X) and Lemma 1 imply that δ_L(X) > δ. Hence, P(δ ∈ [δ_L(X), δ_U(X)]|A) = 0. Now, consider X ∈ B. The definition of δ_U(X) and Lemma 1 imply that δ ≤ δ_U(X). For δ_L(X), there are two cases: either (a) F_X(X; ν₁, ν₂, 0) ≥ 1 − α₁ or (b) F_X(X; ν₁, ν₂, 0) < 1 − α₁. In case (a), the definition of δ_L(X) and Lemma 1 imply that 0 < δ_L(X) ≤ δ. In case (b), the definition of δ_L(X) and Lemma 1 imply that δ_L(X) = 0 < δ. Either way, we have δ_L(X) ≤ δ, and thus, P(δ ∈ [δ_L(X), δ_U(X)]|B) = 1. Finally, consider X ∈ C. If F_X(X; ν₁, ν₂, 0) ≥ α₂ then the definition of δ_U(X) and Lemma 1 imply that δ_U(X) < δ. Otherwise, if F_X(X; ν₁, ν₂, 0) < α₂, then the definition of δ_U(X) and Lemma 1 imply that δ_U(X) = 0 < δ. Thus, P(δ ∈ [δ_L(X), δ_U(X)]|C) = 0.

Therefore, the coverage probability is

$$P(\delta \in [{\delta }_L(X),{\delta }_U(X)])=P(\delta \in [{\delta }_L(X),{\delta }_U(X)]|A)P(A)+P(\delta \in [{\delta }_L(X),{\delta }_U(X)]|B)P(B)+P(\delta \in [{\delta }_L(X),{\delta }_U(X)]|C)P(C)=(0)({\alpha }_1)+(1)(1-\alpha )+(0)({\alpha }_2)=1-\alpha .$$

Lemma 3

Let g(δ) be a continuous, strictly increasing function of δ. If [δ_L, δ_U] is a 1 − α confidence interval for δ, then [g(δ_L), g(δ_U)] is a 1 − α confidence interval for g(θ).

Proof

See Lemma 3 in [30].

Theorem 1 and Lemma 2 imply that [δ_L(X), δ_U(X)] is an 1 − α exact confidence interval for δ. Finally, since SNR and AUC are strictly increasing functions of δ, Lemma 3 yields the stated result for Theorem 2.