Evaluation of methodology for the analysis of “time-to-event” data in pharmacogenomic genome-wide association studies

Abstract

Aim

To evaluate the power to detect associations between single nucleotide polymorphisms (SNPs) and time-to-event outcomes across a range of pharmacogenomic study designs whilst comparing alternative regression approaches.

Materials and methods

Simulations were conducted to compare Cox proportional hazards modelling accounting for censoring and logistic regression modelling of a dichotomised outcome at the end of the study.

Results

The Cox proportional hazards model was demonstrated to be more powerful than the logistic regression analysis. The difference in power between the approaches was highly dependent on the rate of censoring.

Conclusion

Initial evaluation of SNP association signals using computationally efficient software with dichotomised outcomes provide an effective screening tool for some design scenarios, and thus has important implications for the development of analytical protocols in pharmacogenomic studies.

Background

Methodology for the analysis of genome-wide association studies (GWAS) has focused primarily on binary (case-control) phenotypes and quantitative traits [1]. Software implementing these methods, such as PLINK [2] and SNPTEST [3], can efficiently handle the scale and complexity of genetic data from GWAS, allowing for imputed genotypes at millions of single nucleotide polymorphisms (SNPs). However, in pharmacogenomic studies, the outcome of interest is often “time to event” after treatment intervention, where the event could be death, disease remission, or the occurrence of an adverse drug reaction. The traditional approach to the analysis of time to event data is through survival modelling, which can allow for censoring due to patient drop-out before the end of the study, or because the event has not occurred before the end of the trial. However, such outcomes cannot be directly accommodated in widely-used GWAS software such as PLINK and SNPTEST. One approach to circumvent this problem is to consider the occurrence of the event as a dichotomous outcome at some fixed time point, such as the end of the study; patients in which the event has occurred are considered as “cases”, whilst those in which the event has not occurred are considered as “controls” [4]. Nevertheless, this approach would be expected to result in a loss of power to detect association with SNPs because: (i) the event times are not directly considered, thereby losing information; and (ii) the binary outcome cannot allow for censoring before the end of the study, in which case patients will be treated as “missing” observations.

The Cox proportional hazards model is the basis of the most commonly applied framework for the analysis of time to event outcomes. It is a semi-parametric model where the hazard ratio takes a parametric form in terms of the regression coefficients, but the baseline hazard is unspecified. The aim of this paper is to evaluate the power to detect association between SNPs and time to event outcomes under different pharmacogenomic study designs, including censoring before the end of the study, treatment effects, SNP-treatment interactions, and a variable recruitment period. We will compare the power for the analysis of event times: (i) under a Cox proportional hazards model; and (ii) within a logistic regression framework with a dichotomised outcome at the end of the study. Our investigation incorporates detailed simulations and empirical evaluation in a candidate gene study of anti-epileptic drug response with SNPs mapping to/near ABCB1 [5]. Although we expect that Cox proportional hazards modelling will be uniformly most powerful, our aim is to identify scenarios for which the difference in power is minimised. In these scenarios, existing GWAS analysis software for binary phenotypes could be applied to dichotomised time to event outcomes in an initial screen to identify SNPs for further evaluation with more rigorous, and computationally demanding, survival modelling, thereby providing insight into study design and appropriate analytical protocols.

Materials & Methods

Consider a sample of unrelated patients in a pharmacogenomic study investigating the association of a time to event outcome with SNPs after treatment intervention. We denote the time to event for the ith patient by t_i, and their treatment by a vector of covariates x_i. We also denote their genotype at a SNP of interest by S_i, coded under an additive dosage model (directly typed or imputed) for the minor allele. Under the assumption of proportional hazards, we can express the hazard of the event occurring at some time t in the ith individual by:

$$h_i(t)=h_0(t)e^{{\beta }_s{S}_i+{\mathbf{\beta }}_{\mathbf{\text{x}}}{\mathbf{\text{x}}}_{\mathbf{\text{i}}}}.$$ (1)

In this model, h₀(t) is the baseline hazard at time t, and the parameters β_s and β_x correspond to the effect on hazard of the minor allele at the SNP, and a vector of treatment effect(s), respectively.

Alternatively, we can dichotomise the time to event outcome of patients at the end of the study. Let y_i denote the dichotomised outcome of the ith patient, given by y_i = 1 if the event has occurred, and by y_i = 0 if not. Note that patients who are censored before the end of the study are excluded from this analysis since we do not know whether the event has occurred or not and thus are treated as missing. Within a logistic regression framework, we can model the log-odds of the occurrence of the event by:

$$\text{logit}(y_i)={\omega }_0+{\omega }_s{S}_i+{\mathbf{\omega }}_{\mathbf{\text{x}}}{\mathbf{\text{x}}}_{\mathbf{\text{i}}}$$ (2)

In this expression, ω_s corresponds to the log-odds of the minor allele at the SNP, and ω_x represents a vector of treatment effect(s).

For both models, we can form a likelihood ratio test of association of the SNP with outcome by maximising the unrestricted models (1) and (2) and comparing with that under the null hypothesis, for which the allelic effects, β_s and ω_s, are zero. Both models can also be generalised to incorporate additional covariates or a SNP-treatment interaction effect.

Simulation study

We considered four pharmacogenomic GWAS designs to evaluate SNP association with time to event outcomes, selected after examination of published studies in the literature, including Clarke et al. [6] and Han et al. [7]. The scenarios considered, described in detail below, allowed for variable end of study time and recruitment period, censoring before the end of the study, multiple treatment effects, and SNP-treatment interaction. In all scenarios, we considered a study undertaken for a maximum of 60 days. However, we consider the impact on the analysis of fixing the end of the study, Z, at 20, 30, 40, 50 or 60 days. We assumed that patients who do not experience the event before the end of the study to be censored at that point. However, in some scenarios, we also allowed for the possibility of censoring before the end of the study due to the occurrence of an adverse treatment reaction or other reasons for drop-out. In these scenarios, patients who are censored before the end of the study are excluded from the logistic regression analysis at the end of the study because we cannot determine whether the event has occurred or not.

For each scenario, we considered SNP effects, β_s, on the hazard of the occurrence of the event in the range of 0 (null model to evaluate false positive error rates) to 0.4. For each simulation, we generated 1,000 replicates of data for a sample of 1,000 patients. For each replicate, we simulated genotype data for the ith patient, S_i, from a multinomial distribution with minor allele frequency of 0.4, under the assumption of Hardy-Weinberg equilibrium. The time to the occurrence of the event, t_i, was simulated from an exponential distribution with scale parameter dependent on the genotype S_i, SNP effect β_s, and other scenario-specific factors outlined below.

Scenario 1. No treatment effect and censoring occurs only at the end of the study. The hazard of the event at time t was given by h_i(t) = h₀(t)e^β_sS_i, where we considered two baseline hazards: h₀(t) = 15 and h₀(t) = 50. A larger value for the baseline hazard means a patient’s survival time is longer. Since there was no censoring before the end of the study, the observed event time for the ith patient was τ_i = t_i if the event occurred before the end of the study; otherwise τ_i = Z (i.e. was replaced by the end of study time).

Scenario 2. Random censoring due to drop-out before the end of the study. The hazard of the event at time t is given by h_i(t) = h₀(t)e^β_sS_i, where we considered a baseline hazard of h₀(t) = 15. The censoring time of the ith individual, c_i, was simulated from a Weibull distribution with scale parameter 20, 40 or 60. The end of study time is fixed at 40 days, therefore a Weibull scale parameter of 20 for censoring times corresponds to approximately 50% censored observations during the study, a scale of 40 corresponds to approximately 30% censored observations, and a scale of 60 corresponds to approximately 20% censored observations. If censoring occurred before the end of the study for the ith patient, they were assumed to have dropped out at that time, and their observed time τ_i = c_i. If the simulated censoring occurred after the end of the study for the ith patient, their observed event time was τ_i = t_i if the event occurred before the end of the study; otherwise τ_i = Z (i.e. was replaced by the end of study time).

Scenario 3. Recruitment period during first ten days of the study and censoring occurs only at the end of the study. The hazard of the event is given by h_i(t) = h₀(t)e^β_sS_i, where we considered a baseline hazard of h₀(t) = 15. The recruitment time, r_i, was simulated from a Uniform distribution over the first ten days of the study. Since there was no censoring before the end of the study, the observed event time for the ith patient was τ_i = t_i – r_i, if the event occurred before the end of the study; otherwise τ_i = Z - r_i.

Scenario 4. Multiple treatments with variable effects on outcome and censoring. Patients were randomly assigned to one of four treatments (A, B, C or D). Treatment A increased the hazard of the event at any given time, whilst treatment C resulted in increased random censoring due to adverse drug reaction before the end of the study. The hazard of the event is given by $h_i(t)=h_0(t)e^{{\beta }_s{S}_i+{\mathbf{\beta }}_{\mathbf{\text{x}}}{\mathbf{\text{x}}}_{\mathbf{\text{i}}}}$, where we considered a baseline hazard of h₀(t) = 15, β_x = 0.2 is the effect of treatment A, and x_i is an indicator variable taking the value 1 if the ith patient is assigned to treatment A, and 0 otherwise. If the patient is assigned to treatment C, censoring occurs more frequently before the end of the study, with time, c_i, simulated from a Weibull distribution with a scale parameter of 10. All other treatments have a scale parameter of 30. As for Scenario 2, If censoring occurred before the end of the study, the patient was assumed to have dropped out at that time, so that τ_i = c_i. If censoring occurred after the end of the study, the observed event time for the ith patient was τ_i = t_i if the event occurred before the end of the study; otherwise τ_i = Z (i.e. was replaced by the end of study time). Under this same design we also simulate survival times with a significant SNP-treatment interaction effect. The hazard now becomes h_i(t) = h₀(t)e^{β_sS_i+β_xx_i+β_intS_ix_i} with β_int = 0.2, and x_i defined as above.

For each scenario, the event time was dichotomised at the end of the study, Z, such that the binary outcome for the ith patient, y_i = 1 if t_i < Z, and 0 otherwise. For scenarios 2 and 4, patients censored before the end of the study were treated as missing for the binary outcome. For each scenario, we tested for association of the SNP with the time to event under a Cox proportional hazards model and with the binary outcome in a logistic regression framework. For scenarios 1, 2 and 3, the linear component of the regression model included an effect of the SNP only. However, in scenario 4, the linear predictor was extended to include an indicator variable to account for treatment (but not an interaction effect). We evaluated the power and type I error rate of each test to detect association of the SNP with outcome at a 5% significance threshold, approximated by the proportion of replicates for which p < 0.05 for the SNP effect. All simulation scripts and analyses were performed in R 3.2.0.

Application to the SANAD Study

The Standard And New Anti-epileptic Drugs (SANAD) Study was initiated to investigate the impact of genetic variation on response to anti-epileptic drugs. Leschziner et al. [5] considered 503 patients receiving one of six anti-epileptic drugs over a follow-up period of between 84 and 2296 days. They evaluated the evidence of association of 501 SNPs mapping to/near the ABCB1 gene with time to 12-month remission, time to first seizure, and time to drug withdrawal due to inadequate seizure control or adverse reactions. Here, the original dataset was manipulated to illustrate similar designs to that of the simulation study. Specifically, we tested for association of SNPs with time to first seizure within the first 12, 24, or 36 months of follow-up using a Cox proportional hazards model. We also tested for association with a dichotomised outcome, at the same follow-up time points, in a logistic regression model. As these end of study follow up times were implemented a censoring outcome and binary outcome were created influenced by the time to seizure and time to withdrawal outcomes. The number of missing observations due to censoring before the end of the study, for the logistic regression model at 12, 24 and 36 months, were 56, 69 and 95, of the 503 patients, respectively. Before analysis, we eliminated SNPs with MAF less than 1% and missing genotype rate greater than 5%.

Results

Simulation study

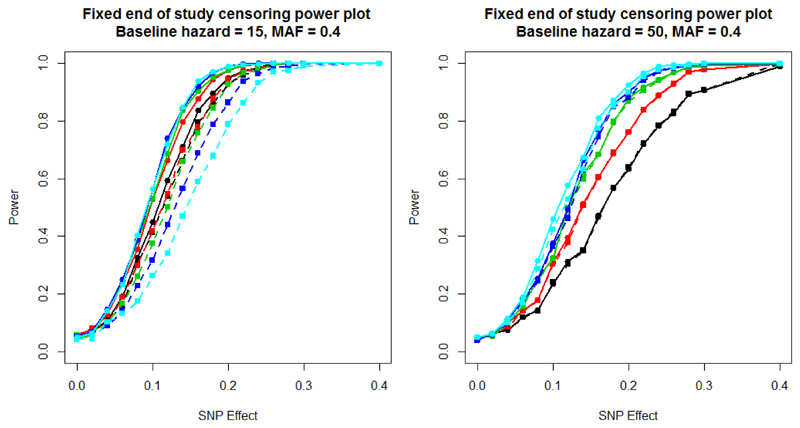
Figure 1 presents the power to detect association of the SNP, under scenario 1, with time to event using a Cox proportional hazards model and with the dichotomised outcome at the end of the study in a logistic regression framework. The two plots present power, for different end of study times, for a baseline hazard of 15 (left) and 50 (right). For a baseline hazard of 15, the majority of patients will have experienced an event by day 20, and almost all will have experienced the event by day 60. In this setting, the number of censored observations at the end of the study is low, and the Cox proportional hazards model can directly account for the times at which the events occurred. On the other hand, the logistic regression model loses power as the end of study time increases, because the number of cases and controls becomes more imbalanced. As a result, the difference in power between the two models increases with the end of study time. On the other hand, for a baseline hazard of 50, far fewer events occur during the study period. As a consequence, there is less to be gained through direct modelling of event times, and the logistic regression analysis has almost identical power to the Cox proportional hazards model. An end of study of 60 is the most favourable cut-off point for the logistic regression model as it has the greatest balance of events and non-events occurring during the trial. Supplementary Figure 1 presents a comparison of - log₁₀ p-value and estimated effect sizes from scenario 1 for a baseline hazard of 15, MAF of 0.4, SNP effect of 0.1 and an end of study time of 40. These parameter settings achieve a power of 50% to detect associations using the Cox proportional hazards model. These results highlight that effect sizes from the two approaches are highly correlated, but the signal of association is more often stronger under the Cox proportional hazards model than logistic regression model.

Figure 1.

Scenario 1 power plots, where the end of study time varied, and with fixed end of study time censoring. Power is estimated at a 5% significance threshold. Lines with circular points characterise the Cox proportional hazards model and lines with square points the logistic regression model. The colour of the line represents the end of study time: 20 days (black); 30 days (red); 40 days (green); 50 days (blue); and 60 days (cyan).

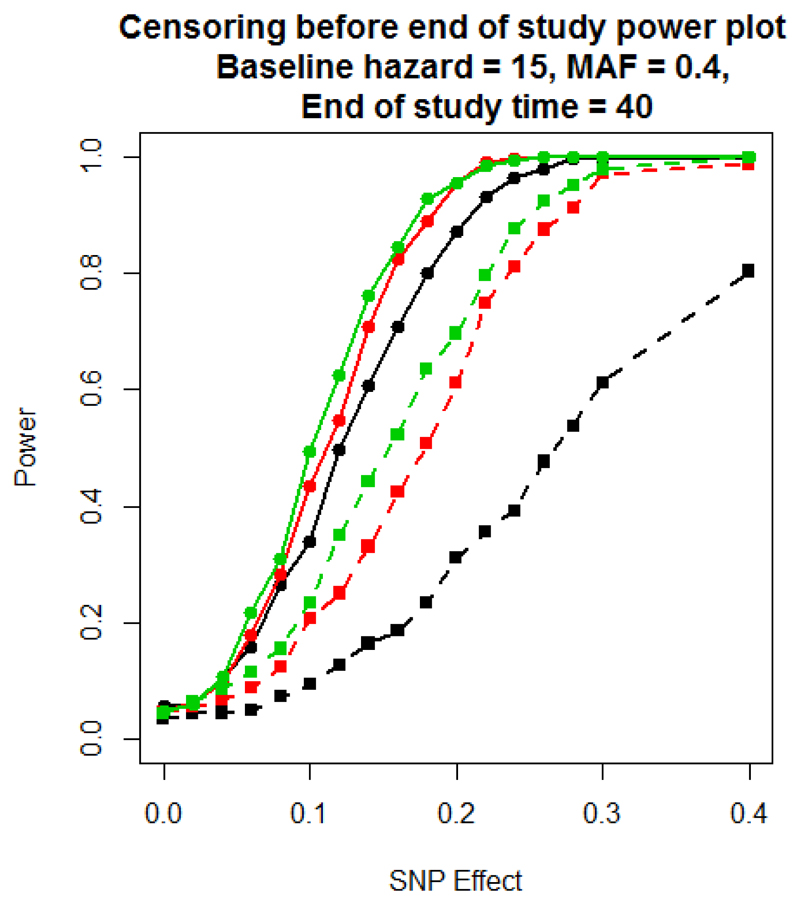
Figure 2 presents the power to detect association of the SNP, under scenario 2, where censoring can occur before the end of the study. As censoring increases, the power of both models decreases. However, the reduction is more dramatic for the logistic regression modelling of dichotomised outcomes because the number of patients contributing to this analysis decreases, with a consequent reduction in power. Supplementary Figure 2 presents a comparison of - log₁₀ p-value and estimated effect sizes from scenario 2 for a baseline hazard of 15, MAF of 0.4, SNP effect of 0.1, a weibull censoring scale parameter of 60 and an end of study time of 40. These parameter settings achieve a power of 50% to detect associations using the Cox proportional hazards model. These results highlight that effect sizes from the two approaches are again highly correlated, and the signal of association is typically weaker under logistic regression modelling of the dichotomised outcome than the Cox proportional hazards model.

Figure 2.

Scenario 2 power plot, where the end of study time is fixed at 40 days, but with random censoring during the study period. Power is estimated at a 5% significance threshold. Lines with circular points characterise the Cox proportional hazards model and lines with square points the logistic regression model. The colour of the line corresponds to the rate of censoring defined by the scale parameter of the Weibull distribution: scale 20 (black); scale 40 (red); scale 60 (green).

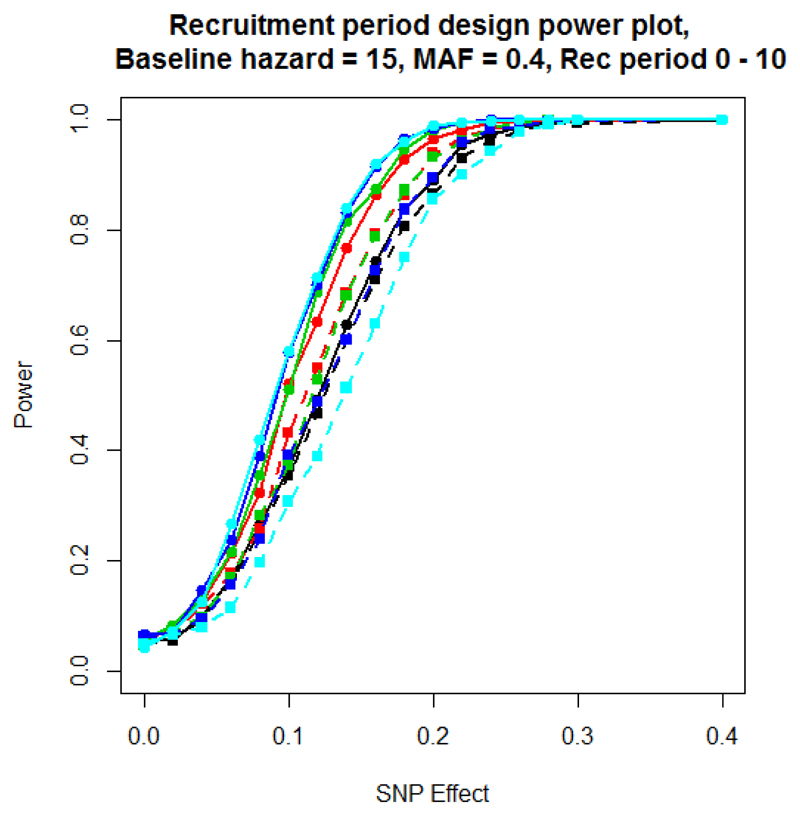
Figure 3 presents the power to detect association of the SNP, under scenario 3, which incorporates a variable recruitment period for patients at the start of the study. The results are similar to those observed for scenario 1 with a baseline hazard of 15. Like scenario 1, the difference in power between the two modelling approaches depends on the proportion of patients in which the event has occurred, and is maximised for an end of study time of 60 days because most patients will have experienced the event by this time, even with a variable recruitment period. An end of study of 20 days shows the smallest difference in power between the models because very few events occur with the majority of patients surviving to the end of the study. Supplementary Figure 3 presents a comparison of - log₁₀ p-value and estimated effect sizes from scenario 3 for a baseline hazard of 15, MAF of 0.4, SNP effect of 0.1 and an end of study time of 40. These parameter settings achieve a power of 50% to detect associations using the Cox proportional hazards model. As with previous scenarios, the effect size estimates obtained from the two models are highly correlated, but signals of association are generally stronger under the Cox proportional hazards model than the logistic regression model.

Figure 3.

Scenario 3 power plot, with variable recruitment period, but with fixed end of study time censoring. Power is estimated at a 5% significance threshold. The recruitment period is between 0 and 10 days. Lines with circular points characterise the Cox proportional hazards model and lines with square points the logistic regression model. The colour of the line represents the end of study time: 20 days (black); 30 days (red); 40 days (green); 50 days (blue); and 60 days (cyan).

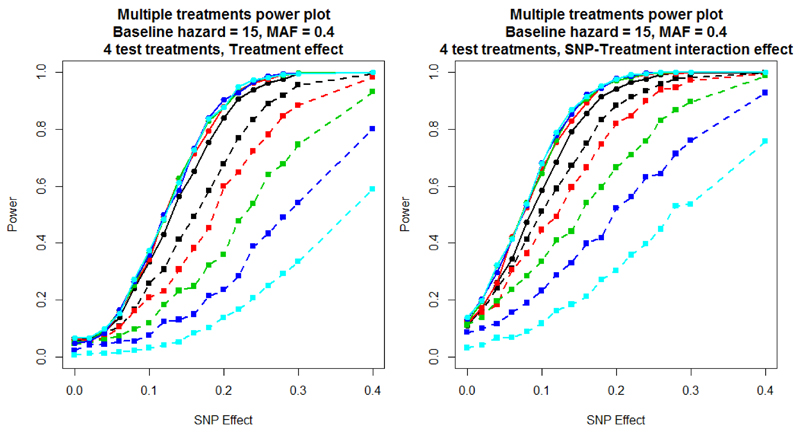
Figure 4 presents the power of the two modelling approaches for scenario 4, where time to event is dependent on treatment. The first plot (left) includes a treatment effect of 0.2 on survival times with both analysis models adjusting for the treatment covariate. The second plot (right) includes both a treatment effect of 0.2 and a SNP-treatment interaction of 0.2, but incorporates only the treatment covariate in the analysis models (because an interaction effect is not typically assumed, a priori). It is clear from both plots that as the end of study time increases, which results in more censoring during the study period, the power of the logistic regression model is substantially reduced. Introducing a SNP-treatment interaction increases power for both analytical approaches because the marginal effect of the SNP is increased, even if the interaction effect itself is not taken account of in the analysis model. Supplementary Figure 4 presents a comparison of - log₁₀ p-value and estimated effect sizes from scenario 4 for a baseline hazard of 15, MAF of 0.4, SNP effect of 0.1, treatment effect of 0.2, interaction effect of 0.2 and an end of study time of 40. These parameter settings achieve a power of 50% to detect associations using the Cox proportional hazards model. These results highlight that the effect sizes from the two approaches are correlated, but the signal of association is more often stronger under the Cox proportional hazards model with very few replicates with more significant associations found towards the logistic regression model.

Figure 4.

Scenario 4 power plots, where the end of study time varied, and there was random censoring during the study period. Power is estimated at a 5% significance threshold. Lines with circular points characterise the Cox proportional hazards model and lines with square points the logistic regression model. The colour of the line represents the end of study time: 20 days (black); 30 days (red); 40 days (green); 50 days (blue); and 60 days (cyan).

For all parameter settings, the Cox proportional hazards analysis of time to event was always at least as powerful as the logistic regression model, as expected. Across scenarios, the greatest difference in power occurred when the end of study time was extended because the number of individuals experiencing the event was maximised, and there was more information in the event times themselves. Whilst the power of the Cox proportional hazards model stays relatively constant, that of the logistic regression approach gets substantially weaker because of the increased imbalance in the number of cases and controls.

Application to the SANAD Study

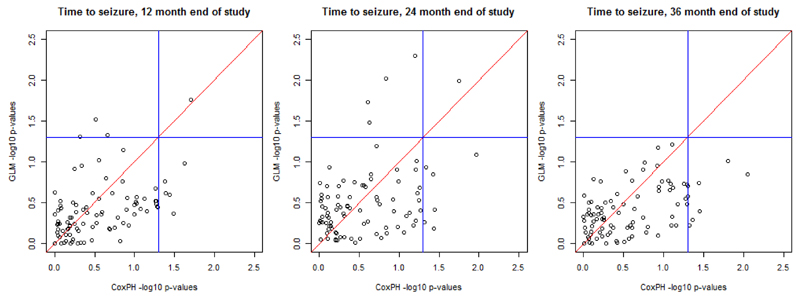
Figure 5 depicts the - log₁₀ p-value for association of SNPs with time to event outcomes from the SANAD study. Each point corresponds to a SNP, with the p-value for the SNP effect from the Cox proportional hazards model on the x-axis and the p-value for the SNP effect from the logistic regression model on the y-axis. The two blue lines indicate a nominal 5% significance threshold for association. The top left quadrant indicates significant SNPs found only by the logistic regression model, the bottom right quadrant shows significant SNPs found only by the Cox proportional hazards model, and the top right quadrant indicates significant SNPs found by both models. The key observation from this analysis is that, as the study period increases, the number of associated SNPs found by the logistic regression model is reduced. This result supports the findings of the simulation study because, as the end of study time increases, there are more censored events within the sample. For the outcomes of times to seizure at 12 and 24, months there is little difference between significant SNPs found by the logistic regression or Cox proportional hazards models. However, for an end of study time of 36 months, the logistic regression model fails to detect any associations.

Figure 5.

- log₁₀ p-value plots for the outcomes time to seizure at 12 months, time to seizure at 24 months and time to seizure 36 months. Blue lines represent 0.05 significance levels.

Discussion

As expected, the Cox proportional hazards model was demonstrated to be uniformly more powerful than the logistic regression analysis of dichotomised outcomes across simulation scenarios and generated stronger signals of association in the SANAD study. However, the difference in power between methods was highly dependent on the rate of censoring and number of events occurring within the study period. If few events occur and the majority of subjects survive until the end of study then there is little to be gained by modelling time to event outcomes. However, the power of the logistic regression model is significantly affected by the two types of censoring: (i) at the end of study because the event has yet to occur; and (ii) during the study period because of the occurrence of an adverse event or drop-out. If there is a lot of censoring during the study, these observations are treated as missing in the logistic regression model, and therefore result in a lack of power to detect associations between SNPs and outcome. The rate of censoring at the end of the study (i.e. the number of events that have occurred) will impact the ratio of cases to controls in the dichotomised outcome. For a given sample size, imbalanced studies will have less power than those for which the number of cases and controls is equal.

There are other survival models available for the analysis of time to event data such as Weibull regression. Parametric models, such as this, are beneficial as they assume the statistical distribution of the data and have completely specified hazard and survivor functions. We might expect the power of these approaches to be greater than the Cox proportional hazards model when the assumption of proportional hazards is not appropriate. However, we expect the scenarios in which the logistic regression model of dichotomised outcomes provides equivalent power to the survival modelling of time to event outcomes to hold under these alternative approaches.

The results of our study have important implications for the development of analytical protocols in the analysis of time to event data in pharmacogenomic studies. We have highlighted scenarios for which the difference in power between the two analysis models is minimised. In these scenarios, existing GWAS analysis software could be applied to dichotomised time to event outcomes in an initial screen to identify SNPs for further evaluation with more rigorous, and computationally demanding, survival modelling. Our study also highlights the need for flexible software for the analysis of time to event data that can efficiently handle the scale and complexity of genetic data throughout the genome.

Executive summary.

Background

• Methodology for genome-wide pharmacogenomic studies with time to event outcomes is not well developed.

Materials & Methods

• We evaluate the power to detect associations between SNPs and time to event outcomes comparing two regression modelling approaches.

• A wide range of trial designs for pharmacogenomic studies with time to event outcomes are covered.

Results

• As expected, the Cox proportional hazards model is more powerful at detecting associations between SNPs and time to event outcomes over logistic regression analysis of dichotomised outcomes at the end of the study.

• Rate of censoring and number of events occurring during the study is correlated to the performance of methods.

Conclusions

• Results highlight the need for software to enable the efficient analysis of GWAS of time to event outcomes with a range of survival models.

• Pharmacogenomic data has more complexities that need to be accounted for by the analysis, so extensions to existing methods are needed.