Abstract
It is difficult for learning models to achieve high classification performances with imbalanced data sets, because with imbalanced data sets, when one of the classes is much larger than the others, most machine learning and data mining classifiers are overly influenced by the larger classes and ignore the smaller ones. As a result, the classification algorithms often have poor learning performances due to slow convergence in the smaller classes. To balance such data sets, this paper presents a strategy that involves reducing the sizes of the majority data and generating synthetic samples for the minority data. In the reducing operation, we use the box-and-whisker plot approach to exclude outliers and the Mega-Trend-Diffusion method to find representative data from the majority data. To generate the synthetic samples, we propose a counterintuitive hypothesis to find the distributed shape of the minority data, and then produce samples according to this distribution. Four real datasets were used to examine the performance of the proposed approach. We used paired t-tests to compare the Accuracy, G-mean, and F-measure scores of the proposed data pre-processing (PPDP) method merging in the D3C method (PPDP+D3C) with those of the one-sided selection (OSS), the well-known SMOTEBoost (SB) study, and the normal distribution-based oversampling (NDO) approach, and the proposed data pre-processing (PPDP) method. The results indicate that the classification performance of the proposed approach is better than that of above-mentioned methods.
1. Introduction
Imbalanced data set problems are the issue in the real world and present challenges to both academics and practitioners. It should be noted that the imbalanced dataset is quite common in medical fields due to the imbalance of their class labels. In addition, the high risk/target patients tend to appear in the minority class of the medical dataset. The risk/cost of miss-classification in the minority class is much higher than that in the majority class in medical fields. Most existing classification methods do not have the required qualities in the performance of classification especially when the dataset is extremely imbalanced. For example, Murphey et al. [1], Cohen et al. [2], Sun et al. [3], Sun et al. [4], Li et al. [5, 6], Song et al. [7], Wang et al. [8], and Zou et al. [9] have shown that when limited training data are available, the small size of the minority data will significantly affect the accuracy of medical diagnoses. With imbalanced datasets, when some classes are much larger than the others, most machine learning and data mining classifiers are overly influenced by the larger classes and ignore the smaller ones. As a result, the classification algorithms often exhibit poor learning performances due to slow convergence in the minority classes [3, 4, 10, 11].
A number of solutions for dealing with class imbalance problems have been proposed to handle classification problems in various fields. These approaches can be divided into two types. One creates new algorithms or modifies existing algorithms; example of this type can be found in Hong et al. [11], Peng and King [12], Nguwi and Cho [13], and Lo et al. [14]. For certain types of data sets, this approach can be highly effective for specific classifiers, but the performance of those classifiers is still less than optimal with data sets that have varied characteristics because it is usually difficult to transform the modification procedures from one algorithm to another. The other type of approach in the literature utilizes sampling techniques; these include undersampling and oversampling to adjust the sizes of data to balance the data sets [2–5, 15–18]. The undersampling method reduces the size of data by eliminating samples from the majority class, thus decreasing its degree of influence. However, eliminating data raises the risk of partially removing the complete characteristics that may be represented in the majority class samples. Researchers have discussed various undersampling methods such as the random and directed approaches. These approaches include Kubat and Matwin [19] presented a method called one-sided selection (OSS) that randomly eliminates examples from majority class data sets until the amount of data for the majority class is equal to that of the minority class. Yen and Lee [20] proposed a cluster-based undersampling approach to select representative examples from the majority data to avoid the loss of crucial information.
As for undersampling approach, this study differs from other approaches that randomly draw data from the majority data, raising the probability of imprecisely characterizing the majority data due to the increased influence of noise or outliers in the samples set [21, 22]. Therefore, we propose a systematic procedure using the box-and-whisker plot approach to exclude outliers and the Mega-Trend-Diffusion (MTD) method proposed by Li et al. [23] to construct the distribution of the majority data. The MTD which is a data expansion method used in this study is to reasonably evaluate the domain range of the observed data. Within the estimated domain range, it includes both the reasonable/fitting data and the outliers. MTD is used to construct the membership function of the observed data and to calculate the membership degree of them. The smaller value the membership degree of the data, the more likely an outlier. This study uses theα-cut based on the MTD method to keep the suitable data and to eliminate the outliers. Further, under the estimated distribution of data, this paper takes representative samples from the majority data by settingα-cut values, providing a suitable value forα-cut to determine an appropriate amount of the majority data.
With regard to oversampling, direct resampling is a widely used strategy to balance a class distribution by duplicating minority class examples. Many researchers have adopted oversampling techniques such as those described in Piras and Giacinto [24], Xie and Qiu [21], Tahir [22], and Fernández-Navarro et al. [25]. However, these approaches may suffer from the overfitting problem. In Chawla et al. [26], rather than duplicate examples from a data set, the authors proposed the synthetic minority oversampling technique (SMOTE) to generate synthetic samples in a feature space. Many subsequent studies such as AdaBoost [27] and SMOTEBoost (SB) [28] have adopted this method, and all have confirmed the effectiveness of this approach with regard to enhancing the classification accuracy of minority class data. Unfortunately, these oversampling methods focus on resampling from rare minority class data. Therefore, when the ratio of the minority data to the overall samples is decreasing, the resampling will be too conservative to behave realistically with imbalanced data sets.
Other oversampling methods consider the underlying minority class data distributions. For instance, working in a feature space, Zhang and Wang [29] proposed a normal distribution-based oversampling (NDO) approach to generate normal-synthetic samples with characteristics that are close to those of the raw minority class data with regard to the expected mean and variance. However, with the imbalanced data sets, when there are very few data in the minority class, it is difficult to know whether the data follow a normal distribution.
Therefore, in this paper, based on a two-parameter Weibull distribution, we propose a new oversampling method for generating representative synthetic samples to extend the minority class data. One reason for this is that the distribution used can appropriately characterize the shape of a data set through various shape parameters of the density function [30–32]. Consequently, the method presented in this work is more flexible with regard to the shape of small data sets. Moreover, in our approach, a uniquely counterintuitive hypothesis-testing procedure is constructed to evaluate the shape parameter of the Weibull distribution by choosing the maximal p-value of a small data size.
This paper uses four real data sets, Wisconsin Diagnostic Breast Cancer (WDBC) and Parkinson's Disease (PD), Vertebral Column (VC) with two categories: normal and abnormal, and Haberman's Survival (HS), to illustrate the performance of the proposed method. Although accuracy is an appropriate criterion for measuring classification performance, it is not adequate for imbalanced data sets due to the impact of the minority class. As a result, the three criteria including Accuracy (ACC), Geometric Mean (G-mean), and F-measure (F1) are recommended to measure the performance of learning with imbalanced data sets [33]. For the learning tool, we tested the support vector machine (SVM) with a linear kernel function (SVM-linear), Naïve Bayes (NB), k-nearest neighbor (KNN), and another type of SVM with a polynomial kernel function (SVM-poly). The experiments show that the SVM with the polynomial kernel function has the best classification performance for raw imbalanced data sets; thus, it is chosen as the learning tool in the subsequent performance comparison among the OSS method, the SB method, the NDO method, the proposed data pre-processing (PPDP) method, the D3C method, and PPDP+D3C method. The D3C is a new hybrid model which combines the ensemble pruning based on k-means clustering and dynamic selection and circulating combination. The D3C model was proposed by Lin et al. [34] to improve the learning of imbalance dataset. It is noted that our proposed method mainly focuses on data pre-processing and the D3C is an ensemble method. Hence, the study proposes the concept of combination of PPDP with LibD3C (PPDP+D3C), that is, the imbalanced datasets are pre-processed by PPDP+D3C, and then are trained by D3C method. The four classifiers set in D3C includes NB, KNN(K = 3), SVM-linear, and SVM-poly. The results show that the combination of PPDP with LibD3C (PPDP+D3C) method has the best classification performance for imbalanced data sets.
The remainder of this paper is organized as follows: Section 2 reviews the literature on the related criteria for evaluating classification performance, the box-and-whisker plot method, and the MTD method. Section 3 introduces the detailed procedure of the proposed method. In Section 4, we present the four real data sets and the detailed experiment methodology, and then compare the results derived from the OSS, SB, NDO, PPDP, D3C, and PPDP+D3C methods. Finally, we present conclusions in Section 5.
2. Related techniques
In this section, we review the literature on the evaluation criteria for classification performance, the box-and-whisker plot method, and the MTD method.
2.1 Evaluation criteria
By convention, the minority class data is the positive class label, and the majority class data is the negative class label. For imbalanced class distributions, the accuracy rate for the minority class is frequently close to zero, which means that evaluations of learning results are not appropriate for use with minority class data. Consequently, the accuracy rate measure is not used to consider the classification performance in this work; instead, other criteria are described in this section. Table 1 shows a confusion matrix, which is used in this work to construct the relevant criteria for a two-class classification problem.
Table 1. Confusion matrix.
| Predicted class | |||
|---|---|---|---|
| Positive | Negative | ||
| Actual class | Positive | TP | FN |
| Negative | FP | TN | |
The items in the confusion matrix are as follows: TP is the number of true positive examples; FN is the number of false negative examples; FP is the number of false positive examples; and TN is the number of true negative examples. The three criteria used in this study are defined as follows:
Accuracy (ACC): ;
Geometric mean (G-mean): , where and ;
F-measure (F1): , where and
2.2 Review of the box-and-whisker plot
The box-and-whisker technique was first proposed by Tukey [35] to show the distribution of data, examine its symmetry, and indicate outliers. Box-and-whisker plots are used to exclude outliers, where the box’s lower boundary is the lower quartile (Q1) of the data and the upper boundary is the upper quartile (Q3). The length of the box is the interquartile range (IQR), which is calculated by
| (1) |
where Q3 and Q1 are the 75th and 25th percentiles of the samples, respectively. In addition, Q2 is the median of the data set. There are two inner fences in a box plot: the lower inner fence (LIF) and upper inner fence (UIF). When data are outside the [LIF,UIF], they are considered suspected outliers. The calculations for this region are as follows:
| (2) |
| (3) |
2.3 The MTD method
Li et al. [23] proposed the MTD method to construct the distribution of manufacturing data. The MTD method which combines mega diffusion and data trend estimation is used to generate virtual samples to provide a strategy for the knowledge of small data set learning and obtain a higher degree of classification accuracy.
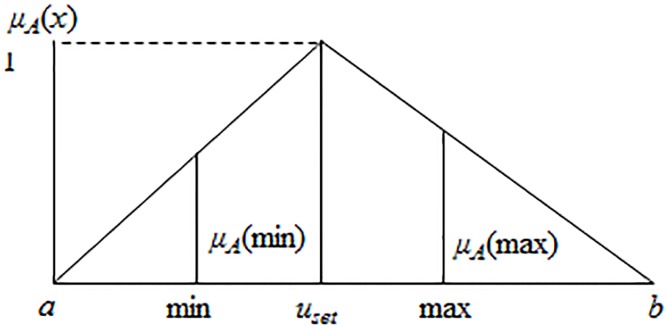
As shown in Fig 1, a triangular membership function μA(x) is constructed from the MTD method to calculate the domain range of observed/collected data x, which is the interval [a,b], described mathematically as:
| (4) |
| (5) |
where is the variance of observed data xi, i = 1,2,…,N, N is the sample size. SL = NL/(NL + NU) is the left of the skewness degree of and SU = NU/(NL + NU) is the right of the skewness degree of . NL and NU indicate the number of data less than and greater than uset that are equal to (min + max)/2, respectively, and “min” and “max” are the actual minimum and maximum values in the observed/collected data set. From Eqs (4) and (5), we can calculate the lower bound a and the upper bound b. That is, the values of a and b are the estimated domain range of observed/collected data set. Note that a = min/5 when NL = 0 and b = max × 5 when NU = 0. In addition, the related parameter settings are: μA(uset) = 1, μA(a) = μA(b) = 0, μA(min) = 1/NU and μA(max) = 1/NL.
Fig 1. Data trend estimation.
3. The model structure
This section describes the proposed procedure to deal with imbalanced data set classification problems. It describes the undersampling process and explains the oversampling technique to find the shape of the data distribution with limited samples to generate synthetic samples for learning the skewed class distribution.
3.1 The proposed procedure
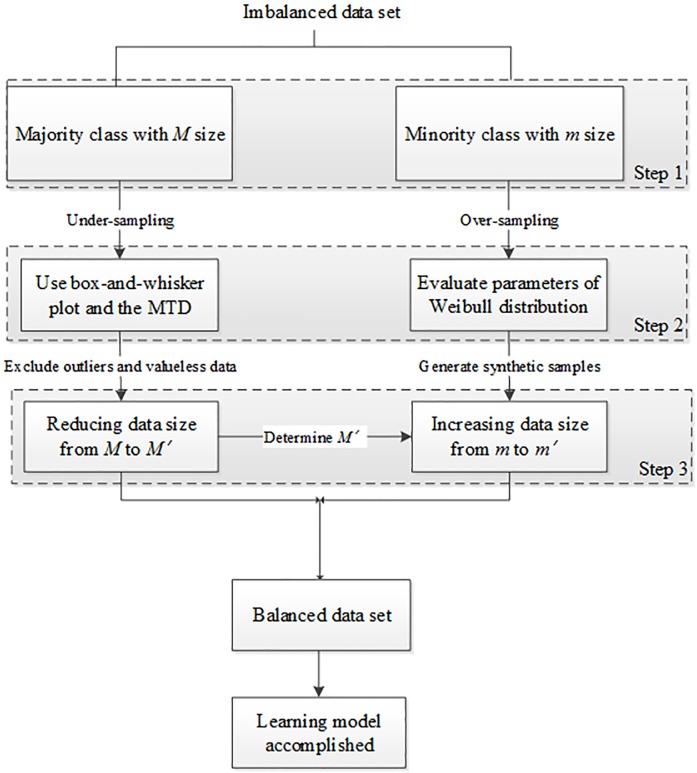
Fig 2 shows the detailed procedure of the proposed method, which contains three main steps.
Fig 2. The proposed procedure for learning imbalanced data sets.
In Step 1, the imbalanced data set is separated into two sets by class, where the majority class has M data and the minority class has m data. In Step 2, based on the undersampling strategy, we utilize the box-and-whisker plot to determine whether data are outliers in each feature. Then, we delete the outliers in the majority class. The MTD method is then applied to draw representative observations from the majority class. Regarding the oversampling strategy, because the number of samples in the minority class is small and may follow an arbitrary probability distribution, we consider the two-parameter Weibull distribution recommended by Little [36] to fit the data in the minority class and form various shapes of density functions, including skewed and mound-shaped curves, thus achieving greater flexibility. Therefore, by assuming that the minority class data are distributed into a two-parameter Weibull density function, we propose a method to evaluate the two parameters of the Weibull distribution and generate synthetic samples from that estimated distribution. In Step 3, given that these valuable parameters have been found and the data size in the majority class has been reduced from M to M', the size of synthetic data becomes M'−m, and we can then form the learning model by inputting the new balanced data set.
3.2 The undersampling method
The following method is proposed to rebuild the model of the data in the majority class. First, we employ the box-and-whisker plot to detect outliers and eliminate them from the majority data. Second, we use the remaining data to compute the range of the data, that is, the interval [a,b], as explained in Section 2.3. As shown in Fig 1, the triangular membership function μA(x) is formed based on the interval [a,b], as follows:
| (6) |
where X is assumed to be a universal set, and x is an element in X. The A set is a fuzzy set of X, and the value of μA(x) is the membership function with regard to each x in [0,1].
Here, we apply theα-cut to draw the valuable data from the corresponding μA(x) in X, where theα-cut of A is a crisp set that contains the total number of x in X that have values of μA(x) greater than or equal toα-cut, denoted as follows:
where Aα can be derived from Eq (6) as
| (7) |
We then use the data set in which all the data belong to Aα as a learning model for the majority class. In the majority class, when setting the value ofα-cut, we can implement this undersampling process to find the representative majority data.
3.3 The oversampling method
In this section, we first describe some basic properties of a two-parameter Weibull distribution, and then present the proposed method for oversampling in detail.
3.3.1 Preparation for a two-parameter Weibull distribution
Given a data set x = {xi}, i = 1,2,⋯,N that can be denoted by a two-parameter Weibull distribution, the probability density function and cumulative distribution function of the Weibull distribution are respectively expressed as follows:
| (8) |
| (9) |
where λ is the scale parameter and β is the shape parameter.
With regard to the shape parameter, Nelson et al. [37] demonstrated that the Weibull distribution has some special expressions. For example, when the value of β is one or two, the Weibull distributions are identical to the Exponential and Rayleigh distributions, respectively, and the shape of the Weibull density function is close to a normal distribution when the value of β is within [3,4]. The least square estimation (LSE) is widely utilized by researchers to estimate the β and λ of Eq (8). The sum of squares error (SSE) can be derived from Eq (9) as
| (10) |
where x(i) is the observed data, i = 1,⋯,N, N is the sample size, and the Bernard’s median rank estimator is . This study executes the shape-first method to fit the optimal value of β. Then the different values of are used to estimate λ based on the minimized SSE, as Eq (10).
3.3.2 The estimation of the two parameters
The proposed method utilizes the Gini statistic [38] in counterintuitive hypothesis testing to find the best-fitting shape parameter β of the Weibull distribution. With a given level of significance α and a data size of N, the proposed testing procedure is constructed as follows:
-
Step 1The null hypothesis is set to
-
Step 2The alternative hypothesis is set to
-
Step 3The testing statistic uses the Gini statistic as shown below:
where , and x(0) ≡ 0.(11) -
Step 4I. The rejection region for a sample size of N between 3 and 20 is set to
where the critical value ξα/2 is the 100(α/2) percentile of the GN statistic. Moreover, the p-value = P{|GN| > |gN||β = β0}, where gN indicates the estimated value of GN, as follows:
where cj = (N−j)/(N−1), and m is the largest index, such that x ≤ cm. Note that the corresponding two-tailed percentiles ξα/2 of the Gini statistic GN are described in Gail and Gastwirth [38].(12) II. The rejection region for a sample size of N that is greater than 20 is set to
where gN is the observed value of [12(N−1)]1/2 (GN−0.5) which follows an approximately standard normal distribution (normal(0,1)) expressed as shown below:(13) -
Step 5
The decision rule of the statistical test is designed as follows:
When β = β0, the p-value has a maximal value, which means that there is strong evidence that the null hypothesis, H0 should be accepted. The best-fitting shape parameter β can be found based on this testing procedure. After β is estimated, we can compute the scale parameter λ using the following equation:
where Bernard’s median rank estimator is , i = 1,⋯,N.(14)
3.3.3 Synthetic sample generation
As mentioned above, the minority class data are assumed to fit a two-parameter Weibull distribution. For a given data set, we employ the inversion method to derive the Weibull variate, which is the approach used here to create synthetic samples. In the inversion method, a random variable X is distributed in a Weibull distribution containing both a scale parameter λ and a shape parameter β (i.e., X ∼ Weibull(λ,β)). Given that F(x,λ,β) is the CDF of the data shown in Eq (9), it can be used to derive the formula of the Weibull variate as follows:
| (15) |
where x ≥ 0, λ ≥ 0, β > 0. Subsequently, in the generation of the synthetic samples , Eq (16) is modified to
| (16) |
where the Bernard’s median rank estimator , a desired number of N', and the two estimators and are calculated by the proposed approach.
3.4 The detailed procedure
Assume that a training data set has N samples with P mutually independent features denoted as T = {(X1,y1),(X2,y2),…,(XN,yN)}, and the two-class data set where each sample Xi, i = 1,…,N has P features (means Xi = (xi1, xi2,…xiP)), and yi ∈ {+,−} is the target value of Xi. Note that the class label of the minority class is positive (+), and the negative (−) label is for the majority data set. To explain the proposed procedure in detail, we provide the following steps:
-
Step 1
Separate the data set T into minority and majority data by the corresponding target value, denoted as , where , j = {+,−} and I(⋅) is an indicator function that is selected if the condition in I holds and excluded otherwise.
-
Step 2
Use the box-and-whisker plot and the MTD method as the undersampling methods to exclude outliers and select the valuable data to reduce the data size of the majority class from M to M'. Note that the number of items in the majority class becomes M', which can be calculated as M−Sbox−Smtd, where Sbox and Smtd are the quantity of outliers and valueless samples, respectively. Sbox is the sample quantity that lies outside of [LIF,UIF], they are considered suspected outliers. LIF and UIF are shown as Eqs (2) and (3). Smtd is the sample quantity that exceeds the value of Aα, Aα = [(uset−a) × α-cut + a,b−(b−uset) × α-cut], given anα-cut. That means the data which exceeds the range of Aα will be removed.
-
Step 3
Utilize the oversampling method to increase the data size in the minority class from m to m', where the number of synthetic samples in is M'−m.
-
Step 4
The reduced and extended sets are merged into a new training data set to establish a learning model.
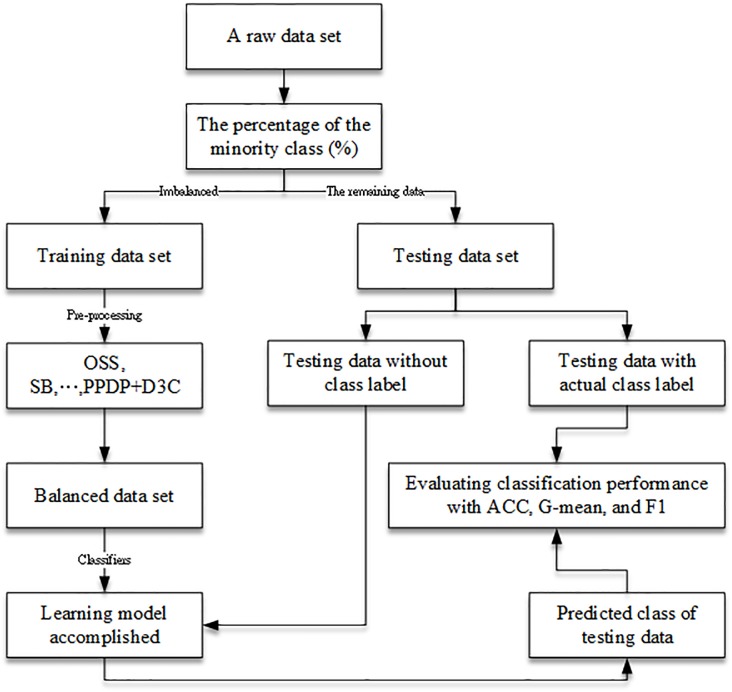
For every data set, we can implement the above steps to balance the raw data set from (M + m) × P into (M' + m') × P dimensions. Besides, the remainder of the raw data set functioned as the testing data set. As for the testing procedure, this study will use the testing data and iterate the experiment 50 times concerning all of the scenarios given anα-cut to compare the result with that of the OSS, SB, NDO, PPDP, D3C methods. The testing procedure is shown as Fig 3.
Fig 3. The testing procedure for imbalanced data sets.
4. Experiments
To demonstrate the classification performance of the PPDP+D3C method, we used four real data sets and compared the result with that of the OSS, SB, NDO, PPDP, D3C methods. Furthermore, paired t-tests were used in the comparison among them to examine the significance of the results with various sets of imbalanced data.
4.1 Four real data sets and classifier selection
In this section, we employ four real data sets (WDBC (available at: https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29), PD (available at: https://archive.ics.uci.edu/ml/datasets/parkinsons), VC (available at: http://archive.ics.uci.edu/ml/datasets/vertebral+column), and HS (available at: https://archive.ics.uci.edu/ml/datasets/Haberman's+Survival), downloaded from the UCI Machine Learning Repository database [39]) to demonstrate the performance of the PPDP+D3C with regard to the imbalanced two-class classification problems. The details of these four data sets are summarized in Table 2, where “r” indicates the percentage of minority classes in the samples.
Table 2. Data set description.
| Data Set | No. Instances | No. Features | Feature Characteristics | r |
|---|---|---|---|---|
| WDBC | 569 | 30 | Numeric | 37.26 |
| PD | 195 | 22 | Numeric | 24.62 |
| VC | 310 | 6 | Numeric | 32.22 |
| HS | 306 | 3 | Numeric | 26.47 |
This study applied four different classifiers including NB, KNN, and two types of SVM to the raw data of these four data sets. In KNN, the parameter of k was set to 3. The kernel functions in the two SVMs were linear and polynomial (notated as SVM-linear and SVM-poly, respectively); the cost parameter was set to 1 and the degree in kernel function set to 2 in the linear and polynomial kernel functions. The algorithms of the NB and KNN classifiers were implemented in Matlab, using the Statistics Toolbox. The SVM-linear and SVM-poly classifiers use LIBSVM [40] as the analysis tool. We selected the best classifier among the four classifiers in the imbalanced scenario (r = 5), using G-mean and F1 as the criteria for assessing classification performance with an imbalanced data set. Using the four raw data sets, we ran the experiment 50 times, set the training data size (N) as 60. The percentage of the minority classes was 5%, and the results, including ACC, G-mean, and F1, are shown in Table 3. The results show that the SVM-poly has a greater G-mean and F1 than NB, 3-NN, and SVM-linear. The bold values indicate that the SVM-poly achieved the best classification performance on both the WDBC, PD, VC, and HS data sets; it has the best G-mean and F1 scores.
Table 3. The results of four classifiers for the WDBC, PD, VC, and HS data set.
| Data set | WDBC | |||
| classifiers | NB | 3-NN | SVM-linear | SVM-poly |
| ACC | 61.39 | 59.63 | 62.20 | 61.12 |
| G-mean | 53.68 | 47.88 | 53.29 | 66.19 |
| F1 | 49.71 | 44.14 | 49.34 | 64.85 |
| Data set | PD | |||
| classifiers | NB | 3-NN | SVM-linear | SVM-poly |
| ACC | 66.31 | 67.73 | 53.91 | 55.41 |
| G-mean | 51.71 | 10.13 | 37.30 | 40.70 |
| F1 | 42.72 | 6.73 | 27.52 | 31.80 |
| Data set | VC | |||
| classifiers | NB | 3-NN | SVM-linear | SVM-poly |
| ACC | 63.77 | 62.25 | 49.15 | 48.56 |
| G-mean | 30.55 | 15.98 | 44.61 | 46.66 |
| F1 | 20.56 | 7.32 | 37.21 | 40.83 |
| Data set | HS | |||
| classifiers | NB | 3-NN | SVM-linear | SVM-poly |
| ACC | 68.88 | 68.32 | 43.86 | 41.46 |
| G-mean | 18.57 | 7.62 | 28.75 | 32.46 |
| F1 | 10.05 | 2.71 | 14.97 | 19.92 |
4.2 The suggested value ofα-cut
In the majority class, the value ofα-cut is important because it creates a region that controls the amount of representative data. To find an appropriate parameter setting forα-cut, we examined the classification performances of variousα-cut settings for both the WDBC, PD, VC, and HS data sets. According to the classifier selection results in Section 4.1, we utilized the SVM-poly classifier to analyze data based on the same parameter settings. Considering the imbalanced data set at (r,N) = (5,60) and performing the experiment 50 times, the results of the classifier's performance on ACC, G-mean, and F1 for different values ofα-cut are given in Table 4. As shown in Table 4, we can achieve better classification performance when the values of α-cut are 0.4 or 0.5. In our opinion, with a smallerα-cut, the data in the created region do not effectively represent the majority class, and the nature of the minority class gradually becomes fuzzy because of the corresponding increase in the number of synthetic samples M'−m. For other, higherα-cut values, the learning model may experience overfitting because the total amount of data (M' + m') becomes smaller. For this reason, we suggest that the value of α-cut should be set to 0.5.
Table 4. The results for differentα-cut values.
| Data set | α-cut | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| WDBC | ACC | 71.57 | 72.41 | 73.69 | 72.28 | 75.24 | 71.28 | 73.21 | 74.06 | 74.47 |
| G-mean | 64.73 | 66.51 | 68.77 | 65.85 | 71.28 | 64.16 | 66.85 | 69.36 | 69.65 | |
| F1 | 58.82 | 61.05 | 64.01 | 60.33 | 67.11 | 58.10 | 61.51 | 64.57 | 64.91 | |
| Sbox | 13 | 13 | 13 | 13 | 13 | 14 | 13 | 13 | 13 | |
| Smtd | 13 | 13 | 13 | 13 | 13 | 14 | 15 | 17 | 25 | |
| M’-m | 41 | 41 | 41 | 41 | 41 | 40 | 39 | 37 | 29 | |
| M’+m’ | 88 | 88 | 88 | 88 | 88 | 86 | 84 | 80 | 64 | |
| Data set | α-cut | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| PD | ACC | 67.25 | 67.61 | 64.84 | 67.21 | 68.48 | 64.53 | 67.62 | 67.70 | 67.64 |
| G-mean | 60.03 | 61.08 | 58.60 | 59.19 | 62.23 | 57.46 | 60.81 | 59.72 | 60.35 | |
| F1 | 50.27 | 51.54 | 48.00 | 49.21 | 52.73 | 46.60 | 51.11 | 50.03 | 50.61 | |
| Sbox | 10 | 10 | 10 | 10 | 11 | 11 | 10 | 10 | 10 | |
| Smtd | 10 | 10 | 11 | 10 | 12 | 12 | 14 | 19 | 29 | |
| M’-m | 44 | 44 | 43 | 44 | 42 | 42 | 40 | 35 | 25 | |
| M’+m’ | 94 | 94 | 92 | 94 | 90 | 90 | 86 | 76 | 56 | |
| Data set | α-cut | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| VC | ACC | 58.66 | 59.50 | 59.38 | 58.61 | 59.85 | 56.70 | 57.82 | 56.28 | 53.90 |
| G-mean | 56.47 | 54.88 | 56.72 | 55.44 | 57.82 | 55.62 | 57.76 | 57.42 | 54.84 | |
| F1 | 47.91 | 45.76 | 48.36 | 46.80 | 49.79 | 47.49 | 50.38 | 50.44 | 48.51 | |
| Sbox | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| Smtd | 8 | 9 | 12 | 14 | 18 | 23 | 29 | 35 | 46 | |
| M’-m | 46 | 45 | 42 | 40 | 36 | 31 | 26 | 19 | 8 | |
| M’+m’ | 98 | 96 | 90 | 86 | 78 | 68 | 58 | 44 | 22 | |
| Data set | α-cut | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| HS | ACC | 57.51 | 57.11 | 55.30 | 58.23 | 57.67 | 57.84 | 55.49 | 54.63 | 52.35 |
| G-mean | 51.39 | 51.11 | 49.46 | 53.32 | 51.71 | 51.87 | 50.64 | 50.18 | 48.04 | |
| F1 | 38.29 | 38.18 | 36.54 | 40.70 | 38.92 | 39.08 | 37.93 | 37.37 | 36.66 | |
| Sbox | 6 | 7 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | |
| Smtd | 16 | 18 | 22 | 24 | 27 | 31 | 37 | 40 | 50 | |
| M’-m | 38 | 36 | 32 | 30 | 27 | 23 | 17 | 14 | 4 | |
| M’+m’ | 82 | 78 | 70 | 66 | 60 | 52 | 40 | 34 | 14 |
4.3 Experiment design
To create imbalanced scenarios, this experiment drew samples from a raw data set according to the percentage of the minority class, which was variously set to 5%, 10%, 15%, and 20% (r = {5,10,15,20}). The training data size, N, was set to 60, 80, 100 and 150 (a total of 16 scenarios). For example, when r = 5 and N = 60, there are four scenarios (M,m) = {(57,3),(76,4),(95,5),(142,8)}. The remainder of the raw data set functioned as the testing data set. Note that the minority class size must be at least three due to the limitation with regard to sample size described in Step 4 in Section 3.3.2. To comply with this restriction, any value of r(%)×N less than three was changed to three. Using the four data sets (WDBC, PD, VC and HS), we iterated this experiment 50 times (16 scenarios at one time) at α-cut = 0.5. The results in Tables 5, 6, 7 and 8 are the averages of the values of ACC, G-mean and F1 for the imbalanced data sets taken from the WDBC, PD, VC and HS data sets. We used the paired t-test to examine whether the PPDP+D3C achieved statistically significant superiority compared with those methods such as OSS, SB, NDO, PPDP, and D3C based on the ACC, G-mean and F1 measures. The statistical test results are listed in Tables 5, 6, 7 and 8. In these tables, the bold values indicate the highest values among the six methods, the values in the parentheses represent the P-value of paired t-test for PPDP+D3C and other mentioned methods. It shows PPDP+D3C had strong statistical significance (P-value < 0.05) with regard to its classification performance.
Table 5. The results of the six methods on WDBC dataset.
| r = 5 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 74.98 | (0.00) | 74.58 | (0.00) | 73.23 | (0.00) | 71.74 | (0.00) |
| SB | 69.83 | (0.00) | 70.15 | (0.00) | 68.77 | (0.00) | 67.17 | (0.00) | |
| NDO | 74.01 | (0.00) | 74.87 | (0.00) | 73.19 | (0.00) | 71.21 | (0.00) | |
| PPDP | 73.51 | (0.00) | 74.37 | (0.00) | 72.38 | (0.00) | 71.42 | (0.00) | |
| D3C | 88.28 | (0.00) | 89.20 | (0.03) | 89.54 | (0.09) | 91.03 | (0.03) | |
| PPDP+D3C | 89.83 | - | 89.95 | - | 90.30 | - | 91.85 | - | |
| G-mean | OSS | 68.01 | (0.00) | 68.89 | (0.00) | 68.33 | (0.00) | 69.40 | (0.00) |
| SB | 59.53 | (0.00) | 62.13 | (0.00) | 61.27 | (0.00) | 63.19 | (0.00) | |
| NDO | 68.07 | (0.00) | 70.37 | (0.00) | 68.76 | (0.00) | 69.08 | (0.00) | |
| PPDP | 67.91 | (0.00) | 70.74 | (0.00) | 68.97 | (0.00) | 70.67 | (0.00) | |
| D3C | 85.85 | (0.02) | 87.37 | (0.06) | 88.29 | (0.13) | 90.91 | (0.05) | |
| PPDP+D3C | 87.98 | - | 88.28 | - | 89.14 | - | 91.76 | - | |
| F1 | OSS | 63.44 | (0.00) | 64.70 | (0.00) | 64.10 | (0.00) | 65.56 | (0.00) |
| SB | 52.70 | (0.00) | 56.04 | (0.00) | 55.07 | (0.00) | 57.77 | (0.00) | |
| NDO | 63.12 | (0.00) | 66.29 | (0.00) | 64.42 | (0.00) | 65.18 | (0.00) | |
| PPDP | 62.66 | (0.00) | 66.50 | (0.00) | 64.46 | (0.00) | 66.98 | (0.00) | |
| D3C | 84.05 | (0.01) | 86.05 | (0.04) | 87.20 | (0.13) | 90.51 | (0.05) | |
| PPDP+D3C | 86.63 | - | 87.14 | - | 88.17 | - | 91.41 | - | |
| r = 10 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 75.08 | (0.00) | 74.85 | (0.00) | 75.22 | (0.00) | 73.72 | (0.00) |
| SB | 71.30 | (0.00) | 71.34 | (0.00) | 71.61 | (0.00) | 70.03 | (0.00) | |
| NDO | 74.82 | (0.00) | 74.99 | (0.00) | 75.14 | (0.00) | 72.81 | (0.00) | |
| PPDP | 73.96 | (0.00) | 75.02 | (0.00) | 74.63 | (0.00) | 74.36 | (0.00) | |
| D3C | 90.85 | (0.03) | 90.66 | (0.08) | 92.11 | (0.58) | 92.35 | (0.00) | |
| PPDP+D3C | 91.77 | - | 91.33 | - | 92.31 | - | 93.62 | - | |
| G-mean | OSS | 69.00 | (0.00) | 70.00 | (0.00) | 71.54 | (0.00) | 71.92 | (0.00) |
| SB | 63.50 | (0.00) | 64.92 | (0.00) | 66.66 | (0.00) | 67.40 | (0.00) | |
| NDO | 69.66 | (0.00) | 70.79 | (0.00) | 72.05 | (0.00) | 71.22 | (0.00) | |
| PPDP | 69.41 | (0.00) | 72.23 | (0.00) | 72.87 | (0.00) | 74.60 | (0.00) | |
| D3C | 89.57 | (0.05) | 89.48 | (0.08) | 91.55 | (0.36) | 92.26 | (0.00) | |
| PPDP+D3C | 90.66 | - | 90.24 | - | 91.91 | - | 93.69 | - | |
| F1 | OSS | 64.63 | (0.00) | 66.00 | (0.00) | 67.92 | (0.00) | 68.65 | (0.00) |
| SB | 57.46 | (0.00) | 59.51 | (0.00) | 61.76 | (0.00) | 63.05 | (0.00) | |
| NDO | 65.12 | (0.00) | 66.82 | (0.00) | 68.47 | (0.00) | 67.81 | (0.00) | |
| PPDP | 64.55 | (0.00) | 68.25 | (0.00) | 69.15 | (0.00) | 71.74 | (0.00) | |
| D3C | 88.20 | (0.04) | 88.29 | (0.08) | 90.69 | (0.41) | 91.85 | (0.00) | |
| PPDP+D3C | 89.48 | - | 89.15 | - | 91.05 | - | 93.36 | - | |
| r = 15 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 76.83 | (0.00) | 76.37 | (0.00) | 75.61 | (0.00) | 75.23 | (0.00) |
| SB | 74.31 | (0.00) | 73.27 | (0.00) | 73.23 | (0.00) | 73.13 | (0.00) | |
| NDO | 77.10 | (0.00) | 76.42 | (0.00) | 75.04 | (0.00) | 75.22 | (0.00) | |
| PPDP | 75.99 | (0.00) | 75.62 | (0.00) | 75.41 | (0.00) | 76.45 | (0.00) | |
| D3C | 92.07 | (0.03) | 91.82 | (0.13) | 91.98 | (0.02) | 92.51 | (0.00) | |
| PPDP+D3C | 92.78 | - | 92.45 | - | 92.81 | - | 93.67 | - | |
| G-mean | OSS | 71.89 | (0.00) | 72.43 | (0.00) | 72.12 | (0.00) | 73.67 | (0.00) |
| SB | 68.32 | (0.00) | 67.77 | (0.00) | 69.10 | (0.00) | 71.04 | (0.00) | |
| NDO | 72.93 | (0.00) | 72.84 | (0.00) | 71.83 | (0.00) | 73.98 | (0.00) | |
| PPDP | 72.55 | (0.00) | 73.18 | (0.00) | 73.55 | (0.00) | 76.74 | (0.00) | |
| D3C | 90.82 | (0.00) | 91.07 | (0.04) | 91.03 | (0.01) | 92.24 | (0.00) | |
| PPDP+D3C | 91.98 | - | 92.03 | - | 92.21 | - | 93.68 | - | |
| F1 | OSS | 68.27 | (0.00) | 68.83 | (0.00) | 68.55 | (0.00) | 70.73 | (0.00) |
| SB | 63.52 | (0.00) | 63.01 | (0.00) | 64.74 | (0.00) | 67.49 | (0.00) | |
| NDO | 69.22 | (0.00) | 69.29 | (0.00) | 68.11 | (0.00) | 71.09 | (0.00) | |
| PPDP | 68.40 | (0.00) | 69.36 | (0.00) | 69.90 | (0.00) | 74.18 | (0.00) | |
| D3C | 89.73 | (0.01) | 89.91 | (0.06) | 90.18 | (0.01) | 91.70 | (0.00) | |
| PPDP+D3C | 90.88 | - | 90.88 | - | 91.37 | - | 93.22 | - | |
| r = 20 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 76.11 | (0.00) | 77.48 | (0.00) | 76.61 | (0.00) | 77.16 | (0.00) |
| SB | 73.97 | (0.00) | 75.14 | (0.00) | 75.08 | (0.00) | 74.11 | (0.00) | |
| NDO | 76.25 | (0.00) | 77.70 | (0.00) | 76.97 | (0.00) | 75.64 | (0.00) | |
| PPDP | 75.76 | (0.00) | 77.13 | (0.00) | 77.17 | (0.00) | 76.17 | (0.00) | |
| D3C | 91.48 | (0.00) | 92.35 | (0.00) | 92.46 | (0.07) | 93.78 | (0.03) | |
| PPDP+D3C | 92.78 | - | 93.05 | - | 92.99 | - | 94.33 | - | |
| G-mean | OSS | 71.33 | (0.00) | 74.26 | (0.00) | 73.61 | (0.00) | 75.98 | (0.00) |
| SB | 68.60 | (0.00) | 70.90 | (0.00) | 71.75 | (0.00) | 71.92 | (0.00) | |
| NDO | 72.25 | (0.00) | 74.79 | (0.00) | 74.44 | (0.00) | 74.10 | (0.00) | |
| PPDP | 72.84 | (0.00) | 75.66 | (0.00) | 76.16 | (0.00) | 76.22 | (0.00) | |
| D3C | 90.22 | (0.00) | 91.45 | (0.00) | 91.65 | (0.00) | 93.57 | (0.00) | |
| PPDP+D3C | 92.42 | - | 92.77 | - | 92.79 | - | 94.42 | - | |
| F1 | OSS | 67.27 | (0.00) | 71.01 | (0.00) | 70.20 | (0.00) | 73.36 | (0.00) |
| SB | 63.73 | (0.00) | 66.66 | (0.00) | 67.82 | (0.00) | 68.41 | (0.00) | |
| NDO | 68.25 | (0.00) | 71.45 | (0.00) | 71.15 | (0.00) | 71.08 | (0.00) | |
| PPDP | 68.67 | (0.00) | 72.23 | (0.00) | 72.94 | (0.00) | 73.39 | (0.00) | |
| D3C | 88.82 | (0.00) | 90.38 | (0.00) | 90.73 | (0.01) | 93.06 | (0.01) | |
| PPDP+D3C | 91.07 | - | 91.59 | - | 91.71 | - | 93.87 | - | |
Table 6. The results of the six methods on PD dataset.
| r = 5 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 69.31 | (0.00) | 65.85 | (0.00) | 64.66 | (0.00) | 47.76 | (0.00) |
| SB | 67.28 | (0.00) | 64.17 | (0.00) | 62.07 | (0.00) | 44.96 | (0.00) | |
| NDO | 67.47 | (0.00) | 66.74 | (0.00) | 65.17 | (0.00) | 53.40 | (0.00) | |
| PPDP | 67.86 | (0.36) | 65.92 | (0.09) | 63.93 | (0.03) | 51.53 | (0.00) | |
| D3C | 71.35 | (0.00) | 70.78 | (0.01) | 68.67 | (0.01) | 62.98 | (0.03) | |
| PPDP+D3C | 73.73 | - | 72.71 | - | 70.82 | - | 66.76 | - | |
| G-mean | OSS | 55.09 | (0.00) | 54.39 | (0.00) | 58.89 | (0.00) | 62.99 | (0.00) |
| SB | 50.31 | (0.00) | 50.62 | (0.00) | 54.79 | (0.00) | 59.97 | (0.00) | |
| NDO | 60.54 | (0.00) | 61.18 | (0.00) | 62.50 | (0.00) | 64.91 | (0.00) | |
| PPDP | 58.88 | (0.00) | 61.61 | (0.00) | 61.86 | (0.00) | 66.24 | (0.00) | |
| D3C | 62.84 | (0.01) | 65.02 | (0.02) | 65.54 | (0.00) | 69.75 | (0.02) | |
| PPDP+D3C | 66.71 | - | 67.62 | - | 68.72 | - | 73.54 | - | |
| F1 | OSS | 45.53 | (0.00) | 45.33 | (0.00) | 52.12 | (0.00) | 61.58 | (0.00) |
| SB | 39.48 | (0.00) | 40.69 | (0.00) | 46.84 | (0.00) | 59.19 | (0.00) | |
| NDO | 50.83 | (0.00) | 53.39 | (0.00) | 56.97 | (0.00) | 67.40 | (0.00) | |
| PPDP | 49.04 | (0.00) | 53.70 | (0.00) | 56.05 | (0.00) | 66.58 | (0.00) | |
| D3C | 52.81 | (0.00) | 57.48 | (0.02) | 60.59 | (0.00) | 75.52 | (0.03) | |
| PPDP+D3C | 57.52 | - | 60.56 | - | 64.36 | - | 78.80 | - | |
| r = 10 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 71.99 | (0.05) | 70.72 | (0.00) | 70.77 | (0.32) | 66.56 | (0.46) |
| SB | 69.67 | (0.00) | 69.66 | (0.00) | 68.33 | (0.00) | 62.33 | (0.00) | |
| NDO | 69.68 | (0.00) | 70.93 | (0.00) | 68.47 | (0.00) | 63.22 | (0.00) | |
| PPDP | 68.44 | (0.76) | 70.57 | (0.03) | 67.44 | (0.44) | 62.47 | (0.90) | |
| D3C | 73.69 | (0.95) | 74.19 | (0.30) | 73.33 | (0.01) | 69.82 | (0.03) | |
| PPDP+D3C | 73.73 | - | 73.60 | - | 71.64 | - | 67.64 | - | |
| G-mean | OSS | 62.29 | (0.00) | 66.01 | (0.00) | 67.92 | (0.05) | 72.66 | (0.16) |
| SB | 56.79 | (0.00) | 62.42 | (0.00) | 64.04 | (0.00) | 69.42 | (0.35) | |
| NDO | 64.77 | (0.00) | 68.32 | (0.01) | 66.69 | (0.00) | 69.39 | (0.37) | |
| PPDP | 63.78 | (0.02) | 69.02 | (0.77) | 66.90 | (0.33) | 69.94 | (0.37) | |
| D3C | 66.25 | (0.03) | 70.41 | (0.69) | 71.49 | (0.05) | 73.84 | (0.01) | |
| PPDP+D3C | 68.51 | - | 70.73 | - | 69.92 | - | 70.63 | - | |
| F1 | OSS | 53.30 | (0.03) | 58.55 | (0.01) | 62.64 | (0.45) | 74.34 | (0.57) |
| SB | 46.75 | (0.00) | 54.37 | (0.00) | 57.73 | (0.00) | 70.18 | (0.00) | |
| NDO | 55.18 | (0.09) | 61.19 | (0.37) | 61.02 | (0.04) | 71.43 | (0.00) | |
| PPDP | 53.72 | (0.06) | 61.75 | (0.68) | 61.16 | (0.27) | 71.68 | (0.08) | |
| D3C | 56.22 | (0.05) | 62.78 | (0.64) | 66.35 | (0.07) | 77.70 | (0.08) | |
| PPDP+D3C | 58.56 | - | 63.23 | - | 64.55 | - | 76.14 | - | |
| r = 15 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 72.63 | (0.71) | 71.24 | (0.08) | 73.48 | (0.30) | 71.04 | (0.27) |
| SB | 71.93 | (0.32) | 71.89 | (0.27) | 71.72 | (0.49) | 70.07 | (0.66) | |
| NDO | 71.36 | (0.09) | 72.86 | (0.96) | 71.91 | (0.61) | 70.02 | (0.67) | |
| PPDP | 69.81 | (0.08) | 69.68 | (0.05) | 70.22 | (0.00) | 67.76 | (0.01) | |
| D3C | 75.39 | (0.00) | 75.72 | (0.00) | 74.88 | (0.00) | 71.91 | (0.04) | |
| PPDP+D3C | 72.99 | - | 72.82 | - | 72.38 | - | 69.47 | - | |
| G-mean | OSS | 67.38 | (0.02) | 66.92 | (0.00) | 71.74 | (0.31) | 73.79 | (0.12) |
| SB | 63.63 | (0.00) | 65.82 | (0.00) | 67.71 | (0.02) | 73.463 | (0.18) | |
| NDO | 66.95 | (0.00) | 70.24 | (0.29) | 70.26 | (0.83) | 73.31 | (0.19) | |
| PPDP | 66.96 | (0.33) | 68.59 | (0.58) | 70.17 | (0.09) | 71.74 | (0.07) | |
| D3C | 71.41 | (0.09) | 72.27 | (0.29) | 72.30 | (0.04) | 74.65 | (0.01) | |
| PPDP+D3C | 70.04 | - | 71.17 | - | 70.49 | - | 71.60 | - | |
| F1 | OSS | 57.45 | (0.91) | 58.32 | (0.08) | 65.81 | (0.02) | 73.38 | (0.28) |
| SB | 53.55 | (0.01) | 57.57 | (0.01) | 61.07 | (0.42) | 73.78 | (0.42) | |
| NDO | 56.56 | (0.40) | 62.36 | (0.19) | 63.93 | (0.18) | 74.03 | (0.30) | |
| PPDP | 56.14 | (0.73) | 59.74 | (0.90) | 63.47 | (0.07) | 73.10 | (0.22) | |
| D3C | 60.71 | (0.04) | 63.63 | (0.17) | 65.56 | (0.03) | 74.96 | (0.33) | |
| PPDP+D3C | 58.63 | - | 61.91 | - | 63.24 | - | 73.62 | - | |
| r = 20 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 74.05 | (0.62) | 74.70 | (0.18) | 74.96 | (0.14) | 73.67 | (0.08) |
| SB | 73.40 | (0.83) | 74.65 | (0.10) | 74.39 | (0.32) | 75.40 | (0.00) | |
| NDO | 72.30 | (0.20) | 74.20 | (0.26) | 74.28 | (0.34) | 74.96 | (0.01) | |
| PPDP | 70.51 | (0.09) | 71.92 | (0.00) | 72.28 | (0.00) | 73.22 | (0.00) | |
| D3C | 76.19 | (0.00) | 77.63 | (0.00) | 78.51 | (0.00) | 75.64 | (0.00) | |
| PPDP+D3C | 73.59 | - | 73.41 | - | 73.58 | - | 71.20 | - | |
| G-mean | OSS | 70.97 | (0.33) | 71.78 | (0.80) | 73.88 | (0.05) | 75.35 | (0.04) |
| SB | 67.11 | (0.00) | 70.04 | (0.15) | 72.14 | (0.90) | 77.12 | (0.00) | |
| NDO | 69.92 | (0.06) | 72.02 | (0.51) | 73.90 | (0.02) | 76.59 | (0.00) | |
| PPDP | 69.12 | (0.40) | 71.44 | (0.04) | 73.12 | (0.00) | 75.89 | (0.00) | |
| D3C | 72.21 | (0.85) | 73.70 | (0.01) | 76.01 | (0.00) | 76.52 | (0.00) | |
| PPDP+D3C | 72.05 | - | 71.47 | - | 72.03 | - | 72.23 | - | |
| F1 | OSS | 60.67 | (0.12) | 63.03 | (0.03) | 66.56 | (0.00) | 74.97 | (0.01) |
| SB | 56.65 | (0.16) | 61.43 | (0.12) | 64.59 | (0.02) | 76.80 | (0.00) | |
| NDO | 58.89 | (0.80) | 63.03 | (0.00) | 66.23 | (0.00) | 76.51 | (0.00) | |
| PPDP | 57.57 | (0.98) | 61.76 | (0.01) | 64.96 | (0.00) | 76.15 | (0.00) | |
| D3C | 60.64 | (0.34) | 64.27 | (0.00) | 68.10 | (0.00) | 75.03 | (0.00) | |
| PPDP+D3C | 59.53 | - | 60.51 | - | 62.71 | - | 71.28 | - | |
Table 7. The results of the six methods on VC dataset.
| r = 5 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 58.70 | (0.00) | 58.68 | (0.00) | 58.91 | (0.00) | 59.49 | (0.00) |
| SB | 58.92 | (0.00) | 60.89 | (0.00) | 60.62 | (0.00) | 62.34 | (0.00) | |
| NDO | 62.76 | (0.00) | 63.30 | (0.00) | 64.56 | (0.00) | 66.84 | (0.01) | |
| PPDP | 59.17 | (0.00) | 58.97 | (0.00) | 60.59 | (0.00) | 60.04 | (0.00) | |
| D3C | 67.84 | (0.65) | 67.66 | (0.37) | 67.42 | (0.85) | 67.38 | (0.15) | |
| PPDP+D3C | 67.36 | - | 66.90 | - | 67.26 | - | 68.73 | - | |
| G-mean | OSS | 52.71 | (0.00) | 55.49 | (0.00) | 57.71 | (0.00) | 61.88 | (0.00) |
| SB | 50.60 | (0.00) | 56.36 | (0.00) | 58.48 | (0.00) | 64.84 | (0.00) | |
| NDO | 59.86 | (0.00) | 62.02 | (0.00) | 64.97 | (0.05) | 69.06 | (0.54) | |
| PPDP | 56.74 | (0.00) | 58.39 | (0.00) | 62.03 | (0.00) | 62.93 | (0.00) | |
| D3C | 62.26 | (0.24) | 63.36 | (0.44) | 64.46 | (0.06) | 67.95 | (0.47) | |
| PPDP+D3C | 64.07 | - | 64.53 | - | 66.68 | - | 68.61 | - | |
| F1 | OSS | 43.41 | (0.00) | 48.05 | (0.00) | 52.21 | (0.00) | 61.70 | (0.00) |
| SB | 40.49 | (0.00) | 48.56 | (0.00) | 52.49 | (0.00) | 64.65 | (0.00) | |
| NDO | 51.99 | (0.01) | 55.91 | (0.03) | 61.16 | (0.07) | 70.62 | (0.44) | |
| PPDP | 47.96 | (0.00) | 51.71 | (0.00) | 58.20 | (0.00) | 64.98 | (0.00) | |
| D3C | 54.43 | (0.24) | 57.06 | (0.30) | 59.48 | (0.00) | 68.15 | (0.00) | |
| PPDP+D3C | 56.54 | - | 59.00 | - | 64.12 | - | 72.24 | - | |
| r = 10 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 60.02 | (0.00) | 58.26 | (0.00) | 61.62 | (0.00) | 63.89 | (0.00) |
| SB | 60.74 | (0.00) | 60.33 | (0.00) | 64.40 | (0.00) | 67.36 | (0.00) | |
| NDO | 63.68 | (0.00) | 65.34 | (0.00) | 67.30 | (0.07) | 68.93 | (0.00) | |
| PPDP | 60.21 | (0.00) | 59.71 | (0.00) | 62.10 | (0.03) | 63.46 | (0.00) | |
| D3C | 68.75 | (0.48) | 69.64 | (0.45) | 71.58 | (0.00) | 71.06 | (0.97) | |
| PPDP+D3C | 68.33 | - | 69.00 | - | 68.42 | - | 71.09 | - | |
| G-mean | OSS | 58.13 | (0.00) | 57.56 | (0.00) | 62.70 | (0.00) | 65.72 | (0.00) |
| SB | 56.91 | (0.00) | 58.92 | (0.00) | 65.04 | (0.00) | 69.29 | (0.04) | |
| NDO | 62.92 | (0.00) | 66.09 | (0.01) | 68.51 | (0.77) | 70.88 | (0.95) | |
| PPDP | 59.55 | (0.00) | 60.65 | (0.00) | 64.03 | (0.00) | 65.93 | (0.00) | |
| D3C | 63.92 | (0.01) | 64.19 | (0.00) | 69.08 | (0.44) | 71.12 | (0.77) | |
| PPDP+D3C | 66.76 | - | 68.65 | - | 68.30 | - | 70.92 | - | |
| F1 | OSS | 49.84 | (0.00) | 50.80 | (0.00) | 58.84 | (0.00) | 66.99 | (0.00) |
| SB | 47.89 | (0.00) | 51.80 | (0.00) | 60.93 | (0.01) | 70.19 | (0.00) | |
| NDO | 55.64 | (0.00) | 60.81 | (0.06) | 65.11 | (0.26) | 71.77 | (0.11) | |
| PPDP | 51.57 | (0.00) | 54.40 | (0.00) | 60.34 | (0.00) | 68.06 | (0.00) | |
| D3C | 55.85 | (0.01) | 57.07 | (0.00) | 64.34 | (0.56) | 69.64 | (0.00) | |
| PPDP+D3C | 59.91 | - | 63.85 | - | 65.06 | - | 73.79 | - | |
| r = 15 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 59.06 | (0.00) | 61.15 | (0.00) | 63.71 | (0.00) | 65.56 | (0.00) |
| SB | 62.22 | (0.00) | 63.81 | (0.00) | 65.85 | (0.00) | 68.45 | (0.00) | |
| NDO | 64.61 | (0.00) | 67.20 | (0.00) | 68.68 | (0.22) | 69.23 | (0.03) | |
| PPDP | 60.26 | (0.00) | 62.42 | (0.00) | 62.49 | (0.00) | 63.59 | (0.00) | |
| D3C | 71.95 | (0.00) | 72.88 | (0.00) | 73.46 | (0.00) | 72.91 | (0.00) | |
| PPDP+D3C | 68.63 | - | 69.72 | - | 69.32 | - | 70.04 | - | |
| G-mean | OSS | 59.15 | (0.00) | 62.03 | (0.00) | 65.11 | (0.00) | 67.25 | (0.00) |
| SB | 60.95 | (0.00) | 63.50 | (0.00) | 66.87 | (0.00) | 70.23 | (0.98) | |
| NDO | 65.34 | (0.00) | 67.95 | (0.00) | 70.17 | (0.82) | 71.04 | (0.03) | |
| PPDP | 61.03 | (0.00) | 64.21 | (0.00) | 65.27 | (0.00) | 66.26 | (0.00) | |
| D3C | 66.31 | (0.16) | 69.38 | (0.66) | 71.13 | (0.19) | 72.46 | (0.00) | |
| PPDP+D3C | 68.31 | - | 69.71 | - | 70.04 | - | 70.24 | - | |
| F1 | OSS | 51.17 | (0.00) | 56.07 | (0.00) | 60.96 | (0.00) | 67.73 | (0.00) |
| SB | 52.63 | (0.00) | 56.95 | (0.00) | 62.35 | (0.00) | 70.36 | (0.86) | |
| NDO | 58.20 | (0.04) | 62.32 | (0.17) | 66.16 | (0.50) | 71.34 | (0.04) | |
| PPDP | 53.16 | (0.00) | 58.10 | (0.00) | 61.76 | (0.00) | 67.28 | (0.00) | |
| D3C | 58.38 | (0.06) | 63.11 | (0.19) | 65.96 | (0.42) | 70.46 | (0.22) | |
| PPDP+D3C | 61.36 | - | 64.34 | - | 66.77 | - | 71.46 | - | |
| r = 20 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 60.69 | (0.00) | 60.09 | (0.00) | 61.42 | (0.00) | 66.19 | (0.00) |
| SB | 63.57 | (0.00) | 63.83 | (0.00) | 66.00 | (0.00) | 69.40 | (0.01) | |
| NDO | 65.23 | (0.00) | 66.46 | (0.00) | 67.76 | (0.00) | 70.69 | (0.12) | |
| PPDP | 60.93 | (0.00) | 61.52 | (0.00) | 62.80 | (0.00) | 65.20 | (0.03) | |
| D3C | 73.38 | (0.00) | 73.87 | (0.00) | 74.93 | (0.00) | 74.45 | (0.00) | |
| PPDP+D3C | 69.34 | - | 69.59 | - | 70.68 | - | 71.51 | - | |
| G-mean | OSS | 62.23 | (0.00) | 62.24 | (0.00) | 63.57 | (0.00) | 68.06 | (0.00) |
| SB | 63.52 | (0.00) | 64.62 | (0.00) | 67.54 | (0.00) | 71.25 | (0.30) | |
| NDO | 66.10 | (0.00) | 68.18 | (0.00) | 69.50 | (0.00) | 72.61 | (0.27) | |
| PPDP | 62.63 | (0.00) | 64.14 | (0.00) | 65.57 | (0.00) | 68.04 | (0.00) | |
| D3C | 68.62 | (0.50) | 69.93 | (0.78) | 72.53 | (0.22) | 72.91 | (0.36) | |
| PPDP+D3C | 69.37 | - | 70.25 | - | 71.60 | - | 72.01 | - | |
| F1 | OSS | 54.73 | (0.00) | 56.57 | (0.00) | 59.05 | (0.00) | 67.68 | (0.00) |
| SB | 55.44 | (0.00) | 57.94 | (0.00) | 62.41 | (0.00) | 70.34 | (0.57) | |
| NDO | 58.62 | (0.01) | 62.32 | (0.05) | 64.68 | (0.00) | 71.56 | (0.14) | |
| PPDP | 54.72 | (0.00) | 57.94 | (0.00) | 60.76 | (0.00) | 67.45 | (0.00) | |
| D3C | 60.83 | (0.31) | 63.19 | (0.24) | 66.96 | (0.65) | 69.69 | (0.08) | |
| PPDP+D3C | 62.18 | - | 64.73 | - | 67.36 | - | 71.75 | - | |
Table 8. The results of the six methods on HS dataset.
| r = 5 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 59.46 | (0.53) | 56.78 | (0.06) | 56.48 | (0.03) | 52.44 | (0.00) |
| SB | 61.06 | (0.54) | 57.72 | (0.35) | 57.01 | (0.04) | 52.74 | (0.01) | |
| NDO | 60.87 | (0.62) | 57.18 | (0.11) | 58.30 | (0.28) | 55.14 | (0.27) | |
| PPDP | 56.25 | (0.27) | 54.05 | (0.66) | 54.90 | (0.50) | 50.35 | (0.32) | |
| D3C | 66.07 | (0.00) | 63.62 | (0.00) | 64.72 | (0.00) | 58.86 | (0.03) | |
| PPDP+D3C | 60.33 | - | 58.71 | - | 59.29 | - | 56.32 | - | |
| G-mean | OSS | 44.36 | (0.00) | 45.82 | (0.00) | 47.27 | (0.00) | 49.22 | (0.00) |
| SB | 42.20 | (0.00) | 43.56 | (0.00) | 46.20 | (0.00) | 49.24 | (0.00) | |
| NDO | 48.43 | (0.01) | 49.08 | (0.24) | 50.67 | (0.00) | 52.88 | (0.25) | |
| PPDP | 51.08 | (0.98) | 48.62 | (0.67) | 51.89 | (0.34) | 49.55 | (0.03) | |
| D3C | 49.50 | (0.08) | 45.83 | (0.00) | 48.08 | (0.00) | 46.46 | (0.00) | |
| PPDP+D3C | 53.05 | - | 51.28 | - | 55.21 | - | 54.41 | - | |
| F1 | OSS | 30.53 | (0.00) | 32.87 | (0.01) | 35.69 | (0.00) | 41.63 | (0.00) |
| SB | 28.27 | (0.00) | 30.27 | (0.00) | 34.16 | (0.00) | 41.37 | (0.00) | |
| NDO | 35.42 | (0.03) | 37.08 | (0.47) | 39.90 | (0.01) | 46.32 | (0.11) | |
| PPDP | 38.48 | (0.82) | 36.60 | (0.56) | 41.64 | (0.17) | 43.22 | (0.01) | |
| D3C | 36.62 | (0.05) | 33.30 | (0.00) | 35.02 | (0.00) | 36.40 | (0.00) | |
| PPDP+D3C | 40.90 | - | 41.69 | - | 45.98 | - | 49.93 | - | |
| r = 10 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 58.27 | (0.08) | 58.07 | (0.00) | 57.64 | (0.00) | 56.05 | (0.00) |
| SB | 59.21 | (0.29) | 58.88 | (0.00) | 58.58 | (0.00) | 57.94 | (0.00) | |
| NDO | 60.10 | (0.82) | 60.74 | (0.00) | 60.76 | (0.32) | 58.79 | (0.00) | |
| PPDP | 54.66 | (0.46) | 58.72 | (0.62) | 55.58 | (0.16) | 54.92 | (0.00) | |
| D3C | 67.91 | (0.00) | 68.07 | (0.00) | 67.81 | (0.00) | 63.04 | (0.09) | |
| PPDP+D3C | 60.33 | - | 64.05 | - | 61.63 | - | 61.82 | - | |
| G-mean | OSS | 46.66 | (0.00) | 50.16 | (0.00) | 52.19 | (0.00) | 53.26 | (0.00) |
| SB | 44.88 | (0.00) | 48.45 | (0.00) | 52.36 | (0.00) | 55.46 | (0.00) | |
| NDO | 50.25 | (0.00) | 52.48 | (0.00) | 53.27 | (0.00) | 55.04 | (0.00) | |
| PPDP | 50.51 | (0.13) | 54.72 | (0.02) | 53.86 | (0.00) | 54.34 | (0.00) | |
| D3C | 48.38 | (0.00) | 47.88 | (0.00) | 49.70 | (0.00) | 49.68 | (0.00) | |
| PPDP+D3C | 54.56 | - | 59.43 | - | 59.66 | - | 60.32 | - | |
| F1 | OSS | 32.53 | (0.00) | 37.41 | (0.00) | 40.86 | (0.00) | 45.44 | (0.00) |
| SB | 30.56 | (0.00) | 35.36 | (0.00) | 40.87 | (0.00) | 48.04 | (0.00) | |
| NDO | 36.77 | (0.01) | 40.27 | (0.00) | 42.28 | (0.00) | 47.57 | (0.00) | |
| PPDP | 37.05 | (0.07) | 42.58 | (0.01) | 43.17 | (0.00) | 47.23 | (0.00) | |
| D3C | 35.10 | (0.00) | 36.60 | (0.00) | 37.98 | (0.00) | 39.37 | (0.00) | |
| PPDP+D3C | 41.76 | - | 48.32 | - | 50.55 | - | 55.24 | - | |
| r = 15 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 56.58 | (0.00) | 57.30 | (0.00) | 57.14 | (0.00) | 58.88 | (0.00) |
| SB | 58.41 | (0.00) | 59.63 | (0.00) | 58.76 | (0.00) | 59.99 | (0.00) | |
| NDO | 61.19 | (0.03) | 62.78 | (0.71) | 62.49 | (0.00) | 61.50 | (0.00) | |
| PPDP | 55.55 | (0.00) | 54.75 | (0.00) | 56.96 | (0.00) | 55.58 | (0.00) | |
| D3C | 70.77 | (0.00) | 69.88 | (0.00) | 69.91 | (0.00) | 65.47 | (0.00) | |
| PPDP+D3C | 63.24 | - | 63.10 | - | 65.15 | - | 63.67 | - | |
| G-mean | OSS | 50.50 | (0.00) | 50.18 | (0.00) | 51.19 | (0.00) | 56.49 | (0.00) |
| SB | 49.46 | (0.00) | 50.15 | (0.00) | 50.96 | (0.00) | 57.01 | (0.00) | |
| NDO | 52.97 | (0.00) | 53.71 | (0.00) | 54.11 | (0.00) | 54.85 | (0.00) | |
| PPDP | 51.48 | (0.00) | 51.44 | (0.00) | 54.50 | (0.00) | 54.99 | (0.00) | |
| D3C | 49.46 | (0.00) | 45.30 | (0.00) | 49.54 | (0.00) | 49.69 | (0.00) | |
| PPDP+D3C | 59.46 | - | 60.00 | - | 62.18 | - | 61.36 | - | |
| F1 | OSS | 35.99 | (0.00) | 36.65 | (0.00) | 38.59 | (0.00) | 48.09 | (0.00) |
| SB | 34.84 | (0.00) | 36.68 | (0.00) | 38.29 | (0.00) | 48.54 | (0.00) | |
| NDO | 39.07 | (0.00) | 41.20 | (0.00) | 42.29 | (0.00) | 45.49 | (0.00) | |
| PPDP | 37.32 | (0.00) | 38.16 | (0.00) | 42.59 | (0.00) | 46.62 | (0.00) | |
| D3C | 31.54 | (0.00) | 32.47 | (0.00) | 37.52 | (0.00) | 38.64 | (0.00) | |
| PPDP+D3C | 46.63 | - | 48.66 | - | 51.56 | - | 54.09 | - | |
| r = 20 | N | ||||||||
| Method | 60 | 80 | 100 | 150 | |||||
| ACC | OSS | 56.25 | (0.00) | 58.23 | (0.00) | 57.41 | (0.00) | 59.78 | (0.00) |
| SB | 59.24 | (0.00) | 60.13 | (0.00) | 59.98 | (0.00) | 60.63 | (0.00) | |
| NDO | 61.76 | (0.01) | 63.73 | (0.01) | 62.62 | (0.00) | 62.32 | (0.00) | |
| PPDP | 55.72 | (0.00) | 58.63 | (0.00) | 57.33 | (0.00) | 57.32 | (0.00) | |
| D3C | 71.11 | (0.00) | 71.09 | (0.00) | 70.59 | (0.00) | 67.53 | (0.00) | |
| PPDP+D3C | 64.04 | - | 66.13 | - | 65.09 | - | 65.42 | - | |
| G-mean | OSS | 50.56 | (0.00) | 52.48 | (0.00) | 54.39 | (0.00) | 57.93 | (0.00) |
| SB | 50.65 | (0.00) | 51.28 | (0.00) | 55.97 | (0.00) | 57.28 | (0.00) | |
| NDO | 53.80 | (0.00) | 54.26 | (0.00) | 55.56 | (0.00) | 55.63 | (0.00) | |
| PPDP | 52.34 | (0.00) | 54.98 | (0.00) | 55.03 | (0.00) | 56.29 | (0.00) | |
| D3C | 48.40 | (0.00) | 45.64 | (0.00) | 50.34 | (0.00) | 48.24 | (0.00) | |
| PPDP+D3C | 60.68 | - | 61.23 | - | 61.89 | - | 62.05 | - | |
| F1 | OSS | 35.78 | (0.00) | 38.53 | (0.00) | 41.46 | (0.00) | 48.34 | (0.00) |
| SB | 35.83 | (0.00) | 37.15 | (0.00) | 43.20 | (0.00) | 47.40 | (0.00) | |
| NDO | 39.72 | (0.00) | 41.23 | (0.00) | 43.02 | (0.00) | 45.39 | (0.00) | |
| PPDP | 37.79 | (0.00) | 41.44 | (0.00) | 42.18 | (0.00) | 46.45 | (0.00) | |
| D3C | 35.06 | (0.00) | 32.52 | (0.00) | 37.68 | (0.00) | 36.45 | (0.00) | |
| PPDP+D3C | 47.19 | - | 48.68 | - | 49.97 | - | 53.02 | - | |
4.4 Experiment results
The experiment results are listed in Tables 5, 6, 7 and 8 for the 16 scenarios (r = {5,10,15,20} and N = {60,80,100,150}). For instance, with (r,N) = (5,60) in the WDBC data set, the PPDP+D3C achieved a better classification performance than the D3C method; the differences of the G-mean and F1 are 87.98–85.85 = 2.13(%) and 86.63–84.05 = 2.58(%) with a group of class sizes (M,m) = (57,3), respectively, and the P-values based on the G-mean and F1 are smaller than 0.05. From Tables 5, 6, 7 and 8, the comparative results of above-mentioned methods are as follows:
For a fixed N and r, the OSS, SB, NDO, PPDP methods have very close ACC values, and there are no statistically significant differences between the other five methods and PPDP+D3C.
For a fixed N, when r is increasing, the values of G-mean and F1 increase for all six methods, and the improvement in ACC is not significant.
For a fixed N, when r has become large, the PPDP+D3C consistently achieves better G-mean and F1 scores than the other five methods do, although this superiority is not statistically significant with regard to D3C in a few scenarios.
For a fixed r, when N is increasing, the PPDP+D3C consistently achieves higher G-mean and F1 scores than D3C does in the most scenarios.
For a small r and N, the results of the paired t-tests between PPDP+D3C and D3C are significant with regard to G-mean and F1 in the some scenarios.
As shown in Tables 5, 6, 7 and 8, we can see in the WDBC dataset the performance of PPDP+D3C in ACC, G-mean and F1 is better compared to the other methods. In other data sets, the D3C can achieve better performance concerning ACC, but less statistically significant differences. While the PPDP+D3C method achieves excellent performance concerning G-mean and F1 compared to the other methods and most of which have statistically significant differences. These results show that the PPDP+D3C method achieves higher classification performance on imbalanced data sets among the other five tested methods. In other words, the results show that the proposed method can effectively achieve better classification performance with small values of r and N. Thus, it is obvious that when a data set includes imbalanced classes, the classification performance can be significantly improved by using the PPDP+D3C method. In addition, for a fixed N, when r is increasing, the number of generated synthetic samples M'−m becomes smaller, as shown in Table 9.
Table 9. The number of Sbox, Smtd, M'−m, and M'+m' with N = 60.
| Dataset | N = 60 | Dataset | N = 60 | ||||||
| WDBC | PD | ||||||||
| r | 5 | 10 | 15 | 20 | r | 5 | 10 | 15 | 20 |
| Sbox | 13 | 13 | 12 | 12 | Sbox | 10 | 10 | 9 | 9 |
| Smtd | 14 | 13 | 12 | 12 | Smtd | 12 | 11 | 10 | 10 |
| M'−m | 40 | 37 | 32 | 28 | M'−m | 42 | 39 | 34 | 30 |
| M'+m' | 86 | 84 | 80 | 76 | M'+m' | 90 | 88 | 84 | 80 |
| Dataset | N = 60 | Dataset | N = 60 | ||||||
| VC | HS | ||||||||
| r | 5 | 10 | 15 | 20 | r | 5 | 10 | 15 | 20 |
| Sbox | 3 | 3 | 3 | 3 | Sbox | 6 | 6 | 6 | 6 |
| Smtd | 18 | 18 | 16 | 14 | Smtd | 27 | 26 | 24 | 23 |
| M'−m | 36 | 32 | 28 | 26 | M'−m | 27 | 24 | 20 | 17 |
| M'+m' | 78 | 74 | 72 | 72 | M'+m' | 60 | 58 | 56 | 54 |
4.5 Summary and discussion
Four data sets, the WDBC, PD, VC, and HS, were used in this research to show the performance of the PPDP+D3C method with regard to learning with imbalanced data sets. Based on the results of experiments, as shown in Tables 5, 6, 7 and 8, the findings can be summarized as follows. The merging of the PPDP+D3C achieves better classification performance than the other five methods, and this superiority is statistically significant. In a few scenarios, when the value of r is 15 or 20 with a larger N, the PPDP+D3C has better G-mean and F1 scores than those of the D3C method, although some comparisons of the results of the paired t-test between the PPDP+D3C and the D3C showed no significant differences with regard to the G-mean and F1 scores. This may be because the ratio of minority data to the overall samples is rather large, and the amount of data in the minority part is thus sufficient for learning to occur based on the minority class. For instance, in the VC data set, the P-value of the paired t-test for F1 is 0.08, which is greater than 0.05 at (r,N) = (20,150). In fact, the results in Tables 5, 6, 7 and 8 show that when the value of r(%)×N is smaller, the PPDP+D3C method improves significantly in classification performance with regard to the G-mean and F1 measures.
5. Conclusion
Imbalanced data classification problems are common in the field of data mining, often leading to low classification performances because the existing learning algorithms are more suitable for the majority class data. In this work, we combined undersampling and oversampling to balance the training data sets; the undersampling method uses the box-and-whisker plot and the MTD method to reduce the size of the majority class data, while the oversampling method extends the minority class data set by adding generated synthetic samples. Experiments were carried out based on four imbalanced data sets. In particular, imbalanced data of a certain disease may differ based on different region, era, and medical environment. It leads to the phenomenon of diverse distribution concerning the certain disease. When the distributed condition of imbalanced data is not severe, a good diagnostic model could be obtained using a general analysis method. Otherwise, the proposed method in this study can assist to obtain a more correct diagnostic model. The results showed that our approach achieves a better classification performance than the other methods. Thus our approach can be considered an effective way to enhance the analytical performance for learning imbalanced class distributions. Our plans for future research include exploring how to find better density functions to generate useful synthetic samples to enhance classification performance for specific applications.
Data Availability
The raw data necessary to replicate this study can be downloaded from the UCI Machine Learning Repository database. We used the following data sets: WDBC (available at: https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29); PD (available at: https://archive.ics.uci.edu/ml/datasets/parkinsons); VC (available at: http://archive.ics.uci.edu/ml/datasets/vertebral+column); and HS (available at: https://archive.ics.uci.edu/ml/datasets/Haberman's+Survival).
Funding Statement
The work was supported by MOST 104-2221-E-006-105, https://www.most.gov.tw/. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Murphey YL, Guo H, Feldkamp LA. Neural learning from unbalanced data. Applied Intelligence. 2004;21(2):117–28. [Google Scholar]
- 2.Cohen G, Hilario M, Sax H, Hugonnet S, Geissbuhler A. Learning from imbalanced data in surveillance of nosocomial infection. Artif Intell Med. 2006;37(1):7–18. doi: 10.1016/j.artmed.2005.03.002 . [DOI] [PubMed] [Google Scholar]
- 3.Sun Y, Kamel MS, Wong AKC, Wang Y. Cost-sensitive boosting for classification of imbalanced data. Pattern Recognition. 2007;40(12):3358–78. doi: 10.1016/j.patcog.2007.04.009 [Google Scholar]
- 4.Sun Y, Wong AK, Kamel MS. Classification of imbalanced data: A review. International Journal of Pattern Recognition and Artificial Intelligence. 2009;23(04):687–719. [Google Scholar]
- 5.Li DC, Liu CW, Hu SC. A learning method for the class imbalance problem with medical data sets. Comput Biol Med. 2010;40(5):509–18. doi: 10.1016/j.compbiomed.2010.03.005 . [DOI] [PubMed] [Google Scholar]
- 6.Li DC, Liu CW, Hu SC. A fuzzy-based data transformation for feature extraction to increase classification performance with small medical data sets. Artif Intell Med. 2011;52(1):45–52. doi: 10.1016/j.artmed.2011.02.001 . [DOI] [PubMed] [Google Scholar]
- 7.Song L, Li D, Zeng X, Wu Y, Guo L, Zou Q. nDNA-prot: identification of DNA-binding proteins based on unbalanced classification. BMC bioinformatics. 2014;15(1):298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang CY, Hu LL, Guo MZ, Liu XY, Zou Q. imDC: an ensemble learning method for imbalanced classification with miRNA data. Genet Mol Res. 2015;14(1):123–33. doi: 10.4238/2015.January.15.15 . [DOI] [PubMed] [Google Scholar]
- 9.Zou Q, Xie S, Lin Z, Wu M, Ju Y. Finding the Best Classification Threshold in Imbalanced Classification. Big Data Research. 2016;5:2–8. doi: 10.1016/j.bdr.2015.12.001 [Google Scholar]
- 10.Zhao Z-Q. A novel modular neural network for imbalanced classification problems. Pattern Recognition Letters. 2009;30(9):783–8. doi: 10.1016/j.patrec.2008.06.002 [Google Scholar]
- 11.Hong X, Chen S, Harris CJ. A kernel-based two-class classifier for imbalanced data sets. IEEE Transactions on neural networks. 2007;18(1):28–41. doi: 10.1109/TNN.2006.882812 [DOI] [PubMed] [Google Scholar]
- 12.Peng X, King I. Robust BMPM training based on second-order cone programming and its application in medical diagnosis. Neural Netw. 2008;21(2–3):450–7. doi: 10.1016/j.neunet.2007.12.051 . [DOI] [PubMed] [Google Scholar]
- 13.Nguwi Y-Y, Cho S-Y, editors. Support vector self-organizing learning for imbalanced medical data. Neural Networks, 2009 IJCNN 2009 International Joint Conference on; 2009: IEEE.
- 14.Lo H-Y, Chang C-M, Chiang T-H, Hsiao C-Y, Huang A, Kuo T-T, et al. Learning to improve area-under-FROC for imbalanced medical data classification using an ensemble method. ACM SIGKDD Explorations Newsletter. 2008;10(2):43–6. [Google Scholar]
- 15.He H, Garcia EA. Learning from imbalanced data. IEEE Transactions on knowledge and data engineering. 2009;21(9):1263–84. [Google Scholar]
- 16.Mazurowski MA, Habas PA, Zurada JM, Lo JY, Baker JA, Tourassi GD. Training neural network classifiers for medical decision making: the effects of imbalanced datasets on classification performance. Neural Netw. 2008;21(2–3):427–36. doi: 10.1016/j.neunet.2007.12.031 ; PubMed Central PMCID: PMCPMC2346433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Farquad MAH, Bose I. Preprocessing unbalanced data using support vector machine. Decision Support Systems. 2012;53(1):226–33. doi: 10.1016/j.dss.2012.01.016 [Google Scholar]
- 18.Estabrooks A, Jo T, Japkowicz N. A multiple resampling method for learning from imbalanced data sets. Computational intelligence. 2004;20(1):18–36. [Google Scholar]
- 19.Kubat M, Matwin S, editors. Addressing the curse of imbalanced training sets: one-sided selection. ICML; 1997: Nashville, USA. [Google Scholar]
- 20.Yen S-J, Lee Y-S. Under-sampling approaches for improving prediction of the minority class in an imbalanced dataset Intelligent Control and Automation: Springer; 2006. p. 731–40. [Google Scholar]
- 21.Xie J, Qiu Z. The effect of imbalanced data sets on LDA: A theoretical and empirical analysis. Pattern Recognition. 2007;40(2):557–62. doi: 10.1016/j.patcog.2006.01.009 [Google Scholar]
- 22.Tahir MA, Kittler J, Yan F. Inverse random under sampling for class imbalance problem and its application to multi-label classification. Pattern Recognition. 2012;45(10):3738–50. doi: 10.1016/j.patcog.2012.03.014 [Google Scholar]
- 23.Li D-C, Wu C-S, Tsai T-I, Lina Y-S. Using mega-trend-diffusion and artificial samples in small data set learning for early flexible manufacturing system scheduling knowledge. Computers & Operations Research. 2007;34(4):966–82. doi: 10.1016/j.cor.2005.05.019 [Google Scholar]
- 24.Piras L, Giacinto G. Synthetic pattern generation for imbalanced learning in image retrieval. Pattern Recognition Letters. 2012;33(16):2198–205. doi: 10.1016/j.patrec.2012.08.003 [Google Scholar]
- 25.Fernández-Navarro F, Hervás-Martínez C, Antonio Gutiérrez P. A dynamic over-sampling procedure based on sensitivity for multi-class problems. Pattern Recognition. 2011;44(8):1821–33. doi: 10.1016/j.patcog.2011.02.019 [Google Scholar]
- 26.Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. SMOTE: synthetic minority over-sampling technique. Journal of artificial intelligence research. 2002;16:321–57. [Google Scholar]
- 27.Freund Y, Schapire RE, editors. Experiments with a new boosting algorithm. icml; 1996. [Google Scholar]
- 28.Chawla NV, Lazarevic A, Hall LO, Bowyer KW, editors. SMOTEBoost: Improving prediction of the minority class in boosting. European Conference on Principles of Data Mining and Knowledge Discovery; 2003: Springer.
- 29.Zhang H, Wang Z, editors. A normal distribution-based over-sampling approach to imbalanced data classification. International Conference on Advanced Data Mining and Applications; 2011: Springer.
- 30.Li D-C, Lin L-S. Generating information for small data sets with a multi-modal distribution. Decision Support Systems. 2014;66:71–81. doi: 10.1016/j.dss.2014.06.004 [Google Scholar]
- 31.Williamson JM, Kim HY, Manatunga A, Addiss DG. Modeling survival data with informative cluster size. Stat Med. 2008;27(4):543–55. doi: 10.1002/sim.3003 . [DOI] [PubMed] [Google Scholar]
- 32.Wahed AS, Luong TM, Jeong JH. A new generalization of Weibull distribution with application to a breast cancer data set. Stat Med. 2009;28(16):2077–94. doi: 10.1002/sim.3598 ; PubMed Central PMCID: PMCPMC3057135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chen M-C, Chen L-S, Hsu C-C, Zeng W-R. An information granulation based data mining approach for classifying imbalanced data. Information Sciences. 2008;178(16):3214–27. doi: 10.1016/j.ins.2008.03.018 [Google Scholar]
- 34.Lin C, Chen W, Qiu C, Wu Y, Krishnan S, Zou Q. LibD3C: Ensemble classifiers with a clustering and dynamic selection strategy. Neurocomputing. 2014;123:424–35. doi: 10.1016/j.neucom.2013.08.004 [Google Scholar]
- 35.Tukey JW. Exploratory data analysis. 1977. [Google Scholar]
- 36.Little SN. Weibull diameter distributions for mixed stands of western conifers. Canadian Journal of Forest Research. 1983;13(1):85–8. [Google Scholar]
- 37.Nelson W. Applied Life Data Analysis, John Wiley; &. New York: 1982. [Google Scholar]
- 38.Gail M, Gastwirth J. A scale-free goodness-of-fit test for the exponential distribution based on the Gini statistic. Journal of the Royal Statistical Society Series B (Methodological). 1978:350–7. [Google Scholar]
- 39.Asuncion A, Newman DJ. UCI Machine Learning Repository [http://www.ics.uci.edu/~mlearn/MLRepository.html]. Irvine, CA: University of California. School of Information and Computer Science; 2007;12. [Google Scholar]
- 40.Chang C-C, Lin C-J. LIBSVM: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST). 2011;2(3):27. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The raw data necessary to replicate this study can be downloaded from the UCI Machine Learning Repository database. We used the following data sets: WDBC (available at: https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29); PD (available at: https://archive.ics.uci.edu/ml/datasets/parkinsons); VC (available at: http://archive.ics.uci.edu/ml/datasets/vertebral+column); and HS (available at: https://archive.ics.uci.edu/ml/datasets/Haberman's+Survival).