A Review on Medical Image Registration as an Optimization Problem

Abstract

Objective:

In the course of clinical treatment, several medical media are required by a phy-sician in order to provide accurate and complete information about a patient. Medical image registra-tion techniques can provide a richer diagnosis and treatment information to doctors and to provide a comprehensive reference source for the researchers involved in image registration as an optimization problem.

Methods:

The essence of image registration is associating two or more different images spatial asso-ciation, and getting the translation of their spatial relationship. For medical image registration, its pro-cess is not absolute. Its core purpose is finding the conversion relationship between different images.

Result:

The major step of image registration includes the change of geometrical dimensions, and change of the image of the combination, image similarity measure, iterative optimization and interpo-lation process.

Conclusion:

The contribution of this review is sort of related image registration research methods, can provide a brief reference for researchers about image registration.

1. INTRODUCTION

In the course of clinical treatment, several medical media are required by a physician in order to provide accurate and complete information about a patient. For example, a CT scan provides information on the structure of bones, an MRI scan provides information on the structure of tissues such as muscles and blood vessels, while ultrasound images focus on organs, lesions, and luminal structures. With the development of digital image, medical image could transfer into digital information which made the image process deal with the computer. The integration of these imagery information media requires aid from image registration techniques. Such techniques essentially involve the process of correlating images from different temporal and spatial sources in order to ensure spatial consistency between given points in all images, especially matching anatomical points to allow a physician to obtain improved and detailed information. Some scholars have reviewed the registration in [1-5]. At the same time, medical image registration techniques serve as the fundamental basis for procedures such as image-guided radiation therapy, image-guided radiation surgery, and image-guided minimally invasive treatments [6-8]. Apart from the above function, image registration can also be further used in retinal imaging which achieve a comprehensive description of retinal morphology [9]. However, differential imaging principles and modalities, sampling time, and the physical state of a patient are variables that need to be considered when accessing various medical media simultaneously, and are serious issues that need resolution in image registration techniques. Improving the accuracy, time sensitivity, and robustness of image registration are issues that need to be resolved in current investigations. Further, automatic diagnose need to integrate more medical information which have to be registries.

The principle of image registration is the correlation of spatial transformation between the images, which could be converted from a registration issue into a parameter optimization issue in mathematics. From the perspective of parameter iterative optimization of angles it can classify and summarize the existing algorithms used in medical image registration. The organization of this review is as follows: Section 2 describes the issues in image registration, Section 3 introduces cross-modal conversions used in images and interpolation algorithms, Section 4 provides an overview on the geometric transformation of images, Section 5 describes the methods used in detecting similarity between images, Section 6 introduces iterative optimization algorithms, and Section 7 evaluates the results from each of the registration methods.

2. Description of issues in image registration

Image registration is one of the basic tasks of image processing, mainly used in matching different images with different time, different sensors, different perspectives and different shooting conditions. Any medical image registration could be divided into three steps:

1. Determine transformation between the source image and target image;

2. Measure similarity degree of the source image and target image;

3. Adopt some optimization methods, make the similarity measure degree better and faster to reach the optimal value.

Combining the above part and the digital image technology, image registration problem can transform into optimization problem.

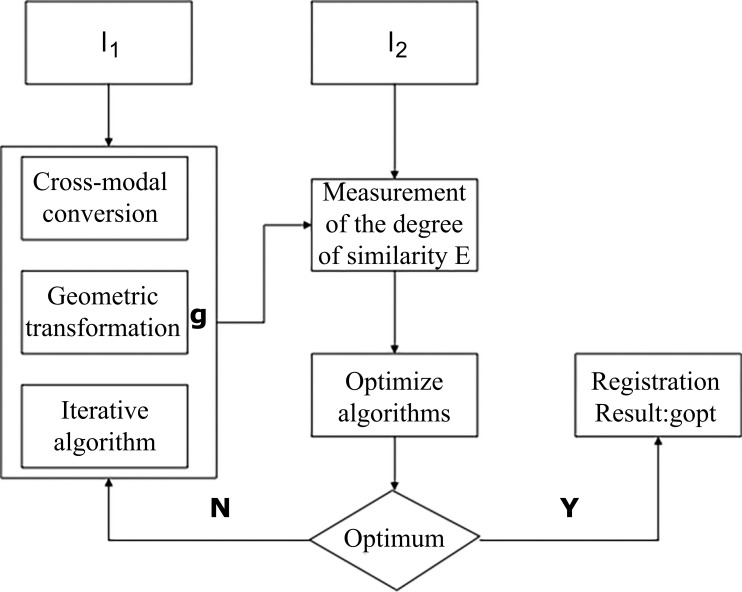
The aim of image registration is to search for the transformation correlation operator g between two images I₁ and I₂, which are used as examples for the registration process, and obtain the optimized measurement of similarity or function E, which ultimately serves to obtain the optimized transformation g_opt, represented as:

g_opt: I₁ → I₂= optimum (E(I₁ – g (I₂))) (1)

The current conventional registration process can be separated into several main steps: (1) cross-modal conversion, (2) geometric transformation, (3) measurement of the degree of similarity, and (4) iterative optimization search, as illustrated in Fig. (1). First, image I₂ undergoes cross-modal conversion and a geometric transformation process to arrive at g’ (I₂). Post transformation, the pixelated position of g’(I₂) may not be a whole integer in pixel position; therefore, interpolation is required in order to assess the pixel. If the interpolation is necessary, the interpolation of g’(I₂) will equate the value of g(I₂); otherwise, g’(I₂) will directly be equivalent to g(I₂). Then, g (I₂) and I₁ are measured for similarity in order to obtain the measurement indicator, or the function E. The goal of image registration is to optimize algorithms derived from the complexity of similarity measurements through the measurement of the similarity indicator or the function E in order to simplify similarity detection in images. Therefore, the efficiency of registration is enhanced using the algorithm. When the similarity indicator (function E) reaches the most optimum state, the optimal transformation correlation g_opt will be obtained. Thus, image registration becomes a problem in parameter optimization in the transform operator g.

Fig. (1).

Process of image registration.

In each specific case of image registration, not all the aforementioned steps are absolutely required. Appropriate adjustments can be made to the methods based on the specific application. For example, a cross-modal conversion process would not be necessary if the images to be registered have the same modality. Similarly, if registration employs manual identification, the similarity detection step can be omitted.

At present, another difficulty encountered in image registration is the assessment of algorithms. The assessment is performed for determining the performance level and the application scope for a given registration method. In addition, the assessment of results from a registration illustrates its potential in clinical applications and scope for improvement.

3. Cross-modal conversion and interpolative algorithms

As a unique case of parameter optimization, image registration can primarily be characterized by its input variable, which is image data. Medical images can have multiple modalities because of the differences in imaging principles and instruments, ultimately resulting in the complexity of the input variable. The cross-modal conversion of images with different modalities into the same modality reduces registration complexity.

Medical imaging provides information on several modalities for clinical diagnosis, including CT images, MRI images, X-ray images, and ultrasound images. For the registration of images with different modalities, it is often required to convert them into images having the same modality. The principle involved in this process is manipulating the physical principles used in producing the images, such that images with different modalities can be converted to images with a single modality. The physical basis of medical image registration is that images with different modalities describe the anatomical structures of the body.

Minimally invasive interventions or surgeries usually rely on fluoroscopic and ultrasound images. As fluoroscopic images consist of projections only, it poses difficulties for a physician to accurately position the three-dimensional coordinates of anatomical structures. Therefore, the conversion of CT and MRI images into X-ray images, or vice versa, has important significance in image-guided minimally invasive surgeries.

Presently, maximum intensity projection are the main methods of generating X-ray images from CT or MRI images [10, 11]. However, these methods have two shortcomings. First, MRI images cannot be used to simulate and generate X-ray images, and second, a partial loss of information occurs when a highly precise CT image is generated into an X-ray image. Based on these shortcomings, some researchers have made improvements in ray-casting and maximum intensity projection methods to achieve more realistic projections [12, 13]. Alternatively, X-ray images can be converted into CT or MRI images by using reverse algorithms [14, 15].

Furthermore, another common conversion of image modality is the conversion of CT or MRI images into ultrasound images. Roche used the magnetic resonance intensity and grayscale information in MRI images to predict the grayscale of ultrasound images, but omitted some of the noisy situations such as signal attenuation and spotting [16]. Similarly, Wein used a physical model of ultrasound image production to convert CT images into ultrasound images in order to realize the registration of CT–ultrasound images [17].

Another means of solving the cross-modal image registration problem is to convert all images into the same modality, ultimately simplifying the question. There are two methods of performing this conversion. The first method involves converting an image into an existing modality, as described in the present article. The second method involves converting all modalities into a modality that is different from all images to be registered. For example, Michel and Paragios used an expertise hybrid model to learn about the conditional probabilities of objectives to achieve cross-modal conversion of images [18]. Although the modalities of images to be registered vary, all images possess the same anatomical structure. Therefore, the isolation of such structures can be extracted into single-modal images, following which single-modal image registration can be used to complete the cross-modal conversion [19, 20].

After cross-modal conversion and spatial transformation, the position of a specified pixel may not lie on an integer pixel in the resulting image, or in other words, at a non-grid position. Therefore, it is necessary to assess the grayscale of the resulting image at the new projected position. The goal of the interpolation process is to regenerate an image at the new projected position, and the process of interpolation can increase the accuracy and speed of image registration.

The most frequently used techniques in interpolation include nearest-neighbor interpolation, linear interpolation, polynomial interpolation, and the Hanning window Sinc function. The simplest method in this list is the nearest-neighbor interpolation technique, which selects the grayscale of the nearest similar pixel as the grayscale of the sampling point. Linear interpolation is relatively simple as well: it obtains the grayscale information of a neighboring pixel or voxel in the spatial orientation of the pixel, and conducts an interpolation in every direction to enhance the precision of the overall interpolation. However, in situations of drastic changes in grayscale, linear interpolation will result in the blurring of edges, which affects the accuracy of interpolation. Therefore, Lagrange or Gaussian interpolation and Fourier or Wavelet transformation should be used in case non-smooth or non-robust grayscale exists in images [21].

4. Geometric transformation

Geometric transformation in image registration corresponds to parameter to be optimized g in parameter optimization. Based on the presence or absence of uncertainty in the parameter, the geometric transformation of an image can be categorized into two main types: linear transformation and non-linear transformation. Choosing the correct type of parameter can enhance the efficiency and accuracy of registration.

4.1. Linear Transformation

Linear transformation is performed through the calculation of translational and rotational vectors, which is mainly used in situations where the internal structure of an image does not show obvious distortion or deformation, for the registration of bone structures and tissues [22]. The main disadvantage of linear transformation is the lack of solution to local or soft tissue deformation. Linear transformations of an image primarily include rigid transformation, affine transformation, and projective transformation. Linear transformations are rotational, translational, and scaling under the insurance that structures remain unchanged and the integrity and consistency of the structure is maintained. The time sensitivity of linear transformation is relatively high.

4.2. Non-linear Transformation

With regard to tissues or structures in the human body, deformation of soft tissue can lead to local deformations that will further affect the accuracy of linear transformation. In contrast to linear transformation, the greatest advantage of non-linear transformation is that it has the capacity for registering local deformations, thus achieving more accurate registration. Non-linear image registration can be further categorized into two subtypes based on the physical basis of registration: registration based on a physical model, and registration based on basis functions.

4.2.1. Non-linear Registration Based on Physical Model

Non-linear transformations can be based on physical models, such as linear elasticity, fluid flow, and optical flow, and statistical models that are based on medical information. Linear elasticity transformation is predominantly based on stress and strain theory, in which a contact force is applied to a given position in an orthogonal plane, and stress is used to confirm deformation in the image [23]. Deformation can be determined by means of solid elasticity [24] (Solid elasticity views an object as a deformable body, and deformations are introduced by the application of an external force.), and finite element method [25] (Finite element method divides the image into several regions, each of which is assigned an organizational property.) A necessary presumption for elastic deformation is that the changes in the image to be registered should occur only in a small range. Thus, it is clearly inapplicable to tissues or organs, which are subjected to large deformations. Christensen et al. proposed a fluid flow model for image registration [26]. The basic idea in the fluid flow model is to view an image as a fluid with a continuous motion toward the other image, and by detecting the similarity between the two images, convert the process of image registration into a motion problem [27]. Optical flow registration algorithm, which is based on the principle of strength conservation in an image, is another algorithm that is similar to fluid flow [28]. Its main application lies in tracking objects with small-scale movement in temporally different images [29, 30]. Furthermore, if an image is transformed from a grayscale image to a gradient image, this method can be used in the registration of images with different modalities. Although each individual has different tissues, most of the tissues are in line with a statistics model. Therefore, some researchers have proposed non-linear methods of image registration based on the statistics model; these methods are based either on the distribution model [31] or the portfolio theory [32].

Elastic models are used in cases with small deformations, but are not applicable in medical image registration mainly because soft tissues undergo large deformations. Fluid flow or optical flow not only solves this problem of large deformations, but also preserves the topological structures of tissue to the maximum extent. However, fluid flow registration does not define the organizational components of soft tissues, i.e., in certain situations, it is not realistic to register the deformation in soft tissue. In practicality, tissue deformation is a very complex physical behavior, and soft tissues can be assumed as an elastic or viscoelastic material only under specific conditions, as soft tissues generally exhibit anisotropy. Therefore, a model that can include the biomechanics of soft tissues more precisely is required.

4.2.2. Image Registration Using Basis Functions

In contrast to physical models, image registration based on basis functions does not draw support from physical models, but rather registers the deformed regions by setting coefficients to the basis functions. Its mathematical structure relies on the function differential theory [33] or the approximation theory [34]. Basis functions used in image registration mainly include radius basis function, thin-plate splines (TPS), and B-splines.

(1) Radius basis function

Radius basis function is defined as the distance function between the interpolation point and the central or identification point of the basis function [35]. Registration using radius basis function works by setting the function approximate as 0. Examples of radius basis functions are the Gaussian method or multivariate quadratic radius basis function. Medical image registration mainly utilizes the radius basis function based on the identification point in medical images [36].

(2) Thin-plate splines

TPS uses the movement of a series of control points toward a specified direction, and performs an adequate amount of similarity detection [37, 38]. TPS can be applied to interpolation in multiple modalities, and has an inherent smooth property. It often makes use of homologous features, anatomical identifications, and other characteristics of an image that can be manually registered. TPS is a global registration method; however, it cannot describe local deformations with high accuracy.

(3) B-splines

B-splines were proposed by Schoenberg in 1946 [39], and it has been widely used in several areas since then. Similar to TPS, B-splines also optimize the projective correlation between images by solving a series of parameters [40]. The B-splines used in medical image registration mainly consist of linear interpolation B-splines, convex nuclear B-splines, and cubic B-splines, which are the most commonly used B-splines [41]. B-splines also used for registration to analyze the plantar pressure image sequences and attain geometric transformation models, so that enhance methodology [42].

As image registration using basis functions does not depend on physical modals, but rather on building a model from interpolation or approximation, the registration process is not affected by changes in physical or biological aspects. Most basic functions are compactly supported, and thus, can accurately describe local deformations and reduce the complexities in calculation and time used in optimization. Identification points are used in registration conducted using radius basis function, which makes the method applicable for registering images of different modalities, and an analytical solution is achieved. B-splines and TPS have similar algorithms, both of which do not measure vectors by using distance, but rather by using a multimodal basis function consisting of a single variable linear combination.

5. Methods in measuring similarity

The similarity measurement indicator E is required during parameter optimization in order to determine whether the optimal parameters are achieved. The methods of measuring similarity in image registration are mostly used to determine if the registration process was optimal. Based on the differences in the feature details of an image, the common methods of similarity measurement include features-based or grayscale-based method.

5.1. Features-based Measurement of Similarity

The extraction of features can drastically reduce the amount of information in a given image, and this increases the speed of similarity detection. There are some examples as global-to-local matching [43], hierarchical model refinement [44], and dual-bootstrap [45]. Based on the nature of selected features, the method can be further specified into two subtypes: registration based on artificial identification and registration based on anatomical identification.

5.1.1. Artificial Identification Points

Artificial identification points are identifications that are artificially implanted on patients, which can be seen and used as features during the sampling process of images. These identifications can be a three-dimensional framework [46], implanted bone structures [47], soft tissues [48], or identified parts of skin adherents [49]. These identification points are usually spherical in order to facilitate the recognition of images. With the exception of the relatively stable positions of the artificial identification points implanted on bones, those implanted on the skin or soft tissues usually undergo movement or translation because of deformations in the structure of soft tissue, thus resulting in deviations in positioning. In spite of this disadvantage, the registration process based on artificial identification points is still being used on tissues that do have the structural organization of bones, such as the liver, the lungs, the prostate, and the pancreas [49].

Measurement of similarity by artificial identification points can be completed using specially designed identification points. Therefore, this method can be very easily performed, requiring only a simple optimization using the least squares method, making the process rapid as well. Thus, the key to measuring similarity by using artificial identification is the rapid and precise recognition of the marker. However, at present, there are two issues with this method. First, error in registration is smaller when identification points are closer to the target region and vice versa [50]. Thus, in special cases where identification points cannot be placed at ideal positions, the accuracy of registration is reduced. Second, this method requires the implantation and stabilization of identification points before image sampling, which needs additional surgical procedures on the patient.

5.1.2. Anatomical Identifications

Anatomical identifications are identifications that are shown in image obviously, which can be seen and used as features during the sampling process of images. The method of measuring similarity based on anatomical identification calculates the “distance” between the same set of anatomical identification in the two images, and uses these “distances” to determine the degree of similarity. Here, “distances” are usually Euclidean distances, or other distances, such as the Mahalanobis distance, or a link that relates the identifications to transformational means. The anatomical identifications can be further classified into feature points, feature curvatures, and feature surfaces or contours.

Based on different anatomical identifications, image registration methods based on anatomical identification to measure similarity can be classified into similarity between feature point / feature point, feature curvature / feature curvature, and feature surface / feature surface.

The method of similarity measurement of feature point / feature point first recognizes the clear anatomical structures in an image, and then positions the corresponding feature points though linear or non-linear geometric transformations to correlate the images, similar to some of the results published previously [6, 51]. The similarity measurement of feature point/ feature point mainly consists of two steps: recognition of feature points and registration of feature points. In contrast to conventional images, the information obtained is not abundant in medical images [52], and the internal similarities of an image can lead to a lack of clarity in feature points. Thus, feature points should have obvious features that are not easily mistaken for. The Harris detection algorithm uses the detection of corners to achieve the detection of features in different images [53]. The application of the Harris detection algorithm in medical imaging reduces uncertainty [54] and realizes linear or non-linear transformation. The focus of studies on feature points is the analysis of scalar spaces.

For each point, it was represented by a descriptor. The “corresponding costs” are the “distance” between descriptor [55-57]. The translation between images is decided by minimum cost between descriptor.

The scale invariant feature transform (SIFT) algorithm proposed by Lowe [58] has been widely used in medical image registration [59, 60]. Han used an improved SIFT operator, the SURF operator [61], to conduct the registration in lung CT [62]. Although this algorithm is widely used in the extraction of feature points in medical images, the diverse and complex nature of medical imaging dictates that the algorithm is not applicable for all types of images. Some researchers have established specific ways of feature point recognition for the images of specific organs [63].

For most point-based registration methods, the feature point is independent, in [64], the positional relation is considered which feature point is defined as a node to enhance the accuracy of registration.

Measurement of similarity from feature curvatures / feature curvature [65, 66] or feature surface / feature surface [67] is achieved by searching the image for characteristic curves or surfaces, and then determining the similarity by using these features. In comparison to the measurement method using feature point/feature point, these two methods have the advantage of easy extraction. Feature-based similarity measurements require the feature to possess robustness; therefore, an incorrect selection of feature will lead to an outlier. Such outliers can lead to catastrophic consequences in image registration because of the high registration accuracy required for medical images. The establishment of a correct correlation value for registration and detection as well as the elimination of outliers is another problem in feature-based similarity measurement that needs to be resolved.

The most important step in methods used for detecting similarities between images is the automatic division and recognition of identification features, and the correlation or registration of these features in various images. Some researchers have proposed methods to reduce the error rate in recognizing features [68, 69]. The most direct method in correlating features is to take advantage of the feature descriptor, through a strategic selection of features that satisfy certain requirements. The simplest requirement is a similarity threshold; the surpassing of the threshold reflects the success in feature registration. Another strategy is to measure the Euclidean distance of candidate features, which are observed around each identifiable feature, and select features by using that Euclidean distance as a feature descriptor. However, as this method allows the inclusion of Pseudo-features, researchers proposed another registration method based on Euclidean distance and feature similarities [70], which selects the best and second-best points by using Euclidean distances and then calculates the feature similarities based on those points.

The ICP algorithm proposed by Besl and McKay is a common alternative to optimize the selection of identification feature points, which is rather rapid. This method reiterates the process of “confirm corresponding points–calculate optimal transformation” until a certain convergence criterion is met. The registration of medical images based on the ICP algorithm is applicable to the image registration of organs with different modalities [71, 72].

Some other methods of state estimation, for example, extended Kalman filters, such as colorless Kalman filters, can also be used to reduce the impact from pseudo-features [73]. The limitations of feature structures can also be used in the correlation of features through the correlation of unique shapes, but this method is applied infrequently in medical image registration because of the uncertainties present in medical images.

5.2. Intensity Registration

As usual, intensity registration is appropriate for the status when the number of feature is insufficient [74]. Intensity similarity measurement strategies are often designed based on the correlation of grayscales. In contrast to anatomical structure-based image registration, this method does not utilize the distance between features, but instead utilizes the pixel information from different images. This requires a strategy that can obtain grayscale information from images generated using different physical principles. Meanwhile, the use of a similarity function can reduce the impact of image generation from various physical principles and achieve the ideal registration outcomes.

5.2.1. Mutual Information

The method based on mutual information basically detects the degree of mutual information of two images. Its advantage is that no presumptions need to be made, which results in its popularity in the registration of medical images [22, 75-79]. In 1997, Viola and Wells described the application of mutual information for registration between magnetic resonance and real scene with gradient descent optimization [80]. The major difference between algorithms of mutual information is the method by which entropy is estimated. Shannon entropy is used in standard mutual information algorithms. The normalization of mutual information can be understood as a change in the algorithm of mutual information in Shannon entropy, which resolves the registration of images with small regions of overlap [76]. Another method to measure similarity by using mutual information is the differential detection method based on joint distribution, which obtains the distribution of joint strength from the order of the images or the separation of corresponding anatomical structures [22]. Other entropies, such as Renyi entropy [77], Tsallis entropy [78], and Havrda-Charvat entropy, [79] have also been used in medical image registration. Standard mutual information algorithms and its derivative algorithms are global statistical methods with low local accuracy. Thus, some researchers have focused on enhancing the accuracy of locally deformed images in registration methods based on mutual information. Studholme [81] suggested a method of regional mutual information, which calculates weighted linear regions to decrease errors induced by regional changes in grayscale. Sundar [82] proposed an Octree method that adaptively covers an image to enhance robustness in cases of regional changes in grayscale. Bardera [83] suggested an NMI method based on the elements of an image to convert multi-modal mutual information into unimodal mutual information. Woo [84] also suggested a similar method. All the aforementioned algorithms require the calculation of mutual information from regional pixels. However, there is a method that uses the extraction and analysis of local information to describe the characteristics of the region [85].

Mutual information is a commonly used method in clinical settings, as it does not require the pre-treatment of images. Moreover, the initialization or adjustment of the parameters is not required in this method. However, its non-generic nature is a disadvantage. During the registration of images with different modalities, if images are not converted for their modalities, both the accuracy and speed will be lower in the registration process. In addition, the adaptiveness to local changes is relatively low when mutual information is used for registration. Likar and Pernus researched on the performance of different algorithms for the joint probability estimation of registration on muscle fibre images [86].

5.2.2. Statistics Method

The similarity measurement can directly use the intensity as statistics information to complete image registration. Examples of this method include the sum of squared differences [87] or cross-correlation [88]. In [89], the authors determined the vector displacement by local cross-correlation to ensure the translation between images. However, this presumption is not robust. To address this, Myronenko proposed a method of residual complexity to increase the robustness for determining the similarity of unimodal images [90].

5.2.3. Joint Registration

For intensity registration, there are some problems, such as mutual information was not suitable for small images. Thus some authors have use two or more methods to finish registration.

In [91] the authors used the mutual information for global registration and further the cross-correlation to register the small image patches. In [92], a two-stage strategy was used on retinal images. First coarse stage used cross-correlation method, and second stage, parabolic interpolation on the peak of the cross-correlation or maximum-likelihood estimation were used for sharp information. Moreover, some methods combine feature-based registration and intensity-based registration [93].

6. Iterative optimization algorithms

Iterative optimization algorithms utilize the results from similarity detection in order to select the optimal search strategy and obtain the optimal transform operator g. The optimization value of E reflects the registration outcome at the point where the similarity measurement function E is optimum. An iterative optimization algorithm aims at reducing the search time in optimization in order to increase the time sensitivity of the algorithm.

Optimization algorithms can be separated into two categories depending on the nature of the variable: continuous variables and discrete variables. The former optimizes function E through true values, while the latter extracts discrete variables from a discrete set.

6.1. Continuous Variables

Optimization method based on continuous variables essentially solves the differential in an objective function, with its parameters defined in several ways. For example, if the length of each step is constant, each iteration aims toward minimizing the direction of search. The direction of search usually takes advantage of first-order or second-order specific information. Based on the differences in search methods, the commonly used methods in the optimization of continuous variables include (1) gradient descent method (GD), (2) conjugate gradient method (CG), (3) Powell optimization method, (4) Quasi-Newton method (QN), (5) Levenberg-Marquardt method (LM), and (6) stochastic gradient descent method.

The objective optimization function of the GD method moves in a direction that reduces the difference, or the direction, of its negative gradient, and has been used in solving a series of issues in registration. The consistent image registration algorithm proposed by Johnson and Christensen [94] and the FFD registration algorithm proposed by Rueckert [95] are both GD methods of optimization.

The conjugate gradient method has a faster convergence time compared to GD. Compared to the convergence search strategy of GD, CG uses prior knowledge from gradient descent to advance in the conjugate direction of search [96].

The Powell optimization method aims at reducing objective functions in the conjugate direction. Its difference from CG lies in that it does not make use of gradients in the image [95]. Also, Powell’s method has used as the optimization algorithm with a three level multi-resolution strategy to assist in the diagnosis of Parkinson's disease by SPECT brain images [97]. Therefore, the Powell method is a non-gradient optimization search method, and is applied in image registrations with less degrees of freedom. A pitfall of the Powell method is that its direction of search is often linear, and thus is not applicable to image registration searches with higher degrees of freedom.

The Quasi-Newton method has a convergence rate that is higher than that of GD. In addition, compared to the CG method, the QN method uses second-order information to speed up its convergence. Other factors contributing to the quick convergence in QN are its accumulation and the use of iterative information [78, 98].

The Levenberg-Marquardt is a method that determines the minimum or maximum value in a linear function by using the gradient to solve the optimal state. It combines the advantages of the GD and QN methods [99].

The aforementioned techniques include gradient convergence as a common optimization method in image registration. Medical image registration requires an abundance of derivative images for improving the data and multi-dimensionality of search space. In order to reduce the burden of calculations, researchers have proposed to use the method of stochastic gradient descent [100].

6.2. Discrete Variables

Compared to optimization methods based on continuous variables, discrete optimization of variables is restricted to discrete values. In image registration applications, discrete variable optimization essentially uses the Markov random field to conduct the optimization. Therefore, discrete optimization is fundamentally utilized to determine the lowest cost curve in a transformed image, where proper restrictions are placed on the respective coordinates and the connections in between a transformed grid. Discrete variable optimization has the advantage of high calculation efficiency, and is currently used in medical image registration [101]. Also, the point based registration could optimize transformation between images through the well-known Procrustes method which is similar least squares method [102].

7. Assessment of the registration outcomes

The measurement of similarity during the optimization of image registration can be viewed as a rough approximation or an initial assessment of the registration outcomes. However, not all registration methods possess clear physical or geometrical identifiers.

At present, several means exist that can be employed to assess each image registration method utilized in the research of medical image registration. An example is determining the smoothness coefficient in gradient optimization methods, or consistent reversal in order to check if the registration of image A to image B yields identical results as the registration of image B to image A. An evaluation method based on pixelated grayscale difference between pre- and post-registration images is used to assess the registration of unimodal images. The most commonly used method involves determining the means square error (MSE) between images in order to ultimately calculate the peak signal noise ratio (PSNR) for evaluating the quality of image registration. For affine and non-linear transformations, MSE and PSNR do not have global consistency, and thus, a more direct measurement of registration quality is performed by estimating the registration error using redundant information in registered regions after transformation steps [103].

Furthermore, identification points can also be used for assessing the outcomes of medical image registration. The target registration error (TRE) can be calculated using corresponding identification points in the image [104]. However, because deviations in the position of identification points can lead to reduction in registration accuracy, an assessment method based on morphology has been proposed. Some studies have further improved the assessment method based on identification points and morphology of image registration [21].

A standard assessment method should be defined in medical image registration in order to facilitate the comparison of the advantages and disadvantages of different algorithms.

CONCLUSION

Image registration has been widely studied and has formed a relatively isolated system in its own. Currently, a key target for research in medical image registration is the improvement and application of this technique for clinical use.

This article discussed the conventional methods in image registration from the aspects of cross-modal conversion and geometric transformation of an image, measurement of similarity, iteration and optimization, in addition to other areas.

In the field of medical image analysis, image registration remains one of the most studied areas. However, several problems remain to be resolved in this area. One such problem is that medical images are mostly grayscale images, which mandates higher requirements in parameter optimization and adjustments. Other problem is that how to promote the accuracy and speed of registration. Also, the robust is one of the problem which impedes the development of registration. Further investigation in this area should focus on effectively using the limited information to conduct high-accuracy registration, while reducing the registration and calculation time to increase the time sensitivity of registrations.

The concluding lines of the article may be presented in a short section of conclusion.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.