Reparameterization of Protein Force Field Nonbonded Interactions Guided by Osmotic Coefficient Measurements from Molecular Dynamics Simulations

Abstract

There is a small, but growing, body of literature describing the use of osmotic coefficient measurements to validate and reparameterize simulation force fields. Here we have investigated the ability of five very commonly used force field and water model combinations to reproduce the osmotic coefficients of seven neutral amino acids and five small molecules. The force fields tested include AMBER ff99SB-ILDN, CHARMM36, GROMOS54a7, and OPLS-AA, with the first of these tested in conjunction with the TIP3P and TIP4P-Ew water models. In general, for both the amino acids and the small molecules, the tested force fields produce computed osmotic coefficients that are lower than experiment; this is indicative of excessively favorable solute-solute interactions. The sole exception to this general trend is provided by GROMOS54a7 when applied to amino acids: in this case, the computed osmotic coefficients are consistently too high. Importantly, we show that all of the force fields tested can be made to accurately reproduce the experimental osmotic coefficients of the amino acids when minor modifications – some previously reported by others and some that are new to this study – are made to the van der Waals interactions of the charged terminal groups. Special care is required, however, when simulating Proline with a number of the force fields, and a hydroxyl-group specific modification is required in order to correct Serine and Threonine when simulated with AMBER ff99SB-ILDN. Interestingly, an alternative parameterization of the van der Waals interactions in the latter force field, proposed by the Nerenberg and Head-Gordon groups, is shown to immediately produce osmotic coefficients that are in excellent agreement with experiment. Overall, this study reinforces the idea that osmotic coefficient measurements can be used to identify general shortcomings in commonly used force fields’ descriptions of solute-solute interactions, and further demonstrates that modifications to van der Waals parameters provides a simple route to optimizing agreement with experiment.

Introduction

There is currently considerable interest in identifying ways to properly validate, and improve if necessary, the force fields that are widely used in molecular dynamics (MD) simulations of biological macromolecules. The osmotic coefficient, ϕ, is an experimental metric that provides information on the combined effect of solute-solute, solute-solvent and solvent-solvent interactions in a system. ϕ relates the osmotic pressure of an aqueous solution to that of a corresponding solution that contains instead ideal (i.e. non-interacting) solute molecules. It thus provides a reasonably direct measure of the extent to which solute-solute interactions are net attractive (ϕ<1) or repulsive (ϕ>1) in aqueous solution.^1–2 Importantly, there is a considerable amount of experimental osmotic coefficient data available in the literature, which provide, in principle, a means of parameterizing the strengths of solute-solute interactions for a wide range of molecule types. These data have only recently begun to be exploited in simulation, using a MD setup proposed by Murad and Powles³ and implemented by Luo and Roux, who used it to parameterize ion-ion interactions for NaCl and KCl.⁴ Since then, osmotic coefficients and pressures have been used to reparametrize other salts,^5–6 organic ions,^7–8 carbohydrates,^9–10 and even amino acid-carbohydrate systems.¹¹ Still, the use of osmotic coefficients to parameterize molecular interactions remains in a nascent stage, which allows for a great deal of exploration and investigation.

While a number of interesting simulation studies have been performed on the self-interactions of peptide systems,^12–14 there have, to our knowledge, only been three studies in which osmotic coefficients of amino acids have been computed using existing force fields in an attempt to place comparisons with experiment on a quantitative level. In the first,¹⁵ the Smith group used osmotic pressures to validate the self-interactions of Glycine (Gly) modeled using their Kirkwood-Buff derived force field.^16–18 In the second,⁷ Yoo and Aksimentiev simulated the self-interactions of Gly in water and found them to be too favorable using both the AMBER and CHARMM force fields. Importantly, they then dramatically improved the agreement with experiment by making subtle adjustments to the van der Waals (vdW) terms describing interactions of the charged amino and carboxyl groups. In the third study,¹⁹ we calculated osmotic coefficients for a variety of amino acids using the AMBER ff99SB-ILDN²⁰ force field in combination with three different water models. We found the osmotic coefficients to be sensitive to the water model used and showed that, while the interactions of aliphatic amino acids were in very good agreement with experiment when simulated with the TIP4P-Ew water model, the interactions of amino acids containing hydroxyl groups (Ser, Thr) were too favorable. In addition, we showed that self-interactions of two-residue peptides (Ala-Ala, Ala-Gly, Gly-Ala, Gly-Gly) could be described much more accurately by recalculating partial charges for the entire peptide in preference to using the charges already assigned to N-terminal and C-terminal residues in the AMBER force field.²¹

In the present study, we extend our previous work by: (a) computing osmotic coefficients for seven different neutral amino acids with latter-day variants of the AMBER,²² CHARMM,²³ GROMOS,²⁴ and OPLS-AA²⁵ force fields, and (b) testing previously proposed modifications, or introducing new ones, in order to improve the agreement with experiment for each force field. We also use the same force fields to measure the osmotic coefficients for five small molecules containing hydroxyl, amide, and aromatic functional groups, whose interactions we suspected in our earlier work¹⁹ were likely to be too favorable. Our results indicate that excessively favorable solute-solute interactions are likely to be a common, but not universal, feature of each of the tested force fields and suggest that reparameterization of the interactions of certain types of functional group (e.g. the hydroxyl group) may be required if more transferable simulation force fields are to be developed.

Computational Methods

Simulation Setup

All simulations were run using GROMACS version 5.0.^26–28 Five force field and water model combinations were used to describe amino acids and small molecules in aqueous solution (Table 1): the AMBER ff99SB-ILDN force field^{20, 29} (hereafter referred to as “AMBER”), which was used with both the TIP4P-Ew³⁰ and the TIP3P³¹ water models; CHARMM36^32–34 (“CHARMM”), with the CHARMM-modified version of TIP3P water;^{33, 35} GROMOS54a7^36–37 (“GROMOS”) with SPC water,³⁸ and OPLS-AA³⁹ (“OPLS-AA”) with TIP4P water.³¹ Osmotic coefficients were calculated and compared to experiment for the following natural amino acids: Glycine (Gly),⁴⁰ Alanine (Ala),⁴¹ Valine (Val),⁴¹ Proline (Pro),⁴² Serine (Ser),⁴³ and Threonine (Thr)⁴² (Figure S1). To provide a further test of aliphatic interactions, we additionally simulated the non-proteinogenic α-amino butyric acid (αABA, Figure S1C), which is intermediate in size between Ala and Val, and for which experimental data have been reported up to 2 m.⁴¹ Since the experimental data all refer to pH 7, all amino acids were modeled in their zwitterionic state. The partial charges for isolated amino acids in the AMBER force field were recently reported by Horn;⁴⁴ those for αABA were calculated in the same way in-house using GAMESS^45–46 and the R.E.D. server utilities⁴⁷ with AMBERTools11⁴⁸ as described in our previous study (see below).¹⁹ For the six natural amino acids in CHARMM, GROMOS, and OPLS-AA, partial charges and vdW parameters were given directly by the force field; for αABA, partial charges were assigned by analogy using Val as a reference compound. Parameter files for αABA can be found in the Supporting Information.

Table 1.

Force Fields, Water Models, and Modifications.

Force Fielda	Water Modelb	Modificationc	Notesd
AMBER ff99SB-ILDN20, 29	TIP4P-Ew30	Used σ and ε values derived by Nerenberg et al.59 & Chapman et al.60	Modifications were applied to both solute-solute and solute-water interactions
AMBER ff99SB-ILDN20, 29	TIP3P31	Increased σ as suggested by Yoo & Aksimentiev7	Additional modifications were required for hydroxyl groups in Ser and Thr
CHARMM3632–34	TIP3P 33	Increased σ as suggested by Yoo & Aksimentiev7	Modifications were not required for Pro
GROMOS54a736–37	SPC38	Decreased σ as described in Computational Methods	Nitrogen parameters originally used for other amino acids were applied to Pro
OPLS-AA39	TIP4P31	Increased σ as described in Computational Methods	Separate σ modification was required for Pro

^aList of force fields used to simulate amino acids and small molecules.

^bWater model used with a given force field.

^cApproach used to modify the LJ parameters of the force field.

^dAdditional considerations for applying modified parameters.

Osmotic pressure simulations of amino acids

For osmotic pressure simulations, we used the same system setup described in our previous reports.^{9, 19} We implemented a modified version of the GROMACS code, edited to report forces exerted by a flat-bottomed potential (FBP) function acting on non-hydrogen solute atoms at each time step. Solutes at concentrations of 1 M (67 molecules) or 2 M (133 molecules) were first placed in a 48 × 48 × 48 Å box, before the box was extended along the z-axis by 24 Å on either side with pure water. The total number of water molecules in each system was approximately 6500 (2 M) or 6900 (1 M). Energy minimization was carried out using the steepest descent algorithm for 1000 steps, followed by an incremental heating up to 298 K over 350 ps. At this stage, the FBP was applied (using a force constant of 1000 kJ mol⁻¹ nm⁻²) to act as a semi-permeable membrane, and a 1 ns equilibration MD simulation was carried out prior to the beginning of the 100 ns production runs.

Simulations were run in the NPT ensemble, with the temperature maintained at 298 K using the Nosé-Hoover thermostat,^49–50 and the pressure maintained at 1 bar using the Parrinello-Rahman barostat.⁵¹ Semi-isotropic pressure coupling was applied so that changes in the simulation box size in the z-direction occurred independently of changes in the x- and y-directions, which were held constant following the simulation setup proposed by Luo and Roux.⁴ For AMBER, CHARMM, and OPLS-AA, long-range electrostatic interactions were calculated using the smooth particle mesh Ewald method;⁵² for GROMOS, long-range electrostatic interactions were calculated using the Reaction Field method⁵³ with the relative dielectric constant of the reaction field set to 62.^{36, 54} Following the recommendations of the force field developers, the cutoffs for van der Waals and short-range electrostatic interactions were set to 10 Å for AMBER²⁰ and OPLS-AA,³⁹ 14 Å for GROMOS,³⁶ and 12 Å for CHARMM; with the latter force field, a force switch function was applied between 10 and 12 Å.⁵⁵ Long-range dispersion corrections⁵⁶ were applied for energy and pressure when using AMBER and OPLS-AA. In all simulations, bonds were constrained to their equilibrium distances using the LINCS algorithm,⁵⁷ thereby allowing a time step of 2.5 fs to be used. Atomic coordinates of both the solute and the solvent molecules were saved every 1 ps for further analysis. All simulation parameters can be found in the GROMACS .MDP files in the Supporting Information.

Osmotic coefficients were calculated as described previously.^{9, 19} The force exerted on the FBP was written out at every time step and averaged over 20 ns blocks. This average force was then converted to a pressure by dividing by the surface area of the semi-permeable membrane, and this pressure was converted to the molal osmotic coefficient (ϕ) according to the equation:^1–2

$$\mathrm{\phi }=\frac{\mathrm{\pi }·{\mathrm{V}}_{\mathrm{w}}}{\mathrm{R}·\mathrm{T}·\mathrm{m}·\mathrm{\nu }·{\mathrm{M}}_{\mathrm{w}}}$$

where V_W is the partial molal volume of water (taken to be 0.018 L·mol⁻¹), R is the gas constant, T is the temperature, m is the molality (calculated by counting the number of water molecules in the central region of the system using VMD software⁵⁸), M_W is the molecular weight of water (0.018013 kg·mol⁻¹), and ν is the van’t Hoff factor (1 for non-electrolytes).

Force Field Modifications

In an effort to improve the agreement with the experimental osmotic coefficients, modifications were made to the vdW parameters describing solute-solute interactions for each force field/water model combination. In each of the force fields examined here, vdW parameters are described by a Lennard-Jones 12-6 (LJ) potential function, and are fully defined by an energy term, ε, which describes the well-depth of the interaction, and a distance term, σ, which describes the interatomic distance at which the interaction switches from being favorable to unfavorable. Some force fields (e.g. CHARMM) use the term r_min (the distance at which the interaction is most energetically favorable) instead of σ to represent this distance, but this can be directly converted to σ by dividing by 2^1/6. Other force fields (e.g. GROMOS) describe LJ interactions in terms of repulsive (C12) and attractive (C6) terms, and these can be (and were) directly converted to ε and σ.²⁸

In order to describe the vdW interaction between two atoms of different type, LJ terms are combined by so-called mixing rules. With the exception of GROMOS, all of the force fields tested here use the Lorentz-Berthelot mixing rule, which takes the geometric mean of the ε values of atoms i and j (i.e. ε_ij = √ε_iε_j) and the arithmetic mean of their σ values (i.e. σ_ij = (σ_i + σ_j) / 2); GROMOS uses the geometric mean for both terms. Any modifications made to these ε_ij and σ_ij values were explicitly defined in the GROMACS topology file, as suggested in the GROMACS manual.²⁸ We applied different sets of adjustments to the vdW parameters for each force field/water model combination as follows:

Modifications to AMBER/TIP4P-Ew

The Head-Gordon⁵⁹ and Nerenberg⁶⁰ groups (hereafter “Nerenberg”) have reported two studies modifying the vdW parameters for a wide range of solutes modeled with an AMBER force field (ff9x/ff12) in conjunction with the TIP4P-Ew water model. In the first study,⁵⁹ attention was focused on improving the force field’s description of solute-water (SW) interactions. To this end, the LJ terms describing interactions between selected solute atoms and water oxygen atoms were scaled in order to best match the free energies of hydration, ΔG_hyd, of a range of molecules within the same family; for example, in order to optimize parameters for the –OH group’s interaction with the water oxygen, methanol, ethanol, isopropanol, and 1,2-ethanediol were used in the fitting to ΔG_hyd data. In the second study,⁶⁰ a similar strategy was followed in an attempt to improve the force field’s description of solute-solute (SS) interactions. To accomplish this, entirely new LJ terms for individual solute atom types were developed in order to best match the enthalpies of vaporization, ΔH_vap, as well as density data, of a range of molecules within the same family. In the present work, we have applied both sets of modifications in an attempt to determine whether they improve the description of osmotic coefficients for a range of solute molecules. In addition, for the specific cases of Ser and Thr we tested both sets of modifications independently in order to determine the relative influence of the proposed modifications to SS and SW interactions (see Results).

Modifications to AMBER/TIP3P and CHARMM

Yoo and Aksimentiev have recently reported modifications to the AMBER force field – when used in conjunction with the TIP3P water model – as well as to the CHARMM force field, that quantitatively reproduce the experimental osmotic coefficient of Gly.⁷ Their proposed modification is to increase σ (AMBER) or r_min (CHARMM) for the interaction between the amino nitrogen and carboxylate oxygen atoms by 0.08 Å. Here we have tested the extent to which these proposed modifications also improve the behavior of other amino acids. In the cases of Ser and Thr with the AMBER force field, which we have previously shown to produce anomalously low osmotic coefficients,¹⁹ we carried out a second set of simulations in which the Gly modification was supplemented with an identical increase to the σ value for interactions of the hydroxyl oxygen (OH) with both the amino nitrogen and carboxylate oxygen atoms (see Results). Finally, in the case of Pro, which in contrast to the other amino acids contains a secondary amine, we performed simulations both with and without the modification proposed by the Aksimentiev group (see Results).

Modifications to GROMOS and OPLS-AA

These were derived in-house by adjusting the σ value of the interaction between the amino nitrogen and carboxylate oxygens using the same approach proposed by the Aksimentiev group. For both force fields, simulations of 2 M Gly were run with a range of incremental adjustments to the σ value (Figures S2A and S2B). With the GROMOS force field, optimal reproduction of the osmotic coefficient of Gly was achieved when the σ value was decreased by 0.11 Å (Figure S2A); with the OPLS-AA force field, best results were obtained when σ was increased by 0.13 Å (Figure S2B). As with the other force fields, the optimized σ values were then applied directly to the other amino acids tested. As outlined in Results, however, much better agreement with experiment was obtained for Pro with the GROMOS force field when the atom type for the nitrogen was changed from its original type (NT) to that used by all other amino acids (NL);⁶¹ for this amino acid only, the original GROMOS parameters were then left unchanged. For Pro modeled with the OPLS-AA force field, on the other hand, the modifications derived for Gly were found to noticeably over-estimate the osmotic coefficient (see Results). For this second special case, therefore, a separate optimization of σ was carried out: optimal reproduction of the osmotic coefficient was achieved by increasing the σ value by 0.08 Å (Figure S2C).

Radial distribution function calculations

In order to probe self-interactions of Gly in an isotropic system (i.e. free from the potentially complicating presence of the semi-permeable membrane), additional 100 ns MD simulations were performed at a 2 M concentration in a 30 × 30 × 30 Å box using the same force fields both with and without the parameter modifications described above. All other aspects of the setup of these simulations were identical to those described above, with the exception of the pressure coupling algorithm, which was switched from semi-isotropic to isotropic. Radial distribution functions (RDF), g(r), for the inter-solute amino nitrogen – carboxyl oxygen interactions, were calculated using the GROMACS rdf utility with a 0.1 Å bin size.

Association constants (K_A) were then calculated from g(r) using the method described by Zhang and McCammon⁶² according to the integral:

$${\mathrm{K}}_{\mathrm{A}}=4\mathrm{\pi }{\int }_0^{5.7}\mathrm{g}(\mathrm{r}){\mathrm{r}}^2\text{dr}$$

where r is the distance expressed in units of 1660^1/3 Å, which results in K_A values in units of M⁻¹; as in our previous study,⁶³ we integrated to a distance of 5.7 Å.

Osmotic pressure simulations of other small molecules

In addition to amino acids, osmotic coefficients were also computed and compared to experiment for five small molecules—methanol (MeOH),⁶⁴ n-butanol (BuOH),⁶⁴ t-butanol (tBuOH),⁶⁴ propionamide (PNMD),⁶⁵ and nicotinamide (NCTD)⁶⁶ (Figure S3)—at 1 M (67 molecules) using the same simulation setup as described for amino acids. The structures of these small molecules were initially built using the build and sculpt functions in PyMOL.⁶⁷ The resulting structures underwent geometry optimization performed at the Hartree-Fock level of theory with the 6–31G* basis set using the GAMESS quantum mechanical software package.^45–46 Partial charges were then assigned for each of the force fields as follows. For AMBER, the partial charges were derived, according to the force field’s recommended strategy, using a two-stage RESP fitting procedure.⁶⁸ Briefly, the electrostatic potential map was computed using GAMESS at the same level of theory as above, and R.E.D. tools utilities⁴⁷ (downloaded from an archive of the R.E.D. server⁶⁹) were used to generate intermediate files and to run AMBERTools.⁴⁸ Once partial charges were calculated, van der Waals terms were assigned to atom types by analogy with similar functional groups already in the force field. For simulations using CHARMM, all charge and vdW parameters were taken directly from the CHARMM General Force Field (CGenFF) library,^70–71 with the exception of n-butanol (which was not present in the library), for which the charges and vdW parameters were assigned by analogy with octanol (present in CGenFF). For simulations using GROMOS and OPLS-AA, parameters were again assigned by analogy with other, similar small molecules. The necessary parameter files can be found in the Supporting Information. As was the case with the amino acids, additional simulations using the AMBER/TIP4P-Ew force field combination were also run using the Nerenberg group’s proposed modifications to solute-solute⁶⁰ and solute-water⁵⁹ vdW interactions.

Conversion and Validation of Experimental Osmotic Coefficients for Small Molecules

For the amide-containing molecules, propionamide and nicotinamide, experimental osmotic coefficients were measured directly at 25 °C using isopiestic equilibration (propionamide)⁶⁵ and vapor-pressure osmometry (nicotinamide).⁶⁶ For the remaining molecules, all of which are alcohols (methanol, n-butanol and t-butanol), osmotic coefficients were instead obtained from freezing point depression experiments.⁶⁴ This technique yields an osmotic coefficient at the freezing point (i.e. <0 °C), whereas our primary interest is in the osmotic coefficient at 25 °C. In order to convert between the two temperatures, therefore, we used the following equation:

$${\mathrm{\phi }}_{\mathrm{R}}={\mathrm{\phi }}^{\prime }-\left(\frac{1}{\mathrm{R}}\right)\left(\frac{1}{\mathrm{T}}-\frac{1}{{\mathrm{T}}_{\mathrm{R}}}\right)({\mathrm{h}}_2\mathrm{m}+2{\mathrm{h}}_3{\mathrm{m}}^2+\cdots )+\left(\frac{1}{\mathrm{R}}\right)\left[{\mathrm{T}}_{\mathrm{R}}\left(\frac{1}{\mathrm{T}}-\frac{1}{{\mathrm{T}}_{\mathrm{R}}}\right)+ln\left(\frac{\mathrm{T}}{{\mathrm{T}}_{\mathrm{R}}}\right)\right]({\mathrm{c}}_2\mathrm{m}+2{\mathrm{c}}_3{\mathrm{m}}^2+\cdots )$$

derived by Desnoyers, Ostiguy, and Perron,⁷² and used extensively by the Wood group for a number of small molecules (see for example refs ^73–76). Here, ϕ_R is the osmotic coefficient at 25 °C (298.15 K), ϕ’ is the osmotic coefficient at the freezing point, R is the gas constant, T and T_R are the temperatures at the freezing point and 298.15 K, respectively, and m is the molality of the solute. Conversion also requires taking into account the two-body and three-body interaction enthalpies (h₂, h₃) and heat capacities (c₂, c₃), which are usually provided in studies that report osmotic coefficients obtained from freezing point depression measurements. For an excellent example of how to convert these data, see Spitzer, Tasker, and Wood.⁷⁵

Given that the osmotic coefficient at 25 °C obtained from freezing point depression studies relies on measurements made at a quite different temperature, we felt it was important to validate the resulting values by comparisons with alternative sources of data. There is a paucity of experimental osmotic coefficient data for alcohols in the literature, but one way to obtain a second estimate is using the gas chromatography measurements made by Sagert and Lau at 20 °C,⁷⁷ who reported the activity coefficients on the mole fraction scale (γ_x) for a variety of alcohols in water. We first converted these into activity coefficients on the molal scale, and then converted them into osmotic coefficients. The first stage was accomplished using the approach outlined in Appendix B of Bart⁷⁸ and in chapters 9 and 12 of DeVoe.⁷⁹ Specifically, we made use of the following equation from Bart:⁷⁸

$${\mathrm{\gamma }}_{\mathrm{i}}^{\mathrm{m}}={\mathrm{\gamma }}_{\mathrm{i}}^{\mathrm{x}}\left(\frac{{\mathrm{x}}_{\mathrm{i}}}{{\mathrm{c}}_{\mathrm{i}}}\right)\left(\frac{{\mathrm{m}}_{\mathrm{s}}}{{\mathrm{\gamma }}_{\mathrm{i}}^{\infty }}\right)$$

where γ_i^m and γ_i^x are the activity coefficients on the molal and mole fraction scales, respectively; x_i and c_i are the solute concentrations on the mole fraction and molar scales, respectively; m_s is the molal solvent concentration (here, 55.508 mol/kg water), and γ_i^∞ is the infinite dilution activity coefficient of the solute provided in the study. Our calculations assumed an equivalence between the molar and molal scales at low concentrations, as suggested by DeVoe in section 9.1 (green squares in Figure S4A and S4B).⁷⁹ However, we further tested this assumption for t-butanol by calculating γ_i^m using molar concentrations calculated directly from density data⁸⁰ (yellow squares in Figure S4A; see below). In the second stage, the computed γ_m values were converted to osmotic coefficients as in our previous work¹⁹ by plotting molality versus ln(γ_m) and integrating using the Trapezoid rule, described by Hamer,⁸¹ up to the concentration of interest.

Importantly, the osmotic coefficients computed from gas chromatography data for n-butanol and t-butanol were very similar to those obtained from the freezing point depression studies (see Figures S4A and S4B). For t-butanol, the osmotic coefficients obtained using c_i values computed explicitly from density data were ~10% higher at 1 M (yellow squares in Figure S4A). At least for the alcohols, therefore, conversion of the gas chromatography data by making the assumption that m_i = c_i appears to provide a lower bound on the true osmotic coefficient. Regardless of this issue, we think that the osmotic coefficients obtained by converting freezing point depression data to 25 °C appear valid. To further validate the conversion, however, we also compared the freezing point depression data for propionamide (blue circles in Figure S4C)⁷³ with data collected using isopiestic equilibration⁶⁵ at 25 °C (green squares in Figure S4C). The data were again in reasonable agreement, although the freezing point data were slightly higher than those from isopiestic equilibration. For comparison with simulation for propionamide, therefore, we used the data from isopiestic equilibration because: (a) it was collected at 25 °C and thus required no conversion and (b) it also provided a lower bound on the osmotic coefficient as above.

Results

Osmotic Coefficients for Amino Acids

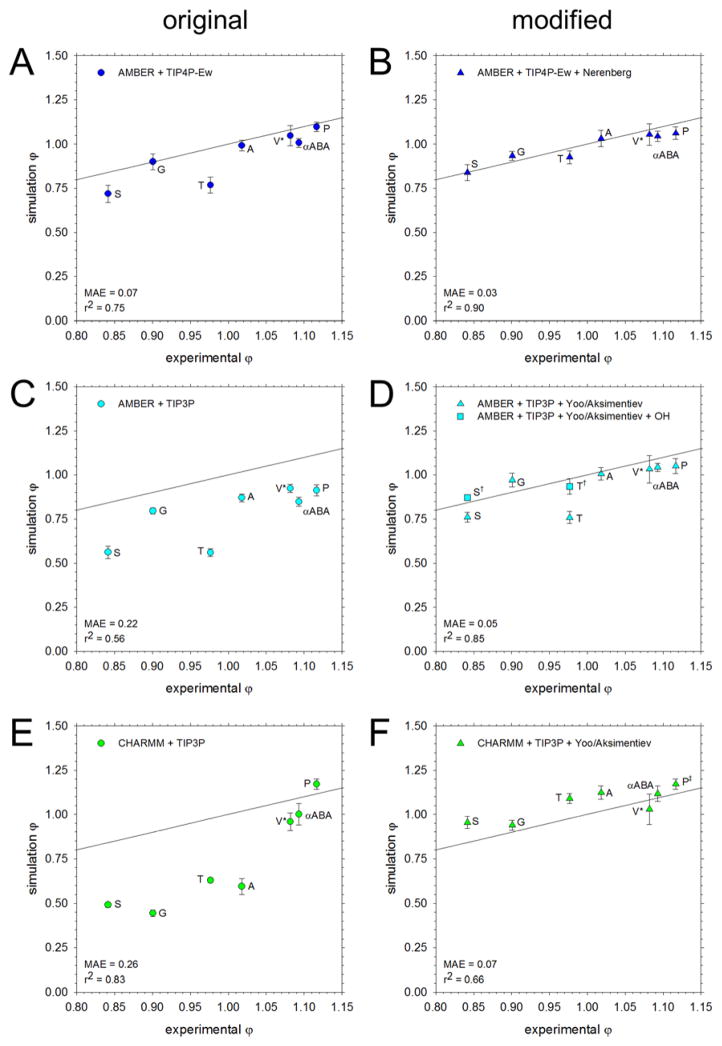
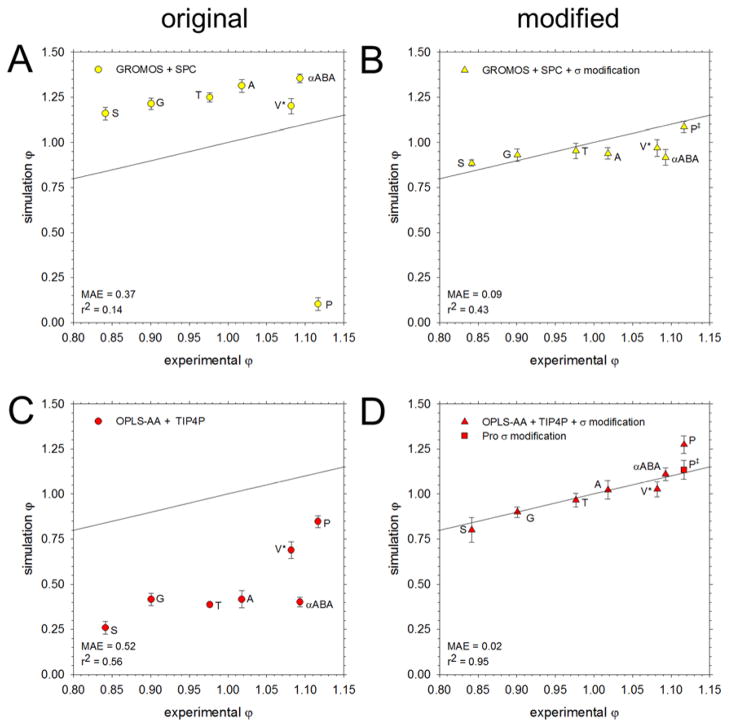
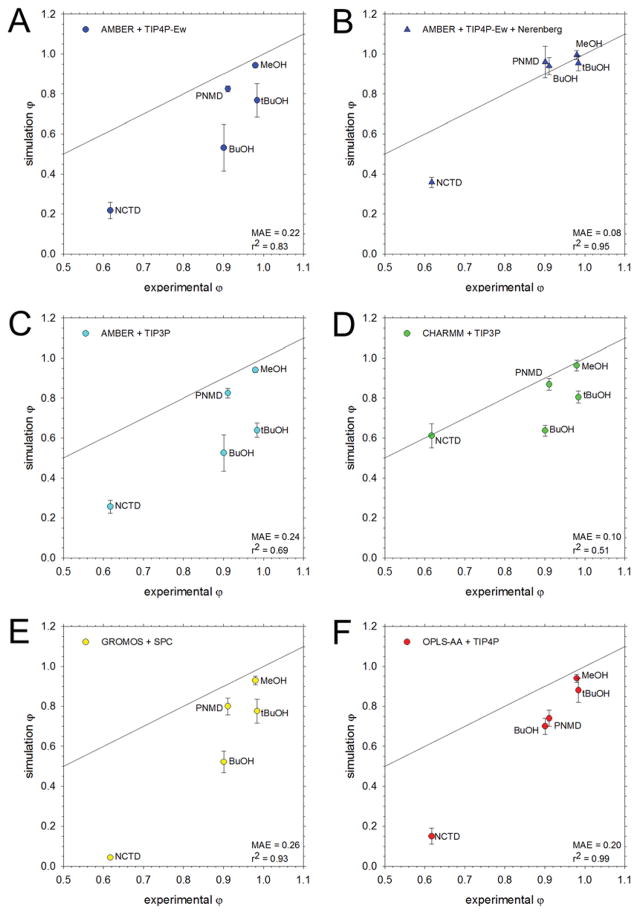
The full set of osmotic coefficients obtained from simulations of amino acids using five different force field/water model combinations are compared with those from experiment in Figures 1 and 2: Figure 1 shows data for the AMBER and CHARMM force fields; Figure 2 shows data for the GROMOS and OPLS force fields. In both figures, panels on the left-hand side show the results obtained with the original force fields, while panels on the right-hand side show those obtained using modified versions of the force fields. In Figure 1, the modifications were proposed in previous work by the Head-Gordon⁵⁹ and Nerenberg⁶⁰ groups (Figure 1B) and by Yoo and Aksimentiev⁷ (Figure 1D and 1F). In Figure 2, the modifications were derived in-house using the same methodology as that developed by Yoo and Aksimentiev. A comparison of the mean average errors (MAE) obtained with each set of simulations reveals the extent to which the proposed modifications improve the description of osmotic coefficients. The same data shown in Figures 1 and 2 are depicted in a molecule-by-molecule form in Figure S5.

Figure 1.

Comparison of osmotic coefficients of the amino acids from simulation with experiment. All simulations were run at 2 M except for Val, which was run at 1 M (V*). The black line represents perfect correspondence between simulation and experiment; the mean average error (MAE) from experiment and the r² value for the linear regression are noted in the bottom left corner. A. Results obtained using the AMBER force field solvated with the TIP4P-Ew water model. B. Same as A, but using the Nerenberg group’s modifications to solute-solute⁶⁰ and solute-water⁵⁹ interactions C. Same as A, but using the TIP3P water model. D. Same as C, but with amino N and carboxylate O interactions adjusted according to the Aksimentiev group.⁷ The data for Ser and Thr with additional adjustments to the OH:OH, OH:N, and OH:O interactions are shown as squares (S^†, T^†). E. Results obtained using the CHARMM force field with the TIP3P water model. F. Same as E, but with interactions between amino N and carboxylate O adjusted according to the Aksimentiev group.⁷ Modifications were not applied for Pro (P^‡, see text).

Figure 2.

Comparison of osmotic coefficients of the amino acids from simulation with experiment. All simulations were run at 2 M except for Val, which was run at 1 M (V*). The black line represents perfect correspondence between simulation and experiment; the mean average error (MAE) from experiment and the r² value for the linear regression are noted in the bottom right corner. A. Results obtained using the GROMOS force field with the SPC water model. B. Same as A, but with amino N and carboxylate O interactions modified using in-house optimization. For Pro (P^‡), the atom type describing the amino N was changed from NT to NL. C. Using the OPLS-AA force field with the TIP4P water model. D. Same as C, but with amino N and carboxylate O interactions modified using in-house optimization. The Pro-specific modification is shown as a square (P^‡).

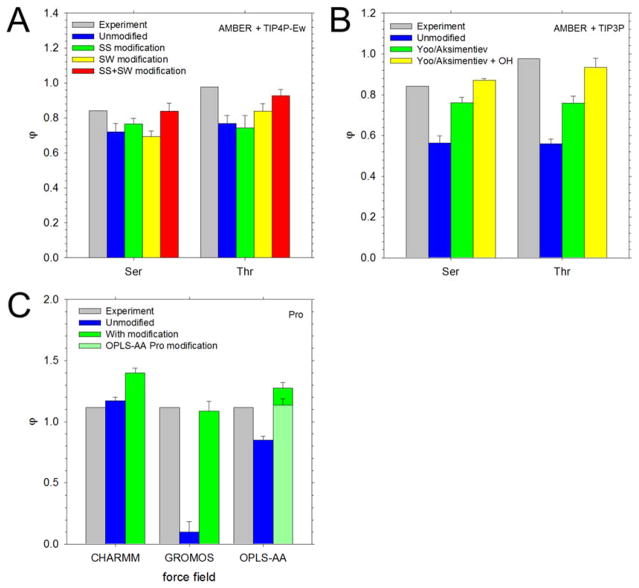
Figure 1A shows the osmotic coefficients that we recently reported for simulations performed using the AMBER/TIP4P-Ew model.¹⁹ As noted previously, for the aliphatic amino acids, Ala, Pro, Val and αABA, the computed values are in very good agreement with experiment, but for Ser and Thr the computed values are too low (Figure 1A). Figure 1B shows the results obtained when we apply the modifications proposed by the Nerenberg and Head-Gordon groups to improve solute-water⁵⁹ and solute-solute⁶⁰ interactions for the same force field combination. Clearly, the results are much improved in terms of both the overall correlation and in terms of the MAE, which is reduced from 0.07 with the original parameters to 0.03 with the proposed modifications. Since these modifications were not specifically devised to match osmotic coefficient data, the results shown in Figure 1B can be considered an important independent test of their ability to describe inter-solute interactions in water. Interestingly, separate simulations of Ser and Thr applying only the solute-water modifications, ⁵⁹ or applying only the solute-solute interactions,⁶⁰ did not produce significantly improved results (Figure 3A), suggesting that both aspects of solute behavior require modification in order to match experiment.

Figure 3.

Notes of caution when modifying LJ parameters for different force fields. In all panels, the experimental osmotic coefficients are shown in gray. A. Computed osmotic coefficients of Ser and Thr at 2 M obtained using the AMBER force field with the TIP4P-Ew water model (blue), and after applying the Nerenberg group’s modifications to solute-solute interactions (SS, green), to solute-water interactions (SW, yellow), and to both types of interaction (SS+SW, red). B. Computed osmotic coefficients of Ser and Thr at 2 M obtained using the AMBER force field with TIP3P water (blue), after applying the modification described by the Aksimentiev group (green), and after applying an additional modification to the hydroxyl O interactions (yellow). C. Computed osmotic coefficients of Pro at 2 M obtained using the CHARMM, GROMOS, and OPLS-AA force fields (blue), and after applying modifications (green); for OPLS-AA, the osmotic coefficient obtained with in-house modified parameters for Pro is shown in light green.

Figure 1C shows the osmotic coefficients that we recently reported for simulations performed using the AMBER/TIP3P model. As noted previously, the computed osmotic coefficients are, in all cases, lower than those reported experimentally,^{7, 19} and this is especially true for Ser and Thr (compare blue bars with grey bars in Figure 3B). The Aksimentiev group has reported a similar underestimation of the osmotic coefficient for Gly and has shown that a simple increase of the σ value describing the interaction between amino nitrogen and carboxylate oxygen atoms can correct the behavior (see Computational Methods). ⁷ Figure 1D (triangles) shows the results that are obtained when we apply the Aksimentiev group’s proposed modification to the other amino acids. In all cases, the modification improves the osmotic coefficients. For the aliphatic amino acids, Ala, Pro, Val and αABA, in particular, the computed values are in very good agreement with experiment. For Ser and Thr, on the other hand, the computed values remain somewhat low (see upward triangles in Figure 1D; see also green bars in Figure 3B): this, however, is expected given that the proposed modification applies to backbone atoms only. In an attempt to correct the remaining errors for Ser and Thr, we also applied the same σ increase to the hydroxyl oxygen’s interaction with amino nitrogen, carboxylate oxygen, and hydroxyl oxygen atoms. The results obtained when these additional modifications are applied are in much better agreement with experiment (see squares in Figure 1D; see also yellow bars in Figure 3B).

Figure 1E shows the osmotic coefficients that we obtained here from simulations performed using the CHARMM/TIP3P model. With the notable exception of Pro, the computed osmotic coefficients are in all cases too low. As was the case with the AMBER/TIP3P model, the Aksimentiev group has previously reported a similar result for Gly,⁷ and again, has shown that an increase of the σ value describing the interaction between amino nitrogen and carboxylate oxygen atoms corrects the behavior. Figure 1F shows the results that are obtained when the same modification is applied to the other amino acids with the exception of Pro, for which the computed value is already in excellent agreement with experiment (Figure 3C shows that application of the modification to Pro worsens its agreement with experiment). As before, the osmotic coefficients all become much closer to experiment, and while the overall correlation with experiment is reduced somewhat, the MAE improves from 0.26 to 0.07.

Figure 2A shows the results obtained when simulations are performed with the GROMOS/SPC model. The correlation coefficient for the full set of data is poor, but when the values for Pro and Val (the latter simulated at a different concentration) are omitted, the correlation coefficient jumps to 0.98. In marked contrast to what was seen with the previous force fields, GROMOS predicts, with one notable exception, osmotic coefficients that are too high compared with experiment. The exception is again Pro, for which an extremely low osmotic coefficient is obtained (Figure 2A; blue bar in Figure 3C). Examination of simulation snapshots reveals that this is due to the formation of very stable – but unrealistic – helical assemblies (Figure S6). In GROMOS, the secondary amino nitrogen of Pro is assigned quite different parameters from the primary amino nitrogen of all other amino acids. Interestingly, however, we found that application of the amino nitrogen parameters of the other amino acids to Pro abolished the formation of helical assemblies and produced an osmotic coefficient in excellent agreement with experiment (Figure 2B; Figure 3C). In an attempt to correct the behavior of the other amino acids, we followed an approach identical to that used previously by the Aksimentiev group for the AMBER and CHARMM force fields. Specifically, we: (a) performed a series of simulations of Gly in order to optimize the σ value for the interaction of the amino nitrogen and carboxylate oxygen atoms, and (b) applied the same modification to each of the other (non-Pro) amino acids. For Gly, we found that optimal results were obtained when σ was decreased by 0.11 Å (see Figure S2A). The results obtained when this same modification is applied to the other non-Pro amino acids are shown in Figure 2B: as with the other force fields tested, the osmotic coefficients are much improved, although the values for the aliphatic amino acids Ala, Val, and αABA are now somewhat too low. In principle, one could further optimize the interactions of these aliphatic amino acids by modifying carbon-carbon interactions, as was very recently done for the AMBER force field, albeit not using osmotic pressure data, by the Aksimentiev group.⁸²

Figure 2C shows the results of simulations performed using the OPLS-AA/TIP4P model; in all cases, the computed osmotic coefficients are much too low compared with experiment. Applying the same approach used for GROMOS (see above), we found that optimal results were obtained for Gly when σ was increased by 0.13 Å (Figure S2B). Applying this same modification to the other amino acids results in a dramatic improvement in the osmotic coefficients with the exception of Pro, for which the final value is now too high (Figure 2D; dark green bar in Figure 3C). We thus optimized the osmotic coefficient for Pro independently, using the same approach used for Gly (Figure S2C). Increasing σ between the amino nitrogen and carboxylate oxygen by 0.08 Å was sufficient to reproduce the experimental osmotic coefficient (square data point in Figure 2D; light green bar in Figure 3C). After correcting the interactions of Pro, the modifications made to the OPLS-AA force field resulted in the greatest improvement in agreement with experiment for any of the tested force fields (MAE decreased from 0.52 to 0.02).

Radial Distribution Functions and Association Constants

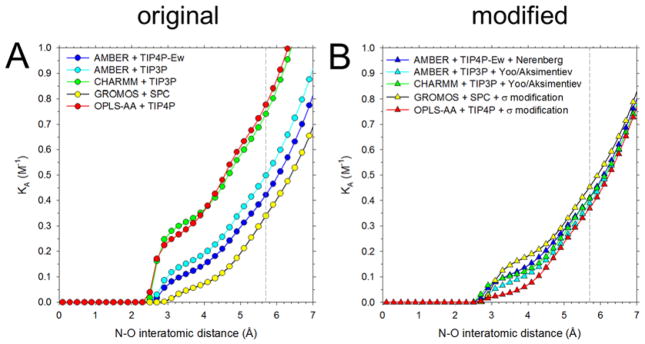
The modifications described above affect the structures of intermolecular associations in ways that are largely in line with expectations. Figure S7 compares the radial distribution functions (RDFs) for intermolecular interactions of amino nitrogen and carboxylate oxygen atoms in simulations of 2 M Gly using each of the original (circles) and modified (triangles) force fields. With the original force fields, the maximum peak heights at close distance are entirely consistent with the osmotic coefficients shown above, with large peak heights corresponding to low osmotic coefficients, and vice versa. They are also qualitatively consistent with those from our previous report,⁸³ with the peak heights decreasing in the order: CHARMM > OPLS-AA ≫ AMBER/TIP3P > AMBER/TIP4P-Ew > GROMOS. Unsurprisingly, given that it was the amino nitrogen – carboxylate oxygen interaction that was adjusted in order to match the experimental osmotic coefficients, the primary changes in the RDFs are to the position and height of the first peak in the RDFs. Interestingly, however, even though all five force field combinations can be made to match the experimental osmotic coefficient for Gly, and even though the RDFs that result from the five modified force fields become much more similar to each other, there remain clear points of difference (Figure S7F).

The strength of pairwise interactions of solutes can also be expressed in terms of association constants (K_A) calculated by integrating the RDFs⁶³ with respect to distance up to a cutoff characteristic of the bound state. Plots of K_A as a function of this cutoff are shown in Figure 4 for each of the original and modified force fields. Using 5.7 Å as the cutoff (see dashed gray line in Figure 4) the association constants computed using the original force field parameters (Figure 4A), range from 0.34 to 0.78 with an average of 0.55 ± 0.19 M⁻¹. The corresponding K_A values obtained with the modified force fields range instead from 0.37 to 0.45 with an average K_A of 0.41 ± 0.03 M⁻¹ (Figure 4B). The much smaller standard deviation indicates, as expected, that the association constants obtained with the modified force fields exhibit a much higher degree of similarity to each other. The fact that the shapes and heights of the RDFs remain different suggests, however, that there are many interaction energy ‘landscapes’ that can produce behavior consistent with the experimental osmotic coefficients.

Figure 4.

Association constants, K_A, of Gly calculated by integrating radial distribution functions for amino N and carboxylate O interactions (see Computational Methods). The dashed line indicates the upper limit of the integration (5.7 Å) used for comparing K_A with previous literature estimates (Figure S9). A. K_A values (M⁻¹) for the five unmodified force field and water model combinations considered here. B. Same as A, but using modified force fields (see Table 1).

Osmotic Coefficients for Small Molecules

As noted in our previous work, we think that it is reasonable to think that force fields may describe the interactions of certain functional groups better than others. As one example, the fact that the osmotic coefficients of Ser and Thr using the AMBER force field are anomalously low, at least in comparison to the other amino acids tested, suggests that interactions of hydroxyl groups are likely to be excessively favorable in this force field. As a second example, in our previous work we suggested that the osmotic coefficients for the amino acids Phe and Gln might also be too low – thereby bringing into question the strengths of interaction of aromatic and amide groups – but the absence of direct experimental data on these two amino acids prevented this from being stated with certainty. Experimental osmotic coefficient data are, however, available for other small molecules that contain each of these functional groups. Specifically, data are available for the alcohols methanol, n-butanol, and t-butanol, and for the amide-containing molecules propionamide (an excellent mimic of the Gln sidechain) and nicotinamide (which is also aromatic).^65–66 We therefore computed osmotic coefficients for each of these small molecules using the five force field combinations described above in an attempt to identify functional groups whose interactions may be excessively strong or weak.

Interestingly, each of the force fields tested tends to underestimate the osmotic coefficients of the small molecules (Figures 5A and 5C–F), indicating that solute-solute interactions in aqueous solution are generally described as being too favorable. The force fields produce quite accurate osmotic coefficients for methanol (results for all force fields are compared in Figure S8A), but the results are significantly worse for the larger alcohols and are especially low for n-butanol (Figure S8B). The force fields also produce osmotic coefficients that are somewhat too low for propionamide (Figure S8D), and results that are far too low for nicotinamide, with the exception of CHARMM, for which the experimental value is nicely reproduced (green bar in Figure S8E). With regard to the AMBER force fields, we find again that the inclusion of the LJ modifications proposed by the Nerenberg group dramatically improves the interactions of all the small molecules, although the computed osmotic coefficient for nicotinamide remains much too low (Figure 5B; see light blue bars in Figure S8E). Finally, we obtain nearly identical osmotic coefficients for all five small molecules when using the AMBER/TIP4P-Ew and AMBER/TIP3P force fields (Figures 5A and 5C): this is in contrast to our findings for amino acids, for which there was a clear dependence on water model.¹⁹

Figure 5.

Comparison of osmotic coefficients of five small molecules from simulation with experiment. The black line represents perfect correspondence with experiment; the mean average error (MAE) from experiment and the r² value for the linear regression are noted in the bottom right corner. A. Results obtained using the AMBER force field with the TIP4P-Ew water model. B. Same as A, but using the Nerenberg group’s LJ parameters C. Same as A but with TIP3P water. D. Same as A but using the CHARMM force field with the TIP3P water model E. Same as A but using the GROMOS force field with the SPC water model F. Same as A but using the OPLS-AA force field with the TIP4P water model.

Discussion

This work attempts to add to a growing body of literature describing the use of osmotic coefficient measurements as a means of identifying inaccuracies in, and if necessary reparametrizing, simulation force fields.^{4–9, 19} The five force field combinations used here all have different issues with reproducing the osmotic coefficients of the amino acids. But in each case we have shown that corrections to the LJ parameters can be applied that dramatically improve results.

The simplest set of results to describe is that obtained with the CHARMM force field. Yoo and Aksimentiev have shown previously that increasing the LJ σ value for interactions of amino nitrogens with carboxylate oxygens increases the osmotic coefficient for Gly significantly, bringing it into good agreement with experiment.⁷ The fact that the osmotic coefficient is sensitive to this parameter indicates that the charge-charge interaction of the amino and carboxylate groups is a key determinant of the (simulated) interactions of Gly molecules. But a proper description of protein folding thermodynamics and protein-protein interactions requires that other types of interaction – especially those of the amino acid sidechains – also be correctly reproduced. It is therefore important to find here that application of the modification proposed by the Aksimentiev group to other (non-Pro) amino acids also leads to much improved osmotic coefficients (compare Figures 1E and 1F): this argues that, at least for the amino acids tested, sidechain interactions are likely to be reasonably well described by the CHARMM force field. The one amino acid that does not require modification is Pro, for which the original parameters already produce an osmotic coefficient in good agreement with experiment. As noted below, Pro is found to be exceptional with other force fields, and while this proves to be a challenge for the development of concise parameter sets, it should be remembered that discrepancies with this residue refer only to its zwitterionic form. We have no reason to believe, based solely on the results reported here, that special problems are likely to be encountered with internal Pro residues in protein chains.

Qualitatively similar behaviors are obtained with the GROMOS and OPLS force fields which, to our knowledge, have not previously been applied in osmotic pressure simulations. Our results for the amino acids with GROMOS and OPLS are systematically too high and too low, respectively, but both discrepancies can be rectified by applying the same approach, pioneered by the Aksimentiev group, of making modest changes to the LJ σ value for interactions of amino nitrogens with carboxylate oxygens (Figure 2). Again, however, care is needed with Pro. In the case of GROMOS, the original LJ parameters – which are different from those of non-Pro amino acids – result in aggregation of Pro molecules into non-physical helical assemblies (see Figure S6). Replacing these parameters with those used for the other amino acids, however, produces much more realistic behavior. In the case of OPLS, on the other hand, application of the σ adjustment that corrects the behavior of the other amino acids leads to an overestimated osmotic coefficient for Pro; we thus undertook a separate adjustment of the σ value for Pro (Figure S2C). In general, however, it is to be noted that the results obtained with the adjusted LJ parameters for OPLS are in excellent qualitative and quantitative agreement with experiment: again, this argues in favor of the description of sidechain interactions with this force field.

The results obtained with the AMBER force field require more extensive discussion. As was the case with the CHARMM force field, the Aksimentiev group has previously shown that, with TIP3P water, increasing the LJ σ value for interactions of amino nitrogens with carboxylate oxygens by 0.08 Å improves the osmotic coefficient for Gly.⁷ We find here that applying this same modification to the other amino acids increases—and therefore improves—their osmotic coefficients as well (Figures 1C and 1D). The fact that the resulting values for the aliphatic amino acids, in particular, are in very good agreement with experiment could be seen as surprising because it has recently been suggested that this force field and water model combination overestimates hydrophobic interactions: aggregates of the largely hydrophobic N-acetyl-leucine-methyl-amide were successfully solubilized only by modifying the interactions of aliphatic carbon groups.⁸² The role of aliphatic carbons, however, remains somewhat ambiguous. We have previously demonstrated⁸⁴ that this force field (and interestingly, OPLS-AA as well) can, in a different setting, accurately describe interactions involving hydrophobic side chains: specifically, when conservative mutations were made to small aliphatic amino acids in a protein kinase’s binding site, simulations accurately reproduced the relative free energies of ligand binding. Similarly, we demonstrate here that the osmotic coefficients for the small aliphatic amino acids Ala, αABA, Val, and Pro are nicely reproduced by adjusting only the interactions between amino nitrogen and carboxylate oxygen, while leaving unaltered the interactions involving aliphatic carbons. What the modification to the charged termini does not do, however, is solve the problem, identified in our previous work,¹⁹ with the anomalously low osmotic coefficients for Ser and Thr: these remain too low. As a result, we set about making modifications that involve the hydroxyl oxygen of these amino acids. It is interesting to find, therefore, that the same σ modification that was applied to amino nitrogens and carboxylate oxygens, when applied to solute-solute interactions involving the hydroxyl oxygen atoms, produces osmotic coefficients in much closer agreement with experiment for Ser and Thr (see Figure 3B). This may hint at a general failing with this force field’s descriptions of favorable hydrogen bonding interactions.

In the case of AMBER with the TIP4P-Ew water, we have previously shown that this force field combination produces excellent osmotic coefficients for the tested amino acids with the exception, again, of Ser and Thr. In principle, we could, therefore, seek to correct the behavior of these two amino acids by applying an ad hoc modification – similar to that outlined above for TIP3P water – to the σ value of interactions involving the hydroxyl oxygen atoms. Instead, however, we considered it of greater interest to ask whether more realistic behavior might be produced by applying more systematic sets of modifications such as those proposed by the Nerenberg group to improve the description of solute-water⁵⁹ and solute-solute⁶⁰ interactions. The results shown in Figure 1B indicate that this is indeed the case: the Nerenberg group’s modifications not only leave unchanged the results for amino acids that we had previously shown to be correct, but also significantly improve the results for Ser and Thr. Given that these modifications were not intended for use in osmotic pressure simulations, nor in the context of amino acids, the good results obtained argue strongly in favor of the Nerenberg group’s approach as a way of developing accurate, transferable descriptions of solute-solute interactions in aqueous solution. This suggestion can be seen to be largely confirmed when the same parameters are applied to the five neutral small molecules tested here: in comparison with the original AMBER parameter set, the results for all molecules are much improved, with the only major discrepancy being the result for nicotinamide, which remains significantly underestimated (Figure 5B).

As should be expected, the use of parameter adjustments that improve the agreement with experimental osmotic coefficients also results in the association constants computed with the different force fields becoming more similar to each other. The K_A values that we obtain here for Gly can be broadly compared with values reported recently by the Chong group for simulations of butylammonium with acetate.⁸⁵ Their results demonstrated the same qualitative behavior that is observed here: large K_A values are obtained from simulations using the CHARMM and OPLS force fields, while smaller K_As are obtained using AMBER, with the value obtained with the TIP3P water model being greater than that obtained with TIP4P-Ew. In fact, the two sets of K_A values are highly correlated (r²=0.99; see Figure S9), even though somewhat different variants of force fields and water models were used for CHARMM and OPLS. The average K_A calculated here for Gly-Gly interactions (0.55 M⁻¹) is also on the same order of magnitude as the values reported by the Chong group, which ranged from 0.43–2.22 M⁻¹, depending on the force field used.⁸⁵

With regard to the small molecules calculations, it is clear that all force fields produce osmotic coefficients that are lower than the experimental values and that they, therefore, provide descriptions of solute-solute interactions that are excessively favorable. This result, while disappointing, is at least consistent with the results reported by the Zagrovic group,⁸⁶ demonstrating that protein-protein interactions in commonly used force fields are generally too attractive, and it is consistent with results reported by a number of groups,^87–93 indicating that intrinsically disordered proteins often undergo an unrealistic collapse with common force fields. As such, it reinforces the notion that the nonbonded parameters of extant force fields may in many cases require reexamination. In terms of the MAE, the best-performing of the original parameter sets is CHARMM: it is the only original force field capable of reproducing with any degree of accuracy the osmotic coefficient of nicotinamide, it performs the best for propionamide, and performs the second-best for n-butanol and t-butanol. Notably, with respect to the small molecules, the only force field combination tested that approaches CHARMM in terms of overall accuracy is the AMBER + TIP4P-Ew force field when combined with the Nerenberg group’s modifications.

Of the five small molecules tested, it is clear that the most difficult osmotic coefficient to reproduce is that of nicotinamide. Since nicotinamide is both aromatic and contains an exocyclic amide group it is possible that either or both groups might be responsible for the poor results. The osmotic coefficients obtained for the other amide-containing molecule that was tested, propionamide, are in somewhat better agreement with experiment, but in all cases are underestimated, suggesting therefore that amide interactions are likely to be excessively favorable. At least in the case of the AMBER force field, this would be consistent with the suggestion made in our previous work¹⁹ that interactions of the amide-containing amino acids Asn and Gln are likely to be excessively favorable. Whether aromatic interactions are also modeled as being excessively favorable in the present force fields is not yet clear.

With regard to the alcohols, it is notable that the results are significantly worse for the larger aliphatic alcohols n-butanol and t-butanol than for the much simpler methanol. While this might be interpreted as suggesting that interactions of the aliphatic groups are more likely to be at fault than those of the hydroxyl groups, it is important to note that this need not be the case. Using a very simple statistical mechanical model, it can be shown that any errors in the description of the hydroxyl group’s interactions could easily be exacerbated in the presence of additional attractive (e.g. aliphatic) interactions that bring solutes into contact (see Supporting Text). As such, it is quite possible that the larger errors seen with the larger alcohols are nevertheless entirely attributable to errors in the hydroxyl group’s interactions. In this regard, therefore, it is worth noting that all of the original force fields also underestimate the osmotic coefficient of methanol, albeit to a smaller degree than seen with the butanols. Again, therefore, these results may point to a general problem – in all of the tested force fields – with the description of the hydroxyl group’s interactions with other solutes.

In closing, it is worth considering how the approach pursued here compares with other ways in which force field parameterization efforts might be conducted. Here, using the approach pioneered first by Luo and Roux,⁴ and then by Yoo and Aksimentiev,⁵ only the van der Waals interactions between selected solute atom types have been adjusted, and other solute-solute, and all solute-solvent interactions have been deliberately left unchanged. In some respects this might be seen as doing little more than applying a “bandaid” to a force field in order to correct a specific problem (i.e. the reproduction of osmotic pressure data). But parameters modified in this way have also been shown, by us and others,^{5, 7, 9} to improve the description of other properties: e.g. the Aksimentiev group showed that modifications developed for phosphate-cation interactions improved both the packing density and the internal pressure of DNA arrays,⁵ and we showed that osmotic pressure-optimized parameters developed for glucose also dramatically improved the conformational behavior of dextran.⁹ In addition, the present work’s demonstration that the same approach works well for all of the force fields tested here, suggests that it is likely to be a useful weapon to add to the arsenal of approaches already used to develop force fields for modeling biomolecular interactions in aqueous solution.

That said, an approach that focuses solely on modifying specific solute-solute interactions is not likely to provide a general solution to problems that stem instead from an incorrect description of solute-solvent interactions. For such cases, it may instead be preferable to adjust either: (a) the partial charges of the solutes, or (b) the van der Waals parameters describing solute-solvent interactions. An example of the first approach comes from the Smith group’s efforts to develop a KBFF model for urea in which it was specifically noted that parameterization efforts based on adjusting only LJ parameters were unsuccessful;⁹⁴ the same approach of adjusting partial charges has proven successful in subsequent parameterization efforts by the same group.^16–18 Examples of the second kind of approach can be found in works from Best, Zheng and Mittal,⁸⁷ and from the MacKerell group,⁹⁵ both of which showed that targeting solute-solvent van der Waals parameters is a promising approach to improving the description of both native and intrinsically disordered proteins. With respect to the latter application, still another possible approach to take is to develop a new water model, as exemplified by the Shaw group’s recent report of the TIP4P-D model.⁸⁸

Finally, we note that force field development – especially when it involves efforts to reproduce many properties simultaneously – is becoming an increasingly automated procedure. Examples include the Pande group’s development of the Force Balance method,⁹⁶ which has led to a water model⁹⁷ that matches water’s properties over a very wide range of conditions, and the Chong group’s very recent report of a new iteration of the AMBER force field for proteins – AMBERff15ipq⁹⁸ – that was derived in only a few months in a largely automated fashion. It seems reasonable to suggest that similar force field parameterization efforts might, in the future, benefit from incorporating osmotic pressure data as an additional target for optimization.