Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2017 Jun 9;174(4):2289–2301. doi: 10.1104/pp.17.00357

Root Tip Shape Governs Root Elongation Rate under Increased Soil Strength1,[OPEN]

Tino Colombi a,2, Norbert Kirchgessner a, Achim Walter a, Thomas Keller b,c
PMCID: PMC5543947  PMID: 28600344

Root tip shape in wheat is a pivotal trait governing root tip 11 penetration stress and thus root elongation rate in soils of greater strength.

Abstract

Increased soil strength due to soil compaction or soil drying is a major limitation to root growth and crop productivity. Roots need to exert higher penetration force, resulting in increased penetration stress when elongating in soils of greater strength. This study aimed to quantify how the genotypic diversity of root tip geometry and root diameter influences root elongation under different levels of soil strength and to determine the extent to which roots adjust to increased soil strength. Fourteen wheat (Triticum aestivum) varieties were grown in soil columns packed to three bulk densities representing low, moderate, and high soil strength. Under moderate and high soil strength, smaller root tip radius-to-length ratio was correlated with higher genotypic root elongation rate, whereas root diameter was not related to genotypic root elongation. Based on cavity expansion theory, it was found that smaller root tip radius-to-length ratio reduced penetration stress, thus enabling higher root elongation rates in soils with greater strength. Furthermore, it was observed that roots could only partially adjust to increased soil strength. Root thickening was bounded by a maximum diameter, and root tips did not become more acute in response to increased soil strength. The obtained results demonstrated that root tip geometry is a pivotal trait governing root penetration stress and root elongation rate in soils of greater strength. Hence, root tip shape needs to be taken into account when selecting for crop varieties that may tolerate high soil strength.

Crops, like most other terrestrial plant species, acquire essential resources they need for growth from soil. To do so, roots need to grow through soil to access water and nutrient pools. Increased mechanical impedance, which can be caused by compacted soil layers or soil drying, is the major limitation to root elongation and, hence, adversely affects soil exploration and resource uptake (Masle and Passioura, 1987; Materechera et al., 1992; Bengough et al., 2006, 2011; Kautz et al., 2013). Under increased soil strength, roots need to exert higher forces in order to penetrate soil successfully. This leads to higher penetration stresses; therefore, root growth and soil exploration require more energy when soil strength is increased (Atwell, 1990b; Bengough et al., 2011; Ruiz et al., 2015, 2016). When soil mechanical impedance is increased, root elongation rate decreases within hours and may cease entirely, leading to significant yield losses (Bengough and Mullins, 1991; Young et al., 1997; Valentine et al., 2012). The integration of functional root traits, which enable resource acquisition at minimum energetic costs, into breeding programs is a promising approach to improve agricultural productivity under limited soil fertility (Bishopp and Lynch, 2015). Soil penetration mechanics needs to be combined with investigations of the root phenotype in order to identify functional root properties enabling an efficient exploration of high-strength soil.

Plants use different strategies to overcome the limitations imposed by increased soil strength on root growth and crop productivity. Barley (Hordeum vulgare) and wheat (Triticum aestivum) have been found to preferentially increase the extension of their root systems into loose compartments of the soil when other compartments are compacted (Bingham and Bengough, 2003). Furthermore, roots of different cereals, maize (Zea mays) and soybean (Glycine max), have been shown to use natural or artificial macropores as pathways of least resistance in compacted soil or dense subsoils (Stirzaker et al., 1996; White and Kirkegaard, 2010; Colombi et al., 2017). Compensatory root growth into loose compartments and the use of macropores in soils of high strength were found to be beneficial for shoot growth compared with uniformly compacted soil (Stirzaker et al., 1996; Bingham and Bengough, 2003; Colombi et al., 2017). However, to ensure adequate root-soil contact, which is required for the uptake of plant nutrients (Stirzaker et al., 1996; Tracy et al., 2011), roots need to grow into bulk soil.

Root thickening is one of the most common responses of roots when growing through soil with higher mechanical impedance. This adjustment of roots to increased soil strength reduces the risk of root buckling and decreases the mechanical stress acting on the root during penetration (Materechera et al., 1992; Kirby and Bengough, 2002; Chimungu et al., 2015). Root thickening in response to increased soil strength has been observed in a wide range of species under field and laboratory conditions and often coincides with increased cortical area (Atwell, 1990a; Materechera et al., 1992; Grzesiak et al., 2013; Siczek et al., 2013; Chen et al., 2014; Hernandez-Ramirez et al., 2014; Colombi and Walter, 2016). Since root thickening decreases penetration stress and stabilizes roots, thick roots are likely to be an advantage in soils with increased mechanical impedance (Materechera et al., 1992; Kirby and Bengough, 2002; Chimungu et al., 2015). A recent study showed that the genotypic cortical thickness in maize is related to bending strength and, hence, to the risk of root buckling (Chimungu et al., 2015). As a consequence of the increased volume-to-length ratio in thicker roots, plants need to invest more resources into soil exploration when soil strength increases (Atwell, 1990b). Cell turnover and cell detachment rates at the root cap were reported to increase when soil is compacted (Iijima et al., 2003a), which further increases the metabolic costs of root growth and resource acquisition. These cells, which are released from the root cap into the rhizosphere, act together with mucilage as a lubricant, reducing the interfacial friction between the growing root tip and the soil (Bengough and McKenzie, 1997; McKenzie et al., 2013).

There is evidence that the penetrability of soil is influenced not only by the diameter of the root but also by the geometry of the root tip. Model predictions have shown that the stress experienced by a growing root is concentrated around the root tip (Kirby and Bengough, 2002). Simulations of stress field distributions around cones inserted into soil show that this distribution changes with changing cone geometry. For cones with an acute opening angle, the stress field is distributed around the cone, whereas for blunt cones, the stress field is located at the cone forefront (Ruiz et al., 2016). Similar results were obtained when comparing local soil compaction that was induced by growing roots between maize roots lacking an intact cap and maize roots with a cap (Vollsnes et al., 2010). These findings can be related to the form of cavity expansion and the soil deformation pattern. Blunting of a root tip or a cone leads to a shift from a rather cylindrical to a more spherical deformation pattern, which causes penetration forces and stresses to increase (Greacen et al., 1968). This increase has been shown to happen when root tips are blunted due to the removal of the root cap (Iijima et al., 2003b). Furthermore, the lack of a root cap results in decreased root elongation rates in comparison with roots with an intact cap (Iijima et al., 2003b; Vollsnes et al., 2010). The forces and stresses that occur at a root tip during soil penetration can be measured directly in soil (Iijima et al., 2003b) or in free air and nutrient solutions (Misra et al., 1986; Bengough and Kirby, 1999; Azam et al., 2013; Bizet et al., 2016). As an alternative, cone penetrometer measurements combined with quantifications of root tip and cone geometry can be used to calculate root tip penetration forces and stresses (McKenzie et al., 2013). Despite the available information, mechanical processes governing root elongation are still poorly understood (Bengough et al., 2011). Thus, conclusive information about root traits that may improve soil penetrability, resource acquisition, and crop productivity when soil strength is increased is missing.

The aims of this study were (1) to quantify whether and how the genotypic diversity of root tip geometry and root diameter are related to root elongation rate in soil of different strengths and (2) to quantify adjustments in root tip properties, root morphology, and root anatomy to increased mechanical impedance. This information was then used to (3) discuss the mechanical and physiological implications of the observed genotypic differences and phenotypic adjustments to increased soil strength. Experiments were performed with 14 winter wheat cultivars in soil columns with bulk densities of 1.3, 1.45, and 1.6 g cm−3, representing loose, moderately, and severely compacted soil, respectively. Root tip geometry, morphology, and elongation rate in 2-d-old seedlings were quantified from high-resolution flatbed scans. Combining this information with cone penetrometer tests enabled root penetration forces and stresses occurring during growth to be calculated. Furthermore, root morphology and anatomy were quantified in embryonic and postembryonic roots of 23-d-old plants.

RESULTS

The axial penetration force obtained from cone penetrometer measurements (semiapex angle, 30°; base radius, 2.5 mm) at −100 hPa matric potential was 6.7 n (se = 0.8), 8.7 n (se = 0.3), and 20.9 n (se = 2.1) for soil bulk densities of 1.3, 1.45, and 1.6 g cm−3, respectively (n = 4). Thus, mechanical impedance calculated for the cone penetrometer was 0.34 MPa (se = 0.04), 0.44 MPa (se = 0.01), and 1.06 MPa (se = 0.1) under low, moderate, and high soil bulk density, respectively.

Effects of Soil Mechanical Impedance and Genotype on Root Elongation Rate, Root Tip Properties, and Root Diameter

Soil mechanical impedance affected root morphology and root growth in 2-d-old seedlings. Since the shoot had not yet emerged, the influence of photosynthesis on root elongation could be excluded. Increased mechanical impedance resulted in reduced root length and root volume. The root elongation rate decreased by 40% and 64% under moderate and high soil bulk density, respectively, compared with roots grown in low-density soil (Table I). Root volume also decreased significantly, but the decrease was smaller than that in length, because root diameter increased with increasing soil mechanical impedance. Root shaft diameter, which was determined as the mean of three random diameter measurements along the root, increased with soil strength. Increases in soil bulk density from 1.3 to 1.45 and to 1.6 g cm−3 resulted in increases in root diameter of 16% and 44%, respectively (Table I). The geometry of the root tip was determined from high-resolution flatbed scans with a pixel edge length of 0.1 mm using an automated image-processing tool (Fig. 1). These scans showed that the radius and the length of the root tip increased significantly under high soil strength compared with low and moderate soil strength (Table I). The shape of the root tip was quantified as the inverse of the shape factor for a cone (Eq. 11) or half spheroid (Eq. 12), respectively. Both factors were calculated using information on root tip radius and length. Despite the effects of soil strength on the size of the root tip, the geometry of the root tip was not affected significantly by increasing soil mechanical impedance (Table I).

Table I. Effects of genotype (GT), soil bulk density (BD), and their interaction on root tip geometry and root morphology after 48 h of growth, analyzed with ANOVA.

Trait ANOVA
 Bulk Density Average
GT BD GT-BD 1.3 g cm−3 1.45 g cm−3 1.6 g cm−3
Tip radius (mm) P = 0.06 ** n.s. 0.255 a 0.264 a 0.300 b
Tip length (mm) * ** n.s. 1.13 a 1.16 a 1.31 b
iSFcone (mm mm−1) ** n.s. n.s. 0.230 0.232 0.233
Tip semiopening angle (°) ** n.s. n.s. 13.1 13.0 13.2
iSFspheroid (mm mm−1) ** n.s. n.s. 0.148 0.147 0.148
Root tip base area (mm2) P = 0.08 ** n.s. 0.206 a 0.221 a 0.290 b
Root length (mm) ** ** n.s. 45.45 a 27.45 b 16.35 c
Root elongation rate (mm d−1) ** ** n.s. 22.73 a 13.72 b 8.17 c
Root diameter (mm) ** ** * 0.524 a 0.609 b 0.754 c
Root volume (mm3) ** ** n.s. 10.01 a 8.05 b 7.35 b
Open in a new tab

Asterisks denote significant effects at P < 0.05 (*) and P < 0.01 (**); n.s. denotes nonsignificant effects (n = 6). Different letters indicate significant differences between different soil bulk densities using Tukey’s honestly significant difference test at P < 0.05. iSF, Inverse of cone (rroot tip/lroot tip) and spheroid shape factor (2rroot tip/πlroot tip); rroot tip, radius at the base of a root tip, lroot tip, length of a root tip.

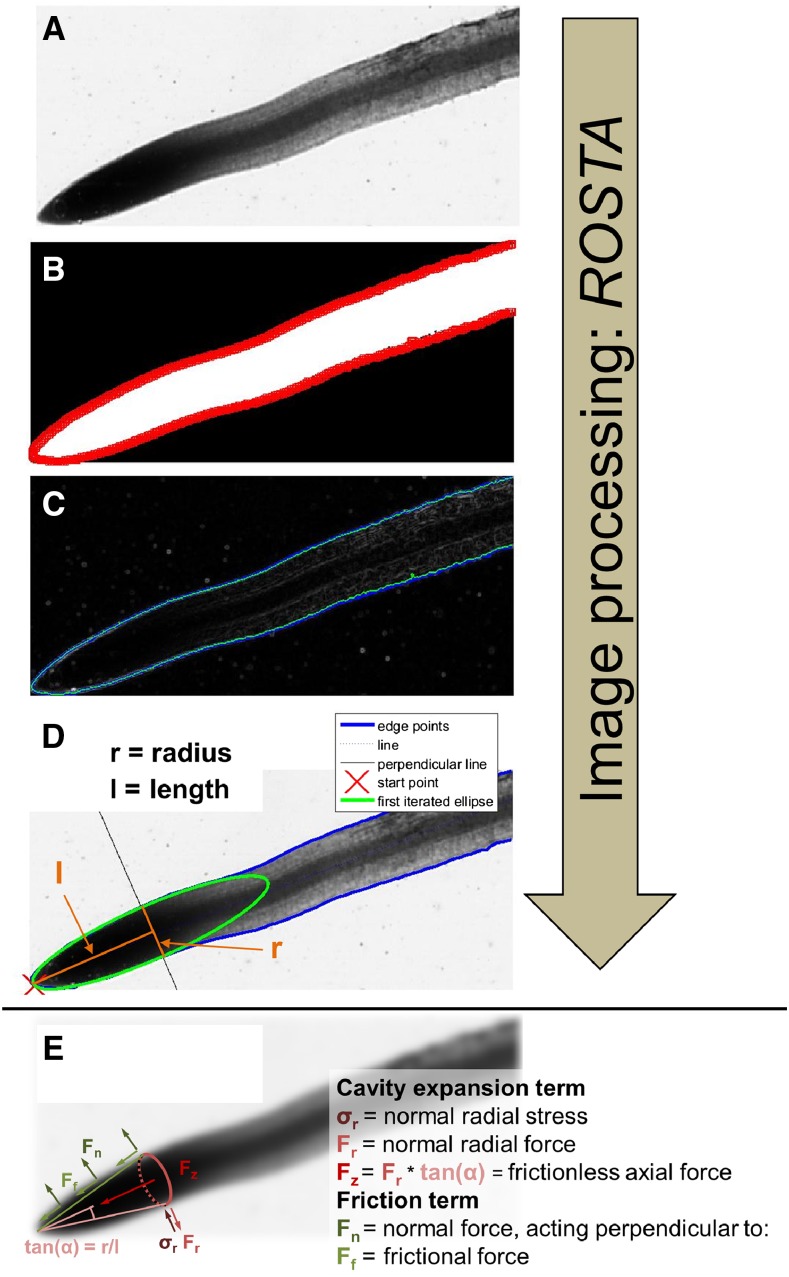
Figure 1.

Figure 1.

Open in a new tab

Image processing and determination of root tip geometry using Root Scan Tip Analysis (ROSTA) software. A, Area of interest containing a root tip with a pixel edge length of ∼0.01 mm. B, Segmented root tip and contour. C, Refinement of the contour using active fitting. D, Fitting of the ellipse on the refined root tip boundary and determination of root tip radius and length. E, Schematic representation of different force components used to calculate total axial force exerted by the root tip during elongation in soil.

Apart from the radius and the area at the base of the root tip, root properties determined in 2-d-old seedlings were influenced significantly by genotype. Genotypic differences were observed for root elongation rate (Supplemental Fig. S1) and root volume as well as root tip length and root shaft diameter (Table I). Particularly under high soil bulk density (1.6 g cm−3), significant genotypic diversity was observed for root tip geometry (Supplemental Fig. S1). To assess the genotypic variability among the cultivars, broad-sense mean-based heritability (Eq. 13) was calculated. Heritability estimations of 51%, 57%, and 80% were obtained for root tip geometry, root diameter, and elongation rate, respectively, indicating considerable genotypic variability among the assessed cultivars (Supplemental Table S1). Analysis of covariance models applied on treatment level mean values showed that root tip geometry significantly affected root elongation rate, whereas for root diameter this was not observed (Table II).

Table II. Summary statistics from an analysis of covariance model of root length as influenced by root tip geometry or root diameter, soil bulk density (1.3, 1.45, or 1.6 g cm−3), and their interaction, based on mean values (n = 6) of genotype-bulk density combinations.

Assumed Root Tip Shape Effect Root Elongation Rate
mm d−1
Cone Bulk density 121.1**
iSFcone 5.2*
Bulk density:iSFcone 0.5 n.s.
R2 0.87
Spheroid Bulk density 121.1**
iSFspheroid 5.2*
Bulk density:iSFspheroid 0.5 n.s.
R2 0.87
Bulk density 107.3**
dmroot 0.1 n.s.
Bulk density:dmroot 18.8 n.s.
R2 0.86
Open in a new tab

Numbers indicate F values. Asterisks denote significant effects at P < 0.05 (*) and P < 0.01 (**); n.s. denotes nonsignificant effects. iSF, Inverse of cone (rroot tip/lroot tip) and spheroid shape factor (2rroot tip/πlroot tip); rroot tip, radius at the base of a root tip; lroot tip, length of a root tip; dmroot, root diameter.

Influence of Root Tip Geometry and Root Diameter on Root Elongation Rate

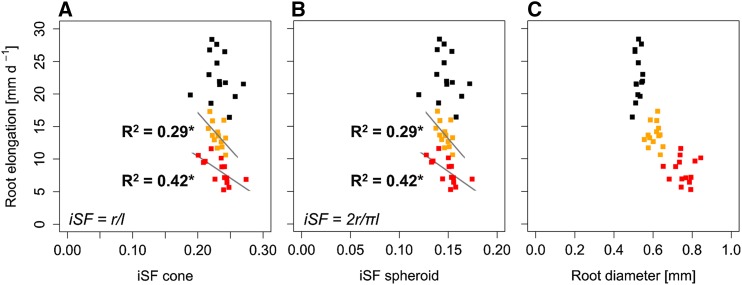
As indicated by the results obtained from analysis of covariance (Table II), root tip geometry was related to root elongation rate. The genotypic diversity of root tip geometry resulted in different root elongation rates, an effect that was particularly pronounced under high soil bulk density (Fig. 2). Root tip radius-to-length ratio, which was used to calculate the inverted shape factor of the conical and spheroid tip geometry (Eqs. 11 and 12), was negatively correlated to root elongation rate (R2 = 0.42, P < 0.05) in the soil with bulk density of 1.6 g cm−3. A similar relationship was observed under moderately increased soil bulk density (1.45 g cm−3), whereas under low soil bulk density (1.3 g cm−3), root tip geometry was not related to root elongation rate (Fig. 3). Despite significant genotypic effects on root diameter (Table I), no significant correlation between root elongation rate and root diameter could be observed under any of the soil bulk densities tested (Fig. 3). Similar to root elongation rate, root volume was negatively correlated (R2 = 0.44, P < 0.01) with root tip radius-to-length ratio under high soil bulk density (Supplemental Fig. S2). These results strongly suggest that the shape of the root tip is a better predictor than root diameter for genotypic root elongation rate under increased soil strength. Seed dry weight, which was determined as a measure of initial energy reserves, was not correlated to root elongation rate, root volume, or root diameter (Supplemental Fig. S3).

Figure 2.

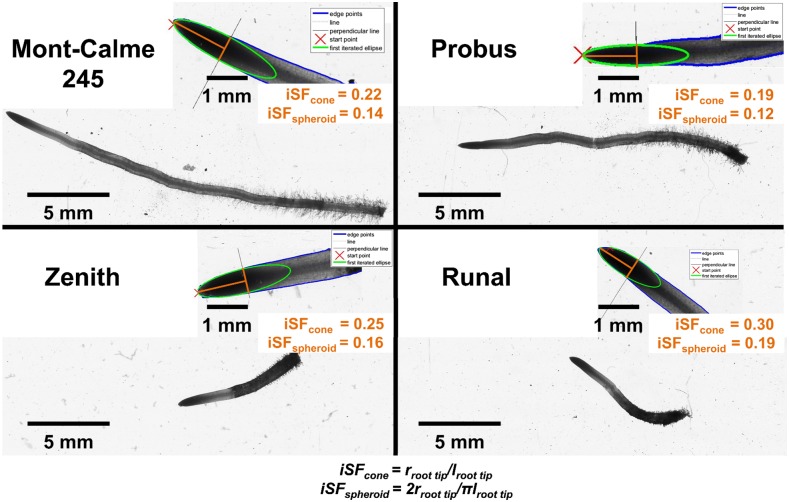
Figure 2.

Open in a new tab

Illustration of the genetic diversity of root tip geometry expressed as the inverse shape factor (iSF) of a cone or spheroid and root length after 48 h of growth into soil with 1.6 g cm−3 bulk density. Mont-Calme 245 and Probus represent genotypes with a small iSF, whereas Zenith and Runal are characterized by a large iSF.

Figure 3.

Figure 3.

Open in a new tab

Influence of root tip geometry and root diameter on root elongation rate determined in 14 wheat genotypes (n = 6). Linear regressions are shown between root elongation rate and inverse shape factor (iSF; calculated using root tip radius [r] and length [l]) of a cone (A) and a spheroid (B) geometry and root diameter (C). Black, orange, and red symbols represent soil bulk density of 1.3, 1.45, and 1.6 g cm−3, respectively. Asterisks denote significant regression at P < 0.05.

Relating Root Penetration Forces and Stresses to Root Elongation Rate and Root Diameter

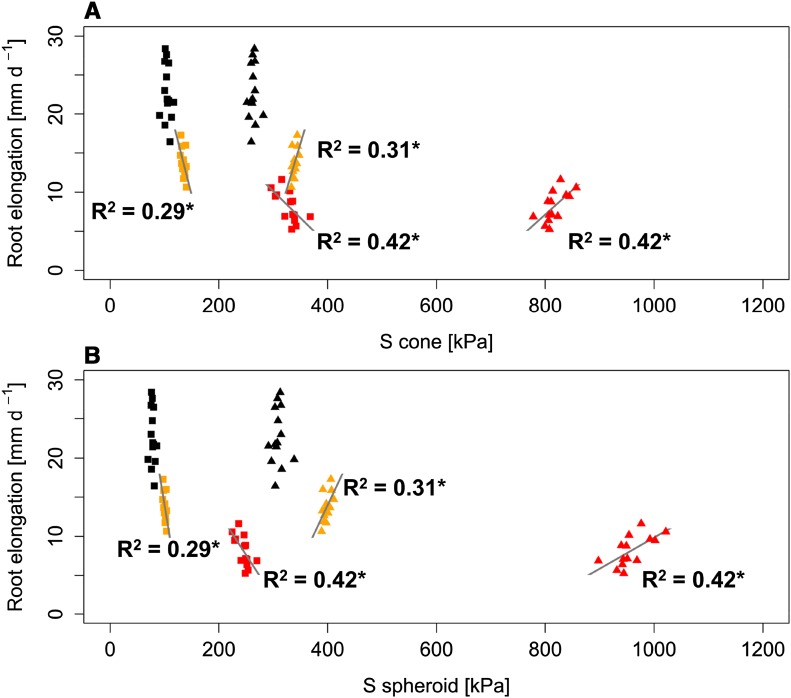
Combining cone penetrometer measurements with information about the geometry of the cone and the root tips permitted the calculation of penetration forces (Eqs. 6 and 8) and stresses (Eqs. 9 and 10) occurring at the root tip during root elongation. Penetration forces and stresses are known to be influenced by the geometry of the tip and the resulting soil deformation field around the root tip. To account for the differences in tip geometry between the steel cone and the roots and between the roots of different genotypes (Table I; Supplemental Fig. S1), we introduced a geometry factor (GF; Eqs. 11 and 12). The values for GF ranged from 0.33 to 0.48 if root tips were assumed to have a conical shape and from 0.21 to 0.3 if root tips were assumed to have a spheroid shape (Supplemental Table S2). Calculated penetration forces ranged between 19 and 143 mn under the assumption of a conically shaped root tip and from 14 to 105 mn for a spheroid tip shape. The resulting root tip penetration stresses were between 91 and 368 kPa and between 69 and 270 kPa for conical and spheroid tip geometry, respectively (Supplemental Table S3). Calculated genotype mean penetration stresses were significantly related to root elongation rate under high (R2 = 0.42, P < 0.05) and moderate (R2 = 0.29, P < 0.05) soil strength. Lower root tip penetration stress resulted in increased root elongation rate under high and moderate soil strength, whereas under low soil bulk density, no such correlation was observed (Fig. 4). It is worth mentioning that these relationships changed when the differences in tip geometry and, hence, the form of the cavity were not taken into account. The exclusion of GF in the calculations of penetration stresses resulted in positive correlations between root tip penetration stress and the root elongation rate (Fig. 4). Furthermore, root tip and root shaft diameter was not related significantly to root tip penetration stress under any of the assessed levels of soil strength (Supplemental Fig. S4).

Figure 4.

Figure 4.

Open in a new tab

Linear regressions between root tip penetration stress (S) and root elongation rate determined in 14 wheat genotypes (n = 6) for conical (A) and spheroid (B) root tip geometry. Penetration stresses were calculated excluding (triangles) or including (squares) GFs (Eqs. 11 and 12). Black, orange, and red symbols represent soil bulk density of 1.3, 1.45, and 1.6 g cm−3, respectively. Asterisks denote significant regression at P < 0.05.

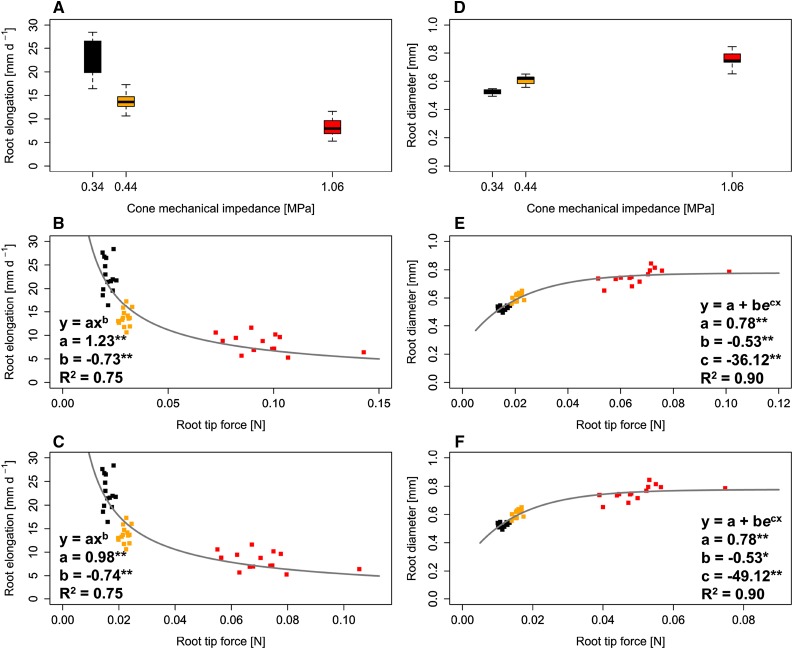
Figure 5 presents root elongation rate and root shaft diameter as functions of calculated penetration forces exerted by roots while elongating in soil. Axial root tip penetration force was related to root elongation rate following a negative power law function (R2 = 0.75) for both conical (Eqs. 6 and 10) and spheroid (Eqs. 8 and 11) tip shape. An exponential function, which asymptotically approached an upper limit, was used to relate root shaft diameter and root tip penetration force (R2 = 0.90). For both tip geometries assumed, this upper limit was at a root diameter of 0.78 mm (Fig. 5), suggesting that adjustment to increased soil strength in the form of root thickening is limited. The same relationships between root tip penetration force and root elongation rate and root diameter, respectively, were obtained when GF was excluded from the calculations (Supplemental Fig. S5).

Figure 5.

Figure 5.

Open in a new tab

Root elongation rate (A–C) and diameter (D–F) of 14 wheat genotypes (n = 6) grown at soil bulk densities of 1.3 (black), 1.45 (orange), and 1.6 (red) g cm−3. A and D, Cone mechanical impedance was obtained from penetrometer measurements. B, C, E, and F, Root tip radial force for conical (B and E) and spheroid (C and F) geometry was calculated according to Equations 11 and 12. Asterisks denote significant regression coefficients at P < 0.05 (*) and P < 0.01 (**).

Effects of Soil Mechanical Impedance and Genotype on Root Anatomy

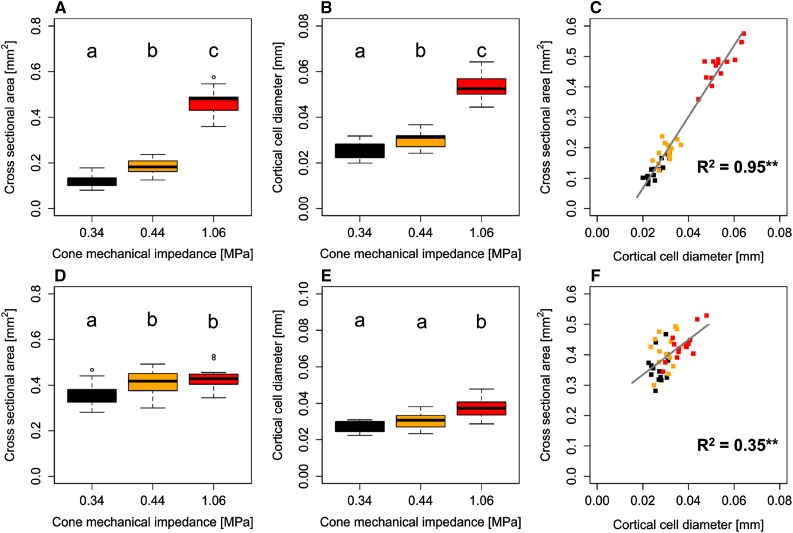
In embryonic and postembryonic roots of 23-d-old plants, root cross-sectional area, the area of the stele and the root cortex, as well as the cortical cell file number were affected significantly by genotype (Table III). Remarkably, the observed root anatomical responses to increased soil strength were not always consistent between embryonic and postembryonic roots. In embryonic roots, the cross-sectional area increased from 0.12 mm2 under low soil bulk density to 0.19 mm2 under moderate soil bulk density and to 0.47 mm2 under high soil bulk density. In postembryonic roots, this response was much less pronounced, and no significant difference was observed between roots grown under moderate and high bulk density (Fig. 6). The average root cross-sectional area under high soil bulk density corresponded to calculated root diameters of 0.77 and 0.74 mm in embryonic and postembryonic roots, respectively (Table III). These values coincided well with the upper limit of 0.78 mm, to which root diameters of 2-d-old seedlings asymptotically converged with increasing penetration force (Fig. 5). Similar results were obtained for root cortical area and cortical cell file number, both of which increased in embryonic roots with increasing soil mechanical impedance. In postembryonic roots, however, cortical area was less affected and cell file number remained unaffected by soil bulk density (Table III). The stele cross-sectional area of embryonic roots increased due to soil compaction, whereas in postembryonic roots, the stele area decreased in response to compaction (Table III).

Table III. Effects of genotype (GT), soil bulk density (BD), and their interaction on root anatomical traits in embryonic and postembryonic roots after 23 d of growth, analyzed with ANOVA.

Root Class Trait ANOVA
 Bulk Density Average
GT BD GT-BD 1.3 g cm−3 1.45 g cm−3 1.6 g cm−3
Embryonic Cross-section area (mm2) ** ** n.s. 0.123 a 0.186 b 0.469 c
Stele area (mm2) ** ** * 0.049 a 0.059 b 0.059 b
Cortical area (mm2) * ** n.s. 0.074 a 0.128 b 0.410 c
RCA (mm2) n.s. ** n.s. 0.002 a 0.011 a 0.088 b
RCA (%) n.s. ** n.s. 1.6 a 7.6b 21.8 c
Cortical cell file number ** ** * 2.3 a 3.0b 4.9 c
Cortical cell diameter (mm) * ** n.s. 0.025 a 0.030 b 0.053 c
Postembryonic Cross-section area (mm2) ** ** n.s. 0.359 a 0.413 b 0.430 b
Stele area (mm2) ** ** n.s. 0.079 a 0.080 a 0.065 b
Cortical area (mm2) ** ** n.s. 0.281 a 0.333 b 0.365 b
RCA (mm2) ** ** n.s. 0.084 a 0.102 b 0.111 b
RCA (%) n.s. n.s. n.s. 29.9 30.5 30.3
Cortical cell file number ** n.s. ** 6.3 6.5 6.2
Cortical cell diameter (mm) n.s. ** n.s. 0.027 a 0.030 a 0.037 b
Open in a new tab

Asterisks denote significant effects at P < 0.05 (*) and P < 0.01 (**); n.s. denotes nonsignificant effects (n = 4). Different letters indicate significant differences between levels of soil strength using Tukey’s honestly significant difference test at P < 0.05. RCA, Root cortex aerenchyma.

Figure 6.

Figure 6.

Open in a new tab

Root anatomy in embryonic (A–C) and postembryonic (D–F) roots of 14 wheat genotypes 23 d after planting. A and D, Total root cross-sectional area. B, C, E, and F, Cortical cell diameter (B and E) and linear correlations between cross-sectional area and cortical cell diameter (C and F), based on treatment means (n = 4). Colors indicate soil bulk density (black, 1.3 g cm−3; orange, 1.45 g cm−3; red, 1.6 g cm−3). Different letters indicate significant differences using Tukey’s honestly significant difference test at P < 0.05. Asterisks denote significant regression at P < 0.01 (**).

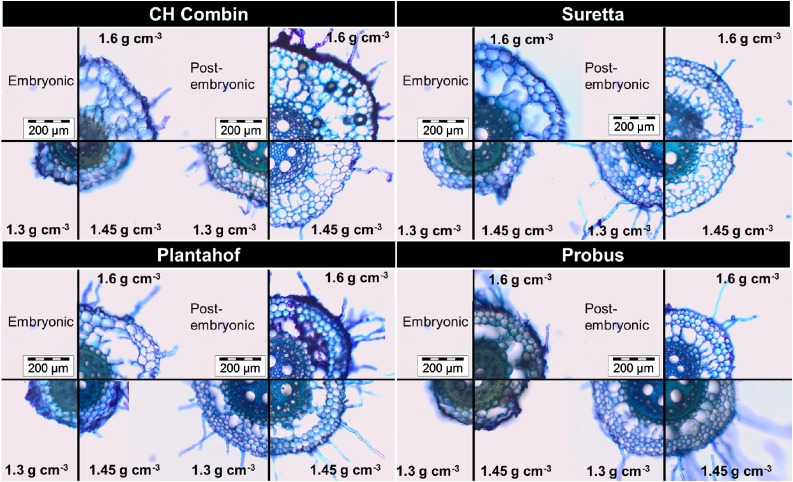
Consistent responses to increased soil strength between both root classes were observed for root cortex aerenchyma and cortical cell diameter. In embryonic roots, the percentage of the root cortex occupied with aerenchyma was several orders of magnitude higher under moderate and high soil bulk density when compared with roots from the low bulk density treatment. In particular, under high soil bulk density, aerenchyma formation in embryonic roots was far advanced. Hence, the quantified response also could have resulted from cortical senescence (Fig. 7). No difference in the proportion of aerenchyma within the cortex of postembryonic roots was observed between different levels of soil bulk density. The area of root cortex aerenchyma increased significantly in response to increased soil strength in both root classes (Table III). Cortical cell diameter increased in response to increased soil bulk density (Fig. 6) and coincided, particularly under high bulk density, with increasing root cross-sectional area (Fig. 7). Linear regressions between root cross-sectional area and cortical cell diameter showed that root thickening in response to increased soil strength was related to increased cortical cell diameter in both embryonic (R2 = 0.95, P < 0.01) and postembryonic (R2 = 0.35, P < 0.01) roots (Fig. 6). Despite the differences between different root classes, these results showed that root morphological adjustments to soil compaction in the form of root thickening coincided with increased cortical cell diameter and an accelerated formation of cortical aerenchyma.

Figure 7.

Figure 7.

Open in a new tab

Illustration of genotypic diversity in root anatomy sampled 23 d after planting 3 cm from the root base of embryonic and postembryonic roots under soil bulk densities of 1.3, 1.45, and 1.6 g cm−3.

DISCUSSION

The quantification of root traits in 14 wheat genotypes allowed the identification of functional root traits that determine genotypic root elongation rates under increased soil strength. Furthermore, it proved possible to show how and to what extent roots may adjust to increased mechanical impedance with respect to root tip properties, root morphology, and anatomy. Combining this phenotypic information with calculated penetration forces and stresses revealed mechanical and physiological implications of genotypic differences and root phenotypic adjustments to increased soil strength.

The root elongation rate decreased with increasing soil bulk density (Table I), which is in agreement with previous findings (Atwell, 1990a; Bengough and Mullins, 1991; Young et al., 1997; Jin et al., 2013; Colombi and Walter, 2016). However, while the root elongation rate decreased with increasing soil strength in all genotypes assessed, the magnitude of this response differed significantly between genotypes (Table I). Significant genotypic differences and considerable degrees of heritability were observed for root elongation rate, root diameter, and root tip shape and size (Table I; Supplemental Table S1). Under high soil bulk density (1.6 g cm−3) in particular, but also under moderate soil bulk density (1.45 g cm−3), it was observed that genotypic root elongation rate correlated with root tip shape. Roots of genotypes with a small root tip radius-to-length ratio elongated faster in soil with high and moderate soil bulk density compared with roots of genotypes with a rather large root tip radius-to-length ratio (Fig. 3). Similar results have been reported for root cap removal, which results in blunted root tips, on root elongation in maize (Iijima et al., 2003b; Vollsnes et al., 2010). This effect of root tip geometry on root elongation rates could be attributed to the distribution of local soil compaction around the root tip induced by the growing root. The lack of an intact root cap resulted in increased penetration stress (Iijima et al., 2003b) due to increased soil compaction at the tip forefront rather than around the tip, as observed for roots with intact caps (Vollsnes et al., 2010). Theoretical considerations showed that a smaller tip radius-to-length ratio causes a shift in the form of cavity expansion from a more spherical to a rather cylindrical deformation field (Greacen et al., 1968; Ruiz et al., 2016). Moreover, Ruiz et al. (2016) found that differences between measured and modeled penetration stress in cone penetrometer experiments are influenced by the cone geometry. Bengough et al. (2016) found that root hairs may support root penetration by anchoring the root to the surrounding soil. Hence, there might be synergistic effects between root tip geometry and the abundance of root hairs that further influence root elongation in high-strength soils.

Based on the observed correlations between root tip shape and root elongation rate, a factor (GF; Eqs. 11 and 12) was introduced in this study to account for the influence of genotypic differences in root tip geometry on the form of cavity expansion. It was shown that decreased penetration stress caused by a smaller root tip radius-to-length ratio (Eqs. 11 and 12) resulted in an increased elongation rate under high and moderate soil bulk density (Fig. 4). Inclusion of the GF resulted in penetration forces and stresses that were between 25% and 44% of the values calculated without the GF (Supplemental Table S3). These reductions are almost identical to the values presented by Greacen et al. (1968). Penetration force was highly correlated (R2 = 0.75) with root elongation rate, following a negative power law function (Fig. 5). We are aware that the reported penetration forces and stresses may differ from the actually occurring values. In this study, the radial stress of cavity expansion (σr) was assumed to be the same for the steel cone and root tip despite their differing diameters. Furthermore, the different penetration rates of roots (0.004–0.02 mm min−1) and the cone penetrometer (4 mm min−1) might further influence penetration forces and stresses (Bengough et al., 1997). However, the penetration forces and stresses as calculated in this study (Eqs. 1–12) are within the range of previously reported results for different plant species (Misra et al., 1986; Bengough and McKenzie, 1997; Iijima et al., 2003b; Azam et al., 2013; Bizet et al., 2016).

It has been argued that root diameter is a crucial trait for root growth in compacted soil, since thick roots may reduce penetration stress and prevent the buckling of roots (Materechera et al., 1992; Chimungu et al., 2015). In this study, genotypic differences in root diameters (Table I) were not related to root elongation rate (Fig. 3) or penetration stress (Supplemental Fig. S4), and root buckling was not observed. As observed for different small-grain cereals in previous studies (Barraclough and Weir, 1988; Materechera et al., 1992; Grzesiak et al., 2013; Hernandez-Ramirez et al., 2014; Colombi and Walter, 2016), root diameters of 2-d-old seedlings increased with increasing soil bulk density (Table I). However, the data obtained from our study strongly suggest that this acclimation of root morphology to increased soil strength was limited by a maximum root diameter. This limitation was observed when comparing root thickening in response to increased bulk density between embryonic and postembryonic roots, which was determined in 23-d-old plants (Fig. 6). In embryonic roots, average root cross-sectional area increased clearly with increasing soil bulk density (Table III). In postembryonic roots, which are inherently thicker than embryonic roots, this response was much less pronounced and root cross-sectional area was similar under moderate and high soil bulk density (Table III). The same conclusions were reached on examining the regression between root tip penetration force and root diameter (Fig. 5). This relationship closely followed an exponential function that asymptotically converged to an upper limit (R2 = 0.90), which may be interpreted as a maximum root diameter. It is worth noting that this upper limit, which was 0.78 mm, corresponded to the diameter calculated from the observed average cross-sectional area of embryonic and postembryonic roots under high bulk density (Table III). To our knowledge, such saturation of phenotypic or physiological adjustment in response to soil physical stress has not been reported previously. The saturation of phenotypic or physiological adjustment has been observed for root exudation in response to increasing aluminum toxicity (Pellet et al., 1995; Li et al., 2000) and for the activity of antioxidative enzymes with increasing shoot manganese concentrations (de la Luz Mora et al., 2009). The limitation of root thickening as observed in this study can be most likely explained by root surface-to-volume ratio, which is critical for nutrient and water uptake (Varney and Canny, 1993; Casper and Jackson, 1997). A further increase in root diameter would probably have resulted in root surface-to-volume ratios being too low for an adequate supply of water and nutrients. The finding that there was no significant adjustment of root tip shape in response to increased bulk density (Table I) is a further indication of the limited potential of roots to adjust to increased soil strength.

Results from previous studies suggest that the metabolic costs of root elongation increase with increasing soil strength due to lower root length-to-volume ratios (Atwell, 1990b) and due to increased root meristem activity and cell detachment rate at the root cap (Iijima et al., 2003a). The results from this study support these findings, since root diameter and root tip size (Table I) were increased in response to increased soil strength. Furthermore, root anatomical properties indicated that plants seek to counterbalance the increased energy demand by altering the anatomy of the root cortex. As shown before (Atwell, 1990a; Colombi and Walter, 2016), high soil strength led to an increased abundance of root cortical aerenchyma and increased cortical cell diameter (Table III). A high abundance of aerenchyma, accelerated cortical senescence, and large cortical cells enable the plant to reduce the metabolic costs of soil exploration (Chimungu et al., 2014; Saengwilai et al., 2014; Schneider et al., 2017), which may fuel root growth under conditions of abiotic stress such as increased soil strength. In these and this study, root anatomy was determined near the root base, whereas mechanical stress is perceived primarily at the root tip (Kirby and Bengough, 2002). Therefore, these root anatomical properties cannot be related directly to the energy that is required for root penetration but rather to the energy that is consumed in the already grown root. However, it has been shown that the penetration stress relates to the energy requirements of soil penetration (Ruiz et al., 2015). Taking into account the influence of root tip shape on the form of cavity expansion and the resulting penetration stress (Greacen et al., 1968; Ruiz et al., 2016) strongly suggests that the root tip shape governs not only the root elongation rate but also the energy needed for root elongation in soils of increased strength. Therefore, root tips with a small radius-to-length ratio are a promising target trait that can be integrated into plant breeding programs aiming to develop crop cultivars that can better explore soils of increased strength at low metabolic costs.

CONCLUSION

In this study, it was shown that the shape of the root tip in wheat is a pivotal trait determining genotypic root elongation rate in soil of increased strength. Combining information about the geometry of the root tip with cone penetrometer measurements and cavity expansion theory enabled us to relate the root elongation rate with root tip geometry. A small root tip radius-to-length ratio resulted in lower penetration forces and stresses due to a more cylindrical form of cavity expansion. Roots could only partially adjust to increased mechanical impedance, since root tips of a certain genotype did not become more acute with increasing soil strength and root thickening was limited. Hence, the geometry of the root tip and the resulting penetration forces and stresses must be taken into account when selecting for crop varieties that tolerate high-strength soils. Future studies could investigate how synergistic effects between root tip geometry, root hairs, and the allocation of photoassimilates to roots relate to root growth in soils of increased strength.

MATERIALS AND METHODS

Soil Physical Conditions, Plant Material, and Growth Conditions

The soil used was homogenized and sieved field soil (2 mm) that was excavated from the top 15 cm of an agricultural field at Agroscope Zurich (8°31′E, 47°27′N, 443 m above sea level). The soil is classified as a Pseudogleyed Cambisol with a topsoil pH (CaCl2) of 6.9. The textural composition is 25% clay, 50% silt, and 25% sand, and the organic carbon content in the topsoil is 1.7%. After sieving, the soil was stored at 3°C until further use. Different levels of soil mechanical impedance were achieved by different packing densities. The soil was packed in six layers of 2 cm height into PVC columns of 4.9 cm diameter and 15 cm height to low (1.3 g cm−3), moderate (1.45 g cm−3), and high (1.6 g cm−3) soil bulk density. The surface of each layer was slightly abraded to ensure homogenous packing. In addition, four soil cores of 5.1 cm diameter and 5 cm height per soil bulk density treatment were packed in 1-cm layers and slowly saturated from below. They were equilibrated on a ceramic plate to determine gravimetric water content at −100 hPa suction potential, which is commonly taken to represent field capacity (Schjonning and Rasmussen, 2000). Soil mechanical impedance was measured by two individual cone penetrometer insertions into the center of the bottom of these soil cores at an insertion speed of 4 mm min−1. The steel cone used (2.5 mm radius, 4.33 mm length, semiopening angle of 30°) had a recessed shaft and was connected to a force transducer (LC 703; Omega Engineering). To calculate the mean penetration force, values from the point at which the cone was fully inserted into the soil to 1.5 cm penetration depth were averaged (∼650 force measurements).

Experiments were conducted with 14 Swiss winter wheat (Triticum aestivum) cultivars released from public breeding programs between 1910 and 2010 (Supplemental Table S4). The plants were grown in a growth chamber at 63% relative humidity and an average temperature of 21.4°C with a day/night cycle of 14/10 h. Incident light was 510 (sd = 33) µmol s−1 m−2, and soil moisture was kept constant at a gravimetric water content corresponding to −100 hPa by daily weighing and watering during the duration of the experiments. To have a measure for initial carbon reserves of each cultivar, 200 seeds were dried at 60°C for 48 h and weighed.

Experiment 1: Root Tip Geometry, Morphology, and Root Elongation Rate

Root Growth and Image Acquisition

Seeds were pregerminated at 25°C for 48 h. For each soil bulk density-genotype combination, four seeds of similar size in which the tip of the first embryonic roots were just visible were selected. They were placed with the emerging roots facing downward into a small pit of around 5 mm height and 3 mm diameter pinched out from the soil and then covered with loose soil (1 g cm−3). To ensure that roots were penetrating the soil and to avoid artifacts of root pull-out effects, the soil columns were covered with cotton tissue and a perforated steel plate. Limiting the growth period to 48 h ensured that root growth was only fueled by seed-derived carbon, as shoots did not yet emerge at the soil surface. After this period, roots were washed out from the soil, and for each treatment level, six individual roots, which were not touching the border of the PVC column, were selected, fixed in acetic formaldehyde:alcohol:acetic acid:distilled water (10:50:5:35), and stored at 3°C. The roots were scanned in a flatbed scanner (Epson Expression 11000 XL; Seiko Epson) at a resolution of 2,400 dpi, resulting in a pixel edge length of 10.6 μm.

Image Processing

Root tip geometry was analyzed using a novel tool called ROSTA, which was programmed in a MatLab 2016a environment (Mathworks). In ROSTA, regions of interest containing single root tips are selected manually from the scans obtained, while subsequent steps run completely automatically. Using the method of Otsu (1979), root tips were segmented from the background, and the perimeter of the root tip was recognized. The root tip perimeter was then refined by applying an active contour on the gray value gradient as a feature map (inspired by Blake and Isard, 1998), and an ellipse was fitted on the refined root tip boundary. To do so, the boundary point closest to the best-fit line was taken as the initial point, around which 25 points in both directions along the root tip perimeter were taken into account for a first fit of the ellipse. The second and final fit of the ellipse was based on all boundary points located in the half of the ellipse facing the root tip (Mitchell, 2008). Root tip length and root tip radius were then determined as the semimajor and semiminor axes of the ellipse, respectively (Fig. 1). Root length and root diameter were measured manually in ImageJ version 1.50b (National Institutes of Health). Root shaft diameter was measured at three random positions along the root and averaged. Since the root tip diameter was slightly smaller than the diameter along the root shaft, root volume was calculated using the average of the three manual diameter measurements along the root.

Calculation of Root Penetration Force and Stress

The total axial force measured with a cone penetrometer (FZ C) is composed of a radial cavity expansion term and a tangential friction term (Greacen et al., 1968; Bengough and Mullins, 1990, 1991; Ruiz et al., 2016). Based on cavity expansion theory, Ruiz et al. (2016) showed that the radial force exerted by the cone (Fr C) can be calculated as:

graphic file with name PP_PP2017RA00357R1_equ1.jpg (1)

where rC is the radius at the cone basis, αC is the semiapex angle of the cone, and σr is the radial stress. The frictionless axial force (Fz C), or cavity expansion term, is then:

graphic file with name PP_PP2017RA00357R1_equ2.jpg (2)

To calculate the total axial force for the cone (FZ C), the frictional force (Ff,z C) between the cone surface and the soil has to be considered, yielding (Ruiz et al., 2016):

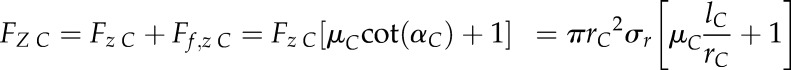graphic file with name PP_PP2017RA00357R1_equ3.jpg (3)

where µC, rC, and lC represent the interfacial friction coefficient, the base radius, and the length of the cone, respectively. The radial stress (σr) is then readily calculated as:

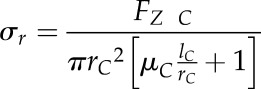graphic file with name PP_PP2017RA00357R1_equ4.jpg (4)

Assuming a conical shape of the root tip, the total axial force of the root tip (FZ Rc) is:

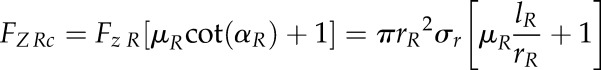graphic file with name PP_PP2017RA00357R1_equ5.jpg (5)

where rR and lR represent the base radius and the length of the root tip, respectively. Substituting Equation 4 into Equation 5 allows calculating the total axial penetration force exerted by a root tip during soil penetration under the assumption of a conical shape (FZ Rc) as a function of cone penetrometer force (FZ C):

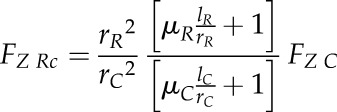graphic file with name PP_PP2017RA00357R1_equ6.jpg (6)

For a spheroid shape of the root tip, Equation 5 needs to be modified slightly. The shape factor of an elliptical half-spheroid was used in a previous study to account for the spheroid shape (McKenzie et al., 2013). For the total axial force of a spheroid root tip shape (FZ Rs), the following applies:

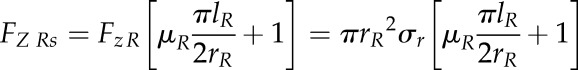graphic file with name PP_PP2017RA00357R1_equ7.jpg (7)

Substituting Equation 4 into Equation 7 allows estimation of the total axial penetration force exerted by a root tip during soil penetration under the assumption of a spheroid shape (FZ Rs) as a function of cone penetrometer force (FZ C):

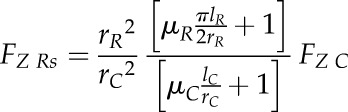graphic file with name PP_PP2017RA00357R1_equ8.jpg (8)

For our calculations, we used a coefficient of friction at the root-soil interface (µR) of 0.1, which is suggested to be typical for boundary lubricants (Hutchings, 1992), and a metal-soil friction coefficient (µC) of 0.5 (Bengough et al., 1997). Root penetration stress for a conical (SRc) and spheroid (SRs) root tip shape was then calculated by dividing axial root force by root tip base area (πrR2):

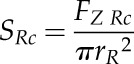graphic file with name PP_PP2017RA00357R1_equ9.jpg (9)
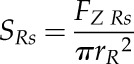graphic file with name PP_PP2017RA00357R1_equ10.jpg (10)

It has been shown that the geometry of a cone or a root tip affects root penetration force and stress due to the differences in cavity form (Iijima et al., 2003b; Vollsnes et al., 2010; Ruiz et al., 2016). If the tip radius-to-length ratio of a root tip or a cone increases, the soil deformation pattern changes from cylindrical to spherical; thus, soil deformation at the front of the tip or cone increases (Vollsnes et al., 2010; Ruiz et al., 2016). Greacen et al. (1968) showed that expansion of a cylindrical cavity (i.e. small tip radius-to-length ratio) requires only 25% to 40% of the pressure required to expand a spherical cavity (i.e. large tip radius-to-length ratio) of the same diameter. The radius-to-length ratio of the cone used in the study was 0.58, whereas for roots, the average tip radius-to-length ratio was 0.23 (Table I). Furthermore, the root tip radius-to-length ratio varied considerably between the different genotypes assessed (Supplemental Fig. S1). To include the effect of the different geometries between the cone and the root tips, as well as among the root tips of the different genotypes, we included a factor (GF) into our calculations of penetration forces and stresses. Based on the radius and length of the steel cone and the root tip, the GF for a conical (GFcone) and spheroid (GFspheroid) root tip was calculated as:

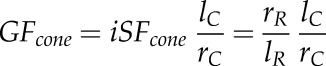graphic file with name PP_PP2017RA00357R1_equ11.jpg (11)

and

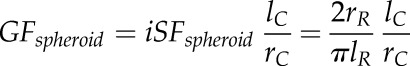graphic file with name PP_PP2017RA00357R1_equ12.jpg (12)

where iSFcone and iSFspheroid represent the inverse shape factor of a conical and spheroid root tip geometry, respectively.

Experiment 2: Root Anatomy of Embryonic and Postembryonic Roots

Four individual pregerminated seeds (25°C, 48 h) of similar size for each treatment combination were selected and grown for 23 d under the conditions described above. After 23 d, roots were washed out from the soil, and 20-mm-long root samples were taken 3 cm from the root base for anatomical measurements. It was ensured that the sampled root segments were taken from the bulk soil and not at the column wall. Root anatomy was investigated in seed-borne roots and nodal roots from the first whorl, which represent embryonic and postembryonic roots, respectively. The samples were fixed and stored in acetic formaldehyde:alcohol:acetic acid:distilled water (10:50:5:35) at 3°C until further analysis. Root cross sections of around 150 μm thickness were cut manually with a razor blade and stained with Toluidine Blue (0.25% in distilled water) for 1 min. Cross sections were imaged using a one-megapixel camera (Olympus XC10; Olympus) connected to a bright-field microscope (Olympus AX70; Olympus). The cross-sectional area of the root, the cortex, and the stele, the area of the cortex occupied with aerenchyma, as well as the cortical cell file number were assessed in ImageJ 1.50b. Furthermore, cortical cell diameter was determined for typical cortical cells (i.e. excluding epidermal and endodermal cells). To do so, the diameter of three individual cells from different cell files was measured in the radial direction.

Statistics

Statistical analyses were performed in R version 3.1.3 (R Core Team, 2015). Two-way ANOVA was used to evaluate the effects of soil bulk density and genotype on root traits. Treatment means were compared using Tukey’s honestly significant difference test at P < 0.05. Broad-sense heritability for root traits from experiment 1 was calculated to assess the genotypic variability among the cultivars. Genotypic variance was obtained from linear mixed models using the lme4 package (Bates et al., 2015), with bulk density and replicate as fixed factors and genotype and genotype-bulk density interaction as random factors. Mean-based heritability was calculated as proposed by Hallauer and Miranda (1981):

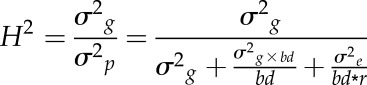graphic file with name PP_PP2017RA00357R1_equ13.jpg (13)

where σ2g and σ2p represent genotypic and phenotypic variance, respectively, σ2g×bd denotes the variance covered by the genotype-bulk density interaction, and bd and r represent the number of bulk density levels and replications, respectively. Analysis of covariance models based on treatment-level means were used to determine whether root diameter or root tip geometry significantly influenced root growth. Nonlinear regressions were performed based on treatment level means with the nonlinear least square method (nls) provided by the R package stats.

Supplemental Data

The following supplemental materials are available.

  • Supplemental Figure S1. Diversity of root traits determined after 48 h of growth in 14 wheat genotypes at soil bulk densities of 1.3, 1.45, and 1.6 g cm−3.

  • Supplemental Figure S2. Influence of root tip geometry and root diameter on root volume after 48 h of growth in 14 wheat varieties at soil bulk densities of 1.3, 1.45, and 1.6 g cm−3.

  • Supplemental Figure S3. Relationship between seed dry weight and root elongation rate, root volume, and average root diameter in 14 wheat varieties at soil bulk densities of 1.3, 1.45, and 1.6 g cm−3.

  • Supplemental Figure S4. Relationship between root tip penetration stress and root tip diameter and average root diameter in 14 wheat varieties at soil bulk densities of 1.3, 1.45, and 1.6 g cm−3.

  • Supplemental Figure S5. Root elongation rate and root diameter of 14 wheat genotypes grown at soil bulk densities of 1.3, 1.45, and 1.6 g cm−3.

  • Supplemental Table S1. Mean-based broad-sense heritability after 48 h of growth.

  • Supplemental Table S2. Inverse shape factors for root tip shape and resulting GFs used to account for different geometries.

  • Supplemental Table S3. Influence of GF on axial force and penetration stress exerted by root tips during soil penetration.

  • Supplemental Table S4. Winter wheat varieties of Swiss origin used in the study ordered according to the year of market release with respective seed dry weights.

Acknowledgments

We thank Dr. Andreas Hund (ETH Zurich) and Dr. Dario Fossati (Agroscope Changins) for providing the wheat varieties used; Dr. Steven Yates (ETH Zurich) for statistical advice; Siul Ruiz, Dr. Stan Schymanski, Daniel Breitenstein, and Prof. Dani Or (ETH Zurich) for help with penetrometer tests and stimulating discussions; Patrick Meyer (ETH Zurich) for help with microscopy; and two anonymous reviewers for constructive comments that helped to improve the article.

Glossary

ROSTA

Root Scan Tip Analysis

Footnotes

1

This project was funded by the Swiss National Science Foundation (Schweizerische Nationalfonds) within the National Research Programme 68, Sustainable Use of Soil as a Resource (http://www.nrp68.ch), project number 406840-143061.

[OPEN]

Articles can be viewed without a subscription.

References

  1. Atwell BJ. (1990a) The effect of soil compaction on wheat during early tillering. I. Growth, development and root structure. New Phytol 115: 29–35 [Google Scholar]
  2. Atwell BJ. (1990b) The effect of soil compaction on wheat during early tillering. III. Fate of carbon transported to the roots. New Phytol 115: 43–49 [Google Scholar]
  3. Azam G, Grant CD, Misra RK, Murray RS, Nuberg IK (2013) Growth of tree roots in hostile soil: a comparison of root growth pressures of tree seedlings with peas. Plant Soil 368: 569–580 [Google Scholar]
  4. Barraclough PB, Weir AH (1988) Effects of a compacted subsoil layer on root and shoot growth, water use and nutrient uptake of winter wheat. J Agric Sci 110: 207–216 [Google Scholar]
  5. Bates D, Mächler M, Bolker B, Walker S (2015) Fitting linear mixed-effects models using lme4. J Stat Softw 67: 18637 [Google Scholar]
  6. Bengough AG, Bransby MF, Hans J, McKenna SJ, Roberts TJ, Valentine TA (2006) Root responses to soil physical conditions: growth dynamics from field to cell. J Exp Bot 57: 437–447 [DOI] [PubMed] [Google Scholar]
  7. Bengough AG, Kirby JM (1999) Tribology of the root cap in maize (Zea mays) and peas (Pisum sativum). New Phytol 142: 421–425 [Google Scholar]
  8. Bengough AG, Loades K, McKenzie BM (2016) Root hairs aid soil penetration by anchoring the root surface to pore walls. J Exp Bot 67: 1071–1078 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bengough AG, McKenzie BM (1997) Sloughing of root cap cells decreases the frictional resistance to maize (Zea mays L.) root growth. J Exp Bot 48: 885–893 [Google Scholar]
  10. Bengough AG, McKenzie BM, Hallett PD, Valentine TA (2011) Root elongation, water stress, and mechanical impedance: a review of limiting stresses and beneficial root tip traits. J Exp Bot 62: 59–68 [DOI] [PubMed] [Google Scholar]
  11. Bengough AG, Mullins CE (1990) The resistance experienced by roots growing in a pressurised cell: a reappraisal. Plant Soil 123: 73–82 [Google Scholar]
  12. Bengough AG, Mullins CE (1991) Penetrometer resistance, root penetration resistance and root elongation rate in two sandy loam soils. Plant Soil 131: 59–66 [Google Scholar]
  13. Bengough AG, Mullins CE, Wilson G (1997) Estimating soil frictional resistance to metal probes and its relevance to the penetration of soil by roots. Eur J Soil Sci 48: 603–612 [Google Scholar]
  14. Bingham IJ, Bengough AG (2003) Morphological plasticity of wheat and barley roots in response to spatial variation in soil strength. Plant Soil 250: 273–282 [Google Scholar]
  15. Bishopp A, Lynch JP (2015) The hidden half of crop yields. Nat Plants 1: 15117. [DOI] [PubMed] [Google Scholar]
  16. Bizet F, Bengough AG, Hummel I, Bogeat-Triboulot MB, Dupuy LX (2016) 3D deformation field in growing plant roots reveals both mechanical and biological responses to axial mechanical forces. J Exp Bot 67: 5605–5614 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Blake A, Isard M (1998) Active Contours: The Application of Techniques from Graphics, Vision, Control Theory and Statistics to Visual Tracking of Shapes in Motion; Springer-Verlag, London [Google Scholar]
  18. Casper BB, Jackson RB (1997) Plant competition underground. Annu Rev Ecol Syst 28: 545–570 [Google Scholar]
  19. Chen YL, Palta J, Clements J, Buirchell B, Siddique KHM, Rengel Z (2014) Root architecture alteration of narrow-leafed lupin and wheat in response to soil compaction. Crop Res 165: 61–70 [Google Scholar]
  20. Chimungu JG, Brown KM, Lynch JP (2014) Large root cortical cell size improves drought tolerance in maize. Plant Physiol 166: 2166–2178 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Chimungu JG, Loades KW, Lynch JP (2015) Root anatomical phenes predict root penetration ability and biomechanical properties in maize (Zea mays). J Exp Bot 66: 3151–3162 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Colombi T, Braun S, Keller T, Walter A (2017) Artificial macropores attract crop roots and enhance plant productivity on compacted soils. Sci Total Environ 574: 1283–1293 [DOI] [PubMed] [Google Scholar]
  23. Colombi T, Walter A (2016) Root responses of triticale and soybean to soil compaction in the field are reproducible under controlled conditions. Funct Plant Biol 43: 114–128 [DOI] [PubMed] [Google Scholar]
  24. de la Luz Mora M, Rosas A, Ribera A, Rengel Z (2009) Differential tolerance to Mn toxicity in perennial ryegrass genotypes: involvement of antioxidative enzymes and root exudation of carboxylates. Plant Soil 320: 79–89 [Google Scholar]
  25. Greacen EL, Farrell DA, Cockroft B (1968) Soil resistance to metal probes and plant roots. Trans 9th Congr Int Soc Soil Sci 1: 769–779 [Google Scholar]
  26. Grzesiak S, Grzesiak MT, Hura T, Marcińska I, Rzepka A (2013) Changes in root system structure, leaf water potential and gas exchange of maize and triticale seedlings affected by soil compaction. Environ Exp Bot 88: 2–10 [Google Scholar]
  27. Hallauer AR, Miranda JB (1981) Quantitative Genetics in Maize Breeding. Iowa State University Press, Ames, IA [Google Scholar]
  28. Hernandez-Ramirez G, Lawrence-Smith EJ, Sinton SM, Tabley F, Schwen A, Beare MH, Brown HE (2014) Root responses to alterations in macroporosity and penetrability in a silt loam soil. Soil Sci Soc Am J 78: 1392–1403 [Google Scholar]
  29. Hutchings LM. (1992) Triblology. Edward Arnold, London [Google Scholar]
  30. Iijima M, Barlow PW, Bengough AG (2003a) Root cap structure and cell production rates of maize (Zea mays) roots in compacted sand. New Phytol 160: 127–134 [DOI] [PubMed] [Google Scholar]
  31. Iijima M, Higuchi T, Barlow PW, Bengough AG (2003b) Root cap removal increases root penetration resistance in maize (Zea mays L). J Exp Bot 54: 2105–2109 [DOI] [PubMed] [Google Scholar]
  32. Jin K, Shen J, Ashton RW, Dodd IC, Parry MA, Whalley WR (2013) How do roots elongate in a structured soil? J Exp Bot 64: 4761–4777 [DOI] [PubMed] [Google Scholar]
  33. Kautz T, Amelung W, Ewert F, Gaiser T, Horn R, Jahn R, Javaux M, Kemna A, Kuzyakov Y, Munch J, et al. (2013) Nutrient acquisition from arable subsoils in temperate climates: a review. Soil Biol Biochem 57: 1003–1022 [Google Scholar]
  34. Kirby JM, Bengough AG (2002) Influence of soil strength on root growth: experiments and analysis using a critical-state model. Eur J Soil Sci 53: 119–127 [Google Scholar]
  35. Li XF, Ma JF, Matsumoto H (2000) Pattern of aluminum-induced secretion of organic acids differs between rye and wheat. Plant Physiol 123: 1537–1544 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Masle J, Passioura J (1987) The effect of soil strength on the growth of young wheat plants. Aust J Plant Physiol 14: 643–656 [Google Scholar]
  37. Materechera SA, Alston AM, Kirby JM, Dexter AR (1992) Influence of root diameter on the penetration of seminal roots into a compacted subsoil. Plant Soil 144: 297–303 [Google Scholar]
  38. McKenzie BM, Mullins CE, Tisdall JM, Bengough AG (2013) Root-soil friction: quantification provides evidence for measurable benefits for manipulation of root-tip traits. Plant Cell Environ 36: 1085–1092 [DOI] [PubMed] [Google Scholar]
  39. Misra RK, Dexter AR, Alston AM (1986) Maximum axial and radial growth pressures of plant roots. Plant Soil 326: 315–326 [Google Scholar]
  40. Mitchell T. (2008) Contour dynamics simulation of Kirchhoff elliptical vortex. https://ch.mathworks.com/matlabcentral/fileexchange/19306-kirchhoff-vortex-contour-dynamics-simulation (date accessed November 11, 2009)
  41. Otsu N. (1979) A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern 9: 62–66 [Google Scholar]
  42. Pellet DM, Grunes DL, Kochian LV (1995) Organic acid exudation as an aluminum-tolerance mechanism in maize (Zea mays L.). Planta 196: 788–795 [Google Scholar]
  43. R Core Team (2015) R: A Language and Environment for Statistical Computing. R Development Core Team, Vienna, Austria
  44. Ruiz S, Or D, Schymanski SJ (2015) Soil penetration by earthworms and plant roots: mechanical energetics of bioturbation of compacted soils. PLoS ONE 10: e0128914. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Ruiz S, Straub I, Schymanski SJ, Or D (2016) Experimental evaluation of earthworm and plant root soil penetration: cavity expansion models using cone penetrometer analogs. Vadose Zone J 15: [Google Scholar]
  46. Saengwilai P, Nord EA, Chimungu JG, Brown KM, Lynch JP (2014) Root cortical aerenchyma enhances nitrogen acquisition from low-nitrogen soils in maize. Plant Physiol 166: 726–735 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Schjonning P, Rasmussen KJ (2000) Soil strength and soil pore characteristics for direct drilled and ploughed soils. Soil Tillage Res 57: 69–82 [Google Scholar]
  48. Schneider HM, Wojciechowski T, Postma JA, Brown KM, Lücke A, Zeisler V, Schreiber L, Lynch JP (2017) Root cortical senescence decreases root respiration, nutrient content and radial water and nutrient transport in barley. Plant Cell Environ 40: 1392–1408 [DOI] [PubMed] [Google Scholar]
  49. Siczek A, Lipiec J, Wielbo J, Szarlip P, Kidaj D (2013) Pea growth and symbiotic activity response to Nod factors (lipo-chitooligosaccharides) and soil compaction. Appl Soil Ecol 72: 181–186 [Google Scholar]
  50. Stirzaker RJ, Passioura JB, Wilms Y (1996) Soil structure and plant growth: impact of bulk density and biopores. Plant Soil 185: 151–162 [Google Scholar]
  51. Tracy SR, Black CR, Roberts JA, Mooney SJ (2011) Soil compaction: a review of past and present techniques for investigating effects on root growth. J Sci Food Agric 91: 1528–1537 [DOI] [PubMed] [Google Scholar]
  52. Valentine TA, Hallett PD, Binnie K, Young MW, Squire GR, Hawes C, Bengough AG (2012) Soil strength and macropore volume limit root elongation rates in many UK agricultural soils. Ann Bot (Lond) 110: 259–270 [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Varney GT, Canny MJ (1993) Rates of water uptake into the mature root system of maize plants. New Phytol 123: 775–786 [Google Scholar]
  54. Vollsnes AV, Futsaether CM, Bengough AG (2010) Quantifying rhizosphere particle movement around mutant maize roots using time-lapse imaging and particle image velocimetry. Eur J Soil Sci 61: 926–939 [Google Scholar]
  55. White RG, Kirkegaard JA (2010) The distribution and abundance of wheat roots in a dense, structured subsoil: implications for water uptake. Plant Cell Environ 33: 133–148 [DOI] [PubMed] [Google Scholar]
  56. Young IM, Montagu K, Conroy J, Bengough AG (1997) Mechanical impedance of root growth directly reduces leaf elongation rates of cereals. New Phytol 135: 613–619 [Google Scholar]

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES