Frequency-specific directed interactions in the human brain network for language

Significance

The brain’s remarkable capacity for language requires bidirectional interactions between functionally specialized brain regions. Although the functional role of individual regions in the brain network for language has been well studied, as of yet little is known about the mechanisms that facilitate the information exchange between these brain regions. In this paper we show that communication between language-relevant areas in the brain is supported by rhythmic neuronal synchronization and that different rhythms reflect the direction of information flow. These findings likely reflect a generic mechanism that allows for dynamic routing of information in a network of task-relevant brain regions during cognitive processing.

Abstract

The brain’s remarkable capacity for language requires bidirectional interactions between functionally specialized brain regions. We used magnetoencephalography to investigate interregional interactions in the brain network for language while 102 participants were reading sentences. Using Granger causality analysis, we identified inferior frontal cortex and anterior temporal regions to receive widespread input and middle temporal regions to send widespread output. This fits well with the notion that these regions play a central role in language processing. Characterization of the functional topology of this network, using data-driven matrix factorization, which allowed for partitioning into a set of subnetworks, revealed directed connections at distinct frequencies of interaction. Connections originating from temporal regions peaked at alpha frequency, whereas connections originating from frontal and parietal regions peaked at beta frequency. These findings indicate that the information flow between language-relevant brain areas, which is required for linguistic processing, may depend on the contributions of distinct brain rhythms.

The human brain is capable of effortlessly extracting meaning from sequences of written or spoken words by means of a sophisticated interplay between dedicated neocortical regions. Neuroanatomical research has revealed a number of white-matter pathways that facilitate these interregional interactions (1). Electrophysiological research with electro- and magnetoencephalography (EEG/MEG) has revealed with high temporal precision the sequential activation of individual nodes embedded within the human brain network for language (2, 3). However, the nature of the functional interactions that enable the efficient flow of information between the nodes of this network has yet to be elucidated.

One important feature of cortical interregional connections is that they are frequently reciprocal in nature (4), which implies that information can be exchanged in a bidirectional fashion. Moreover, the information flow between cortical regions may be facilitated by interregional rhythmic synchronization (5), where neuronal rhythms of specific different frequencies reflect the direction in which the information is flowing (6, 7). This bidirectional flow of information should also be a crucial feature of the neurobiological system that supports language processing. Linguistic processing is not a simple bottom-up process where incoming linguistic information (for instance, when reading a sentence) drives a sequence of activations of cortical areas that gradually transforms a string of letters into a representation of sentence and discourse meaning. Rather, contextual information, which is either already available, or built up while a sentence unfolds, can also provide top-down information, affecting the response in lower-order areas.

Here, we show that interregional interactions in the human brain network for language are subserved by rhythmic neuronal synchronization at specific frequencies. Specifically, we found that rhythmic activity in the alpha frequency range (8–12 Hz) propagates from temporal cortical areas to frontal cortical areas, and that beta frequency rhythmic activity (15–30 Hz) propagates in the opposite direction. These results indicate the functional relevance of rhythmic directed interactions during language processing, where interactions between areas are supported by different frequency bands, depending on the direction of the interaction. This functional relevance likely extends to other cognitive domains, reflecting a generic mechanism that allows for dynamic routing of information in a network of task-relevant brain regions.

Results

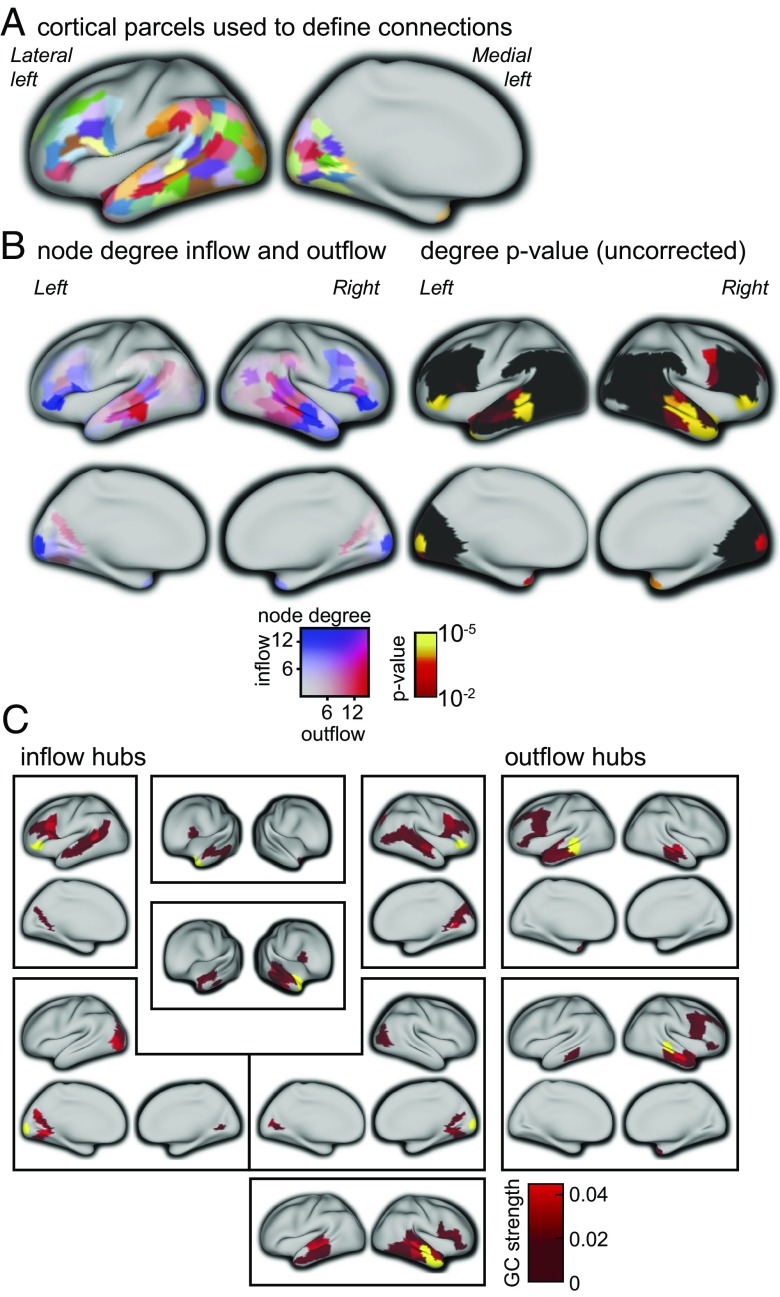
We used MEG to record neuromagnetic signals while participants were reading sequences of words. We reconstructed the cortical activity in a set of predefined brain areas (consisting of 156 cortical parcels), encompassing areas that are part of the core language system, areas in the visual system, and homolog areas in the contralateral hemisphere (8) (Fig. 1A). Next, we computed frequency-resolved Granger causality (GC) to quantify directed rhythmic neuronal interactions between brain areas for language that are known to be anatomically connected (9–11). Because the interpretation of connectivity estimated from neuromagnetic recordings is highly confounded by spatial leakage of source activity (12), we statistically compared, across the sample of 102 participants, the estimated GC with an estimate of GC after time reversal of the signals (13). This allowed us to conservatively discard a substantial subset of the predefined connections for which the direction and/or the strength of the estimated Granger causal interaction is likely confounded by spatial leakage of activity. This left us with a subset of 713 connections from the initial 4,350 connections formed between 156 modeled cortical parcels. We subsequently explored the topology of the resulting network and observed an uneven distribution in the number of connections for the cortical parcels involved (Fig. 1 B and C). Specifically, for each of the cortical parcels we quantified the number of in- and outgoing directed connections (i.e., the node degree). We observed left and right middle temporal cortical parcels to serve as a sender node in a large number of connections, projecting to ipsilateral anterior middle and superior temporal cortex [Brodmann areas (BA) 21/22/38], to contralateral middle and superior temporal cortex (BA 21/22), and to frontal cortex (BA 6/9/44/45/47) (P < 0.05, Bonferroni corrected randomization test). Left and right inferior frontal regions (BA 47), however, were observed to receive Granger causal input from ipsilateral frontal cortex (BA 44/45/46), ipsilateral superior temporal cortex (BA 22), ipsilateral angular gyrus (BA 39), and ipsilateral extrastriate visual cortex (BA 19, area 17/18 present in the right hemisphere only) (P < 0.05, Bonferroni corrected randomization test). Additionally, regions receiving substantial inflow were located bilaterally in the anterior temporal pole (receiving input from superior and middle temporal regions, as well as from inferior frontal cortex), in the occipital pole (receiving input from extrastriate regions as well as from inferior temporal and occipito-temporal cortex), and in the right anterior temporal cortex.

Fig. 1.

Topology of the brain network for language as quantified with GC. (A) Overview of the left hemispheric anatomical parcels used for source reconstruction and serving as network nodes, displayed on the inflated cortical surface. Lateral and medial surfaces are shown on the Left and Right, respectively. Right hemispheric homologous parcels were also considered for network estimation, yet not displayed here. (B, Left) Node degree for inflow (i.e., the number of nodes from which each of the nodes receives significant Granger causal input) (P < 0.05, nonparametric permutation test, Bonferroni corrected) and outflow (i.e., the number of nodes to which each of the nodes sends significant Granger causal output). (B, Right) Uncorrected P values associated with the statistical comparison (nonparametric permutation) of the topology observed in the left panels, and randomly connected networks, keeping the overall degree distribution constant. Orange/yellow parcels survive Bonferroni correction for multiple comparisons (the number of edges) and reflect hubs in the network. (C) Topology of the connections for each of the highly connected hubs identified in B, and the other cortical areas, for inflow hubs (blue parcels in B) and outflow hubs (red parcels in B), with the hubs displayed in yellow, and the Granger causal strength to sending/receiving areas in red.

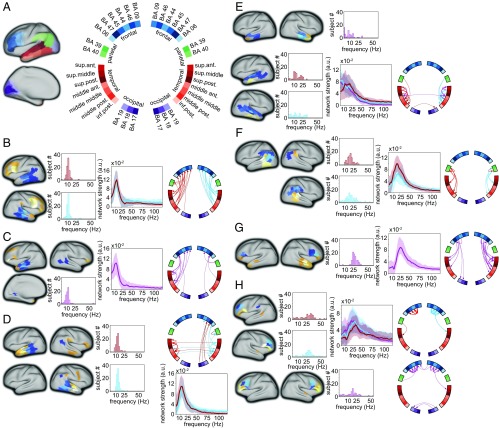
To gain more detailed insight into the spatial and spectral structure of this brain wide network we applied nonnegative matrix factorization (NMF) to the group-level connectivity data (8). Specifically, we modeled the connectivity data as a mixture of a limited number of spatially static network components, each with a subject-specific spectral profile. The decomposition algorithm did not incorporate any specific constraints with respect to the spatial or spectral structure of the underlying components. In particular, no assumptions were made about the spatial clustering of edges (i.e., the decomposition algorithm did not favor sets of connections to end up in the same component when the cortical parcels on each end of the directed connection were spatially clustered). However, the majority of extracted network components were physiologically interpretable, judging from the spatial clustering of the cortical parcels participating in component-specific directed interactions. Fig. 2 shows the network components with predominant connections between language-relevant cortical areas (components with predominant connections between visual cortical areas and components with more spatially diffuse connections are shown in Fig. S1). The components’ cortical locations for outflow and inflow are depicted in blue and orange/yellow, respectively, in the leftmost panel for each quadruplet of columns. For some of the components, the subject-averaged spectral profiles were band-limited to a certain frequency range, which moreover showed a consistent peak frequency across subjects (Fig. 2 B–H, middle panels for each quadruplet of columns). This suggests that these components represent frequency-specific rhythmic directed interactions between key regions in this large-scale network. We categorized the extracted components based on the dominant region for outflow. The majority of the components reflected predominantly intrahemispheric connections (Fig. 2 B–H, right panel for each quadruplet of columns). We identified left and right hemispheric directed rhythmic interactions from posterior and midtemporal cortical regions to ipsilateral frontal cortex (mainly inferior frontal), with a median peak frequency at 12 Hz [interquartile range (IQR) 11–13 Hz] (Fig. 2B). A somewhat spatially more diffuse component with predominantly left intrahemispheric connections led from midtemporal areas to inferior and superior frontal areas (Fig. 2C). Connections from posterior and midtemporal regions to ipsilateral anterior temporal cortex had a slightly higher median peak frequency of 14 Hz (with an IQR of 12–15 Hz and 13–15 Hz for the left and right hemispheric components), compared with the temporo-frontal connections (Fig. 2D). Next, there was a set of components predominantly interconnecting temporal cortical regions that showed somewhat more variability in their spectral profile across subjects (Fig. 2E). These components reflected connections from superior and middle temporal cortex (along the whole anterior–posterior axis) to mid and anterior inferior temporal cortex, and connections from midmiddle and superior anterior temporal cortex to the temporal pole.

Fig. 2.

Network components obtained with NMF show frequency, regional, and direction-specific interactions. (A) Location of the cortical nodes, displayed on an inflated cortical sheet (Left) with color coding and labeling convention (Right), as used in B–H. Circular grouping was according to anatomical location, using BA labeling for the parcels outside temporal cortex, and using their relative location along the anterior/posterior and superior/inferior axis for temporal parcels. (B–H) Components reflecting connections between language-relevant cortical areas. Leftmost panels show the location of the parcels involved. Dark/light blue colors: regions for outflow (the lighter the color of the parcel, the stronger the relative contribution of the parcel to the component). Orange/yellow/white colors: regions for inflow. The histograms show for each of the components the distribution of the subject-specific peak frequency. The spectra show the median (and IQR) spectral profiles across subject. The circular plots show the directed connections between the parcels. The thickness of the arrows reflects the relative strength of the connection. Components with predominantly left-hemispheric, right-hemispheric, or bilateral connections are displayed in red, light blue, and purple, respectively. (B) Left and right hemispheric components from temporal regions to ipsilateral frontal regions. (C) Component with bilateral intrahemispheric temporal-to-frontal connections. (D) Left and right hemispheric components with predominant connections from middle to anterior temporal regions. (E) Components with predominantly intratemporal connections from superior to inferior regions (upper two rows), and from midanterior regions to the temporal pole (bottom row). (F) Components with predominant connections from the angular gyrus (BA 39) and supramarginal gyrus (BA 40) to posterior temporal cortex. (G) Component from frontal regions to temporal regions. (H) Components with predominantly fronto-frontal connections.

Fig. S1.

Network components obtained by group-level NMF with predominant connections between visual cortical areas (A) and with spatially diffuse connections (B).

In contrast to the network components with the outflow regions in temporal cortex, the rhythmic interactions with predominant outflow from parietal (Fig. 2F) and frontal (Fig. 2 G and H) regions consistently showed a higher peak frequency of interaction. Components reflecting parietal-to-posterior temporal interactions had a median peak frequency of 20 Hz (with an IQR of 17–22 Hz and 15–26 Hz for the left and right hemispheric components, respectively) and frontal-to-temporal rhythmic interactions had a median peak frequency of 27 Hz (with an IQR of 25–30 Hz). Intrafrontal interactions had a somewhat more broadband spectral profile, with a median peak frequency of 24 Hz (IQR: 19–29 Hz) for directed interactions from BA 44 to BA 45/46/47. Interactions from BA 46 to BA 44/45/47 had a median peak frequency of 30 Hz (IQR: 23–35 Hz) and 29 Hz (IQR: 25–33 Hz) for left and right hemispheric connections, respectively. We statistically evaluated the peak frequency of the rhythmic interactions between components with predominant connections between parietal, frontal, and temporal brain areas (Fig. 3A). Overall, the component-specific median peak frequencies ranged from the upper end of the alpha range (12 Hz) to the upper end of the beta range (30 Hz). Moreover, components with rhythmic Granger causal outflow predominantly from temporal areas had a consistently lower peak frequency than components with Granger causal outflow from parietal or frontal areas (P < 0.05, nonparametric permutation test, multiple comparison corrected). Notably, based on the NMF we could distinguish temporo-frontal interactions, with a peak frequency of 12 Hz (Figs. 2 A and B and 3 B and C, connection in dark red), from fronto-temporal interactions, with a peak frequency of 27 Hz (Figs. 2F and 3 B and C, connection in dark blue). Fig. 3B shows a schematic summary of the dominant rhythmic interactions, with the corresponding spectral profile in Fig. 3C.

Fig. 3.

Rhythmic interactions originating from temporal/parietal cortex have consistently lower peak frequencies than those originating from frontal cortex. (A) Pairwise comparison of the component-specific peak frequencies (nonparametric permutation test, corrected for multiple comparisons). Each colored element represents the median of the subject-specific difference in peak frequency (row component – column component). The values in the black boxes along the main diagonal reflect the median peak frequency for each component. (B) Schematic representation of the directed rhythmic cortico-cortical interactions in the language system, grouped according to the cortical output area. The temporal lobe is split into two ”nodes,” to be able to display the rhythmic mid to anterior connection. The colored arrows refer to the spectra shown in C. The black spectrum in C is the average of the components shown in (Fig. 2E), with dominant connections from superior temporal to middle temporal gyrus, and is not displayed as a separate connection in B.

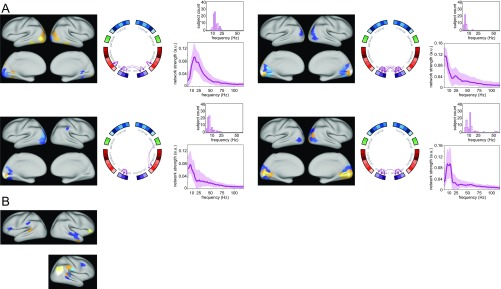
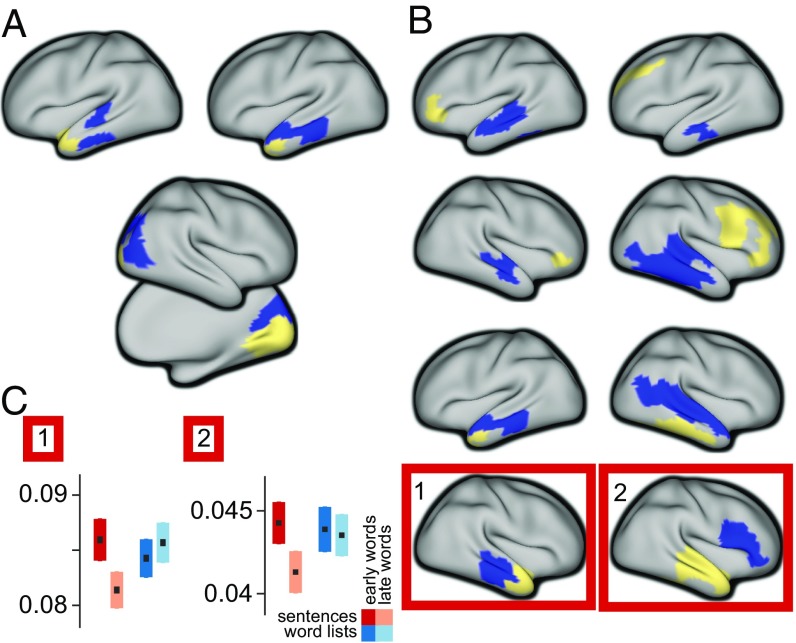
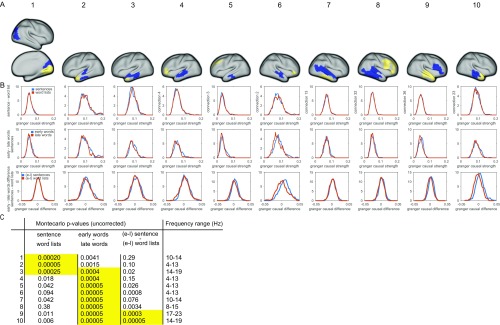
We proceeded to test whether the strength of the rhythmic interactions was modulated by the functional requirements imposed by the perceptual input. To this end, we divided the stimulus material into four conditions, based on whether the subjects were reading a well-structured sentence or a pseudorandom sequence of words (sentences and word lists), and based on the ordinal position of the words (early and late words). Importantly, we stratified the data for lexical frequency and overall signal variance, to avoid as much as possible interpretational confounds for the estimated connectivity (12, 14) due to differences in univariate signal and stimulus properties (8). Subsequently we computed the Granger causal interactions for each subject and condition for the most prominent functional connections, which were extracted from the NMF results by means of spatial clustering. We constrained the analysis to band-limited estimates of GC, averaging across frequencies and edges. The connection-specific frequency bands were obtained from the components’ peak frequencies and IQRs. Contrasting sentences with sequences, we observed the strength of the interactions to be modulated from left middle temporal regions to the left temporal pole, where sequences elicited stronger interactions than sentences, and from right striate to extrastriate visual regions (Fig. 4A, P < 0.05, nonparametric permutation test, Holm–Bonferroni correction for multiple comparisons). Comparing early words with late words in the sentence condition showed several significantly modulated connections, with rhythmic interactions being stronger early in the sentence (Fig. 4B). These connections were bilateral from temporal to frontal regions, and from middle temporal regions to the temporal pole. In addition, in the right hemisphere we identified significantly modulated connections from frontal regions to temporal regions, and from the superior temporal gyrus to the middle temporal gyrus (P < 0.05, nonparametric permutation test, Holm–Bonferroni correction for multiple comparisons). Moreover, we identified two right hemispheric connections that showed a significant interaction effect between early vs. late words and sentences vs. sequences (Fig. 4B and Fig. S2).

Fig. 4.

The strength of directed interactions is modulated by the linguistic input. (A) Connections showing stronger interactions in the word list condition than in the sentence condition (P < 0.05, corrected Bonferroni–Holm). Blue parcels indicate nodes for outflow and yellow parcels indicate nodes for inflow. (B) Connections showing stronger interactions for early words in the sentences, compared with late words in the sentences. The connections shown in the red boxes show a significant interaction effect (P < 0.05, corrected), on top of a significant early vs. late effect. (C) Bar graphs show condition-specific mean (±SEM) Granger causal strength for the outlined connections.

Fig. S2.

Connection-specific data for the condition comparisons. (A) Spatial location of outgoing (blue) and ingoing (yellow) parcels. (B) Distribution of data values across subjects of Granger causal strength for the different conditions compared. Upper row: sentences vs. word lists. Middle row: early words vs. late words. Bottom row: difference values (early words minus late words) for sentences and word lists. (C) Table with uncorrected P values for the condition-specific comparisons, including a specification of the connection-specific frequency range.

Discussion

We have provided evidence for directed interactions between cortical regions in the human brain network for language during sentence reading. Topological analysis of the overall network revealed a high degree of Granger causal inflow into anterior inferior frontal cortical regions, right anterior temporal cortex, and the temporal pole bilaterally. This is in line with these regions’ being “high-order” regions, involved in the processing of more abstract features of the linguistic input, which requires integration of converging information. Frontal regions are engaged in unification operations (15), integrating lexical units into the larger context. Anterior temporal cortex is associated with conceptual object representations (16, 17).

Middle temporal cortical regions, however, displayed a high degree of Granger causal outflow. This is in agreement with the middle temporal gyrus’ crucial role in language comprehension at the level of single words (18, 19). Its functional connections to more anterior temporal areas, as well as to inferior frontal cortex, reflect the necessity to propagate information about individual lexical items to areas that subserve integration operations. Notably, we did not observe a clear lateralization in the pattern of connections, which lends support to the evolving notion that both cerebral hemispheres are involved in the processing of linguistic stimuli (20).

Data-driven decomposition of the overall network into smaller subnetworks revealed several spatially constrained components, corresponding with local and long-range directed interactions. The clear frequency-resolved profile displayed by some of these components displayed is indicative of the interactions’ being mediated by rhythmic interareal synchronization. Connections originating from temporal cortical areas showed a consistently lower peak frequency (alpha and low beta) than connections originating from parietal or frontal regions (high beta). As a specific example, temporal-to-frontal interactions are subserved by rhythmic synchronization at ∼12 Hz, whereas interactions in the opposite direction, from frontal to temporal regions, peak at a frequency of ∼27 Hz.

At first glance, these findings correspond well with recent work in the visual system in which it was shown that feedforward and feedback connections, as defined by their characteristic cortical laminar connectivity profile (21), could be distinguished in terms of their frequency of interaction (6, 7, 22). However, in the visual system, feedforward connections have been functionally characterized by gamma band synchronization (>50 Hz) (and to a lesser extent by theta band synchronization) and feedback connections by alpha/beta synchronization. A GC spectral peak in the gamma frequency range was absent in our data. Although studies in the visual system allow for experimental paradigms eliciting robust and strongly modulated gamma band rhythmicity, language paradigms do not typically lead to similarly strong local gamma-band responses (23), rendering the likelihood of detecting gamma-band interactions low. In addition, characterization of feedforward and feedback connections based on their cytoarchitectonic connectivity profiles is likely to be more distinct in peripheral sensory systems than in higher cortical regions (24), such as the higher-order areas in the human brain network for language. Consequently, there is no reason to assume that the emergent functional properties of the language network, in terms of the frequency of interactions, should directly map onto observations in the visual system. Nevertheless, our data reveal frequency-specific subnetworks in the brain system for language.

Further exploration of the potential functional significance of these interactions revealed that the linguistic context modulates left lateralized midtemporal-to-anterior temporal interactions, as well as right lateralized extrastriate-to-striate interactions. In these connections, Granger causal influences were stronger in the word list condition. This suggests that the absence of syntactic structure intensifies the need for information transfer to the anterior temporal lobe, possibly to facilitate access to word meaning. In addition, our findings indicate that even the generation of a word form percept might require stronger interactions for effective processing in the absence of context constraining syntactic structure. Next, in a sentential context, the incremental availability of contextual information allows for the generation of constraining predictions about the upcoming input, likely facilitating processes such as lexical selection. Bilateral interactions from temporal to frontal regions, from midtemporal to anterior temporal regions, from right lateralized frontal to temporal regions, and from superior temporal to middle temporal regions are stronger early in the sentence, when the constraining context is still relatively weak, as opposed to later in the sentence. These stronger interactions early in the sentence might reflect the increased need for information exchange between these regions, to establish a linguistic context.

In conclusion, this study shows directional interactions in the highly dynamic cortical network of language-relevant areas, with salient differences in the specific frequencies that support the communication protocols in the temporo-frontal and the fronto-temporal directions. Although our findings are in line with earlier reports of a frequency difference between feedforward and feedback connections, the carrier frequencies in the language network shown here deviate from what has been observed in the visual system. However, the effect of linguistic context on the strength of some of these connections suggests the functional relevance of dynamic rhythmic cortical interactions during cognitive processing in general, and language processing in particular (25). An interesting avenue for further research would be to relate these rhythmic interactions to local measures of activation, to gain insight into how the interplay between local cortical activity and long-range interactions shapes cognition.

Materials and Methods

Experimental Procedure and MEG Data Acquisition.

Native Dutch speakers (n = 102, 51 males), with an age range of 18–33 y, participated in the experiment. All participants were right-handed, had normal or corrected-to-normal vision, and reported no history of neurological, developmental, or language deficits. The study was approved by the local ethics committee (CMO, the local “Committee on Research Involving Human Participants” in the Arnhem–Nijmegen region) and followed the guidelines of the Helsinki declaration. All participants gave written informed consent before participation. The participants read sequences and lists of words (total number of 240, with 9–15 words per sequence), presented sequentially on a back-projection screen, placed in front of them. MEG data were collected with a sampling frequency of 1,200 Hz. Throughout the measurement the head position was continuously monitored using custom software (26).

Artifact Rejection and Subtraction of Single-Trial Activity.

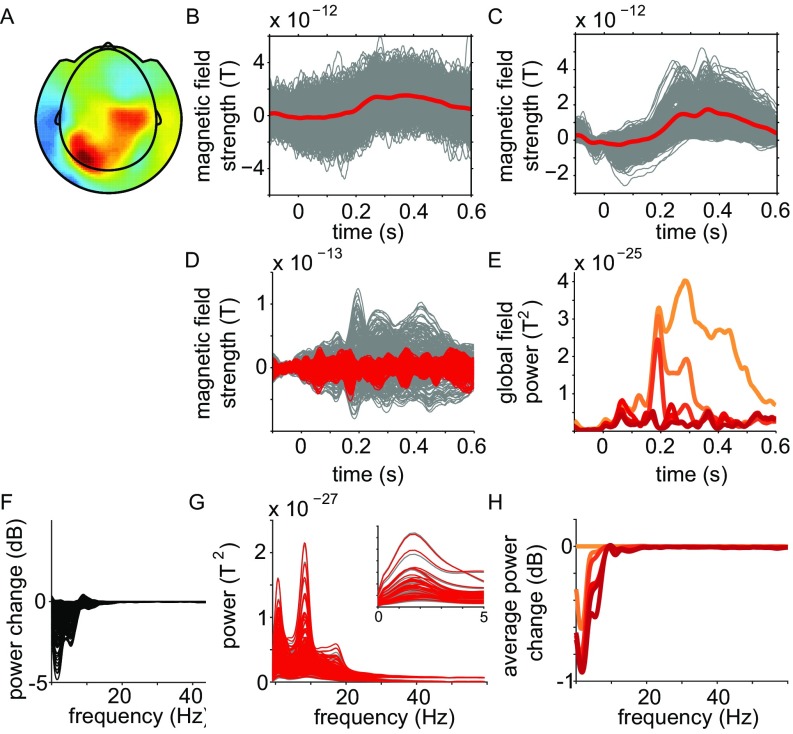
All analyses were done with custom-written MATLAB scripts and FieldTrip (27). Data were epoched from −100 to 600 ms relative to word onset, and segments contaminated by artifacts were discarded before further analysis. We subtracted the event-related response from the single-trial data with the ASEO algorithm (28), aiming to attenuate the effects of evoked transients on the estimation (and subsequent interpretation) of GC (29). Transients in the signals violate the underlying assumption of stationarity and result in nonzero GC estimates, due to systematic latency differences of the peak of the transient signals across regions. We combined the ASEO algorithm with a blind source separation technique [denoising source separation (DSS) (30)]. We modeled single-trial signals as a combination of ongoing activity and event-related components (31) and subtracted the modeled single-trial evoked responses from the data (Fig. S3).

Fig. S3.

Illustration of combined DSS/ASEO procedure tor the removal of word-onset event-related signal transients. (A) Spatial topography of the mixing coefficients for the first extracted DSS component for an example subject. (B) Single-trial time courses (in gray) of the first DSS component, time-locked to word onset, average across trials in red. (C) Single-trial estimates of the stimulus-locked transient response, estimated with the ASEO algorithm, average across trials in red. (D) Overlay of single channel event-related averages before (gray) and after (red) the cleaning procedure. (E) Global field power across channels of the event-related average (light orange) and after iterative removal of five DSS components (ranging from orange to dark red). (F–H) Effect of the DSS/ASEO procedure on spectral quantities. (F) Overlay of single-channel relative change in power after removal of event-related activity. (G) Overlay of single-channel power spectra before (gray) and after (red) the cleaning procedure. The magnified subpanel zooms in on a subset of channels for the low-frequency range. (H) Reduction in power (average across channels) during iterative removal of five DSS components.

Source Reconstruction and Parcellation of Source-Reconstructed Activity.

We performed source reconstruction using a linearly constrained minimum variance beamformer (LCMV) (32), estimating a spatial filter at 8,196 locations of the subject-specific reconstructed midcortical surface. Next, we applied an atlas-based parcellation scheme to reduce the dimensionality of the data. We used a refined version the Conte69 atlas, resulting in a parcellation scheme consisting of 191 parcels per hemisphere. Spatial filters were concatenated across vertices comprising a parcel, and we obtained a set of time courses of the event-related field at each parcel and selected for each parcel the first two spatial components explaining most of the variance in the signal. We opted for this method, rather than averaging, because we used rank-reduced forward solutions (excluding the most noise-sensitive dipole orientations), which might result in signal cancellation effects upon averaging, due to sign ambiguity of the resulting cardinal dipole orientations.

Preselection of the Connections Between Language-Relevant Areas.

We constrained ourselves a priori to a subset of connections between parcel pairs, using known “long-range” macroanatomical fiber pathways between parcels comprised of core language regions and the visual system as described in the literature (1, 9–11). In addition, we allowed a priori for direct connections between neighboring nodes, based on the characteristics of cortico-cortical connections (e.g., refs. 24 and 33). We included intrahemispheric connections from both hemispheres and also included interhemispheric connections between homologous areas. Fig. 2A shows how the individual nodes were labeled. Connections between directly adjacent parcels were excluded for further analysis to reduce spurious estimates of connectivity due to spatial leakage of source-reconstructed activity. The selection scheme resulted in 4,350 connections between pairs of parcels, which notably consisted of a sparse subset of all possible pairwise connections between the 156 parcels used for the GC analysis.

GC Computation and Statistical Evaluation of Overall Network Topology.

We computed the spectral representation of the signals at the sensor level and projected this into source space, using the parcel-specific spatial filters. The spectral representation of the signals was obtained using the fast Fourier transform in combination with multitapers (using 5-Hz smoothing) on the time domain data from 200 until 600 ms after word onset. For each pair of parcels we computed the cross-spectral density matrix and used this to compute GC using nonparametric spectral matrix factorization and a blockwise approach (34, 35). We also computed GC based on the source-projected Fourier transform of time-reversed data, to distinguish “weak” asymmetries from “strong” asymmetries, as described by Haufe and coworkers (13) and Haufe et al. (36). A weak asymmetry is an apparent directional interaction between a pair of network nodes, which is due to a difference in signal-to-noise ratio (SNR) across nodes (14), often caused by a linear mixture of underlying sources (37). We selected only parcel pairs for subsequent analysis for which the difference between GC and reverse GC was statistically significant (across subjects) at a P value <0.05, corrected for multiple comparisons (one-sided t test, with Bonferroni correction). This reduced the number of connections that were used for subsequent analysis from 4,350 to 713.

NMF and Network Visualization.

We explored the network topology by performing NMF with sparsity constraints (38) on the resulting GC spectra. The purpose of this analysis is to describe the reconstructed connectivity data as a low-dimensional mixture of network components, each of which with a subject–specific spectral profile. This technique has successfully been applied to sensor-level MEG-signals before (39). We opted for sparse NMF, because the nonnegativity constraint facilitates the interpretation of the components, as opposed to, for example, a statistical independence constraint as applied in independent component analysis. This is because GC is strictly nonnegative. The outcome of NMF is dependent on the number of components. We explored a range of “number of components” but settled on the number 20 for the remainder of the paper, providing a reasonable balance between providing a small number of interpretable components, while at the same time maintaining a good separation between subnetworks. We used the Icasso framework (40), with 40 repeated random initialization, which applies a hierarchical clustering procedure on the outcome to extract the underlying structure of the data, irrespective of the random initializations of the NMF algorithm.

Condition-Specific Statistical Evaluation.

We estimated condition-specific GC in the dominant connections extracted from the identified network components. The individual conditions were defined according to whether the words were presented in a well-formed sentence context (or were part of a word list) and according to whether the words were presented early in the sentence/word list (words two to four) or late in the sentence/word list (n − 3 until n − 1, with n the number of words in the sentence/word list). To account for potential interpretational confounds of the resulting GC estimates we used a stratification procedure to ensure that the marginal distributions of the epochwise signal variances as well as the words’ lexical frequencies were equalized across conditions. As a consequence only a subset of epochs is used for the GC estimation, where the parcel-pair specific number of epochs varies across parcel pairs. On average 50% of the epochs were retained (range: 20–75%), corresponding to 147 (range: 45–235) epochs. We defined dominant connections as spatially clustered sets of edges. We computed subject- and condition-specific GC and performed a nonparametric permutation test to evaluate (i) sentence – word list words, (ii) for the sentence condition: early – late words, and (iii) an interaction effect: (early-late words sentences) – (early-late words sequences).

SI Materials and Methods

Experimental Procedure and MEG Data Acquisition.

A total of 102 native Dutch speakers (51 males), with an age range of 18–33 y (mean of 22 y), participated in the experiment. All participants were right-handed, had normal or corrected-to-normal vision, and reported no history of neurological, developmental, or language deficits. The study was approved by the local ethics committee (CMO, the local “Committee on Research Involving Human Participants” in the Arnhem–Nijmegen region) and followed the guidelines of the Helsinki declaration. Participants received monetary compensation for their participation.

The participants were seated comfortably in a magnetically shielded room and were instructed to read sequences of words (total number of 240, with 9–15 words per sequence), which were presented sequentially on a back-projection screen, placed in front of them. All words were presented at the center of the screen within a visual angle of 4°, in a black monospaced font, on a gray background using Presentation software (Version 16.0; Neurobehavioral Systems, Inc.). The vertical refresh rate of the LCD projector was 60 Hz. The sequences of words formed either well-formed sentences or consisted of a scrambled version of a sentence, where the word order was randomly shuffled. For the remainder we refer to these latter stimulus sequences as word lists. See Lam et al.(23) for more details about the stimulus material used. Sentences and word lists were presented in small blocks, of five sentences (or word lists) each, to a total of 120 stimuli per condition. To check for task compliance, in a random 10% of the word sequences they were followed by a yes/no question about the content of the previous sentence/word list.

MEG data were collected with a 275 axial gradiometer system (CTF). The signals were analog low-pass-filtered at 300 Hz and digitized at a sampling frequency of 1,200 Hz. The participant’s head was registered to the MEG-sensor array using three coils attached to the participant’s head (nasion and left and right ear canals). Throughout the measurement the head position was continuously monitored using custom software (26). During breaks the participant was allowed to reposition to the original position if needed. Participants were able to maintain a head position within 5 mm of their original position. Three bipolar Ag/AgCl electrode pairs were used to measure the horizontal and vertical electrooculogram and the electrocardiogram.

Artifact Rejection and Subtraction of Single-Trial Activity.

All analyses were done with custom-written MATLAB scripts and FieldTrip (27). Data were initially epoched from −100 to 600 ms relative to word onset. Segments contaminated by artifacts due to eye movements, muscular activity, and superconducting quantum interference device jumps were discarded before further analysis. Next, we subtracted the event-related response from the single-trial data with the ASEO algorithm (28). The acronym ASEO stands for analysis of single-trial ERP and ongoing activity, and the aim of the application of this algorithm in this context was to attenuate the effects of evoked transients on the estimation (and subsequent interpretation) of GC (29). Transients in the signals violate the underlying assumption of stationarity and moreover may result in nonzero GC estimates, due to systematic latency differences of the peak of the transient signals across regions. Although such latency differences may reflect an actual interaction (where temporal precedence of a transient signal peak in region A, compared with region B, may be an indication that A is causing B), their spurious effect on the estimated GC is unwanted, if the aim is to interpret the frequency domain GC in terms of directed synchronized interactions. In our experimental setup, transient brain responses could not be avoided (as opposed to, for instance, ref. 7), and we developed a procedure (performed at the sensor level) to attenuate the effect of transient evoked components, combining the ASEO algorithm with a blind source separation technique (DSS) (30). In short, the ASEO algorithm models single-trial signals as a combination of ongoing activity and event-related components, where the latter are modeled as a set of “canonical” components, each with a trial-specific latency and amplitude. In a typical application (31), the single-trial estimates of latencies and amplitude are used as dependent variables for subsequent analysis. Here, however, we subtracted the single-trial evoked responses that were reconstructed from the latency and amplitude estimates, which results in a better account of ongoing activity, compared with the subtraction of a fixed average event-related response from each signal. DSS was used to iteratively unmix the sensor-level data into a set of components, where the DSS framework allows for the unmixing algorithm to capitalize on specific features of the requested components. Specifically, we applied an iterative procedure, where each iteration consisted of the following steps:

• i)
  Estimation of the dominant DSS component using quasiperiodic averaging, which essentially extracts components with strong evoked transients, time-locked to word onset. This step yields a spatial map of mixing weights, describing for each MEG sensor the extent to which this component is present in the MEG signals, as well as an observations-by-time matrix of the component time series. Mathematically, the sensor-level data are modeled as:

  $$\left[X_1\hspace{0.17em}{X}_2\hspace{0.17em}\dots X_R\right]=a\ast \left[y_1\hspace{0.17em}{y}_2\dots y_R\right]+N,$$

  where matrix X_r has channels in the rows and time points in the columns for trial r. Column vector a represents the mixing weights, and row vector y_r represents the single-trial time courses of the estimated component. For the implementation we used the software provided by the authors (30) (available from www.cis.hut.fi/projects/dss/), which is part of FieldTrip and can be deployed using ft_componentanalysis, with cfg.method = ‘dss.’
• ii)
  Application of the ASEO algorithm to the single-trial time series of the estimated DSS component (vector y in our notational convention), yielding single-trial estimates of the evoked transients. The data model underlying the ASEO algorithm models each single-trial response as a combination of ongoing activity and a weighted combination of latency shifted event-related canonical signal components, as per the following equation:

  $$y_r\left(t\right)={\displaystyle \sum _{n=1}^N{\beta }_{rn}{s}_n}\left(t-{\tau }_{rn}\right)+z_r\left(t\right)={\stackrel{\sim }{y}}_r\left(t\right)+z\left(t\right),$$

  where y_r(t) is the signal for trial r as a function of time t. z_r(t) is the ongoing activity, and s_n(t) is a canonical signal component, which is shifted by latency parameter τ and weighted by amplitude parameter β. The ASEO algorithm parameterizes the single-trial signals using an iterative approach in the frequency domain. For the implementation used in the current work we adapted the code that was kindly provided to us by Mingzhou Ding, University of Florida, Gainesville, FL, and which was used for the original implementation (28).
• iii)
  Backprojection of the component’s single-trial evoked transients ${\stackrel{\sim }{y}}_r$ to the MEG sensor level, using the spatial map of mixing weights, obtained in step i:

  $$\left[{\stackrel{\sim }{X}}_1\hspace{0.17em}{\stackrel{\sim }{X}}_2\hspace{0.17em}\dots {\stackrel{\sim }{X}}_R\right]=a\ast \left[{\stackrel{\sim }{y}}_1\hspace{0.17em}{\stackrel{\sim }{y}}_2\dots {\stackrel{\sim }{y}}_R\right].$$
• iv)Subtraction of the back-projected evoked transients from the MEG sensor data, yielding MEG-sensor data that served as input data for the next iteration.

We performed five iterations (i.e., we removed five time-locked components). Removal of additional components did not affect the global field power appreciably (Fig. S3E). The different steps and the effect of this cleaning procedure are illustrated in Fig. S3.

Source Reconstruction and Parcellation of Source-Reconstructed Activity.

After the cleaning of the sensor data with the combined DSS-ASEO procedure we performed source reconstruction using an LCMV (32). For this, we computed the covariance matrix between all MEG-sensor pairs, as the average covariance matrix across the cleaned single trial covariance estimates. This covariance matrix was used in combination with the forward model, defined on a set of 8,196 locations on the participant-specific reconstruction of the cortical sheet to generate a set of spatial filters, one filter per dipole location. Individual cortical sheets were generated with the Freesurfer package (version 5.1) (surfer.nmr.mgh.harvard.edu), coregistered to a template with a surface-based coregistration approach, using Caret software (brainvis.wustl.edu/wiki/index.php/Caret:Operations/Freesurfer_to_fs_LR, brainvis.wustl.edu/wiki/index.php/Caret:Download), and subsequently downsampled to 8,196 nodes, using the MNE software (martinos.org/mne/stable/index.html). The forward model was computed using FieldTrip’s “singleshell” method (41), where the required brain/skull boundary was obtained from the subject-specific T1-weighted anatomical images.

Next, we applied an atlas-based parcellation scheme to further reduce the dimensionality of the data. To this end, we used the Conte69 atlas (brainvis.wustl.edu/wiki/index.php//Caret:Atlases/Conte69_Atlas), which provides a parcellation of the neocortical surface, based on Brodmann’s cytoarchitectonic atlas, consisting of 41 labeled parcels per hemisphere. This parcellation scheme was further refined, breaking up the larger parcels into a set of subparcels, respecting the original boundaries (e.g., breaking up the middle temporal gyrus in smaller parcels along the anterior/posterior axis). This resulted in a parcellation scheme consisting of 191 parcels per hemisphere.

For each parcel, we obtained a parcel-specific spatial filter as follows. We concatenated the spatial filters of the vertices comprising the parcel, obtained a set of time courses of the event-related field at each parcel, and performed a principal component analysis on the result. We selected for each parcel the first two spatial components explaining most of the variance in the signal. We opted for this method, rather than averaging, because we used rank-reduced forward solutions (excluding the most noise sensitive dipole orientations), which might result in signal cancellation effects upon averaging, due to sign ambiguity of the resulting cardinal dipole orientations. For the parcels used the two dominant spatial components explained on average 90% of the signal variance within each parcel (range: 74–96%).

Preselection of the Connections Between Language-Relevant Areas.

For the connectivity analysis we constrained ourselves a priori to a subset of connections between parcel pairs, using known “long-range” macroanatomical fiber pathways between parcels comprised of core language regions and the visual system as described in the literature (1, 9–11). This preselection was motivated by the fact that direct functional connections should be supported by direct anatomical connections. In addition, we allowed a priori for direct connections between neighboring nodes, which is a fair assumption given the characteristics of cortico-cortical connections observed in anatomical tracing studies (e.g., refs. 24 and 33), where local connections are abundant. We included intrahemispheric connections from both hemispheres and also included interhemispheric connections between homologous areas. The nodes were defined based on the labeling scheme of Brodmann, where each of these nodes could consist of one or more subparcels (where subparcels were defined as described above). In addition, nodes in temporal cortex were classified according to their position along the anterior–posterior axis (distinguishing anterior, middle, and posterior parts) and along the superior–inferior axis (distinguishing superior, middle, and inferior parts). Fig. 2A in the main text shows how the individual nodes were labeled. As major long-range fiber pathways we included the arcuate fasciculus (AF), the superior longitudinal fasciculus (SLF), the extreme capsule (EC), the uncinate fasciculus (UC), and the inferior fronto-occipital fasciculus (IFOF). The AF provides widespread connections between the temporal cortex (predominantly the middle and superior temporal gyri) and various frontal areas (BA44/45/6/9). The SLF connects frontal areas (notably BA44) with posterior superior temporal and parietal areas. The EC connects frontal areas with the middle part of superior and middle temporal gyrus. The UC connects frontal areas with the temporal pole, and the IFOF connects frontal areas with occipital areas. Connections between directly adjacent parcels were excluded for further analysis to reduce spurious estimates of connectivity due to spatial leakage of source reconstructed activity. The selection scheme resulted in 4,350 connections between pairs of parcels, which notably consisted of a sparse subset of all possible pairwise connections between the 156 parcels used for the GC analysis.

GC Computation and Statistical Evaluation of Overall Network Topology.

For computational efficiency we computed the spectral representation of the signals at the sensor level and projected this into source space, using the parcel-specific spatial filters. The spectral representation of the signals was obtained using the fast Fourier transform in combination with multitapers (using 5-Hz smoothing) on the time domain data from 200 until 600 ms after word onset. The sensor-level Fourier-transformed data were projected into source space, and for each pair of parcels we computed the cross-spectral density matrix. Subsequently we performed nonparametric spectral matrix factorization for each pair of parcels, followed by computation of GC (34, 35).

We used a blockwise approach (35) in combination with nonparametric spectral factorization (34). Rather than using a parametric approach, which requires the estimation of multivariate autoregressive models, and subsequently uses the Fourier transforms of the model coefficients (along with variance estimates of the residuals) to obtain an estimate of frequency-resolved GC, we used a nonparametric technique, which is implemented in FieldTrip and has successfully been used before (6, 42).

The factorization algorithm decomposes a (by definition conjugate symmetric) cross-spectral density matrix, into a (frequency-specific) asymmetric spectral transfer matrix, and a frequency independent symmetric matrix, according to

$$S\left(\omega \right)=H\left(\omega \right)\mathrm{\Sigma }{H}^{\ast }\left(\omega \right),$$

where S(ω) is the cross-spectral density as a function of frequency ω, H(ω) is the spectral transfer matrix, and Σ is a square symmetric matrix, representing the equivalent of the residuals’ covariance matrix in a parametric estimation context. In a bivariate context, that is, where each of the signals consists of a univariate time series, and thus the cross-spectral density S is a 2 × 2 matrix for each frequency bin, GC from signal 1 to signal 2 is defined as

$${\text{GC}}_{1\to 2}\left(\omega \right)=\ln \left(\frac{S_{22}\left(\omega \right)}{S_{22}\left(\omega \right)-\left({\mathrm{\Sigma }}_{11}-\frac{{\mathrm{\Sigma }}_{21}^2}{{\mathrm{\Sigma }}_{22}}\right)abs{\left(H_{21}\left(\omega \right)\right)}^2}\right),$$

where the subscripts in the variables reflect the row and column indices for the individual elements of the 2 × 2 matrices. In a blockwise context, where each of the signals is a multivariate (in our case, a bivariate) time series, GC from signal 1 to signal 2 is defined, according to ref. 35, as

$${\text{GC}}_{1\to 2}\left(\omega \right)=\ln \left(\frac{\left|S_{22}\left(\omega \right)\right|}{\left|{\stackrel{\sim }{H}}_{22}\left(\omega \right){\mathrm{\Sigma }}_{11}{\stackrel{\sim }{H}}_{22}\left(\omega \right)\right|}\right),$$

where the subscripts in the variables reflect the row and column indices of the individual blocks of the 4 × 4 matrices, |X| denotes the determinant of a matrix, and $\stackrel{\sim }{H}$ is a modified version of the spectral transfer matrix, defined as

$$\stackrel{\sim }{H}\left(\omega \right)=H\left(\omega \right)P^{-1},$$

where P is defined as:

$$\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& -{\mathrm{\Sigma }}_{12}{\mathrm{\Sigma }}_{22}^{-1}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right].$$

For the implementation we used custom-written code (to improve computational efficiency), which was adopted from the FieldTrip functions sfactorization_wilson, sfactorization_wilson2×2, and ft_connectivity_granger.

In addition to computing GC, we also computed GC based on the source-projected Fourier transform of time-reversed data, where time reversal is essentially equivalent to complex conjugation of the Fourier coefficients, to distinguish “weak” asymmetries from “strong” asymmetries, as described by Haufe and coworkers (13) and Haufe et al. (36). Essentially, a weak asymmetry is an apparent directional interaction between a pair of network nodes, which is the consequence of a difference in SNR across nodes (14) and difficult to avoid when the signals consist of a linear mixture of underlying sources (37). We compared GC with reverse GC and selected only parcel pairs for subsequent analysis for which the parametric null hypothesis of the means (across subjects) could be rejected at a P value < 0.05, corrected for multiple comparisons (one-sided t test, with Bonferroni correction). This reduced the number of connections that were used for subsequent analysis from 4,350 to 713. Next, we evaluated the topology of this resulting network by quantifying the node degree for each of the 156 parcels involved, identifying “hubs” for inflow and outflow (Fig. 1). We quantified the probability of observing the computed node degree under the null hypothesis of the 713 connections’ being a random subset of the originally included 4,350 connections, using a permutation test. Using Bonferroni correction, a P value of 0.05/(2*156) = 1.6 × 10⁻⁴ was considered significant (each of the 156 parcels was tested twice, once for the degree for inflow and once for the degree for outflow).

As an important control analysis, we computed, across parcels, the Spearman’s rank correlation between the inflow and outflow degree on the one hand and signal variance, the norm of the spatial filter, and the SNR on the other hand. The norm of the spatial filter corresponds with an estimate of the projected noise, and the ratio between the signal variance and the spatial filter’s norm corresponds with an SNR estimate. The motivation for this analysis is to check whether there is a relationship between the node degree and simple univariate signal(-to-noise) properties, which may give rise to spurious inferences about the directionality of estimated interactions (14). Specifically, assuming the worst, one could hypothesize that parcels with a large degree of inflow (outflow) also show on average a low (high) signal(-to-noise), when comparing across parcels. The results of this control analysis are shown in Table S1. Based on this analysis, which did not reveal any significant correlations, we argue that the observed patterns of node degree in the brain network for language are not consequences of systematic differences in univariate signal properties.

Table S1.

Correlation between node degree and univariate signal properties

	Node degree inflow		Node degree outflow
Signal property	Correlation	P value	Correlation	P value
Signal variance	0.054	0.51	0.077	0.34
Spatial filter norm	0.096	0.23	0.12	0.15
SNR	−0.097	0.23	0.032	0.69

NMF and Network Visualization.

We explored the network topology by performing NMF with sparsity constraints, using an open-source toolbox (38). Specifically, we used the sparsenmfnnls routine from this toolbox, to group-concatenated data matrix X according to

$$X\approx AY,$$

where X, A, and Y are nonnegative matrices and A and Y aim to minimize the following quantity:

$$X-A{Y}_F^2+\eta A_F^2+\lambda {\displaystyle \sum _{i=1}^N{y_i}_1^2},$$

where η and λ are sparsity parameters.

Because typically the outcome of NMF depends on the random starting conditions, we repeated the factorization multiple times (n = 40), and used a hierarchical clustering procedure, as implemented in the Icasso toolbox (40) (research.ics.aalto.fi/ica/icasso). In particular, we used the hcluster function, using as a similarity matrix a matrix that was defined as

$$1-corr\left(\left[\begin{array}{c}{Y}_1\\ Y_2\\ ⋮\\ Y_{40}\end{array}\right]\right),$$

where corr(Y) is the sample correlation matrix between all pairs of rows in Y, and where the matrix Y was constructed as a concatenation of the network topologies extracted by each of the 40 runs of the NMF algorithm. We fixed the number of clusters to 20. From each of the clusters, we extracted the component that on average had the highest correlation with the other members of that cluster, to obtain the spatial topology and spectral content of that cluster.

The purpose of this analysis is to describe the reconstructed connectivity data as a low-dimensional mixture of network components, each of which with a subject-specific spectral profile. This technique has successfully been applied to sensor-level MEG-signals before (39). We opted for sparse NMF, because the nonnegativity constraint facilitates the interpretation of the components, as opposed to, for example, a statistical independence constraint as applied in independent component analysis. This is because GC is strictly nonnegative. The data matrix that was subjected to the factorization algorithm was constructed by concatenating across subjects GC spectra, normalized for the SD per subject. The columns in this matrix reflect the individual connections (across subjects and frequencies), and the rows in this matrix (number of frequency bins times number of subjects) reflected the connections for a given frequency bin and subject. Typically, the outcome of NMF is dependent on the number of components (which has to be chosen a priori) and of the initial random starting conditions. We explored a range of “number of components” but settled on the number 20, because this number provided a reasonable balance between providing a small number of easily interpretable components, while at the same time maintaining a good separation between subnetworks.

The outcome of this procedure consisted of two matrices. One matrix represents the network component spatial fingerprints, quantifying for each of the edges its relative contribution to the network components. The other matrix contains for each network component a subject-specific spectral profile, quantifying the subjectwise relative and frequency-specific contribution to the network components. For visualization purposes we assigned each of the edges to a unique network component based on its relative weight. Subsequently, the different aspects of the network components were depicted as follows. To obtain spatial maps of the nodes (i.e., anatomical parcels) participating in a particular component, we summed across each node’s contributing edges the outflow and inflow separately and displayed these onto an inflated representation of the cortical sheet, using hcp-workbench (www.humanconnectome.org/software/connectome-workbench.html).

To visualize the connections between the parcels, for each pair of parcels we averaged the connection weights across all pairs of subparcels that constituted the parcel pair. Connections were drawn as directed arrows, where the thickness of the lines reflects the overall weight of the connection. The spectral profiles of the network components were visualized as the median across subjects and their IQR. For display purposes we ordered the components according to their dominant regions for outflow. Fig. 2 in the main text shows the components that are made up predominantly by connections between language-relevant cortical parcels.

Components that are made up predominantly by connections between visual cortical parcels as well as components with spatially very diffuse connections are displayed in Fig. S1.

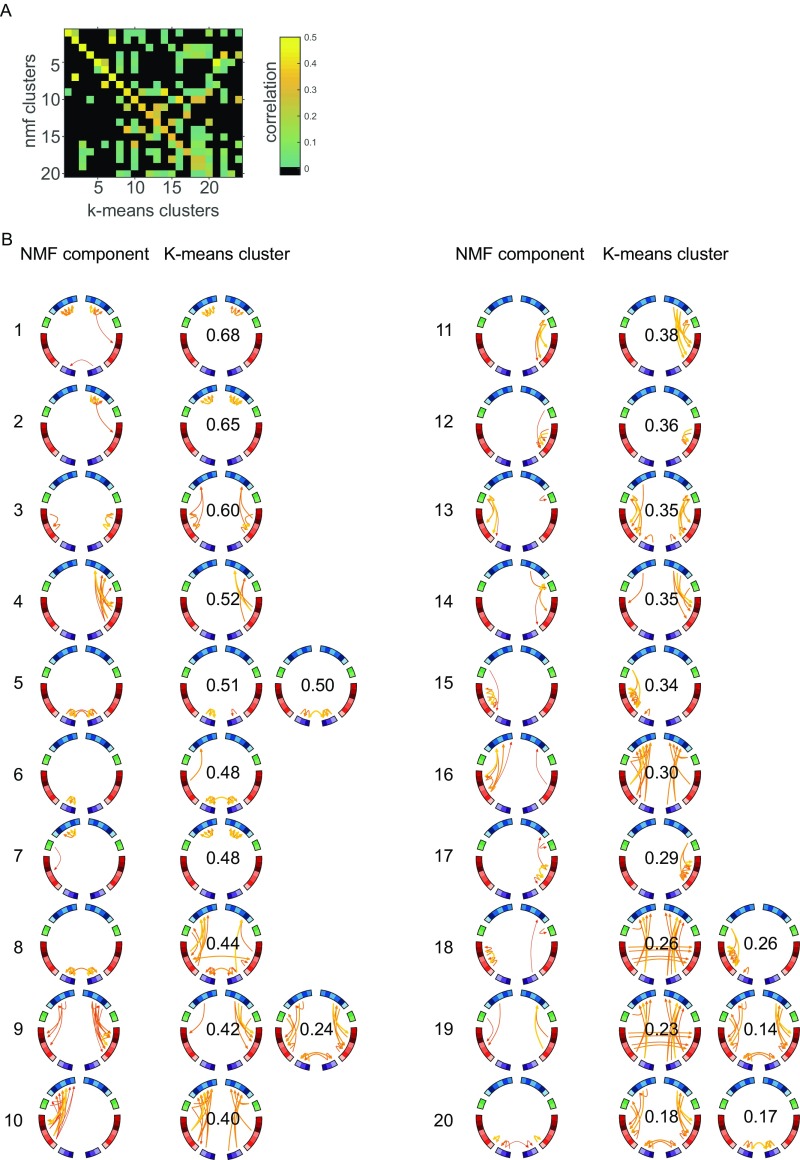
As a sanity check, we compared the NMF-based results with K-means clustering scheme, which in theory should give very similar results (43, 44). The results of this comparison are displayed in Fig. S4. We used the MATLAB built-in kmeans.m function, with cityblock as distance metric. Overall, both clustering approaches yield very similar patterns, where the K-means clusters were topologically less sparse than their corresponding NMF-based counterparts.

Fig. S4.

Comparison between NMF and K-means clustering. (A) Pairwise correlation matrix between the spatial topology of network components identified with NMF and with K-means clustering. The components are ordered such that for each of the NMF components the most highly correlated K-means cluster is on the diagonal. (B) Spatial topology of NMF component (left columns) with corresponding highly correlated K-means cluster (right columns).

Condition-Specific Statistical Evaluation.

To investigate whether the involvement of the network components was modulated by functional constraints of the linguistic input, we estimated condition-specific GC in the dominant connections extracted from the identified network components. The individual conditions were defined according to whether the words were presented in a well-formed sentence context (or were part of a word list), and according to whether the words were presented early in the sentence/word list (words two to four) or late in the sentence/word list (n − 3 until n − 1, with n being the number of words in the sentence/word list). To account for potential interpretational confounds of the resulting GC estimates we adopted a stratification procedure to ensure that, for each of the parcel pairs in each of the subjects, the marginal distributions of the epochwise signal variances as well as the words’ lexical frequencies were equalized across conditions. Lexical frequencies were estimated using the Subtlex-NL database (crr.ugent.be/programs-data/subtitle-frequencies/subtlex-nl). Condition-specific histograms for lexical frequency were generated using 13 log-spaced bins. Histograms for signal variance were generated using six log-spaced bins. The consequence of this procedure is that only a subset of epochs is used for the subsequent estimation of GC, where the parcel-pair-specific number of epochs varies across parcel pairs. On average 50% of the epochs were retained (range: 20–75%), corresponding to 147 (range: 45–235) epochs.

From each of the extracted network components we defined a dominant connection as a spatially clustered set of edges that fulfilled the following criteria: (i) Each cluster consisted of at least four edges, (ii) the inflow/outflow nodes consisted of spatially adjacent cortical parcels, and (iii) nodes that for a given cluster of edges served both as input and output node were discarded, as well as the edges to which these nodes contributed.

This resulted in 42 connections for which we computed subject- and condition-specific GC, as an average across the contributing edges, and across the component-specific frequency range, defined by the IQR across subjects. We performed a nonparametric permutation test to evaluate the following contrasts: i) sentence – word list words, ii) for the sentence condition: early – late words, and iii) interaction effect: (early-late words sentences) – (early-late words sequences).

The statistical test performed was a two-sided permutation test (using 20,000 permutations) on Wilcoxon’s signed rank statistic (Z-score) with a Bonferroni–Holm stepdown control for the familywise error rate. Fig. S2 shows in more detail data from the individual connections that showed statistically significant effects for one (or two) of the contrasts mentioned above.

Power Analysis.

Our large sample of subjects provides a unique opportunity to perform a power analysis, to estimate the minimum sample size required to reliably identify the beta-band fronto-temporal and alpha-band temporo-frontal interaction patterns.

We randomly sampled from our pool of 102 subjects, using two different approaches. These approaches differed in the extent of reanalysis upon random sampling from our pool of 102 subjects. Our general approach was as follows. We randomly drew from the pool of subjects subsets of 10, 20, 30, or 40 subjects, and for each of these subsets we did this random selection 100 times. Next, we performed the NMF on the reduced-number-of-subjects concatenated GC spectra. In the first approach, we included only those edges that survived the statistical pruning procedure (based on a Bonferroni corrected parametric statistical evaluation of GC vs. reverse-time GC, as described in the main text), where this procedure was performed on the subselection of the subjects. In the second approach we included the 713 edges that were determined based on the statistical evaluation of the full batch of subjects. Next, we paired the NMF components obtained from the subsampled data with the 102-subject results, by computing pairwise correlations between the spatial topology of the components. The subsampled components with the highest spatial correlation with the original components were subsequently used. We focused on the temporo-frontal and fronto-temporal components, corresponding to the components in Fig. 2 B and G of the main text, respectively. Next, we defined a frontotemporal directionality index:

$$di=\left(F{T}_l-T{F}_l\right)+\left(F{T}_r-T{F}_r\right),$$

where FT_l is the average of the nonzero left-hemispheric fronto-temporal edges for a given component and TF_l is the average of the nonzero left-hemispheric temporo-frontal edges. We used Monte Carlo resampling to estimate the expected value of di under random allocation of the edge weights and subtracted the average across 500 Monte Carlo estimates from the di estimated from the observed component to obtain a corrected value. Thus, a di value >0 would indicate that the corresponding component is a predominantly frontal to temporal connection, and the a di value <0 would indicate a temporal to frontal connection.

Correct detection performance was calculated as the percentage of random subsets yielding a di value with the expected sign. The results are shown in the Table S2. When using the previously determined subset of 713 edges the detection performance was extremely good, even at low subject numbers, suggesting that only a moderate sample size is needed for a reliable detection of fronto-temporal beta-band and temporo-frontal alpha-band interactions. However, when using a more conservative approach, and using a data-driven approach to statistically prune the edges (using Bonferroni correction), based on the subset of subjects in the sample, detection performance became rather poor. This performance decrease was primarily caused by the conservative edge detection process’s not selecting sufficient fronto-temporal and temporo-frontal edges to begin with. Extending the number of subjects in the subselection to 50 and 60 increased the detection performance, but not in a satisfactory way. Relaxation of the statistical selection threshold (arbitrarily setting the edge acceptance threshold to 0.0005 uncorrected) recovered the detection rate to beyond 80% with a sample size between 30 and 40. Thus, based on these analyses we conclude that using a data-driven edge selection procedure with a statistical selection criterion that is not too strict would require a sample size of 30–40 subjects to detect the fronto-temporal and temporo-frontal connections with a probability of at least 80%.

Table S2.

Detection probability of beta-band fronto-temporal and alpha-band temporo-frontal connections, based on subsampling of the subjects

No. of subjects	Fronto-temporal, %	Temporo-frontal 1, %	Temporo-frontal 2, %
Fixed set of edges (713), based on 102 subjects’ results
10	100	92	100
20	100	95	96
30	100	99	99
40	100	99	96
Data-driven edge detection (Bonferroni corrected P value)
10	0	0	0
20	0	1	1
30	0.1	0.4	0.2
40	9	0.8	5
50	47	17	40
60	68	21	51
Data-driven edge detection (P < 0.0005, uncorrected)
10	43
20	90	41	35
30	90	77	77
40	95	91	87
50	96	92	93
60	95	94	91