Entanglement and thermodynamics after a quantum quench in integrable systems

Significance

Understanding how statistical ensembles arise from the out-of-equilibrium dynamics of isolated pure systems has been a fascinating question since the early days of quantum mechanics. Recently, it has been proposed that the thermodynamic entropy of the long-time statistical ensemble is the stationary entanglement of a large subsystem in an infinite system. Here, we combine this concept with the quasiparticle picture of the entanglement evolution and integrability-based knowledge of the steady state to obtain exact analytical predictions for the time evolution of the entanglement in arbitrary 1D integrable models. These results explicitly show the transformation between the entanglement and thermodynamic entropy during the time evolution. Thus, entanglement is the natural witness for the generalized microcanonical principle underlying relaxation in integrable models.

Abstract

Entanglement and entropy are key concepts standing at the foundations of quantum and statistical mechanics. Recently, the study of quantum quenches revealed that these concepts are intricately intertwined. Although the unitary time evolution ensuing from a pure state maintains the system at zero entropy, local properties at long times are captured by a statistical ensemble with nonzero thermodynamic entropy, which is the entanglement accumulated during the dynamics. Therefore, understanding the entanglement evolution unveils how thermodynamics emerges in isolated systems. Alas, an exact computation of the entanglement dynamics was available so far only for noninteracting systems, whereas it was deemed unfeasible for interacting ones. Here, we show that the standard quasiparticle picture of the entanglement evolution, complemented with integrability-based knowledge of the steady state and its excitations, leads to a complete understanding of the entanglement dynamics in the space–time scaling limit. We thoroughly check our result for the paradigmatic Heisenberg chain.

Since the early days of quantum mechanics, understanding how statistical ensembles arise from the unitary time evolution of an isolated quantum system has been a fascinating question (1–7). A widely accepted mechanism is that, although the entire system remains in a pure state, the reduced density matrix of an arbitrary finite compact subsystem attains a long time limit that can be described by a statistical ensemble (8). In the last decade, groundbreaking experiments with cold atoms (9–19) simulated with incredible precision the unitary time evolution of many-body quantum systems, reviving the interest in this topic. The simplest out-of-equilibrium protocol in which these ideas can be theoretically and experimentally tested is the quantum quench (20, 21). A system is prepared in an initial state $|{\mathrm{\Psi }}_0⟩$, typically the ground state of a local Hamiltonian $H_0$, and it evolves with a many-body Hamiltonian $H$. At asymptotically long times, physical observables relax to stationary values, which for generic systems, are described by the Gibbs (thermal) ensemble (3–7), whereas for integrable systems, a generalized Gibbs ensemble has to be used (8, 22–45).

Although these results suggest a spectacular compression of the amount of information needed to describe steady states, state of the art numerical methods, such as the time-dependent density matrix renormalization group (46–49) (tDMRG), can only access the short-time dynamics. Physically, the origin of this conundrum is the fast growth of the entanglement entropy $S\equiv -{\text{Tr}}_A{\rho }_A\ln {\rho }_A$, with ${\rho }_A$ being the reduced density matrix of an interval $A$ of length $\mathrm{\ell }$ embedded in an infinite system. It is well-understood that $S$ grows linearly with the time after the quench (50). This linear behavior implies an exponentially increasing amount of information manipulated during typical tDMRG simulations. Remarkably, the entanglement dynamics has been successfully observed in a very recent cold-atom experiment (19).

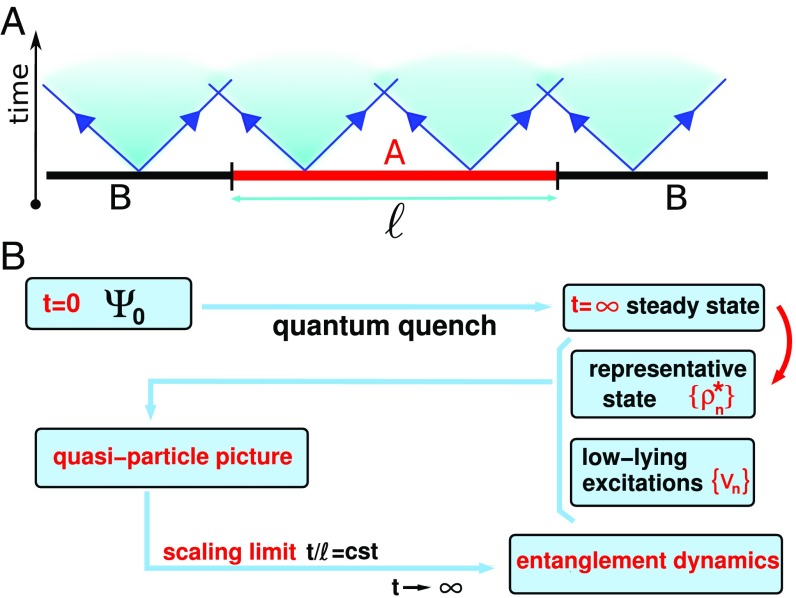
In this work, using a standard quasiparticle picture (50), we show that, in integrable models, the steady state and its low-lying excitations encode sufficient information to reconstruct the entanglement dynamics up to short times. According to the quasiparticle picture (50), the prequench initial state acts as a source of pairs of quasiparticle excitations. Let us first assume that there is only one type of quasiparticles identified by their quasimomentum $\lambda$ and moving with velocity $v(\lambda )$. Although quasiparticles created far apart from each other are incoherent, those emitted at the same point in space are entangled. Because these propagate ballistically throughout the system, larger regions get entangled. At time $t$, $S(t)$ is proportional to the total number of quasiparticle pairs that, emitted at the same point in space, are shared between A and its complement (Fig. 1A). Specifically, one obtains

$$S(t)\propto 2t\underset{2|v|t<\mathrm{\ell }}{\int }d\lambda v(\lambda )f(\lambda )+\mathrm{\ell }\underset{2|v|t>\mathrm{\ell }}{\int }d\lambda f(\lambda ),$$ [1]

where $f(\lambda )$ depends on the production rate of quasiparticles. Eq. 1 holds in the space–time scaling limit $t,\mathrm{\ell }\to \mathrm{\infty }$ at $t/\mathrm{\ell }$ fixed. When a maximum quasiparticle velocity $v_M$ exists [e.g., because of the Lieb–Robinson bound (51)], for $t\le \mathrm{\ell }/(2v_M)$, $S$ grows linearly in time, because the second term in Eq. 1 vanishes. In contrast, for $t\gg \mathrm{\ell }/(2v_M)$, the entanglement is extensive (i.e., $S\propto \mathrm{\ell }$). This light-cone spreading of entanglement has been confirmed analytically only in free models (52–57), numerically in several studies (58–60), in the holographic framework (61–68), and in a recent experiment (19). The validity of the quasiparticle picture Eq. 1 for the entanglement dynamics has been proven for free models in ref. 52. In the presence of interactions, few results are known. For instance, the validity of Eq. 1 has been proven for rational CFTs (Conformal Field Theories) in ref. 69. In interacting integrable models à la Yang–Baxter, the quasiparticle picture has been used to describe the out-of-equilibrium dynamics after an inhomogeneous quench, and it is at the foundation of the integrable hydrodynamics approach for transport in integrable models (70, 71).

Fig. 1.

Entanglement dynamics after a quantum quench: theoretical scheme. (A) Quasiparticle picture. Full lines denote quasiparticles with maximum velocity emitted in the initial state. Shaded cones show the halo of slower quasiparticles. (B) Main steps to calculate the entanglement dynamics using Bethe ansatz and the quasiparticle picture.

Results

In a generic interacting integrable model, there are different species of stable quasiparticles corresponding to bound states of an arbitrary number of elementary excitations. Integrability implies that different types of quasiparticles must be treated independently. It is then natural to conjecture that

$$S(t)=\sum _n\left[2t\underset{2|v_n|t<\mathrm{\ell }}{\int }d\lambda v_n(\lambda )s_n(\lambda )+\mathrm{\ell }\underset{2|v_n|t>\mathrm{\ell }}{\int }d\lambda s_n(\lambda )\right],$$ [2]

where the sum is over the types of particles $n$, $v_n(\lambda )$ is their velocity, and $s_n(\lambda )$ is their entropy. To give predictive power to Eq. 2, in the following, we show how to determine $v_n(\lambda )$ and $s_n(\lambda )$ in the Bethe ansatz framework for integrable models. Eq. 2 is straighforwardly generalized to the mutual information between two intervals (see SI Materials and Methods and Fig. S1).

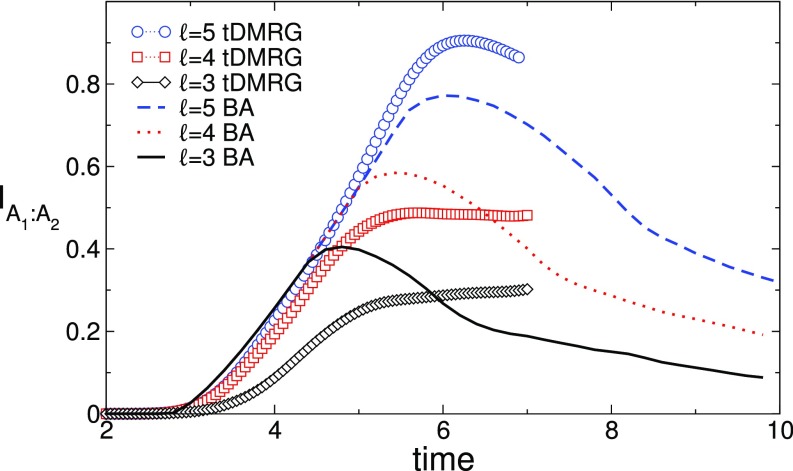
Fig. S1.

Mutual information $I_{A_1:A_2}$ between the two intervals $A_1$ and $A_2$ after the quench from the Néel state in the open $XXZ$ chain. Here, $A_1$ and $A_2$ are at the two edges of the chain and of equal length $\mathrm{\ell }$. The distance between $A_1$ and $A_2$ is $d=10$ lattice sites. The symbols are tDMRG results for $\mathrm{\ell }=3,4,5$. All of the data are for $\mathrm{\Delta }=2$. The lines are the analytical results using the quasiparticle picture (Eq. S18). BA, Bethe ansatz.

The eigenstates of Bethe ansatz solvable models are in correspondence with a set of pseudomomenta (rapidities) $\lambda$. In the thermodynamic limit, these rapidities form a continuum. One then introduces the particle densities ${\rho }_{n,p}(\lambda )$, the hole (i.e., unoccupied rapidities) densities ${\rho }_{n,h}(\lambda )$, and the total densities ${\rho }_{n,t}(\lambda )={\rho }_{n,p}(\lambda )+{\rho }_{n,h}(\lambda )$. Every set of densities identifies a thermodynamic “macrostate.” This macrostate corresponds to an exponentially large number of microscopic eigenstates, any of which can be used as a “representative” for the macrostate. The total number of representative microstates is $e^{S_{YY}}$, with $S_{YY}$ as the thermodynamic Yang–Yang entropy of the macrostate

$$S_{YY}=s_{YY}L=L\sum _{n=1}^{\mathrm{\infty }}\int d\lambda [{\rho }_{n,t}(\lambda )\ln {\rho }_{n,t}(\lambda )-{\rho }_{n,p}(\lambda )\ln {\rho }_{n,p}(\lambda )-{\rho }_{n,h}(\lambda )\ln {\rho }_{n,h}(\lambda )]\equiv L\sum _{n=1}^{\mathrm{\infty }}\int d\lambda s_{YY}^{(n)}[{\rho }_{n,p},{\rho }_{n,h}](\lambda ).$$ [3]

Physically, $S_{YY}$ corresponds to the total number of ways of assigning the quasimomentum label to the particles, similar to free fermion models.

In the Bethe ansatz treatment of quantum quenches (72–74), local properties of the postquench stationary state are described by a set of densities ${\rho }_{n,p}^{\ast }(\lambda )$ and ${\rho }_{n,h}^{\ast }(\lambda )$. Calculating these densities is a challenging task that has been performed only in a few cases (75–87). From the densities, the thermodynamic entropy of the stationary ensemble Eq. 3 is $s_{YY}[{\rho }_{n,p}^{\ast },{\rho }_{n,h}^{\ast }](\lambda )$. Physically, $e^{L{s}_{YY}}$ is the number of microscopic eigenstates entering in a generalized microcanonical ensemble for quenches, in which all of the microstates corresponding to the macrostate have the same probability.

We now present our predictions for the entanglement dynamics (Fig. 1B gives a survey of our theoretical scheme). First, in the stationary state, the density of thermodynamic entropy coincides with that of the entanglement entropy in Eq. 2, as it has been shown analytically for free models (52, 88, 89). This identification implies that $s_n(\lambda )=s_{YY}[{\rho }_{n,p}^{\ast },{\rho }_{n,h}^{\ast }](\lambda )$. Moreover, it is natural to identify the entangling quasiparticles in Eq. 2 with the low-lying excitations around the stationary state ${\rho }^{\ast }$. Their group velocities $v_n$ depend on the stationary state, because the interactions induce a state-dependent dressing of the excitations. These velocities $v_n$ can be calculated by Bethe ansatz techniques (90) (SI Materials and Methods and Figs. S2 and S3).

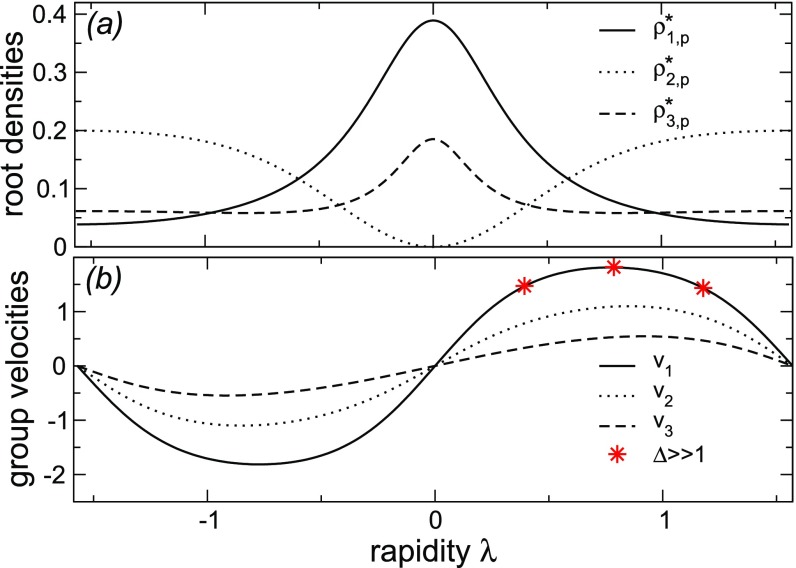
Fig. S2.

The postquench steady state and the low-lying excitations around it. Results for the quench from the Néel state in the $XXZ$ chain with $\mathrm{\Delta }=2$. (A) The macrostate densities ${\rho }_{n,p}^{\ast }$ characterizing the steady state. The first three particle densities ${\rho }_n^{\ast }(\lambda )$ plotted against the rapidity $\lambda$. (B) Group velocities of the low-lying excitations around the steady-state macrostate as a function of $\lambda$. Note that $v_n(-\lambda )=-v_n(\lambda )$. The star symbols are the results for $\mathrm{\Delta }\gg 1$.

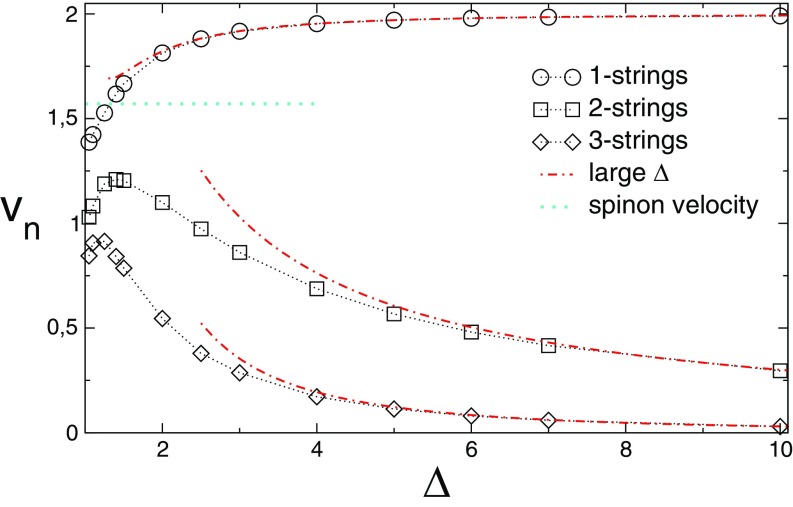
Fig. S3.

Group velocities of the low-lying excitations around the steady state after the quench from the Néel state in the $XXZ$ chain. The maximum velocity in each string sector (different symbols used in the figure) is plotted against the anisotropy $\mathrm{\Delta }$. The dashed–dotted lines are the analytical results of Eq. S14 in the large $\mathrm{\Delta }$ limit. The horizontal dotted line is the (low-energy) spin-wave velocity $v_{sw}=\pi /2$ at $\mathrm{\Delta }=1$.

To substantiate our idea, we focus on the spin-$1/2$ anisotropic Heisenberg ($XXZ$) chain, considering quenches from several low-entangled initial states, namely the tilted Néel state, the Majumdar–Ghosh (dimer) state, and the tilted ferromagnetic state (Materials and Methods). For these initial states, the densities ${\rho }_{n(h),p}^{\ast }$ are known analytically (77–79).

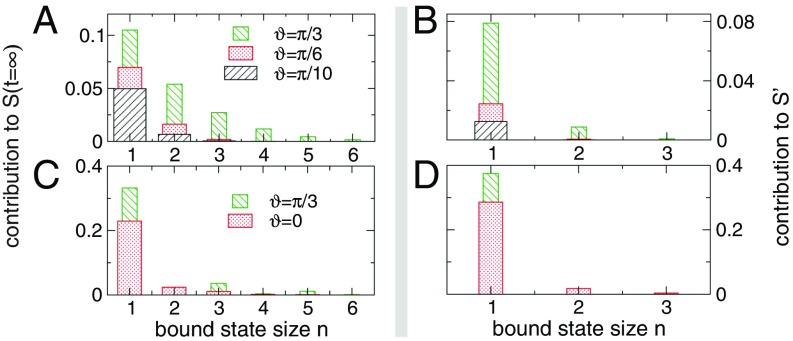
Fig. 2 summarizes the expected entanglement dynamics in the space–time scaling limit, plotting $S/\mathrm{\ell }$ vs. $v_{M}t/\mathrm{\ell }$. Interestingly, $S/\mathrm{\ell }$ is always smaller than $\ln 2$ (i.e., the entropy of the maximally entangled state). For the Néel quench, because the Néel state becomes the ground state of Eq. 4 in the limit $\mathrm{\Delta }\to \mathrm{\infty }$, $S/\mathrm{\ell }\approx \ln (\mathrm{\Delta })/{\mathrm{\Delta }}^2$ vanishes, whereas it saturates for all of the other quenches. For the Majumdar–Ghosh state, one obtains $S/\mathrm{\ell }=-1/2+\ln 2$ at $\mathrm{\Delta }\to \mathrm{\infty }$. For the tilted ferromagnet with $\vartheta \to \mathrm{\hspace{0.17em}0}$ (Fig. 2E), $S/\mathrm{\ell }$ is small at any $\mathrm{\Delta }$, reflecting that the ferromagnet is an eigenstate of the $XXZ$ chain. Surprisingly, the linear growth seems to extend for $v_{M}t/\mathrm{\ell }>1$. However, $dS/dt$ (Fig. 2F) is flat only for $v_{M}t/\mathrm{\ell }\le 1$, which signals true linear regime only for $v_{M}t/\mathrm{\ell }\le 1$. This peculiar behavior is caused by the large entanglement contribution of the slow quasiparticles. In Fig. 3, we report the bound-state resolved contributions to the entanglement dynamics. Fig. 3 A and C focuses on the steady-state entropy (second term in Eq. 2), whereas Fig. 3 B and D shows the bound-state contributions to the slope of the linear growth (first term in Eq. 2). The contribution of the bound states, although never dominant, is crucial to ensure accurate predictions.

Fig. 2.

Analytical predictions for the $XXZ$ chain. Entanglement entropy per site $S/\mathrm{\ell }$ vs. $v_{M}t/\mathrm{\ell }$, with $v_M$ as the maximum velocity. Different panels correspond to the different initial states: Néel (A), tilted Néel (B), Dimer (C), and tilted ferromagnet (D and E). Different lines correspond to different $\mathrm{\Delta }$. For $\mathrm{\Delta }\to \mathrm{\infty }$, $S\to \mathrm{\hspace{0.17em}0}$ for the Néel quench, whereas it saturates in the other cases. Note in E the substantial entanglement increase for $v_{M}t/\mathrm{\ell }>\mathrm{\hspace{0.17em}1}$. (F) The numerical derivative $S\prime (v_{M}t/\mathrm{\ell })\times 100$ for the quench in E.

Fig. 3.

Bound-state contributions to the entanglement dynamics. On the $x$ axis, $n$ is the bound-state size. (A and B) Quench from the tilted ferromagnet. (A) Bound-state contributions to steady-state entropy density (second term in Eq. 2). (B) Bound-state contributions to the slope of the entanglement growth for $t<\mathrm{\ell }/v_M$ (first term in Eq. 2). Different histograms denote different tilting angles $\vartheta$. All of the data are for $\mathrm{\Delta }=\mathrm{\hspace{0.17em}2}$. (C and D) Same as in A and B for the quench from the tilted Néel state.

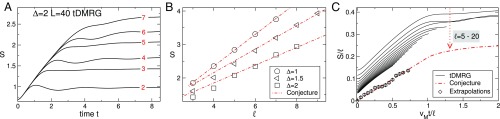
Fig. 4A shows tDMRG results for $S(t)$ for the quench from the symmetrized Néel state $(|\uparrow \downarrow \uparrow \mathrm{\dots }⟩+|\downarrow \uparrow \downarrow \mathrm{\dots }⟩)/\sqrt{2}$. The data are for the open $XXZ$ chain and subsystems starting from the chain boundary. The qualitative agreement with Eq. 2 is apparent. Fig. 4B reports the steady-state entanglement entropy as a function $\mathrm{\ell }$ (data at $t\approx \mathrm{\hspace{0.17em}8}$ in Fig. 4A). The volume law $S\propto \mathrm{\ell }$ is visible. The dashed–dotted lines in Fig. 4B are fits to $S\propto s_{YY}^{\ast }\mathrm{\ell }$, supporting the equivalence between entanglement and thermodynamic entropy. Fig. 4C focuses on the full-time dependence, plotting $S/\mathrm{\ell }$ vs. $v_{M}t/\mathrm{\ell }$. The dashed–dotted line in Fig. 4C is Eq. 2 with $t\to t/2$ because of the open boundary conditions (58). Deviations from Eq. 2 because of the finite $\mathrm{\ell }$ are visible. The diamonds in Fig. 4C are numerical extrapolations to the thermodynamic limit. The agreement with Eq. 2 is perfect. Finally, we provide a more stringent check of Eq. 2, focusing on the linear entanglement growth. Fig. 5 shows infinite time-evolving block decimation (iTEBD) results in the thermodynamic limit for $S\prime (v_{M}t)$, with $S\prime (x)\equiv dS(x)/dx$ taken from ref. 91. For all of the quenches, the agreement with Eq. 2 (horizontal lines in Fig. 5) is spectacular.

Fig. 4.

Comparison with numerical simulations. Entanglement entropy dynamics after the quench from the Néel state in the $XXZ$ chain. (A) tDMRG results for a chain with $L=\mathrm{\hspace{0.17em}40}$ sites and $\mathrm{\Delta }=\mathrm{\hspace{0.17em}2}$. Different curves correspond to different subsystem sizes $\mathrm{\ell }$ (accompanying numbers). (B) The entropy saturation values (tDMRG results at $t\approx 8$) as a function of the block length $\mathrm{\ell }$ for several $\mathrm{\Delta }$. The dashed–dotted lines are the conjectured volume-law behavior $S\propto s_{YY}^{\ast }\mathrm{\ell }$ (compare with Eq. 3). (C) The scaling limit: $S/\mathrm{\ell }$ plotted vs. $v_{M}t/\mathrm{\ell }$. The continuous curves are the tDMRG results for $\mathrm{\ell }=5-20$. The diamonds are numerical extrapolations to the thermodynamic limit. The dashed–dotted line is the conjecture Eq. 2.

Fig. 5.

Comparison with numerical simulations: the short-time regime. Derivative $S\prime (v_{M}t)$ as a function of time. Different panels correspond to different initial states: tilted Néel (A), tilted ferromagnet (B), and dimer state (C); $\vartheta$ is the tilting angle. In each panel, the different curves are iTEBD results for different $\mathrm{\Delta }$. The horizontal lines are the conjecture Eq. 2.

SI Materials and Methods

In this supplementary material, we provide some details on

• i)the Bethe ansatz solution of the $XXZ$ chain,
• ii)the Bethe ansatz treatment of the postquench steady state,
• iii)the calculation of the group velocities of the low-lying excitations around the steady state, and
• iv)the entanglement and the mutual information of two disjoint intervals.

Bethe Ansatz Solution of the XXZ Chain.

In the Bethe ansatz (94) solution of the $XXZ$ chain, the eigenstates of the $XXZ$ chain in the sector with $M$ down spins (particles) are in correspondence with a set of rapidities ${\lambda }_j$. These rapidities are obtained by solving the Bethe equations (94)

$${\left[\frac{\sin ({\lambda }_j+i\frac{\eta }{2})}{\sin ({\lambda }_j-i\frac{\eta }{2})}\right]}^L=-\prod _{k=1}^M\frac{\sin ({\lambda }_j-{\lambda }_k+i\eta )}{\sin ({\lambda }_j-{\lambda }_k-i\eta )},$$ [S1]

where $\eta \equiv \text{arccosh}(\mathrm{\Delta })$.

In the thermodynamic limit, the solutions of the Bethe equations (Eq. S1) form string patterns in the complex plane. The rapidities forming an $n$ string are parametrized as

$${\lambda }_{n,\gamma }^j={\lambda }_{n,\gamma }+i\frac{\eta }{2}(n+1-2j)+{\delta }_{n,\gamma }^j,$$ [S2]

where $j=1,\mathrm{\dots },n$ labels the different string components, ${\lambda }_{n,\gamma }$ is the “string center,” and ${\delta }_{n,\gamma }^j$ are the so-called string deviations. Typically (i.e., for the majority of the eigenstates of the $XXZ$ chain), one has ${\delta }_{n,\gamma }^j=\mathcal{O}(e^{-L})$, implying that the string deviations can be neglected (94) (string hypothesis). Physically, $n$ strings correspond to bound states of $n$ down spins. The string centers ${\lambda }_{n,\gamma }$ are solutions of the Bethe–Gaudin–Takahashi (BGT) equations (94):

$$L{\theta }_n({\lambda }_{n,\alpha })=2\pi I_{n,\alpha }+\sum _{(n,\alpha )\ne (m,\beta )}{\mathrm{\Theta }}_{n,m}({\lambda }_{n,\alpha }-{\lambda }_{m,\beta }).$$ [S3]

For $\mathrm{\Delta }>1$, one has ${\lambda }_{n,\gamma }\in [-\pi /2,\pi /2)$. Here, we define ${\theta }_n(\lambda )\equiv 2\arctan [\tan (\lambda )/\tanh (n\eta /2)]$. The scattering phases ${\mathrm{\Theta }}_{n,m}(\lambda )$ are defined as

$${\mathrm{\Theta }}_{n,m}(\lambda )\equiv (1-{\delta }_{n,m}){\theta }_{|n-m|}(\lambda )+2{\theta }_{|n-m|+2}(\lambda )+\mathrm{\cdots }+{\theta }_{n+m-2}(\lambda )+{\theta }_{n+m}(\lambda ).$$ [S4]

Each different choice of the so-called BGT quantum numbers $I_{n,\alpha }\in \frac{1}{2}\mathbb{Z}$ identifies a different set of solutions of Eq. S3 and in turn, a different eigenstate of the model. The corresponding eigenstate energy $E$ and total momentum $P$ are obtained by summing over all of the BGT rapidities (94) as $E={\sum }_{n,\alpha }{ϵ}_n({\lambda }_{n,\alpha })$ and $P={\sum }_{n,\alpha }{z}_n({\lambda }_{n,\alpha })$ with

$${ϵ}_n(\lambda )\equiv -\frac{\sinh (\eta )\sinh (n\eta )}{\cosh (n\eta )-\cos (2\lambda )},\hspace{1em}{z}_n({\lambda }_{n,\alpha })=\frac{2\pi I_{n,\alpha }}{L}.$$ [S5]

Note that $P$ depends only on the $I_{n,\alpha }$.

The Steady State: Bethe Ansatz Treatment.

Here, we provide some details on how to derive the steady-state densities ${\rho }_{n,p}^{\ast },{\rho }_{n,h}^{\ast }$ in Bethe ansatz. The root densities ${\rho }_{n,p}$ are defined as (95)

$${\rho }_{n,p}(\lambda )\equiv \underset{L\to \mathrm{\infty }}{lim}\frac{1}{L({\lambda }_{n,\alpha +1}-{\lambda }_{n,\alpha })}.$$ [S6]

Instead of working with the hole densities ${\rho }_{n,h}$, it is convenient to define ${\eta }_n={\rho }_{n,h}/{\rho }_{n,p}$. For all of the initial states considered in this work, the corresponding steady-state densities ${\rho }_{n,h}^{\ast },{\eta }_n^{\ast }$ obey the recursive relations (74, 80)

$${\eta }_n^{\ast }(\lambda )=\frac{{\eta }_{n-1}^{\ast }(\lambda +i\frac{\eta }{2}){\eta }_{n-1}^{\ast }(\lambda -i\frac{\eta }{2})}{1+{\eta }_{n-2}^{\ast }(\lambda )}-1,$$ [S7]

$${\rho }_{n,h}^{\ast }(\lambda )={\rho }_{n,t}^{\ast }(\lambda +i\frac{\eta }{2})+{\rho }_{n,t}^{\ast }(\lambda )-{\rho }_{n-1,h}^{\ast }(\lambda ),$$ [S8]

with ${\eta }_0^{\ast }=0$ and ${\rho }_{0,h}^{\ast }=0$. In Eqs. S7 and S8, the initial conditions ${\rho }_{1,h}^{\ast }$ and ${\eta }_1^{\ast }$ encode the information about the prequench initial state. For all of the quenches considered in this work, these initial conditions are known analytically. For instance, for the quench from the Néel state, one has (80)

$$\begin{array}{c}{\eta }_1^{\ast }=\frac{2[2\cosh (\eta )+2\cosh (3\eta )-3\cos (2\lambda ){\sin }^2(\lambda )]}{[\cosh (\eta )-\cos (2\lambda )][\cosh (4\eta )-\cos (4\lambda )]}\\ {\rho }_{1,h}^{\ast }=\frac{{\theta }_1^{\prime }(\lambda )}{2\pi }(1-\frac{4{\cosh }^2(\eta )}{{[{\theta }_1^{\prime }(\lambda )\sin (2\lambda )]}^2+4{\cosh }^2(\eta )}),\end{array}$$ [S9]

where ${\theta }_1^{\prime }(\lambda )\equiv d{\theta }_1(\lambda )/d\lambda$ [with ${\theta }_1(\lambda )$ as defined in Eq. S4]. For the dimer state, ${\rho }_{1,p}^{\ast }$ and ${\eta }_1^{\ast }$ have been calculated in ref. 81, whereas for the tilted Néel and the tilted ferromagnet, they have been derived recently (79, 87). Fig. S2A shows ${\rho }_{n,p}^{\ast }$ for $n=\mathrm{1,2,3}$ for the quench from the Néel state in the $XXZ$ chain with $\mathrm{\Delta }=2$.

Group Velocities of the Entangling Quasiparticles.

Here, we detail the calculation of the group velocities of the entangling quasiparticles, which explain the linear entanglement growth after the quench. The low-lying excitations around the postquench steady state can be constructed as particle hole excitations over the corresponding macrostate. Notice that it has been verified in ref. 96 that the low-lying excitations around the stationary state can be used to reconstruct “back in time” the postquench out-of-equilibrium dynamics of local observables. First, one can imagine choosing among the eigenstates of the $XXZ$ chain a representative of the macrostate, identified by some BGT quantum numbers $I_{n,\alpha }^{\ast }$. Second, a particle hole excitation, in each $n$-string sector, is obtained as $I_{n,h}^{\ast }\to I_{n,p}$, where $I_{n,p}(I_{n,h}^{\ast })$ is the BGT number of the added particle (hole). Because the $XXZ$ chain is interacting, this local change in quantum numbers affects all of the new rapidities. The excess energy of the particle hole excitation is

$$\delta E_n=e_n({\lambda }_{n,p}^{\ast })-e_n({\lambda }_{n,h}^{\ast }).$$ [S10]

Remarkably, apart from the dressing of the “single-particle” energy $e(\lambda )$ (see below for its calculation), Eq. S10 is the same as for free models. The change in the total momentum is obtained from Eq. S5 as

$$\delta P=z_n({\lambda }_{n,p}^{\ast })-z_n({\lambda }_{n,h}^{\ast }).$$ [S11]

Finally, the group velocity of the particle hole excitations is by definition

$$v_n(\lambda )\equiv \frac{\partial e_n}{\partial z_n}=\frac{e_n^{\prime }(\lambda )}{2\pi {\rho }_{n,t}^{\ast }}.$$ [S12]

Here, we used that (94) $d{z}_n(\lambda )/d\lambda =2\pi {\rho }_{n,t}^{\ast }$, with ${\rho }_{n,t}^{\ast }\equiv {\rho }_{n,p}^{\ast }(1+{\eta }_n^{\ast })$, and we defined $e_n^{\prime }(\lambda )$ as the derivative of $e(\lambda )$. Importantly, $e_n^{\prime }(\lambda )$ is determined by an infinite system of Fredholm integral equations of the second kind as

$$e_n^{\prime }(\lambda )+\frac{1}{2\pi }\sum _{m=1}^{\mathrm{\infty }}\int d\mu e_m^{\prime }(\mu )\frac{{\mathrm{\Theta }}_{m,n}^{\prime }(\mu -\lambda )}{1+{\eta }_m^{\ast }(\mu )}={ϵ}_n^{\prime }(\lambda ),$$ [S13]

where ${\mathrm{\Theta }}_{n,m}^{\prime }(\lambda )\equiv d{\mathrm{\Theta }}_{n,m}(\lambda )/d\lambda$ and ${ϵ}_n^{\prime }(\lambda )\equiv d{ϵ}_n(\lambda )/d\lambda$ (compare Eq. S4 with Eq. S5). The solutions of Eq. S13 can be obtained numerically very effectively after truncating the system considering $n\le n_{max}$. We should mention that the method outlined above has been used to study transport properties in the $XXZ$ chain starting from inhomogeneous initial conditions (70, 71) and the spreading of correlations after quantum quenches (20, 90, 97–105).

Importantly, in the limit $\mathrm{\Delta }\to \mathrm{\infty }$, the solution of Eq. S13 and the group velocities (Eq. S12) can be obtained analytically as a power series in $z\equiv e^{-\eta }\approx 1/(2\mathrm{\Delta })$. For instance, for the quench from the Néel state, one obtains

$$\begin{array}{c}{v}_1(\lambda )=2\sin (2\lambda )+z^2[\sin (2\lambda )+4\cos (4\lambda )\sin (2\lambda )]+z^3[2\cos (2\lambda )\sin (2\lambda )]-z^4[2\cos (4\lambda )\sin (2\lambda )-\sin (2\lambda )-4\cos (8\lambda )\sin (2\lambda )]+\mathcal{O}(z^5)\\ v_2(\lambda )=6z\sin (2\lambda )+\mathcal{O}(z^3)\\ v_3(\lambda )=12z^2\sin (2\lambda )+\mathcal{O}(z^3).\end{array}$$ [S14]

A similar result can be obtained for the Majumdar–Ghosh state as

$$\begin{array}{c}{v}_1(\lambda )=2\sin (2\lambda )+4z^2\cos (4\lambda )\sin (2\lambda )+z^3[8\cos (2\lambda )\sin (2\lambda )+4\sin (2\lambda )]+z^4[6\sin (2\lambda )-4\cos (2\lambda )\sin (2\lambda )+-8\cos (4\lambda )\sin (2\lambda )+4\cos (8\lambda )\sin (2\lambda )]+\mathcal{O}(z^5)\\ v_2(\lambda )=4z\sin (2\lambda )+z^2[4\sin (2\lambda )+4\cos (2\lambda )\sin (2\lambda )]+z^3[4\cos (4\lambda )\sin (2\lambda )-6\sin (2\lambda )]+z^4[4\cos (6\lambda )\sin (2\lambda )-28\sin (2\lambda )-32\cos (2\lambda )\sin (2\lambda )]+\mathcal{O}(z^5)\\ v_3(\lambda )=12z^2\sin (2\lambda )+\mathcal{O}(z^3).\end{array}$$ [S15]

As an example of calculation of group velocities, we plot in Fig. S2B $v_n^{\ast }(\lambda )$ for $n=1,2,3$ for the quench from the Néel state in the $XXZ$ chain with $\mathrm{\Delta }=2$. In Fig. S1B, $v_n$ are plotted vs. the rapidity $\lambda$. The star symbols in Fig. S2B are the perturbative results (Eq. S14) in the large $\mathrm{\Delta }$ limit. Moreover, in Fig. S3, we plot the maximum group velocity in each string sector as a function of $\mathrm{\Delta }$. The dashed–dotted lines in Fig. S3 are the analytical results (Eq. S14) in the limit $\mathrm{\Delta }\to \mathrm{\infty }$. Note that, in the limit $\mathrm{\Delta }\to \mathrm{\infty }$, one has $v_1\to 2$, whereas the group velocities are vanishing in the other string sectors. At $\mathrm{\Delta }=1$, $v_1$ is different from the low-energy spin-wave velocity $v_{sw}=\pi /2$ (shown as the horizontal dotted line in Fig. S3).

Two Disjoint Intervals.

In this section, we investigate the entanglement of two disjoint spin blocks after a quench. This study is motivated by some recent holographic results, which also apply to irrational $1$ + $1$ CFT (64, 67, 69, 106, 107), that are in contrast with the quasiparticle picture. We focus on the behavior of the von Neumann mutual information $I_{A_1:A_2}$ after a global quench. We consider the tripartition of the chain as $A_1\cup A_2\cup B$, where $A_1$ and $A_2$ are two disjoint intervals of equal length $\mathrm{\ell }$ and at distance $d$, whereas $B$ is the remainder of the chain. The mutual information $I_{A_1:A_2}$ is defined as

$$I_{A_1:A_2}\equiv S_{A_1}+S_{A_2}-S_{A_1\cup A_2},$$ [S16]

with $S_{A_{1(2)}}$ and $S_{A_1\cup A_2}$ being the entanglement entropies of $A_{1(2)}$ and $A_1\cup A_2$, respectively.

For an infinite system and two intervals of length $\mathrm{\ell }$ at a distance $d$, it is straightforward to derive the contribution to the mutual information of each quasiparticle with velocity $v$, namely (50)

$$I_{A_1:A_2}\propto -2\max (\frac{(d+\mathrm{\ell })}{2},vt)+\max (\frac{d}{2},vt)+\max (\frac{(d+2\mathrm{\ell })}{2},vt),$$ [S17]

which predicts $I_{A_1:A_2}=0$ for $vt\le d/2$, a linear increase for $d/2<vt\le (d+\mathrm{\ell })/2$ followed by a linear decrease up to $vt=(d+2\mathrm{\ell })/2$. In stark contrast, it has been suggested that the quasiparticle picture for the entanglement propagation does not hold in holographic contexts. The scenario of ref. 69 predicts $I_{A_1:A_2}=0$ at any time: the idea is that quasiparticles originated at the same point in space and traveling with one in $A_1$ and the other in $A_2$, do not remain maximally entangled when they are far apart from each other (a phenomenon known as scrambling).

To clarify whether the quasiparticle picture applies to interacting integrable models, here we discuss the behavior of $I_{A_1:A_2}$ after the quench from the Néel state $|\uparrow \downarrow \uparrow \mathrm{\cdots }⟩$ in the $XXZ$ chain. We restrict ourselves to the open $XXZ$ spin chain. We always consider the situation with the two intervals $A_1$ and $A_2$ at the opposite edges of the chain, because it is convenient for the numerical simulations. This geometry implies $L=2\mathrm{\ell }+d$.

In this case, the contribution of each quasiparticle is given by Eq. S17 with the replacement $\mathrm{\ell }\to 2\mathrm{\ell }$, but the formula is valid only before the revival time $t_{rev}=L/v$. Similar to Eq. 2, the final quasiparticle prediction for the mutual information is obtained by summing (and integrating) the contribution of all quasiparticles: that is,

$$I_{A_1:A_2}=\sum _n\int d\lambda s_n(\lambda )[-2\max (\frac{(d+2\mathrm{\ell })}{2},v_n(\lambda )t)+\max (\frac{d}{2},v_n(\lambda )t)+\max (\frac{(d+4\mathrm{\ell })}{2},v_n(\lambda )t)],$$ [S18]

which again, it is valid before the revival time (i.e., for $t$, such that $v_{M}t<L$). In the following, we compare Eq. S18 with tDMRG results.

It is well-known that extracting the entanglement entropy of multiple disjoint intervals in density matrix renormalization group (DMRG) simulations is a formidable task in contrast with the single-interval entropy. Specifically, given the matrix product state (MPS) representation of the state, the computational cost scales as ${\chi }^6$ for the multiinterval, whereas it is only ${\chi }^3$ for the single interval, with $\chi$ being the bond dimension of the MPS. This issue is even more dramatic out of equilibrium, where $\chi$ grows exponentially with time. For this reason, we can provide reliable data for $I_{A_1:A_2}$ only for very small intervals and up to short times after the quench.

Our results are presented in Fig. S1. The symbols are the tDMRG data for $I_{A_1:A_2}$ plotted as a function of the time after the quench. We show the data for $\mathrm{\ell }=3,4,5$, which are the only sizes that we can simulate reliably, and only $t\lesssim 7$. In our simulations, for all values of $\mathrm{\ell }$, the two intervals are at fixed distance $d=10$. The lines in Fig. S1 are the analytic results obtained using Eq. S18. Clearly, the system sizes and timescales accessible in our tDMRG simulations do not allow us to reach a quantitative conclusion on the validity of Eq. S18 for the mutual information. However, we observe that the DMRG data are in a good overall qualitative agreement with the quasiparticle predictions in Eq. S18. Indeed, the mutual information is zero for $t<d/(2v_M)$; then, it starts growing (seemingly) linearly with time, up to a maximum value that is clearly visible for $\mathrm{\ell }=5$ (but not for smaller $\mathrm{\ell }$). The few results available in the literature for the mutual information of two disjoint intervals for free systems (55, 108) show very similar effects when the lengths of the subsystems are very small, such as in our simulations. Hence, these DMRG results provide a strong support for the validity of the quasiparticle picture for $I_{A_1:A_2}$, signaling the absence of scrambling that takes place for CFTs with large central charge (69).

Conclusions

The main result of this work is the analytical prediction in Eq. 2 for the time-dependent entanglement entropy after a generic quantum quench in an integrable model. We tested our conjecture for several quantum quenches in the $XXZ$ spin chain, although we expect Eq. 2 to be more general. Additional checks of Eq. 2 (e.g., for the Lieb–Liniger gas) are desirable. It would be also interesting to generalize Eq. 2 to quenches from inhomogeneous initial states, exploiting the recent analytical results (70, 71, 92). Although we are not able yet to provide an ab initio derivation of Eq. 2, we find it remarkable that it is possible to characterize analytically the dynamics of the entanglement entropy, whereas its equilibrium behavior is still an open challenge. Finally, we believe that Eq. 2 represents a deep conceptual breakthrough, because it shows in a single compact formula the relation between entanglement and thermodynamic entropy for integrable models. An analogous description for nonintegrable systems, where quasiparticles have finite lifetime or do not exist at all, could lead to a deeper understanding of thermalization (19).

Materials and Methods

The anisotropic spin-$1/2$ Heisenberg chain is defined by the Hamiltonian

$$H=\sum _{i=1}^L\left[\frac{1}{2}(S_i^{+}{S}_{i+1}^{-}+S_i^{+}{S}_{i+1}^{-})+\mathrm{\Delta }\left(S_i^z{S}_{i+1}^z-\frac{1}{4}\right)\right],$$ [4]

where $S_i^{\alpha }$ are spin-$1/2$ operators, and $\mathrm{\Delta }$ is the anisotropy parameter. Here, we considered as prequench initial states the tilted Néel state $|\vartheta ,\nearrow \swarrow \mathrm{\cdots }⟩\equiv e^{i\vartheta {\sum }_j{S}_j^y}|\uparrow \downarrow \mathrm{\cdots }⟩$, the Majumdar–Ghosh (dimer) state $|MG⟩\equiv {((|\uparrow \downarrow ⟩-|\downarrow \uparrow ⟩)/2)}^{\otimes L/2}$, and the tilted ferromagnetic state $|\vartheta ,\nearrow \nearrow ⟩\equiv e^{i\vartheta {\sum }_j{S}_j^y}|\uparrow \uparrow \mathrm{\cdots }⟩$. The Heisenberg spin chain is the prototype of all integrable models. Moreover, for all of the initial states considered in this work, the postquench steady state can be characterized analytically via the macrostate densities ${\rho }_{p(h)}^{\ast }$. Specifically, a set of recursive relations for these densities can be obtained (SI Materials and Methods). The group velocities of the low-lying excitations around the steady state (i.e., the entangling quasiparticles) are obtained by solving numerically an infinite set of second-type Fredholm integral equations (details are in SI Materials and Methods).

The numerical data for the postquench dynamics of the entanglement entropy presented in Fig. 4 were obtained using the standard tDMRG (46–49) in the framework of matrix product states. For the implementation, we used the ITENSOR library (itensor.org/). The data presented in Fig. 5 are obtained using the iTEBD method (93) and they are a courtesy of Mario Collura.