Leveraging Multi-ethnic Evidence for Risk Assessment of Quantitative Traits in Minority Populations

Abstract

An essential component of precision medicine is the ability to predict an individual’s risk of disease based on genetic and non-genetic factors. For complex traits and diseases, assessing the risk due to genetic factors is challenging because it requires knowledge of both the identity of variants that influence the trait and their corresponding allelic effects. Although the set of risk variants and their allelic effects may vary between populations, a large proportion of these variants were identified based on studies in populations of European descent. Heterogeneity in genetic architecture underlying complex traits and diseases, while broadly acknowledged, remains poorly characterized. Ignoring such heterogeneity likely reduces predictive accuracy for minority individuals. In this study, we propose an approach, called XP-BLUP, which ameliorates this ethnic disparity by combining trans-ethnic and ethnic-specific information. We build a polygenic model for complex traits that distinguishes candidate trait-relevant variants from the rest of the genome. The set of candidate variants are selected based on studies in any human population, yet the allelic effects are evaluated in a population-specific fashion. Simulation studies and real data analyses demonstrate that XP-BLUP adaptively utilizes trans-ethnic information and can substantially improve predictive accuracy in minority populations. At the same time, our study highlights the importance of the continued expansion of minority cohorts.

Introduction

An important component of precision medicine is to incorporate the genetic variation of an individual in disease risk assessment, as well as in optimizing disease prevention and treatment strategies. In the context of complex traits, such as blood glucose level, lipid concentration, and body mass index, this goal has proven challenging for two reasons: first, these traits are strongly influenced by an array of genetic, environmental, and lifestyle risk factors, most of which are not systematically measured; second, the genetic components of complex traits feature polygenic architecture, meaning hundreds or thousands of genes influence an individual’s phenotype, of which our current knowledge—largely derived from regions reaching statistical significance in genome-wide association studies (GWASs)—represents only the tip of the iceberg.¹ At the same time, studies with expanding cohorts continue to uncover variants associated with a variety of traits and diseases, indicating moderate to high heritability.^{2, 3, 4, 5} Therefore, while genetic variation alone is insufficient for accurate disease or trait prediction, it is reasonable to expect that a summary score of all trait-relevant variants can meaningfully quantify the heritable component that underlies variation in complex traits or disease risks. Furthermore, this genetic score complements conventional non-genetic risk factors, and integration of genetic and non-genetic risk factors may lead to more accurate health assessment. The goal of this paper is to develop an analytical approach to quantifying the genetic risk score that influences the trait; the term “trait prediction” is used as shorthand, but it should be emphasized that the output of this “trait prediction” aims to capture only the genetic risk factors, and is meant to be combined with non-genetic risk factors such as age, gender, or smoking status.

Although a number of methods have been developed for complex trait prediction, most of these methods are designed for and applied to populations of European descent (EUR). These methods fall into two categories. One group of methods builds regularized regression models based on established or suggestive trait loci.⁶ In its simplest form, such a method selects independent SNPs reaching a pre-specified p value threshold. At each SNP, one allele is designated as the trait-increasing allele, while the other allele is a trait-decreasing allele. The genetic risk simply tallies the number of trait-increasing alleles across all selected SNPs.^{7, 8} More sophisticated methods have been developed to weigh SNPs by the corresponding allelic effects, which are estimated from an independent training cohort.^{9, 10} These methods are computationally efficient and perform well in populations where large cohorts are available. However, for minority individuals, who are under-represented in GWASs, these methods are sub-optimal because much less information is available for selecting relevant SNPs and for estimating allelic effects. Consequentially, under this framework, trait prediction may be considerably less precise in minority populations.

The second group of methods is based on best linear unbiased prediction (BLUP) for predicting random effects in linear mixed effects models (LMMs).^{11, 12} Originally applied to animal and plant breeding,^{13, 14} LMMs have become a powerful method to estimate SNP-based heritability using GWAS data.^{15, 16} By assuming a common distribution that describes the allelic effects at all SNPs and focusing on the aggregated genetic effects rather than individual genetic effects, LMMs and BLUP are particularly attractive for modeling polygenic architecture. On the other hand, to capture minute effects spread over a majority of the genome, this assumed common distribution—usually a Gaussian distribution—fails to capture major trait loci with large effects efficiently. To cope with this problem, a number of methods have been proposed that use multiple random effect terms with distinct variances to represent classes of SNPs with varying allelic effects.^{17, 18, 19} External biological annotation offers a natural grouping of SNPs into classes that correspond to the multiple random effects terms; Speed and Balding¹⁷ developed an algorithm that groups genomic regions based on their observed regional heritability. In parallel, Bayesian hierarchical models have been developed, which consider the underlying allelic effects as drawn from a mixture of Gaussian distributions, thus providing a probabilistic framework that allocates a sparse fraction of the SNPs to have moderate to large effects.^{18, 19, 20} Although these methods differ in how the SNP classes are defined, simulation and real data analyses results consistently suggest that very large GWAS sample sizes are needed to achieve good predictive performance. Under favorable simulation settings, a sample size of ∼100,000 is recommended.¹⁶ While such a sample size is becoming feasible for some common traits in European populations, it remains infeasible for minority populations.

In this paper, we present a trans-ethnic framework for assessing genetic risk for minority individuals. Previously we have shown that complex traits genetic architecture overlaps substantially between ethnicities and that harnessing trans-ethnic information leads to substantial improvement in our ability to discover trait loci that are relevant in minority populations.^{21, 22} Therefore, we reason that trait prediction in minority populations may also benefit from integrating much larger GWAS data generated from populations of European descent. Our proposed approach, termed cross-population BLUP (XP-BLUP), is a multiple-component LMM model designed specifically to address the need for efficient prediction in minority populations. The SNPs are placed into classes defined using GWAS evidence from any ethnicity, while the variances of the random-effects and BLUP are computed using population-specific data. We use simulation to illustrate the usefulness of trans-ethnic information, as well as the importance of minority-specific GWAS data. Application to real data of lipid concentration indicates that the genetic risk factor formulated by XP-BLUP on a moderate sized African American (AA) cohort achieves similar predictive accuracy as commonly measured non-genetic risk factors, such as age and BMI.

Material and Methods

LMM and BLUP for Complex Traits

Our proposed trans-ethnic prediction approach is based on LMM and BLUP; the statistical theory and computation are well established. To facilitate the comparison and to set up notations, we briefly summarize the standard LMM and BLUP for complex traits. Details about the computation and the underlying model assumptions have been described in the context of SNP-based heritability estimation.^{15, 17, 23}

Let X be the N × M genotype matrix of N individuals and M markers, and Y be the vector of length N, representing the quantitative phenotype centered at 0. Following convention, let Z be the centered and scaled genotype matrix: if $X_{jm}\in \left(\mathrm{0,1,2}\right)$ denotes genotypes of individual j at SNP m, then $Z_{jm}=\left(X_{jm}-2f_m\right)/\sqrt{2f_m\left(1-f_m\right)}$ where f_m is the allele frequency.¹⁵ Y is modeled as the sum of the genetic (g) and non-genetic (e) contributions: Y = g + e. (In what follows, all boldfaced symbols represent vectors or matrices.) For cohorts in which individuals are not close relatives, it is convenient to assume that the non-genetic contribution e_j is drawn independently from a Gaussian distribution, $N\left(0,{\sigma }_e^2\right)$. Under a polygenic architecture, the additive genetic component can be represented as a linear combination of the standardized genotypes (Z) weighted by the corresponding allelic effects, u: g = Zu. In its simplest form, we consider the allelic effects, u_m, as independently sampled from a Gaussian distribution with mean 0 and variance ${\sigma }^2/M$, $N\left(0,{\sigma }^2/M\right)$. It can be shown that $\mathit{g}\sim N\left(0,\mathit{A}{\sigma }^2\right)$, where $\mathit{A}=\mathit{Z}{\mathit{Z}}^{\mathit{\prime }}/M$ is a genetic relationship matrix (GRM). Covariates, such as age and gender, can be included in the model as fixed effects terms. We will refer to this basic model as the single-component model.

Building upon the single-component model, a number of studies have aimed to use multiple random effects terms to represent groups of SNPs with different allelic effects.^{18, 20, 24} Let Z_k denote the sub-matrix (columns of matrix Z) that corresponds to the SNPs in group k. The general form of a K-component LMM can be written as:

$$\mathit{Y}=\sum _{k=1}^K{\mathit{g}}_k+\mathit{e}$$ (Equation 1)

where ${\mathit{g}}_k={\mathit{Z}}_k{\mathit{u}}_k$ represents the genetic contribution of group k. This model allows SNPs in group k to have allelic effects drawn from a group-specific Gaussian distribution, $u\sim N\left(0,{\sigma }_k^2/\left|C_k\right|\right)$, where $\left|C_k\right|$ is the number of markers in group k. Analogous to the single-component model, ${\mathit{g}}_{\mathit{k}}\sim N\left(0,{\mathit{A}}_{\mathit{k}}{\sigma }_k^2\right)$, where ${\mathit{A}}_{\mathit{k}}={\mathit{Z}}_k{\mathit{Z}}_{\mathit{k}}^{\mathit{\prime }}/\left|C_k\right|$ can be thought of as the GRM based on SNPs in group k. It should be noted that the SNP groups do not need to be disjoint; a SNP belonging to both groups k₁ and k₂ has an effect size drawn from $N\left(0,{\sigma }_{k_1}^2/\left|C_{k_1}\right|+{\sigma }_{k_2}^2/\left|C_{k_2}\right|\right)$.

The variance parameters ${\sigma }_1^2,\dots ,{\sigma }_K^2$ and ${\sigma }_e^2$ are estimated by restricted maximum likelihood (REML).^{25, 26} Given that the variance parameters have been estimated, the BLUP of allelic effects for SNPs in class k is:

$${\hat{\mathit{u}}}_k={\hat{\sigma }}_k^2{\mathit{A}}_k{\mathit{Z}}_{\mathit{k}}^{\prime }{\mathit{V}}^{-1}\mathit{Y}$$

where $\mathit{V}={\sum }_k{\hat{\sigma }}_k^2{\mathit{A}}_k+{\hat{\sigma }}_e^2{\mathit{I}}_N$, and I_N is the identity matrix of dimension N.

Finally, the predicted trait values of individuals, with genotype Z^test, are computed by

$${\hat{\mathit{Y}}}^{\text{test}}=\sum _{k=1}^K{\mathit{Z}}_k^{\text{test}}{\hat{\mathit{u}}}_k.$$ (Equation 2)

Trans-ethnic Genetic Prediction

We now describe the problem of trans-ethnic trait prediction. Consider a setting in which GWASs have been conducted for a trait in a target population of primary interest (e.g., AA) and the goal is to predict the trait value of other individuals from the same population. We will refer to the first set of individuals, for whom both genotype data and trait values are used to build the prediction model, as the training set; the second set of individuals, for whom we wish to predict trait values using genotype data, is the testing set. In simulation studies, the (simulated) true trait values of the test set are used as the gold standard to evaluate the predictive accuracy. For trans-ethnic auxiliary information, we use the summary-level statistics—specifically SNP-level p values—from an independent auxiliary GWAS of matching trait (e.g., EUR). We make no assumption with regard to the genetic similarity between the target and the auxiliary GWAS—in fact, the auxiliary GWAS can be trans-ethnic or multi-ethnic; the “independent” assumption merely requires that the target GWAS and the auxiliary GWAS consist of non-overlapping individuals.

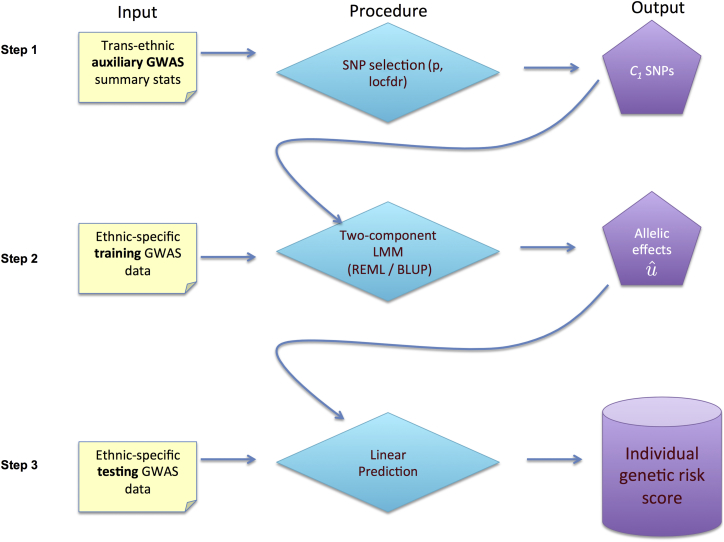
Figure 1 shows a flow chart of the trans-ethnic prediction approach, which utilizes a two-component LMM (K = 2 in Equation 1). The grouping of the SNPs is based on the summary statistics of the auxiliary GWAS. One component, denoted as C₂, consists of all genotyped SNPs; the other component, C₁, includes only SNPs showing evidence of association in the auxiliary GWAS. The variance parameters of the LMM and the BLUP of the allelic effects are estimated using genotypes of the training set in the target population. The predicted trait values on the testing individuals are computed using their genotype, according to Equation 2. Note that individual-level data from the auxiliary GWAS are not needed in the trans-ethnic prediction.

Figure 1.

Overview of the XP-BLUP Procedure

Step 1: SNPs are sorted into two classes based on summary statistics in a trans-ethnic auxiliary GWAS. Step 2: A two-component linear mixed-effects model (LMM) and ethnic-specific training GWAS data are used to compute the allelic effects associated with each variant in the target population. Step 3: Trait value of an individual of unknown phenotype can be estimated using his/her genotypes and the allelic effects estimated in step 2.

To select SNPs with strong evidence of association in the base GWAS, we use program XPEB to compute the local false discovery rate (locfdr) defined by Equation 5 in Coram et al.²² In brief, this approach assumes that the observed test statistics, S (chi-square statistics that can be computed from the p values), arise from a mixture of null and non-null distributions. By maximizing the joint likelihood of all observed test statistics in the base GWAS, the mixture proportions can be estimated. The locfdr at a marker, m, is then computed as the posterior probability that S_m is drawn from the null component. We pre-specify a locfdr threshold, ${\upsilon }^{\ast }$, such that a SNP is included in C₁ only if its locfdr falls below ${\upsilon }^{\ast }$. For all simulations presented below, ${\upsilon }^{\ast }=0.05$. Alternatively, one can pre-specify a p value threshold, ${\tau }^{\ast }$, such that a SNP is included in C₁ if its p value in the base GWAS falls below ${\tau }^{\ast }$. Since there is a monotonic relationship between the p value and locfdr, using a locfdr criterion is equivalent to using some p value threshold. In the Discussion, we propose approaches that adaptively choose ${\upsilon }^{\ast }$ (equivalently, ${\tau }^{\ast }$).

Simulation

We evaluate the proposed prediction algorithm using simulated genotype and trait data generated in a previous study.²² The genotype data consist of ∼727,000 autosomal SNPs on the Illumina 1M SNP array with minor allele frequencies greater than 1%. It is simulated using program HAPGEN2 and HapMap Phase 3 genotypes and includes eight CEU-like cohorts (simEUR) and one YRI-like cohort (simAFR) of 10,000 individuals each. To simulate the phenotypes, 1,000 SNPs are sampled as causal variants in each ethnic population; the proportions of causal variants that overlap between the simEUR and the simAFR cohorts $\left(\delta \right)$ range from 0.001 to 1, with $\delta =0.001$ representing independent genetic architecture and $\delta =1$ representing complete overlap in causal variants. The true allelic effects at these causal variants are sampled from a Gaussian distribution; the correlation between the allelic effects in simEUR and simAFR is 0.7. Lastly, trait values are simulated using the allelic effects, the simulated genotypes, and a random non-genetic component, whose variance is calibrated to achieve a heritability ranging from 40% to 90%. For each value of $\delta$, 20 sets of trait values are simulated, with causal variants independently sampled from run to run. In practice, not all causal variants are genotyped. To consider such situations, we additionally analyzed simulated data removing all causal variants in both simEUR and simAFR.

To apply the proposed trans-ethnic prediction model, the eight simEUR cohorts are meta-analyzed (total N = 80,000) and treated as the auxiliary GWAS. Within simAFR, we randomly sample 8,000 individuals to form the training dataset, leaving the remaining 2,000 individuals as the testing set for evaluating the predictive accuracy, for which we focus on correlation (r) between the simulated true trait values and the predicted values. For each simulated trait, we compute the locfdr that the SNP is associated with the trait in simEUR using meta-analysis summary statistics. SNPs with locfdr below 0.05 are selected to C₁; all SNPs are included in set C₂. Next, we compute the two-component LMM and BLUP on the simAFR training set, recording the BLUP of allelic effects. These BLUP estimates are then used to predict the corresponding trait values in the 2,000 testing individuals. The accuracy measure reported is $cor\left({\mathit{y}}^{\mathit{\ast }},{\hat{\mathit{y}}}^{\ast }\right)$, where ${\hat{\mathit{y}}}^{\ast }$ is defined by Equation 2.

We compare the proposed method with two alternative approaches. First, we consider a single-component LMM on the simAFR training set (N = 8,000) alone. This comparison assesses the contribution of trans-ethnic information. Second, we consider a two-component LMM that uses only European individuals. For this analysis, a ninth simEUR cohort is simulated as described above and used as the training dataset. For all comparisons, the testing set is the 2,000 simAFR individuals. These comparisons are designed to assess the importance of trans-ethnic and population-specific training data.

Predicting Genetic Scores for Lipid Concentration in African American Women

As a real data example, we analyze lipid concentration in African American females in the Women’s Health Initiative SNP Health Association Resource (WHI-SHARe), which includes 8,153 post-menopausal AA women. All WHI participants have provided written informed consent, and institutional review board approval has been obtained at each of the 40 WHI clinical centers and at the clinical coordinating center at the Fred Hutchinson Cancer Research Center. For analyses described in this manuscript, which uses de-identified data, institutional review board approval has been obtained at Stanford University. We randomly sample four non-overlapping sets of 2,000 individuals as test sets; for each test set the remaining individuals are used to compute the BLUP. Prediction accuracy reported in Results are averaged across the four testing sets. For auxiliary GWAS, we use the meta-analysis of the Global Lipids Genetics Consortium (GLGC), which consists largely of individuals of European descent, with no overlap with WHI-SHARe.³ In GLGC, 47, 37, and 32 loci meet the genome-wide significance threshold of 5 × 10⁻⁸ and are associated with high-density lipoprotein (HDL) cholesterol, low-density lipoprotein (LDL) cholesterol, and triglyceride (TG) levels, respectively. Using the p value threshold of 5 × 10⁻⁸ selects approximately the same SNPs as using a locfdr of 0.05. In the WHI-SHARe AA cohort, genome-wide African ancestry proportion explains less than 1% of the observed phenotypic variance in HDL, LDL, and TG. Nonetheless, to eliminate the effects of admixture, we first regress out the estimated proportion of African ancestry from each lipid trait and use the residuals in XP-BLUP. To assess the effect of the pre-specified threshold, we also apply XP-BLUP varying the p value threshold from 5 × 10⁻³ to 5 × 10⁻⁸. To compare the predictive accuracy of XP-BLUP with other risk factors, we use the same training individuals to estimate the predictive models that are based on (1) age or (2) BMI. To compare XP-BLUP with a conventional polygenic risk scores (PRSs) approach, we performed single-marker GWAS analysis using training individuals (independent loci are defined as being at least 250 kb apart). PRSs in testing individuals are computed using PLINK’s score option, which weighs the index SNPs by the corresponding estimated allelic effects.²⁷

Computation

For all results reported in the next section, we used GCTA to perform REML and BLUP estimation, although a number of available software programs can perform similar tasks.^{12, 17, 28} The BLUP output of GCTA is re-processed to account for the two classes of SNPs using a customized script, and the predicted trait values on the testing set are produced in PLINK.²⁷

Results

Predictive Accuracy on Simulated Data

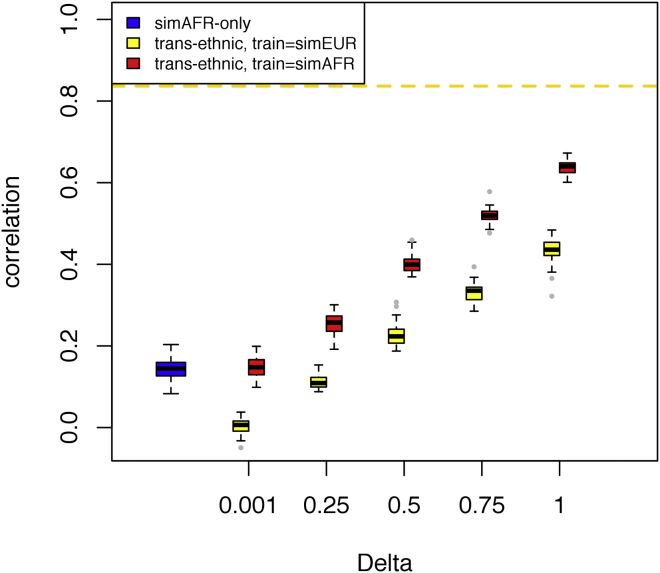
Figure 2 compares the predictive accuracy, measured by correlation coefficients, of the proposed trans-ethnic prediction (XP-BLUP) with two alternative LMM methods. Since the simulation model assumes a genetic architecture with a heritability of 0.7, the maximum achievable correlation between the predicted and observed traits is $\sqrt{0.7}=0.84$. Using the standard, single-component LMM and simAFR data alone (N = 8,000), the mean predictive accuracy on the out-of-sample testing individuals is 0.14 (Figure 2, blue box). As expected, the predictive accuracy of the proposed XP-BLUP increases with the degree of overlap between the auxiliary simEUR and the target simAFR population. When the trait loci completely overlap in the two populations, the predictive accuracy is 0.64, indicating that the summary-level statistics from simEUR GWAS provide substantial information. On the other hand, for any level of genetic overlap, the predictive accuracy trained entirely on simEUR (Figure 2, yellow boxes) is lower than that trained on simAFR, emphasizing the importance of ethnically matched training cohorts. Additional simulations confirm that the same trend holds for various levels of underlying heritability and when some or all causal variants are not genotyped (Figures S1 and S2).

Figure 2.

Comparison of Predictive Correlation

XP-BLUP (red) compares favorably to a single-component linear mixed-effects model (LMM, blue) and a two-component LMM model trained only on simulated European GWAS data (yellow). Delta specifies the proportion of overlapping loci between ethnicities. Dashed line is the theoretical maximum.

It should be noted that the improved predictive accuracy of XP-BLUP does not require that all true trait loci in the target population are included in C₁ class. This is because, even with completely overlapping genetic architecture $\left(\delta =1\right)$ and a sample size of 80,000, not all simEUR trait loci can be detected. Over all simulations, the average number of loci discovered in the simEUR GWAS is 550 out of 1,000 (range 523–581). The moderate simAFR training samples and the incomplete knowledge of all trait loci in the simAFR population account for the discrepancy between the observed predictive accuracy (0.64) and the theoretical maximum possible accuracy (0.84) at $\delta =1$. On the other hand, XP-BLUP does not assume all SNPs in C₁ are indeed trait relevant in simAFR. For instance, at $\delta =0.5$, half of the SNPs in C₁ are expected to bear no predictive information in simAFR, yet XP-BLUP still outperforms the single-component LMM. Lastly, when the genetic architecture is independent in simEUR and simAFR $\left(\delta =0.001\right)$, the auxiliary GWAS provides no useful information. In this scenario, XP-BLUP achieves similar accuracy as a single-component LMM, demonstrating its ability to ignore irrelevant auxiliary information. In contrast, a two-component LMM trained on simEUR can perform substantially worse than a single-component LMM when $\delta =0.001$. Taken together, this set of analyses demonstrates two features of the XP-BLUP framework: first, the predictive model needs to be trained in a population-specific context; second, regardless of the underlying overlap in genetic architecture, trans-ethnic auxiliary information will not negatively impact the predictive accuracy.

BLUP of Allelic Effects

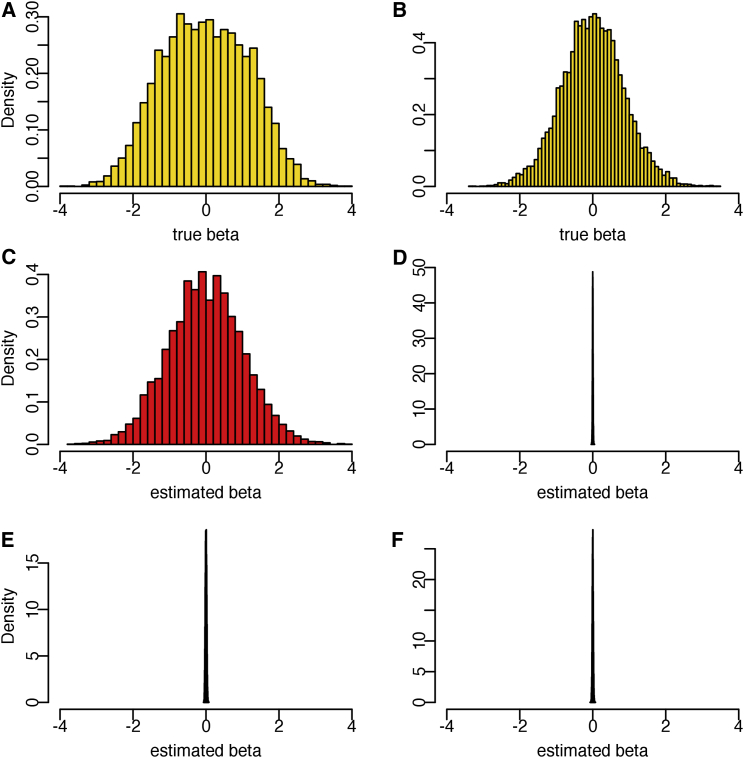
To better understand why the two-component LMM outperforms the single-component LMM, it is instructive to examine the BLUP allelic effects under the two approaches (Figures 3 and S3). Focusing on loci that affect trait values in simAFR (e.g., ${\mathit{u}}_k\ne 0)$, we form two groups based on whether a variant is selected into C₁ in the XP-BLUP analysis, which requires that locfdr < 0.05 in simEUR. The two histograms in the first row (Figures 3A and 3B) represent the true simulated allelic effects in simAFR for each of the two groups. The slight flattening of the histogram representing C₁ (Figure 3A) is due to requiring the variant to pass a significance threshold in the simEUR.

Figure 3.

True and BLUP of Trait-Relevant SNP Effects in Simulated Data

True SNP effects (A and B), BLUP under trans-ethnic model (C and D), and BLUP under a single-component model (E and F). SNPs in C₁ (A, C, and E); SNPs not in C₁ (B, D, and F).

The predicted allelic effects using XP-BLUP and a single-component LMM are shown in the second (Figures 3C and 3D) and third (Figures 3E and 3F) rows, respectively. Under a single-component LMM, the allelic effects of all variants are assumed to have come from a common Gaussian distribution. The REML estimate of this common Gaussian distribution features a small variance of ${\hat{\sigma }}_G^2/M$. In consequence, it heavily shrinks the estimated allelic effects toward 0. Such shrinkage captures the reality that a majority of the variants in the genome have zero or infinitesimal effects, in which case shrinkage is an effective strategy to reduce sampling variability of the prediction. Undesirably, however, true trait variants with moderate or even large effects are similarly shrunk (Figures 3E and S3). As the true trait variants are relatively sparse, the noise from non-associated variants overwhelms the true signal, leading to poor predictions.

In contrast, XP-BLUP allows the allelic effects of C₁ SNPs to be drawn from a different Gaussian distribution than the rest of the variants. Consider that for $\delta =0.75$, approximately 75% of the SNPs in C₁ are associated with the trait in simAFR and the remaining 25% are simEUR specific. The allelic effects of C₁ SNPs estimated by XP-BLUP are much less attenuated (Figure 3C), compared with the corresponding estimates using a single-component LMM (Figure 3E). On the other hand, simAFR trait variants that are not included in C₁, either because they are simAFR specific or because the SNPs did not reach genome-wide significance in the simEUR GWAS, show similar level of shrinkage as those in a single-component LMM (Figures 3D and 3F). This observation suggests that the success of XP-BLUP depends on constructing C₁ SNPs enriched for variants near trait loci in simAFR. At $\delta =0.001$, the SNPs in C₁ are not enriched for simAFR trait variants compared to the rest of the genome; in this situation, XP-BLUP effectively ignores the simEUR auxiliary information and shrinks the C₁ SNPs similarly to the rest of the genome (Figure S3).

Predicting Genetic Scores for Lipid Concentration in African American Women

The Women’s Health Initiative is a US-based study of common health issues in post-menopausal women. Over a period of 15 years, the study has enrolled a total of more than 160,000 women aged 50–79 years old. Among these, 8,153 African American participants have been genotyped as part of the Women’s Health Initiative SNP Health Association Resource (WHI-SHARe). Previously, we have examined the lipid concentrations in this cohort to characterize overlapping genetic architecture.²¹ Here we apply the proposed XP-BLUP method to predict lipid concentrations. For LDL, HDL, and TG, the total estimated heritability on the training set is 0.33, 0.28, and 0.26, respectively. As such, the theoretical maximal predictive correlation coefficients are 0.57, 0.53, and 0.51, respectively. Table 1 summarizes the predictive accuracy achieved, when C₁ is defined by conventional genome-wide significance threshold of 5 × 10⁻⁸. Table 1 also includes the corresponding predictive accuracy for a number of epidemiologic risk factors available in this data, such as age and BMI. We find that XP-BLUP achieves higher accuracy than age and BMI for all three lipid traits. Further, XP-BLUP achieves higher accuracy compared to a polygenic risk score approach that includes only the index SNPs of genome-wide significant loci detected in the training dataset. Finally, combining XP-BLUP scores, age, age², smoking, BMI, and fasting status (for LDL only), the overall predicted risk scores achieve a correlation of 0.22, 0.30, and 0.25 with LDL, HDL, and TG, respectively.

Table 1.

Correlation Coefficients between Predicted Scores and Observed Lipid Concentration in African Americans of the Women’s Health Initiative SNP Health Association Resource

Trait	| C1|	VG/VP	XP-BLUP	LMM	Age	BMI	FE
LDL	413	0.33	0.18	0.095	0.085	0.044	0.16
HDL	569	0.28	0.22	0.086	0.042	0.21	0.17
TG	413	0.26	0.17	0.078	0.066	0.11	0.13

All correlations are evaluated on the African American testing set individuals. Abbreviations are as follows: | C₁|, number of SNPs in C₁ set; VG/VP, SNP-heritability estimated by program GCTA; XP-BLUP, proposed trans-ethnic best linear unbiased prediction; C₁ SNPs are defined by p < 5 × 10⁻⁸ in Global Lipids Genetics Consortium (GLGC) meta-analysis; LMM, standard linear mixed effects model computed by GCTA; age, fixed effects model with age as a single predictor; BMI, fixed effects model with BMI as a single predictor; FE, fixed effects model that includes only index SNPs at genome-wide significant loci in the African American training set.

The definition of p < 5 × 10⁻⁸ or locfdr < 0.05 may seem arbitrary. To investigate the sensitivity of the performance of XP-BLUP with respect to this threshold definition, we re-analyze the lipid traits by varying the threshold ranging from 5 × 10⁻³ to 5 × 10⁻⁸. As the inclusion threshold is relaxed from 5 × 10⁻⁸ to 5 × 10⁻⁵, the number of SNPs included in C₁ increases by a factor of ten, but the predictive correlation remains relatively stable (Tables S1–S3). We reason that this phenomenon reflects a tradeoff between true signal and noise: although a bigger set of C₁ SNPs likely includes more trait variants, an increasing proportion of added SNPs are false positives. Consequentially, the BLUP for C₁ SNPs are increasingly shrunk toward zero. This reasoning is supported by the observation that the phenotypic variance explained by C₁ SNPs does not always increase as more SNPs are included (column VG₁ in Tables S1–S3). The optimal threshold that balances this trade-off depends on the underlying genetic architecture as well as the sample size of training set. With much larger training samples, one can choose an optimal threshold using the following cross-validation (CV) approach.²⁹ The training set is divided into a number of equal parts; to be specific, we describe a ten-fold CV. At each p value threshold, the two-component LMM model is computed on nine parts of the data, and the predictive accuracy is evaluated on the remaining part, termed the validation set. In turn, each of the ten parts is treated as the validation set once; the optimal threshold value is the one that achieves the best predictive accuracy averaging over all ten validation sets. However, at the sample size of WHI-SHARe, we found no substantial differences in the predictive accuracy when the threshold ranges from more than three orders of magnitudes (Tables S1–S3). Therefore, for current studies in minority populations, we recommend applying XP-BLUP with a pre-specified threshold of p < 5 × 10⁻⁸.

Discussion

We have investigated XP-BLUP, a computational approach for assessing the genetic risk of complex traits in minority populations. The underlying idea is to use a two-component LMM, in which one component is highly enriched for trait-associated SNPs that are derived from independent, well powered, but possibly ethnically unmatched GWASs. Although an LMM with multiple random effects is a generally useful approach for integrating external knowledge of candidate regions or SNPs, this framework is particularly appealing for leveraging trans-ethnic GWAS results because it benefits from partial overlap in genetic architectures across populations, without assuming transferability of all trait loci between populations, as we explain in detail next.

First, both simulation (Figure 1) and the lipid data analysis (Table 1) emphasize that the performance of a multi-component LMM for prediction strongly depends on the level of enrichment in SNP set C₁. The ideal C₁ is the set that includes all and only trait-associating SNPs in the target population. The predictive accuracy diminishes when C₁ is heavily contaminated with SNPs not relevant in the target population, or it misses trait-associating SNPs. In theory, it is possible to choose C₁ and compute BLUP using the same GWAS data;^{17, 18} however, for minority studies with moderate sample size, a set constructed this way is likely less accurate. In contrast, for a variety of complex traits studied to date, accumulating evidence suggests considerable numbers of overlap loci between ethnicities.^{30, 31, 32, 33} For these traits, a large proportion of SNPs selected based on a large European GWAS are expected to be relevant in non-European populations. Therefore, a set selected based on a large GWAS in a non-matching population is expected to harbor higher fraction of variants for the target population than a set selected on a small dataset in matching population. Likewise, we expect that the trans-ethnic GWAS data provides more specific information than trait-independent biological annotation, such as chromatin accessibility. It should be noted that C₁ does not need to exclusively contain the causal variants and should be interpreted accordingly. For the purpose of prediction, any SNPs in linkage disequilibrium with causal variants can serve as useful predictors. This feature makes XP-BLUP easier to use in practice than a fixed-effects PRS model that requires “independent” risk SNPs, because defining independent trait loci and identifying likely causal variants, which may vary across populations, are challenging on their own.

Second, while our XP-BLUP approach takes advantage of the strong overlap between ethnicities, it does not assume all SNPs in C₁ to be associated with the trait in the minority population. In other words, the method accommodates incomplete overlap in genetic architecture. This is important because it is difficult to assess, a priori, the degree of overlap for a particular trait. Our simulation results suggest that XP-BLUP is robust to contamination of mis-specified SNPs. SNPs that are strongly associated in European populations but not in the target population tend to have small BLUP estimates because these BLUPs are estimated using training data in the target population. When C₁ includes a substantial fraction of non-associated SNPs, the prediction accuracy deteriorates due to the shrinkage effect; however, even when C₁ consists of randomly sampled SNPs $\left(\delta =0.001\right)$, the performance of XP-BLUP is not worse than a standard one-component LMM model. Furthermore, we choose not to make any assumption regarding the agreement, in sign or magnitude, between the estimated allelic effects in the European GWAS and those in the target population. This choice is based on the empirical evidence that the correlation between allelic effects across ethnicities varies by trait, and currently we do not have sufficient information to accurately model such correlation structure.

The XP-BLUP approach described here can be extended in several directions. First, it is anticipated that GWASs with expanded cohorts will continue to discover loci associated with traits and diseases. As the number of SNPs becomes sufficiently large and includes variants of infinitesimal effects, it may be useful to divide C₁ SNPs into multiple sets, representing variants with varying level of allelic effects. A practical approach is to split C₁ SNPs on the basis of putative contributions of each variant, defined by $2{\hat{\beta }}^{2}p\left(1-p\right)$, where $\hat{\beta }$ is the estimated allelic effects in the auxiliary GWAS and p is allele frequency in the target population. At the same time, expanded minority cohorts may enable us to discover target population-specific variants. These variants can be incorporated in XP-BLUP framework as fixed effects. Second, our current implementation focuses on one trait and makes use of auxiliary GWASs of the matching trait. Recent studies have demonstrated widespread pleiotropy: genetic loci that simultaneously influence related and sometimes seemingly unrelated traits.³⁴ Integrating pleiotropic information to jointly predict related traits has shown promise.³⁵ Extending XP-BLUP to leverage both trans-ethnic and cross-trait information may be particularly useful for under-studied traits. Third, we have focused on quantitative traits and have described XP-BLUP as a linear mixed-effects model. For a binary disease outcome, a commonly adopted approach is the liability-threshold model, which postulates that genetic factors contribute additively to an underlying quantitative trait, liability, and the observed disease status is a dichotomized version of the liability at a specific threshold. However, in most case-control GWASs, affected individuals are over-sampled and therefore the underlying liability in the cohorts may be strongly skewed. Computational strategies for estimating heritability and predicting disease status in case-control designs have been developed and may be adapted for trans-ethnic disease prediction.^{36, 37}

While trans-ethnic information can substantially improve predictive accuracy, our work emphasizes the importance of estimating the allelic effects in ethnically matched cohorts. Therefore, sustained efforts should be dedicated to building large and well-phenotyped cohorts in minority populations. In the coming years, a number of large cohorts, such as the US National Institutes of Health Precision Medicine Initiative and the Millions Veterans Program, will enable researchers to investigate the genetic basis of a wide range of complex traits and diseases in diverse populations. We anticipate that approaches leveraging trans-ethnic information will continue to play an important role in these studies.

Published: July 27, 2017

Web Resources

• GCTA, http://www.complextraitgenomics.com/software/gcta/

• PLINK, http://pngu.mgh.harvard.edu/∼purcell/plink/

• dbGaP, http://www.ncbi.nlm.nih.gov/gap

• XPEB program, http://med.stanford.edu/tanglab/software/

• XP-BLUP script, https://github.com/tanglab/XP-BLUP