Abstract
Repeated measures of various biomarkers provide opportunities for us to enhance understanding of many important clinical aspects of CKD, including patterns of disease progression, rates of kidney function decline under different risk factors, and the degree of heterogeneity in disease manifestations across patients. However, because of unique features, such as correlations across visits and time dependency, these data must be appropriately handled using longitudinal data analysis methods. We provide a general overview of the characteristics of data collected in cohort studies and compare appropriate statistical methods for the analysis of longitudinal exposures and outcomes. We use examples from the Chronic Renal Insufficiency Cohort Study to illustrate these methods. More specifically, we model longitudinal kidney outcomes over annual clinical visits and assess the association with both baseline and longitudinal risk factors.
Keywords: CKD, longitudinal data, repeated measures, GEE, mixed effects model, correlation structures, Biomarkers, Cohort Studies, Disease Progression, GFR, Humans, kidney, Renal Insufficiency, Chronic, risk factors
Introduction
The term repeated measures refers to data observed repeatedly within the same subject, and they are being increasingly collected in many research studies. Aside from being used to evaluate the reproducibility and variability of a novel biomarker (1,2), repeated measures are often generated in the context of longitudinal studies, in which one or more biomarkers are observed over time. For chronic diseases, such as CKD, patterns of biomarker trajectories are crucial for understanding of disease prognosis.
In many studies, the repetitions are predetermined by the study protocol, whereby measures are administered prospectively at specific intervals during scheduled clinical visits or telephone interviews (3,4). In other scenarios, the repeated data (e.g., measures of vital signs, such as BP, heart rate, and respiratory rate) become available at variable time points when certain events (e.g., hospitalization) occur. Repeated measures could also be obtained retrospectively as natural history data through available databases, such as Medicare (5).
Depending on the scientific questions, the longitudinal measures may serve as the outcomes of interest, the exposures, or a combination of both. Examples of these scenarios in kidney disease research include comparisons of the burden of coronary artery calcification for patients at different stages of CKD and ESRD, treating the longitudinal coronary artery calcification measures as the outcome of interest (6); evaluations of the associations of longitudinal measures of GFR with subsequent adverse events, such as ESRD and death, as outcomes (7,8); and an investigation of the causal relationship between BP and kidney function, in which both measures were updated over time (9).
In this paper, we will focus primarily on the appropriate statistical methods for analyzing longitudinal data as outcomes. In particular, we will discuss extensively regression methods that can estimate the rate of change of the longitudinal data in association with certain risk factors (10,11). The terms repeated measures and longitudinal data are used interchangeably.
Motivating Example
The Chronic Renal Insufficiency Cohort (CRIC) Study is a prospective, longitudinal study of patients with CKD, in which repeated measures of serum creatinine and cystatin C, along with several other laboratory measures, were collected from each participant during annual clinical visits (3,7,12). eGFR, calculated on the basis of the CRIC Study eGFR equation that incorporates both serum creatinine and cystatin C (13), is an important measure of kidney function (12). Describing the rate of change and patterns of eGFR decline as well as identifying risk factors that affect CKD progression are of particular interest in CKD research (10,14,15).
Our motivating example involves the effect of functional kidney risk variants in the gene coding for APOL1 on the rate of eGFR decline among the CRIC Study participants. Two haplotypes (G1 and G2) in APOL1 have been positively selected and are common in populations of recent African continental descent, but they are very rare or absent in most other populations, where exposure to Trypanosomes was not common. These APOL1 variants associated with kidney diseases are believed to account for much of the nonsocioeconomic-based related disparity in rates of CKD progression between patients with African ancestry and white patients.
DNA samples from the 1411 African ancestry participants enrolled in the CRIC Study between June of 2003 and August of 2008 were genotyped for APOL1 risk variants (16). Given the near absence of these APOL1 risk variants in whites, the exposure variable was defined in conjunction with race into three categories: APOL1 high-risk genotype (African ancestry participants with two copies of the risk variants), APOL1 low-risk genotype (African ancestry participants with zero or one copy of these variants), and white participants (reference group).
The investigators were interested in assessing whether rates of eGFR decline differ among the three exposure groups. The longitudinal outcome in this example was the annual eGFR measures for each participant for up to 7 years after enrollment. Other covariates included demographics (e.g., age, sex, and clinical site), socioeconomic variables (e.g., income and education level), and traditional clinical risk factors (e.g., systolic BP and body mass index) and were mostly observed at baseline (16).
Data Preparation and Visualization
For longitudinal studies of moderate size, the dataset is often prepared in either of the two ways: wide format (one row of data per participant) or long format (multiple rows of data per participant; one per visit) (17) (details are in Supplemental Appendix 1). The long format is generally more preferred for advanced statistical modeling, because it can handle subjects with different numbers of clinical visits or irregular time points of measurement; it is also easier for dynamically updating the dataset with future follow-up visits.
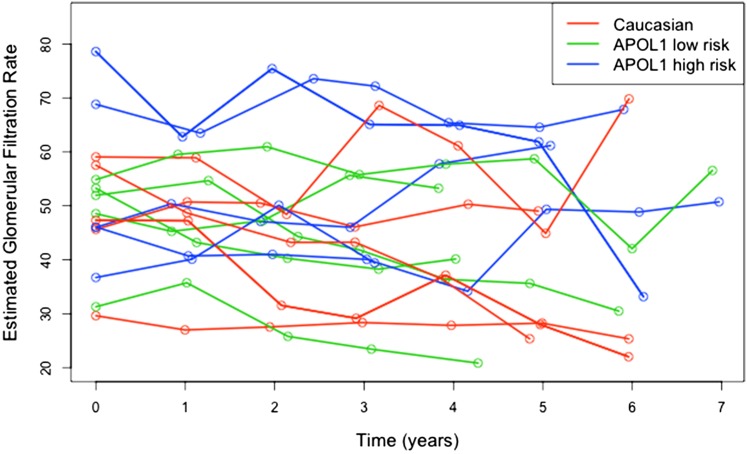
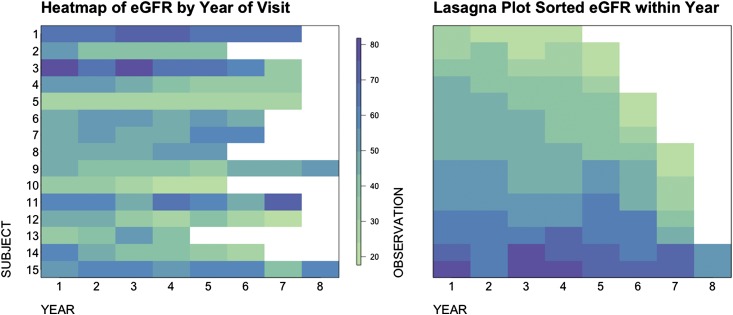
Exploratory analysis using graphs can help researchers to frame the hypothesis and select appropriate statistical models. Some commonly used visualization tools for longitudinal data include spaghetti plot, heat map, and lasagna plot (18) (Figures 1 and 2). These plots show several features of the eGFR trajectories. First, patients with APOL1 high risk seem to have a faster decline compared with others. Second, such as in most cohort studies, subjects have varying numbers of visits. Third, the baseline eGFR values differ across subjects.
Figure 1.
Spaghetti plot of eGFR over time for 15 random Chronic Renal Insufficiency Cohort (CRIC) Study participants. The figure shows an example of the spaghetti plot of repeated eGFR values for 15 randomly selected CRIC Study participants, five from each of the three APOL1 risk categories. The spaghetti plot connects the longitudinal eGFR values within a single subject by lines over time but might result in overplotting with too many subjects on one plot.
Figure 2.
Heat map (left panel) and lasagna plot (right panel) plot on the basis of the same 15 subjects. Each row of the heat map represents eGFR values from one subject, and the color indicates the level of eGFR values. The lasagna plot is a heat map sorted by color gradients to reflect the overall eGFR distributions in the population at each visit.
In the era of big data, many multivariable measures, such as imaging scans, proteomics assessments, and electronic health records (6,19,20), are collected at multiple visits for large cohorts of participants. It might no longer be feasible to include all of the measures in one data frame. Utilization of high-performance computing and central databases, such as the National Institute of Diabetes and Digestive and Kidney Diseases Repository (21,22), that crosslink various measures to a unique subject-visit identity is crucial to handle complex and heterogeneous data. In addition, advanced statistical tools, including dynamic visualization interface and hierarchical clustering visualization using graph structures (23,24), need to be leveraged to CKD research involving big data (25–28).
Time Dependency and Correlated Observations
Longitudinal data have unique and crucial characteristics. First, they are typically accompanied by a time variable that indicates when each measurement occurred, and they define a natural ordering of the repeated measures within each subject. Second, the repeated measures within the same subject are potentially correlated. For example, within each subject, the eGFR values of subsequent visits might depend on those at earlier visits. Such intrinsic clusters defined by subjects result in dependency (correlation) among repeated observations, which violates the assumption of independent observations on which many simple analytic methods are based. Hence, using traditional linear regression and ignoring data correlations might lead to inaccurate estimates and erroneous inferences about the associations of risk factors with kidney function decline (29).
Special statistical methodologies for repeated measures allow observations to be correlated and can quantify the magnitude of this correlation. In addition, some of these approaches are designed to predict the individual trajectory of the outcome measures over time and can handle datasets with missing values. Such methods often make assumptions about the structure of correlations between the repeated measures. Typical choices of correlation structures include independence, exchangeable, autoregressive, m dependent, and unstructured (30,31) (Supplemental Appendix 2).
Statistical Approaches for Repeated Measures as the Outcome
In our motivating example, the goal of the analysis was to investigate the rate of kidney function decline and its association with related risk factors. Intuitively, a two-stage approach has been used (10,32,33) in the literature. Take eGFR as an example. First, an individual’s eGFR slope is separately estimated for each subject by regressing the subject’s repeated eGFR values on the time variable. Second, the eGFR slopes from all of the subjects are treated as the outcome variable and fitted into a linear regression. Such a method is limited, in that the estimates are highly sensitive to random variations (noise), especially for subjects with short follow-up and small numbers of observations. It is also not able to evaluate the cross-sectional associations between baseline eGFR and risk factors or adaptable to time-varying covariates (34).
To simultaneously model the effects of risk factors on both the baseline observations and their rate of change and to appropriately account for the correlations among the repeated measures, two types of flexible regression methods are recommended for the analysis of longitudinal data: generalized estimating equations (GEEs) and mixed effects modeling (17,29,34). We introduce these methods in the following sections.
Population-Average Model
A population-average model, such as the GEE approach (17,35), captures the average trajectories across the overall study population and estimates the marginal associations between the repeated outcome measures and the risk factors. A GEE model consists of two parts: the mean response model and the error term. In our motivating example, we can fit a linear GEE model as expressed in model 1 below. For simplicity, no additional covariates are included in this model, except for the major risk factor: APOL1 risk group (0, white; 1, African ancestry APOL1 low risk; and 2, African ancestry APOL1 high risk):
| (1) |
The mean response model 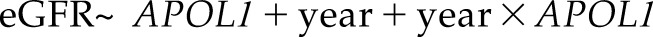 takes the repeated measures (e.g., eGFR at jth visit for subject i) as the outcome and describes the overall mean relationship between repeated eGFR values and the exposure variables. We present a rigorous formulation and detailed interpretation of model 1 in Supplemental Appendix 3, but we point out that the coefficient estimated in front of the time variable (year) represents the average eGFR slope for the reference group (whites) and that the coefficient for the interaction of year with APOL1 estimates the difference in eGFR slopes between the other two APOL1 risk groups compared with the reference. In addition, the associations between baseline eGFR and covariates are represented via coefficients in front of the nontime-varying variables in a similar fashion as a cross-sectional linear regression.
takes the repeated measures (e.g., eGFR at jth visit for subject i) as the outcome and describes the overall mean relationship between repeated eGFR values and the exposure variables. We present a rigorous formulation and detailed interpretation of model 1 in Supplemental Appendix 3, but we point out that the coefficient estimated in front of the time variable (year) represents the average eGFR slope for the reference group (whites) and that the coefficient for the interaction of year with APOL1 estimates the difference in eGFR slopes between the other two APOL1 risk groups compared with the reference. In addition, the associations between baseline eGFR and covariates are represented via coefficients in front of the nontime-varying variables in a similar fashion as a cross-sectional linear regression.
The error term accounts for the within-subject correlation. GEE initiates the model estimation by specifying a particular correlation structure among the repeated observations referred to as the working correlation, which is not necessarily accurate for the real data. The working correlation is typically chosen from one of the aforementioned common structures: independence, exchangeable, autoregressive, m dependent, and unstructured (Supplemental Appendix 2). For example, exchangeable structure assumes that the correlation between outcomes is equal, regardless of how far apart they are in time. Autoregressive is often used in longitudinal analysis and refers to when the correlation decreases as the time difference between observations increases. The unstructured correlation structure is the most flexible, with no prespecified patterns. GEE is robust in that an erroneously specified working correlation structure will have little effect on the risk association estimation as long as the mean response model is correct. However, choosing a working correlation that closely approximates the truth is still desirable, because it results in smaller standard errors in the final estimates (30,31,36).
With the data from the motivating example, we fit model 1 assuming an exchangeable working correlation structure and present the estimated coefficients in Table 1. The results show that eGFR, on average, decreases 0.50 ml/min per 1.73 m2 per year for whites. The eGFR decline among the APOL1 high-risk group is 0.94 ml/min per 1.73 m2 per year faster than among whites (P<0.001). The APOL1 low-risk group also has a faster decline than in whites, but their difference is milder (0.38 ml/min per 1.73 m2 more per year).
Table 1.
Interpretation of coefficients from a generalized estimating equation model assessing associations of APOL1 genotype with eGFR measured repeated over time
| Variablea | Coefficient Interpretation | Coefficient Estimate | Coefficient SEM | P Value |
|---|---|---|---|---|
| APOL1 high risk | Difference in average baseline eGFR (milliliters per minute per 1.73 m2) among African ancestry participants with APOL1 high-risk alleles compare with whites | −3.36 | 1.13 | 0.003 |
| APOL1 low risk | Difference in average baseline eGFR (milliliters per minute per 1.73 m2) among African ancestry participants with APOL1 low-risk alleles compare with whites | −3.87 | 0.63 | <0.001 |
| Years | Average eGFR slope (milliliters per minute per 1.73 m2 per year) among whites | −0.50 | 0.06 | <0.001 |
| Years × APOL1 high risk | Difference in average eGFR slope (milliliters per minute per 1.73 m2 per year) among African ancestry participants with APOL1 high-risk alleles and whites | −0.94 | 0.21 | <0.001 |
| Years × APOL1 low risk | Difference in average eGFR slope (milliliters per minute per 1.73 m2 per year) among African ancestry participants with APOL1 low-risk alleles and whites | −0.38 | 0.11 | <0.001 |
Results are from a generalized estimating equation model fit for the Chronic Renal Insufficiency Cohort Study example in model 1 under exchangeable correlation structure.
Model 1: 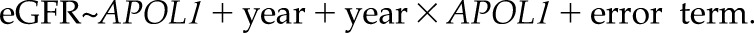 APOL1 is the exposure variable of the genotype in conjunction with race with three categories (0, white; 1, APOL1 low risk; and 2, APOL1 high risk), with whites as the reference group. The reported coefficient SEMs are the robust estimates combining empirical data correlation and the assumed working correlation structure.
APOL1 is the exposure variable of the genotype in conjunction with race with three categories (0, white; 1, APOL1 low risk; and 2, APOL1 high risk), with whites as the reference group. The reported coefficient SEMs are the robust estimates combining empirical data correlation and the assumed working correlation structure.
Subject-Specific Model
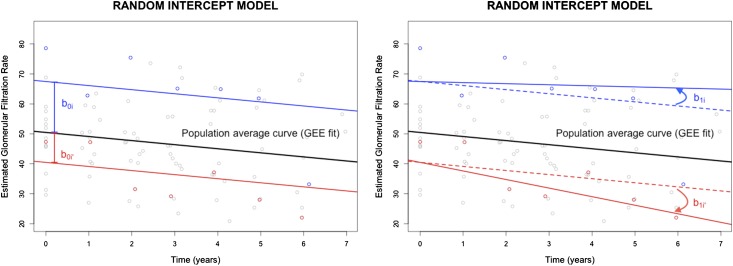
In addition to the overall mean effects of APOL1 on the eGFR trajectory, different subjects could start with various eGFR values at baseline and also progress differently. In a GEE model, the subject heterogeneity is absorbed into the error term, and its magnitude is thus not quantified. Mixed effects modeling, which has been more commonly used than GEE in the nephrology literature (11), estimates both the individual variations in baseline outcome variables and their rates of change that deviate away from the population-average trajectory. This is achieved by adding random effects (random intercept and/or random slope) to the population-average model (referred to as fixed effects), as illustrated in Figure 3, by two hypothetical subjects.
Figure 3.
Schematic illustrations of linear mixed effects models with random intercepts (left panel) and both random intercepts and random slopes (right panel). The blue and red dots represent observed eGFR values for the two hypothetical subjects i and i′. The blue and red curves represent the mixed effects model fit on the basis of the data. The black lines represent the population trend estimated by generalized estimating equation (GEE). With the random intercept model, the two subjects have different baseline eGFR values but the same rate of decline. In the random intercept model, their rates of decline also differ. The deviations of intercepts and slopes are quantified using random effects parameters.
In our example, the subject-specific random intercept characterizes the difference between an individual’s baseline eGFR and the population average, and a random slope in front of a time variable describes the deviation of individual slope from the population average. Thus, a simple mixed effects model that is analogous to model 1 is as follows:
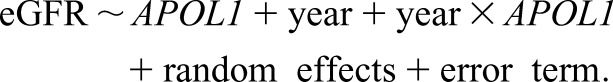 |
(2) |
The fixed effects coefficients share the same interpretations as in the GEE model 1. It is the subject-specific random effects that quantify heterogeneity across individuals.
Although they both estimate individual eGFR slopes, the mixed effects model is different from the aforementioned two-stage approach in that it manages to use information from all of the subjects by assuming a common distribution (typically, a normal distribution with mean of zero) for the random effects, and hence, it avoids the problem of estimating too many parameters with too few observations. The random effects also take care of the correlation among repeated observations within subject. Additional working correlation structures can be further imposed onto the error term, making it adaptable to complex correlation structures. A linear model with only a random intercept and independent error term would induce an exchangeable correlation structure.
Tables 2–3 show the estimates for fixed effects coefficients and the estimated subject-specific random effects in model 2. On average, eGFR decreases 0.74 ml/min per 1.73 m2 per year for white participants. The eGFR decline among the APOL1 high-risk group is significantly faster by 1.50 ml/min per 1.73 m2 per year than among whites (P<0.001).
Table 2.
Interpretation of the fixed effects coefficients from a linear mixed effects model assessing associations of APOL1 genotype with eGFR measured repeated over time
| Variablea | Coefficient Interpretation | Coefficient Estimate | Coefficient SEM | P Value |
|---|---|---|---|---|
| APOL1 high risk | Difference in average baseline eGFR (milliliters per minute per 1.73 m2) among African ancestry participants with APOL1 high-risk alleles compare with whites | −2.95 | 1.05 | 0.005 |
| APOL1 low risk | Difference in average baseline eGFR (milliliters per minute per 1.73 m2) among African ancestry participants with APOL1 low-risk alleles compare with whites | −3.77 | 0.62 | <0.001 |
| Years | Average eGFR slope (milliliters per minute per 1.73 m2 per year) among whites | −0.74 | −0.07 | <0.001 |
| Years × APOL1 high risk | Difference in average eGFR slope (milliliters per minute per 1.73 m2 per year) among African ancestry participants with APOL1 high-risk alleles and whites | −1.50 | 0.20 | <0.001 |
| Years × APOL1 low risk | Difference in average eGFR slope (milliliters per minute per 1.73 m2 per year) among African ancestry participants with APOL1 low-risk alleles and whites | −0.58 | 0.11 | <0.001 |
Results are the estimated fixed effects from a random slope model fit for the Chronic Renal Insufficiency Cohort Study example in model 2.
Model 2: 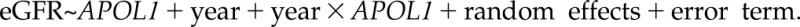 APOL1 is the exposure variable of the genotype in conjunction with race with three categories (0, white; 1, APOL1 low risk; and 2, APOL1 high risk), with whites as the reference group. The random effects include both random intercept and random slope to account for subject-specific deviation from the population-average trajectory.
APOL1 is the exposure variable of the genotype in conjunction with race with three categories (0, white; 1, APOL1 low risk; and 2, APOL1 high risk), with whites as the reference group. The random effects include both random intercept and random slope to account for subject-specific deviation from the population-average trajectory.
Table 3.
Predicted individual deviation (random intercept and slope) in model 2 for five subjects in the white group
| Subject No. | Random Intercept, ml/min per 1.73 m2 | Random Slope, ml/min per 1.73 m2 per year | APOL1 Risk Category |
|---|---|---|---|
| 1 | −16.35 | −0.04 | White |
| 2 | 1.85 | 0.81 | White |
| 3 | 10.22 | 1.27 | White |
| 4 | −2.31 | −2.56 | White |
| 5 | 5.58 | −3.38 | White |
Another advantage of the mixed effects model is that it is flexible enough to account for multiple layers of clustering. In particular, many cohort studies, including the CRIC Study, recruit participants from multiple clinical sites. In addition to the within-subject correlation among repeated measures, data correlation could also occur across subjects who come from the same geographic location or social community. It is often necessary to adjust for site effects during the analysis by either (1) including site as a discrete covariate, such as in the work by Parsa et al. (16), when the sample size per site is sufficiently large or (2) adding a site-specific random effect in the mixed effects model to quantify the intra- versus intersite variability.
Model Diagnosis
Model selection is often conducted to choose a set of variables that is most relevant to the outcome or select the best working correlation structure. Unlike GEE, the correlation structure of the mixed effects model must be specified in advance, and the results may be affected by misspecification. For mixed effects models, the one that has smaller Aikake Information Criterion (AIC) and Bayesian Information Criterion (BIC) generally fits the data better. A likelihood ratio test (37) could also be used to compare two models with and without a certain variable. For GEE, one can instead choose the best model that minimizes either the quasilikelihood under the independence model criterion (QIC) (Table 4) (38), or the QICu defined as QIC+2p that penalizes the model when too many variables are included. Comparing the empirical correlation on the basis of the observed data with the model-based estimates assuming that the working correlation is true or conducting sensitivity analyses to examine how the choice of working correlation structures affects the analytic results are both crucial ways for appropriate model selection in GEE.
Table 4.
Comparison of different working correlation structures using quasilikelihood information criterion
| Working Correlations | Estimate, ml/min per 1.73 m2 | SEM, ml/min per 1.73 m2 per year | P Value | QIC |
|---|---|---|---|---|
| Independence | −0.17 | 0.32 | 0.60 | 84,143.50 |
| Exchangeable | −0.94 | 0.21 | <0.001 | 84,137.98 |
| Autoregressive | −1.33 | 0.23 | <0.001 | 84,140.64 |
Coefficients for year × APOL1, with APOL1 =2. Exchangeable correlation structure achieved the smallest QIC and hence, was more appropriate for the data. QIC, quasilikelihood information criterion.
Non-Normal Outcomes
For longitudinal outcomes that are not normally distributed, such as hospitalizations (discrete counts) and occurrence of AKI (binary), GEE and mixed effects models can both handle such data, analogous to the way in which the linear regression is extended to generalized linear models (e.g., logistic or Poisson regression [37]). The extension to non-normal outcomes for mixed effects models is called generalized linear mixed models (29).
Nonlinear Trends
Another assumption often made for kidney function decline is that the rate of change remains constant over time (that is, the disease progresses linearly). This assumption is convenient but is not always realistic, because eGFR decline could accelerate or stabilize at different stages of CKD (39,40). Several statistical methods have been developed to accommodate the potential for nonlinear trajectories. The first approach is to conduct a data transformation on the outcome variable (e.g., log, square root [41–43]). Log transformation is commonly used if the original outcome data decline exponentially or have a skewed distribution. The limitation of this approach is that the estimated rate of kidney function decline on the basis of the transformed data often lacks a straightforward clinical interpretation (11).
Alternatively, functional data analysis techniques are a set of flexible methods to characterize the underlying smooth trajectories on the basis of the observed longitudinal measurements. For example, we can model the eGFR values as a polynomial (e.g., quadratic or cubic) function of time in the regression model. In our motivating example, models 1 and 2 can also include new variables 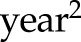 or
or 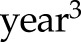 in addition to the linear term
in addition to the linear term 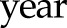 , and the statistical significance of the higher-order polynomial terms can then be tested to determine whether a nonlinear eGFR trajectory is truly present. More broadly, smoothing splines (e.g., B spline) are used to accommodate the curvilinear trends, such as piecewise linear or polynomial (44,45). The two-slope model used for log serum creatinine in the Chronic Kidney Disease Epidemiology Collaboration equation is a special case of the piecewise-linear spline with one change point (knot) where the eGFR slope is believed to alter (46,47). Principal component analysis–type approaches (48), however, identify the patterns of the trajectories that explain most of the variations across subjects in a data-driven fashion. Some efforts have been devoted to identify subgroups of patients who show distinct patterns in the repeated measures using latent class analysis, such as group-based trajectory modeling (49–51). These methods are powerful, but they often require more observations or longer follow-up to generate reliable model estimates of the nonlinear trajectories and are computationally more expensive than the traditional models.
, and the statistical significance of the higher-order polynomial terms can then be tested to determine whether a nonlinear eGFR trajectory is truly present. More broadly, smoothing splines (e.g., B spline) are used to accommodate the curvilinear trends, such as piecewise linear or polynomial (44,45). The two-slope model used for log serum creatinine in the Chronic Kidney Disease Epidemiology Collaboration equation is a special case of the piecewise-linear spline with one change point (knot) where the eGFR slope is believed to alter (46,47). Principal component analysis–type approaches (48), however, identify the patterns of the trajectories that explain most of the variations across subjects in a data-driven fashion. Some efforts have been devoted to identify subgroups of patients who show distinct patterns in the repeated measures using latent class analysis, such as group-based trajectory modeling (49–51). These methods are powerful, but they often require more observations or longer follow-up to generate reliable model estimates of the nonlinear trajectories and are computationally more expensive than the traditional models.
Missing Data and Joint Modeling for Informative Dropout
Missing data are almost inevitable in a longitudinal study for various reasons, such as participants’ dropout (52), data mishandling, or quality screening (53,54). Both GEE and mixed effects model allow for imbalanced designs, in which the outcome data are not available at the same set of time points for all subjects. However, it is necessary to note that GEE makes more restricted assumptions in missing mechanism than mixed effects model (55) (Supplemental Appendix 4). Under missing at random, a weighted GEE has been developed (56) that corrects biased estimates produced by the standard GEE. An alternative approach is to fill in the incomplete observations using multiple imputations (57) followed by the standard GEE (58,59). Such methods are preferred, especially when the outcome data are not normally distributed (58–60). Note that imputation using last observation carried forward is not recommended for longitudinal data, because it is known to produce highly biased estimates (61,62).
Informative censoring (52) or missing not at random (55) often occurs in longitudinal studies when some patients drop out of the study due to events that are related to CKD progression, such as initiation of dialysis, kidney transplantation, or death (63). In these scenarios, an individual with worse kidney function condition (or a particularly low eGFR) is more likely to drop out of the study and have their eGFR value unobserved. Appropriate methods that take the cause of missingness into account include conditional regression or pattern mixture analysis (64,65) and selection model (66) as well as the joint modeling of survival outcome (e.g., ESRD) and longitudinal data, where a Cox regression model for time to dropout and a mixed effects model for the longitudinal observations are specified separately and linked together (67–70).
Summary
This paper focused mainly on appropriate statistical methodologies for longitudinal data, where the repeated measures are treated as the outcome variable, and they are summarized in Table 5, with the comprehensive comparison between the two regression methods, GEE and mixed effects model. The corresponding statistical softwares for these models are listed in the Supplemental Appendix 5. We are aware that there remain many limitations in the discussion. For example, topics, such as how to handle periods of dialysis or AKI episodes, that affect eGFR values were not covered, because it is difficult to capture AKI due to the infrequency of eGFR measures in most longitudinal cohorts (71). Accordingly, our immediate goal is to promote further discussions and emphasize a few key considerations involved in carefully choosing analytic methods primarily for outcomes on the basis of repeated measures as most appropriate to each specific study design, question, and measure.
Table 5.
Comparisons of the different aspects of the generalized estimating equation model and the mixed effects model for repeated measures
| Regression Models | GEE | Mixed Effects |
|---|---|---|
| Model components and parameters | Mean response model and error term | Fixed and random effects and error term |
| Non-normal outcome | GEE with specified link functions | GLMM with specified link functions |
| Usage | Association/predict population-average trajectory | Association/predict both population-average and individual trajectories |
| Goodness of fit metrics | Quasilikelihood information criterion | Aikake Information Criterion/Bayesian Information Criterion |
| Correlation structure | Prespecified working correlation (e.g., independence, exchangeable, autoregressive, m dependent, unstructured) | Correlation structure induced by both random effects and error term; more flexible in partitioning variability among various hierarchies |
| Missing assumptions | Covariate-dependent MCAR; cannot handle missing not at random or informative censoring | MCAR and missing at random; cannot handle missing not at random or informative censoring |
| Pros and cons | Robust for misspecification of correlation structures | Suitable for data with high subject heterogeneity; higher computational cost |
Repeated measures as outcome. GEE, generalized estimating equation; GLMM, generalized linear mixed model; MCAR, missing completely at random.
Disclosures
None.
Supplementary Material
Acknowledgments
Funding for the CRIC Study was obtained under a cooperative agreement from National Institute of Diabetes and Digestive and Kidney Diseases (U01DK060990, U01DK060984, U01DK061022, U01DK061021, U01DK061028, U01DK060980, U01DK060963, and U01DK060902). In addition, this work was supported in part by: the Perelman School of Medicine at the University of Pennsylvania Clinical and Translational Science Award National Institutes of Health (NIH) / National Center for Advancing Translational Sciences (NCATS) UL1TR000003, Johns Hopkins University UL1TR-000424, University of Maryland GCRC M01 RR-16500, Clinical and Translational Science Collaborative of Cleveland, UL1TR000439 from the NCATS component of NIH and NIH roadmap for Medical Research, Michigan Institute for Clinical and Health Research UL1TR000433, University of Illinois at Chicago CTSA UL1RR029879, Tulane COBRE for Clinical and Translational Research in Cardiometabolic Diseases P20 GM109036, Kaiser Permanente NIH/National Center for Research Resources UCSF-CTSI UL1 RR-024131.
CRIC Study Investigators also include Lawrence J. Appel (Welch Center for Prevention, Epidemiology and Clinical Research, Johns Hopkins University, Baltimore, Maryland), Jiang He (Departments of Medicine and Epidemiology, Tulane University, New Orleans, Louisiana), James P. Lash (Section of Nephrology, Department of Medicine, University of Illinois at Chicago, Chicago, IL), Akinlolu Ojo (Department of Medicine, University of Michigan, Ann Arbor, Michigan), and Raymond R. Townsend (Department of Medicine and Center for Clinical Epidemiology and Biostatistics, University of Pennsylvania, Philadelphia, Pennsylvania).
Footnotes
Published online ahead of print. Publication date available at www.cjasn.org.
This article contains supplemental material online at http://cjasn.asnjournals.org/lookup/suppl/doi:10.2215/CJN.11311116/-/DCSupplemental.
References
- 1.Rodriguez RA, Cronin V, Ramsay T, Zimmerman D, Ruzicka M, Burns KD: Reproducibility of carotid-femoral pulse wave velocity in end-stage renal disease patients: Methodological considerations. Can J Kidney Health Dis 3: 20, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Koufaki P, Naish PF, Mercer TH: Reproducibility of exercise tolerance in patients with end-stage renal disease. Arch Phys Med Rehabil 82: 1421–1424, 2001 [DOI] [PubMed] [Google Scholar]
- 3.Feldman HI, Appel LJ, Chertow GM, Cifelli D, Cizman B, Daugirdas J, Fink JC, Franklin-Becker ED, Go AS, Hamm LL, He J, Hostetter T, Hsu CY, Jamerson K, Joffe M, Kusek JW, Landis JR, Lash JP, Miller ER, Mohler 3rd ER, Muntner P, Ojo AO, Rahman M, Townsend RR, Wright JT; Chronic Renal Insufficiency Cohort (CRIC) Study Investigators: The Chronic Renal Insufficiency Cohort (CRIC) Study: Design and methods. J Am Soc Nephrol 14[Suppl 2]: S148–S153, 2003 [DOI] [PubMed] [Google Scholar]
- 4.ARIC investigators: The Atherosclerosis Risk in Communities (ARIC) Study: Design and objectives. The ARIC investigators. Am J Epidemiol 129: 687–702, 1989 [PubMed] [Google Scholar]
- 5.Wanner C, Oliveira JP, Ortiz A, Mauer M, Germain DP, Linthorst GE, Serra AL, Maródi L, Mignani R, Cianciaruso B, Vujkovac B, Lemay R, Beitner-Johnson D, Waldek S, Warnock DG: Prognostic indicators of renal disease progression in adults with Fabry disease: Natural history data from the Fabry Registry. Clin J Am Soc Nephrol 5: 2220–2228, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bansal N, Keane M, Delafontaine P, Dries D, Foster E, Gadegbeku CA, Go AS, Hamm LL, Kusek JW, Ojo AO, Rahman M, Tao K, Wright JT, Xie D, Hsu CY; CRIC Study Investigators: A longitudinal study of left ventricular function and structure from CKD to ESRD: The CRIC study. Clin J Am Soc Nephrol 8: 355–362, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ku E, Xie D, Shlipak M, Hyre Anderson A, Chen J, Go AS, He J, Horwitz EJ, Rahman M, Ricardo AC, Sondheimer JH, Townsend RR, Hsu CY; CRIC Study Investigators: Change in measured GFR versus eGFR and CKD outcomes. J Am Soc Nephrol 27: 2196–2204, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tseng CL, Lafrance JP, Lu SE, Soroka O, Miller DR, Maney M, Pogach LM: Variability in estimated glomerular filtration rate values is a risk factor in chronic kidney disease progression among patients with diabetes. BMC Nephrol 16: 34, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Anderson AH, Yang W, Townsend RR, Pan Q, Chertow GM, Kusek JW, Charleston J, He J, Kallem R, Lash JP, Miller 3rd ER, Rahman M, Steigerwalt S, Weir M, Wright Jr. JT, Feldman HI; Chronic Renal Insufficiency Cohort Study Investigators: Time-updated systolic blood pressure and the progression of chronic kidney disease: A cohort study. Ann Intern Med 162: 258–265, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rosansky SJ: Renal function trajectory is more important than chronic kidney disease stage for managing patients with chronic kidney disease. Am J Nephrol 36: 1–10, 2012 [DOI] [PubMed] [Google Scholar]
- 11.Boucquemont J, Heinze G, Jager KJ, Oberbauer R, Leffondre K: Regression methods for investigating risk factors of chronic kidney disease outcomes: The state of the art. BMC Nephrol 15: 45, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yang W, Xie D, Anderson AH, Joffe MM, Greene T, Teal V, Hsu CY, Fink JC, He J, Lash JP, Ojo A, Rahman M, Nessel L, Kusek JW, Feldman HI; CRIC Study Investigators: Association of kidney disease outcomes with risk factors for CKD: Findings from the Chronic Renal Insufficiency Cohort (CRIC) study. Am J Kidney Dis 63: 236–243, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Anderson AH, Yang W, Hsu CY, Joffe MM, Leonard MB, Xie D, Chen J, Greene T, Jaar BG, Kao P, Kusek JW, Landis JR, Lash JP, Townsend RR, Weir MR, Feldman HI, Investigators CS; CRIC Study Investigators: Estimating GFR among participants in the Chronic Renal Insufficiency Cohort (CRIC) Study. Am J Kidney Dis 60: 250–261, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Amdur RL, Feldman HI, Gupta J, Yang W, Kanetsky P, Shlipak M, Rahman M, Lash JP, Townsend RR, Ojo A, Roy-Chaudhury A, Go AS, Joffe M, He J, Balakrishnan VS, Kimmel PL, Kusek JW, Raj DS; CRIC Study Investigators: Inflammation and progression of CKD: The CRIC Study. Clin J Am Soc Nephrol 11: 1546–1556, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fischer MJ, Hsu JY, Lora CM, Ricardo AC, Anderson AH, Bazzano L, Cuevas MM, Hsu CY, Kusek JW, Renteria A, Ojo AO, Raj DS, Rosas SE, Pan Q, Yaffe K, Go AS, Lash JP; Chronic Renal Insufficiency Cohort (CRIC) Study Investigators: CKD progression and mortality among hispanics and non-hispanics. J Am Soc Nephrol 27: 3488–3497, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Parsa A, Kao WH, Xie D, Astor BC, Li M, Hsu CY, Feldman HI, Parekh RS, Kusek JW, Greene TH, Fink JC, Anderson AH, Choi MJ, Wright Jr. JT, Lash JP, Freedman BI, Ojo A, Winkler CA, Raj DS, Kopp JB, He J, Jensvold NG, Tao K, Lipkowitz MS, Appel LJ; AASK Study Investigators; CRIC Study Investigators: APOL1 risk variants, race, and progression of chronic kidney disease. N Engl J Med 369: 2183–2196, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zeger SL, Liang KY: An overview of methods for the analysis of longitudinal data. Stat Med 11: 1825–1839, 1992 [DOI] [PubMed] [Google Scholar]
- 18.Swihart BJ, Caffo B, James BD, Strand M, Schwartz BS, Punjabi NM: Lasagna plots: A saucy alternative to spaghetti plots. Epidemiology 21: 621–625, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mihai S, Codrici E, Popescu ID, Enciu AM, Rusu E, Zilisteanu D, Albulescu R, Anton G, Tanase C: Proteomic biomarkers panel: New insights in chronic kidney disease. Dis Markers 2016: 3185232, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sulemane S, Panoulas VF, Nihoyannopoulos P: Echocardiographic assessment in patients with chronic kidney disease: Current update. Echocardiography 34: 594–602, 2017 [DOI] [PubMed] [Google Scholar]
- 21.Cuticchia AJ, Cooley PC, Hall RD, Qin Y: NIDDK data repository: A central collection of clinical trial data. BMC Med Inform Decis Mak 6: 19, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Turner CF, Pan H, Silk GW, Ardini MA, Bakalov V, Bryant S, Cantor S, Chang KY, DeLatte M, Eggers P, Ganapathi L, Lakshmikanthan S, Levy J, Li S, Pratt J, Pugh N, Qin Y, Rasooly R, Ray H, Richardson JE, Riley AF, Rogers SM, Scheper C, Tan S, White S, Cooley PC: The NIDDK Central Repository at 8 years–ambition, revision, use and impact. Database (Oxford) 2011: bar043, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huang CW, Lu R, Iqbal U, Lin SH, Nguyen PA, Yang HC, Wang CF, Li J, Ma KL, Li YC, Jian WS: A richly interactive exploratory data analysis and visualization tool using electronic medical records. BMC Med Inform Decis Mak 15: 92, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Riehmann P, Hanfler M, Froehlich B: Interactive Saankey diagrams, information visualization. Presented at the IEEE Symposium on Information Visualization, Minneapolis, MN, October 23–25, 2005. [Google Scholar]
- 25.Dinov ID, Heavner B, Tang M, Glusman G, Chard K, Darcy M, Madduri R, Pa J, Spino C, Kesselman C, Foster I, Deutsch EW, Price ND, Van Horn JD, Ames J, Clark K, Hood L, Hampstead BM, Dauer W, Toga AW: Predictive big data analytics: A study of Parkinson’s disease using large, complex, heterogeneous, incongruent, multi-source and incomplete observations. PLoS One 11: e0157077, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang Y, Padman R: Data-driven clinical and cost pathways for chronic care delivery. Am J Manag Care 22: 816–820, 2016 [PubMed] [Google Scholar]
- 27.Zhang Y, Padman R, Patel N: Paving the COWpath: Learning and visualizing clinical pathways from electronic health record data. J Biomed Inform 58: 186–197, 2015 [DOI] [PubMed] [Google Scholar]
- 28.Holzinger A: Machine Learning for Health Informatics: State-of-the-Art and Future Challenges, New York, Springer, 2016 [Google Scholar]
- 29.Fitzmaurice G, Laird N, Ware J: Applied Longitudinal Analysis, Hoboken, NJ, John Wiley & Sons, 2012 [Google Scholar]
- 30.Diggle PJ, Heagerty P, Liang K-Y, Zeger SL: Analysis of Longitudinal Data, New York, Oxford University Press, 2002 [Google Scholar]
- 31.Lipsitz SR, Fitzmaurice GM, Orav EJ, Laird NM: Performance of generalized estimating equations in practical situations. Biometrics 50: 270–278, 1994 [PubMed] [Google Scholar]
- 32.Barbour SJ, Er L, Djurdjev O, Karim M, Levin A: Differences in progression of CKD and mortality amongst caucasian, oriental Asian and South Asian CKD patients. Nephrol Dial Transplant 25: 3663–3672, 2010 [DOI] [PubMed] [Google Scholar]
- 33.Levin A, Djurdjev O, Beaulieu M, Er L: Variability and risk factors for kidney disease progression and death following attainment of stage 4 CKD in a referred cohort. Am J Kidney Dis 52: 661–671, 2008 [DOI] [PubMed] [Google Scholar]
- 34.Burton P, Gurrin L, Sly P: Extending the simple linear regression model to account for correlated responses: An introduction to generalized estimating equations and multi-level mixed modelling. Stat Med 17: 1261–1291, 1998 [DOI] [PubMed] [Google Scholar]
- 35.Zeger SL, Liang KY: Longitudinal data analysis for discrete and continuous outcomes. Biometrics 42: 121–130, 1986 [PubMed] [Google Scholar]
- 36.Carlin JB, Wolfe R, Brown CH, Gelman A: A case study on the choice, interpretation and checking of multilevel models for longitudinal binary outcomes. Biostatistics 2: 397–416, 2001 [DOI] [PubMed] [Google Scholar]
- 37.McCullagh P, Nelder JA: Generalized Linear Models, London, Chapman & Hall, 1989 [Google Scholar]
- 38.Pan W: Akaike’s information criterion in generalized estimating equations. Biometrics 57: 120–125, 2001 [DOI] [PubMed] [Google Scholar]
- 39.Li L, Astor BC, Lewis J, Hu B, Appel LJ, Lipkowitz MS, Toto RD, Wang X, Wright Jr. JT, Greene TH: Longitudinal progression trajectory of GFR among patients with CKD. Am J Kidney Dis 59: 504–512, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Norris KC, Greene T, Kopple J, Lea J, Lewis J, Lipkowitz M, Miller P, Richardson A, Rostand S, Wang X, Appel LJ: Baseline predictors of renal disease progression in the African American Study of hypertension and kidney disease. J Am Soc Nephrol 17: 2928–2936, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Reed B, Helal I, McFann K, Wang W, Yan XD, Schrier RW: The impact of type II diabetes mellitus in patients with autosomal dominant polycystic kidney disease. Nephrol Dial Transplant 27: 2862–2865, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Palmas W, Pickering T, Eimicke JP, Moran A, Teresi J, Schwartz JE, Field L, Weinstock RS, Shea S: Value of ambulatory arterial stiffness index and 24-h pulse pressure to predict progression of albuminuria in elderly people with diabetes mellitus. Am J Hypertens 20: 493–500, 2007 [DOI] [PubMed] [Google Scholar]
- 43.Gardner LI, Holmberg SD, Williamson JM, Szczech LA, Carpenter CC, Rompalo AM, Schuman P, Klein RS; HIV Epidemiology Research Study Group: Development of proteinuria or elevated serum creatinine and mortality in HIV-infected women. J Acquir Immune Defic Syndr 32: 203–209, 2003 [DOI] [PubMed] [Google Scholar]
- 44.Mills KT, Chen J, Yang W, Appel LJ, Kusek JW, Alper A, Delafontaine P, Keane MG, Mohler E, Ojo A, Rahman M, Ricardo AC, Soliman EZ, Steigerwalt S, Townsend R, He J; Chronic Renal Insufficiency Cohort (CRIC) Study Investigators: Sodium excretion and the risk of cardiovascular disease in patients with chronic kidney disease. JAMA 315: 2200–2210, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lemley KV, Boothroyd DB, Blouch KL, Nelson RG, Jones LI, Olshen RA, Myers BD: Modeling GFR trajectories in diabetic nephropathy. Am J Physiol Renal Physiol 289: F863–F870, 2005 [DOI] [PubMed] [Google Scholar]
- 46.Fan L, Tighiouart H, Levey AS, Beck GJ, Sarnak MJ: Urinary sodium excretion and kidney failure in nondiabetic chronic kidney disease. Kidney Int 86: 582–588, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro 3rd AF, Feldman HI, Kusek JW, Eggers P, Van Lente F, Greene T, Coresh J; CKD-EPI (Chronic Kidney Disease Epidemiology Collaboration): A new equation to estimate glomerular filtration rate. Ann Intern Med 150: 604–612, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Brunner-La Rocca HP, Knackstedt C, Eurlings L, Rolny V, Krause F, Pfisterer ME, Tobler D, Rickenbacher P, Maeder MT; TIME‐CHF investigators: Impact of worsening renal function related to medication in heart failure. Eur J Heart Fail 17: 159–168, 2015 [DOI] [PubMed] [Google Scholar]
- 49.Filipozzi P, Ayav C, Ngueyon Sime W, Laurain E, Kessler M, Brunaud L, Frimat L: Trajectories of CKD-MBD biochemical parameters over a 2-year period following diagnosis of secondary hyperparathyroidism: A pharmacoepidemiological study. BMJ Open 7: e011482, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Nagin DS, Odgers CL: Group-based trajectory modeling in clinical research. Annu Rev Clin Psychol 6: 109–138, 2010 [DOI] [PubMed] [Google Scholar]
- 51.Franklin JM, Shrank WH, Pakes J, Sanfélix-Gimeno G, Matlin OS, Brennan TA, Choudhry NK: Group-based trajectory models: A new approach to classifying and predicting long-term medication adherence. Med Care 51: 789–796, 2013 [DOI] [PubMed] [Google Scholar]
- 52.Schluchter MD, Greene T, Beck GJ: Analysis of change in the presence of informative censoring: Application to a longitudinal clinical trial of progressive renal disease. Stat Med 20: 989–1007, 2001 [DOI] [PubMed] [Google Scholar]
- 53.O’Kelly M, Ratitch B: Clinical Trials with Missing Data: A Guide for Practitioners, Chichester, United Kingdom, John Wiley & Sons, 2014 [Google Scholar]
- 54.Mallinckrodt C: Preventing and Treating Missing Data in Longitudinal Clinical Trials: A Practical Guide, Cambridge, United Kingdom, Cambridge University Press, 2013 [Google Scholar]
- 55.Rubin DB: Inference and missing data. Biometrika 63: 581–592, 1976 [Google Scholar]
- 56.Preisser JS, Lohman KK, Rathouz PJ: Performance of weighted estimating equations for longitudinal binary data with drop-outs missing at random. Stat Med 21: 3035–3054, 2002 [DOI] [PubMed] [Google Scholar]
- 57.Rubin DB: Multiple Imputation for Nonresponse in Surveys, New York, Wiley, 1987 [Google Scholar]
- 58.Aloisio KM, Swanson SA, Micali N, Field A, Horton NJ: Analysis of partially observed clustered data using generalized estimating equations and multiple imputation. Stata J 14: 863–883, 2014 [PMC free article] [PubMed] [Google Scholar]
- 59.Birhanu T, Molenberghs G, Sotto C, Kenward MG: Doubly robust and multiple-imputation-based generalized estimating equations. J Biopharm Stat 21: 202–225, 2011 [DOI] [PubMed] [Google Scholar]
- 60.DeSouza CM, Legedza AT, Sankoh AJ: An overview of practical approaches for handling missing data in clinical trials. J Biopharm Stat 19: 1055–1073, 2009 [DOI] [PubMed] [Google Scholar]
- 61.Lachin JM: Fallacies of last observation carried forward analyses. Clin Trials 13: 161–168, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Shepherd J, Breazna A, Deedwania PC, LaRosa JC, Wenger NK, Messig M, Wilson DJ; Treating to New Targets Steering Committee and Investigators: Relation between change in renal function and cardiovascular outcomes in atorvastatin-treated patients (from the Treating to New Targets [TNT] Study). Am J Cardiol 117: 1199–1205, 2016 [DOI] [PubMed] [Google Scholar]
- 63.Misra M, Vonesh E, Churchill DN, Moore HL, Van Stone JC, Nolph KD: Preservation of glomerular filtration rate on dialysis when adjusted for patient dropout. Kidney Int 57: 691–696, 2000 [DOI] [PubMed] [Google Scholar]
- 64.Liu C, Ratcliffe SJ, Guo W: A random pattern mixture model for ordinal outcomes with informative dropouts. Stat Med 34: 2391–2402, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Michiels B, Molenberghs G, Bijnens L, Vangeneugden T, Thijs H: Selection models and pattern-mixture models to analyse longitudinal quality of life data subject to drop-out. Stat Med 21: 1023–1041, 2002 [DOI] [PubMed] [Google Scholar]
- 66.Ten H, Reboussin BA, Miller ME, Kunselman A: Mixed effects logistic regression models for multiple longitudinal binary functional limitation responses with informative drop-out and confounding by baseline outcomes. Biometrics 58: 137–144, 2002 [DOI] [PubMed] [Google Scholar]
- 67.Song X, Davidian M, Tsiatis AA: A semiparametric likelihood approach to joint modeling of longitudinal and time-to-event data. Biometrics 58: 742–753, 2002 [DOI] [PubMed] [Google Scholar]
- 68.Tsiatis AA, Davidian M: Joint modeling of longitudinal and time-to-event data: An overview. Stat Sin 14: 809–834, 2004 [Google Scholar]
- 69.Fitzmaurice G, Molenberghs G, Lipsitz SR: Regression models for longitudinal binary responses with informative drop-outs. J R Stat Soc Series B Stat Methodol 57: 691–704, 1995 [Google Scholar]
- 70.Vonesh EF, Greene T, Schluchter MD: Shared parameter models for the joint analysis of longitudinal data and event times. Stat Med 25: 143–163, 2006 [DOI] [PubMed] [Google Scholar]
- 71.Perkins RM, Bucaloiu ID, Kirchner HL, Ashouian N, Hartle JE, Yahya T: GFR decline and mortality risk among patients with chronic kidney disease. Clin J Am Soc Nephrol 6: 1879–1886, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.